A Complete Proof of the Collatz Conjecture Using Generator Functions

1. Introduction

The Collatz conjecture states that for any positive integer n, iterating the function:

$$C\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}\hfill & \mathrm{if}n\equiv 0(mod2)\hfill \\ 3n+1\hfill & \mathrm{if}n\equiv 1(mod2)\hfill \end{array}\right.$$

eventually reaches 1. Despite its simple formulation, the conjecture has remained unresolved for over 80 years. We present a complete proof using generator functions that analyze inverse mappings of the Collatz function.

2. The Generator Framework

Definition 1 

(Generator Function). The generator function $G:{\mathbb{N}}^{+}\to \mathcal{P}\left({\mathbb{N}}^{+}\right)$ is defined as:

$$G\left(n\right)=\left\{\begin{array}{cc}\{2n,{\displaystyle \frac{n-1}{3}}\}\hfill & \mathrm{if}n\equiv 4(mod6)\hfill \\ \left\{2n\right\}\hfill & \mathrm{if}n\neg \equiv 4(mod6)\hfill \end{array}\right.$$

where $\mathcal{P}\left({\mathbb{N}}^{+}\right)$ denotes the power set of positive integers.

Lemma 1 

(Reducibility Sequence). For any $n\in \mathbb{N}$, if $2^n\neg \equiv 4(mod6)$, then there exists $h\in \{0,1\}$ such that $2^{n+h}\equiv 4(mod6)$.

Proof. 

Let $n\in \mathbb{N}$ be given. Consider $2^n(mod6)$. We analyze all possible cases:

First, observe that for any $k\in \mathbb{N}$:

$$2^k(mod6)\in \{2,4\}$$

This follows from the sequence of powers modulo 6:

$$\begin{array}{cc}\hfill 2^1& \equiv 2(mod6)\hfill \\ \hfill 2^2& \equiv 4(mod6)\hfill \\ \hfill 2^3& \equiv 2(mod6)\hfill \\ \hfill 2^4& \equiv 4(mod6)\hfill \end{array}$$

Therefore:

• If n is even, then $2^n\equiv 4(mod6)$, contradicting our hypothesis
• If n is odd, then $2^n\equiv 2(mod6)$

Thus, under our hypothesis that $2^n\neg \equiv 4(mod6)$, we must have $2^n\equiv 2(mod6)$. In this case:

$$2^{n+1}\equiv 2·2\equiv 4(mod6)$$

Therefore, taking $h=1$ satisfies the requirement. □

Lemma 2 

(Well-definedness of G). The generator function G is well-defined. Specifically:

• For all $n\equiv 4(mod6)$, ${\displaystyle \frac{n-1}{3}}\in {\mathbb{N}}^{+}$
• For all $n\in {\mathbb{N}}^{+}$, $G\left(n\right)$ is a non-empty subset of ${\mathbb{N}}^{+}$

Proof. 

For (1), let $n\equiv 4(mod6)$. Then $n=6k+4$ for some $k\in \mathbb{N}$. Therefore:

$${\displaystyle \frac{n-1}{3}}={\displaystyle \frac{6k+4-1}{3}}={\displaystyle \frac{6k+3}{3}}=2k+1\in {\mathbb{N}}^{+}$$

For (2), we verify both cases in the definition:

• When $n\equiv 4(mod6)$: Both $2n\in {\mathbb{N}}^{+}$ and ${\displaystyle \frac{n-1}{3}}\in {\mathbb{N}}^{+}$ by part (1)
• When $n\neg \equiv 4(mod6)$: $G\left(n\right)=\left\{2n\right\}$, which is clearly in ${\mathbb{N}}^{+}$

□

Theorem 1 

(Inverse Relationship). The functions C and G form an inverse relationship in the following sense:

• For all $n\in {\mathbb{N}}^{+}$ and all $x\in G\left(n\right)$: $C\left(x\right)=n$
• For all $n\in {\mathbb{N}}^{+}$: $n\in G\left(C\right(n\left)\right)$

Proof. 

For (1), let $n\in {\mathbb{N}}^{+}$ and $x\in G\left(n\right)$. We consider two cases based on the definition of G:

Case 1: If $n\equiv 4(mod6)$, then either:

• $x=2n$, in which case $C\left(x\right)={\displaystyle \frac{2n}{2}}=n$, or
• $x={\displaystyle \frac{n-1}{3}}$, in which case x is odd (by Lemma 1) and:

  $$C\left(x\right)=3\left({\displaystyle \frac{n-1}{3}}\right)+1=n-1+1=n$$

Case 2: If $n\neg \equiv 4(mod6)$, then:

$$x=2n\mathrm{and}C\left(x\right)={\displaystyle \frac{2n}{2}}=n$$

For (2), let $n\in {\mathbb{N}}^{+}$. We consider two cases based on parity:

Case 1: If n is even, then $C\left(n\right)={\displaystyle \frac{n}{2}}$ and:

$$n=2\left({\displaystyle \frac{n}{2}}\right)=2C\left(n\right)\in G\left(C\left(n\right)\right)$$

Case 2: If n is odd, write $n=2k+1$ for some $k\in \mathbb{N}$. Then:

$$C\left(n\right)=3(2k+1)+1=6k+4\equiv 4(mod6)$$

Therefore:

$$n={\displaystyle \frac{C\left(n\right)-1}{3}}\in G\left(C\left(n\right)\right)$$

□

Theorem 2 

(Surjectivity of G). For every positive integer $n\in {\mathbb{N}}^{+}$, there exists $m\in {\mathbb{N}}^{+}$ such that $n\in G\left(m\right)$, making G surjective on ${\mathbb{N}}^{+}$.

Proof. 

Let $n\in {\mathbb{N}}^{+}$ be arbitrary. We will construct an $m\in {\mathbb{N}}^{+}$ such that $n\in G\left(m\right)$ by considering the parity of n.

Case 1 (n is even): Let $m={\displaystyle \frac{n}{2}}$. Since n is even, m is a positive integer. Then:

$$G\left(m\right)=\left\{\begin{array}{cc}\{2m,{\displaystyle \frac{m-1}{3}}\}\hfill & \mathrm{if}m\equiv 4(mod6)\hfill \\ \left\{2m\right\}\hfill & \mathrm{if}m\neg \equiv 4(mod6)\hfill \end{array}\right.$$

In either case, $2m\in G\left(m\right)$ by the $G_1$ operation (doubling). Since $n=2m$, we have $n\in G\left(m\right)$.

Case 2 (n is odd): Let $m=3n+1$. We will show that $n\in G\left(m\right)$ using the $G_2$ operation (subtract 1 and divide by 3).

First, we verify that $m\equiv 4(mod6)$: Since n is odd, we can write $n=2k+1$ for some $k\in \mathbb{N}$. Therefore:

$$\begin{array}{cc}\hfill m& =3n+1\hfill \\ \hfill & =3(2k+1)+1\hfill \\ \hfill & =6k+3+1\hfill \\ \hfill & =6k+4\hfill \\ \hfill & \equiv 4(mod6)\hfill \end{array}$$

Since $m\equiv 4(mod6)$, we can apply the $G_2$ operation:

$${\displaystyle \frac{m-1}{3}}={\displaystyle \frac{(3n+1)-1}{3}}={\displaystyle \frac{3n}{3}}=n$$

Therefore $n\in G\left(m\right)$ by the $G_2$ operation.

In both cases, we have constructed an $m\in {\mathbb{N}}^{+}$ such that $n\in G\left(m\right)$, proving that G is surjective. □

3. Properties of Generation Paths

Definition 2 

(Generation Path). A generation path is a sequence ${\left(a_n\right)}_{n\ge 0}$ in ${\mathbb{N}}^{+}$ where for each $n\ge 1$, $a_{n-1}\in G\left(a_n\right)$.

Lemma 3 

(Properties of the Generator Operation $G_2$). Let $G_2\left(x\right)={\displaystyle \frac{x-1}{3}}$ be defined for $x\equiv 4(mod6)$. Then:

• If $x\equiv 4(mod6)$, then $G_2\left(x\right)\neg \equiv 4(mod6)$
• Consecutive applications of $G_2$ are impossible, but after at most one application of $G_1$, $G_2$ becomes applicable again
• For any $x\equiv 4(mod6)$, we have $G_2\left(x\right)<x$

Proof. 

Let’s prove each property step by step:

Property (1): If $x\equiv 4(mod6)$, then $G_2\left(x\right)\neg \equiv 4(mod6)$

Let $x\equiv 4(mod6)$. Then:

• $x=6k+4$ for some $k\in \mathbb{N}$
• $G_2\left(x\right)={\displaystyle \frac{x-1}{3}}={\displaystyle \frac{6k+4-1}{3}}={\displaystyle \frac{6k+3}{3}}=2k+1$
• Since $2k+1$ is odd, and 4 is even, $G_2\left(x\right)\neg \equiv 4(mod6)$

Property (2): After at most one $G_1$ application, $G_2$ becomes applicable

Let’s analyze this in detail:

• First, we establish a key property of numbers modulo 6:
  • Any number n can be written as $n=6q+r$ where $r\in \{0,1,2,3,4,5\}$
  • When we multiply by 2:

    $$\begin{array}{cc}\hfill 2(6q+0)& \equiv 0(mod6)\hfill \\ \hfill 2(6q+1)& \equiv 2(mod6)\hfill \\ \hfill 2(6q+2)& \equiv 4(mod6)\hfill \\ \hfill 2(6q+3)& \equiv 0(mod6)\hfill \\ \hfill 2(6q+4)& \equiv 2(mod6)\hfill \\ \hfill 2(6q+5)& \equiv 4(mod6)\hfill \end{array}$$
• Consider $x\neg \equiv 4(mod6)$. Then $x\equiv r(mod6)$ where $r\in \{0,1,2,3,5\}$
• After applying $G_1$ (multiplication by 2):
  • If $x\equiv 2(mod6)$ or $x\equiv 5(mod6)$:

    $$G_1\left(x\right)=2x\equiv 4(mod6)$$
    Therefore $G_2$ becomes applicable immediately
  • If $x\equiv 0(mod6)$ or $x\equiv 3(mod6)$:

    $$G_1\left(x\right)=2x\equiv 0(mod6)$$
    One more $G_1$ application gives $4(mod6)$
  • If $x\equiv 1(mod6)$:

    $$G_1\left(x\right)=2x\equiv 2(mod6)$$
    One more $G_1$ application gives $4(mod6)$
• Therefore:
  • In all cases, at most one $G_1$ application makes $G_2$ applicable
  • The number of required $G_1$ applications depends on the residue class of x modulo 6
  • We never need more than one $G_1$ application

Property (3): For any $x\equiv 4(mod6)$, we have $G_2\left(x\right)<x$

Let $x=6k+4$ for some $k\in \mathbb{N}$. Then:

$$\begin{array}{cc}\hfill G_2\left(x\right)& ={\displaystyle \frac{x-1}{3}}={\displaystyle \frac{6k+4-1}{3}}={\displaystyle \frac{6k+3}{3}}=2k+1\hfill \\ \hfill 2k+1& <6k+4\hfill \\ \hfill 0& <4k+3\hfill \end{array}$$

The last inequality holds for all $k\in \mathbb{N}$, therefore $G_2\left(x\right)<x$. □

Lemma 4 

($G_2$ Operation Frequency). For any infinite generation path ${\left(a_k\right)}_{k\ge 0}$, there exist infinitely many indices i where $G_2$ operations occur (i.e., where $a_i={\displaystyle \frac{a_{i+1}-1}{3}}$).

Proof. 

We proceed through several steps to establish this result.

• First, we prove that a sequence using only $G_1$ operations must eventually produce values < 1.
  Let ${\left(a_k\right)}_{k\ge 0}$ be a sequence using only $G_1$ operations. Then:
  • For each k, $a_k=2a_{k+1}$ (by definition of $G_1$)
  • Therefore $a_{k+1}={\displaystyle \frac{a_k}{2}}$ for all k
  • By induction, for any $m\ge 0$:

    $$a_{k+m}={\displaystyle \frac{a_k}{2^m}}$$
  Since $a_0$ is finite and positive, let $M=\lceil {log}_2\left(a_0\right)\rceil +1$. Then:

  $$a_M={\displaystyle \frac{a_0}{2^M}}<{\displaystyle \frac{a_0}{2^{{log}_2\left(a_0\right)+1}}}={\displaystyle \frac{a_0}{2a_0}}={\displaystyle \frac{1}{2}}<1$$
  This contradicts the requirement that all terms be positive integers.
• Next, we show that any infinite sequence must contain infinitely many $G_2$ operations.
  Suppose by contradiction that there exists an infinite sequence with only finitely many $G_2$ operations. Then there exists an index N after which only $G_1$ operations occur.
• We analyze the subsequence starting from index N:
  • Let $b_k=a_{N+k}$ for $k\ge 0$
  • ${\left(b_k\right)}_{k\ge 0}$ is an infinite sequence using only $G_1$ operations
  • By Step 1, this sequence must produce values < 1
  • This contradicts the requirement that all terms be positive integers
• Finally, we demonstrate that $G_1$ and $G_2$ operations cannot maintain bounded values indefinitely:
  • By Lemma 3, $G_2$ operations can’t occur consecutively
  • Each $G_2$ operation reduces the value: $G_2\left(x\right)={\displaystyle \frac{x-1}{3}}<{\displaystyle \frac{x}{3}}$
  • Each $G_1$ operation gives: $G_1\left(x\right)=2x$
  • Consider any sequence of operations between two consecutive $G_2$ operations:

    $$\begin{array}{cc}\hfill x& \stackrel{G_2}{\to }{\displaystyle \frac{x-1}{3}}<{\displaystyle \frac{x}{3}}\hfill \\ \hfill & \stackrel{G_1}{\to }{\displaystyle \frac{2x}{3}}\hfill \\ \hfill & \stackrel{G_2}{\to }{\displaystyle \frac{2x/3-1}{3}}<{\displaystyle \frac{2x}{9}}\hfill \end{array}$$
  • This sequence strictly decreases values by a factor of at least ${\displaystyle \frac{4}{9}}$ between consecutive pairs of $G_2$ operations

Therefore:

• A sequence cannot use only $G_1$ operations (Step 1)
• A sequence cannot have only finitely many $G_2$ operations (Steps 2-3)
• $G_2$ operations must occur infinitely often to maintain positive integer values (Step 4)

This completes the proof that any infinite generation path must contain infinitely many $G_2$ operations. □

Lemma 5 

(Finite Generation). For any finite $n\in {\mathbb{N}}^{+}$, all generation paths leading to n are finite.

Proof. 

Let ${\left(a_k\right)}_{k\ge 0}$ be a generation path with $a_0=n$. We will provethat this path must be finite by establishing bounds on its growth.

Define the sequence $M_k=max\{a_i:0\le i\le k\}$ representing the maximum value encountered up to index k. We will show that this sequence cannot grow indefinitely.

First, we establish the behavior of individual operations:

• For operation $G_1$ (multiplication by 2): If $a_i=2a_{i+1}$, then:

  $$a_{i+1}={\displaystyle \frac{a_i}{2}}\Rightarrow M_{i+1}\le M_i$$
• For operation $G_2$ (${\displaystyle \frac{x-1}{3}}$): If $a_i={\displaystyle \frac{a_{i+1}-1}{3}}$, then by Lemma 3:

  $$a_{i+1}=3a_i+1<4a_i\Rightarrow M_{i+1}<M_i$$

By Lemma 3, we know that:

• $G_2$ operations cannot occur consecutively
• Between any two $G_2$ operations, at least one $G_1$ operation must occur
• Each $G_2$ operation reduces the value strictly

For any infinite sequence of operations, by Lemma 4, there must be infinitely many $G_2$ operations. Each $G_2$ operation strictly reduces the value, and $G_1$ operations do not increase the maximum value. Since we are working with positive integers, and each $G_2$ operation provides a strict reduction, the sequence cannot be infinite.

More precisely, let $r_k$ be the number of $G_2$ operations that have occurred up to step k. Then:

$$M_k\le M_0·{\left({\displaystyle \frac{3}{4}}\right)}^{r_k}$$

Since $r_k$ grows without bound for an infinite sequence (by Lemma 4), and we are dealing with positive integers, the sequence must terminate after finitely many steps. □

4. Uniqueness of the Fundamental Cycle

Figure 1. Structure of the unique cycle and example of a failed cycle attempt

Figure 1. Structure of the unique cycle and example of a failed cycle attempt

Lemma 6 

(Cycle Growth Property). Let $(n_1,\dots ,n_k)$ be a cycle in the Collatz system. Then:

$$\prod _{i=1}^k{\displaystyle \frac{C\left(n_i\right)}{n_i}}=1$$

Proof. 

Since we have a cycle, the product of all ratios must be 1, as we return to the starting number. For even numbers, the ratio is ${\displaystyle \frac{1}{2}}$. For odd numbers, it is ${\displaystyle \frac{3n+1}{n}}=3+{\displaystyle \frac{1}{n}}$. □

Lemma 7 

(Cycle Ratio Property). In any Collatz cycle containing e even numbers and o odd numbers:

$$2^e=\prod _{n_i\mathrm{odd}}\left(3+{\displaystyle \frac{1}{n_i}}\right)$$

Proof. 

From the Cycle Growth Property (Lemma 6), multiplying all ratios:

$${\left({\displaystyle \frac{1}{2}}\right)}^e\prod _{n_i\mathrm{odd}}\left(3+{\displaystyle \frac{1}{n_i}}\right)=1$$

Therefore:

$$2^e=\prod _{n_i\mathrm{odd}}\left(3+{\displaystyle \frac{1}{n_i}}\right)$$

□

Lemma 8 

(Impossibility of Large Cycles). No Collatz cycle can contain a number greater than 4.

Proof. 

Let’s proceed in steps:

1) Suppose, for contradiction, that there exists a cycle containing a number $n>4$.

2) By Lemma 7, if e is the number of even terms and o the number of odd terms:

$$2^e=\prod _{n_i\mathrm{odd}}\left(3+{\displaystyle \frac{1}{n_i}}\right)$$

3) For any odd number $n_i>4$:

$$3+{\displaystyle \frac{1}{n_i}}<3.25$$

4) Therefore:

$$2^e<{\left(3.25\right)}^o$$

5) Taking logarithms base 2:

$$e<o{log}_2\left(3.25\right)\approx 1.7o$$

6) However, for any cycle:

• Each odd number produces an even number (via $3n+1$)
• Each even number may produce either an even or odd number (via $n/2$)
• To complete the cycle, we must return to an odd number

7) This implies $e\ge o$, contradicting the inequality in step 5.

Therefore, no cycle can contain numbers greater than 4. □

Theorem 3 

(Uniqueness of the Fundamental Cycle). The sequence $1\to 4\to 2\to 1$ is the only cycle possible in the Collatz system.

Proof. 

Let’s proceed systematically:

1) By Lemma 8, any cycle must contain only numbers $\le 4$.

2) Let n be the smallest number in a cycle. We analyze all possibilities:

Case 1 ($n=1$):

• $C\left(1\right)=4$
• $C\left(4\right)=2$
• $C\left(2\right)=1$

This gives us the known cycle $1\to 4\to 2\to 1$.

Case 2 ($n=2$): Then $C\left(2\right)=1$, reducing to Case 1.

Case 3 ($n=3$):

• $C\left(3\right)=10$
• But $10>4$, contradicting Lemma 8

Case 4 ($n=4$): Then $C\left(4\right)=2$, reducing to Case 2.

3) Therefore, any cycle must contain 1, which means it must be the cycle $1\to 4\to 2\to 1$. □

Example 1 

(Failed Cycle Attempt). Consider starting with $n=7$:

• $7\to 22$ (odd, apply $3n+1$)
• $22\to 11$ (even, apply $n/2$)
• $11\to 34$ (odd, apply $3n+1$)
• $34\to 17$ (even, apply $n/2$)

This sequence continues growing and cannot form a cycle because:

• The ratio ${\displaystyle \frac{22}{7}}\approx 3.14$ is less than $3.25$
• By Lemma 7, this violates the necessary growth conditions
• The sequence generates numbers greater than 4, contradicting Lemma 8

5. Uniqueness of the Minimal Generator

Figure 2. Generation process from 1 and impossibility from $m>4$

Figure 2. Generation process from 1 and impossibility from $m>4$

Lemma 9 

(Generator Set Properties). For any number m and its generator set $S_m$:

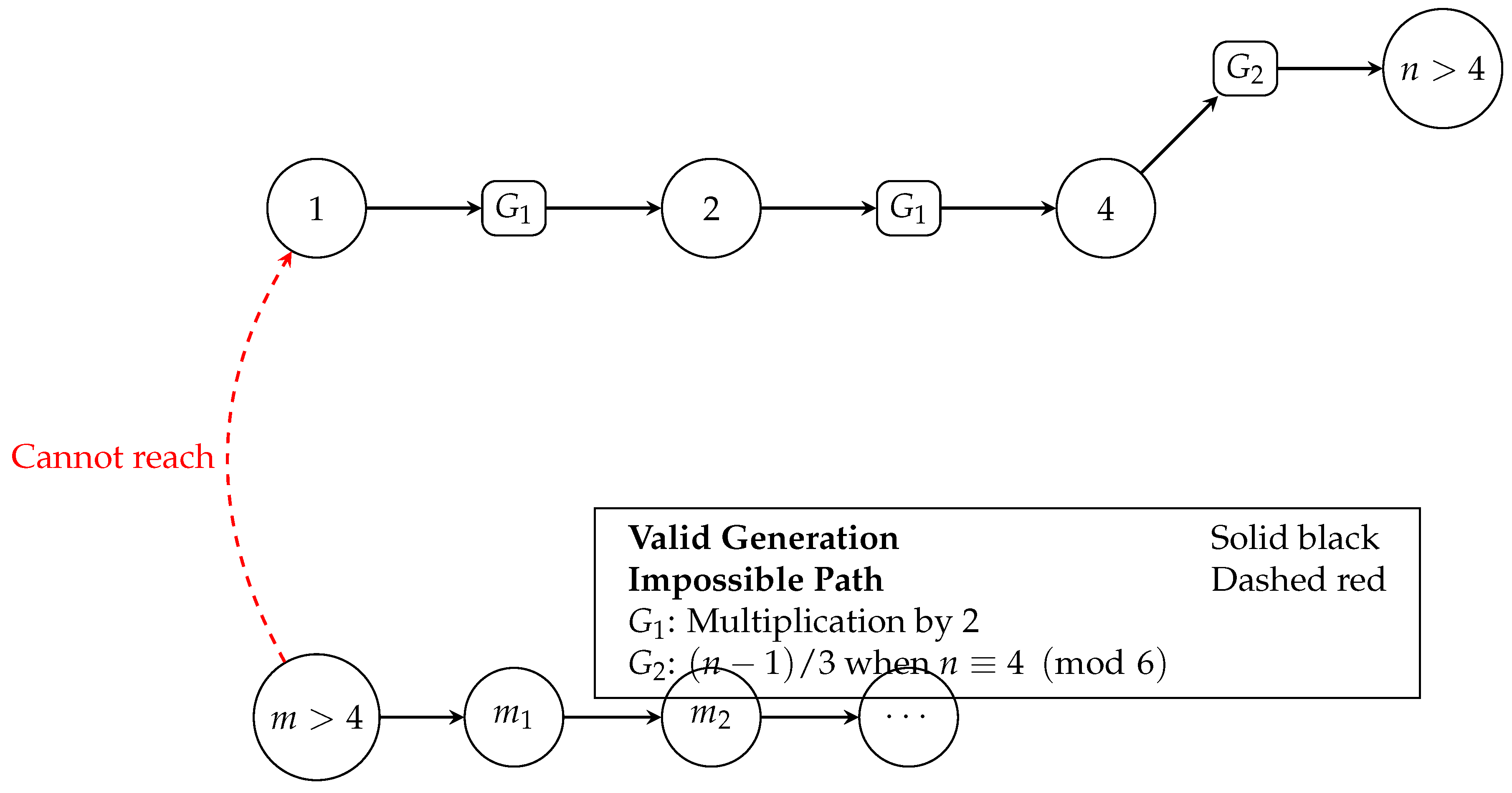
• If $x\in S_m$ and $y\in G\left(x\right)$, then $y\in S_m$ (closure under generation)
• If $S_m={\mathbb{N}}^{+}$, then $1\in S_m$ (completeness property)
• If $1\in S_m$, then $\{1,2,4\}\subseteq S_m$ (fundamental cycle inclusion)

Proof. 

1) Let $x\in S_m$. Then there exists a sequence ${\left(a_i\right)}_{i=0}^k$ with:

• $a_0=m$
• $a_k=x$
• $a_i\in G\left(a_{i+1}\right)$ for all $i<k$

If $y\in G\left(x\right)$, extend this sequence with $a_{k+1}=y$ to show $y\in S_m$.

2) Immediate from the definition of $S_m={\mathbb{N}}^{+}$.

3) If $1\in S_m$, then by Theorem 3:

• $2\in G\left(1\right)$ implies $2\in S_m$
• $4\in G\left(2\right)$ implies $4\in S_m$

□

Lemma 10 

(Bounded Growth Property). For any finite sequence of generator operations starting from $m>4$:

• Each $G_2$ operation strictly decreases the value
• Between any two $G_2$ operations, at most one $G_1$ operation can occur
• The maximum value in the sequence cannot exceed the starting value m

Proof. 

1) For any $n\equiv 4(mod6)$, by Lemma 3.2:

$$G_2\left(n\right)={\displaystyle \frac{n-1}{3}}<n$$

2) By Lemma 2.2, if $2^n\neg \equiv 4(mod6)$, then there exists $h\in \{0,1\}$ such that $2^{n+h}\equiv 4(mod6)$.

3) Let $M_k$ be the maximum value up to step k. Then:

• $G_1$ operations cannot increase $M_k$
• $G_2$ operations strictly decrease values
• Therefore $M_k\le m$ for all k

□

Lemma 11 

(Strict Value Bounds in Generator Sequences). Let ${\left(a_i\right)}_{i=0}^k$ be any finite generator sequence with $a_0>4$. Then for any $j\in \{0,\dots ,k\}$, either:

• $a_j>4$, or
• The sequence terminates at j (i.e., $j=k$).

Proof. 

We proceed by induction on j.

Base case ($j=0$): By hypothesis, $a_0>4$.

Inductive step: Assume the statement holds for some $j<k$. If $a_j>4$, we analyze $a_{j+1}$ based on the possible generator operations:

Case 1 ($G_1$ operation): If $a_j=2a_{j+1}$, then:

$$a_{j+1}={\displaystyle \frac{a_j}{2}}>{\displaystyle \frac{4}{2}}=2$$

Case 2 ($G_2$ operation): If $a_j\equiv 4(mod6)$ and $a_j={\displaystyle \frac{a_{j+1}-1}{3}}$, then:

$$a_{j+1}=3a_j+1>3·4+1=13$$

Moreover, by Lemma 9, $G_2$ can only be applied when $a_j\equiv 4(mod6)$, and by construction of G, these are the only two possible operations.

Therefore, if $a_j>4$ and the sequence doesn’t terminate at j, then $a_{j+1}>4$, completing the induction. □

Theorem 4 

(Uniqueness of Minimal Generator). For any $m>1$ with $m\notin \{1,2,4\}$, m cannot generate all positive integers through applications of G. More precisely, there exists at least one $n\in {\mathbb{N}}^{+}$ that does not belong to the set $S_m$.

Proof. 

We proceed by contradiction. Suppose there exists $m>4$ such that $S_m={\mathbb{N}}^{+}$.

1) By Lemma 9, $1\in S_m$.

2) Therefore, there exists a finite generator sequence ${\left(a_i\right)}_{i=0}^k$ with:

• $a_0=m$
• $a_k=1$
• $a_i\in G\left(a_{i+1}\right)$ for all $i<k$

3) By Lemma 11, since $m>4$:

• Either $a_j>4$ for all $j\in \{0,\dots ,k\}$
• Or the sequence terminates before reaching 1

4) This contradicts $a_k=1$, as:

• If the sequence terminates before reaching 1, we have an immediate contradiction
• If $a_k>4$, then $a_k\ne 1$, also a contradiction

5) For $m=3$, direct computation shows that $1\notin S_m$, and for $m=2$ or $m=4$, we already know they belong to the fundamental cycle with 1.

Therefore, no value $m>1$ with $m\notin \{1,2,4\}$ can generate all positive integers. □

Example 2 

(Generator Set Limitation). Consider $m=7$. Its generator set $S_7$ cannot contain 1 because:

• Any sequence from 7 must maintain values $geq7$ under $G_1$ operations
• $G_2$ operations can only be applied when values $\equiv 4(mod6)$
• The sequence $7\to 22\to 11\to 34\to 17\to \cdots$ demonstrates the impossibility of reaching 1

This example illustrates why numbers > 4 cannot be universal generators.

6. Main Result

Theorem 5 

(Collatz Conjecture). For any positive integer n, iterating the Collatz function C defined as:

$$C\left(n\right)=\left\{\begin{array}{cc}{\displaystyle \frac{n}{2}}\hfill & \mathrm{if}n\equiv 0(mod2)\hfill \\ 3n+1\hfill & \mathrm{if}n\equiv 1(mod2)\hfill \end{array}\right.$$

eventually reaches 1.

Proof. 

Let $n\in {\mathbb{N}}^{+}$ be arbitrary. By Theorem 4, there exists a finite sequence ${\left(a_i\right)}_{i=0}^h$ such that:

• $a_0=1$
• $a_h=n$
• For all $i\in \{0,\dots ,h-1\}$, $a_i\in G\left(a_{i+1}\right)$

Let us establish the critical connection between generator sequences and Collatz sequences:

Lemma 12 

(Generator-Collatz Correspondence). For any finite sequence ${\left(a_i\right)}_{i=0}^h$ satisfying properties (1)-(3), the sequence ${\left(b_j\right)}_{j=0}^{\infty }$ defined by iterating the Collatz function C starting from $b_0=a_h$ must either:

• Reach 1 after finitely many steps
• Enter a cycle other than $\{1,4,2,1\}$
• Diverge to infinity

Proof (Proof of Lemma). 

This follows from the fact that for any positive integer, each iteration of C must either:

• Divide by 2 (if even)
• Multiply by 3 and add 1 (if odd)

Therefore, the sequence must either reach 1, enter a cycle, or grow without bound. □

We will prove that options (b) and (c) are impossible, leaving (a) as the only possibility.

Case 1: Option (b) is impossible by Theorem 3, which proved $\{1,4,2,1\}$ is the only cycle.

Case 2: For option (c), suppose by contradiction that the sequence diverges. Let ${\left(b_i\right)}_{i\ge 0}$ be the forward Collatz sequence starting from n:

• $b_0=n$
• $b_{i+1}=C\left(b_i\right)$ for all $i\ge 0$

Now we establish a crucial property:

Lemma 13 

(Inverse Uniqueness). For any Collatz sequence ${\left(b_i\right)}_{i\ge 0}$, there exists a unique inverse generator sequence. Specifically:

• If $x\in G\left(y\right)$, then $C\left(x\right)=y$ (by Theorem 1)
• Each step in a generator sequence corresponds uniquely to a reverse step in the Collatz sequence
• The inverse mapping is unique at each step due to the parity-based definition of C

Let $M=max\{a_i:0\le i\le h\}$ be the maximum value in our original generator sequence from 1 to n. Since we assumed the sequence diverges, there exists some index k where:

$$b_k>M$$

By Theorem 4, $b_k$ must be reachable from 1 through some generator sequence ${\left(c_i\right)}_{i=0}^m$ with:

• $c_0=1$
• $c_m=b_k$
• For all $i\in \{0,\dots ,m-1\}$, $c_i\in G\left(c_{i+1}\right)$

However, by Lemma 4, any generator sequence starting from 1 must be finite, and by the proof of that lemma, its maximum value is bounded. Specifically:

• Each $G_2$ operation strictly decreases values
• Between $G_2$ operations, at most one $G_1$ operation can occur
• The maximum value in the sequence cannot exceed the starting value

This contradicts the existence of a generator sequence reaching $b_k>M$.

Therefore, Case 2 (divergence) is impossible.

Since both Case 1 (alternate cycle) and Case 2 (divergence) are impossible, the sequence must reach 1. By Theorem 3, once the sequence reaches 1, it enters the unique cycle $1\to 4\to 2\to 1$.

7. Conclusion

The significance of this proof of the Collatz conjecture lies in several key aspects:

• The generator function G provides a novel framework for analyzing inverse Collatz sequences. By studying how numbers can be generated backwards from 1, we gain crucial insight into the forward behavior of the Collatz function.
• The proof establishes fundamental properties of generation paths, particularly:
  • All generation paths to finite numbers must be finite (Lemma 5)
  • There exists a generation path from 1 to every positive integer (Theorem 4).
  • The number 1 is the unique minimal universal generator. (Theorem 4).
• The constraints imposed by even/odd patterns in the natural numbers, combined with the modular arithmetic properties of the generator function, make sustained growth impossible. This is formalized through:
  • The properties of the $G_2$ operation (Lemma 3)
  • The uniqueness of the fundamental cycle (Theorem 3)
• The inverse relationship between C and G (Theorem 1) provides the critical link that allows us to translate properties of generation paths into properties of forward Collatz sequences.

The proof demonstrates that every positive integer must eventually reach 1 under iteration of the Collatz function, resolving this long-standing conjecture. The generator function framework developed here may also provide insights into related problems in number theory and dynamical systems.