Two Methods to Compute the Plastic Bimoment of thin Walled Sections

1. Introduction

The elastic theory to obtain the warping coordinate and bimoment is presented.

To obtain the plastic bimoment the static or lower bound theorem is used. This theorem states if the equilibrium and plastic condition are verified, then factor ξ equals or is less than the plastic load combination. Where ξ is plastification factor that multiplies the combination of internal forces { ξN_Ed ξM_y,Ed ξM_z,Ed ξB_Ed ξV_y,Ed ξV_z,Ed ξT_t,Ed ξT_w,Ed }

In case of Torsion the following should be taken into account { ξB_Ed ξT_t,Ed ξT_w,Ed }, to obtain the plastic bimoment all the other internal forces are zero { ξB_Ed }

1.1. Elastic Theory

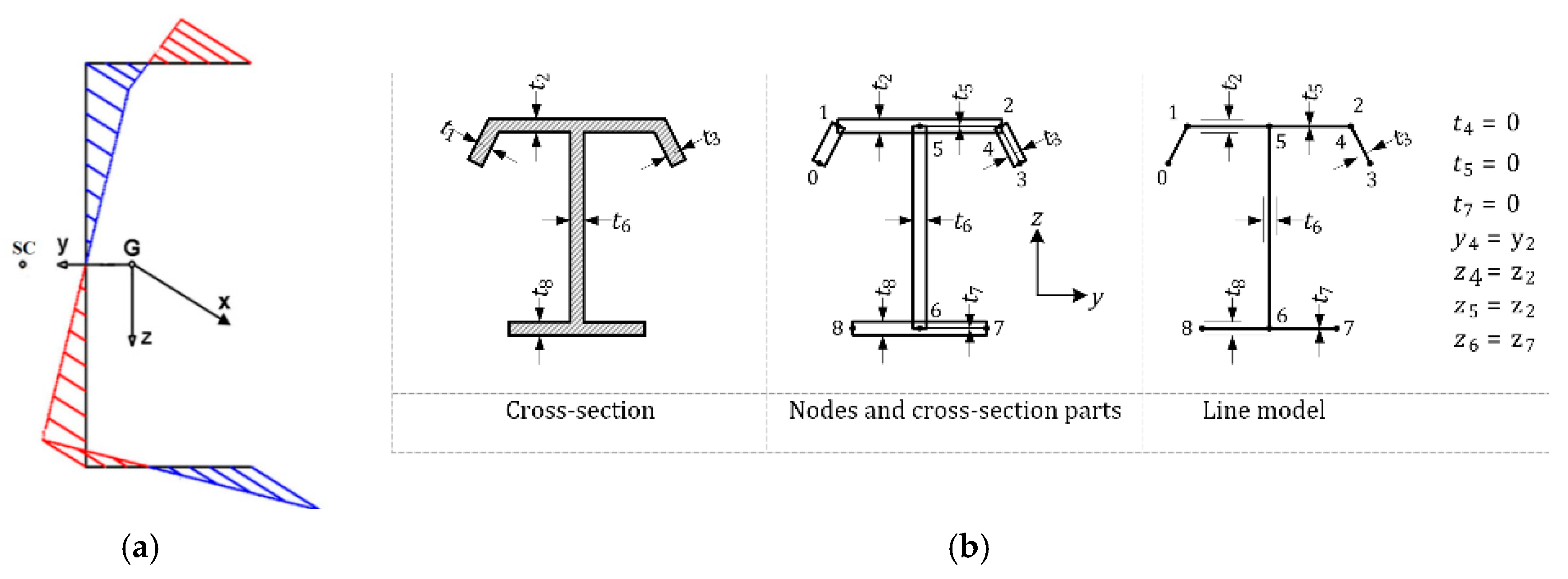
The classical approach to determining section properties is presented including sectorial coordinates using centroidal coordinates y_c and z_c see Figure 1 (a) and (b).

$$I_y=\int z_c^{2}dA={\displaystyle \frac{1}{3}}\sum \left(z_{c,i}^2+z_{c,i}{z}_{c,i-1}+z_{c,i-1}^2\right)A_i$$

(1)

$$I_z=\int y_c^{2}dA={\displaystyle \frac{1}{3}}\sum \left(z_{ci}^2+z_{c,i}{z}_{c,i-1}+z_{c,i-1}^2\right)A_i$$

(2)

$$I_{yz}=\int y_c{z}_{c}dA={\displaystyle \frac{1}{6}}\sum \left(2y_{c,i-1}{z}_{c,i-1}+y_{c,i-1}{z}_{c,i}+y_{c,i}{z}_{c,i-1}+2y_{c,i}{z}_{c,i}\right)A_i$$

(3)

$$I_{y\omega }=\int y_c{\omega }_{c}dA={\displaystyle \frac{1}{6}}\sum \left(2y_{c,i-1}{\omega }_{c,i-1}+y_{c,i-1}{\omega }_{c,i}+y_{c,i}{\omega }_{c,i-1}+2y_{c,i}{\omega }_{c,i}\right)A_i$$

(4)

$$I_{z\omega }=\int z_c{\omega }_{c}dA={\displaystyle \frac{1}{6}}\sum \left(2z_{c,i-1}{\omega }_{c,i-1}+z_{c,i-1}{\omega }_{c,i}+z_{c,i}{\omega }_{c,i-1}+2z_{ci}{\omega }_{c,i}\right)A_i$$

(5)

$${\omega }_{c,i}={\omega }_{c,i-1}+y_{c,i-1}\left(z_{c,i}-z_{c,i-1}\right)-z_{c,i-1}\left(y_{c,i}-y_{c,i-1}\right)$$

(6)

$$={\omega }_{c,i-1}+y_{c,i-1}{z}_{c,i}-y_{c,i}{z}_{c,i-1}\mathrm{where}{\omega }_{c,0}=0$$

(7)

(${\omega }_{c,0}$ can be chosen arbitrarily, typically taken as 0)

$$y_{sc}={\displaystyle \frac{I_z{I}_{z\omega }-I_{yz}{I}_{y\omega }}{I_y{I}_z-I_{yz}^2}}$$

(8)

$$z_{sc}={\displaystyle \frac{I_y{I}_{y\omega }-I_{yz}{I}_{z\omega }}{I_y{I}_z-I_{yz}^2}}$$

(9)

$${\omega }_{s,i}={\omega }_{s,i-1}+\left(y_{c,i-1}-y_{sc}\right)\left(z_{c,i}-z_{c,i-1}\right)-\left(z_{c,i-1}-z_{sc}\right)\left(y_{c,i}-y_{c,i-1}\right)\mathrm{where}{\omega }_{s,0}=0$$

(10)

(${\omega }_{s,0}$ can be chosen arbitrarily, typically taken as 0)

$${\omega }_{n,i}={\omega }_{s,i}-{\omega }_{s,mean}$$

(11)

$${\omega }_{s,mean}={\displaystyle \frac{1}{A}}\int {\omega }_{s}dA={\displaystyle \frac{1}{A}}\sum {\displaystyle \frac{{\omega }_{s,i-1}+{\omega }_{s,i}}{2}}{A}_i$$

(12)

$$I_w=\int {\omega }_n^{2}dA={\displaystyle \frac{1}{3}}\sum \left({\omega }_{n,i}^2+{\omega }_{n,i}{\omega }_{n,i-1}+{\omega }_{n,i-1}^2\right)A_i$$

(13)

$$B=\int \sigma {\omega }_{n}dA$$

(14)

$${\sigma }_w=B{\omega }_n/I_w$$

(15)

$$B_{el}=f_y{I}_w/{\omega }_{n,max}$$

(16)

It is convenient computationally to use any arbitrary starting coordinate system (y, z, ω) and the parallel axis theorem to obtain the centroidal properties. For sectorial coordinates with respect to any pole,

$${\omega }_i={\omega }_{i-1}+y_{i-1}\left(z_i-z_{i-1}\right)-z_{i-1}\left(y_i-y_{i-1}\right)={\omega }_{i-1}+y_{i-1}{z}_i-y_i{z}_{i-1}\mathrm{where}{\omega }_0=0$$

(17)

The normalized sectorial coordinates about the shear center can then be determined using

$${\omega }_{n,i}={\omega }_i-{\omega }_{mean}+z_{sc}{y}_{c,i}-y_{sc}{z}_{c,i}$$

(18)

$${\omega }_{mean}={\displaystyle \frac{1}{A}}\int \omega dA={\displaystyle \frac{1}{A}}\sum {\displaystyle \frac{{\omega }_{i-1}+{\omega }_i}{2}}{A}_i$$

(19)

1.2. Plastic Theory

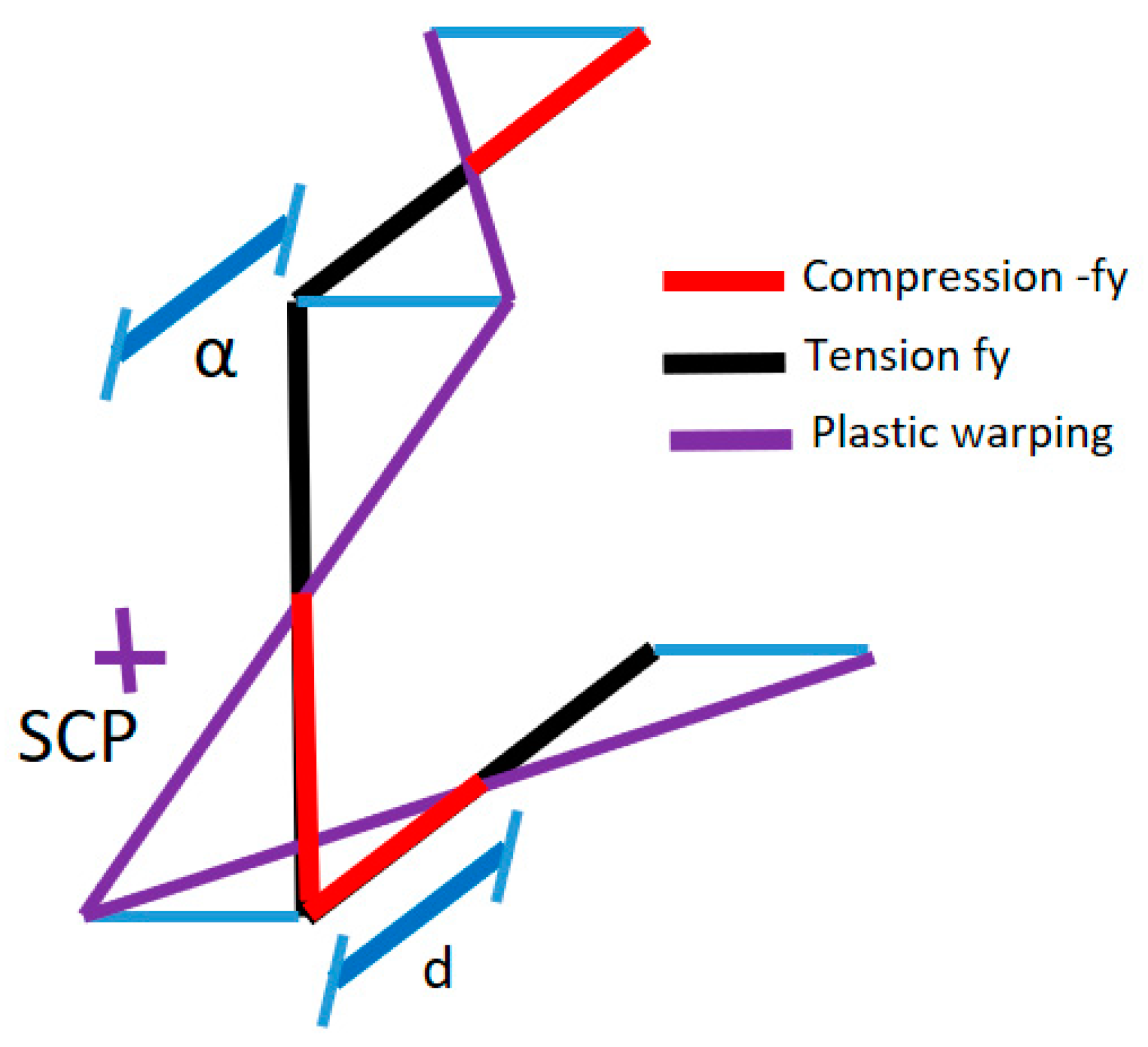
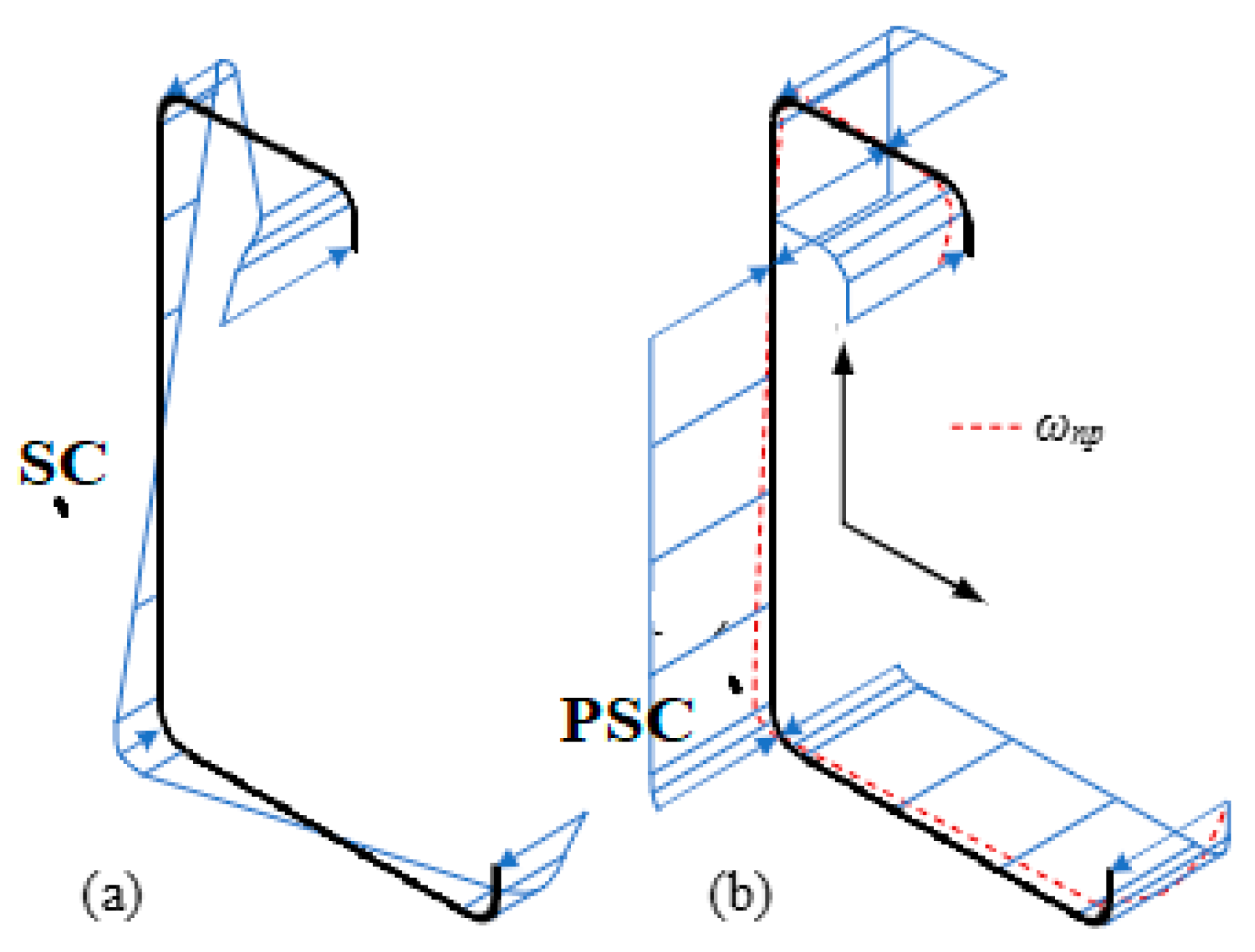
In method 1: The classical approach Glauz [1] is used where the sign of ω_np corresponds to the sign of σ, see Figure 2.

$${\omega }_{sp,i}={\omega }_{sp,i-1}+\left(y_{c,i-1}-y_{psc}\right)\left(z_{c,i}-z_{c,i-1}\right)-\left(z_{c,i-1}-z_{psc}\right)\left(y_{c,i}-y_{c,i-1}\right)\mathrm{where}{\omega }_{sp,0}=0$$

(20)

$${\omega }_{np,i}={\omega }_{sp,i}-{\omega }_{sp,median}$$

(21)

${\omega }_{sp,median}$ is determined such that there are equal areas of positive and negative stress (axial equilibrium). This is similar to locating the plastic neutral axis for flexure resulting in equal areas of positive and negative stress.

$$N=\int {\sigma }_{wp}dA=0,\int d{A}_{{\omega }_{np}^{+}}=\int d{A}_{{\omega }_{np}^{-}}$$

(22)

The plastic shear center is the location where the bimoment yield stresses associated with the sign of ω_np result in flexural equilibrium.

$$M_y=\int {\sigma }_{wp}zdA=0,\int zd{A}_{{\omega }_{np}^{+}}=\int zd{A}_{{\omega }_{np}^{-}}$$

(23)

$$M_z=\int {\sigma }_{wp}ydA=0,\int yd{A}_{{\omega }_{np}^{+}}=\int yd{A}_{{\omega }_{np}^{-}}$$

(24)

$$B_{pl}=\int {\sigma }_{wp}{\omega }_{np}dA\mathrm{where}{\sigma }_{wp}=\pm f_y$$

(25)

$$B_{pl}=f_y\int \left|{\omega }_{np}\right|dA$$

(26)

If the bimoment yield stresses are determined by other means such that the net axial force and moments are zero, the plastic shear center location does not need to be determined.

$${\omega }_{np}=\omega -{\omega }_{sp,median}+z_{psc}{y}_c-y_{psc}{z}_c$$

(27)

$$B_{pl}=\int {\sigma }_{wp}{\omega }_{np}dA=\int {\sigma }_{wp}\left(\omega -{\omega }_{sp,median}+z_{psc}{y}_c-y_{psc}{z}_c\right)dA=\int {\sigma }_{wp}\omega dA$$

(28)

Most terms drop out because ${\omega }_{sp,median}$ is multiplied by $N=\int {\sigma }_{wp}dA=0$, $z_{psc}$ is multiplied by $M_z=\int {\sigma }_{wp}{y}_{c}dA=0$, and $y_{psc}$ is multiplied by $M_y=\int {\sigma }_{wp}{z}_{c}dA=0$.

In the second method by Agüero [2], the bimoment can be obtained using linear programming, maximizing the bimoment obtained by using as pole the elastic shear center that satisfies the constraints N=M_y=M_z=0 and the stress at each point constrained to $-fy<\sigma <$fy

$$B_{pl}=\int {\sigma }_{wp}{\omega }_{s,el}dA=\int {\sigma }_{wp}\left(\omega -{\omega }_{mean}+z_{sc}{y}_{ci}-y_{sc}{z}_{ci}\right)dA=\int {\sigma }_{wp}\omega dA$$

(29)

The plastic bimoment section modulus can be obtained as:

$${Z_w=W_{pl,w}=B}_{pl}/f_y$$

(30)

2. Numerical Examples

The numerical examples are checked with Software by Agüero [3] ( https://labmatlab-was.upv.es/webapps/home/thinwallsectionelasticplastic.html ).

Figure 3. Channel section illustration showing y_psc, z_psc, ω_sp, and σ_wp.

Figure 3. Channel section illustration showing y_psc, z_psc, ω_sp, and σ_wp.

2.1. Channel Section

Middle line dimensions b=75mm h=187mm t_f=13mm t_w=10mm

The traditional approach using sectorial coordinates about the plastic shear center and precisely locating the stress reversals gives Z_w=591.098 cm⁴, where y_psc=38.642mm and z_psc=0mm (distance between plastic shear center and centroid).

To obtain the part of the bottom flange under compression and top flange under tension {d} Fig. 3, the condition My=0 is used equation (31).

$$d{t}_{f}h+{\displaystyle \frac{h^2{t}_w}{4}}=\left(b-d\right)h{t}_f\mathrm{therefore}d={\displaystyle \frac{b}{2}}-{\displaystyle \frac{h{t}_w}{8t_f}}$$

(31)

and taking into account that the shift of the plastic normal stresses from compression to tension takes place where the warping is zero the following equation (32) gives the distance of the plastic shear center to the web.

$$\propto {\displaystyle \frac{h}{2}}-d{\displaystyle \frac{h}{2}}=0\mathrm{therefore}d=\alpha$$

(32)

Method 2: With 10 fibers per element W_pl,w=Z_w=594.874cm⁴, and with 20 fibers per element Z_w= 591.517cm⁴, so the results tend to converge to the precise solution with more fibers, also from equation in table 14 Agüero [2] Z_w= 591.098cm⁴

Y_sc,el=47.559mm distance between elastic shear center and centroid.

Also W_plw=2878cm⁴ was compared with the one obtained by Baláž [4] for a UPE360.

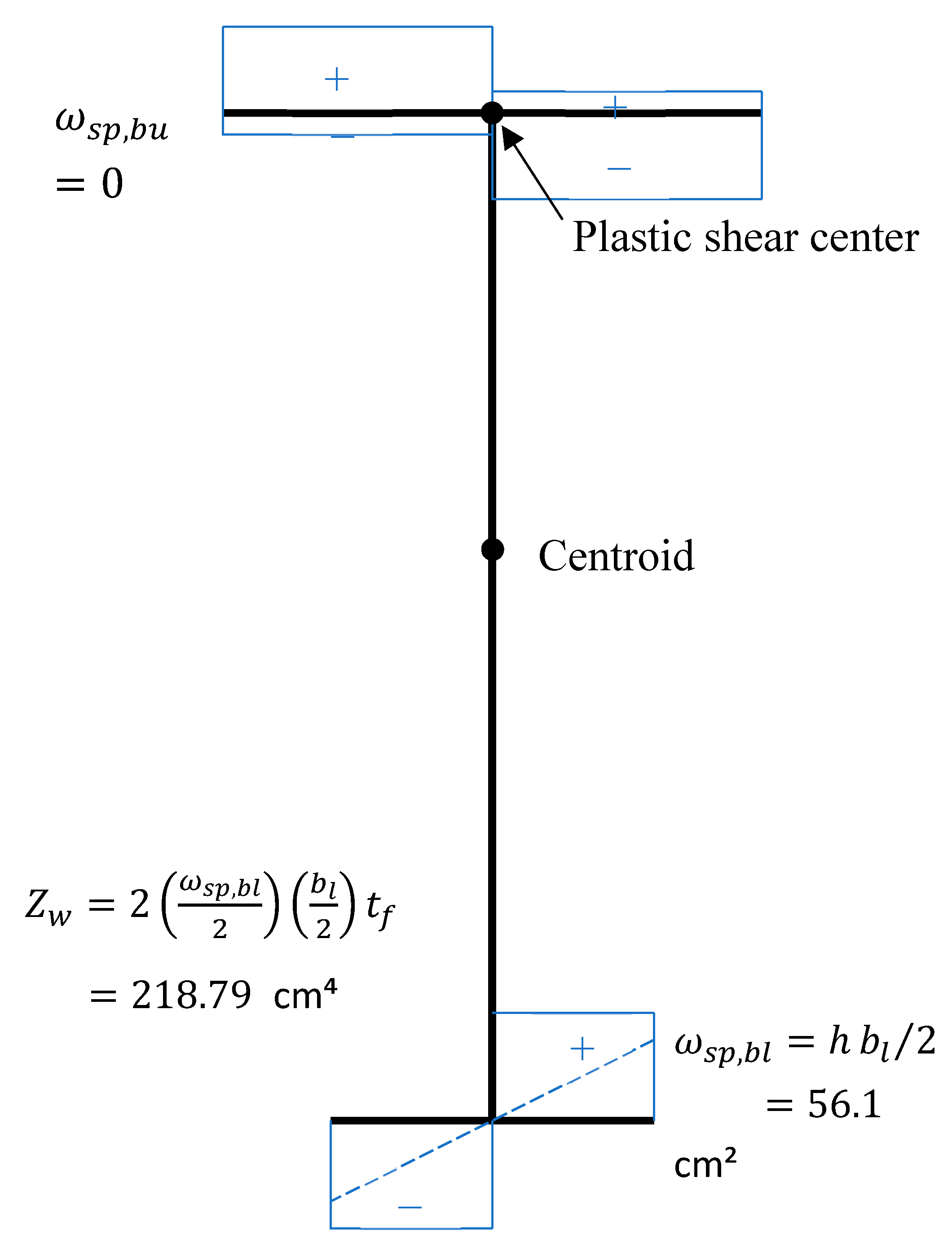
2.2. Mono-Symmetrical I Shape Section

Trahair [5] pointed out that for this section the plastic bimoment did not depend on the pole position to compute the warping coordinate.

Middle line dimensions b_u=100mm b_l=60mm h=187mm t_f=13mm t_w=10mm

The distance {d} from the plastic shear center to the lower part of the upper flange can be obtained applying the condition Mz=0, this results in equation (33).

$$d={\displaystyle \frac{t_f}{2}}\left(1-{\displaystyle \frac{b_l^2}{b_u^2}}\right)$$

(33)

The plastic shear center lies within the thickness of the larger flange: z_psc=78.851mm. The tension and compression stresses are apportioned across the thickness of the larger flange to attain equilibrium but have negligible contribution to the plastic bimoment. Due to symmetry, the normalized plastic sectorial coordinates and plastic bimoment section modulus can easily be determined as shown in Figure 4.

Method 2: With 10 fibers per element Wpl,w=Zw=218.79cm⁴ also from equation in table 13 Agüero [2] the same value is obtained.

Zsc,el=47.974mm distance between elastic shear center and centroid.

2.3. Section Non-Symmetrical

Channel section different width top and bottom flange.

middle line dimensions b_u=75mm b_l=50mm h=187mm t_f=13mm t_w=10mm

The traditional approach using sectorial coordinates about the plastic shear center and precisely locating the stress reversals gives Z_w=303.889 cm⁴, where y_psc=15.118mm and z_psc=84.795mm, distance between plastic shear center and centroid.

Method 2: With 10 fibers per element Wpl,w=Zw=303.875cm⁴

Ysc,el=35.102mm Zsc,el=31.259mm distance between elastic shear center and centroid.

3. Conclusions

The present paper present 2 methods to obtain the plastic bimoment of thin walled sections. In the first method plastic shear center needs to be obtained, while in the second method linear programming is used to maximize the plastic bimoment using as pole to obtain the unit warping the elastic shear center. Numerical examples for monosymmetric I shaped section, channel section and non symmetric section show perfect agreement.

About the interaction with other non zero internal forces { ξN_Ed ξM_y,Ed ξM_z,Ed ξB_Ed ξV_y,Ed ξV_z,Ed ξT_t,Ed ξT_w,Ed } the bimoment is different computed using the plastic shear center to obtain the unit warping as suggested by Osterrieder [6,8] and Trahair [5] than computed using the elastic shear as suggested by Kindmann [7,9] leading to different interaction plastic diagrams.