1. Introduction
The first sustained nuclear chain reaction was conducted within the Chicago Pile, (CP-1) located underneath the University of Chicago’s Stagg Field in 1942. Since then, the scientific value of the subcritical pile grew significantly during the first era of nuclear energy research but now appears to have dwindled from the nuclear community. [
1]
There are three known subcritical piles located at Universities throughout the United States, which strictly act as an educational tool or with limited research use. [
2] Recently, the pile located at Purdue University was re-arranged in late 2023 to accommodate a testbed to explore how thermal neutrons could affect the performance of microelectronics. Prior to the inclusion of the testbed, the pile was well-categorized by students and professors, however, the construction of the pile originally prevented any appreciable size of testing material from being placed within the pile. The inclusion of the testbed establishes a testing volume of approximately 1.5*10^5 cm^3 which exceeds that of any pile in the United States and of many test reactors that also exist in the university setting.
While the testbed was originally designed and constructed with the goal of testing the performance of commercial off-the-shelf microelectronics under neutron and gamma irradiation, the potential research uses extend beyond this topic of interest. Two examples that have received high attention within the nuclear community are the potential for limited isotope production via neutron activation and the use of thermal neutrons for non-destructive imaging. [
3,
4] Both of which could have significant commercial and military applications.
Before the testbed can be used in any experimental capacity, it is important to quantify the spatial and energy distribution of neutrons and gammas internal and external to the testbed. These values allow for the identification of maxima and minima that may justify experimental setup and optimization. The subcritical pile neutron flux can be obtained using metallic foils that are activated and then measured for subsequent gamma decay. A secondary approach is the use of open-source Monte Carlo (MC) simulations to model the geometries of the pile to a high degree of fidelity. [
5] One advantage of the MC methods is the production of large data sets that can be used for educational purposes or training and testing machine learning and artificial intelligence algorithms. [
6]
This article discusses the testbed design and construction, test methods, and data used to conduct metal foil neutron analysis to quantify the total flux within the pile and thermal/epithermal neutrons within the volume of the testbed. A high-fidelity Monte Carlo model of the subcritical pile was produced using MIT’s OpenMC software and then benchmarked using the obtained experimental metal foil measurements. The overall purpose is to classify the modified Purdue subcritical pile in the current testbed configuration to support its role as a scientific instrument for future testing and modeling of radiation environments.
2. Literature Review
A subcritical pile is a unique and safe nuclear facility operating below the criticality threshold, providing distinctive features and advantages. Very few subcritical facilities are currently active around the world that possess a maximum K-eff of 0.96, the known highest neutron flux value of 3.72*10^4 ± 0.0052 n/cm^2 *s, and have minimal space available for testing of cm to mm samples. Typically, subcritical piles are experimentally characterized using He-3 detectors and BF-3 detectors paired with gold foils. These values are used to validate either analytical calculations or Monte Carlo method-based simulation tools. Most of the subcritical piles are used for hands-on experiments, criticality measurements, neutron flux distribution, or neutron transport analysis. An overview of subcritical pile characterization studies and recent projects are described below.
High-fidelity modeling and simulations were performed for the MIT graphite exponential pile (MGEP) using Monte Carlo Neutron Particle (MCNP) transport code, and OpenMC. The results were validated against experimental data, collected by using a He-3 neutron detector on a mobile platform that was placed inside the pile. The comparison results show the error is less than 2.5% in the two upper layers, and less than 4.5% in all four measured layers. [
7]
Another project was conducted on the characterization of the same MIT graphite pile where a detailed neutronic model of the pile was created using MCNP5 software and used to map the spatial source dependence. Count rate measurements were taken using three Quaesta Instruments Neuchrometer Helium-3 detectors inserted into fuel stringers at various locations on the north face of the Pile. The overall flux shapes were similar, and the neutronic model was able to predict the measured flux with less than 15% error at surface locations. The error between the model prediction and the experimentally measured data was greater than 15% for the 6-7 sampling locations that were furthest from the source. The K-effective of the system was also calculated and was compared between the simulated and the analytical results. The simulated mean K-eff value was 0.82483 and the analytically calculated mean K-eff value was 0.82411 while the error was ± 0.00072. [
8]
Another project considered utilizing different reactivity determination methods like the slope fit method, the Sjostrand method, and the source jerk method, which were based on experiments performed at the assembly Yalina in Minsk, Belarus. The results are compared with Monte Carlo simulations performed with various nuclear data libraries. These libraries were also based on experiments performed at the subcritical assembly Yalina in Minsk, Belarus. The Sjostrand Method provides low statistical error in comparison with the MCNP model. The Slope Fit Method is inconvenient to apply to deep subcritical configurations but gives reliable results in comparison with MCNP. The Source Jerk Method gives large uncertainties. The K-eff value was also compared between MCNP and the other methods mentioned above. The K-eff generated by MCNP for various data libraries were 0.91803 ± 0.00005 for ENDF/B-VI, 0.92010 ± 0.00007 for JEFF3.0 and 0.92114 ± 0.00006 for JENDL3.3. In comparison with the MCNP calculations, the Slope Fit Method showed similar results, whereas the Sjostrand Method and the Source Jerk Method underestimate and overestimate K-eff, respectively. [
9]
Fixed source and criticality calculations in MCNP were performed to calculate the power and absolute flux of a source driven subcritical assembly at Jordan University of Science and Technology. The highest total radial flux of 2.572E3 ± 0.0269 n/cm^2*s was identified at the center of the pile while the highest total axial flux of 3.72*10^4 ± 0.0052 n/cm^2 *s, was found below the core. [
10]
Computational modeling of the subcritical reactor of the Army Technology Center (CTEx), namely ARGUS pile, was carried out using MCNP to determine the multiplication factor (K
eff) for different enrichment of various types of fuel. The results show with metal uranium fuel, supercriticality would be achieved with an enrichment greater than 2.4% while for uranium dioxide, supercriticality would be achieved with an enrichment greater than 4.3%. [
11]
A collaborative project between the Atomic Energy of Canada Limited (AECL) and the Deep River Science Academy (DRSA) was conducted to numerically explore the subcritical experiments carried out by the Nuclear Regulatory Commission (NRC) Laboratories by Laurence where Monte Carlo reactor physics code, MCNP6, was utilized to identify and study the key parameters impacting the subcritical pile’s neutron multiplication factor (e.g., moderation, geometry, material impurities) and quantify their effect on the extent of subcriticality. An analytical assessment in deriving theoretical relationships supported a maximum Keff value of 0.7298 ± 0.0003, assuming pure materials, which is closer to the 0.71 value that Laurence reports using “Halban’s method”. [
12]
Yet another K
eff experiment at the Universidad Autonoma de Zacatecas’ Subcritical Pile was calculated using the six-factor formula and the Monte Carlo methods. The results supported the notion that for fuel mass less than 750 kg, the six-factor formula tends to overestimate the Keff in comparison to Monte Carlo methods and underestimate the Keff in comparison to Monte Carlo calculations for a fuel weight of more than 2500 kg. Also, in locations near the center of the pile, the spectrum is strongly affected by the source neutron spectrum. [
13]
At the University of Cincinnati Subcritical facility validation of MCNP simulated model was carried out against experimental measurements for neutron flux distributions and subcritical neutron multiplication factors while illustrating a unique feature of the core being loaded and unloaded. The experimental neutron count measurements were carried out using a standard 60 cm long BF3 detector mounted in the counter transverse mechanism. The calculations display the MCNP model can reasonably predict measured levels of subcriticality, especially for the loaded core, and can predict the neutron flux profiles adequately well, particularly for non-perturbed situations of the fully loaded core. [
14]
At the MIT graphite exponential pile, a digital twin was developed for the system. An OpenMC model was used to create simulated flux readings from a detector that was then used to train an artificial neural network developed using the open-source artificial neural network machine learning code toolkit –
Non-Probability Sampling Network. The neural network would predict the location of the initiating control rod and move the responding control rod to the symmetric position to restore a symmetric neutron flux in the pile. The project successfully implemented an autonomous control system both using a digital twin of the MGEP and a physical digital control system on the actual MGEP. The digital control was able to predict the location of an unknown movement of a control rod and move another control rod to a symmetric position. [
15]
Research work was performed to compare the viability of producing uranium-233 using thorium irradiation in heavy water reactors and accelerator-driven subcritical pile at Texas A&M University. The ADS was not only able to produce a greater quantity of U-233 than the National Research Experimental (NRX) reactor, but the ADS produced U-233 more efficiently as well. This investigation is helpful in evaluating not only the capabilities available to a potential proliferator but also indicates to regulators possible vulnerabilities that exist within the current safeguard regime. [
16]
A detailed neutronic analysis of the Jordan Subcritical Assembly was performed including criticality and reactivity analysis, neutron flux characterization, etc. using various computational models including MCNP5, KENO-V. a (SCALE), and Serpent. The range of Keff values for JSA using different codes and libraries is 0.96151± 0.00009 – 0.96571± 0.00007 with a maximum difference of 420 pcm. Flux mapping was created for a different range of energetic neutrons. At the center of the pile, the contribution from the thermal neutrons dominates while the fast flux increases rapidly as the neutron source location is approached. [
17]
Another characterization project was performed at the subcritical assembly in the Philippines, where an MCNP model was used for criticality calculations to determine the multiplication factor (Keff) and gamma-neutron dose of the subcritical assembly. The calculated Keff when the control rod was fully withdrawn was 0.95518 ± 0.00007, while when it was fully inserted, Keff was 0.94139 ± 0.00007. The horizontal dose distribution results show that at the surface of the pile, the calculated dose rate is about 1 μSv/h. While for the vertical dose distribution, the calculated dose rate just above the water top is ~0.1 μSv/h. The safety of the pile was ensured by the computational models which will later be used in calculating and predicting radiation measurement in the subcritical pile to enhance the facility of research and training purposes. [
18]
3. Modified Subcritical Pile Testbed
3.1. Pile Geometry
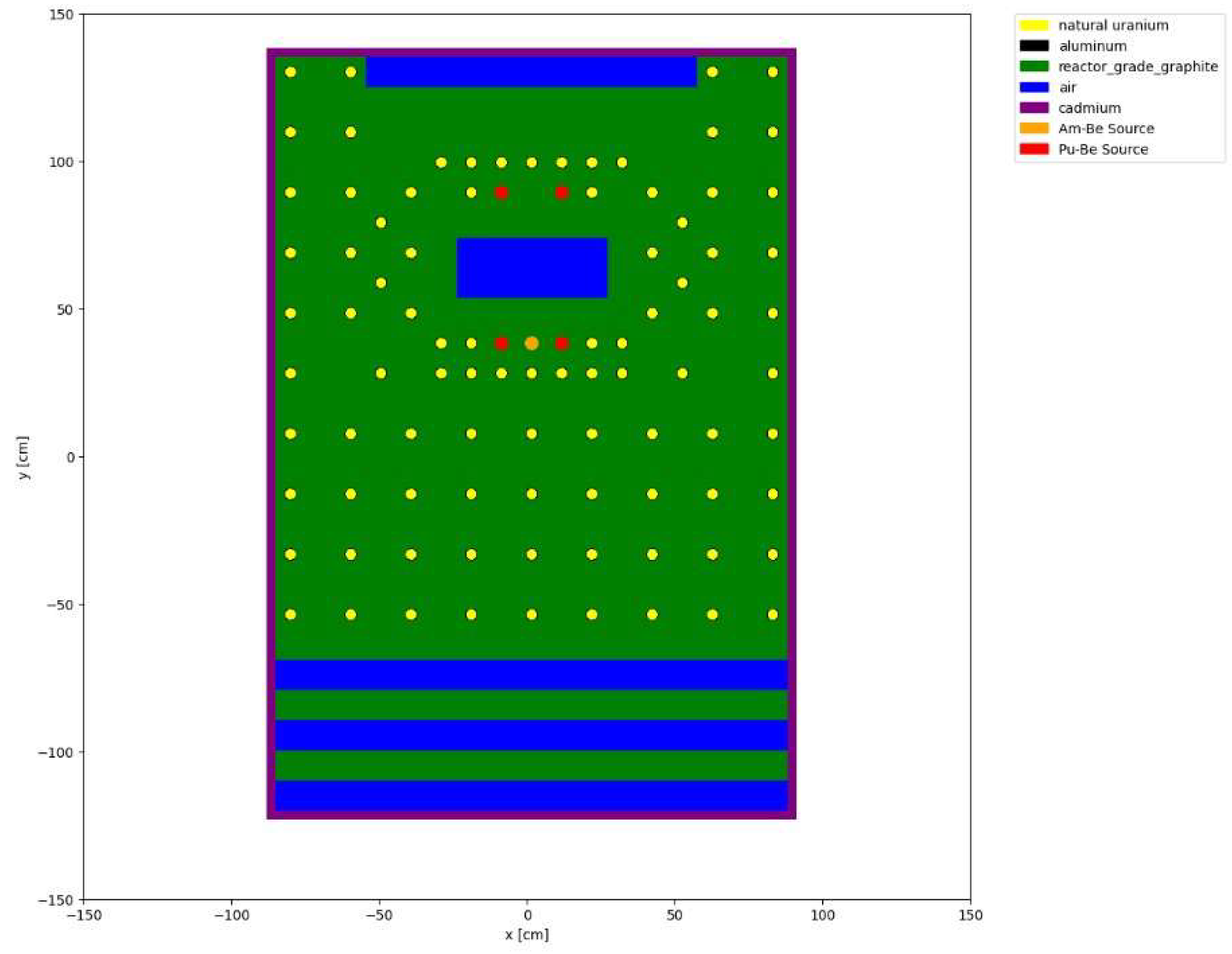
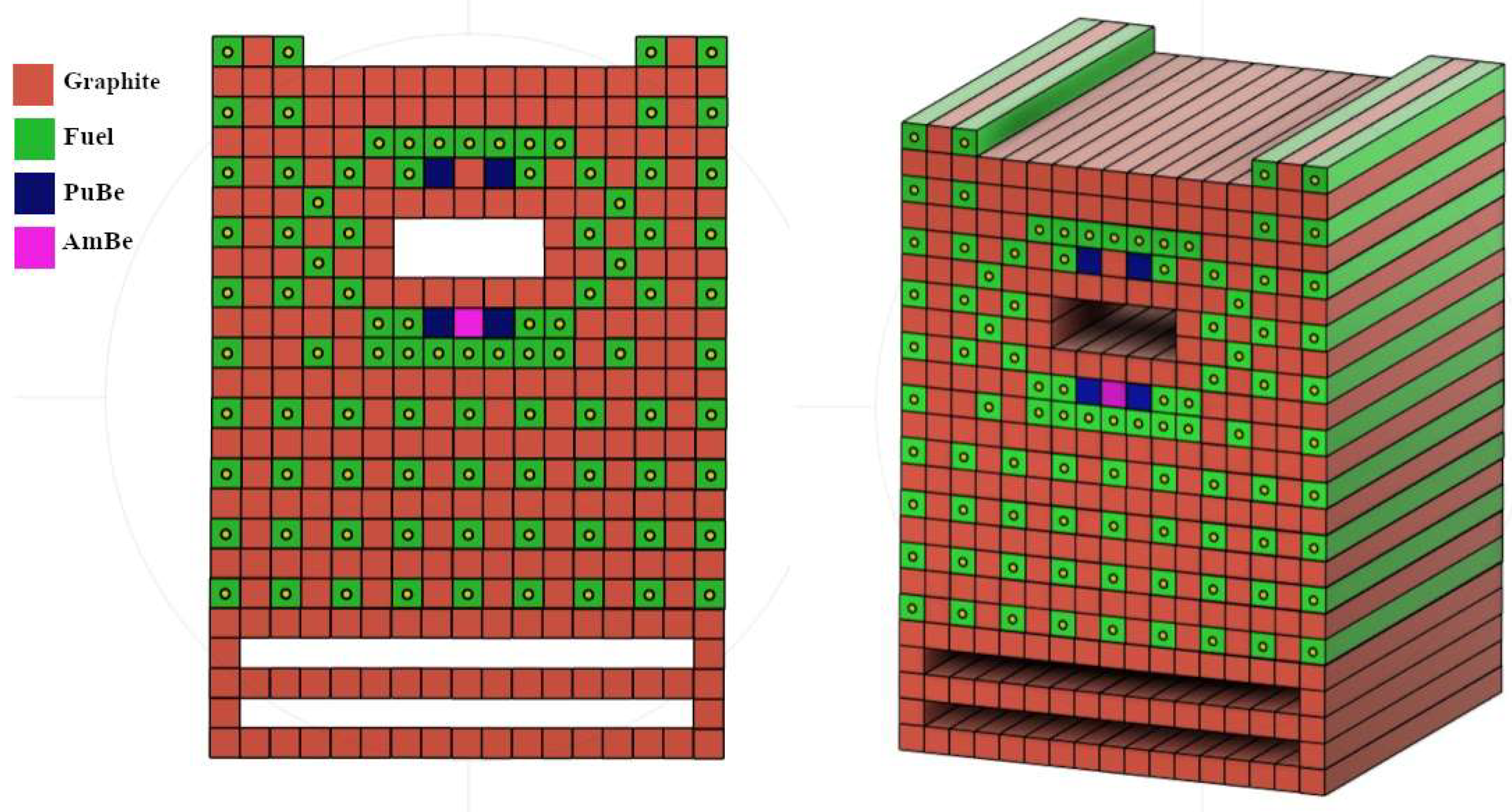
The subcritical pile is a repeating matrix of rectangular prism graphite and fuel. Natural Uranium fuel rods in aluminum cladding are placed inside graphite blocks combining a total of 90 fuel-graphite joint blocks. Another 247 blocks of only graphite are placed as well. Together they form the subcritical pile, being 179 cm in length, 260 cm in height, and 179 cm in depth. A cadmium reflector surrounds the whole pile. 1 Americium-Berylium (AmBe) source of 10 Ci and 4 Plutonium- Berylium (PuBe) sources of 1 Ci each are placed in the pile. These sources are used to emit neutrons inside the pile, initiating and later controlling the fission reaction in the subcritical pile. The AmBe source has a neutron yield of 2.0 – 2.4*10^6 neutrons/sec* Ci, while each PuBe source has a neutron yield of 1.5 – 2.0*10^6 neutrons/second*Ci. [
21]
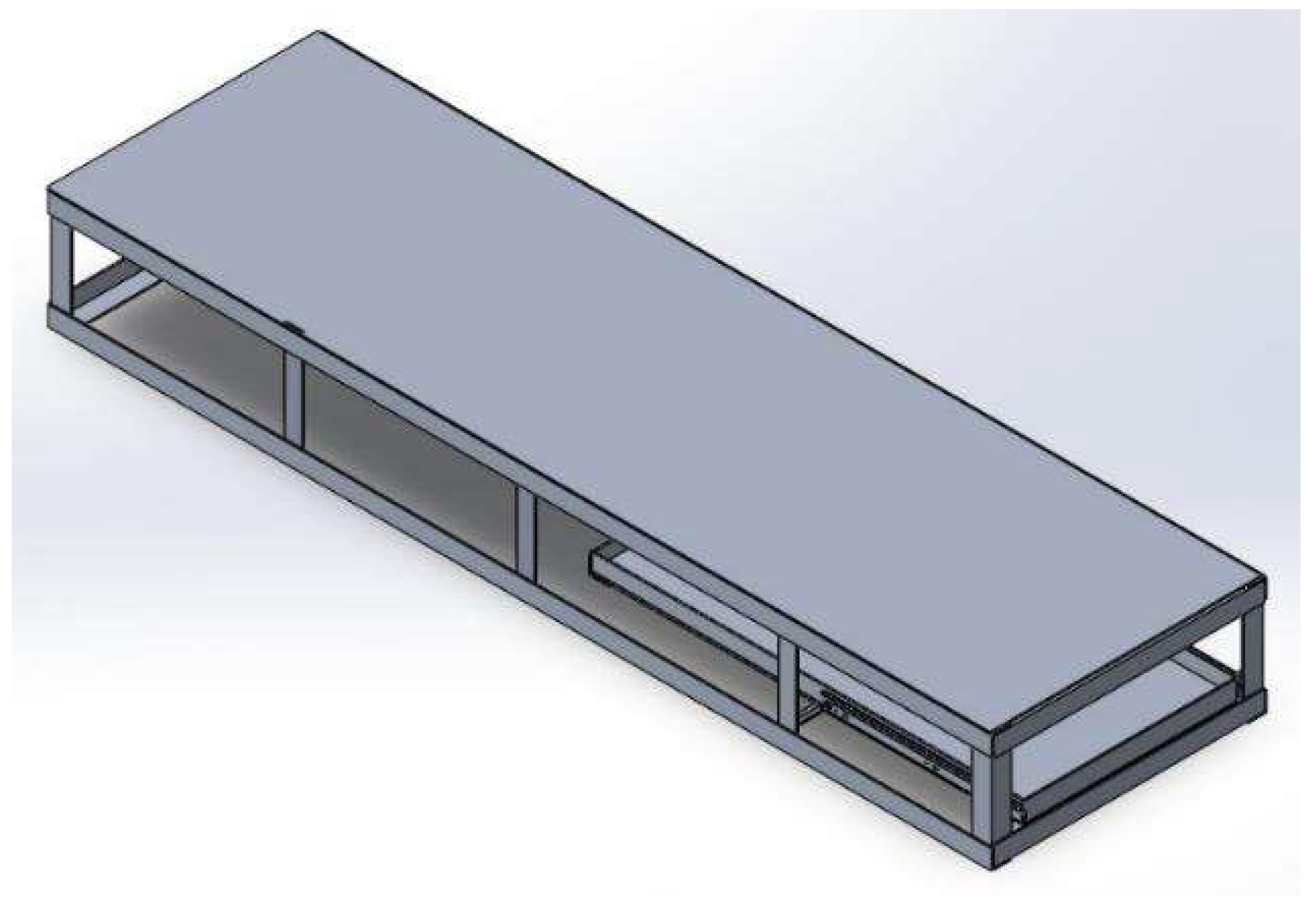
The chief addition to the pile is the rectangular testbed near the upper center in the Z and X planes. This feature was added to the pile in late 2023 and is the focal point of what differentiates the Purdue sub-critical pile from others. The testbed dimensions are 45 cm x 20 cm x 162 cm, the limiting constraint was set to ensure minimal disruption to the original pile configuration. In addition to the test bed volume, there is a removable platform on drawer slides to allow for easy placement of test materials. The platform minimizes the potential for contamination from test materials and minimizes the dose to technicians while conducting measurements. The platform is roughly the same width as the testbed but has half of the depth into the pile. This design feature was selected due to the placement of the neutron sources near the front face of the pile relative to the personnel working space.
Figure 1 displays the front working space as well as a bird’s eye 3D image to give the perspective of the pile’s composition and construction. This is a computer-aided design (CAD) design that was generated by Fusion 360 software complex. Materials are defined in this CAD model by various colors, for example red is the graphite moderator, green is natural uranium, the blue and magenta represent the PuBe and AmBe sources respectively. One added convenience of OpenMC over other standard MC programs is the ability to import CAD geometries.
In addition to volume consideration for the testbed, the secondary concern was the potential for creating long-lived radioactive material. To prevent undesired waste, aluminum was selected as the structural material. While the potential for activation of Al-27 is not low (0.231 b), the half-life of Al-28 is 2.3 minutes, classifying the material as a short-lived isotope. The hardware of the testbed to a reasonable degree is low-cobalt steel. Although the full list of materials cannot be verified for the construction, the bulk of the testbed is aluminum, thus minimizing the production of long-lived waste. A 3D SolidWorks rending of the test bed is shown in
Figure 2. The testbed integrated into the pile from the working face is shown in
Figure 3.
4. Methods
4.1. Neutron Interactions
Neutrons interact with the nuclei of target materials via scattering, absorption, or fission reactions. First, neutrons can undergo elastic or inelastic scattering. During inelastic scattering, a collision between a neutron and a nucleus results in the neutron losing energy, and the nucleus becoming excited. During elastic scattering, the kinetic energy of the system is conserved when a neutron collides with a nucleus. Repeated inelastic scattering events can lead to the thermalization of neutrons which is relevant in environments such as the subcritical pile.
Neutrons may also cause fission reactions to occur. This occurs when a neutron interacts with the nucleus of a fissile material (uranium-235 in the case of the subcritical pile). During fission, the neutron is briefly absorbed into the nucleus to form a compound nucleus before almost instantly splitting into two fission fragments. Released with the fragments is a significant amount of energy, 2-3 neutrons on average, and other subatomic particles. [
20]
Finally, neutrons can be absorbed into the nucleus it interacts with through radiative capture. Absorption tends to dominate at lower neutron energies. If the addition of the neutron causes the nucleus to become unstable, that neutron has activated the nucleus. After neutron activation, the resulting radioisotope will decay according to its properties. This interaction is the basis of the analysis techniques presented in this work. [
20]
The specific isotopes being activated in this work are indium-115 and gold-197. The specific neutron activation reactions are given by reactions (1) and (2).
The gold reaction is straightforward, as gold only has one naturally occurring isotope (Au-197), and it only activates to a single isotope (Au-198). The cross-section for this reaction is 98.65 barns. The indium reaction is more complicated. First, indium-115 is not the only naturally abundant isotope of indium. Indium-113 is also present in natural indium at 4.28% abundance, with indium-115 making up the remaining 95.72%. Indium-113 activates to indium-114. With a half-life of 49.51 days, often times Indium-114 is not activated enough to be taken into consideration during neutron activation analysis. The final consideration to take into account is that indium-115 can activate into multiple different isotopes. 79% of the time, indium-115 activates to indium-116m with half-life 54.29 minutes, so the neutron absorption cross section (202 barns) must be multiplied by 0.79 to yield the appropriate cross section for this specific reaction (159.58 barns). The other isotopes indium-115 activates into (indium-116 and indium-116m2) have half-lives of less than 15 seconds, therefore it is important for those isotopes to decay before measuring the activities of any indium foils during neutron activation analysis. [
21]
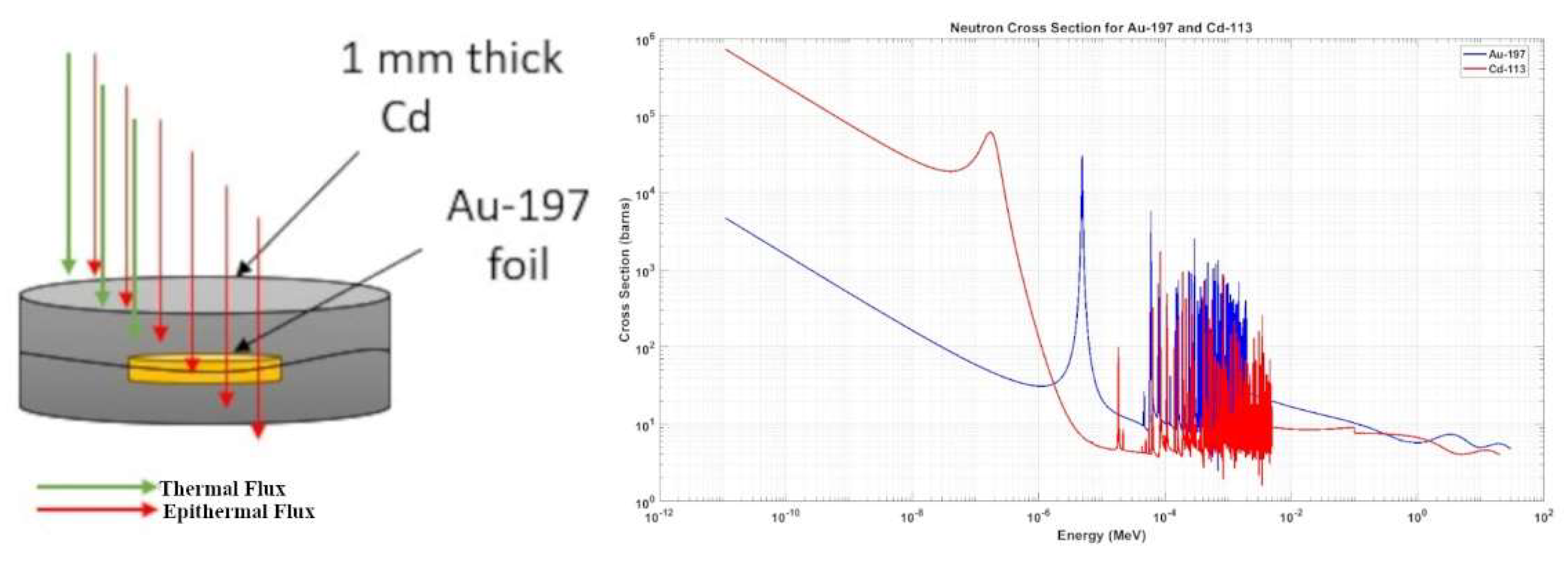
In a similar manner, neutrons are also captured by cadmium-113. Cadmium-113 has an extremely high capture cross section at 0.55 eV (2233 barns). This makes it convenient to block out thermal neutrons from reaching an activation foil by covering the foil with cadmium. The method of cadmium-covered activation foils is covered extensively later in this work. Reaction (3) displays cadmium absorption. [
21]
4.2. Metal Foil Neutron Activation
Au-197 (1.5 cm and 0.1 mm) and In-115 foils (2.5 cm in diameter and 0.25 mm) thickness were activated in the subcritical pile to determine the neutron flux at different locations throughout it. Once activated, the gamma decay energy could be measured in order to determine the neutron flux at that location.
Measurements in both locations followed a consistent procedure. For those measured throughout the pile, they were placed in a long aluminum tray. The tray extends the whole length of the pile and has seventeen slots to place foils. Each slot has an aluminum covering and a label to ensure consistent placement and safety of the handler. Due to only having nine Indium-115 foils, they were placed in every other slot. Each foil was labeled with a letter that corresponded to the numbered slot they were placed in.
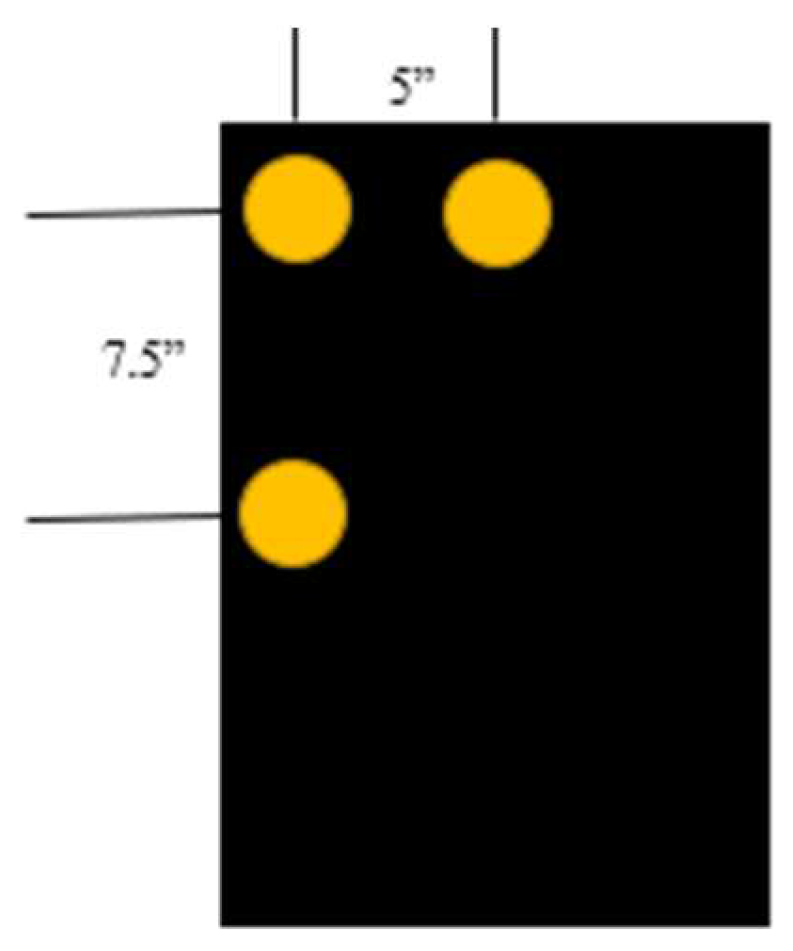
Foils for testbed measurement were set in various measured locations on the platform in order to be activated. There were several orientations, and the placement location was determined by taking the width and the length and then dividing by the number of foils in each respective dimension. For example, a layout of 3 wide by 4 deep was placed on the testbed described in
Figure 4.
All foils were activated in the pile overnight to ensure they reached saturation. When being placed in the pile and removed, proper safety precautions were taken. The handlers wore a dosimeter to track their exposure to radiation, as well as gloves to prevent contamination. When removing the foils from the pile, the long trays were taken out and moved to a separate room with the germanium detector. They were set on a desk on the opposite side of the room from the handler and the detector, still in the tray. When removing the foils from the testbed, tweezers were used to pick up and transport the foils to the detector. Only one foil was moved at a time.
4.3. Diffusion Theory
The diffusion theory of neutrons is an important concept in understanding how spatial neutron flux is distributed within the subcritical pile. Neutron diffusion theory treats all neutrons as belonging to two energy groups. These energy groups are thermal neutrons and fast neutrons, with the cutoff at 0.55 eV. The pile medium is assumed to be homogenous, and the scattering is assumed to be isotropic. The key is treating the neutron population as a group of particles that follow Fick’s Law and diffuse according to the concentration gradient. The result is a smooth and continuous spatial neutron flux. In the case of the subcritical pile, this flux exponentially decays away towards the edges of the pile. The general diffusion equation for two energy groups is shown in (4) and (5). These can be solved for various geometries, but we are concerned with cartesian coordinates which provide a cosine solution.
In this case, is the neutron flux for group 1, or the fast flux. is the thermal flux. and are the macroscopic cross-section for absorption for the respective group. is the macroscopic cross-section for down-scattering. is the macroscopic cross-section for fission multiplied by the neutron production factor (~2.5 for U-235). and are the diffusion coefficients equating the process to Fick’s law.
4.4. Two Group Neutron Profile
The measurement and subsequent calculation of two energy groups of neutrons requires a two-foil approach. This is typically conducted through a cadmium-gold combination, due to the neutron absorption cross-sections of the metals. In the thermal neutron energies (considered less than 1 eV for Cd), the neutron cross section is at least two orders of magnitude larger than gold. A 1 mm thick 1 cm diameter cadmium cover over gold will attenuate 99% of the thermal neutrons. Thus, any gold activation is the result of epithermal neutrons.
Figure 5 displays the setup of the gold foils in the cadmium cover in addition to the neutron cross-section for absorption of the two metals.
The calculation process requires the use of both cadmium-covered and bare foils. The measured activity of the bare foils (A
b) and covered foils (A
c) normalized for mass are used to develop the cadmium ratio (R), shown in equation (6). The gamma-decay constant (λ), activation time (t
a), cooling time (t
w), averaged neutron cross-section for absorption for thermal neutrons (σ
th), the self-shielding for thermal neutrons (Gth) are all required to calculate the thermal flux from activity in equation (7). The value of Gth is 0.8 for gold. [
24] F
cd is a convenience variable that is calculated in equation (8).
Due to the non 1/sqrt(E) relationship of the high-end overlap of the cross-sections, the fast flux is not a direct subtraction of the thermal flux from the total flux. As a result, equation (9) must be used to consider the effects of the multiple decades of energy in which the cross-section data spans. The lower energy limit, again, is set by the cadmium. However, the upper limit is arbitrarily set due to the fission-neutron energy of U-235 in the pile. There are neutrons that are born or up-scatter above 2.5 MeV, but the concentration is numerically insignificant to the energies in the range selected.
4.5. High-Purity Germanium Detectors
These detectors are a type of solid-state instrument used to measure ionizing radiation. They are a semiconductor-based detector, made from germanium crystals. Incoming radiation interacts with the crystals, leading them to form electron-hole pairs. These pairs are proportional to the energy from the incident radiation. The pairs are collected at electrodes within the detector, which converts the measurement into an electrical signal. The other electrical components of the detector setup, including the preamplifier and amplifier, turn this signal into a usable and measurable pulse. From these pulses, the amount of incident radiation, as well as the source of radiation can be determined.
High-purity germanium detectors are frequently used for radiation measurements due to their high resolution and increased accuracy. Resolution is calculated from the full width at the half maximum of an energy peak to the full energy of the peak. Detectors with low resolutions have a wide energy peak, and risk not separating peaks next to each other or background radiation. Detectors with a high resolution, such as the germanium detector, have energy peaks that almost resemble a straight line. They can easily and effectively separate energy peaks and background radiation, increasing the accuracy of the measurement values being recorded.
4.6. OpenMC Modeling
The entire subcritical pile was modeled using the Python language-based OpenMC software. Similar to other Monte Carlo particle transport codes, the geometry and materials are defined. Regions where radioactive particles are counted or discarded are then defined. The source strength, or number of particles, is defined by the user. A series of pseudo-random variables are generated to determine the particle interaction.
The pile geometry was measured and replicated in the software. Material assignments were conducted by referencing technical manuals from the pile construction. The source strength was defined by the known fission rate of the Am-Be and Pu-Be sources placed within graphite channels of the pile. [
21] The geometry of the whole model in OpenMC is defined using constructive solid geometry (CSG), also sometimes referred to as combinational geometry. It is important to note for this particular model that any void space within the pile was assigned to air at standard temperature and pressure.
Figure 6.
Front view of OpenMC subcritical pile model.
Figure 6.
Front view of OpenMC subcritical pile model.
The high-fidelity model of the subcritical pile is validated by comparison with experimental measurements. In the model, the vacant area where the testbed is located is shown in the middle. Two Pu-Be sources and one Am-Be source are located at the bottom of the testbed on the y-axis according to the model. The other two Pu-Be sources are located above the test bed. The Monte Carlo simulation was performed using 3.0*10^6 particles in fixed source mode while 300 active and 20 inactive batches were used. The fixed source simulation considers the subcritical state with the irradiation by an external neutron source. The mesh size of the flux tallies for the testbed was 2.25 cm and a total of 80 nodes were adopted. The ENDF/BVIII. 0 based continuous-energy nuclear data libraries are used for OpenMC code. [
22]
5. Results
5.1. Detector Energy Calibration
The use of the HPGe is standard among radiation detection experiments for its high energy resolution. Compared to other scintillating detectors like sodium-iodide (NaI), the energy resolution of the HPGe is often two orders of magnitude larger. The HPGe detector has around 8,000 channels compared to the 2,048 sodium-iodide. The advantage of this allows gamma energies within a few keV of one another to be resolved. However, the channels require an energy calibration to associate the energy of an incoming gamma to a particular channel. Data used for measurement is found in
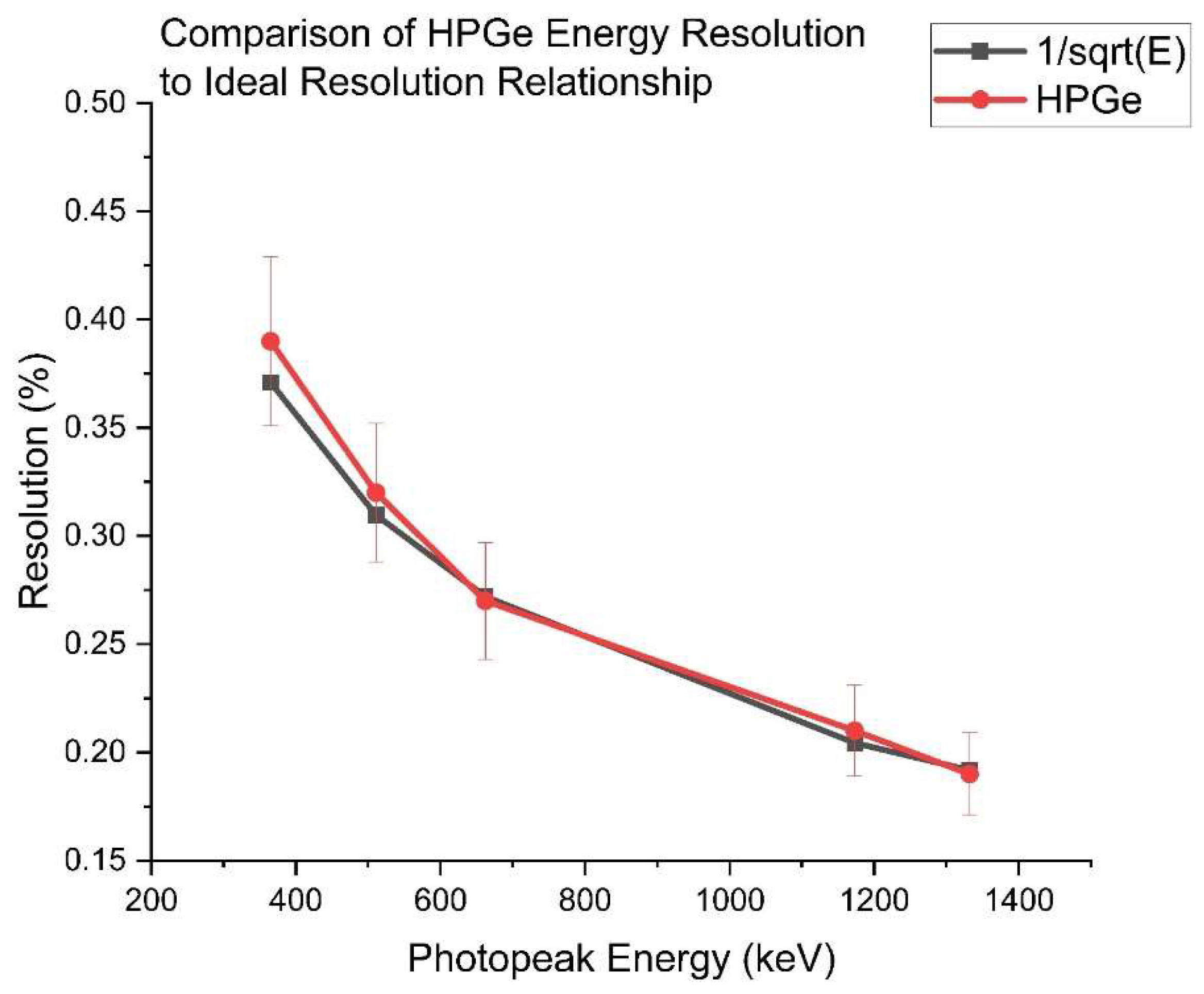
Table 1. Equation (10) displays the method for calculating energy resolution. Where FWHM is the full-width at half maximum. The ideal energy resolution as a function of energy follows the proportional relationship (11).
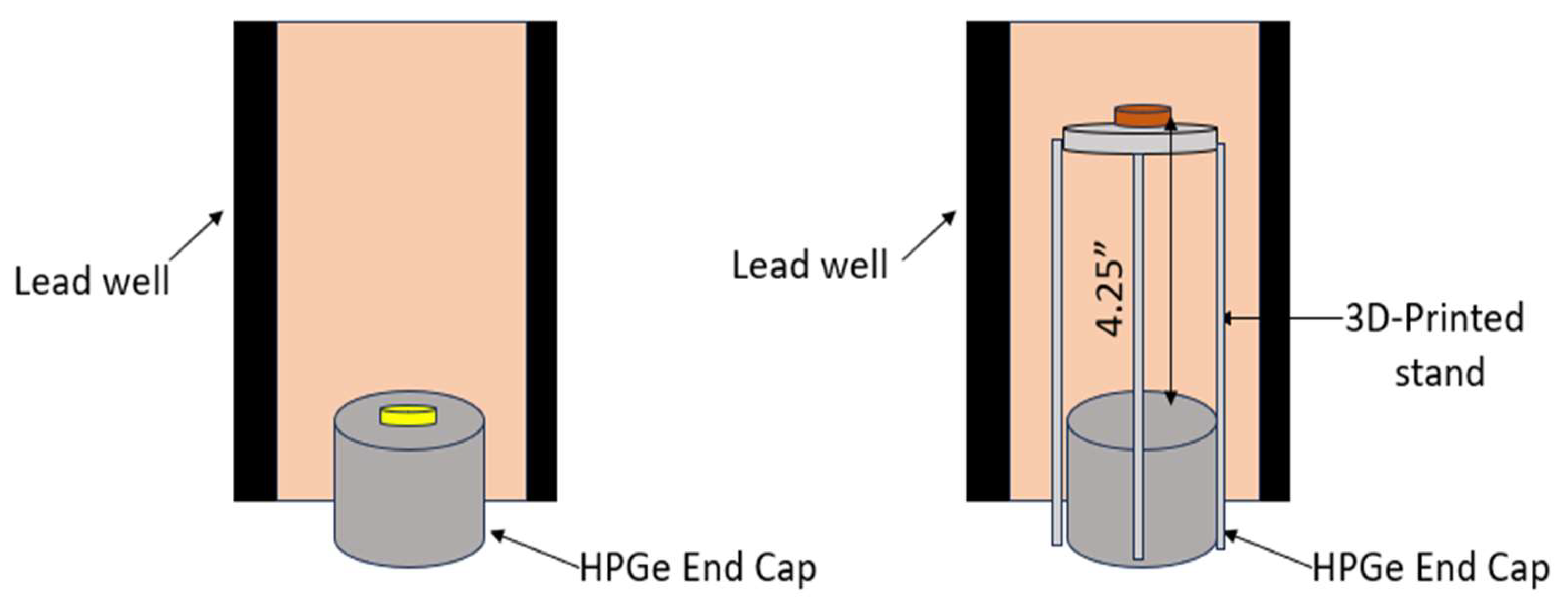
An energy calibration is conducted through the use of known gamma-emitting test sources. The HPGe in the following experiments made use of Na-22, Ba-133, Co-60, and Cs-137 to establish the near-linear channel-to-energy relationship. An ABS 3D printed stand (10.8 cm above the end cap) was built for general use of the HPGe to minimize the potential for end cap contamination.
Figure 7 displays the stand and measurement setup. The Maestro software was used to analyze HPGe radiation counts. The software has a built-in function that allows the assignment of channels to a particular energy.
Table 1 presents the measured resolution and
Figure 8 displays the resolution graphed against photopeak energy, where the measured values are in agreement with the expected values calculated through relationship (11).
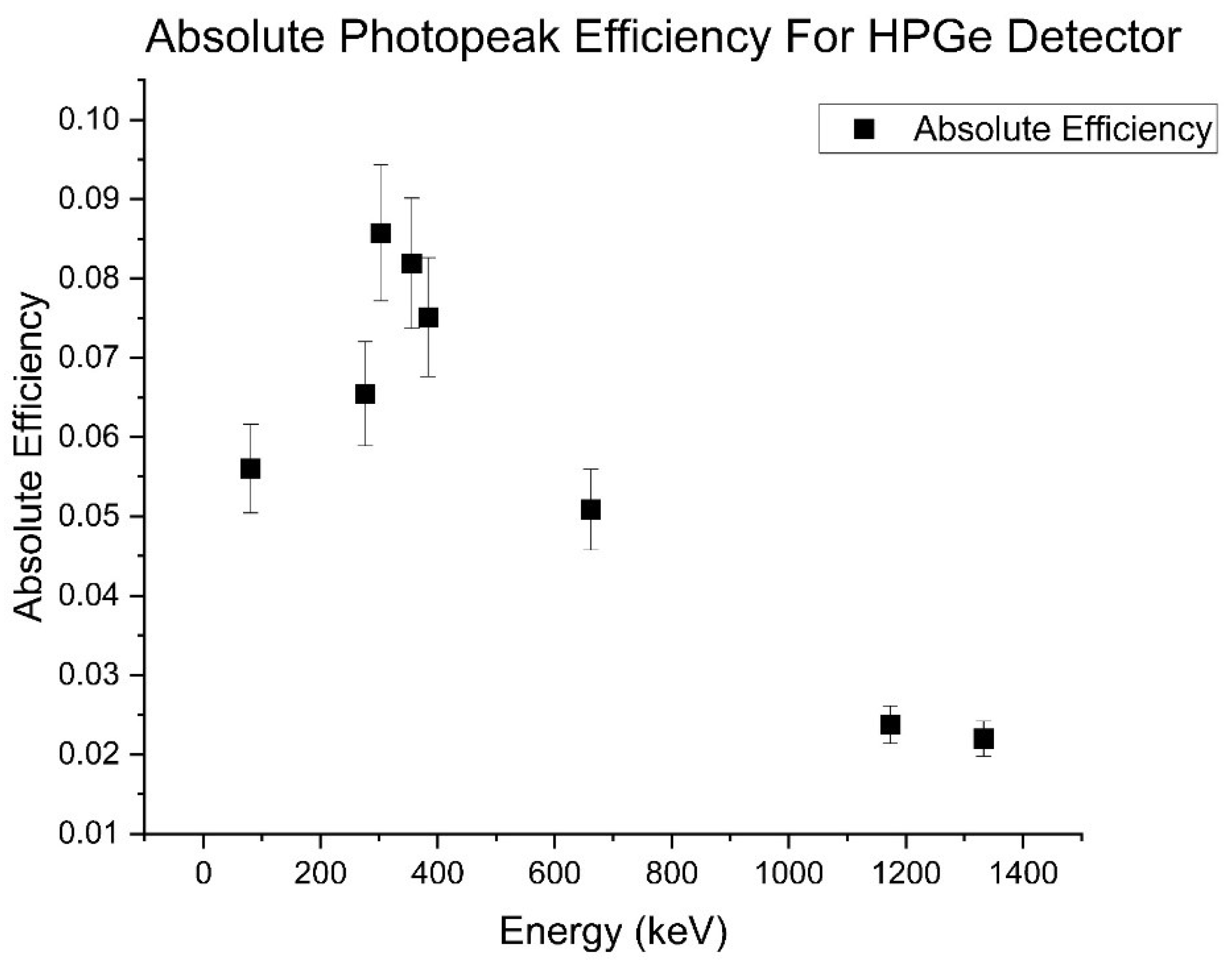
5.2. Absolute Photopeak Efficiency
As is the case with all instruments, the HPGe detectors are not capable of detecting all of the radiation emitted from a source. Geometry, distance, energy, and imperfections in electronics make for a less-than-ideal counting space. The counting error is minimized by investigating the detector’s absolute photopeak efficiency as a function of gamma energy. Again, test sources are used for this calculation. However, the activity of the source must be brought to the current date. In these experiments, the activity of the sources was verified on 01 July 2003. Using the exponential decay equation (12), and the half-life of the isotope of interest, the activity in decays/second could be determined for the date of the measurement.
The ratio of the activity measured by the detector and the current date activity at the particular photopeak is the absolute photopeak efficiceny. These values must be calculated at the location where subsequent measurements are intended to be taken. Distance from the source to the detector face has a strong dependence on absolute efficiency. If there is a deviation from this practice, it is important to consider the distance of the source relative to the detector face to determine if the source should be treated as a point source or a planar source. A general rule includes that any source greater than 10 cm is considered a point source.
Figure 9 provides the calculated absolute photopeak efficiency for the HPGe detector at the distance of the 3D printed stand.
Appendix A contains the data related to the measurements at various distances from the end cap.
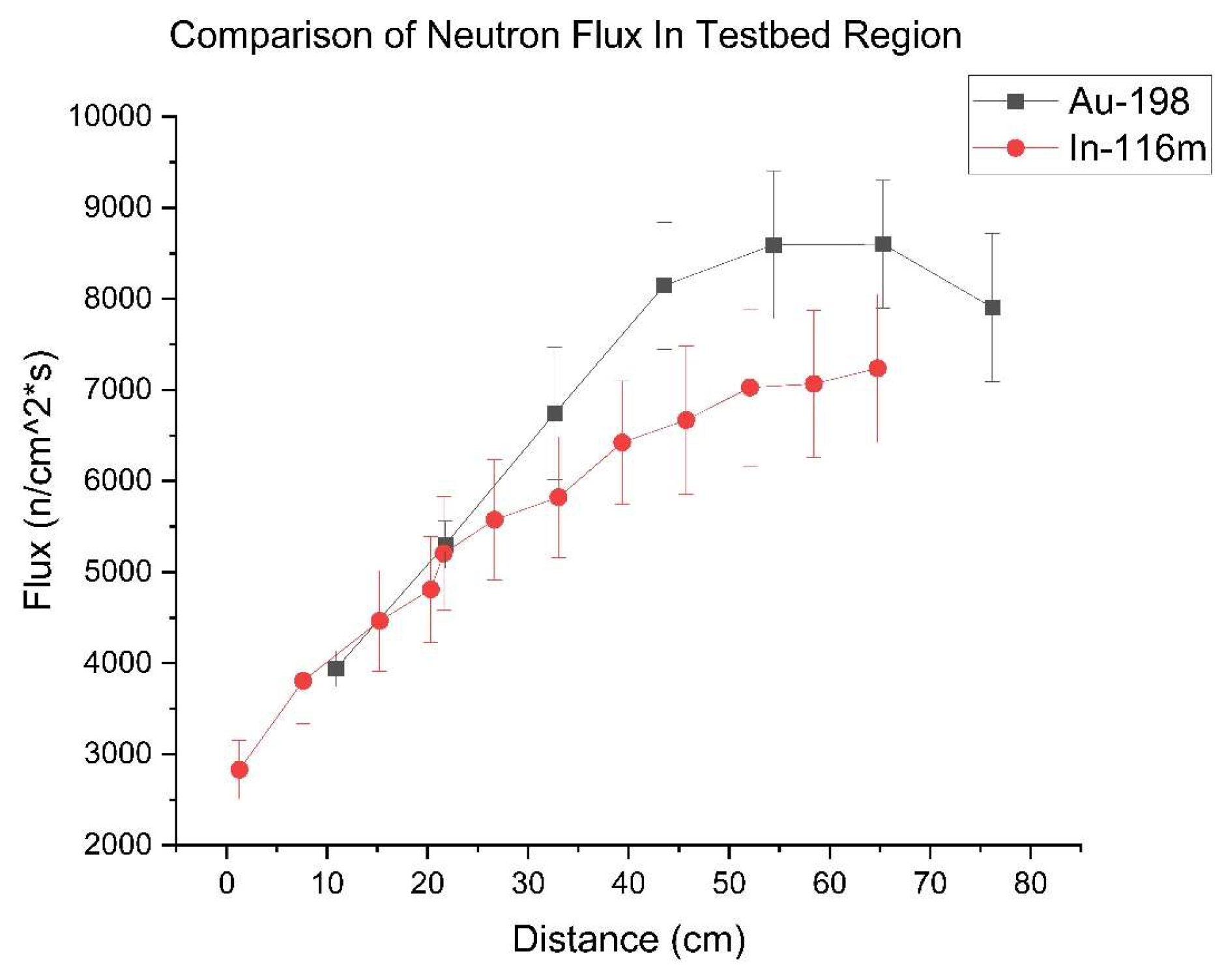
5.4. Testbed Region Neutron Flux Measured by Indium and Gold
The neutron flux within the volume of the testbed was measured using gold foils in a 4-wide by 7-deep configuration. The HPGe photopeak efficiency of gold was determined to be 0.0722 at the 411 keV photopeak. Using this value, the neutron flux as a function of location was determined for the 28 foils. To determine the average value of the flux, the mean of the 4 foils at each depth position was considered. The averaged flux along the depth dimension of the testbed is shown in
Figure 10. The dimensions of the profile are in the Y-Z plane relative to the OpenMC model. However, the origin of the testbed is set at the front face of the pile.
A similar analysis was conducted to verify the results of the gold foil experiments by using indium foils as the activation target. When using indium, multiple photopeaks can be used for the calculation. Similar to gold, each of the absolute photopeak efficiencies and branching ratios must be found.
Table 2 displays the values for the activated indium photopeaks and
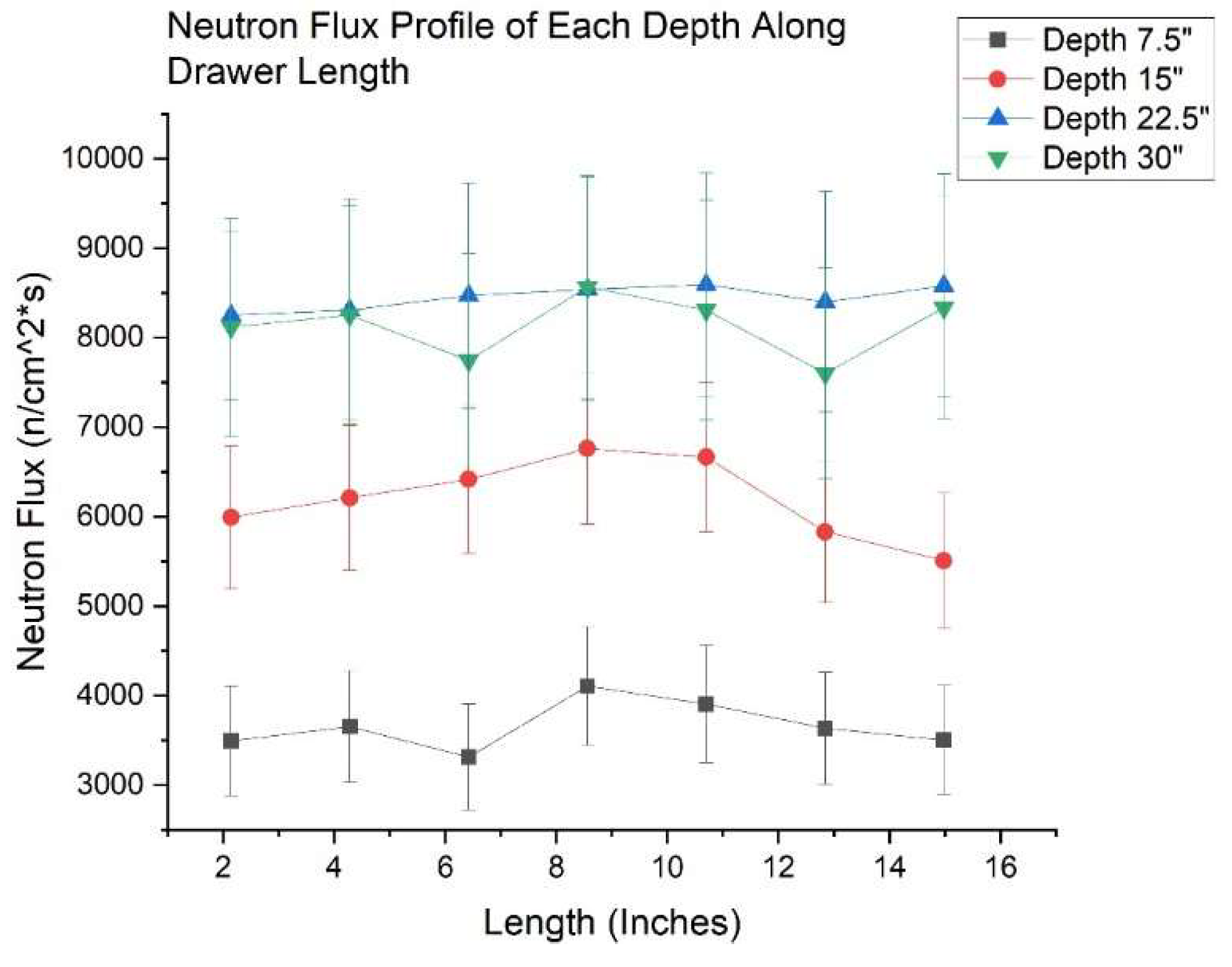
Figure 10 also displays the calculated neutron flux for the approximately same testbed region as displayed above for both the gold-197 and indium-115 foils. It is important to note that there were 4 by 12 foils in the indium trial. The centerline average is considered because the length dimension for each depth position has a relatively flat neutron flux as indicated by
Figure 11 with the gold foils.
5.5. Two Energy Neutron Testbed Profile
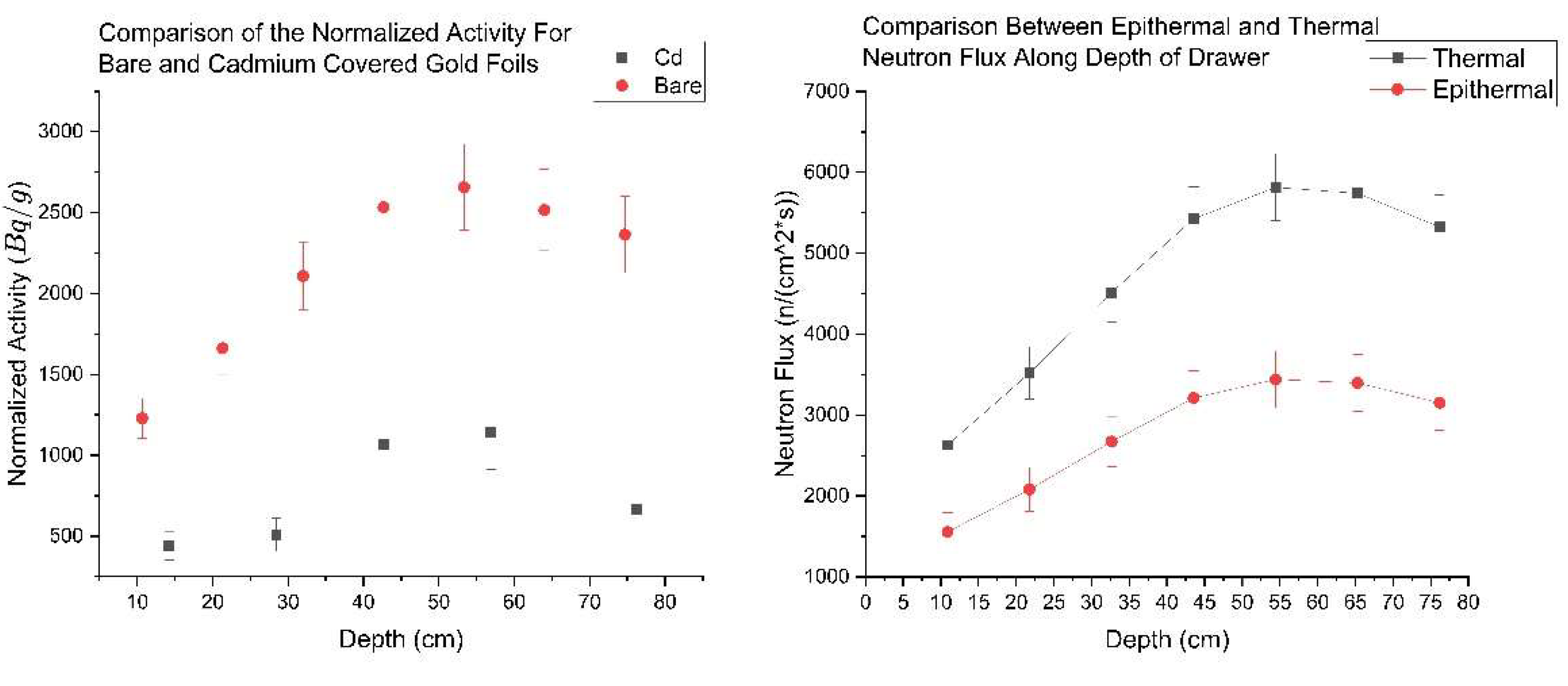
Following the measurement of the bare and cadmium-covered foils from the pile, a mass-normalized activity plot was produced to help determine the R
cd value as a function of depth. The results of the activity as a function of testbed depth are shown in
Figure 12. The cadmium ratio on average is 2.7 across the testbed. This value was assumed to be R
cd for further calculations of epithermal/fast and thermal neutrons. Making use of the equations presented in section 4.4 along with the activity, and estimated R
Cd, the thermal and epithermal/fast neutrons can be calculated as a function of the depth of the test bed. The expected cosine shape per Diffusion theory is displayed, where there are nearly 3 times more thermal neutrons than epithermal/fast. The results of the calculated two-energy group neutron flux are also presented in
Figure 12.
5.6. Complete Pile Volume Neutron Flux via Indium Foils
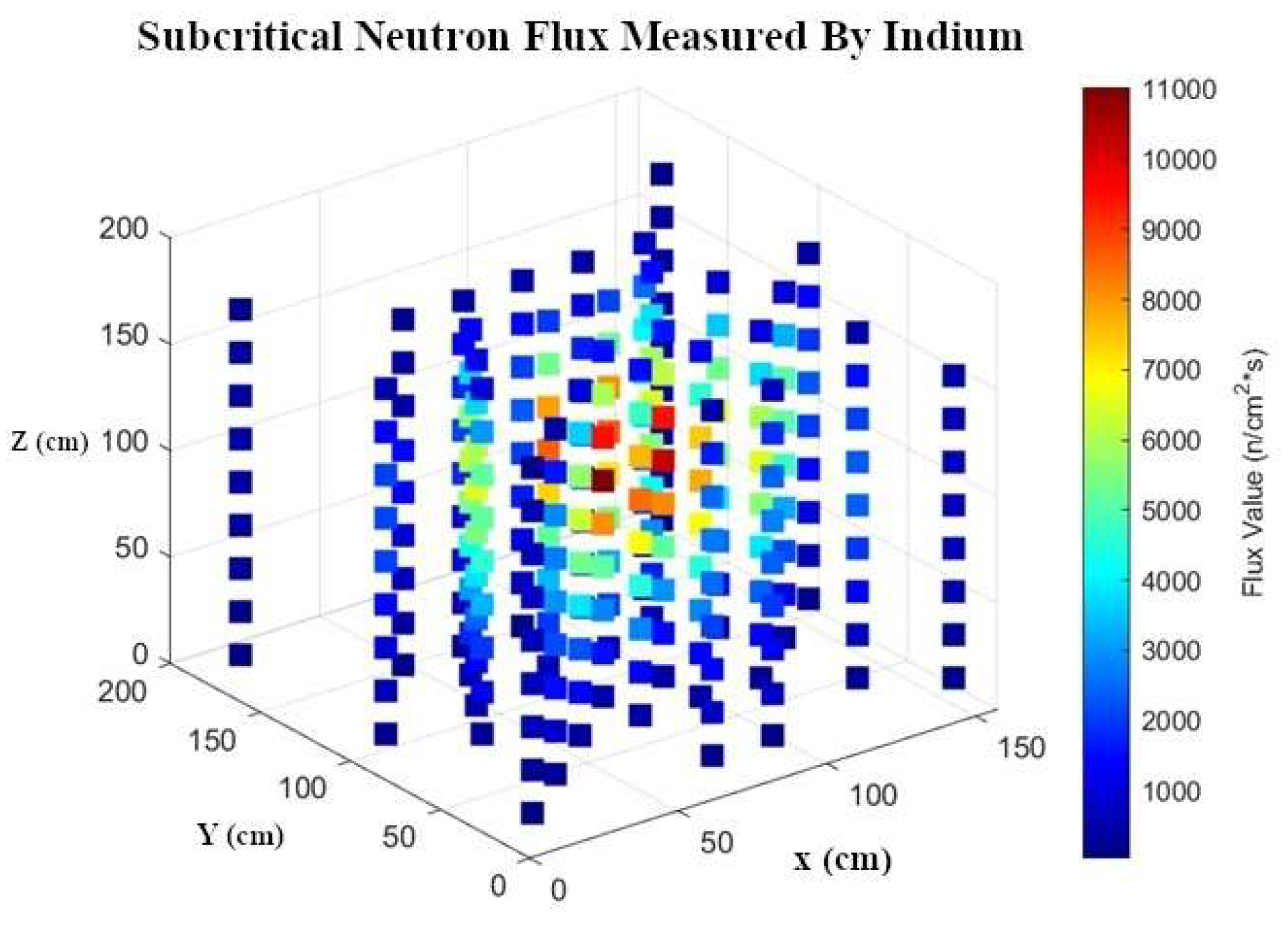
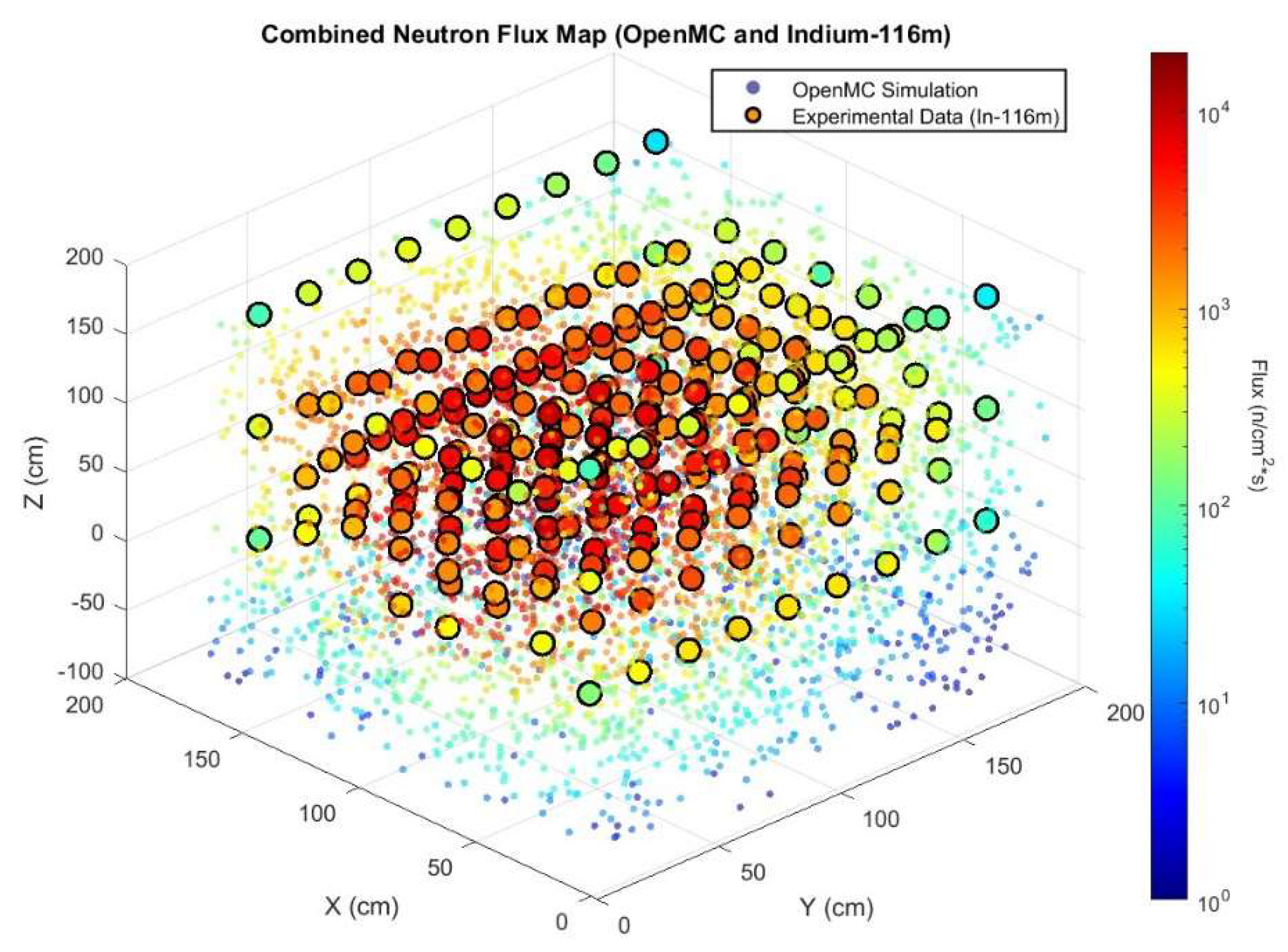
The neutron flux across the full volume of the subcritical pile was measured using Indium foils. 271 foils were placed in various locations throughout the pile in place of graphite rods. The HPGE photopeak efficiency of Indium was measured at 2.24 x 10^-2 at the 1293 keV peak. Using this value along with the other necessary parameters from equation (7), the radiation counts measured from the HPGE detector were converted into flux values for this photopeak. The total flux measured from the 1293 keV photopeak of In-116m throughout the volume of the pile is displayed in
Figure 13 below, where the x, y, and z axis represent the faces of the pile, and the colored blocks represent the flux measurement at that location in the pile. The yellow blocks represent the locations with the highest flux of 1.1E4 n/cm^2*s while the blue represents the lowest flux of 3.7E1 n/cm^2*s.
5.7. OpenMC Modeled Pile
The use of OpenMC allows for a validation of the measurements found using all three methods. In addition to the locations measured physically by metal foils, OpenMC can apply a finer mesh allowing for thousands of flux calculations within the pile. This data can be used for a better visual aid and more robust training of machine learning algorithms simply due to the larger volume of data.
Keff was found to be 0.61648 +/- 0.00084. This value provides a model integrity check, as theoretically, the K-eff of a subcritical pile should be below 1 by the very nature of subcritical multiplication.
A detailed description of the OpenMC modeled characteristics of the subcritical Pile are provided below in the
Table 3 and
Table 4. The coordinates shown are of the original OpenMC coordinate system. It is important to note, that any comparison of the OpenMC data with experimental data is translated such that the origin is placed at the bottom right side of the pile relative to the working face.
Neutron and gamma energy spectra prove useful in characterizing the radiation environment of the Pile. As a result, neutron and gamma energy spectra were generated by OpenMC and plotted below. The neutron energy spectra of the entire pile and within the testbed region are displayed in
Figure 14.
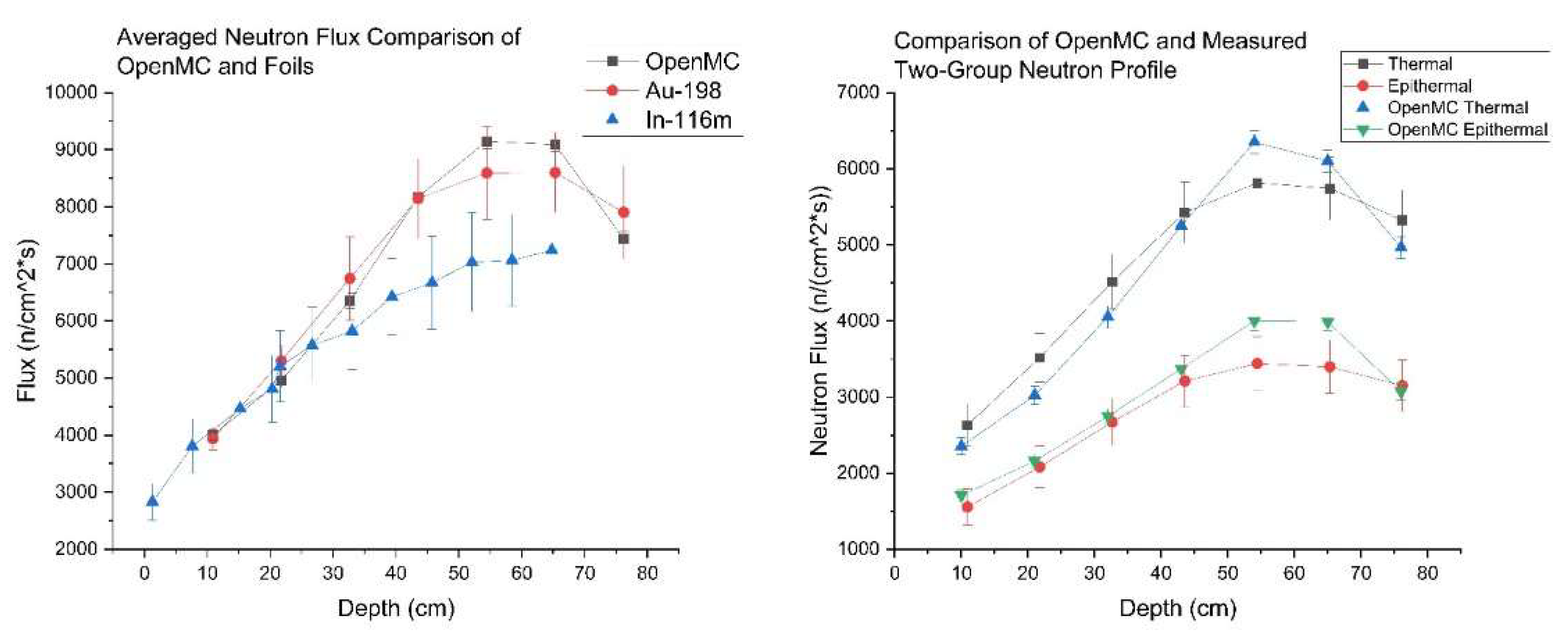
The values computed by both foil experiments and Monte Carlo methods are found to be congruent when comparing the total flux within the testbed as a function of depth. The comparison is displayed in
Figure 15. The flux values generated by OpenMC model show good alignment with the experimentally measured flux by gold foils having an error from 0.5% to 6.5%. The results validate the accuracy of the modeling and simulation. The indium foils do present a slightly lower value for total flux than the other two values, but there is a slight overlap in the error bars. This suggests that the true value of neutron flux most likely exists between the two. Of course, the neutron flux measured by the indium was conducted using three energy peaks which were weighted averaged for each location, then each location was mean averaged again to produce the effective centerline average flux. This is accounted for in the error but certainly may lead to data loss using the mean average twice. Symmetry is assumed across the length of the testbed, but it is important to note there were some outlier data points. The next comparison that can be made among the data sets is the two-group neutron profile within the testbed. Again, there is an agreement between the OpenMC model and the cadmium-covered foil experiment also shown in
Figure 15. The relative amount of thermal to epithermal neutrons is also consistent with diffusion theory.[
19] The amount of thermal neutrons is a critical aspect of the experimental process, as these are what produce a majority of activation reactions. They are also required for experiments such as neutron imaging, due to the high potential for attenuation in varying density materials.
Finally, an entire pile comparison can be conducted to validate the foil measurements further with the Monte Carlo results.
Figure 16 displays the 3D neutron flux map of the pile generated from the OpenMC model overlaid with the full pile of indium foils displayed in
Figure 16. The face to the left is where the testbed was placed within the pile. This model suggests that the largest neutron flux is approximately 2.4*10^4 n/cm^2*s after the normalization and removal of the volumes immediately surrounding the sources. This maximum value is found slightly above and below the testbed. This may be explained by the finer mesh applied to the OpenMC model where regions immediately outside of the source location and within the moderator can be tracked. The foil measurements require a void to be placed, therefore the closest they could be placed to the source was outside one block of moderating material.
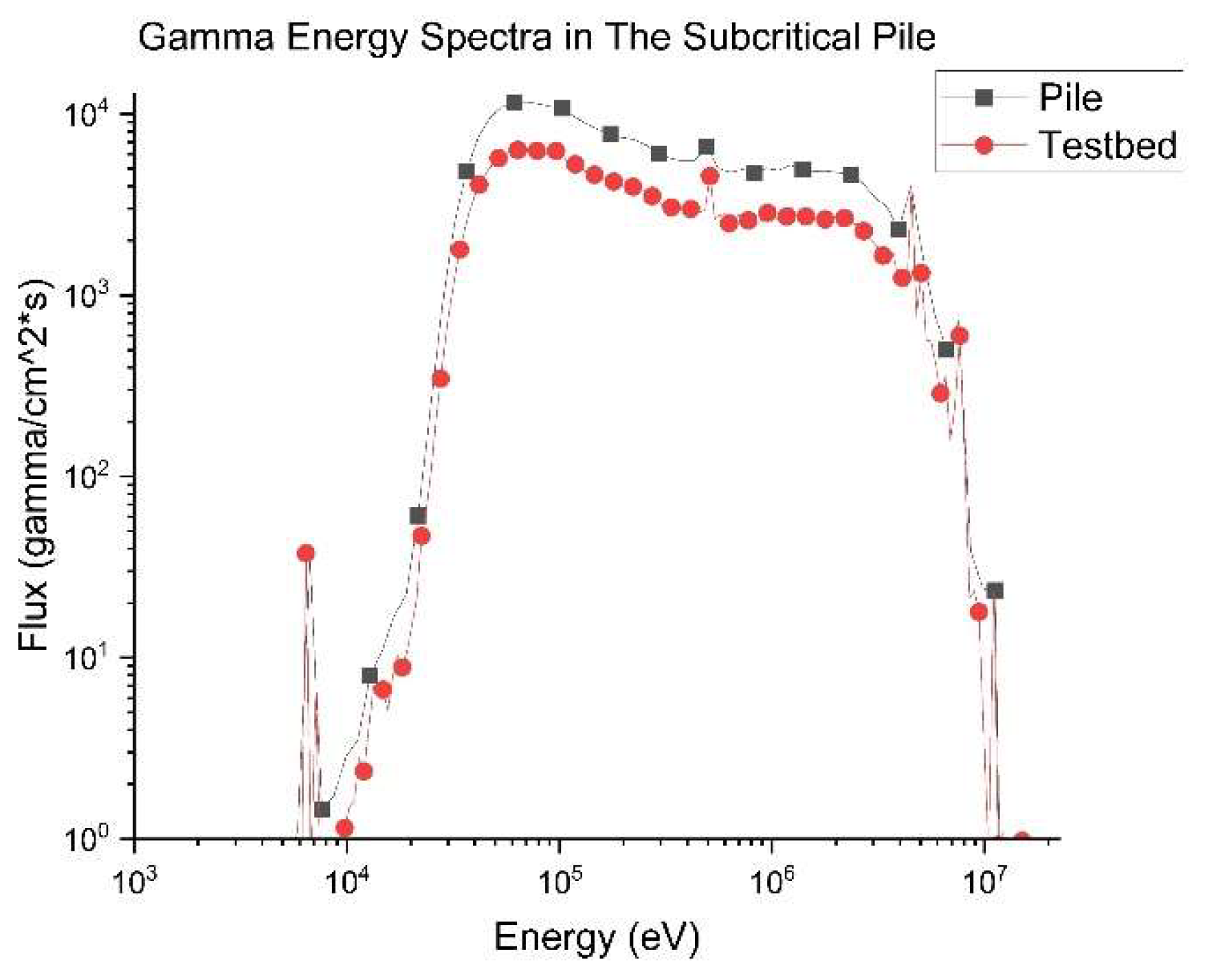
Although physical measurements were not taken related to the gamma flux, the ability of OpenMC to produce the gamma map highlights the software’s utility in similar studies. Often, the gamma measurements of a radiation environment are of concern. To illustrate this feature, an OpenMC gamma map is provided in
Figure 17 with spatial points corresponding to the locations of the indium foils.
Figure 18 displays the gamma energy spectra of the pile and the testbed region.
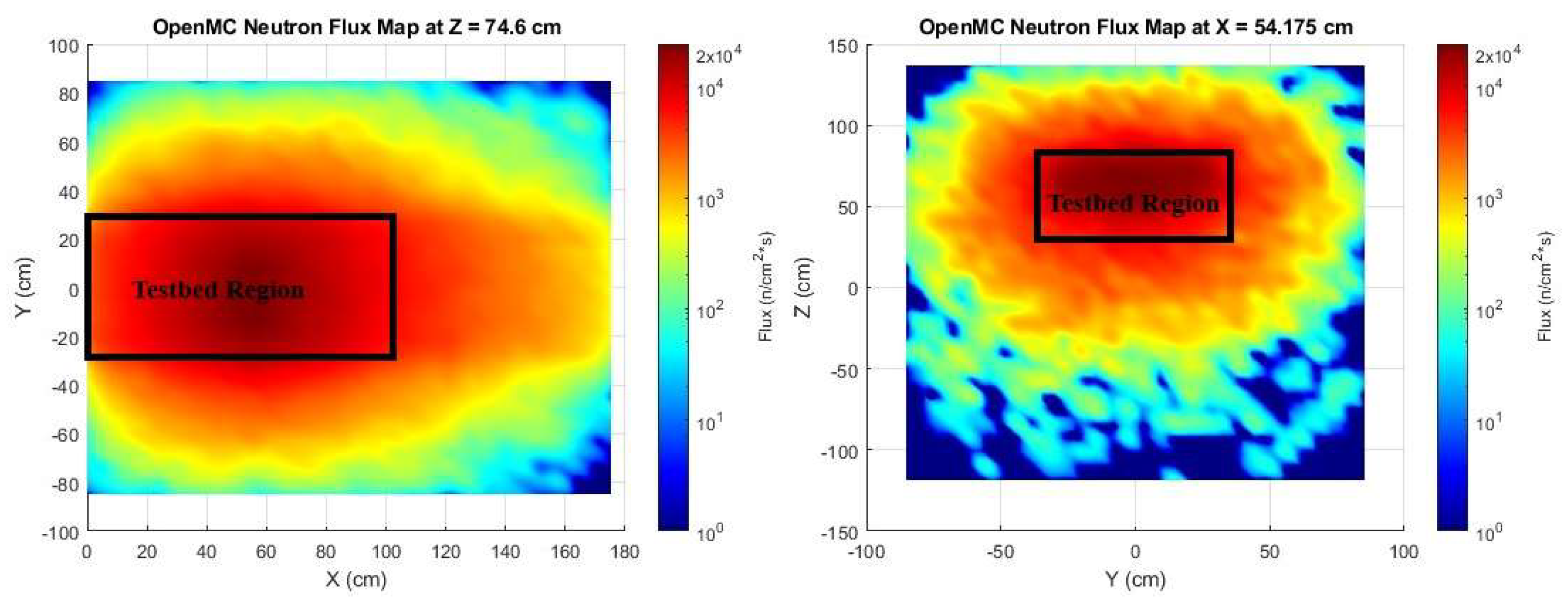
Considering the 2D region where the testbed exists within the pile, there is evidence to support a similar neutron flux profile.
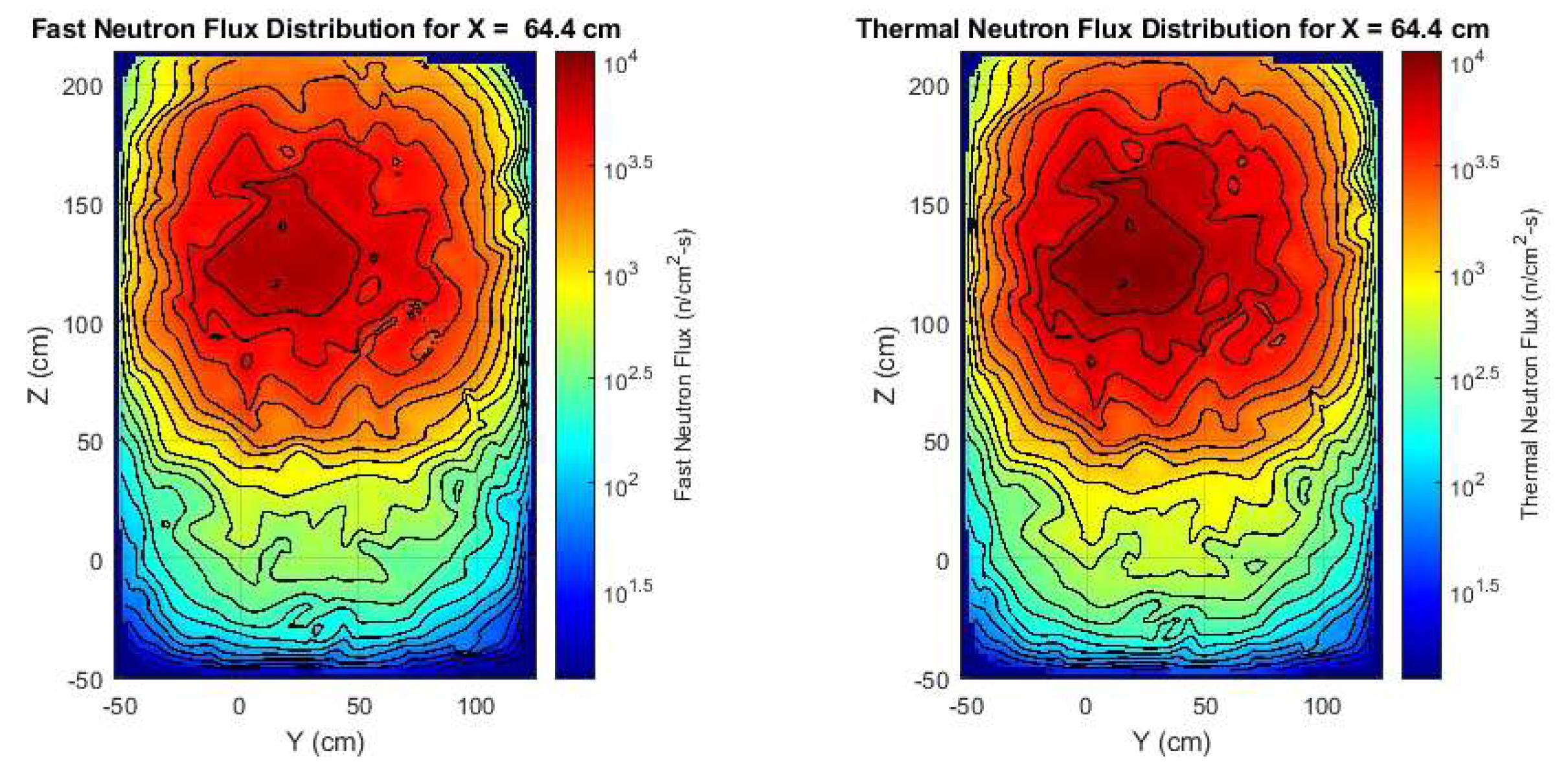
Figure 19 shows the OpenMC generated data in the pile highlighting the position where the testbed is placed. These results suggest that the optimal placement of a test material is at a depth of 60 cm from the front face of the pile where will receive an average flux of 8.5x10^3 n/cm^2*s. The OpenMC model and the experimental values show very good alignment here. To further display the results of the OpenMC model, 2D cross-sections of the thermal and fast at their largest values relative to the X-axis are provided in
Figure 20.
6. Discussion
6.1. Subcritical Pile Error Analysis
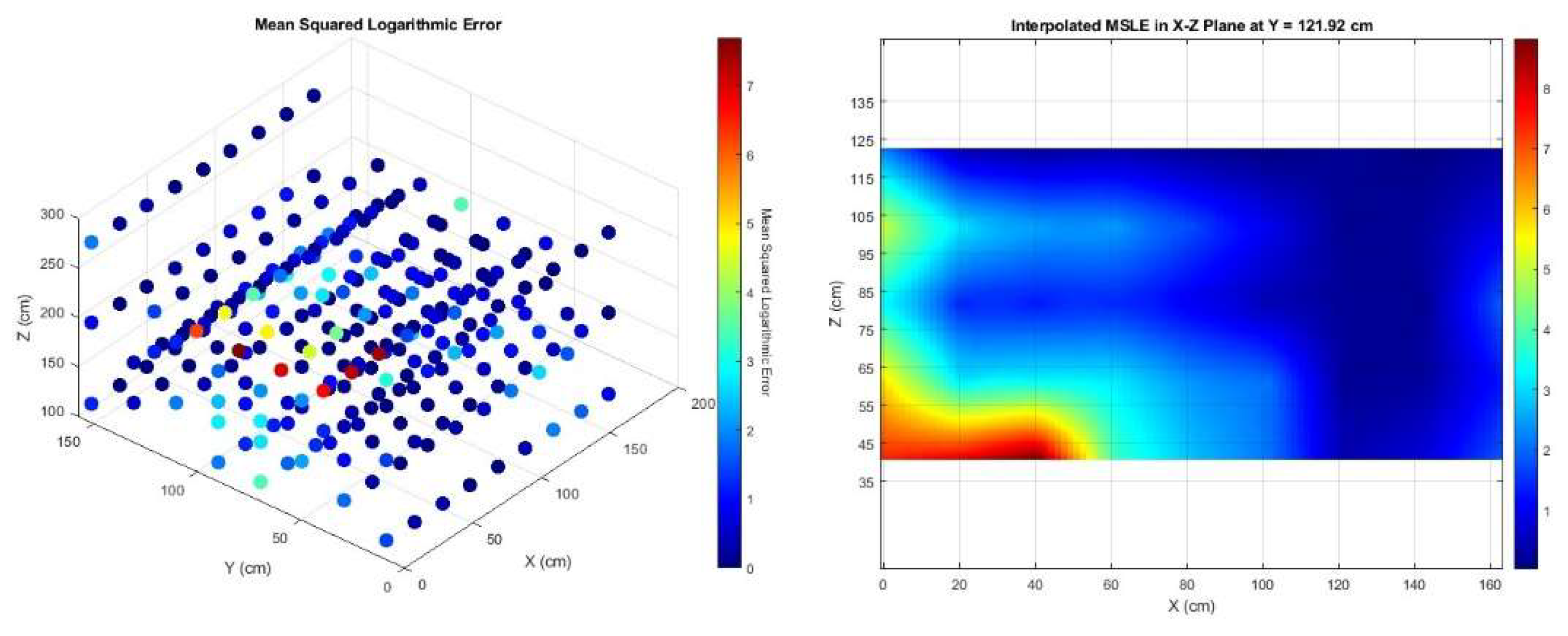
An error analysis was conducted between the indium foil measurements and the OpenMC-generated neutron flux for the entire volume of the pile. The stochastic nature of the MC software, finer mesh size, and ability to generate spatial points in the direct vicinity of the source must be taken into account when compared to the experimental results. In part, this is compensated for by taking the average of the OpenMC flux within a 10-cubic centimeter volume where the center point is the coordinates of the indium foil measurement. The spatially averaged MC flux can then be compared to the foil measurements using standard error analysis methods.
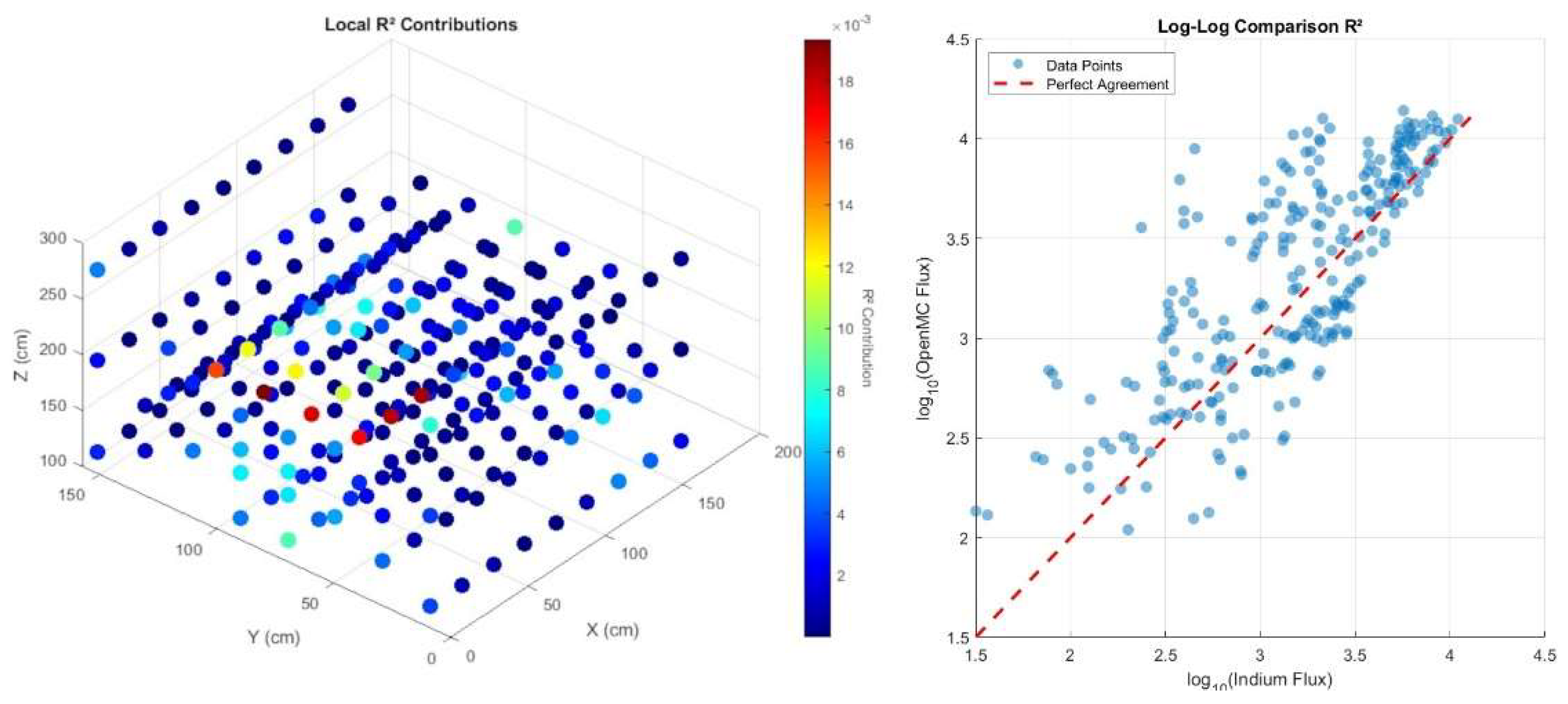
Root Mean Squared Log Error (RMSLE) and log R-squared methods were considered in the analysis to provide a fair representation of the error between data sets. The data of each set spans multiple decades of neutron flux, thus the use of the logarithmic operation was deemed useful. However, it is important to note that taking the log of the data skews the representation of outlying points. The advantage of RMSLE over R-squared is that RMSLE is more sensitive to relative errors, particularly when dealing with data that has a large range of values or exponential growth, while R² provides a better representation of variance. The formula used for RMSLE is provided in equation (13) and R-squared in equation (14). Where
n is the number of points and
Y is the spatial neutron flux. The results of the R-squared methods for error analysis are provided in
Figure 21 and
Figure 22. RMSLE methods are displayed in
Figure 23.
(13)
R² = (14)
The results presented in
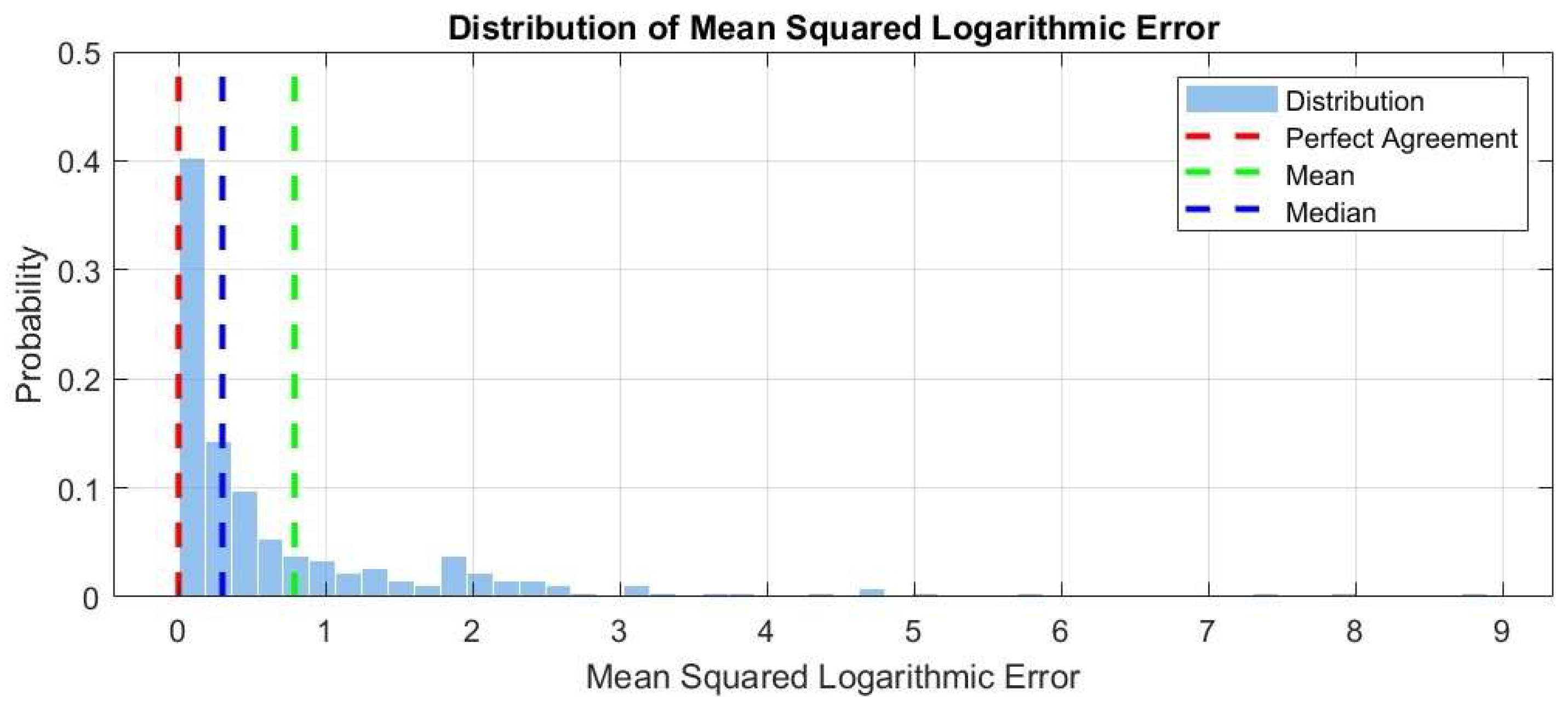
Figure 22 display an MSLE distribution where the mean is not representative of the full data set due to the outliers. The median is a better metric for displaying the average distribution of the MSLE results. Nearly 60% of the data points fall under the mean value, and for this work are considered fair agreement. Again, this can be misleading, so the R-squared values are also presented to argue the validity of the OpenMC data when compared to the measured gold and indium foils.
In general, for both methods, the majority of the OpenMC results agree with the measured data points. The exception appears to be directly near the neutron sources. It is proposed that this occurrence is the inability of foils to be placed in the direct vicinity of the sources due to physical limitations. Due to the nature of the transport-generated data, the simulated volume immediately surrounding the sources produces significantly higher neutron fluxes at those tally locations. The inverse square distance relationship of the source may cause a disparity in the simulated data when compared to the measured data at what would be considered a relatively short distance. A future experiment may consider increasing the foil spatial density when within a few migration lengths of the neutrons relative to the source. This may provide more accurate measured data which reflects the relationship between the source and distance when comparing the two data sets.
6.2. Experimental Discussion
Multiple different data sets have been developed and displayed showing the neutron flux of the subcritical pile and its contained testbed. Three tests were conducted to determine the average neutron flux on the testbed inside the subcritical pile. These included experimentally measuring the decay of activated Au-198 and In-116m, as well as simulating the experiment in OpenMC. A comparison between the two experimental data sets can be seen in
Figure 16. The general trend of the flux with the change in depth in the testbed shows a similar shape between the two experiments. While the flux values are not the same, they are within each other’s error allowance, allowing them to be considered similar. Therefore, the flux values measured from the experiments involving Au-198 and In-116m provide accurate data for the testbed in the pile. A comparison can also be made against the data from the OpenMC simulation. The results from the OpenMC model fall within the error allowance for the measurements from both experimental results and, therefore can also be considered similar. The three data sets including the averaged flux measurements of the testbed in the pile as a function of depth independently produced similar results, confirming their accuracy.
As part of the same experiment and simulation, the two-group neutron profile was measured and can be compared. The thermal and epithermal neutron flux is compared in
Figure 16. Similarly, the results between the experimental and simulated data are consistent, following the same general trend and having similar values.
The neutron flux throughout the pile was measured experimentally using In-116m foils and through another OpenMC simulation.
Figure 13 shows the flux throughout the pile as a heat map for the experimental data. This can be compared to
Figure 17 showing the neutron flux measurements from the simulation. As seen in both Figures, the flux has the highest value towards the center of the pile, however, is slightly skewed to the front, and has the lowest value on the outer edges. This is consistent with neutron activation theory since the neutron sources in the subcritical pile are located between the middle and the front of the pile, and approximately halfway between the shortest and tallest locations in the vertical direction. The data file used to generate these Figures can also be compared to show consistency between the specific flux values at the various locations measured.
7. Conclusions
Purdue University is home to one of three subcritical piles at universities in the United States. It features a testbed located in between neutron sources. The testbed was included in 2023, allowing enough volume for devices and objects to be placed in it and tested. The inclusion of the testbed separates the pile at Purdue University from those at other universities.
To use the subcritical pile and testbed for experiments, the neutron flux present at various locations must be determined. Multiple experiments were conducted in order to establish these values, including measuring the gamma decay of metallic foils after being activated in the neutron flux, and open-source Monte Carlo simulations.
Au-197 and In-115 foils were placed throughout the pile and on the testbed in the neutron flux overnight. Neutron activation is the process of turning stable elements into unstable isotopes. Once removed, the foils were placed in a high-purity germanium detector. The amount of energy given off as the foils decayed back to their original state was measured and recorded in the form of radiation counts. These counts, through calculations, were then converted into flux values. The OpenMC program uses the geometry of the pile and the testbed, along with the properties of the neutron sources to simulate the neutron flux at multiple locations.
The results from the experiments and the simulation were compared to validate the values for the neutron flux at various locations throughout the pile and testbed. The results were similar and showed the same general trends for the neutron flux across the testbed and throughout the pile, confirming the flux values and demonstrating their accuracy.
Future work related to this project may include methods which aim to experimentally measure the gamma flux within the subcritical pile and the testbed region. This can then be used to validate the OpenMC gamma energy spectra and flux maps. Given the correlation between the experimental and MC generated neutron data, it can reasonably be assumed that the gamma data generated has some validity when compared to the subcritical pile. The gamma production results presented should be viewed as, at the very least, a numerical approximation based on a partially characterized OpenMC model.
Author Contributions
Conceptualization, B.J., M.N., T.M., and S.C.; methodology, All; software, N.K.; validation, M.N., R.M., H.P., and N.K.; resources, B.J., T.M., S.C.; data curation, R.M.; writing—original draft preparation, M.N., R.M., H.P. and N.K.; Editing, S.C.; supervision, S.C. All authors have read and agreed to the published version of the manuscript.
Funding
This project did not receive external funding.
Data Availability Statement
Data is available upon request.
Acknowledgments
An additional thank you to the Purdue Military Research Institute for their support in higher education for the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Table A1.
Absolute Photopeak Efficiency at 7.62 cm.
Table A1.
Absolute Photopeak Efficiency at 7.62 cm.
| Energy (keV) |
Resolution (%) |
Error (%) |
356
511
662
1173
1332 |
0.89
0.27
0.33
0.37
0.28 |
0.02
0.03
6E-3
0.02
2E-4 |
Table A2.
Absolute Photopeak Efficiency at 2.54 cm.
Table A2.
Absolute Photopeak Efficiency at 2.54 cm.
| Energy (keV) |
Resolution (%) |
Error (%) |
356
511
662
1173
1332 |
2.50
0.70
0.70
0.81
0.59 |
0.03
0.06
9E-5
0.03
2E-5 |
References
- Manhattan Project: CP-1 Goes Critical, Met Lab, December 2, 1942 Available online: https://www.osti.gov/opennet/manhattan-project-history/Events/1942-1944_pu/cp-1_critical.htm (accessed on 16 December 2024).
- RRDB Available online: https://nucleus.iaea.org/rrdb/#/home (accessed on 16 December 2024).
- Beck, J.N.; Lamberty, C.M. THERMAL NEUTRON ACTIVATION ANALYSIS—AN IMPORTANT ANALYTICAL TOOL. Applied Spectroscopy Reviews 2002, 37, 19–55, doi:10.1081/ASR-120004372. [CrossRef]
- Kardjilov, N.; Manke, I.; Hilger, A.; Strobl, M.; Banhart, J. Neutron Imaging in Materials Science. Materials Today 2011, 14, 248–256, doi:10.1016/S1369-7021(11)70139-0. [CrossRef]
- Lababsa, D.; Mazrou, H.; Belgaid, M. Performance Evaluation and Validation of OpenMC Code for Criticality Analysis of an MTR-Type Research Reactor. Annals of Nuclear Energy 2024, 206, 110617, doi:10.1016/j.anucene.2024.110617. [CrossRef]
- Vasili, K.; Seda Yilmaz; Matthew M. Niichel; Jonah Lau; Shripad Revankar; Lefteri Tsoukalas; Stylianos; Chatzidakis Exploring Quantitative and Qualitative Machine Learning Methods for Predicting Neutron Flux Values from a Simulated Molten Salt Reactor. In Proceedings of the TRANSACTIONS; Las Vegas, 2024.
- Yu, J.; Wilson, J.; Forget, B.; Dave, A.J.; Sun, K.; Phillips, B. Experimental Validation of a High Fidelity Monte Carlo Neutron Transport Model of the MIT Graphite Exponential Pile. Progress in Nuclear Energy 2022, 152, 104368, doi:10.1016/j.pnucene.2022.104368. [CrossRef]
- Sara Hauptman Characterization of the MIT Graphite Exponential Pile. Bachelor’s thesis, Massachusetts Institute of Technology, 2019.
- Persson, C.-M.; Seltborg, P.; Åhlander, A.; Gudowski, W.; Stummer, T.; Kiyavitskaya, H.; Bournos, V.; Fokov, Y.; Serafimovich, I.; Chigrinov, S. Analysis of Reactivity Determination Methods in the Subcritical Experiment Yalina. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2005, 554, 374–383, doi:10.1016/j.nima.2005.07.058. [CrossRef]
- Xoubi, N. Calculation of the Power and Absolute Flux of a Source Driven Subcritical Assembly Using Monte Carlo MCNP Code. Annals of Nuclear Energy 2016, 97, 96–101, doi:10.1016/j.anucene.2016.07.009. [CrossRef]
- Avelino Santos; Ademir X. Da Silva; Wilson F. Rebello; Victor L. Lassance Cunha Modeling of the CTEx Subcritical Unit Using MCNPX Code.; 2011; pp. 1–6.
- Dranga, R.; Blomeley, L.; Carrington, R. AN MCNP PARAMETRIC STUDY OF GEORGE C. LAURENCE’S SUBCRITICAL PILE EXPERIMENT. AECL Nuclear Review 2014, 3, 91–99, doi:10.12943/ANR.2014.00037. [CrossRef]
- Vega-Carrillo, H.R. Subcritical Nuclear Assembly 2015.
- Maldonado, G.I.; Xoubi, N.; Zhao, Z. Enhancement of a Subcritical Experimental Facility via MCNP Simulations. Annals of Nuclear Energy 2008, 35, 263–268, doi:10.1016/j.anucene.2007.06.022. [CrossRef]
- Bren Phillips; Jarod Wilson; Jiankai Yu; Andrea M. Molina-Dejesus; Benoit Forget; Akshay J. Dave; Kaichao Sun Demonstrating Autonomous Control Framework Using Graphite Exponential Pile; 2022; pp. 2–39;.
- Patrick Joseph O’Neal Comparison of 233U Production by Thorium Irradiation in Heavy Water Reactor and Accelerator-Driven Subcritical Pile. Master of Science, Texas A&M, 2020.
- Radaideh, M.I.; Jarrah, I.; Malkawi, S.; Khateeb, A.; Al-Issa, I. Reactivity and Flux Characterization of the Jordan Subcritical Assembly. Progress in Nuclear Energy 2018, 108, 43–53, doi:10.1016/j.pnucene.2018.05.003. [CrossRef]
- Asuncion-Astronomo; Marquez, J.M.; Olivares, R.U.; Romallosa, K.M.D. Utilizing the Philippine Research Reactor-1 TRIGA Fuel in a Subcritical Assembly; International Atomic Energy Agency (IAEA), 2020;
- Niichel, M. Development Of An Electronics Testbed For Radiation Testing In Gamma And Neutron Environments, Purdue University: West Lafayette, IN, 2024.
- Lewis, E.E. Fundamentals of Nuclear Reactor Physics; Academic Press: Amsterdam ; Boston, 2008; ISBN 978-0-12-370631-7.
- E10 Committee ASTM International. Test Method for Determining Thermal Neutron Reaction Rates and Thermal Neutron Fluence Rates by Radioactivation Techniques; DOI: 10.1520/E0262-17. [CrossRef]
- Sirakov; Kopecky; Young Au-197 (N,Tot).
- MUGHABGHAB Cd-113 (N,Tot) 2010.
- Abolaban, F.A.; Alawi, M.A.; Taha, E.M.; Elmoujarkach, E.; Banoqitah, E.M.; Alhawsawi, A.M.; De Maio, P.; Lopopolo, G.; Tolomeo, A.; Dimiccoli, V.; et al. ESTIMATION OF THERMAL & EPITHERMAL NEUTRON FLUX AND GAMMA DOSE DISTRIBUTION IN A MEDICAL CYCLOTRON FACILITY FOR RADIATION PROTECTION PURPOSES USING GOLD FOILS AND GATE 9. Radiation Protection Dosimetry 2021, 193, 176–184, doi:10.1093/rpd/ncab034. [CrossRef]
- 0751 - H122 - Basic Health Physics - 25 - Neutron Sources, US NRC, September 29, 2011. Available online: https://www.nrc.gov/docs/ml1122/ML11229A704.pdf.
- D.A. Brown, M.B. Chadwick, R. Capote, A.C. Kahler, A. Trkov, M.W. Herman, A.A. Sonzogni, Y. D non, A.D. Carlson, M. Dunn, et al., ENDF/B-VIII.0: The 8th Major Release of the Nuclear Reaction Data Library with CIELO-project Cross Sections, New Standards and Thermal Scattering Data. Nuclear data sheets; 2018; 148, pp.: 3-142.
Figure 1.
Purdue subcritical pile CAD model from the perspective of the working space.
Figure 1.
Purdue subcritical pile CAD model from the perspective of the working space.
Figure 2.
3D SolidWorks rending of the electronics testbed drawer placed within the Purdue sub-critical drawer.[
19]
.
Figure 2.
3D SolidWorks rending of the electronics testbed drawer placed within the Purdue sub-critical drawer.[
19]
.
Figure 3.
(a) Modified Purdue subcritical pile. (b) In testing configuration with testbed drawer from the working face of the pile. Testbed dimensions are 45 cm x 20 cm x 162 cm for a total test volume of approximately 1.5E5 cm^3.
Figure 3.
(a) Modified Purdue subcritical pile. (b) In testing configuration with testbed drawer from the working face of the pile. Testbed dimensions are 45 cm x 20 cm x 162 cm for a total test volume of approximately 1.5E5 cm^3.
Figure 4.
Testbed foil placement for a 3x4 configuration.
Figure 4.
Testbed foil placement for a 3x4 configuration.
Figure 5.
Cadmium-covered gold foils under a thermal and epithermal neutron flux. [
22,
23].
Figure 5.
Cadmium-covered gold foils under a thermal and epithermal neutron flux. [
22,
23].
Figure 7.
Experimental setup of 3D printed stand over HPGe within a lead well to minimize contamination.
Figure 7.
Experimental setup of 3D printed stand over HPGe within a lead well to minimize contamination.
Figure 8.
Comparison of HPGE Energy resolution to ideal resolution.
Figure 8.
Comparison of HPGE Energy resolution to ideal resolution.
Figure 9.
Absolute Photopeak Efficiency for HPGE Detector used for experiments.
Figure 9.
Absolute Photopeak Efficiency for HPGE Detector used for experiments.
Figure 10.
Comparison of average neutron flux in testbed calculated by gold and indium foils. Error bars represent 1σ uncertainty.
Figure 10.
Comparison of average neutron flux in testbed calculated by gold and indium foils. Error bars represent 1σ uncertainty.
Figure 11.
Refined 7 by 4 gold foil neutron flux along the length of the drawer.
Figure 11.
Refined 7 by 4 gold foil neutron flux along the length of the drawer.
Figure 12.
(a) The mass normalized activity of the bare and cadmium-covered gold foils. (b) Two energy group average neutron profiles as a function of testbed depth.
Figure 12.
(a) The mass normalized activity of the bare and cadmium-covered gold foils. (b) Two energy group average neutron profiles as a function of testbed depth.
Figure 13.
Flux map of the entire pile as measured by indium foils.
Figure 13.
Flux map of the entire pile as measured by indium foils.
Figure 14.
Neutron energy spectra in the full pile and testbed region.
Figure 14.
Neutron energy spectra in the full pile and testbed region.
Figure 15.
(a) Comparison of total average neutron flux along depth of testbed for each method. (b) Comparison of two-group neutron flux for experimental and OpenMC methods.
Figure 15.
(a) Comparison of total average neutron flux along depth of testbed for each method. (b) Comparison of two-group neutron flux for experimental and OpenMC methods.
Figure 16.
3D OpenMC neutron flux overlaid with 3D Indium foil neutron flux.
Figure 16.
3D OpenMC neutron flux overlaid with 3D Indium foil neutron flux.
Figure 17.
(a) 2D OpenMC maximum gamma flux of XY plane. (b) 2D OpenMC maximum gamma flux of YZ plane.
Figure 17.
(a) 2D OpenMC maximum gamma flux of XY plane. (b) 2D OpenMC maximum gamma flux of YZ plane.
Figure 18.
Gamma energy spectra for the entire subcritical pile.
Figure 18.
Gamma energy spectra for the entire subcritical pile.
Figure 19.
(a) OpenMC 2D neutron flux map of testbed XY plane. (b) OpenMC 2D neutron flux map of testbed YZ plane.
Figure 19.
(a) OpenMC 2D neutron flux map of testbed XY plane. (b) OpenMC 2D neutron flux map of testbed YZ plane.
Figure 20.
(a) OpenMC fast neutron map at X=64.4 cm. (b) OpenMC thermal neutron map at X=64.4 cm.
Figure 20.
(a) OpenMC fast neutron map at X=64.4 cm. (b) OpenMC thermal neutron map at X=64.4 cm.
Figure 21.
(a) The mean squared logarithmic error between OpenMC and Indium foils. (b) 2D mean squared logarithmic error at the maximum Z value.
Figure 21.
(a) The mean squared logarithmic error between OpenMC and Indium foils. (b) 2D mean squared logarithmic error at the maximum Z value.
Figure 22.
The Mean squared logarithmic error frequency distribution for the subcritical pile.
Figure 22.
The Mean squared logarithmic error frequency distribution for the subcritical pile.
Figure 23.
(a) Spatial results of R-squared error analysis. (b) Frequency distribution of R-squared error.
Figure 23.
(a) Spatial results of R-squared error analysis. (b) Frequency distribution of R-squared error.
Table 1.
Measured Energy Resolution of the HPGe Detector.
Table 1.
Measured Energy Resolution of the HPGe Detector.
| Energy (keV) |
Resolution (%) |
Error1 |
356 (Ba-133)
511 (Na-22)
662 (Cs-137)
1173 (Co-60)
1332 (Co-60) |
0.39
0.32
0.27
0.21
0.19 |
0.038
0.030
0.027
0.022
0.017 |
Table 2.
Absolute photopeak efficiencies and branching ratios for indium-116m.
Table 2.
Absolute photopeak efficiencies and branching ratios for indium-116m.
| Energy (keV) |
Efficiency (ε) |
Branching Ratio |
| 416.9 |
7.22E-02 |
0.272 |
| 1097.2 |
2.78E-02 |
0.585 |
| 1293.56 |
2.24E-02 |
0.848 |
Table 3.
Maximum flux values for gammas, epithermal/fast, and thermal neutrons.
Table 3.
Maximum flux values for gammas, epithermal/fast, and thermal neutrons.
| Characteristic |
Flux (n/cm^2*s) |
Coordinates |
| Thermal Flux (Pile) |
1.32E+04 |
(-29.91, 52.24, -31.05) |
| Thermal Flux (Testbed) |
6.66E+03 |
(0.0, 53.0, -30.53) |
| Epithermal Flux (Pile) |
1.03E+04 |
(-29.91, 52.24, -31.05) |
| Epithermal Flux (Testbed) |
3.95E+03 |
(0.0, 53.0, -34.12) |
| Gamma Flux (Pile) |
1.18E+04 |
(-29.91, 52.24, -31.05) |
| Gamma Flux (Testbed) |
5.96E+03 |
(0.0, 65.0, -34.12) |
| Total Neutron Flux (Pile) |
2.43E+04 |
(-29.91, 52.24, -31.05) |
Table 4.
Maximum particle energies in the subcritical pile.
Table 4.
Maximum particle energies in the subcritical pile.
| Characteristic |
Energy (MeV) |
| Neutron Energy (Pile) |
1.70E+01 |
| Gamma Energy (Pile) |
1.44E+01 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).