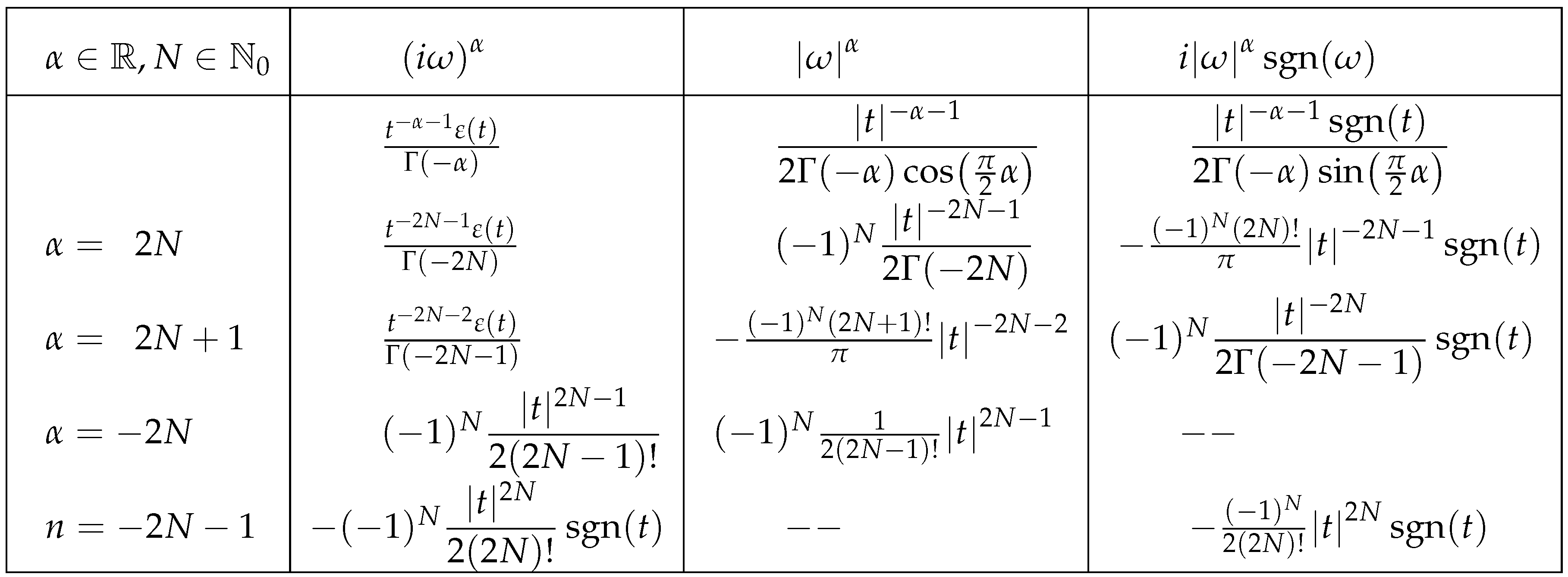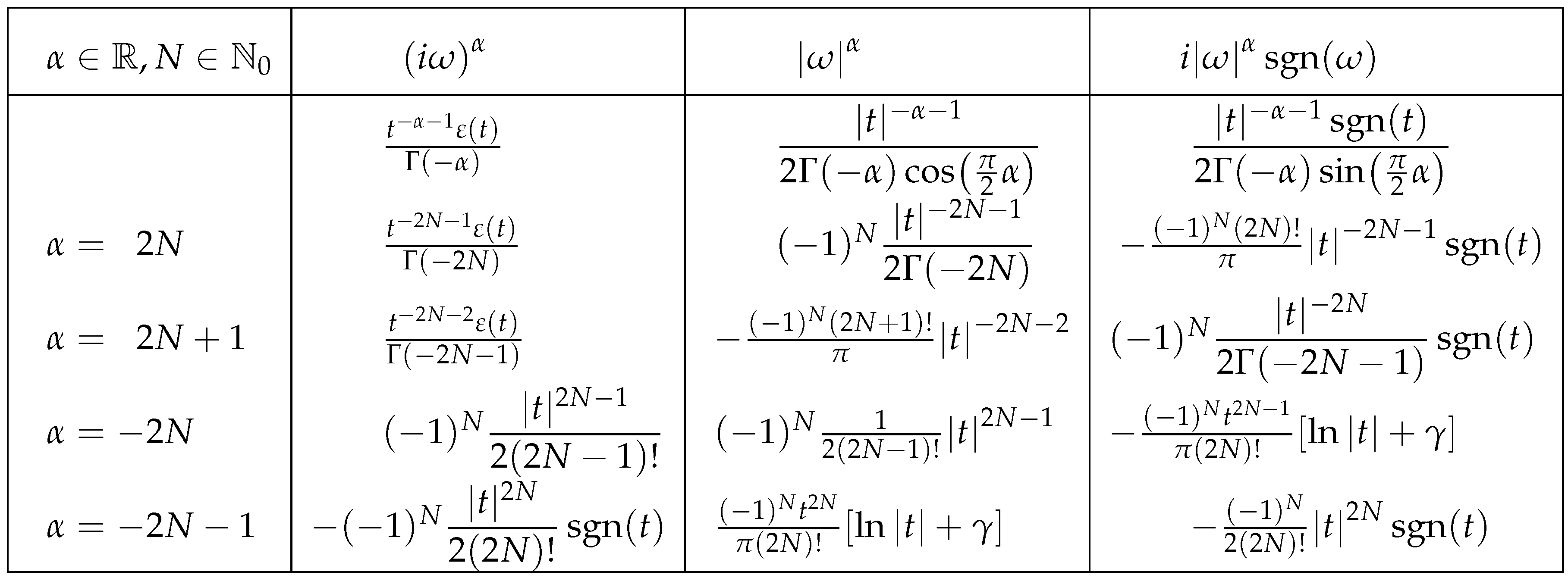The Power Functions and Their Relations to the Unified Fractional Derivative

1. Introduction

The concept of unified fractional derivative (UFD) seems to be introduced by Ortigueira & Trujillo [1] to generalize and unify the notions of one-sided causal/anti-causal (Grünwald-Letnikov) and the two-sided (centred) derivatives [2,3]. Such idea was recovered by Ortigueira & Machado in [4] to introduce fractional derivatives in the context of system theory as part of the movement for coherent definition of fractional derivatives. This led to a deep study in [5] and to generalizations as the tempered derivatives [6,7]. The underlying theory of unified fractional derivative allowed the introduction of formulations in such a way that derivatives/anti-derivatives of any real order could be defined while keeping full coherence with classical results. Namely, as they are shift-invariant, they allow us to define many useful systems, assuming the ARMA form [8] or the diffusion/telegraph form [9,10,11,12,13,14], for Example.

In dealing with shift-invariant linear systems, the exponential functions are their eigenfunctions [8,15,16,17,18]. However, for expressing the impulse and step responses the main role is played by the power functions [18,19]. Their presence/absence is connected with the short and long memory of the system at hand [8,20,21,22,23]. They assume two interlaced aspects: unilateral (tied with causality) and bilateral. Recently, a brief study of some aspects of these functions was done [24], but leaving some unanswered questions. In this paper, we have tried to give an exhaustive presentation of the different expressions of the power functions, their derivatives, and Fourier transforms in relation with particular cases of the UFD.

The paper outlines as follows. In the Section 2, we will describe some useful mathematical tools. The unified fractional derivative will be presented in Section 3, where some of its properties will be introduced. The main objectives of this paper will be treated in Section 4. We will consider the different forms of the power functions and their Fourier transforms. Products by other functions will also be treated. A conjecture about the extrema of functions is also reminded. Finally, some conclusions will be drawn.

2. Some Mathematical Tools

2.1. Laplace and Fourier Transforms

Definition 1. 

The direct Laplace transform is defined by:

$$\mathcal{L}\left[h\left(t\right)\right]=H\left(s\right)=\underset{-\infty }{\overset{\infty }{\int }}h\left(t\right)e^{-st}\mathrm{d}t,s\in \mathbb{C}.$$

(1)

and the inverse reads

$$h\left(t\right)={\mathcal{L}}^{-1}H\left(s\right)={\displaystyle \frac{1}{2\pi i}}\underset{c-i\infty }{\overset{c+i\infty }{\int }}H\left(s\right)e^{st}\mathrm{d}s,t\in \mathbb{R},$$

(2)

where $c\in \mathbb{R}.$ The right hand side represents the Bromwich integral.

Under suitable conditions, the integral in (1) converges absolutely and uniformly in a vertical strip in the complex plane defined by $b<Re\left(s\right)<a$, where $H\left(s\right)$ is analytic. This strip is called region of convergence (ROC), and the values of the constants a and b are the abscissas of convergence. It is possible to show that the inversion integral (1), with $b<c<a,$ converges to the half sum of the lateral values, that is, ${\displaystyle \frac{1}{2}}\left[h\left(t^{+}\right)+h\left(t^{-}\right)\right]$, for any $t\in \mathbb{R}$ [15,16,25].

If the ROC includes the imaginary axis or this is one of the boundaries, we can substitute $s\to i\omega$ getting the Fourier transform by

$$\mathcal{F}\left[h\left(t\right)\right]=H\left(\omega \right)=\underset{-\infty }{\overset{\infty }{\int }}h\left(t\right)e^{-i\omega t}\mathrm{d}t,\omega \in \mathbb{R},$$

(3)

$$h\left(t\right)={\mathcal{F}}^{-1}\left[H\left(\omega \right)\right]={\displaystyle \frac{1}{2\pi }}\underset{-\infty }{\overset{\infty }{\int }}H\left(\omega \right)e^{i\omega t}\mathrm{d}\omega ,t\in \mathbb{R},$$

(4)

which are called analysis and synthesis equations, respectively. The integration must be taken in the sense of the Cauchy principal value. The function $H\left(\omega \right)$ in (3) is the direct FT, while $h\left(t\right)$ given by (4) is the inverse FT. About the existence of the FT (3) we can say that if $h\left(t\right)$ is piecewise continuous, with bounded variation, and absolutely integrable (AI), then the FT exists and the convergence of the integral in (3) is uniform on $\omega \in \left]-\infty ,+\infty \right[$ [15,16].

2.2. On the Distributions

Definition 2. 

Let $f\left(t\right)$ be a continuous function, defined on $\mathbb{R}$ and null for $t<0$ (in abusive language, we call it causal function, by analogy with the impulse response of causal systems). Sometimes the designation “right function” is also used. Represent the usual derivative by D. We define a distribution $g\left(t\right)$ as a derivative of a given order of $f\left(t\right)$

$$g\left(t\right)=D^{n}p\left(t\right),n\in \mathbb{N}.$$

(5)

Several mathematical formulations support this definition and extend the validity of the LT and FT [25,26,27,28,29], but this is out of our objectives.

Example 1. 

Let $r\left(t\right)$ (ramp) be defined by

$$r\left(t\right)=\left\{\begin{array}{cc}t\hfill & t\ge 0\hfill \\ 0\hfill & t<0.\hfill \end{array}\right.$$

Since it is a continuous function, it originates interesting distributions: the Heaviside function

$$\epsilon \left(t\right)=Dr\left(t\right),$$

Dirac’s delta distribution [26,27,28]

$$\delta \left(t\right)=D^{2}r\left(t\right),$$

and its derivatives. Similarly, we can define another sequence, by successive derivations

$$\left|t\right|\to sgn\left(t\right)\to 2\delta \left(t\right).$$

The function $sgn\left(t\right)=2\epsilon \left(t\right)-1$ is the signum function.

Example 2. 

Let $\beta >0$. We define the causal fractional power function by

$${\psi }_{\beta }\left(t\right)={\displaystyle \frac{t^{\beta -1}}{\Gamma \left(\beta \right)}}\epsilon \left(t\right),$$

(6)

where the Gamma function is given by

$$\Gamma \left(\beta \right)={\int }_0^{\infty }{\tau }^{\beta -1}{\mathrm{e}}^{-\tau }\mathrm{d}\tau$$

(7)

for $\beta >0$.

The Laplace transform of ${\psi }_{\beta }\left(t\right)$ reads [30]

$$\mathcal{L}\left[{\psi }_{\beta }\left(t\right)\right]={\displaystyle \frac{1}{s^{\beta }}},Re\left(s\right)>0.$$

(8)

If $\beta <0$ the Gamma function is defined by [31,32,33]

$$\Gamma \left(\beta \right)={\int }_0^{\infty }{\tau }^{\beta -1}\left[{\mathrm{e}}^{-\tau }-\sum _{m=0}^N{\displaystyle \frac{{(-1)}^m{\tau }^m}{m!}}\right]\mathrm{d}\tau$$

(9)

where $-N-1<\beta <-N,N\in \mathbb{N}$.

The distributions obtained by successive applications of the operator D to ${\psi }_{\beta }\left(t\right)$ are called pseudo-functions [26,27,28,34,35]. Frequently, the representation $Pf(.)$ is used. We do not find it necessary. Therefore, $s^{\beta }$ can be considered as the Laplace transform of the pseudo-function ${\displaystyle \frac{t^{-\beta -1}}{\Gamma (-\beta )}}\epsilon \left(t\right).$

We can prove that, in the context of Laplace or Fourier transforms, the convolution of two distributions gives rise to another distribution [25,28,29,35,36]. In such cases, $\delta \left(t\right)$ is the neutral element of the convolution and, if $g\left(t\right)$ and $h\left(t\right)$ are convolutionally inverse, then

$$g\left(t\right)\ast h\left(t\right)=\delta \left(t\right).$$

(10)

The inversion of this convolution has been subject of many publications [37,38]. The causal case, mainly based in the Abel’s algorithm, has attracted the attention recently [22,39,40,41,42].

Remark 1. 

In this paper we deal with the multivalued expression $s^{\beta },\beta \in \mathbb{R}$. To define a function we have to fix a branch cut line and choose a branch (Riemann surface). To deal with right functions a simple correct procedure consists of choosing the negative real half-axis as branch cut line and adopting the principal branch; we assume also that the obtained function is continuous above the branch cut line, so that ${(-1)}^{\beta }=e^{i\beta \pi }$.

2.3. On the Binomial Coefficients

The importance of the binomial coefficients sequence is unquestionable [43,44,45,46]. In our applications we express them in the form:

$$\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{n}}\right)={(-1)}^n{\displaystyle \frac{{(-\alpha )}_n}{n!}},n\in {\mathbb{N}}_0,$$

(11)

where, if $a\in \mathbb{R},$ then ${\left(a\right)}_n=a(a+1)\cdots (a+n-1),$ with ${\left(a\right)}_0=1,$ is the Pochhammer symbol for the raising factorial that can be written as

$${\left(a\right)}_n=\prod _{k=0}^{n-1}{\displaystyle \frac{a+k}{1+k}}.$$

Remark 2. 

It is important to emphasize the fact that this representation of the binomial coefficients avoids the use of the gamma function, simplifying computations.

The absolute value of sequence represented in (11) is increasing for $\alpha <-1$, constant for $\alpha =-1$ and decreasing for $\alpha >-1$. It can be shown that it varies asymptotically as ${\displaystyle \frac{1}{n^{\alpha +1}}}$[46]. It is finite, if $\alpha \in \mathbb{N}$. These expressions allow us to recover well-known characteristics of the binomial series. Let $z\in \mathbb{C}$. The binomial series reads

$${(1-z)}^{\alpha }=\sum _{m=0}^{\infty }{\displaystyle \frac{{(-\alpha )}_m}{m!}}{z}^m.$$

(12)

This series converges absolutely and uniformly for any $\alpha \in \mathbb{R}$ provided that $\left|z\right|<1$[43,46]. If $\left|z\right|>1$ the series diverges except when $\alpha$ is a non-negative integer, in which case the series becomes a finite sum. However, we are interested in the case $z=e^{i\omega },\omega \in \mathbb{R}$ about which we can say that

• the series converges absolutely if and only if $\alpha \ge 0$;
• if $z\ne 1$, the series converges simply, if and only if $\alpha >-1$;
• if $z=1,$ the series diverges for $\alpha <0$.

The relation (12) allows us to obtain an interesting bilateral binomial series, defined on the unit circle, and given by [3]

$$\begin{array}{cc}\hfill {\Psi }_{\theta }^{\alpha }\left(\omega \right)& =\underset{z\to e^{i\omega }}{lim}{(1-z)}^a{(1-z^{-1})}^b={\left|2sin\left(\omega /2\right)\right|}^{\alpha }{e}^{i{\displaystyle \frac{\pi }{2}}\theta sgn\left(\omega \right)}{e}^{i\pi \theta \omega /2}\hfill \\ & =\sum _{n=-\infty }^{+\infty }{(-1)}^n·{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(\frac{\alpha +\theta }{2}-n+1\right)\Gamma \left(\frac{\alpha -\theta }{2}+n+1\right)}}{e}^{in\omega },\hfill \end{array}$$

(13)

where $\alpha =a+b>-1$ and $\theta =a-b\in \mathbb{R}$. It is a simple matter to verify that the coefficients of this series result from the cross-correlation of the binomial coefficients corresponding to orders a and b [3,47]:

$$\sum _{m=0}^{\infty }{\displaystyle \frac{{(-a)}_m}{m!}}{\displaystyle \frac{{(-b)}_{m+n}}{(m+n)!}}={(-1)}^n·{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(\frac{\alpha +\theta }{2}-n+1\right)\Gamma \left(\frac{\alpha -\theta }{2}+n+1\right)}}$$

3. The Unified Fractional Derivative

The unified fractional derivative results from (13) [2,3]. Let $\alpha ,\theta \in \mathbb{R}$ and consider the exponential $e\left(t\right)=e^{i\omega t},\omega ,t\in \mathbb{R}$.

Definition 3. 

The operator $D_{\theta }^{\alpha }$ whose associated frequency response, ${\Psi }_{\theta }^{\beta }\left(\omega \right)$, given by

$${\Psi }_{\theta }^{\alpha }\left(\omega \right)={\left|\omega \right|}^{\alpha }{e}^{i{\displaystyle \frac{\pi }{2}}\theta ·sgn\left(\omega \right)}$$

(14)

verifying

$$D_{\theta }^{\alpha }{e}^{i\omega t}={\Psi }_{\theta }^{\alpha }\left(\omega \right)e^{i\omega t},$$

(15)

is named unified fractional derivative [1,4]; α is the derivative order and θ the asymmetry parameter.

When $\theta =\alpha$, we will omit the $theta$ parameter, $D_{\pm \alpha }^{\alpha }=D^{\alpha };$ In particular, we set, $D_1^1=D.$

This definition has a deep connection with the Fourier transform and allows us to extend two dual properties [48].

Theorem 1. 

Let $F\left(\omega \right)$ be the Fourier transform of a given function or distribution $f\left(t\right)$. Then, the UFD of $f\left(t\right)$ is given by

$$D_{\theta }^{\alpha }f\left(t\right)={\displaystyle \frac{1}{2\pi }}{\int }_{\mathbb{R}}{\left|\omega \right|}^{\alpha }{e}^{i\theta {\displaystyle \frac{\pi }{2}}sgn\left(\omega \right)}F\left(\omega \right)e^{i\omega t}d\omega ,t\in \mathbb{R}.$$

(16)

This is a consequence of (15). The dual is obtained immediately

$$D_{\theta }^{\alpha }F\left(\omega \right)={\int }_{\mathbb{R}}{\left|t\right|}^{\alpha }{e}^{i\theta {\displaystyle \frac{\pi }{2}}sgn\left(t\right)}f\left(t\right)e^{-i\omega t}dt,\omega \in \mathbb{R}.$$

(17)

Remark 3. 

• The above definition is very general. Given a pair, ($\alpha ,\theta$), there exists, at least, one explicit description of the UFD. Suitable choices allow us to recover the causal, anti-causal, and bilateral derivatives. The particular, most interesting, cases are [5]

–

$\theta =\pm \alpha$—forward/backward Liouville and GL derivatives [49,50,51].

–

$\theta =0$— Riesz derivative [52].

–

$\theta =1$—Feller derivative [53]. with $\theta =1$, we obtain the usual discrete-time formulation of the Hilbert transform [54].

• From (15) we conclude easily that [55]
  • The Bode amplitude diagram is a straight line with slope $20\alpha dB/dec$;
  • The Bode phase is an horizontal straight line with ordinate $\theta {\displaystyle \frac{\pi }{2}}rad;$
• Due to the properties of the Fourier transform, the UFD verifies all the required items for really being a fractional derivative [56];
• We must be careful when using (17), since the hermitian property can be lost for some values of the asymmetry parameter.

Some other properties can be drawn [2,3,5]:

• Additivity and commutativity of the orders

  $$D_{\theta }^{\alpha }{D}_{\eta }^{\beta }f\left(t\right)=D_{\theta +\eta }^{\alpha +\beta }f\left(t\right).$$

  (18)
  In applying this property it is convenient to have in mind the periodicity in $theta$.

  $$D_{\theta }^{\alpha }f\left(t\right)=D_{\theta +4n}^{\alpha }f\left(t\right),n\in \mathbb{Z},$$

  as we observe from (14). It is a simple task to verify that

  $$D_{\theta }^{\alpha }f\left(t\right)=-D_{\theta +2n}^{\alpha }f\left(t\right),n\in \mathbb{Z}.$$
  Therefore, we can write

  $$\begin{array}{cc}\hfill & D_0^{\alpha }{D}_0^{\beta }f\left(t\right)=D_0^{\alpha +\beta }f\left(t\right);\hfill \\ \hfill & D_1^{\alpha }{D}_0^{\beta }f\left(t\right)=D_1^{\alpha +\beta }f\left(t\right);\hfill \\ \hfill & D_1^{\alpha }{D}_1^{\beta }f\left(t\right)=-D_0^{\alpha +\beta }f\left(t\right).\hfill \end{array}$$

  (19)
  These relations motivate the introduction of two series analog to Mittag-Leffler’s that may be useful in solving partial differential equations involving space derivatives. They read

  $$s_e\left(t\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{1}{2\Gamma (k\alpha +1)sin\left(k\alpha \frac{\pi }{2}\right)}}{\left|t\right|}^{k\alpha }$$

  and

  $$s_o\left(t\right)=\sum _{k=0}^{\infty }{\displaystyle \frac{1}{2\Gamma ((2k+1)\alpha +1)cos\left((2k+1)\alpha \frac{\pi }{2}\right)}}{\left|t\right|}^{(2k+1)\alpha }sgn\left(t\right).$$
• Existence of inverse derivative
  We define the identity operator

  $$D_0^{0}f\left(t\right)=f\left(t\right).$$

  (20)
  From this definition and (18), the anti-derivative exists when $\beta =-\alpha$ and ${\theta }_1=-{\theta }_2$. Therefore,

  $$D_{\theta }^{\alpha }{D}_{-\theta }^{-\alpha }f\left(t\right)=D_{-\theta }^{-\alpha }{D}_{\theta }^{\alpha }f\left(t\right)=f\left(t\right).$$

  (21)
  It is interesting to note that

  $$D_1^{\alpha }{D}_1^{-\alpha }f\left(t\right)=-f\left(t\right).$$
  Remark 4. We must highlight the difference between anti-derivative and primitive. This one is the right inverse of the derivative, while the anti-derivative is the left and right inverse.
• Hermitian/anti-hermitian decomposition

  $$D_{\theta }^{\alpha }f\left(t\right)=cos\left(\theta {\displaystyle \frac{\pi }{2}}\right)D_0^{\alpha }f\left(t\right)+sin\left(\theta {\displaystyle \frac{\pi }{2}}\right)D_1^{\alpha }f\left(t\right),$$

  (22)

  valid for any pairs $(\alpha ,\theta )$. This property is important enough to demand for its deduction. As $sin\left({\displaystyle \frac{\pi }{2}}\theta sgn\left(\omega \right)\right)=sin\left({\displaystyle \frac{\pi }{2}}\theta \right)sgn\left(\omega \right)$, we have

  $$\begin{array}{cc}\hfill {\Psi }_{\theta }^{\alpha }\left(\omega \right)& ={\left|\omega \right|}^{\alpha }{e}^{i{\displaystyle \frac{\pi }{2}}\theta ·sgn\left(\omega \right)}={\left|\omega \right|}^{\alpha }cos\left({\displaystyle \frac{\pi }{2}}\theta \right)+i{\left|\omega \right|}^{\alpha }sin\left({\displaystyle \frac{\pi }{2}}\theta sgn\left(\omega \right)\right)\hfill \\ & =cos\left({\displaystyle \frac{\pi }{2}}\theta \right){\left|\omega \right|}^{\alpha }+sin\left({\displaystyle \frac{\pi }{2}}\theta \right)i{\left|\omega \right|}^{\alpha }sgn\left(\omega \right),\hfill \end{array}$$

  that leads to (22).
  The hermitian part is obtained from

  $$2{\left|\omega \right|}^{\alpha }cos\left({\displaystyle \frac{\pi }{2}}\theta \right)={\Psi }_{\theta }^{\alpha }\left(\omega \right)+{\Psi }_{\theta }^{\alpha }(-\omega ).$$

  (23)
  Its FT inverse is the impulse response of the Riesz derivative [5]. Similarly, the anti-hermitian is

  $$i2{\left|\omega \right|}^{\alpha }sin\left({\displaystyle \frac{\pi }{2}}\theta \right)sgn\left(\omega \right)={\Psi }_{\theta }^{\alpha }\left(\omega \right)-{\Psi }_{\theta }^{\alpha }(-\omega ).$$

  (24)
  Its impulse response defines the Feller derivative [5].
• Causal/anti-causal decomposition
  Consider the last two relations and choose $\theta =\alpha$, so that ${\Psi }_{\theta }^{\alpha }\left(\omega \right)={\left(i\omega \right)}^{\alpha }$. Then

  $${\left|\omega \right|}^{\alpha }={\displaystyle \frac{{\left(i\omega \right)}^{\alpha }+{(-i\omega )}^{\alpha }}{2cos\left(\frac{\pi }{2}\alpha \right)}}$$

  (25)

  and

  $$i{\left|\omega \right|}^{\alpha }sgn\left(\omega \right)={\displaystyle \frac{{\left(i\omega \right)}^{\alpha }-{(-i\omega )}^{\alpha }}{2sin\left(\frac{\pi }{2}\alpha \right)}}$$

  (26)

  which imply, respectively

  $$D_0^{\alpha }f\left(t\right)={\displaystyle \frac{D_{\alpha }^{\alpha }f\left(t\right)+D_{-\alpha }^{\alpha }f\left(t\right)}{2cos\left(\frac{\pi }{2}\alpha \right)}}$$

  (27)

  and

  $$D_1^{\alpha }f\left(t\right)={\displaystyle \frac{D_{\alpha }^{\alpha }f\left(t\right)-D_{-\alpha }^{\alpha }f\left(t\right)}{2sin\left(\frac{\pi }{2}\alpha \right)}}.$$

  (28)
  These expressions lead to

  $$D_{\theta }^{\alpha }f\left(t\right)={\displaystyle \frac{cos\left[(\alpha +\theta )\frac{\pi }{2}\right]}{sin\left(\alpha \frac{\pi }{2}\right)}}{D}_{\alpha }^{\alpha }f\left(t\right)+{\displaystyle \frac{cos\left[(\alpha -\theta )\frac{\pi }{2}\right]}{sin\left(\alpha \frac{\pi }{2}\right)}}{D}_{-\alpha }^{\alpha }f\left(t\right)$$

  (29)

  showing how the UFD can be expressed in terms of the Liouville causal and anti-causal derivatives.

Remark 5. 

The relations (22) to (29) show that the UFD can be expressed in terms of two simpler derivatives

• Riesz + Feller derivatives;
• Liouville causal + anti-causal derivatives.

Besides the two sets of derivatives are inter-related.

For a given pair, ($\alpha ,\theta$), there is, at least, one explicit formulation for the UFD obtained from one of the following expressions. For some particular cases, it is possible to devise other formulae, deeply related to these [4,5]

• Let $\alpha >-1$ if $\theta \ne \pm \alpha$, or $\alpha \in \mathbb{R}$ if $\theta =\pm \alpha .$ The GL type UFD is given by:

  $$\begin{array}{cc}\hfill D_{\theta }^{\alpha }f\left(t\right)& =\underset{h\to 0^{+}}{lim}{h}^{-\alpha }\sum _{n=-\infty }^{+\infty }{(-1)}^n·{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(\frac{\alpha +\theta }{2}-n+1\right)\Gamma \left(\frac{\alpha -\theta }{2}+n+1\right)}}f(t-nh)\hfill \\ \hfill & ={\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(\frac{\alpha +\theta }{2}+1\right)\Gamma \left(\frac{\alpha -\theta }{2}+1\right)}}\underset{h\to 0^{+}}{lim}{h}^{-\alpha }\sum _{n=-\infty }^{+\infty }{\displaystyle \frac{{\left(-\frac{\alpha +\theta }{2}\right)}_n}{{\left(\frac{\alpha -\theta }{2}+1\right)}_n}}f(t-nh).\hfill \end{array}$$

  (30)
  We can extend the formula (30) to other pairs of the parameters. Interesting cases are $\alpha \in {\mathbb{Z}}^{-}$, with $\left|\theta \right|=0,\mathit{or}1,\mathit{or}2$.
• For $\alpha >0,$ an integral formulation for the unified anti-derivative is given by

  $$D_{\theta }^{-\alpha }f\left(t\right)={\displaystyle \frac{1}{sin\left(\alpha \pi \right)\Gamma \left(\alpha \right)}}{\int }_{\mathbb{R}}f(t-\tau )sin\left[\left(\alpha +\theta ·sgn\left(\tau \right)\right){\displaystyle \frac{\pi }{2}}\right]{\left|\tau \right|}^{\alpha -1}\mathrm{d}\tau .$$

  (31)
  It is possible to regularize (31) so that it becomes valid for any $\alpha$ [5].

4. Power Functions and Their Derivatives

4.1. Types of Powers

In the previous section, we showed that we can express the UFD as linear combinations of causal/anti-causal or hermitian/anti-hermitian derivatives. The former are defined by right/left impulse responses, while the later by symmetric/anti-symmetric ones. In fact, we have to relate the power frequency responses and the time power functions. Such frequency responses are

• Causal Liouville – ${\left(i\omega \right)}^{\alpha };$
• Anti-causal Liouville – ${(-i\omega )}^{\alpha };$
• Hermitian Riesz – ${\left|\omega \right|}^{\alpha };$
• Anti-Hermitian Feller – $i{\left|\omega \right|}^{\alpha }sgn\left(\omega \right).$

They have correspondence with powers of types

• Right – $t^{\beta }\epsilon \left(t\right);$
• Left – ${(-t)}^{\beta }\epsilon (-t);$
• Symmetric (even) – ${\left|t\right|}^{\beta };$
• Anti-symmetric (odd) – ${\left|t\right|}^{\beta }sgn\left(t\right).$

Therefore, we will consider preferably Liouville (and Grünwald-Letnikov), Riesz, and Feller derivatives.

4.2. $\theta =\pm \alpha$ – Liouville

The $\theta =\pm \alpha$ cases underly the causal/anti-causal derivatives. We will treat the causal only, since the anti-causal instances will be obtained from the corresponding causal through a change $-t\to t(\omega \to -\omega ).$

Therefore, we are going to look for the inverse FT of the frequency response

$${\Psi }^{\alpha }\left(\omega \right)={\left|\omega \right|}^{\alpha }{e}^{i{\displaystyle \frac{\pi }{2}}\alpha ·sgn\left(\omega \right)}={\left(i\omega \right)}^{\alpha }$$

(32)

As referred above, we omitted the reference to $\theta$. This expression deserves a careful analysis.

• If $\alpha \in \mathbb{R}\setminus \mathbb{Z}$, the function ${\left(i\omega \right)}^{\alpha }$ is hermitian. Therefore, its inverse FT is a real function, neither even, nor odd. It will be deduced below.
• When $\alpha =N\in {\mathbb{Z}}_0^{+}$ we have two situations corresponding to even and odd orders. If N is even, ${\left(i\omega \right)}^N$ is real even; the same happens to the FT inverse. If N is odd, ${\left(i\omega \right)}^N$ is imaginary odd and its inverse is real odd. In fact it is known that this case is singular, since

  $${\mathcal{F}}^{-1}{\left(i\omega \right)}^N={\delta }^{\left(N\right)}\left(t\right).$$
  Moreover, it can be written as [26]

  $${\mathcal{F}}^{-1}{\left(i\omega \right)}^N={\displaystyle \frac{t^{-N-1}\epsilon \left(t\right)}{\Gamma (-N)}},t\in \mathbb{R},$$

  (33)

  expressed in a form that is coherent with the general expression, as we will se below.
• If the order is a negative integer, ${\left(i\omega \right)}^{-N}$ has also an alternancy real/imaginary giving even/odd FT inverses, therefore bilateral functions (no causality). This case will be treated later.

As observed looking into the items, we were driven into a distribution framework and delt with pseudo-functions [28]. We tried to establish a direct relation between the frequency response ${\left(i\omega \right)}^{\alpha }$ and the causal behaviour. As we verified, such a correspondence only happens when the order is not integer. In such cases, we can show that [46,57,58]

$${\left(i\omega \right)}^{\alpha }={\int }_0^{\infty }\left[e^{-i\omega \tau }-\sum _0^N{\displaystyle \frac{{(-i\omega )}^n}{n!}}{\tau }^n\right]{\displaystyle \frac{{\tau }^{-\alpha -1}}{\Gamma (-\alpha )}}\mathrm{d}\tau$$

(34)

where $N=\lfloor \alpha \rfloor$, the greatest integer less than or equal to $\alpha$. If $N<0$ the summation is null.

Attending to the observations we made above, we conclude that there exists what we can consider as generalized impulse response of the derivative defined by the frequency response ${\left(i\omega \right)}^{\alpha }$. If $\alpha$ is not a negative integer number, such an impulse response assumes the form

$$D^{\alpha }\delta \left(t\right)={\mathcal{F}}^{-1}{\left(i\omega \right)}^{\alpha }={\displaystyle \frac{t^{-\alpha -1}\epsilon \left(t\right)}{\Gamma (-\alpha )}},$$

(35)

being a pseudo-function when $\alpha \ge 0$. Having this in mind we are going to make a brief study of this distribution, by computing it from the derivative definition (30). This objective can be achieved through some manipulations in the definition of GL, using a procedure that follows the one used in [59]. We reduce the difficulties by working with the step response. We know that

$$\delta \left(t\right)=D\epsilon \left(t\right),$$

then the impulse response, $h\left(t\right)$, verifies

$$h\left(t\right)=D{r}_{\epsilon }\left(t\right),$$

where

$$r_{\epsilon }\left(t\right)=h\left(t\right)\ast \epsilon \left(t\right)={\int }_0^{t}h(t-\tau )d\tau .$$

Attending to these relations and using (35) we obtain

$$D^{\alpha }\epsilon \left(t\right)={\displaystyle \frac{{\tau }^{-\alpha }\epsilon \left(t\right)}{\Gamma (-\alpha +1)}}.$$

(36)

We are going to look into this result from a deeper point of view by computing it directly from the GL causal derivative. This one is got from (30) by setting $\theta =\alpha \in \mathbb{R}$

$$\begin{array}{cc}\hfill D^{\alpha }f\left(t\right)& =\underset{h\to 0^{+}}{lim}{h}^{-\alpha }\sum _{n=0}^{\infty }{(-1)}^n{\displaystyle \frac{\Gamma \left(\alpha +1\right)}{\Gamma \left(\alpha -n+1\right)\Gamma \left(n+1\right)}}f(t-nh)\hfill \\ & =\underset{h\to 0^{+}}{lim}{h}^{-\alpha }\sum _{n=0}^{+\infty }{\displaystyle \frac{{(-\alpha )}_n}{n!}}f(t-nh).\hfill \end{array}$$

(37)

Theorem 2. 

Let $f\left(t\right)=\epsilon \left(t\right),t\in \mathbb{R}$ and $\alpha \in \mathbb{R}$. Then

$$D^{\alpha }\epsilon \left(t\right)={\displaystyle \frac{t^{-\alpha }}{\Gamma (-\alpha +1)}}\epsilon \left(t\right),$$

(38)

For a simple proof, let $h=t/L,L\in \mathbb{N}$. We get

$$D^{\alpha }\epsilon \left(t\right)=\underset{h\to 0^{+}}{lim}{h}^{-\alpha }\sum _{n=0}^L{\displaystyle \frac{{(-\alpha )}_n}{n!}}=t^{-\alpha }\underset{L\to \infty }{lim}{L}^{\alpha }\sum _{n=0}^L{\displaystyle \frac{{(-\alpha )}_n}{n!}}$$

However, [46]

$$\sum _{n=0}^L{\displaystyle \frac{{(-\alpha )}_n}{n!}}=\sum _{k=0}^L{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)=\left({\displaystyle \genfrac{}{}{0pt}{}{L-\alpha }{L}}\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\displaystyle \frac{\Gamma (L+1-\alpha )}{\Gamma (L+1)}}$$

A well-known property of the gamma function [46] gives

$${\displaystyle \frac{\Gamma (L+1-\alpha )}{\Gamma (L+1)}}\approx L^{-\alpha }$$

for larger values of L. Therefore,

$$\underset{L\to \infty }{lim}{L}^{\alpha }\sum _{n=0}^L{\displaystyle \frac{{(-\alpha )}_n}{n!}}={\displaystyle \frac{1}{\Gamma (-\alpha +1)}},$$

that leads to the expected result. This Theorem deserves some comments:

• It is valid for any real order;
• For $\alpha \in {\mathbb{Z}}^{-}$ it leads to the well-known result

  $$D^{-N}\epsilon \left(t\right)={\displaystyle \frac{t^N}{N!}}\epsilon \left(t\right),$$

  (39)

  that corresponds to a recursive computation of the anti-derivative;
• If $\alpha =N\ge 0$, we get

  $$D^N\epsilon \left(t\right)={\displaystyle \frac{t^{-N}}{\Gamma (-N+1)}}\epsilon \left(t\right),$$

  (40)

  as we showed above.

This Theorem confirms the correctness of (35).

A similar procedure was used by Miller & Ross [59] to obtain

Corollary 1. 

The α–order derivative of the power function ${\displaystyle \frac{t^N}{\Gamma (N+1)}}\epsilon \left(t\right),N\in \mathbb{N}$ is given by

$$D^{\alpha }{\displaystyle \frac{t^N}{\Gamma (N+1)}}\epsilon \left(t\right)={\displaystyle \frac{t^{N-\alpha }}{\Gamma (N-\alpha +1)}}\epsilon \left(t\right),$$

(41)

for any real α.

From these results and property (18) we can generalize the previous relation to obtain, for any real $\alpha ,\beta$ [60],

$$D^{\alpha }{\displaystyle \frac{t^{\beta }}{\Gamma (\beta +1)}}\epsilon \left(t\right)={\displaystyle \frac{t^{\beta -\alpha }}{\Gamma (\beta -\alpha +1)}}\epsilon \left(t\right).$$

(42)

Remark 6. 

This relation shows something very important: given a power of the type $t^{m\beta }\epsilon \left(t\right)$ the sequence of order β derivatives does not stop

$$D^{n\beta }{\displaystyle \frac{t^{m\beta }}{\Gamma (m\beta +1)}}\epsilon \left(t\right)={\displaystyle \frac{t^{(m-n)\beta }}{\Gamma \left(\right(m-n)\beta +1)}}\epsilon \left(t\right),m,n\in \mathbb{Z}.$$

This highlights the abnormality of the Caputo derivative that stops for $n=m+1$, since a null derivative of the Heaviside function is obtained.

We showed that any causal power function can be considered as a fractional derivative of a suitable order of the Heaviside function

$${\displaystyle \frac{t^{\alpha }}{\Gamma (\alpha +1)}}\epsilon \left(t\right)=D^{-\alpha }\epsilon \left(t\right).$$

(43)

However, this does not mean that all the versions result from inverting ${\left(i\omega \right)}^{\alpha -1}$. In fact, we showed that

$$\mathcal{F}\left[{\displaystyle \frac{t^{\alpha }}{\Gamma (\alpha +1)}}\epsilon \left(t\right)\right]={\left(i\omega \right)}^{\alpha -1},$$

(44)

if $\alpha \notin {\mathbb{Z}}_0^{+}.$ This result leaves out the positive integer order power function ${\displaystyle \frac{t^N}{\Gamma (N+1)}}\epsilon \left(t\right),$ because its FT is not given by a simple expression like ${\left(i\omega \right)}^{N-1}$. In fact, it is not very hard to show that [26,29]

$$\mathcal{F}\left[\epsilon \left(t\right)\right]=\pi \delta \left(\omega \right)+{\displaystyle \frac{1}{i\omega }}.$$

(45)

Using the property (17) with $\theta =\alpha$ we obtain

$$\mathcal{F}\left[t^N\epsilon \left(t\right)\right]=\pi i^N{\delta }^{\left(N\right)}\left(\omega \right)+{\displaystyle \frac{N!}{{\left(i\omega \right)}^{N+1}}}.$$

and so,

$$\mathcal{F}\left[{\displaystyle \frac{t^N}{\Gamma (N+1)}}\epsilon \left(t\right)\right]={\displaystyle \frac{\pi }{N!}}{i}^N{\delta }^{\left(N\right)}\left(\omega \right)+{\displaystyle \frac{1}{{\left(i\omega \right)}^{N+1}}}.$$

(46)

Thus an “abnormal” term appears when comparing with (44). Therefore, the inverse FT of ${\left(i\omega \right)}^{-N}$ is not causal.

Another interesting result can be formulated as

Theorem 3. 

Let us consider the relations (42) and the above involving integer derivative orders. We can show [60] that, if $N\in \mathbb{N}$,

$$D^{\alpha }{t}^{-N}\epsilon \left(t\right)=-{\displaystyle \frac{{\left(\alpha \right)}_N}{(N-1)!(-\alpha +1)}}{t}^{-\alpha -N}\epsilon \left(t\right)\left[log\left(t\right)-\gamma -\psi (-\alpha +1)-\sum _{n=1}^N{\displaystyle \frac{1}{1-\alpha -n}}\right],$$

(47)

where

$$\psi \left(z\right)={\Gamma }^{\prime }\left(z\right)/\Gamma \left(z\right)$$

is the digamma function [31,44].

4.3. $\theta =0\mathit{and}1$ – Riesz and Feller Cases

With $\theta =0,\pm 1$, we are led to what we can call Riesz and Feller derivatives, respectively. From Theorem 1 we get the corresponding frequency responses

$${\Psi }_0^{\alpha }\left(\omega \right)={\left|\omega \right|}^{\alpha }$$

and

$${\Psi }_1^{\alpha }\left(\omega \right)=i{\left|\omega \right|}^{\alpha }sgn\left(\omega \right).$$

From the properties of FT, we know that the corresponding impulse responses, ${\psi }_0^{\alpha }\left(t\right)$ and ${\psi }_1^{\alpha }\left(t\right)$, are even and odd, respectively. Recovering the impulse response ${\displaystyle \frac{t^{-\alpha -1}\epsilon \left(t\right)}{\Gamma (-\alpha )}}$ we got in the previous subsection and using the relations (25) and (26), we deduce

Theorem 4. 

Let $\alpha \in \mathbb{R}\setminus {\mathbb{Z}}^{-}.$ The impulse responses, ${\psi }_0^{\alpha }\left(t\right)$ and ${\psi }_1^{\alpha }\left(t\right)$, are given by

$${\psi }_0^{\alpha }\left(t\right)={\displaystyle \frac{{\left|t\right|}^{-\alpha -1}}{2\Gamma (-\alpha )cos\left(\frac{\pi }{2}\alpha \right)}}$$

(48)

and

$${\psi }_1^{\alpha }\left(t\right)={\displaystyle \frac{{\left|t\right|}^{-\alpha -1}sgn\left(t\right)}{2\Gamma (-\alpha )sin\left(\frac{\pi }{2}\alpha \right)}}$$

(49)

This result comes from inserting (35) into (27) and (28). Of course, we must be careful with the singular cases that appear when $\alpha =M\in \mathbb{Z}$. We are going to study each case step by step. Consider the $\theta =0$ case. We have 4 noteworthy cases: positive/negative and even/odd $M.$ Let $N\in {\mathbb{N}}_0$.

4.3.1. Riesz Case

• $M=+2N$.
  We have,

  $$cos\left({\displaystyle \frac{\pi }{2}}M\right)={(-1)}^N,$$

  and

  $${\psi }_0^{2N}\left(t\right)={(-1)}^N{\displaystyle \frac{{\left|t\right|}^{-2N-1}}{2\Gamma (-2N)}}={(-1)}^N{\delta }^{\left(2N\right)}\left(t\right).$$

  (50)
• $M=-2N$.
  This case is not singular. We obtain directly

  $${\psi }_0^{-2N}\left(t\right)={(-1)}^N{\displaystyle \frac{{\left|t\right|}^{2N-1}}{2(2N-1)!}}.$$

  (51)
• $M=+2N+1$.
  We note that

  $${\displaystyle \frac{1}{2\Gamma (-\alpha )cos\left(\alpha \frac{\pi }{2}\right)}}=-{\displaystyle \frac{\Gamma (\alpha +1)sin(\alpha \pi /2)}{\pi }},$$

  (52)

  that gives

  $${\psi }_0^{2N+1}\left(t\right)=-{(-1)}^N{\displaystyle \frac{{(2N+1)!\left|t\right|}^{-2N-2}}{\pi }}.$$

  (53)
• $M=-2N-1$.
  In this case, the term $cos\left(\alpha {\displaystyle \frac{\pi }{2}}\right)=0$ creates difficulties. We need another approach. We will treat it below.

4.3.2. Feller Case

In the Feller case, we get

• $M=+2N$.
  Note that,

  $${\displaystyle \frac{1}{2\Gamma (-\alpha )sin\left(\frac{\pi }{2}\alpha \right)}}=-{\displaystyle \frac{\Gamma (\alpha +1)cos(\alpha \pi /2)}{\pi }},$$

  (54)

  which gives

  $${\psi }_1^{2N}\left(t\right)=-{\displaystyle \frac{{(-1)}^N\left(2N\right)!}{\pi }}{\left|t\right|}^{-2N-1}sgn\left(t\right).$$

  (55)
• $M=-2N$.
  This case is singular. We leave it for now.
• $M=+2N+1$.
  Using (54), we obtain

  $${\psi }_1^{2N+1}\left(t\right)={(-1)}^N{\displaystyle \frac{{\left|t\right|}^{-2N}}{2\Gamma (-2N-1)}}sgn\left(t\right)={(-1)}^N{\delta }^{(2N+1)}\left(t\right).$$

  (56)
• $M=-2N-1$.
  This case does not have any difficulty. We have

  $${\psi }_1^{-2N-1}\left(t\right)=-{(-1)}^N{\displaystyle \frac{{\left|t\right|}^{2N}}{2\Gamma (2N+1)}}sgn\left(t\right).$$

  (57)

Remark 7. 

Till now, we left unsolved three problems consisting in the inversion of ${\left(i\omega \right)}^{-N}{,\left|\omega \right|}^{-2N-1},{\left|\omega \right|}^{-2N}sgn\left(\omega \right)$. We know already how to solve the first. Consider the ${\left(i\omega \right)}^{\alpha }$ with $\alpha =-M,M\in \mathbb{N}$ a non solved case in the previous subsection. We must make a distinction between the even and odd cases that will come from (51) and (57) respectively, leading to

$${\psi }_0^{-2N}\left(t\right)={(-1)}^N{\displaystyle \frac{{\left|t\right|}^{2N-1}}{2(2N-1)!}}.$$

(58)

and

$${\psi }_1^{-2N-1}\left(t\right)=-{(-1)}^N{\displaystyle \frac{{\left|t\right|}^{2N}}{2\Gamma (2N+1)}}sgn\left(t\right).$$

(59)

Therefore, the inverse of ${\left(i\omega \right)}^{-M}$ is one of the previous relation. At this time, we do not know how to get ${\psi }_0^{-2N-1}\left(t\right)$ and ${\psi }_1^{-2N}\left(t\right).$ To get them, we need another approach that we will describe in a later section [5].

We can resume the FT inversions we made till now, by constructing the following Table 1.

4.3.3. Derivatives of the Power Functions

Given the above relationships and an appropriate change in the parameters, we obtain the derivatives of the power functions. We consider regular cases (orders not equal to negative integers). The others are obtained from the Table 1. Let $\mu \in \mathbb{R}-\mathbb{Z}$. We get:

• Using the symmetry property of the FT, we have

  $$\mathcal{F}\left[D_0^{\alpha }{\left|t\right|}^{\mu }\right]={\left|\omega \right|}^{\alpha }{\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}={\displaystyle \frac{{\pi \left|\omega \right|}^{\alpha -\mu -1}}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}},$$

  and, from (52)

  $${\mathcal{F}}^{-1}\left[{\left|\omega \right|}^{\alpha -\mu -1}\right]={\displaystyle \frac{\Gamma (\alpha -\mu )cos\left(\right(\alpha -\mu )\pi /2)}{\pi }}{\left|t\right|}^{\mu -\alpha }$$
  Therefore,

  $$D_0^{\alpha }{\left|t\right|}^{\mu }={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}{\displaystyle \frac{cos\left((\alpha -\mu )\frac{\pi }{2}\right)}{cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }$$

  (60)
• As above,

  $$\mathcal{F}\left[D_0^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)\right]=-i{\left|\omega \right|}^{\alpha }{\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}sgn\left(\omega \right)}{\Gamma (-\mu )sin\left(\frac{\pi }{2}\mu \right)}}=-i{\displaystyle \frac{{\pi \left|\omega \right|}^{\alpha -\mu -1}sgn\left(\omega \right)}{\Gamma (-\mu )sin\left(\frac{\pi }{2}\mu \right)}},$$

  and, from (54)

  $${\mathcal{F}}^{-1}\left[{i\left|\omega \right|}^{\alpha -\mu -1}sgn\left(\omega \right)\right]=-{\displaystyle \frac{\Gamma (\alpha -\mu )sin\left(\right(\alpha -\mu )\pi /2)}{\pi }}{\left|t\right|}^{\mu -\alpha }sgn\left(t\right).$$

  $$D_0^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}{\displaystyle \frac{sin\left((\alpha -\mu )\frac{\pi }{2}\right)}{sin\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }sgn\left(t\right)$$

  (61)
• With identical procedure we get successively

  $$\mathcal{F}\left[D_1^{\alpha }{\left|t\right|}^{\mu }\right]=i{\left|\omega \right|}^{\alpha }sgn\left(\omega \right){\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}sgn\left(\omega \right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}={\displaystyle \frac{{\pi \left|\omega \right|}^{\alpha -\mu -1}sgn\left(\omega \right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}},$$

  $$D_1^{\alpha }{\left|t\right|}^{\mu }=-{\displaystyle \frac{\Gamma (\alpha -\mu )sin\left((\alpha -\mu )\frac{\pi }{2}\right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }sgn\left(t\right)$$

  (62)
• Similarly,

  $$\mathcal{F}\left[D_1^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)\right]={\left|\omega \right|}^{\alpha }sgn\left(\omega \right){\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}sgn\left(\omega \right)}{\Gamma (-\mu )sin\left(\frac{\pi }{2}\mu \right)}}={\displaystyle \frac{{\pi \left|\omega \right|}^{\alpha -\mu -1}}{\Gamma (-\mu )sin\left(\frac{\pi }{2}\mu \right)}},$$

  and

  $$D_1^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}{\displaystyle \frac{cos\left((\alpha -\mu )\frac{\pi }{2}\right)}{sin\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }$$

  (63)

  similar to (60), as expected, attending to (19).

From these relations, we conclude that, while the Riesz derivative keeps the symmetry characteristic of the power, the Feller inverts it. In fact

• The Riesz derivative of a symmetric/anti-symmetric power is symmetric;
• The Feller derivative of a symmetric/anti-symmetric power is anti-symmetric/symmetric.

Therefore, if we compute the bilateral derivative of a symmetric power for constant order, but varying $\theta$ from 0 to 1, we move from symmetry to anti-symmetry, passing through all the intermmediate asymmetric powers, because

$$\begin{array}{cc}\hfill D_{\theta }^{\alpha }{\left|t\right|}^{\mu }& ={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}\left[{\displaystyle \frac{cos\left((\alpha -\mu )\frac{\pi }{2}\right)cos\left(\theta \frac{\pi }{2}\right)}{cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }-{\displaystyle \frac{sin\left((\alpha -\mu )\frac{\pi }{2}\right)sin\left(\theta \frac{\pi }{2}\right)}{cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }sgn\left(t\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}\left[{\displaystyle \frac{cos\left((\alpha -\mu )\frac{\pi }{2}\right)cos\left(\theta \frac{\pi }{2}\right)-sin\left((\alpha -\mu )\frac{\pi }{2}\right)sin\left(\theta \frac{\pi }{2}\right)sgn\left(t\right)}{cos\left(\frac{\pi }{2}\mu \right)}}\right]{\left|t\right|}^{\mu -\alpha }\hfill \\ \hfill & ={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}\left[{\displaystyle \frac{cos(\alpha -\mu +\theta sgn\left(t\right))\frac{\pi }{2})}{cos\left(\frac{\pi }{2}\mu \right)}}\right]{\left|t\right|}^{\mu -\alpha }\hfill \end{array}$$

(64)

From this result, we can conclude that, if $\alpha <\mu$, the form of the power function on the right depends essentially on the asymmetry parameter. It is not very difficult to deduce the formula for $D_{\theta }^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)$ and relate it with (64).

Definition 4. 

Coherently with (31) define a general asymmetric power function of positive order, $\mu >0$, by

$$p_{\eta }^{\mu }\left(t\right)=-{\displaystyle \frac{cos\left[\left(\mu +\eta ·sgn\left(t\right)\right)\frac{\pi }{2}\right]\Gamma (-\mu )}{\pi }}{\left|t\right|}^{\mu }$$

(65)

having FT

$$P_{\eta }^{\mu }\left(\omega \right)={\left|\omega \right|}^{-\mu -1}{e}^{-i\eta {\displaystyle \frac{\pi }{2}}sgn\left(\omega \right)}$$

(66)

Theorem 5. 

In agreement with definition 4, there are two (quadrature) filters with frequency responses, $F\left(\omega \right)$ and $Q\left(\omega \right),$ that transform a given asymmetric power function into a symmetric and anti-symmetric powers respectively. They are given by

$$F\left(\omega \right)={\left|\omega \right|}^{a-\mu -1}{e}^{-i\eta {\displaystyle \frac{\pi }{2}}sgn\left(\omega \right)}$$

(67)

and

$$Q\left(\omega \right)={\left|\omega \right|}^{a-\mu -1}{e}^{i(1-\eta ){\displaystyle \frac{\pi }{2}}sgn\left(\omega \right)}$$

(68)

where a is any real value. In particular, we can set $a=\mu +1$, so that the two filters are generalized Hilbert transforms.

The proof is immediate, from (32) and (66).

This led us to formulate the following conjecture [61].

Conjecture 1. 

Let $f\left(t\right)$ be a piecewise continuous bounded function defined on $\mathbb{R},$ having Fourier transform. Assume it has an extremum at $t=t_0$. Then, there are derivative orders, $\alpha \in {\mathbb{R}}^{+},$ and one asymmetry parameter $\theta \in [-2,2],$ such that the unified fractional derivative, $D_{\theta }^{\alpha }f\left(t_0\right)$, is null.

To understand it and check its plausibility, let $\theta =\eta \in [-2,2]$ and suppose that

$$f\left(t\right)\approx A-B{p}_{\eta }^{\mu }{(t-t_0)}^{\mu },A,B\mu \in {\mathbb{R}}^{+},$$

in an interval $(t_0-\tau ,t_0+\tau ),\tau >0$. In such a situation, attending to the Theorem 5, the derivative, $D_{1-\eta }^{\alpha }f\left(t\right)$ is null at $t_0$. As it is clear, the derivative $D_{-\eta }^{\alpha }f\left(t\right)$ has a maximum at that point.

4.4. Remaining Cases

4.4.1. Other Singular Powers

In the above subsection we left unsolved two cases corresponding to the FT inversions of the transforms ${\left|\omega \right|}^{-2N-1},i{\left|\omega \right|}^{-2N}sgn\left(\omega \right),N\in {\mathbb{N}}_0$. These express “abnormal” cases that cannot be deduced directly from the general formulae (48) and (49). In [5] the solutions were found through a small trick consisting in doind the ordinary derivation relatively to the fractional order, followed by some simple manipulations. We are led to

$${\mathcal{F}}^{-1}\left[{\left|\omega \right|}^{-2N-1}\right]={\displaystyle \frac{{(-1)}^N{t}^{2N}}{\pi \left(2N\right)!}}\left[ln\left|t\right|+\gamma \right],$$

(69)

and

$${\mathcal{F}}^{-1}\left[{i\left|\omega \right|}^{-2N}sgn\left(\omega \right)\right]=-{\displaystyle \frac{{(-1)}^N{t}^{2N-1}}{\pi \left(2N\right)!}}\left[ln\left|t\right|+\gamma \right].$$

(70)

Therefore we can perform the completition of the above table.

With this table, we can solve some open problems, as the application of mixed Liouville/Riesz-Feller or the computation of the FT of some integer powers.

4.4.2. The Liouville Derivative of Two-Sided Power Functions

In [24], the computation of the Liouville derivative of ${\left|t\right|}^{-\mu },\mu >0$ was addressed and a partial solution was obtained. We have two ways of solving the problem: using the regularized Liouville derivative or through the FT as we did above. In the first case, we are limited by the properties of the gamma and beta integrals that introduce some limitations, although the regularization allows an enlargement of the parameter domains [58]. However, we cannot obtain the derivative of an increasing power, ${\left|t\right|}^{\mu },\mu >0.$ Using the FT, we can solve the problem with greater generality. We will consider the non integer case only. Let $\mu \in \mathbb{R}\setminus \mathbb{Z}$. The FT of ${\left|t\right|}^{\mu }$ is obtained from

$$\mathcal{F}\left[{\displaystyle \frac{{\left|t\right|}^{-\alpha -1}}{2\Gamma (-\alpha )cos\left(\frac{\pi }{2}\alpha \right)}}\right]={\left|\omega \right|}^{\alpha },$$

applying the duality property

$${\mathcal{F}\left[\right|t|}^{\mu }]={\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}.$$

(71)

Write successively

$$\begin{array}{cc}\hfill \mathcal{F}\left[D^{\alpha }{\left|t\right|}^{\mu }\right]& ={\left(i\omega \right)}^{\alpha }{\displaystyle \frac{{\pi \left|\omega \right|}^{-\mu -1}}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}\hfill \\ & ={\displaystyle \frac{{\left|\omega \right|}^{\alpha -\mu -1}{e}^{i\frac{\pi }{2}\alpha sgn\left(\omega \right)}}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}\hfill \\ & ={\displaystyle \frac{cos\left(\frac{\pi }{2}\alpha \right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}{\left|\omega \right|}^{\alpha -\mu -1}+i{\displaystyle \frac{sin\left(\frac{\pi }{2}\alpha \right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}{\left|\omega \right|}^{\alpha -\mu -1}sgn\left(\omega \right)\hfill \\ \end{array}$$

Therefore, using (48) with (52) and (49) with (54), we get

$$\begin{array}{cc}\hfill D^{\alpha }{\left|t\right|}^{\mu }=& -{\displaystyle \frac{cos\left(\frac{\pi }{2}\alpha \right)\Gamma (\alpha -\mu )sin\left((\alpha -\mu -1)\frac{\pi }{2}\right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }\hfill \\ & -{\displaystyle \frac{sin\left(\frac{\pi }{2}\alpha \right)\Gamma (\alpha -\mu )cos\left((\alpha -\mu -1)\frac{\pi }{2}\right)}{\Gamma (-\mu )cos\left(\frac{\pi }{2}\mu \right)}}{\left|t\right|}^{\mu -\alpha }sgn\left(t\right).\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill D^{\alpha }{\left|t\right|}^{\mu }=& {\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}\left[-{\displaystyle \frac{cos\left(\frac{\pi }{2}\alpha \right)sin\left((\alpha -\mu -1)\frac{\pi }{2}\right)+sin\left(\frac{\pi }{2}\alpha \right)cos\left((\alpha -\mu -1)\frac{\pi }{2}\right)sgn\left(t\right)}{cos\left(\frac{\pi }{2}\mu \right)}}\right].\hfill \end{array}$$

(72)

We can simplify this result as

$$D^{\alpha }{\left|t\right|}^{\mu }={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}{\left|t\right|}^{\mu -\alpha }\left\{\begin{array}{cc}{\displaystyle \frac{cos\left(\alpha \pi -\mu \frac{\pi }{2}\right)}{cos\left(\mu \frac{\pi }{2}\right)}}\hfill & t>0\hfill \\ 1\hfill & t<0.\hfill \end{array}\right.$$

(73)

Remark 8. 

It is important to note that

• The result for $t>0$ coincides with the one presented in [24], but with wider generality.
• For $t<0$, the result must be compared with the one stated in (42).
• Using the formulae presented in Table 2 we can obtain the corresponding expressions for $\mu ,\alpha \in \mathbb{Z}$.
• It is a simple task to get $D^{\alpha }{\left|t\right|}^{\mu }sgn\left(t\right)$.

4.4.3. The Fourier Transform of Negative Integer Powers

The presence of the gamma function can produce a major change in the characteristics of a power. For Example, ${\displaystyle \frac{t^{-1}}{\Gamma \left(0\right)}}$ is a delta distribution, while $t^{-1}$ is a hyperbola. Obviously, the corresponding FT are deeply different. The use of Table 2 and the duality property give the FT of some negative power functions. Let $N\in \mathbb{N}$. We have 4 cases

• $t^{-2N}={\left|t\right|}^{-2N}$
  This is immediate from Table 2, since we get

  $${\mathcal{F}}^{-1}{\left|\omega \right|}^{2N+1}=-{\displaystyle \frac{{(-1)}^N(2N+1)!}{\pi }}{\left|t\right|}^{-2N-2}$$

  and [25]

  $$\mathcal{F}{\left|t\right|}^{-2N}={\displaystyle \frac{{(-1)}^N\pi }{(2N-1)!}}{\left|\omega \right|}^{2N-1}$$
• $t^{-2N-1}sgn\left(t\right)={\left|t\right|}^{-2N-1}$
  Again from Table 2 we find

  $${\mathcal{F}}^{-1}\left[{\left|\omega \right|}^{-2N-1}\right]={\displaystyle \frac{{(-1)}^N{t}^{2N}}{\pi \left(2N\right)!}}\left[ln\left|t\right|+\gamma \right]$$

  which gives

  $$\mathcal{F}\left[{\left|t\right|}^{-2N-1}\right]=2{\displaystyle \frac{{(-1)}^N{\omega }^{2N}}{\left(2N\right)!}}\left[ln\left|\omega \right|+\gamma \right]$$
• $t^{-2N-1}={\left|t\right|}^{-2N-1}sgn\left(t\right)$
  Using Table 2 we obtain

  $${\mathcal{F}}^{-1}\left[i{\left|\omega \right|}^{-2N-1}sgn\left(\omega \right)\right]={\displaystyle \frac{{(-1)}^N}{2\left(2N\right)!}}{\left|t\right|}^{2N}sgn\left(t\right)$$
  From this relation, we can write

  $$\mathcal{F}\left[{\left|t\right|}^{-2N-1}sgn\left(t\right)\right]=-i\pi {\displaystyle \frac{{(-1)}^N}{\left(2N\right)!}}{\left|\omega \right|}^{2N}sgn\left(\omega \right)$$
• $t^{-2N}sgn\left(t\right)={\left|t\right|}^{-2N}sgn\left(t\right)$
  In the referred table, we find

  $${\mathcal{F}}^{-1}\left[i{\left|\omega \right|}^{-2N}sgn\left(\omega \right)\right]=-{\displaystyle \frac{{(-1)}^N{t}^{2N-1}}{\pi \left(2N\right)!}}\left[ln\left|t\right|+\gamma \right],$$

  that gives

  $$\mathcal{F}\left[{\left|t\right|}^{-2N}sgn\left(t\right)\right]=i2{\displaystyle \frac{{(-1)}^N{\omega }^{2N-1}}{\left(2N\right)!}}\left[ln\left|t\right|+\gamma \right],$$

4.5. Products of Powers and Other Functions

In some practical applications, we need to find fractional derivatives of the product of power functions and logarithms. We are going to find closed formulae and the corresponding FT. It is a simple task to get such formulae: we only have to pick those we described in the previous Section and compute suitable derivatives relatively to any involved parameter. This can be done both in time or frequency domains. Depending on the used derivative we can obtain several formulae starting from one. The first interesting result can be formulated as

Theorem 6. 

Let us consider the relation (42) and the above relations involving integer derivative orders. We can show [60] that

$$D^{\alpha }{t}^{\beta }log\left(t\right)\epsilon \left(t\right)={\displaystyle \frac{\Gamma (\beta +1)}{\Gamma (\beta -\alpha +1)}}{t}^{\beta -\alpha }\epsilon \left(t\right)\left[log\left(t\right)+\psi (\beta +1)-\psi (\beta -\alpha +1)\right].$$

(74)

In particular, with $\beta =0$, we obtain

$$D^{\alpha }log\left(t\right)\epsilon \left(t\right)={\displaystyle \frac{1}{\Gamma (-\alpha +1)}}{t}^{-\alpha }\epsilon \left(t\right)\left[log\left(t\right)-\gamma -\psi (-\alpha +1)\right].$$

(75)

Theorem 7. 

Consider relation (60) and proceed as above, computing the ordinary derivative relatively to μ.

$$D_0^{\alpha }{\left|t\right|}^{\mu }log\left|t\right|=A\left[\left(\psi (-\mu )-\psi (\alpha -\mu )\right)B+{\displaystyle \frac{\pi }{2}}{\displaystyle \frac{sin\left(\frac{\pi }{2}\alpha \right)}{{cos}^2\left(\frac{\pi }{2}\mu \right)}}\right]{\left|t\right|}^{\mu -\alpha }+{AB\left|t\right|}^{\mu -\alpha }log\left|t\right|,$$

(76)

with

$$A={\displaystyle \frac{\Gamma (\alpha -\mu )}{\Gamma (-\mu )}}$$

and

$$B={\displaystyle \frac{cos\left((\alpha -\mu )\frac{\pi }{2}\right)}{cos\left(\frac{\pi }{2}\mu \right)}}$$

Other similar relations can be obtained from (61) to (64).

More interesting in applications is the multiplication of powers and exponentials [6].

Theorem 8. 

Consider the product $p\left(t\right)=t^N{e}^{at},t\in \mathbb{R}$, where $N\in \mathbb{N},a\in {\mathbb{R}}^{+}$. This function is important in solving linear systems and, in particular, for defining tempered derivatives and systems. The Liouville derivative of $p\left(t\right)$ is given by

$$D^{\alpha }p\left(t\right)=\sum _{k=0}^N{(-1)}^k{(-\alpha )}_k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)a^{\alpha -k}{t}^{N-k}{e}^{at}.$$

(77)

The proof is immediate from the Leibniz rule

$$D^{\alpha }\left[f\left(t\right)g\left(t\right)\right]=\sum _{i=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{i}}\right)D^{i}f\left(t\right)D^{\alpha -i}g\left(t\right),$$

(78)

by using the relations introduced in Section 3. If, instead of a bilateral power, we used a causal one, the summation would have infinite terms. Let $p\left(t\right)=t^N{e}^{at}\epsilon \left(t\right),t\in \mathbb{R}$. This case is interesting, because we can associate the Heaviside function to the power or to the exponential, giving two different expressions

• $$D^{\alpha }p\left(t\right)=\sum _{k=0}^{\infty }{(-1)}^k{\displaystyle \frac{{(-\alpha )}_k}{k!}}{\displaystyle \frac{N!t^{N-\alpha }}{\Gamma (N-\alpha +1)}}\epsilon \left(t\right)a^{\alpha -k}{t}^{N-k}{e}^{at}.$$

  (79)
• $$D^{\alpha }p\left(t\right)=\sum _{k=0}^N{(-1)}^k{(-\alpha )}_k\left({\displaystyle \genfrac{}{}{0pt}{}{\alpha }{k}}\right)t^{N-k}{D}^{\alpha -k}\left[e^{at}\epsilon \left(t\right)\right],$$

  (80)
  We can compute $D^{\alpha -k}\left[e^{at}\epsilon \left(t\right)\right],$ either from the Taylor expansion of the exponential, or from the Liouville integral.

5. Conclusion

We introduced the general forms of power functions, computed their derivatives, and found their Fourier transforms. The unified fractional derivative was used, due to its connection with the powers.