Revetment Rock Armour Stability Under Depth-Limited Breaking Waves

1. Introduction

1.1. Background

Typically, coastal revetments are constructed to prevent wave erosion of dunes and foreshores. Revetments may be subjected to waves that shoal and dissipate on the revetment slope, the revetment toe being in relatively deep water, to waves that shoal on the seabed immediately in front of the revetment, breaking directly onto it, and to waves that have shoaled and broken on the seabed prior to reaching the revetment. The latter conditions have revetment toes in relatively shallow water, being the subject of this research.

The revetment armour is underlain by a separating filter layer overlying fine-grained sediment. While allowing for groundwater seepage, these underlying materials are impermeable to incident wave energy, which is reflected onto the revetment armour. Therefore, the stability of revetment armour is somewhat compromised compared with breakwater armouring that, commonly, overlies a permeable core.

Armour units for revetments subjected to wave impact are designed with formulae developed and calibrated empirically using hydraulic scale models [1,2,3]. Early work defined the median requisite armour mass, M₅₀, as a function of wave height, rock density, water density and revetment slope following the passage of some 1,000 regular waves, being the Hudson formula [1]. These tests were undertaken on sloping structures for permeable breakwaters under regular non-breaking waves. Empirical coefficients for a range of various concrete armour units and rock types for both non-breaking and breaking waves have been developed subsequently. The Hudson formula is:

$$M_{50}={\displaystyle \frac{{\rho }_a{H}_s^3}{K_D{∆}^{3}cot\alpha }}$$

(1)

where M₅₀ is the median armour mass (kg), ρ_a is the armour density (kg/m³), H_s is the incident significant wave height (m), Δ is the relative density of the armour to water ((ρ_a - ρ_w)/ρ_w), K_D is a damage coefficient derived empirically and cotα is the revetment armour slope.

Testing of rock armour and various concrete armour units under breaking waves was undertaken in a wave flume at the University of New South Wales Water Research Laboratory (UNSW WRL) [4,5]. The testing under regular waves found that K_D depended on percentage damage D thus ([4,5] p28):

$$K_D=a{D}^n$$

(2)

where (a, n) = (1.2, 0.51) for two layers of random rock on an impermeable core and D is percentage damage (0 < D < 0.20). This form of expression for the Hudson damage coefficient has been adopted for subsequent modifications to the Hudson formula by others [2,6].

Later research included formulae calibrated empirically for both surging and plunging random waves on sloping revetments and breakwaters. The van der Meer formulae [2] encompassed a larger range of relevant parameters including the Iribarren number (wave period), core permeability, degree of damage and the number of zero-crossing waves. Most of the tests comprised relatively deep water at the structure toe. The requisite armour mass was formulated as a function of wave height cubed for plunging conditions:

$$M_{50}={\displaystyle \frac{{\rho }_a{\epsilon }_m^{1.5}{H}_s^3}{c_{pl}^3{{\left(\frac{S}{\sqrt{N}}\right)}^{0.6}{P}^{0.54}∆}^3}}$$

(3a)

and for surging conditions:

$$M_{50}={\displaystyle \frac{{\rho }_a{P^{0.39}H}_{\mathrm{s}}^3}{c_s^3{{\left(\frac{S}{\sqrt{N}}\right)}^{0.6}{\epsilon }_m^{3P}∆}^3{cot\alpha }^{1.5}}}$$

(3b)

where P is a permeability parameter of the armour underlayers, ε_m is the Iribarren number using the mean wave period, $S=A_E/D_{n50}^2$, A_E is the cross-sectional eroded area, D_n50 is the nominal median diameter of the armour stones, N is the number of zero-crossing waves with calibration coefficients C_pl = 6.2 and C_s = 1.0. As $M_{50}={\rho }_a{D}_{n50}^3$, $S=A_E/D_{n50}^2$ and D_n50 is likely to be included in the derivation of P, although not given in the reference [2], D_n50 is included both in the dependent and independent variables.

The most recent development of these formulae, being that of van Gent [6], included testing of two sloping structures with impermeable underlayers. The van Gent formula can be expressed as:

$$M_{50}={\displaystyle \frac{{\rho }_a{H}_s^3}{5.4{{\left(\frac{S}{\sqrt{N}}\right)}^{0.6}\left(1+\raisebox{1ex}{$D_{n50core}$}\!\left/ \!\raisebox{-1ex}{$D_{n50}$}\right.\right)}^3{∆}^3{cot\alpha }^{1.5}}}$$

(4)

with D_n50 included in both the dependent and independent variables.

With this development, the influence of wave period was considered small compared with the amount of scatter in the data due to other reasons [6]. Therefore, the wave period was not used in this formula and there was no separation between “plunging” conditions and “surging” conditions [6].

These formulae, (3) and (4), have been revised recently with changes made to the calibration coefficients and to the wave period parameters to be used [7,8]. However, their basic structures have remained the same.

Typical conditions studied by van der Meer [2] had revetment toes in relatively deep water, with waves dissipating on the revetment slope, whereas van Gent [3] and Gordon [4,5] considered waves breaking onto the revetment armour directly from the fronting seabed.

More recently, numerical models such as SPH (Smoothed Particle Hydrodynamics), IHFOAM, waves2Foam, and DualSPHysics have been developed for overtopping and armour stability research [9,10,11]. These models can be expensive computationally, particularly when applied to solve large domains and long duration wave trains, which may be required for wave-structure interaction ([11] p80). However, significant progress has been made on wave interaction with porous structures with these models that do not require complex meshes nor any special treatment for the free-surface flows ([11] p80).

As many numerical models rely on physical modelling for validation, the role of physical hydraulic scale modelling of coastal protection structures remains relevant [12]. The empirical approaches based on physical model studies defined the median requisite armour mass as a function of, inter alia, incident wave height cubed [1,2,3]. No explanation for this has been proffered other than it would appear to have been necessary to ensure dimensional integrity of the formulae. However, other researchers have proposed sediment transport as a function of incident wave energy ([13] p27).

1.2. Thesis

It is the energy of breaking waves that applies the disturbing forces to revetment armour and it is the mass of that armour that secures or otherwise its stability. This article examines revetment rock armour stability as a function of incident wave energy, E, which is a function of the product of wave height squared and wavelength ([14] p2-26, eqn(2-38)) thus:

$$E={\displaystyle \frac{{\rho }_{w}g{H}_s^{2}L}{8}}$$

(5)

where g is gravitational acceleration, L is the nearshore wavelength. In shallow water, the nearshore wavelength can be approximated by ([14] p2-25 eqn2-37, [15]):

$$L=T\sqrt{g{h}_{toe}}$$

(6)

where h_toe is the nearshore depth at the revetment.

The following wave energy formula is proposed for the requisite rock armour mass on an impermeable core revetment, adopting the dependence on armour slope from van der Meer [2] and incorporating nearshore depth and wave period through wavelength:

$$M_{50}={\displaystyle \frac{{\rho }_a{H}_s^{2}T\sqrt{g{h}_{toe}}}{{K^{\prime }∆}^3{cot\alpha }^{1.5}}}$$

(7)

The damage coefficient, $K^{\prime }=f\left(D/\sqrt{N}\right)$, is calibrated empirically herein in the form of equation (2) for double layered rough angular rock [4,5]. Noted is that the nearshore wave height also is a function of depth, period and beach slope ([16,17] p81).

2. Method

2.1. Data

Data for this research comprised:

• Physical model test results undertaken in flumes at New South Wales Government Manly Hydraulics Laboratory [18,19] for a commercial project comprising the design of rock armour protection on clay embankments for the Mardie Salt and Potash facility, Western Australia (Figure 1 and Figure 2))
• Research for amour rock stability under breaking waves generated in a flume at Delft Hydraulics [3,6]
• Research from a Master’s degree thesis for amour rock stability under breaking waves undertaken in a flume at UNSW WRL [4,5].

2.2. Physical Modelling

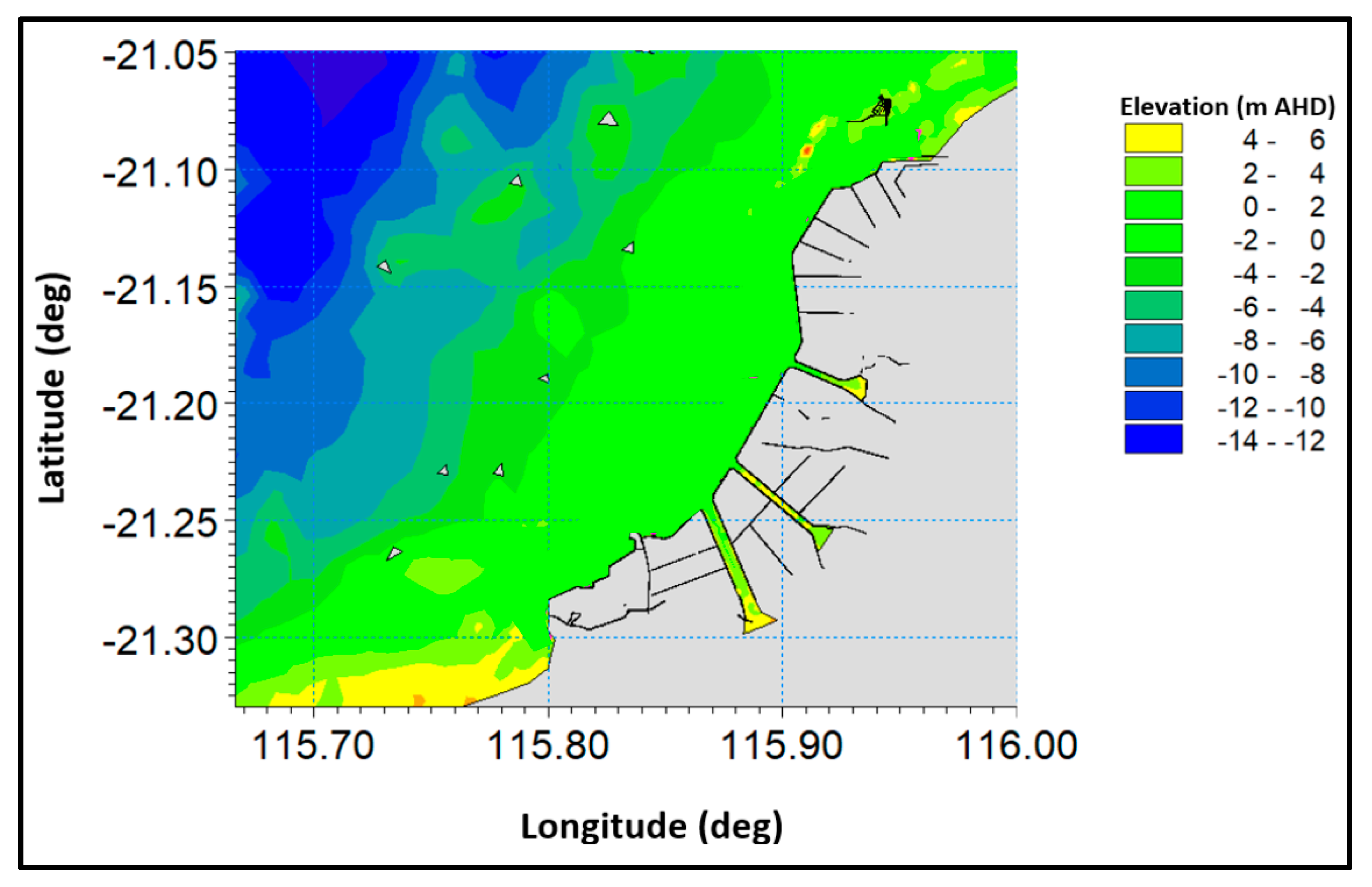
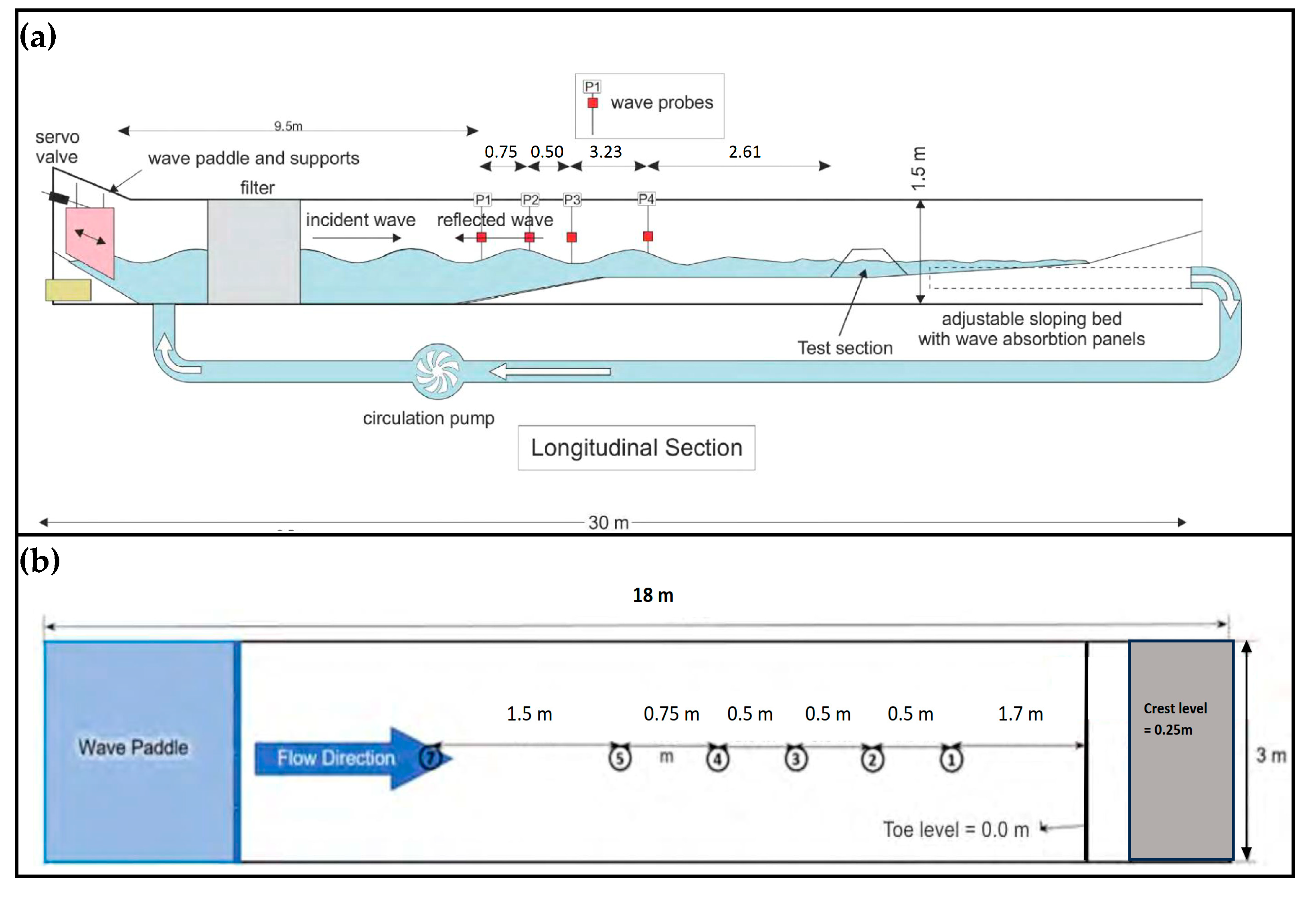
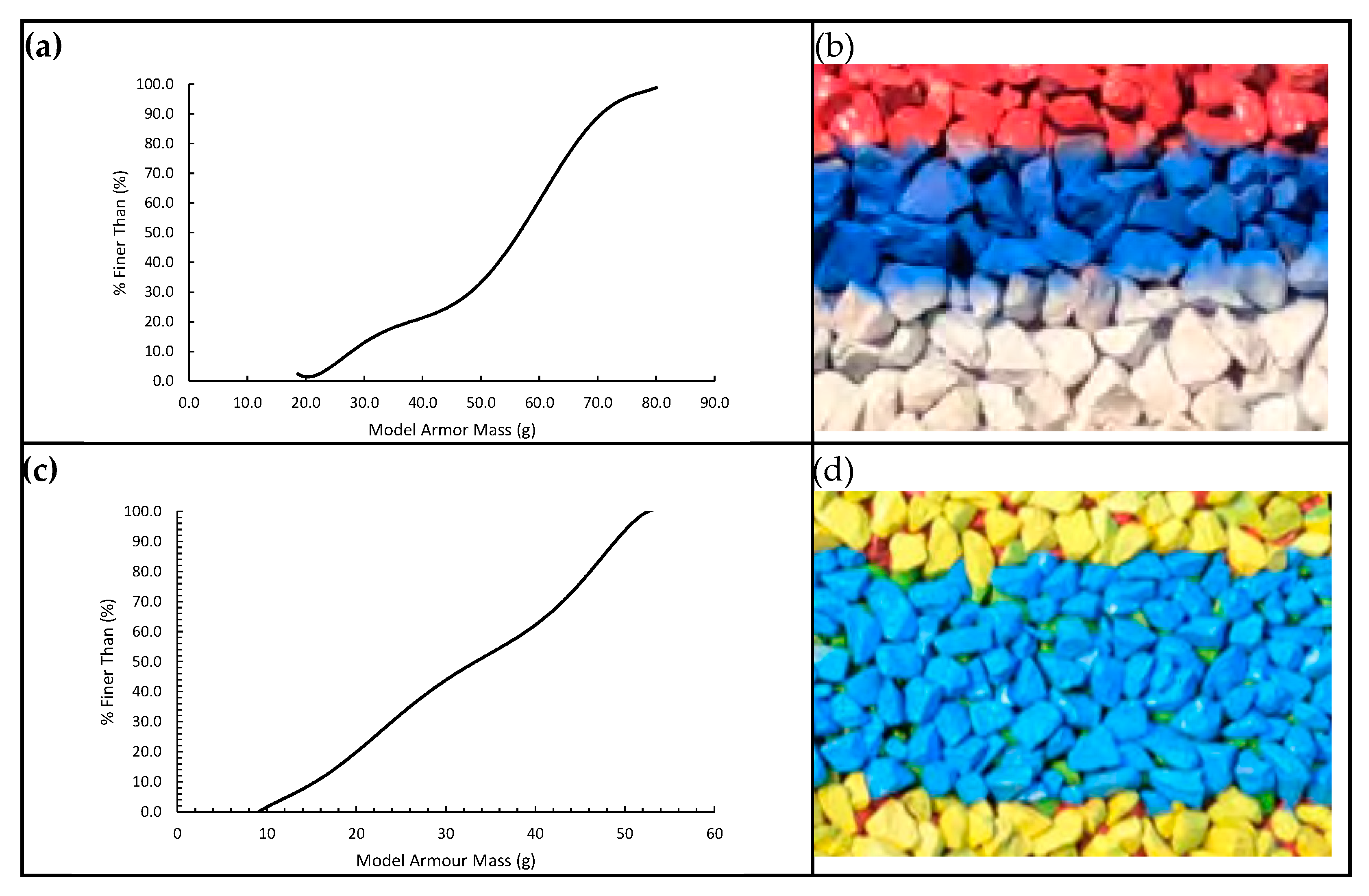
2.2.1. Manly Hydraulics Laboratory

Two-dimensional physical model testing for the rock armoured revetments of the Mardie embankments was undertaken in 1 m and 3 m wide flumes (Figure 3). Model armour comprised two layers of a well graded igneous rock of specific gravity s.g. = 2.76. The rock was placed with a porosity of 40% on an impermeable slope of cotα = 2.5. Testing was undertaken with random waves in fresh water.

For the 1 m wide flume model, the seabed slope was flat (m = 0) and M₅₀ = 0.056 kg (Figure 4(a)). Most of the tests comprised some 3,000 waves of peak period T_p = 1.2 s, although some tests were undertaken with fewer waves (100, 300, 500). For the 3 m wide flume model, the seabed slope was m = 0.006 and M₅₀ = 0.034 kg (Figure 4(c)). Tests comprised some 2,000 zero-crossing waves with peak period T_p = 2.5 s.

The modelling comprised testing the armour rock stability over a range of water levels with depth-limited breaking waves, recording the subsequent damage. Damage was observed by comparing photographs taken before and after exposure to the test conditions. Damage was quantified by counting the number of units displaced by more than one nominal diameter as a percentage of the total number of units within the wave runup/rundown section of the revetment. All rocks in the two armour layers were considered exposed. Only results with damage less than 15% for severe breaking were considered, defined as H_s/h_toe > 0.4 for these very flat slopes on which the maximum wave height that can be sustained is around 55% of the depth [20,21]. Test and reduced data are in Table 1.

2.2.2. Delft Hydraulics

Data were reviewed from tests undertaken in the 1 m wide flume of Delft Hydraulics in 1983-1986 [2] and in 2003 [3,6]. The former are documented comprehensively in the thesis of professor van der Meer, which is publicly and readily available. Included were some 132 tests with rough angular armourstone of D_n50 = 0.036 m on impermeable underlayers of slopes cotα= 2, 3, 4, and 6, T_m varying from 1.3 s to 3.3 s, damage recorded after 1,000 and 3,000 waves with damage after 3,000 waves varying from S = 0.6 to 33.0. As H_s/h_toe varied from 0.06 to 0.32 with an average value of 0.16, the revetment toe was in relatively deep water with waves collapsing and dissipating on the revetment slope, rather than shoaling and breaking onto it from the fronting seabed. These data were not considered in this analysis.

For the tests in 2003, the armour comprised well sorted “standard rough angular rock” of specific gravity 2.75 with D_n50 = 0.026 m [6]. The revetments were on impermeable cores at slopes of cotα = 2 (for Structure No. 6) and cotα = 4 (for Structure No. 7). The seabed slope was m = 0.033. Only considered were results with damage S < 12 (D < 0.15) for severe wave breaking, defined herein as H_s/h_toe > 0.5 for this moderate seabed slope (m = 0.033). The flume test data and reduced test data are in Table 2.

2.2.3. Water Research Laboratory

Testing of rough angular rock armour on slopes of cotα = 1.25, 1.5 and 2.0 with regular waves was undertaken in a flume 1 m wide, 1.5 m deep and 30 m long [4,5]. The flume bed for 8 m fronting the structure had a slope m = 0.033, beyond which the bed was flat. The limestone rock armour had a specific gravity of 2.7, was graded with a ratio of maximum to minimum mass of approximately 2.0, a median mass of M₅₀ = 0.064 kg, an aspect ratio not exceeding 2.0 with edges that were moderately sharp and was placed randomly in two layers, the core being impermeable.

For a given toe depth, the wave height and period were adjusted until the wave formed a plunging break immediately onto the structure. The toe depth was increased by small increments allowing larger waves to break onto the structure. Damage was assessed as the percentage of rock dislodged over the revetment area extending from one wave height below SWL to the limit of wave uprush. The testing regime was set up to enable the effects of up to 10,000 regular waves to be observed for each water level and period combination. Under the limiting conditions progressive damage to the armour was observed up to failure, which occurred generally after around 2,500 waves [4,5]. Progressive damage to failure developed once damage had reached around 20%. For wave attack producing lesser damage levels the structures adopted a stable configuration once the initial damage had occurred. The test data and reduced test data are in Table 3.

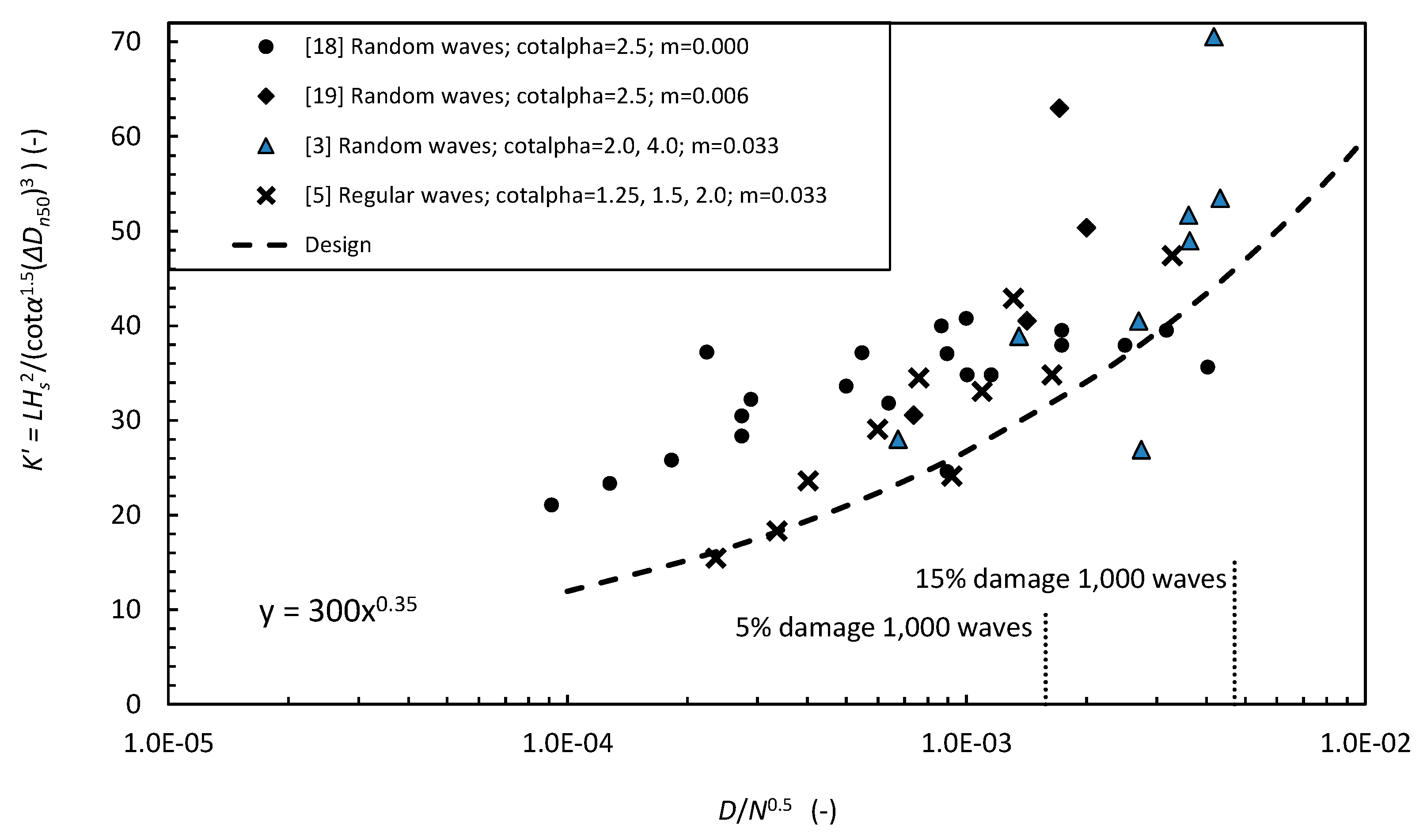
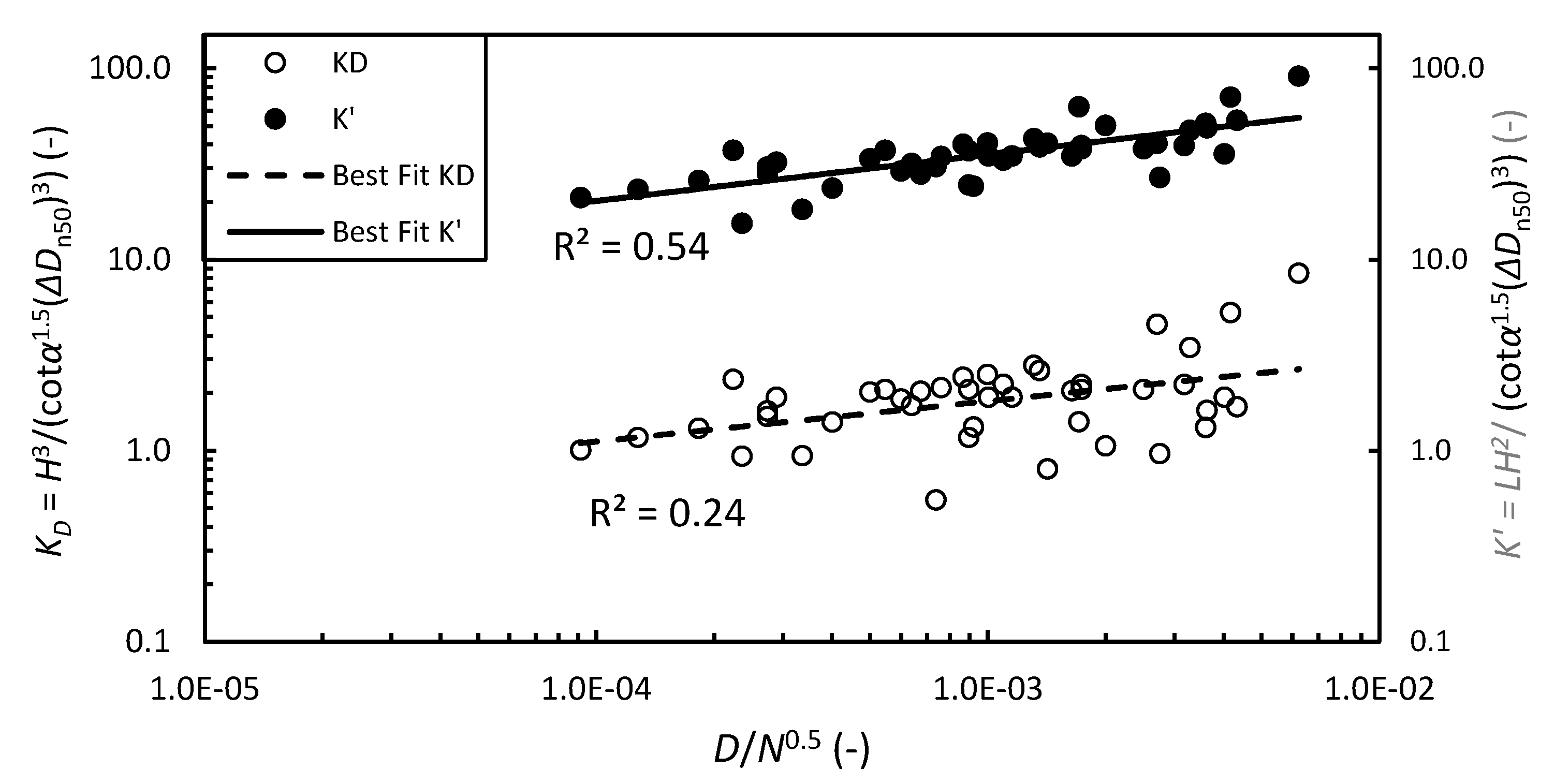
3. Results

The damage coefficient for the wave energy formula, $K^{\prime }=L{H}_s^2/{(\left(∆D_{n50}\right)}^3{cot\alpha }^{1.5}),$ is plotted against normalised damage $D/\sqrt{N}$ in Figure 5. A design condition that over-predicts around 95% of the requisite mass data as modelled is presented as a dashed curve. The resulting calibrated wave energy formula is:

$$M_{50}={\displaystyle \frac{{\rho }_a{H}_s^2{T}_p\sqrt{g{h}_{toe}}}{300{\left(\frac{D}{\sqrt{N}}\right)}^{0.35}{∆}^3{cot\alpha }^{1.5}}}$$

(7)

4. Discussion

Data presented herein have been drawn from a 2023 [18,19] commercial project and 2003 [3] and 1973 [5] research projects. No other data for very shallow waves breaking onto impermeable core, rock armoured revetments were found. The results are qualified as follows.

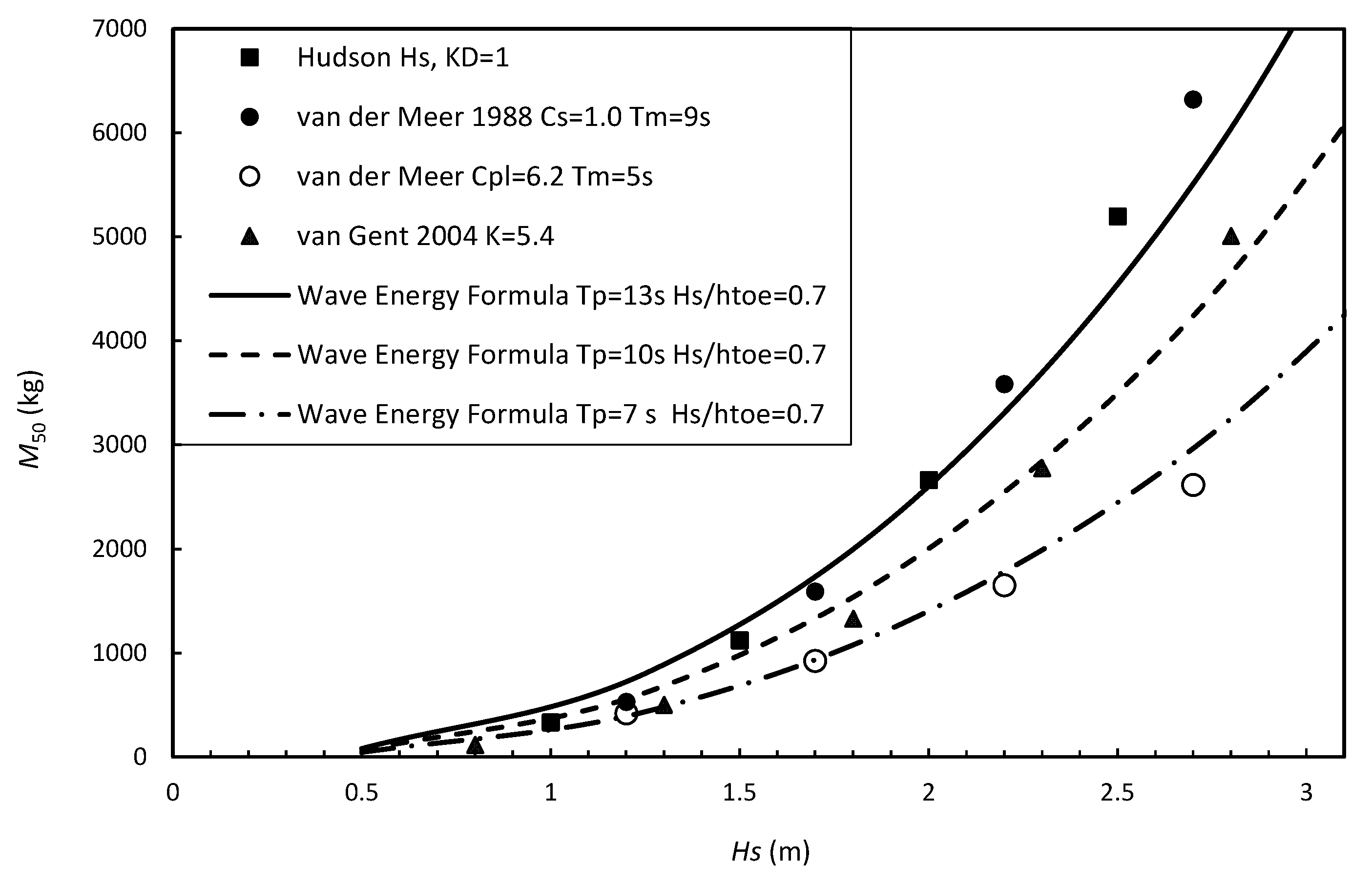
4.1. Comparison with Established Formulae

To compare the wave energy formula, which uses LH² in lieu of H³ with the Hudson formula, in Figure 6 the very shallow water flume data [3,5,18,19] were plotted against normalised damage, $D/\sqrt{N}$, with the wave energy damage coefficient, $K^{\prime }=L{H}_s^2/{cot\alpha }^{1.5}{\left(∆D_{n50}\right)}^3$ and a modified Hudson coefficient $K_D=H_s^3/{cot\alpha }^{1.5}{\left(∆D_{n50}\right)}^3$. The Coefficients of Determination from the “best fit” trend lines (Figure 6) indicated that the wave energy formula (LH²) was significantly more coherent than the Hudson approach (H³), with K’_max/K’_min = 6 whereas K_{D max}/K_{D min} = 15.

Intuitively, the greater the breaking wave energy the larger would be the damage to rock armour. Hence, waves of longer period would require larger armour rock mass for stability. However, neither the Hudson [1] nor the van Gent [6] formulae include a wave period parameter.

Calibrating rock armour damage to the energy of the depth-limited breaking waves introduces both toe depth and wave period to the design formula. As shown in Figure 7, both the wave energy formula and that of van der Meer [2] require larger requisite mass for waves with longer periods. The wave energy formula matches well the results from the Hudson formula [1], as well as those from the van der Meer [2] formulae for both longer and shorter wave periods, but over-estimates and under-estimates results from the van Gent formula [6] for longer and shorter wave periods respectively, which is expected as the van Gent formula does not include wave period.

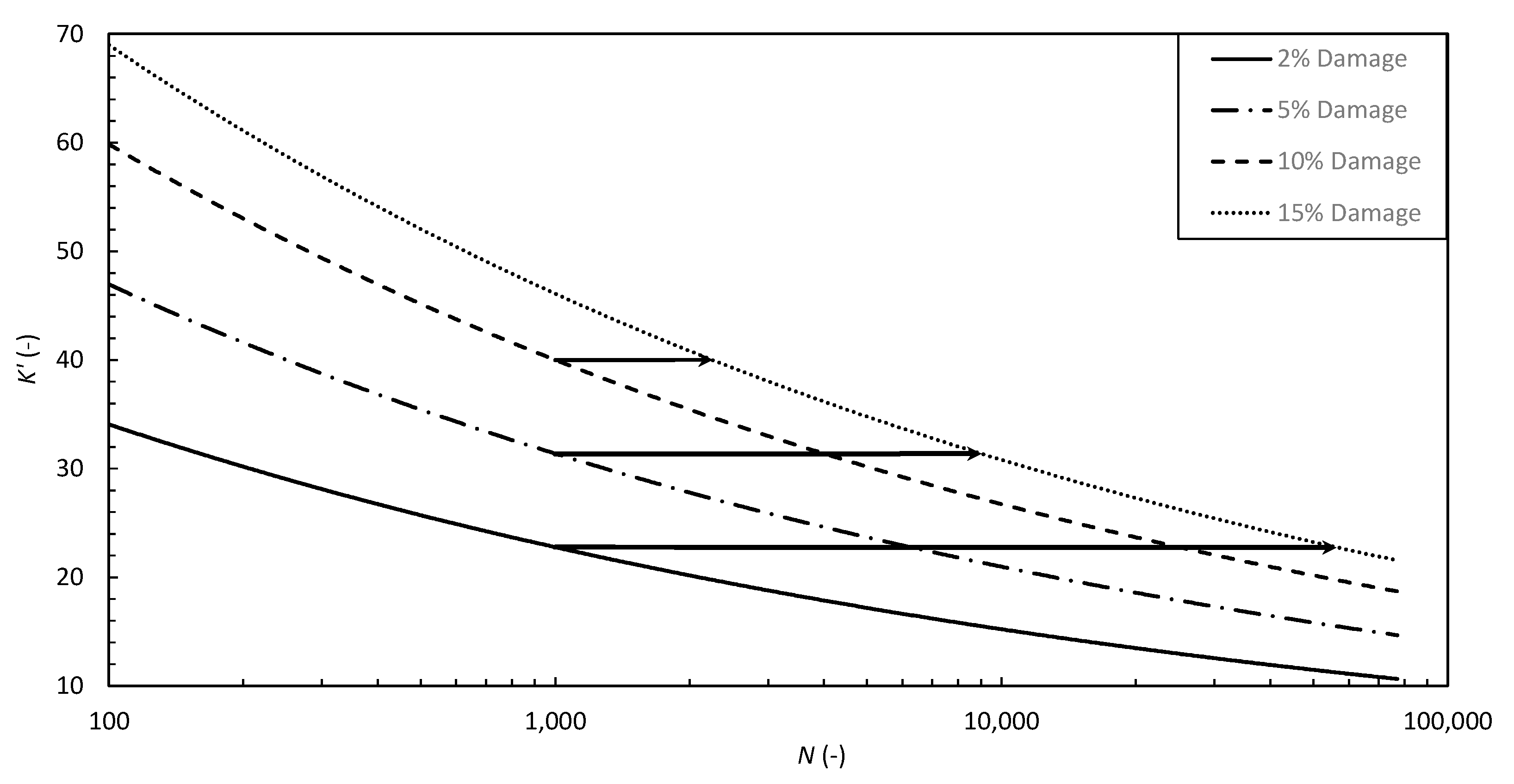
4.2. Storm Duration

Flume testing has found that rip-rap damage may not have stabilised after more than 5,000 to 20,000 zero-crossing waves ([23] Figs7,16,28-29,31,33-34). For many of the tests undertaken herein the duration was some 1,000 to 5,000 zero-crossing waves, which may not have been enough to reach stabilisation of damage.

The number of waves matters. Should a design comprise 2% damage, that is virtually no damage, after a storm of 1,000 waves, then failure of the rock armour protection, assumed to be at 15% damage, is predicted not to occur until the passage of a further 55,000 design waves (Figure 8). Further, however, the predictor indicates that should a concept design comprise 5% damage under 1,000 waves, then failure could occur following the passage of an additional 8,000 design waves (Figure 8). For 10% damage/1,000 waves design criteria, failure is predicted following a further 1,300 design waves (Figure 8). Such considerations could inform an economic analysis of capital cost versus delayed maintenance costs.

4.3. Limits of Application

Ranges in the values of pertinent parameters of the model studies adopted herein are presented in Table 3.

Prototype conditions would lay beyond some of these limits and extrapolating results from the predictor proposed should consider possible scale effects and processes not included in the base data. Paucity of data precluded considering the influence of seabed slope on the rock armour formula proposed.

5. Conclusions

A formula has been presented for coastal revetments in very shallow water that relates the requisite stable mass of armour rock to the energy of the incident breaking waves. This formula includes parameters for significant wave height, wave period, toe depth, degree of damage, the number of waves, revetment slope, armour and water density. The formula has been calibrated using flume data generated by hydraulic laboratories in Australia and the Netherlands. The formula is compared with those of Hudson, and as modified by van der Meer and van Gent, as commonly used, and shows more coherence with the available flume data than those of the modified Hudson formulae. The formula allows for the investigation of capital expenditure versus maintenance for the design of rock armoured revetments. However, this development would benefit from more laboratory data, which is required also to investigate the impact of seabed slope.