Fracture Network Mathematics

1. Introduction

Analytic solutions for elastostatic displacement due to vertical/shear traction applied to the faces of a single crack in a 2D plane are reviewed in Section 2. The purpose of this review is to introduce mathematics relevant to specifying multi-crack elastostatic displacements. In Section 3, the relation between multi-crack elastostatic displacement fields and Riemann surface geometry is discussed. Section 4 explains why 2D multi-crack solutions appear limited to describe idealized cracks in 2 spatial dimensions, and conjectures how 3D fracture networks in the lithosphere can be described in terms of singular spectrum analysis of crack phase fields.

2. Single Crack 2D Elastostatic Displacement

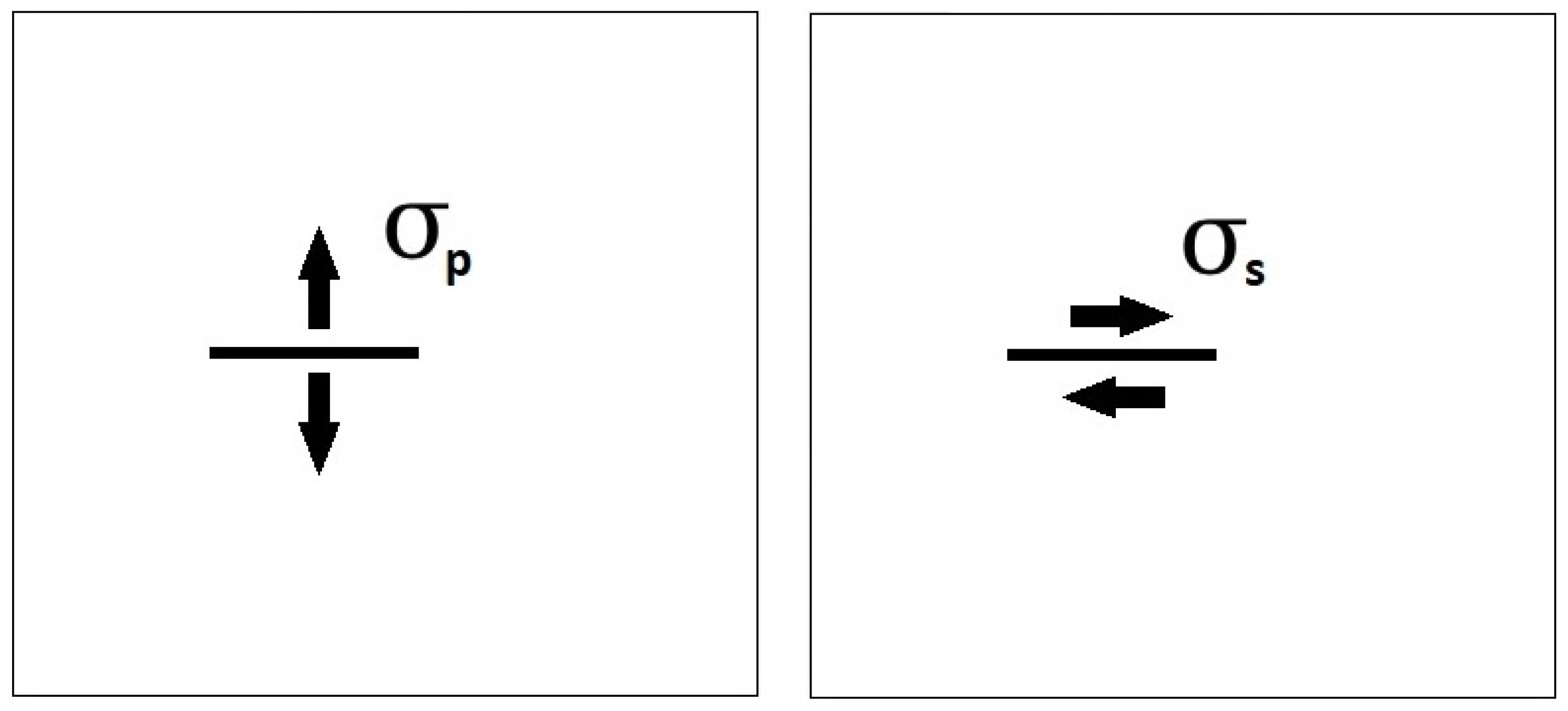
2.1. Yoffe Mode I Crack

Consider a sharp crack of length R propagating with constant velocity v in a uniform elastic material in 2D plane strain conditions, whereby the crack tips are located at $(vt-R,0)$ and $(vt,0)$. In terms of coordinates $(\xi ,y)=(x-vt,y)$ in which the crack tips are fixed at $(-R,0)$ and $(0,0)$, the elastic displacement $\mathbf{u}(x,y,t)$ can be expressed in terms of scalar and vector potentials $\varphi (\xi ,y)$ and $\overrightarrow{\psi }=(0,0,\psi (\xi ,y))$ as:

$$\mathbf{u}(x,y,t)=\nabla \varphi +\nabla \times \overrightarrow{\psi },$$

(1)

where:

$$\begin{array}{ccc}\hfill {\alpha }_P^2{\displaystyle \frac{{\partial }^2\varphi }{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2\varphi }{\partial y^2}}& =& 0,\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\alpha }_S^2{\displaystyle \frac{{\partial }^2\psi }{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2\psi }{\partial y^2}}& =& 0,\hfill \end{array}$$

(3)

for constants ${\alpha }_P=\sqrt{1-v^2/v_P^2}$ and ${\alpha }_S=\sqrt{1-v^2/v_S^2}$ specified by v and the P and SV wave velocities $v_P$ and $v_S$[6]. In turn, the potentials $\varphi (\xi ,y)$ and $\psi (\xi ,y)$ can be expressed in terms of analytic functions $F\left(\zeta \right)$ and $G\left(\zeta \right)$ as:

$$\begin{array}{ccc}\hfill \varphi (\xi ,y)& =& ReF\left({\zeta }_P\right),\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \psi (\xi ,y)& =& ImG\left({\zeta }_S\right),\hfill \end{array}$$

(5)

for ${\zeta }_P=\xi +i{\alpha }_{P}y$ and ${\zeta }_S=\xi +i{\alpha }_{S}y$, whereby elastic displacement field and stress field components are given by the equations:

$$\begin{array}{ccc}\hfill u_x(x,y,t)& =& Re(F^{\prime }\left({\zeta }_P\right)+{\alpha }_S{G}^{\prime }\left({\zeta }_S\right)),\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill u_y(x,y,t)& =& -Im({\alpha }_P{F}^{\prime }\left({\zeta }_P\right)+G^{\prime }\left({\zeta }_S\right)),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\sigma }_{xx}(x,y,t)& =& Re((\lambda +2\mu -\lambda {\alpha }_P^2)F^{\prime \prime }\left({\zeta }_P\right)+2\mu {\alpha }_S{G}^{\prime \prime }\left({\zeta }_S\right)),\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\sigma }_{yy}(x,y,t)& =& -\mu Re((1+{\alpha }_S^2)F^{\prime \prime }\left({\zeta }_P\right)+2{\alpha }_S{G}^{\prime \prime }\left({\zeta }_S\right)),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\sigma }_{xy}(x,y,t)& =& -\mu Im(2{\alpha }_P{F}^{\prime \prime }\left({\zeta }_P\right)+(1+{\alpha }_S^2)G^{\prime \prime }\left({\zeta }_S\right)),\hfill \end{array}$$

(10)

for Lame parameters $\lambda$ and $\mu$.

Now assume the crack is Mode I, in that a uniform vertical traction ${\sigma }_p$ acts on the crack faces while the shear traction applied to the crack faces is 0, as illustrated in Figure 1-left. In this case the $-R<\xi <0$ crack face boundary conditions are:

$$\begin{array}{ccc}\hfill {\sigma }_{yy}(\xi ,0^{\pm })& =& -{\sigma }_p,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\sigma }_{xy}(\xi ,0^{\pm })& =& 0.\hfill \end{array}$$

(12)

and the potentials $\varphi (\xi ,y)$ and $\psi (\xi ,y)$ have the symmetries $\varphi (\xi ,-y)=\varphi (\xi ,y)$ and $\psi (\xi ,-y)=-\psi (\xi ,y)$ imply $u_x(x,-y,t)=u_x(x,y,t)$ and $u_y(x,-y,t)=-u_y(x,y,t)$, in keeping with x-axis reflection symmetry of a Mode I crack displacement solution. Furthermore, the Cauchy-Riemann equations imply $F\left(\overline{\zeta }\right)=\overline{F\left(\zeta \right)}$ and $G\left(\overline{\zeta }\right)=\overline{G\left(\zeta \right)}$.

The symmetries of F and G, together with Equations (10) and (12), imply the function:

$$E\left(\zeta \right)=2{\alpha }_P{F}^{\prime \prime }\left(\zeta \right)+(1+{\alpha }_S^2)G^{\prime \prime }\left(\zeta \right),$$

(13)

is continuous across the crack line between $\zeta =-R$ and $\zeta =0$, and is therefore entire. Given that the elastic velocity and stress fields are zero at points remote from the crack, Lioiuville’s theorem on bounded entire functions implies:

$$G^{\prime \prime }\left(\zeta \right)=-{\displaystyle \frac{2{\alpha }_P}{1+{\alpha }_S^2}}{F}^{\prime \prime }\left(\zeta \right).$$

(14)

Equations (9) and (14) together with condition (11) imply:

$$Re{F}^{\prime \prime }\left(\xi \right)=-{\displaystyle \frac{1+{\alpha }_S^2}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }},-R<\xi <0,$$

(15)

where $D=4{\alpha }_P{\alpha }_S-{(1+{\alpha }_S^2)}^2$, and discontinuity of $Im{F}^{\prime \prime }\left(\zeta \right)$ across the crack line occurs as necessary to account for discontinuity in elastic displacement. Assuming $\sqrt{\zeta (\zeta +R)}$ is defined as a single valued function on the complex plane with a branch cut between $\zeta =-R$ and $\zeta =0$ along $y=0$, the function:

$$\left(F^{\prime \prime }\left(\zeta \right)+{\displaystyle \frac{1+{\alpha }_S^2}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}\right)\sqrt{\zeta (\zeta +R)}-{\displaystyle \frac{1+{\alpha }_S^2}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}(\zeta +R/2),$$

(16)

is continuous across the crack line, and is therefore an entire function that approaches 0 as $\left|\zeta \right|\to \infty$, implying:

$$\begin{array}{c}\hfill F^{\prime \prime }\left(\zeta \right)={\displaystyle \frac{1+{\alpha }_S^2}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}\left({\displaystyle \frac{\zeta +R/2}{\sqrt{\zeta (\zeta +R)}}}-1\right),\end{array}$$

(17)

and:

$$\begin{array}{c}\hfill G^{\prime \prime }\left(\zeta \right)=-{\displaystyle \frac{2{\alpha }_P}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}\left({\displaystyle \frac{\zeta +R/2}{\sqrt{\zeta (\zeta +R)}}}-1\right).\end{array}$$

(18)

Equations (17) and (18) imply the normal stress distribution ${\sigma }_{yy}(\xi ,0)$ on the crack line ahead of the advancing crack tip is:

$${\sigma }_{yy}(\xi ,0)={\sigma }_p\left({\displaystyle \frac{\xi +R/2}{\sqrt{\xi (\xi +R)}}}-1\right),\xi >0.$$

(19)

Integration of Equations (17) and (18) gives equations:

$$\begin{array}{c}\hfill F^{\prime }\left(\zeta \right)={\displaystyle \frac{1+{\alpha }_S^2}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}\left(\sqrt{\zeta (\zeta +R)}-\zeta -R/2\right),\end{array}$$

(20)

and:

$$\begin{array}{c}\hfill G^{\prime }\left(\zeta \right)=-{\displaystyle \frac{2{\alpha }_P}{D}}{\displaystyle \frac{{\sigma }_p}{\mu }}\left(\sqrt{\zeta (\zeta +R)}-\zeta -R/2\right).\end{array}$$

(21)

in which constants of integration have been selected so elastic displacements are 0 at remote points. Assuming $\sqrt{\zeta (\zeta +R)}$ is defined as a single valued function on the complex plane with a branch cut between $\zeta =-R$ and $\zeta =0$ along $y=0$, Equations (20) and (21) together with equation (7) imply the crack opening displacement is:

$$u_y(\xi ,0^{+})={\displaystyle \frac{{\alpha }_P{v}^2}{D{v}_S^2}}{\displaystyle \frac{{\sigma }_p}{\mu }}\sqrt{-\xi (\xi +R)},-R<\xi <0.$$

(22)

2.2. Rice Mode II Crack

Now assume the crack is Mode II, in that a uniform shear traction ${\sigma }_s$ is applied to the crack faces while the vertical traction applied to the crack faces is 0, as illustrated in Figure 1-right[11]. In this case the $-R<\xi <0$ crack face boundary conditions are:

$$\begin{array}{ccc}\hfill {\sigma }_{xy}(\xi ,0^{\pm })& =& -{\sigma }_s,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\sigma }_{yy}(\xi ,0^{\pm })& =& 0,\hfill \end{array}$$

(24)

and the potentials $\varphi (\xi ,y)$ and $\psi (\xi ,y)$ have the symmetries $\varphi (\xi ,-y)=-\varphi (\xi ,y)$ and $\psi (\xi ,-y)=\psi (\xi ,y)$ so that:

$$\begin{array}{ccc}\hfill u_x(x,-y,t)& =& -u_x(x,y,t),\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill u_y(x,-y,t)& =& u_y(x,y,t),\hfill \end{array}$$

(26)

and:

$$\begin{array}{ccc}\hfill F\left(\overline{\zeta }\right)& =& -\overline{F\left(\zeta \right)},\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill G\left(\overline{\zeta }\right)& =& -\overline{G\left(\zeta \right)},\hfill \end{array}$$

(28)

as necessary to satisfy the Cauchy-Riemann equations for analytic functions $F\left(\zeta \right)$ and $G\left(\zeta \right)$.

Equations (27) and (28) imply the function:

$$E\left(\zeta \right)=-(1+{\alpha }_S^2)F^{\prime \prime }\left(\zeta \right)-2{\alpha }_S{G}^{\prime \prime }\left(\zeta \right),$$

(29)

is continuous across the crack line, and therefore entire. Furthermore, vanishing of stress and velocity field displacements as $\left|\zeta \right|\to \infty$ imply $E\left(\zeta \right)$ is bounded at infinity, and thus identically 0 by Liouville’s theorem. Consequently:

$$G^{\prime \prime }\left(\zeta \right)=-{\displaystyle \frac{1+{\alpha }_S^2}{2{\alpha }_S}}{F}^{\prime \prime }\left(\zeta \right),$$

(30)

which together with boundary condition (23) implies that along the crack line:

$$Im{F}^{\prime \prime }\left(\xi \right)={\displaystyle \frac{2{\alpha }_S}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }},-R<\xi <0,$$

(31)

where $D=4{\alpha }_P{\alpha }_S-{(1+{\alpha }_S^2)}^2$, and discontinuity of $Re{F}^{\prime \prime }\left(\zeta \right)$ across the crack line occurs as necessary to account for discontinuity in elastic displacement. Assuming $\sqrt{\zeta (\zeta +R)}$ is defined as a single valued function on the complex plane with a branch cut between $\zeta =-R$ and $\zeta =0$ along $y=0$, the function:

$$\left(F^{\prime \prime }\left(\zeta \right)-{\displaystyle \frac{2i{\alpha }_S}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}\right)\sqrt{\zeta (\zeta +R)}+{\displaystyle \frac{2i{\alpha }_S}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}(\zeta +R/2),$$

(32)

is continuous across the crack line, and is therefore an entire function that approaches 0 as $\left|\zeta \right|\to \infty$, implying:

$$\begin{array}{c}\hfill F^{\prime \prime }\left(\zeta \right)=-{\displaystyle \frac{2i{\alpha }_S}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}\left({\displaystyle \frac{\zeta +R/2}{\sqrt{\zeta (\zeta +R)}}}-1\right),\end{array}$$

(33)

and:

$$\begin{array}{c}\hfill G^{\prime \prime }\left(\zeta \right)={\displaystyle \frac{i(1+{\alpha }_S^2)}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}\left({\displaystyle \frac{\zeta +R/2}{\sqrt{\zeta (\zeta +R)}}}-1\right).\end{array}$$

(34)

Integration of Equations (33) and (34) gives equations:

$$\begin{array}{c}\hfill F^{\prime }\left(\zeta \right)=-{\displaystyle \frac{2i{\alpha }_S}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}\left(\sqrt{\zeta (\zeta +R)}-\zeta -R/2\right),\end{array}$$

(35)

and:

$$\begin{array}{c}\hfill G^{\prime }\left(\zeta \right)={\displaystyle \frac{i(1+{\alpha }_S^2)}{D}}{\displaystyle \frac{{\sigma }_s}{\mu }}\left(\sqrt{\zeta (\zeta +R)}-\zeta -R/2\right),\end{array}$$

(36)

in which constants of integration have been selected so elastic displacements are 0 at remote points. Assuming $\sqrt{\zeta (\zeta +R)}$ is defined as a single valued function on the complex plane with a branch cut between $\zeta =-R$ and $\zeta =0$ along $y=0$, Equations (35) and (36) together with equation (6) imply the crack opening displacement is:

$$u_x(\xi ,0^{+})={\displaystyle \frac{{\alpha }_S{v}^2}{D{v}_S^2}}{\displaystyle \frac{{\sigma }_s}{\mu }}\sqrt{-\xi (\xi +R)},-R<\xi <0.$$

(37)

3. Multi-Crack 2D Elastostatic Displacement

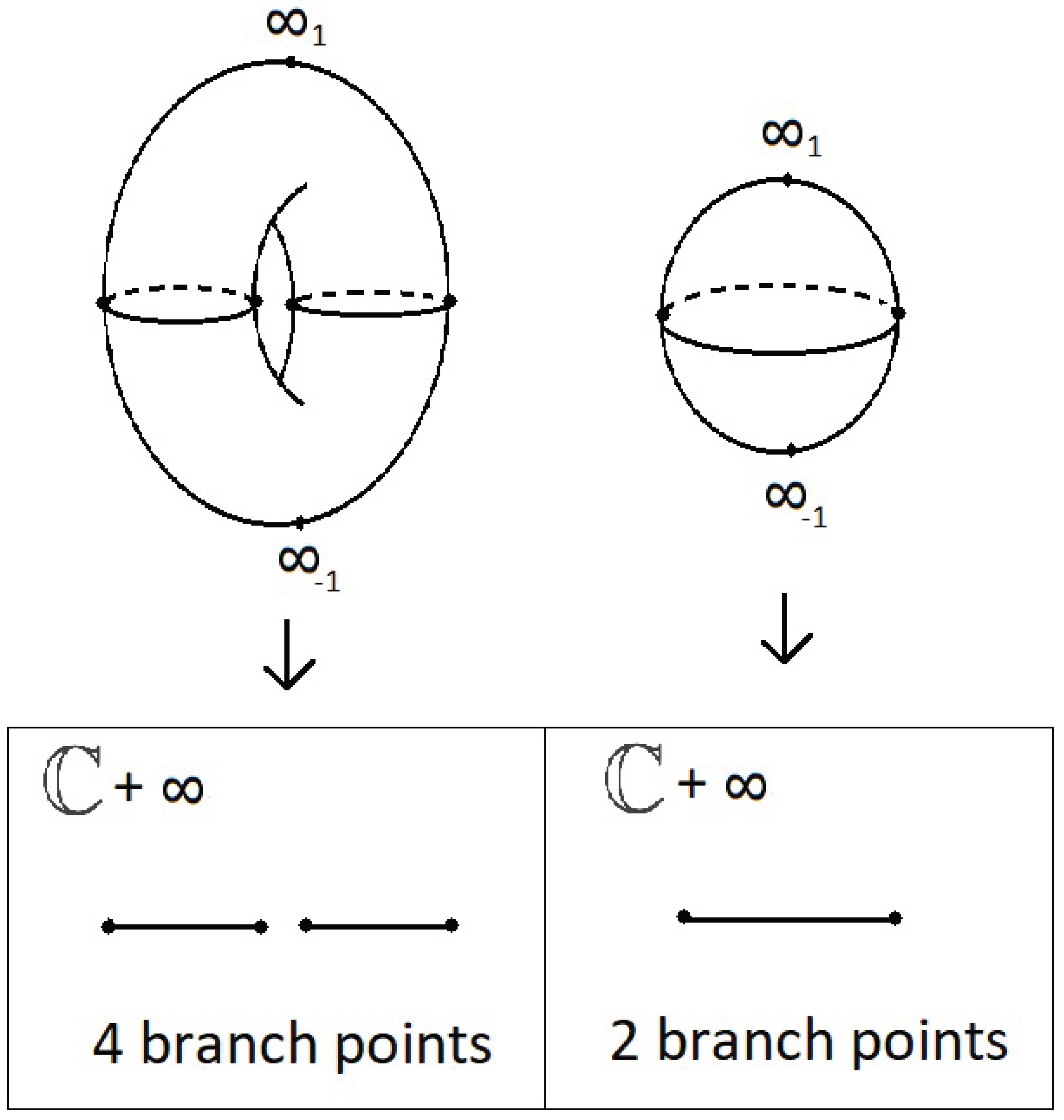
3.1. Crack Geometry: Hyperelliptic Curves

For the purpose of calculating multi-crack 2D elastostatic displacements, cracks will be identified with branch cuts of the complex plane specifying sheets of Riemann surfaces. To explain this statement in detail, consider the equation:

$$Y^2=(X-b_1)(X-b_2)\dots (X-b_{2g+1})(X-b_{2g+2}),$$

(38)

relating complex variables Y and $\zeta$ with $2g+2$ different complex values $b_i$. For each pair of values $(b_{2i-1},b_{2i})$ the expression:

$$\sqrt{(X-b_{2i-1})(X-b_{2i})},$$

(39)

can be a singled valued analytic function on the complex X-plane with a branch cut joining the points $b_{2i-1}$ and $b_{2i}$, and this function is unique up to choice of sign. Iterating selection of a branch for square root for $1\le i\le g+1$, it the product:

$$Y=\sqrt{(X-b_1)(X-b_2)\dots (X-b_{2g+1})(X-b_{2g+2})},$$

(40)

can be defined as a single valued analytic function on the complex X-plane, up to choice of sign, away from a finite set of branch cuts joining branch points $b_{2i-1}$ and $b_{2i}$ in pairs. For this reason, the projection:

$$(X,Y)\to X,$$

(41)

from points satisfying equation (38) to the complex X-plane is a double cover of the complex plane away from the branch cuts.

The projective completion of non-compact hyperelliptic curve (38) is the compact hyperelliptic curve:

$$Y^2{Z}^{2g}=(X-b_{1}Z)(X-b_{2}Z)\dots (X-b_{2g+1}Z)(X-b_{2g+2}Z),$$

(42)

in $\mathbb{C}{P}^2$. From this point of view, the projection:

$$(X:Y:Z)\to (X:Z),$$

(43)

from points on curve (42) to the Riemann sphere $\mathbb{C}{P}^1$ is a double cover with branch points at $X/Z=b_i$. When $|X/Z|\gg max|b_i|$, equation (42) implies:

$${\left({\displaystyle \frac{Y}{Z}}\right)}^2\approx {\left({\displaystyle \frac{X}{Z}}\right)}^{2g+2},$$

(44)

so the point $(X:Z)$ with $Z\ne 0$ is covered by the two points $\left(X:\pm X^{g+1}/Z^g:Z\right)$. Therefore, for $g=0$ the point at infinity $(1:0)$ is double covered by $(1:1:0)$ and $(1:-1:0)$ while for $g\ge 1$ the point at infinity $(1:0)$ is double covered by $(0:1:0)$. With resolution of the $g\ge 1$ singularity at $(X:Y:Z)=(0,1,0)$, projection (43) can be drawn as a projection from a non-singular genus g Rieman surface to the Riemann sphere as shown in Figure 2. In this image, the inverse image of each branch cut is shown as a closed loop on the surface.

3.2. Elastostatic Displacement: Differential Forms

For a superposition of vertical/shear traction acting on the crack faces, the Mode I and Mode II single crack elastostatic displacement potentials $\varphi$ and $\psi$ independently solve the 2D Laplace equation:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2\varphi }{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2\varphi }{\partial y_P^2}}& =& 0,\hfill \end{array}$$

(45)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\partial }^2\psi }{\partial {\xi }^2}}+{\displaystyle \frac{{\partial }^2\psi }{\partial y_S^2}}& =& 0,\hfill \end{array}$$

(46)

away from the crack lines in the $(\xi ,y_P)=(\xi ,{\alpha }_{P}y)$ and $(\xi ,y_S)=(\xi ,{\alpha }_{S}y)$ planes. By Gauss’ and Stokes’ theorems, the line integrals:

$${\oint }_{{\mathcal{C}}_{\mathcal{P}}}\mathbf{u}·\mathbf{n}ds={\oint }_{{\mathcal{C}}_{\mathcal{P}}}\nabla \varphi ·\mathbf{n}ds=Im\left({\oint }_{{\mathcal{C}}_{\mathcal{P}}}{F}^{\prime }\left({\zeta }_P\right)d{\zeta }_P\right)={\displaystyle \frac{\pi {\alpha }_P{v}^2{R}^2}{4D{v}_S^2\mu }}{\sigma }_P,$$

(47)

and:

$${\oint }_{{\mathcal{C}}_{\mathcal{S}}}\mathbf{u}·\mathbf{t}ds={\oint }_{{\mathcal{C}}_{\mathcal{S}}}(\nabla \times \overrightarrow{\psi })·\mathbf{t}ds=Re\left({\oint }_{{\mathcal{C}}_{\mathcal{S}}}{G}^{\prime }\left({\zeta }_S\right)d{\zeta }_S\right)=-{\displaystyle \frac{\pi {\alpha }_S{v}^2{R}^2}{4D{v}_S^2\mu }}{\sigma }_S,$$

(48)

each obtain a constant value for any closed contours ${\mathcal{C}}_P$ and ${\mathcal{C}}_S$ encircling the crack once counterclockwise in the ${\zeta }_P$ and ${\zeta }_S$ planes. Moreover, these constant values can be non-zero because the analytic functions $F\left(\zeta \right)$ and $G\left(\zeta \right)$ are multi-valued, as may be anticipated based on $1/\left|\zeta \right|$ dependence of elastostatic displacement at points remote from the cracks. This dependence can be extracted from singular behavior of differential forms $F^{\prime }\left(\zeta \right)d\zeta$ and $G^{\prime }\left(\zeta \right)d\zeta$ at infinity evaluated using the substitution $\overline{\zeta }=1/\zeta$. Noting that:

$$\sqrt{\zeta (\zeta +R)}-\zeta -R/2=-{\displaystyle \frac{R^2/4}{\sqrt{\zeta (\zeta +R)}+\zeta +R/2}}\propto \overline{\zeta },$$

(49)

for $\left|\zeta \right|\gg R$, and $d\zeta =-d\overline{\zeta }/{\overline{\zeta }}^2$, it is evident that both $F^{\prime }\left(\zeta \right)d\zeta$ and $G^{\prime }\left(\zeta \right)d\zeta$ have a simple pole at infinity. For this reason, the integral of the pullback of either form to a Riemann sphere around the closed contour shown in Figure 2 is non-zero, because the form has a simple pole on both the inside and outside of the contour.

For $g\ge 1$, $g+1$ cracks in the ${\zeta }_P$ or ${\zeta }_S$ plane can be viewed as branch cuts for a double cover of the plane by a hyperelliptic curve of genus g, and multi-crack elastostatic displacement solutions for constant vertical or shear surface tractions are associated with meromorphic 1-forms on the curve. The Riemann-Roch theorem applies to calculate the dimension of the complex vector space $V_{\omega }$ of meromorphic 1-forms $\omega$ on a non-singular Riemann surface of genus g with simple poles at 2 prescribed points as being $g+1$. More specifically, the theorem for curves states that if $\mathcal{K}$ is a canonical divisor on a non-singular Riemann surface of genus g, then:

$$\begin{array}{ccc}\hfill {dim}_{\mathbb{C}}{V}_{\omega }& =& l(\mathcal{K}+{\infty }_1+{\infty }_{-1})\hfill \end{array}$$

(50)

$$\begin{array}{ccc}& =& g-1+l(-{\infty }_1-{\infty }_{-1})-deg(-{\infty }_1-{\infty }_{-1})\hfill \end{array}$$

(51)

$$\begin{array}{ccc}& =& g-1+0-(-2)\hfill \end{array}$$

(52)

$$\begin{array}{ccc}& =& g+1.\hfill \end{array}$$

(53)

where $l\left(D\right)$ is the complex dimension of the vector space of meromorphic functions on the Riemann surface bounded by divisor D[7]. Consequently, if an elastostatic displacement vector field $\mathbf{u}$ in the multi-cracked $(x-vt,y)$ plane is associated with meromorphic 1-forms $F^{\prime }\left({\zeta }_P\right)d{\zeta }_P$ and $G^{\prime }\left({\zeta }_S\right)d{\zeta }_S$ in the ${\zeta }_P$ and ${\zeta }_S$ planes via Helmholtz decomposition (1) and Equations (4) and (5), the pullback of either 1-form to a non-singular genus g Riemann surface can each be expressed as a linear combination of a basis ${\omega }_1$, ${\omega }_2$, ..., ${\omega }_g$, ${\omega }_{\infty }$ for a vector space of mermomorphic 1-forms $V_{\omega }$ on the respective curve, where each ${\omega }_i$ is holomorphic and ${\omega }_{\infty }$ has simple poles at the points ${\infty }_{\pm 1}$. When $v=0$, the ${\zeta }_P$ and ${\zeta }_S$ planes coincide and both meromorphic 1-forms $F^{\prime }\left({\zeta }_P\right)d{\zeta }_P$ and $G^{\prime }\left({\zeta }_S\right)d{\zeta }_S$ pullback to 1-forms on the same Rieman surface. In this case, the complex dimension $g+1$ is in agreement with the fact there are $2g+2$ real parameters ${\sigma }_{P,i}$ and ${\sigma }_{S,i}$ available to specify constant vertical and shear surface tractions on crack faces of the multi-crack system, since the elastostatic displacement fields $\mathbf{u}$ associated with sets of constant surface tractions form a real vector space.

4. 3D Fracture Networks

Correspondence between 2D multi-crack configurations with hyperelliptic curves suggests a change in 2D crack configuration (e.g. crack growth) may be modeled as a change in the shape of a Riemann surface. This fact is of scientific interest because current methods of modeling and simulating crack growth invoke empirical time evolution equations for crack phase fields (i.e. damage fields), and these methods may be advanced by more systematic time evolution modeling [8]. However, practical application of the multi-crack Riemann surface model to modeling crack growth in laboratory rock samples and the lithosphere appears lacking for at least two reasons:

• It is not clear how the 2D Riemann surface model can be generalized to describe cracks of arbitrary orientation and finite width in 3 spatial dimensions.
• It is not clear how the 2D Riemann surface model can be generalized to describe elastostatic displacement of a material whose elastic parameters vary in space and time.

To address these problems, an introductory discussion of 3D fracture in laboratory rock samples and the lithosphere is presented, and 3D fracture network dynamics preceding an earthquake are characterized in terms of singular spectrum analysis of a crack phase field. Mathematically, specification of a time dependent crack phase field in a laboratory rock sample or region of the lithosphere can be used to specify a time dependent elasto-plastic tangent stiffness operator, with an increase in the crack phase field at a particular spatial location corresponding to a reduction in effective shear modulus of material. Consequently, shear band instability leading to rock fracture is associated with increase in the crack phase field where material is damaged due to inelastic deformation. Within the lithosphere, changes in material shear modulus can be detected as changes in local earthquake coda wave signals on seismograms, allowing for detection of a fault damage zone formed before earthquake fault rupture. Conjecturally, time evolution of the crack phase field preceding an earthquake is governed by a finite dimensional nonlinear dynamical system with phase space dimension equal to a number of dynamic modes of fault damage. From this point of view, it remains possible that the underlying nonlinear dynamical system phase space of a 3D crack phase field is related to the geometry of Riemann surfaces, although more detailed investigation is required to determine whether or not this is the case.

4.1. Laboratory Brittle Rock Fracture

Consider a triaxial compression test on a rock sample for which axial compressive strain is applied along principal axis 1 while compressive stresses in the direction of principal axes 2 and 3 are held constant. Assume the initial compressive stresses satisfy ${\sigma }_1>{\sigma }_2>{\sigma }_3$, and as ${\sigma }_1$ is increased towards a maximum value ${\sigma }_{1,max}$, plastic strain hardening of the rock sample occurs according to a Mohr-Coulomb yield criterion with a mobilized friction angle and a non-associated plastic flow rule [15]. Also assume that when ${ϵ}_1$ is increased beyond the strain ${ϵ}_{1,max}$ at which ${\sigma }_1={\sigma }_{1,max}$, strain softening of the rock occurs with formation of a shear band along a plane where the rock ultimately undergoes shear failure.

Physically accurate and well defined mathematical description of the rock strain softening regime requires addition of at least two features to the strain hardening non-associated plasticity model:

• Strain rate softening of rock shear strength [2].
• Regularization of rock plastic flow introducing a non-zero shear band width [5].

If it is assumed that with consideration of these technical details, and definition of a finite element mesh, a global elasto-plastic tangent stiffness operator $K_T^{ep}\left(\tau \right)$ can be defined for the rock sample throughout triaxial compression at a constant strain rate at each time $\tau$, Newton’s equation of motion dictates that the equation:

$$M\ddot{\mathbf{U}}\left(t\right)+C\left(\tau \right)\dot{\mathbf{U}}\left(t\right)+K_T^{ep}\left(\tau \right)\mathbf{U}\left(t\right)=\mathbf{F}\left(t\right),$$

(54)

describes time evolution of a vector perturbation $\mathbf{U}\left(t\right)$ to the finite element nodal elasto-plastic displacements at time $\tau$, where M is a lumped mass matrix, $C\left(\tau \right)$ is a damping matrix at time $\tau$, and $\mathbf{F}\left(t\right)$ is a perturbation of the externally applied nodal force vector [3].

During strain hardening, the lowest eigenvalue ${\beta }_0\left(\tau \right)$ of $K_T^{ep}\left(\tau \right)$ decreases to 0 at which point a strain rate bifurcation occurs and a shear band along the rock failure plane is formed with incremental displacement described by an eigenvector ${\overrightarrow{v}}_0\left(\tau \right)$ of $K_T^{ep}\left(\tau \right)$ with eigenvalue 0. However, prior to final shear band formation, there may exist other eigenvalues ${\beta }_1\left(\tau \right),{\beta }_2\left(\tau \right),...,{\beta }_p\left(\tau \right)$ of $K_T^{ep}\left(\tau \right)$ for which $|{\beta }_i\left(\tau \right)|\ll 1$, associated with other dynamic modes of increasing material damage. The respective eigenvectors ${\overrightarrow{v}}_1\left(\tau \right),...,{\overrightarrow{v}}_p\left(\tau \right)$ of $K_T^{ep}\left(\tau \right)$, together with ${\overrightarrow{v}}_0\left(\tau \right)$, span a vector space $\mathcal{V}$, and the motion of a point in this vector space describes the time evolution of strain rate in a fault damage zone surrounding the shear band/rock fracture plane.

4.2. Lithospheric Fracture Network Statistics

In seismology, detecting fault damage zone formation by monitoring real time variation of local earthquake coda wave signals on seismograms has been identified as a possible method of predicting earthquakes [1]. According to this method, in a frequency band centered at angular frequency $\omega$, time variation of the local earthquake coda $Q\left(\omega \right)$ value at a particular seismic station can be attributed to time variation of the anelastic and/or scattering Q values $Q_i\left(\omega \right)$ and $Q_s\left(\omega \right)$ according to the equation:

$${\displaystyle \frac{1}{Q\left(\omega \right)}}={\displaystyle \frac{1}{Q_i\left(\omega \right)}}+{\displaystyle \frac{1}{Q_s\left(\omega \right)}},$$

(55)

and decrease of $Q_s\left(\omega \right)$ in time reflects earthquake precursor dynamics in the lithosphere. More specifically, based on a single backscattering model of coda wave signals, $Q_s$ scales with signal frequency according to the power law:

$$Q_s\left(\omega \right)\propto {\omega }^{2H},$$

(56)

and may therefore contribute to real time variation of $Q\left(\omega \right)$ if the Hurst exponent H changes in time [16]. Fundamentally, the Hurst exponent H is related to the power spectrum of random S-wave velocity model inhomogeneities in the lithosphere $W_{3D}\left(k\right)$, where k is wave number, via the relation [14]:

$$W_{3D}\left(k\right)\propto k^{-2H-3}.$$

(57)

These random inhomogeneities can be attributed to a fracture network superimposed on a fixed seismic velocity model background, such as a 1D layered velocity model, with fracture size statistics characterized by equation (57).

4.3. Crack Phase Field Singular Spectrum Analysis

Suppose a scalar crack phase field influences Lame parameters $\lambda (x,y,z,\tau )$ and $\mu (x,y,z,\tau )$ of an uncracked 3D laboratory rock sample or lithospheric region via the equations:

$$\begin{array}{ccc}\hfill \lambda (x,y,z,\tau )& =& {\lambda }_0(x,y,z)+{\lambda }_r\varphi (x,y,z,\tau )\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill \mu (x,y,z,\tau )& =& {\mu }_0(x,y,z)+{\mu }_r\varphi (x,y,z,\tau ),\hfill \end{array}$$

(59)

where ${\lambda }_0(x,y,z)$ and ${\mu }_0(x,y,z)$ are the Lame parameters of uncracked rock at location $(x,y,z)$, $\varphi (x,y,z,\tau )$ is the crack phase field with value 0 for uncracked material and 1 for maximally damaged material, and ${\lambda }_r$ and ${\mu }_r$ are constants [9]. If the crack phase field can be directly measured at a particular 3D location P at regular time intervals, the sequence of phase field values ${\varphi }_i=\varphi (P,{\tau }_0+(i-1)\Delta \tau )$ can be used to write a trajectory matrix $\mathcal{X}\left({\varphi }_i\right)$:

$$\mathcal{X}\left({\varphi }_i\right)={\displaystyle \frac{1}{\sqrt{N}}}\left[\begin{array}{ccccc}{\varphi }_1& {\varphi }_2& {\varphi }_3& \dots & {\varphi }_n\\ {\varphi }_2& {\varphi }_3& {\varphi }_4& \dots & {\varphi }_{n+1}\\ \dots & \dots & \dots & \dots & \dots \\ {\varphi }_N& {\varphi }_{N+1}& {\varphi }_{N+2}& \dots & {\varphi }_{N+n-1}\end{array}\right],$$

(60)

whose singular value decomposition can be used to identify dominant signal components in the discrete time series ${\varphi }_i$[4]. More generally, the scalar time series ${\varphi }_i$ can be replaced with a vector of phase field values at different 3D locations, and multichannel singular spectrum analysis can be applied to identify dominant vector signal components.

Realistically, crack phase field values are not measured at individual points in a laboratory sample or the lithosphere, but rather, inferred from changes in local earthquake coda wave signals. Therefore, it is noted that single/multi-channel singular spectrum analysis allows for replacement of the scalar/vector time series of crack phase field measurements ${\varphi }_i$ with a scalar/vector time series ${\Phi }_i$ of experimentally observed data, such as relative changes in average S-wave velocity between seismic station pairs measured by monitoring coda wave signals [10]. Therefore, assuming each ${\Phi }_i$ is the measurement of an observable on a nonlinear dynamical system with a finite dimensional phase space, the rows of the trajectory matrix $\mathcal{X}\left({\Phi }_i\right)$ provide an embedding of the phase space trajectory into ${\mathbb{R}}^n$. Physically, it appears reasonable to conjecture that the phase space itself is the vector space of damage modes $\mathcal{V}$ defined in Section 4.1 [12]. Alternatively, if the $\tau$ dependent coefficients of the eigenvectors are functions of the elasto-plastic stiffness matrix eigenvalues ${\beta }_0\left(\tau \right),{\beta }_1\left(\tau \right),...,{\beta }_p\left(\tau \right)$, a nonlinear dynamical system:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\beta }_0}{d\tau }}& =& F_0({\beta }_0,{\beta }_1,...,{\beta }_p)\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\lambda }_1}{d\tau }}& =& F_1({\beta }_0,{\beta }_1,...,{\beta }_p)\hfill \end{array}$$

(62)

$$\begin{array}{ccc}& ⋮& \end{array}$$

(63)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\beta }_p}{d\tau }}& =& F_p({\beta }_0,{\beta }_1,...,{\beta }_p)\hfill \end{array}$$

(64)

with phase space consisting of points $({\beta }_0,{\beta }_1,...,{\beta }_{p+1})\in {\mathbb{C}}^{p+1}$ underlies coda wave signal observations. An estimate of the dimension of this underlying phase space trajectory is provided by computing the correlation dimension of the phase space trajectory embedded in ${\mathbb{R}}^n$.

5. Conclusions

Further computational and experimental effort is required to distinguish fundamental models of crack growth models based on applied mathematics from those based on mathematical concoction. In particular, an example of simulating crack phase field time evolution in a laboratory rock sample and using singular spectrum analysis to characterize this time evolution should be provided to clarify what dynamical system governs formation of the fault damage zone. If the results of an initial computational investigation are promising, an example of approximating crack phase field phase space dimension from singular spectrum analysis of coda wave data should be provided as evidence for real world applicability of phase field singular spectrum analysis. Theoretically, to the point of providing analytic models of phase field time evolution, which may be deterministic or probabilistic, it may be useful to investigate if time evolution of the elasto-plastic tangent stiffness operator eigenvalue distribution can be cast in terms of renormalization of a statistical mechanical system, such as a 2D Coulomb gas [13].