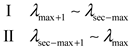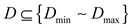1. Introduction
Space activities, including not only commercial satellite launches and on-orbit service, but also space exploration missions by more and more countries and international organizations, are increasing day by day which has made space environment more complex. The importance of Space Traffic Management (STM) is becoming increasingly prominent. Space Traffic Management refers to the planning, supervision, coordination, and emergency response activities carried out by relevant management agencies through technical, legal, and other means to ensure the safe, efficient, and orderly launch, orbit operation, re-entry, and other activities of satellite, as well as to maintain the space environment and prevent unsafe factors such as electromagnetic interference, physical collisions, and environmental damage [
1,
2,
3,
4].
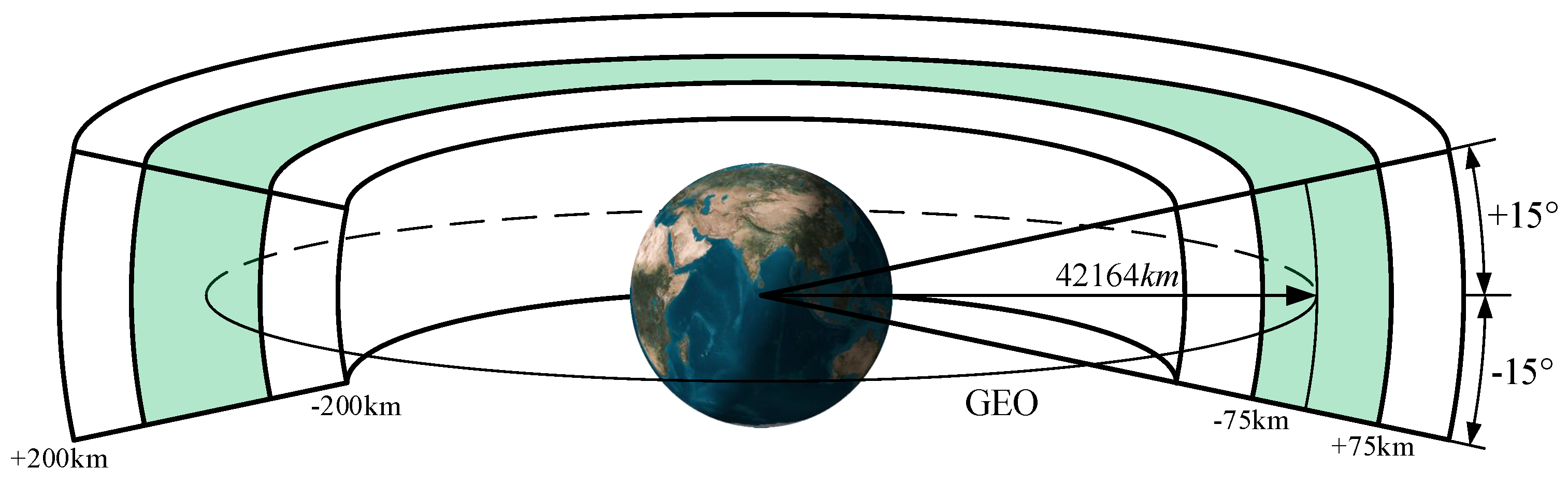
Space Traffic Management revolves around three core goals: safety, orderliness, and sustainability. Safety is primary consideration, which means ensuring the normal operation of satellite and related equipment, and preventing the occurrence of various accidents and incidents. As an important component of Space Traffic Management, the Space Situational Awareness (SSA) system is primarily responsible for monitoring and tracking of space targets, ensuring the safety and sustainable use of the space environment. In the vast expanse of space, GEO Zone is a key area for Space Traffic Management. It is generally considered that the GEO is a circular orbit with inclination of 0° and earth-radius of 42164km. In a strict sense, there is only one GEO in space. In order to effectively use and protect GEO, Inter-Agency Space Debris Coordination Committee (IADC) has artificially delineated a GEO Zone as shown in
Figure 1 [
5]. It can be seen that the GEO Zone’s upper and lower height is 35786km±200km, and the north-south range is latitude ±15°. In the Zone, the inner ±75km zone is GEO working zone while the rest is GEO maneuver zone. Satellites in GEO Zone are widely used in navigation, communication, early warning and other fields due the unique orbital advantage, such as the sub-satellite point trajectory and global coverage [
6].
The prerequisite for Space Traffic Management in GEO is to obtain the status information of GEO targets quickly and accurately. However, due to the long distance and poor tracking accuracy, the ground-based space situation awareness system for GEO satellites inspection is limited. Space-based observation, which can achieve close range, long-term, and multi-angle tracking and observation of space targets, becomes the only means to obtain detailed information of GEO satellite. Due to the vastness of GEO, GEO SSA typically adopts a method of traverse patrol, which is similar to traffic patrol, called Space Traffic Patrol. Space Traffic Patrol means to go around a Zone or an area at regular times to check that it is safe and that there is no trouble at close range by using one or more satellite.
According to the UCS database, as of May 2023, there are 590 controllable GEO satellites [
7]. In terms of satellite types, GEO satellites can be divided into three categories: military, civilian/government, and commercial. The number of commercial satellites is largest, accounting for about 57%, and the military and civilian/government is equivalent, accounting for 21% and 22%. When considering that the perigee and apogee are both in working zone, the number of qualified satellites are 495, accounting for about 84%. When considering the distribution of orbital inclination, it can be seen that although most GEO satellites have a small inclination angle, but the number of satellite inclinations exceed 0.1° is 179, accounting for more than 30%. Those satellites belong to a different orbital plane from the patrol satellite due to its inclination, which poses a huge challenge to Space Traffic Patrol. In this article, we define an inclined geosynchronous orbit (IGSO) target is a satellite with inclination angle exceed 0.1°.
Essentially, the Space Traffic Patrol problem belongs to the problem of multiple targets rendezvous. There are a lot of domestic and international researchers who engage in it, especially in terms of On-Orbit-Services. Those articles can be divided into four categories: One-to-Multiple (OTM), Multiple-to-Multiple (MTM), Peer-to-Peer (PTP), and Mixed.
OTM means that one service satellite refuels multiple targets. In OTM, most scholars consider service order as the main variable for optimization, with the minimum consumption as the optimization objective. Those scholars transform it into a Travel Salesman Problem (TSP) or a Mixed Integer Nonlinear Programming (MILP) problem. Ref. [
8] studied the OTM service order problem with the service satellite and targets in same circular orbit. Ref. [
9] studied the route problem of servicing GEO targets with small inclination, while same question as in Ref. [
10]. In addition, a spiral cruise orbit for GEO satellites traverse was designed by using relative orbit equations in Ref. [
11,
12]. Genetic algorithms (GA), Particle Swarm Optimization (PSO) and other optimization algorithms are also used to solve the problem [
13,
14,
15,
16,
17,
18].
MTM means that multiple service satellites refuel multiple targets. MTM problem is much more complex than OTM. Many factors, such as initial position and traverse cost, will affect the path planning. Moreover, considering the limited capacity of service satellite, it is necessary to place the location and number of fuel stations to affect the final result. For MTM, different scenarios are set and different models are established. Ref. [
19] assumes that the service satellite can return to fuel station for refueling and continue the service. Taking the service sequence and the time of return to station as variables, the service plan with lowest consumption is optimized. By converting the problem into a Location-Route Problem (LRP), a service plan is given in Ref. [
20], same as in Ref [
25,
26,
27,
28,
29]. Some others solved the problem by converting it into an Optimal Matching Problem (OMP) [
21,
22] or a mixed mode [
23,
24].
PTP assumes that each service satellite and target have the ability to maneuver. PTP is actually an optimal matching problem, and the model is established depending on the constraints of the scene conditions. All models were varying slightly. To make all targets fuel-abundant with lowest cost, the PTP problem was transformed into an optimal matching problem model and solved by using auction algorithms. Ref. [
30] studied the PTP traverse mode assuming that targets in a circular orbit with uneven fuel distribution. The PTP refueling model added fuel quantity threshold as a new parameter, where targets with larger quantity as fuel-abundant and smaller quantity as fuel deficient [
31]. Furthermore, some scholars assumed that each service satellite can return to the original position of anyone after rendezvous, transformed it into a three-index assignment problem, also called E-PTP (Egalitarian Peer to Peer) problem, and solved it by using search algorithms [
32].
Mixed traverse is relatively complex, and generally two or more categories are used to achieve the goal of reducing fuel consumption or more effective traverse. Ref. [
33,
34,
35] simplifies the MTM and PTP to achieve equilibrium through weighting, resulting in a relatively ideal state for fuel consumption and fuel gap between targets. Ref. [
36] selected some service satellites to only provide fuel for some targets in the constellation. After these targets receive fuel, they transform into service satellites to provide fuel for other targets. Through enumeration and PSO comprehensive algorithm comparison, it was verified that the hybrid traverse strategy is more cost-effective than other strategies.
Although there are many literature studies on this topic, most of them focus on the coplanar rendezvous, and there is relatively little research on non-coplanar rendezvous problem. Bai et al. used the dual target rendezvous orbit cluster to obtain the rendezvous orbit approaching multiple non-coplanar targets by searching and calculating the closest distance to other targets [
37,
38,
39]. Zhang et al. used Lambert's theorem to determine the service satellite orbit that were close to two targets, and then improved the orbit by using least squares method and genetic algorithm, obtained the orbit that approaches three non-coplanar targets [
40,
41,
42]. Ref [
43] demonstrated a service satellite orbit that can rendezvous with multiple satellites in Walker constellation without orbit maneuver. Based on this, the author summarized the rendezvous orbit constraints for maximum number of constellation satellites, and then used phase modulation to change the initial phase of service satellite to rendezvous with all satellites in the orbit plane. The strategy is verified that fuel consumption is less compared to the Lambert's theorem. Mana et al. designed the traversal orbit for GPS satellites by using single pulse coplanar orbit maneuver. After traversing one orbit plane, the maneuver is carried out at the intersection with next one, and repeating the same operation until the traversal of all satellites [
44].
The above articles mainly focus on Walker constellation, but IGSO orbit is not a regular Walker constellation, but rather an irregular problem. To solve the rendezvous multiple targets problem on general orbital plane, Zhang et al. proposed the crossing point method, and achieving the rendezvous orbit based on the method [
45,
46,
47].
In this article, we propose a patrol route design approach based on gradient longitude drift rate and crossing points to patrol IGSO targets. Sec. Ⅱ introduces the approach in detail. And, the proposed approach is illustrated in Sec. Ⅲ by using numerical experiment. Additionally, the discussion is illustrated in Section Ⅳ. Finally, the conclusion and future work directions are provided in Section Ⅴ.
2. Materials and Methods
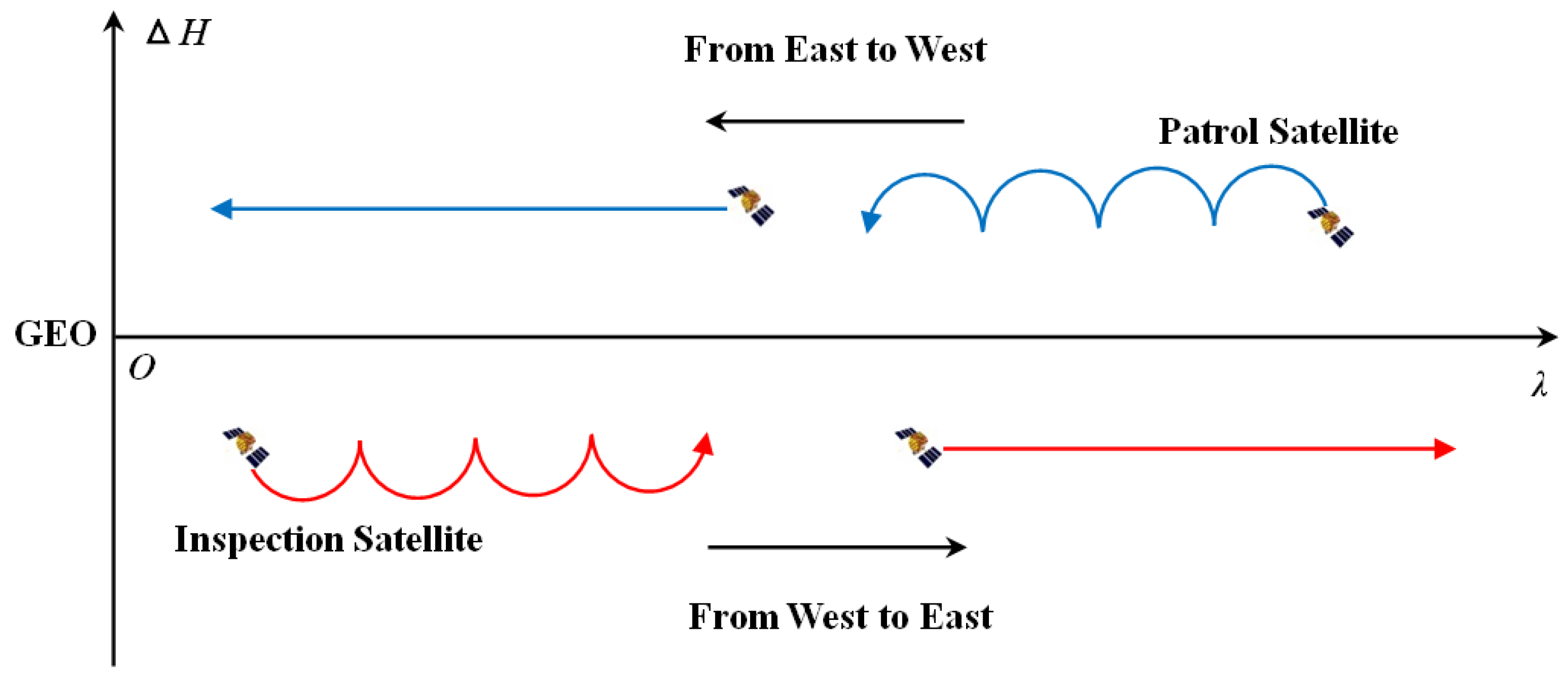
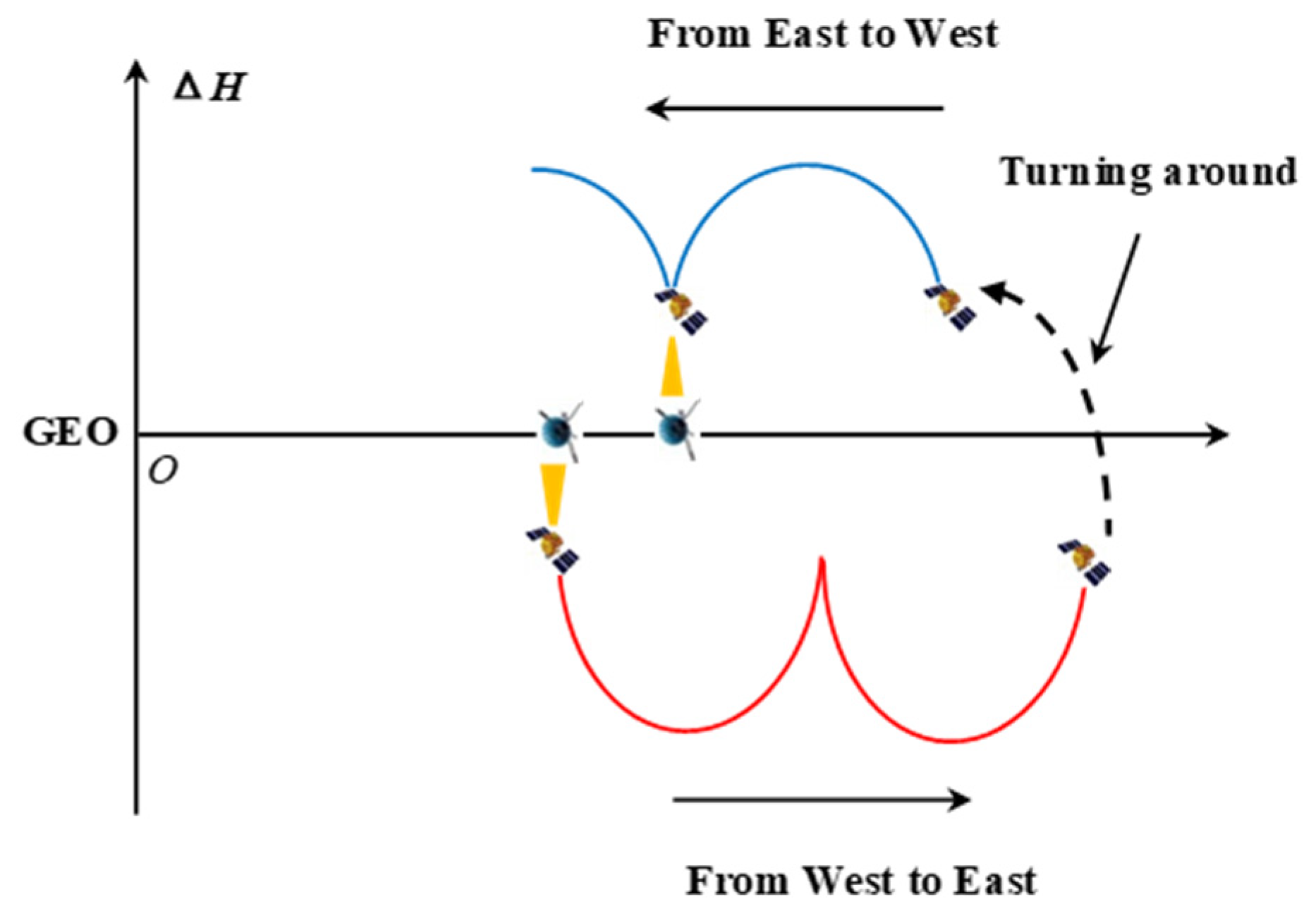
For safety, the patrol satellite should not frequently pass through the GEO working zone, and not affect the normal satellites in working zone. Thus, the patrol satellite should be located in GEO maneuver zone defined by IADC. It can be seen from the definition that the GEO maneuver zone is divided into two in-dependent parts, above or below GEO. Therefore, the patrol orbit zone should be located in a part of the maneuver zone. When the satellite is in the maneuver zone, it will drift relative to GEO. Taking the standard GEO as the reference coordinate system, the patrol route relative to the GEO is shown in
Figure 2.
It can be seen from the figure that when the satellite is located below GEO, its trajectory relative to GEO is wave-shaped (elliptical orbit) or linear (circular orbit). The sub-satellite point longitude becomes larger, and drifts from west to east. Conversely, when located above the GEO, its relative trajectory is also wave or linear with sub-satellite point longitude becomes smaller and drifts from east to west.
By utilizing the relative drift, it is possible to patrol the GEO targets. The longitude drift rate
D is
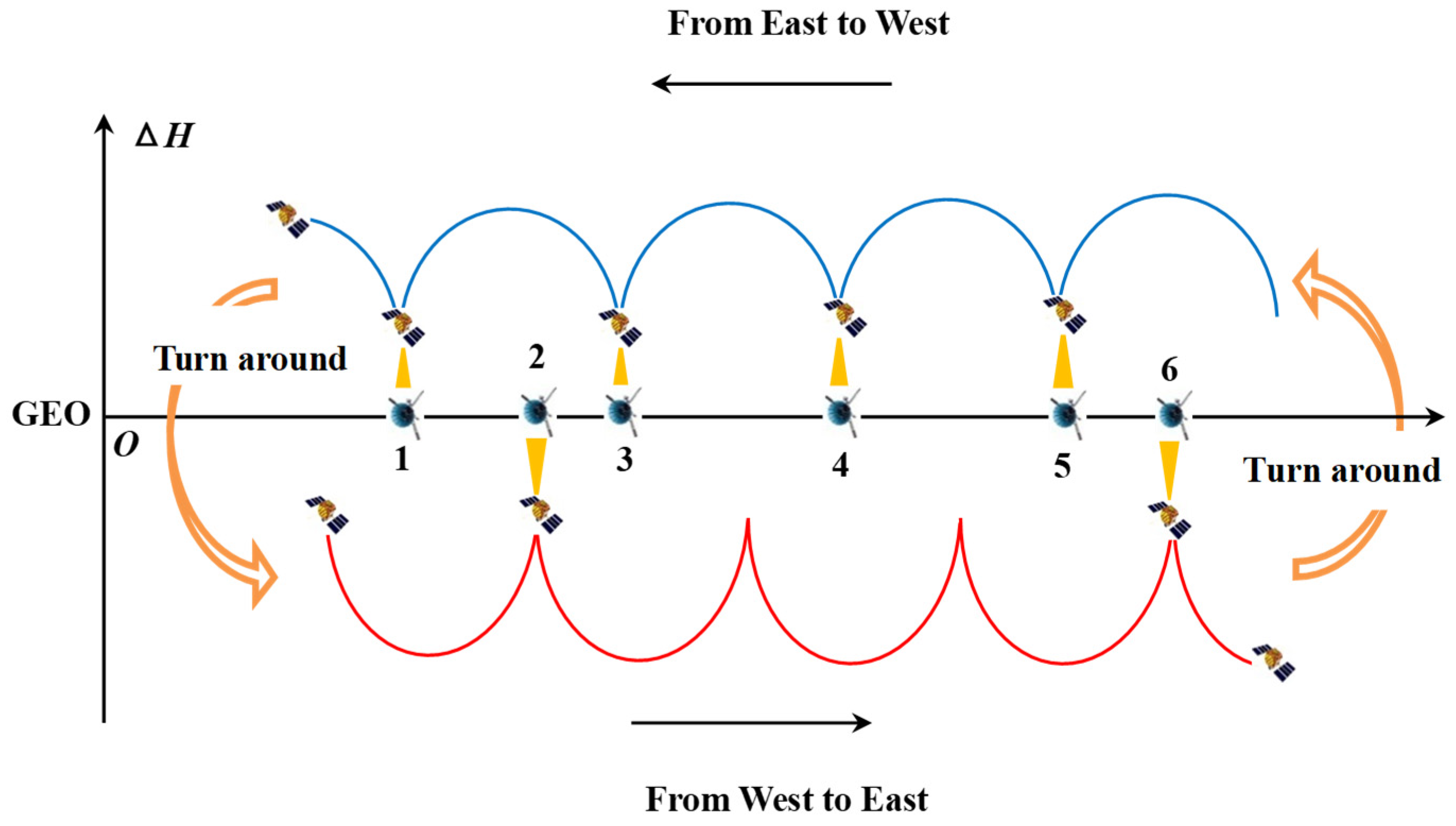
Therefore, by designing drift rate reasonably, it is possible to achieve a natural patrol of all targets in GEO zone. As shown in
Figure 3, assume that a GEO zone contains six targets. The patrol satellite first drifts from west to east, observing target 2 and 6 at apogee, and then implementing orbital maneuver at the zone boundary, turn around and drifts from east to west, observing target 1, 3, 4, and 5 at perigee. Thereby, the satellite achieves the patrol of the entire zone's targets. Afterwards, through orbital maneuver, the satellite will turn around again and enter the East-Drift orbit, conducting periodic patrol of targets in the zone.
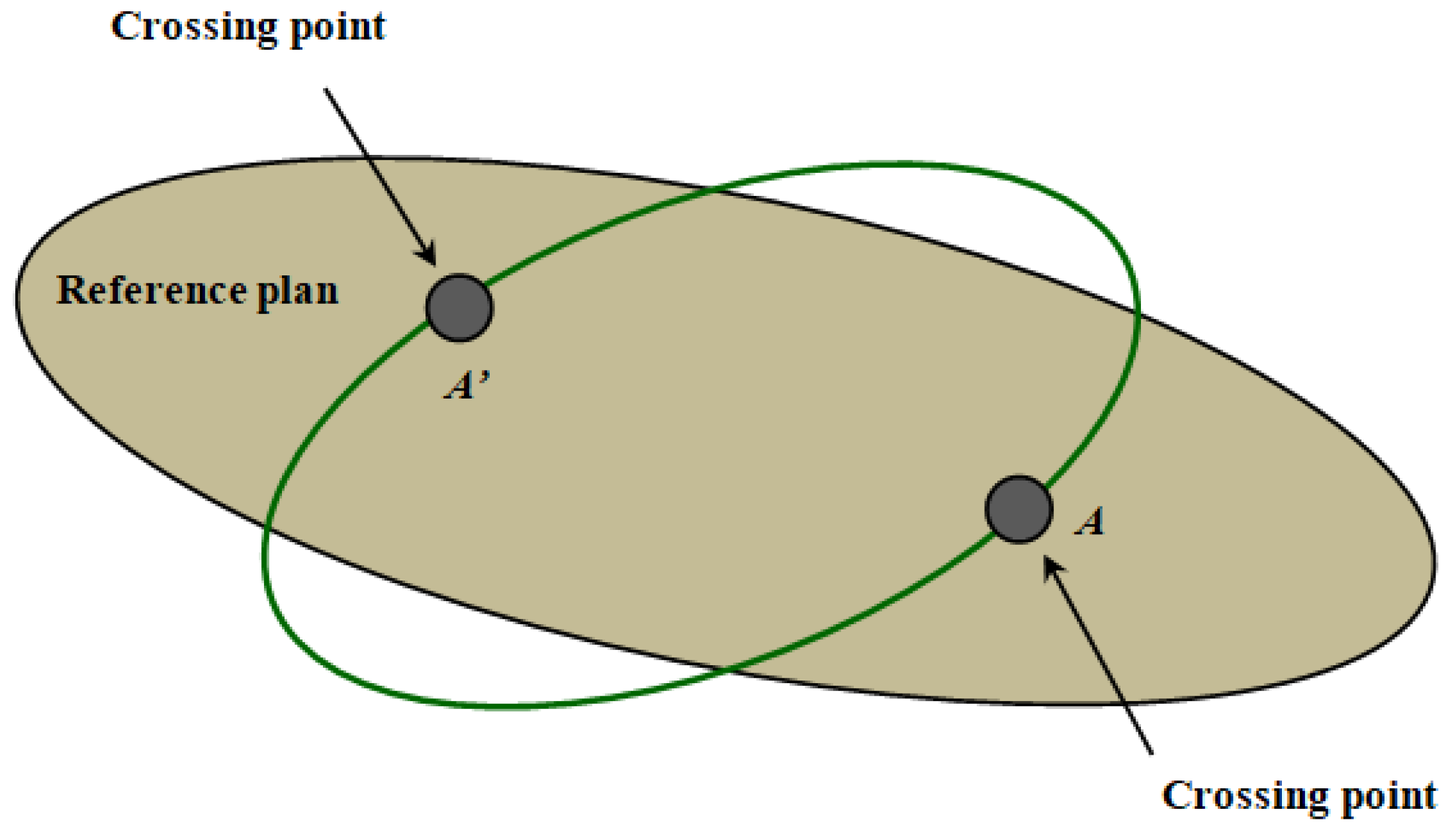
The above strategy is very effective when the target is stationary, but IGSO targets exhibit up and down relative to the equatorial plane. Patrolling these targets not only requires consideration of relative position, but also relative time, which is a more complex spatiotemporal problem. According to orbital dynamics, each satellite is in a plane passing through the center of Earth. That is, the orbital planes of any two satellites will inevitably intersect, forming two intersection points, called crossing points, as shown in the following
Figure 4.
Select any orbit plane as the reference plane, and the target orbit passes through the reference plane and intersects at points A and A', where point A north of the equatorial plane is called the north crossing point, and point A' south of the equatorial plane is called the south crossing point. The two points have a phase difference of 180 ° within the reference plane.
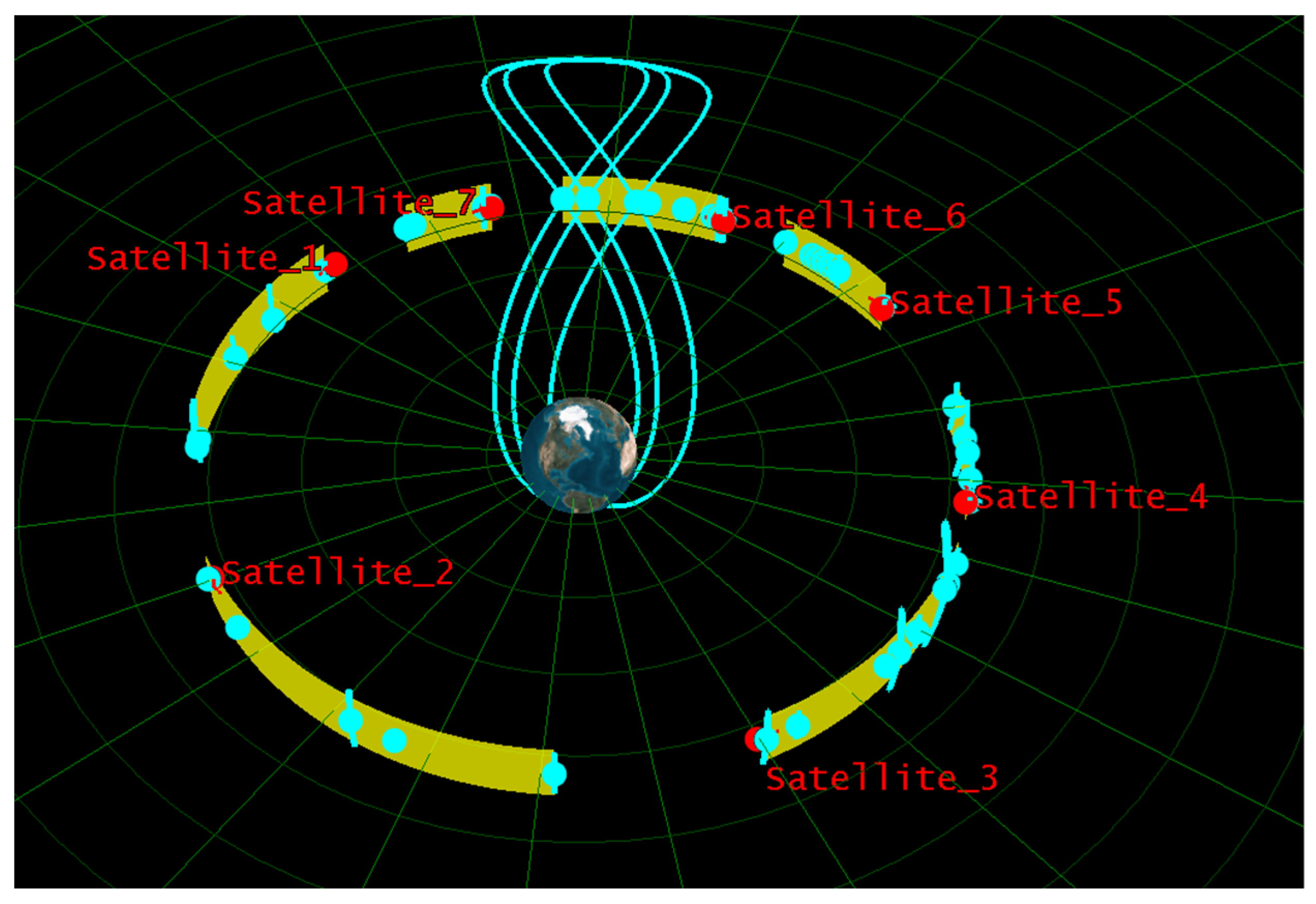
If we use the strategy above to implement the patrol of IGSO targets, there will be a situation where the patrol satellite nears the crossing point, but the target does not reach the crossing point. If the patrol satellite could hold on near the crossing point for a period of time, waiting the target crosses the reference plane, then the problem can be smoothly transformed into the stationary problem. According to the space special orbit design theory [
47], when the height difference meets certain conditions, it can achieve a spiral holding-on effect as shown in
Figure 5.
When the target crosses the reference plane, the patrol satellite happens to be on the spiral ring. By designing the spiral ring reasonably, the cycle of the spiral ring can cover the crossing time within a day. This transforms the patrol problem of IGSO targets into a stationary target problem, and uses the gradient longitude drift rate method to achieve patrol of IGSO targets.
This article proposes a gradient longitude drift rate patrol configuration approach based on crossing points and spiral rings to patrol IGSO targets, includes:
(1) Calculate the crossing position and crossing time of the IGSO targets;
(2) Design the spiral trajectory that satisfies desired patrol time;
(3) Divide IGSO targets into regions based on dichotomy approach;
(4) Calculate the bidirectional longitude drift rate within each region;
(5) Determine the starting position of patrol for each region;
(6) Determine the transfer trajectory for each region.
2.1. Calculate the Crossing Position and Crossing Time of the igso Targets
Assuming a IGSO target crosses the orbital plane, the target orbital element is
. Set the orbital plane of patrol satellite as reference plane, which can be represented by
. The coordinates of crossing point in reference plane can be represented as
, where
is the moment when target crosses through the plane,
is the geocentric distance of the crossing point, and
is the ascending intersection angle of the crossing point. If crossing point is
, thus
Among them,
is the argument of latitude of the target, which can be obtained by
The crossing time can be obtained from the Kepler equation:
The south crossing point and north crossing point are symmetrical relative to the center of the earth, then the south crossing point (
) is
Due to the periodic motion, the target periodically crosses the reference plane, with a time interval of orbital period
Tt , i.e
In this article, the patrol satellite operates within the equatorial plane, thus
Then, the crossing point becomes the ascending and descending node of target, and the crossing point can be represented by
. Thus, formulas (5)~(8) derive the crossing time as
Considering that most IGSO targets is in near circular orbit, thus
Formula (9) can be simplified as:
ac is the radius of geostationary orbit. It can be seen that the change of crossing time is closely related to the semi major axis difference between target and
ac. The difference between two consecutive crossing times is
If the semi major axis difference is 100km, it can be obtained that the daily variation of crossing time is about 306.5 seconds. Considering that the semi major axis change is only a few kilometers under the perturbation, it can be considered that the crossing time of IGSO target in this article remains basically unchanged. The
Ω will also experience precession drift due to the perturbation influence, and the drift pattern is as follows
It can be obtained that the Ω decreases by about 0.0089 ° per day. However, under controlled conditions, the Ω will remain within ± 0.1 ° of its sub-point longitude. Therefore, in this paper, we consider that the crossing points of selected targets remain unchanged.
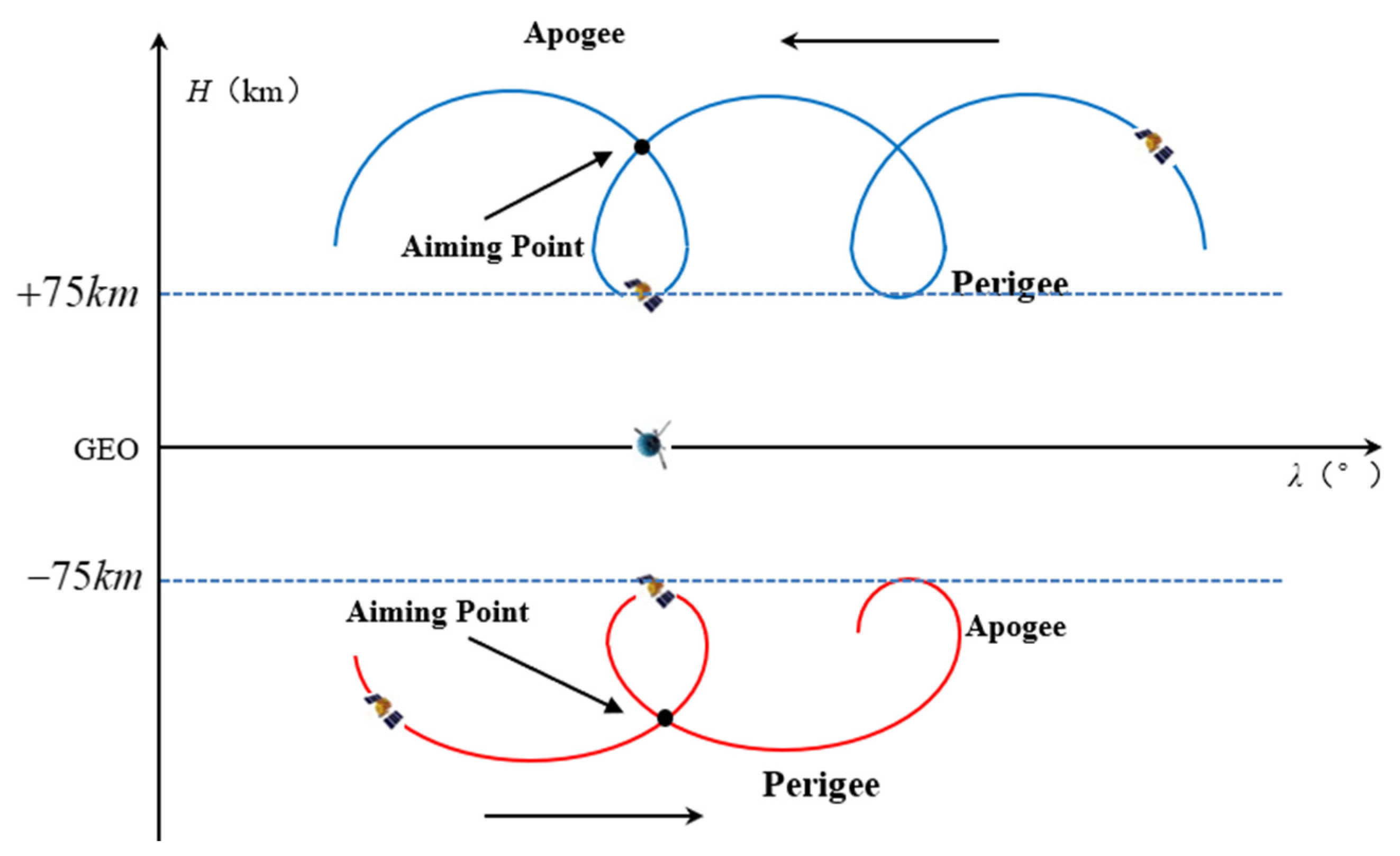
2.2. Design the Spiral Trajectory That Satisfies Desired Patrol Time
As shown in Figure5, the intersection point is called aiming point, and the point where the trajectory turns from west to east or from east to west is called turning point. Satellite passes through the same aiming point twice is called a spiral loop, which is a closed teardrop trajectory relative to GEO. The turning point is the point where the velocity of patrol satellite is equal to the GEO. Using the vitality formula, turning point is
Among them,
v is the velocity of the turning point,
a is the semi major axis of the patrol satellite,
r is the position of the turning point, and
µ is the gravitational constant of the Earth. The turning point position is
According to the displacement difference between aiming point and turning point, it is approximately equal to half of the difference between the aiming point and the satellite, that is, the position of the aiming point is
The period of the spiral ring is the time interval where the satellite continuously passing through the same aiming point, which is approximately twice the time between turning points. Similarly, it can be obtained that:
where
vs is the energy parameter at the turning point, which is:
Assuming that the crossing times within a day is {T
1,T
2,…,T
n}, and the earliest aiming point is T
ins, thus.
2.3. Divide IGSO Targets into Regions Based on Dichotomy Approach
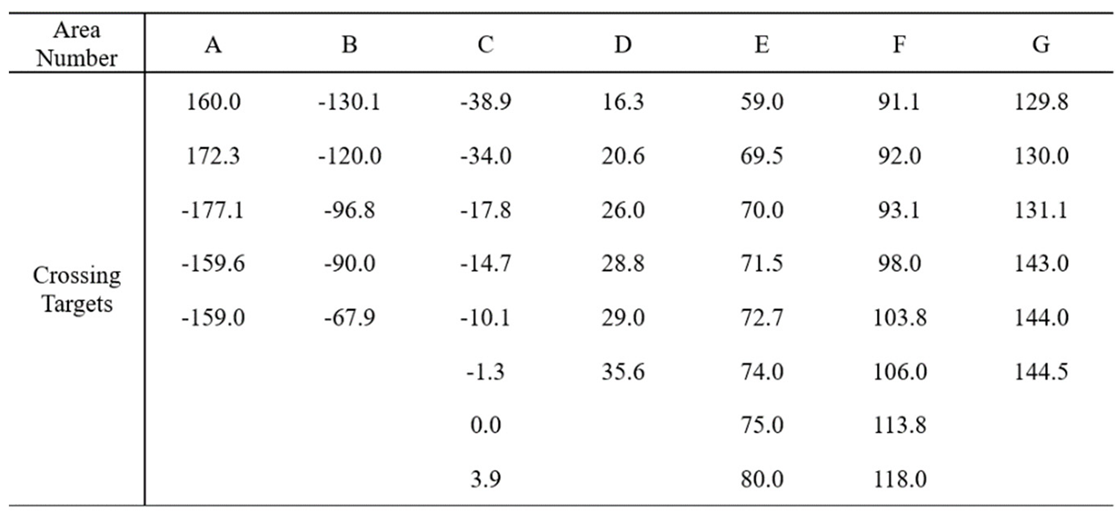
It can be seen that when the longitude drift rate is constant, the patrol period of targets depends on the maximum longitude difference. On the other hand, if the distribution of longitude differences between targets within the zone is uneven, there will be a situation where the targets are concentrated on both sides, which causes a great waste of time. Therefore, when designing the patrol configuration, it is necessary to consider dividing all targets reasonably to ensure that the longitude differences within each zone are consistent, so that the patrol periods of each zone are not significantly different, and thus achieve periodic patrol of all targets.
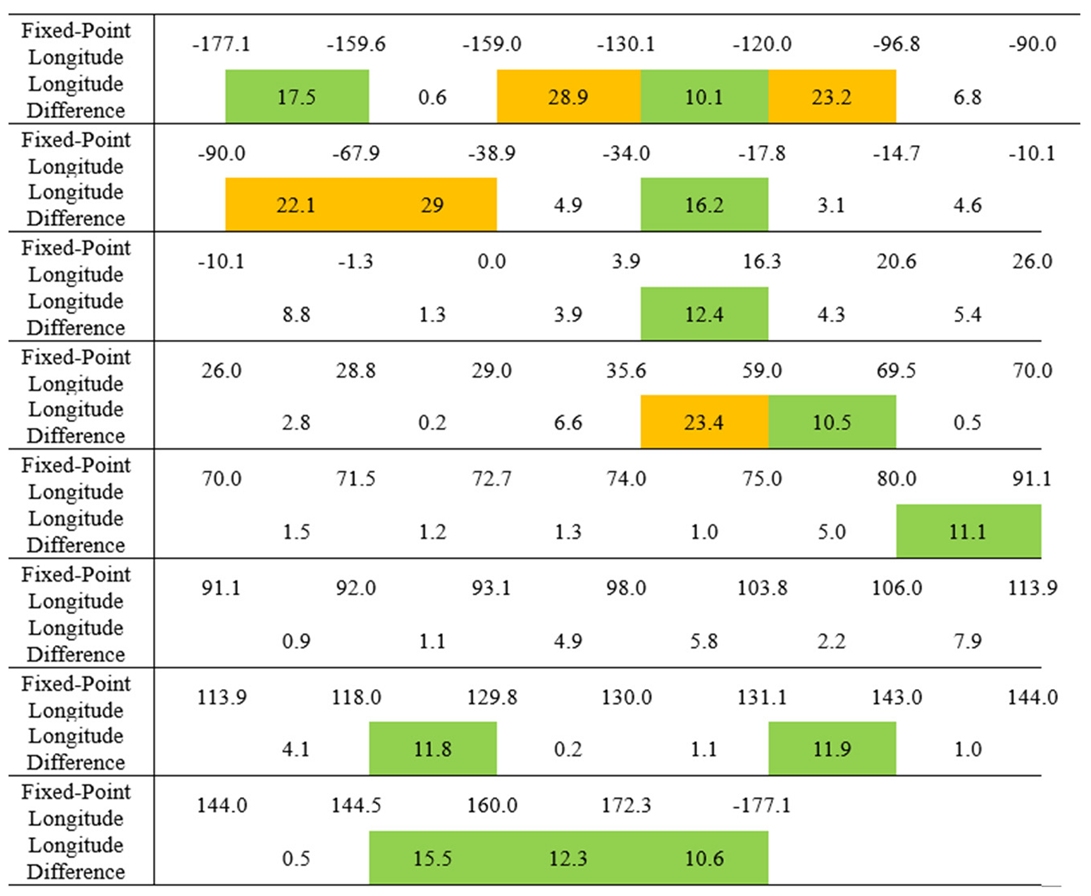
Without losing generality, sort n GEO targets in ascending order according to their sub-satellite point longitude, and record the longitude as λ
i (i=1, 2,..., n), and λ
1< λ
2<…< λ
n. Distributed on GEO orbits, the difference in longitude between adjacent targets is recorded as Δλ
i (i=1, 2,..., n), then there is
When the distribution of GEO targets is uneven, there will inevitably be several large longitude gaps. If the divided area covers the gaps, there will be a significant in-crease in patrol period due to a single target. Therefore, when dividing zones, it is necessary to avoid these huge gaps as much as possible.
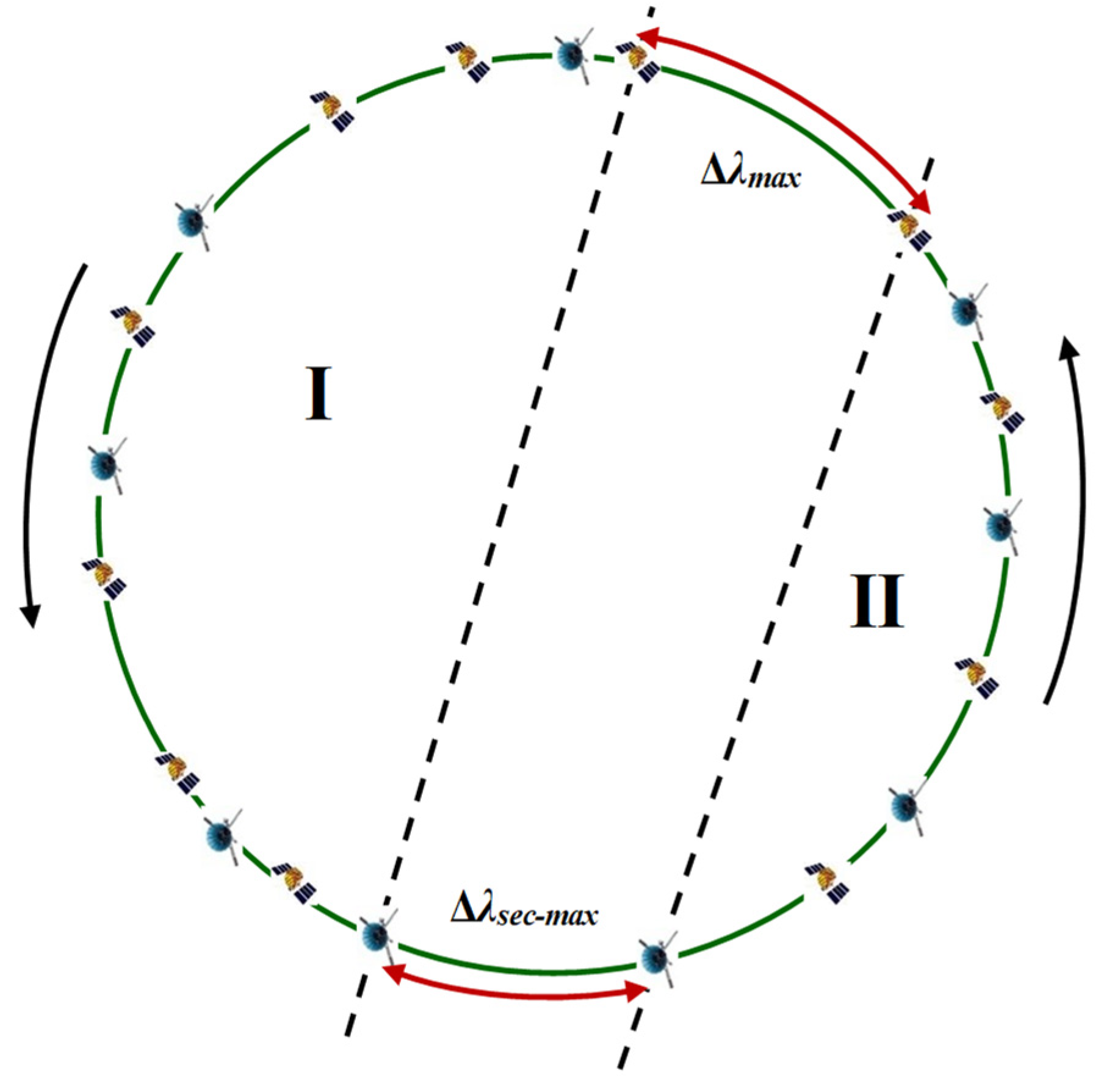
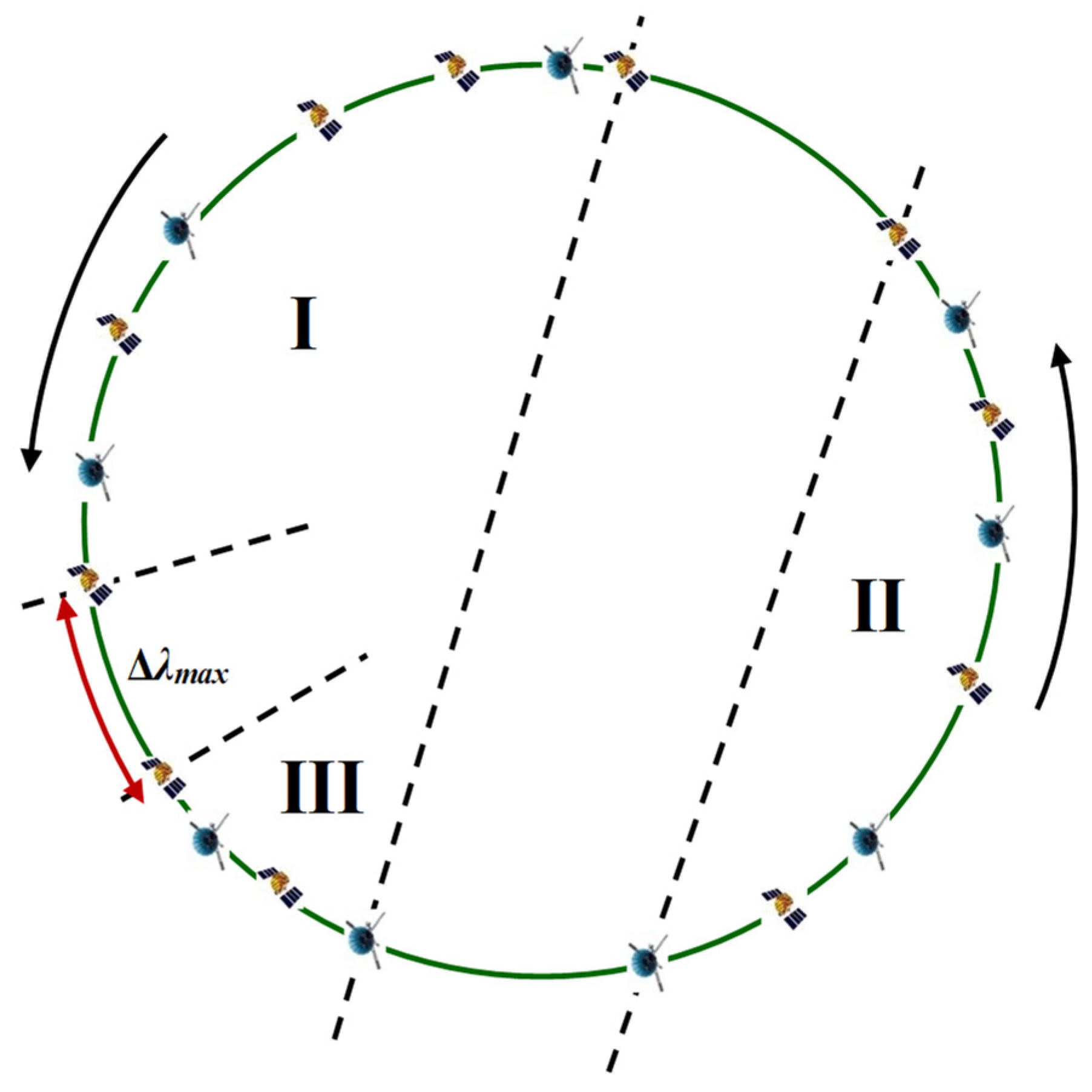
This paper presents a zone division method based on dichotomy approach, which can quickly perform zone division. Set the maximum and second largest longitude difference gap between targets as
Due to the characteristic of circular distribution, these two longitude differences divide all targets into two zones, as shown in
Figure 6.
The longitude coverage ranges of the two zones are
Set the range of longitude drift rate to
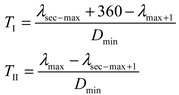
Then the maximum patrol period of the two zones can be calculated as
Compare the sizes of T
I and T
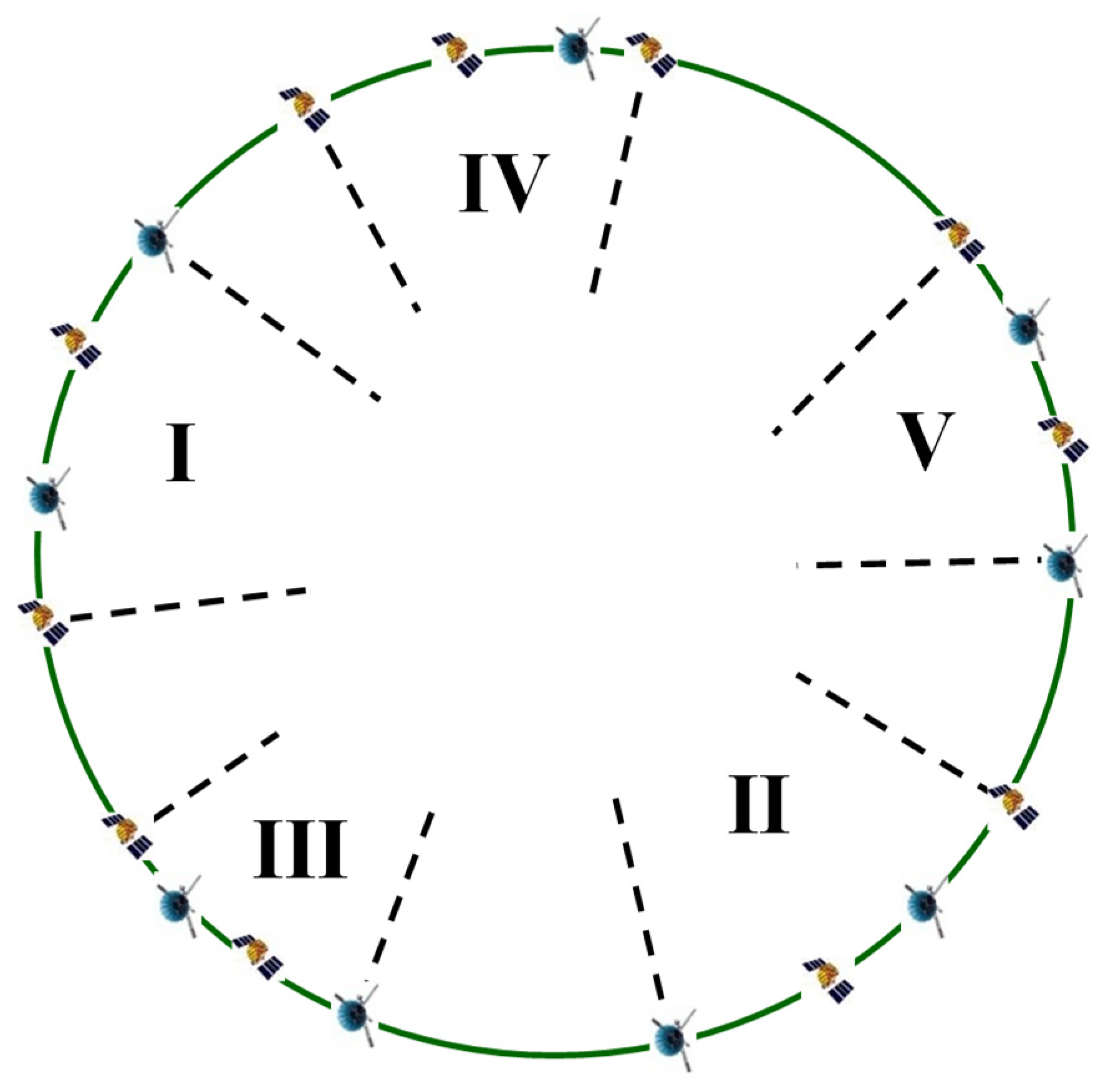
II, select the zone with a larger period, select the maximum longitude difference gap within the zone, and perform secondary division, as shown in
Figure 7.
Compare the periods of the three zones T
I , T
II and T
III, and also select the zones with larger periods for segmentation using the maximum longitude difference gap until all zones meet the patrol period T
0 (T
0 is the given limitation period), as shown in
Figure 8.
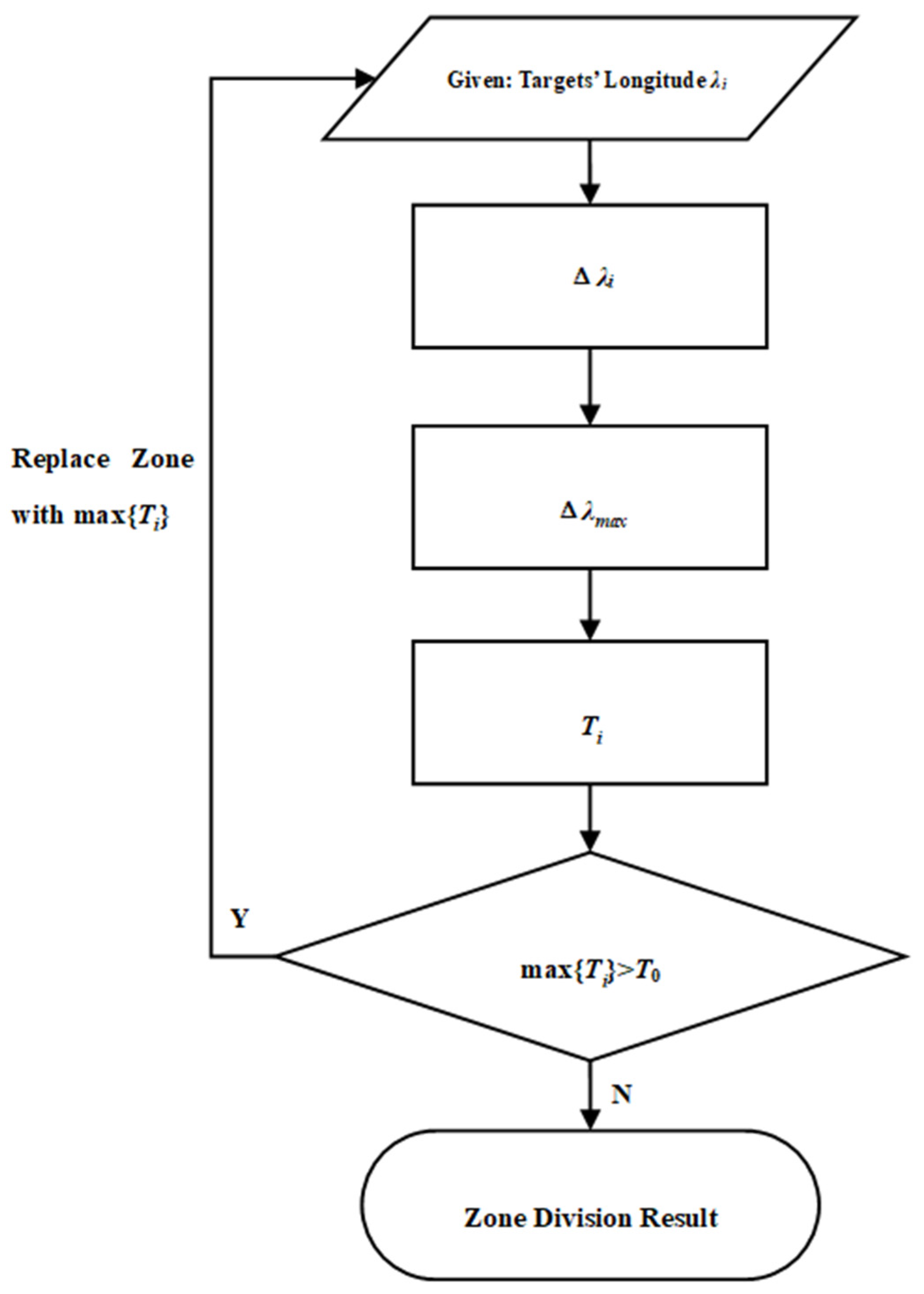
The process steps for dividing the entire zone are shown in
Figure 9.
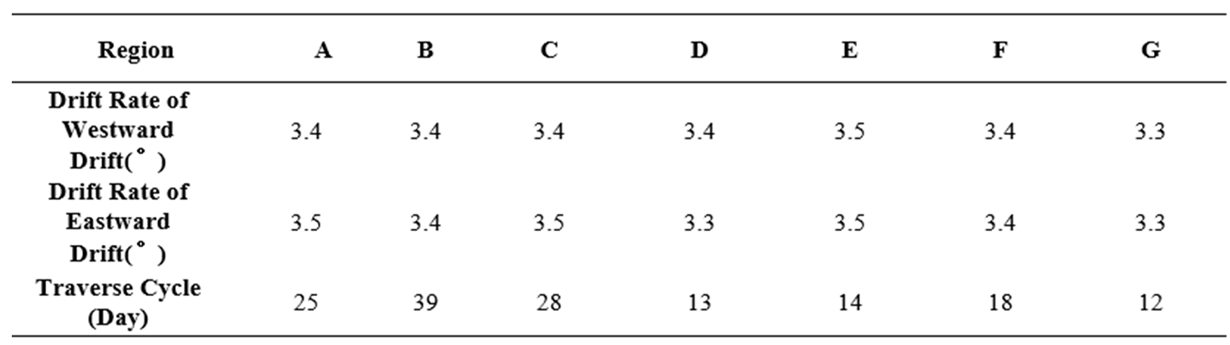
2.4. Calculate the Bidirectional Longitude Drift Rate within Each Region
After dividing the entire target into multiple zones, it is necessary to determine the east/west longitude drift rate within each zone. Assuming n targets are divided into N zones, denoted as Z
i (i=1, 2, ..., N), each zone contains M
i targets, represented by their sub-satellite point longitude, denoted as λ
ij (i=1, 2, ..., N, j=1, 2, ..., M
i). Thus
It can be seen from
Figure 4 that if target k and target l can be observed in one patrol, their longitude difference needs to be an integral multiple of the drift rate, which is
The above equation also indicates that the remainder of t drift rate D for target k and target l is the same, which is
Assuming that the eastward longitude drift rate of the patrol satellite is D
E and the westward is D
W. It can be inferred from the above analysis that the conditions for achieving patrol of targets can be transformed into the existence of D
E and D
W, so that the eastward target set Q
E with the same remainder of D
E, and the westward target set Q
W with the same remainder of D
W, meet the union of the Q
E and Q
W can include all targets
Taking zone N as an example for analysis, the sub-satellite point longitude of the targets is λ
j (j=1, 2, ..., M
N). Considering the existence of the GEO satellite box, keep the sub-satellite point to one decimal, denoted as λ
j* (j=1, 2, ..., M
N). Simultaneously, simplify the longitude drift rate to one decimal
order
Take Q corresponding to the mode of the above set, denoted as Q
Di, then
Join the above target sets until patrol of all targets is achieved
Considering that the orbital periods for patrol satellite are not significantly different, the drift rate affects the number of patrol cycles under certain longitude difference conditions. The larger the drift rate, the more longitudes drift each day, the fewer cycles required for patrol, and the shorter the corresponding patrol cycle. On the contrary, the smaller the drift rate, the longer the patrol period. Therefore, patrol satellites with high longitude drift rates should be selected firstly. When satellites with high longitude drift rates do not meet the requirements for patrol, they choose to use smaller longitude drift rates for patrol.
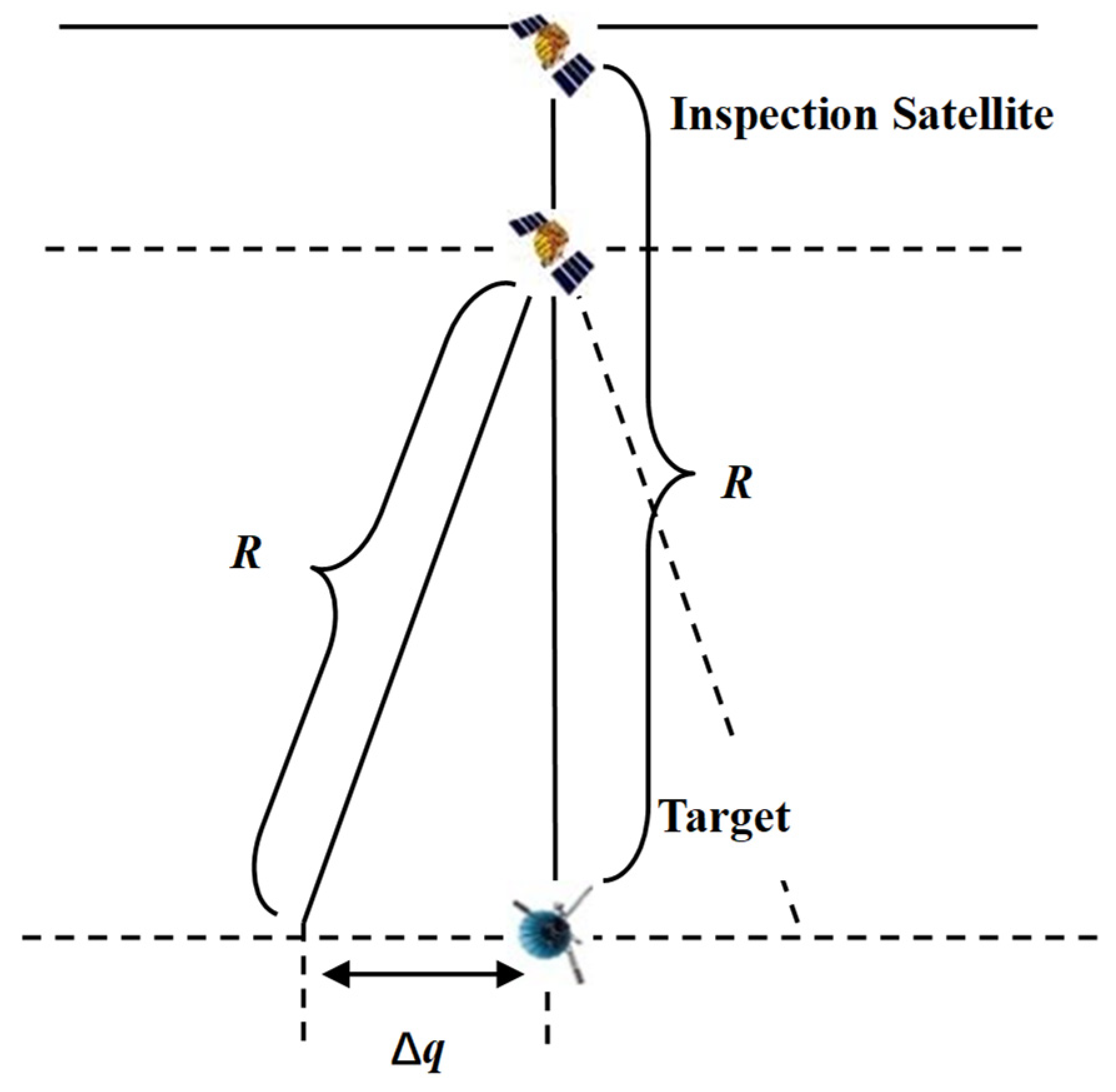
In addition, according to the constraint analysis, there is redundancy in the observation distance. By adjusting the observation distance, a certain sub-satellite point longitude threshold can be brought to the target's sub-satellite point longitude, as shown in
Figure 10.
Set the point longitude threshold to Δq. The same remainder condition is trans-formed into
Correspondingly, the target set corresponding to the mode becomes the target set corresponding to the same set of residues with the most elements
Take the intersection of the target set Q generated by each longitude drift rate mentioned above, and find two sets of longitude drift rates, which are the east-west longitude drift rates used by the satellite for patrol.
2.5. Determine the Starting Position of Patrol for Each Region
Assuming that the set of eastward drift targets and westward drift targets are Q
E and Q
W, the initial position λ
E and λ
W is
At this point, the initial time TE of the eastward drift is the 0 o'clock of λE local time, and the initial time TW of the westward drift is the 12 o'clock of λW local time.
2.6. Determine the Transfer Trajectory for Each Region
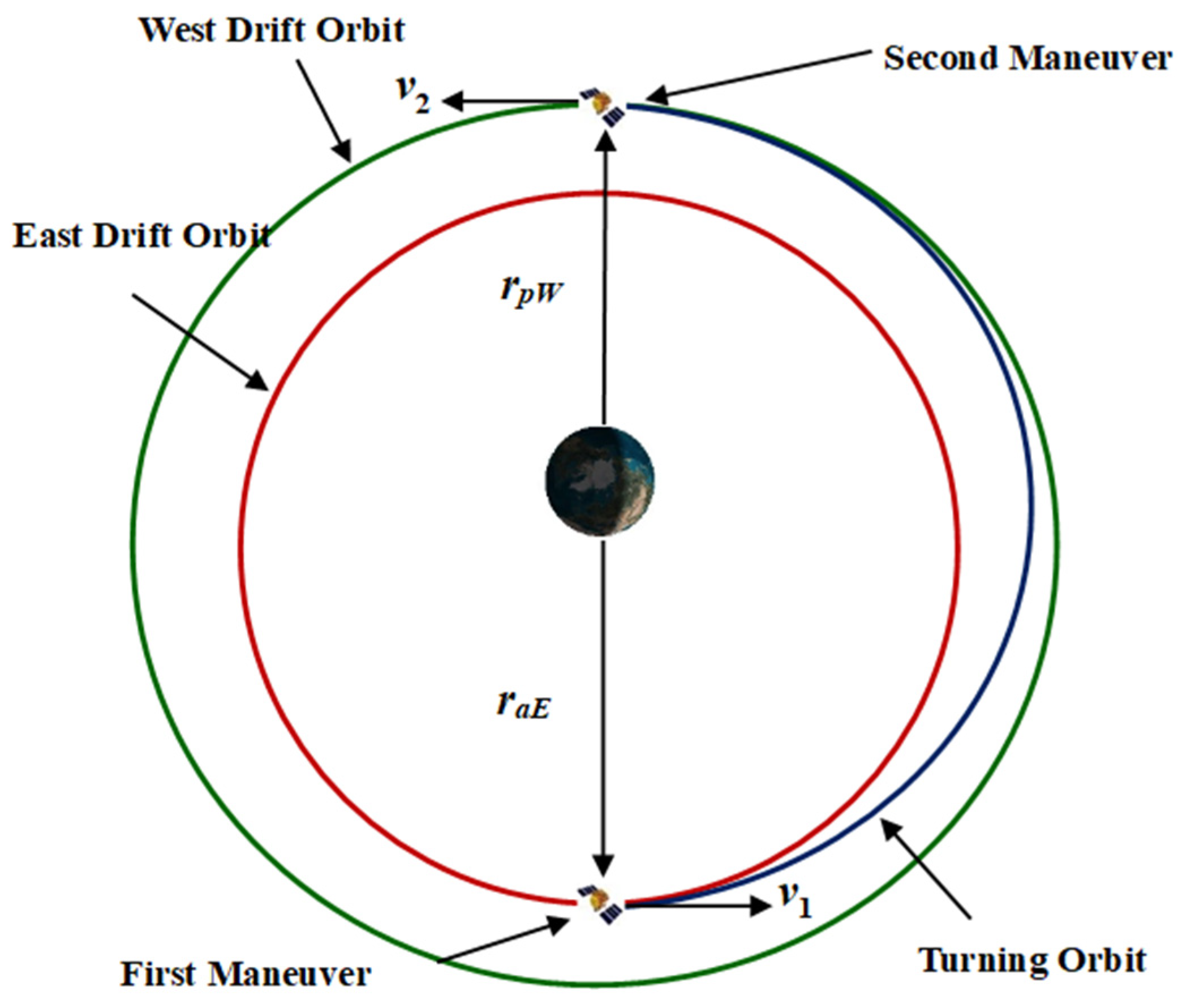
Assuming that the patrol satellite does not consume fuel during the westward and eastward drifts (ignoring the pulses applied during orbit maintenance), the classic double pulse orbit transfer method is used for the turning process. Eastward drift first and then westward, as shown in
Figure 11.
From the previous section, it can be seen that when patrol satellite turns around from east drift to west drift, it should maneuver from the apogee of east drift orbit to the perigee of west drift orbit. As previously analyzed, the patrol position of eastward drift orbit is apogee, while the position of westward drift orbit is perigee, and the period is approximately 24 hours. The above transfer orbit allows the patrol satellite to carry out normal missions after turning around. The specific transfer process is shown in
Figure 12.
According to formula (1), the semi-major axes of east and west drift orbit are
The perigee of the transfer orbit is the eastward drift orbit apogee r
aE, and the apogee of the transfer orbit is the westward drift orbit perigee r
pW, then its semi-major axis is
Based on orbital knowledge, it is easy to obtain the velocity of the eastward drift orbit apogee v
aE, and the velocity of westward drift orbit apogee v
pW, and v
1 and v
2 of the transfer orbit apogee, respectively
Therefore, the energy consumption required for the transition is
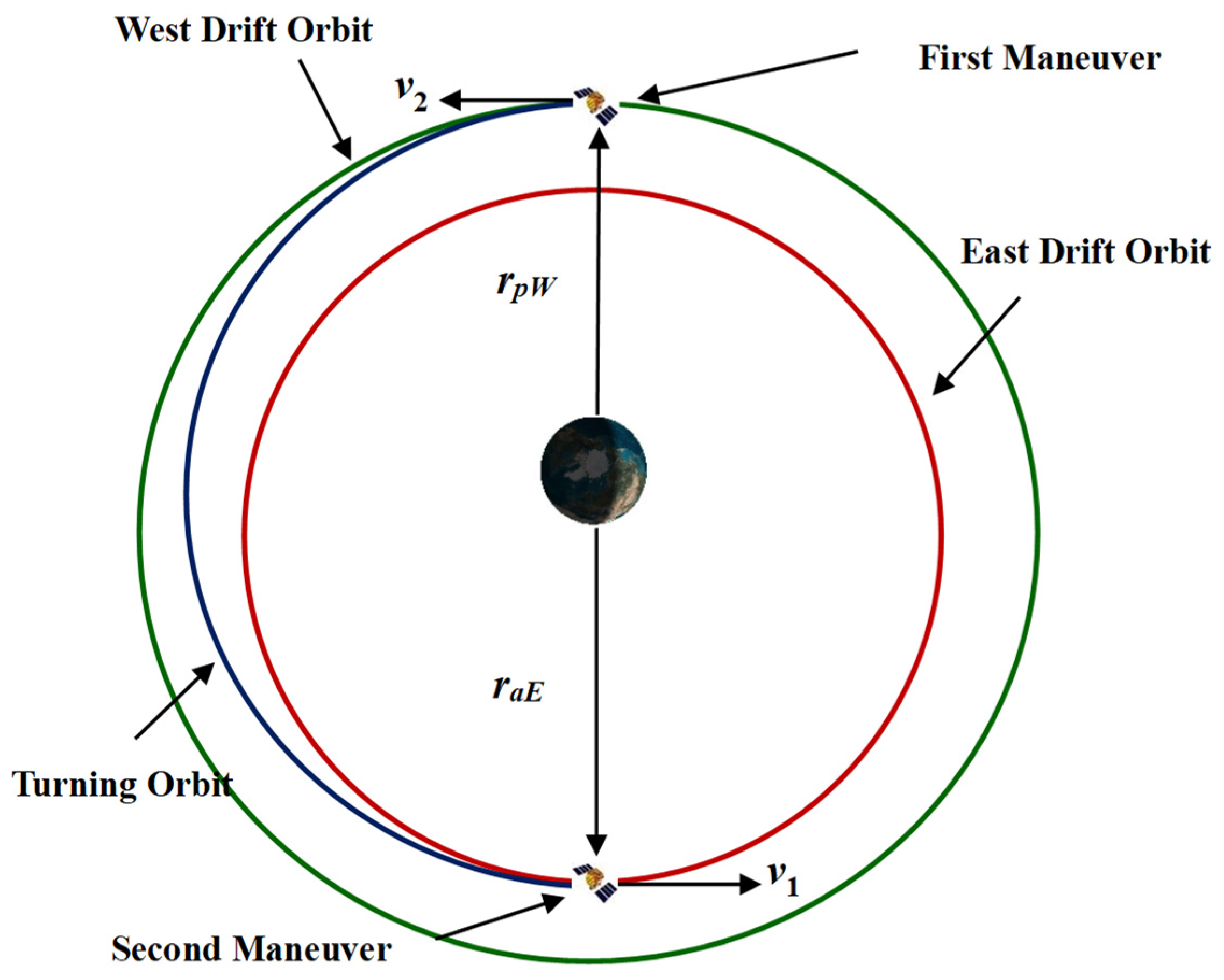
Similarly, when the patrol satellite transitions from a west to east, it shifts from the perigee of the westward drift orbit to the apogee of the eastward drift orbit, as shown in
Figure 13.
It can be seen that the required energy consumption is also
Thus, it can be obtained that the energy consumption of patrol of the targets in the zone once is
Figure 1.
GEO Zone Defined by IADC.
Figure 1.
GEO Zone Defined by IADC.
Figure 2.
Patrol route relative to GEO orbit.
Figure 2.
Patrol route relative to GEO orbit.
Figure 3.
Schematic diagram of patrol strategy.
Figure 3.
Schematic diagram of patrol strategy.
Figure 4.
Schematic diagram of satellite crossing point.
Figure 4.
Schematic diagram of satellite crossing point.
Figure 5.
Schematic diagram of spiral cruise.
Figure 5.
Schematic diagram of spiral cruise.
Figure 6.
Schematic diagram of zone division.
Figure 6.
Schematic diagram of zone division.
Figure 7.
Schematic diagram of second zone division.
Figure 7.
Schematic diagram of second zone division.
Figure 8.
Schematic diagram of zone division result.
Figure 8.
Schematic diagram of zone division result.
Figure 9.
Zone division process.
Figure 9.
Zone division process.
Figure 10.
Schematic diagram of a certain sub-satellite point longitude threshold.
Figure 10.
Schematic diagram of a certain sub-satellite point longitude threshold.
Figure 11.
Schematic diagram of turning around.
Figure 11.
Schematic diagram of turning around.
Figure 12.
Schematic diagram of turning around orbit.
Figure 12.
Schematic diagram of turning around orbit.
Figure 13.
Schematic diagram of turning around orbit.
Figure 13.
Schematic diagram of turning around orbit.
Figure 14.
Schematic diagram of observation positions for patrol satellite.
Figure 14.
Schematic diagram of observation positions for patrol satellite.
Figure 15.
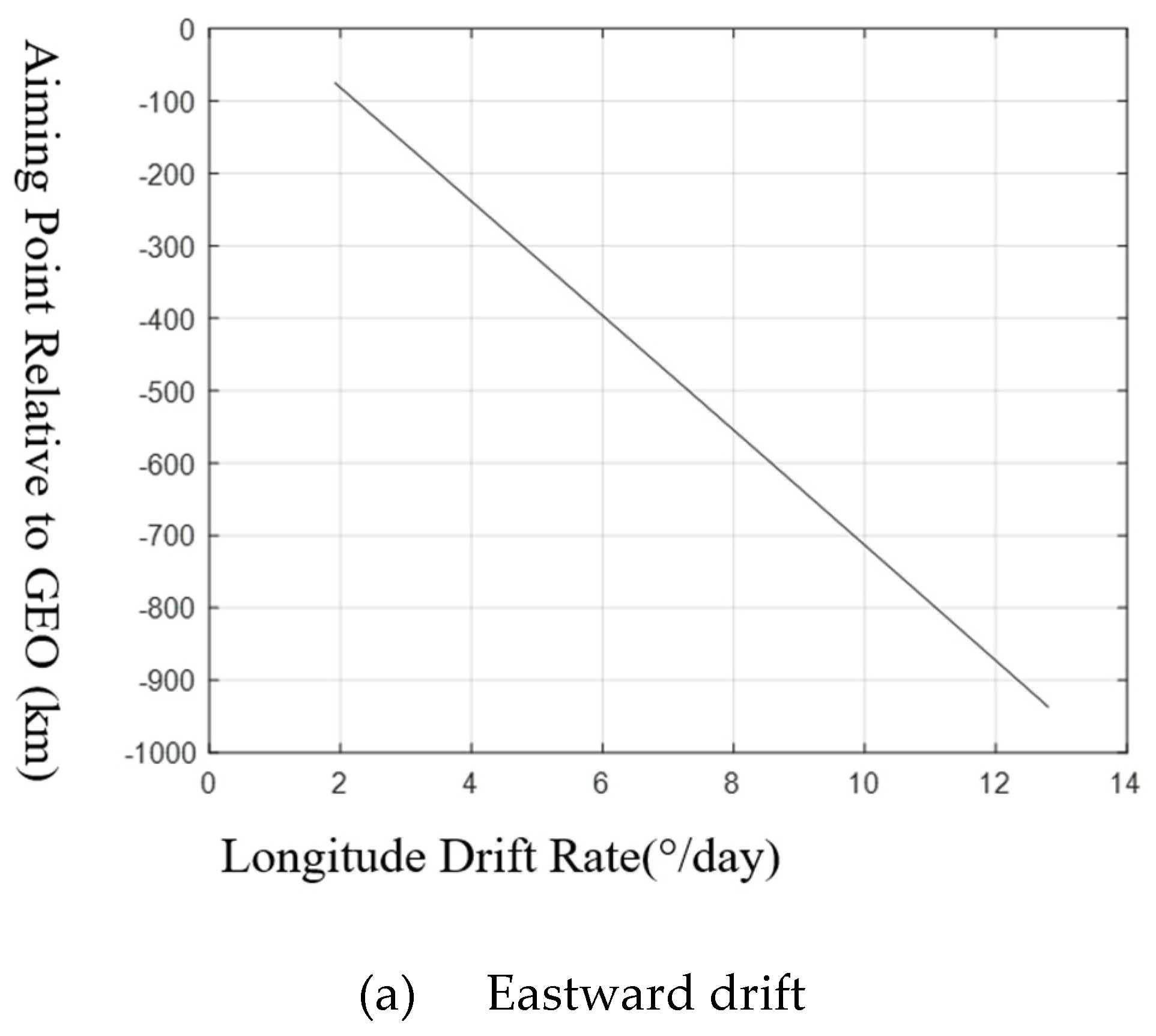
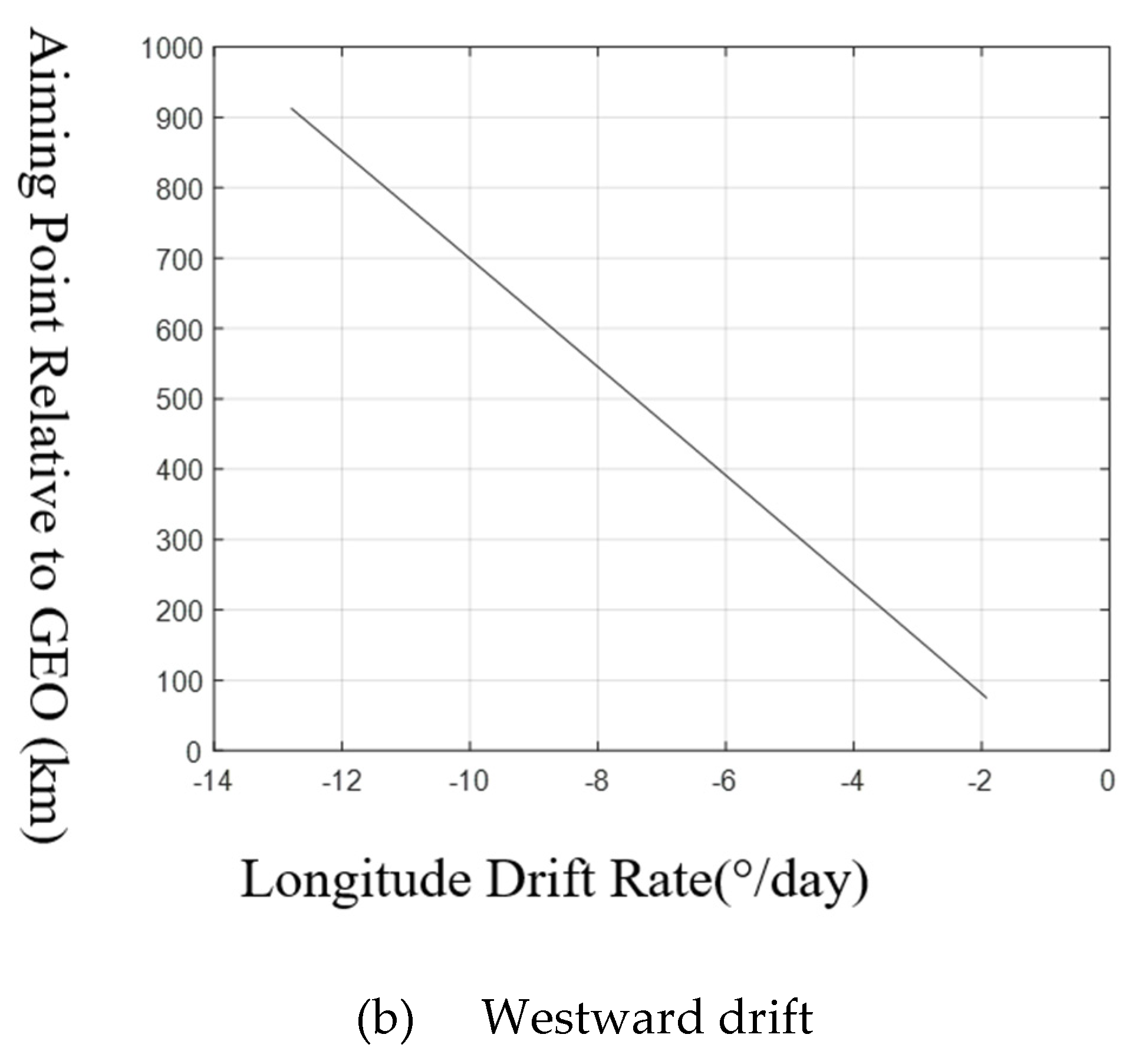
Diagram of the aiming point position relative to GEO with longitude drift rate.
Figure 15.
Diagram of the aiming point position relative to GEO with longitude drift rate.
Figure 16.
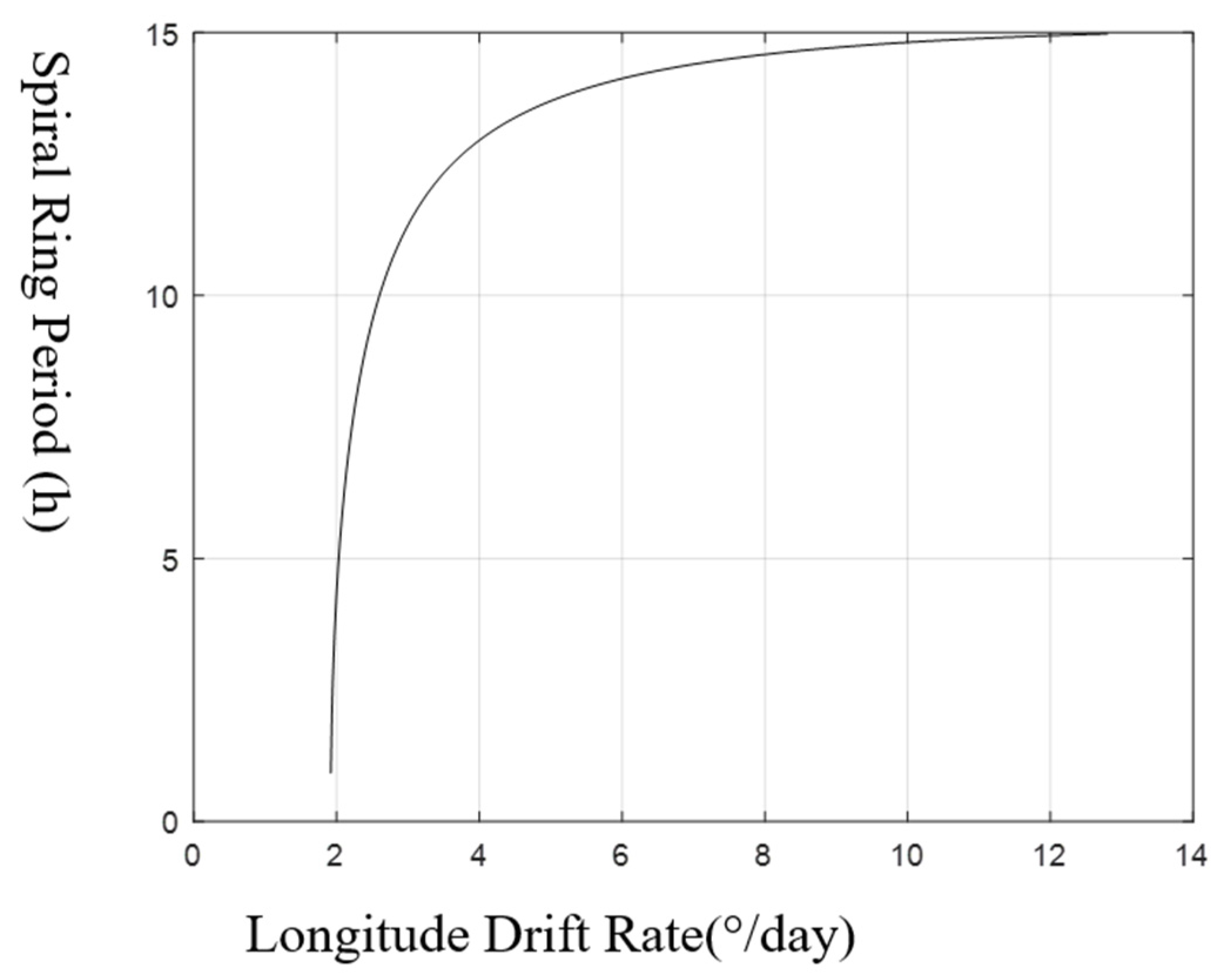
Diagram of spiral ring period variation with longitude drift rate.
Figure 16.
Diagram of spiral ring period variation with longitude drift rate.
Figure 17.
Schematic diagram of the IGSO patrol configuration.
Figure 17.
Schematic diagram of the IGSO patrol configuration.
Figure 18.
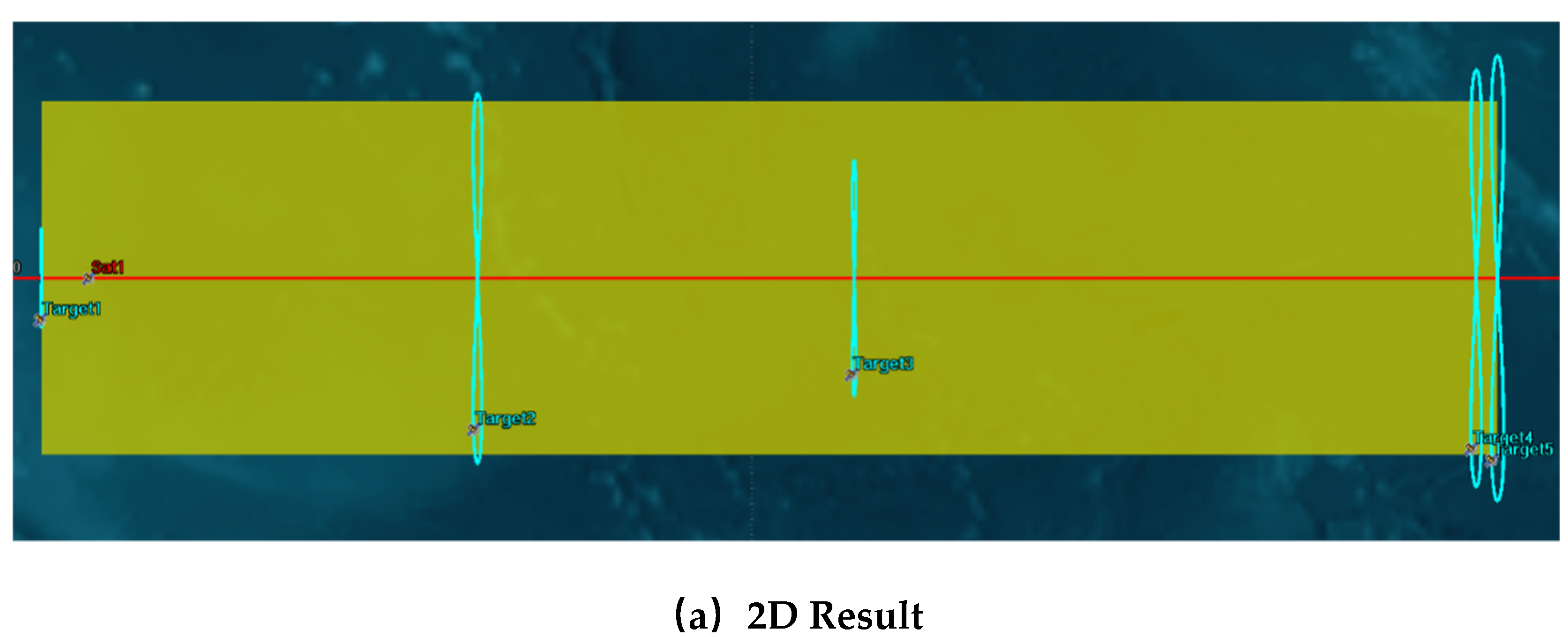
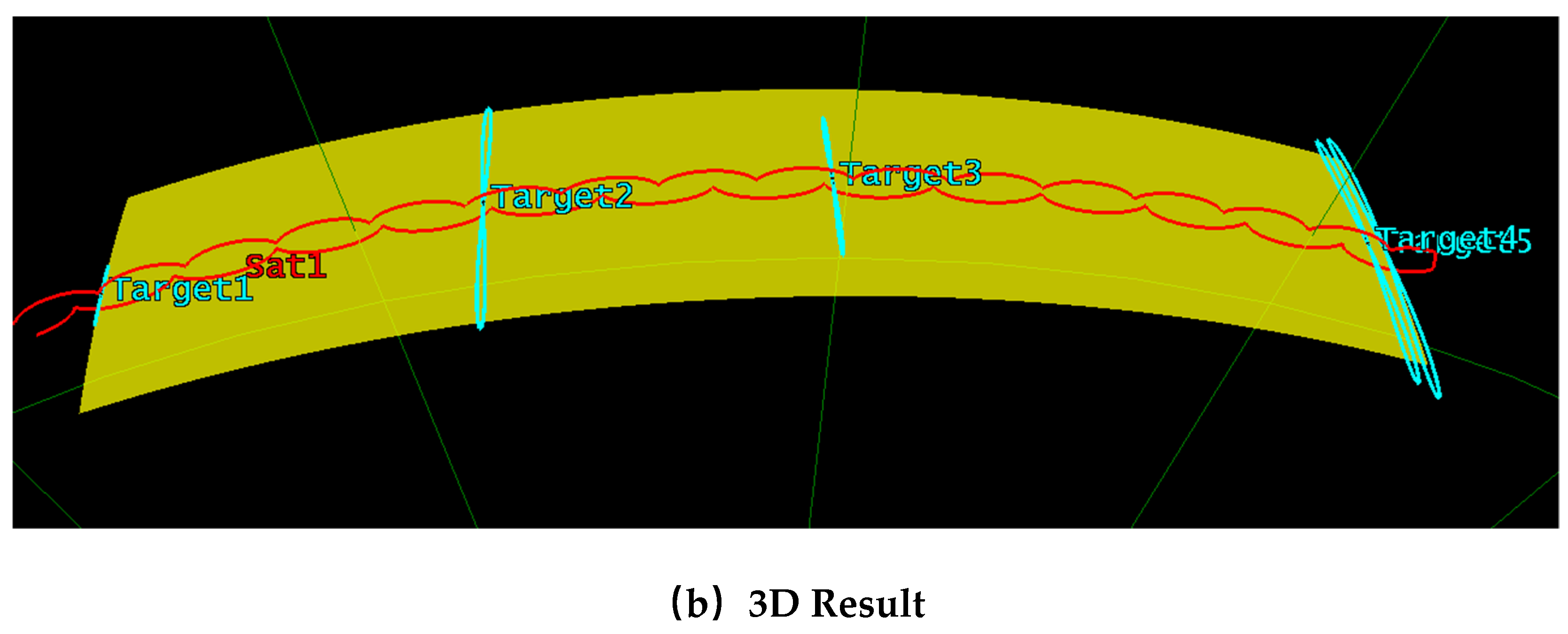
Patrol simulation results of zone A.
Figure 18.
Patrol simulation results of zone A.
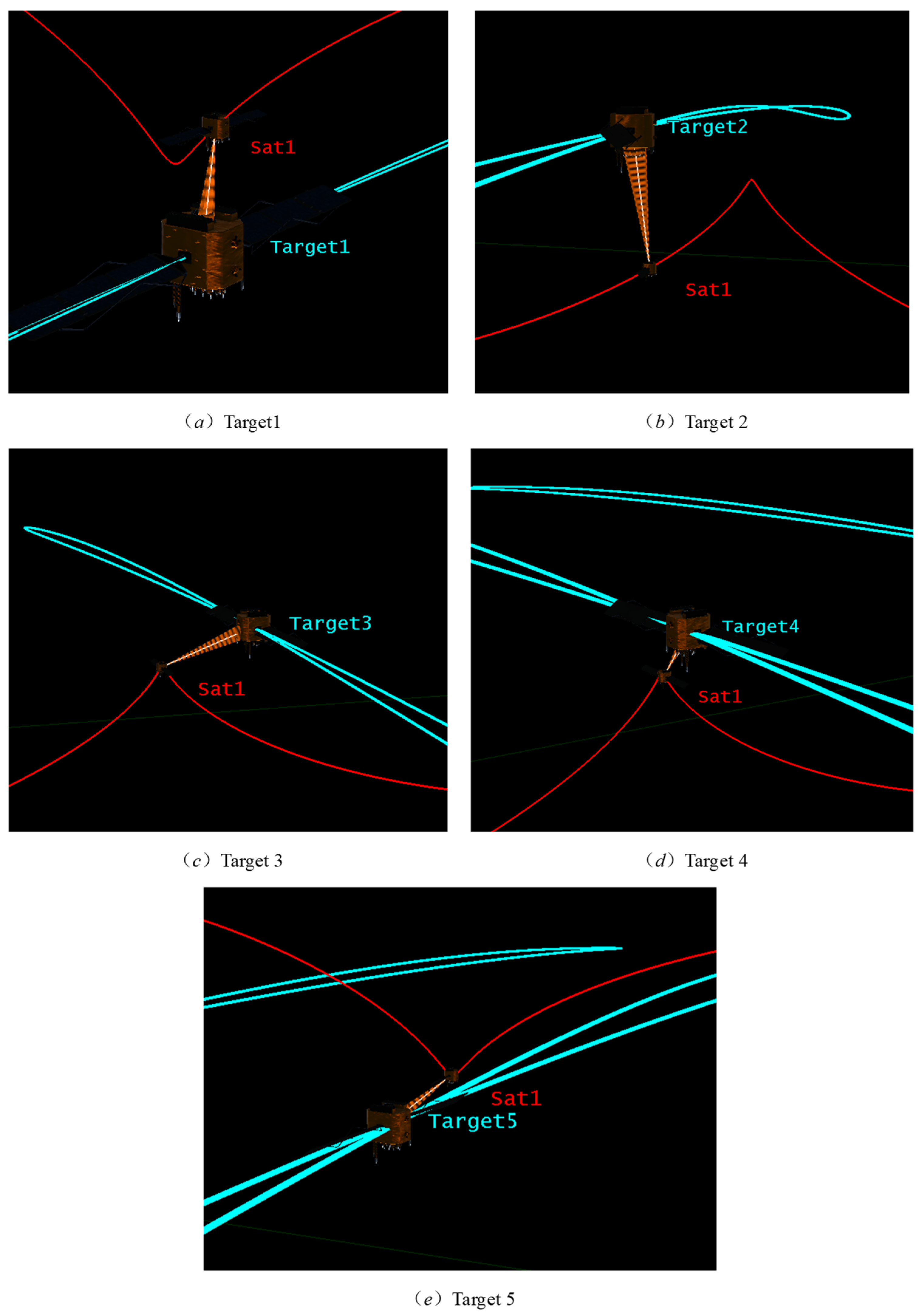
Figure 19.
Patrol of various targets by patrol satellite.
Figure 19.
Patrol of various targets by patrol satellite.
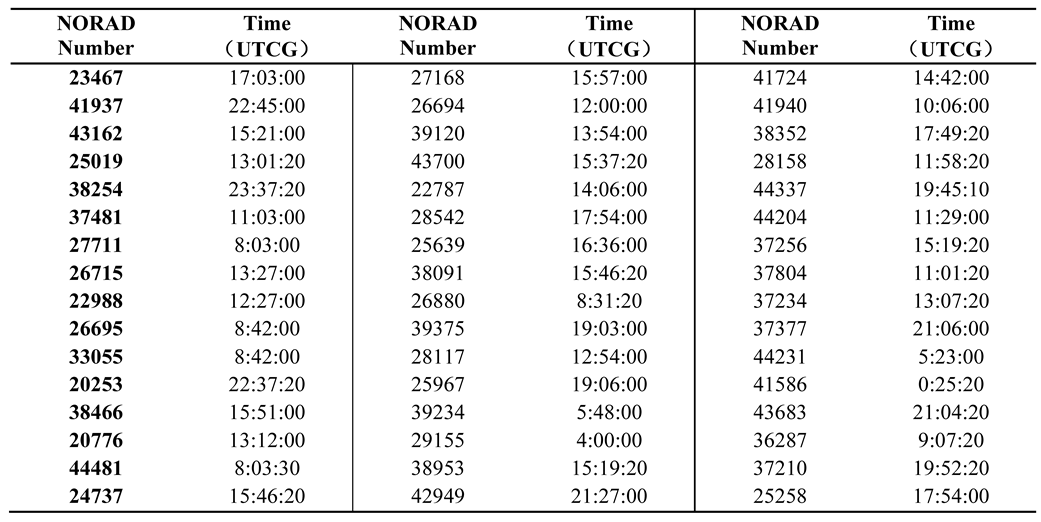
Table 1.
The time of crossing the target.
Table 1.
The time of crossing the target.
Table 2.
IGSO targets position and its longitude difference.
Table 2.
IGSO targets position and its longitude difference.
Table 3.
IGSO targets division.
Table 3.
IGSO targets division.
Table 4.
Longitude drift rate and patrol period of geo crossing target regions.
Table 4.
Longitude drift rate and patrol period of geo crossing target regions.
Table 5.
The initial positions of each region.
Table 5.
The initial positions of each region.
Table 6.
Energy consumption for one patrol cycle.
Table 6.
Energy consumption for one patrol cycle.
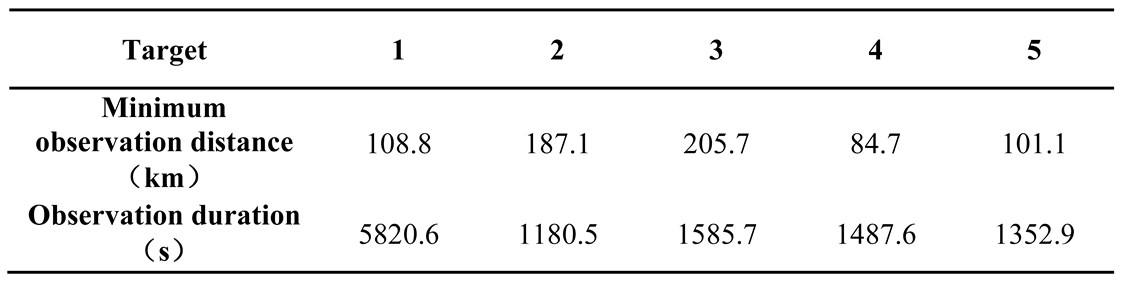
Table 7.
The minimum observation distance and duration for each target.
Table 7.
The minimum observation distance and duration for each target.