Research on Predictive Control Strategy for Phase Shift Full Bridge Transform Based on Improved Nonlinear Disturbance Observer

1. Introduction

With the continuous development of modern industrial manufacturing, the sophisticated development of modern equipment and materials has placed higher demands on traditional electrolytic plating processes. The phase-shifted full-bridge converter (PSFB) has become one of the key components in the development of high-power electrolytic plating equipment due to its high power density, electrical isolation, and ease of achieving soft switching [1].

As a complex system with high-order nonlinearity, the control strategy of the phase-shifted full-bridge converter often adopts control methods that do not rely on mathematical models, including Proportional-Integral (PI) control, sliding mode variable structure control, and hysteresis loop control. Among them, PI control has become the main control method for traditional electrolytic plating power supply design due to its simple structure and fast dynamic response capability. However, the response capability of the PI controller is greatly limited by the design of PI parameters. Therefore, to solve the problem of complex parameter design for PI controllers and further improve the dynamic response capability of the phase-shifted full-bridge converter, Model Predictive Control (MPC) has received widespread attention from scholars.

The rapid development of modern electronic processors has driven research on model predictive control. Its working principle is based on the theoretical model of the controlled object for digital calculation and the application of optimal control quantities using a cost function. It has the characteristics of simple parameter design and faster dynamic response speed. Currently, model predictive control algorithms have achieved certain results in the research of DCDC converters. Literature [2] establishes a reduced-order model for the dual active bridge, proposes a predictive current mode control algorithm, which greatly improves the dynamic performance of the dual active bridge converter during load switching. Literature [3] analyzes the circuit model of the interleaving parallel DCDC converter and combines predictive current control with the least squares method, making the system have faster dynamic performance and smaller output ripple. The dynamic compensation strategy for the Buck-type bidirectional DCDC converter based on model predictive control proposed in literature [4] effectively solves the problem of current fluctuations in DC microgrids.

Although model predictive control can improve the dynamic performance of converters, it also has certain deficiencies. Since the control idea of model predictive control is based on the theoretical model of the controlled object, it requires high accuracy in system modeling. Therefore, when the parameters of the converter components change, the overall control performance of the system will be affected. In addition, external random disturbances also have a certain impact on controllers that solely adopt model predictive control algorithms. To address the above issues, literature [5] combines online parameter identification methods with direct power fast model predictive control strategies to solve the problem of inductor parameter mismatch in converter control systems. Literature [6] designs a voltage outer loop with self-disturbance rejection capability and a predictive direct power control current inner loop, which improves both the anti-disturbance capability and the response speed of the inner loop. Literature [7] combines nonlinear sliding mode control with predictive control, establishes a sliding mode surface predictive control model based on the discrete mathematical model of the bidirectional converter, and ultimately improves the output current ripple of the photovoltaic energy storage converter and enhances system robustness.

Another method to improve system stability is to adopt a disturbance observer. Its basic principle is to equivalently treat the output difference between the actual model and the ideal model caused by external disturbances and changes in model parameters as control input, and introduce equivalent compensation in the loop design to achieve disturbance suppression. For example, literature [8] uses an inductor current disturbance observer to accurately observe and compensate for the input signal of the control inner loop of a three-phase inverter, eliminating the impact of circuit parameter changes and uncertain disturbances on the system and improving system robustness.

To enhance the dynamic response capability of the output current of the phase-shifted full-bridge converter in modern electrolytic plating equipment, this paper combines an improved nonlinear disturbance observer (NDOB) with model predictive control to propose a novel control strategy to improve the dynamic response and anti-disturbance capabilities of the system.

2. PSFB Converter Modeling

2.1. PSFB Working Principle

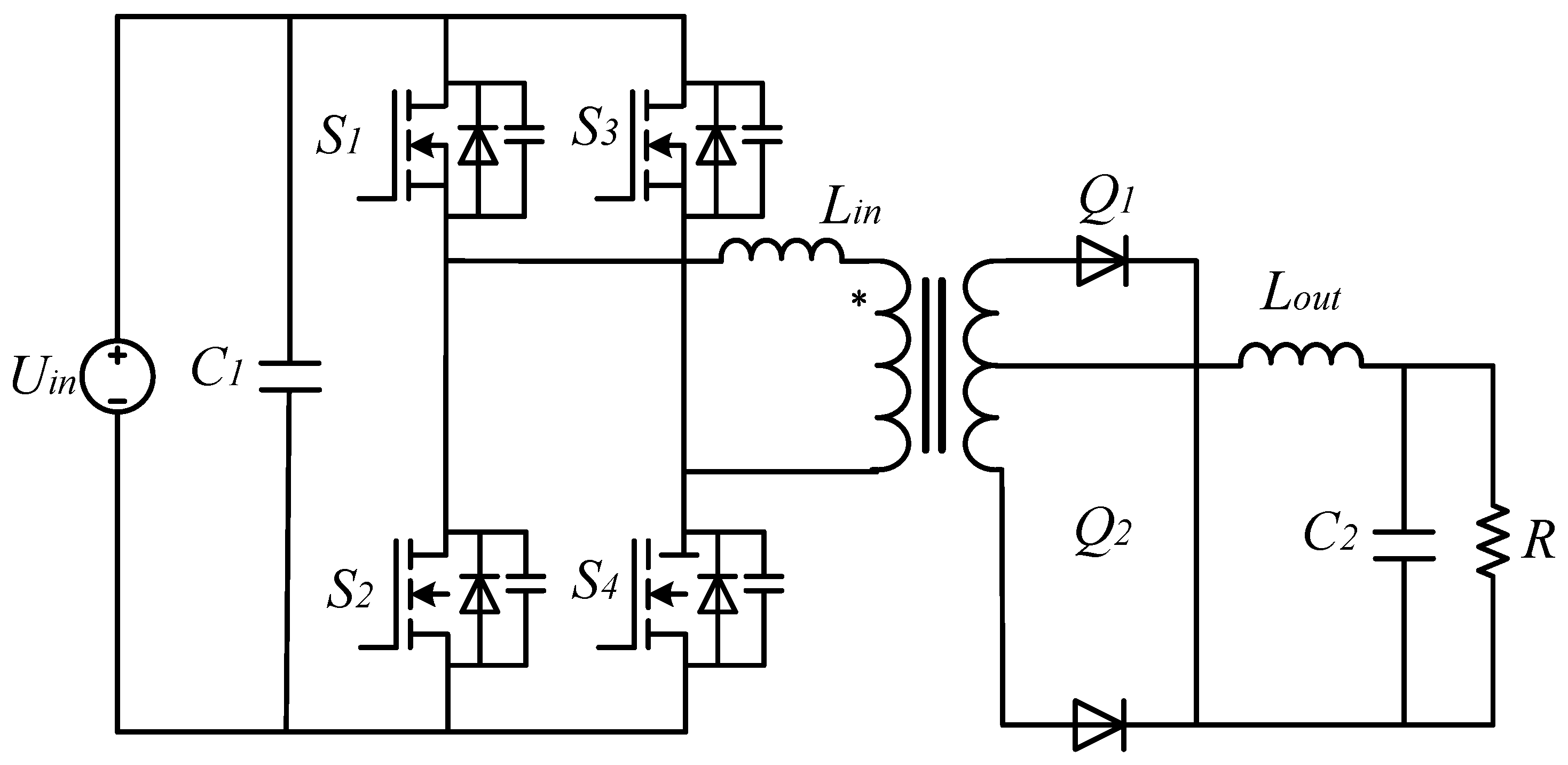
Based on the existing design of electrolytic plating power supplies [9], the topology of the phase-shifted full-bridge converter used in this paper is shown in Figure 1. The structure is mainly divided into a high-voltage input side and a low-voltage output side. The high-voltage input side consists of the input power supply $U_{in}$, the stabilizing capacitor $C_1$, the switches $S_1$ to $S_4$, the resonant inductor $L_{in}$, and the transformer. The low-voltage output side is composed of diodes $Q_1$ and $Q_2$, the output filter inductor $L_{out}$, and the filter capacitor $C_2$. The turns ratio between the primary and secondary sides of the isolation transformer is $N_1:N_2$, and the ratio is denoted as n.

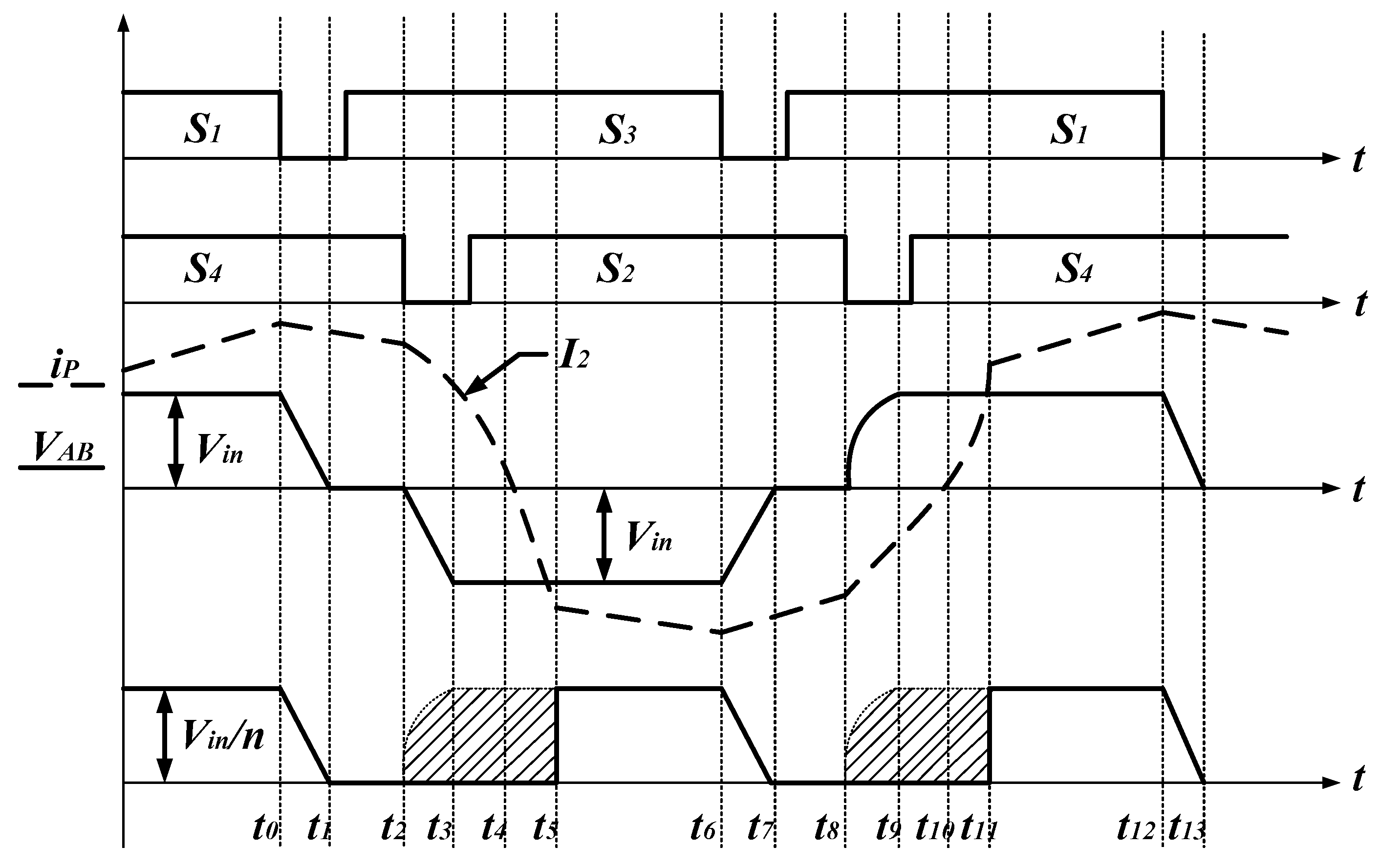
The phase-shift control process of the converter is shown in Figure 2, where switches $S_1$ and $S_2$ are the leading leg, and $S_3$ and $S_4$ are the lagging leg. The conduction time interval between the leading leg and the lagging leg is the phase-shift angle, which determines the magnitude of the full-bridge output voltage. Ts represents the minimum period of a PWM switch, and the maximum duty cycle of the input-side leg is 0.5Ts.

2.2. Equivalent Mathematical Model

Analyzing the circuit principles of the phase-shifted full-bridge converter, the input side primary can be treated as an equivalent voltage source, and the operation process of the secondary side can be approximated as a Buck circuit. Under continuous current operation mode, the theoretical model of the converter satisfies the following relationship [10]:

$$\left\{\begin{array}{c}{\displaystyle \frac{d{\mathrm{u}}_c}{dt}}=-{\displaystyle \frac{1}{R{C}_2}}{u}_c+{\displaystyle \frac{1}{C_2}}{i}_L\\ {\displaystyle \frac{d{\mathrm{i}}_L}{dt}}=-{\displaystyle \frac{1}{L_f}}{i}_L+{\displaystyle \frac{1}{L_f}}{U}_{in}\end{array}\right.$$

(1)

In the formula, R represents the load, $i_L$ is the output current, and $u_c$ is the output voltage. Given a duty cycle of D, the relationship between the output voltage $u_c$ and the input voltage $U_{in}$ is given by the following formula:

$$u_c=D·U_{in}/n$$

(2)

2.3. Control Framework Design

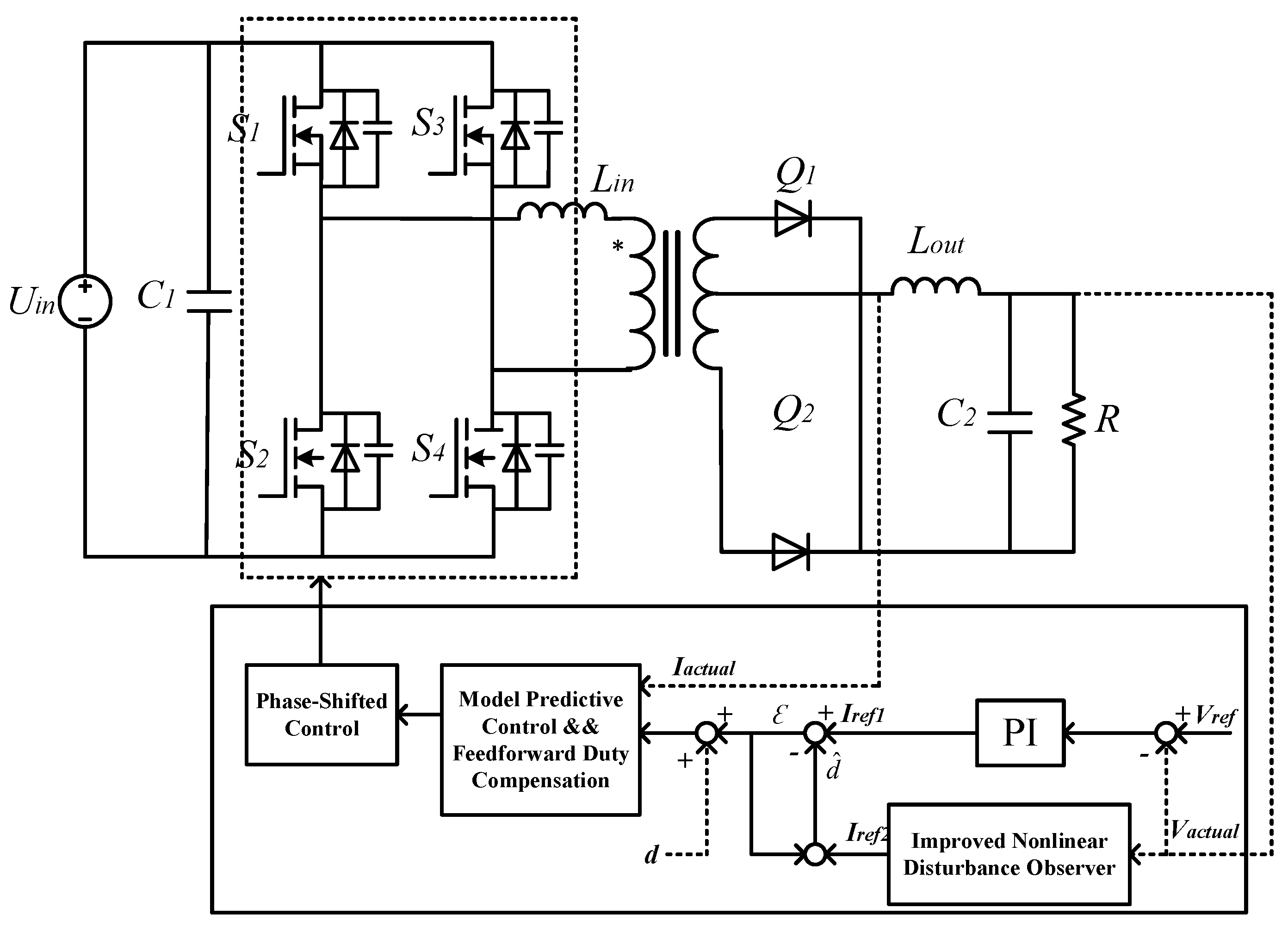
Based on the topology and mathematical model derivation of the phase-shifted full-bridge converter, this paper designs the control framework shown in Figure 3 below. The core of this framework is divided into four main modules: model predictive control design, disturbance observer design, duty cycle compensation, and phase-shift control. Model predictive control serves as the primary inner loop control structure, aiming to enhance the dynamic response capability of the system. The disturbance observer is responsible for real-time monitoring of sudden changes in system parameters and external random disturbances, thereby improving system robustness. Duty cycle compensation specifically addresses the issue of duty cycle loss in phase-shifted full-bridge control. Phase-shift control converts the calculated equivalent duty cycle into an actual controlled phase-shift angle, achieving precise control of the output voltage.

3. PSFB Controller Design

3.1. Model Predictive Control Strategy

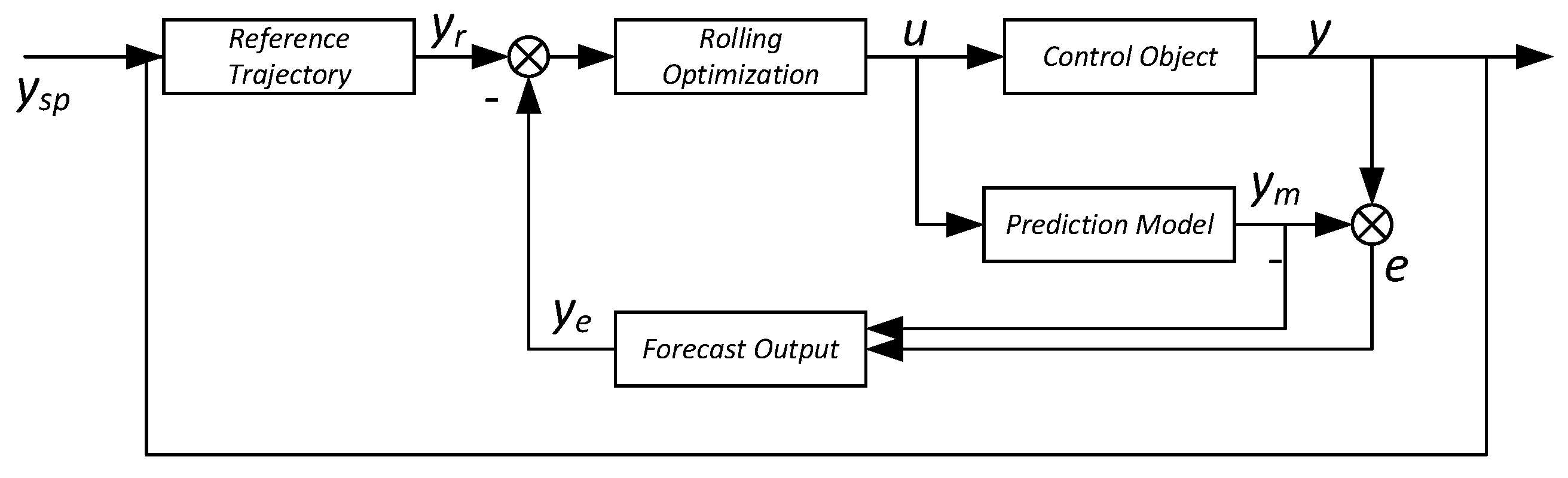
In this paper, the model predictive control algorithm is applied to the control process of the phase-shifted full-bridge converter, following three key steps: prediction model establishment, rolling optimization control, and feedback correction. The specific implementation process is shown in Figure 4.

Firstly, the implementation of the model predictive control strategy requires precise modeling of the controlled system. By utilizing the state-space equation to represent the phase-shifted full-bridge converter [11], the following expression can be obtained:

$$\dot{x}=Ax+Bu$$

(3)

Wherein: $\begin{array}{cc}& x=\left[\begin{array}{c}{u}_c\\ i_L\end{array}\right],u=\left[\begin{array}{c}0\\ U_{in}\end{array}\right]\hfill \\ & A=\left[\begin{array}{cc}-{\displaystyle \frac{1}{R{C}_2}}& {\displaystyle \frac{1}{C_2}}\\ -{\displaystyle \frac{1}{L_f}}& 0\end{array}\right],B=\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{L}}\end{array}\right]\hfill \end{array}$

Secondly, based on the first-order Euler formula, a discretized state space expression is established for the phase-shifting full bridge converter as follows:

$$\left\{\begin{array}{c}{u}_c^{k+1}=(1-{\displaystyle \frac{{\mathrm{T}}_{\mathrm{s}}}{R{C}_2}})u_c^k+{\displaystyle \frac{{\mathrm{T}}_{\mathrm{s}}}{C_2}}{i}_L^k\\ i_L^{k+1}=-{\displaystyle \frac{{\mathrm{T}}_{\mathrm{s}}}{L_f}}{u}_L^k+i_L^k+{\displaystyle \frac{D·{\mathrm{T}}_{\mathrm{s}}}{L_f}}{U}_{in}\end{array}\right.$$

(4)

Finally, considering that model predictive control has an enhancing effect on the dynamic response capability of the system and can effectively achieve the controlled system to follow current changes, the current reference value is selected as the core consideration factor for the cost function[12]. The expression for the cost function g is as follows:

$$g=\left|i_L^{ref}-i_L^{k+1}\right|$$

(5)

3.2. Disturbance Observer Design

To suppress external random disturbances and sudden changes in controlled system parameters, this paper designs a nonlinear disturbance observer to observe them. The definition of random disturbances and parameter changes during the operation of a phase-shifting full bridge converter is lumped disturbance dtotal, and the expression of the converter model with added lumped disturbance is:

$$\dot{x}=Ax+Bu+d_{total}$$

(6)

The disturbance observer observation value is defined as ${\widehat{d}}_{total}$, and the disturbance estimation error ${\widehat{d}}_{total}$ satisfies the following equation:

$${\tilde{d}}_{total}=d_{total}-{\widehat{d}}_{total}$$

(7)

It can be assumed that the variation of external random disturbances is very slow, and its derivative is estimated to be 0. Therefore, the differential of disturbance estimation error satisfies the following equation:

$${\dot{\tilde{d}}}_{total}={\dot{d}}_{total}-{\dot{\widehat{d}}}_{total}\approx -{\dot{\widehat{d}}}_{total}$$

(8)

To ensure effective convergence of disturbance estimates, a convergence law can be designed to ensure that the error estimate tends towards 0. The perturbation estimation approach law is defined in the following form:

$${\dot{\widehat{d}}}_{total}=l\left(x\right)·{\dot{\tilde{d}}}_{total}=l\left(x\right)·(d_{total}-{\dot{\widehat{d}}}_{total})$$

(9)

After substituting the above equation into the nonlinear system equation, a naive nonlinear disturbance observer can be obtained.

$${\dot{\widehat{d}}}_{total}=l\left(x\right)·(\dot{x}-Ax-Bu)-l\left(x\right)·{\widehat{d}}_{total}$$

(10)

Due to the need for naive disturbance observers to utilize parameters, most systems typically cannot directly obtain the measured value. Therefore, based on the basic principle of improving the NDOB observer, an improved NDOB model can be obtained [13]:

$$\left\{\begin{array}{c}{\widehat{d}}_{total}=z+p\left(x\right)\\ \dot{z}=l\left(x\right)·[-Ax-Bu+p\left(x\right)]-l\left(x\right)·z\end{array}\right.$$

(11)

In the formula, z is the intermediate variable, and $p\left(x\right)$ satisfies the following relationship:

$${\displaystyle \frac{dp\left(x\right)}{dt}}=l\left(x\right)·\dot{x}$$

(12)

3.3. Duty Cycle Compensation and Phase Shift Control

Duty cycle loss refers to the difference between the effective duty cycle $D_{ass}$ of the secondary side and the duty cycle D of the primary side given by the driving signal, denoted as $D_{loss}$, which satisfies the following expression.

$$D_{loss}=D-D_{ass}$$

(13)

The problem of duty cycle loss is a major challenge in the control process of phase-shifting full bridge converters. The reason for this is that the voltage drop at both ends of the resonant inductor in the transformer’s primary side causes a decrease in the actual output voltage. Therefore, to solve this problem, based on consulting relevant literature [14], this article derives the calculation logic of the duty cycle $D_{loss}$ and obtains the following relationship:

$$D_{loss}={\displaystyle \frac{2i_L-0.5u_c(1-D)T_s/L_{out}}{n·\frac{U_{in}}{L_{in}}·\frac{T_s}{2}}}$$

(14)

After algebraic simplification of the above equation, it can be concluded that:

$$D_{loss}={\displaystyle \frac{4L_{in}{i}_L-(1-D)u_c{L}_{in}{T}_s}{n{L}_{out}{U}_{in}{T}_s}}$$

(15)

Phase shift control is the core step of the main phase-shifting full bridge converter studied in this article, and its phase-shifting angle modulation method satisfies the following equation:

$$\theta =(1-D)·{180}^{\circ }$$

(16)

4. Simulation Verification

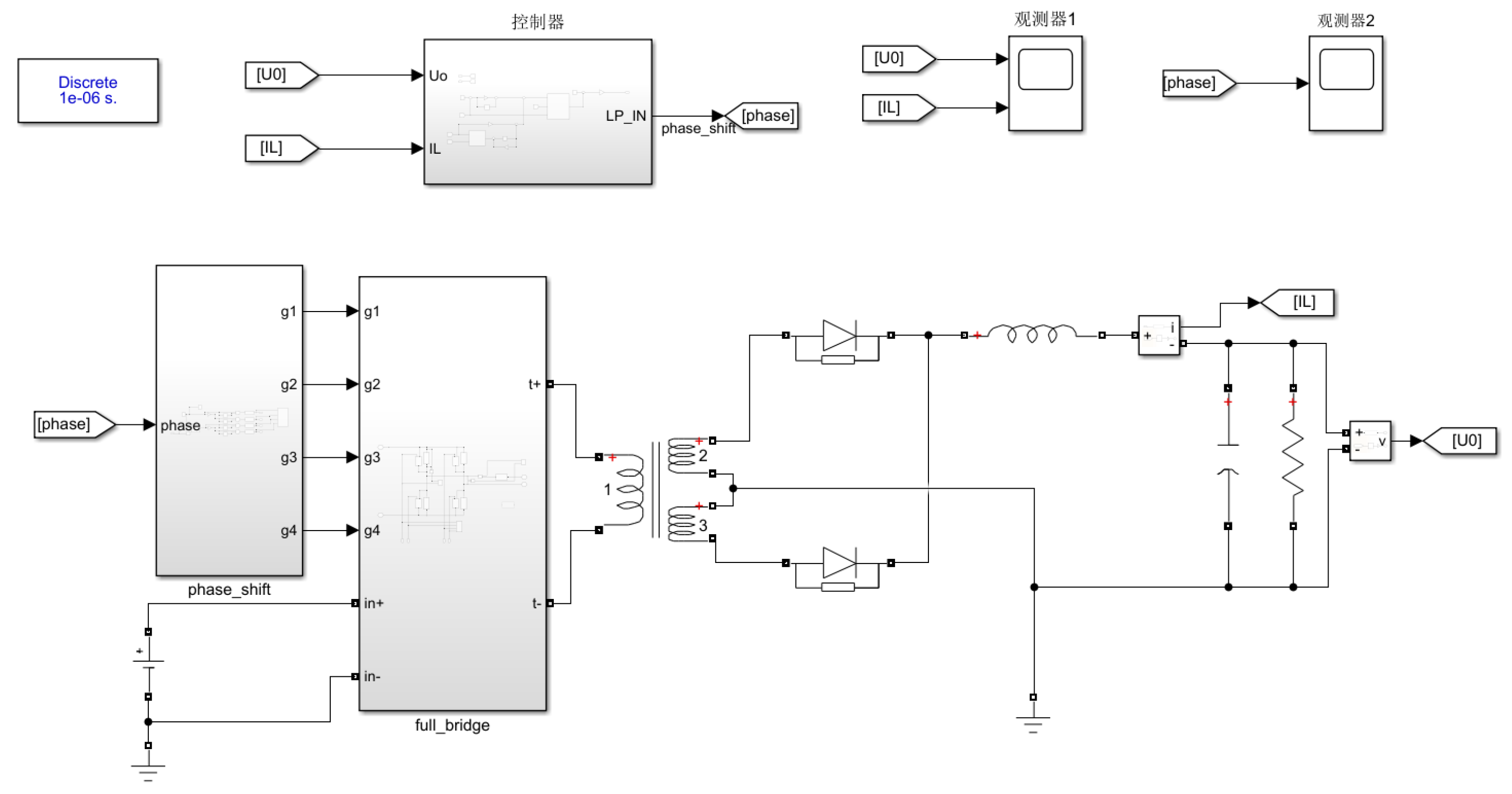
To effectively verify the superiority of the proposed strategy, this paper builds a simulation of a 12.5KW phase-shifting full bridge DC/DC converter as shown in Figure 5 based on the Matlab/Simulink platform.

Among them, the main equipment parameters in the electrical system are shown in Table 1. Based on the same electrical equipment parameters, discuss the control effects of two control strategies separately.

4.1. Comparison Experiment of Traditional PI Control

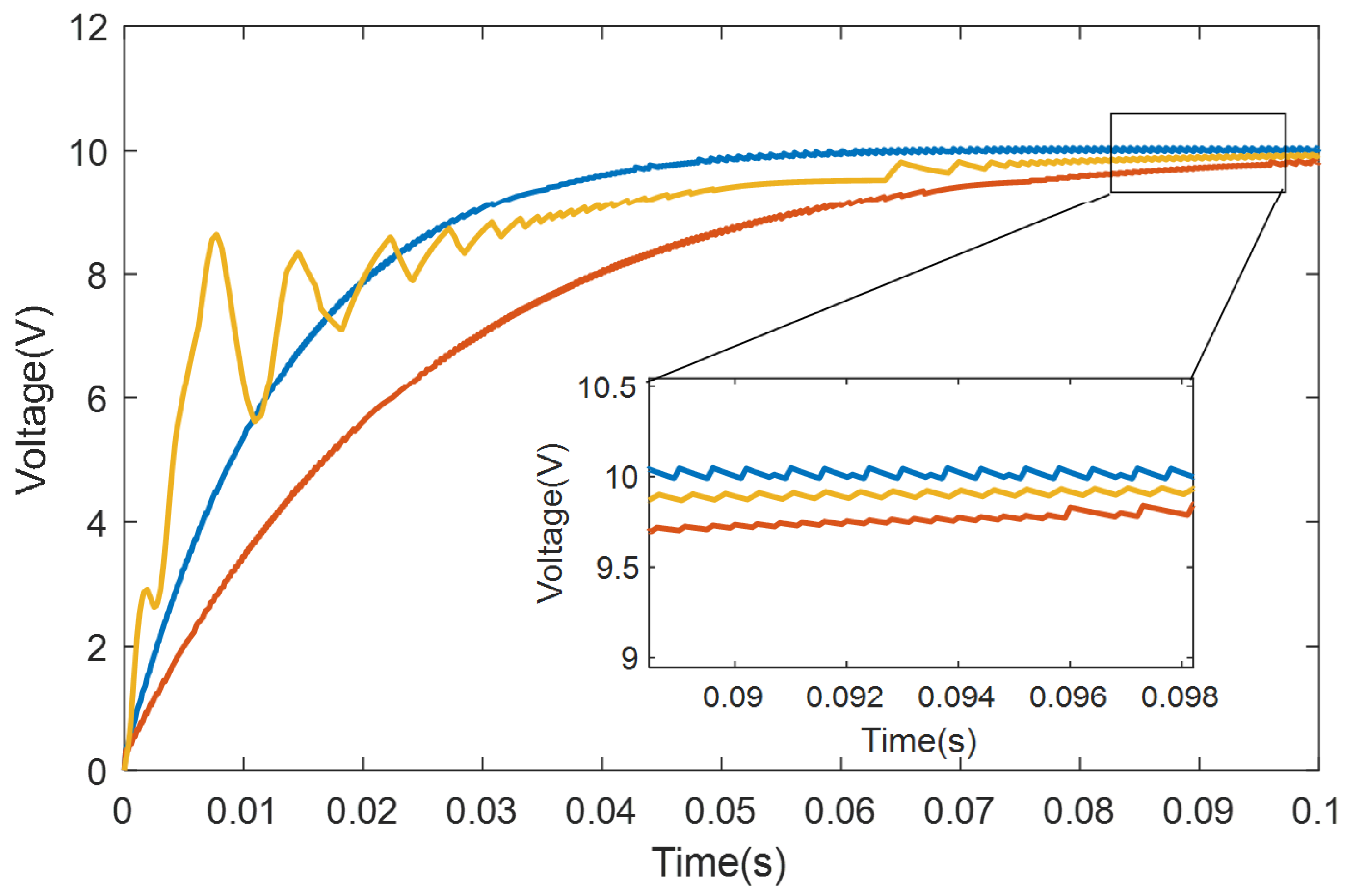
To verify the proposed strategy’s ability to solve complex PI parameter tuning, this paper uses three sets of current loop PI parameter results to discuss the control effects of different parameters on the phase-shifting full bridge topology. As shown in Figure 6, the yellow curve represents the voltage response curve with a proportional parameter of 1e-5 and an integral parameter of 5e-2; The red curve represents the voltage response curve with a proportional parameter of 7e-4 and an integral parameter of 1e-4; The blue curve represents the voltage response curve with a proportional parameter of 7e-4 and an integral parameter of 5e-2. It can be seen that when different PI parameters are selected for the current loop, the response effect of the controlled system will be greatly affected. Moreover, when the PI parameters are not within a reasonable range, the system will not be able to respond correctly to the corresponding voltage.

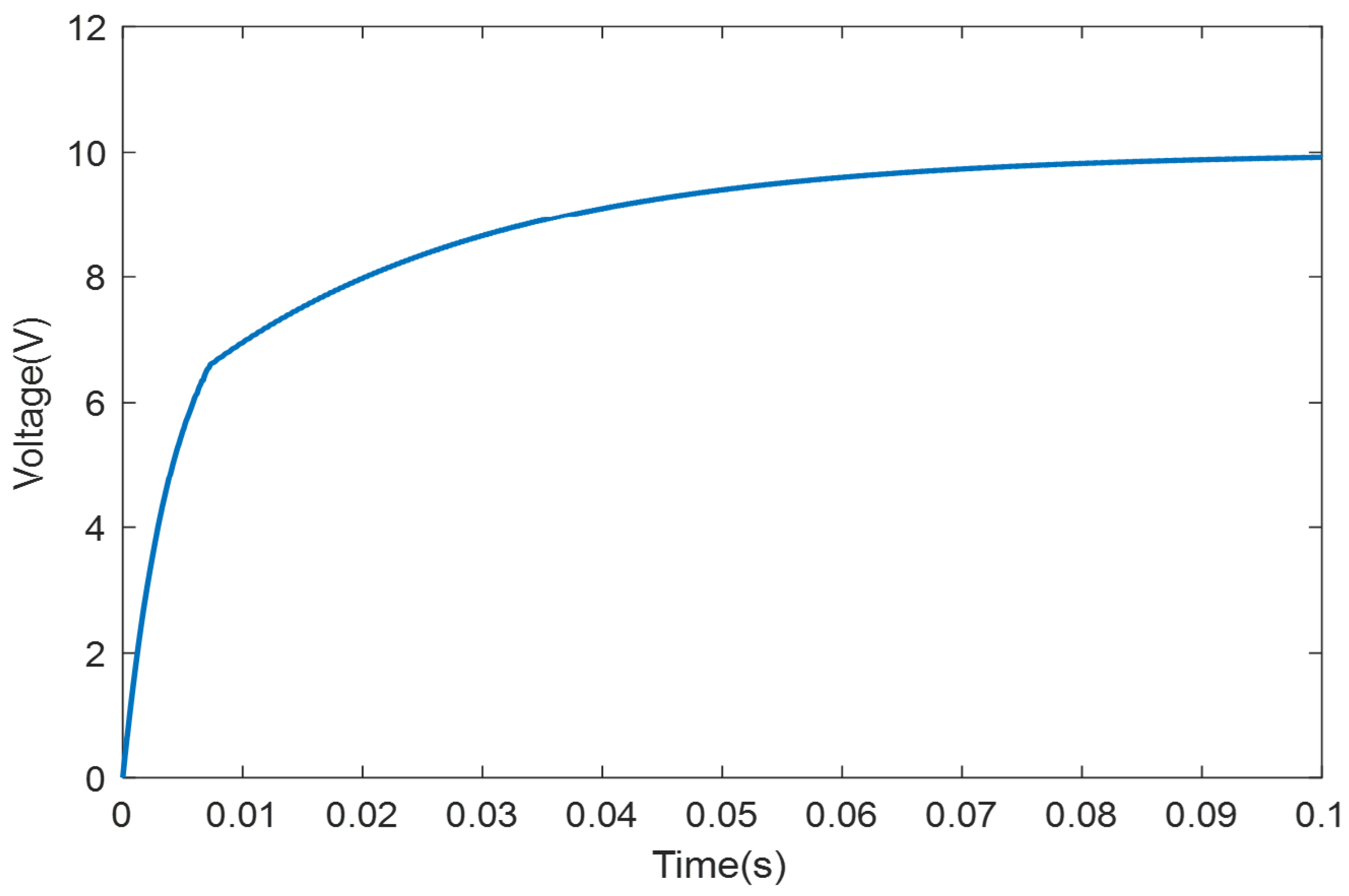
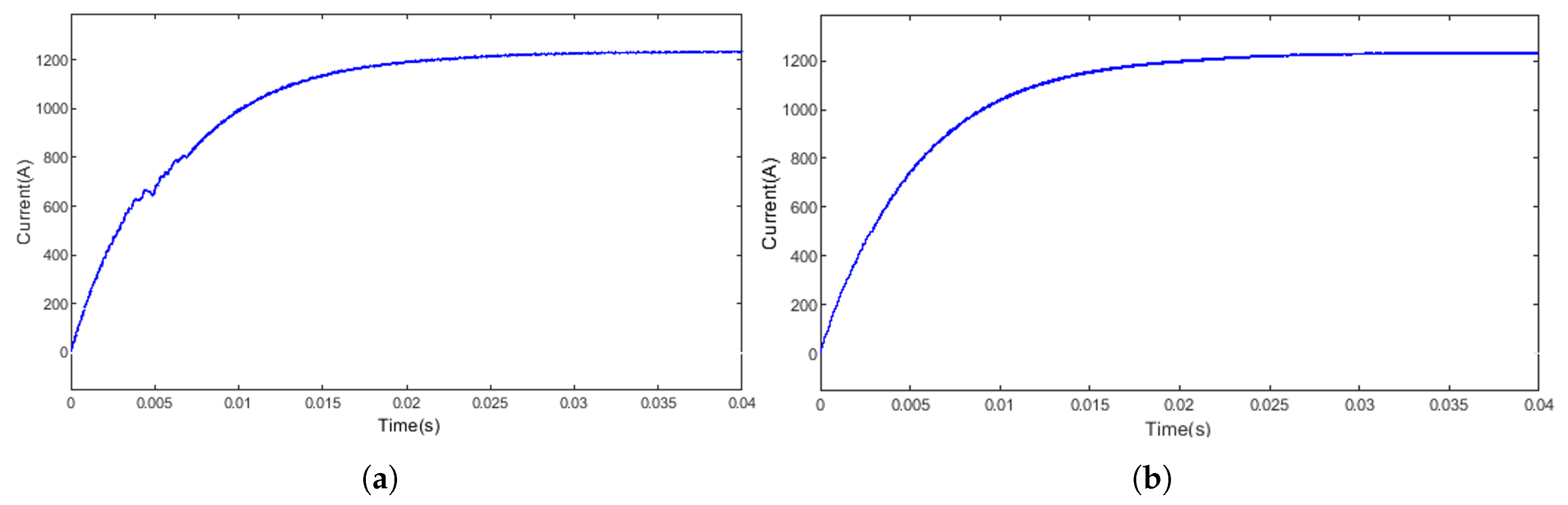
However, when the model predictive control algorithm is applied to the current loop, the control effect of the system is shown in Figure 7, and its voltage control effect will no longer be affected by parameters and the control effect will be excellent.

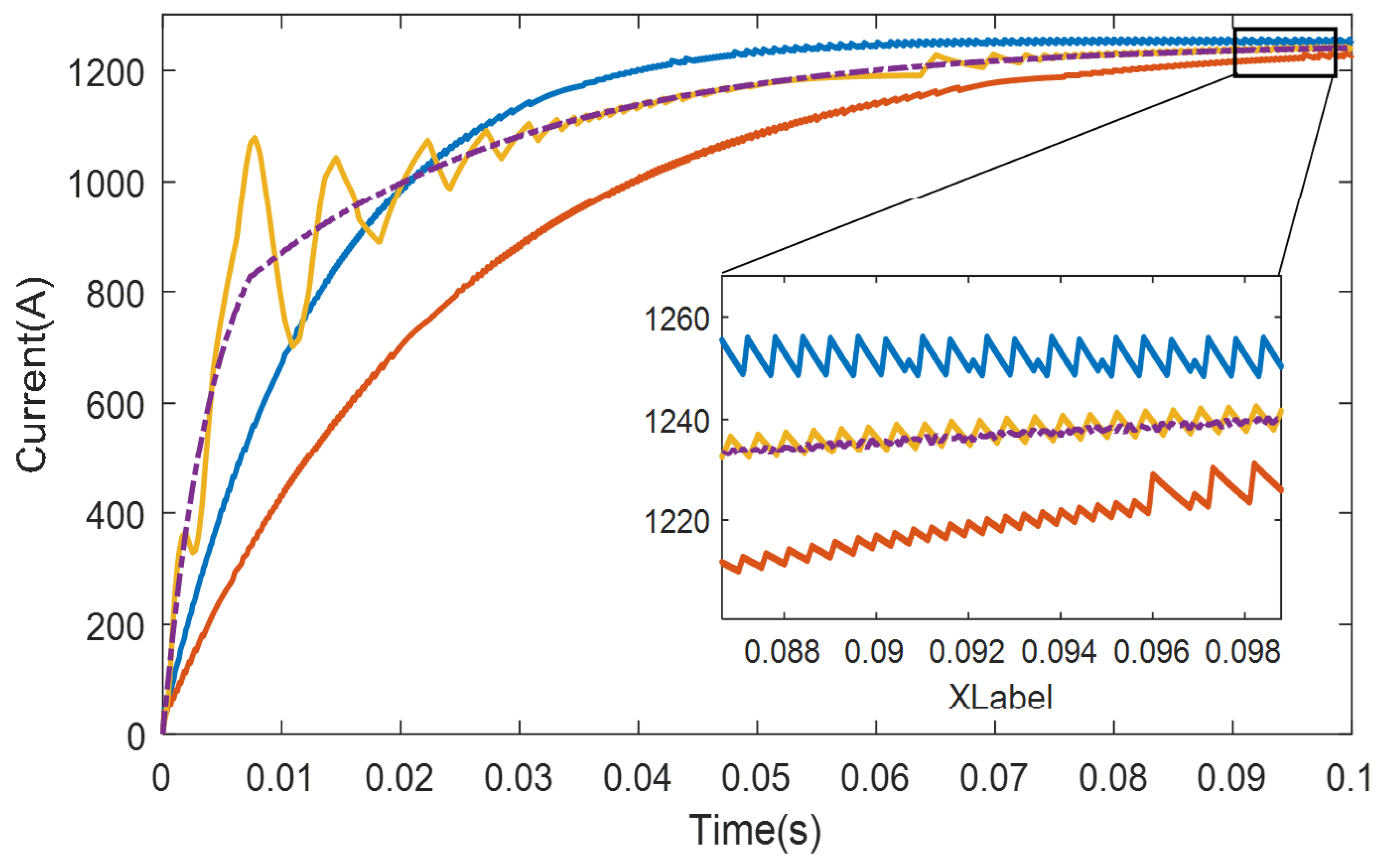
Similarly, as shown in Figure 8, the above experiment has almost the same effect on current to ground as on voltage, where the dashed line represents the control effect of the model predictive control strategy.

4.2. Load Mutation Experiment

To verify the response ability of traditional PI control strategy and MPC control strategy to resistance changes, a load sudden change experiment was designed. Drop the load suddenly from the initial 0.016$\Omega$ to 0.008$\Omega$ and observe the response ability of the two control strategies. The results are shown in Figure 9, where the blue curve represents the current under the load sudden change condition under PI control, and the brown curve represents the current under the load sudden change condition under MPC control. Obviously, the current ripple of PI control is small, but the current response ability of MPC is faster.

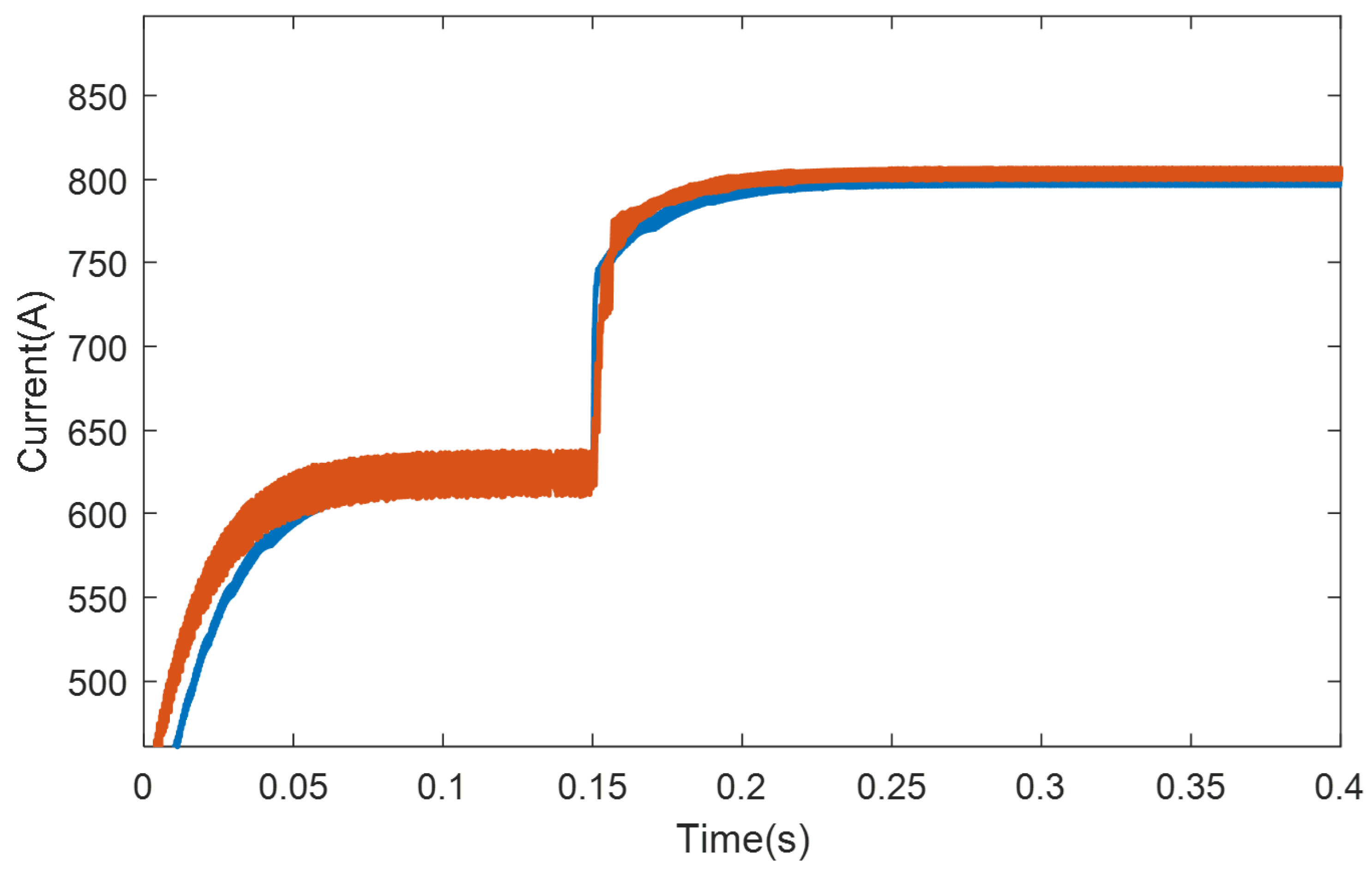
4.3. Inductance Parameter Mismatch Experiment

To verify the disturbance compensation ability of the observer in the case of system inductance parameter mismatch, a comparative experiment was designed between traditional predictive control and predictive control strategy with improved disturbance observer. The experimental results are shown in Figure 10. The blue curve represents the current response of traditional predictive control under the condition of mismatched output inductance parameters, while the brown curve represents the current response of traditional predictive control under the condition of mismatched output inductance parameters. The results show that although the predictive control strategy using an improved nonlinear disturbance observer lacks a certain response speed, the final effect on current ripple suppression is superior, It can effectively suppress system disturbances caused by parameter mismatch and other situations.

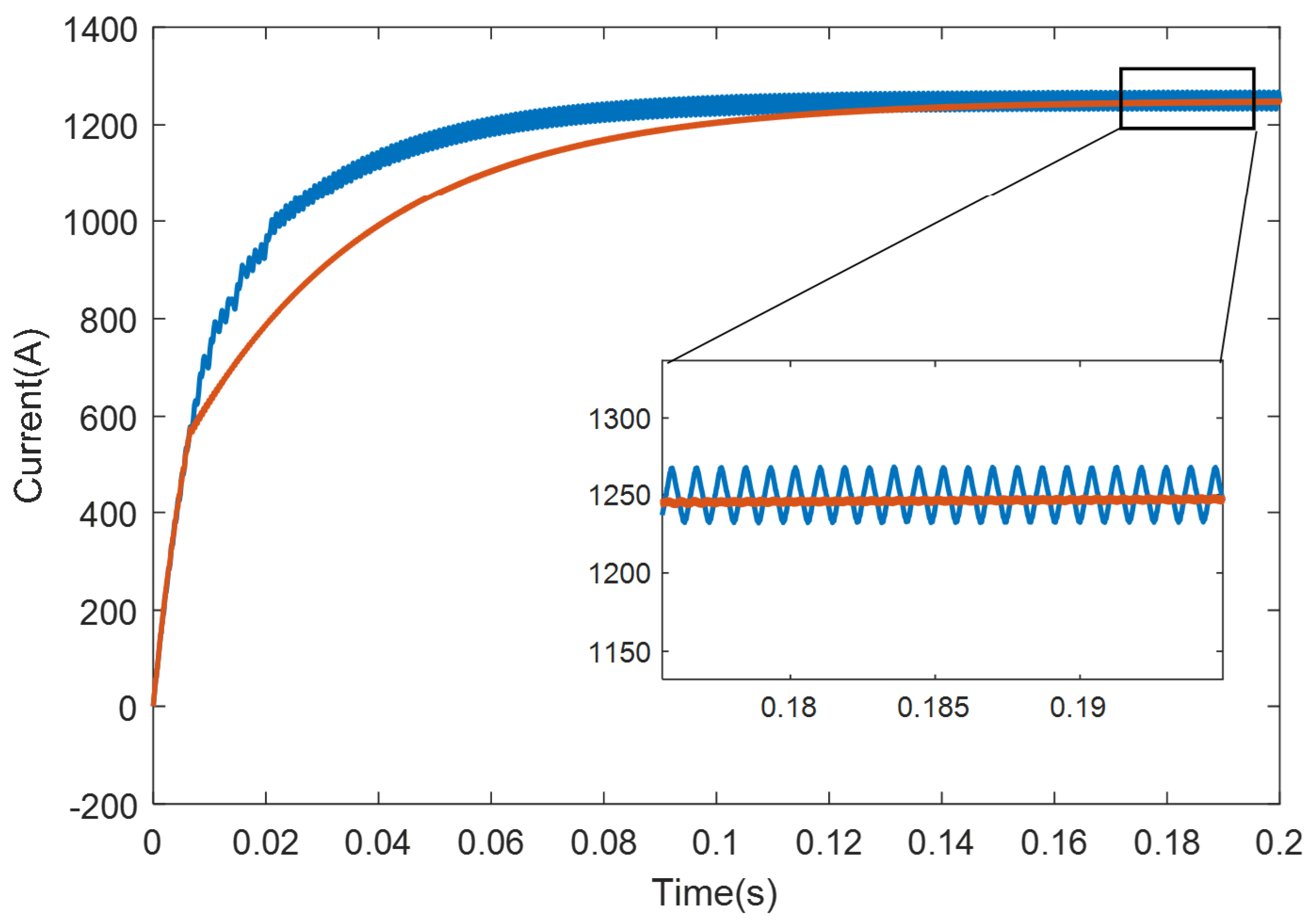
4.4. Current Random Disturbance Experiment

To verify the disturbance compensation ability of the observer in the presence of random current disturbances in the system, relevant comparative experiments were designed. Among them, the current random disturbance value is set to a maximum disturbance value of 60A based on 5% of the rated output current. The experimental results are shown in Figure 11. The controller using traditional model predictive control strategy is susceptible to interference and poses a risk of fluctuation in current response, while the predictive control strategy using improved nonlinear disturbance observer is almost unaffected by interference.

5. Conclusions

To improve the control effect of traditional electrolytic electroplating power supply, this paper proposes a control strategy that combines model predictive control with disturbance observer based on the topology of phase-shifting full bridge DC/DC converter. Firstly, the model predictive control algorithm is used to design the control inner loop to improve the dynamic response capability of the converter; Secondly, using an improved nonlinear disturbance observer to estimate the lumped disturbance received by the system and improve its anti-interference ability; Finally, design a feedforward compensation loop to address the issue of duty cycle loss during the circulation process. The simulation results show that compared with traditional PI control strategies, this strategy can effectively solve the inherent complex PI parameter adjustment problem in traditional control strategies; Secondly, compared to traditional predictive control strategies, incorporating an improved nonlinear disturbance observer can effectively improve the system’s anti-interference ability and enhance its robustness.