Submitted:
06 February 2025
Posted:
07 February 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
3. Methodologies
3.1. Deep Neural Networks
3.1. Multi-Objective Optimization
4. Experiments
4.1. Experimental Setup
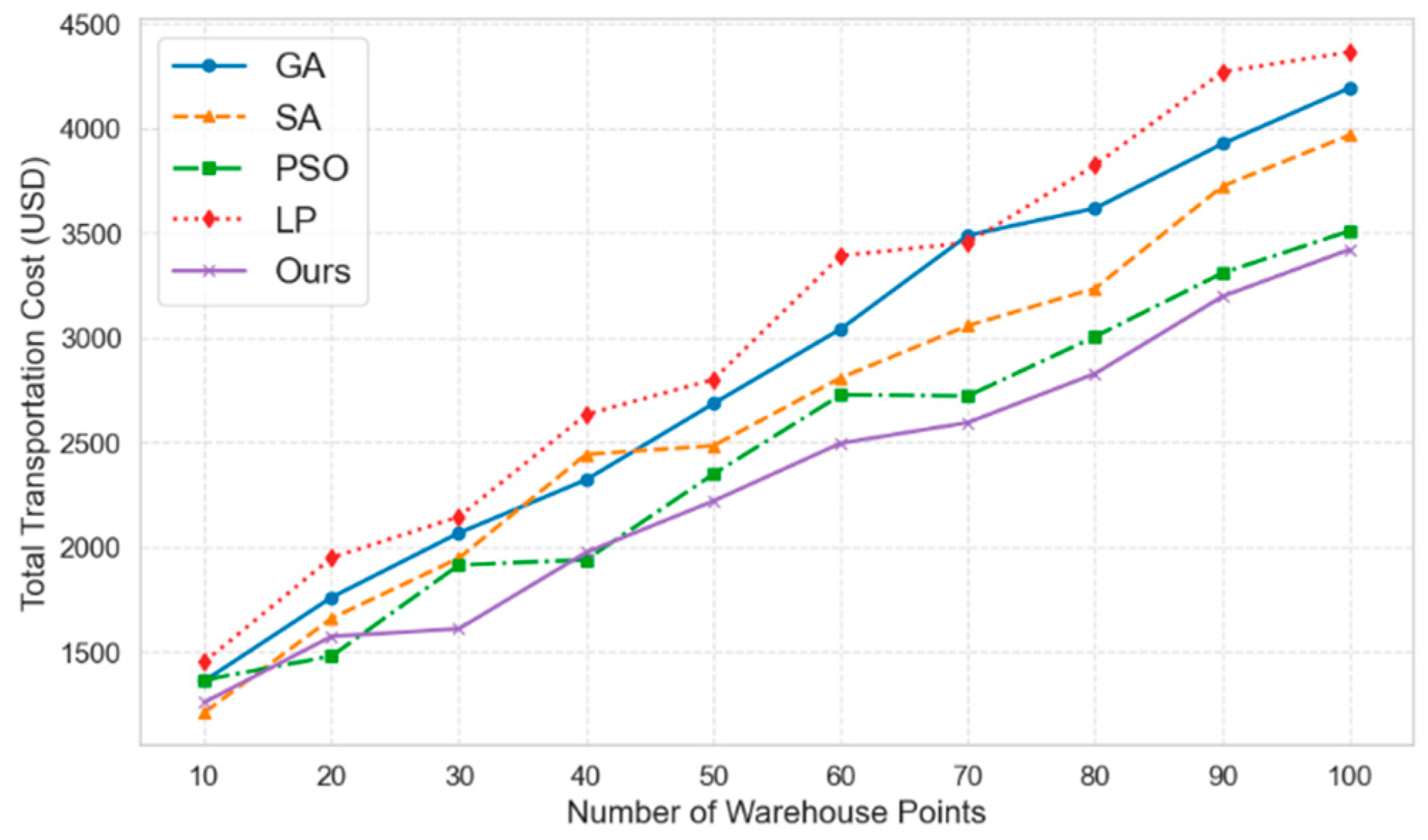
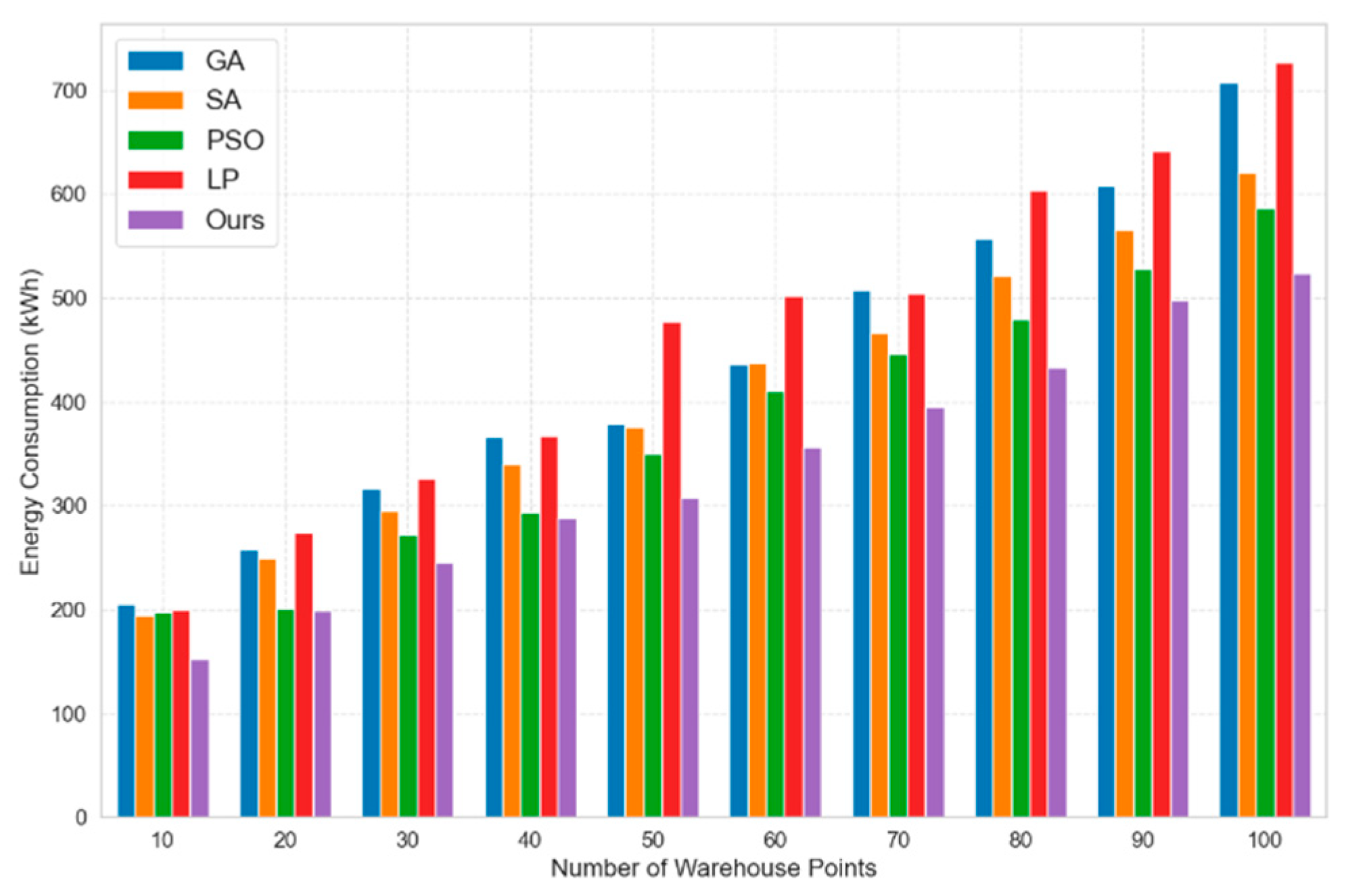
4.2. Experimental Analysis
5. Conclusion
References
- Ghoushchi, Saeid Jafarzadeh, et al. "Landfill site selection for medical waste using an integrated SWARA-WASPAS framework based on spherical fuzzy set." Sustainability 13.24 (2021): 13950. [CrossRef]
- Zhao, S., Zhang, T., & Li, N. (2024). Machine learning analysis of key features in household financial decision-making. Academic Journal of Science and Technology, 12(2), 1-6. [CrossRef]
- Tripathi, Ashutosh Kumar, Sonam Agrawal, and Rajan Dev Gupta. "Comparison of GIS-based AHP and fuzzy AHP methods for hospital site selection: a case study for Prayagraj City, India." GeoJournal (2021): 1-22. [CrossRef]
- Wang, H. (2025). Joint Training of Propensity Model and Prediction Model via Targeted Learning for Recommendation on Data Missing Not at Random. In AAAI 2025 Workshop on Artificial Intelligence with Causal Techniques.
- Eren, Ezgi, and Burak Yiğit Katanalp. "Fuzzy-based GIS approach with new MCDM method for bike-sharing station site selection according to land-use types." Sustainable Cities and Society 76 (2022): 103434. [CrossRef]
- Mishra, Arunodaya Raj, Pratibha Rani, and Abhijit Saha. "Single-valued neutrosophic similarity measure-based additive ratio assessment framework for optimal site selection of electric vehicle charging station." International journal of intelligent systems 36.10 (2021): 5573-5604. [CrossRef]
- Pittman, Simon J., et al. "Rapid site selection to prioritize coastal seascapes for nature-based solutions with multiple benefits." Frontiers in Marine Science 9 (2022): 832480. [CrossRef]
- Xu, Xiaofeng, and Yangyang He. "Blockchain application in modern logistics information sharing: A review and case study analysis." Production Planning & Control 35.9 (2024): 886-900. [CrossRef]
- Kannan, Jeevitha, Vimala Jayakumar, and Mahalakshmi Pethaperumal. "Advanced fuzzy-based decision-making: the linear diophantine fuzzy CODAS method for logistic specialist selection." Spectrum of Operational Research 2.1 (2025): 41-60. [CrossRef]
- Deveci, Muhammet, et al. "Type-2 neutrosophic number based multi-attributive border approximation area comparison (MABAC) approach for offshore wind farm site selection in USA." Engineering Applications of Artificial Intelligence 103 (2021): 104311. [CrossRef]
- Deveci, Muhammet, et al. "Hybrid q-rung orthopair fuzzy sets based CoCoSo model for floating offshore wind farm site selection in Norway." CSEE Journal of Power and Energy Systems 8.5 (2022): 1261-1280. [CrossRef]
- Mishra, Arunodaya Raj, Pratibha Rani, and Kiran Pandey. "Fermatean fuzzy CRITIC-EDAS approach for the selection of sustainable third-party reverse logistics providers using improved generalized score function." Journal of ambient intelligence and humanized computing (2022): 1-17. [CrossRef]
- Deveci, Muhammet, Umit Cali, and Dragan Pamucar. "Evaluation of criteria for site selection of solar photovoltaic (PV) projects using fuzzy logarithmic additive estimation of weight coefficients." Energy Reports 7 (2021): 8805-8824. [CrossRef]
- Wang, Chia-Nan, Thanh-Tuan Dang, and Julius Bayer. "A two-stage multiple criteria decision making for site selection of solar photovoltaic (PV) power plant: A case study in Taiwan." IEEE Access 9 (2021): 75509-75525. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




