1. Introduction
Let V be a vector space of dimension n and let be the third-degree exterior power space of V over the field K. Any element of is named trivector on V. By virtue of the canomical identification , there is no diffrence between trivectors and trilinear alternating form. The classification of trilinear alternating forms is the study of the action of on : . For , this classification was completed for any fields and the number of orbits is finite. In dimension 9, the number of classes of trivectors over is infinite (see [3]) and over is finite (there are 317 classes, see [6]).
In this paper we examine the general cause for the trivector in dimension , called standard trilinear alternating form, the form of the transitive automorphism group over L in which L is the extension of the field K and the trivector in dimension with the isotropic hyperplane. We computed their groups of automorphisms and their radical polynomials. The main results are the Tables 1, 2, 3, 4 and 5 containing the trivectors and with the sizes of the group of automorphisms, the radical polynomials and the number of orbits of trivectors in dimension eight. The commutant of a trivector with a maximum rank of eight forms a Frobenius algebra with (See [10] Theorem 2.8, p.49), we show that this result is not true for .
The motivation behind this research stems from the graph theory, complexity and cryptography, in which they are interested in the alternating trilenear form equivalence (ATFE) problem and code loops, see [12] and [15]. We note that Frobenius algebras are significant in the algebraic approach.
2. Preliminaries
Let be a trilinear alternating form on a vector space V over a field . The trivector satisfies the equality for every permutation . Two forms and are equivalent, , if there exists a homomorphism bijective of V verifying:
One of the possible approaches to the classification of trivectors is to use invariants. We recall three invariants of trivectors: the automorphism group
, the radical polynomial
of
introduced by J.Hora [6] and the commutant
.
Definition 1.
The group of automorphisms of ω, , is defined by
Example 1. Let be the trivector , then .
Definition 2. The set is called the radical of ω and denoted by . If is trivial , then ω is called non degenerate.
Fix and define radical of V as . is a subspace of V. The rank of , is an even number.
Definition 3.
Let be a finite field. The polynomial defined by:
where and , is the radical polynomial of ω.
Definition 4. Two vectors are orthogonal , if . The subspaces and of V are orthogonal , if for all and .
Definition 5.
We say that a non degenerate trilinear alternating form ω on V is decomposable if , and whenever . The restrictions of ω to are denoted by . is compatible with the orthogonal decomposition:
Example 2.
Let be the trivector . The radical polynomial of is equal to
Definition 6.
The commutant of ω, is
Definition 7. Let A be an algebra of finite dimension over a field K. We say that A is a F.algebra if (isomorphic as A-modules).
Note that if A is finite-dimensional algebra over a field K. Then A is a Frobenius algebra if and only if there is a non-degenerate symmetric bilinear form such that for all .
3. Invariants on Dimension
Standard Trilinear Form
Definition 8. Let V be a - dimensional vector space over K and let be a fixed basis of V. A standard trilinear alternating form can be expressed as
Since is a decomposable form, then is compatible with the orthogonal decomposition and we have
Proposition 1.
Let be the automorphism of , then it satisfies the exact sequence
If
Proof. The domain where , is invariant i.e. if . So that for permutation , we can define a groups homomorphism.
where
is surjective, we deduce that the sequence
is exact.
Let , then and from the equality , hence
We can write the matrix of
f as follows
with
then
. □
The first Galois cohomology where , is the algebraic closure of K, distinguishes forms over K and .
We consider . If L is the extension of K, there exists a trivector such that and is L-isomorphic to . Let C be the set of orbits of the forms of . Since . The exact sequence of Galois cohomology sets gives us . Where of degree .
We obtain the following lemma
Lemma 1.
The trivector has a K-form with the automorphisms group verify the following exact sequence:
If , and .
Since contain and contain the finite cyclic group , then is semi-direct product .
The only non trivial trivector over with a transitive automorphisms group is the trivector arising from the three dimensional determinant over (see J. Hora[6], page 11). So is the only trivector in dimension with the transitive automorphisms group.
The trivector
is the only trivector with equal ranks of all non zero vectors
v,
. Its radical polynomial is equal to
We get the following Table 1.
Table 1.
Automorphisms group and radical polynomial of .
Table 1.
Automorphisms group and radical polynomial of .
Remark 1. If , , we have
For , and
For , , and ,
For , , and , . (See J. Hora [6] Appendix A and B page 12-13).
Remark 2. The trivector has three K-forms , and in which and where .
Proof. Let L be an extension of degree 3 of K and F is a space of dimension 3 over L. We consider a standard basis of F, the determinant form is defined by: where . The trace form is , we put , is a trivector of rank nine on .
We take with in this case, the basis of V is
.
We can calculate:
and
otherwise. We obtain
and it follows that
If
,
where
, is a quadratic extension of
K, in this case, the basis of
V is
. Then,
and
otherwise.
We obtain
and it follows that
If then , by the same method we obtain . □
If finite field of order q, and .
We get the following Table 2.
Table 2.
Automorphisms group and its size of
Table 2.
Automorphisms group and its size of
Remark 3. In dimension , the expression of the trivector seems to be a difficult problem (see Table 1.).
4. Invariants on Dimension
4.1. General Rule for the Non Trivial Forms with an Isotropic Hyperplane
Let
V be a vector space of dimension
n,
and let
be a trivector of rank
. There exists a basis
such that
It is the only trivector in dimension with an isotropic hyperplane (Hyperplane W such that the restriction on W is the zero form).
Proposition 2.
Let be the automorphism of , then it satisfies the exact sequence
i.e.
If , then
Proof. We consider the set . If ∈, we have , then and , for . Then and there exists / . The matrix of f with a basis must have the form , this we define a group of homomorphism surjective , .
Let : , which means with
. We consider the linear application with the matrix . The homomorphism
defined by , is surjective and . □
While observing the radical polynomial of and , we deduce
The radical polynomial of
is equal to
We get the following Table 3.
Table 3.
Automorphisms group and radical polynomial of
Table 3.
Automorphisms group and radical polynomial of
Remark 4. If finite field of order 2, we have:
For , and
For , and
For , and , it is the class with the largest group of automorphisms. (See J. Hora [6] Appendix A and B page 12-13).
4.2. General Rule for the Form of the Type
Let V be a vector space of dimension n, and let be a trivector of rank . There exists a basis such that
Proposition 3.
Let be the automorphism of , then it satisfies the exact sequence
If
Proof. We observe the domain (linear span)
is invariant. We obtain
Then therefore, stabilizer each of the two subspaces and
. We can define a group homomorphisms
If , f acts on and as .
We obtain the exact sequence
If f is the identity over and (modulo ),
where , then
, ,...,
is an additive group isomorphic to □
We get the following Table 4.
Table 4.
Automorphisms group and its size of
Table 4.
Automorphisms group and its size of
Remark 5.
Remark 4.If , we have
For , ,
For , , (See J. Hora [6] Appendix A and B page 12-13).
5. Commutant of a Trivector and Frobenius Algebra
Proposition 4. There exists a vector space V of dimension nine and in which is not a F.algebra and .
Proof. Let
be a trivector of rank nine (See [3] Table 1):
We consider
f, an element of the commutant and
, the matrix of
f, where
B is the standard basis, then by direct competitions we have:
has the form
thus
with
and the matrices of
,
,
and
are presented by
and
By computation we prove that , , and satisfy:
If
is a Frobenius algebra, there exists a non-degenerate symmetric bilinear form
in which
where
We put
the matrix of
in the basis
, then
The matrix
C is represented by
The rank of , different from 5, hence this contradicts the non-degeneracy of . We conclude that is not a F.algebra and . We deduce that . □
6. Classification of Trivectors in Dimension 8 over a Finite Field of Characteristic 2
For , the classification of trivectors over finite fields, except for characteristic 2 or 3, and over a finite field of two elements has been done in [7] and [5] respectively. More recently a classifications have appeared for a finite field of characteristic 3 [9]. We give the following classification over .
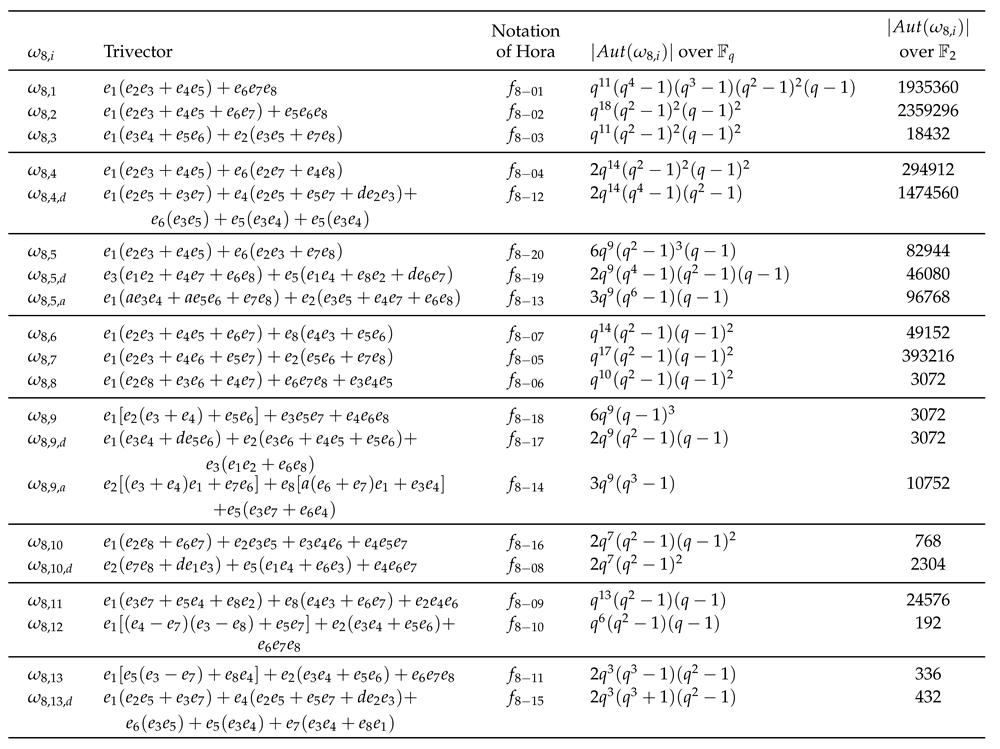
Theorem 1. Let V be a vector space of dimension eight over a finite field of characteristic 2, . If m is odd, there are 20 inequivalent trivectors in which are of a full rank.
Table 5.
The cardinality of the automorphisms groups for trivectors of rank 8 over . ,
Table 5.
The cardinality of the automorphisms groups for trivectors of rank 8 over . ,
Remark 6. This classification was done over (see table 2 page 3468 in [5] or see Appendix A page 12 in [6]).
7. Weight Varieties of a Non-Degenerate Form
We can use the classification of trivectors in the theory of codes (See [13]).
Some undefined terms can be found in [13, page 426-429].
Similar arguments applied in [13] are used for determining the varieties and for some trivectors and we have:
Proposition 5.
The varieties and for are given by:
8. Conclusions
In this paper, by using the invariants of the trivectors, we deduce the general rule for some trivectors. As a future work, one can calculate the cardinalities of and and use them to fully determine the spectrum of .
References
-
A. M. CohenandA. G. Helminck: Trilinear alternating forms on a vector space of dimension 7,Communications in algebra., 16 (1988) 1–25.
-
D. Djokovic: Classification of trivectors of an eight dimensional real vector space, Linear Multilinear Algebr., 13 (1983) 3–39..
- A.G. Elashvili and E.B. Vinberg. Classification des trivecteurs d’un espace de dimension 9 ( en russe ). Trudy sem.Vekt ,Tenz. Anlisu XVIII 55 (1978), 197–233.
-
G. B. Gurevitch: Foundations of the Theory of Algebraic Invariants, P. Noordhoff Ltd.,Groningen, the Netherlands (1964).
-
J. HoraandP. Pudlák: Classification of 8-dimensional trilinear alternating forms over GF(2), Commun Algebra., 34 (2015) 3459–3471.
-
J. HoraandP. Pudlák:Classification of 9-dimensional trilinear alternating forms over GF(2), Finite Fields and Their Applications., 70 (2021) 101788.
-
N. MidouneandL. Noui: Trilinear alternating forms on a vector space of dimension 8 over a finite field, Linear and Multilinear Algebra., 61 (2013) 15–21.
- N. Midoune, L. Noui. K-forms of 2-step splitting trivectors. Int. J. Algebra 2 (2008), 369–382.
- N. Midoune , M.A. Rakdi . Trilinear alternating forms and related CMLs and GECs. International Journal of Group Theory 12 (2023), 227–235.
- L. Noui and Ph. Revoy. Formes multilinéaires alternées. Linear and Multilinear Algebra 1 (1994), 43–69. Blaise Pascal 1: 43-69.
-
L. Noui: Transvecteur de rang 8 sur un corps algébriquement clos,Comptes Rendus de l’Académie des Sciences-Series I-Mathematics, 324 (1997) 611–614.
- E.O’Brien ,P. Vojtěchovskỳ Code loops in dimension at most 8. Journal of Algebra 2017, 473, 607–626.
- M.A. Rakdi , N. Midoune. Weights of the Fq-forms of 2-step splitting trivectors of rank 8 over a finite field. Carpathian Mathematical Publications 11 (2019), 422–430.
- J. Schouten. Klassifizierung der alternierenden Gröszen dritten Grades in 7 Dimensionen. Rendiconti del Circolo Matematico di Palermo (1884-1940) 55(1931), 137–156. [CrossRef]
- G. Tang, D. H. Duong, A. Joux, T. Plantard, Y. Qiao, and W. Susilo. Practical post-quantum signature schemes from isomorphism problems of trilinear forms. In O. Dunkelman and S. Dziembowsk, editors,Advances in Cryptology - EURO- Crypt 2022 - 41st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Trondheim, Norway, May 30 - June 3, 2022, Proceedings, Part III, volume 13277 of Lecture Notes in Computer Science, pages 582-612, Springer, 2022.
- Borovoi, Mikhail, Willem A. de Graaf, and Hông Vân Lê. "Classification of real trivectors in dimension nine." Journal of Algebra 603 (2022), 118-163. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).