Submitted:
03 February 2025
Posted:
06 February 2025
You are already at the latest version
Abstract
We present novel implementations of Starobisky-like inflation within Supergravity adopting Kahler potentials for the inflaton which parameterize hyperbolic geometries known from the T-model inflation. The associated superpotentials are consistent with an R and a global or gauge U(1)X symmetries. The inflaton is represented by a gauge singlet or non-singlet superfield and is accompanied by a gauge-singlet superfield successfully stabilized thanks to its compact contribution into the total Kahler potential. Keeping the Kahler manifold intact, a conveniently violated shift symmetry is introduced which allows for a slight variation of the predictions of Starobinsky inflation: The (scalar) spectral index exhibits an upper bound which lies close to its central observational value whereas the constant scalar curvature of the inflaton-sector Kahler manifold increases with the tensor-to-scalar ratio.
Keywords:
1. Introduction
- Wess-Zumino models with a matter-like inflaton [19,20,21,22,23,24]. Polynomial superpotentials, W, – of the Wess-Zumino form [11] – are adopted in this class of models and the Kähler potentials K parameterize specific Kähler manifolds of the form , inspired by the no-scale models [25,26] of SUSY breaking. The stabilization of the inflaton-accompanying modulus at a Planck-scale value [20] is achieved by a deformation of the internal geometry.
- Ceccoti-like [27] models with a modulus-like inflaton [20,28,29,30,31,32,33,34,35,36,37]. Similar K’s are used here whereas W is linear [38] with respect to the matter-like inflaton-accompanying field which may be stabilized at the origin via several mechanisms [6,10,35,39,40,41,42,43]. In a subclass of these models [31,32,33,34,36,37], the conjecture of induced gravity [44,45] is incorporated leading to a dynamical generation of the reduced Planck scale, through the vacuum expectation value (v.e.v) of the inflaton at the end of its evolution.
-
Models which exhibit a pole [51,52,53,54,55] of order one in the kinetic term of the inflaton [56,57,58]. As in every SI model, the inflationary potential develops one shoulder for large values, where is the canonically normalized inflaton which can be expressed in terms of the original field as [58]The presence of the real positive variable N – aligned with the conventions of [58] – leads to a generalized version of SI called -SI [20] or E-Model inflation. This model can be contrasted with the T-Model inflation [59,60] which arises thanks to a pole of order two in the inflaton kinetic term and features a potential with two symmetric plateaus away from the origin. Namely, the relation assumes the form
2. SUGRA Framework
2.1. General Set-Up
2.2. Guidelines
2.2.1. Achieving D-Flatness.
- If the inflaton is (the radial part of) a gauge-singlet superfield . In this case, has obviously zero contribution to .
- If the inflaton is the radial part of a conjugate pair of Higgs superfields, and , in the fundamental representation of . In a such case – see Section 4.3 below – we obtain . The same result can be obtained if is more structured than employing just one superfield in the adjoint representation of and using as inflaton its neutral component – see e.g. Ref. [85].
2.2.2. Selecting the Suitable W
- It assists in determining W. To achieve it, we require that S appears linearly in W and so both are equally charged under a global R symmetry.
-
It can be stabilized at without invoking higher order terms, if we select [35]
- It assures the boundedness of . Indeed, if we set , then for , and . Obviously, non-vanishing values of the last term may render unbounded from below.
-
It generates for and for monomial W the numerator of in Eq. (1.3) via the only term of which remains “alive”. Indeed, we obtainAssuming that no mixing terms between S and the inflaton exist in K, we obtain and so the numerator of in Eq. (1.3) emerges if W has the formgiven that the assumption yields mostly stable configuration – here we focus on a gauge-singlet . On the other hand, the denominator of in Eq. (1.3) may be generated via the exponential prefactor in Eq. (2.3) through logarithmic contributions to K – as we explain below.
2.2.3. Selecting the Convenient Kähler Potential
-
It has to generate the desired relation in Eq. (1.2). Therefore, we need to introduce a contribution into K including and in the same function. After inspection – see Appendix of Ref. [86] – we infer that a pole of order two in the kinetic term of inflaton is achieved if whereHere and the subscript “T” indicates that this part of the total K is responsible for the T-model Kähler metric – see Eq. (2.1b). However, from Eq. (2.3), we remark that K affects – besides the kinetic mixing – via the prefactor . Therefore, is generically expected to emerge also in the denominator of making difficult the establishment of an inflationary era. This problem can be surpassed [58,66] by two alternative strategies:
- -
- -
- Replacing with so that the desired kinetic terms in Eq. (2.1a) remain unaltered and, simultaneously [56,58,66]In other words, the symmetry of is augmented by some shift symmetry – see Appendix A – without disturbing in Eq. (2.1b). To accomplish this, includes holomorphic and anti-holomorphic terms which yield vanishing contribution to the mixed derivatives of . Taking into account the form of in Eq. (2.5), we may select formallyNote that the same construction is valid even in case of polynomial K’s if we check the structure of the relevant K’s in Refs. [70,74,75,76,77,78,79].
3. Gauge-Singlet Inflaton
3.1. Set-Up
3.2. Canonical Normalization
3.3. Inflationary Potential
4. Gauge Non-Singlet Inflaton
4.1. Set-Up
4.2. Canonical Normalization
4.3. Inflationary Potential
4.4. Phase Transition
5. Inflation Analysis
5.1. Analytic Results
5.2. Numerical Results
5.2.1. SI with a Gauge-Singlet Inflaton (CSI)
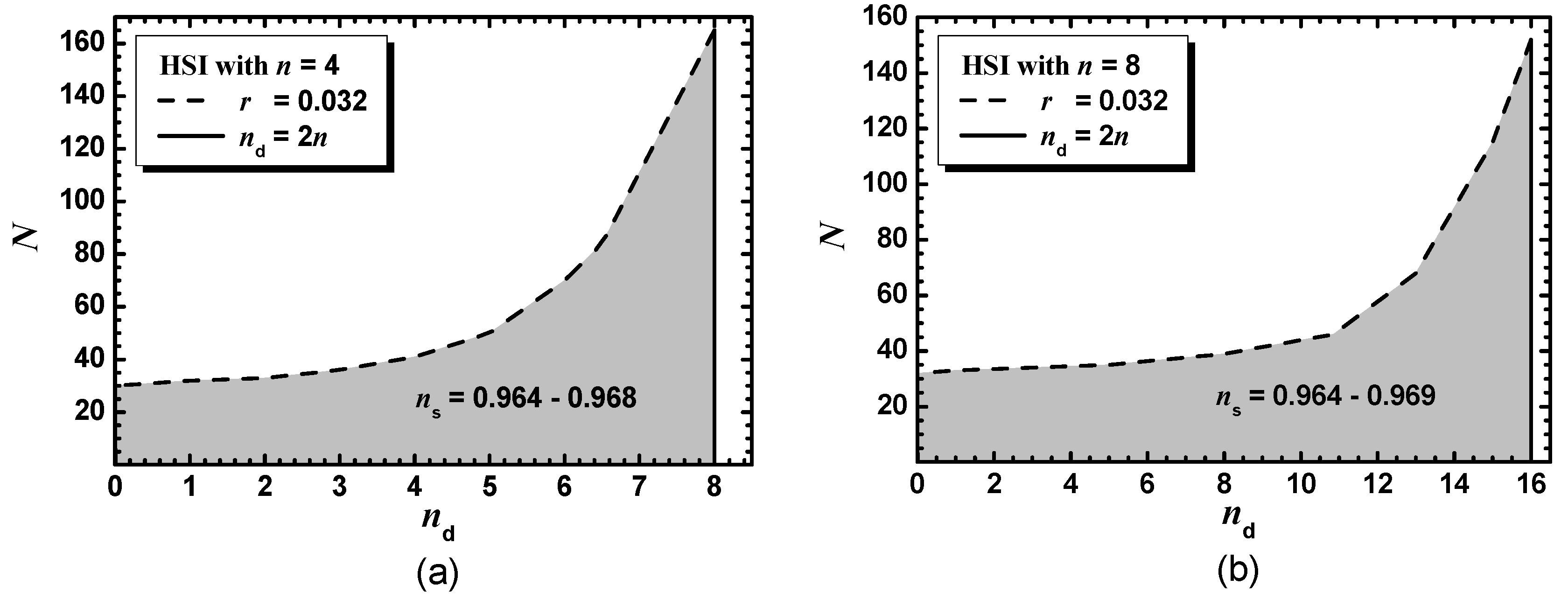
5.2.2. SI with a Higgs Field (HSI)
6. Conclusions
Acknowledgments
Appendix A. Shift Symmetry & Hyperbolic Kähler Geometries
Appendix A.1. Shift Symmetry for CSI
Appendix A.2. Shift Symmetry for HSI
Appendix A.2.1. Kähler Manifold M (11) 2
Appendix A.2.2. Kähler Manifold M 21
References
- A.A. Starobinsky, A New Type of Isotropic Cosmological Models Without Singularity, Phys. Lett. B91, 99 (1980).
- J. Martin, C. Ringeval and V. Vennin, Encyclopædia Inflationaris, Phys. Dark Univ. 5, 75 (2014) [arxiv:1303.3787].
- J. Martin, C. Ringeval R. Trotta and V. Vennin, The Best Inflationary Models After Planck, 03, no. 14, 039 (2014) [arXiv:1312.3529]. [CrossRef]
- . Grøn, Predictions of Spectral Parameters by Several Inflationary Universe Models in Light of the Planck Results, Universe 4, no.2, 15 (2018).
- Y. Akrami et al. [Planck Collaboration], Planck 2018 results. X. Constraints on inflation, Astron. Astrophys.641, A10 (2020) [arxiv:1807.06211].
- C. Kounnas, D. Lüst and N. Toumbas, R2 inflation from scale invariant supergravity and anomaly free superstrings with fluxes, Fortsch. Phys. 63, 12 (2015) [arxiv:1409.7076]. [CrossRef]
- M. Galante, R. Kallosh, A. Linde, and D. Roest, Unity of Cosmological Inflation Attractors, Phys. Rev. Lett.114, no. 14, 141302 (2015) [arxiv:1412.3797]. [CrossRef]
- J. Ellis, D.V. Nanopoulos, K.A. Olive and S. Verner, A general classification of Starobinsky-like inflationary avatars of SU(2,1)/SU(2)×U(1) no-scale supergravity, J. High Energy Phys. 03, 099 (2019) [arxiv:1812.02192]. [CrossRef]
- J. Ellis, M.A.G. Garcia, N. Nagata, D.V. Nanopoulos, K.A. Olive and S. Verner, Building Models of Inflation in No-Scale Supergravity, Int. J. Mod. Phys. D 29, 16, 2030011 (2020) [arxiv:2009.01709]. [CrossRef]
- C. Pallis and N. Toumbas, Starobinsky Inflation: From Non-SUSY To SUGRA Realizations, Adv. High Energy Phys.2017, 6759267 (2017) [arxiv:1612.09202]. [CrossRef]
- See, e.g., P. Binétruy, Supersymmetry: Theory, experiment and cosmology, Oxford (2006).
- S. Navas et al. [Particle Data Group], Review of particle physics, Phys. Rev. D110, no.3, 030001 (2024).
- F. Wang, W. Wang, J. Yang, Y. Zhang and B. Zhu, Low Energy Supersymmetry Confronted with Current Experiments: An Overview, Universe 8, no. 3, 178 (2022) [arxiv:2201.00156].
- W. Buchmuller, V. Domcke and K. Kamada, The Starobinsky Model from Superconformal D-Term Inflation, Phys. Lett. B 726, 467 (2013) [arxiv:1306.3471]. [CrossRef]
- S. Basilakos, N.E. Mavromatos and J. Sola, Starobinsky-like inflation and running vacuum in the context of Supergravity, Universe 2, no. 3, 14 (2016) [arxiv:1505.04434]. [CrossRef]
- S.V. Ketov and A. A. Starobinsky, Embedding (R+R2)-Inflation into Supergravity, Phys. Rev. D 83, 063512 (2011) [arxiv:1011.0240].
- R. Blumenhagen, A. Font, M. Fuchs, D. Herschmann and E. Plauschinn, Towards axionic Starobinsky-like inflation in string theory, Phys. Lett. B746, 217 (2015) [arxiv:1503.01607]. [CrossRef]
- T. Li, Z. Li and D.V. Nanopoulos, Helical phase in ation via non-geometric flux compactifications: from natural to Starobinsky-like inflation, J. High Energy Phys. 10, 138 (2015) [arxiv:1507.04687].
- J. Ellis, D.V. Nanopoulos and K.A. Olive, No-Scale Supergravity Realization of the Starobinsky Model of Inflation, Phys. Rev. Lett. 111, 111301 (2013) – Erratum: Phys. Rev. Lett. 111, no. 12, 129902 (2013) [arxiv:1305.1247].
- J. Ellis D. Nanopoulos and K. Olive, Starobinsky-like Inflationary Models as Avatars of No-Scale Supergravity, 10, 009 (2013) [arXiv:1307.3537].
- J. Ellis, H.-J. He and Z.-Z. Xianyu, New Higgs inflation in a no-scale supersymmetric SU(5) GUT, Phys. Rev. D 91 021302 (2015) [arxiv:1411.5537]. [CrossRef]
- I. Garg and S. Mohanty, No-scale SUGRA SO(10) derived Starobinsky model of inflation, Phys. Lett. B 751, 7 (2015) [arxiv:1504.07725]. [CrossRef]
- J. Ellis, M.A.G. Garcia, N. Nagata, D.V. Nanopoulos and K.A. Olive, Starobinsky-like Inflation, Supercosmology and Neutrino Masses in No-Scale Flipped SU(5), 07, 006 (2017) [arxiv:1704.07331].
- J. Ellis, M.A.G. Garcia, N. Nagata, D.V. Nanopoulos and K.A. Olive, Starobinsky-Like Inflation and Neutrino Masses in a No-Scale SO(10) Model, 11, 018 (2016) [arXiv:1609.05849].
- E. Cremmer, S. Ferrara, C. Kounnas and D.V. Nanopoulos, Naturally Vanishing Cosmological Constant in N=1 Supergravity, Phys. Lett. B133, 61 (1983); [CrossRef]
- A.B. Lahanas and D.V. Nanopoulos, The Road to No-Scale Supergravity, Phys. Rept.145, 198 (1987). [CrossRef]
- S. Cecotti, Higher Derivative Supergravity Is Equivalent To Standard Supergravity Coupled To Matter, Phys. Lett. B 190, 86 (1987). [CrossRef]
- F. Farakos, A. Kehagias and A. Riotto, On the Starobinsky Model of Inflation from Supergravity, Nucl. Phys. B876, 187 (2013) [arxiv:1307.1137].
- R. Kallosh and A. Linde, Superconformal generalizations of the Starobinsky model, 062013028 [arxiv:1306.3214].
- A.B. Lahanas and K. Tamvakis, Inflation in no-scale supergravity, Phys. Rev. D91, 085001 (2015) [arxiv:1501.06547].
- C. Pallis, Linking Starobinsky-Type Inflation in no-Scale Supergravity to MSSM, 042014024; 07, 01(E) (2017) [arxiv:1312.3623].
- C. Pallis, Induced-Gravity Inflation in no-Scale Supergravity and Beyond, 057 (2014) [arXiv:1403.5486].
- C. Pallis, Reconciling induced-gravity inflation in supergravity with the Planck 2013 & BICEP2 results, 10, 058 (2014) [arXiv:1407.8522]. [CrossRef]
- R. Kallosh, More on Universal Superconformal Attractors, Phys. Rev. D89, no. 8, 087703 (2014) [arxiv: 1402.3286]. [CrossRef]
- C. Pallis and N. Toumbas, Starobinsky-Type Inflation With Products of Kähler Manifolds, 05, no. 05, 015 (2016) [arXiv:1512.05657]. [CrossRef]
- C. Pallis and Q. Shafi, Induced-Gravity GUT-Scale Higgs Inflation in Supergravity, Eur. Phys. J. C78, no.6, 523 (2018) [arxiv:1803.00349].
- C. Pallis, Starobinsky-Type B-L Higgs Inflation Leading Beyond MSSM, PoS CORFU2022, 101 (2023) [arxiv:2305.00523].
- R. Kallosh, A. Linde and T. Rube, General inflaton potentials in supergravity, Phys. Rev. D83, 043507 (2011) [arxiv:1011.5945]. [CrossRef]
- H.M. Lee, Chaotic inflation in Jordan frame supergravity, 08, 003 (2010) [arXiv:1005.2735]. [CrossRef]
- I. Antoniadis, E. Dudas, S. Ferrara and A. Sagnotti, The Volkov – Akulov – Starobinsky Supergravity, Phys. Lett. B 733, 32 (2014) [arxiv:1403.3269].
- Y. Aldabergenov, Volkov–Akulov–Starobinsky supergravity revisited, Eur. Phys. J. C 80, no. 4, 329 (2020) [arxiv:2001.06617].
- S. Ferrara, R. Kallosh and A. Linde, Cosmology with Nilpotent Superfields, J. High Energy Phys. 10, 2014 (143) [arxiv:1408.4096]. [CrossRef]
- I. Antoniadis, D.V. Nanopoulos and K.A. Olive, R2–Inflation Derived from 4d Strings, the Role of the Dilaton, and Turning the Swampland into a Mirage, arxiv:2410.16541.
- A. Zee, A Broken Symmetric Theory of Gravity, Phys. Rev. Lett.42, 417 (1979). [CrossRef]
- G.F. Giudice and H.M. Lee, Starobinsky-like inflation from induced gravity, Phys. Lett. B733, 58 (2014) [arxiv:1402.2129]. [CrossRef]
- C. Pallis and Q. Shafi, Non-minimal chaotic inflation, Peccei-Quinn phase transition and non-thermal leptogenesis, Phys. Rev. D 86, 023523 (2012) [arxiv:1204.0252].
- C. Pallis and Q. Shafi, Gravity Waves From Non-Minimal Quadratic Inflation, 03, 023 (2015) [arxiv:1412.3757]. [CrossRef]
- C. Pallis, Unitarity-Safe Models of Non-Minimal Inflation in Supergravity, Eur. Phys. J. C 78, no.12, 1014 (2018) [arxiv:1807.01154]. [CrossRef]
- C. Pallis, Unitarizing non-Minimal Inflation via a Linear Contribution to the Frame Function, Phys. Lett. B789, 243 (2019) [arXiv:1809.10667]. [CrossRef]
- A. Kehagias, A.M. Dizgah and A. Riotto, Remarks on the Starobinsky model of in ation and its descendants, Phys. Rev. D 89, 043527 (2014) [arxiv:1312.1155].
- T. Terada, Generalized Pole Inflation: Hilltop, Natural, and Chaotic Inflationary Attractors, Phys. Lett. B760, 674 (2016) [arxiv:1602.07867].
- B.J. Broy, M. Galante, D. Roest and A. Westphal, Pole inflation, Shift symmetry and universal corrections, J. High Energy Phys. 12, 149 (2015) [arxiv:1507.02277]. [CrossRef]
- T. Kobayashi, O. Seto and T.H. Tatsuishi, Toward pole inflation and attractors in supergravity : Chiral matter field inflation, Prog. Theor. Phys. 123B04, no.12 (2017) [arxiv:1703.09960]. [CrossRef]
- C. Pallis, Pole Inflation in Supergravity, PoS CORFU 2021, 078 (2022) [arXiv:2208.11757].
- S. Karamitsos and A. Strumia, Pole inflation from non-minimal coupling to gravity, J. High Energy Phys. 05, 016 (2022) [arxiv:2109.10367]. [CrossRef]
- J.J.M. Carrasco, R. Kallosh, A. Linde and D. Roest, Hyperbolic geometry of cosmological attractors, Phys. Rev. D92, no. 4, 041301 (2015) [arxiv:1504.05557].
- J.J.M. Carrasco, R. Kallosh and A. Linde, α-Attractors: Planck, LHC and Dark Energy, J. High Energy Phys. 10, 147 (2015) [arxiv:1506.01708].
- C. Pallis, An Alternative Framework for E-Model Inflation in Supergravity, Eur. Phys. J. C 82, no. 5, 444 (2022) [arxiv:2204.01047]. [CrossRef]
- R. Kallosh, A. Linde, and D. Roest, Superconformal Inflationary a-Attractors, J. High Energy Phys. 11, 198 (2013) [arxiv:1311.0472]. [CrossRef]
- R. Kallosh and A. Linde, Universality Class in Conformal Inflation, 07, 002 (2013) [arxiv:1306.5220].
- R. Kallosh and A. Linde, BICEP/Keck and cosmological attractors, 12, no.12, 008 (2021) [arXiv:2110.10902]. [CrossRef]
- J. Ellis, M.A.G. Garcia, D.V. Nanopoulos, K.A. Olive and S. Verner, BICEP/Keck constraints on attractor models of inflation and reheating, Phys. Rev. D 105, no. 4, 043504 (2022) [arxiv:2112.04466]. [CrossRef]
- S. Bhattacharya, K. Dutta, M.R. Gangopadhyay and A. Maharana, α-attractor inflation: Models and predictions, Phys. Rev. D107, no. 10, 103530 (2023) [arxiv:2212.13363].
- K. Dimopoulos, Introduction to Cosmic Inflation and Dark Energy, CRC Press, ISBN 978-0-367-61104-0 (2020).
- J. Ellis, D. V. Nanopoulos, K. A. Olive and S. Verner, Unified No-Scale Attractors, 09, 040 (2019) [arXiv:1906.10176]. [CrossRef]
- C. Pallis, Pole-induced Higgs inflation with hyperbolic Kähler geometries, 05, 043 (2021) [arXiv:2103.05534]. [CrossRef]
- C. Pallis, SU(2,1)/(SU(2)×U(1)) B-L Higgs Inflation, J. Phys. Conf. Ser.2105, no. 12, 12 (2021) [arxiv:2109.06618].
- C. Pallis, T-Model Higgs Inflation in Supergravity, arXiv:2307.14652.
- G. ’t Hooft, Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking, NATO Sci. Ser. B59, 135 (1980).
- M. Kawasaki, M. Yamaguchi and T. Yanagida, Natural chaotic inflation in supergravity, Phys. Rev. Lett. 85, 3572 (2000) [hep-ph/0004243]. [CrossRef]
- P. Brax and J. Martin, Shift symmetry and inflation in supergravity, Phys. Rev. D 72, 023518 (2005) [hep-ph/0504168]. [CrossRef]
- S. Antusch, K. Dutta and P.M. Kostka, SUGRA Hybrid Inflation with Shift Symmetry, Phys. Lett. B 677, 221 (2009) [arxiv:0902.2934].
- T. Li, Z. Li and D.V. Nanopoulos, Supergravity Inflation with Broken Shift Symmetry and Large Tensor-to-Scalar Ratio, 02, 028 (2014) [arXiv:1311.6770].
- C. Pallis, Kinetically modified nonminimal chaotic inflation, Phys. Rev. D91, 123508 (2015) [arxiv: 1503.05887].
- C. Pallis, Kinetically Modified Non-Minimal Inflation With Exponential Frame Function, Eur. Phys. J. C 77, no. 9, 633 (2017) [arxiv:1611.07010]. [CrossRef]
- I. Ben-Dayan and M.B. Einhorn, Supergravity Higgs Inflation and Shift Symmetry in Electroweak Theory, 12, 002 (2010) [arXiv:1009.2276]. [CrossRef]
- G. Lazarides and C. Pallis, Shift Symmetry and Higgs Inflation in Supergravity with Observable Gravitational Waves, J. High Energy Phys. 11, 114 (2015) [arxiv:1508.06682]. [CrossRef]
- C. Pallis, Kinetically modified nonminimal Higgs inflation in supergravity, Phys. Rev. D92, no. 12, 121305 (2015) [arxiv:1511.01456].
- C. Pallis, Variants of Kinetically Modified Non-Minimal Higgs Inflation in Supergravity, 10, 037 (2016) [arXiv:1606.09607].
- R. Kallosh, A. Linde, D. Roest and T. Wrase, Sneutrino inflation with α-attractors, 11, 046 (2016) [arXiv:1607.08854].
- T.E. Gonzalo, L. Heurtier and A. Moursy, Sneutrino driven GUT Inflation in Supergravity, J. High Energy Phys. 06, 109 (2017) [arxiv:1609.09396]. [CrossRef]
- K. Kaneta, Y. Mambrini, K. A. Olive and S. Verner, Inflation and Leptogenesis in High-Scale Supersymmetry, Phys. Rev. D101, no.1, 015002 (2020) [arxiv:1911.02463]. [CrossRef]
- J. Ellis, M.A.G. Garcia, D.V. Nanopoulos and K.A. Olive, Phenomenological aspects of no-scale inflation models, 10, 003 (2015) [arxiv:1503.08867]. [CrossRef]
- Y. Ema, M.A. G. Garcia, W. Ke, K.A. Olive and S. Verner, Inflaton Decay in No-Scale Supergravity and Starobinsky-like Models, Universe 10, no. 6, 239 (2024) [arxiv:2404.14545]. [CrossRef]
- C. Pallis, T-Model Higgs Inflation and Metastable Cosmic Strings, J. High Energy Phys. 01, ?? (2025) [arxiv:2409.14338].
- C. Pallis, E- and T-model hybrid inflation, Eur. Phys. J. C 83, no. 1, 2 (2023) [arxiv:2209.09682]. [CrossRef]
- N. Aghanim et al. [Planck Collaboration], Planck 2018 results. VI. Cosmological parameters, Astron. Astrophys.641, A6 (2020) – Erratum: Astron. Astrophys.652, C4 (2021) [arxiv:1807.06209].
- M.S. Turner, Coherent Scalar-Field Oscillations in an Expanding Universe Phys. Rev. D 28, 1243 (1983).
- J. Martin and C. Ringeval, First CMB Constraints on the Inflationary Reheating Temperature, Phys. Rev. D 82, 023511 (2010) [arxiv:1004.5525]. [CrossRef]
- J. Ellis, M.A.G. Garcia, D.V. Nanopoulos and K.A. Olive, Calculations of Inflaton Decays and Reheating: with Applications to No-Scale Inflation Models, 07, 050 (2015) [arxiv:1505.06986]. [CrossRef]
- C.M. Lin, On the oscillations of the inflaton field of the simplest α-attractor T-model, Chin. J. Phys. 86, 323 (2023) [arxiv:2303.13008].
- M. Tristram et al., Improved limits on the tensor-to-scalar ratio using BICEP and Planck, Phys. Rev. Lett. 127, 151301 (2021) [arxiv:2112.07961].
- P.A.R. Ade et al. [BICEP and Keck Collaboration], Improved Constraints on Primordial Gravitational Waves using Planck, WMAP, and BICEP/Keck Observations through the 2018 Observing Season, Phys. Rev. Lett.127, no. 15, 151301 (2021) [arxiv:2110.00483].
- K. Abazajian et al., CMB-S4 Science Case, Reference Design, and Project Plan, arxiv:1907.04473.
- P. Andre et al. [PRISM Collaboration], PRISM (Polarized Radiation Imaging and Spectroscopy Mission): A White Paper on the Ultimate Polarimetric Spectro-Imaging of the Microwave and Far-Infrared Sky, arxiv:1306.2259.
- L. Montier et al. [LiteBIRD Collaboration], Overview of the Medium and High Frequency Telescopes of the LiteBIRD satellite mission, Proc. SPIE Int. Soc. Opt. Eng. 11443, 114432G (2020) [arxiv:2102.00809].
- D. Baumann et al. [CMBPol Study Team Collaboration], CMBPol Mission Concept Study: Probing Inflation with CMB Polarization, AIP Conf. Proc.1141, 10 (2009) [arxiv:0811.3919].
- R. Kallosh and A. Linde, Polynomial α-attractors, 04, no. 04, 2022 (017) [arXiv:2202.06492].
- F. Bauer and D.A. Demir, Higgs-Palatini Inflation and Unitarity, Phys. Lett. B698, 425 (2011) [arxiv: 1012.2900]. [CrossRef]
- V.M. Enckell, K. Enqvist, S. Rasanen and L.P. Wahlman, Inflation with R2 term in the Palatini formalism, Phys. Lett. B02, 022 (2019) [arxiv:1810.05536].
- I. Antoniadis, A. Karam, A. Lykkas and K. Tamvakis, Palatini inflation in models with an R2 term, Phys. Lett. B11, 028 (2018) [arxiv:1810.10418].
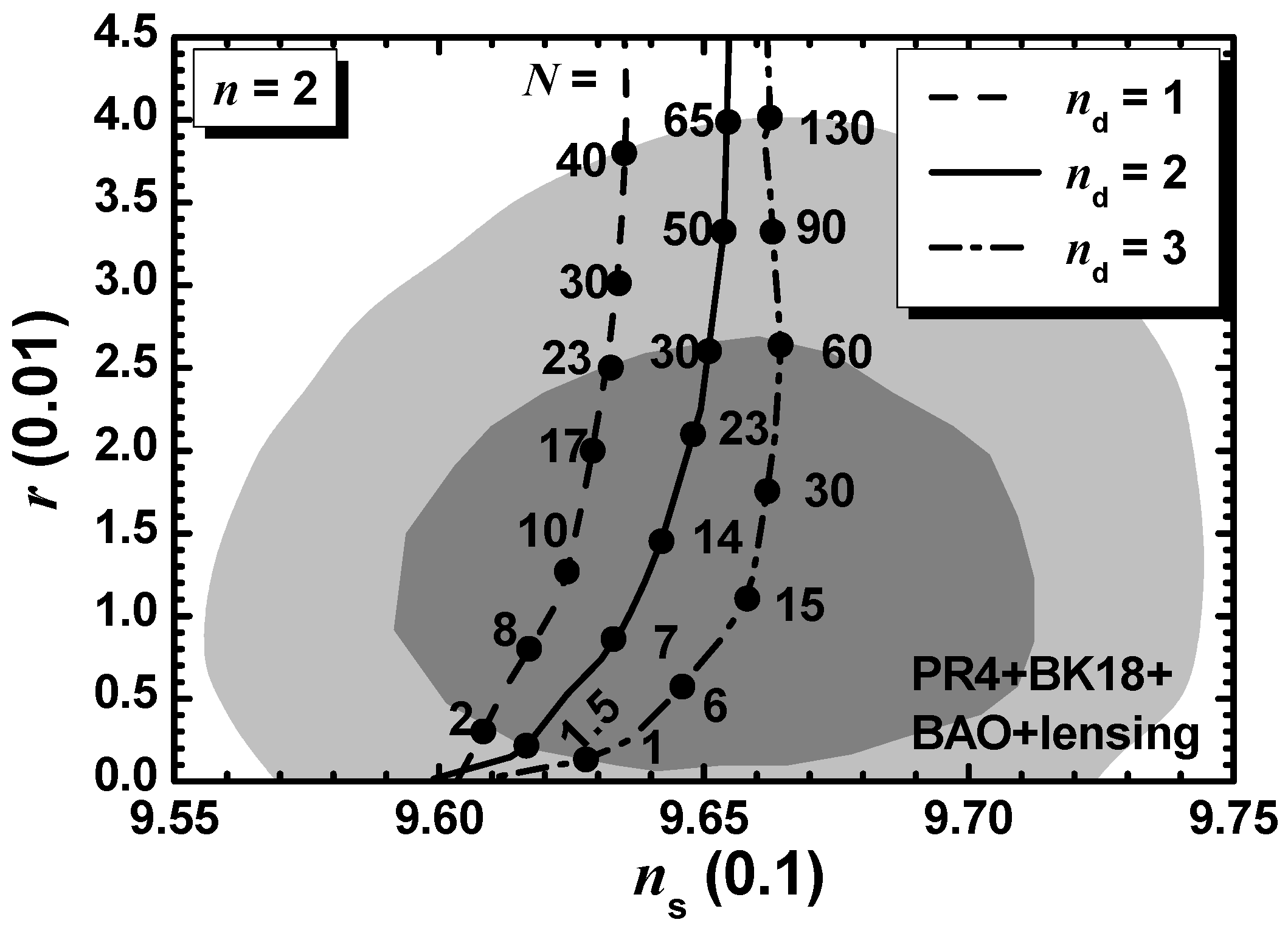
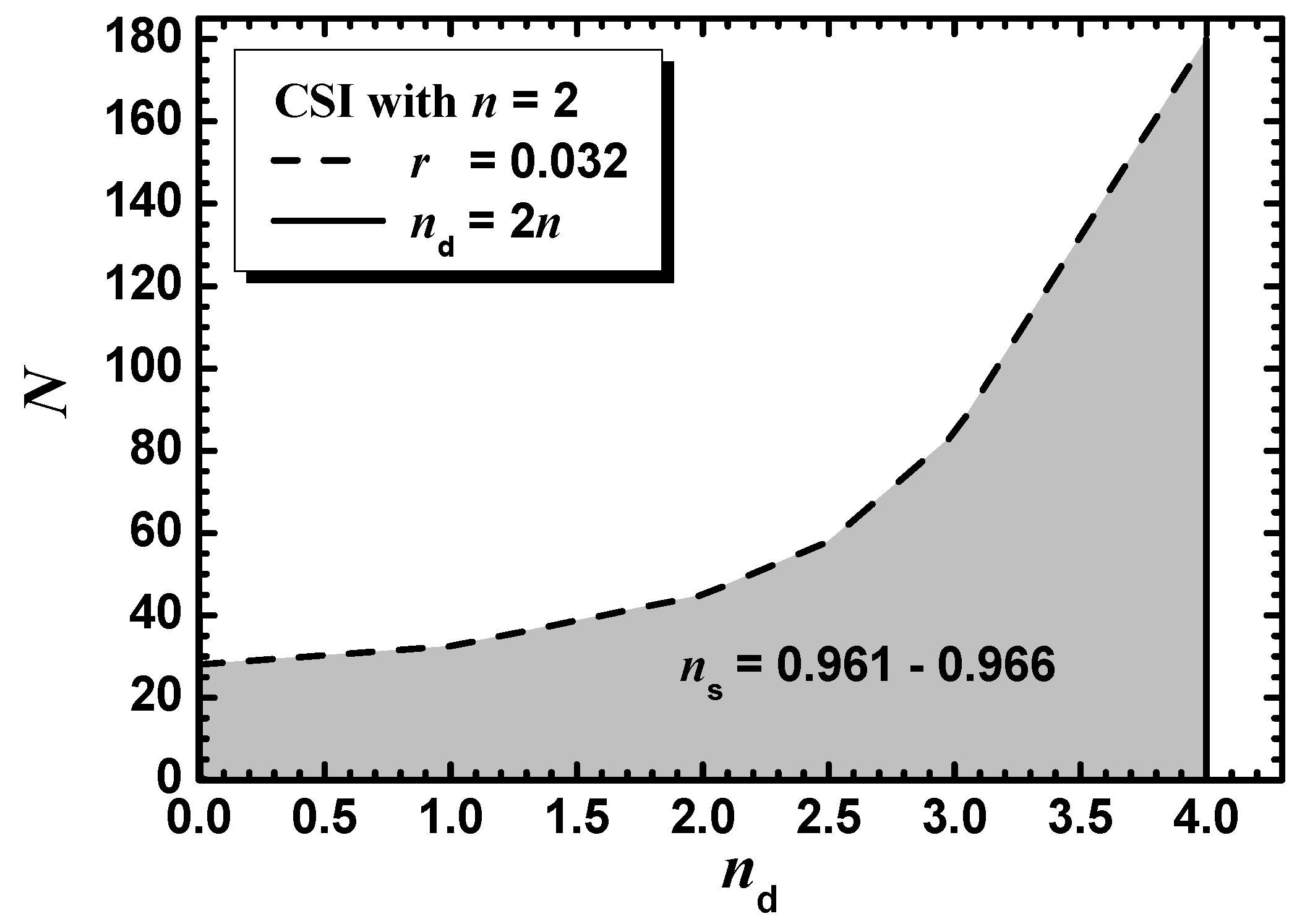
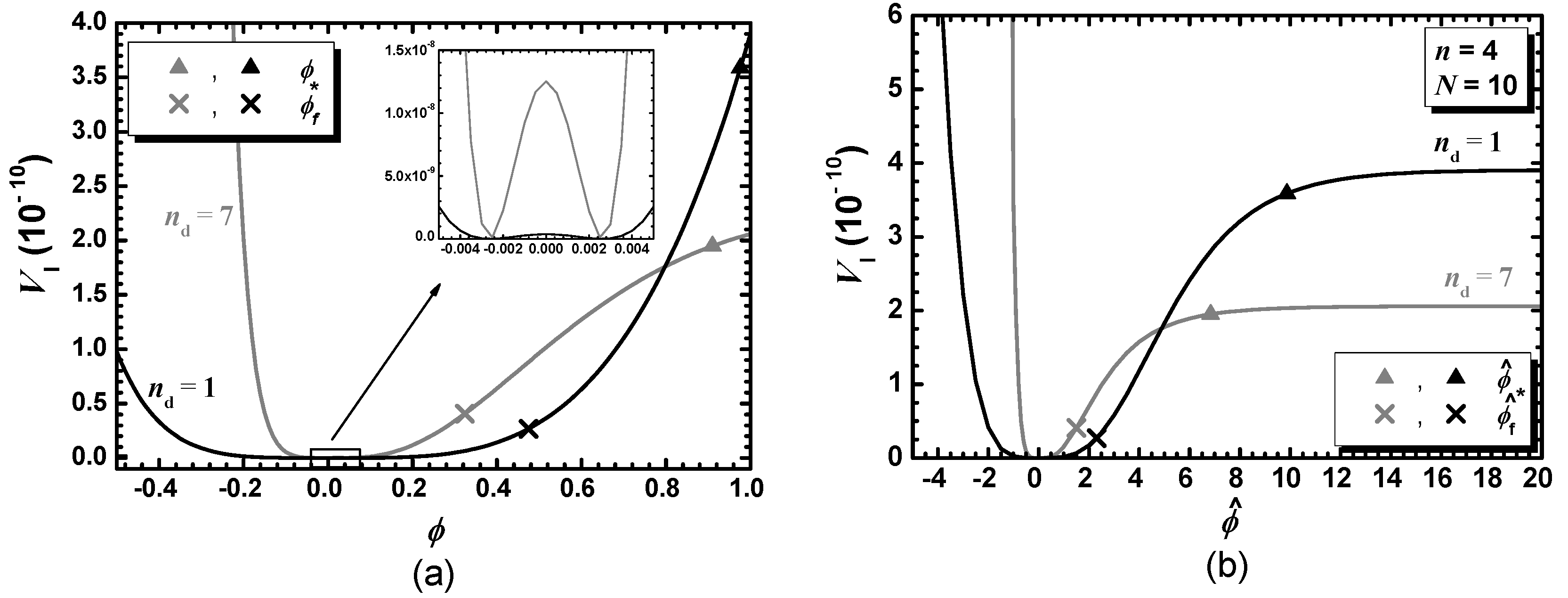
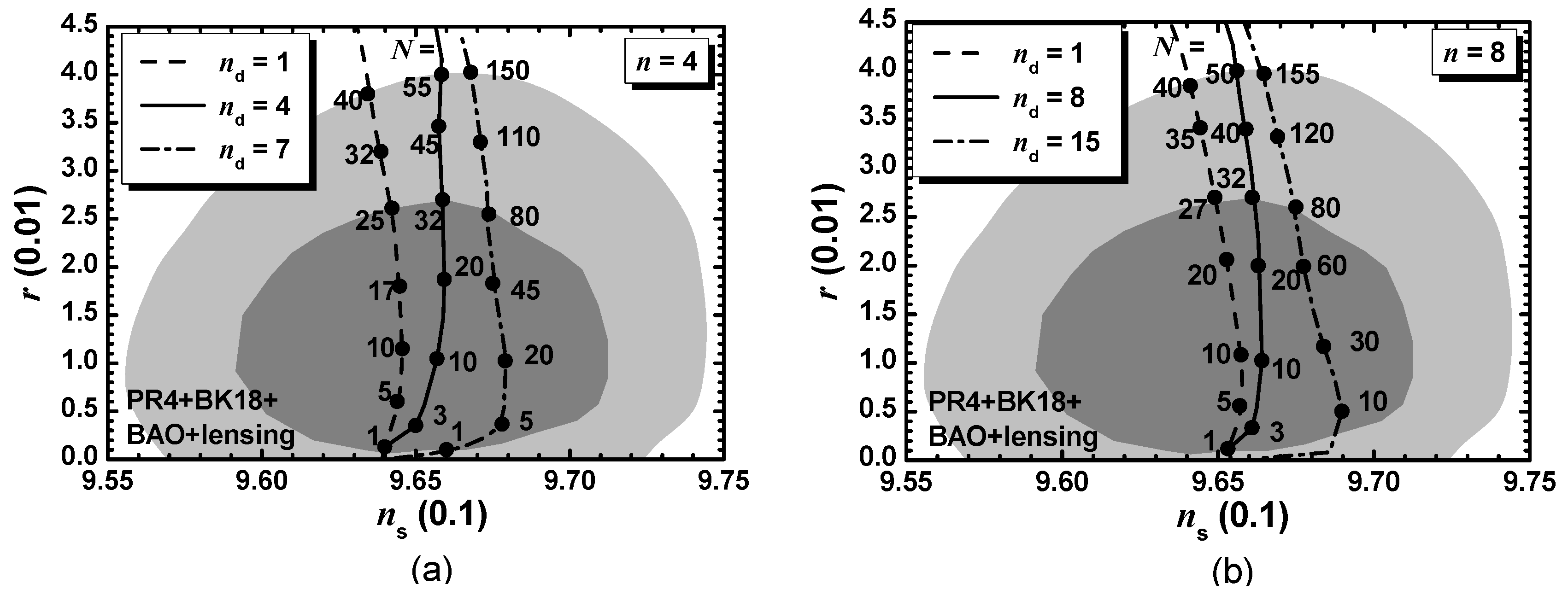
| Fields | Eigenstates | Masses Squared | ||
|---|---|---|---|---|
| 1 real scalar | ||||
| 2 real scalars | ||||
| 2 Weyl spinors | ||||
| Fields | Eigen- | Masses Squared | ||
|---|---|---|---|---|
| states | ||||
| 4 | ||||
| real | ||||
| scalars | ||||
| 1 gauge boson | ||||
| 4 Weyl | ||||
| spinors | ||||
| Model: | CSI | HSI | HSI | |||
|---|---|---|---|---|---|---|
| n | 2 | 4 | 8 | |||
| 1 | 3 | 1 | 7 | 1 | 15 | |
| 9 | 7 | |||||
| {1.9} | ||||||
| M | − | |||||
| 22.6 ZeV | 36.4 ZeV | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




