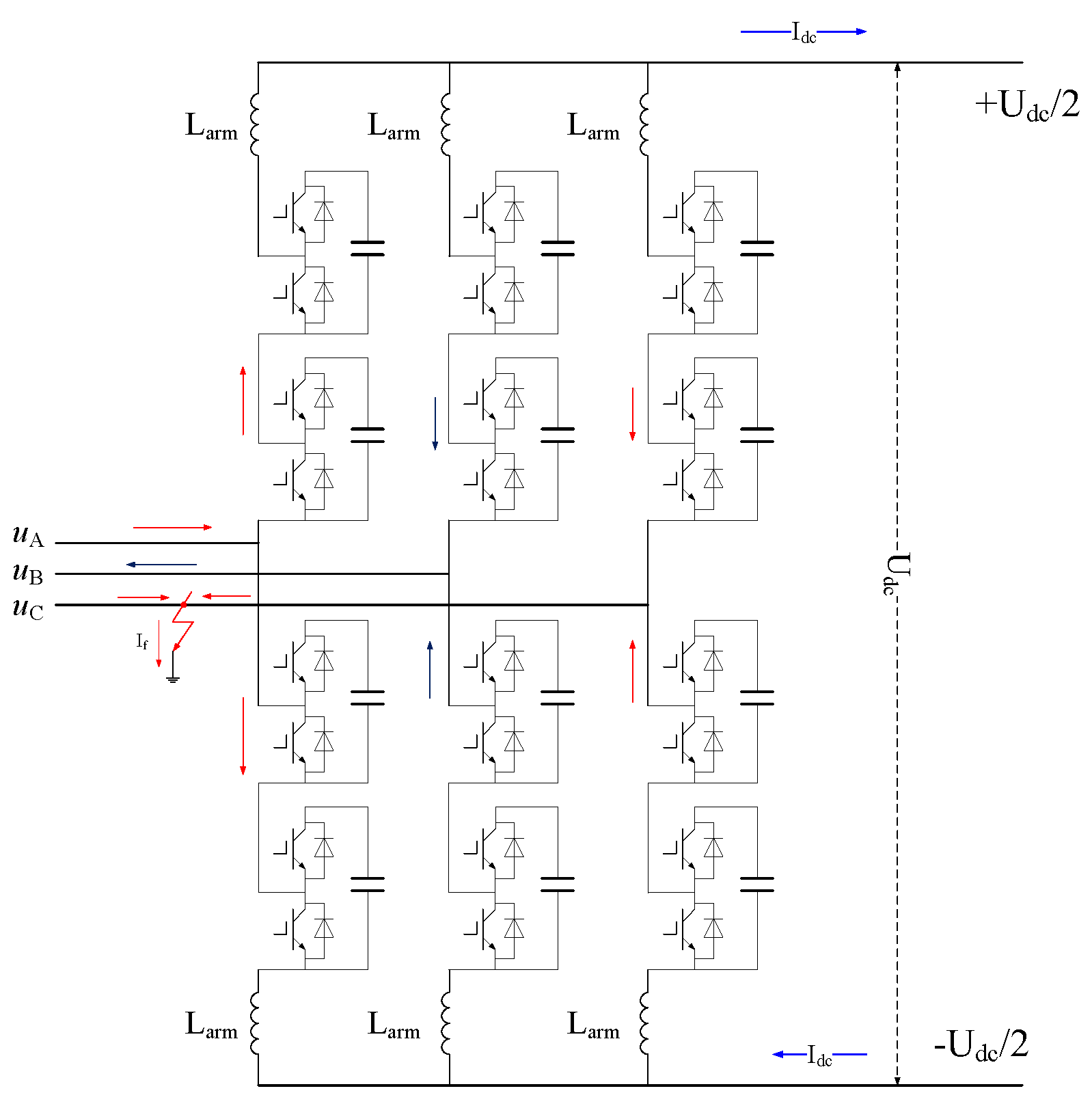Research on Overcurrent in Offshore MMC and Suppression Strategies Based on Field-Circuit Coupling Analysis

1. Introduction

The modular multilevel converter based high voltage direct current (MMC-HVDC) transmission system as a primary solution for large-scale renewable energy integration. With the continuous maturation of MMC-HVDC technology, an increasing number of offshore wind farms, both domestically and internationally, are expected to be connected to the grid via this system, particularly those located in deep-sea areas [1]. However, the high maintenance costs, long maintenance cycles, and significant challenges associated with offshore converter stations pose numerous unresolved issues [2]. Among these, the safety and stability of the MMC valves are particularly prominent. The core equipment of MMC consists of sub-modules based on semiconductor devices, such as half-bridge sub-modules with two power devices (e.g., IGBTs) and full-bridge sub-modules with four power devices (e.g., IGBTs). These power devices in the converter valves serve dual functions: circuit switching and power transmission. Unlike conductors, semiconductors have both free electrons and holes as charge carriers, and factors such as carrier concentration, diffusion current, and mobility can all affect the current-carrying characteristics of the semiconductor. Therefore, the overcurrent capability of MMC converter valves is very limited, and improper handling can lead to severe consequences [3].

Overcurrent in valves is generally caused by system faults or equipment failures. The control and protection strategies, protection settings, the timing of fault occurrence, and the circuit characteristics after a fault can all influence the fault current. After a fault occurs, the operating states of nonlinear components in the circuit change, altering the characteristics of the fault current. Furthermore, under high-frequency excitation, the impact of distributed parameters in the MMC valves becomes more pronounced, making the analysis of overcurrent more complex and challenging [4]. Therefore, research on the overcurrent characteristics of valves is of great importance, and the study of the development process and influencing factors of overcurrent is both complex and challenging.

The low safety margin caused by overcurrent in MMC valve has always been a major concern for the safe operation of offshore wind power MMC-HVDC transmission systems. Currently, research on the fault characteristics of offshore MMC valve remains a hot topic in the industry [5,6,7]. A protection scheme for modular multilevel converter based HVDC grids is proposed by Xiuyong Yu to meet the ultra-fast, selective, and reliable requirements of the dc fault protection in 2021[8]. Current-limiting requirement of MMC-HVDC system and studies the performance of three types of SFCL were proposed by Xiangyu Tan in 2021[9]. Hongyu Zhou analyzed dynamic reactive current optimization strategy that combines MMC energy control capability with transient overload capability to achieve onshore AC fault ride-through in 2024[10]. Geon-Woong Kim used the SFCL on short circuit to Limit characteristics of capacitor discharge current of MMC-based system in 2022[11]. The influence of new energy of AC system on DC fault current characteristics in MMC-HVDC system was studied by Siyuan Liu in 2023[12].

The electric field characteristics and stray parameters of the MMC valves under fault conditions have not been considered in existing research. The behavior of nonlinear elements in the system during faults has not been accounted in these studies. The overcurrent of the MMC valves calculated using these methods might be incomplete in terms of operational conditions and might lack sufficient accuracy. This deficiency poses risks for subsequent engineering commissioning and testing. Additionally, comprehensive strategies for suppressing overcurrent in valves have not been thoroughly addressed. In this paper, a field-circuit coupling analysis method is proposed for overcurrent research in MMC valve. The method integrated the electric field characteristics of valves, stray parameters, and transient characteristics of nonlinear devices during the fault process with the analysis of the MMC-HVDC system. Firstly, the development process and influencing factors of overcurrent in MMC valve within offshore wind power MMC-HVDC systems are analyzed. Subsequently, the stray parameters induced by the valve structure and valve hall layout were calculated. A comprehensive overcurrent analysis model for MMC valves, incorporating field-circuit coupling analysis, is established. This model includes the electric field characteristics of the MMC valves, stray parameters, and the nonlinear model of the surge arresters in the MMC-HVDC system. Finally, the proposed field-circuit coupling method was used to accurately calculate the overcurrent in converter valves. Based on these calculations, a rational overcurrent suppression strategy for offshore MMC valve was proposed. The effectiveness and practicality of the proposed method were verified through comprehensive case studies conducted on the ±500kV offshore MMC-HVDC valve overcurrent calculation and suppression. The numerical results demonstrate the efficacy and accuracy of the method presented in this paper.

2. Influencing Factors of MMC Valve Overcurrent

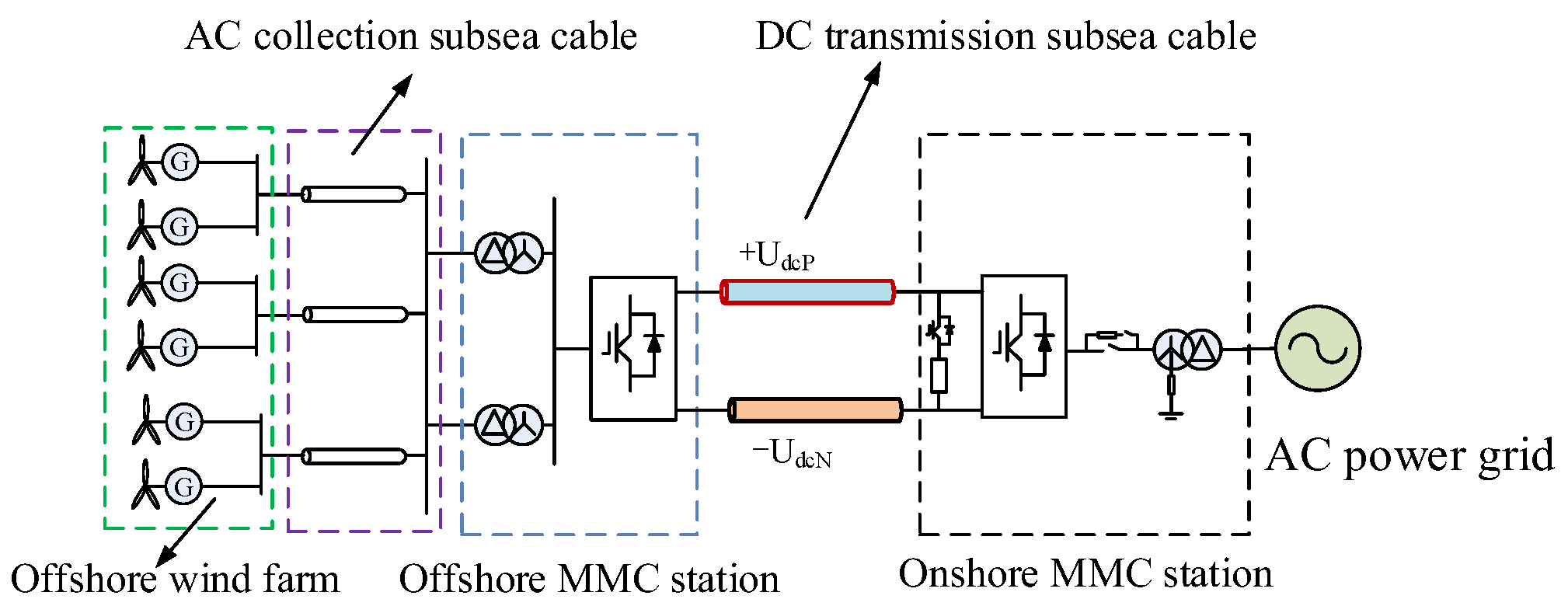
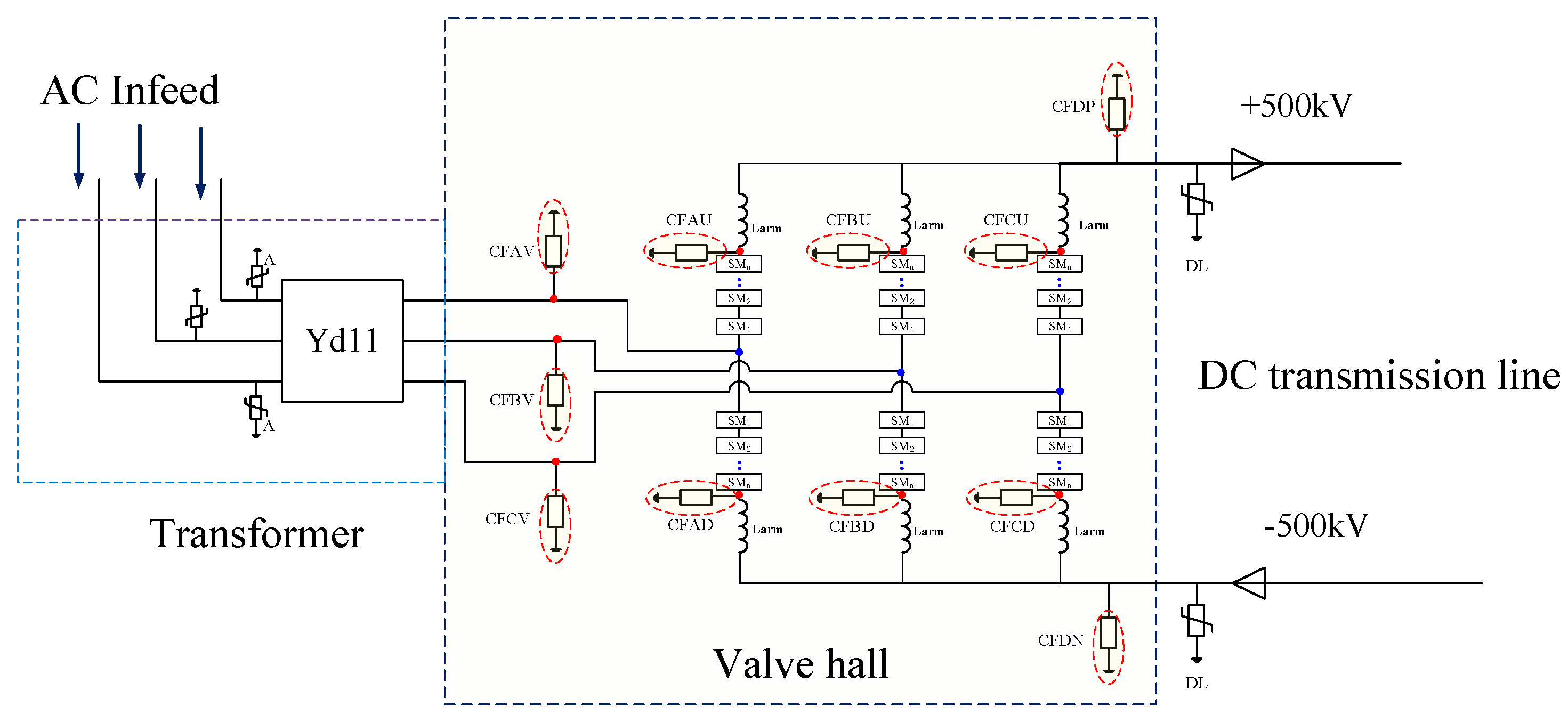
The offshore wind power MMC-HVDC transmission system is the primary method for delivering electrical energy from large-scale, deep-sea wind farms. Currently, several offshore wind power MMC-HVDC transmission projects have already been implemented[13]. The schematic diagram of offshore wind power MM-HVDC transmission system is shown in Figure 1.

As shown in Figure 1, the offshore wind power MMC-HVDC transmission system consists of the offshore wind farm, the AC collection system, the offshore converter station, the DC submarine cable, the onshore converter station, and the DC energy dissipation device.

In the offshore wind power MMC-HVDC system, half-bridge sub-modules are utilized to construct the MMC. The offshore converter station is arranged in the form of an offshore platform located in deep-sea areas, designed to withstand harsh marine environments while ensuring reliable power conversion and transmission.

Overcurrent phenomena in the MMC valves of offshore MMC-HVDC system are typically caused by severe faults occurring in the converter station area or within the DC transmission lines. These faults can lead to significant transient currents that may exceed the rated capacity of the valves, posing risks to the safe and stable operation of the system.

The principle of overcurrent caused by faults in the valve hall area of the offshore converter station is illustrated in Figure 2.

As shown in Figure 2, the offshore wind power MMC-HVDC system employs a monopolar connection configuration. Each converter station consisting of six bridge arms. Each bridge arm is composed of a series connection of N half-bridge sub-modules. During operation, power transmission is achieved by controlling the switching of sub-modules.

When a fault occurs within the offshore converter platform, whether it is a short-circuit fault, a ground fault, or an open-circuit fault, the physical characteristics of the power transmission system are altered. Due to the change in the circuit, the impedance characteristics of the MMC system are also affected.

The relationship between the bridge arm current and voltage during operation is defined as:

$$\left\{\begin{array}{l}{u}_{\mathrm{armupC}}=-u_{\mathrm{Cn}}+{\displaystyle \frac{{\mathrm{U}}_{\mathrm{dc}}}{2}}\\ u_{\mathrm{armdownC}}=u_{\mathrm{Cn}}+{\displaystyle \frac{{\mathrm{U}}_{\mathrm{dc}}}{2}}\\ i_{\mathrm{arm}}=f(u{}_{\mathrm{arm}})={\displaystyle \frac{P_{\mathrm{dc}}}{{3\mathrm{U}}_{\mathrm{dc}}}}+{\displaystyle \frac{\sqrt{{P_{\mathrm{dc}}}^2+Q^2}}{6u_{\mathrm{Cn}}}}\end{array}\right.$$

(1)

In the Equation (1), iarm is the bridge arm current of MMC. u_Cn is the ground voltage on the valve side. U_dc is the DC voltage of the MMC. uarmupC and uarmdownC are the voltages of the upper and lower bridge arms. Pdcand Q are the active power and reactive power of MMC.

As shown in Figure 2, during the transient process following a fault, the expression for the bridge arm current is defined as:

$$\left\{\begin{array}{l}{u}_{\mathrm{armup}}=i_{arm}{Z}_{arm}(\mathrm{t})\\ Z_{arm}(\mathrm{t})=Z_{\mathrm{on}}{N}_1+Z_{\mathrm{off}}（\mathrm{N}-N_1）+Z_{\mathrm{F}}+Z_{\mathrm{g}}\end{array}\right.$$

(2)

In the Equation (2), Z_arm is the equivalent impedance of the bridge arm. Z_on and Z_off are the impedances of the sub-modules in the on-state and off-state. N and N1are the total number of modules in the bridge arm and the number of sub-modules in the on-state.

Bridge arm current of MMC. Z_F is the impedance in the fault loop. Z_g is the impedance resulting from MMC valve stray parameters.

According to the Equation (2), it can be seen that during steady-state operation, Z_F​ is zero, and the effect of Z_g​ can be neglected. In this case, the current through the valve can be indirectly controlled based on power.

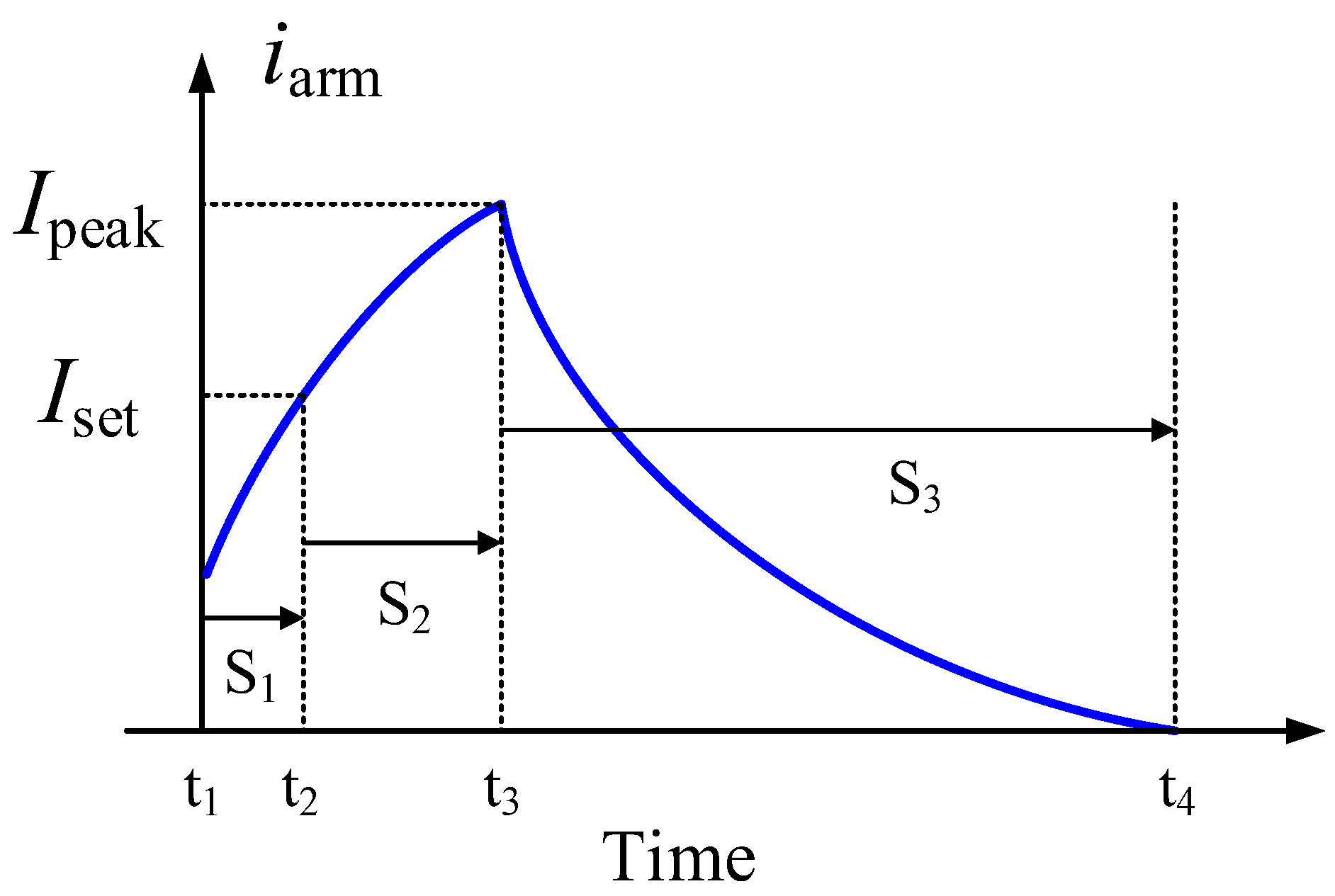
In the overcurrent protection of the MMC valve, the instantaneous current value is detected by the bridge arm current transformer. When the peak current of the bridge arm reaches the protection setting Iset​ (or other conditions), the MMC current protection signal is triggered. Following the protection action, the bridge arm current is reduced. The development process of the bridge arm fault current in MMC is shown in Figure 3.

As shown in Figure 3, a severe fault occurs within the station at time t1​, causing the bridge arm current to increase rapidly. When the current iarm​ reaches the protection setting Iset​, the protection is triggered, and the system is blocked. After the protection chain delay(S₂), the blocking is completed, and the MMC valve current reaches its peak value Ipeak​.

In practical engineering applications of HVDC transmission, the rated gate-emitter voltage for IGBT drivers is typically around 15V. Additionally, the maximum safe turn-off current of IGBT is generally about twice the rated current. Therefore, the peak current Ipeak​ during a fault must be less than twice the rated current of IGBT to ensure device safety[14,15,16].

During time intervals S1​and S2​, the development of the fault current is closely related to the characteristics of the fault loop. The time interval S2​ is determined by the hardware of the control and protection system. Unreasonable design of the main circuit parameters and stray parameters of the equipment can cause current distortion and rapid increase, leading to device damage under certain operating conditions.

As shown in the (2), the fault-induced changes in impedance characteristics lead to overcurrent, especially under impulse excitation, where the effect of Z_g​ becomes more pronounced.

Because of the different positions and geometric dimensions of the metal components, a large number of stray parameters exist in the MMC valve, especially stray capacitances.

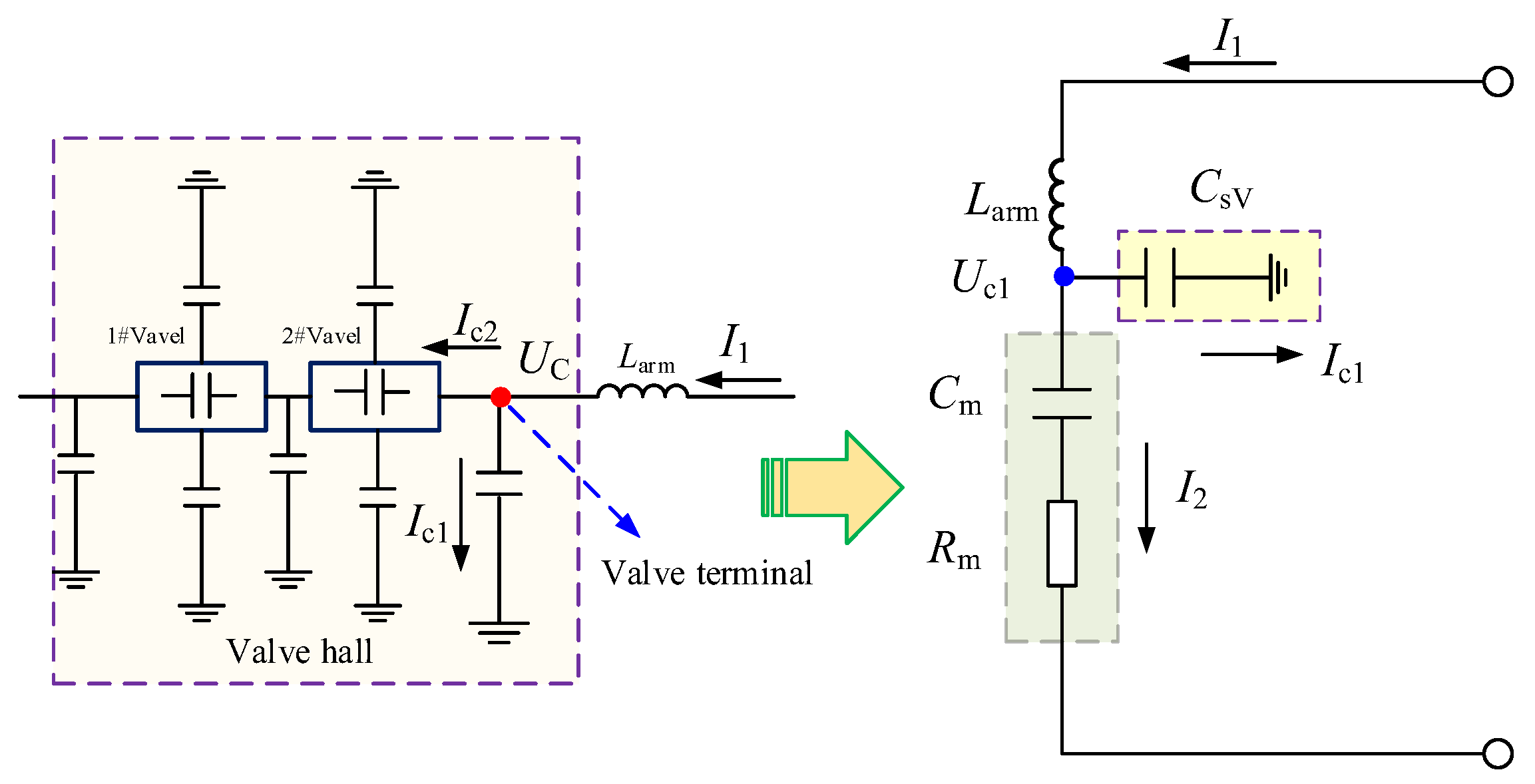
The impact of stray capacitance in the MMC valve on the current is shown in Figure 4.

As shown in the Figure 4, L_arm is the bridge arm reactor, and C_SV is the stray ground capacitance at the terminal of the MMC valve.

U_C is the voltage to ground at the terminal of the MMC valve. C_m and R_m are the equivalent capacitance and equivalent resistance of the MMC. I₁ is the bridge arm current. The presence of stray capacitance may lead to changes in the bridge arm current.

The impact of stray capacitance on the bridge arm current is defined as:

$$\left\{\begin{array}{l}{U}_{c1}=j\omega C_{\mathrm{sV}}{I}_{c1}\\ I_{c1}=-j{\displaystyle \frac{U_{c1}}{\omega C_{\mathrm{sV}}}}\\ Z_2=R_m-j{\displaystyle \frac{1}{\omega C_{\mathrm{m}}}}\end{array}\right.$$

(3)

In the Equation (3), I_c1 is the current generated by stray capacitance. U_C1 is the voltage to ground at the terminal of the MMC valve. Cm and Rm are the equivalent capacitance and equivalent resistance of the MMC. I₁ is the bridge arm current. ω is angular frequency of voltage or current.

Stray capacitance can cause changes in the bridge arm current. The impact factor of stray capacitance on the bridge arm current is defined as:

$$f_{CI}(\omega )={\displaystyle \frac{I_{c1}}{I_{c2}}}={\displaystyle \frac{C_{\mathrm{sV}}}{C_{\mathrm{m}}}}+j\omega C_{\mathrm{sV}}{R}_m$$

(4)

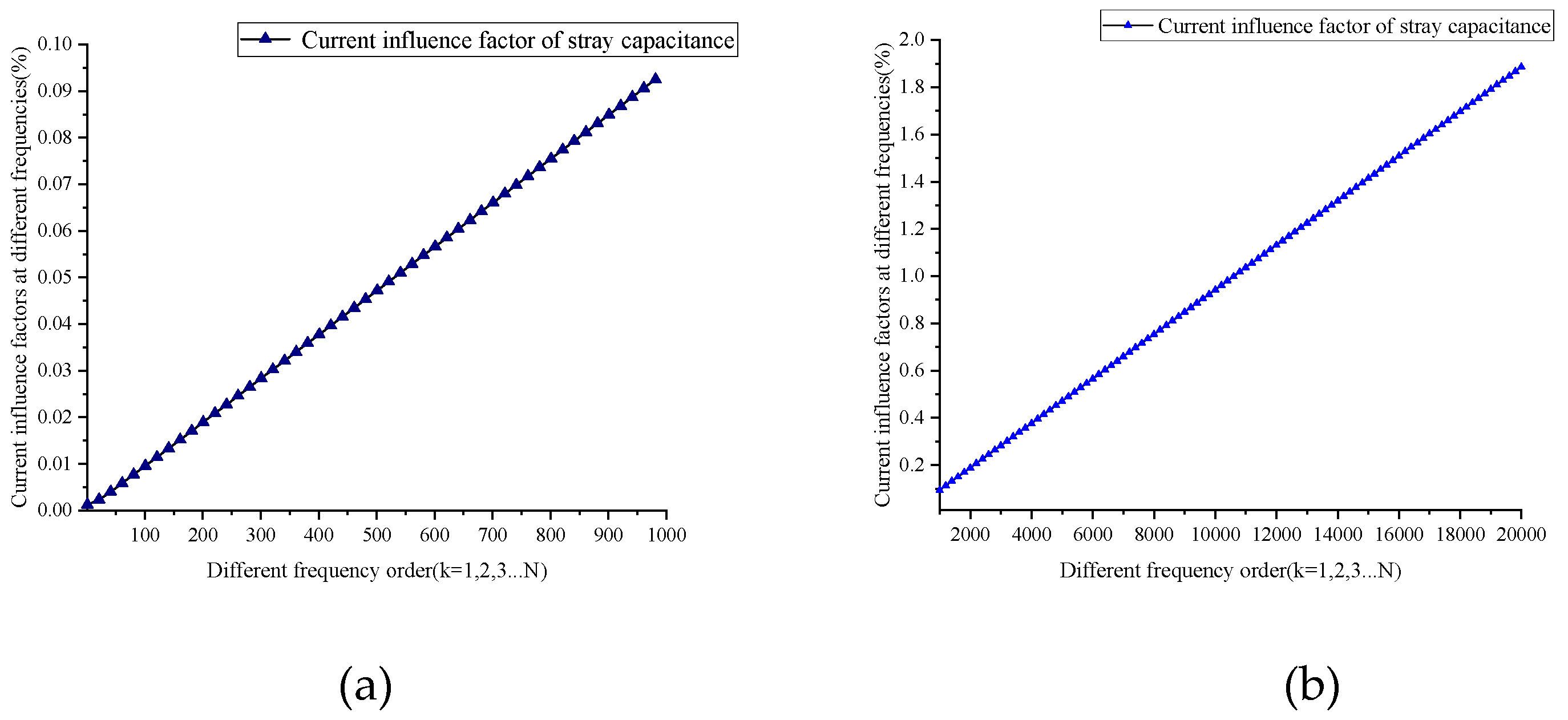
In the Equation (4), f_CI is the impact factor of stray capacitance on the bridge arm current. The magnitude of this impact factor is related to the frequency of the current.

The impact factor of stray capacitance on the bridge arm current (f_CI) at different frequencies is shown in Figure 5.

As shown in the Figure 5, the impact of stray capacitance on the bridge arm current is very small at low frequencies. Specifically, higher frequencies tend to result in a more pronounced effect due to the capacitive reactance characteristics.

At lower frequencies, the impact factor is relatively small, while at higher frequencies, it can significantly alter the current waveform.

When the frequency is below 50th order, the impact factor f_CI is essentially zero. At a frequency of 150th order, the impact factor is only 0.01%. When the frequency reaches 1000th order, the impact factor increases to 0.1%, and the influence begins to become more pronounced. When the frequency reaches 1000th order(500kHZ), the impact factor fCI increases to 1%, impact of stray capacitance becomes very significant.

In the offshore wind power MMC-HVDC transmission system, MMC valve overcurrent caused by severe station faults is typically in the form of impulses. The rise time of the MMC valve voltage and current waveforms is very short, resulting in the presence of high-frequency components in the waveforms. Therefore, the impact of stray capacitance in the MMC valve must be considered in the analysis of overcurrent

3. Field-Circuit Coupling Analysis Method

3.1. Field-Circuit Coupling Analysis Model

In offshore wind power MMC-HVDC transmission system, the overcurrent levels of the valves are typically high, and the current rises rapidly after a fault occurs[17]. As illustrated in Figure 2, the variation of fault current is primarily determined by the current loop formed after the fault.

According to Figure 4, the transient parameter variations of nonlinear components, stray parameters of the converter valve, and the electric field distribution can all influence the fault loop during transient conditions.

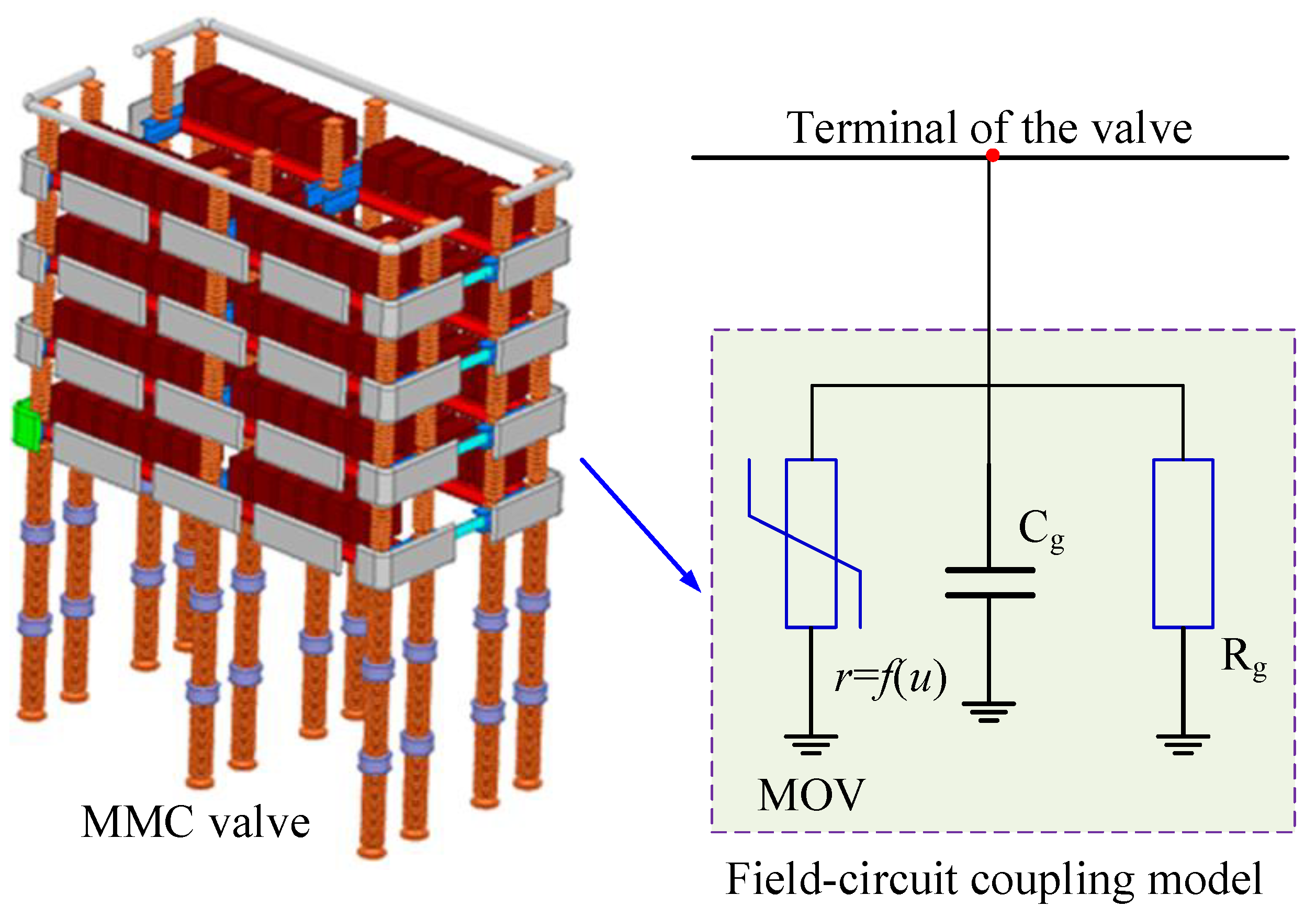
A field-circuit coupled analysis model for overcurrent calculation is established, as shown in Figure 6.

As shown in the Figure 6, the field-circuit coupled model incorporates the electric field characteristics of the MMC valve, stray parameters of the MMC valve, and the nonlinear model of the surge arrester within the MMC-HVDC system.

3.2. Electric Field and Stray Parameters Calculation

In the offshore wind power MMC-HVDC transmission system, severe station faults lead to the operation of control and protection systems, which in turn cause the MMC valve to be blocked.

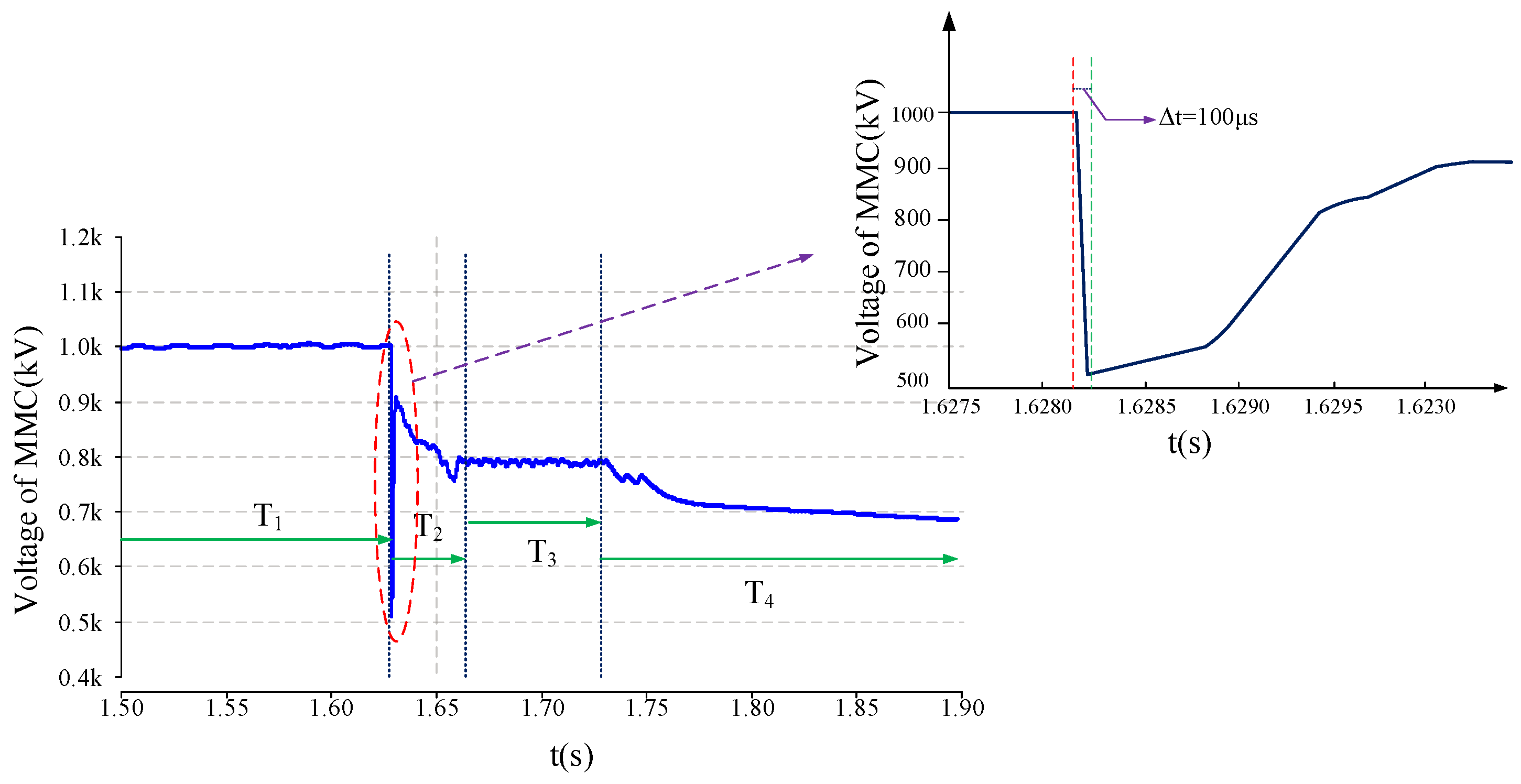
Following the fault described in Figure 2, the voltage of the MMC valve is shown in Figure 7.

As shown in Figure 7, following a severe system fault, the voltage variation can be divided into four stages. It can be observed from that the terminal voltage of the MMC valve experiences the largest fluctuation and the most severe impulse during stage T₂, with the voltage falling edge at the terminal occurring approximately 100 μs after the fault occurs.

After estimation, the high-frequency components are expected to exceed 1 MHz. As shown in Figure 5(b), the f_CI will exceed 1.5%, indicating that the stray parameters of the MMC valve will have a significant influence on the overcurrent.

From the Figure 7, it is evident that during system faults, the terminal voltage of the MMC valve is subjected to impulse excitation, characterized by relatively steep voltage rise and fall edges.

In summary, under the influence of this impulse voltage, the following characteristics appear at the terminal location of the converter valve:

1) Under impulse excitation, the stray parameters of the valve cause more pronounced changes in the fault loop. Therefore, it is necessary to calculate the stray parameters of the MMC valve under impulse excitation, primarily the stray capacitance.

2) When the voltage peak is high, it may lead to a higher electric field strength at the terminal of the MMC valve. If partial discharge occurs, it will also cause changes in the fault loop.

3) Under impulse excitation, when the voltage peak is large, the surge arrester at the terminal location of the MMC valve may be activated, leading to changes in the fault loop.

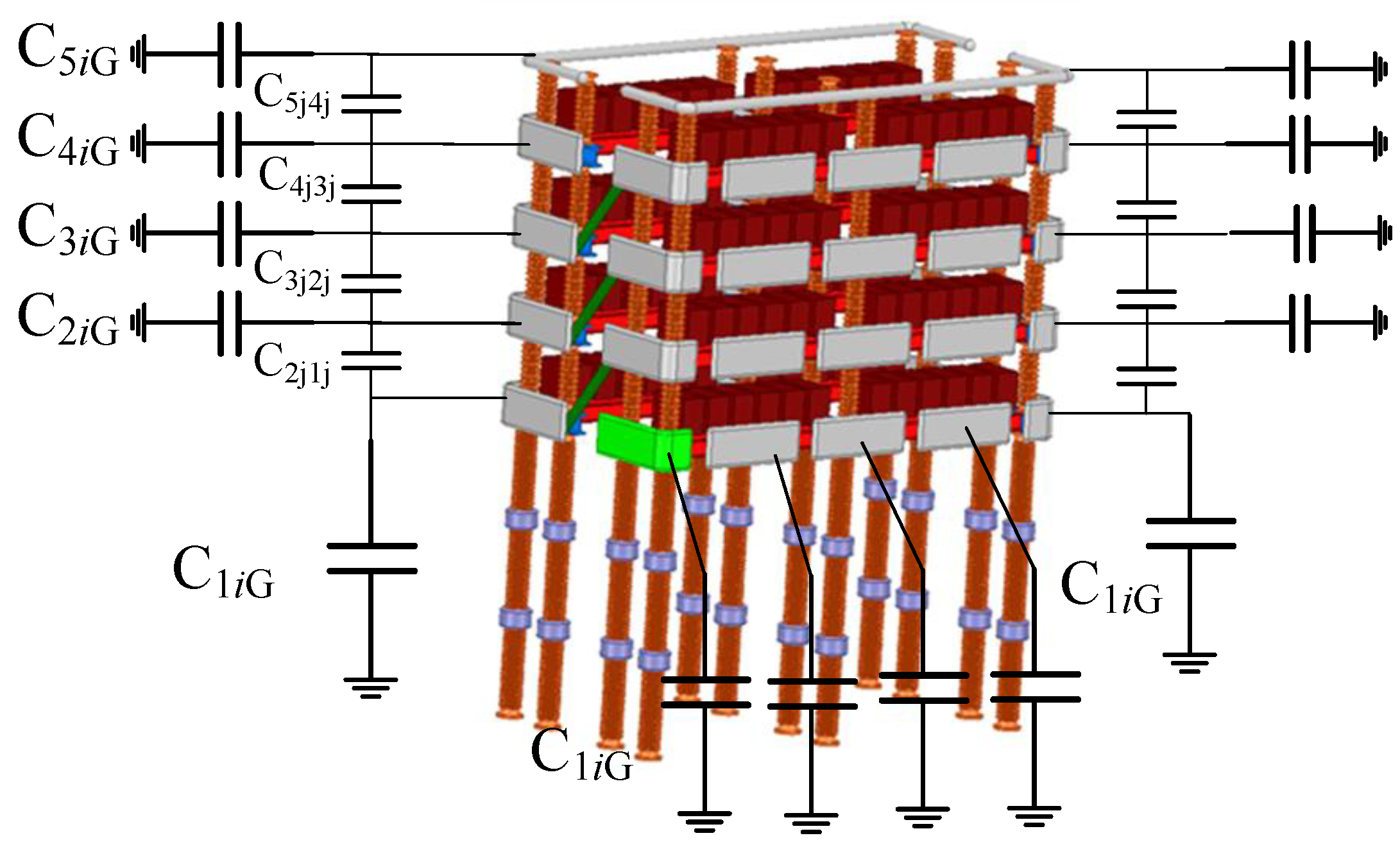
The MMC valve is composed of multiple conductors, and all conductors need to be processed in the capacitance calculation. The capacitances of the valve shields are shown in Figure 8.

As shown in Figure 8, C_1iG is the ground capacitance of conductor i in the layer 1. C_1ij is the capacitance between conductor i and conductor j in layer 1. The C1iand2i is the capacitance between conductor i in layer 1 and conductor i in layer 2. From the (2), a change in Zg​will lead to alterations in the characteristics of the fault current.

According to the physical definition, capacitance is a measure that describes the ability to store electric field energy. The structure of the MMC valve is relatively complex, with a large number of conductors of various shapes.

The accurate calculation method of stray capacitance based on electric field energy calculation is defined as:

$$\left\{\begin{array}{l}{W}_{\mathrm{c}}={\displaystyle \frac{1}{2}}\mathrm{C}(\Delta {\mathrm{U})}^2\\ \Delta \mathrm{U}={\phi }_1-{\phi }_2\\ {\mathrm{C}}_{\mathrm{gij}}=f_{\mathrm{C}}(E_{ij})={\displaystyle \frac{{\epsilon }_r{\epsilon }_0{\displaystyle \int E^{2}dV}}{{(\Delta \mathrm{U})}^2}}\end{array}\right.$$

(5)

In the Equation (5), E_ij is the electric field between conductors i and j. φij are the potential distributions of conductors. ε_r is the relative permittivity of the insulating structure between conductors. ε₀ is the acuum permittivity. W_C is the electric field energy stored between conductors. C_gij is the capacitance between conductors. ΔU is the voltage between conductors.

Due to the influence of factors such as terminal connectors and bus-bars, the electric field at the terminal of the MMC valve is often large and unevenly distributed.

Therefore, the electric field characteristics at the terminal of the converter valve are described through ground impedance. The electric field coupling impedance is defined as:

$$R_{\mathrm{g}}=f(E_i)$$

(6)

In the Equation (6), E_i is the instantaneous electric field strength between MMC terminal conductor and ground. Rg is the electric field coupling impedance of MMC terminal.

The value of electric field coupling impedance R_g is determined by the electric field strength. When the transient electric field E_i​ is less than the air breakdown field strength at the position, the value of resistance R_g​ is considered to be infinite. Conversely, when the transient electric field E_i​ reaches the air breakdown field strength, the resistance value R_g​ becomes a relatively small value, approximately several 1 to 5ohm or even lower.

From the Equation(5), it can be deduced that the MMC stray capacitances can be obtained through electric field analysis. A 3-Dimensional electric field calculation method was used to perform detailed calculations of the MMC valve stray parameters and electric field distribution characteristics.

In the electric field calculation model, the computed capacitance and electric field values are coupled into the system field-circuit coupling analysis model. During the system calculation process, the electric field characteristics of the MMC valve influence the fault characteristics

3.3. Nonlinear Modeling of Arresters

According to the insulation coordination design of the MMC-HVDC transmission system, it is necessary to install surge arresters in the converter stations to suppress overvoltage levels. In the offshore wind power MMC-HVDC transmission system shown in Figure1, zinc oxide surge arresters were installed on the valve side of the bridge-arm reactors and the valve side of the transformers.

The characteristics of the metal oxide varistor (MOV) model for the surge arresters are defined as:

$$\left\{\begin{array}{l}U=\mathrm{C}{I}^{\alpha }\\ r(i)={\displaystyle \frac{dU}{dI}}=\mathrm{C}\alpha I^{\alpha -1}\end{array}\right.$$

(7)

In the Equation (7), U and I are the voltage and current of the surge arrester. C is the material constant, and α is the nonlinearity coefficient. Typically, the value range of α is:0.02<α<0.1. Therefore, by transforming the Equation (7), the resistive characteristic of the surge arrester can be expressed as a function of the current flowing through it.

The resistive characteristic of the surge arrester is defined as:

$$r_{\mathrm{MOV}}(i)=C{\displaystyle \frac{\alpha }{i^{1-\alpha }}}$$

(8)

From the Equation (8), when the current through the surge arrester is small, the nonlinear resistance of the surge arrester exhibits a high-resistance state. In this case, the resistance r_MOV​ is large and can be considered negligible. When the voltage at the end of the surge arrester exceeds the reference voltage, the current i begins to increase, leading to a decrease in r_MOV​. This, in turn causes a further increase in the current through the surge arrester. During the energy absorption process, the surge arrester exhibits an instantaneous low-resistance characteristic.

The nonlinear impedance models of surge arresters at all locations within the system are calculated and incorporated into the CF model as shown in Fig.6.

Since faults within the valve hall are generally permanent faults, the converter station can only be shut down and locked. During the fault process, the voltage and current of the MMC valve exhibit transient impulse characteristics. Therefore, it is necessary to consider the field-circuit coupling characteristics of the MMC valve

4. Simulation Verification of MMC Overcurrent Calculation

Research manuscripts reporting large datasets that are deposited in a publicly available database should specify where the data have been deposited and provide the relevant accession numbers. If the accession numbers have not yet been obtained at the time of submission, please state that they will be provided during review. They must be provided prior to publication.

Based on the aforementioned discussion, a field-circuit coupling model has been integrated into the offshore wind power MMC-HVDC transmission system model, as shown in Figure 9[18,19,20].

As shown in the Figure9, a ±500 kV, 2000 MW offshore wind power MMC-HVDC transmission system model incorporating field-circuit coupled models has been established. This integration allows for a more comprehensive analysis of the system behavior under various operating conditions, particularly during transient events.

The main parameters of ±500 kV, 2000 MW offshore wind power MMC-HVDC transmission system are shown in Table 1.

Concurrently, an electric field calculation model for the MMC valve has been developed. The voltages at critical locations within the system serve as input conditions for the electric field model calculations.

The voltage-current (V-I) characteristics model of the MOV at these locations is also integrated into the field-circuit coupled models. The electric field strength, stray parameter values calculated by the electric field model, and the instantaneous system voltages are then input into the corresponding field-circuit coupled model at each location.

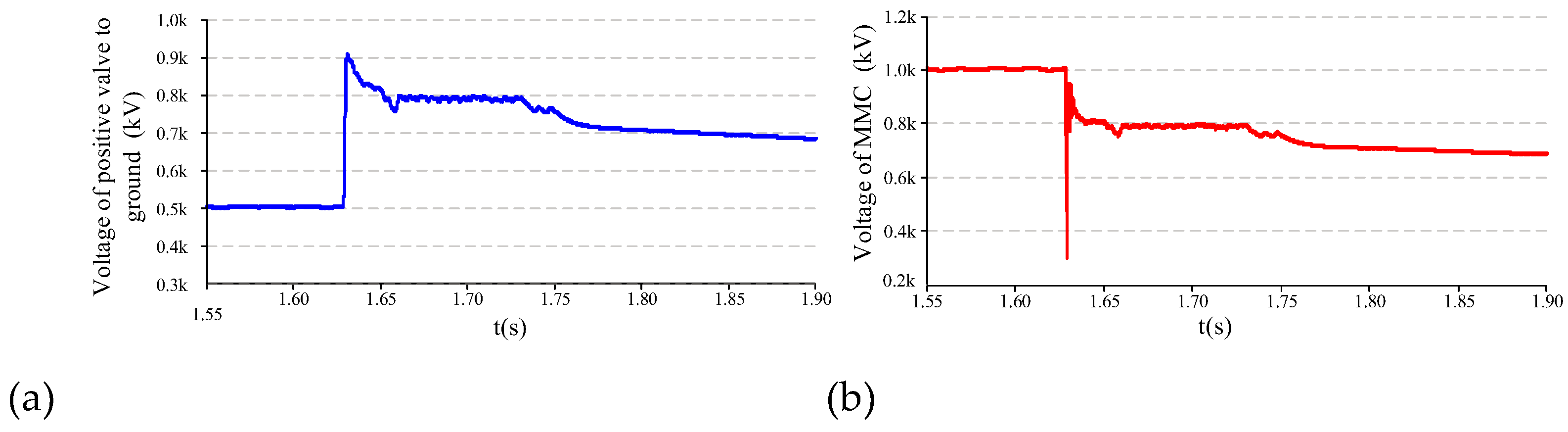
When a valve-bottom ground fault occurs at the offshore station, the voltage waveform at the MMC and the ground voltage waveform at the terminal of the positive valve tower are shown in Figure 10.

As shown in Figure 10, after a ground fault occurs at the valve bottom of the system, the control and protection system detects the fault and performs a lockout and shutdown protection action. During the fault process, severe overvoltage is generated in the system. The voltage values are then input into the electric field calculation model of the MMC valve.

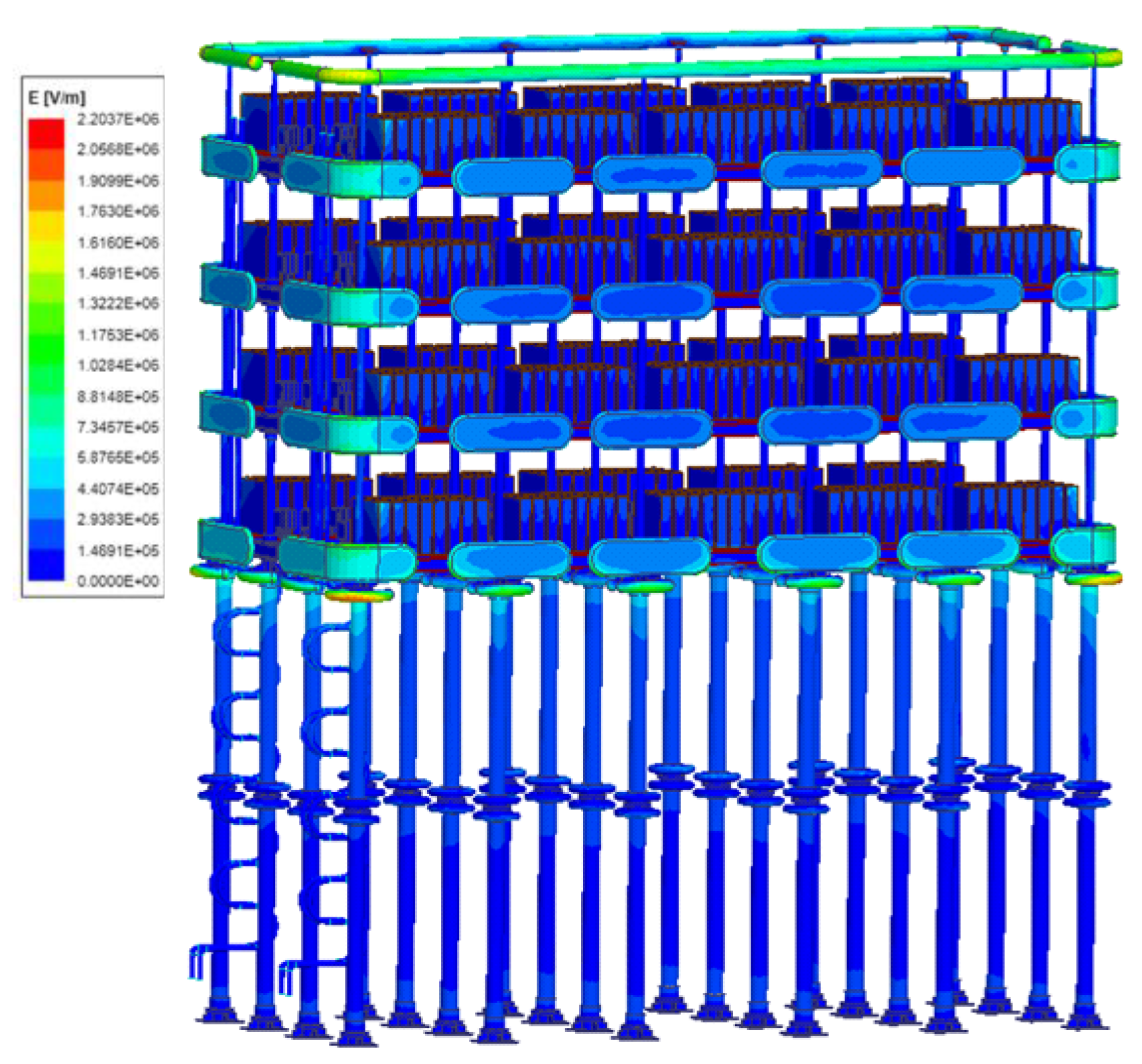
When a severe fault occurs within the offshore converter station, the electric field distribution when the converter valve voltage reaches its maximum increase is shown in Figure 11.

As shown in Figure 11, during a fault in the system, the electric field distribution characteristics and stray capacitance under the fault impulse excitation are calculated.

Through the electric field calculation, the maximum electric field strength at the end of the MMC valve reaches 2.2 kV/mm under the voltage peak condition. The maximum electric field strength is lower than the air breakdown field strength of 3.0 kV/mm.

Therefore, the resistance R_g​ is infinite. By the electric field calculation, the ground capacitance at the end of the converter valve is approximately 108 pF.

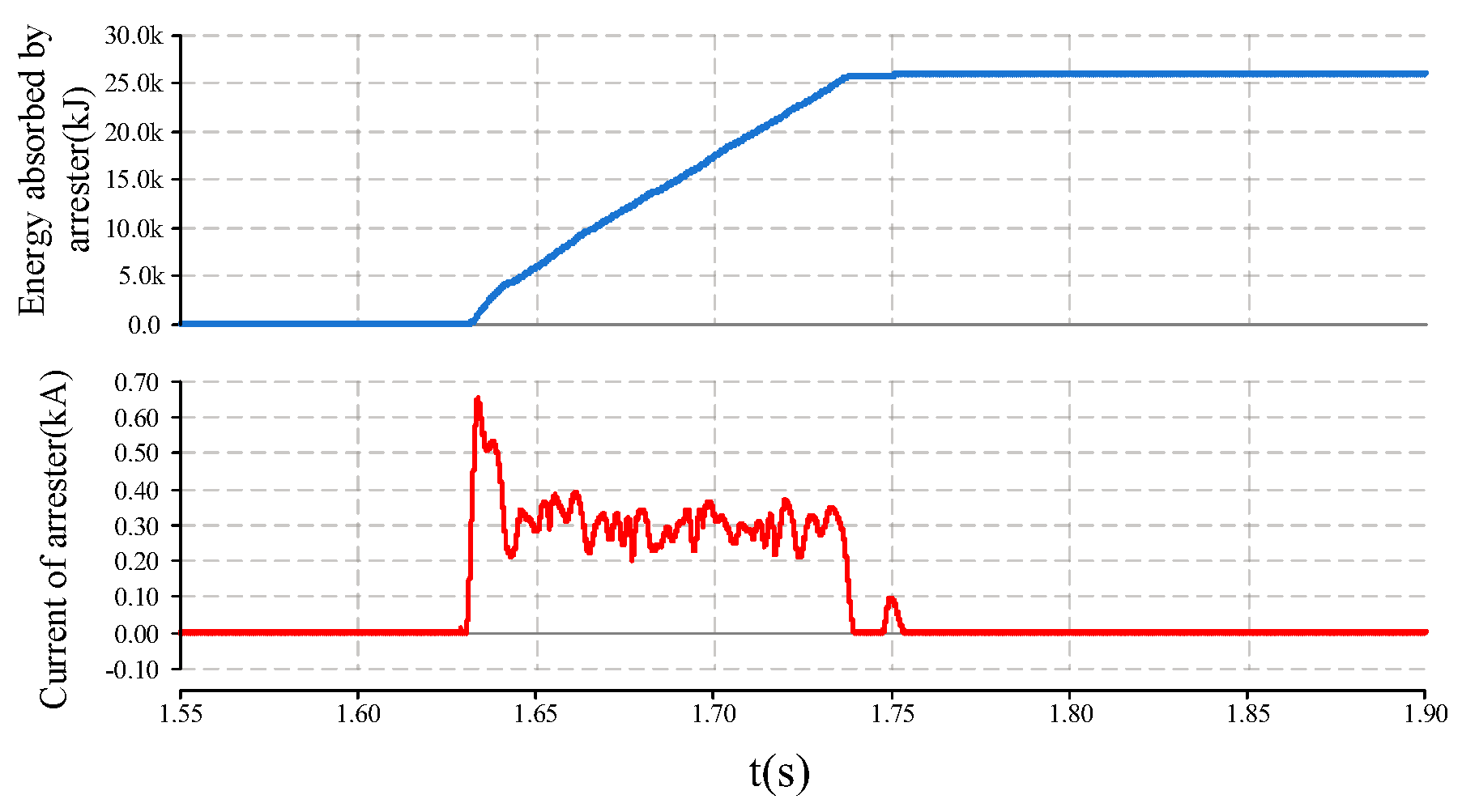
The calculated stray capacitance and the results of the electric field analysis are input in real-time into the offshore MMC-HVDC system model as shown in Figure 9. The MOV arrester current and absorbed energy in the CF model are shown in the Figure 12.

As shown as in Figure 12, the results of the field-circuit coupled model demonstrate that the occurrence of significant overvoltage during the fault event leads to the activation of the surge arrester.

As stated in the Equation (3), the passage of large currents through the metal oxide varistor (MOV) results in the manifestation of a low-impedance characteristic of the MOV within the CF model as shown in Figure 6.This low-impedance state allows the MOV to effectively divert fault currents, thereby protecting the system from overvoltage damage.

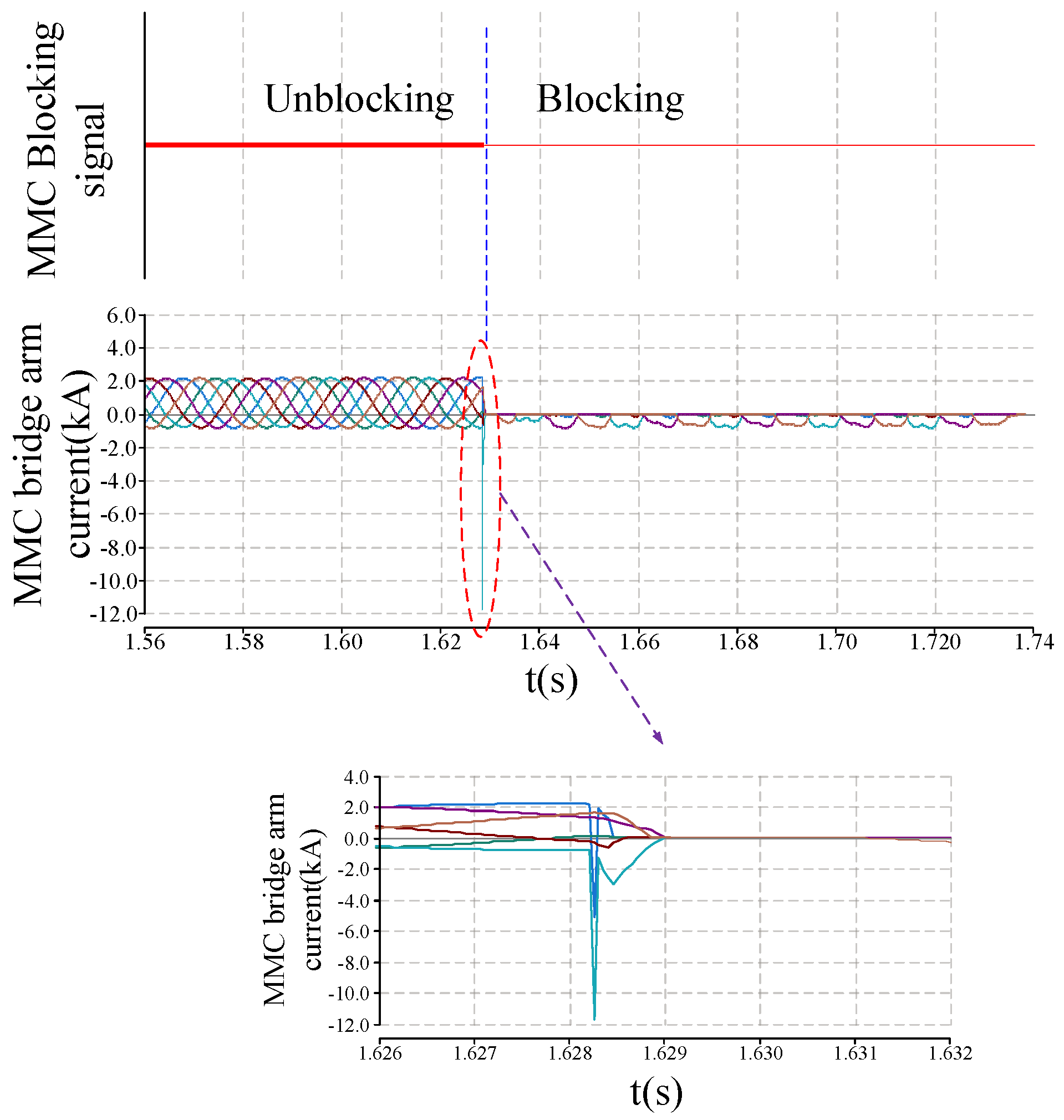
The current of the MMC valve during the fault, analyzed using the field-circuit coupled model of the ±500kV MMC-HVDC transmission system, is shown in the Figure 13.

As shown in Figure 13, the establishment of the CF model in the system fault analysis takes into account the stray capacitance of the MMC valve.

The electric field and MOV nonlinear parameters are also applied to the establishment of the CF model. The current through the MMC valve becomes distorted before the system is locked out, with its peak exceeding 6000A. This may lead to the damage of IGBT.

Based on the calculation results from Figure 13, it is evident that the preliminary system parameters, including overcurrent protection strategy and settings, might not be reasonable. The initial design parameters of the MMC valve structure might also be unreasonable. Therefore, it is necessary to optimize the system design in response to the distortion of the MMC valve current.

5. Overcurrent Suppression Strategy and Verification

Research manuscripts reporting large datasets that are deposited in a publicly available database should specify where the data have been deposited and provide the relevant accession numbers. If the accession numbers have not yet been obtained at the time of submission, please state that they will be provided during review. They must be provided prior to publication.

Based on the development process of overcurrent in the MMC valve shown in Figure3, the magnitude of the overcurrent in the MMC valve is primarily determined by the fault current during the two stages S1​ and S2​​. The rate of current rise and the delay in protection action determine the peak value Ipeak​. Due to hardware limitations, optimization of the valve control link delay (t2~t3​) is limited.

As shown in Figure 3, the overcurrent suppression can theoretically be approached from two directions:

1) Reducing the rate of current rise during the fault, keeping I_peak​ within a reasonable range during the time interval when the control and protection system is enabled. To achieve this, it is necessary to optimize the loop parameters or structure of the MMC-HVDC system to improve the fault loop characteristics.

2) Enhancing the sensitivity of overcurrent protection. Reducing the duration of time interval S1​ and enabling rapid activation of overcurrent protection. Effective suppression of Ipeak​ can be achieved.

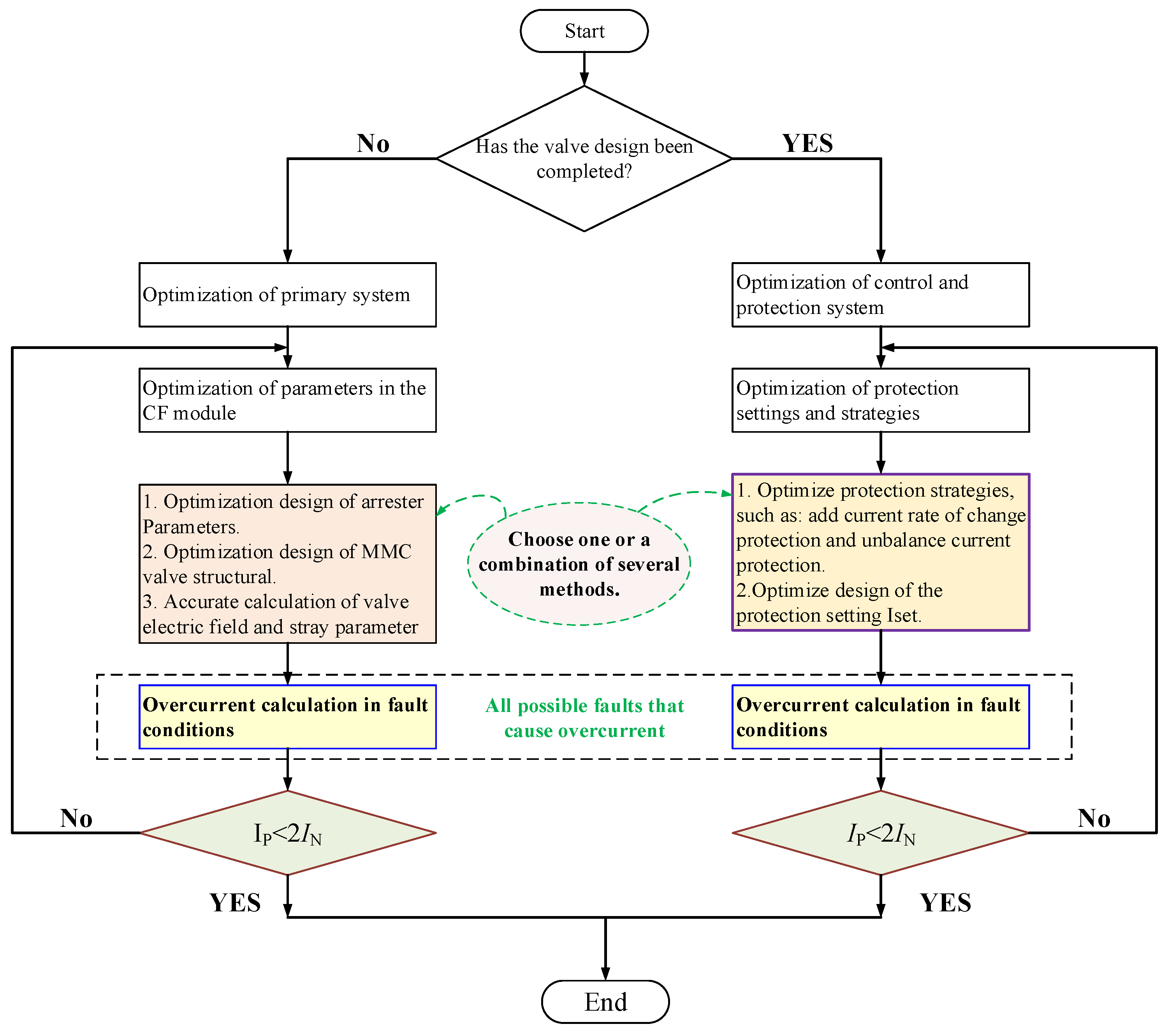
In summary, the suppression strategy for overcurrent of MMC valve is shown in Figure 14.

As shown in Figure 14, once the MMC valve design is finalized, the only options for overcurrent suppression are to modify the fault detection time: t1~ t2​ and the setting Iset​.

More sensitive protection methods, such as rate-of-rise protection and unbalance current protection, can be employed to reduce t₂​. Alternatively, without changing the original protection strategy, the setting I_set​ can be optimized within a reasonable range, such as by adopting a two-stage overcurrent protection strategy for the bridge arm.

If the offshore wind power MMC-HVDC transmission system is still in the design phase and has not yet been finalized.

The optimal solution for suppressing overcurrent is to optimize the parameters of the primary system.

By employing the field-circuit coupled analysis method demonstrated in this paper, a comprehensive investigation of overcurrent in MMC valves can be conducted.

This approach enables the identification of factors that lead to high overcurrent levels in advance and, based on these findings, proposes effective strategies for overcurrent suppression.

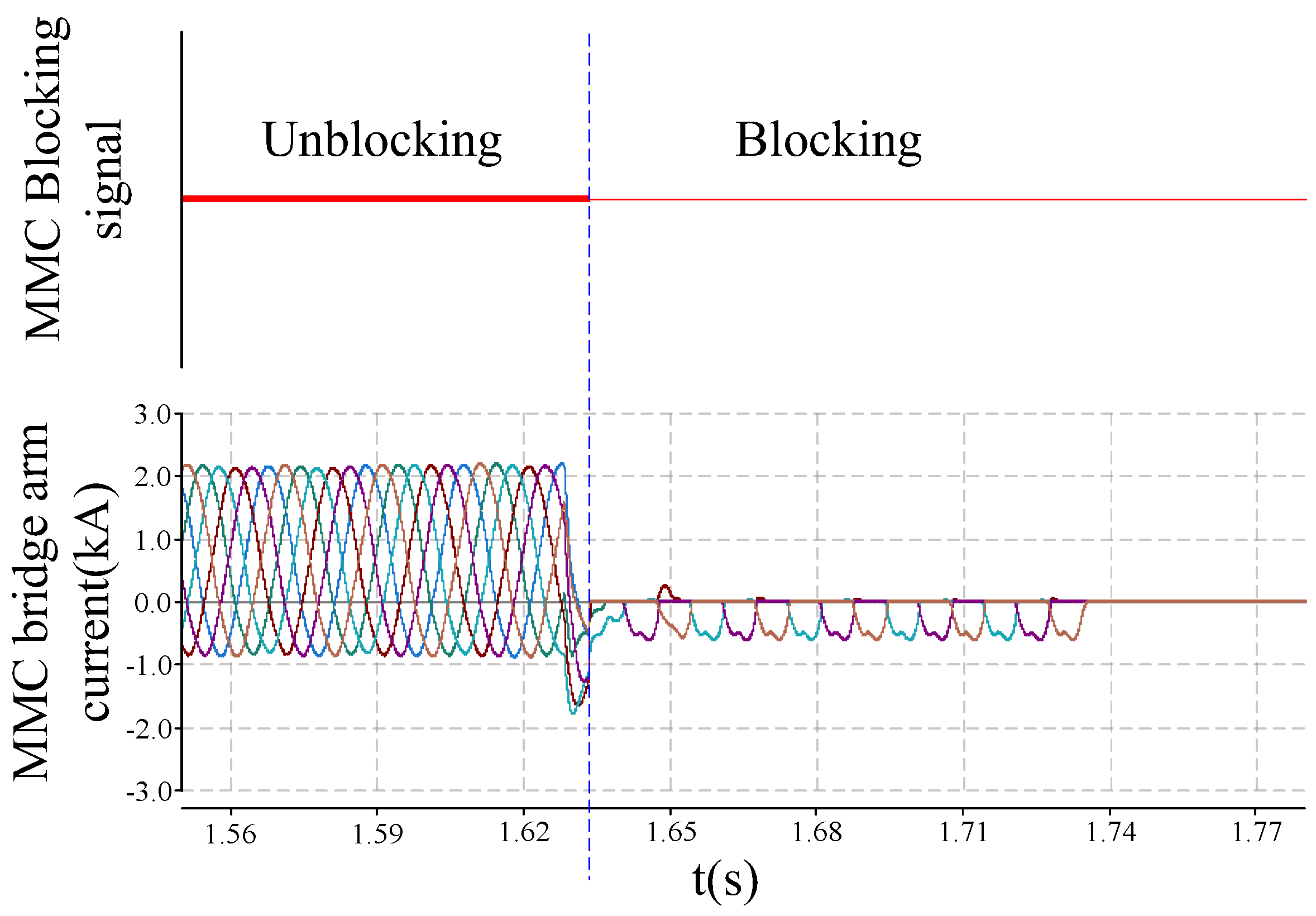
The ±500 kV MMC-HVDC system shown in Figure 9 is still in the validation process. Drawing on the simulation waveforms from Figure 11, 12, and 13, the arrester scheme in the CF model is optimized by reasonably increasing the reference voltage of the arresters.

After re-evaluating and verifying the insulation coordination design, the MMC valve current under the same fault condition shown in Figure 9 is indicated in Figure 15.

As shown in Figure 15, the CF model within the system has been optimized through a refined design approach.

Consequently, the system simulation no longer exhibits any additional discharge paths. During the fault process, the current through the MMC valve does not display any spikes. The peak current of the converter valve is approximately 2800 A, which is less than 2IN​(4000A). Thus, the MMC valve current complies with the safety requirements for system operation during the fault process.

6. Conclusions

A field-circuit coupling analysis method for overcurrent research in MMC valve is proposed in this paper. The method integrated the electric field characteristics of MMC valve with the analysis of MMC-HVDC system. Given the limited overcurrent capability of semiconductor devices in MMC valves and the significant impact of overcurrent phenomena on the safe operation and system parameter design, accurate calculation of overcurrent in MMC valves is essential and complex.

Firstly, the method investigates the characteristics and influencing factors of fault currents in valves. Control and protection strategies, protection settings, and post-fault circuit characteristics all contribute to variations in fault currents.

Additionally, transient parameter changes in nonlinear components, stray parameters of valve, and electric field distribution can influence the fault loop under transient conditions. Subsequently, a field-circuit coupling model and an electric field calculation model for valves were established, with the system instantaneous voltage serving as the input for electric field calculation and surge arrester transients. The electric field strength and capacitance values obtained from the electric field calculation were used as inputs for C_g​ and R_g​ in the field-circuit coupling model. Through this model, the operational circuit characteristics of the system were combined with the electric field characteristics of the valve, enabling precise calculation of overcurrent and accurate design of suppression strategies. Finally, the method proposed in this paper was applied to the ±500 kV offshore MMC-HVDC system for overcurrent analysis and suppression strategy design.

Simulation experiments were conducted, and the numerical results demonstrate the effectiveness and correctness of the method presented in this paper. This research provides a solid basis for the accurate calculation of overcurrent protection strategies and settings and for improving the utilization rate of power devices in offshore MMC-HVDC valve.