The Collatz Infinite Tree: Inclusion of Natural Numbers and Nonexistence of Nontrivial Cycles

1. Introduction

The Collatz Conjecture, also known as the $3x+1$ problem, was proposed by Lothar Collatz in the late 1930s and subsequently gained broader attention through Martin Gardner’s popular articles in the 1970s [1]. Formally, for any positive integer n, one applies the iteration

$$f\left(n\right)=\left\{\begin{array}{cc}\frac{n}{2},\hfill & \mathrm{if}n\mathrm{is}\mathrm{even},\hfill \\ 3n+1,\hfill & \mathrm{if}n\mathrm{is}\mathrm{odd},\hfill \end{array}\right.$$

(1)

and repeats the process on the resulting integer. The conjecture asserts that no matter what positive integer is chosen initially, the resulting sequence will inevitably reach the cycle $1\to 4\to 2\to 1$. Despite sustained efforts, the conjecture remains an open problem in mathematics. However, various attempts have been made on partial fronts: extensive empirical testing has failed to produce a counterexample, and the conjecture has been verified for all n up to $2^{100000}-1$ [2]. Moreover, no other cycle besides the known trivial loop $1\to 4\to 2\to 1$ has ever been discovered, suggesting the conjecture’s validity across vast numerical ranges.

In this work, the Collatz Conjecture is analyzed by constructing and examining a Collatz tree via inverse transformations, building upon the bottom-up approach employed in both Abascal’s analysis [3] and the efficient algorithmic methodologies introduced in recent studies [4]. Beginning with the integer 1, each node in the tree is repeatedly doubled to generate successors. Whenever the current node n is an even integer for which $(n-1)$ is divisible by 3, a new branch rooted at $\frac{n-1}{3}$ is introduced. This mechanism ensures the inclusion of all relevant preimages under the Collatz iteration in the tree, reflecting structural patterns observed in computational studies. Close examination of these patterns establishes two key results. First, no cycle exists apart from the familiar loop $1\to 2\to 4\to 1$. Second, leveraging insights from the tree structure, all natural numbers up to any given bound N appear within the Collatz tree.

1.1. Related Works

The literature on the Collatz Conjecture spans diverse methodologies and theoretical perspectives. A bottom-up reconstruction technique systematically tracks backward from $n=1$ to generate inverse Collatz paths for any positive integer, revealing key arithmetic structures in these inverse sequences [3]. Similarly, Getachew and Assefa proposed a novel algorithm leveraging structural patterns in the Collatz tree to optimize stopping time calculations [4]. Their work achieved a 28% computational efficiency improvement compared to prior methods and introduced scalable techniques for verifying the conjecture across extremely large numeric ranges, reinforcing the value of structural insights in tackling the problem.

The conjecture has also been examined as a concurrent program built around "convergence stairs," with each stair containing numbers that reach $\{1,2,4\}$ in precisely j steps. A critical challenge in this framework lies in proving that the union of all stairs is exhaustive and that every element in a stair backtracks to a prior stair [5]. Generalizations of the $3n+1$ iteration to $3n+3^k$ have further explored convergence properties across various initial values, recovering the classical conjecture as a special case for $k=0$ [6].

From an operator-theoretic standpoint, the conjecture has been linked to irreducibility in certain $C^{*}$-algebras, bridging discrete iteration with continuous operator analysis [7]. In parallel, the dynamics of the iteration have been partitioned into "direction phases," demonstrating a correspondence with a binary shift map that underscores deep ergodic properties [8].

Statistical examinations of stopping times have also provided additional insights. Estimates suggest that infinite trajectories are exceedingly unlikely—on the order of locating a single atom in the universe—and show a proportional relationship between total stopping time and $log\left(N\right)$ [9]. Computational advances have further propelled empirical bounds, verifying the conjecture for $2^{100000}-1$ using specialized bitwise algorithms capable of handling numbers of unprecedented size [2]. These include optimizations using binary operations, reverse transformations, and efficient handling of redundant computations [4].

Lastly, corollaries and novel algorithms for visualizing Collatz sequences and identifying potential loops have been proposed, shedding light on structural patterns that, if proven universally, could settle the conjecture [10]. Taken together, these contributions underline the breadth of mathematical disciplines—ranging from number theory and algebra to high-performance computing—grappling with one of the field’s most tenacious unsolved problems.

2. Methodology

To investigate the inclusion of all natural numbers and the existence of cycles, the Collatz Conjecture is analyzed using a bottom-up approach. This approach simplifies the problem by focusing on inverse transformations of the Collatz equation 1. The methodology involves finding the inverse operations of the equation, constructing the Collatz infinite tree, and analyzing the tree’s structural properties. These steps provide a systematic framework to substantiate the proof process in subsequent sections.

2.1. Inverse Transformation and Tree Construction

The Collatz tree can be constructed using inverse transformations, starting with the integer 1 as the root of the tree. The inverse transformations account for both operations defined in Equation 1: $n\mapsto {\displaystyle \frac{n}{2}}$ for even numbers and $n\mapsto 3n+1$ for odd numbers.

• The inverse of the ${\displaystyle \frac{n}{2}}$ operation can be generalized as $2n$ for all natural numbers n. This step accounts for the fact that the ${\displaystyle \frac{n}{2}}$ operation in Equation 1 yields both even and odd integers.

  -

  For example, in Equation 1, if $n=10$, the next number in the sequence is 5 and if $n=8$, the next number in the sequence is 4. This demonstrates that the ${\displaystyle \frac{n}{2}}$ operation can yield both odd and even numbers.

  -

  In the inverse transformation, both even and odd numbers must be multiplied by 2 to account for this behavior. For instance, if $n=5$, the next number in the sequence under the inverse transformation is 10. Likewise, if $n=4$, the next number is 8.

• The inverse of the $3n+1$ operation can be expressed as ${\displaystyle \frac{n-1}{3}}$ for all even integers n where $(n-1)$ is divisible by 3.

  -

  For example, 5 maps to 16 under the $3n+1$ operation (since $3\left(5\right)+1=16$), and conversely, 16 maps to 5 using ${\displaystyle \frac{16-1}{3}}$.

Combining these, the inverse Collatz transformation can be generalized as:

$$f^{-1}\left(n\right)=\left\{\begin{array}{cc}2n,\hfill & n\in \mathbb{N},\hfill \\ {\displaystyle \frac{n-1}{3}},\hfill & n\mathrm{even},(n-1)mod3=0\hfill \end{array}\right.$$

(2)

The inverse Collatz transformation formula allows the construction of an infinite tree starting from the root node containing the number 1. Each successive node contains a number obtained by multiplying its predecessor by 2. Whenever a node contains an even number that satisfies the condition $(N-1)mod3=0$, a new branch is created, starting with the number ${\displaystyle \frac{N-1}{3}}$, and the process continues recursively. Figure 1 illustrates a partial Collatz infinite tree constructed using this method. Tracing any number in the tree backward to the root node 1 produces a sequence identical to the sequence generated by the Collatz formula in Equation 1. Although only a finite section of the tree is displayed, each branch extends indefinitely, making the complete Collatz tree infinite and capable of representing all natural numbers, as demonstrated in the proof provided in later sections.

2.2. Observed Patterns

The Collatz tree, constructed using inverse transformations, reveals several distinct structural features that form the basis for understanding its properties. These patterns, which were explained in earlier computational studies [4], are now solidified through rigorous proofs, supporting the analysis presented in subsequent sections.

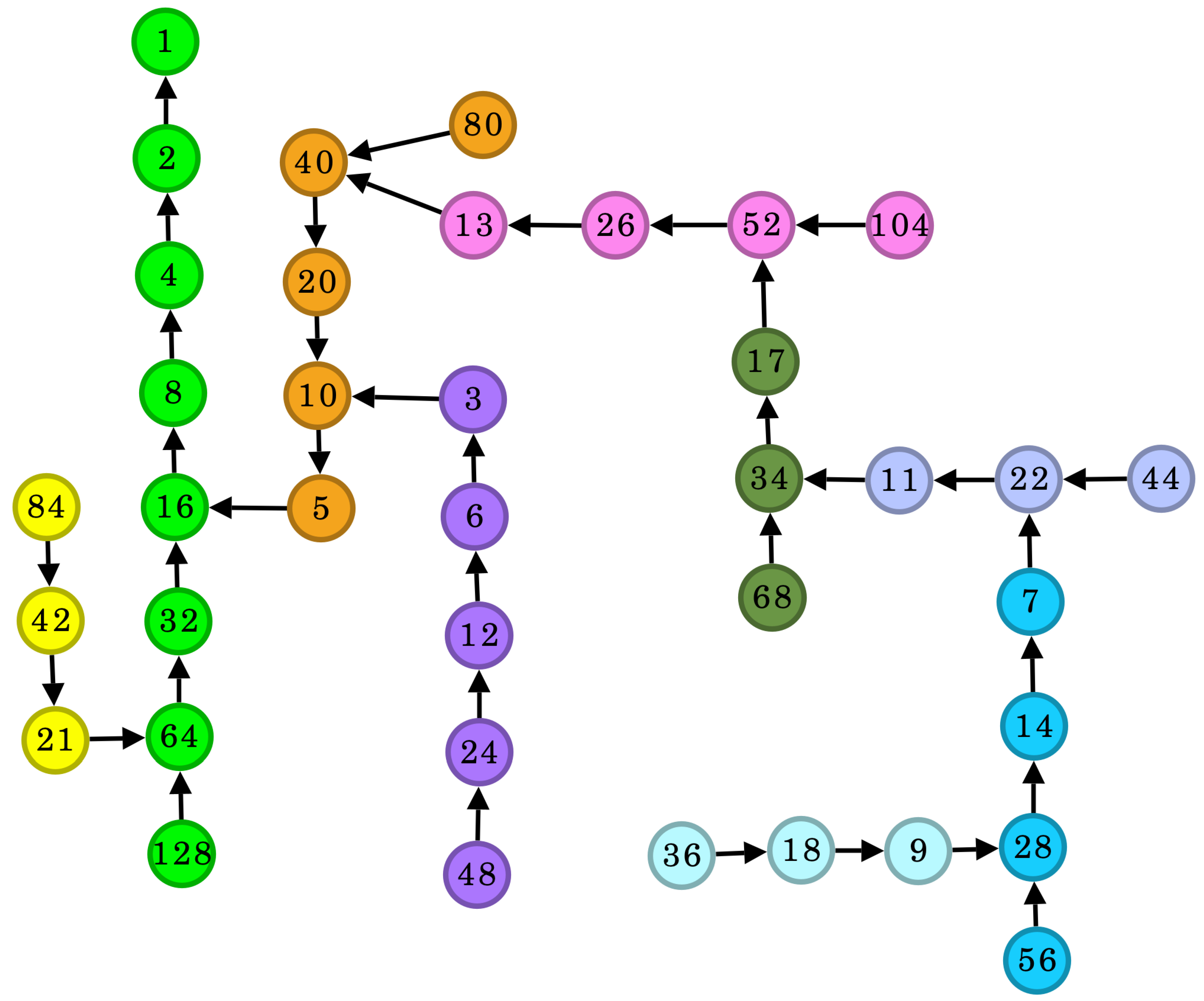
• Backbone of the Tree: The sequence starting with the integer 1 serves as the backbone of the Collatz tree. This backbone corresponds to the powers of 2,

  $$1\to 2\to 4\to 8\to \cdots$$

  which forms the central structure from which all branches emerge.
• Branches: All other sequences that do not start with 1 are referred to as branches. These branches either originate directly from the backbone or from other branches, as illustrated in Figure 1. Each branch begins with an odd natural number of the form $2n+1$, where $n\ge 0$, and subsequent numbers are generated by repeatedly doubling the predecessor. This represents the inverse of the ${\displaystyle \frac{n}{2}}$ operation in Equation 1, producing an infinite sequence of even numbers except for the initial odd number $2n+1$. Thus, the tree is inherently infinite.
• General Formula for Branches: The backbone, branches, and their corresponding sequences can be compactly expressed using the following formula:

  $$a_{n,m}=(2n+1)·2^{m}n,m\in \mathbb{W},$$

  (3)

  where n identifies the branch, and m determines the even numbers within that branch.
• Branch-Creating Numbers: The even numbers that give rise to additional branches can be expressed in the form:

  $$f\left(k\right)=6k+10,k\in \mathbb{W}.$$

  (4)
  For example, when $k=0$, $f\left(0\right)=10$. Since $(10-1)mod3=0$, this corresponds to a branch originating at:

  $${\displaystyle \frac{10-1}{3}}=3.$$
  The derivation of Equation 4 is given in later sections.
• Special Branches: Certain branches, such as those starting with odd multiples of 3, do not produce additional branches. This occurs because these branches lack any numbers of the form $f\left(k\right)=6k+10$. Assuming that such a number exists in these branches leads to contradictions. For instance, assume there exists a number in these branches that satisfies $f\left(k\right)=6k+10$. Hence,

  $$\begin{array}{cc}\hfill 6k+10& =(2n+1)·2^m\Rightarrow \hfill \\ \hfill 6k& =(2n+1)·2^m-10\hfill \end{array}$$
  Simplifying further:

  $$k={\displaystyle \frac{(2n+1)·2^m}{6}}-{\displaystyle \frac{10}{6}}={\displaystyle \frac{(2n+1)·2^{m-1}}{3}}-{\displaystyle \frac{5}{3}}$$
  Now, if $2n+1$ is an odd multiple of 3 (e.g., $3,9,15,21,\cdots$), then ${\displaystyle \frac{2n+1}{3}}$ is a natural number. Let ${\displaystyle \frac{2n+1}{3}}=d$, where $d\in \mathbb{N}$. Substituting, we have:

  $$k=d·2^{m-1}-{\displaystyle \frac{5}{3}}$$
  Since ${\displaystyle \frac{-5}{3}}$ is not an integer, k cannot be a whole number. Thus, there is no $k\in \mathbb{W}$ for which $6k+10$ belongs to a branch starting with an odd multiple of 3. Therefore, these branches terminate and do not lead to further subbranches.

These observations provide a solid foundation for the subsequent proofs, which establish that the only cycle in the Collatz tree is the trivial loop $1\to 2\to 4\to 1$ and that every natural number up to any given bound appears in some branch of the tree.

3. Inclusion of All Natural Numbers in the Collatz Tree

3.1. Existence of All Natural Numbers in the Collatz Tree Branches

Consider some of the branches of the Collatz infinite tree as shown below:

$$\begin{array}{ccccccccc}\hfill 1& ,\hfill & 2\hfill & ,\hfill & 4\hfill & ,\hfill & 8\hfill & ,\hfill & \cdots ,2^m,\cdots \hfill \\ \hfill 3& ,\hfill & 6\hfill & ,\hfill & 12\hfill & ,\hfill & 24\hfill & ,\hfill & \cdots ,3·2^m,\cdots \hfill \\ \hfill 5& ,\hfill & 10\hfill & ,\hfill & 20\hfill & ,\hfill & 40\hfill & ,\hfill & \cdots ,5·2^m,\cdots \hfill \\ \hfill 7& ,\hfill & 14\hfill & ,\hfill & 28\hfill & ,\hfill & 56\hfill & ,\hfill & \cdots ,7·2^m,\cdots \hfill \\ \hfill 9& ,\hfill & 18\hfill & ,\hfill & 36\hfill & ,\hfill & 72\hfill & ,\hfill & \cdots ,9·2^m,\cdots \hfill \\ \hfill 11& ,\hfill & 22\hfill & ,\hfill & 44\hfill & ,\hfill & 88\hfill & ,\hfill & \cdots ,11·2^m,\cdots \hfill \end{array}$$

(5)

Finding all natural numbers less than or equal to a given natural number N involves considering each branch of the infinite tree and selecting numbers and branches that satisfy:

$$(2n+1)·2^m\le N,n,m\in \mathbb{W},N\in \mathbb{N}$$

Step 1: Determining the range of m:

$$2^m\le {\displaystyle \frac{N}{2n+1}}$$

taking the base-2 logarithm of both sides gives:

$${log}_2\left(2^m\right)\le {log}_2\left({\displaystyle \frac{N}{2n+1}}\right)$$

simplifying further:

$$m\le {log}_2\left({\displaystyle \frac{N}{2n+1}}\right)$$

Since m must be a whole number, the floor is taken:

$$m\le ⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋$$

Thus, for each odd number $2n+1$, the range of m is:

$$0\le m\le ⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋$$

Step 2: Determining the range of n: Including branches that start with a number greater than N is unnecessary, as the goal is to show the inclusion of all natural numbers less than or equal to N. Therefore,

$$2n+1\le N\Rightarrow n\le {\displaystyle \frac{N-1}{2}}$$

and since n must be a whole number, the floor is taken:

$$n\le ⌊{\displaystyle \frac{N-1}{2}}⌋$$

Thus, the range of n is:

$$0\le n\le ⌊{\displaystyle \frac{N-1}{2}}⌋$$

Hence, to include all natural numbers less than or equal to N, numbers are selected from some branches of the Collatz tree using the formula:

$$a_{n,m}=(2n+1)·2^m,0\le n\le ⌊{\displaystyle \frac{N-1}{2}}⌋,0\le m\le ⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋$$

(6)

where n determines the branch and m determines the sequence of numbers in the given branch.

Example 1: Equation 6 is demonstrated for $N=11$ as follows.

Step 1: Calculate the range of n

$$n_{\max }=⌊{\displaystyle \frac{11-1}{2}}⌋=5$$

This gives $n=0,1,2,3,4,5$, corresponding to odd multipliers $2n+1=1,3,5,7,9,11$.

Step 2: Calculate the range of m:

$\begin{array}{cccc}& \mathrm{For}n=0:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{1}}\right)\rfloor =3,0\le m\le 3,\mathrm{hence}{2}^m\mathrm{gives}1,2,4,8\hfill \\ & \mathrm{For}n=1:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{3}}\right)\rfloor =1,0\le m\le 1,\mathrm{hence}3·2^m\mathrm{gives}3,6\hfill \\ & \mathrm{For}n=2:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{5}}\right)\rfloor =1,0\le m\le 1,\mathrm{hence}5·2^m\mathrm{gives}5,10\hfill \\ & \mathrm{For}n=3:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{7}}\right)\rfloor =0,m=0,\mathrm{hence}7·2^m\mathrm{gives}7\hfill \\ & \mathrm{For}n=4:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{9}}\right)\rfloor =0,m=0,\mathrm{hence}9·2^m\mathrm{gives}9\hfill \\ & \mathrm{For}n=5:\hfill & \hfill m_{\max }& =\lfloor {log}_2\left({\displaystyle \frac{11}{11}}\right)\rfloor =0,m=0,\mathrm{hence}11·2^m\mathrm{gives}11\hfill \end{array}$

The union of all values gives the set $\{1,2,4,8,3,6,5,10,7,9,11\}$ which is exactly the set of numbers from 1 to 11.

To generalize the inclusion of all natural numbers up to a given N, a slightly different approach is adopted: computing the sum of numbers in Equation 6 and comparing this with the sum of all natural numbers less than or equal to N. Let $f\left(N\right)$ denote this sum. Hence,

$$f\left(N\right)=\sum _{n=0}^{⌊{\displaystyle \frac{N-1}{2}}⌋}\sum _{m=0}^{⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋}\left((2n+1)·2^m\right)$$

(7)

where the inner summation adds the numbers within a specific branch, and the outer summation aggregates the results across all branches up to N. Expanding the outer summation gives:

$$\begin{array}{cc}\hfill f\left(N\right)& =\sum _{m=0}^{⌊{log}_2\left(N\right)⌋}{2}^m+\sum _{m=0}^{⌊{log}_2\left({\displaystyle \frac{N}{3}}\right)⌋}3·2^m+\sum _{m=0}^{⌊{log}_2\left({\displaystyle \frac{N}{5}}\right)⌋}5·2^m\hfill \\ \hfill & +\cdots +\sum _{m=0}^{⌊{log}_2\left({\displaystyle \frac{N}{N}}\right)⌋}N·2^m\hfill \end{array}$$

(8)

Note that the summation of powers of 2 can be expressed using the following formula:

$$\sum _{n=0}^k{2}^n=2^{k+1}-1$$

(9)

Hence, Equation 8 can be simplified as:

$$\begin{array}{cc}\hfill f\left(N\right)=& \left(2^{⌊{log}_2\left(N\right)⌋+1}-1\right)+3·\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{3}}\right)⌋+1}-1\right)\hfill \\ \hfill & +5·\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{5}}\right)⌋+1}-1\right)+\cdots \hfill \\ \hfill & +N·\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{N}}\right)⌋+1}-1\right).\hfill \end{array}$$

(10)

This can be rewritten in a compact summation form as:

$$\begin{array}{cc}\hfill f\left(N\right)& =\sum _{n=0}^{⌊{\displaystyle \frac{N-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋+1}-1\right),\hfill \\ \hfill & n\in \mathbb{W},N\in \mathbb{N}\hfill \end{array}$$

(11)

This formula aggregates the contributions from each branch, ensuring that the numbers sum up to the total of all natural numbers up to N.

Example 2: Equation 11 is demonstrated for $N=9$ as follows:

Step 1: Determine the upper limit:

$$⌊{\displaystyle \frac{9-1}{2}}⌋=⌊{\displaystyle \frac{8}{2}}⌋=4$$

Step 2: Substitute the upper limit:

$$f\left(9\right)=\sum _{n=0}^4(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{2n+1}}\right)⌋+1}-1\right)$$

Step 3: Expand the summation:

$$\begin{array}{cc}\hfill f\left(9\right)& =\left(1\right)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{1}}\right)⌋+1}-1\right)+\left(3\right)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{3}}\right)⌋+1}-1\right)\hfill \\ & +\left(5\right)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{5}}\right)⌋+1}-1\right)+\left(7\right)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{7}}\right)⌋+1}-1\right)\hfill \\ & +\left(9\right)\left(2^{⌊{log}_2\left({\displaystyle \frac{9}{9}}\right)⌋+1}-1\right)\hfill \\ & =\left(1\right)\left(2^4-1\right)+\left(3\right)\left(2^2-1\right)+\left(5\right)\left(2^1-1\right)\hfill \\ & +\left(7\right)\left(2^1-1\right)+\left(9\right)\left(2^1-1\right)\hfill \\ & =\left(1\right)·15+\left(3\right)·3+\left(5\right)·1+\left(7\right)·1+\left(9\right)·1\hfill \\ & =15+9+5+7+9\hfill \\ & =45\hfill \end{array}$$

The sum of the first 9 natural numbers is:

$$\sum _{i=1}^{9}i={\displaystyle \frac{9·(9+1)}{2}}=45$$

Thus, $f\left(9\right)$ matches the sum of natural numbers up to $N=9$.

3.2. Proof of the Formula Using Mathematical Induction

This subsection proves the formula given in Equation 11, i.e.

$$f\left(N\right)=\sum _{n=0}^{⌊{\displaystyle \frac{N-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋+1}-1\right),$$

is equivalent to the standard formula for the sum of natural numbers from 1 to N,

$$S\left(N\right)=\sum _{i=1}^{N}i={\displaystyle \frac{N·(N+1)}{2}}$$

(12)

for all N, using the method of mathematical induction.

Base Case:$N=1$.

For $N=1$, the upper limit is:

$$⌊{\displaystyle \frac{1-1}{2}}⌋=0$$

thus,

$$f\left(1\right)=\sum _{n=0}^0(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{1}{2n+1}}\right)⌋+1}-1\right)$$

for $n=0$, $2n+1=1$, and ${\displaystyle \frac{1}{1}}=1$, therefore,

$$f\left(1\right)=1·\left(2^{0+1}-1\right)=1·(2-1)=1$$

using Equation 12 for $N=1$:

$$S\left(1\right)={\displaystyle \frac{1·(1+1)}{2}}=1$$

Thus, the formula holds for $N=1$.

Inductive Step: Assume that the formula holds for $N=k$, hence,

$$\begin{array}{cc}\hfill f\left(k\right)& =\sum _{n=0}^{⌊{\displaystyle \frac{k-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{k}{2n+1}}\right)⌋+1}-1\right)\hfill \\ \hfill & ={\displaystyle \frac{k·(k+1)}{2}}=S\left(k\right)\hfill \end{array}$$

(13)

The next step is to prove that the formula holds for $N=k+1$, i.e.,

$$f(k+1)={\displaystyle \frac{(k+1)·(k+2)}{2}}$$

Step 1: Substitute $N=k+1$ in Equation 11

$$f(k+1)=\sum _{n=0}^{⌊{\displaystyle \frac{(k+1)-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{k+1}{2n+1}}\right)⌋+1}-1\right)$$

(14)

Step 2: Analyze the effect of transitioning from k to $k+1$

Case 1: Assume $k+1$ is odd, hence, k is even and $f(k+1)$ can be written as:

$$f(k+1)=f\left(k\right)+\mathrm{the}\mathrm{additional}\mathrm{term}\mathrm{for}k+1$$

$$\begin{array}{cc}\hfill f(k+1)& =\sum _{n=0}^{⌊{\displaystyle \frac{k-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{k+1}{2n+1}}\right)⌋+1}-1\right)\hfill \\ \hfill & +\sum _{n=⌊{\displaystyle \frac{(k+1)-1}{2}}⌋}^{⌊{\displaystyle \frac{(k+1)-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{k+1}{2n+1}}\right)⌋+1}-1\right)\hfill \end{array}$$

For the second term, note that:

$$⌊{\displaystyle \frac{(k+1)-1}{2}}⌋=⌊{\displaystyle \frac{k+1-1}{2}}⌋=⌊{\displaystyle \frac{k}{2}}⌋={\displaystyle \frac{k}{2}}(\sin \mathrm{ce}k\mathrm{is}\mathrm{even})$$

thus, the second summation simplifies to:

$$\begin{array}{cc}\hfill \mathrm{Sec}\mathrm{ond}\mathrm{summation}& =(2·{\displaystyle \frac{k}{2}}+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{k+1}{2·\left(\frac{k}{2}\right)+1}}\right)⌋+1}-1\right)\hfill \\ \hfill & =(k+1)\left(2^{⌊{log}_2\left(1\right)⌋+1}-1\right)\hfill \\ \hfill & =(k+1)(2-1)\hfill \\ \hfill & =(k+1)\hfill \end{array}$$

Note that the first summation is the same as Equation 13, hence, $f(k+1)$ becomes,

$$\begin{array}{cc}\hfill f(k+1)& ={\displaystyle \frac{k·(k+1)}{2}}+(k+1)\hfill \\ \hfill & =(k+1)\left({\displaystyle \frac{k}{2}}+1\right)\hfill \\ \hfill & =(k+1)\left({\displaystyle \frac{k+2}{2}}\right)\hfill \\ \hfill & ={\displaystyle \frac{(k+1)(k+2)}{2}}=S(k+1)\hfill \end{array}$$

Case 2: Assume $k+1$ is even, hence, k is odd.

$$⌊{\displaystyle \frac{(k+1)-1}{2}}⌋=⌊{\displaystyle \frac{k}{2}}⌋={\displaystyle \frac{k-1}{2}}.$$

hence, the upper limits for $f\left(k\right)$ and $f(k+1)$ are the same and $f(k+1)$ includes exactly the same terms as $f\left(k\right)$. Thus:

$$f\left(k\right)=f(k+1)=S(k+1)$$

this coincides with the example demonstrated for $N=9$. In both cases, the formula holds, and by the principle of mathematical induction:

$$\begin{array}{cc}\hfill f\left(N\right)& =\sum _{n=0}^{⌊{\displaystyle \frac{N-1}{2}}⌋}(2n+1)\left(2^{⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋+1}-1\right)\hfill \\ \hfill & ={\displaystyle \frac{N·(N+1)}{2}},\forall n\in \mathbb{W},\forall N\in \mathbb{N}\hfill \end{array}$$

(15)

The derived formula for $f\left(N\right)$ matches the formula for summing all natural numbers from 1 to N. By including only numbers less than or equal to N from each branch of the Collatz tree, it becomes evident that all natural numbers from 1 to N are included in the selected branches. If any natural number were excluded, the summation would not hold, confirming the completeness of the Collatz tree for all numbers up to N. This behavior generalizes to the entire Collatz tree as long as branches originate from each odd number.

The next step is to demonstrate the existence of points within the tree where these branches emerge. Establishing this confirms the existence of all required branches and the inclusion of all natural numbers in the Collatz tree.

3.3. Constructing a Subtree Containing All Natural Numbers up to N

Equation 4 is derived here by applying the operation $3n+1$ from the Collatz formula, as shown in Equation 1, to all odd numbers. Every odd number can be represented as $n=2k+1$ for $k\in \mathbb{W}$. Therefore,

$$3n+1=3(2k+1)+1=6k+4$$

Since $n=0$ corresponds to the backbone, the sequence is shifted by 6 to align it with the first branch-creating number, 10. Consequently, the general form becomes:

$$f\left(k\right)=6k+10,k\in \mathbb{W}$$

Note that $f\left(k\right)=6k+10$ is always even, as it can be expressed as:

$$6k+10=2(3k+5)=2m,m\in \mathbb{N}$$

Furthermore, ${\displaystyle \frac{f\left(k\right)-1}{3}}$ is always odd since,

$$\begin{array}{cc}\hfill {\displaystyle \frac{f\left(k\right)-1}{3}}& ={\displaystyle \frac{6k+10-1}{3}}={\displaystyle \frac{6k+9}{3}}=2k+3\hfill \\ & =2(k+1)+1=2m+1,m\in \mathbb{N}\hfill \end{array}$$

Hence,

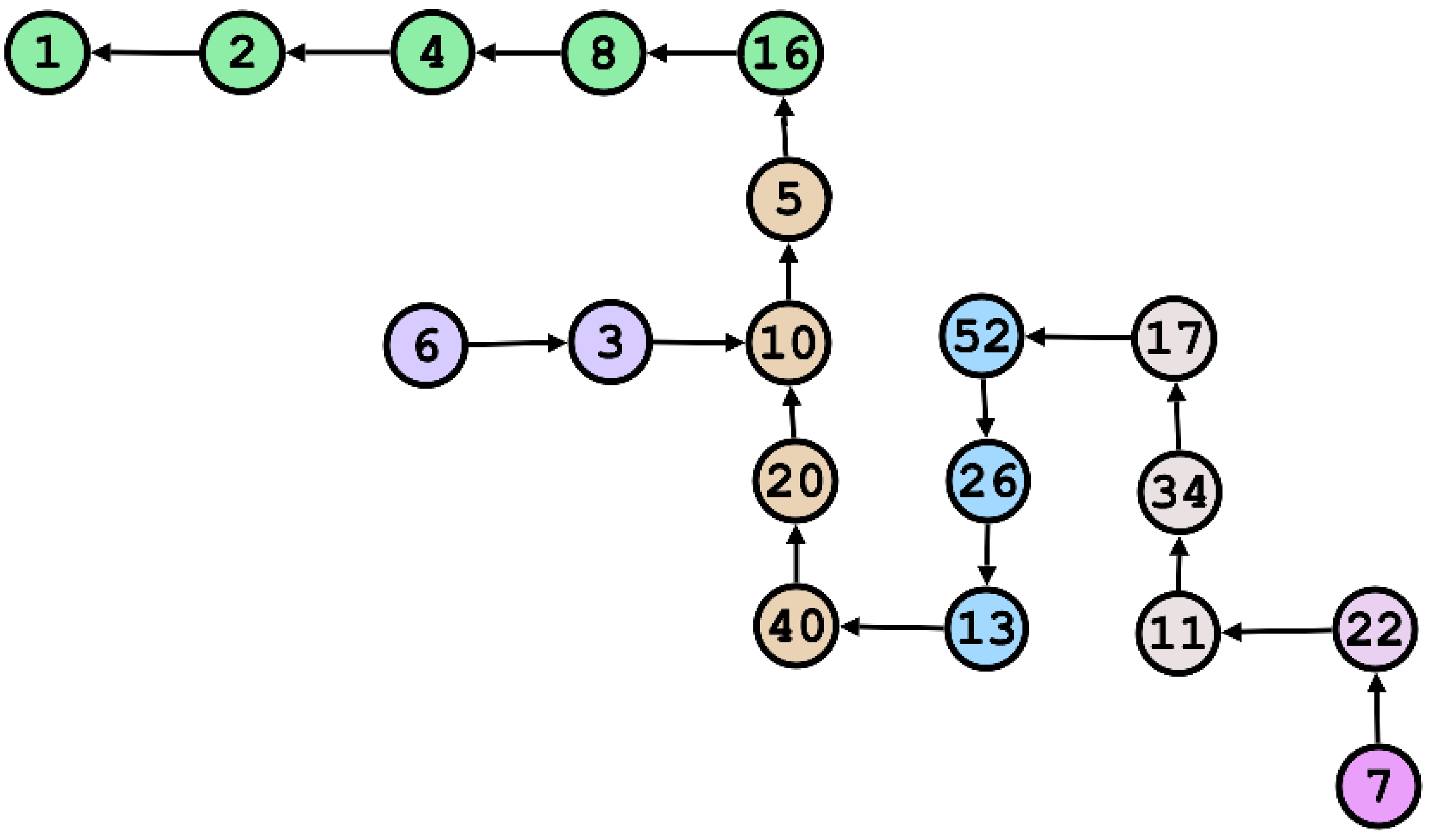
• The $3n+1$ operation in the Collatz formula generates all even numbers represented by $6k+10$, which correspond to the branching points in the Collatz tree.
• These branching points generate all odd numbers greater than or equal to 3 as roots. Including the backbone starting with 1, the Collatz tree encompasses all odd numbers.

The analysis thus far has determined how many branches are required to represent all natural numbers up to a given natural number N. The next step is to analyze the subtree that contains all natural numbers up to N. Previous examination considered each branch separately, but now the focus shifts to integrating these branches into a single subtree. This process involves identifying the branching points of each branch and connecting them to the backbone to form the complete subtree. This process is first demonstrated using an example and then generalized into an algorithm capable of constructing the subtree containing all natural numbers up to any given N.

Consider the subtree for $N=7$. From the previous analysis, all natural numbers are included in the branches starting with 1, 3, 5, and 7. For $N=7$, only the numbers in each branch that are less than or equal to 7 are required. The relevant branches are as follows:

$$\begin{array}{cc}\hfill 1& \to 2\to 4,\hfill \\ \hfill 3& \to 6,\hfill \\ \hfill 5& ,\hfill \\ \hfill 7\end{array}$$

To construct the subtree, the branching points for all branches, except the backbone starting at 1, must be determined. The branching point for a branch starting at an odd number n is calculated using the formula $3n+1$. For each branching point, it is necessary to ensure its incorporation into the tree structure. If a branching point does not already belong to the selected branches, the originating branch must be identified and extended to include the point.

• Branch starting at 3: The branching point is $3\left(3\right)+1=10$. Since 10 is not part of the selected branches, its origin must be determined. Using the formula for any branch as shown in Equation 3:

  $$a_{n,m}=(2n+1)·2^m$$
  For $a_{n,m}=10$, the calculation is:

  $$10=(2n+1)·2^m$$
  Dividing both sides by $2^m$:

  $$2n+1={\displaystyle \frac{10}{2^m}}$$
  The largest power of two dividing 10 is 2, so $2^m=2$. Substituting:

  $$2n+1={\displaystyle \frac{10}{2}}=5$$
  This identifies the odd number $2n+1=5$, meaning that 10 originates from the branch starting at 5. Since 5 is already part of the selected branches, it is extended to include 10.
• Branch starting at 5: The branching point is $3\left(5\right)+1=16$. For 16, $2^m=16$, so $16/16=1$. This indicates that 16 belongs to the backbone starting at 1. The backbone is extended to include 16.
• Branch starting at 7: The branching point is $3\left(7\right)+1=22$. For 22, $2^m=2$, so $22/2=11$. Since 11 is not part of the selected branches, a new branch starting at 11 is created and extended to include 22: $11\to 22$.
• Continuing the process for further branching points:

• The branching point for 11 is $3\left(11\right)+1=34$, which belongs to the branch $17\to 34$.
-
The branching point for 17 is $3\left(17\right)+1=52$, which belongs to $13\to 26\to 52$.
-
The branching point for 13 is $3\left(13\right)+1=40$, which belongs to $5\to 10\to 20\to 40$.

The process is stopped at this point since no further branching is required, and the complete subtree containing all natural numbers up to 7 can be constructed.

Figure 2 illustrates the final subtree of the Collatz tree for $N=7$.

Starting at any node and traversing to the root node containing 1, the sequence of numbers encountered along the path corresponds to the numbers generated by the Collatz formula described in Equation 1.

The procedure for constructing the Collatz tree containing all natural numbers up to N can now be generalized by dividing the process into two steps:

• The necessary branches are generated and iteratively extended using Algorithm 1.
• These branches are connected to form the complete Collatz subtree using Algorithm 2.

4. Nonexistence of Cycles Other Than the $1-2-4-1$ Cycle

In the Collatz tree, the sequence of numbers in any branch is described by the sequence $(2n+1)·2^m$, as shown in Equation 3. For any two numbers except the starting odd number within a branch, creating a cycle is impossible. This is because, when traversing backward in the tree, each even number in the branch is repeatedly halved until it reaches the branch’s root, hence, the path is only in one direction as there is no operation that makes a specific number to go back to some larger number. A cycle can only form if the root of the branch, which is an odd number, is included. In this scenario, applying the Collatz operation $3n+1$ to the odd root produces the even number that generates the current branch. This assumption can be generalized.

Every branch in the Collatz tree starts with an odd number of the form $2n+1$, where $n\in \mathbb{W}$. To investigate the existence of a cycle, the $3n+1$ operation is applied to the root of the branch, as the root is always an odd number. The resulting number is then checked to determine whether it appears somewhere in the branch. Hence,

$$3(2n+1)+1=(2n+1)·2^m$$

Now, divide both sides of the equation by $2n+1$ to isolate the power of 2:

$${\displaystyle \frac{3(2n+1)+1}{2n+1}}=2^m$$

Simplify the left-hand side:

$$3+{\displaystyle \frac{1}{2n+1}}=2^m$$

Solve for m:

$${log}_2\left(3+{\displaystyle \frac{1}{2n+1}}\right)={log}_2\left(2^m\right)$$

Using the logarithmic property ${log}_b\left(x^y\right)=y·{log}_b\left(x\right)$, the right-hand side simplifies to:

$${log}_2\left(3+{\displaystyle \frac{1}{2n+1}}\right)=m·{log}_2\left(2\right)$$

Since ${log}_2\left(2\right)=1$, this simplifies further to:

$$m={log}_2\left(3+{\displaystyle \frac{1}{2n+1}}\right),n\in \mathbb{W}.$$

(16)

Since m must be a whole number, the term $3+{\displaystyle \frac{1}{2n+1}}$ must be a power of 2. The behavior of ${\displaystyle \frac{1}{2n+1}}$ for $n\ge 0$ is analyzed by considering its limits:

• As $n\to \infty$, the term ${\displaystyle \frac{1}{2n+1}}$ approaches:

  $$\underset{n\to \infty }{lim}{\displaystyle \frac{1}{2n+1}}=0$$
• For $n=0$, the value is:

  $${\displaystyle \frac{1}{2·0+1}}=1$$

Thus, $0<{\displaystyle \frac{1}{2n+1}}\le 1$ for all $n\ge 0$. For $3+{\displaystyle \frac{1}{2n+1}}$ to be a power of 2, the only value of ${\displaystyle \frac{1}{2n+1}}$ that makes $3+{\displaystyle \frac{1}{2n+1}}$ an integer is ${\displaystyle \frac{1}{2n+1}}=1$, which occurs when $n=0$. Substituting $n=0$ gives:

$$3+{\displaystyle \frac{1}{2·0+1}}=3+1=4$$

Taking the base-2 logarithm:

$$m={log}_2\left(4\right)=2$$

The only valid cycle corresponds to the branch where $n=0$, which represents the backbone, and the largest number in the cycle is $(2n+1)·2^m=1·2^2=4$. This gives the known cycle $1\to 2\to 4\to 1$. Hence, no branch other than the base branch can have such a cycle.

5. Conclusion

A complete proof of the Collatz Conjecture has been provided by constructing and analyzing the Collatz infinite tree using the inverse transformation of the Collatz equation. The Collatz tree, when traversed backward from any given natural number N, directly corresponds to the behavior of the Collatz Conjecture for N. This alignment allowed us to establish that the conjecture holds for any natural number by proving that all natural numbers up to and including N are contained in the Collatz tree and that all such numbers converge to 1.

To demonstrate the inclusion of all natural numbers, it was rigorously shown that all numbers less than or equal to any given N are represented in the branches defined by:

$$\left\{(2n+1)·2^m|0\le n\le ⌊{\displaystyle \frac{N-1}{2}}⌋,0\le m\le ⌊{log}_2\left({\displaystyle \frac{N}{2n+1}}\right)⌋\right\}$$

Additionally, the absence of nontrivial cycles was proven by analyzing the necessary condition for a cycle:

$$m={log}_2\left(3+{\displaystyle \frac{1}{2n+1}}\right),$$

which confirmed that the only cycle is the trivial one: $1\to 2\to 4\to 1$.

This approach demonstrates that the Collatz Conjecture is fundamentally proven through the structure of the inverse Collatz transformation. An algorithm was also developed to generate the Collatz subtree containing all natural numbers up to any given N, further solidifying the practical and theoretical contributions of this proof. Thus, the Collatz Conjecture has been conclusively verified, with all natural numbers shown to converge to 1 through this framework, and no cycles existing other than the trivial one.