Mathematical Modeling for the Optimal Surface of T-Shaped Combined Footing Assuming That the Contact Area with the Ground Woks Partially Under Compression

1. Introduction

The ground pressure below a footing depends on the type of soil, the relative stiffness of the soil and the footing, and the depth of the foundation at the level of contact between the footing and the ground.

Figure 1 shows the distribution of ground pressure below of the contact surface of a footing depending on the ground type for a rigid footing. Figure 1(a) presents a rigid footing on sandy soil. Figure 1(b) shows a rigid footing on clay soil. Figure 1(c) presents the uniform distribution used in the current design [1].

The proposed model considers that the distribution of the pressures on the ground is linear for T-shaped combined footings subjected to biaxial bending in each column.

The load capacity studies by analytical and/or experimental methods for different types of foundations have been investigated by several authors, such as: Shahin and Cheung [2], Dixit and Patil [3], ErzÍn and Gul [4], Colmenares et al. [5], Cure et al. [6], Fattah et al. [7], Uncuoğlu [8], Anil et al. [9], Khatri et al. [10], Mohebkhah [11], Zhang [12], Turedi et al. [13], Gnananandarao [14], Gör [15].

The most important investigations on rectangular isolated footings for the efficient management of soil-footing interaction problems have been carried out through the use of analytical methods [16,17,18,19,20,21,22,23,24,25], for graphics or design aids [26,27,28], and by analytical methods and graphics or design aids [29,30]. These documents are developed to obtain the axial load capacity and biaxial moment of the footing, or the pressure distribution in the contact area of a rigid rectangular isolated footing resting on the ground, and the dimensions of the footing are obtained through an iterative procedure.

The most important contributions on the studies of combined footings have been investigated by several researchers, such as: For rectangular footings by Maheshwari and Khatri [31], Konapure and Vivek [32], Vivek et al. [33], Ravi Kumar Reddy et al. [34], Kashani et al. [35]; For trapezoidal footings by Al-Douri [36], Luévanos-Rojas et al. [37]; T-shaped footings by Luévanos-Rojas et al. [38,39], Moreno-Landeros et al. [40]; For corner Footings by Aishwarya, K.M.; Balaji [41]; For strap footings by Luévanos-Rojas et al. [42].

The papers more related to this paper are: Luévanos-Rojas et al. [38] investigated an analytical model to obtain the dimensions of the reinforced concrete T-shaped combined footings in contact with the ground. Luévanos-Rojas et al. [39] proposed a design mathematical model to obtain the thickness and reinforcing steel for reinforced concrete T-shaped combined footings. Moreno-Landeros et al. [40] developed an optimal cost design for reinforced concrete T-shaped combined footings. All these works are developed under the criterion that the area of the footing works totally in compression.

Thus, the review of the previous studies shows that there are no works with the current level of knowledge on the minimum area of T-shaped combined footings, considering that the area works partially in compression.

This work presents an analytical model to obtain the minimum area for T-shaped combined footings assuming that the area in contact with the ground works partially in compression, i.e., a part of the footing contact area is subject to compression and another part without pressure (zero pressure). This paper shows the fifteen possible cases of footings subjected to biaxial bending and three special cases of uniaxial bending (M_y1 and M_y2 are equals to zero), and the resultant force R and the orthogonal moments on the X and Y axes are obtained by integration and are verified by the properties of a pyramid with a triangular base for biaxial bending and the properties of a triangular prism for uniaxial bending. Three numerical examples are presented in this paper. Example 1 is for biaxial bending; Example 2 is the same example 1, but M_x1 and M_x2 are equals to zero; Example 3 is the same example 1, but M_y1 and M_y2 are equals to zero. Each example presents four types of constraints, which are: Constraint 1 is for a footing with unconstrained sides; Constraint 2 is for a footing with one side constrained in column 1; Constraint 3 is for a footing with a side constrained in column 2; Constraint 4 is for a footing with two sides constrained (opposite sides). Also, a comparison is made with the current model (area works completely under compression) and the new model (area works partially under compression) to observe the different.

2. Formulation of the Model

This work makes the following considerations: the footing is supported on an elastic and homogeneous ground and the footing is totally rigid, i.e., the ground pressure on the footing behaves linearly.

Figure 2 shows a T-shaped combined footing (free sides at its ends) that supports two columns aligned on a Y axis (longitudinal axis), and each column transfers to the footing an axial load and two bending moments on the X and Y axes.

The geometric properties of the T-shaped combined footing viewing in plan are:

$$A=\left(a_1-a_2\right)b+a_2{h}_y,$$

(1)

$$y_t={\displaystyle \frac{\left(a_1-a_2\right)b^2+a_2{h_y}^2}{2\left[\left(a_1-a_2\right)b+a_2{h}_y\right]}},$$

(2)

$$y_b={\displaystyle \frac{\left(2h_y-b\right)\left(a_1-a_2\right)b+a_2{h_y}^2}{2\left[\left(a_1-a_2\right)b+a_2{h}_y\right]}},$$

(3)

$$I_x={\displaystyle \frac{a_2{h}_{y}b{\left(a_1-a_2\right)\left(h_y-b\right)}^2\left[a_2{h}_y+b\left(a_1-a_2\right)\right]}{4{\left[\left(a_1-a_2\right)b+a_2{h}_y\right]}^2}}+{\displaystyle \frac{\left(a_1-a_2\right)b^3+a_2{h_y}^3}{12}},$$

(4)

$$I_y={\displaystyle \frac{b{a_1}^3+\left(h_y-b\right){a_2}^3}{12}},$$

(5)

where: A = Area of ​​the footing in plan (m²), y_t = Distance from center of footing to positive end (m), y_b = Distance from center of footing to negative end (m), I_x = Moment of inertia about the X axis (m⁴), I_y = Moment of inertia about the Y axis (m⁴).

2.1. Biaxial Bending

In this subsection, the fifteen possible cases for a T-shaped combined footing subjected to axial load and two orthogonal bending moments in each column are presented.

For case I, it is assumed that the entire bottom surface of the footing works under compression. The pressures generated by the ground on the footing are obtained by the following equation (biaxial bending equation):

$$\sigma ={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}y}{I_x}}+{\displaystyle \frac{M_{yT}x}{I_y}}.$$

(6)

where: σ = Allowable soil pressure (kN/m²), M_x = Bending moment about X axis (kN-m), M_y = Bending moment about Y axis (kN-m).

Note: R, M_x and M_y can be determined as follows:

$$R=P_1+P_2,$$

(7)

$$M_{xT}=M_{x1}+M_{x2}+P_1\left(y_t-L_1\right)-P_2\left(h_y-y_t-L_2\right),$$

(8)

$$M_{yT}=M_{y1}+M_{y2}.$$

(9)

For cases II to XV, it is assumed that the entire bottom surface of the footing works partially under compression, i.e., part of the contact area there is no pressure, and by integration and/or by the geometric properties of a pyramid with a triangular base, the resultant force R, the moment on the X axis M_xT and the moment on the Y axis M_yT are obtained.

The pressures generated by the ground on the footing are obtained by means of the general equation of the pressure plane, starting from three known points.

The general equation of a 3-D pressure plane of the ground on the footing is:

$$Ax+By+C{\sigma }_z+D=0.$$

(10)

For cases II to XV, the three known points of the pressure plane are:

$$p_1\left({\displaystyle \frac{a_1}{2}},y_t,{\sigma }_{max}\right);p_2\left({\displaystyle \frac{a_1}{2}}-L_{x1},y_t,0\right);p_3\left({\displaystyle \frac{a_1}{2}},y_t-L_{y1},0\right).$$

(11)

The general equation of the pressure plane is obtained as follows:

$$\left|\begin{array}{ccc}x-\left({\displaystyle \frac{a_1}{2}}\right)& y-\left(y_t\right)& {\sigma }_z-{\sigma }_{max}\\ {\displaystyle \frac{a_1}{2}}-L_{x1}-\left({\displaystyle \frac{a_1}{2}}\right)& y_t-\left(y_t\right)& 0-{\sigma }_{max}\\ {\displaystyle \frac{a_1}{2}}-\left({\displaystyle \frac{a_1}{2}}\right)& y_t-L_{y1}-\left(y_t\right)& 0-{\sigma }_{max}\end{array}\right|.$$

(12)

Solving the determinant of Equation (12) gives the pressure at any point σ_z:

$${\sigma }_z={\displaystyle \frac{{\sigma }_{max}\left[2L_{x1}\left(L_{y1}+y-y_t\right)+L_{y1}\left(2x-a_1\right)\right]}{2L_{x1}{L}_{y1}}}.$$

(13)

The equation of the straight line that forms the neutral axis is:

$$2L_{x1}\left(L_{y1}+y-y_t\right)+L_{y1}\left(2x-a_1\right)=0.$$

(14)

Figure 3 shows Case I assuming that the entire bottom surface of the footing works under compression.

Figure 4 shows Cases II to XV assuming that the entire bottom surface of the footing works partially under compression.

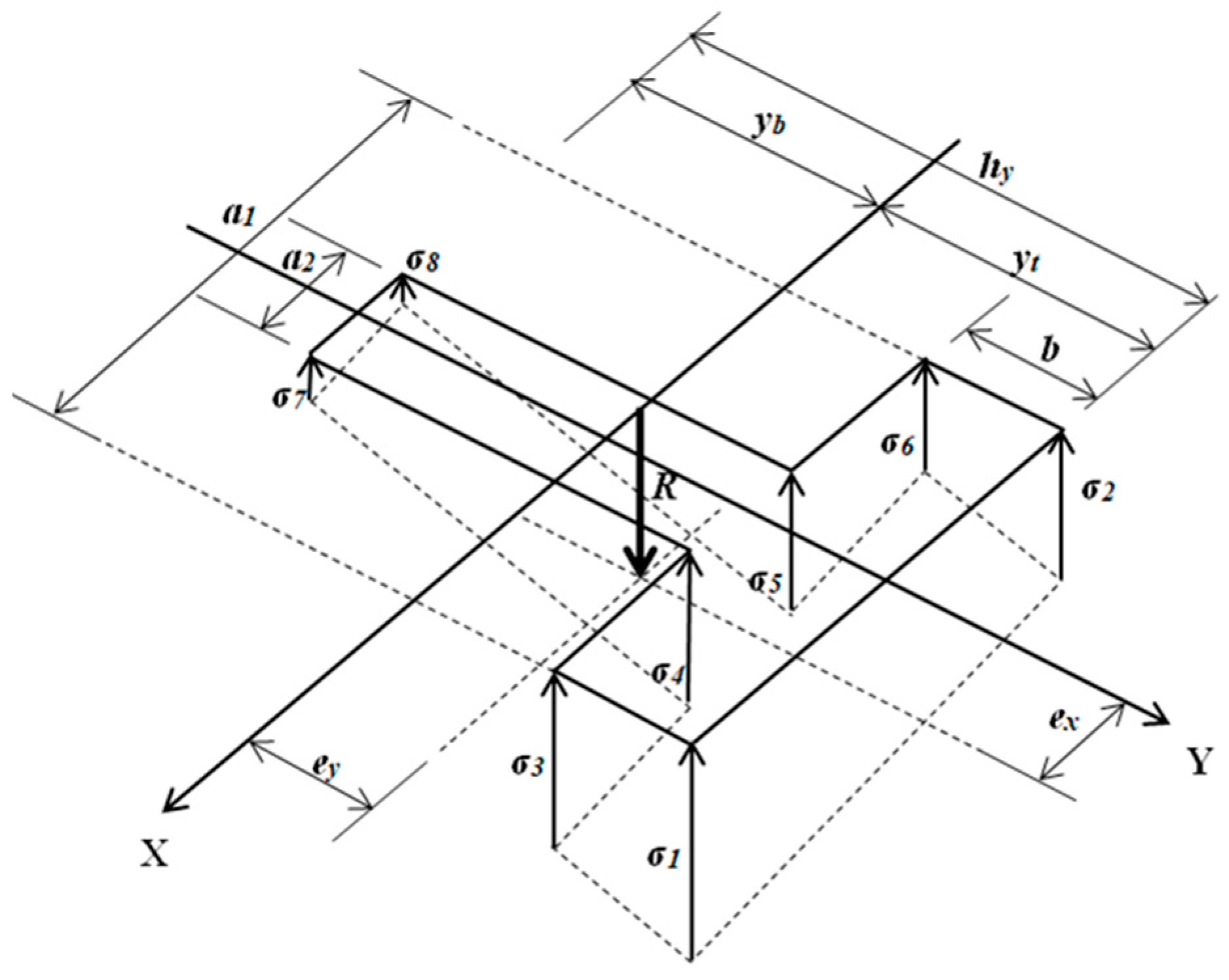
2.1.1. Case I

The general equations for the soil pressure at each vertex of a footing subjected to biaxial bending are obtained from equation (6) as follows:

$${\sigma }_1={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}{y}_t}{I_x}}+{\displaystyle \frac{M_{yT}{a}_1}{2I_y}},$$

(15)

$${\sigma }_2={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}{y}_t}{I_x}}-{\displaystyle \frac{M_{yT}{a}_1}{2I_y}},$$

(16)

$${\sigma }_3={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}\left(y_t-b\right)}{I_x}}+{\displaystyle \frac{M_{yT}{a}_1}{2I_y}},$$

(17)

$${\sigma }_4={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}\left(y_t-b\right)}{I_x}}+{\displaystyle \frac{M_{yT}{a}_2}{2I_y}},$$

(18)

$${\sigma }_5={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}\left(y_t-b\right)}{I_x}}-{\displaystyle \frac{M_{yT}{a}_2}{2I_y}},$$

(19)

$${\sigma }_6={\displaystyle \frac{R}{A}}+{\displaystyle \frac{M_{xT}\left(y_t-b\right)}{I_x}}-{\displaystyle \frac{M_{yT}{a}_1}{2I_y}},$$

(20)

$${\sigma }_7={\displaystyle \frac{R}{A}}-{\displaystyle \frac{M_{xT}\left(h_y-y_t\right)}{I_x}}+{\displaystyle \frac{M_{yT}{a}_2}{2I_y}},$$

(21)

$${\sigma }_8={\displaystyle \frac{R}{A}}-{\displaystyle \frac{M_{xT}\left(h_y-y_t\right)}{I_x}}-{\displaystyle \frac{M_{yT}{a}_2}{2I_y}}.$$

(22)

The general equations of R, M_xT and M_yT for cases II to XV are presented below.

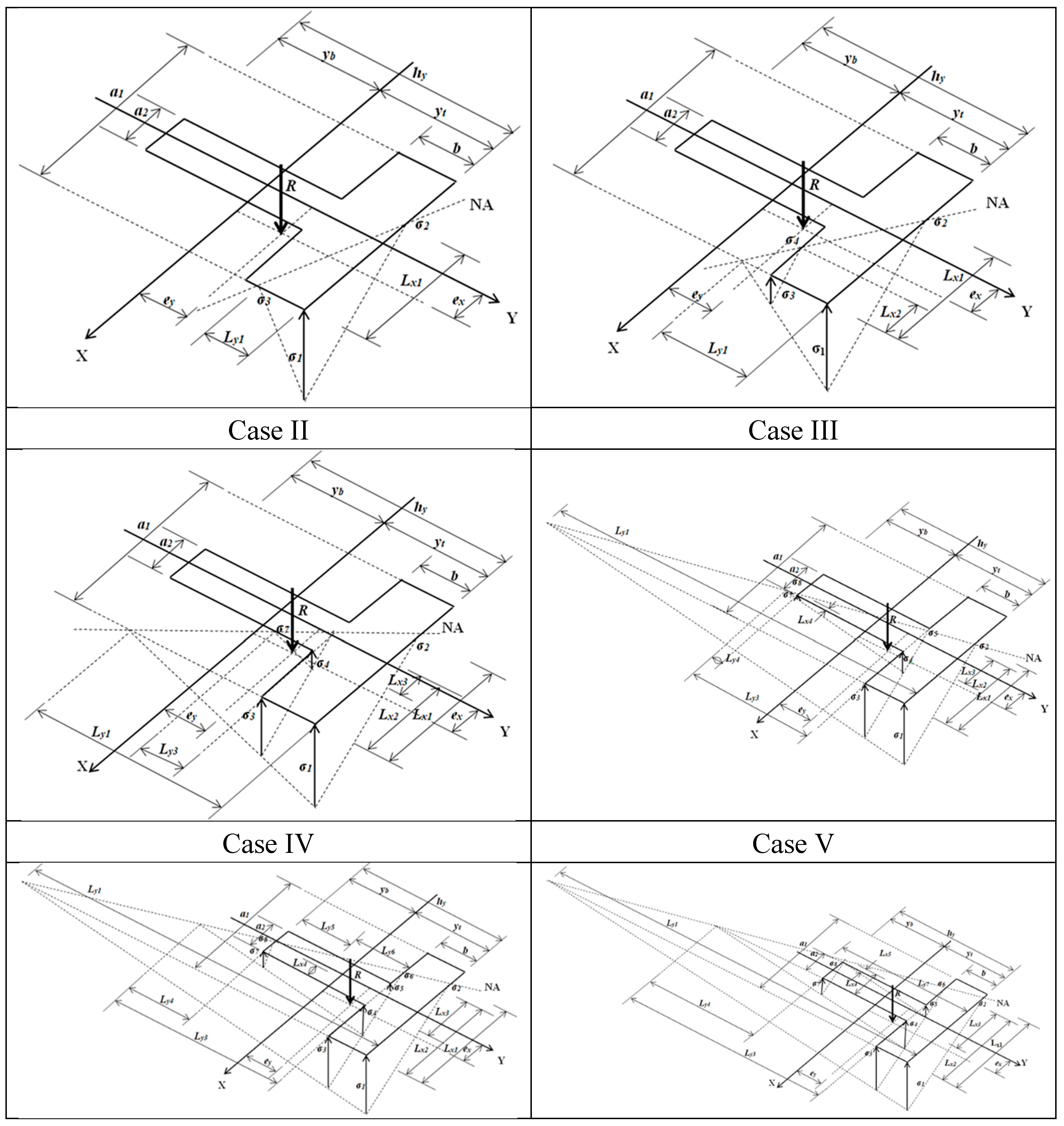
2.1.2. Case II

$$R={\int }_{y_t-L_{y1}}^{y_t}{\int }_{{\displaystyle \frac{a_1}{2}}+{\displaystyle \frac{\left(y_t-L_{y1}-y\right)L_{x1}}{L_{y1}}}}^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}dxdy,$$

(23)

$$R={\displaystyle \frac{{\sigma }_{max}{L}_{x1}{L}_{y1}}{6}},$$

(24)

$$M_{xT}={\int }_{y_t-L_{y1}}^{y_t}{\int }_{{\displaystyle \frac{a_1}{2}}+{\displaystyle \frac{\left(y_t-L_{y1}-y\right)L_{x1}}{L_{y1}}}}^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}ydxdy,$$

(25)

$$M_{xT}={\displaystyle \frac{{\sigma }_{max}{L}_{x1}{L}_{y1}\left(4y_t-L_{y1}\right)}{24}},$$

(26)

$$M_{yT}={\int }_{y_t-L_{y1}}^{y_t}{\int }_{{\displaystyle \frac{a_1}{2}}+{\displaystyle \frac{\left(y_t-L_{y1}-y\right)L_{x1}}{L_{y1}}}}^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}xdxdy,$$

(27)

$$M_{yT}={\displaystyle \frac{{\sigma }_{max}{L}_{x1}{L}_{y1}\left(2a_1-L_{x1}\right)}{24}}.$$

(28)

2.1.3. Case III

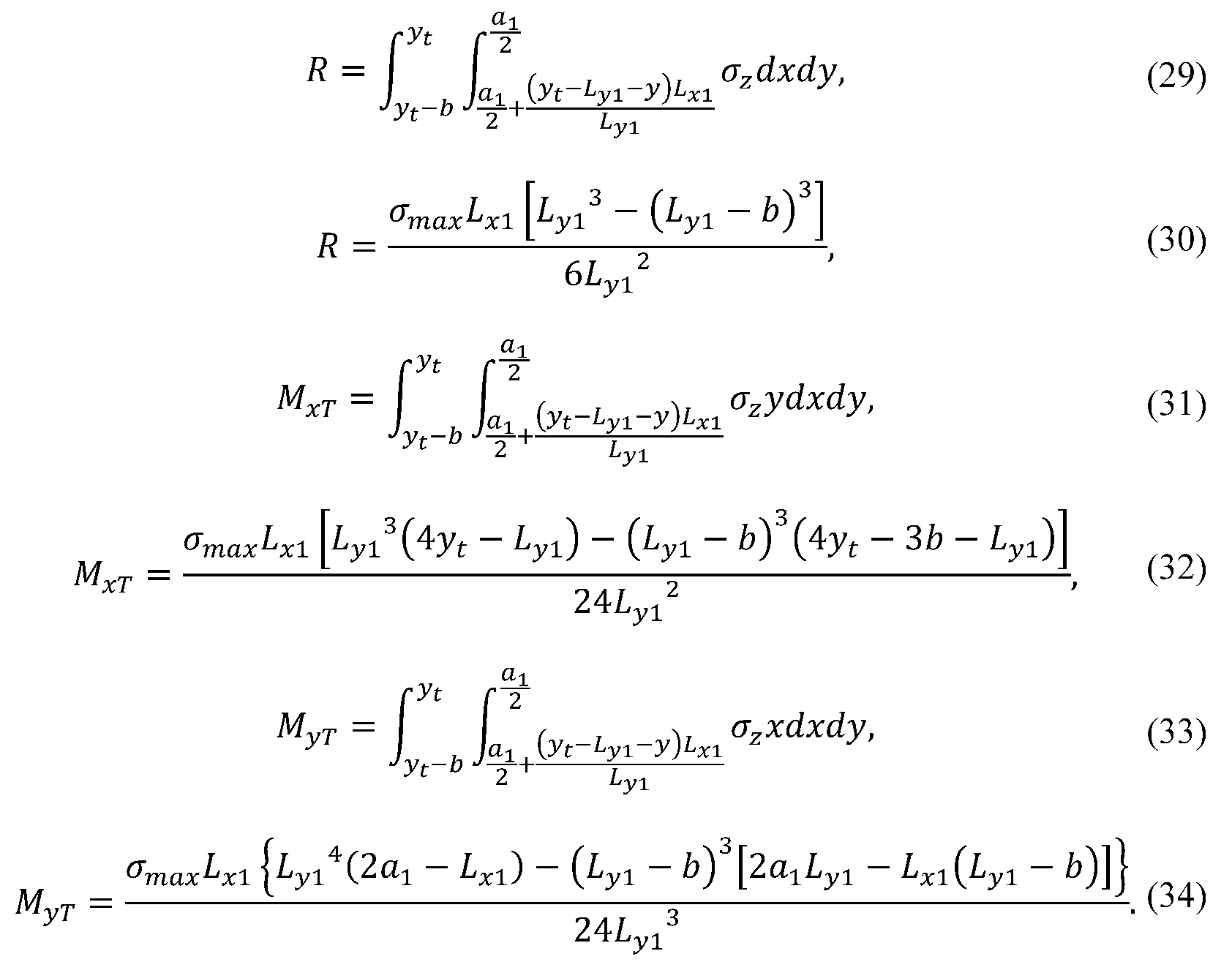
2.1.4. Case IV

2.1.5. Case V

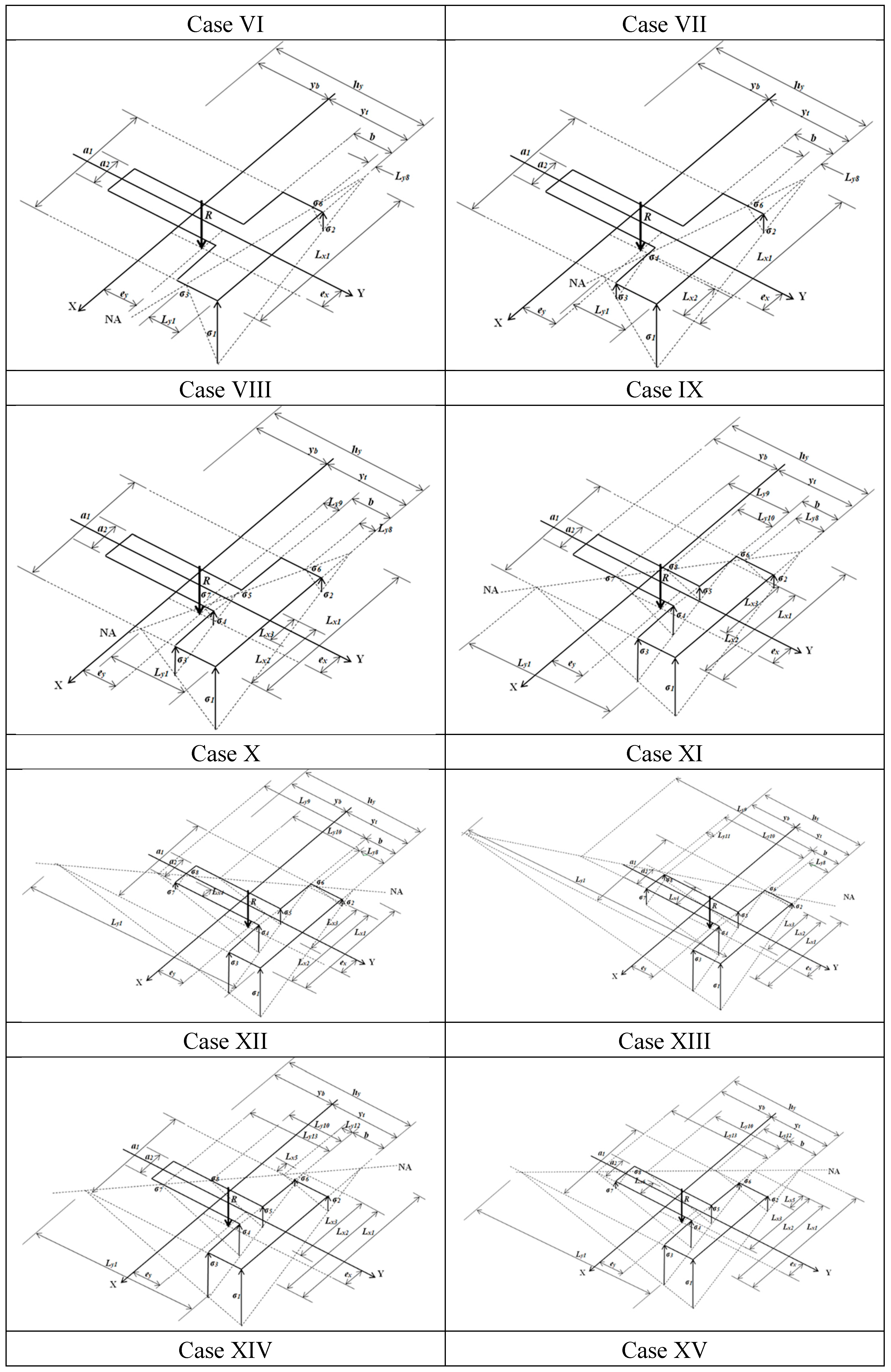
2.1.6. Case VI

2.1.7. Case VII

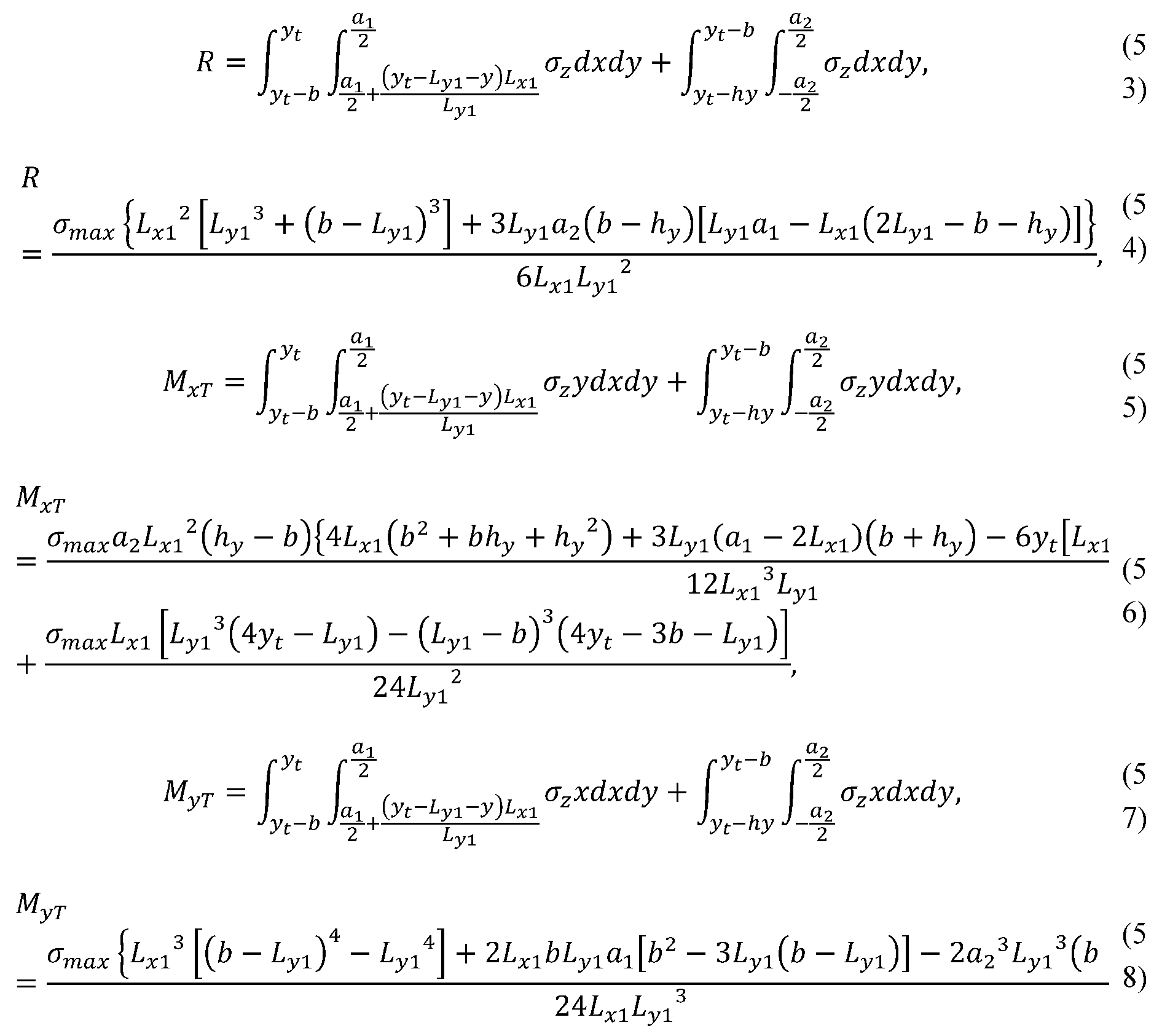
2.1.8. Case VIII

2.1.9. Case IX

2.1.10. Case X

2.1.11. Case XI

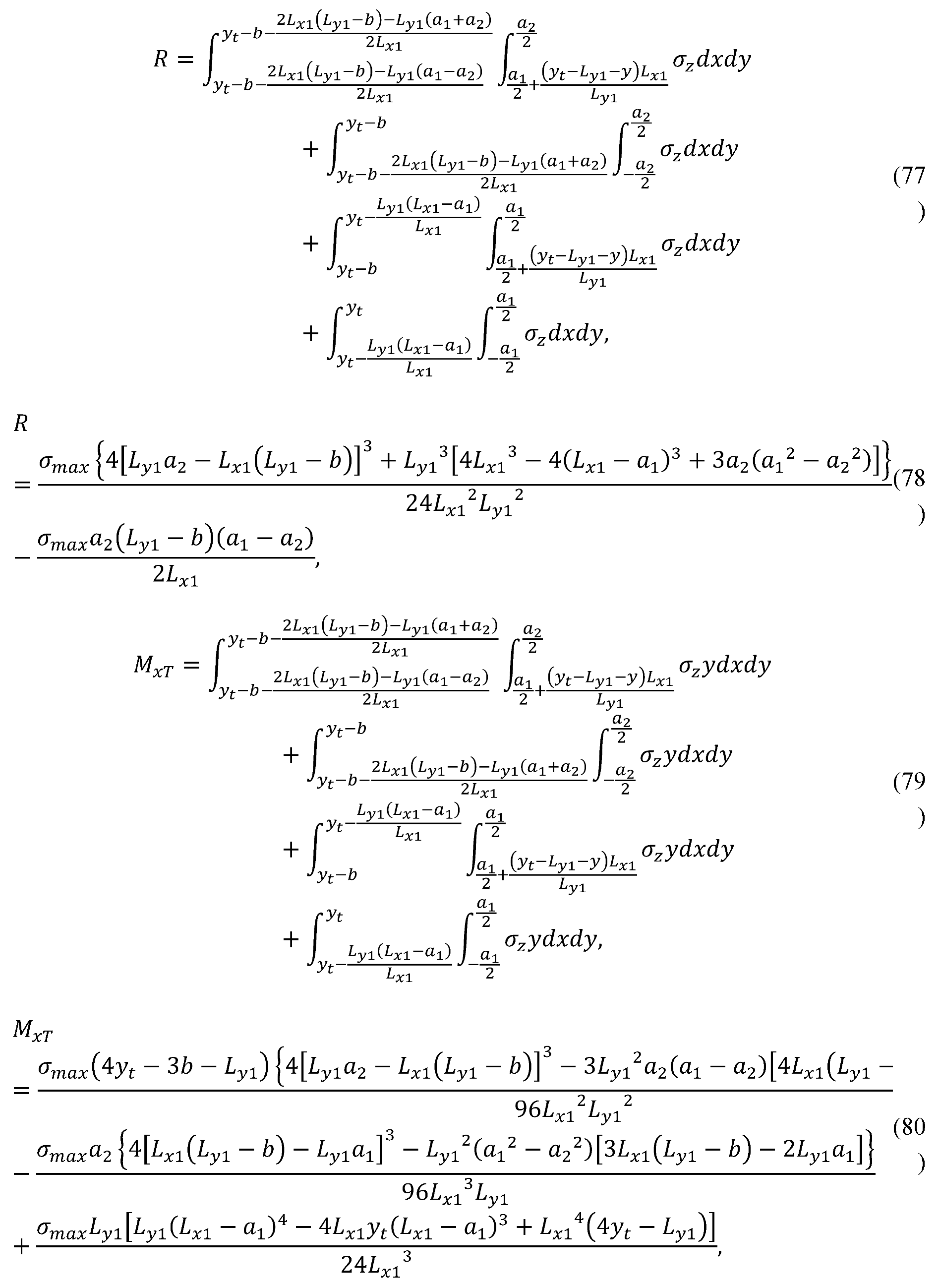
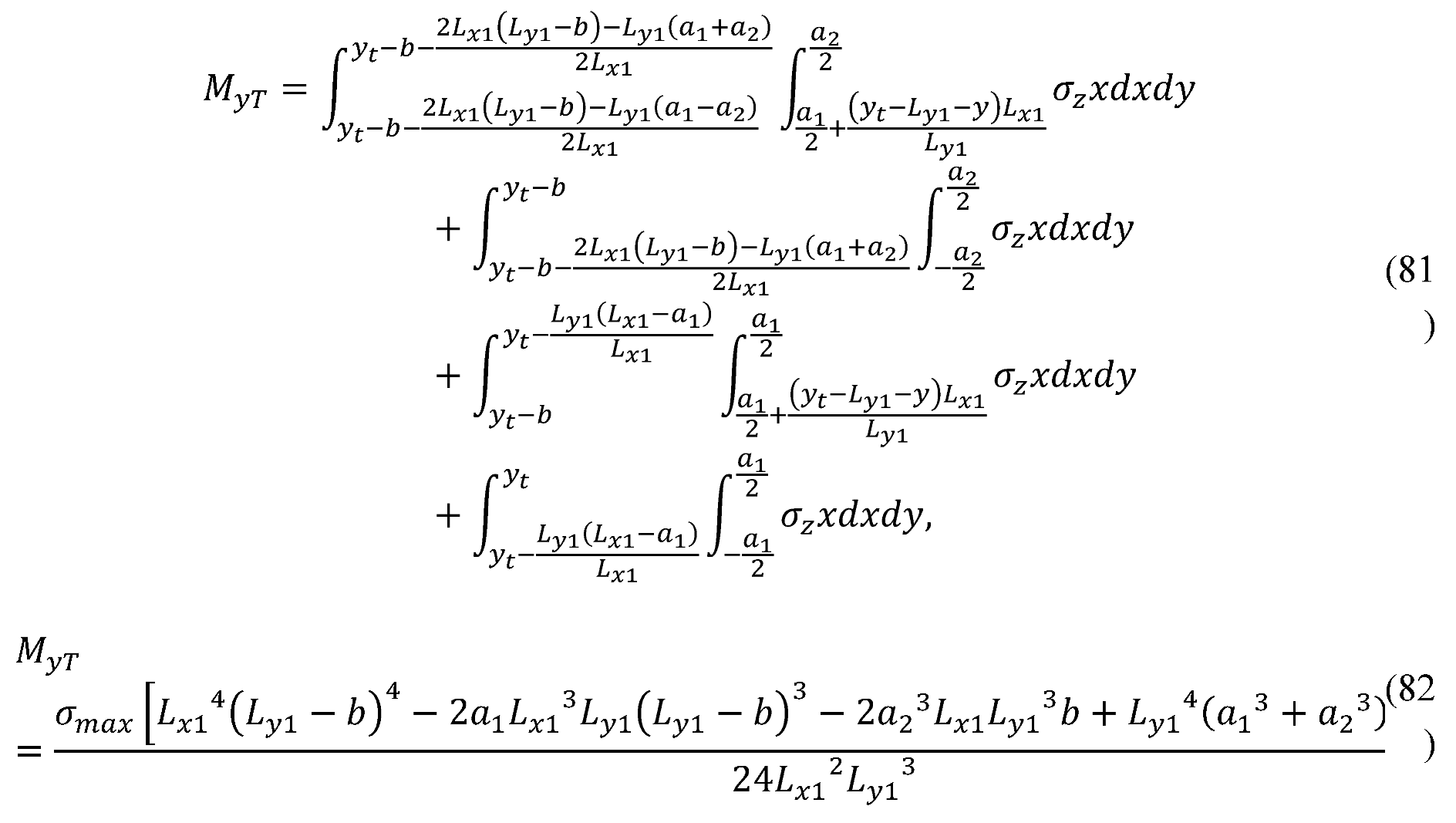
2.1.12. Case XII

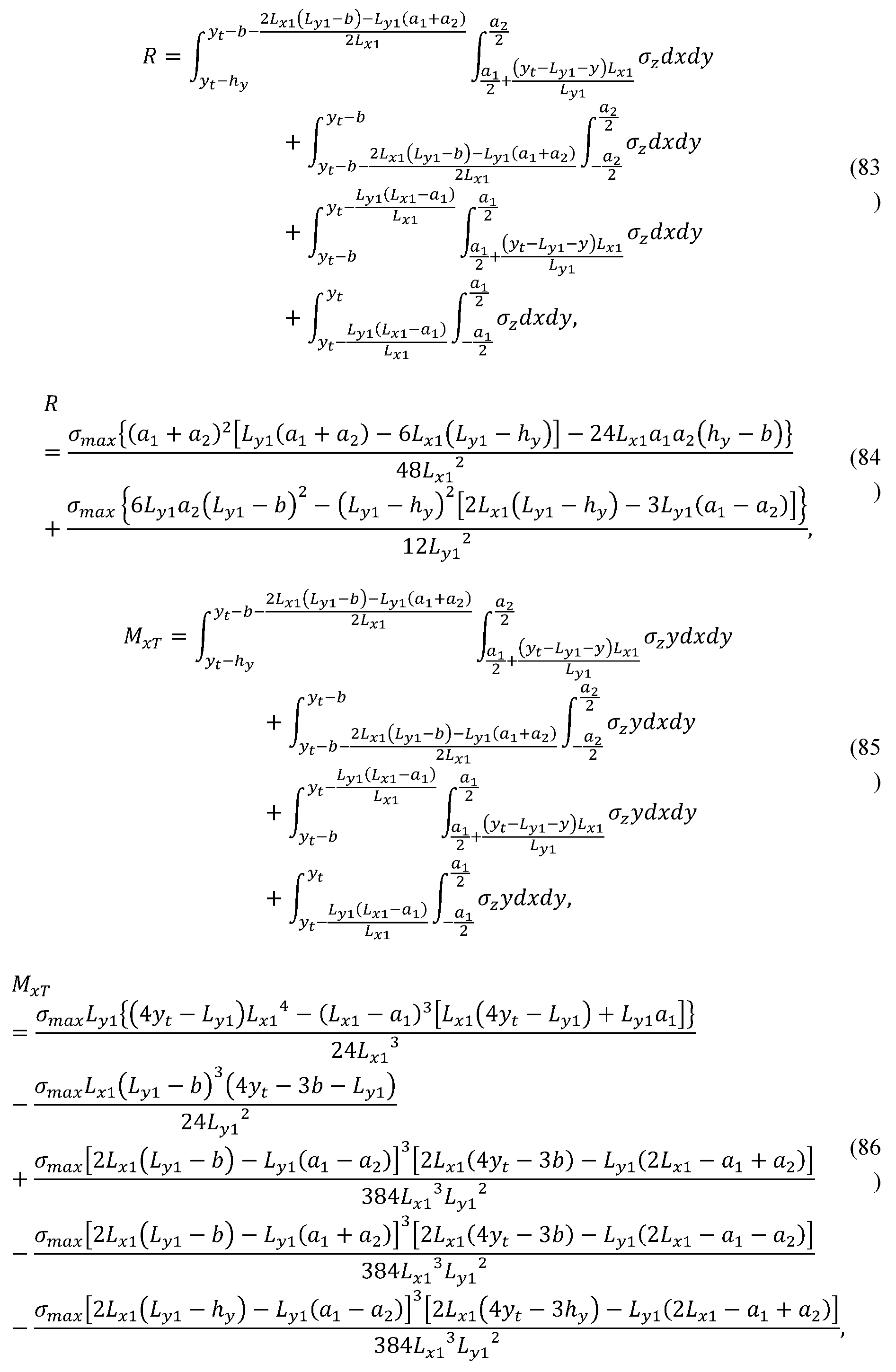
2.1.13. Case XIII

2.1.14. Case XIV

2.1.15. Case XV

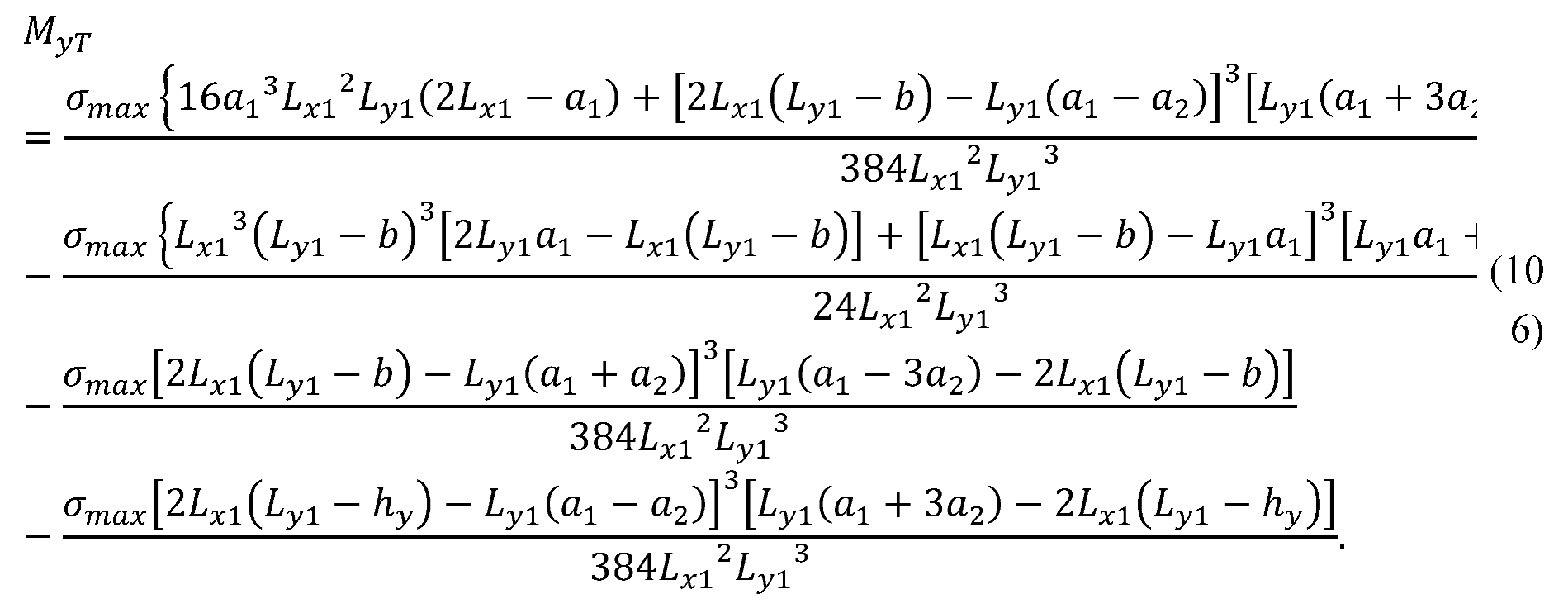
2.2. Special Cases

There are two cases: Case X) when the moments M_x1 and M_x2 are zero; Case Y) when moments M_y1 and M_y2 are zero.

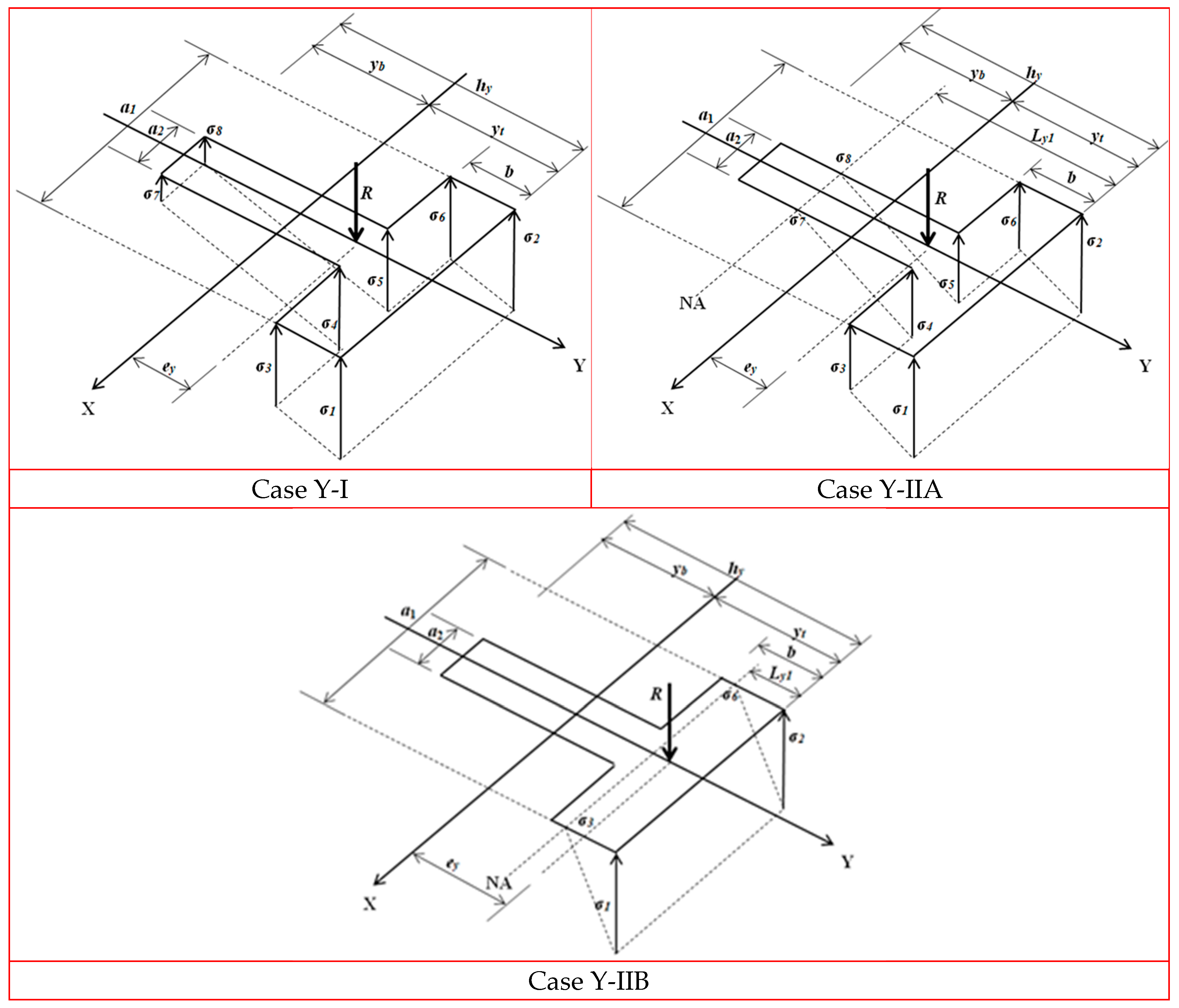
2.2.1. Case Y

Figure 5 shows the three possible cases for a T-shaped combined footing subjected to axial load and a bending moment around the X axis provided by each column (M_y1 and M_y2 are zero).

For case Y-I, it is assumed that the entire bottom surface of the footing works under compression, and equations (15) to (22) are used.

For cases Y-IIA and Y-IIB, it is assumed that the entire bottom surface of the footing works partially under compression

The pressures generated by the ground on the footing are obtained by means of the general equation of the pressure plane, starting from three known points.

Now, the three known points of the pressure plane are:

$$p_1\left({\displaystyle \frac{a_1}{2}},y_t,{\sigma }_{max}\right);p_2\left(-{\displaystyle \frac{a_1}{2}},y_t,{\sigma }_{max}\right);p_3\left({\displaystyle \frac{a_2}{2}},y_t-L_{y1},0\right).$$

(107)

The general equation of the pressure plane is obtained as follows:

$$\left|\begin{array}{ccc}x-{\displaystyle \frac{a_1}{2}}& y-y_t& {\sigma }_z-{\sigma }_{max}\\ -a_1& 0& 0\\ {\displaystyle \frac{a_2-a_1}{2}}& -L_{y1}& -{\sigma }_{max}\end{array}\right|.$$

(108)

Solving the determinant of equation (108) gives the pressure at any point “σ_z”:

$${\sigma }_z={\displaystyle \frac{{\sigma }_{max}\left(L_{y1}-y_t+y\right)}{L_{y1}}}.$$

(109)

2.2.1.1. Case Y-IIA

The general equations for R and M_xT are:

$$R=2{\int }_{y_t-b}^{y_t}{\int }_0^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}dxdy+2{\int }_{y_t-L_{y1}}^{y_t-b}{\int }_0^{{\displaystyle \frac{a_2}{2}}}{\sigma }_{z}dxdy,$$

(110)

$$R={\displaystyle \frac{{\sigma }_{max}\left[a_{1}b\left(2L_{y1}-b\right)+a_2{\left(L_{y1}-b\right)}^2\right]}{2L_{y1}}},$$

(111)

$$M_{xT}=2{\int }_{y_t-b}^{y_t}{\int }_0^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}ydxdy+2{\int }_{y_t-L_{y1}}^{y_t-b}{\int }_0^{{\displaystyle \frac{a_2}{2}}}{\sigma }_{z}ydxdy,$$

(112)

$$M_{xT}={\displaystyle \frac{{\sigma }_{max}b\left(a_1-a_2\right)\left[2b^2+6L_{y1}{y}_t-3b\left(L_{y1}+y_t\right)\right]}{6L_{y1}}}+{\displaystyle \frac{{\sigma }_{max}\left\{a_2{L_{y1}}^2\left(3y_t-L_{y1}\right)\right\}}{6L_{y1}}}.$$

(113)

2.2.1.2. Case Y-IIB

The general equations for R and M_xT are:

$$R=2{\int }_{y_t-L_{y1}}^{y_t}{\int }_0^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}dxdy,$$

(114)

$$R={\displaystyle \frac{{\sigma }_{max}{a}_1{L}_{y1}}{2}},$$

(115)

$$M_{xT}=2{\int }_{y_t-L_{y1}}^{y_t}{\int }_0^{{\displaystyle \frac{a_1}{2}}}{\sigma }_{z}ydxdy,$$

(116)

$$M_{xT}={\displaystyle \frac{{\sigma }_{max}{a}_1{L}_{y1}\left(3y_t-L_{y1}\right)}{6}}.$$

(117)

2.2.2. Case X

For the T-shaped combined footing subjected to axial load and a bending moment around the Y axis provided by each column (M_x1 and M_x2 are zero).

For the case X, all the equations of the biaxial bending must be used, because there are resultant moments M_xT.

2.3. Minimum Surface for T-Shaped Combined Footings

Minimum surface (objective function) for all cases is:

$$A_{min}=\left(a_1-a_2\right)b+a_2{h}_y.$$

(118)

Table 1 shows the equations of the constraint functions for biaxial bending in each case.

The functions that must be limited in the Y-axis direction are:

Not limited: L₁ ≥ c₁/2 and L₂ ≥ c₃/2.

Limited in column 1: L₁ = c₁/2 and L₂ ≥ c₃/2.

Limited in column 2: L₁ ≥ c₁/2 and L₂ = c₃/2.

Limited in the two columns: L₁ = c₁/2 and L₂ = c₃/2.

Note: c₁ and c₃ are the sides of the columns in the Y direction.

Table 2 shows the equations of the constraint functions for uniaxial bending in each case (Case Y).

3. Numerical Examples

Three numerical examples are shown for T-shaped combined footings supporting two columns, and each example presents four types of constraints, the constraints are: Constraint 1 is for unconstrained sides (L₁ ≥ c₁/2 and L₂ ≥ c₃/2); Constraint 2 is for a side constrained in column 1 (L₁ = c₁/2 and L₂ ≥ c₃/2); Constraint 3 is for a side constrained in column 2 (L₁ ≥ c₁/2 and L₂ = c₃/2); Constraint 4 is for two sides constrained (opposite sides) (L₁ = c₁/2 and L₂ = c₃/2). Example 1 is for a T-shaped combined footing subjected to axial load and moments on the X and Y axes due to the columns. Example 2 is for a T-shaped combined footing subjected to axial load and a moment on the Y axis due to the columns. Example 3 is for a T-shaped combined footing subjected to axial load and a moment on the X axis due to the columns.

The data for example 1 are: c₁ = 0.40 m, c₃ = 0.40 m, P₁ = 1250 kN, P₂ = 250 kN, M_x1 = 300 kN-m, M_x2 = 150 kN-m, M_y1 = 200 kN-m, M_y2 = 200 kN-m, L = 6.00 m, σ_max = 200 kN/m². The data for example 2 are: the same as for example 1, but M_x1 = 0 kN-m, M_x2 = 0 kN-m. The data for example 3 are: the same as for example 1, but M_y1 = 0 kN-m, M_y2 = 0 kN-m.

Table 3 shows the results of the example 1.

Table 4 shows the results of the example 2.

Table 5 shows the results of the example 3.

4. Results

The results of the table 3 show the following:

1.- The value of “A_min” is the same for constraint 1 and 3, except in cases II and IV that there is no solution available in constraint 3.

2.- The value of “A_min” is the same for constraint 2 and 4, except in case VI that there is solution available, but it is different.

3.- The minimum areas “A_min” are presented in case VI for constraints 1, 2 and 3, and case XIV for constraint 4.

The results of the table 4 show the following:

1.- The value of “A_min” is the same for constraint 1 and 3, except in cases II and IV that there is no solution available in constraint 3, and also for cases III, VI, VII, XI XII, XV these are different.

2.- The value of “A_min” is the same for constraint 2 and 4, except in cases VI and XV that there is solution available, but these are different.

3.- The minimum areas “A_min” are presented in case XV for constraint 1, in case VI for constraint 2, in case XI for constraint 3 and in case XV for constraint 4.

The results of the table 5 show the following:

1.- The value of “A_min” is the same for constraint 1 and 3.

2.- The value of “A_min” is the same for constraint 2 and 4.

3.- The minimum areas “A_min” are presented in case YIIA for all the constraints.

Table 6, Table 7 and Table 8 show in detail the mechanical and geometric properties of the cases that present the minimum areas of each example.

The results of the table 6 show the following:

1.- All the values are the same for constraints 1 and 3.

2.- The smaller value of “a₁” occurs in constraint 2, and the largest appears in constraint 4. All the values of “a₂” are the same. The smaller value of “b” occurs in constraint 4, and the largest appears in constraints 1 and 3. The largest value of “h_y” occurs in constraint 2, and the smaller appears in constraints 1, 3 and 4.

3.- The minimum area “A_min” is presented in case VI for constraints 1 and 3, and the largest appears in case XIV for constraint 4.

The results of the table 7 show the following:

1.- The smaller value of “a₁” occurs in constraint 3, and the largest appears in constraint 4. All the values of “a₂” are the same. The largest value of “b” occurs in constraint 3, and the smaller appears in constraint 1, 2 and 4. The largest value of “h_y” occurs in constraint 4, and the smaller appears in constraint 4.

2.- The minimum area “A_min” is presented in case XI for constraint 3, and the largest appears in case VI for constraint 2.

3.- The constraint 3 shows a rectangular combined footing.

The results of the table 8 show the following:

1.- All the values are the same for constraints 1 and 3, and for constraints 2 and 4.

2.- The smaller value of “a₁” occurs in constraints 1 and 3, and the largest appears in constraints 2 and 4. All the values of “a₂” are the same. All values of “b” are the same. The largest value of “h_y” occurs in constraints 1 and 3, and the smaller appears in constraints 2 and 4.

3.- The minimum area “A_min” is presented in case YIIA for constraints 1 and 3, and the largest appears in case YIIA for constraints 2 and 4.

Figure 6 shows a comparison between the CM (current model) and the NM (new model).

In three examples it shows a saving using the NM with respect to the CM. For example 1, largest savings occurs with 31.40% by limiting L₁. For example 2, largest savings occurs with 17.26% by limiting L₂. For example 3, largest savings occurs with 29.09% by limiting L₁, and by limiting L₁ and L₂.

5. Conclusions

The model presented in this document applies only for minimum area of a T-shaped combined footing that supports two columns aligned on a longitudinal axis. The considerations of this work are: the footing is rigid and the soil that supports to the footing is elastic and homogeneous, that comply with the biaxial bending, i.e., the variation of soil pressure is linear.

This paper concludes the following:

1.- Some authors present equations to find the dimensions of the footing and the minimum surface, but the entire surface of the footing works under compression (see Case I for the three examples).

2.- The proposed model presents the minimum surface and the constraint functions for the fifteen possible cases.

3.- The model can be used as a review of the allowable load capacity of the soil, taking into account the objective function “σ_max”, and the same constraint functions for biaxial bending or uniaxial bending.

4.- The proposed model can be used for rectangular combined footings, simply set a₁ = a₂ and b = h_y (see Table 7).

5.- When M_xT is zero, the resultant force lies along the X axis (see Table 7).

6.- When M_yT is zero, the resultant force lies along the Y axis (see Table 8).

7.- The model can be used for the following considerations:

a) Unconstrained sides (L₁ ≥ c₁/2 and L₂ ≥ c₃/2)

b) A constrained side in column 1 (L₁ = c₁/2 and L₂ ≥ c₃/2)

c) A constrained side in column 2 (L₁ ≥ c₁/2 and L₂ = c₃/2)

d) Two constrained sides (opposite sides) (L₁ = c₁/2 and L₂ = c₃/2)

The next investigations can be: 1) Minimum area for corner combined footings assuming that the contact area with the ground woks partially under compression. 2) Minimum area for strap combined footings assuming that the contact area with the ground woks partially under compression.