Submitted:
21 January 2025
Posted:
22 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
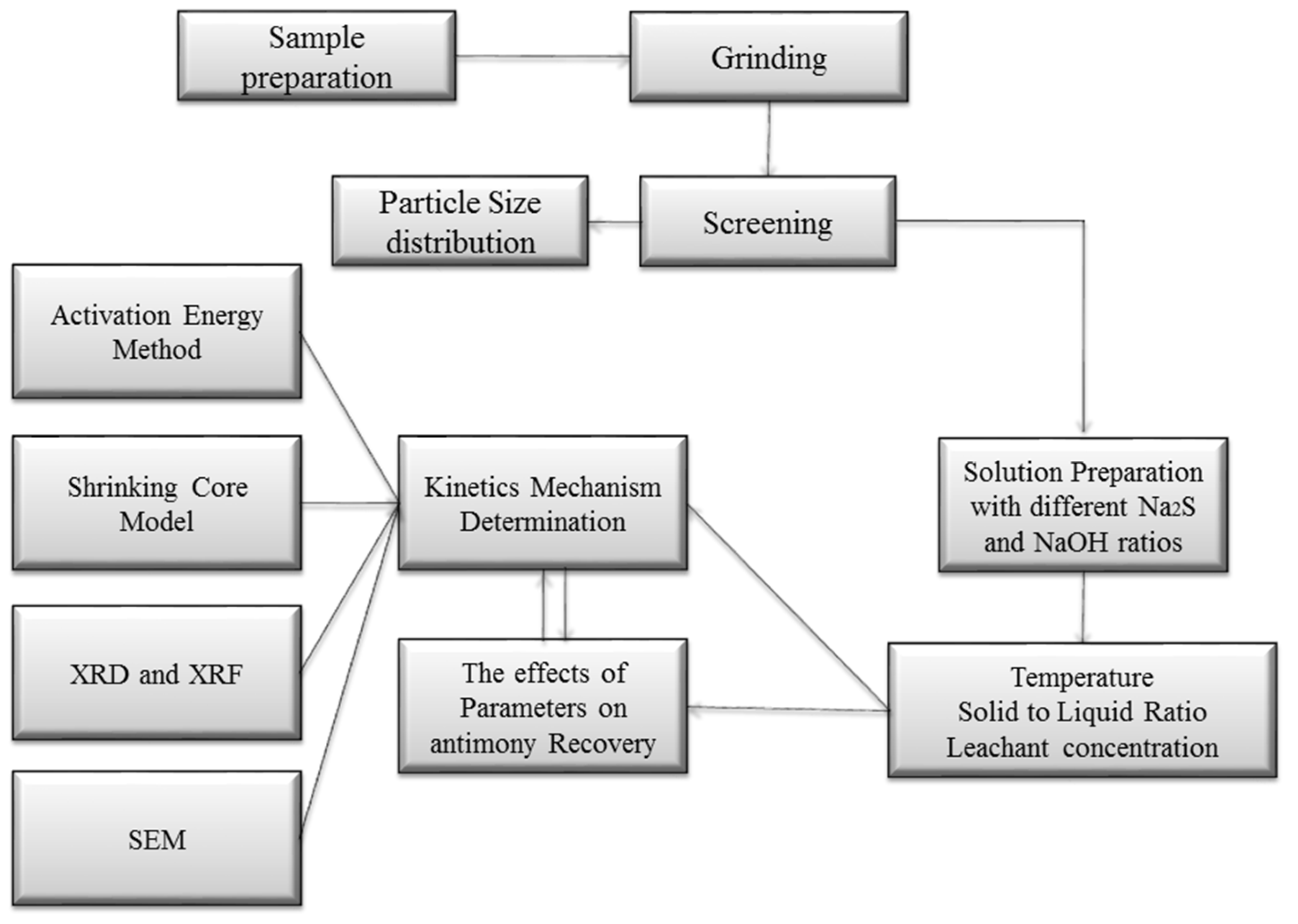
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Results and Discussion
3.1. The Effect of Leaching Parameters on Antimony Recovery
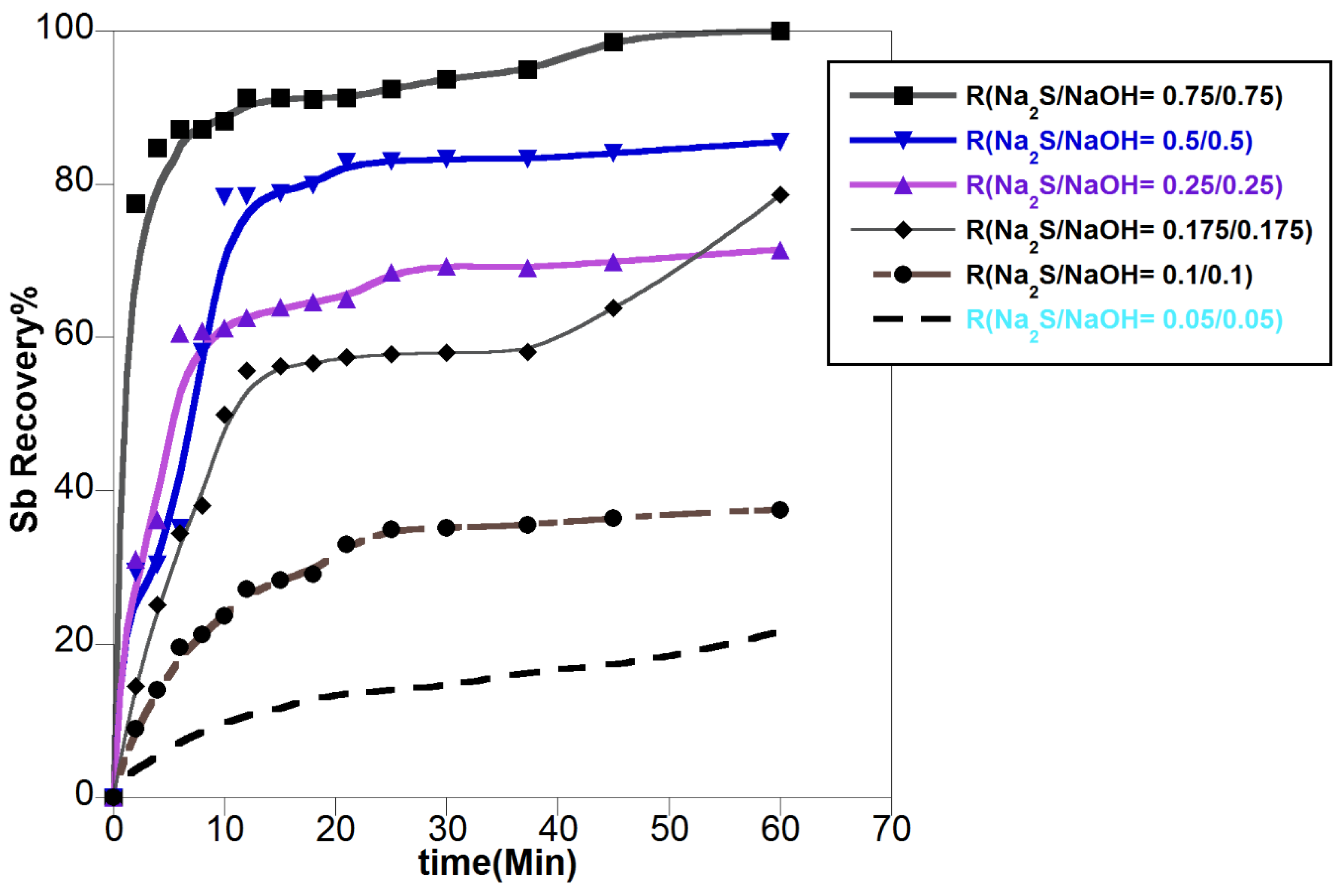
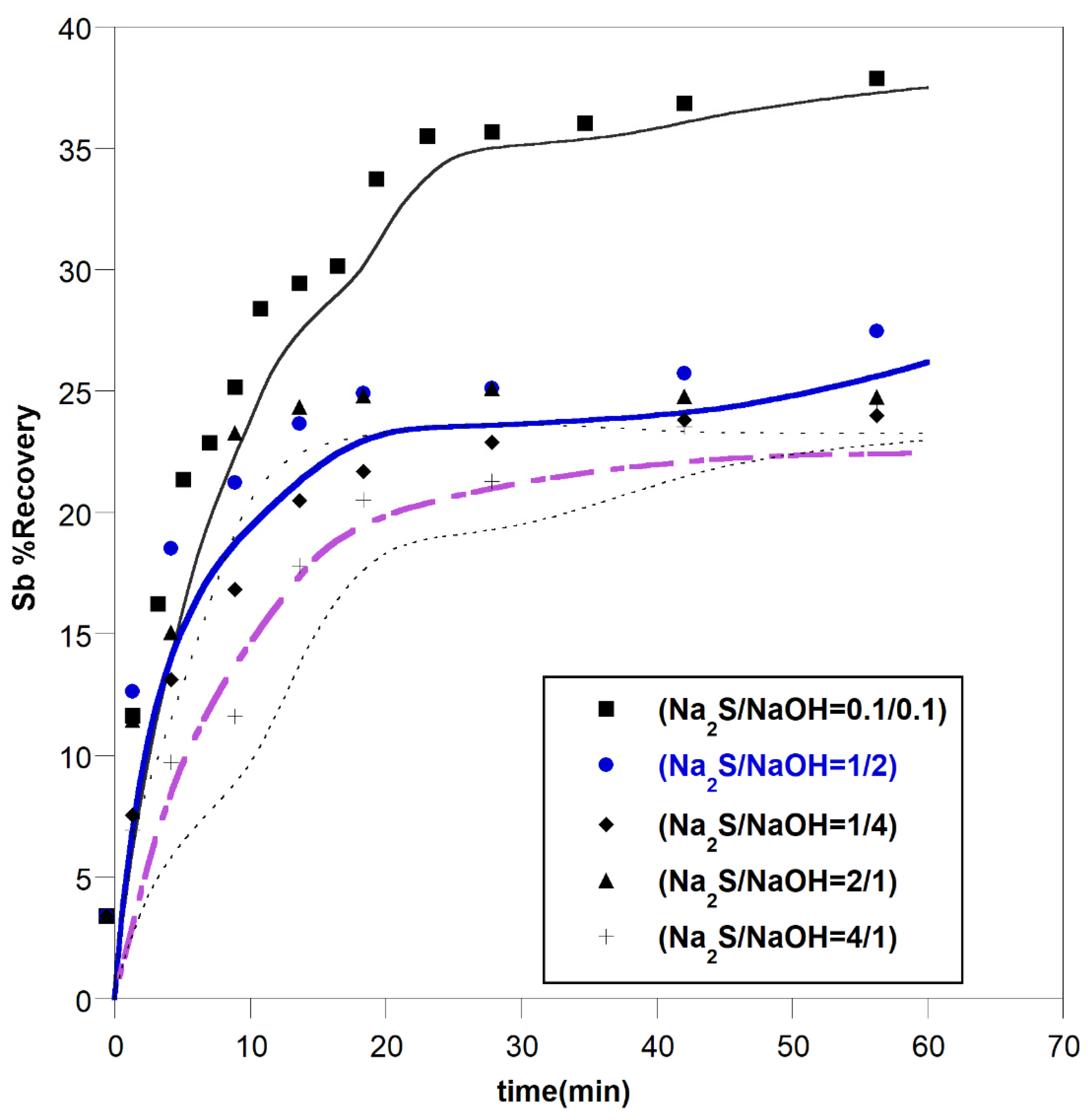
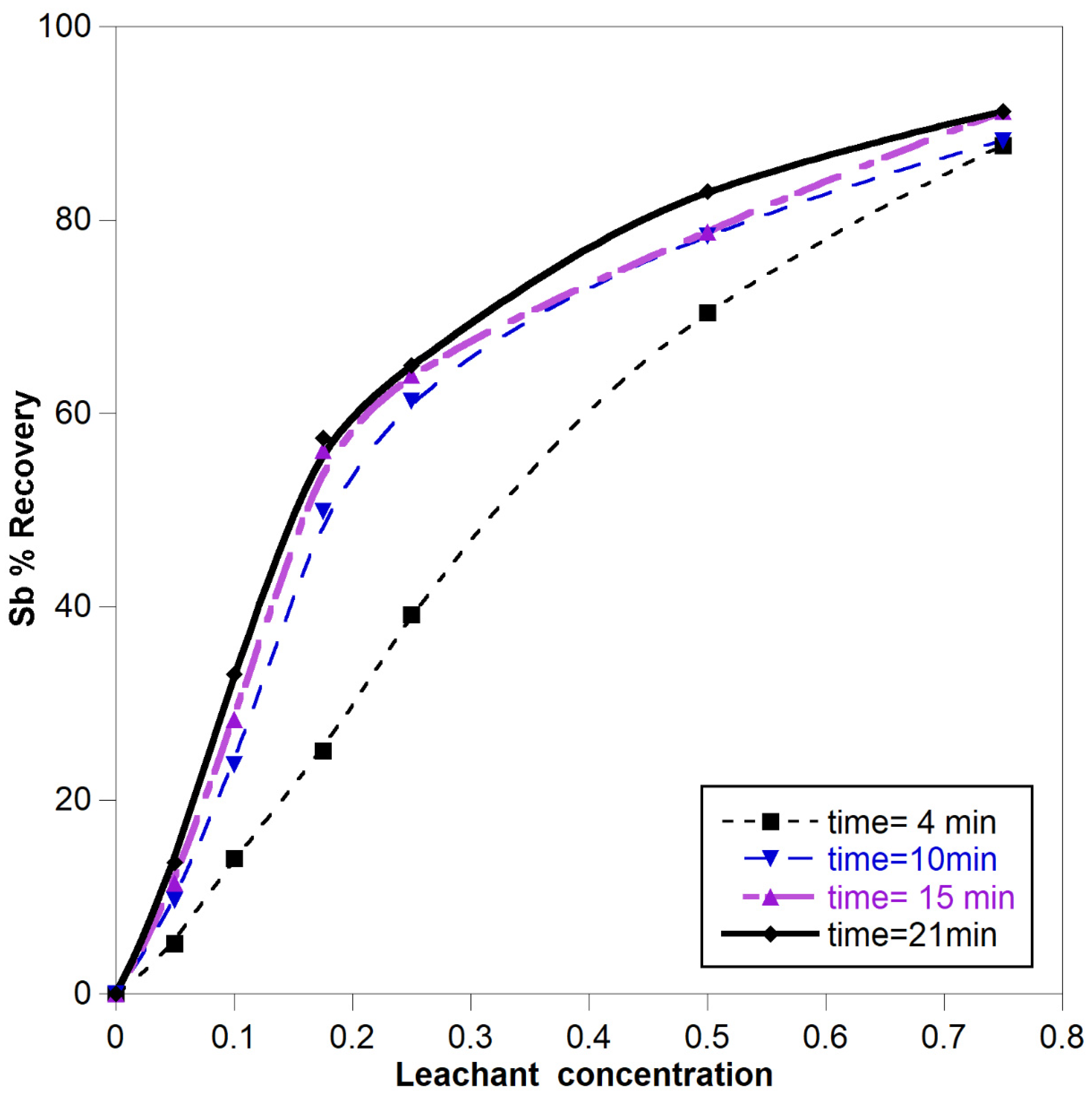
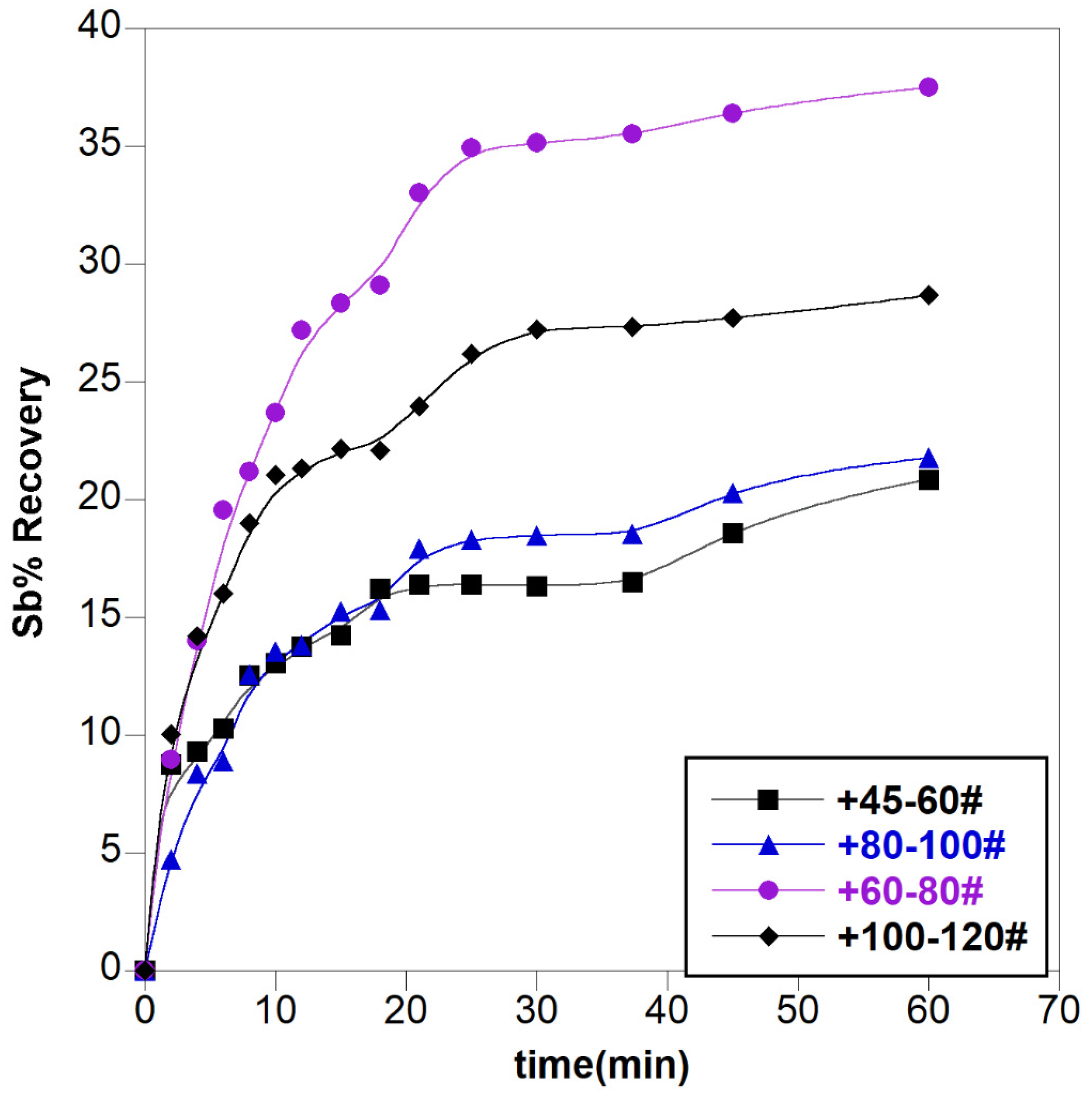
3.1.1. Effect of Leachant Concentration
- -
- Time for the start of the reaction
- -
- Time for middle of the reaction
- -
- Time near to equilibrium point
3.1.2. Effect of Other Parameters
3.2. Kinetic Consideration
- A.
- Accuracy of the Shrinking Core Model
- B.
- Effect of Leaching Parameters on Reaction Kinetics
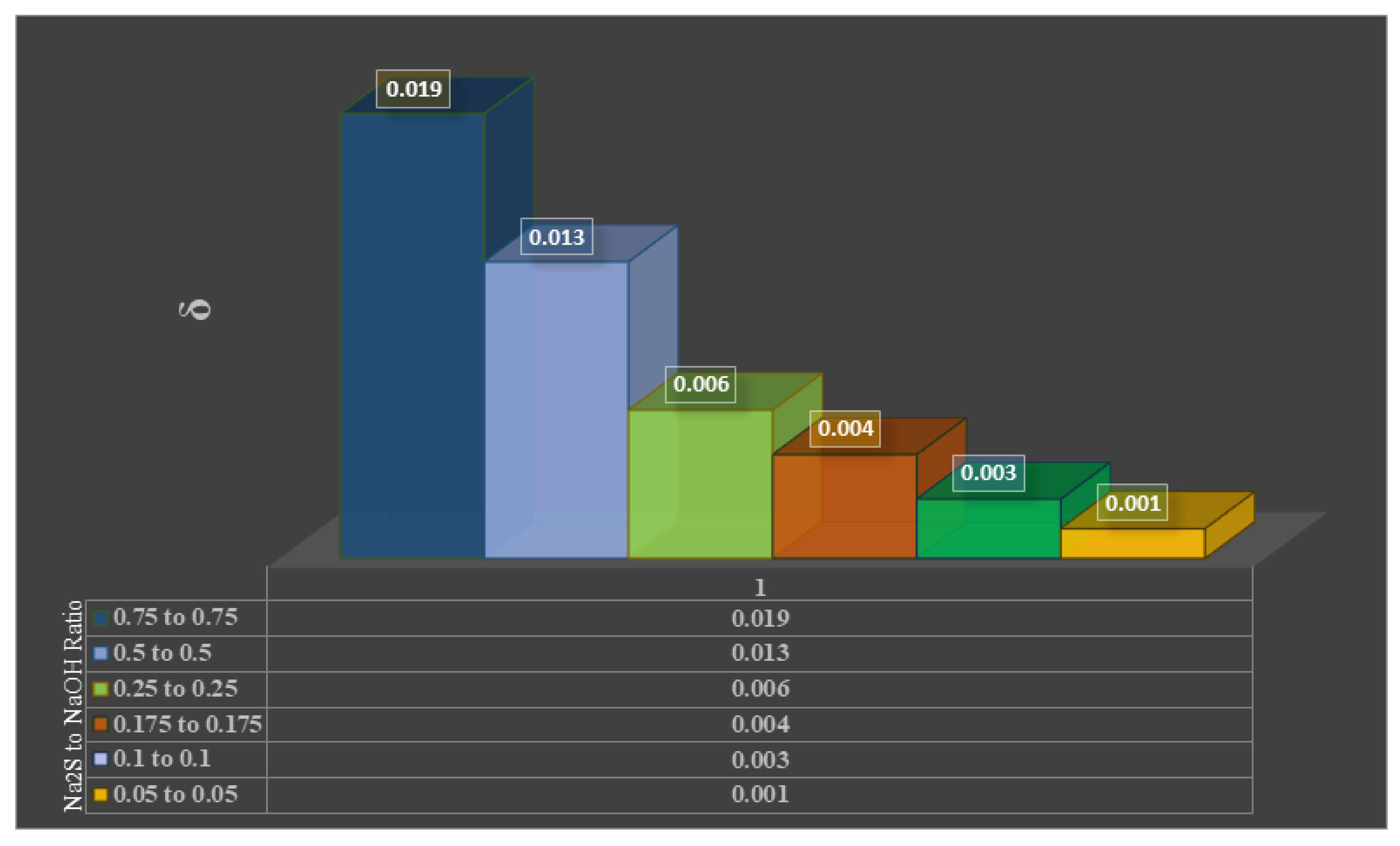
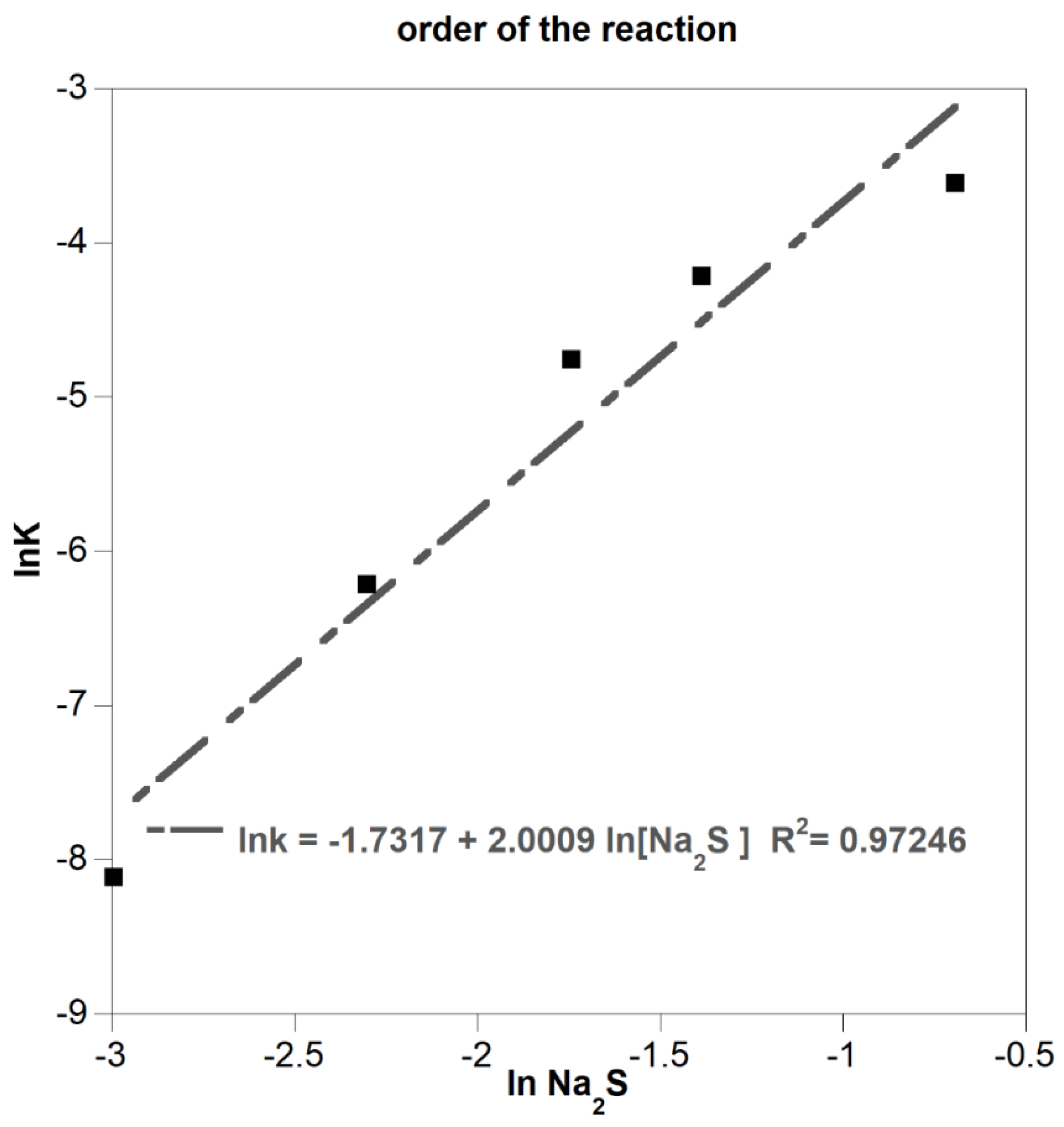
3.2.1. Effect of Leachant Concentration
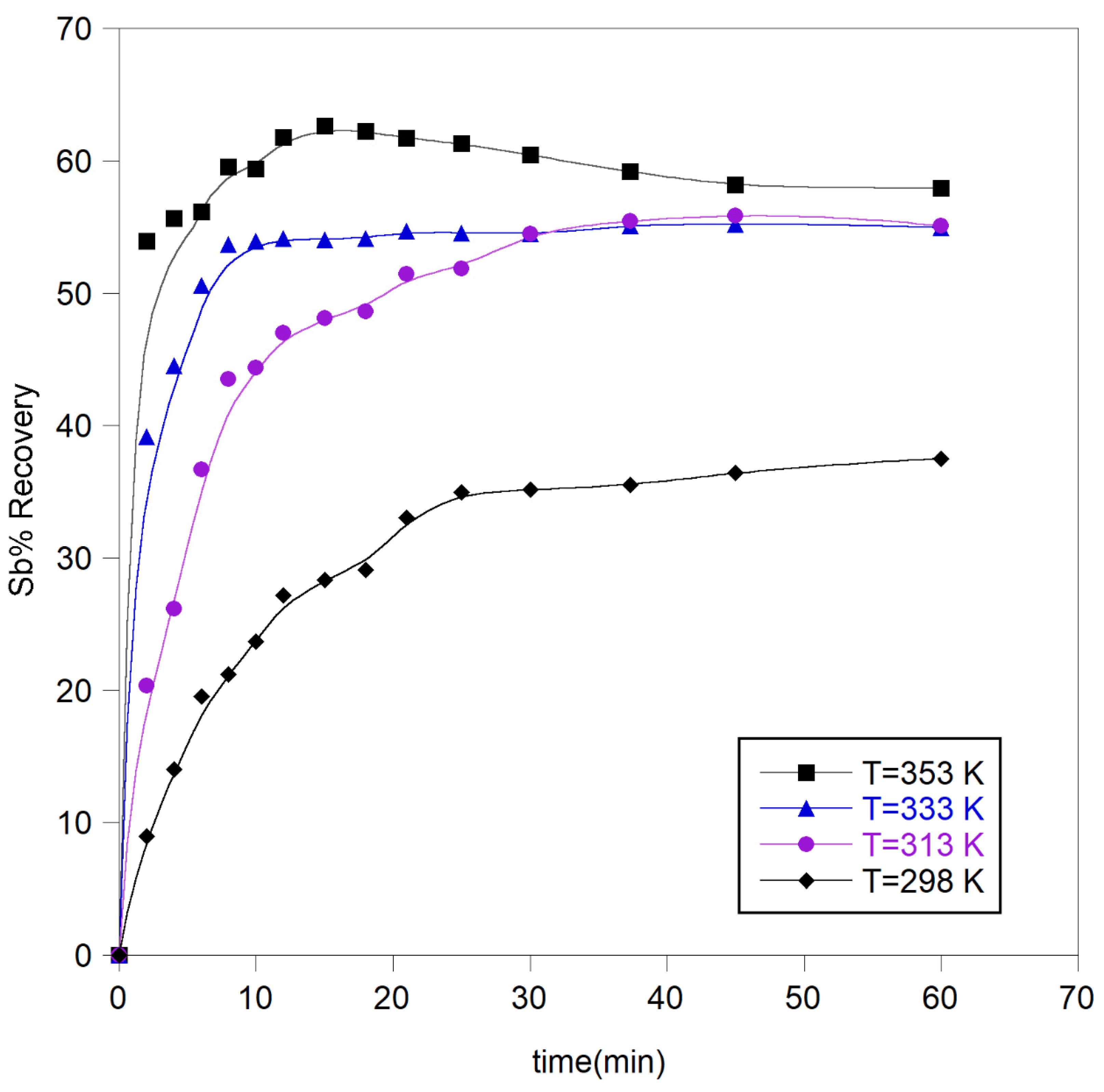
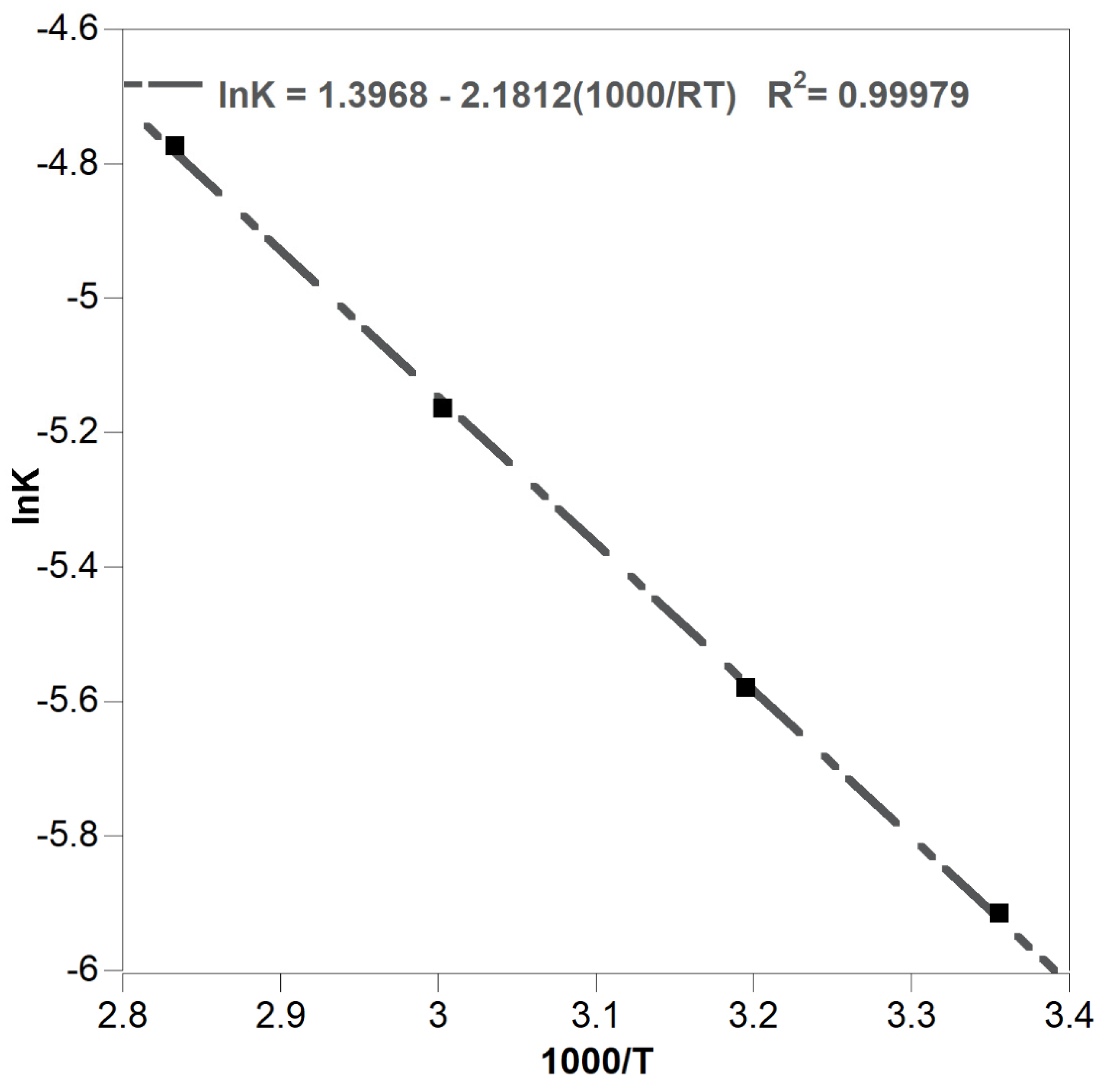
3.2.2. Effect of Temperature
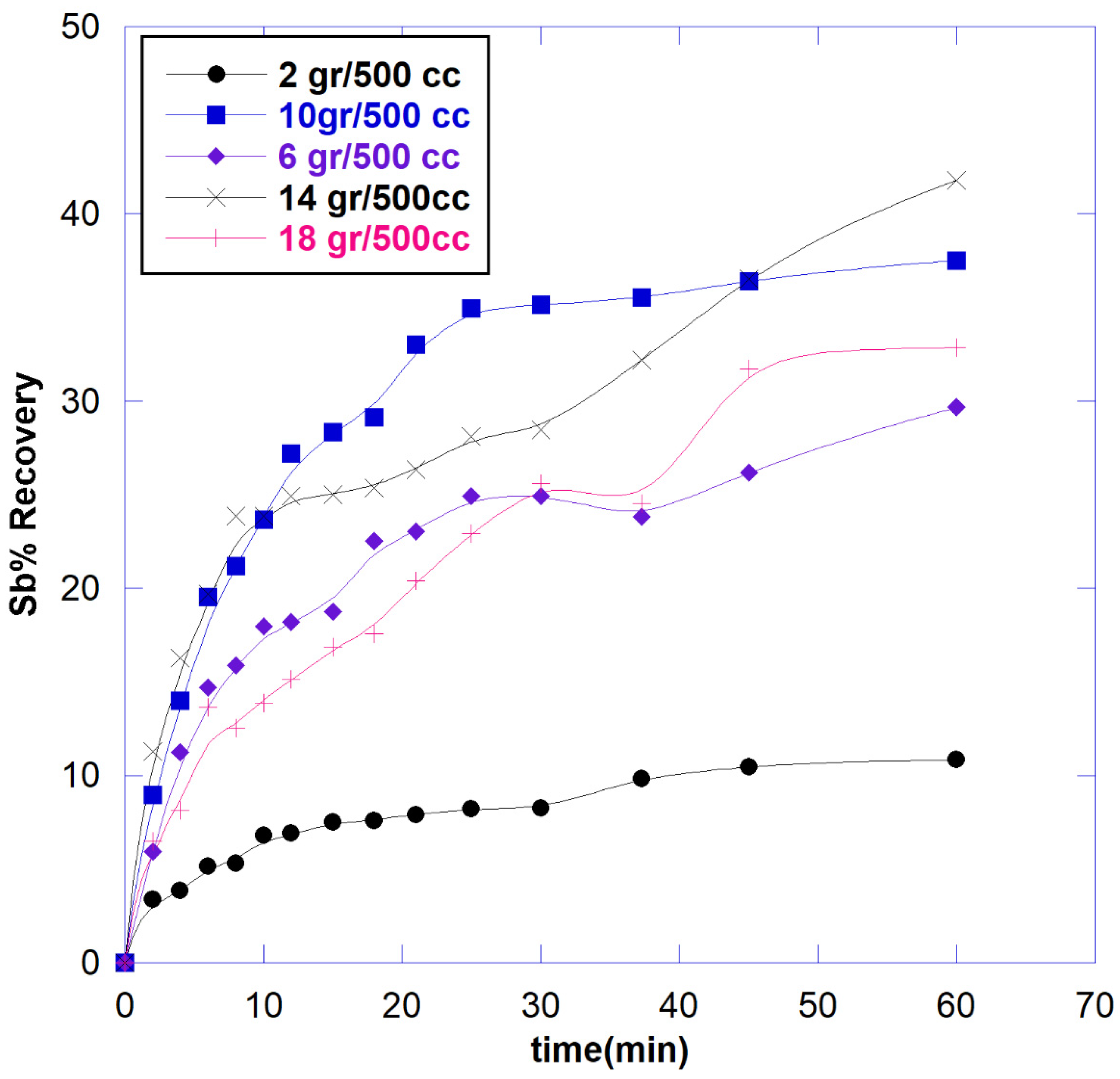
3.2.3. Effect of Solid to Liquid Ratio
3.2.4. Effect of Particle Size
3.3. Comparison of the Ash Layer Diffusion Model in SCM to Other Diffusion Models
3.4. The Consideration of Silica Formation as an Ash Layer
4. Conclusions
References
- Mahlangu, T.; Gudyanga, F.; Simbi, D. Reductive leaching of stibnite (Sb 2 S 3) flotation concentrate using metallic iron in a hydrochloric acid medium I: Thermodynamics. Hydrometallurgy 2006, 84, 192–203. [Google Scholar] [CrossRef]
- Li, L. et al. Separation and Recovery of Antimony from High Arsenic-bearing Flue Dusts through Selective Oxidation Using MnO2. ISIJ International 2017, 57, 581–586. [Google Scholar] [CrossRef]
- Qin, W.-q. et al. Mechanism of stibnite volatilization at high temperature. Journal of Central South University 2015, 22, 868–873. [Google Scholar] [CrossRef]
- Adelman, J. Mineral interactions in a gold mining environment: change in oxidation rate of stibnite as affected by the addition of varying amounts of pyrite in an oxygenated flow through system; McGill University, 2010. [Google Scholar]
- Kwong, Y.J.; Pratt, A.; Botton, G. Antimony leaching from stibnite and complex ores. In 7th International Conference on Acid Rock Drainage (ICARD); American Society of Mining and Reclamation (ASMR): St. Louis, MI, USA, 2006. [Google Scholar]
- Sminčáková, E. Leaching of natural stibnite using sodium hydroxide solution. JOM 2009, 61, 32. [Google Scholar] [CrossRef]
- Sminčáková, E.; Komorová, Ľ. Leaching of stibnite in NaOH solutions. Reactions 2008, 1, 10. [Google Scholar]
- Multani, R.S.; Feldmann, T.; Demopoulos, G.P. Antimony in the metallurgical industry: a review of its chemistry and environmental stabilization options. Hydrometallurgy 2016, 164, 141–153. [Google Scholar] [CrossRef]
- Tian, Q. et al. Ozonation leaching of a complex sulfidic antimony ore in hydrochloric acid solution. Hydrometallurgy 2016, 159, 126–131. [Google Scholar] [CrossRef]
- Ubaldini, S. et al. Process flow-sheet for gold and antimony recovery from stibnite. Hydrometallurgy 2000, 57, 187–199. [Google Scholar] [CrossRef]
- Biver, M.; Shotyk, W. , Stibnite (Sb2S3) oxidative dissolution kinetics from pH 1 to 11. Geochimica et Cosmochimica Acta 2012, 79, 127–139. [Google Scholar] [CrossRef]
- Raschman, P.; Sminčáková, E. Kinetics of leaching of stibnite by mixed Na 2 S and NaOH solutions. Hydrometallurgy 2012, 113, 60–66. [Google Scholar] [CrossRef]
- Dodangeh, A. et al. Leaching kinetics of stibnite in sodium hydroxide solution; 2014. [Google Scholar]
- Tian-cong, Z. The metallurgy of antimony/Central South University of Technology; Press Changsha the Peoples Republic, 1988; Volume 731. [Google Scholar]
- Zunkel, A.; Habashi, F. Principles of Extractive Metallurgy, Vol. 1: General Principles. Vol. 2: Hydrometallurgy; JSTOR, 1971. [Google Scholar]
- Levenspiel, O.; Levenspiel, C. Chemical reaction engineering; Wiley: New York, 1972. [Google Scholar]
- Prosser, A.P. Review of uncertainty in the collection and interpretation of leaching data. Hydrometallurgy 1996, 41, 119–153. [Google Scholar] [CrossRef]
- Lindman, N.; Simonsson, D. On the application of the shrinking core model to liquid—solid reactions. Chemical Engineering Science 1979, 34, 31–35. [Google Scholar] [CrossRef]
- Awe, S.A.; Samuelsson, C.; Sandström, Å. Dissolution kinetics of tetrahedrite mineral in alkaline sulphide media. Hydrometallurgy 2010, 103, 167–172. [Google Scholar] [CrossRef]
- Demopoulos, G.; Papangelakis, V. Sulfuric Acid Pressure Leaching of a Limonitic Laterite: Chemistry and Kinetics. Hydrometallurgy 1998, 49, 23–46. [Google Scholar]
- Georgiou, D.; Papangelakis, V. Sulphuric acid pressure leaching of a limonitic laterite: chemistry and kinetics. Hydrometallurgy 1998, 49, 23–46. [Google Scholar] [CrossRef]
- Živković, Ž. et al. Kinetics and mechanism of Sb 2 S 3 oxidation process. Thermochimica Acta 2002, 383, 137–143. [Google Scholar] [CrossRef]
- Younesi, S. , et al. Kinetic mechanisms of cementation of cadmium ions by zinc powder from sulphate solutions. Hydrometallurgy 2006, 84, 155–164. [Google Scholar]
- Havlík, T. Hydrometallurgy: Principles and applications; Elsevier, 2014. [Google Scholar]
- Sminčáková, E.; Komorová, L. Kinetika lúhovania Sb2S3 v roztoku NaOH. Acta Montanistica Slovaca 2007, 12, 328–333. [Google Scholar]
- Anderson, C. Hydrometallurgically treating antimony-bearing industrial wastes. JOM 2001, 53, 18–20. [Google Scholar] [CrossRef]
- Wen, C. Noncatalytic heterogeneous solid-fluid reaction models. Industrial & Engineering Chemistry 1968, 60, 34–54. [Google Scholar]
- Baláž, P.; Achimovičová, M. Selective leaching of antimony and arsenic from mechanically activated tetrahedrite, jamesonite and enargite. International Journal of Mineral Processing 2006, 81, 44–50. [Google Scholar] [CrossRef]
- Baláž, P. et al. Non-oxidative leaching of mechanically activated stibnite. Hydrometallurgy 1992, 31, 201–212. [Google Scholar] [CrossRef]
- Baláž, P. et al. Mechano-chemical treatment of tetrahedrite as a new non-polluting method of metals recovery. In Hydrometallurgy’94; Springer, 1994; pp. 209–218. [Google Scholar]
- Bischoff, K. Accuracy of the pseudo steady state approximation for moving boundary diffusion problems. Chemical Engineering Science 1963, 18, 711–713. [Google Scholar] [CrossRef]
- Bischoff, K. Further comments on the pseudo steady state approximation for moving boundary diffusion problems. Chem. Eng. Sci. 1965, 20, 783–784. [Google Scholar] [CrossRef]
- Stakgold, I.; Bischoff, K.; Gokhale, V. Validity of the pseudo-steady-state approximation. International Journal of Engineering Science 1983, 21, 537–542. [Google Scholar] [CrossRef]
- Lapidus, G. Mathematical modelling of metal leaching in nonporous minerals. Chemical engineering science 1992, 47, 1933–1941. [Google Scholar] [CrossRef]
- Liddell, K.C. Shrinking core models in hydrometallurgy: What students are not being told about the pseudo-steady approximation. Hydrometallurgy 2005, 79, 62–68. [Google Scholar] [CrossRef]
- Dickinson, C.; Heal, G. Solid–liquid diffusion controlled rate equations. Thermochimica Acta 1999, 340, 89–103. [Google Scholar] [CrossRef]
- Falayi, T.; Ntuli, F.; Okonta, F.N. Kinetic and thermodynamic parameters of silica leaching from Camden power station fly ash; 2015. [Google Scholar]
- Koech, L. et al. Leaching kinetics of bottom ash waste as a source of calcium ions. Journal of the Air & Waste Management Association 2015, 65, 126–132. [Google Scholar]
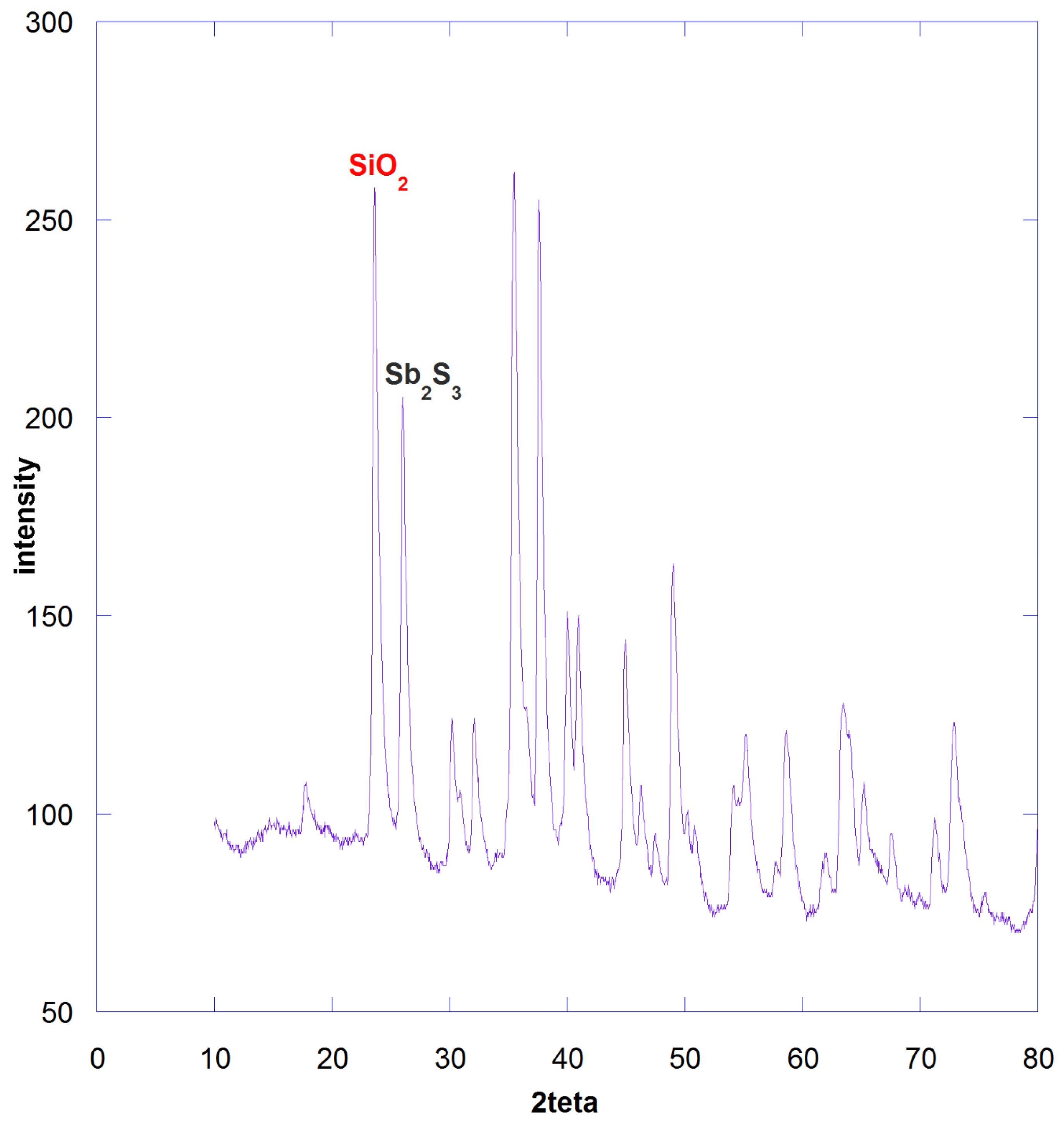
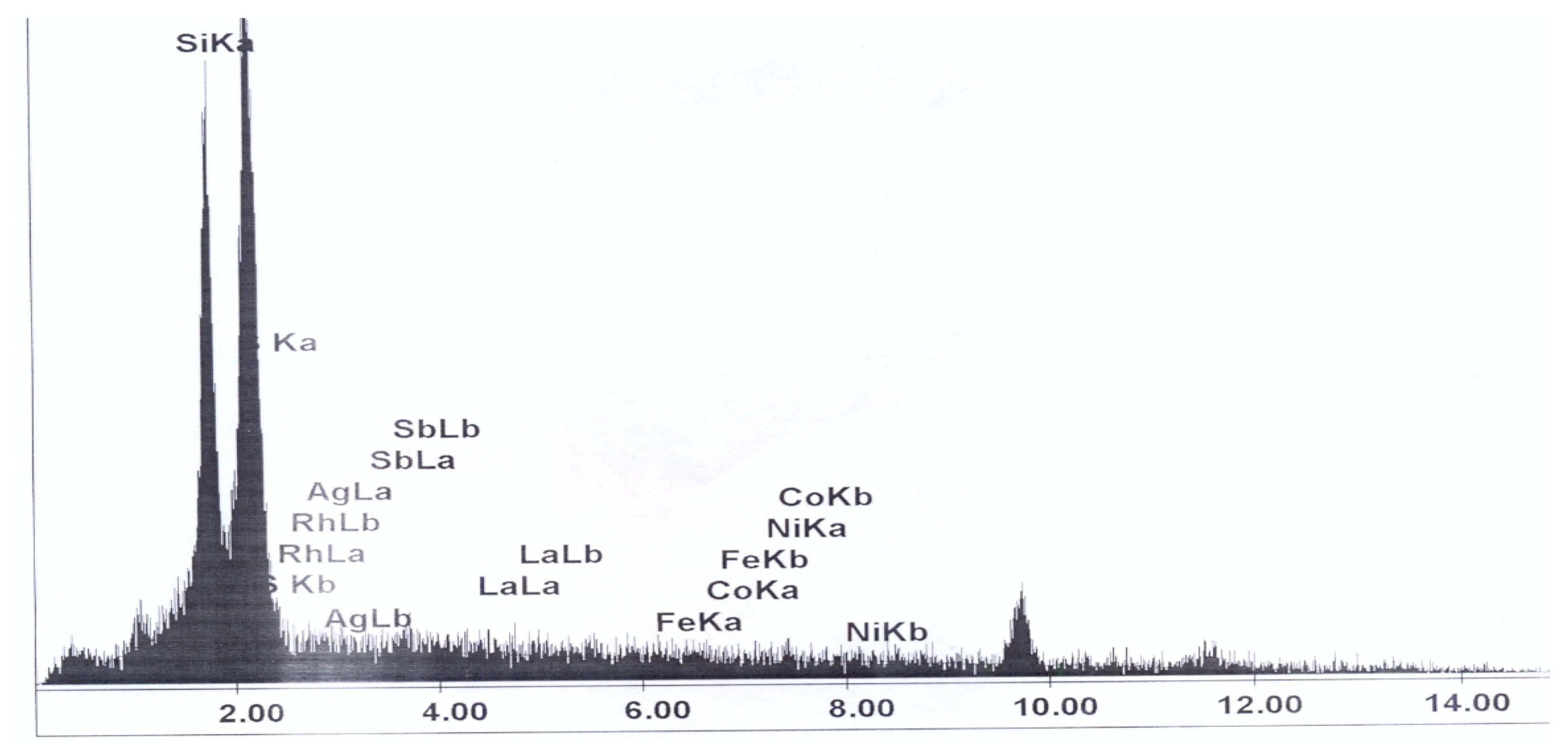

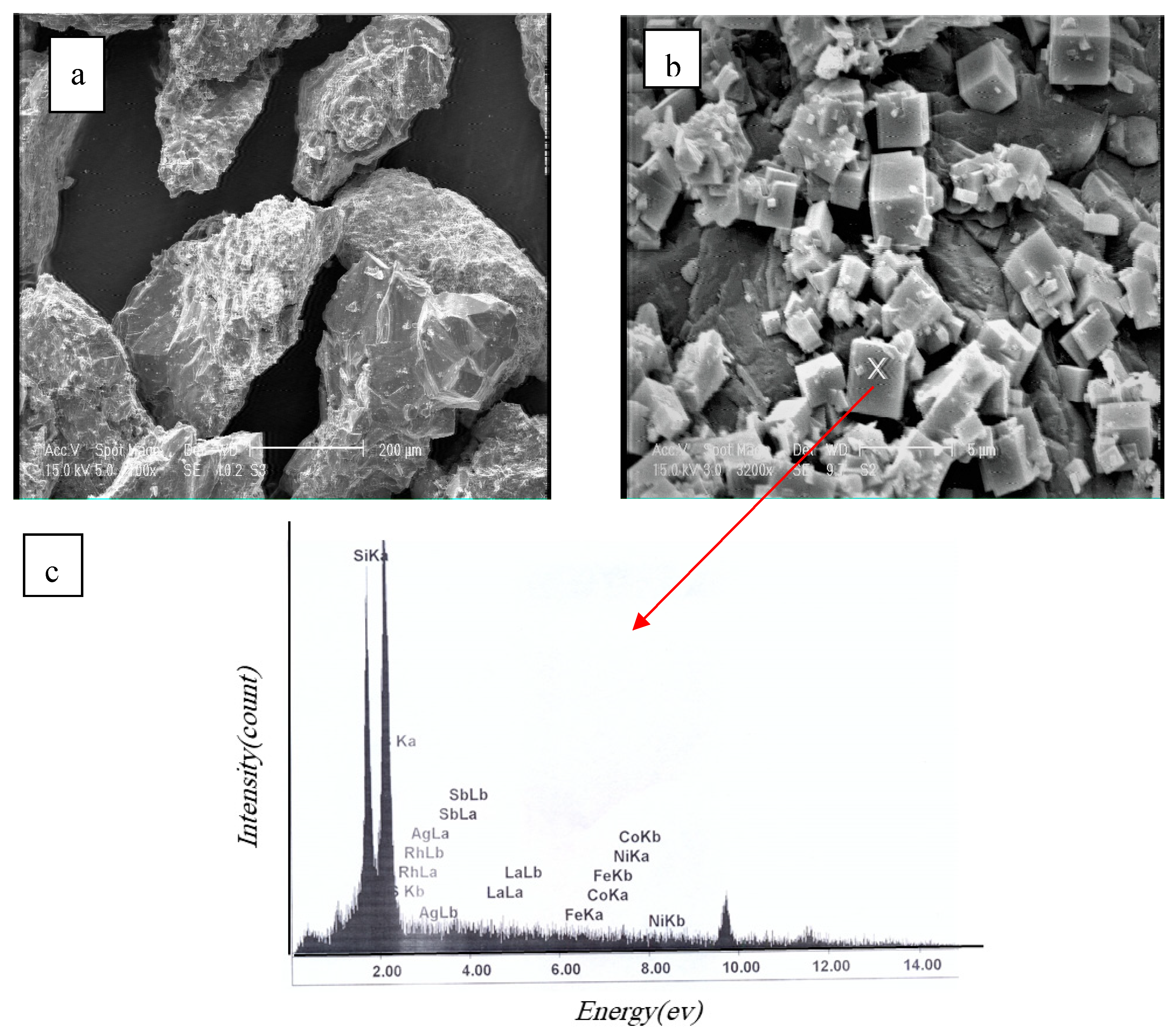
| Element of Mixture | Weight Percent |
|---|---|
| Sb | 44.3 |
| SiO2 | 31.2 |
| S | 17.8 |
| Mo | 1.12 |
| Al2O3 | 1.03 |
| TiO2 | 0.14 |
| Fe | 0.30 |
| As | 0.079 |
| Rh | 0.11 |
| Cd | 0.01 |
| In2O3 | 0.09 |
| Pb | 1.05 |
| Element of Mixture | Weight Percent |
|---|---|
| Sb | 3.86 |
| SiO2 | 84.5 |
| S | 1.71 |
| Mo | 0.3 |
| Al2O3 | 1.26 |
| TiO2 | 0.22 |
| Fe | 1.79 |
| As | - |
| Rh | 0.01 |
| Cd | 0.018 |
| In2O3 | 0.042 |
| Pb | 1.23 |
| Mechanism | f(x) |
|---|---|
|
Controlled by diffusion from ash layer Controlled by chemical reaction Controlled by diffusion from film layer |
1-3(1-x) 2 / 3+2(1-x)=k1t 1-(1-x)1/3=k2t x=k3t |
| Different Ratios | ||||||
|---|---|---|---|---|---|---|
| Ratio Na2S/NaOH | K1(s-1) | R12 | K2(s-1) | R22 | K3(s-1) | R32 |
| 0.25 | 0.0007 | 0.993 | 0.0052 | 0.746 | 0.0145 | 0.714 |
| 0.5 | 0.0011 | 0.953 | 0.0041 | 0.929 | 0.0117 | 0.918 |
| 2 | 0.0011 | 0.944 | 0.0052 | 0.834 | 0.014 | 0.814 |
| 4 | 0.0005 | 0.961 | 0.002 | 0.924 | 0.008 | 0.915 |
| Equal Ratios | ||||||
| Ratio Na2S/NaOH | K1(s-1) | R12 | K2(s-1) | R22 | K3(s-1) | R32 |
| 0.05/0.05 | 0.003 | 0.993 | 0.0027 | 0.885 | 0.0078 | 0.872 |
| 0.1/0.1 | 0.0021 | 0.992 | 0.0064 | 0.856 | 0.0173 | 0.809 |
| 0.175/0.175 | 0.008 | 0.95 | 0.0157 | 0.884 | 0.0035 | 0.826 |
| 0.25/0.25 | 0.0148 | 0.955 | 0.0234 | 0.647 | 0.043 | 0.85 |
| 0.5/0.5 | 0.023 | 0.968 | 0.0201 | 0.899 | 0.0321 | 0.882 |
| 0.75/0.75 | 0.01 | 0.951 | 0.0075 | 0.869 | 0.0058 | 0.832 |
| Different Ratios | ||||||
|---|---|---|---|---|---|---|
| Temperature(K) | K1(s-1) | R12 | K2(s-1) | R22 | K3(s-1) | R32 |
| 298 | 0.002 | 0.992 | 0.0064 | 0.856 | 0.0173 | 0.809 |
| 313 | 0.0065 | 0.925 | 0.0131 | 0.712 | 0.0324 | 0.6 |
| 333 | 0.0066 | 0.929 | 0.0158 | 0.709 | 0.0377 | 0.826 |
| 353 | 0.003 | 0.9 | 0.0027 | 0.898 | 0.0045 | 0.897 |
| Solid to Liquid Ratio(gr/cc) | Equation | Regression Coefficient (R2) |
|---|---|---|
| 2/500 | F(x)=0.0011t | 0.958 |
| 6/500 | F(x)=0.0006t | 0.978 |
| 10/500 | F(x)=0.0020t | 0.992 |
| 14/500 | F(x)=0.001t | 0.931 |
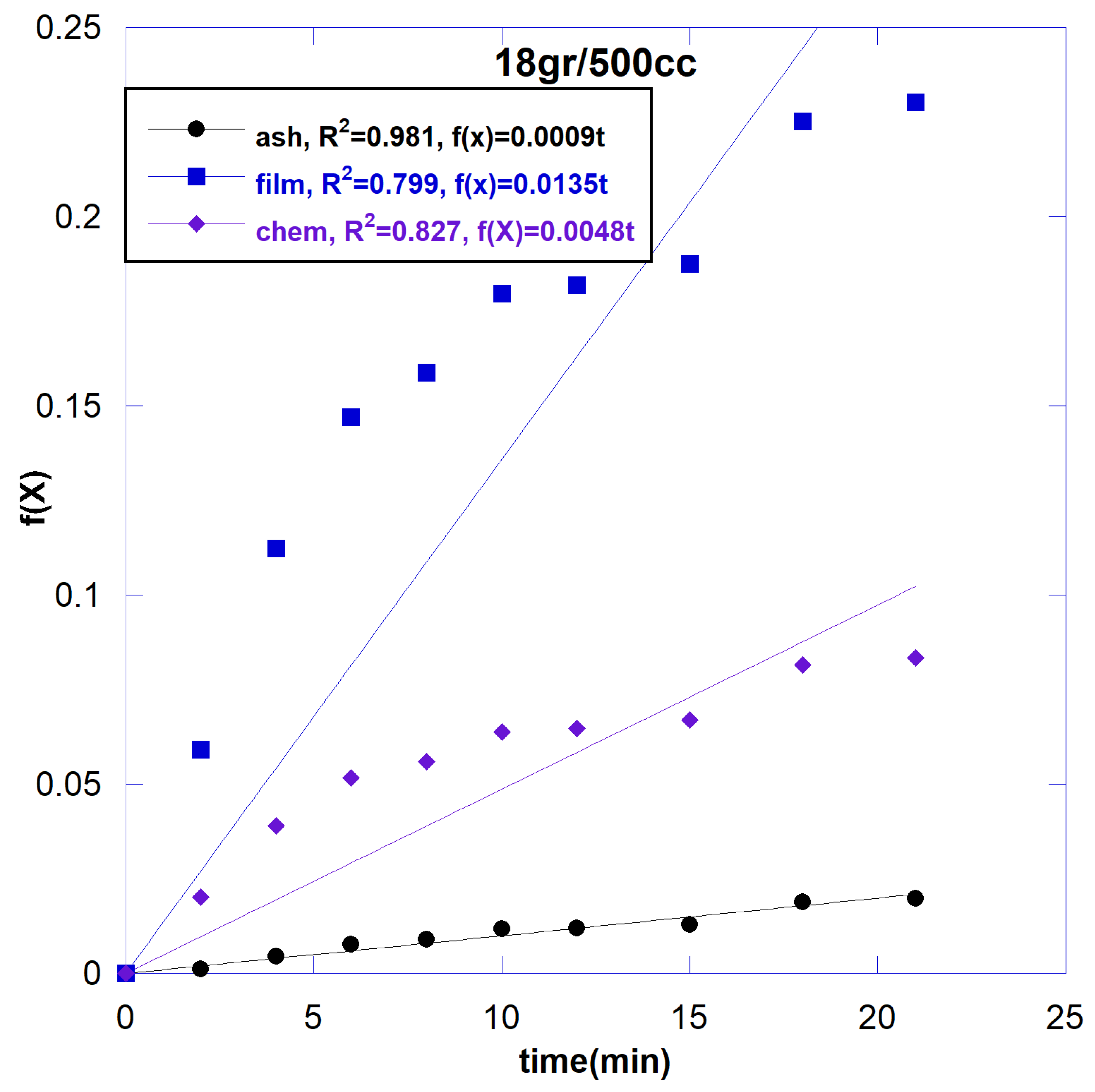
| 18/500 | F(x)=0.0008t | 0.981 |
| Particle Size (Micrometer) | Equation | R2 |
|---|---|---|
| 250-350 | F(x)=0.0011t | 0.979 |
| 175-250 | F(x)=0.002t | 0.992 |
| 150-175 | F(x)=0.0005t | 0.949 |
| 105-150 | F(x)=0.0011t | 0.919 |
| Model | equation | Rate Coefficient(s-1) | R2 |
| Ash Layer Diffusion [16] | F(x)= 1-3(1-x) 2 / 3+2(1-x) =k1t | 0.0021 | 0.992 |
| D5 [36] | F(x)=((1-x)-1/3-1)2=k5t | 0.0010 | 0.980 |
| D12 [36] | F(x)=0.2(1-x)-5/3-0.25(1-x)-4/3+0.05=k9t | 0.0006 | 0.973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




