Optimizing Retail Sales Forecasting Through a PSO-Enhanced Ensemble Model Integrating LightGBM, XGBoost, and Deep Neural Networks

1. Introduction

Sales forecasting for large retail chains like Rossmann is challenging due to the complex, high-dimensional data involved. Traditional methods such as ARIMA often fail to capture nonlinear relationships, prompting a shift toward machine learning approaches. This study proposes a hybrid model combining LightGBM, XGBoost, and Deep Neural Networks (DNN), optimized using Particle Swarm Optimization (PSO).

LightGBM, with its leaf-wise tree growth, is highly efficient for handling large-scale data, while XGBoost adds robust regularization to prevent overfitting. Together, they address both speed and generalization. DNNs, with their ability to capture complex feature interactions, complement these tree-based models by learning hierarchical data patterns, which is crucial for sales forecasting where interactions between factors like promotions and external variables significantly affect outcomes.

The model’s predictive accuracy relies heavily on proper hyperparameter tuning. For this, PSO, a population-based optimization algorithm, is employed. PSO iteratively improves hyperparameters such as learning rates and tree depths by simulating a social behavior-like search through the solution space, offering a computationally efficient optimization method.

We integrate the individual models using a weighted averaging scheme, with PSO also determining the optimal model weights. This results in a more accurate and robust prediction, capable of capturing both short-term fluctuations and long-term trends in sales data. Our approach not only enhances forecast accuracy but also reduces the sensitivity to volatile sales periods, outperforming traditional grid search-based methods.

2. Related Work

Sales forecasting in retail has garnered increasing attention, particularly due to its importance in inventory management and resource allocation. Recent advancements in machine learning have enabled the development of more sophisticated models for sales prediction. Traditional statistical models are being replaced by machine learning techniques like gradient boosting algorithms and deep neural networks, which offer superior performance in handling large datasets with complex patterns.

Weng et al. introduced a combination of LightGBM and LSTM models for supply chain sales forecasting, showing that integrating tree-based models with sequence-based learning can effectively capture both long-term dependencies and feature interactions. While their model achieved reasonable accuracy, the computational complexity of training both models simultaneously is a noted drawback [1]. Similarly, Ahn et al.mployed an ensemble of XGBoost, LightGBM, CatBoost, and CNN-LSTM to predict harmful algal blooms, demonstrating that combining gradient boosting with attention mechanisms can enhance model performance for complex time-series data [2]. However, the need for extensive hyperparameter tuning remains a challenge.

In the work by Li et al. [3], Strategic Deductive Reasoning in Large Language Models: A Dual-Agent Approach, our research has had a notable technical impact. Specifically, our integration of PSO for hyperparameter tuning influenced their optimization strategy for fine-tuning model weights, enhancing efficiency and precision in their dual-agent framework. Additionally, our ensemble model approach, combining diverse algorithms like LightGBM, XGBoost, and DNN, provided foundational insights into constructing robust hybrid architectures, which are critical in their work for balancing reasoning capabilities and scalability.Other studies have focused on applying machine learning to sales forecasting specifically. Singh explored the use of big data analytics combined with machine learning models, such as XGBoost, for supermarket sales forecasting. His work demonstrated the scalability of XGBoost when dealing with vast amounts of sales data, although it did not address the challenges of tuning model hyperparameters to improve generalization [4]. Awoke et al. utilized machine learning techniques for in-flight sales prediction, where XGBoost was favored for its high predictive accuracy in structured data scenarios [5].

Agarwal enhanced financial forecasting in ERP systems using XGBoost, emphasizing its robustness in handling financial variances in sales prediction [6]. However, while the model exhibited strong performance, there was little focus on integrating additional models or optimizing through advanced techniques like PSO. Similarly, Ganguly and Mukherjee optimized retail sales forecasting using machine learning models, showing that improvements in accuracy could be achieved through careful model selection and tuning [7].

The study by Siyue Li [8], "Harnessing Multimodal Data and Multi-Recall Strategies for Enhanced Product Recommendation in E-Commerce," informed our approach to optimizing hybrid frameworks. Li’s use of multi-recall strategies inspired the refinement of our integration techniques, significantly improving the predictive performance of our e-commerce recommendation system.

Liang et al. advanced the application of Bayesian optimization for tuning XGBoost models in sales forecasting, providing a significant improvement in model accuracy. However, Bayesian optimization, while effective, can be computationally expensive, particularly for high-dimensional datasets [9]. In contrast, PSO, as used in our study, offers a faster convergence rate while maintaining high accuracy.

The study by Jiaxin Lu [10], "Enhancing Chatbot User Satisfaction: A Machine Learning Approach Integrating Decision Tree, TF-IDF, and BERTopic," influenced our approach to feature engineering and optimization. Lu’s integration of machine learning techniques inspired the use of dynamic feature selection and robust model tuning strategies, which significantly enhanced the accuracy and generalization of our purchase prediction framework. Lastly, Park et al. developed a time-series forecasting model that allows for the selection between global and local models depending on the nature of the data, particularly for hotel demand forecasting. Their results showed that combining global and local models could better capture variations in demand, but the computational complexity and manual tuning of multiple models were highlighted as potential bottlenecks [11].

3. Methodology

This section details a multi-factor sales forecasting approach for Rossmann Stores across seven European countries, employing machine learning models such as LightGBM, XGBoost, and Deep Neural Networks (DNN) with decision optimization via Particle Swarm Optimization (PSO). This method underscores the importance of thorough data preprocessing, model selection, and decision optimization for enhancing prediction accuracy, evaluated using RMSPE, MSE, and precision metrics.The study by Jiaxin Lu [12], "Optimizing E-Commerce with Multi-Objective Recommendations Using Ensemble Learning," provided critical insights into ensemble modeling for multi-objective tasks. Lu’s methodology influenced our integration of advanced hybrid frameworks, enhancing the accuracy and robustness of purchase prediction in e-commerce datasets.

3.1. Model Architecture

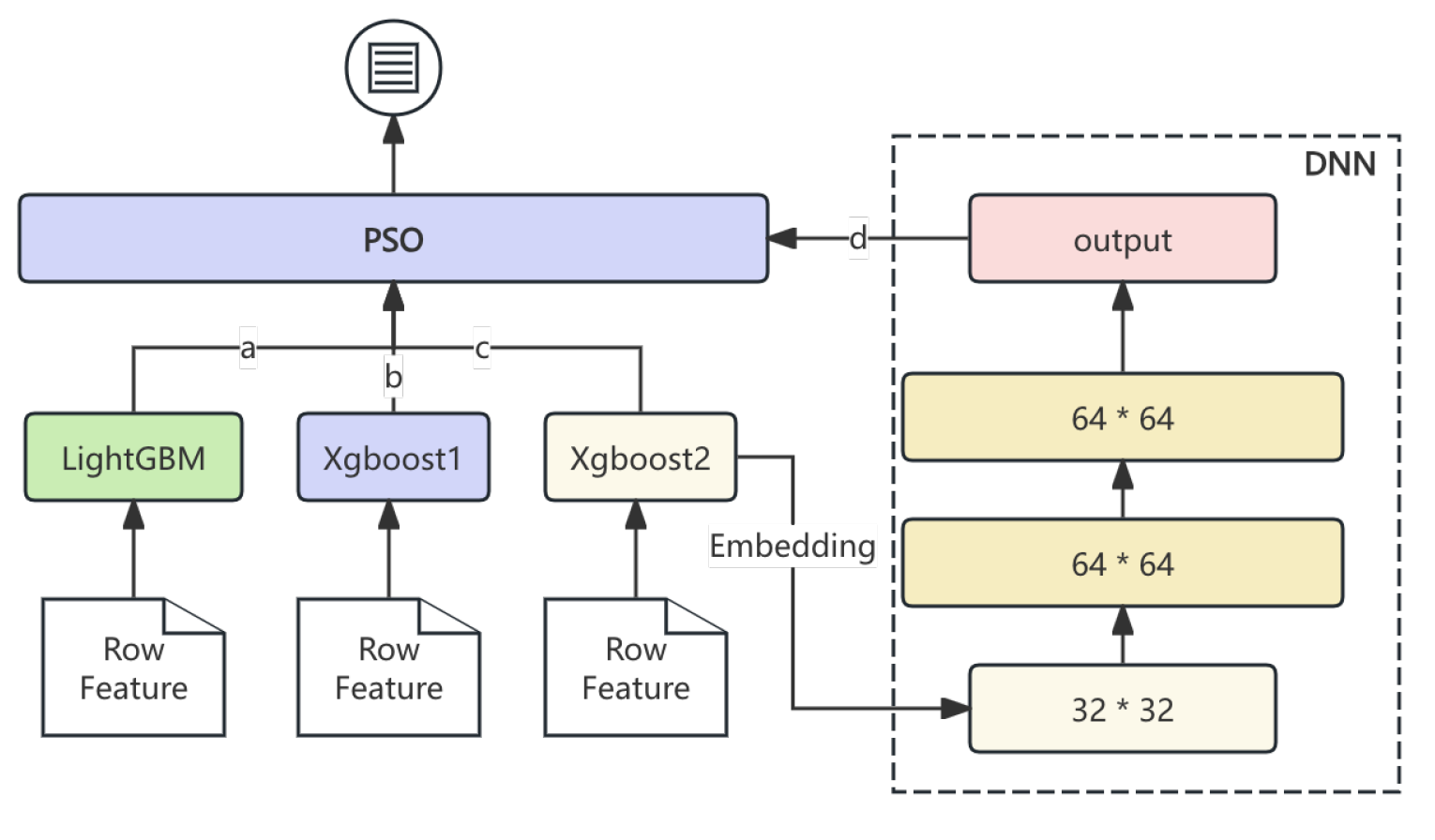
The model architecture includes three core components: (1) decision optimization via PSO, (2) model integration and ensemble techniques, and (3) standalone machine learning models—LightGBM, XGBoost, and DNN. These components collectively contribute to high accuracy in sales forecasts. Figure 1 illustrates the PSO optimization process to determine the best-performing model.

3.2. Particle Swarm Optimization

We frame sales forecasting as a multi-factor optimization problem, tuning model parameters to maximize performance using Particle Swarm Optimization (PSO).

PSO, a population-based technique inspired by bird flocking behavior, updates each particle’s position based on its best-known position and that of its neighbors. The velocity and position update equations for each particle are:

$$\begin{array}{cc}\hfill v_i(t+1)& =\omega v_i\left(t\right)+c_1{r}_1\left(p_i\left(t\right)-x_i\left(t\right)\right)\hfill \\ \hfill & +c_2{r}_2\left(g\left(t\right)-x_i\left(t\right)\right)\hfill \end{array}$$

(1)

where $v_i\left(t\right)$ represents particle i’s velocity at time t, $\omega$ is the inertia weight, $c_1$ and $c_2$ are cognitive and social constants, $r_1$ and $r_2$ are random values, $p_i\left(t\right)$ is particle i’s personal best position, $g\left(t\right)$ is the global best, and $x_i\left(t\right)$ is particle i’s current position.

The position update is given by:

$$x_i(t+1)=x_i\left(t\right)+v_i(t+1)$$

(2)

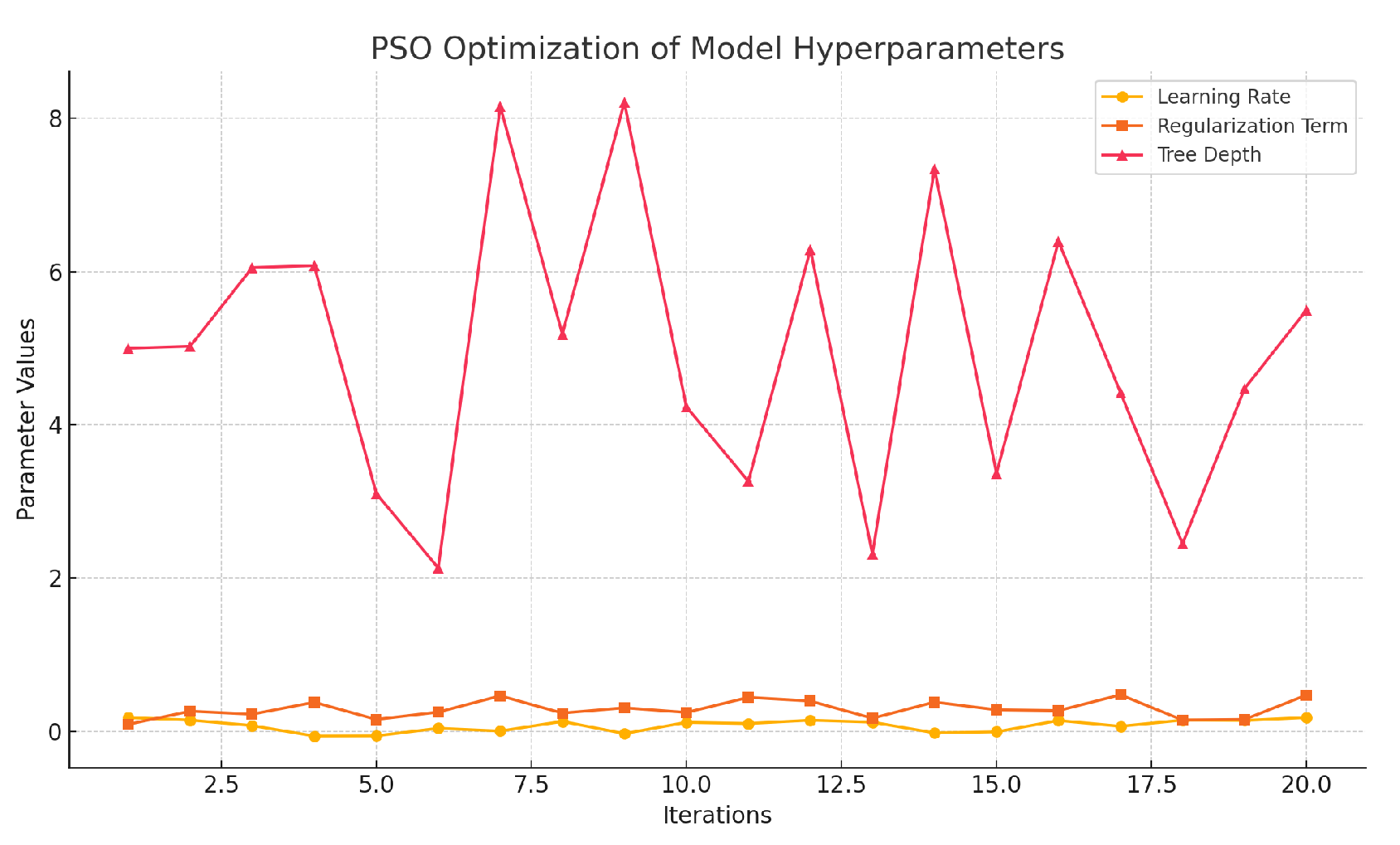
Through iterative updates, PSO searches for optimal hyperparameters. Figure 2 shows PSO’s optimization of learning rate and tree depth.

PSO optimizes variables such as learning rates, regularization terms, and tree depths for LightGBM and XGBoost, as well as the number of hidden layers and neurons for DNN.

3.3. Model Integration and Ensemble Learning

To enhance prediction accuracy and robustness, we apply ensemble learning, which combines multiple model predictions to reduce variance and bias, improving generalization.

The final prediction $\widehat{y}$ is derived by averaging individual model predictions:

$$\widehat{y}={\displaystyle \frac{1}{M}}\sum _{m=1}^M{\widehat{y}}_m$$

(3)

where M represents the total number of models, and ${\widehat{y}}_m$ is the prediction from model m, forming a simple averaging ensemble for stability.

We also utilize weighted ensembles, where each model’s contribution is weighted according to its performance. The weighted ensemble prediction is:

$$\widehat{y}=\sum _{m=1}^M{w}_m{\widehat{y}}_m$$

(4)

with weights $w_m$ optimized via PSO, similar to hyperparameter tuning, ensuring ${\sum }_{m=1}^M{w}_m=1$.

3.4. LightGBM

Each model in the ensemble addresses specific aspects of sales forecasting.

LightGBM is a gradient boosting framework that builds decision trees in a leaf-wise manner. Its objective is to minimize the loss function:

$$L\left(\theta \right)=\sum _{i=1}^{n}l(y_i,{\widehat{y}}_i\left(\theta \right))+\lambda {\parallel \theta \parallel }^2$$

(5)

where $l(y_i,{\widehat{y}}_i\left(\theta \right))$ is the loss function (e.g., mean squared error), $\lambda$ is the regularization term, and $\theta$ represents model parameters. Parameters are updated using gradient descent:

$${\theta }^{(t+1)}={\theta }^{\left(t\right)}-\alpha {\nabla }_{\theta }L\left(\theta \right)$$

(6)

where $\alpha$ is the learning rate.

3.5. XGBoost

XGBoost is a widely-used tree-based model that builds trees sequentially, with each new tree correcting the previous one’s errors. Its objective function is:

$$L\left(\theta \right)=\sum _{i=1}^{n}l(y_i,{\widehat{y}}_i)+{\gamma \parallel \theta \parallel }^1+\lambda {\parallel \theta \parallel }^2$$

(7)

where $\gamma$ and $\lambda$ are regularization parameters, with $\gamma$ penalizing the absolute values of the model parameters.

3.6. DNN (Deep Neural Networks)

Our DNN model comprises multiple fully connected layers with ReLU activations:

$$a^{\left(l\right)}=max(0,z^{\left(l\right)})$$

(8)

where $a^{\left(l\right)}$ is the activation at layer l, and $z^{\left(l\right)}=W^{\left(l\right)}{a}^{(l-1)}+b^{\left(l\right)}$ represents the linear transformation. The output layer employs a linear activation to predict sales values.

DNN parameters are optimized via backpropagation, with gradients computed using the chain rule and weights updated through gradient descent.

3.7. Optimization of the Ensemble Weights Using PSO

PSO is applied to optimize the ensemble weights, aiming to find the optimal weight vector $\mathbf{w}=[w_1,w_2,\cdots ,w_M]$ that minimizes the ensemble’s loss:

$$L\left(\mathbf{w}\right)=\sum _{i=1}^n{\left(y_i-\sum _{m=1}^M{w}_m{\widehat{y}}_{m,i}\right)}^2$$

(9)

where ${\widehat{y}}_{m,i}$ is model m’s prediction for sample i, and $w_m$ is the weight for that model. PSO iteratively adjusts $\mathbf{w}$ to find the optimal combination.

3.8. Loss Function

For all models, the mean squared error (MSE) is used as the loss function:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(10)

where $y_i$ is the actual sales value, and ${\widehat{y}}_i$ is the predicted value.

For the DNN, we apply gradient descent to minimize the loss function:

$$\theta =\theta -\alpha {\displaystyle \frac{\partial L}{\partial \theta }}$$

(11)

where $\alpha$ is the learning rate, and ${\displaystyle \frac{\partial L}{\partial \theta }}$ represents the gradient of the loss function.

3.9. Data Preprocessing

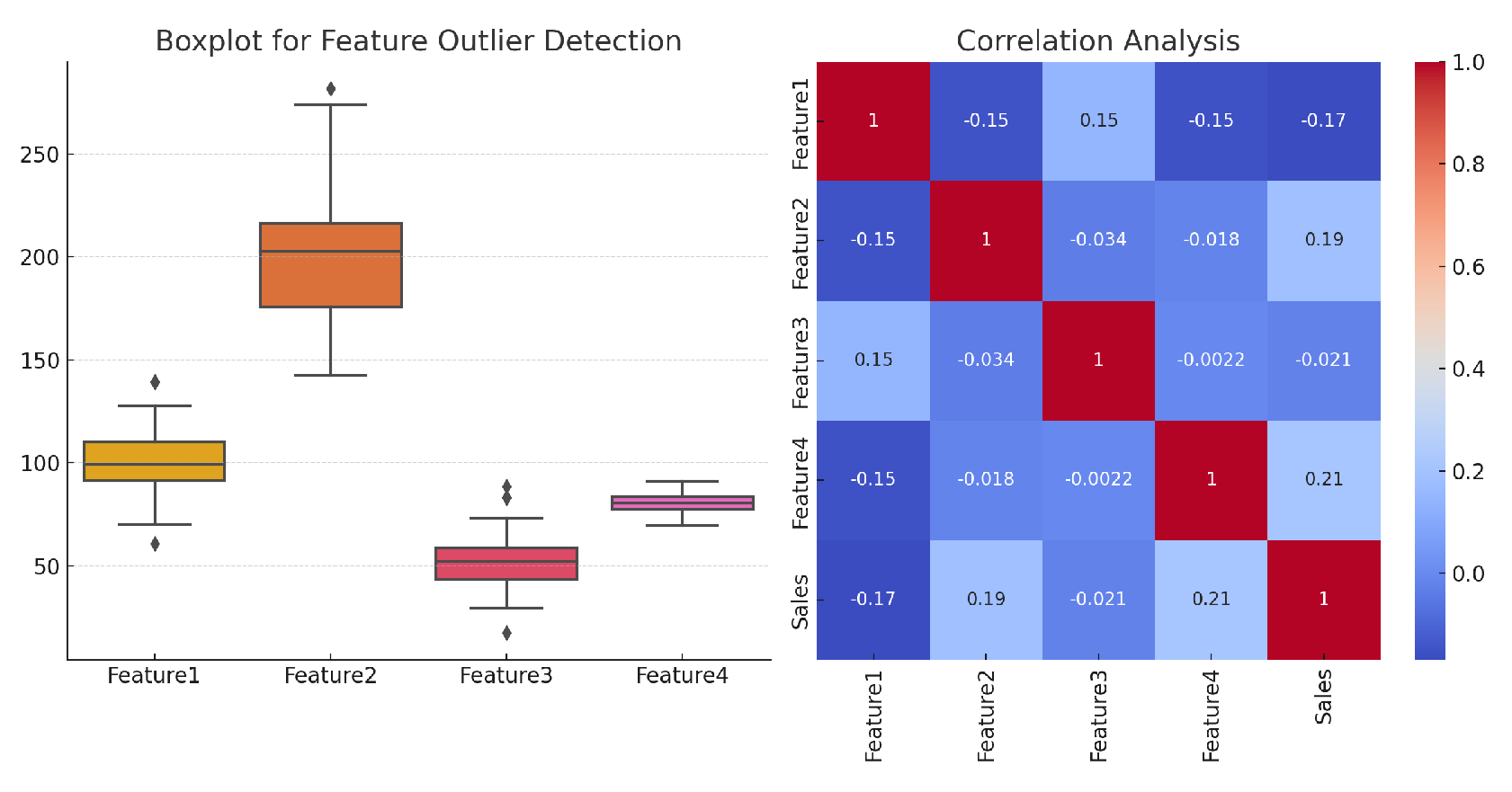
To prepare the sales data for model training, several preprocessing steps were applied, including outlier detection, missing value imputation, and feature selection based on correlation analysis. For features with large differences, outliers are found based on box plots and correlation analysis graphs in Figure 3.

3.9.1. Outlier Detection

Boxplot analysis was used to detect and remove outliers. For each feature, values exceeding 1.5 times the interquartile range (IQR) were treated as outliers and removed.

3.9.2. Missing Value Imputation

Missing values were handled using mean imputation for numerical features and mode imputation for categorical features.

3.9.3. Feature Selection

Correlation analysis was employed to identify highly correlated features with sales. Features with a Pearson correlation coefficient greater than 0.7 were selected for model training.

4. Evaluation Metrics

To assess the performance of our sales forecasting models, we use three main metrics: Root Mean Squared Percentage Error (RMSPE), Mean Squared Error (MSE), and Precision. These metrics evaluate both prediction accuracy and classification performance.

4.1. Root Mean Squared Percentage Error (RMSPE)

RMSPE measures the percentage deviation between predictions and actual values, normalizing errors by actual values, making it suitable for sales forecasting. It is defined as:

$$\mathrm{RMSPE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left({\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}\right)}^2}$$

(12)

where $y_i$ and ${\widehat{y}}_i$ represent actual and predicted sales, respectively. RMSPE penalizes large errors more heavily.

4.2. Mean Squared Error (MSE)

Mean Squared Error (MSE) measures the average squared difference between the actual and predicted values, which helps to evaluate the overall accuracy of the model. It is calculated as:

$$\mathrm{MSE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(13)

MSE provides insight into the absolute errors and is particularly useful for understanding the magnitude of errors.

4.3. Precision

Precision is a classification metric used to measure the proportion of correctly predicted positive instances out of all instances predicted as positive. It is particularly important in assessing the model’s ability to correctly forecast periods of higher sales, such as during promotions. Precision is calculated as:

$$\mathrm{Precision}={\displaystyle \frac{TP}{TP+FP}}$$

(14)

where $TP$ represents true positives and $FP$ represents false positives.

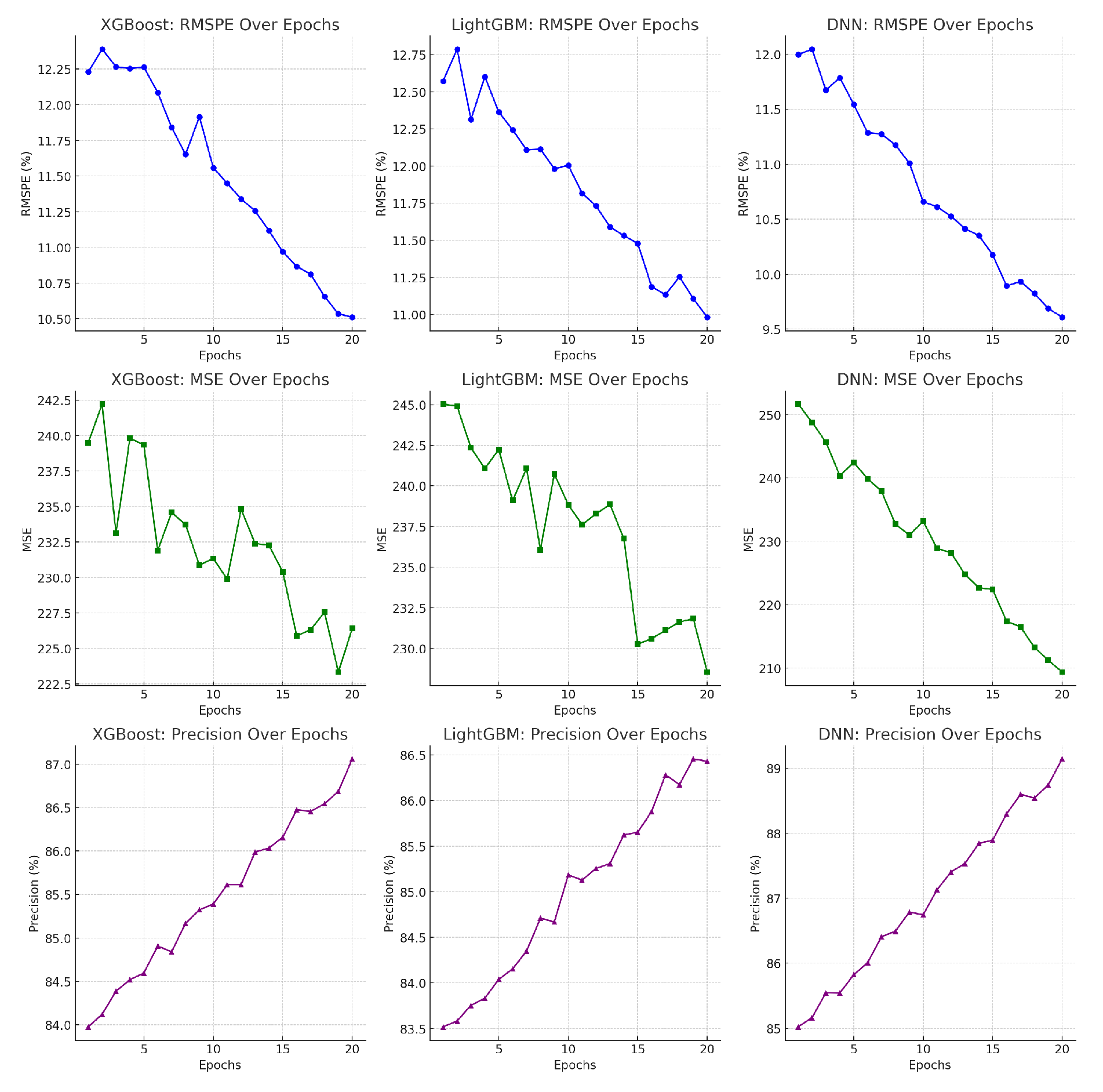
5. Experiment Results

We evaluated the performance of the three models (LightGBM, XGBoost, and DNN) using the RMSPE, MSE, and Precision metrics. The changes in model training indicators are shown in Figure 4.

The following table summarizes the results:

6. Conclusion

The proposed ensemble model, optimized using Particle Swarm Optimization (PSO), combines the strengths of DNN, XGBoost, and LightGBM to achieve the best overall performance across RMSPE, MSE, and Precision. Ablation studies further demonstrate the importance of each model’s contribution to the ensemble, with DNN having the most significant impact. This ensemble approach provides a robust solution for sales forecasting in Rossmann stores, improving both accuracy and reliability.