Euler and Gourava Sombor Coindices: Theoretical Bounds and QSPR Applications for Butane Derivatives

1. Introduction

Consider a simply connected graph, denoted $\mathfrak{S}$, whose vertices and edge sets are $\mathfrak{Ѵ}\left(\mathfrak{S}\right)$ and $\mathfrak{E}\left(\mathfrak{S}\right)$, respectively. The graph $\overline{\mathfrak{S}}$, whose set of vertices is the same as the Ѵ(S) and set of edges is $\mathfrak{E}\left(\overline{\mathfrak{S}}\right)$($\left|\mathfrak{E}\left(\overline{\mathfrak{S}}\right)\right|=\overline{\mu }$) is the complement of $\mathfrak{S}$. For other graph-theoretical notation and terminology, we refer to [1,2].

In this article, $\mathfrak{S}$ will be considered as a simple connected graph with $\mu$ edges and $\eta$ vertices. The degree of the vertices in this graph is ${\omega }_{\mathfrak{S}}\left(x\right)$, where ∆ and δ denote the maximum and minimum degrees, respectively.

Topological indices are among the prominent subjects of Graph Theory. Chemical graph theory generally considers various topological indices (molecular descriptors) of molecular graphs and examines how strongly they are related to various properties of the corresponding molecules. Thus, mathematical representations of these relationships are obtained with QSAR and QSPR studies in the literature.

There are studies in the literature on topological indices and coindices [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. In Table 1, we give some degree based topological indices and coindices.

In the light of these definitions, Euler Sombor and Gourava Sombor co-indices defined as

$$\overline{\mathrm{E}\mathrm{U}}\left(\mathfrak{S}\right)={\displaystyle \sum _{\mathrm{x}\mathrm{y}\notin \mathfrak{E}\left(\mathfrak{S}\right)}}\sqrt{{{\mathsf{\omega }}_{\mathfrak{S}}\left(\mathrm{x}\right)}^2+{{\mathsf{\omega }}_{\mathfrak{S}}\left(\mathrm{y}\right)}^2+\left({\mathsf{\omega }}_{\mathfrak{S}}\left(\mathrm{x}\right){\mathsf{\omega }}_{\mathfrak{S}}\left(\mathrm{y}\right)\right)}$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}\sqrt{{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)}.$$

The bounds for Euler Sombor and Gourava Sombor co-indices depending on the Zagreb coindices, Hyper Zagreb coindices and forgetten topological coindex were obtained. The bounds are computed for these indices of several graph operations like union, sum, cartesian product and composition of graphs [25]. Euler Sombor coindex and Gourava Sombor coindex of some chemical graphs are studied. An analysis of the physicochemical properties of butane and its derivatives was performed to evaluate the effects of Euler Sombor and Gourava Sombor indices and co-indices in QSPR studies. A non-linear model was developed using the QSPR approach to predict the specified properties and the results showed that the indices have satisfactory performance in comparative tests in predicting all the properties.

2. The Euler Sombor and Gourava Sombor Coindices

In this section, the bounds for Euler Sombor and Gourava Sombor coindices depending on the Zagreb coindices, Hyper Zagreb coindices and forgetten topological coindex were obtained. The bounds are computed for these indices of the graph operations like union, sum, cartesian product and composition of graphs.

2.1. Bounds for Euler Sombor Coindex and Gourava Sombor Coindex Depending on Some Other Topological Coindices

First, let's give the necessary inequalities for the obtained results.

Lemma 2.1.1. 

(P´olya-Szegö Inequality [26])

Let $x_1$, $x_2$, … $x_s$ and $y_1$, $y_2$, … $y_s$ be two sequences of positive real numbers. If there exists real numbers $x$, $y$, $X$ and $Y$ such that $0<k\le x_i\le K<\mathrm{\infty }$ and $0<l\le y_i\le L<\mathrm{\infty }$ for $i=\mathrm{1,2},\dots ,t$ then

$${\displaystyle \frac{{\displaystyle {\sum }_{i=1}^t}{x}_i^2{\displaystyle {\sum }_{i=1}^t}{y}_i^2}{{\left[{\displaystyle {\sum }_{i=1}^t}{x}_i{y}_i\right]}^2}}\le {\displaystyle \frac{{\left(kl+KL\right)}^2}{4klKL}}.$$

Lemma 2.1.2. 

(Radon’s inequality [26])

If $x_i,y_i>0$ for $i=\mathrm{1,2},\dots ,r$ and $p>0$,

$${\displaystyle \sum _{i=1}^r}{\displaystyle \frac{x_i^{p+1}}{{y_i}^p}}\ge {\displaystyle \frac{{\left({\displaystyle {\sum }_{i=1}^r}{x}_i\right)}^{p+1}}{{\left({\displaystyle {\sum }_{i=1}^r}{y}_i\right)}^p}}.$$

Theorem 2.1.3. 

Let $\mathfrak{S}$ be a graph on $\eta$ vertices and $\mu$ edges. Then

$${\displaystyle \frac{2\delta \Delta \sqrt{\overline{\mu }\left(\overline{F}\left(\mathfrak{S}\right)+{\overline{M}}_2\left(\mathfrak{S}\right)\right)}}{\left({\delta }^2+{\Delta }^2\right)}}\le \overline{EU}\left(\mathfrak{S}\right)\le \sqrt{{\displaystyle \frac{3}{2}}\Delta \overline{\mu }{\overline{M}}_1\left(\mathfrak{S}\right)}$$

(2.1)

Proof.

Letting $x_i=\sqrt{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2+\left({\omega }_{\mathfrak{S}}\left(x\right){\omega }_{\mathfrak{S}}\left(y\right)\right)}$ and $y_i=\delta$ in Lemma 2.1.1, and choosing

$k=\sqrt{3}\delta ,l=\delta ,$ $K=\sqrt{3}\Delta$ and $L=\Delta$, we get $0<k\le x_i\le K<\mathrm{\infty }$ and $0<l\le y_i\le L<\mathrm{\infty }$for $i=\mathrm{1,2},\dots ,\overline{\mu }.$ Applying Lemma 2.1.1 with the sums running over the edges in $\overline{\mathfrak{S}}$, we have

$${\displaystyle \frac{{\displaystyle {\sum }_{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2+\left({\omega }_{\mathfrak{S}}\left(x\right){\omega }_{\mathfrak{S}}\left(y\right)\right){\displaystyle {\sum }_{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{\delta }^2}{{\delta }^2{\left[\overline{EU}\left(\mathfrak{S}\right)\right]}^2}}\le {\displaystyle \frac{{\left(\sqrt{3}{\delta }^2+\sqrt{3}{∆}^2\right)}^2}{12{\delta }^2{\Delta }^2}}.$$

Using the definitions of Forgetten and Second Zagreb coindices, we get

$${\displaystyle \frac{\overline{\mu }(\overline{F}\left(\mathfrak{S}\right)+{\overline{M}}_2\left(\mathfrak{S}\right))}{{\left[\overline{EU}\left(\mathfrak{S}\right)\right]}^2}}\le {\displaystyle \frac{{\left({\delta }^2+{\Delta }^2\right)}^2}{4{\delta }^2{\Delta }^2}}$$

Hence we obtain the lower bound as

$${\displaystyle \frac{2\delta \Delta \sqrt{\overline{\mu }(\overline{F}\left(\mathfrak{S}\right)+{\overline{M}}_2\left(\mathfrak{S}\right)}}{\left({\delta }^2+{\Delta }^2\right)}}\le \overline{EU}\left(\mathfrak{S}\right).$$

For the upper bound, letting $x_i=\sqrt{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2+\left({\omega }_{\mathfrak{S}}\left(x\right){\omega }_{\mathfrak{S}}\left(y\right)\right)}$ and $y_i={\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)$ in Lemma 2.1.2 with the sums running over the edges in $\overline{\mathfrak{S}}$, we have

$${\displaystyle \sum _{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{\displaystyle \frac{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2+\left({\omega }_{\mathfrak{S}}\left(x\right){\omega }_{\mathfrak{S}}\left(y\right)\right)}{{\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)}}\ge {\displaystyle \frac{{\left[\overline{EU}\left(\mathfrak{S}\right)\right]}^2}{{\displaystyle {\sum }_{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)}}.$$

Notice that

$${\displaystyle \frac{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2+\left({\omega }_{\mathfrak{S}}\left(x\right){\omega }_{\mathfrak{S}}\left(y\right)\right)}{{\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)}}\le {\displaystyle \frac{3}{2}}\Delta .$$

Thus, we get

$$\overline{EU}\left(\mathfrak{S}\right)\le \sqrt{{\displaystyle \frac{3}{2}}\Delta \overline{\mu }{\overline{M}}_1\left(\mathfrak{S}\right)}$$

Theorem 2.1.4. 

Let $\mathfrak{S}$ be a graph on $n$ vertices and $m$ edges. Then

$${\displaystyle \frac{\sqrt{8\delta \Delta \sqrt{{\delta }^2+4}\overline{\mu }\sqrt{{\Delta }^2+4}\left({\overline{HM}}_1\right(\mathfrak{S})+{\overline{HM}}_2(\mathfrak{S}\left)\right)}}{\delta \sqrt{{\delta }^2+4}+2\Delta \sqrt{{\Delta }^2+4}}}\le \overline{GSO}\left(\mathfrak{S}\right)\le \sqrt{{\displaystyle \frac{\overline{\mu }\left({\Delta }^2+4\right)\overline{F}\left(\mathfrak{S}\right)}{2}}}$$

(2.2)

Proof.

Letting $x_i=\sqrt{{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)}$ and $y_i=1$ in Lemma 2.1.1, and choosing $k=\delta \sqrt{{\delta }^2+4},l=1,$ $K=\Delta \sqrt{{\Delta }^2+4}$ and $L=2$, we get $0<k\le x_i\le K<\mathrm{\infty }$ and $0<l\le y_i\le L<\mathrm{\infty }$ for $i=\mathrm{1,2},\dots ,\overline{\mu }.$ Applying Lemma 2.1.1 with the sums running over the edges in $\overline{\mathfrak{S}}$, we get

$${\displaystyle \frac{{\displaystyle \sum _{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)\overline{\mu }}{{\left[\overline{GSO}\left(\mathfrak{S}\right)\right]}^2}}\le {\displaystyle \frac{{\left(\delta \sqrt{{\delta }^2+4}+2\Delta \sqrt{{\Delta }^2+4}\right)}^2}{8\delta \Delta \sqrt{{\delta }^2+4}\sqrt{{\Delta }^2+4}}}.$$

Using the definitions of Hyper Zagreb coindices, we have

$${\displaystyle \frac{\sqrt{8\delta \Delta \sqrt{{\delta }^2+4}\overline{\mu }\sqrt{{\Delta }^2+4}\left({\overline{HM}}_1\left(\mathfrak{S}\right)+{\overline{HM}}_2\left(\mathfrak{S}\right)\right)}}{\delta \sqrt{{\delta }^2+4}+2\Delta \sqrt{{\Delta }^2+4}}}\le \overline{GSO}\left(\mathfrak{S}\right)$$

For the upper bound, letting $x_i=\sqrt{{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)}$ and $y_i={{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2$in Lemma 2.1.2 with the sums running over the edges in $\overline{\mathfrak{S}}$, we have

$${\displaystyle \sum _{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{\displaystyle \frac{{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)}{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2}}\ge {\displaystyle \frac{{\left[\overline{GSO}\left(\mathfrak{S}\right)\right]}^2}{{\displaystyle {\sum }_{xy\notin \mathfrak{E}\left(\mathfrak{S}\right)}}{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2}}.$$

Notice that

$${\displaystyle \frac{{\left({\omega }_{\mathfrak{S}}\left(x\right)+{\omega }_{\mathfrak{S}}\left(y\right)\right)}^2+\left({{\omega }_{\mathfrak{S}}\left(x\right)}^2{{\omega }_{\mathfrak{S}}\left(y\right)}^2\right)}{{{\omega }_{\mathfrak{S}}\left(x\right)}^2+{{\omega }_{\mathfrak{S}}\left(y\right)}^2}}\le {\displaystyle \frac{{\Delta }^2+4}{2}}.$$

Hence, we get

$$\overline{GSO}\left(\mathfrak{S}\right)\le \sqrt{{\displaystyle \frac{\overline{\mu }\left({\Delta }^2+4\right)\overline{F}\left(\mathfrak{S}\right)}{2}}}.$$

2.2. Bounds on the Euler Sombor Coindex and Gourava Sombor Coindex of Graph Operations

In this section, the minimum degree of the graph ${\mathfrak{S}}_i$ $(i=\mathrm{1,2}$) will be taken as ${\delta }_i$ and the maximum degree will be taken as ${\Delta }_i$.

Theorem 2.2.1. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, respectively. Then, the the union of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Euler Sombor coindex has the lower and upper bounds as

$$\overline{EU}\left({\mathfrak{S}}_1\right)+\overline{EU}\left({\mathfrak{S}}_2\right)+{\eta }_1{\eta }_2\left({{\delta }_1}^2+{{\delta }_2}^2+{(\delta }_1{\delta }_2\right)\le \overline{EU}\left({\mathfrak{S}}_1\cup {\mathfrak{S}}_2\right)\le \overline{EU}\left({\mathfrak{S}}_1\right)+\overline{EU}\left({\mathfrak{S}}_2\right)$$

$$+{\eta }_1{\eta }_2\left({{\Delta }_1}^2+{{\Delta }_2}^2+{(\Delta }_1{\Delta }_2\right)$$

(2.3)

Moreover, the equality holds if ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ are regular.

Proof.

By the definition of Euler Sombor coindex, we have

$$\overline{EU}\left({\mathfrak{S}}_1\cup {\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right)+{{\omega }_{{\mathfrak{S}}_1}}^2\left(y\right)+{\omega }_{{\mathfrak{S}}_1}\left(x\right){\omega }_{{\mathfrak{S}}_1}\left(y\right)}$$

$$+{\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_2}}^2\left(x\right)+{{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right)+{\omega }_{{\mathfrak{S}}_2}\left(x\right){\omega }_{{\mathfrak{S}}_2}\left(y\right)}$$

$$+{\displaystyle \sum _{x\in Ѵ\left({\mathfrak{S}}_1\right)}}\left({\displaystyle \sum _{y\in Ѵ\left({\mathfrak{S}}_2\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right)+{{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right){+(\omega }_{{\mathfrak{S}}_1}\left(x\right){\omega }_{{\mathfrak{S}}_2}\left(y\right))}\right).$$

Using the minimum and maximum degrees, we obtain the desired result.

Theorem 2.2.2.  

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, respectively. Then, the the union of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Gourava Sombor coindex has the lower and upper bounds as

$$\overline{GSO}\left({\mathfrak{S}}_1\right)+\overline{GSO}\left({\mathfrak{S}}_2\right)+{\eta }_1{\eta }_2\sqrt{{\left({(\delta }_1+{\delta }_2\right)}^2+{{\delta }_1}^2{{\delta }_2}^2}\le \overline{GSO}\left({\mathfrak{S}}_1\cup {\mathfrak{S}}_2\right)\le \overline{GSO}\left({\mathfrak{S}}_1\right)+\overline{GSO}\left({\mathfrak{S}}_2\right)$$

$$+{\eta }_1{\eta }_2\sqrt{{\left({(\Delta }_1+{\Delta }_2\right)}^2+{{\Delta }_1}^2{{\Delta }_2}^2}$$

(2.4)

Moreover, the equality holds if ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ are regular.

Proof.

By the definition of Gourava Sombor coindex, we have

$$\overline{GSO}\left({\mathfrak{S}}_1\cup {\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\omega }_{{\mathfrak{S}}_1}\left(y\right)\right)}^2{+{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right){{\omega }_{{\mathfrak{S}}_1}}^2\left(y\right)}$$

$$+{\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\omega }_{{\mathfrak{S}}_2}\left(y\right)\right)}^2{+{\omega }_{{\mathfrak{S}}_2}}^2\left(x\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right)}$$

$$+{\displaystyle \sum _{x\in Ѵ\left({\mathfrak{S}}_1\right)}}\left({\displaystyle \sum _{y\in Ѵ\left({\mathfrak{S}}_2\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\omega }_{{\mathfrak{S}}_2}\left(y\right)\right)}^2+{{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right)}\right).$$

Hence, we get the desired result.

Theorem 2.2.3. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the the sum of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Euler Sombor coindex has the lower and upper bounds as

$$\sqrt{3}\left[\overline{{\mu }_1}\left({\delta }_1+{\eta }_2\right)+\overline{{\mu }_2}\left({\delta }_2+{\eta }_1\right)\right]\le \overline{EU}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)\le \sqrt{3}\left[\overline{{\mu }_1}\left({\Delta }_1+{\eta }_2\right)+\overline{{\mu }_2}\left({\Delta }_2+{\eta }_1\right)\right]$$

$$+{\eta }_1{\eta }_2\left({{\Delta }_1}^2+{{\Delta }_2}^2+{(\Delta }_1{\Delta }_2\right)$$

(2.5)

Here, the number of edges of the graph ${\mathfrak{S}}_{\mathrm{i}}$ for i=1,2 is ${\mu }_i$. Moreover, the equality holds if ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ are regular.

Proof.

By the definition of Euler Sombor coindex, we get

$$\overline{EU}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right)+{{\omega }_{{\mathfrak{S}}_1}}^2\left(y\right)+{\omega }_{{\mathfrak{S}}_1}\left(x\right){\omega }_{{\mathfrak{S}}_1}\left(y\right)}$$

$$+{\displaystyle {\sum }_{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_2}}^2\left(x\right)+{{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right)+{\omega }_{{\mathfrak{S}}_2}\left(x\right){\omega }_{{\mathfrak{S}}_2}\left(y\right)}$$

Using the definition of the sum of two graphs, we get

$$\overline{EU}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\eta }_2\right)}^2+{\left({\omega }_{{\mathfrak{S}}_1}\left(y\right)+{\eta }_2\right)}^2+\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\eta }_2\right)\left({\omega }_{{\mathfrak{S}}_1}\left(y\right)+{\eta }_2\right)}$$

$$+{\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\eta }_1\right)}^2+{\left({\omega }_{{\mathfrak{S}}_2}\left(y\right)+{\eta }_1\right)}^2+\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\eta }_1\right)\left({\omega }_{{\mathfrak{S}}_2}\left(y\right)+{\eta }_1\right).}$$

Using the minimum and maximum degrees, we obtain

$$\sqrt{3}\left[\overline{{\mu }_1}\left({\delta }_1+{\eta }_2\right)+\overline{{\mu }_2}\left({\delta }_2+{\eta }_1\right)\right]\le \overline{EU}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)\le \sqrt{3}\left[\overline{{\mu }_1}\left({\Delta }_1+{\eta }_2\right)+\overline{{\mu }_2}\left({\Delta }_2+{\eta }_1\right)\right]$$

$$+{\eta }_1{\eta }_2\left({{\Delta }_1}^2+{{\Delta }_2}^2+{(\Delta }_1{\Delta }_2\right)$$

Theorem 2.2.4. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the the sum of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Gourava Sombor coindex has the lower and upper bounds as

$$\left[\overline{{\mu }_1}\left({\delta }_1+{\eta }_2\right)\sqrt{4+{\left({\delta }_1+{\eta }_2\right)}^2}\right]+\left[\overline{{\mu }_2}\left({\delta }_2+{\eta }_1\right)\sqrt{4+{\left({\delta }_1+{\eta }_1\right)}^2}\right]\le \overline{GSO}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)\le \left[\overline{{\mu }_1}\left({\Delta }_1+{\eta }_2\right)\sqrt{4+{\left({\Delta }_1+{\eta }_2\right)}^2}\right]+\left[\overline{{\mu }_2}\left({\Delta }_2+{\eta }_1\right)\sqrt{4+{\left({\Delta }_1+{\eta }_1\right)}^2}\right]$$

(2.6)

Here, the number of edges of the graph ${\mathfrak{S}}_{\mathrm{i}}$ for i=1,2 is $\overline{m_{\mathrm{i}}}$. Moreover, the equality holds if ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ are regular.

Proof.

By the definition of Gourava Sombor coindex, we have

$$\overline{GSO}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\omega }_{{\mathfrak{S}}_1}\left(y\right)\right)}^2{+{\omega }_{{\mathfrak{S}}_1}}^2\left(x\right){{\omega }_{{\mathfrak{S}}_1}}^2\left(y\right)}$$

$$+{\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\omega }_{{\mathfrak{S}}_2}\left(y\right)\right)}^2{+{\omega }_{{\mathfrak{S}}_2}}^2\left(x\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(y\right)}$$

Using the definition of the sum of two graphs, we get

$$\overline{GSO}\left({\mathfrak{S}}_1+{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1\right)}}\sqrt{\left[\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\eta }_2\right)+{\left({\omega }_{{\mathfrak{S}}_1}\left(y\right)+{\eta }_2\right)}^2\right]+{\left({\omega }_{{\mathfrak{S}}_1}\left(x\right)+{\eta }_2\right)}^2{\left({\omega }_{{\mathfrak{S}}_1}\left(y\right)+{\eta }_2\right)}^2}$$

$$+{\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_2\right)}}\sqrt{\left[\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\eta }_1\right)+{\left({\omega }_{{\mathfrak{S}}_2}\left(y\right)+{\eta }_1\right)}^2\right]+{\left({\omega }_{{\mathfrak{S}}_2}\left(x\right)+{\eta }_1\right)}^2{\left({\omega }_{{\mathfrak{S}}_2}\left(y\right)+{\eta }_1\right)}^2}.$$

Using the minimum and maximum degrees, we get the desired result.

Theorem 2.2.5. 

Let ${\mathfrak{S}}_1$and ${\mathfrak{S}}_2$be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the cartesian product of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Euler Sombor coindex has the lower and upper bounds as

$$2\alpha \sqrt{{{\delta }_1}^2+{{\delta }_2}^2+\left({\delta }_1{\delta }_2\right)}\le \overline{EU}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)\le 2\alpha \sqrt{{{\Delta }_1}^2+{{\Delta }_2}^2+\left({\Delta }_1{\Delta }_2\right)}$$

(2.7)

dir. Here, the number of edges of the graph ${\mathfrak{S}}_1◻{\mathfrak{S}}_2$ is $\alpha ={\eta }_1{\mu }_2+{\mu }_1{\eta }_2$.

Proof.

Let $x=(x_1,x_2)$ and $y=(y_1,y_2)$. By the definition of Euler Sombor coindex, we have

$$\overline{EU}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)}}\sqrt{{{\omega }_{{\mathfrak{S}}_1}}^2\left(x_1\right)+{{\omega }_{{\mathfrak{S}}_2}}^2\left(x_2\right)+{\omega }_{{\mathfrak{S}}_1}\left(x_1\right){\omega }_{{\mathfrak{S}}_2}\left(x_2\right)}$$

$$+\sqrt{{{\omega }_{{\mathfrak{S}}_1}}^2\left(y_1\right)+{{\omega }_{{\mathfrak{S}}_2}}^2\left(y_2\right)+{\omega }_{{\mathfrak{S}}_1}\left(y_1\right){\omega }_{{\mathfrak{S}}_2}\left(y_2\right).}$$

Hence, we get the desired bounds.

Theorem 2.2.6. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the the cartesian product of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Gourava Sombor coindex has the lower and upper bounds as

$$2\alpha \sqrt{{{{\left({\delta }_1+{\delta }_2\right)}^2+\delta }_1}^2{{\delta }_2}^2}\le \overline{GSO}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)\le 2\alpha \sqrt{{{{\left({\Delta }_1+{\Delta }_2\right)}^2+\Delta }_1}^2{{\Delta }_2}^2}$$

(2.8)

Here, the number of edges of the graph ${\mathfrak{S}}_1◻{\mathfrak{S}}_2$ is $\alpha ={\eta }_1{\mu }_2+{\mu }_1{\eta }_2$.

Proof.

Let $x=(x_1,x_2)$ and $y=(y_1,y_2)$. By the definition of Gourava Sombor coindex, we have

$$\overline{GSO}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)={\displaystyle \sum _{xy\notin \mathfrak{E}\left({\mathfrak{S}}_1◻G_2\right)}}\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(x_1\right)+{\omega }_{{\mathfrak{S}}_2}\left(x_2\right)\right)}^2+\left({{\omega }_{{\mathfrak{S}}_1}}^2\left(x_1\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(x_2\right)\right)}$$

$$+\sqrt{{\left({\omega }_{{\mathfrak{S}}_1}\left(y_1\right)+{\omega }_{{\mathfrak{S}}_2}\left(y_2\right)\right)}^2+\left({{\omega }_{{\mathfrak{S}}_1}}^2\left(y_1\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(y_2\right)\right)}.$$

Hence, we get

$$2\alpha \sqrt{{{{\left({\delta }_1+{\delta }_2\right)}^2+\delta }_1}^2{{\delta }_2}^2}\le \overline{GSO}\left({\mathfrak{S}}_1◻{\mathfrak{S}}_2\right)\le 2\alpha \sqrt{{{{\left({\Delta }_1+{\Delta }_2\right)}^2+\Delta }_1}^2{{\Delta }_2}^2}.$$

Theorem 2.2.7. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the the composition of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Euler Sombor coindex has the lower and upper bounds as

$$2\beta \sqrt{{{\eta }_2}^2{{\delta }_1}^2+{{\delta }_2}^2+{(\eta }_2{\delta }_1{\delta }_2)}\le \overline{EU}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)\le 2\beta \sqrt{{{\eta }_2}^2{{\Delta }_1}^2+{{\Delta }_2}^2+{(\eta }_2{\Delta }_1{\Delta }_2)}$$

(2.9)

Here, the number of edges of the graph ${\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]$ is $\beta ={{\eta }_1{\mu }_2+{\mu }_1{\eta }_2}^2.$

Proof.

Let $x=(x_1,x_2)$ and $y=(y_1,y_2)$. By the definition of Euler Sombor coindex, we get

$$\overline{EU}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)={\displaystyle \sum _{uv\notin \mathfrak{E}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)}}\sqrt{{\left({{\eta }_2\omega }_{{\mathfrak{S}}_1}\left(x_1\right)\right)}^2+{{\omega }_{{\mathfrak{S}}_2}}^2\left(x_2\right)+{{\eta }_2\omega }_{{\mathfrak{S}}_1}\left(x_1\right){\omega }_{{\mathfrak{S}}_2}\left(x_2\right)}+\sqrt{{\left({{\eta }_2\omega }_{{\mathfrak{S}}_1}\left(y_1\right)\right)}^2+{{\omega }_{{\mathfrak{S}}_2}}^2\left(y_2\right)+{{\eta }_2\omega }_{{\mathfrak{S}}_1}\left(y_1\right){\omega }_{{\mathfrak{S}}_2}\left(y_2\right)}.$$

Hence, we obtain

$$2\beta \sqrt{{{\eta }_2}^2{{\delta }_1}^2+{{\delta }_2}^2+{(\eta }_2{\delta }_1{\delta }_2)}\le \overline{EU}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)\le 2\beta \sqrt{{{\eta }_2}^2{{\Delta }_1}^2+{{\Delta }_2}^2+{(\eta }_2{\Delta }_1{\Delta }_2)}.$$

Theorem 2.2.8. 

Let ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ be two graphs on ${\eta }_1$ and ${\eta }_2$ vertices, ${\mu }_1$ and ${\mu }_2$edges respectively. Then, the the composition of the graphs ${\mathfrak{S}}_1$ and ${\mathfrak{S}}_2$ on the Gourava Sombor coindex has the lower and upper bounds as

$$2\beta \sqrt{{{(\eta }_2{\delta }_1{+\delta }_2)}^2+\left({{\eta }_2}^2{{\delta }_1}^2{{\delta }_2}^2\right)}\le \overline{GSO}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)\le 2\beta \sqrt{{{(\eta }_2{\Delta }_1{+\Delta }_2)}^2+\left({{\eta }_2}^2{{\Delta }_1}^2{{\Delta }_2}^2\right)}$$

(2.10)

Here, the number of edges of the graph ${\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]$ is $\beta ={{\eta }_1{\mu }_2+{\mu }_1{\eta }_2}^2.$

Proof.

Let $x=(x_1,x_2)$ and $y=(y_1,y_2)$. By the definition of Gourava Sombor coindex, we get

$$\overline{EU}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)={\displaystyle \sum _{uv\notin \mathfrak{E}\left({\mathfrak{S}}_1\left[{\mathfrak{S}}_2\right]\right)}}\sqrt{{{{(\eta }_2\omega }_{{\mathfrak{S}}_1}\left(x_1\right)+{\omega }_{{\mathfrak{S}}_2}\left(x_2\right))}^2+\left({{\eta }_2}^2{{\omega }_{{\mathfrak{S}}_1}}^2\left(x_1\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(x_2\right)\right)}+\sqrt{{{{(\eta }_2\omega }_{{\mathfrak{S}}_1}\left(y_1\right)+{\omega }_{{\mathfrak{S}}_2}\left(y_2\right))}^2+\left({{\eta }_2}^2{{\omega }_{{\mathfrak{S}}_1}}^2\left(y_1\right){{\omega }_{{\mathfrak{S}}_2}}^2\left(y_2\right)\right)}.$$

Hence, we get the desired bounds.

3. The Euler Sombor and Gourava Sombor Coindices of SOME chemical Graphs

$\mathfrak{S}$ is a chemical graph if ${\omega }_{\mathfrak{S}}\left(x\right)\le 4$ for all $x\in \mathfrak{Ѵ}\left(\mathfrak{S}\right)$. We denote by ${\eta }_i$ the number of vertices of degree $i$. Let ${\mu }_{i,j}$ and ${\overline{\mu }}_{i,j}$ be the number of adjacent and non-adjacent vertex of degree $i$ to a vertex of degree $j$ respectively. Here, ${\overline{\mu }}_{i,i}=\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_i}{2}}\right)-{\mu }_{i,i}$ and ${\overline{\mu }}_{i,j}={\eta }_i{\eta }_j-{\mu }_{i,j}$, for $1\le i,j\le 4.$

Proposition 3.1. If $\mathfrak{S}$ is a chemical graph, then the Euler Sombor coindex and the Gourava Sombor coindex are are as follows respectively:

$$\overline{EU}\left(\mathfrak{S}\right)=\sqrt{3}{\overline{\mu }}_{\mathrm{1,1}}+\sqrt{7}{\overline{\mu }}_{\mathrm{1,2}}+\sqrt{13}{\overline{\mu }}_{\mathrm{1,3}}+\sqrt{21}{\overline{\mu }}_{\mathrm{1,4}}+2\sqrt{3}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{19}{\overline{\mu }}_{\mathrm{2,3}}+2\sqrt{7}{\overline{\mu }}_{\mathrm{2,4}}+3\sqrt{3}{\overline{\mu }}_{\mathrm{3,3}}+\sqrt{37}{\overline{\mu }}_{\mathrm{3,4}}$$

$$+{4\sqrt{3}\overline{\mu }}_{\mathrm{4,4}}$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)=\sqrt{5}{\overline{\mu }}_{\mathrm{1,1}}+\sqrt{13}{\overline{\mu }}_{\mathrm{1,2}}+5{\mu }_{\mathrm{1,3}}+\sqrt{41}{\overline{\mu }}_{\mathrm{1,4}}+4\sqrt{2}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{61}{\overline{\mu }}_{\mathrm{2,3}}+10{\overline{\mu }}_{\mathrm{2,4}}+3\sqrt{13}{\overline{\mu }}_{\mathrm{3,3}}+\sqrt{193}{\overline{\mu }}_{\mathrm{3,4}}+{8\sqrt{5}\overline{\mu }}_{\mathrm{4,4}}.$$

Proof. For a chemical graph $\mathfrak{S}$, there exist only $\left(\mathrm{1,1}\right),\left(\mathrm{1,2}\right),\left(\mathrm{1,3}\right),\left(\mathrm{1,4}\right),\left(\mathrm{2,2}\right),\left(\mathrm{2,3}\right),\left(\mathrm{2,4}\right),\left(\mathrm{3,3}\right),$ $\left(\mathrm{3,4}\right),\left(\mathrm{4,4}\right)$ type of vertex pairs. Using the definitions of the Euler and Gourava coindices, the desired result can be get easily.

Dendrimer has a special structure that is generally divided into three parts: inner layer, middle layer and surface functional group layer. If the molecular graph of porphyrin core polyamidoamine dendrimers synthesized by microwave method[27] is shown with PDP(k), where $k\ge 1$ is the production step, the following theorem is obtained.

Theorem 3.2. Let $k\ge 1$. Then the Euler and Gourava coindices of PDP(k) are

$$\overline{EU}\left(\mathfrak{S}\right)={\displaystyle \frac{\sqrt{3}{\eta }_1}{2}}\left({\eta }_1+{\displaystyle \frac{2\sqrt{21}}{3}}{\eta }_2-1\right)+2\sqrt{2}{\eta }_2\left({\eta }_2+{\displaystyle \frac{\sqrt{122}}{4}}{\eta }_3-1\right)+{\displaystyle \frac{3\sqrt{13}}{2}}{\eta }_3\left({\eta }_3-1\right)$$

$$-2^{k+1}\left(24\sqrt{2}+\sqrt{7}+2\sqrt{13}+7\sqrt{61}\right)-32\sqrt{13}-16\sqrt{61}$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)={\displaystyle \frac{\sqrt{5}{\eta }_1}{2}}\left({\eta }_1+{\displaystyle \frac{2\sqrt{65}}{5}}{\eta }_2+2\sqrt{5}{\eta }_3-1\right)+2\sqrt{2}{\eta }_2\left({\eta }_2+{\displaystyle \frac{\sqrt{122}}{4}}{\eta }_3-1\right)+{\displaystyle \frac{3\sqrt{13}}{2}}{\eta }_3\left({\eta }_3-1\right)$$

$$-2^{k+1}\left(24\sqrt{2}+\sqrt{7}+2\sqrt{13}+7\sqrt{61}\right)-32\sqrt{13}-16\sqrt{61}$$

where ${\eta }_1=2^{k+2}+2^{k+1}-4,{\eta }_2={5.2}^{k+2}+8,{\eta }_3=3.2^{k+1}+12.$

Proof. Using the values of ${\mu }_{i,j}$ from [28], ${\overline{\mu }}_{i,j}$ are found as follows:

$${\overline{\mu }}_{\mathrm{1,1}}=\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_1}{2}}\right),{\overline{\mu }}_{\mathrm{1,2}}={\eta }_1{\eta }_2-2^{k+1},{\overline{\mu }}_{\mathrm{1,3}}={\eta }_1{\eta }_3-2^{k+2}+4,{\overline{\mu }}_{\mathrm{2,2}}=\left[\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_2}{2}}\right)-3.2^{k+2}\right],$$

$${\overline{\mu }}_{\mathrm{2,3}}={\eta }_2{\eta }_3-2^{k+4}+2^{k+1}-16,{\overline{\mu }}_{\mathrm{3,3}}=\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_1}{2}}\right)-12.$$

Then the Euler and Gourava coindices of PDP(k) are

$$\overline{EU}\left(\mathfrak{S}\right)={\displaystyle \frac{\sqrt{3}{\eta }_1}{2}}\left({\eta }_1+{\displaystyle \frac{2\sqrt{21}}{3}}{\eta }_2+{\displaystyle \frac{2\sqrt{39}}{3}}{\eta }_3-1\right)+\sqrt{3}{\eta }_2\left({\eta }_2+{\displaystyle \frac{\sqrt{57}}{3}}{\eta }_3-1\right)+{\displaystyle \frac{3\sqrt{3}}{2}}{\eta }_3\left({\eta }_3-1\right)$$

$$-2^{k+1}\left(12\sqrt{3}+\sqrt{7}+2\sqrt{13}+7\sqrt{19}\right)-36\sqrt{3}+4\sqrt{13}-16\sqrt{19p}$$

$$\overline{GSO}\left(\mathfrak{S}\right)={\displaystyle \frac{\sqrt{5}{\eta }_1}{2}}\left({\eta }_1+{\displaystyle \frac{2\sqrt{65}}{5}}{\eta }_2+2\sqrt{5}{\eta }_3-1\right)+2\sqrt{2}{\eta }_2\left({\eta }_2+{\displaystyle \frac{\sqrt{122}}{4}}{\eta }_3-1\right)+{\displaystyle \frac{3\sqrt{13}}{2}}{\eta }_3\left({\eta }_3-1\right)$$

$$-2^{k+1}\left(24\sqrt{2}+\sqrt{7}+2\sqrt{13}+7\sqrt{61}\right)-32\sqrt{13}-16\sqrt{61}$$

Graphene is a material with a two-dimensional honeycomb lattice structure consisting of a single layer of atoms and is denoted by $GN(\eta ,k)$.

Theorem 3.3. Let $G$ be the graphene $GN(\eta ,k)$ where $1\le k\le \eta .$ Then the Euler and Gourava coindices of $GN(\eta ,k)$ are

$$\overline{EU}\left(\mathfrak{S}\right)=24\sqrt{3}{\eta }^2{k}^2+\left(8\sqrt{19}-24\sqrt{3}\right){\eta }^{2}k+\left(16\sqrt{19}-24\sqrt{3}\right)\eta k^2+\left(4\sqrt{3}-12\sqrt{19}\right)\eta k$$

$$+\left(10\sqrt{3}-4\sqrt{19}\right){\eta }^2+\left(22\sqrt{3}-8\sqrt{19}\right)k^2+\left(16\sqrt{3}-4\sqrt{19}\right)\eta +\left(10\sqrt{3}-4\sqrt{19}\right)k+8\sqrt{19}-20\sqrt{3},$$

$$\overline{GSO}\left(\mathfrak{S}\right)=24\sqrt{13}{\eta }^2{k}^2+\left(8\sqrt{61}-24\sqrt{13}\right){\eta }^{2}k+\left(16\sqrt{61}-24\sqrt{13}\right)\eta k^2$$

$$+\left(32\sqrt{2}-12\sqrt{3}-12\sqrt{61}\right)\eta k+\left(8\sqrt{2}+6\sqrt{13}-4\sqrt{61}\right){\eta }^2+\left(32\sqrt{2}+6\sqrt{13}-8\sqrt{61}\right)k^2$$

$$+\left(-4\sqrt{2}+18\sqrt{13}-4\sqrt{61}\right)\eta +\left(-16\sqrt{2}+18\sqrt{13}-4\sqrt{61}\right)k-16\sqrt{2}+8\sqrt{61}-12\sqrt{13}.$$

Proof. Since $GN(\eta ,k)$ has only $\left(\mathrm{2,2}\right),\left(\mathrm{2,3}\right)$ and $\left(\mathrm{3,3}\right)$-type of vertex pairs, we can see easy that ${\overline{\mu }}_{\mathrm{2,2}}=2{\eta }^2+8k^2+8\eta k-\eta -4k-4$, ${\overline{\mu }}_{\mathrm{2,3}}=4\left(2-k-2k^2-\eta -3\eta k-{\eta }^2+4k^2\eta +2{\eta }^{2}k\right),{\overline{\mu }}_{\mathrm{3,3}}=2\left(-2+3k+k^2+3\eta -2\eta k+{\eta }^2-4{\eta }^{2}k-4k^2\eta +4{\eta }^2{k}^2\right),{\eta }_2=2n+4$ and ${\eta }_3=2\left(2\eta k-\eta -k\right).$ If these values ​​are written in the equations, we obtain

$$\overline{EU}\left(\mathfrak{S}\right)=2\sqrt{3}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{19}{\overline{\mu }}_{\mathrm{2,3}}+3\sqrt{3}{\overline{\mu }}_{\mathrm{3,3}}$$

$$=2\sqrt{3}\left(2{\eta }^2+8k^2+8\eta k-\eta -4k-4\right)$$

$$+\sqrt{19}\left(4\left(2-k-2k^2-\eta -3\eta k-{\eta }^2+4k^2\eta +2{\eta }^{2}k\right)\right)$$

$$+3\sqrt{3}(2\left(-2+3k+k^2+3\eta -2\eta k+{\eta }^2-4{\eta }^{2}k-4k^2\eta +4{\eta }^2{k}^2\right)$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)=4\sqrt{2}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{61}{\overline{\mu }}_{\mathrm{2,3}}+3\sqrt{13}{\overline{\mu }}_{\mathrm{3,3}}$$

$$=4\sqrt{2}(2{\eta }^2+8k^2+8\eta k-\eta -4k-4)$$

$$+\sqrt{61}\left(4\left(2-k-2k^2-\eta -3\eta k-{\eta }^2+4k^2\eta +2{\eta }^{2}k\right)\right)$$

$$+3\sqrt{13}(2\left(-2+3k+k^2+3\eta -2\eta k+{\eta }^2-4{\eta }^{2}k-4k^2\eta +4{\eta }^2{k}^2\right).$$

If the necessary calculations are made, the desired results are obtained.

Carbon nanocones are conical structures with a loop of length $k$ at the core and $n$ hexagonal layers arranged on a conical surface around the center, denoted by $CN{C}_k\left(\eta \right)$.

Theorem 3.4. Let $G$ be the carbon nanocone structure $CN{C}_k\left(\eta \right)$ with $k>4$ and $\eta \ge 1.$ Then,

$$\overline{EU}\left(\mathfrak{S}\right)={\displaystyle \frac{3\sqrt{3}}{2}}{\eta }^4{k}^2+\left(3\sqrt{3}+\sqrt{19}\right){\eta }^3{k}^2+\left({\displaystyle \frac{5\sqrt{3}}{2}}+2\sqrt{19}\right){\eta }^2{k}^2-4{\eta }^{2}k+\left(2\sqrt{3}+\sqrt{19}\right)\eta k^2-\left(4\sqrt{3}+2\sqrt{19}\right)\eta k+\sqrt{3}{k}^2-3\sqrt{3}k,$$

$$\overline{GSO}\left(\mathfrak{S}\right)={\displaystyle \frac{3\sqrt{13}}{2}}{\eta }^4{k}^2+\left(3\sqrt{13}+\sqrt{61}\right){\eta }^3{k}^2+\left(2\sqrt{2}+{\displaystyle \frac{3\sqrt{13}}{2}}+2\sqrt{61}\right){\eta }^2{k}^2-6\sqrt{13}{\eta }^{2}k+\left(4\sqrt{2}+\sqrt{61}\right)\eta k^2-\left(2\sqrt{2}+3\sqrt{13}+2\sqrt{61}\right)\eta k+2\sqrt{2}{k}^2-6\sqrt{2}k.$$

Proof. It is easy to check that${\eta }_2=k\left(\eta +1\right),{\eta }_3=\eta k\left(\eta +1\right)$ ${\overline{\mu }}_{\mathrm{2,2}}=\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_2}{2}}\right)-{\mu }_{\mathrm{2,2}}$, ${\overline{\mu }}_{\mathrm{2,3}}={\eta }_2{\eta }_{3-}{\mu }_{\mathrm{2,3}},{\overline{\mu }}_{\mathrm{3,3}}=\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_3}{2}}\right)-{\mu }_{\mathrm{3,3}}.$If we calculate $\overline{EU}\left(\mathfrak{S}\right)=2\sqrt{3}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{19}{\overline{\mu }}_{\mathrm{2,3}}+3\sqrt{3}{\overline{\mu }}_{\mathrm{3,3}}$ and $\overline{GSO}\left(\mathfrak{S}\right)=4\sqrt{2}{\overline{\mu }}_{\mathrm{2,2}}+\sqrt{61}{\overline{\mu }}_{\mathrm{2,3}}+3\sqrt{13}{\overline{\mu }}_{\mathrm{3,3}}$, the desired results are obtained.

A tree is a caterpillar if and only if all vertex of degree greater than equal $3$ are surrounded by at most two vertices of degree two or greater.

Proposition 3.5. Let $G$ be the caterpillar $〈S_4,S_3,\dots ,S_3,S_4;z_1,z_2,\dots ,z_n〉$. Then we have

$$\overline{EU}\left(\mathfrak{S}\right)=\left(4\sqrt{3}+2\sqrt{21}\right){\eta }^2-3\sqrt{3}\eta +5\sqrt{3}-2\sqrt{21}$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)=\left(10\sqrt{5}+2\sqrt{41}\right){\eta }^2-\left(3\sqrt{5}+32\sqrt{15}\right)\eta +\sqrt{5}-2\sqrt{41}+32\sqrt{15}.$$

Proof. It is seen from the structure of $\mathfrak{S}$ that ${\eta }_1=2\eta +2,{\eta }_4=\eta ,{\mu }_{\mathrm{1,1}}=0,{\mu }_{\mathrm{1,4}}=2\eta +2$ and ${\mu }_{\mathrm{4,4}}=\eta -1$. Then we get

$$\overline{EU}\left(\mathfrak{S}\right)=\sqrt{3}\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_1}{2}}\right)+\sqrt{21}({\eta }_1{\eta }_4-2\eta -2)+4\sqrt{3}\left[\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_4}{2}}\right)-\eta +1\right]$$

and

$$\overline{GSO}\left(\mathfrak{S}\right)=\sqrt{5}\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_1}{2}}\right)+\sqrt{41}\left({\eta }_1{\eta }_4-2\eta -2\right)+8\sqrt{5}\left[\left({\displaystyle \genfrac{}{}{0pt}{}{{\eta }_4}{2}}\right)-\eta +1\right].$$

When the values ​​of ${\eta }_1$ and ${\eta }_4$ are substituted into the equations above, the desired results are obtained.

4. The Use of Selected Sombor Topological Indices and Coindices in QSPR Studies

QSPR studies have become an important field of study for both mathematicians and chemists with the advantage of rapid calculation of topological indices to predict the properties of compounds. In this section, we have shown that Euler Sombor and Gourava Sombor indices and their coindices play an important role in the prediction of Hydrogen bond acceptor count (HBAC), Heavy atomic count (HAC), Complexity (COMP), and Surface Tension(ST) properties.

Table 2. Experimental values of physicochemical properties of Butane derivatives [29].

Compound	HBAC	HAC	COMP	ST
1,4-butanedithiol	2	6	17.5	31.1
2-butanone	1	5	38.5	22.9
1,3-butanediol	2	6	28.7	34.9
butane dinitrile	2	6	92	40.7
butanediamide	2	8	96.6	53
butane-1-sulfoamide	3	8	133	41.9
1-butanethiol	1	5	13.1	24.8
1,4-diaminobuane	2	6	17.5	35.8
butane-1,4-disulfonic acid	6	12	266	77.9
butyraldehyde	1	5	24.8	23.1
2,3-butanedione	2	6	71.5	27.3
1-butanesufonylchloride	2	8	133	36.4

Table 2. Experimental values of physicochemical properties of Butane derivatives [29].

Compound	HBAC	HAC	COMP	ST
1,4-butanedithiol	2	6	17.5	31.1
2-butanone	1	5	38.5	22.9
1,3-butanediol	2	6	28.7	34.9
butane dinitrile	2	6	92	40.7
butanediamide	2	8	96.6	53
butane-1-sulfoamide	3	8	133	41.9
1-butanethiol	1	5	13.1	24.8
1,4-diaminobuane	2	6	17.5	35.8
butane-1,4-disulfonic acid	6	12	266	77.9
butyraldehyde	1	5	24.8	23.1
2,3-butanedione	2	6	71.5	27.3
1-butanesufonylchloride	2	8	133	36.4

Table 3. Gourava and Sombor indices(coindices) of Butane derivatives.

Compound	$\mathit{G}\mathit{S}\mathit{O}$	$\mathit{E}\mathit{U}$	$\overline{\mathit{E}\mathit{U}}$	$\overline{\mathit{G}\mathit{S}\mathit{O}}$
1,4-butanedithiol	24.18	15.68	27.99	40.83
2-butanone	30	17.81	17.71	25.11
1,3-butanediol	27.07	17.67	26.38	37.54
butane dinitrile	53.44	26.21	52.30	96.91
butanediamide	58.46	33.79	77.47	130.05
butane-1-sulfoamide	85.92	49.98	91.83	149.39
1-butanethiol	18.52	17.51	26.36	22.31
1,4-diaminobuane	24.18	20.97	27.99	40.83
butane-1,4-disulfonic acid	121.94	66.77	231.47	390.13
butyraldehyde	24.88	14.82	20.18	31.33
2,3-butanedione	50.69	30.13	35.52	55.12
1-butanesufonylchloride	67.40	37.76	74.23	118

Table 3. Gourava and Sombor indices(coindices) of Butane derivatives.

Compound	$\mathit{G}\mathit{S}\mathit{O}$	$\mathit{E}\mathit{U}$	$\overline{\mathit{E}\mathit{U}}$	$\overline{\mathit{G}\mathit{S}\mathit{O}}$
1,4-butanedithiol	24.18	15.68	27.99	40.83
2-butanone	30	17.81	17.71	25.11
1,3-butanediol	27.07	17.67	26.38	37.54
butane dinitrile	53.44	26.21	52.30	96.91
butanediamide	58.46	33.79	77.47	130.05
butane-1-sulfoamide	85.92	49.98	91.83	149.39
1-butanethiol	18.52	17.51	26.36	22.31
1,4-diaminobuane	24.18	20.97	27.99	40.83
butane-1,4-disulfonic acid	121.94	66.77	231.47	390.13
butyraldehyde	24.88	14.82	20.18	31.33
2,3-butanedione	50.69	30.13	35.52	55.12
1-butanesufonylchloride	67.40	37.76	74.23	118

• Non-linear Regression Model:

Here, we based on the below non-linear regression model:

$$In\left(P\right)=X+YIn\left(I\right)$$

where $\left(P\right)$ indicates the selected properties of Butane derivatives, and $\left(I\right)$ indicates the Gourava and Sombor indices(coindices).

The Gourava Sombor index $GSO$:

$$In\left(HBAC\right)=-1.8291+0.6650In\left(GSO\right)$$

$$In\left(HAC\right)=0.4569+0.3813In\left(GSO\right)$$

$$In\left(COMP\right)=-2.0591+1.6116In\left(GSO\right)$$

$$In\left(ST\right)=1.5964+0.5277In\left(GSO\right)$$

The Euler Sombor index $EU$:

$$In\left(HBAC\right)=-2.1247+0.8513In\left(EU\right)$$

$$In\left(HAC\right)=0.2910+0.4871In\left(EU\right)$$

$$In\left(COMP\right)=-2.0480+1.8395In\left(EU\right)$$

$$In\left(ST\right)=1.6338+0.5919In\left(EU\right)$$

The Gourava Sombor coindex $\overline{GSO}$:

$$In\left(HBAC\right)=-1.4831+0.5106In\left(\overline{GSO}\right)$$

$$In\left(HAC\right)=0.6819+0.2864In\left(\overline{GSO}\right)$$

$$In\left(COMP\right)=-0.3666+1.0325In\left(\overline{GSO}\right)$$

$$In\left(ST\right)=1.9833+0.3782In\left(\overline{GSO}\right)$$

The Euler Sombor coindex $\overline{EU}$:

$$In\left(HBAC\right)=-1.5213+0.5747In\left(\overline{EU}\right)$$

$$In\left(HAC\right)=0.6308+0.3302In\left(\overline{EU}\right)$$

$$In\left(COMP\right)=-0.2987+1.1236In\left(\overline{EU}\right)$$

$$In\left(ST\right)=1.936+0.4305In\left(\overline{EU}\right)$$

When the necessary calculations are made here, it is seen that the predicted values ​​of the properties are as in Table 4, Table 5, Table 6 and Table 7. The correlation coefficients of the experimental values ​​and the exact values ​​of the selected physicochemical properties of the butane derivative are given in Table 8. The $R^2$ values ​​for the nonlinear QSPR model are shown in Table $9$.

The following figures indicates how much the predicted values of physio-chemical properties are correlated with the wellknown physio-chemical properties.

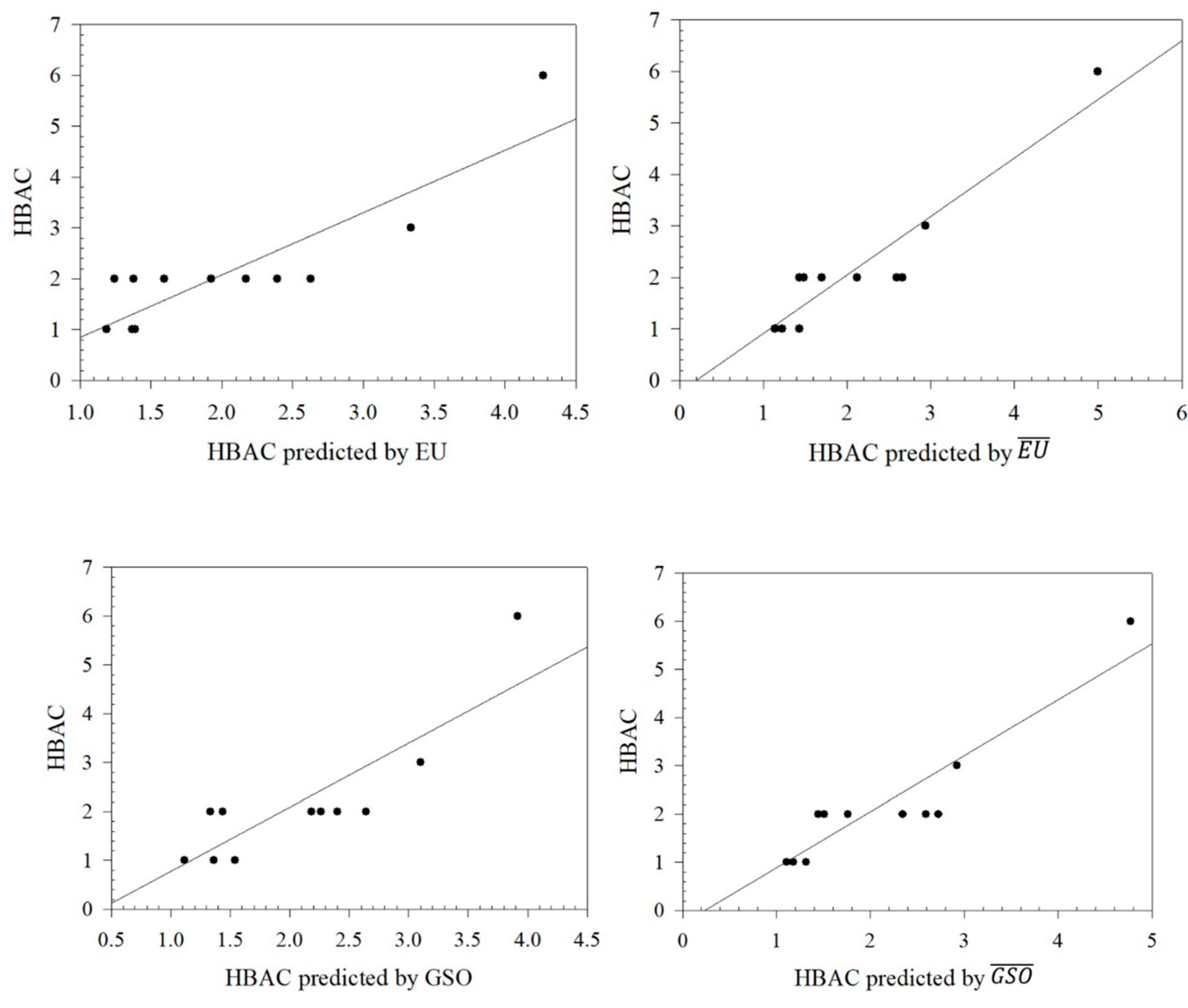
Figure 1. Graphical relationships between predicted values of HBAC and its exact values.

Figure 1. Graphical relationships between predicted values of HBAC and its exact values.

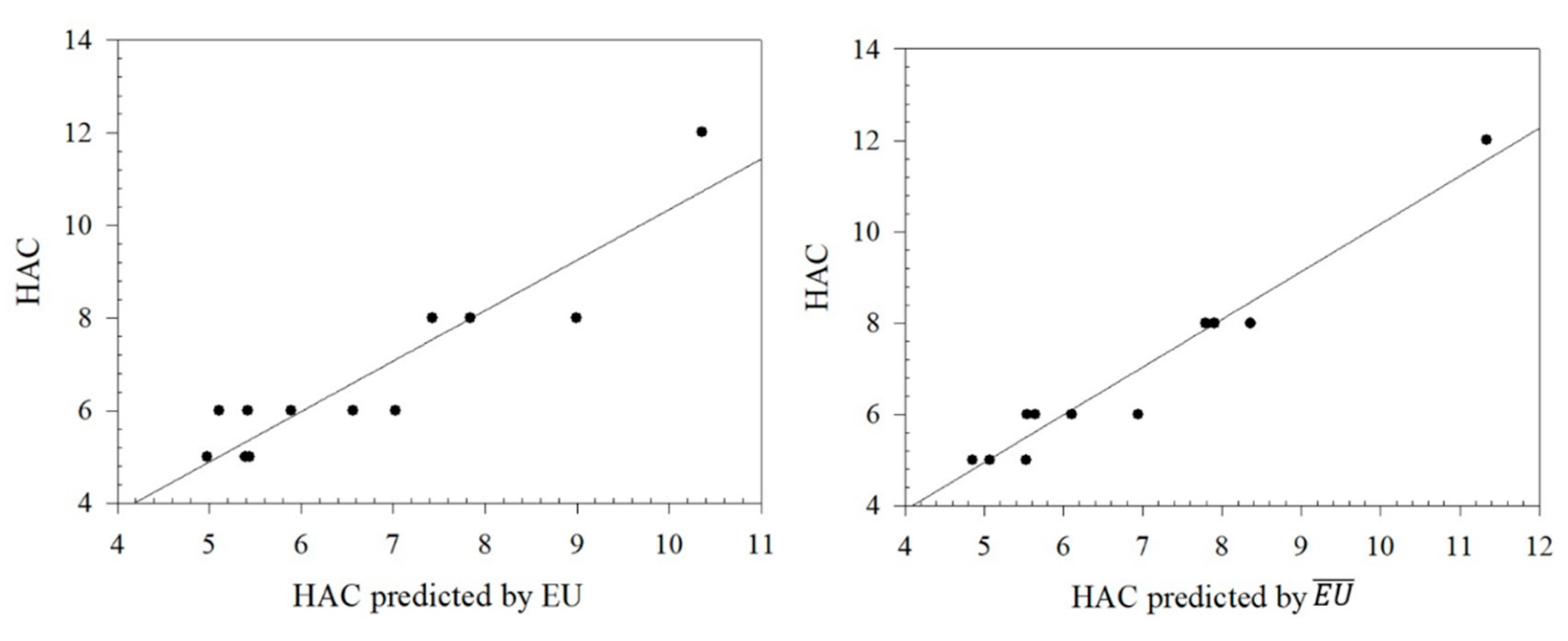
Figure 2.1. Graphical relationships between predicted values of HAC and its exact values $EU$ and $\overline{EU}$.

Figure 2.1. Graphical relationships between predicted values of HAC and its exact values $EU$ and $\overline{EU}$.

Figure 2.2. Graphical relationships between predicted values of HAC and its exact values $GSO$ and $\overline{GSO}$.

Figure 2.2. Graphical relationships between predicted values of HAC and its exact values $GSO$ and $\overline{GSO}$.

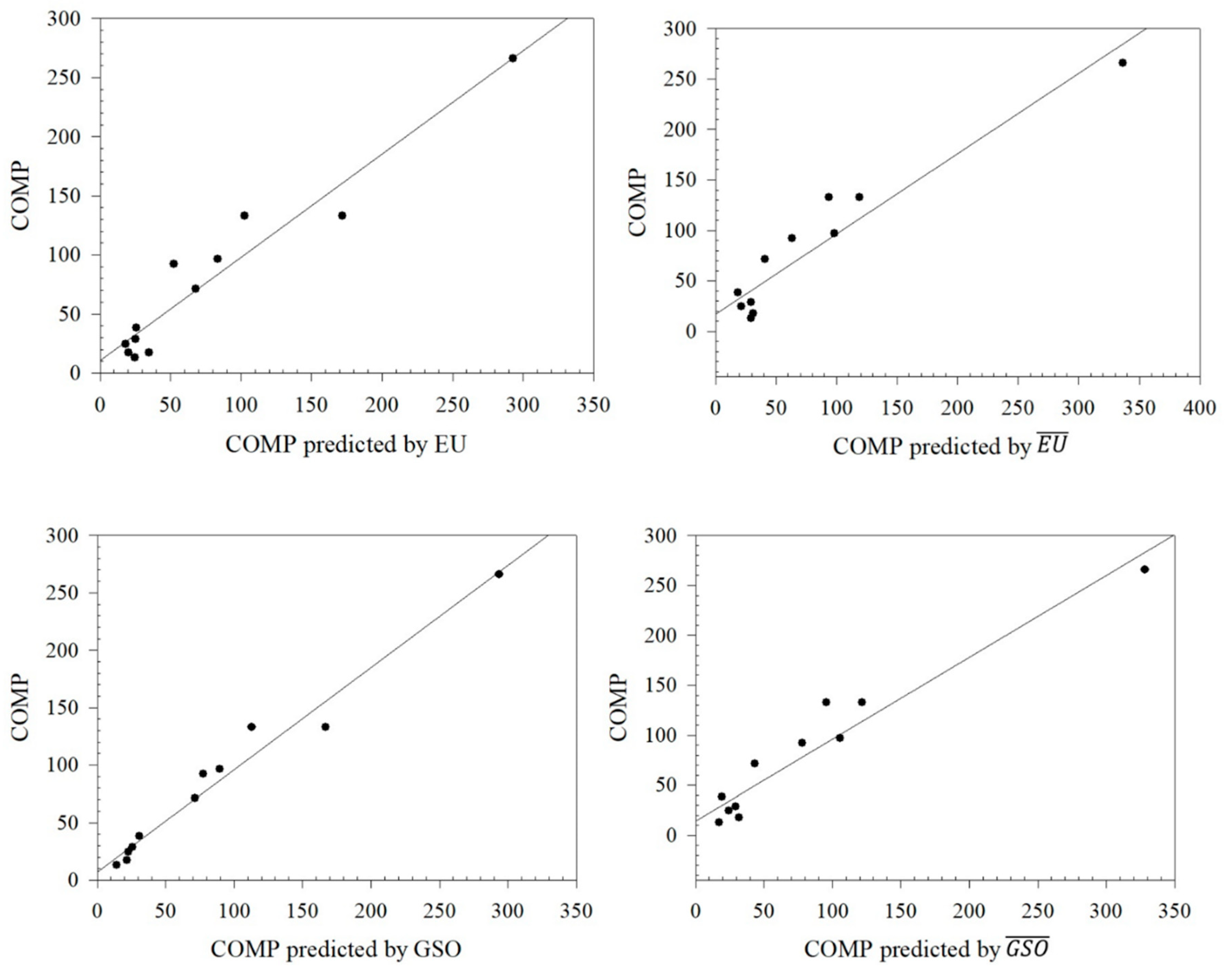
Figure 3. Graphical relationships between predicted values of COMP and its exact values.

Figure 3. Graphical relationships between predicted values of COMP and its exact values.

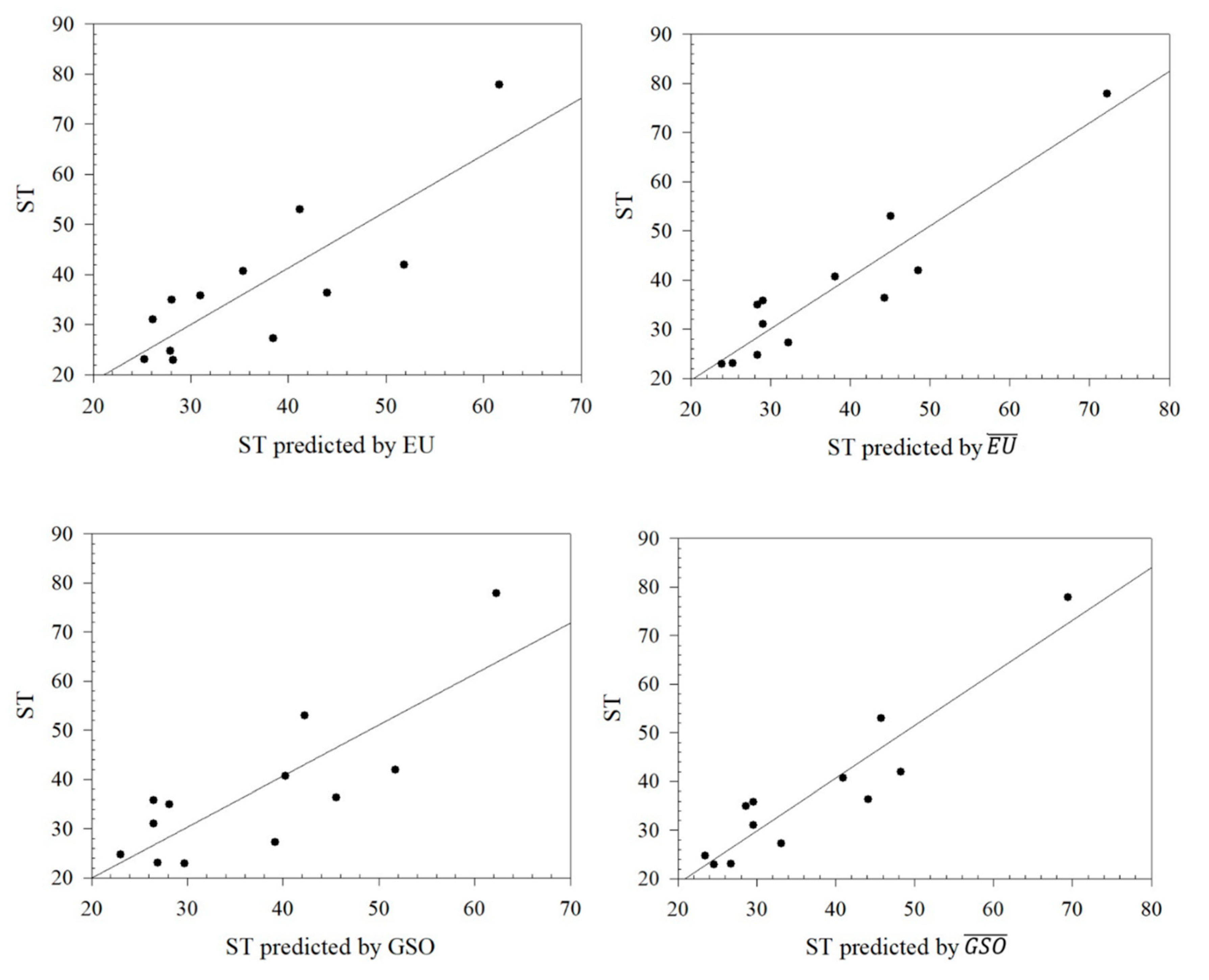
Figure 4. Graphical relationships between predicted values of ST and its exact values.

Figure 4. Graphical relationships between predicted values of ST and its exact values.

5. Results and Discussion

In this study, Gourava Sombor and Euler Sombor coindices are introduced as a new tool in mathematical chemistry and bounds are obtained through union, sum, cartesian product and composition graph operations. Also these indices are studied in some chemical graphs. These results show the important relationship between graph structure and degree concept.

From Table 8, it can be seen that the Euler Sombor and Gourava Sombor topological indices and their coindices are particularly effective in predicting the HBAC, HAC, COMP, and ST properties of butane derivatives. It is observed that the correlation coefficient of the predicted values ​​and the exact values ​​of HBAC is in the range of 0.8419 ≤ R ≤ 0.9277, with the Euler Sombor coindex having the best correlation coefficient of 0.9277. In addition, the correlation coefficient of the predicted and exact values ​​of HAC is in the range of 0.8897 ≤ R ≤ 0.9748, and it gives the best correlation coefficient of 0.9748 with the Euler Sombor coindex, and it is seen that ST is in the range of 0.8137 ≤ R ≤ 0.9344, with the best correlation coefficient being 0.9344 in this index. Finally, the correlation range for Comp is 0.9506 ≤ R ≤ 0.9855, and its best correlation is with the GSO index. It is clear that especially the EU coindex and GSO coindex show very strong correlations with the exact values ​​of the predicted values ​​of the selected physicochemical properties. These strong correlations show that the selected indices are reliable estimators in predicting the physicochemical properties of butane derivatives.

In a related study by Shashidhara et al. [30], the correlation coefficient of predicted and exact values for the studied domination topological indices was in the range of 0.58 ≤ R ≤ 0.88 for HAC, while it was in the range of 0.8897 ≤ R ≤ 0.9748 in our study, For ST, it was in the range of 0.53 ≤ R ≤ 0.83 in [30], while it was in the range of 0.8137 ≤ R ≤ 0.9344 in our study. For Comp, it was in the range of 0.53 ≤ R ≤ 0.90 in [30], while it was in the range of 0.9506 ≤ R ≤ 0.9855 in our study. Thus, in the literature, the highest performance results were obtained with the Gourava Sombor and Euler Sombor indices and especially the coindices in predicting the HAC, COMP and ST physicochemical properties of butane derivatives.