Vector Map Encryption Method Based on Secret Sharing

1. Introduction

In modern information age, Geographic Information Systems (GIS) have been widely applied in various fields such as urban planning, environmental monitoring, traffic management, and the military industry [1,2,3,4,5]. Vector maps, as one of the main GIS data, contain rich geographic coordinate information [6,7]. However, with the popularity of vector maps, how to protect the security and privacy of this sensitive data has become an increasingly prominent challenge [8,9,10,11]. Currently, there are two main issues for the security protection of vector maps: confidentiality protection and copyright protection [12]. Copyright protection mainly includes technologies such as blockchain [13] and digital watermarking [14,15] which can embed copyright information into vector maps while ensuring data integrity. Confidentiality protection is mainly based on encryption technology, which converts the plaintext data into unreadable ciphertexts to prevent unauthorized users to access data. At present, a few vector map encryption schemes have been proposed and applied to the field of geographic information protection [16]. Existing encryption schemes can be roughly divided into three categories: Classical cryptography-based encryption schemes [17], spatial domain-based encryption schemes [23,24], and transform domain-based encryption schemes [18,19].

Classical cryptography-based encryption schemes treat the vector map as a binary file and encrypt and decrypt the vector map as a whole. These encryption algorithms can be either symmetric encryption techniques or asymmetric encryption techniques. Symmetric encryption schemes mainly employ Advanced Encryption Standard (AES) [20] and Data Encryption Standard (DES) [21], etc. while asymmetric encryption schemes mainly employ the Rivest Shamir Adleman algorithm (RSA) [22] and the ellipse curve cryptography algorithm (ECC) [23], etc. The algorithms of these encryption types are simple to implement and consume few resources. However, these algorithms have limited randomness and do not consider the structural characteristics of vector data, resulting in poor usability.

Spatial domain-based encryption schemes directly shuffle the spatial distribution of map vertices through various chaotic systems, scrambles, and obfuscations. In terms of chaotic systems, the local encryption method proposed in [24], uses the SM3 algorithm and a four-dimensional hyperchaotic system to generate pseudo-random sequences, and utilizes these sequences to perform confusion, scrambling, and encryption processing on vertex coordinates. Another example is the encryption method based on the double random position permutation strategy [25], which uses the double random position permutation strategy to encrypt all the coordinates of the vector map. This method can prevent a one-to-one mapping relationship between the plaintext and the ciphertext vector maps. But the encryption effect of this algorithm on points is relatively weak. The encryption algorithm based on image scrambling regards the vector map as a special kind of image and encrypts it using image scrambling techniques. Common scrambling methods include the Arnold transformation [26] and nonlinear scrambling [27], etc. These encryption algorithms have a fast encryption speed and wide applicability. However, they have poor probabilistic property, not semantically secure.

Transform domain-based encryption schemes, converting data from the spatial domain to the transform domain for encryption, belong to another classic type of encryption method. Commonly used transforms in these encryption methods include the Discrete Cosine Transform (DCT), the Discrete Wavelet Transform (DWT), and the Discrete Fourier Transform (DFT) [28]. Pham et al. [29] employed the Advanced Encryption Standard and keys to encrypt the feature vertices of the backbone objects and randomized all the vertices of the backbone objects through the random Gaussian distribution algorithm. Van et al. [30] proposed to classify the objects in each map layer, and all the coordinates of important objects are encrypted by using Discrete Wavelet Transform (DWT) and Discrete Fourier Transform (DFT).

In summary, although some representative models and algorithms for vector map data encryption have been proposed, there still exist the following deficiencies for these methods: (1) Plaintext map data is encrypted into only one ciphertext map, and only one ciphertext map is required for data decryption. The security of such encryption models is not very sufficient for the sensitive vector map data. (2) When the only encrypted map data is lost or damaged, it is difficult to restore the encrypted map to its original version, which will lead to permanent data loss and leakage or damage to the integrity of the data. (3) In most classical cryptography algorithms, when the same plaintext data is encrypted twice, the results of each encryption are the same. This enables attackers to discover the patterns of the encryption algorithm by analyzing a large number of plaintext and ciphertext pairs collected, and then crack the key or the plaintext. Moreover, some asymmetric encryption algorithms have poor diffusion properties, which reduces the security of the algorithms. (4) Many existing algorithms lack robustness to data RST (Rotation, Scaling and Translation) transformations which are the very common operations for vector map data. Thus, decryption for the encrypted data often fails after RST operations. (5) Some methods lack versatility. The encryption algorithms cannot support all 2D vector data types (points, polylines, polygons), or the encryption effect varies depending on the data elements, which will affect the overall security of the methods.

To address the issues above, this paper proposes a novel vector map encryption method based on $\left(k,n\right)$-threshold secret sharing, which encrypts one map into $n$ map shares and reconstructs the plaintext map by collecting at least $k$ shares, thus improving the algorithm’s security and achieving the disaster tolerance property. Moreover, random numbers and cipher-feedback mode are cooperated into the encryption process in the proposed method to achieve probabilistic and diffusion properties. In addition, quantized polar coordinate is defined and original map coordinates are transformed into quantized polar coordinates before encryption and decryption process to achieve robustness to data RST transformations.

The remainder of this paper is organized as follows. Section 2 introduces the Shamir’s secret sharing method. Section 3 describes in detail the methodology of the proposed method. Experimental results and performance of the proposed method are discussed and evaluated in Section 4. Finally, a conclusion is drawn in Section 5.

2. Shamir’s Secret Sharing Method

In 1979, Shamir and Blakley proposed a $(k,n)$-threshold secret sharing scheme [31]. The method is to divide the secret information $s$ into $n$ shares and distribute them to $n$ respective participants. Any set that contains at least $k$participants is an authorized subset and can reconstruct $s$ correctly, while a set that contains $k-1$ or fewer participants is an unauthorized subset and cannot get any information of $s$. Shamir’s secret sharing scheme is widely used. The implementation process is as follows:

Select a finite field $F_p$, where $p\ge n$. Select $k-1$ random numbers $a_i$ ($i=\mathrm{1,2},\cdots ,k-1$) from $F_p$ and construct the polynomial

$$f\left(x\right)=\mathrm{s}+a_{1}x+a_2{x}^2+\cdots +a_{k-1}{x}^{k-1}modp$$

(1)

Select $n$ non-zero elements $x_1,x_2,\cdots ,x_n$ from $F_p$ which are different from each other and publicly known. Then, the $n$ shares for $s$ are obtained as $f\left(x_q\right)$, $q=\mathrm{1,2},\cdots ,n$.

When at least $k$ shares $f\left(x_{t_j}\right)$ ($j=\mathrm{1,2},\cdots ,kand{t}_j\in \{\mathrm{1,2},\cdots ,n\})$ are collected, the original data $s$ can be reconstructed. The reconstruction of the original data is achieved through Lagrange interpolation, represented as:

$$f\left(x\right)=\sum _{j=1}^k\left(f\left(x_{t_j}\right)\prod _{\begin{array}{c}1\le l\le k\\ l\ne j\end{array}}{\displaystyle \frac{x-x_{t_l}}{x_{t_j}-x_{t_l}}}\right) mod p$$

(2)

Substituting $x=0$ into the above formula, the original data $s=f\left(0\right)$ can be obtained.

3. Methodology

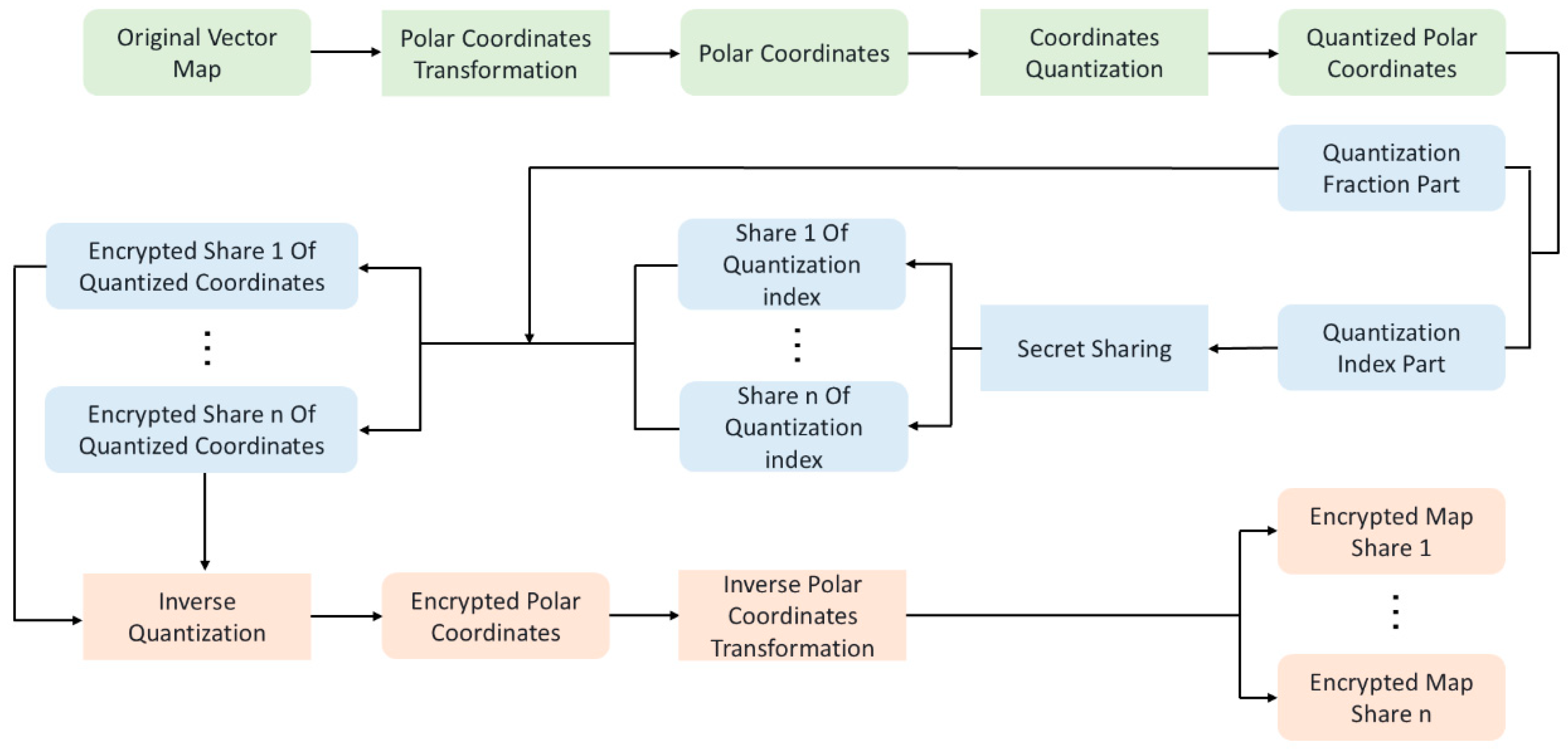
Vector maps use the vector data model to represent geographical entities and describe geospatial phenomena through geometric objects such as points, polylines, and polygons as well as their attributes. The geometric objects consist of ordered 2D coordinates sequences. The encryption operation is performed on each coordinate to obtain encrypted map data. In this paper, each coordinate is encrypted into $n$ cipher coordinates by using $\left(k,n\right)$ threshold secret sharing. After all coordinates are encrypted, $n$ cipher map shares are obtained. Only by collecting at least $k$ cipher shares can the plaintext map be reconstructed. As the secret sharing model processes data in the finite field, the map coordinates represented by real data are converted into integers on finite field before secret sharing operations. The conversion from real coordinates to integer coordinates is completed by using a data quantization process based on predefined quantization steps. In addition, in order to make the map decryption robust to the RST (Rotation, Scaling and Translation) operations which are the common operations for map data, the data quantization process and the secret sharing based encryption are all performed under a constructed polar coordinate system.

Specifically, the encryption process for a vector map data includes four sub-processes: (1) The original map coordinates are transformed into polar coordinates under a constructed polar coordinate system. (2) Quantization processes are performed to the polar coordinates using predefined quantization steps to obtain quantized polar coordinates. Each quantized polar coordinate is then divided into quantization index part and quantization fraction part. (3) Secret sharing operation is performed to each quantization index part and $n$ ciphertexts for each index part are obtained accordingly. Each ciphertext for index part is then combined with the fraction part to form $n$ ciphertexts for each quantized polar coordinate. (4) The $n$ ciphertexts of each quantized polar coordinate are then processed using inverse quantization and inverse polar coordinate transformation in sequence and $n$ encrypted map shares for the original map are finally obtained. The flowchart of the encryption process is shown in Figure 1.

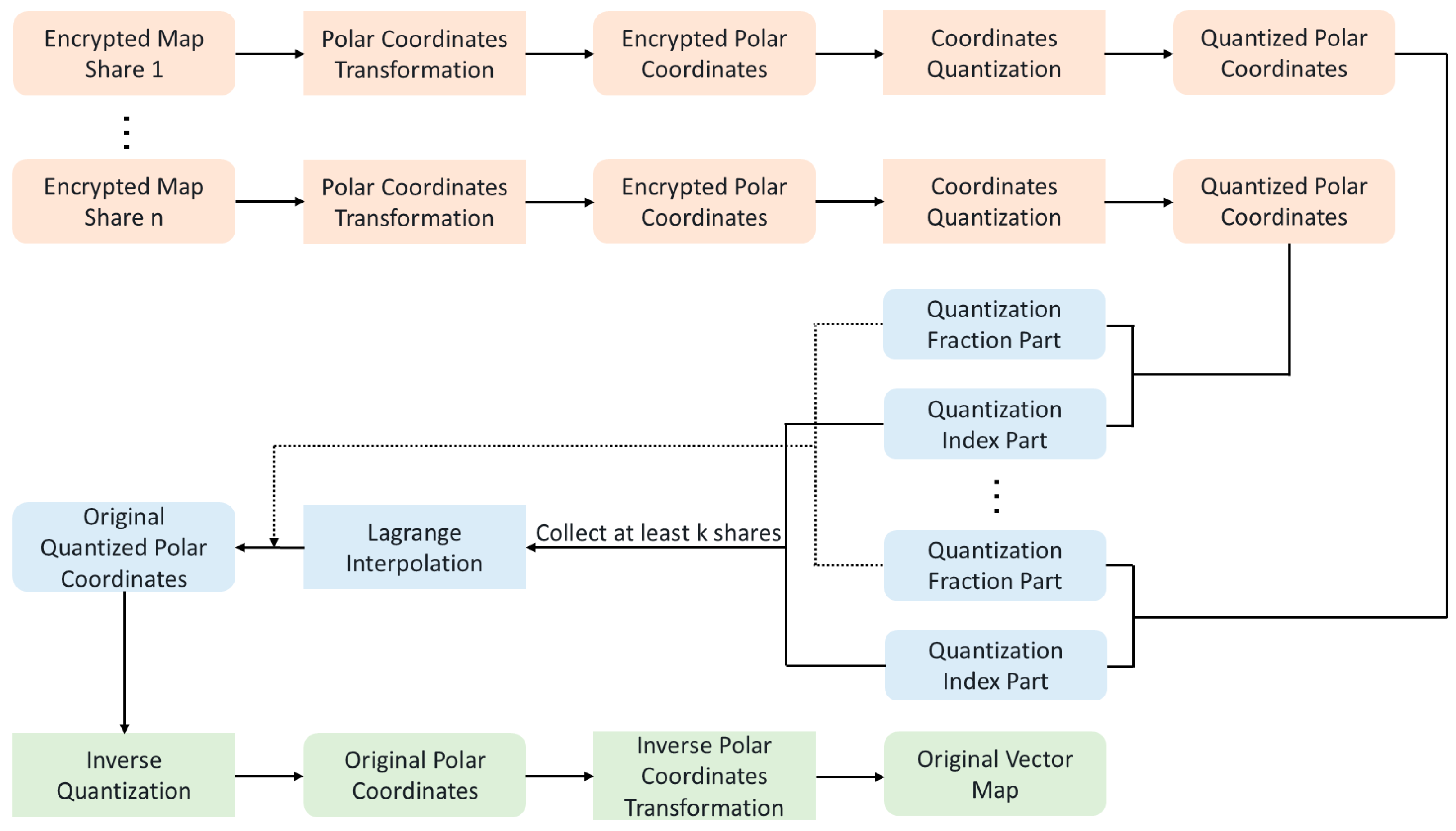
The decryption process consists of four sub-processes as follows. (1) For each encrypted map share, polar coordinate transformation is performed to all the encrypted coordinates, producing encrypted polar coordinates. (2) Quantization processes are performed to all the encrypted polar coordinates using the corresponding quantization steps to produce quantized cipher polar coordinates. And each quantized cipher polar coordinate is divided into quantization index part and fraction part. (3) For each index part, collect at least $k$ corresponding shares to reconstruct the original index part. The original index part is then combined with the corresponding fraction part to form the original quantized polar coordinate. (4) The original quantized polar coordinates are performed inverse quantization operations and inverse polar coordinate transformations sequentially to obtain the original vector map data. The flowchart of the decryption process is shown in Figure 2.

3.1. Construction of Polar Coordinate System

RST transformations do not affect data usage and are common operations for vector map data. To ensure that the decryption of cipher map is robust to the RST operations, map encryption and decryption are performed in a constructed polar coordinate system. The construction of the polar coordinate system and the transformation from Cartesian coordinates to polar coordinates are described as follows.

For a given 2D vector map, its vertex sequence$\left\{V_i\left(x_i,y_i\right)\right|i=\mathrm{1,2},\cdots ,N\}$ is first obtained, where $N$ is the number of vertices. Choose two vertices $V_{p_1}$ and $V_{p_2}$ in the sequence according to a predefined key ${key}_1$ with $V_{p_1}$ as the pole and the ray $V_{p_1}{V}_{p_2}$ as the initial ray to construct a polar coordinate system. Then, the vertex coordinates $V_i\left(x_i,y_i\right)$($i=\mathrm{1,2},\cdots ,N$) are transformed into coordinates under the constructed polar system to obtain the polar coordinates $V_i\left(r_i,{\theta }_i\right)$. The transformation from Cartesian coordinates to polar coordinates can be represented by

$$r_i=‖V_{p_1}{V}_i‖$$

(3)

$$\left\{\begin{array}{l}{\theta }_i=sign(\overrightarrow{V_{p_1}{V}_{p_2}}\times \overrightarrow{V_{p_1}{V}_{\dot{i}}}•\overrightarrow{e_z})\times \mathrm{a}\mathrm{r}\mathrm{c}\cos \left({\displaystyle \frac{{‖V_{p_1}{V}_i‖}^2+{‖V_{p_1}{V}_{p_2}‖}^2-{‖V_{p_2}{V}_i‖}^2}{2‖V_{p_1}{V}_i‖\times ‖V_{p_1}{V}_{p_2}‖}}\right) if ‖\overrightarrow{V_{p_1}{V}_{p_2}}\times \overrightarrow{V_{p_1}{V}_{\dot{i}}}‖\ne 0\\ {\theta }_i=\mathrm{a}\mathrm{r}\mathrm{c}\cos \left({\displaystyle \frac{{‖V_{p_1}{V}_i‖}^2+{‖V_{p_1}{V}_{p_2}‖}^2-{‖V_{p_2}{V}_i‖}^2}{2‖V_{p_1}{V}_i‖\times ‖V_{p_1}{V}_{p_2}‖}}\right) if ‖\overrightarrow{V_{p_1}{V}_{p_2}}\times \overrightarrow{V_{p_1}{V}_{\dot{i}}}‖=0\end{array}\right.$$

(4)

where $\overrightarrow{e_z}$ is the unit vector of $Z\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$. And the inverse polar coordinate transformation can be represented by

$$x_i=r_i\mathit{cos}({\theta }_i)+x_{p_1}$$

(5)

$$y_i=r_i\mathit{sin}({\theta }_i)+y_{p_1}$$

(6)

3.2. Quantization Process to Polar Coordinates

There are two necessities for performing quantization process to all the polar coordinates. (1) Although the polar radii keep invariant under the map rotation and translation operations, their values will be changed under map scaling operation. Consequently, if encryption process is directly performed to the polar coordinates, the decryption of cipher map will fail after map scaling transformation. Thus, to ensure that the decryption of cipher map is robust to map scaling operation, before encryption and decryption processes, each polar radius is quantized by using a quantization step which is defined as a fixed proportion of the length between the two chosen vertices $V_{p_1}$ and $V_{p_2}$. The quantized polar radii possess RST-invariant capability. (2) The polar coordinates are real numbers, while the secret sharing model is defined on integers in finite field. Thus, the polar coordinates are transformed into integers on a finite field before secret sharing operations. The polar coordinates’ transformation from real numbers to integer numbers is achieved by quantization process.

For a given vertex $V_i\left(r_i,{\theta }_i\right)$, the quantization formula is as follows:

$$\left\{\begin{array}{c}{r}_i^q={\displaystyle \raisebox{1ex}{$r_i$}\!\left/ \!\raisebox{-1ex}{$q_r$}\right.}\\ {\theta }_i^q={\displaystyle \raisebox{1ex}{${\theta }_i$}\!\left/ \!\raisebox{-1ex}{$q_{\theta }$}\right.}\end{array}\right.$$

(7)

where $q_r$ is the quantization step for polar radii and $q_{\theta }$ is the quantization step for polar angles. $q_r$ is defined as a fixed proportion of the length between vertices $V_{p_1}$ and $V_{p_2}$ and computed as formula (8).

$$q_r=\rho \sqrt{{\left(x_{p_1}-x_{p_2}\right)}^2+{\left(y_{p_1}-y_{p_2}\right)}^2}$$

(8)

where $\rho$is an adaptation factor for the quantization step, and the value of $q_r$ can be tuned by tuning the value of $\rho$.

The inverse quantization process is represented by

$$\left\{\begin{array}{c}{r}_i=q_r\times r_i^q\\ {\theta }_i=q_{\theta }\times {\theta }_i^q\end{array}\right.$$

(9)

$V_i^q\left(r_i^q,{\theta }_i^q\right)$ represents the quantized polar coordinates. A quantization index number is defined as the integer part of the quantized polar coordinate and a quantization fraction number is defined as the decimal part of the quantized polar coordinate. For polar radius, the quantization index number is denoted as $r_i^{q\_int}$, and the quantization fraction number is denoted as $r_i^{q\_dec}$. For polar angle, the quantization index number is denoted as ${\theta }_i^{q\_int}$, and the quantization fraction number is denoted as ${\theta }_i^{q\_dec}$. It is obvious that $r_i^q=r_i^{q\_int}+r_i^{q\_dec} \mathrm{a}\mathrm{n}\mathrm{d} {\theta }_i^q={\theta }_i^{q\_int}+{\theta }_i^{q\_dec}$. The quantization index number set $\left\{\left(r_i^{q\_int},{\theta }_i^{q\_int}\right)|i\ne p_1 and i\ne p_2\right\}$ constitutes the encryption domain. Secret sharing operations will be performed on the encryption domain.

3.3. Map Encryption Based on Secret Sharing

In the original Shamir’s secret sharing scheme [31], the constant item $s$ can be replaced by elements in the encryption domain to produce the shares of the quantization index numbers, and the coefficients $a_1,\cdots ,a_{k-1}$are all randomly selected integers. The use of random numbers in the sharing process can promote the security level. However, the scheme cannot achieve diffusion properties. One bit change in secret $s$ can only change the shares for itself and has no impact to the shares of other elements in the encryption domain, which may lead to the failure of resisting differential cryptanalysis, chosen-plaintext attack, and so on. Therefore, the cipher-feedback mode of AES is cooperated into the original Shamir’s secret sharing scheme by using a random share of the previous sharing result as the last coefficient of the polynomial in the current sharing operation [32].

Then, the proposed $(k,n)$-threshold secret sharing scheme can be constructed as follows. (1) Generate $n$ different integers $\{x_1,x_2,\cdots ,x_n\}$ from a secret key denoted as ${key}_2$; (2) for the $i$-th element in the encryption domain, two $k-1$ degree polynomials are constructed by

$$\left\{\begin{array}{c}{f}_i^r\left(x\right)=(r_i^{q\_int}+\sum _{c=1}^{k-2}{a}_c{x}^c+f_{i-1}^r\left(x_{t_r}\right)x^{k-1}) mod p_r\\ f_i^{\theta }\left(x\right)=({\theta }_i^{q\_int}+\sum _{c=1}^{k-2}{b}_c{x}^c+f_{i-1}^{\theta }\left(x_{t_{\theta }}\right)x^{k-1}) mod p_{\theta }\end{array}\right.$$

(10)

where $a_1,\cdots ,a_{k-2}$ and $b_1,\cdots ,b_{k-2}$ are all randomly selected integers. $f_{i-1}^r\left(x_{t_r}\right)$ and $f_{i-1}^{\theta }\left(x_{t_{\theta }}\right)$ are randomly selected previous sharing results, in which $t_r$ and $t_{\theta }$ are random in each sharing and randomly selected from $\{\mathrm{1,2},\cdots ,n\}$. For the first element $i=1$, $f_0^r\left(x_{t_r}\right)$ and $f_0^{\theta }\left(x_{t_{\theta }}\right)$ can be any random integers satisfying $f_0^r\left(x_{t_r}\right)<p_r$ and $f_0^{\theta }\left(x_{t_{\theta }}\right)<p_{\theta }$. When $x\in \{x_1,x_2,\cdots ,x_n\}$, $n$ shares for polar radius and polar angle can be generated as $\{f_i^r\left(x_1\right),f_i^r\left(x_2\right),\cdots f_i^r\left(x_n\right)\}$ and $\{f_i^{\theta }\left(x_1\right),f_i^{\theta }\left(x_2\right),\cdots f_i^{\theta }\left(x_n\right)\}$, respectively. Then, $V_i^{q\_int\_j}\left(r_i^{q\_int\_j}=f_i^r\left(x_j\right),{\theta }_i^{q\_int\_j}=f_i^{\theta }\left(x_j\right)\right)$ represents the $i$-th encrypted quantization index number of share $j$.

In the above secret sharing scheme, a change of one element only influences the shares of itself and the following elements, and has no impact to the shares of preceding elements. In order to make the change of one element diffuse across the shares of all elements in the encryption domain, the above secret sharing operations can be performed in two rounds, and the sharing result of the second round is used as the final encryption result. In the second round, it is noted that, for the first element, the last coefficient of the secret sharing polynomial is randomly selected from the shares of the last element produced in the first round.

After secret sharing operations on encryption domain, the encrypted quantization index numbers represented as $V_i^{q\_int\_j}\left(r_i^{q\_int\_j},{\theta }_i^{q\_int\_j}\right)$($i=\mathrm{1,2},\cdots ,N$, $i\ne p_1,i\ne p_2$ and $j=\mathrm{1,2},\cdots ,n$) are combined with the quantization fraction numbers to form $n$ shares of the quantized polar coordinates. For the $i$-th vertex in share $j$, its encrypted quantized polar coordinates denoted as $V_i^{q\_j}(r_i^{q\_j},{\theta }_i^{q\_j})$ are computed as formula (11).

$$\left\{\begin{array}{c}{r}_i^{\mathrm{q}\_\mathrm{j}}=r_i^{\mathrm{q}\_\mathrm{i}\mathrm{n}\mathrm{t}\_\mathrm{j}}+r_i^{\mathrm{q}\_\mathrm{d}\mathrm{e}\mathrm{c}}\\ {\theta }_i^{\mathrm{q}\_\mathrm{j}}={\theta }_i^{\mathrm{q}\_\mathrm{i}\mathrm{n}\mathrm{t}\_\mathrm{j}}+{\theta }_i^{\mathrm{q}\_\mathrm{d}\mathrm{e}\mathrm{c}}\end{array}\right.$$

(11)

Finally, sequential operations of inverse quantization and inverse polar coordinate transformation are performed to all encrypted quantized polar coordinates $V_i^{q\_j}(r_i^{q\_j},{\theta }_i^{q\_j})(i=\mathrm{1,2},\cdots ,N,i\ne p_1,i\ne p_2\mathrm{a}\mathrm{n}\mathrm{d}j=\mathrm{1,2},\cdots ,n)$ to obtain the final $n$ shares denoted as $\left\{\left(j,{share}_j\right)|j\in \{\mathrm{1,2},\cdots ,n\}\right\}$ of encryption results for the original vector map. $KEY=({key}_1,{key}_2)$ is saved for decryption process.

3.4. Decryption Process

The flowchart for decryption process is shown as Figure 2. When any $k$ shares with their identities $\left(t_s,{share}_{t_s}\right),s\in \left\{\mathrm{1,2},\cdots ,k\right\},t_s\in \{\mathrm{1,2},\cdots ,n\}$ have been collected, polar coordinate transformation and quantization process are first performed to all the coordinates of each share sequentially, obtaining the encrypted quantized polar coordinates $V_i^{q_{\_}{t}_s}(r_i^{q_{\_}{t}_s},{\theta }_i^{q_{\_}{t}_s})(i=\mathrm{1,2},\cdots ,N,i\ne p_1,i\ne p_2,s=\mathrm{1,2},\cdots ,kand{t}_s\in \{\mathrm{1,2},\cdots ,n\left\}\right)$. Then, the encrypted quantization index numbers $r_i^{q\_int\_t_s}$($s=\mathrm{1,2},\cdots ,k$) for polar radius can be obtained as the integer part of $r_i^{q_{\_}{t}_s}$ and the quantization fraction numbers $r_i^{q\_dec}$ for polar radius can be obtained as the decimal part of $r_i^{q_{\_}{t}_s}$. Similarly, the encrypted quantization index numbers ${\theta }_i^{q\_int\_t_s}(s=\mathrm{1,2},\cdots ,k)$ for polar angle and the quantization fraction numbers${\theta }_i^{q\_dec}$ for polar angle can be obtained as the integer part and decimal part of ${\theta }_i^{q_{\_}{t}_s}$, respectively. It is easy to see that $r_i^{q\_int\_t_s}=f_i^r\left(x_{t_s}\right)$ and ${\theta }_i^{q\_int\_t_s}=f_i^{\theta }\left(x_{t_s}\right)$. Finally, one can compute $x_{t_s}$based on ${key}_2$, and reconstruct the polynomials $f_i^r$ and $f_i^{\theta }$ using the Lagrange interpolation as formula (2), recovering the original quantization index numbers $r_i^{q\_int}$ and ${\theta }_i^{q\_int}$ as $f_i^r\left(0\right)$ and $f_i^{\theta }\left(0\right)$, respectively.

The decrypted original quantization index numbers $\left(r_i^{q\_int},{\theta }_i^{q\_int}\right)$ are combined with the quantization fraction numbers $\left(r_i^{q\_dec},{\theta }_i^{q\_dec}\right)$ to form the original quantized polar coordinates $V_i^q(r_i^q,{\theta }_i^q)$ by using $r_i^q=r_i^{q\_int}+r_i^{q\_dec}\mathrm{a}\mathrm{n}\mathrm{d}{\theta }_i^q={\theta }_i^{q\_int}+{\theta }_i^{q\_dec}$. Subsequently, inverse quantization process and inverse polar coordinate transformation are performed to all the decrypted quantized polar coordinates $V_i^q(r_i^q,{\theta }_i^q)$ to obtain the final decrypted original vector map.

4. Experiments

4.1. Testing Environment and Datasets

The proposed algorithm is implemented using the Java (JDK8) language and the open-source library for geospatial data processing–GDAL. The experimental programs were run on 64-bit Windows 11 with AMD Ryzen™ 7 6800H CPU @ 3.20 GHz and 16G of memory.

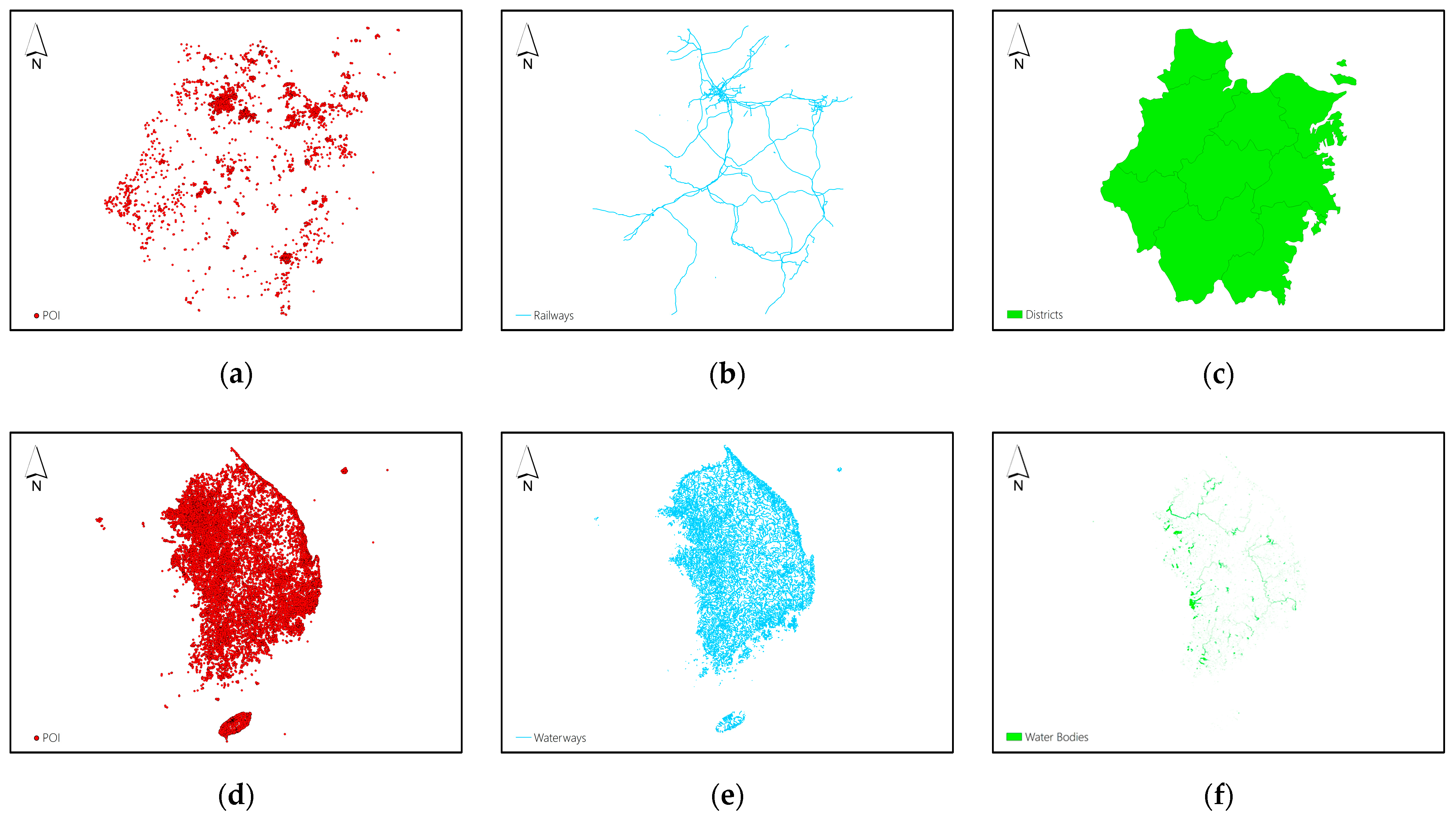
Experiments on point, polyline and polygon feature maps were designed to validate the effectiveness and efficiency of the proposed method for vector map encryption. To better demonstrate the applicability of the proposed method, as shown in Figure 3, vector map datasets from OpenStreetMap (OSM) were used in the experiments, covering different volumes, feature types, and precisions. Specifically, Datasets A to C are the Points of Interest (POI), railways network and administrative division of prefecture-level cities in Zhejiang Province, China, respectively. Datasets D to F are the Points of Interest (POI), waterway network and water bodies of South Korea, respectively. The statistical information of these datasets is listed in Table 1.

4.2. Encryption and Decryption Results

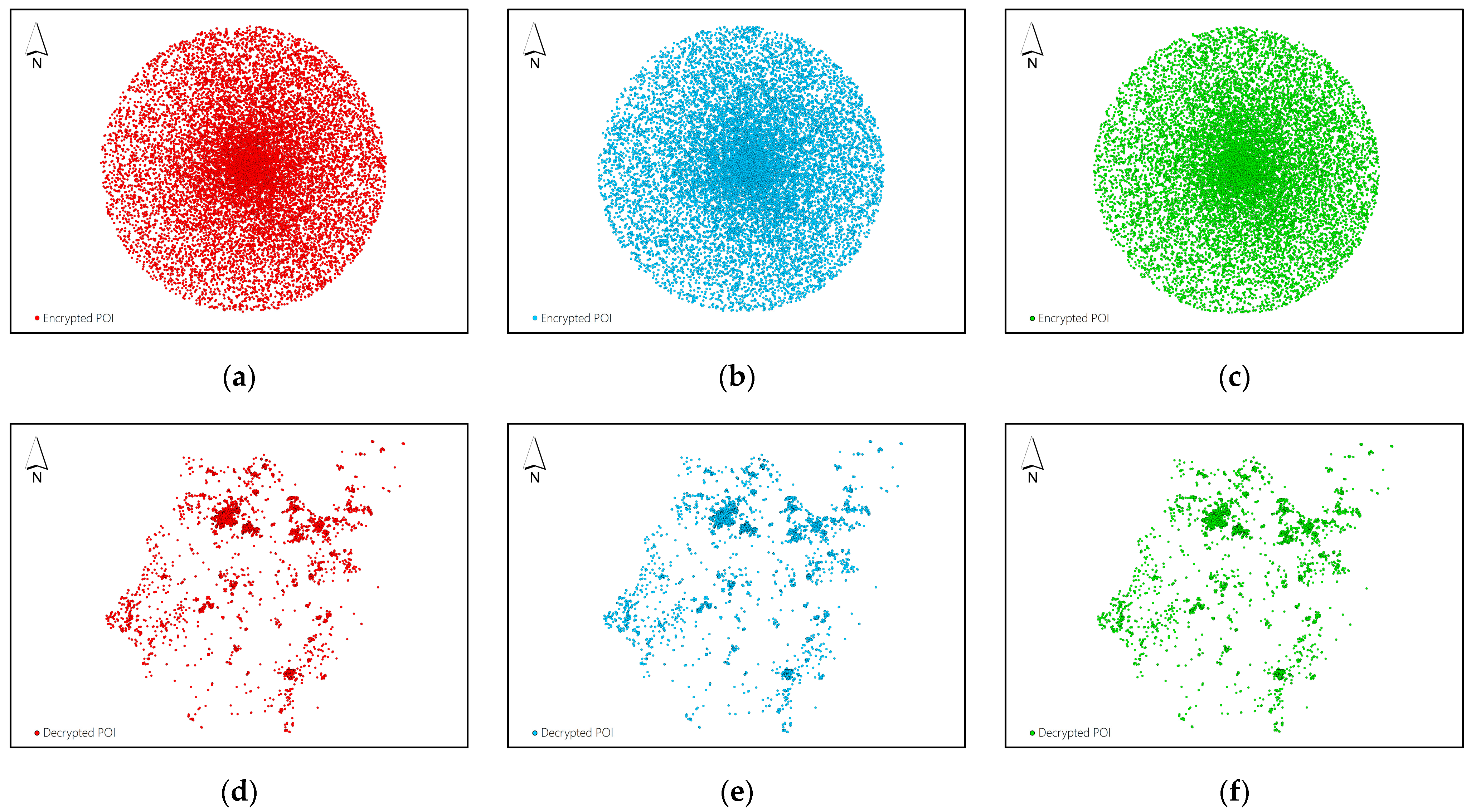
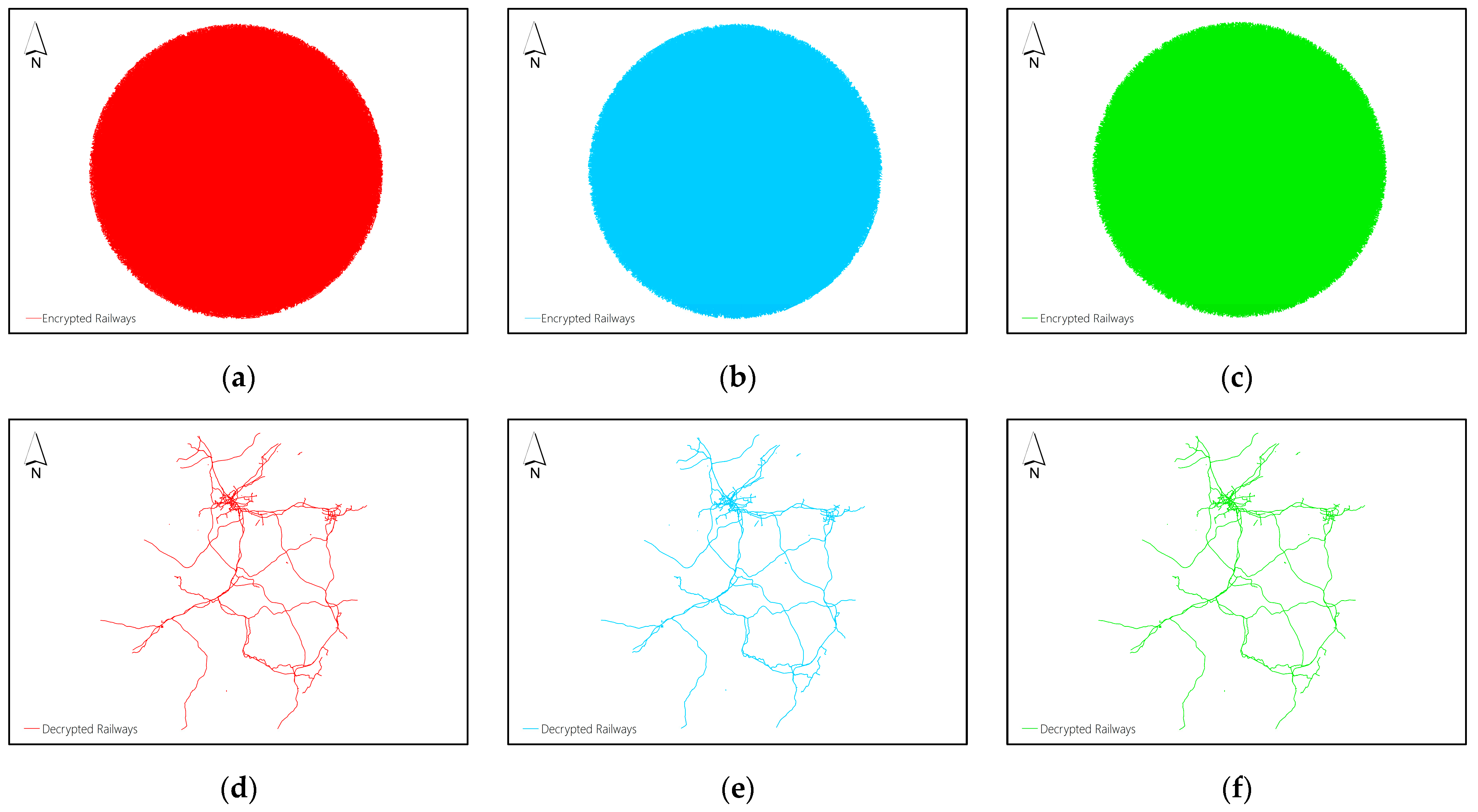
The encryption and decryption operations on the vector map data are performed utilizing the proposed method. The threshold secret sharing schemes of $\left(\mathrm{2,3}\right)$, $\left(\mathrm{3,5}\right)$ and $\left(\mathrm{5,9}\right)$ are implemented in the experiments, and some results are shown in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8. Figure 4(a-c) display the three shares of Dataset A obtained by using the proposed $\left(\mathrm{2,3}\right)$-threshold secret sharing method, and Figure 4(d-f) display the decryption results obtained by collecting any two shares to reconstruct the plaintext data. Figure 5(a-c) display the three shares of Dataset B obtained by using the proposed (2,3)-threshold secret sharing method, and Figure 5(d-f) display the decryption results obtained by collecting any two shares to reconstruct the plaintext data. 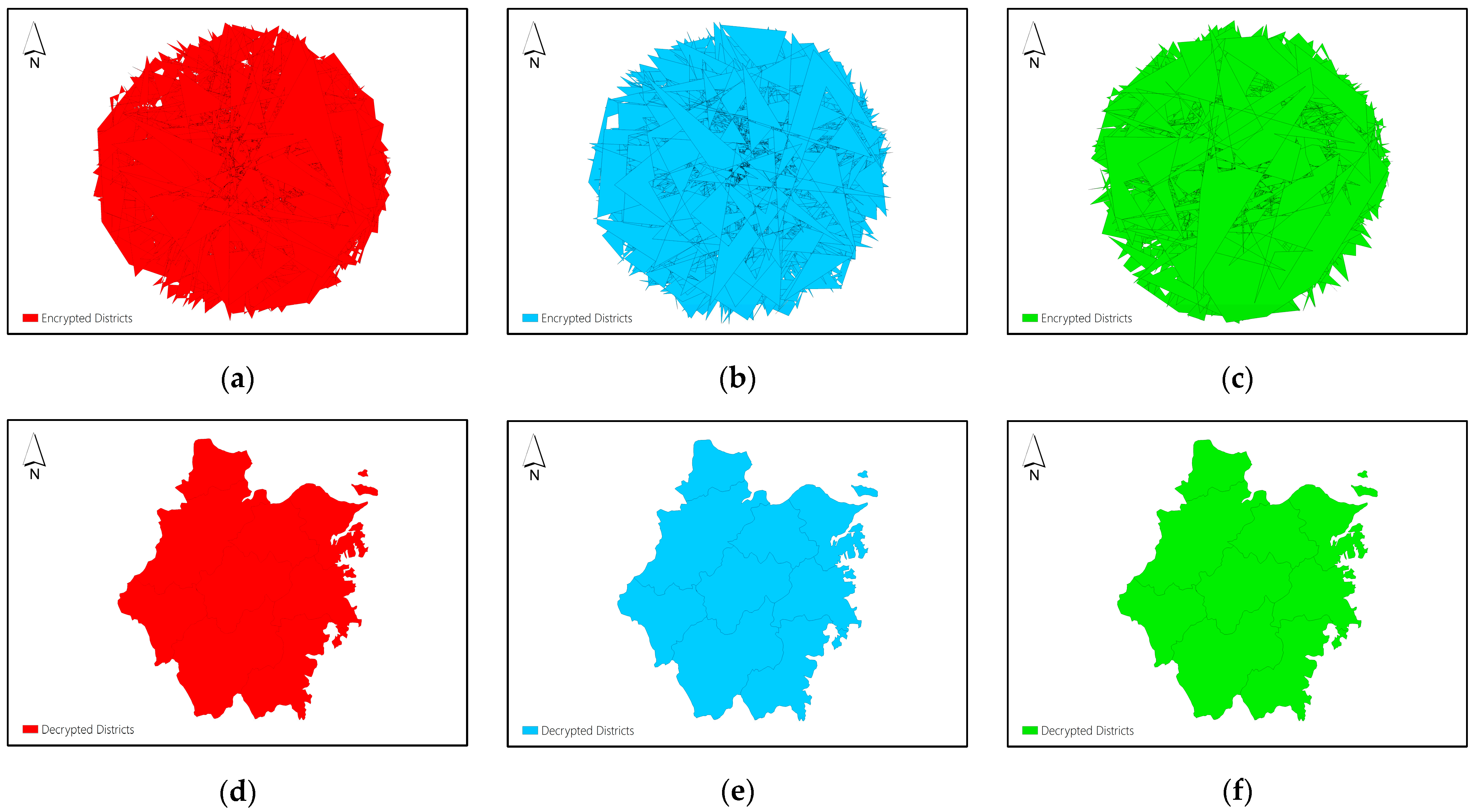Figure 6(a-c) display the three shares of Dataset C obtained by using the proposed (2,3)-threshold secret sharing method, and Figure 6(d-f) display the decryption results obtained by collecting any two shares to reconstruct the plaintext data. 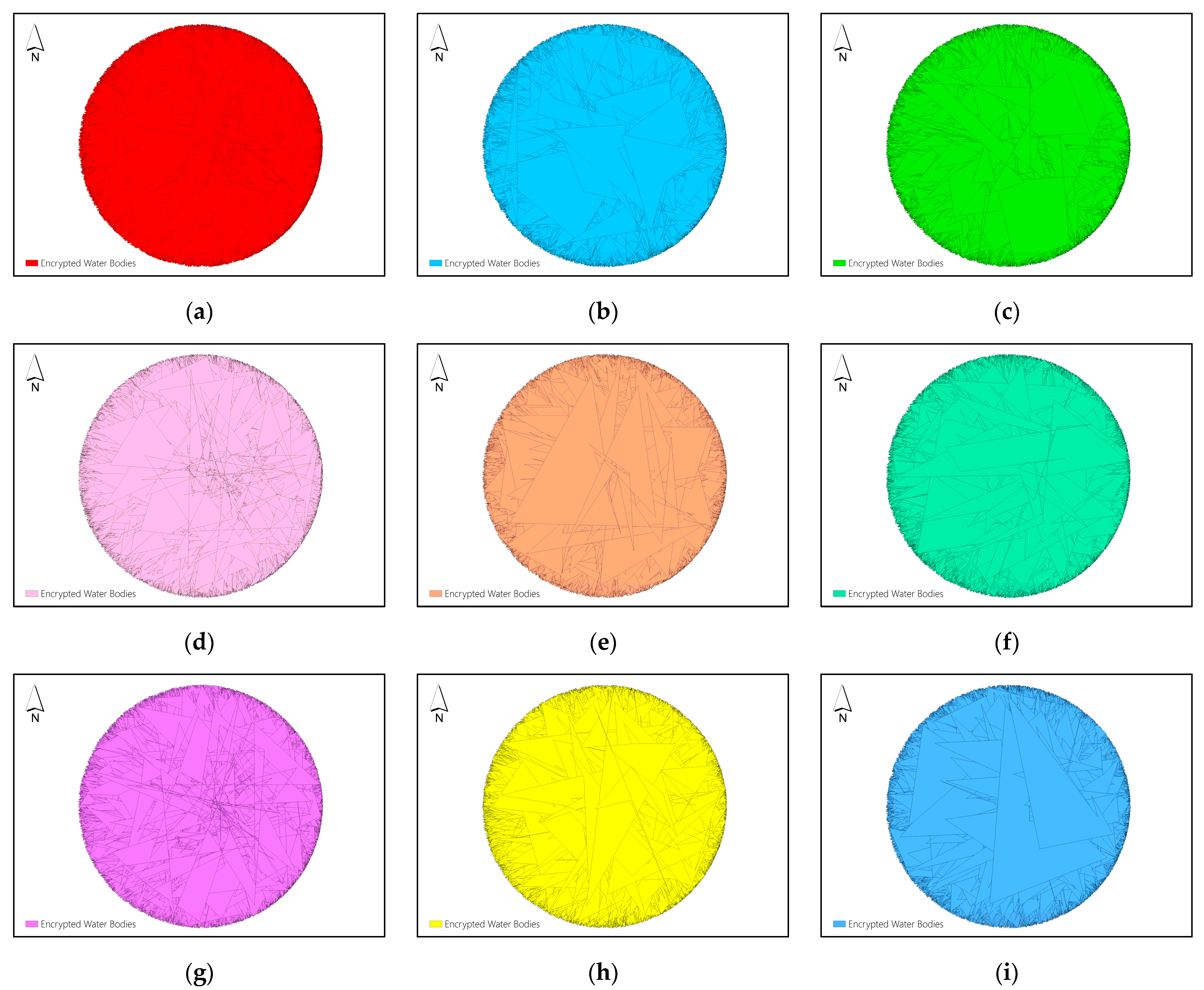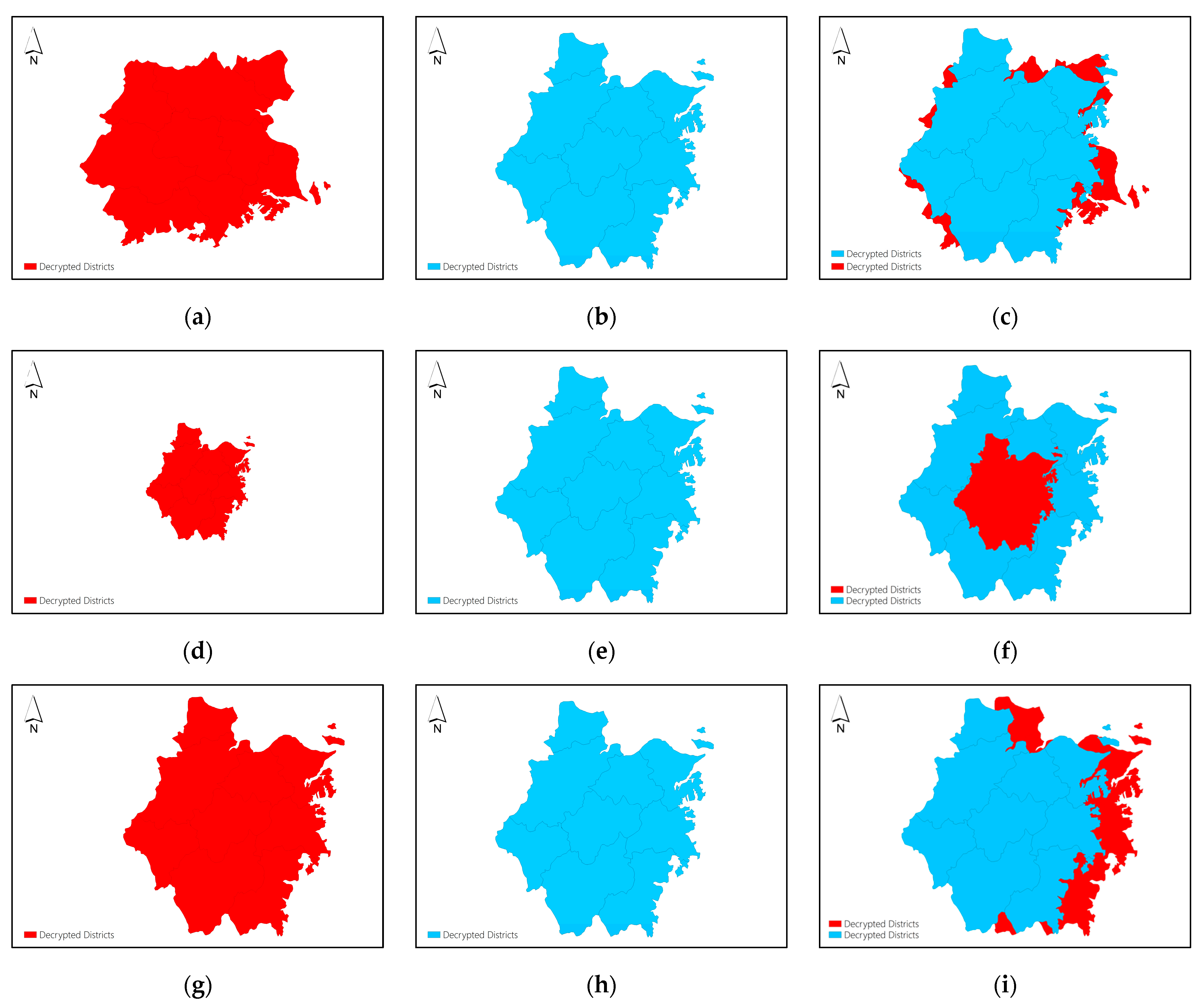Figure 7(a-i) display the nine shares of Dataset F obtained by using the proposed (5,9)-threshold secret sharing method. 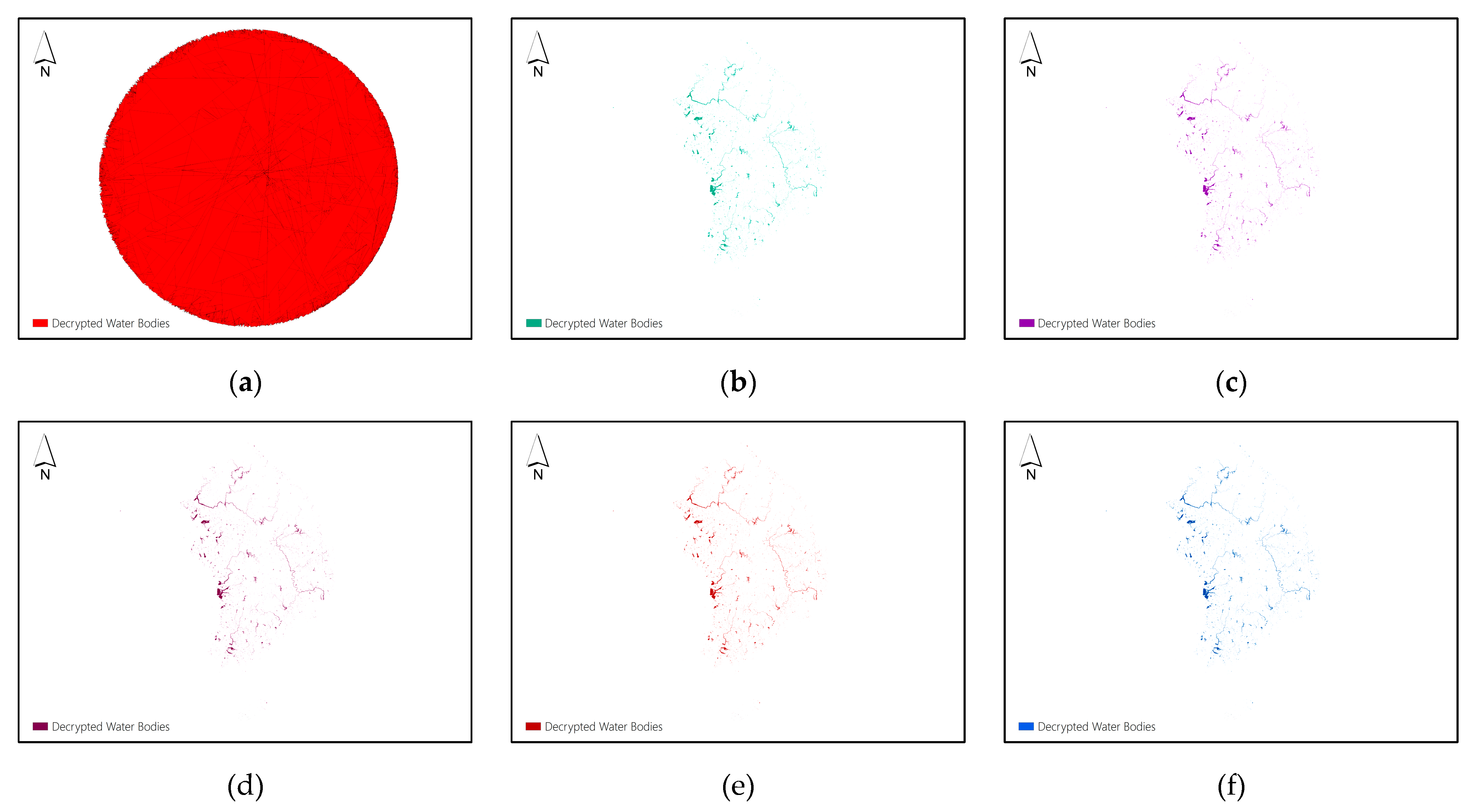Figure 8(a) displays the decryption result of Dataset F by collecting 4 of 9 shares to reconstruct the plaintext data, and Figure 8(b-f) display the decryption results of Dataset F by collecting 5, 6, 7, 8 and 9 shares to reconstruct the plaintext data, respectively.

From the results, it can be found that the vertex distribution of the shares produced by the proposed $\left(k,n\right)$-threshold secret sharing scheme is chaotic from the visual effect, and it is difficult to get a bit of valuable information and patterns about the original maps, thus realizing the protection of the map information. The decryption results shown in Figure 4(d-f), Figure 5(d-f) and Figure 6(d-f) validate that collecting any $k$ of $n$ shares produced by the proposed $\left(k,n\right)$-threshold secret sharing can reconstruct the plaintext data correctly. It means that if no more than $n-k$ shares are destroyed, the plaintext data still can be reconstructed correctly by the remaining shares. This verifies the disaster tolerance property and promotes the security level of the proposed encryption scheme.

The decryption results shown in Figure 8(a-f) indicate that collecting less than $k$ shares can not obtain any information of the original vector map, while collecting no less than $k$ shares can reconstruct the plaintext data correctly, and this further proves the high security level of the proposed encryption scheme.

4.3. Encryption Effects

In vector maps, the adjacent coordinates generally exhibit strong correlations. An effective encryption process should disrupt such correlations between coordinates and scramble all the vertices in the vector map in a random way. Thus, the RMSE (Root Mean Square Error) between the original map and the encrypted map will be high. In this section, the correlation of adjacent coordinates and the RMSE between the original and encrypted maps are adopted to measure the efficacy of the proposed encryption method.

4.3.1. Correlation of Adjacent Coordinates (CAC)

The correlation between adjacent coordinates in the vector map is calculated as:

$$\overline{x}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{x}_i$$

(12)

$${\sigma }_x=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(x_i-\overline{x}\right)}^2}$$

(13)

$$cov\left(x,y\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)$$

(14)

$$r_{xy}={\displaystyle \frac{cov\left(x,y\right)}{{\sigma }_x{\sigma }_y}}$$

(15)

Table 2 shows the results of the adjacency coordinate correlation in dataset B and C. It can be seen that the CAC of the original map is quite high, while that of the encrypted map shares are close to zero. The CAC of the decrypted map is the same as that of the original map, indicating that the decrypted map data is identical to the original map data. This demonstrates that the proposed encryption algorithm in this paper can effectively break the correlation within the original map data.

4.3.2. RMSE Between the Original and Encrypted Maps

RMSE is used to describe how big the offset distance between the two corresponding vertices in the original map and encrypted map is. To eliminate the influence of dimensionality, normalized RMSE ($NRMSE$) is proposed in this paper by normalizing the original RMSE using the maximum distance between two vertices in the original map. The calculation of $NRMSE$ is represented by formula (16), where $d_i$ is the offset distance between two corresponding vertices in the original and encrypted maps, $N$ is the number of vertices, and $maxdis$ is the maximum distance between two vertices in the original map. Obviously, the larger the $NRMSE$, the greater the difference between the original and encrypted maps. Table 3 shows the normalized minimum offset distance (N-Min offset distance), normalized maximum offset distance (N-Max offset distance) and $NRMSE$ between original and encrypted maps for Dataset A, B and C. The results shown in Table 3 suggest that the encrypted maps are totally different from the original maps and the proposed encryption method has very good encryption effects.

$$NRMSE={\displaystyle \frac{1}{maxdis}}\sqrt{{\displaystyle \frac{{\sum }_{i=1}^{i=N}{d}_i^2}{N}}}$$

(16)

4.4. Encryption and Decryption Security

An encryption scheme which possesses probabilistic property encrypts the same plaintext data into two different ciphertexts in two encryption processes, thus, achieving semantic security. Furthermore, if an encryption scheme possesses diffusion property, a bit change in plaintext data will diffuse across the whole dataset in ciphertext version after encryption process, resulting in totally different encrypted data, which enable the encryption scheme to resist differential cryptanalysis, chosen-plaintext attack, and so on. Probabilistic property and diffusion property are very important properties for promoting the security of the encryption algorithms. Many existing vector map encryption schemes lack these properties, which greatly affects the security of the algorithms. Thus, the probabilistic and diffusion properties of the proposed encryption method are evaluated in this section. In addition, the robustness of the proposed decryption process to RST transformations is also evaluated in this section, since the RST transformations are very common data operations for vector maps.

4.4.1. Probabilistic Property

Probabilistic property ensures that the encryption process results in different ciphertexts when a plaintext is encrypted twice. In this section, plaintext maps are encrypted twice using the proposed encryption method. The normalized minimum offset distance (N-Min offset distance), normalized maximum offset distance (N-Max offset distance) and N-RMSE between two corresponding shares produced by encryption twice are computed and the results are listed in Table 4. Table 4 demonstrates that the offset distances between corresponding shares obtained by encrypting the same dataset twice are big, and the corresponding shares are completely different, which proves that the proposed vector map encryption method possesses probabilistic property.

4.4.2. Diffusion Property

Diffusion property ensures that one bit change in a vertex coordinate will diffuse across all the vertex coordinates after encryption process, which promotes the encryption algorithm’s ability of resisting differential cryptanalysis, chosen-plaintext attack, and so on. In this section, one bit of a vertex coordinate in a dataset is changed first. Then, the proposed encryption algorithm is performed to the dataset before and after change, respectively. Finally, the N-Min offset distance, N-Max offset distance and N-RMSE between two corresponding shares produced by encrypting the dataset before and after change are computed, and the results are listed in Table 5. Table 5 shows that the offset distances between corresponding shares are big, and that the corresponding shares obtained by encryption before and after one bit change are totally different, which verifies that the proposed vector map encryption method possesses diffusion property.

4.4.3. Robustness of Decryption Process

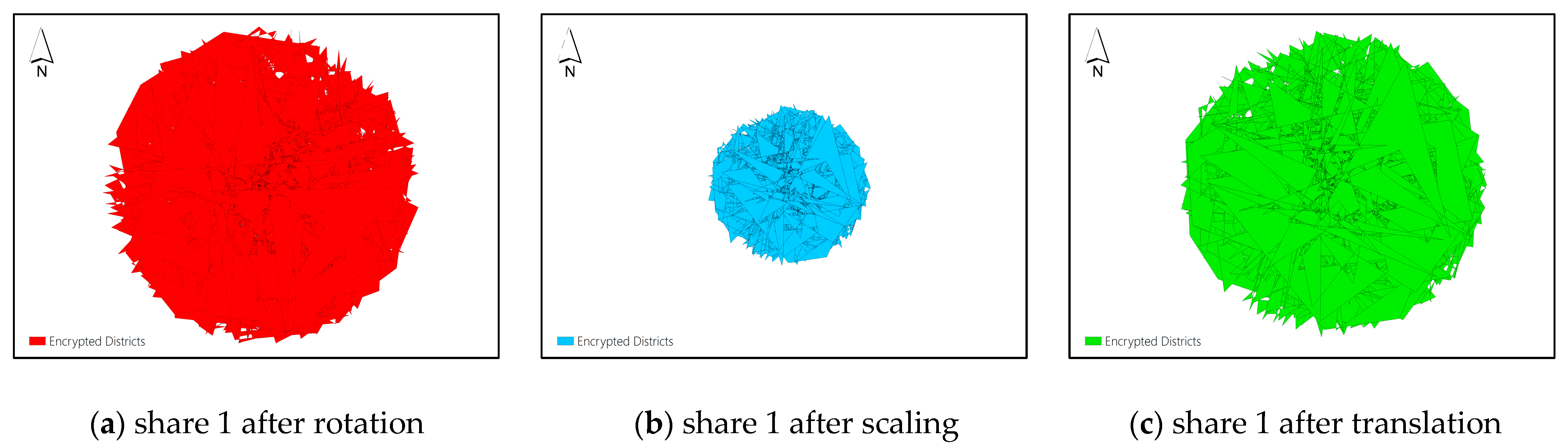
RST transformations are very common data operations for vector maps. The corresponding decryption algorithm for an encryption scheme should be robust to RST transformations so that the encrypted map can be correctly decrypted even after the RST transformations are performed to it. In this section, Dataset C is encrypted using the proposed $\left(\mathrm{2,3}\right)$-threshold secret sharing scheme shown as Figure 6(a-c), and one of three shares is selected to perform RST transformations. Share 1 is selected for example. The transformed share 1 after rotation, scaling and translation operations is shown in Figure 9(a), 9(b) and 9(c), respectively. Then, the transformed share 1 and share 2 are selected to reconstruct the plaintext map. As the coordinate system of the transformed share 1 is different from the original coordinate system used by share 2, the reconstructed plaintext map can use either the transformed coordinate system of share 1 or the original coordinate system of share 2. The decrypted maps using the transformed coordinate system and the original coordinate system and the overlay of the two decrypted maps are shown in the sub figures of Figure 10, respectively. Figure 10 demonstrates that even the shares involved in decryption are transformed by RST operations, the plaintext map can still be correctly decrypted, and the decrypted map can use any coordinate system used by the shares involved in the decryption.

4.5. Efficiency Analysis

Computational efficiency is an important metric for evaluating encryption algorithms. Experiments were conducted using vector maps of three types (point, polyline, polygon) with different data volumes to demonstrate the efficiency of the proposed method. Through theoretical analysis of the algorithm, it can be seen that the parameters $n$, $k$ used in the $\left(k,n\right)$-threshold secret sharing process and the data volumes are key factors that affect the efficiency of the proposed algorithm. The following experiments were conducted to demonstrate how these factors affect the encryption and decryption efficiency.

4.5.1. Encryption Efficiency

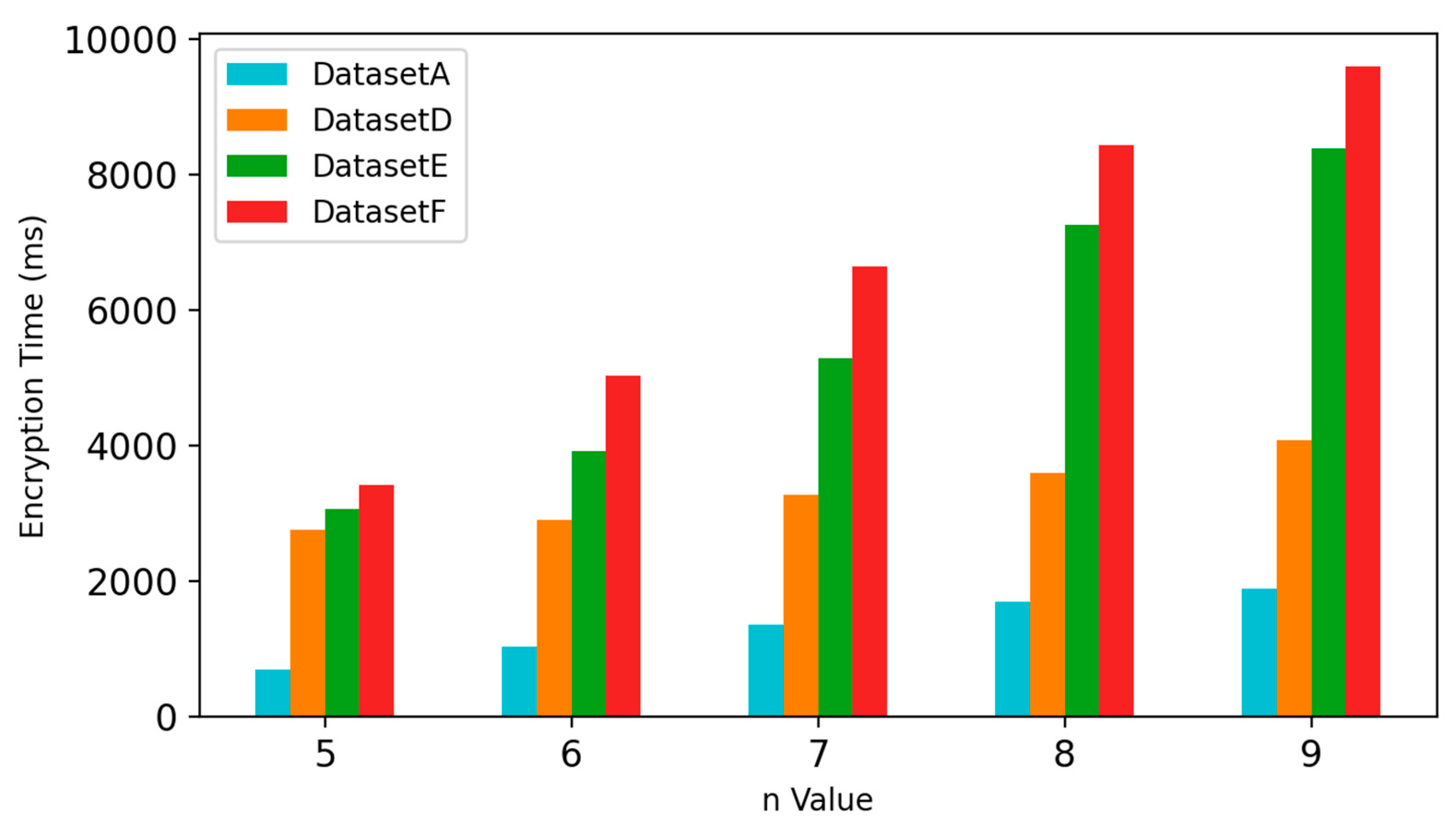
In this section, Datasets A, D, E and F of different data types with different data volumes are selected for experiments. Five encryption experiments are set to test the encryption time of the proposed method. The number $n$ of the shares produced by encryption process is set to 1, 3, 5, 7 and 9 for each respective experiment. Encryption operations are performed to all the selected datasets in each experiment, and each encryption operation is performed 30 times, taking the average value as the result. The experimental results for the five experiments are displayed in Figure 11, which shows the increase in encryption time with the increase of data volume and the number of shares. It can be found in Figure 11 that compared to data volume, the number of shares has a greater impact on encryption time. When $n$ increases, the encryption time increases significantly. However, when the $n$ value is not too much big, it is found that the encryption time of the proposed method is comparable to that of the Local Encryption algorithm [24] and DRPP algorithm [25] which is not demonstrated here due to the limitation in paper length.

4.5.2. Decryption Efficiency

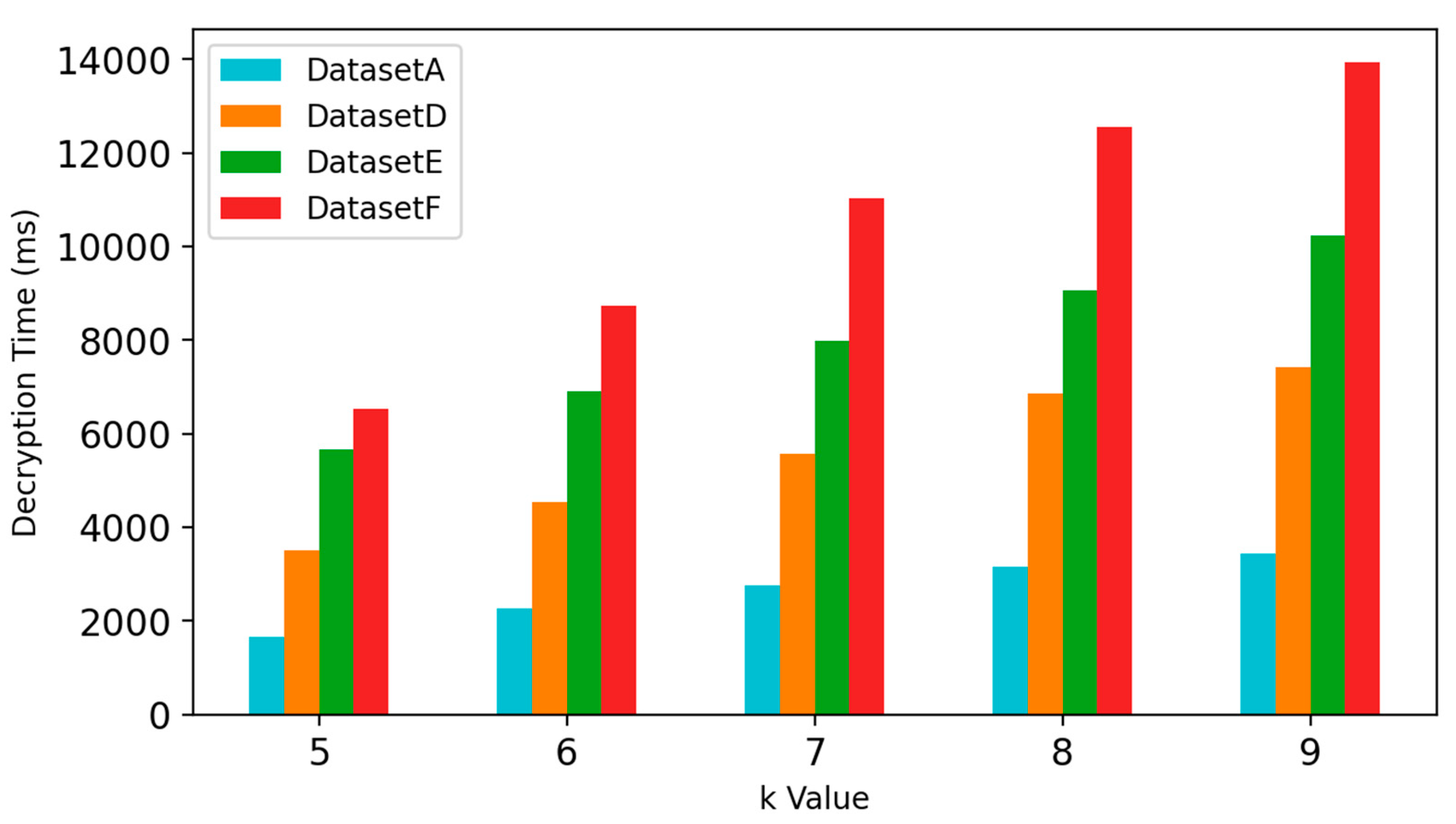
In this section, the impact of the $k$ value used in the $\left(k,n\right)$-threshold secret sharing process and the data volume on the decryption time is evaluated. In the experiments, $n$ is set to 9, and $k$ is set to 5, 6, 7, 8 and 9, respectively. The selected datasets in section 4.5.1 are used in the decryption experiments. Each decryption operation is performed 30 times, taking the average value as the result. The decryption time for each selected dataset under different $k$ values is displayed in Figure 12, which shows the increase in the decryption time with the increase of data volume and $k$ value. It is noted in Figure 12 that compared to $k$ value, data volume has a much greater impact on decryption time. This is because Lagrange interpolation for decrypting each vertex coordinate is time-consuming and as the number of vertices increases, time consumption becomes more significant. For this reason, the time efficiency of decryption operations is much lower than that of encryption operations for the proposed method.

4.6. Comparison with Existing Methods

To evaluate the applicability and effectiveness of the proposed method, a comparison is made with other methods from five aspects, namely, whether the encryption method has disaster tolerance property, probabilistic property, diffusion property, the robustness to data RST transformations and whether it is applicable to points, polylines, and polygons. The comparison results are listed in Table 6. As shown in Table 6, (1) Compared with references [9,24,25,29,30], the proposed method has disaster tolerance property, which means that even some map shares are unavailable, the plaintext map can still be correctly decrypted; (2) Compared with references [9,24,25], the proposed method has probabilistic property. That is, different ciphertexts will be generated after encrypting the same plaintext twice, thus achieving semantic security; (3) Compared with references [29,30], the proposed method has diffusion property, which enhances the algorithm’s ability of resisting differential cryptanalysis, chosen-plaintext attack, and so on; (4) Compared with references [24,29,30], the proposed method is robust to data RST transformations, which means the plaintext map can still be decrypted after RST transformations are performed to the ciphertext map; (5) Compared with references [25,29], the proposed method is applicable to different data types such as points , polylines and polygons. Overall, the proposed method is superior compared with the existing methods.

5. Conclusions

This research proposes a novel vector map encryption method based on $\left(k,n\right)$-threshold secret sharing, which encrypts one vector map into $n$ map shares, and only by collecting at least k shares can the plaintext map be reconstructed. The encryption process consists of polar coordinate transformation and quantization, secret sharing process to produce $n$ shares, and inverse quantization and inverse polar coordinate transformation. The corresponding decryption process consists of polar coordinate transformation and quantization, plaintext reconstruction by collecting at least $k$ shares, and inverse quantization and inverse polar coordinate transformation. To validate the effectiveness of the proposed method, encryption results of different datasets using different secret sharing schemes are given, and encryption effects, security and efficiency were analyzed on vector map data of different types with different data volumes. Compared with available representative methods, the proposed encryption method has many very good properties, such as disaster tolerance property, probabilistic property, diffusion property and the robustness to data RST transformations, which greatly enhance the security and practicality of the method.

The proposed vector map encryption method encrypts a vector map into $n$ shares, and the $n$ shares can be managed by $n$ respective data administrators. Decryption of data can only be carried out with the consent of at least $k$ data administrators, making it particularly suitable for protecting the security of sensitive vector map data. To our knowledge, our work is the first to achieve vector map encryption using $\left(k,n\right)$-threshold secret sharing.

However, the proposed method also has some limitations. The encryption method encrypts one vector map into $n$ map shares, expanding data volume by $n$ times and bringing challenges to data storage. In addition, for the proposed method, as $n$ increases, the encryption efficiency rapidly decreases. Moreover, due to that the Lagrange interpolation for decrypting each vertex coordinate is time-consuming, the decryption efficiency is not very high, too. Avenues for future investigation include exploring more efficient ways to achieve $\left(k,n\right)$-threshold secret sharing to improve the efficiency of the method.