Multi-Model Approach for Stock Price Prediction and Trading Recommendations

1. Introduction

The increasing complexity and scale of modern financial markets have transformed stock trading [1] into a data-intensive domain, where conventional manual analysis and intuition-driven strategies [2,3] often fall short. Markets such as China’s A-share exchange encompass over 2,000 listed companies with historical records spanning decades, producing massive volumes of dynamic, nonlinear, and highly volatile data [4]. These characteristics render traditional analytical techniques inadequate for extracting timely and robust insights.

In response, machine learning (ML) and deep learning techniques has opened new avenues for financial time series modeling [5]. These methods are increasingly used in market prediction tasks due to their ability to process large volumes of historical data and uncover complex, nonlinear patterns [6,7]. Unlike traditional analytical tools, ML-based approaches can generate predictive insights that are difficult to obtain through manual or rule-based techniques [8].

Building on these advancements, this study presents a unified forecasting framework that integrates both classical statistical techniques and modern deep learning models. We propose a unified stock forecasting framework comprising five models: LR, ARIMA, LSTM, an ARIMA-LSTM ensemble, and a Transformer-based model. These models are evaluated across five representative U.S. stocks–AAPL, KO, NVDA, PFE, and TSLA–which were selected to reflect diverse volatility patterns and sectoral characteristics. By featuring sliding window segmentation and window-based normalization, we enable fair and generalizable model comparison. Our study emphasizes modularity, preprocessing rigour, and volatility-aware evaluation, showing that preprocessing strategies can significantly influence forecasting performance and that statistical models may outperform deep learning methods under certain volatility regimes.

2. Related Work

Recent advances in stock price prediction have introduced a range of techniques spanning from statistical models to deep learning-based methods. They can be broadly categorized into three streams: classical statistical models, deep learning architectures, and hybrid or comparative approaches. However, many existing studies exhibit limitations in comparative breadth and generalizability. This section briefly reviews representative techniques from each category, highlighting their core mechanisms, typical applications, and limitations relevant to our study.

2.1. Classical and Deep Learning Models (ARIMA / LSTM / LR)

For short-term prediction of stationary sequences, traditional models such as Autoregressive Integrated Moving Average (ARIMA) is particularly effective. It combines three key components - Autoregression (AR), Integration (I), and Moving Average (MA) - to capture different aspects of time series behavior [9]. The AR component models lag-based dependencies, the MA component addresses error autocorrelation, and the Integration component ensures stationarity through differencing. Figure 1 illustrates the modeling pipeline and workflow of ARIMA.

ARIMA models have maintained their relevance in stock price prediction despite the emergence of newer methods. Ariyo’s 2014 study [10] provided a systematic approach to ARIMA model selection, utilizing metrics such as Standard Error of Regression (SER), Adjusted R-square values, Bayesian Information Criteria. Wang’s Proposed Hybrid Model (PHM) combined ARIMA with ESM and BPNN [11], analyzing weekly data to demonstrate superior performance over single-model approaches. Similarly, Zhang’s research [12] integrated ARIMA with recurrent neural networks (RNNs), achieving improved prediction in both linear and nonlinear settings.

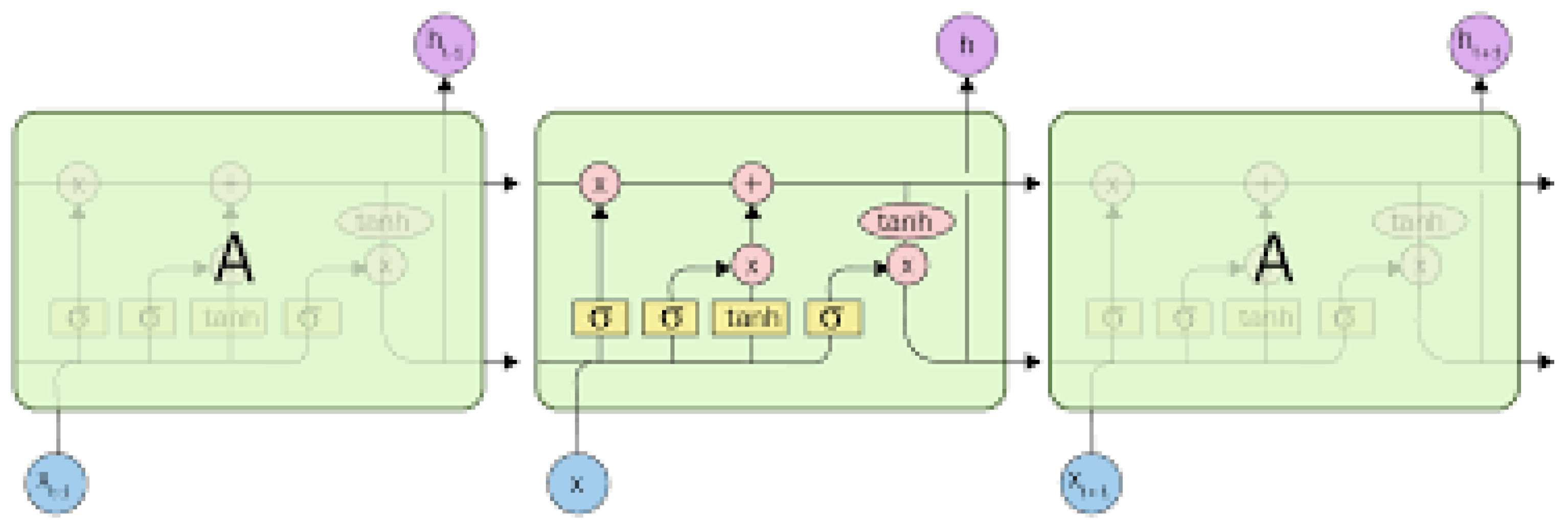
In contrast, Long Short-Term Memory (LSTM) networks, a type of RNN, address the limitations of traditional RNNs in modelling long-term dependencies [13]. As designed for sequential data, their architecture includes specialized memory cells containing input, forget, and output gates [14]. Each LSTM unit processes information through these gates, enabling selective information retention and update. The structure of an LSTM network (as shown in Figure 2) can be visualized as a chain of repeating units, each processing sequential inputs.

The memory cell maintains state information over arbitrary time intervals, while the gates control information flow:

$$C_t=f_t·C_{t-1}+i_t·tanh(W_C·[h_{t-1},x_t]+b_C)$$

(1)

where $f_t$ represents the forget gate, $i_t$ the input gate, and $C_t$ the cell state at time t.

Recent applications of LSTM in stock prediction have demonstrated remarkable success. Di Persio and Honchar [15] demonstrated LSTM’s superior performance compared to traditional Recurrent Neural Networks (RNN) and Gated Recurrent Units (GRU) in predicting Google stock prices using five-day period data. Their work established LSTM as a particularly effective method for short-term price predictions.

While models like ARIMA and LSTM offer sophistication and modeling depth, simpler alternatives like Linear Regression (LR) remain valuable as fast, interpretable baselines. LR assumes a linear relationship between input features and target prices and performs well in stable market conditions. Its simplicity, speed, and interpretability make it valuable in scenarios where market behavior is relatively stable or linear. Although it lacks the capacity to model nonlinear patterns, LR provides a benchmark for understanding whether additional model complexity yields significant improvements. Bhuriya et al. (2017) [16] reported competitive performance of LR on stable stocks under carefully selected features.

2.2. Hybrid Models and Transformer Architectures

Recent literature has explored hybrid architectures that combine statistical models and deep learning to improve forecasting accuracy. One of the earliest examples is the work by Fischer and Krauss (2018) [17], which combined deep neural networks with market indicators to outperform traditional financial models. More recently, Livieris et al. (2020) [18] proposed an ARIMA-LSTM hybrid model for stock price prediction, demonstrating improved generalization on financial time series. These hybrid systems leverage ARIMA’s efficiency in modeling short-term trends and LSTM’s capacity to handle nonlinear, long-term dependencies. Their integration often results in enhanced robustness in volatile environments and better adaptability to structural market changes.

Transformer models, originally designed for natural language processing, have also been adapted for time series forecasting. Their self-attention mechanism enables modeling of long-range dependencies in sequential data without relying on recurrence. Notable implementations such as Informer, Temporal Fusion Transformer (TFT), and Time Series Transformer have shown competitive results in financial and energy domains. Wu et al. (2021) [19] demonstrated that Informer reduces computation time while retaining accuracy, whereas Lim et al. (2021) [20] showed TFT’s ability to integrate static and time-varying covariates with interpretable attention layers. Despite these advantages, transformers often require large datasets and careful regularization to avoid overfitting in noisy financial environments.

2.3. Advanced Integration Strategies

Building upon the foundational models discussed, recent research has focused on advanced integration strategies that combine traditional statistical models, deep learning, and modern attention mechanisms to enhance robustness and adaptability across diverse market conditions. These strategies are particularly effective when addressing complex financial signals that exhibit both short-term fluctuations and long-range dependencies. For instance, to further capture sequential relevance, attention mechanisms have been embedded within LSTM frameworks to dynamically weigh input sequences, improving interpretability and forecast accuracy [21,22,23].

Reinforcement learning has also been applied to financial scenarios, aiming to optimize trading strategies through reward-based policies [24]. Recent advances in multi-armed bandit models [25] and scalable neural kernels [26,27] offer promising directions for adaptive decision-making in dynamic financial environments, particularly in real-time trading scenarios. Extensions to contextual bandits under unbounded context distributions further improve robustness in non-stationary, high-dimensional financial settings [28]. Building upon this, Drift2Matrix [29] addresses concept drift in co-evolving time series. Additionally, recent work explores cross-modal fusion techniques to harmonize heterogeneous financial signals, such as combining visual and temporal data [30]. However, these works often focus on narrow model comparisons, lack consistent preprocessing pipelines, or apply limited cross-stock evaluation.

In addition to model integration strategies, recent advances in data-centric AI propose automatic feature refinement as a complementary approach to improve forecasting quality. Studies have explored reinforcement-guided selection [31], and symbolic-autoregressive embedding [32] to identify or transform salient input features in high-dimensional tabular and temporal datasets. Other research introduces contrastive or topology-aware transformations to enhance representation fidelity [33,34]. While these methods are primarily applied in domains such as biomedical signals or material science, their implications for volatility-aware financial modeling—especially in guiding input construction for LSTM or Transformer—remain a promising avenue for future integration.

3. Data Collection and Processing

3.1. Dataset Description and Selection

We collected historical stock price data for five publicly traded U.S. companies—Apple (AAPL), Coca-Cola (KO), NVIDIA (NVDA), Pfizer (PFE), and Tesla (TSLA)—using Yahoo Finance. These companies were selected to represent a broad range of market sectors and volatility profiles: AAPL represents a large-cap technology firm, KO reflects the consumer staples sector with stable price behavior, NVDA offers exposure to high-volatility tech stocks, PFE captures dynamics from the pharmaceutical industry, and TSLA embodies a high-growth, high-volatility automotive innovator. This diversity ensures that our model evaluation spans a spectrum of market behaviors, from stable to turbulent.

The dataset spans a five-year period. Each stock’s historical time series was aligned to a total of 1,250 trading days after synchronizing trading calendars to ensure temporal consistency across all assets. For each day, six key metrics were recorded: open, high, low, close, adjusted close, and volume. These fundamental attributes are standard in financial forecasting tasks and offer a rich basis for temporal and cross-sectional analysis.

3.2. Data Preprocessing Methodology

To accommodate the unique input requirements of each model type, we applied targeted preprocessing strategies.

3.2.1. Linear Regression Preprocessing

We implement temporal aggregation by combining five consecutive trading days into a single observation unit (creating a 25-dimensional input vector), with the closing price five days ahead serving as the prediction target. This structure enables capturing short-term price patterns while maintaining computational efficiency.

3.2.2. ARIMA Time Series Transformation

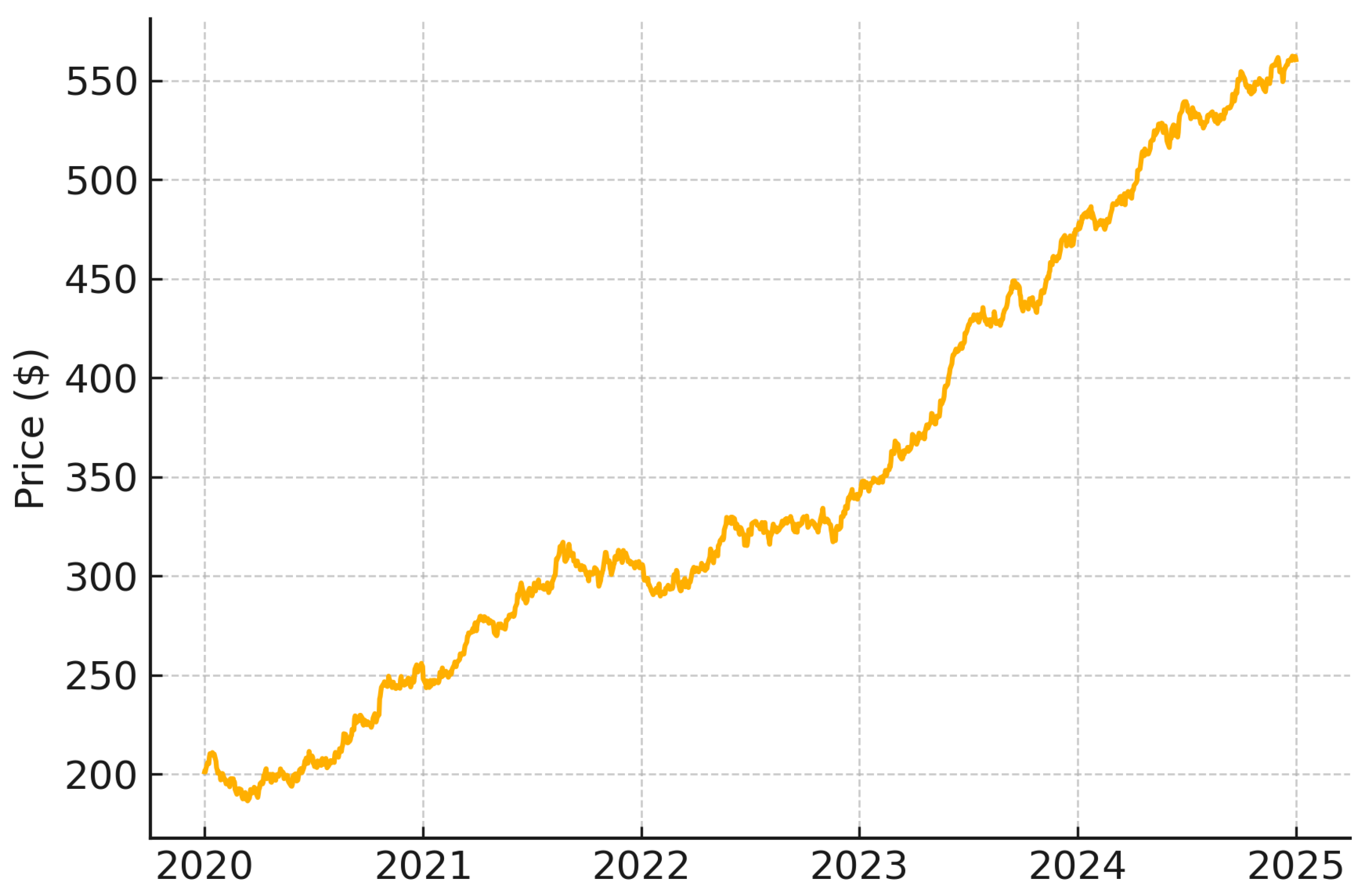
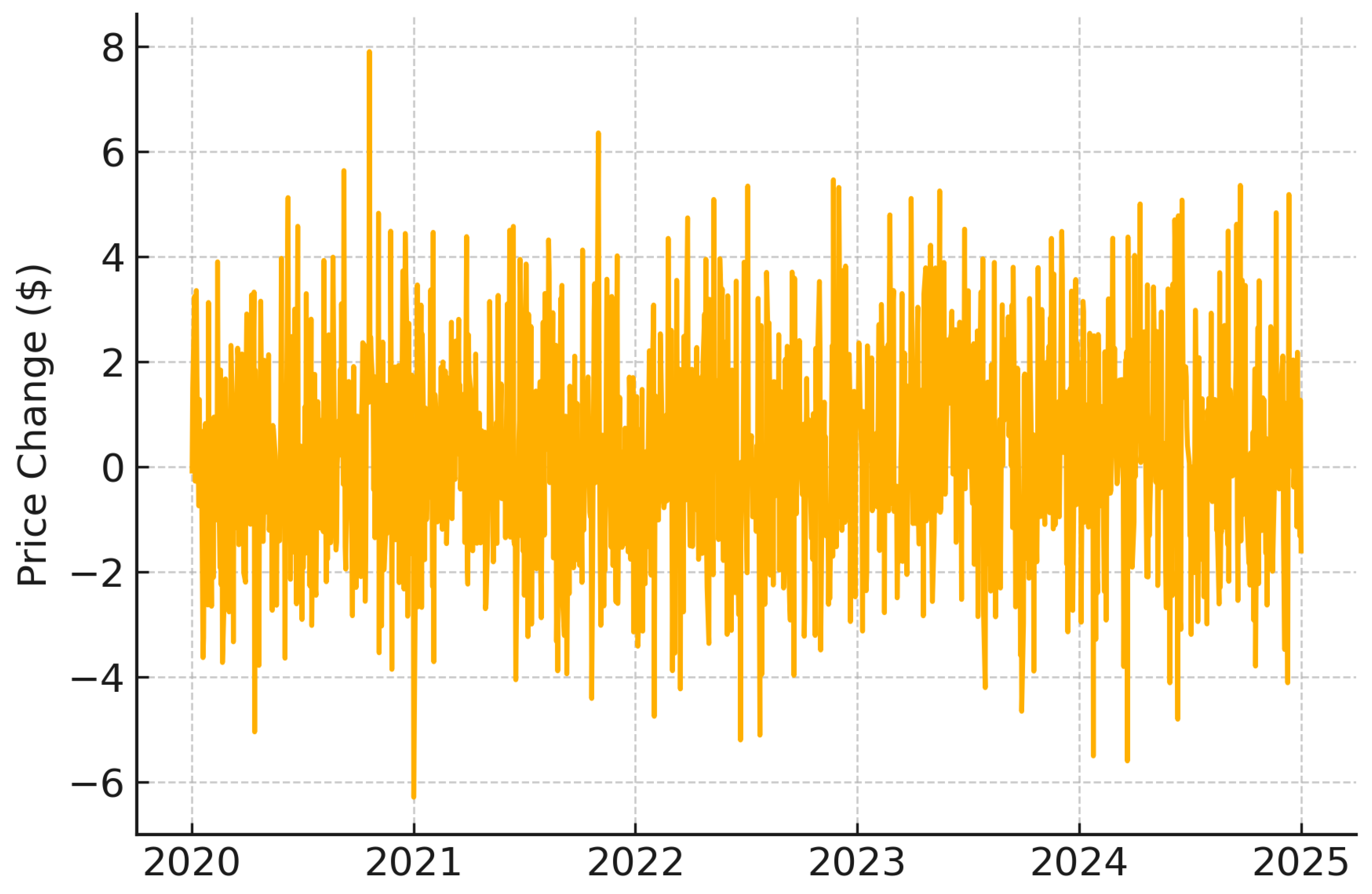
The ARIMA model implementation required careful attention to time series stationarity. We applied first-order differencing to the closing price sequence to generate a stationary time series, as illustrated in Figure 3 and Figure 4 using NVIDIA stock data as an example. Figure 3 illustrates the raw price series of NVIDIA, showing trend and non-stationarity, while Figure 4 presents the first-order differenced series, confirming stationarity post-transformation. The stationarity of the transformed series was rigorously validated through unit root testing, with all stocks showing p-values below ${10}^{-10}$. This statistical validation confirmed that first-order differencing was sufficient to achieve stationarity, eliminating the need for higher-order transformations.

3.2.3. LSTM Sequential Data Processing

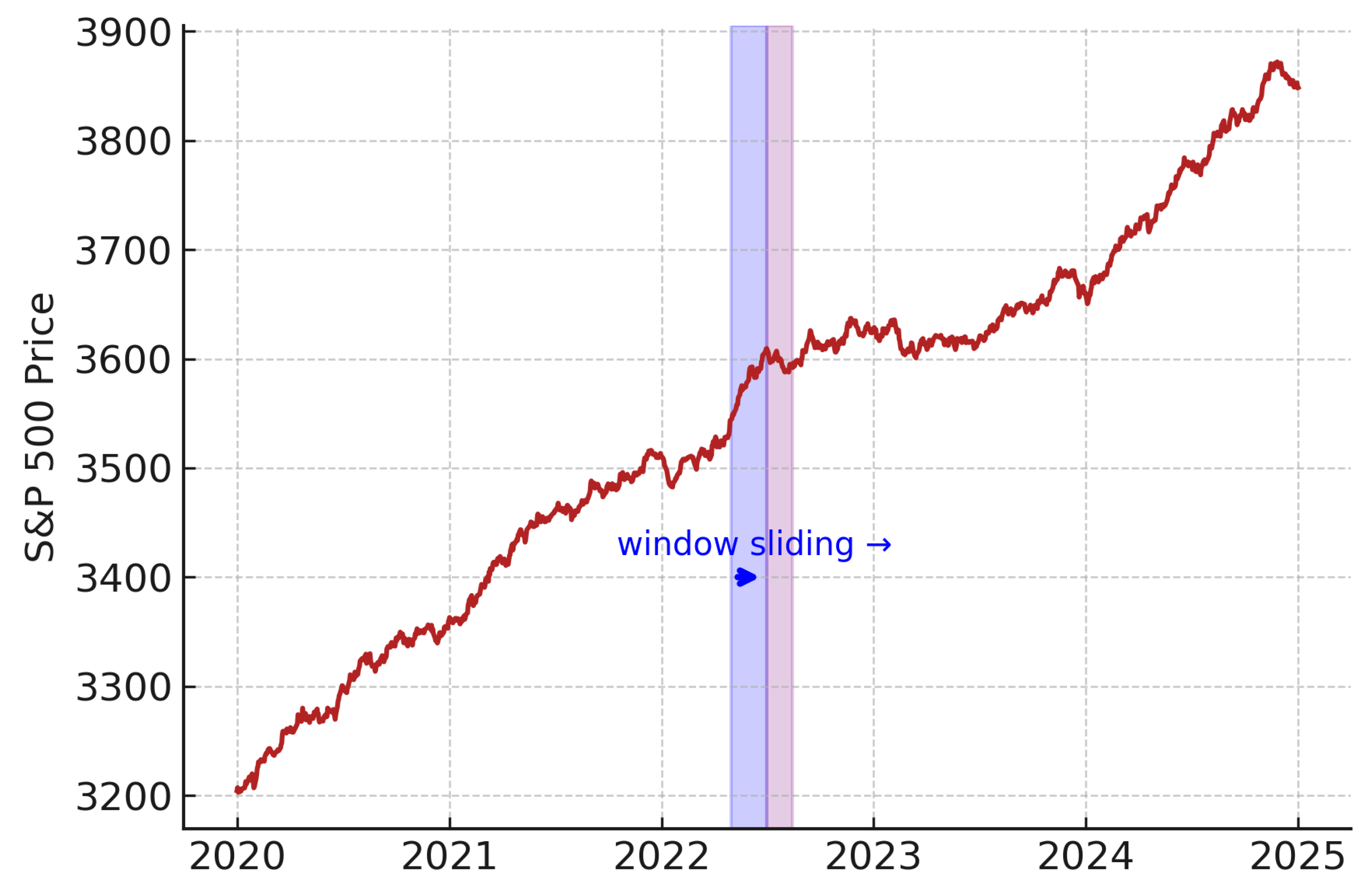
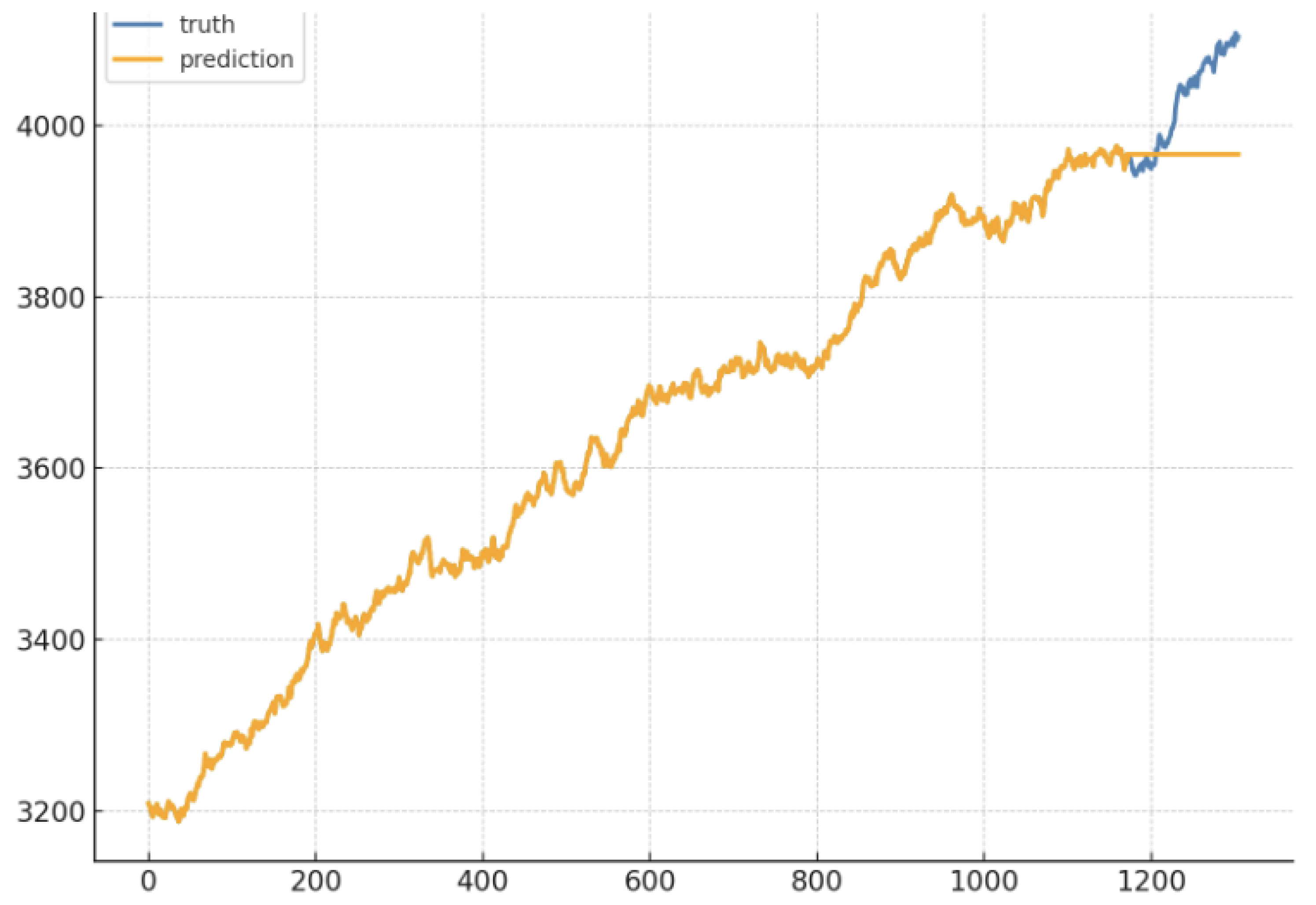
For the LSTM model, we implemented a sliding window approach to preserve temporal structure. Each window spans several consecutive trading days, forming a sequence used for training. As shown in Figure 5, we reserved the most recent 10% of the data for testing, using S&P 500 data for illustration.

To address distribution drift and price-level variance across windows, we applied window-specific normalization. Each price window $W_t$ was normalized by dividing all values by the last price of the preceding window $P(t-1)$:

$$W_t^{\prime }=W_t/P(t-1)$$

(2)

This converts absolute price prediction into modelling relative change, enhancing generalization across stocks with different price scales. Figure 6 shows the model’s poor performance on non-normalized inputs, where unseen price levels impair accuracy. This transformation also implicitly reshapes the local distribution of input sequences, aligning with principles in nonparametric density estimation such as k-nearest neighbor smoothing [35].

This combined use of sliding segmentation and relative normalization forms a key methodological innovation in our pipeline, supporting model-agnostic adaptation across volatility regimes.

3.3. Quality Control and Validation

High-quality input data is critical for effective forecasting. We implemented a data validation pipeline to handle missing values, outliers, and inconsistent timestamps. Trading calendars were synchronized across all stocks to account for market holidays and ensure temporal alignment. We also verified trading volume ranges and cross-checked price integrity across multiple sources. These efforts minimized noise and ensured that performance comparisons reflected model differences rather than data artifacts.

To further ensure the validity of model performance comparisons, we adopted a temporally consistent data splitting strategy. Each stock’s historical time series was aligned to a total of 1,250 trading days, covering a five-year period, after synchronizing trading calendars to ensure temporal consistency across all assets. The data was chronologically partitioned into three segments: approximately 80% of the earliest data points (∼1,000 trading days) were used for model training, the following 10% (∼125 trading days) served as a validation set for hyperparameter tuning and early stopping, and the most recent 10% (∼125 trading days) were held out as an independent test set for final evaluation. This approach preserves the temporal ordering of the data and prevents information leakage from future observations into the training or validation phases. While this study focuses on a fixed temporal holdout split, extended validation results using rolling-window cross-validation are reported in Section V.D.

This rigorous data preparation stage established a reliable foundation for downstream modelling, allowing us to isolate the effects of model architecture and preprocessing decisions in the subsequent evaluation.

4. Methodology

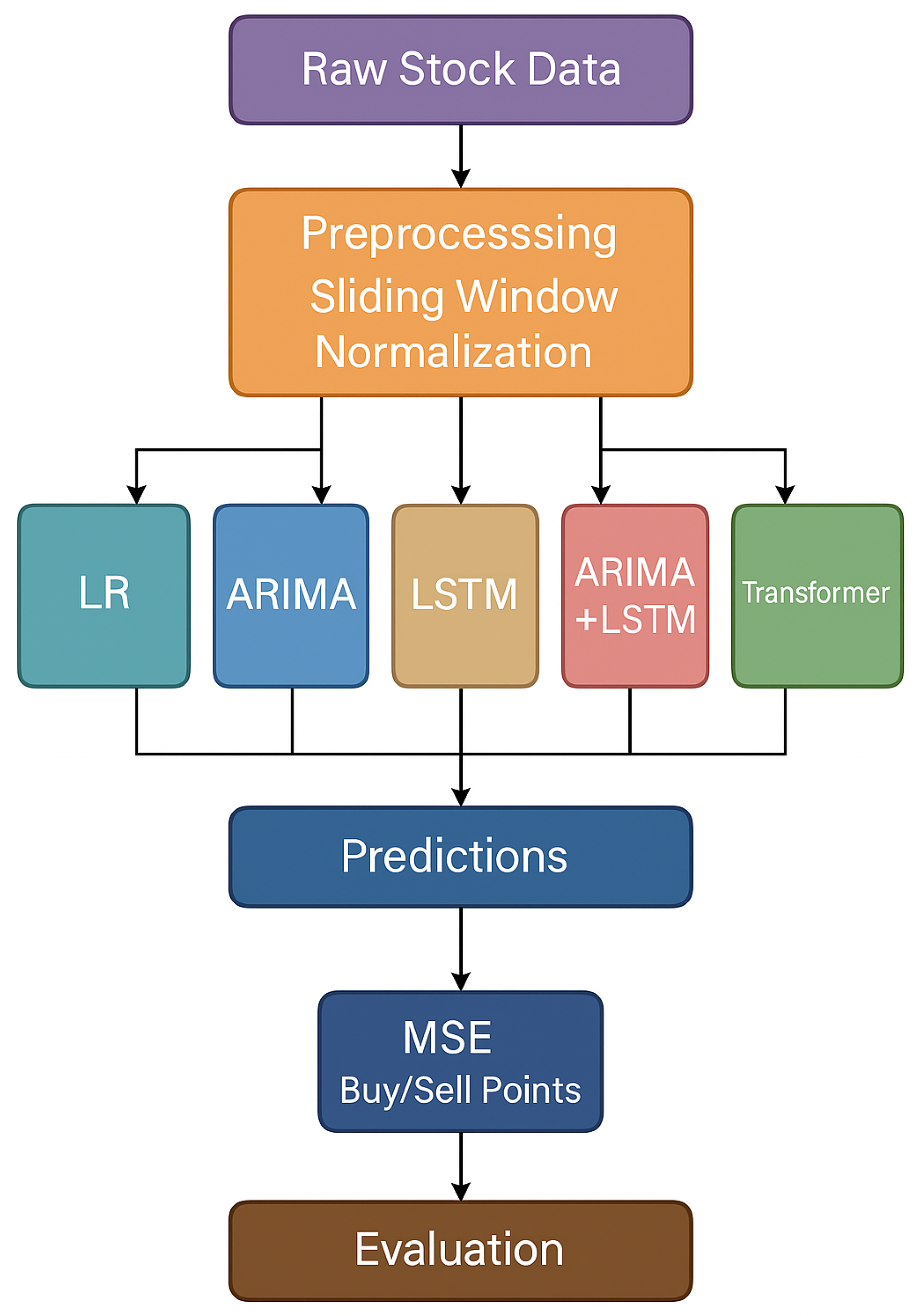
In this section, we describe five forecasting models employed in our study: Linear Regression, ARIMA, Long Short-Term Memory (LSTM), an ARIMA-LSTM ensemble, and a Transformer-based model. Each contributes a different modeling perspective—from linear interpretability to sequential memory and attention-based reasoning—enabling a comprehensive analysis across diverse market behaviors. The pipeline is shown in Figure 7.

The primary prediction task in this study is defined as next-day closing price forecasting at a daily time granularity. All models are trained to predict the closing price of the next trading day based on historical sequences of daily stock data. In addition, for the Linear Regression model, we also explored a five-day ahead forecasting variant to assess the model’s ability to capture short-term trends. Unless otherwise specified, all reported results correspond to the next-day prediction task.

4.1. Baseline Models

For LSTM, the input to the model is structured using a sliding window over normalized stock prices. Each window contains a fixed-length sequence of prior trading days, and the model is trained to predict the price on the day immediately following the window. Normalization is applied per window to stabilize the training process and enhance generalization across varying price ranges. The architecture consists of one or two LSTM layers followed by a fully connected output layer. This configuration enables the model to learn complex temporal dependencies while mitigating the risk of overfitting. We selected LSTM for its ability to capture nonlinear patterns and memory dynamics in volatile stock series, especially when preprocessing steps such as window normalization are incorporated.

For ARIMA time series modeling, we applied first-order differencing to each stock’s closing price to ensure stationarity, as verified through unit root tests. Model parameters (p, d, q) were selected based on inspection of the autocorrelation function (ACF) and partial autocorrelation function (PACF), and performance was validated through cross-validation. ARIMA’s structure makes it particularly effective on stable or autoregressive stock series, and its transparent parameterization offers interpretability for short-term trend modeling.

Meanwhile, Linear Regression serves as a benchmark model due to its low complexity and interpretability. We constructed fixed-length input vectors by concatenating multiple days of raw price features, forming a tabular input structure. The target label is the future closing price at a defined prediction horizon (e.g., five days ahead). While LR does not model temporal dynamics explicitly, it provides a baseline for assessing the added value of more complex sequence-based models. It is particularly relevant for stable stocks where linear assumptions are not severely violated.

These three baseline models provide complementary perspectives on stock price prediction, with varying capabilities in handling temporal dependencies and nonlinear relationships. Their comparative performance across different stock types establishes the foundation for evaluating our advanced model architectures described in the following section.

4.2. Extended Architectures

Building upon our baseline models, we incorporated several supplementary modeling strategies that go beyond the core models described. These extensions serve both as validation tools and as forward-looking modules aligned with modern trends in financial time series forecasting.

First, we assess the impact of input normalization in LSTM performance by conducting a controlled comparison between normalized and unnormalized inputs. The results, discussed in Section V-F, reveal that normalization substantially improves prediction stability, particularly for high-volatility stocks such as TSLA.

Second, we implement an ensemble model that linearly combines the outputs of ARIMA and LSTM. This strategy is designed to exploit the complementary strengths of statistical structure modeling and deep sequence learning. As evidenced in our experiments, the ensemble yields more stable and accurate forecasts on volatile assets than either model alone. The ARIMA-LSTM ensemble combines the individual model predictions through a simple linear weighted average:

$$\begin{array}{cc}\hfill {\widehat{y}}_{ensemble}\left(t\right)& =w·{\widehat{y}}_{ARIMA}\left(t\right)+(1-w)·{\widehat{y}}_{LSTM}\left(t\right)\hfill \end{array}$$

(3)

where $w\in [0,1]$ denotes the fusion weight assigned to the ARIMA model, with $(1-w)$ assigned to LSTM. To identify an effective fusion configuration, we performed a simple grid search over the range $w\in \{0.0,0.25,0.5,0.75,1.0\}$, and evaluated the ensemble performance across multiple stocks. This allowed us to examine the contribution of each model and assess the robustness of different fusion strategies.

Third, we integrate a lightweight Transformer model as a contemporary deep learning baseline. The Transformer employs positional encoding and multi-head attention mechanisms [36], aligning with recent instruction-tuned models designed for robust domain adaptation [37]. Although not outperforming ARIMA in most cases, the Transformer shows competitive results for stable stocks like KO, offering promise for future integration into hybrid forecasting systems.

Collectively, these extensions enhance the practical relevance of our approach. They demonstrate that our framework is modular and adaptable to a range of modeling paradigms, which is critical for applications in dynamic financial environments.

To ensure fairness in evaluation, all models were trained and tested on the same data splits and were evaluated using the Mean Squared Error (MSE) metric. Preprocessing steps were aligned with each model’s structural needs but kept consistent in scope. This unified setup allows us to isolate model-specific behaviors and assess comparative strengths across different market conditions.

5. Experiments

Our experimental study presents a systematic evaluation of five predictive models across diverse market conditions and stock characteristics. We focused on comparing the performance across five representative stocks: Apple (AAPL), Coca-Cola (KO), NVIDIA (NVDA), Pfizer (PFE), and Tesla (TSLA). All models are evaluated using historical daily closing prices and each time series is segmented via a sliding window mechanism with a fixed look-back period to forecast the next day’s price. For ARIMA and LR, model parameters are determined via AIC-guided grid search and cross-validation. For LSTM and Transformer models, early stopping is applied based on validation loss. The following analysis encompasses multiple dimensions of model performance, from feature engineering effectiveness to architectural optimization, revealing significant insights into the relative strengths and limitations of each method.

5.1. Individual Model Results and Comparative Analysis

Linear Regression served as a baseline benchmark due to its simplicity and computational efficiency. Each input consisted of a 25-dimensional feature vector formed by concatenating five consecutive days of six daily stock metrics. The model predicted the closing price five days ahead.

Table 1 shows the MSE results under different feature configurations. Results indicate that using a broader feature set (OHLCV) yields slightly lower MSE than relying solely on closing prices. Linear Regression performs competitively on low-volatility stocks like KO and PFE but degrades significantly on high-volatility assets like NVDA and TSLA, where nonlinear dynamics dominate. This observation underscores the model’s limitation in complex temporal pattern learning.

The LSTM model received sequential windowed input normalized relative to the final price in each window. Architecture variations were explored, with one or two stacked LSTM layers and dropout regularization. For this comparison, we specifically selected NVDA and TSLA due to their high volatility, where the impact of input normalization on LSTM generalization becomes particularly pronounced.

Table 2 reports the performance under different configurations. Experimental results reveal that LSTM benefits substantially from input normalization, particularly in stabilizing predictions for volatile stocks such as NVDA and TSLA. Without normalization, the model tended to plateau or diverge outside the training data distribution. Despite its flexibility, LSTM showed sensitivity to hyperparameters like sequence length and layer width, requiring careful tuning to achieve optimal performance.

For ARIMA models, first-order differencing was applied to enforce stationarity, and (p,d,q) parameters were selected based on PACF and ACF plots. ARIMA models were retrained separately for each stock to accommodate different underlying autocorrelation structures.

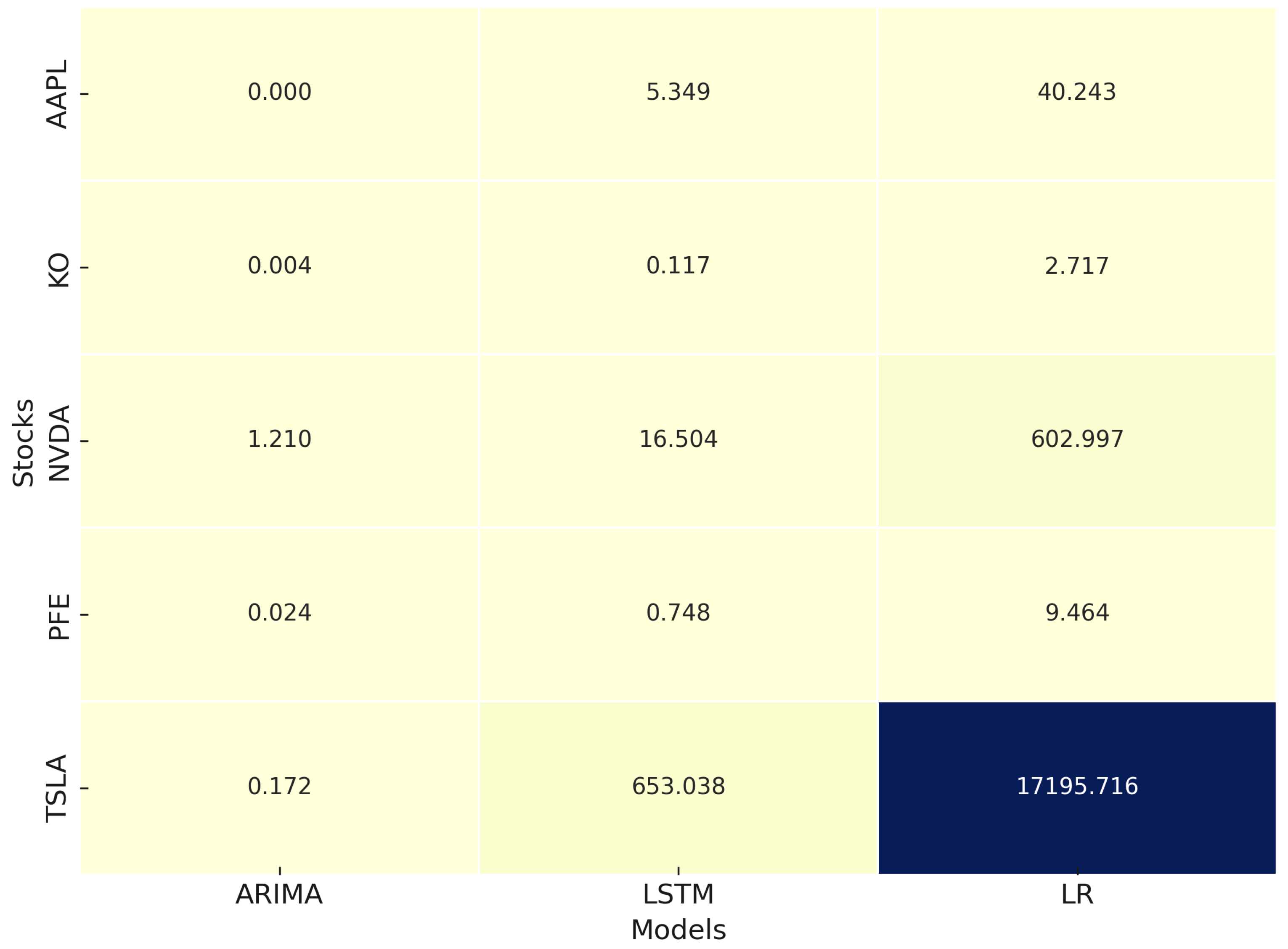
Table 3 lists the best-selected parameters and corresponding MSE for each stock. Across most stocks, ARIMA achieved the best or near-best MSE scores, particularly excelling on highly volatile assets like TSLA and NVDA. The model’s ability to directly model temporal dependencies without overfitting to noise proved advantageous compared to more flexible but data-hungry architectures like LSTM.

To further probe the model behaviors and expand the analysis, we visualize the MSE performance in Figure 8. The stock selection reflects diverse volatility profiles: TSLA and NVDA are highly volatile, KO and PFE are more stable, while AAPL represents a mid-range asset. As shown in Fig. 13, ARIMA consistently achieves the lowest MSE for high-volatility stocks, showcasing its strength in modeling short-term dynamics. Linear Regression performs adequately on KO and PFE, confirming that simple models suffice for stable assets. LSTM shows competitive performance but varies across assets, indicating sensitivity to data characteristics.

5.2. Extended Models

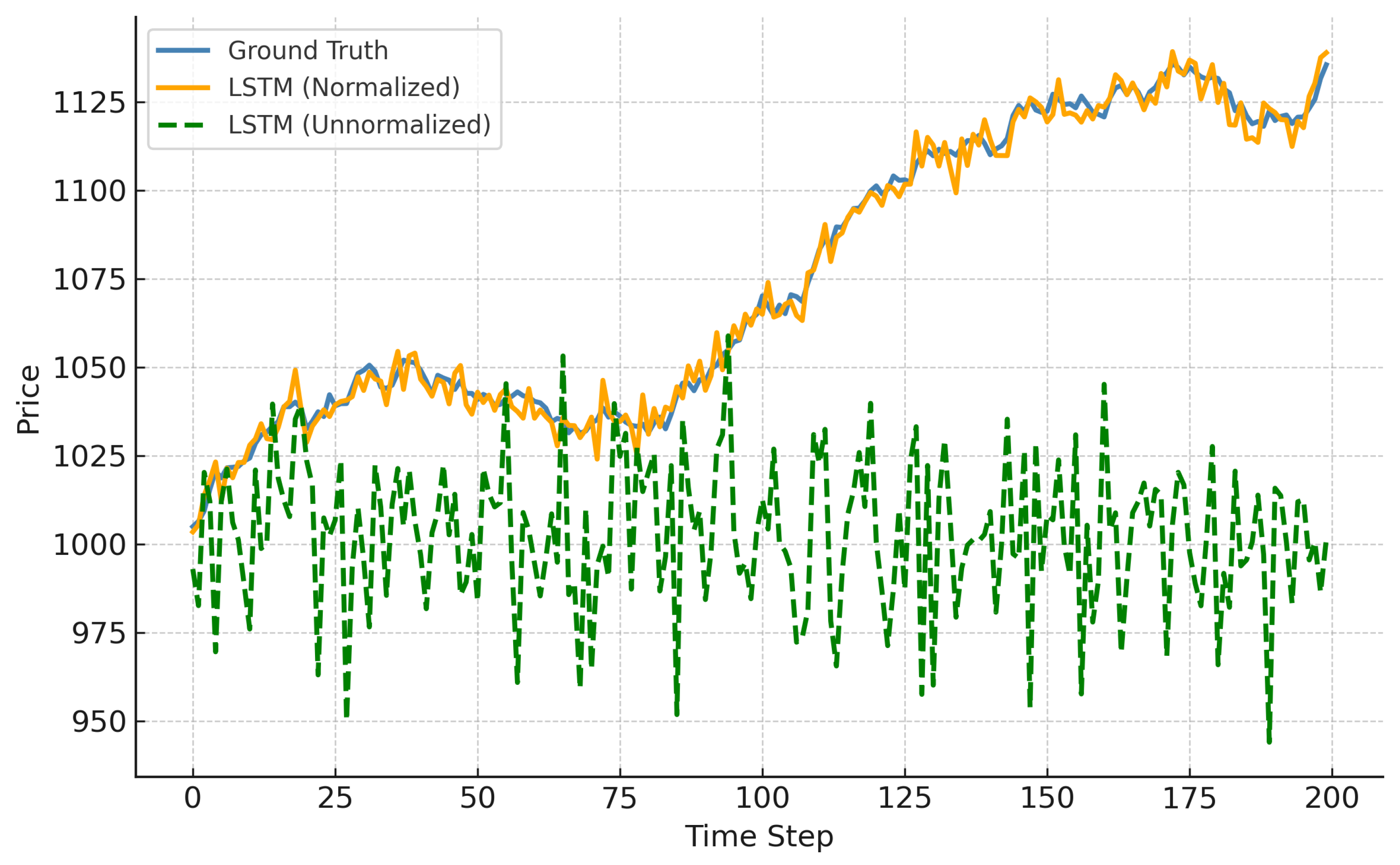
Normalization significantly impacts LSTM’s performance, particularly for volatile stocks. In Figure 9, we contrast LSTM predictions on TSLA with and without normalization. TSLA, characterized by large price swings and rapid trend changes, presents a challenge for sequence models. Without normalization, the LSTM’s predictions drift and exhibit poor generalization. Normalized input windows stabilize learning by reducing variance in price scales, allowing the model to focus on relative temporal patterns rather than absolute magnitude, thereby improving forecast accuracy.

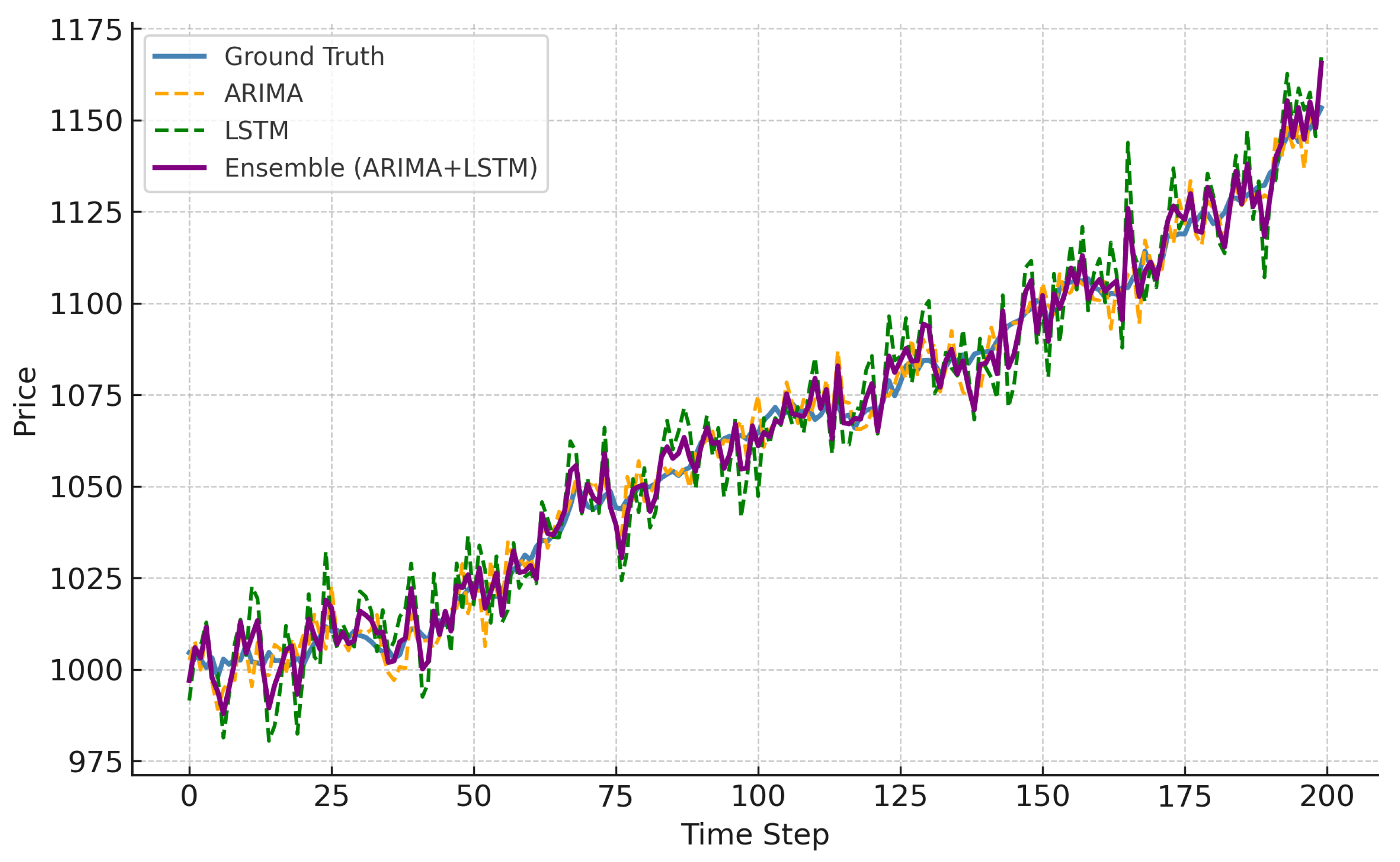
To explore hybrid model advantages, we created an ensemble averaging the outputs of ARIMA and LSTM. We targeted TSLA and NVDA, as these stocks exhibit substantial volatility where pure models show performance limitations. Figure 10 shows that the ensemble yields smoother and more accurate predictions than either individual model. The improvement stems from ARIMA capturing short-term autocorrelations while LSTM models longer nonlinear dependencies. This complementary dynamic helps reduce prediction error resulting in smoother and more accurate predictions under challenging market conditions, which reflects findings in multimodal ensemble learning systems [38].

To further examine the effectiveness of the ensemble fusion strategy, we performed a grid search over five different fusion weights for each target stock. Specifically, we tested weight settings of $w\in \{0.0,0.25,0.5,0.75,1.0\}$, corresponding respectively to using LSTM only, LSTM-dominant fusion, equal fusion, ARIMA-dominant fusion, and ARIMA only. Table 4 summarizes the Mean Squared Error (MSE) results across different configurations for representative stocks.

As shown in Table 4, the results indicate that ARIMA-dominant configurations (e.g., $w=0.75$ or $w=1.0$) generally outperform pure LSTM or equal-weighted ensembles in this daily forecasting context. This is consistent with the characteristics of financial time series at daily resolution, where linear autoregressive patterns dominate and short-term memory effects are prevalent. Nonetheless, in more volatile or nonlinear settings—such as NVDA and PFE—fusing in a portion of LSTM predictions improved performance relative to pure ARIMA. This suggests that LSTM contributes complementary learning capacity under certain market dynamics..

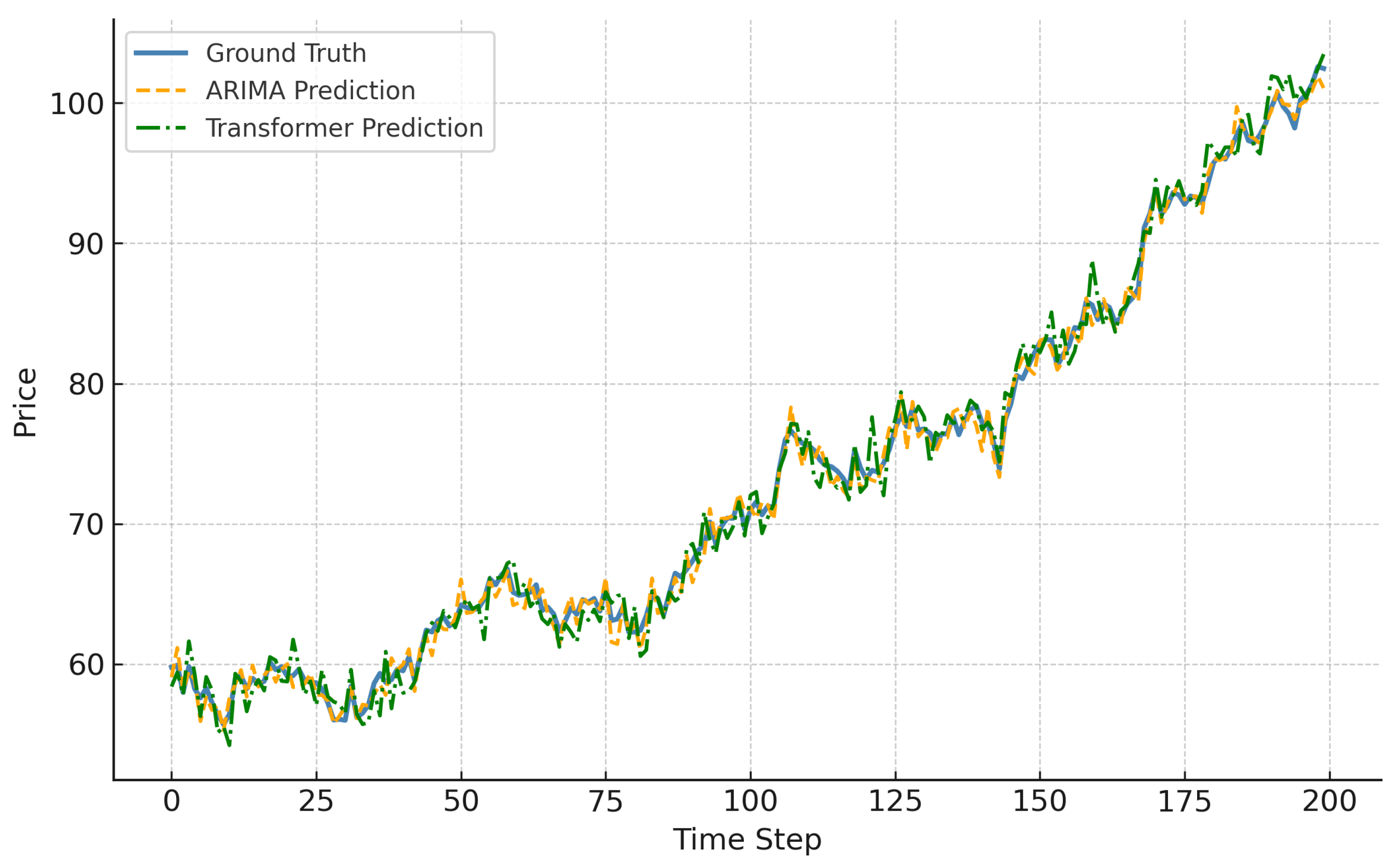
Based on the ensemble strategy, we introduce a Transformer-based model to assess the adaptability of modern architectures to financial time series. The Transformer was tested primarily on KO, a stock with low volatility and stable trends, because Transformer models benefit from long-range dependency capture but are sensitive to noise. Figure 11 shows that Transformer predictions on KO align closely with ARIMA, albeit with slightly higher variance. This result suggests that attention-based models are promising for stable financial assets but may require further regularization or hybridization for volatile environments.

Table 5 summarizes the MSE scores across the extended experiments, reaffirming the nuanced relationship between model architecture, preprocessing strategies, and asset characteristics.

5.3. Validation with Rolling Window Cross-Validation

To further evaluate the generalization capability of the proposed models across different market periods and to mitigate potential biases introduced by a single train-test split, we performed an extended validation using rolling-window cross-validation. This approach provides a more robust assessment of model stability under varying temporal dynamics, which is particularly critical for financial time series exhibiting non-stationarity and regime shifts.

In this experiment, each stock’s time series was segmented into five overlapping folds, using a rolling window configuration with a window size of 250 trading days (∼1 year) and a step size of 50 trading days (∼2 months). For each fold, models were trained on the historical data within the window and evaluated on the subsequent segment. The mean squared error (MSE) and standard deviation across the five folds are reported in Table 6.

5.4. Key Insights

Our comprehensive experimental evaluation demonstrates that no single model universally dominates across all stock types and volatility regimes. Instead, the results reveal a nuanced landscape of model suitability, emphasizing the need for context-specific forecasting strategies.

ARIMA models consistently achieve the best performance on highly volatile stocks such as TSLA and NVDA by effectively capturing short-term autocorrelations through differencing and autoregression. Their simplicity and low risk of overfitting make them particularly effective under rapid market fluctuations. In contrast, LSTM models exhibit strong adaptability when combined with appropriate input normalization strategies. On volatile assets, normalization substantially enhances LSTM’s ability to track price movements and prevent divergence, though without rigorous preprocessing and careful hyperparameter tuning, LSTM models can suffer from significant instability.

Linear Regression, despite its simplicity, serves as a surprisingly strong baseline for low-volatility, stable assets such as KO and PFE. Its robustness under simple linear assumptions provides reliable predictions without requiring complex architectures or extensive computational resources. Meanwhile, Transformer-based models show promising results for relatively stable assets, benefiting from their ability to capture long-range dependencies with minimal recurrence mechanisms. However, their sensitivity to noise limits their effectiveness in more volatile environments unless further regularization techniques are applied.

Moreover, ensemble strategies that combine ARIMA and LSTM outputs yield more robust forecasts on volatile assets. The ensemble approach leverages ARIMA’s strength in short-term structure learning and LSTM’s capacity for nonlinear sequence modeling, resulting in smoother and more accurate predictions under challenging market conditions.

Collectively, these findings advocate for a portfolio- and asset-specific model selection strategy in stock price forecasting, rather than reliance on a single modeling paradigm. They also underscore the critical role of data preprocessing, model hybridization, and architecture-market alignment in building resilient, adaptive financial forecasting systems capable of addressing diverse market challenges. This adaptability also extends to varying prediction horizons and data frequencies, providing a foundation for future exploration of both high-frequency and low-frequency forecasting tasks. Furthermore, the computational efficiency of different models aligns with their practical deployability: ARIMA and Linear Regression are well-suited for latency-sensitive applications, while LSTM and Transformer architectures, with appropriate optimization, can support real-time or near-real-time forecasting workflows in modern trading systems.

6. Conclusions

In this study, we developed and evaluated a multi-model framework for stock price prediction, integrating traditional statistical methods, deep learning architectures, and ensemble strategies. Our comparative experiments across five representative stocks reveal that no single model universally outperforms others; rather, model effectiveness varies based on market characteristics and volatility profiles [39].

Through rigorous experimentation, we demonstrate that ARIMA models excel at capturing short-term structures in highly volatile stocks, LSTM models provide adaptable learning capabilities when supported by careful preprocessing, and Linear Regression remains a strong and interpretable baseline for low-volatility assets. Furthermore, we highlight that Transformer-based architectures hold promise for stable financial environments, while hybrid approaches like ARIMA-LSTM ensembles offer enhanced robustness in unpredictable markets.

This work contributes a systematic and extensible methodology for stock forecasting model selection and performance benchmarking. By unifying input preprocessing pipelines, including feature selection to optimize model inputs [40], and exploring hybridization, we provide practical insights for both academic research and real-world financial forecasting applications.

From an application perspective, the proposed multi-model forecasting framework is designed with practical deployment considerations in mind. Classical models such as ARIMA and Linear Regression offer fast inference with sub-second latency on standard CPU infrastructure, making them suitable for integration into real-time trading systems. The LSTM and Transformer components, while more computationally intensive, can achieve acceptable inference times (typically under 100 ms per stock) when optimized with modern serving pipelines (e.g., ONNX, TensorRT) on GPU-accelerated platforms. The ensemble approach introduces moderate additional overhead but remains feasible for batch inference in intraday trading scenarios. The preprocessing pipeline, based on sliding window segmentation and normalization, is compatible with streaming data architectures and can be incorporated into low-latency data processing pipelines. Future work will further explore full integration of this framework within real-time trading environments, including latency benchmarking, adaptive retraining schedules, and risk-aware decision integration.

Looking ahead, future work may explore multi-horizon forecasting capabilities and evaluate model adaptability across different data frequencies, alongside deeper integration of multi-modal features, such as incorporating sentiment analysis [41], macroeconomic indicators, and graph-based representation learning frameworks [42,43]. Additionally, techniques from multi-label image classification [44] could inspire approaches for identifying overlapping patterns or co-occurring events in financial markets. Likewise, contrastive learning frameworks that combine traditional financial instruments like US Treasuries with cryptocurrencies [45] can help calibrate cross-market dynamics under macroeconomic uncertainty. Moreover, integrating visual representations such as candlestick charts or technical heatmaps may offer a complementary view of market dynamics. Recent segmentation networks like DDUNet [46], UCloudNet [47], and CP2M [48] provide efficient mechanisms for extracting spatial patterns and could inspire future multimodal financial models.

Complementing these perception-driven approaches, reinforcement learning-based methods represent a promising avenue for modelling sequential decision-making in dynamic trading environments. In particular, recent work on nearest-neighbor-based Q-learning demonstrates minimax optimality under infinite-horizon settings, offering theoretical support for sample-efficient, policy-driven strategy optimization in financial markets [49].

Taken together, these directions highlight the rich potential of combining diverse data modalities with principled learning algorithms. We hope that this line of research can inspire more holistic and adaptive solutions for next-generation financial decision-making systems.