Electromagnetic Nanocoils Based on InGaN Nanorings

1. Introduction

Low dimensional semiconductor structures such as quantum dots, nanorings and nanowires give rise to new physical phenomena that have been applied in optoelectronic and electronic devices with novel functionalities, such as quantum dot (QD) laser diodes (LDs) [1] and single-electron transistors [2]. In particular, semiconductor nanorings are more complex quantum systems. On the one hand, the inner hole in the semiconductor nanorings provides a capability of trapping a single magnetic flux and offers the exciting opportunity to observe electronic wave-function phases in magneto-optical experiments. Thus, this unique nanostructure has attracted intense interest on quantum interference phenomenon and excitonic Aharonov–Bohm (AB) effect [3,4] in transport and optical properties recently [5,6,7,8,9,10,11,12,13,14,15]. On the other hand, this structure also provides a current path in nanoscale systems, in which a current can be induced, and furthermore, a magnetic field can be generated only in the inner hole. This kind of semiconductor nanocoil is significant for electromagnetic signal generation, detection and energy conversion in integrated nanosystems for optoelectronic and biological applications.

To date, the formation of semiconductor nanorings is often through self-organized processes, mostly controlled by the Stranski-Krastanow (S-K) growth mode [16]. By this method, semiconductor nanorings were fabricated [5,17,18,19,20,21,22]. Some researchers control structure morphology to form nanorings by modulating adatom migration rate, controlling surface free energy balance [23] or using lithographic techniques [7]. However, the random distribution of the ring sizes and locations usually occurred. Besides the S-K mode, some researchers developed a few unique methods to create nanorings. By using polar surface–induced spontaneous self-coiling process, freestanding single-crystal complete nanorings of zinc oxide were formed [24]. Hollow nanocrystals can be synthesized through a mechanism analogous to the Kirkendall Effect, in which pores form because of the difference in diffusion rates between two components in a diffusion couple [25].

In order to achieve uniform and periodic structure arrays, many different surface processing methods were carried out to promote nucleation at expected sites, including surface states control [26,27,28], shallow modulated substrate surfaces [29,30] and nanoscale selective area epitaxy (NSAE) on patterned surfaces [31,32,33,34]. By using the NSAE, we have produced uniform and periodic nanodot/ nanoring/nanowire arrays, which have a mean lateral size less than 100 nm with a standard deviation of only 2.94% for the nanodots/nanorings [35].

Here, we present the work on electromagnetic induction from the long-range ordered InGaN nanoring arrays on the patterned GaN surface. The nanopatterns were defined by electron-beam lithography (EBL). The InGaN nanoring arrays were grown by the NSAE in metalorganic chemical vapour deposition (MOCVD). The electromagnetic induction from the nanorings was detected by the movement of refractive high-energy electron diffraction (RHEED) in a modulated external magnetic field.

2. Materials and Methods

To fabricate the nanostructures, first a semi-insulating GaN film was grown on a c-plane sapphire up to a thickness of 2 μm. Next 80 nm SiO₂ was deposited onto the GaN film, and then processed by EBL to create nanopatterns in the SiO₂. The fabrication details have been described elsewhere [34,35], Supporting Online Material: Figure S1. InGaN was then grown on the patterned SiO2/GaN in the MOCVD reactor at 750 ℃, resulting in the formation of nanodots or nanorings, depending on the pattern sizes and growth durations. The nominal thickness of the InGaN is about 10 nm. On top of the InGaN, another 10 nm GaN cap layer was grown. Finally, the samples were dipped in diluted hydrofluoric acid to remove all SiO2 to assess the sample morphology. The samples were investigated by means of scanning electron microscopy (SEM), continues wave (CW) photoluminescence (PL) at low temperature and RHEED at 200 ℃.

A typical SEM image of the InGaN nanoring arrays grown on the patterned GaN surface is shown (Figure 1). The nanorings are about 100 nm in diameter and spaced by 200 nm. The inset is a three-dimensional view of a few nanorings. In this sample, the InGaN nanorings are well developed. The InGaN nanorings have very uniform size and regular symmetry. The standard deviation of the nanorings in diameter is around 3%.

3. Results

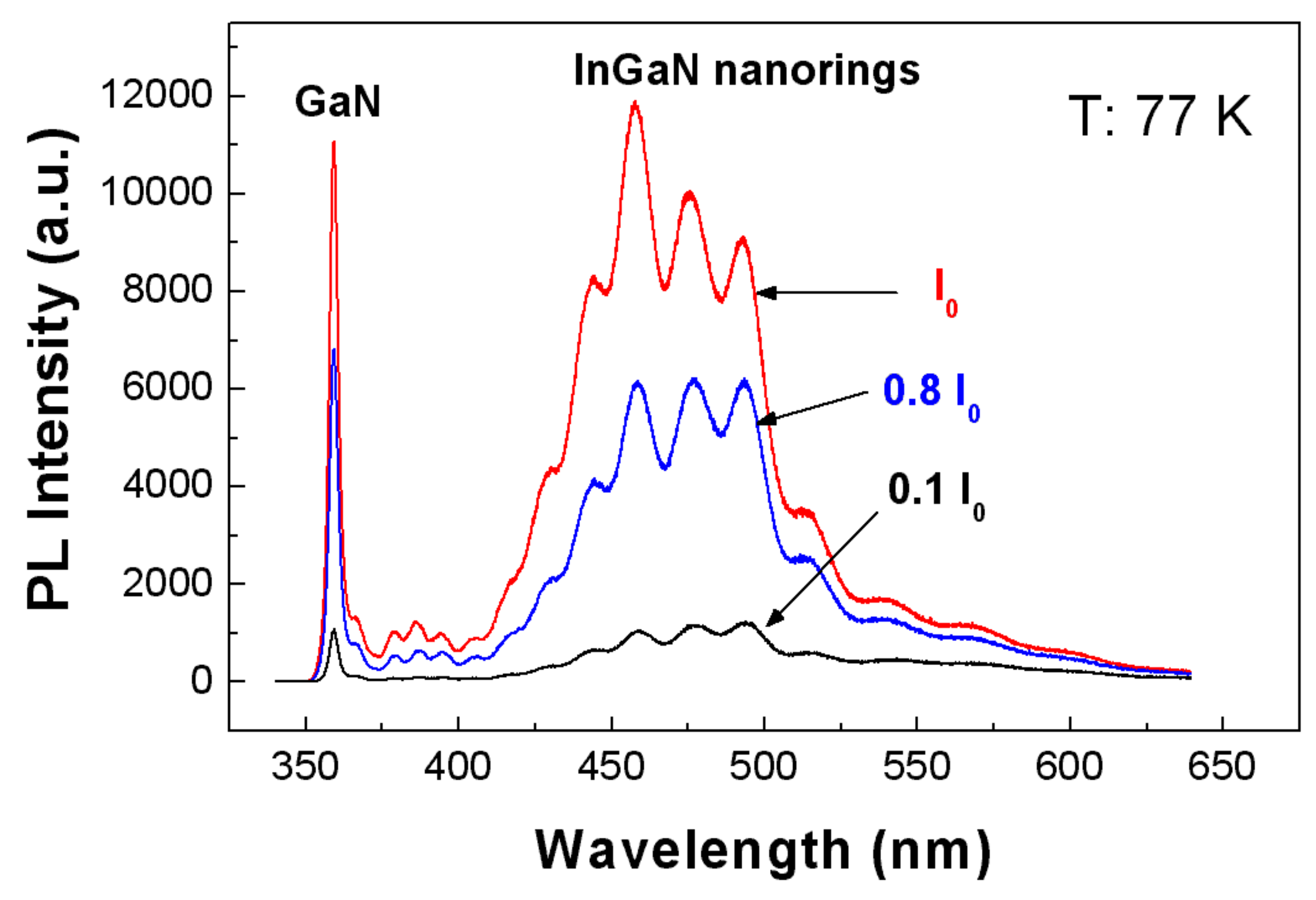
PL spectra from the 100 nm InGaN nanoring arrays were obtained (Figure 2) under different excitation levels of 0.1I₀, 0.8I₀ and I₀, where I₀ is the highest excitation power. The excitation source is a 325 nm He-Cd CW laser. It is seen that the emission from the nanorings is broad. The fringes in the spectra are caused by light interference in the epilayer. Clearly, the broadening is not due to the size non-uniformity, but due to the nonuniform indium composition across the ring. The ring-shape profile indicates the different growth rates between the edge area and centre area in those patterned holes. Furthermore, the indium composition is influenced by the growth rate. A higher growth rate induced higher indium incorporation efficiency in this experiment. As shown in Figure 2, by increasing the excitation power, the emission at the shorter wavelength part (around 460 nm) was enhanced more than the part in longer wavelength range (around 500 nm), which indicates more excitons recombining at higher energy levels under higher excitation power. Due to the large photo-energy difference between 460 nm (2.70 eV) and 500 nm (2.48 eV), this photo energy increment cannot be fully explained by band filling effect. So, it means that the indium composition is not uniform in a nanoring. According to the growth rate difference in a nanohole, it is deemed that a higher growth rate at the edge area results in a higher indium composition. The indium accumulation effect at the edge area can be directly observed in the growth with a larger selective area (Supporting Online Material: Figure S2). Thus, these InGaN structures not only have ring-shape profile in geometry image, but also a ring-shape potential in energy picture. From the PL results, the largest potential is about 820 meV deep with reference to the semi-insulating GaN layer.

It is well known that normal InGaN by epitaxy is unintentionally n-type semiconductor. The InGaN nanorings also are not exceptional and have free electrons with a concentration of 10¹⁸ ~ 10¹⁹/cm³ estimated from InGaN epilayers at room temperature. Namely, there should be a few hundred free electrons in a single InGaN nanoring. Once these electrons flow along the ring, there will be an additional magnetic field generated by the ring current. To observe electromagnetic induction from the nanorings, we plan to create the ring current by modulating the external magnetic field.

The electromagnetic induction from the InGaN nanorings is measured by RHEED in a high vacuum chamber (~ 10^-9 Torr). The movement of the RHEED patterns is recorded by RHEED monitoring software. The sample is mounted on a Molybdenum holder equipped with a heater at the backside. Because the heater is a wreathed filament, it can provide a modulated external magnetic field by flowing a DC current. To confirm the environment is clean for the RHEED measurement, i.e. without any other source to generate a magnetic field, a bare GaN/sapphire sample is used for reference.

After desorption of all impurities by keeping the sample in the high vacuum chamber for 24 hours, the samples were heated to 200 ℃ for RHEED. The RHEED patterns from the InGaN nanoring surface and the bare GaN surface were obtained respectively (Figure 3, a and b) without external magnetic field. As expected, spotty patterns were observed on the InGaN nanoring surface (Figure 3a), while streaky patterns were observed on the bare GaN surface (Figure 3b). When an external magnetic field is exerted, these patterns will shift in the direction as indicated by the white arrows in Figure 3. Obviously, the shifting of the patterns is decided by how the external magnetic field alters. In order to record how the patterns shift, we choose to record the time-dependent light intensity of a pattern in the selected area, as indicated by the white box in Figure 3. When the pattern moves away, the light intensity drops. However, if there is any undulation during the movement of the pattern, so is the intensity recorded. In this experiment, the external magnetic field is modulated by the heater current switched between 0 A and 17 A.

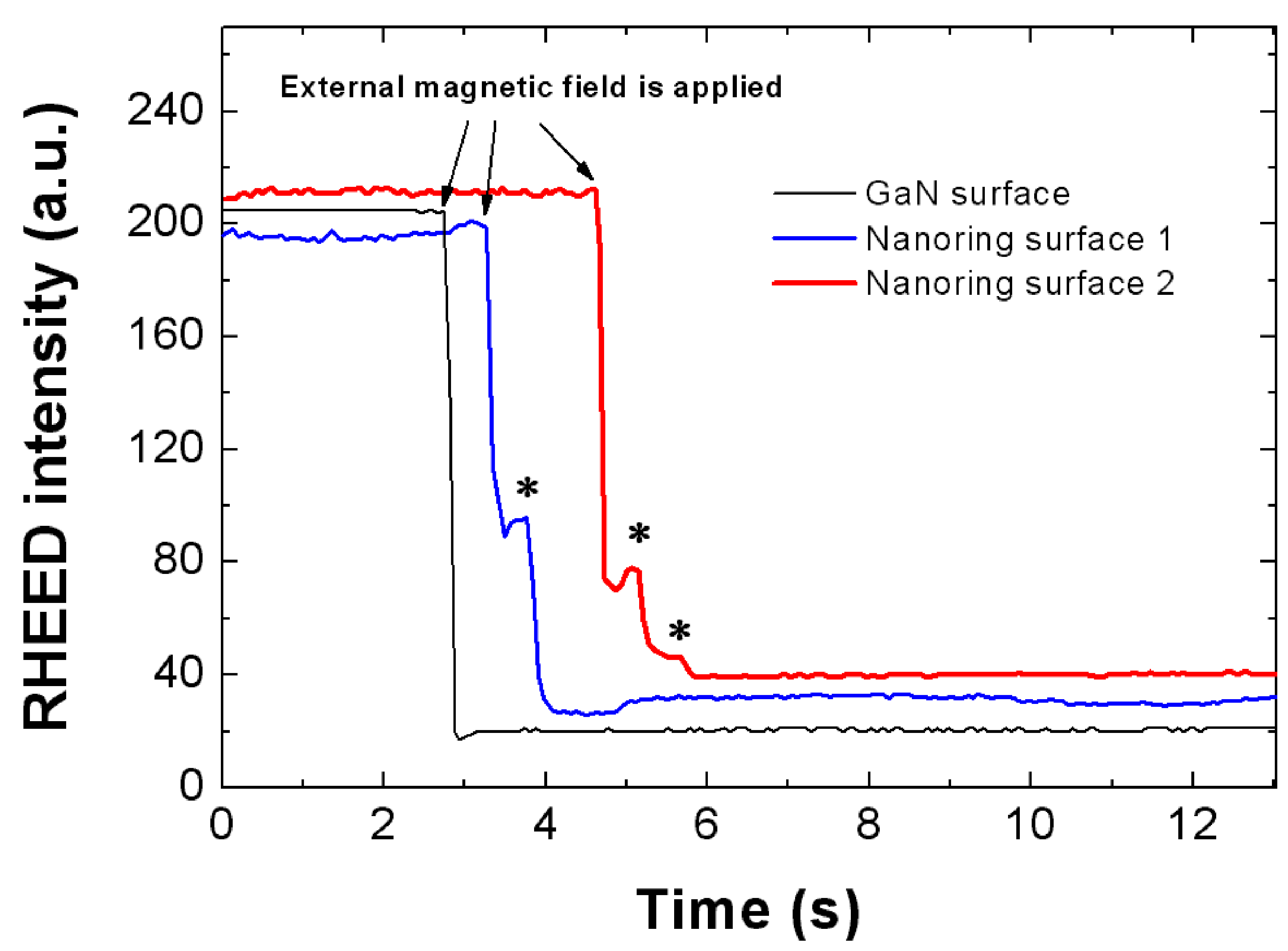
The intensity change in the presence of the external magnetic field has been recorded (Figure 4). For the bare GaN reference sample, the intensity dropped monotonously till to the background value, which indicates that the bare GaN does not generate any induced magnetic field. This can be easily understood, since the GaN is semi-insulating and does not have any ring-shape potential to confine the movement of electrons. However, the intensity evolvement is different for the InGaN nanoring surface - there are several rebounds during the intensity drop, as marked by the stars in Figure 4. These rebounds indicate that the patterns were not monotonously shifting in direction; instead, the patterns have been pulled back a little during the shift. This indicates the existence of an additional magnetic field generated during the process. The only source for the new magnetic field is the InGaN nanoring arrays. A ring current is first induced in the InGaN nanorings during the increase/decrease of the external magnetic field. In turn, the ring current produces the new magnetic field. Because the increase/decrease of the external magnetic field is not linear, the ring current density and the induced magnetic field intensity were varying during the process. The direction of the induced magnetic field can be the same or opposite to the external magnetic field. Indeed, we observed several rebounds during one shift, which indicates the variation of the induced magnetic field. For whole process of the shift, please refer to the video clips attached in the Supporting Online Material. This phenomenon proves the electromagnetic induction from the InGaN nanorings, acting as electromagnetic nanocoils.

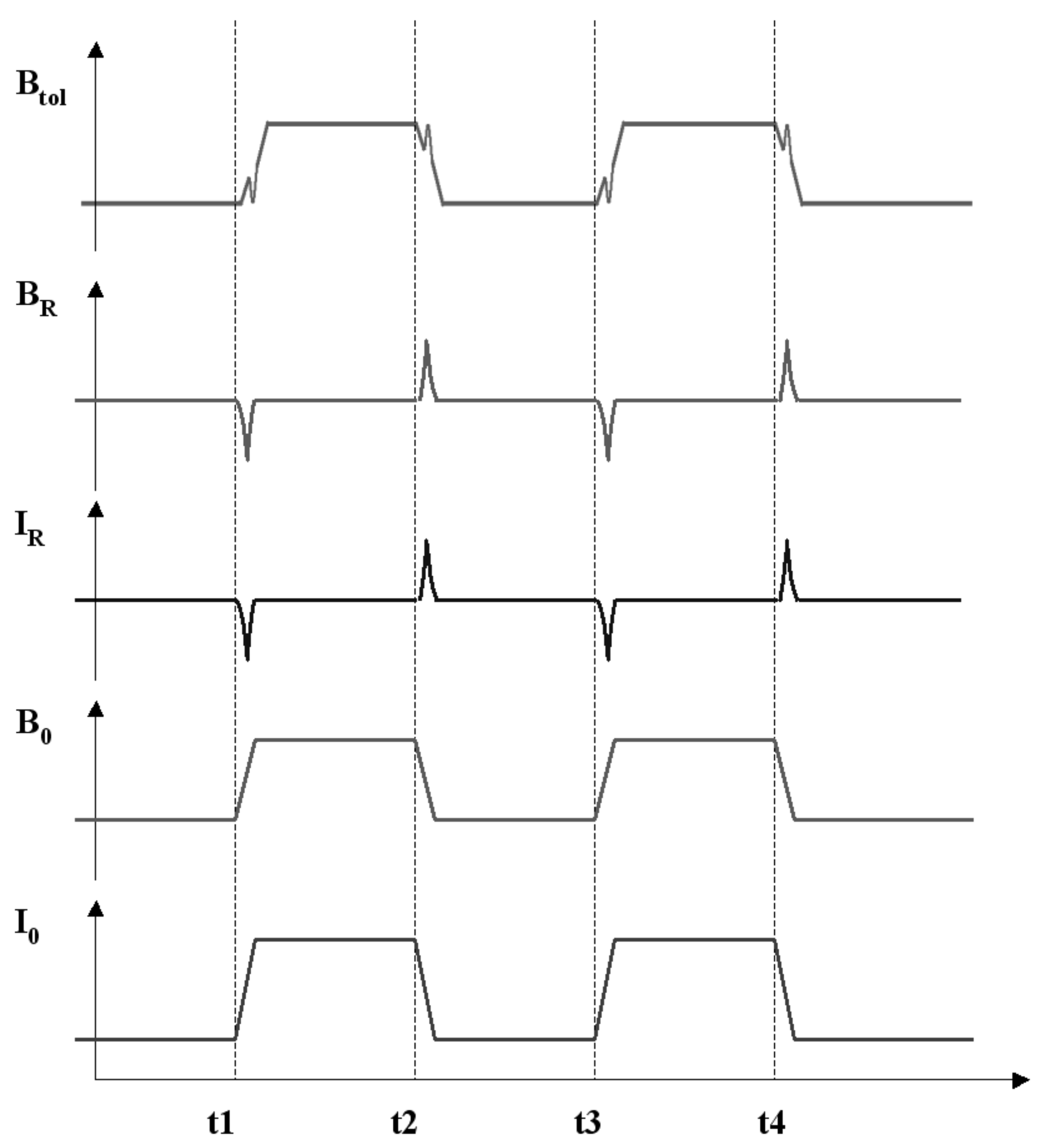
The detailed process is schematically described (Figure 5). The external magnetic field (B₀) is modulated by turning on and off the DC current (I₀) of 17 A through the heater. A linear variation of B₀ is assumed. Due to the ring-shape InGaN nanostructure existing in the magnetic field, an inductive ring current (I_R) will be induced in the nanorings during the appearance and disappearance of B₀. Furthermore, the inductive ring current, I_R, generates an additional magnetic field (B_R) that can be the same or opposite to B₀. Thus, in this system, the total magnetic field (B_tol) is the vector sum of B₀ and B_R (Figure 5). The movement of the RHEED patterns embodies the behaviour of the total magnetic field in this system. Appearing and disappearing of the B₀ cause the major shift of the RHEED patterns. When there is no other magnetic field source, B₀ is the only factor to cause the shift of RHEED patterns, as in the case of the bare GaN sample. However, I_R and B_R will be induced on the InGaN nanoring surface, and B_R will also contribute to B_tol. Thus, in this case, the movement of the RHEED patterns also presents the influence from B_R.

4. Conclusions

In this study, the InGaN nanorings show the capability of generating ring current and magnetic field in the nanoscale. Based on this nanostructure and phenomenon, a variety of nanodevices and nanosystems can be built, which can work under either active or passive mode serving various functionalities. In the active mode, i. e. when the ring current is artificially injected, the nanorings can produce magnetic field that is concentrated in the ring. In this case, the nanorings could work as a nanotransmitter, which can transfer energy over a space to a receiver through its magnetic field. If the receiver consists of multiple-ring structures, then the whole nanosystem can work as a nanotransformer. In the passive mode, i.e. when the ring current is induced by an external magnetic field, the nanoring arrays could be used as nanoscale sensors, transducers and resonators.6. Patents

The demonstration of uniform and periodic InGaN nanoring arrays by NSAE presented here should be universal and transferable to other materials and structures [35]. The successful demonstration of electromagnetic induction based on the nanorings may not only benefit fundamental study on quantum effects, but also open a way for energy conversion, transfer and detection in nanosystems.