Modeling the Knowledge Production Function Based on Bibliometric Information

1. Introduction

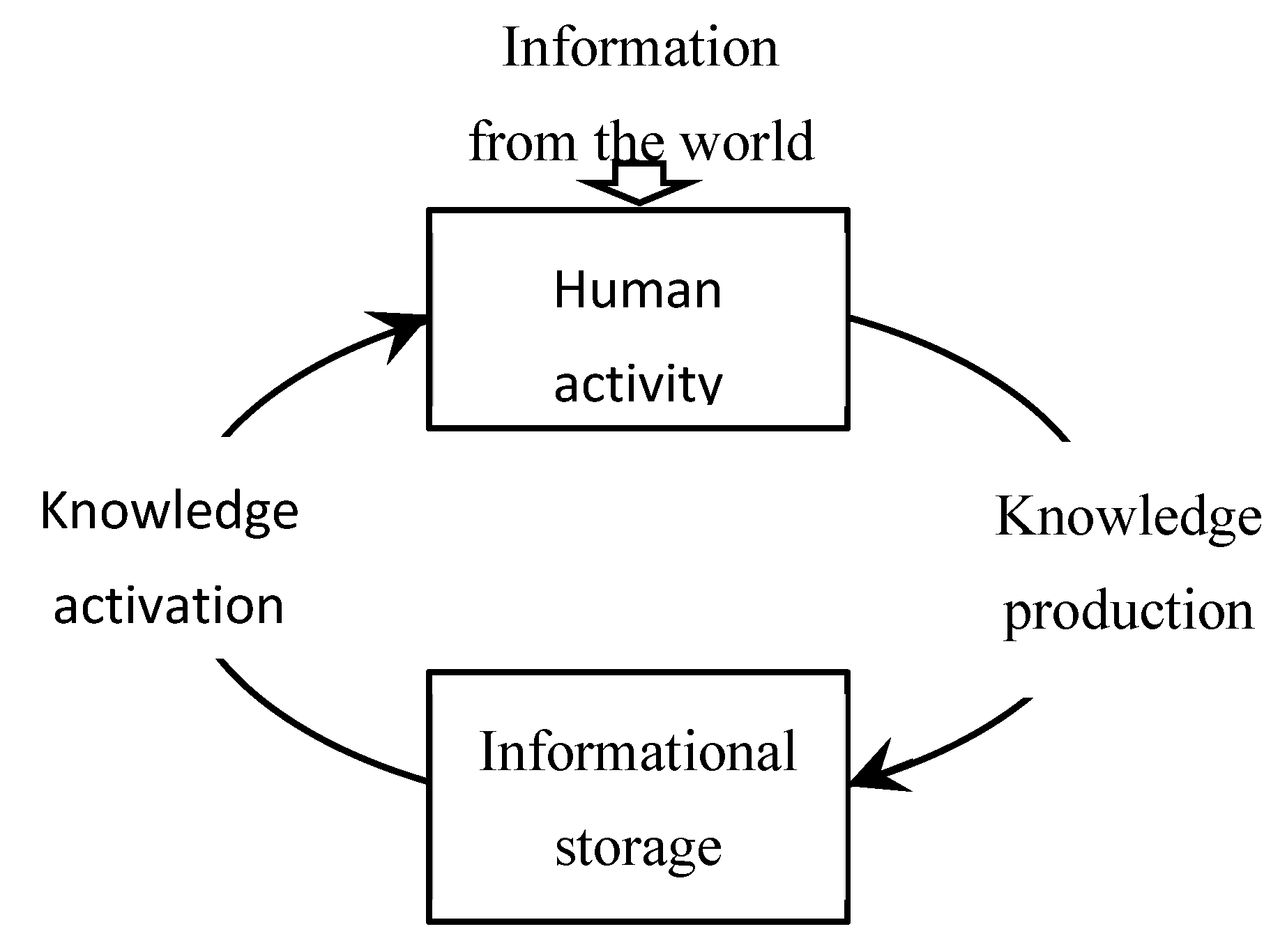
The development of society is directly related to the accumulation of knowledge both in the field of science and technology, and in the cultural and humanitarian sphere. Knowledge is produced at a rate that depends on its amount and population. In turn, knowledge production controls population growth. The corresponding dynamic equations were obtained by Dolgonosov and Naidenov (2006). In this approach, a crucial factor is per capita productivity of knowledge $w\left(q,t\right)$, which depends on knowledge amount $q$ and time $t$. Knowledge production $\dot{q}=dq/dt$ can be represented in general form as

$$\dot{q}=w\left(q,t\right)N+J\left(t\right)$$

(1)

where $N$ is the population size, $J\left(t\right)$ is an external source of knowledge. We assume in (1) that the number of knowledge producers is proportional to the total population, as is usually the case in econometric models (Romer, 1986, 1990; Kremer, 1993; Abdih and Joutz, 2006; Dong et al., 2016, Kato, 2016). In our previous studies (Dolgonosov, 2016, 2020) we looked at the problem of knowledge production by assuming that productivity is constant. This assumption has reasonable grounds for a pre-information society with its undeveloped computing capabilities. However, at present, when we have an information society, the rapid progress of computer technology and artificial intelligence leads to increased productivity, which should be reflected in the rate of knowledge accumulation and, as a consequence, in demographic dynamics. The problem is to figure out what the function $w\left(q,t\right)$ is, how justified the constant productivity approximation is, and under what conditions it can be applied. We consider the problem in this work.

Further development of the theory requires consideration of the general case where productivity depends on accumulated knowledge. This problem has also been addressed in econometric models describing the relationship between technological development and population growth. Unlike technologies, knowledge is understood somewhat more broadly: it includes all the components of human culture, which undoubtedly influence population growth to a certain extent. Nevertheless, econometric models capture the essential features of the phenomenon. First of all, it is worth mentioning Romer's (1986, 1990) model, which was written for technology, but we will extend it to knowledge in general. Romer's model can be presented as

$$\dot{q}=w\left(q\right)N_1^{\lambda }$$

(2)

with the only difference that Romer's variable $q$ is the sum of technologies (although this is not all knowledge), $N_1$ is the number of only those people who work in science and technology, and per capita productivity is expressed as

$$w\left(q\right)=w_0{q}^{\epsilon }$$

(3)

where $w_0$, $\lambda$ and $\epsilon$ are parameters (everything is in our notation). Ultimately, Romer accepts $\lambda$ and $\epsilon$ equal to 1.

Kato (2016) analyzes a model similar to (2)-(3), with the only difference that the total population $N$ is used instead of $N_1$. The author expresses the following thought about the exponent $\epsilon$ (in the original it is designated as $\phi$):

• “When $\phi >1$, then the growth rate of technological progress would rise rapidly with increasing level of technology. However, such situations have not been observed in developed nations through postwar periods, so Barro and Sala-i-Martin (1992) imposed the condition $\phi \le 1$.”

We use this remark when constructing the productivity function.

Kremer's (1993) model can also be represented as equation (1). Unlike Romer's model (2), Kremer uses the total population $N$ instead of the number of S&T personnel $N_1$, but the parameters $\lambda$ and $\epsilon$ are still equal to 1. So, instead of (3) we have

$$w\left(q\right)=w_{0}q$$

(4)

A similar model of technology development was used by Collins et al (2013) in their evolutionary theory of long-run economic growth.

Jones (1995, 1999) modified Romer's model by setting $\epsilon <1$ in (3), which after a series of transformations led him to the equation

$${\displaystyle \frac{\dot{q}}{q}}=\alpha {\displaystyle \frac{\dot{N_1}}{N_1}}$$

(5)

where $\alpha =\lambda /\left(1-\epsilon \right)$. The meaning of this equation can be clarified after integrating it, which yields

$$q=k{N}_1^{\alpha }$$

(6)

$k$ is a constant. From (6) it follows that the technologies accumulated to date are only the output of currently working technology producers. However, this approach does not reflect the influence of previous generations, whose work also contributed to the development of technology. Obviously, the equation for $q$ must contain an integral term summing up the contribution of past generations.

The same problem was noted by Dong et al. (2016), who, based on an analysis of well-known econometric models and extensive empirical material, showed that technological growth depends not only on the current generation of people, but also on the achievements of past generations. The authors found deviations from the proportionality law $N_1\propto N$ between the number of technology producers and the total population when dealing with the long-term evolution of society over millennia.

Okuducu and Aral (2017) suggested that productivity could be a constant, linear, quadratic, or exponential function of knowledge amount, and used these representations to compute various hypothetical scenarios of knowledge dynamics.

There is a difference between the knowledge approach (1) and the econometric one (2)-(4). Productivity $w\left(q\right)$ is the per capita knowledge product (different forms of publication, e.g. patents, articles, books; cf. Abramo et al., 2019) in the first case or the per capita gross product in the second one. Knowledge is measured in information units, while technology and gross product in monetary units.

The question arises (Court and McIsaac, 2020): is the information approach to demographic dynamics divorced from reality and is it possible to calibrate the corresponding model? The answer to this question is one of the objectives of this work. As for the reality and prospects of such an approach, we can refer to the work (Dolgonosov, 2020), in which a general global-scale model was proposed, including economic, environmental, demographic and information components, and which was successfully calibrated using extensive empirical data.

In connection with the development of artificial intelligence, a dilemma has arisen about how to describe the presence of intelligent machines, whether to include them among the producers of knowledge, thereby expanding the number $N$, or to continue to believe that knowledge is produced by people, and the machine is still only a tool that helps them in the production of knowledge. Sadovnichy, Akaev and Korotayev (2022) develop the former approach, believing that intelligent machines can now be considered producers of knowledge and hence included in the number $N$ along with humans. This is a promising direction of research, especially given the rapid development of AI. But for now, following the analysis of Akaev and Sadovnichii (2021), we will remain with the traditional approach, according to which it is people who produce knowledge, while intelligent machines only help them in this matter. Then the effect of AI manifests itself through an increase in the amount of knowledge and a corresponding increase in human productivity.

The above-mentioned productivity functions proposed by various authors require verification based on empirical material. To this end, we revisit the issue of productivity as a function of knowledge and verify the theoretical results using literature data.

Another nontrivial problem is how to determine the amount of knowledge. The most consistent approach is to estimate memory capacity that knowledge takes up. However, at the moment such information is unlikely to exist. Meanwhile, there is evidence that digital memory is rapidly increasing over time, in what appears to be a global information explosion during the digitization period (1986-2007 onwards) (Hilbert, 2014).

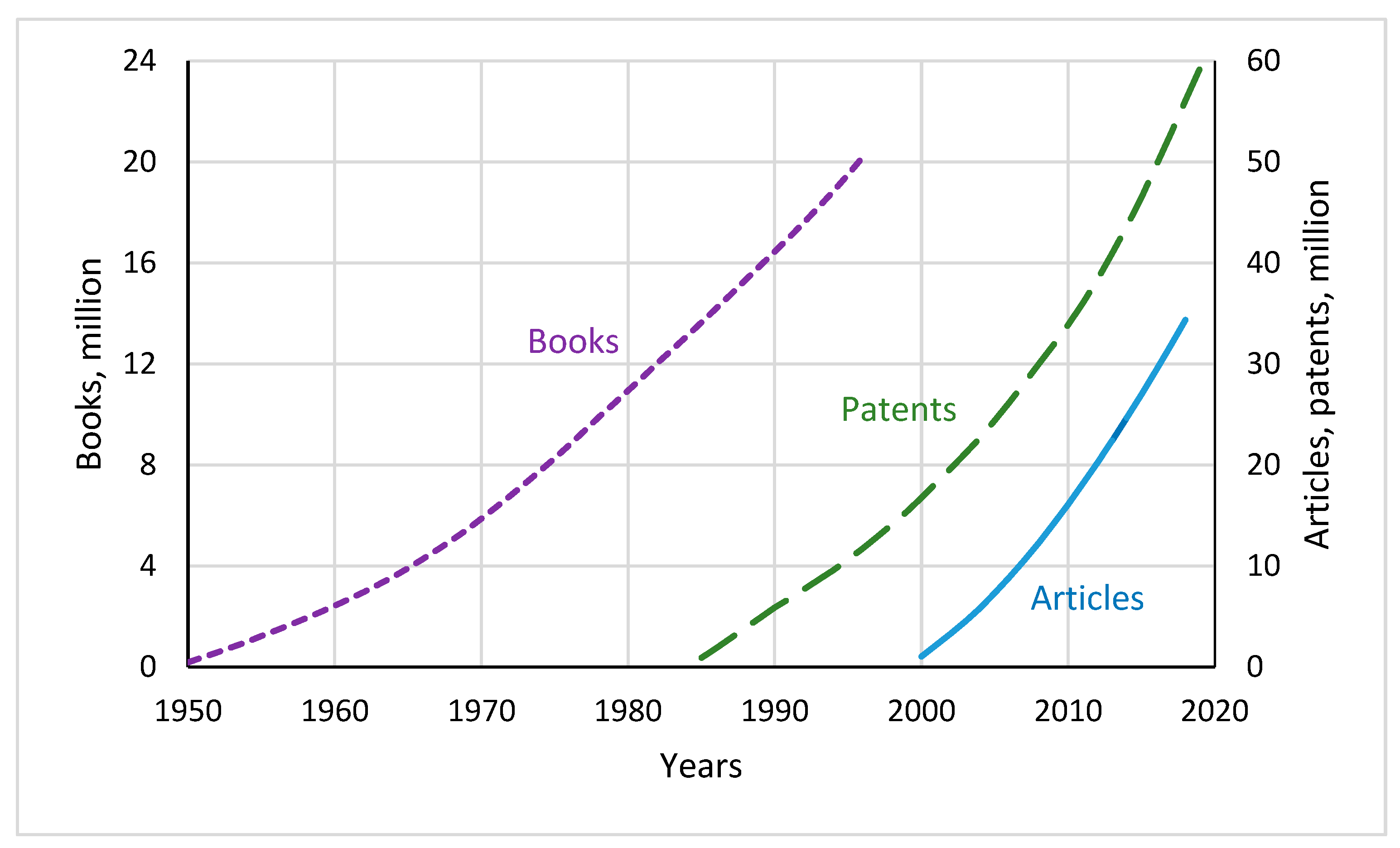
It should be expected that the total memory capacity far exceeds knowledge capacity due to repeated replication of useful information, especially in graphic and video formats. In this situation, it is necessary to use data on different types of knowledge representation, such as patent applications, original articles and books. These data have been largely cleared of duplication. Knowledge production should be assessed separately for each type. Below we use this approach.

2. Model

2.1. Knowledge Production and Accumulation

The need to solve non-standard problems that life poses to people encourages knowledge production (Figure 1). Knowledge is professionally produced only by a part of the population. As in many econometric models, we assume that this part is proportional to population size. Dong et al. (2016) found deviations from this law for individual countries, but there is reason to believe that the deviations are likely to be smoothed out when moving to a global scale, as usually happens when a statistical system is enlarged. Then the overall rate of knowledge production will be equal to average productivity multiplied by population size, as expressed by equation (1). However, for humanity as a global system, this equation can be simplified by keeping in mind the following fact. Human civilization does not have extraterrestrial contacts, hence there are no external sources of knowledge, so in (1) we must put $J=0$. Due to this isolation, the system is autonomous, which means that productivity does not depend on time explicitly, but only through $q\left(t\right)$, so that equation (1) reduces to the form

$$\dot{q}=w\left(q\right)N$$

(7)

Equation (7) can be written as

$${\displaystyle \frac{dq}{w\left(q\right)}}=N\left(t\right)dt$$

(8)

Integrating (8) with the initial condition

$$t=t_0, q=q_0$$

(9)

and introducing functions

$$F\left(q\right)={\int }_{q_0}^q{\displaystyle \frac{d{q}^{\mathrm{\text{'}}}}{w\left(q^{\mathrm{\text{'}}}\right)}}$$

(10)

$$S\left(t\right)={\int }_{t_0}^{t}N\left(t^{\mathrm{\text{'}}}\right)d{t}^{\mathrm{\text{'}}}$$

(11)

we come to the equation

$$F\left(q\right)=S\left(t\right)$$

(12)

which implicitly specifies $q$ as a function of the cumulative population number $S\left(t\right)$, thereby formalizing the accumulation of knowledge over time.

2.2. Productivity Function

To reveal the dependence of productivity on knowledge amount, we will consider two opposite cases: an extremely undeveloped society and a highly developed information society. The productivity function should have the following properties:

• in an extremely undeveloped society, knowledge has not yet been accumulated ($q=0$), but knowledge is produced with a non-zero initial productivity $w\left(0\right)=w_0$;
• in a highly developed information society, productivity increases slowly according to the power law $w\left(q\right)\propto q^{\epsilon }$ with an exponent ε not exceeding 1 (since an average knowledge producer uses a very limited amount of knowledge in his creative process — this is close to the opinion of Barro and Sala-i-Martin (1992), mentioned in the Introduction).

The simplest interpolation formula with these properties is

$$w\left(q\right)=w_0{\left(1+hq\right)}^{\epsilon }$$

(13)

$$w_0>0, h\ge 0, 0\le \epsilon \le 1$$

(14)

where $w_0,h,\epsilon$ are parameters. If $hq\ll 1$, we can use the constant productivity approximation as in our previous works. Substitution of (13) into (10) yields

$$F\left(q\right)={\displaystyle \frac{1}{h{w}_0}}\left({\ln }_{\epsilon }\left(1+hq\right)-{\ln }_{\epsilon }\left(1+h{q}_0\right)\right)$$

(15)

and according to (12) we find

$$1+hq=\left(1+h{q}_0\right) {\exp }_{\epsilon }\left({\displaystyle \frac{h{w}_{0}S}{{\left(1+h{q}_0\right)}^{1-\epsilon }}}\right)$$

(16)

where we use the deformed logarithm and deformed exponential, which are defined as (Umarov et al., 2008)

$${\ln }_{\epsilon }\left(x\right)={\displaystyle \frac{x^{1-\epsilon }-1}{1-\epsilon }}$$

(17)

$${\exp }_{\epsilon }\left(x\right)={\left(1+\left(1-\epsilon \right)x\right)}^{1/\left(1-\epsilon \right)}$$

(18)

In the limit $\epsilon \to 1$, we get the natural logarithm and natural exponential:

$${\ln }_1\left(x\right)=\ln \left(x\right), {\exp }_1\left(x\right)=\exp \left(x\right)$$

(19)

At the ends of the $\epsilon$ range, we have:

• a constant productivity

$$\epsilon =0, w=w_0, q=q_0+w_{0}S$$

(20)

• productivity as a linear function of knowledge

$$\epsilon =1, w=w_0\left(1+hq\right), 1+hq=\left(1+h{q}_0\right)\exp \left(h{w}_{0}S\right)$$

(21)

In (20) and (21), accumulated knowledge is, respectively, a linear and exponential function of the total number of people $S$ over the period under study $\left(t_0,t\right)$. All people are taken into account here, not just the direct producers of knowledge, since the number of producers is assumed to be proportional to the population.

The presence of the integral quantity $S$ in (16) describes the contribution of past generations to the accumulation of knowledge, as discussed by Dong et al. (2016), in contrast to formula (6), which refers only to the current population.

2.3. Asymptotics

Let us consider a situation where the most probable values of the parameters in equation (16) correspond to the limit $h\to \infty$. Minimizing the standard deviation of the model from data by varying $h$ causes $w_0$ to depend on $h$. The asymptotic form of equation (16) is

$$q\approx {\left({q_0}^{1-\epsilon }+\left(1-\epsilon \right)h^{\epsilon }{w}_{0}S\right)}^{1/\left(1-\epsilon \right)}$$

(22)

In the limit $h\to \infty$, expression (22) must be independent of $h$, which implies

$$w_0\approx c{h}^{-\epsilon }$$

(23)

and

$$q\approx q_0{\left(1+{\displaystyle \frac{\left(1-\epsilon \right)cS}{{q_0}^{1-\epsilon }}}\right)}^{1/\left(1-\epsilon \right)}$$

(24)

where $c$ is a positive constant. Productivity (13) asymptotically obeys the power law

$$w\left(q\right)\approx c{q}^{\epsilon }$$

(25)

Thus, the general productivity function (13) includes three special cases: a constant (20), linear (21) and power (25) function. There is another special case, which we consider in the next item.

2.4. Exponential Productivity

Kato (2016) expressed the opinion that the option $\epsilon >1$ in (3) and, accordingly, in (13) gives an unrealistically rapid increase in human productivity (see the quote in the Introduction). This option can even lead to a singularity, nevertheless, for the sake of completeness, we will consider it. In particular, let us look at the case where productivity is converted from (13) to an exponential function of knowledge. Previously, Okuducu and Aral (2017) considered productivity as an exponential function of $q$ as an option.

Let us adopt that in (13) there is no upper limit for $\epsilon$ and the coefficient $h$ decreases with increasing $\epsilon$ according to the law $h=a/\epsilon , a>0$. Then $w\left(q\right)=w_0{\left(1+aq/\epsilon \right)}^{\epsilon }$, and in the limit $\epsilon \to \mathrm{\infty }$ we get

$$w\left(q\right)=w_0{e}^{aq}$$

(26)

From (10)-(12) it is easy to find

$$q=q_0+{\displaystyle \frac{1}{a}}\ln {\displaystyle \frac{1}{1-bS}}$$

(27)

where $b=a{w}_0{e}^{a{q}_0}$. The cumulative population number $S\left(t\right)$ increases with time, hence at some point in time it reaches the value $S=1/b$, at which a singularity occurs. Thus, in a finite time the accumulated knowledge $q$ becomes infinite, which now seems weird, but if we bear in mind the rapid development of artificial intelligence, the singularity in (27) may be associated with the use of AI as an incredibly powerful tool for knowledge production, resulting in exponential growth in productivity (26) as knowledge accumulates.

3. Model Calibration

3.1. From Continuous to Discrete

The productivity function (13) is calibrated by varying its parameters in order to minimize the standard deviation from data. Due to the annual discreteness of demographic data, integral (11) should be replaced by the sum of the population over the years $t_0$ to $t$:

$$S=\sum _{i=t_0}^t{N}_i$$

(28)

where $N_i$ is the $i$th year population, $i$ is a year number.

According to Abramo et al. (2019), knowledge can be measured through its publication. We will consider three forms of publication: patents, articles and books. Each form accumulated up to and including a certain year $t$ is the sum

$$q=q_0+\sum _{i=t_0}^t{X}_i$$

(29)

where $X$ is knowledge production measured on a case-by-case basis by the annual publication of patents, articles or books (what is denoted as $\dot{q}$ in the basic equation (7)), $X_i$ corresponds to the $i$th year, $q_0$ is knowledge (number of patents, articles or books) accumulated up to year $t_0$ (not including $t_0$ itself). This equality is also used to determine informational storage capacity.

3.2. Bibliometric Data

To calibrate model equations (16) and (24), we used the bibliometric data presented in Figure 2. Articles in scientific and technical journals (for 2000-2018) and patent applications (for 1985-2020) are represented by global data (WB, 2022; OECD, 2022). Data on new book titles (for 1950-1996) are selected for a group of 30 countries based on information provided by Fink-Jensen (2015). The group composition is indicated in the note to Table 1. The criterion for including a country in the group is the availability of data on books published for 1950-1996. For other countries, the data range is less than specified. There are gaps in the data for individual years that are filled by linear interpolation. When calibrating the model, we used group population for books and world population for articles and patents (Figure 3).

3.3. Initial Amount of Knowledge

The informational storage capacity at the beginning of the digitization period is known from the literature (Hilbert, 2014). However, this cannot be said about the initial amount of knowledge $q_0$, represented in the form of patents, articles and books. To find $q_0$, we use an indirect estimate based on the relationships between annual knowledge production $X\left(t\right)$ (as denoted in (29)), gross domestic product $G\left(t\right)$, and population $N\left(t\right)$. All these quantities are provided with literature data (for links, see captions to Figure 2 and Figure 3). The problem is that the time series $X\left(t\right)$ is usually very short, and in order to find $q_0$ it is necessary to sum $X\left(t\right)$ over a fairly long retrospective period. This can be done using the following algorithm:

1° generate a function $N\left(t\right)$ based on demographic data;

2° generate functions $X\left(G\right)$ and $G\left(N\right)$ on ranges provided with data;

3° approximate $X\left(G\right)$ and $G\left(N\right)$ with suitable functions and continue the functions to the origin (where $G$ and $N$ are zero);

4° make up a composition of functions $X\left(t\right)=X\left(G\left(N\left(t\right)\right)\right)$, continuing it into the distant past, where $X$ tends to zero;

5° take the sum of $X\left(t\right)$ for the entire previous period up to point $t_0$ (not including it), where the data for $X$ begins:

$$q_0=\sum _{i=-\infty }^{t_0-1}{X}_i$$

(30)

Formally, the summation starts from $-\infty$, but in fact it is permissible to take a fairly distant point in the past, where $X\left(t\right)$ is very small. We took 1900 as such a point, when the production of patents, articles and books was negligible compared to modern amounts;

6° calculate $q\left(t\right)$ using formula (29) in two ways: (i) using the available data for $X$, and (ii) using the results of model calculations according to item 4° (to compare the model with the data).

An example of applying this algorithm to finding the initial number of articles $q_0$ accumulated by the year $t_0=2000$ is shown in Figure 4. Data on articles are available in the range 2000-2018. Despite such a short data range, the use of this algorithm allows us to estimate the accumulation of articles in a much wider range: 1900-2020. The agreement between the model and the data is satisfactory. This algorithm was also applied to patents and books (Figure 5).

4. Results and Discussion

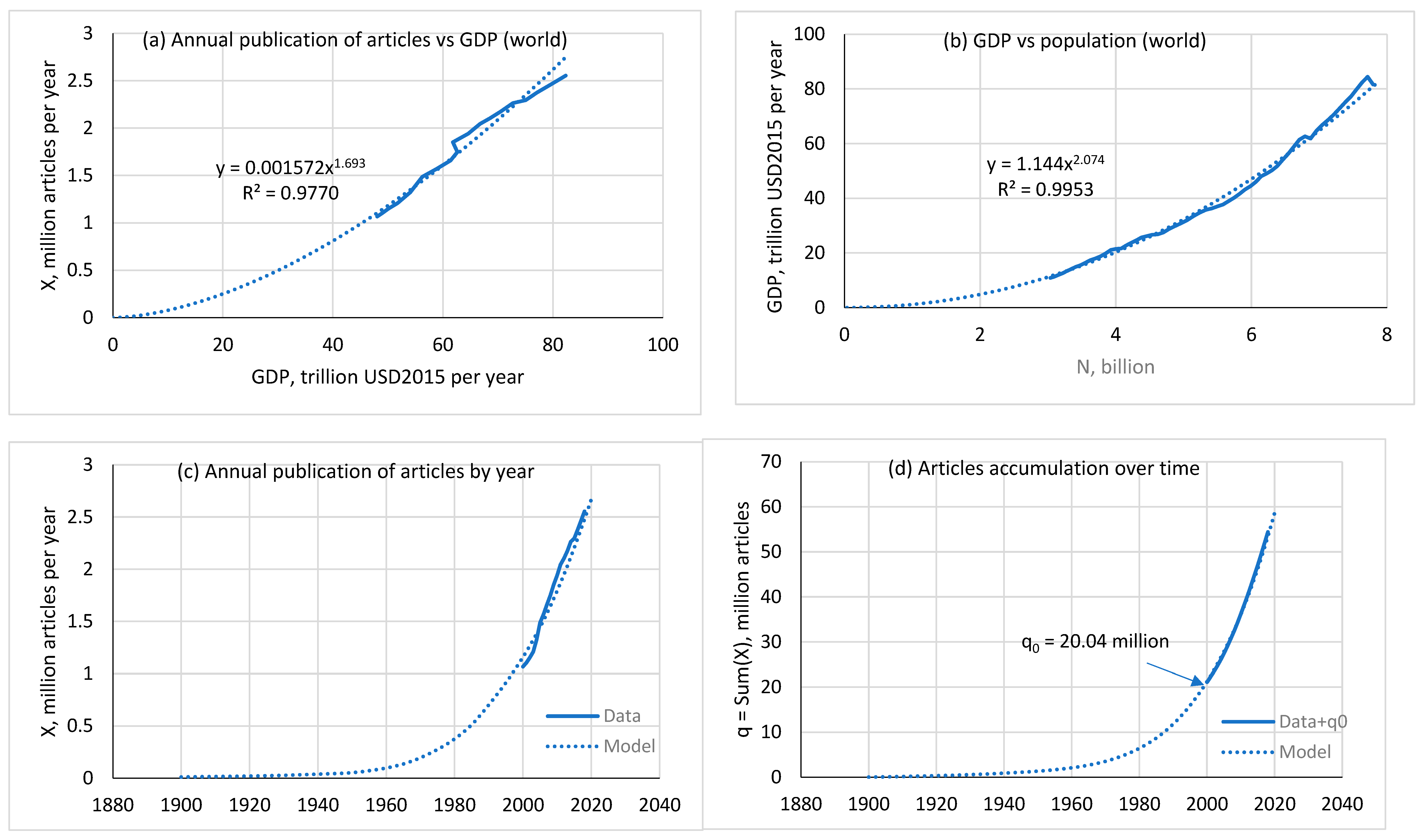
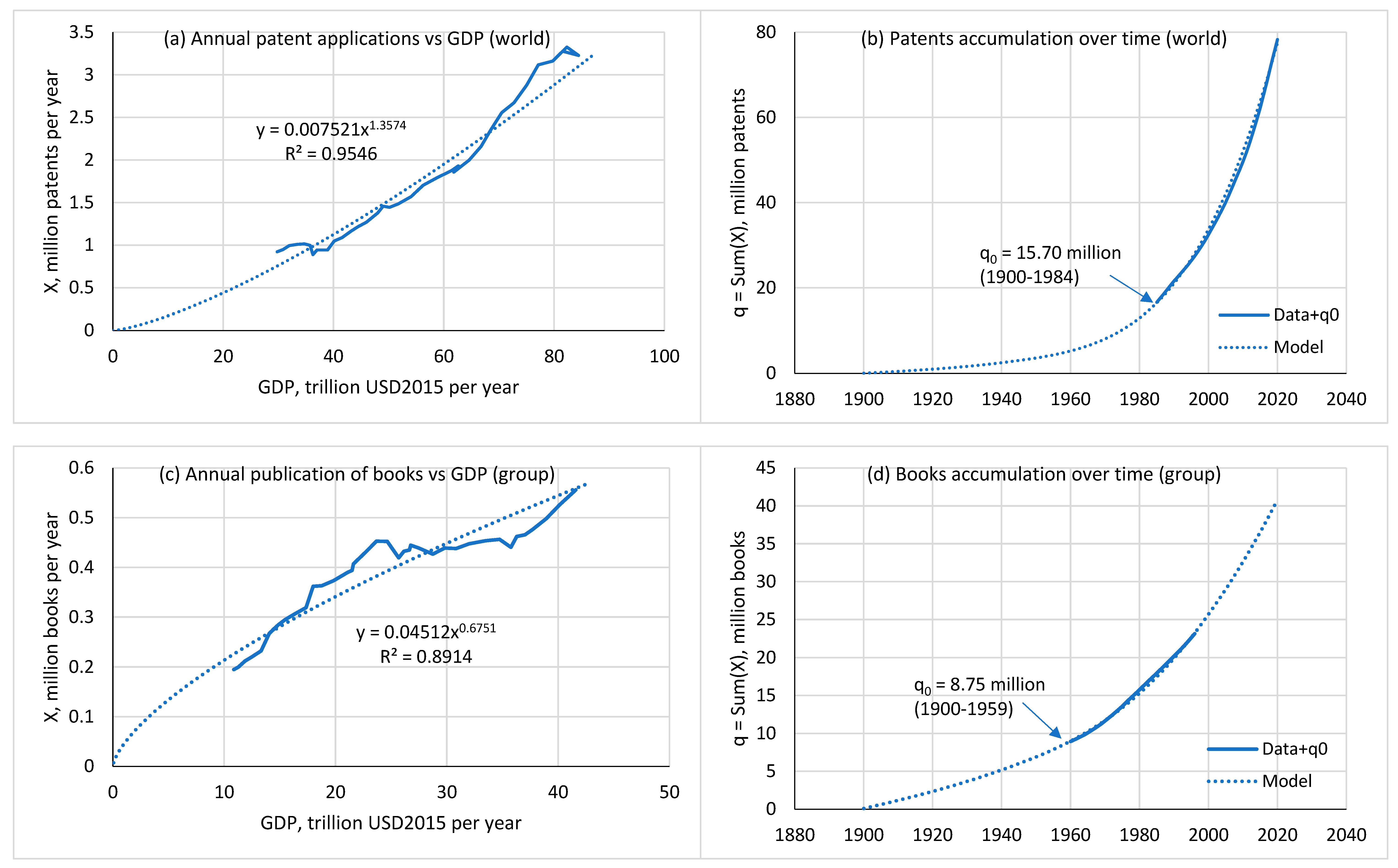
The parameter values found as a result of model calibration are presented in Table 1 and Figure 6. The accuracy of matching the model with the data is very high, as evidenced by the determination coefficient $R^2$, the values of which are close to 1.

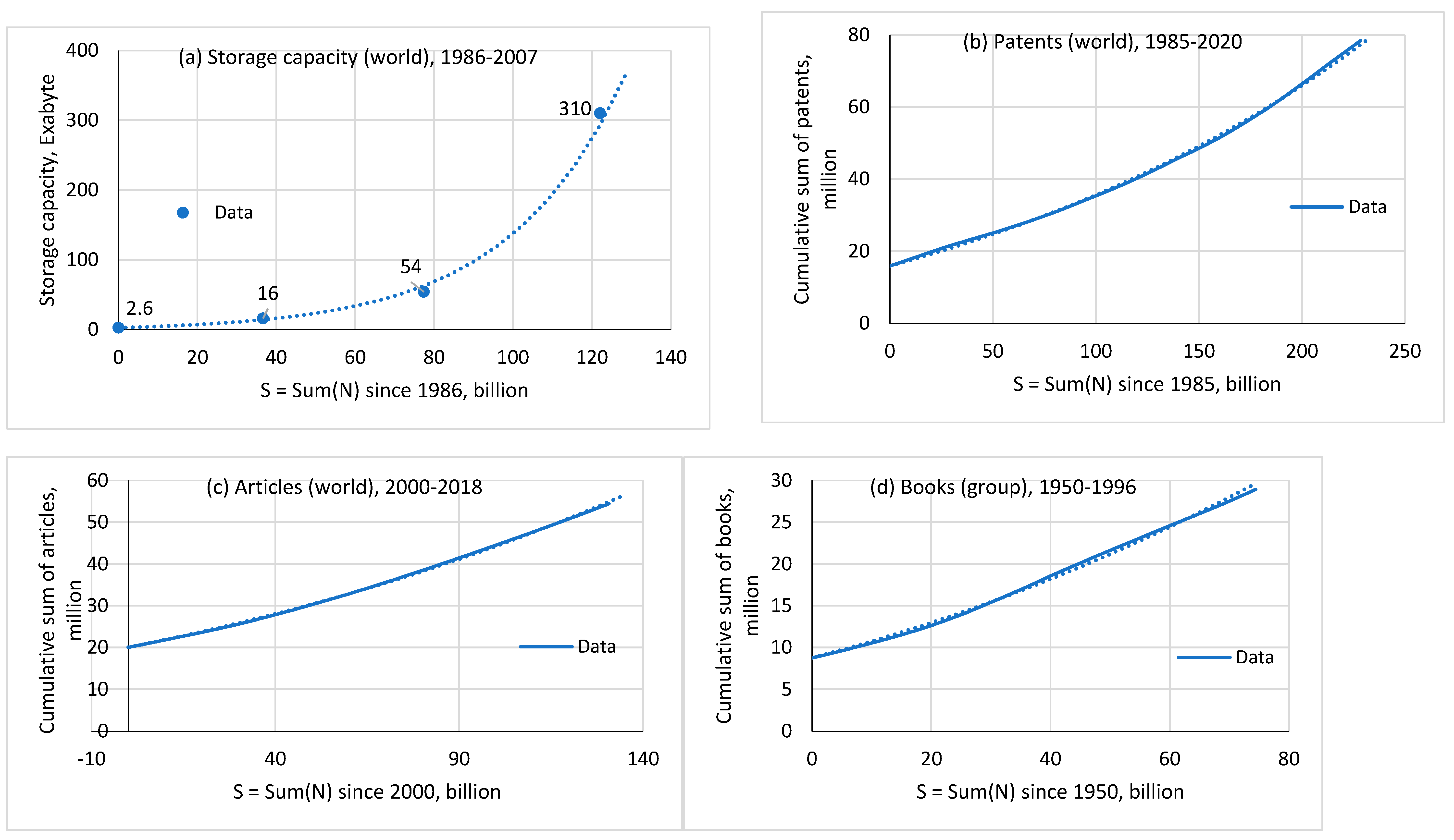
4.1. Storage Capacity

The best fit of equation (16) to the data is achieved at $\epsilon =1$, when a linear productivity (21) is the case:

$$q=q_h\left(\rho e^{S/\sigma }-1\right)$$

(31)

$$q_h=2.053, \rho =2.266,\sigma =29.42$$

(32)

where

$$q_h={\displaystyle \frac{1}{h}}, \rho =1+h{q}_0, \sigma ={\displaystyle \frac{1}{h{w}_0}}$$

(33)

$q$ is measured in Exabytes (only in this case), $S$ and $\sigma$ are measured in billion people×year.

4.2. Patents

Kong et al. (2023) found that patents created absorb much more knowledge from patents than from articles. Then we can neglect the contribution of articles to the production of patents.

The number of patents is also best suited to the linear case $\epsilon =1$, see (21), and obeys equation (31) with parameters (33) having values

$$q_h=20.41, \rho =1.770,\mathrm{}\mathrm{}\mathrm{}\sigma =230.8$$

(34)

here and further in (35) $q$ is measured in million texts.

4.3. Articles

Equation (16) when applied to the number of articles in scientific and technical journals gives the best result in the asymptotic limit $h\to \infty$, which corresponds to equation (24) at $\epsilon =0.7580$ (Table 1). Equation (24) can be rewritten as

$$q=q_0{\left(1+{\displaystyle \frac{S}{\sigma \tau }}\right)}^{\tau }$$

(35)

$$q_0=20.04,\mathrm{}\mathrm{}\mathrm{}\sigma =114.5,\mathrm{}\mathrm{}\mathrm{}\tau =4.132$$

(36)

where

$$\sigma ={\displaystyle \frac{q_{0 }^{1-\epsilon }}{c}}, \tau ={\displaystyle \frac{1}{1-\epsilon }}$$

(37)

4.4. Books

For the number of new book titles (in all genres of literature), the best result corresponds to the same asymptotic formula (35) as for articles, with $\epsilon =0.5814$ and parameter values

$$q_0=8.749,\mathrm{}\mathrm{}\mathrm{}\sigma =46.74,\mathrm{}\mathrm{}\mathrm{}\tau =2.389$$

(38)

4.5. Memory Capacity Assessment

To estimate the memory capacity (in bytes) occupied by patents, articles and books, we use estimates of the average sizes of these texts. Analysis of samples of several hundred patents and articles yields an average size of approximately 1.5 Megabytes per patent (or article). Similarly for books, we get an average size of 14 Megabytes per book. The latest storage capacity value of 310 Exabytes dates back to 2007. Memory capacity estimates for various types of knowledge representation as of 2007 are shown in Table 2.

We see that the memory capacity occupied by each text type is 6 orders of magnitude less than the total storage capacity. The storage capacity is filled primarily with visual information (photos, films, archives of TV programs, video surveillance, digitized museum exhibits, etc.). It is also necessary to consider the repeated duplication of visual and textual information, copied by almost every interested user to their devices. The need to store such immense information causes an accelerated growth in the capacity of storage devices, which is what we are seeing in reality (Figure 6a).

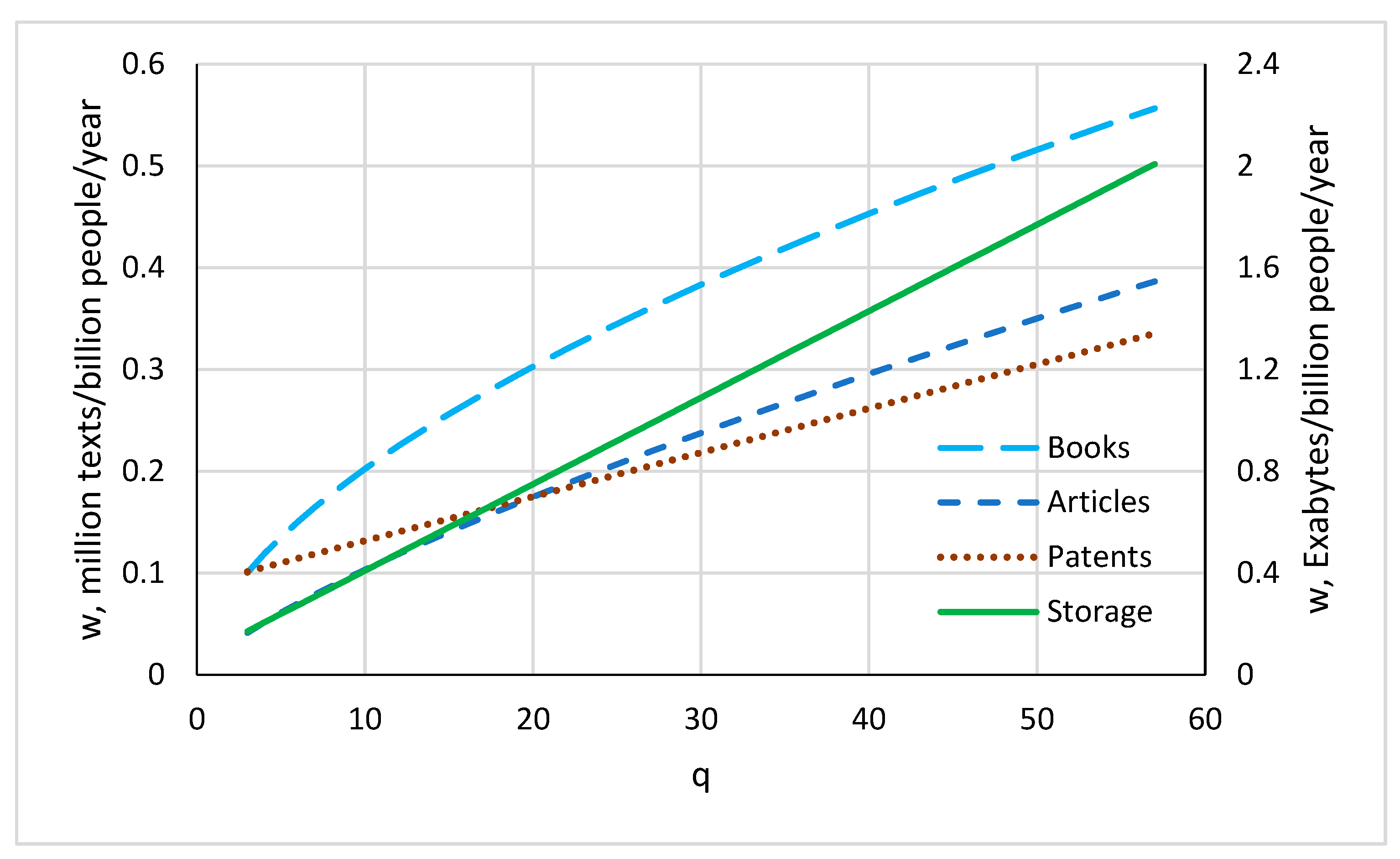
4.6. Productivity Increase

According to the adopted model, productivity increases for all types of texts studied here (patents, articles and books), as depicted in Figure 7. With an increase in knowledge by 5 times ($q$ from 10 to 50 units), productivity increases by 2.3, 2.5 and 3.4 times for patents, books and articles, respectively. For the same increase in storage capacity, productivity increases by 4.3 times. So, productivity grows more slowly than knowledge.

Table 3 shows that during the observation period productivity increases by 2 – 2.7 times. Unlike knowledge, the information storage stands apart: its capacity $q$ increased over the observation period by 113 times, and its productivity $w$ increased by 63 times. We see that memory is expanding much faster than new texts (patents, articles, books) are created. Apparently, producing storage devices is a simpler process than creating new knowledge.

4.7. Constant Productivity Approximation

Consider the condition under which the constant productivity approximation may be acceptable. According to (13), this condition is $q\ll q_h$, where $q_h=1/h$ is a threshold value. Referring to Table 1, we find $q_h=2.053$ for storage and $q_h=20.41$ for patents. The former corresponds to 1983, the latter to 1989.

For articles and books, their productivity $w$ and accumulated knowledge $q$ obey nonlinear laws (25) and (35). As shown above (see (20)), constant productivity causes a linear increase in knowledge. Equation (35) can be linearized if the condition $S\ll \sigma$ is satisfied, then $w\approx c{q}_0^{\epsilon }$. According to (36) and (38), $\sigma =114.5$ for articles and $\sigma =46.74$ for books. The threshold value $S=\sigma$ is reached in 2016 for articles and in 1982 for books.

So, we can use the constant productivity approximation (20) as long as we do not get too close to the specified dates, staying in the range of $q$ where the condition $q\ll q_h$ for storage and patents or $S\ll \sigma$ for articles and books holds. To summarize, as we approach the 1980s, the constant productivity approximation loses its adequacy (for articles it happens later).

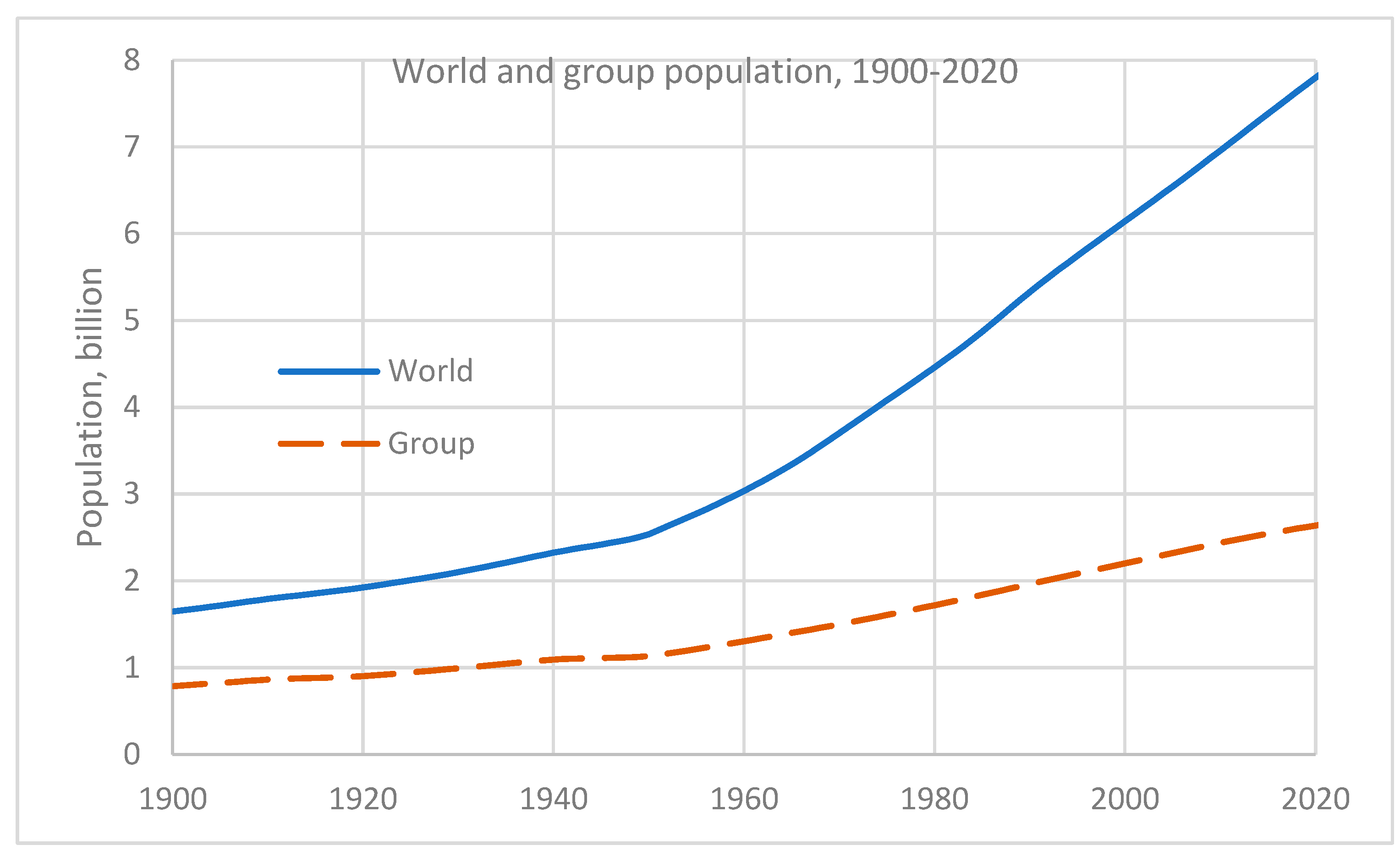
The dependence of knowledge production on population size (7), supplemented by the equation of knowledge dynamics, allows us to obtain the equation of demographic dynamics (Dolgonosov, 2016). The constant productivity approximation $w=w_0$ leads to the well-known hyperbolic law of world population growth (von Foerster et al., 1960), which operated for over a thousand years. However, deviations from this law become increasingly apparent as we approach the 1980s, which is associated with a significant accumulation of knowledge and an increase in productivity — it can no longer be taken as constant. This fact is usually considered as a demographic and technological phase transition (Korotayev et al., 2015; Grinin et al., 2020a, b), and at the same time it can be interpreted as a transition from a pre-information society, where the constant productivity approximation operates, to a more developed information society with advanced computer technologies and growing human productivity.

After the 1980s, personal computers became widespread and the information society continued to develop. Digital memory grew, reaching the level of analog memory and then surpassing it. The share of digital memory increased as follows: 0.8% in 1986, 3% in 1993, 25% in 2000, 94% in 2007 (Hilbert and López, 2011). The capacities of both types of memory became equal in 2003. Thus, the early 2000s can be considered a milestone in the maturation of digital civilization. Currently, the majority of world's technological memory is organized in the most accessible and fastest digital format.

5. Conclusion

The amount of knowledge correlates with the number of patents, articles and books published in the world over the entire previous period, which allowed us to trace the dynamics of knowledge accumulation. The production of knowledge depends on its amount and population size. This dependence plays a crucial role in knowledge dynamics and related demographic dynamics. The goal of this work was to find out the form of this dependence and check how well it corresponds to real data.

We have proposed a model in which the total rate of knowledge production is expressed as the product of average human productivity and population size. Productivity increases as knowledge accumulates and information technology advances. At the early stage of society development, knowledge is very scarce, but productivity is still not zero, which is a necessary condition for further development.

As knowledge grows, productivity gradually increases, reaching high values in a developed information society. In the asymptotic limit, when knowledge amount $q$ becomes large, productivity can be described by a power-law dependence on $q$. To combine the extreme cases of an undeveloped society and a highly developed one, we described productivity by the interpolation dependence representing a linear form of $q$ raised to a certain power. This dependence generalizes important special cases where productivity can be a constant, linear, power or exponential function of knowledge.

In a developed society, information is stored primarily in digital format on various types of devices, which, together with analog memory, form the global informational storage. With the development of digital technology, storage capacity is rapidly increasing. To describe this process, we used the proposed model.

The model was calibrated using literature data for the world as a whole (applied to patents, articles and informational storage) and for the group of 30 countries (applied to books, given the lack of data for many countries). Good agreement with the data was achieved. The general dependence of human productivity on knowledge amount was reduced to two special cases: a linear function of $q$ for patents and storage capacity, and a power function of $q$ for articles and books.

The analysis showed that in a pre-information society, with a relatively small amount of knowledge, the constant productivity approximation can be used. The transition to a developed information society occurred in the 1980s. Productivity can no longer be considered constant: it grows with the accumulation of knowledge according to a linear law in the case of patents, and according to a power law in the case of articles and books.

Digital memory surpassed analog memory after 2003. The population's need for repeated duplication of useful information led to a rapid increase in the number of storage devices and, consequently, to an increase in the total capacity of informational storage, which by 2007 exceeded the memory capacity occupied by patents, articles and books by 6 orders of magnitude.

The results obtained open up an opportunity to advance in describing the dynamics of various forms of knowledge and predicting their development in the future.