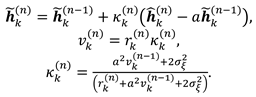Multi-User MIMO Downlink Precoding with Dynamic Users Selection for Limited Feedback

1. Introduction

MIMO (Multiple Input Multiple Output) technology along with modulation and coding schemes selection provides a sensible compromise between noise immunity (error correction capability) and data transfer rate in wireless communication systems [1,2]. MIMO systems can, under certain conditions, approach the theoretical limit of channel capacity [3,4,5]. This technology is a highly efficient way of transmitting data and is widely used in modern radio communication systems such as WiFi 5 - 7 wireless communication systems, LTE, LTE-Advanced, 5G mobile communication systems, etc. It is worth noting the key role of Massive MIMO technology in modern mobile communication systems (5G-Advanced), Beyond 5G (B5G) systems and multi-user wireless sensor networks to achieve high throughput, capacity and reliability of data transmission [2,6,7,8].

However, to fully capitalize on the advantages of MIMO systems, especially for the multi-user (MU) scenario, additional signal processing technologies are required, the most important of which is the precoding technology [9,10,11,12,13]. The precoding improves the performance of MIMO systems by using the channel information to pre-process signals transmitted. The precoding is especially effective in Multi-User MIMO (MU-MIMO) systems, as it allows for simultaneous downlink data transmission for users with a small number of receiving antennas using the same frequency resources. Precoders are typically designed in accordance with the information theory, so the throughput, the capacity, the mutual information, and other criteria may be used for optimization [2,6,14,15,16].

Precoders that use full MIMO channel state information (full CSI) are well known. References [6,11,12,13,14,17] detail linear precoding approaches that allow for transmission of users’ signals in the downlink while avoiding interference (i.e. facilitate the full separation of signals. However, the availability of full CSI without feedback is only possible in TDD mode for low-mobility (stationary) subscribers or in MIMO systems with Full Duplex technology [18]. In most other cases, the full information is not available on the transmitting side, so a feedback channel from each user to the base station is used [19,20,21]. With a large number of antennas at the base station (BS) and a large number of users in Massive MIMO systems, the amount of channel information transmitted over feedback channel from mobile stations (MS) can be comparable to the total traffic amount, which is a significant limitation. Therefore, the partial channel state information (partial CSI) precoding systems that do not require large feedback amount are of great interest.

For example, in 5G and B5G systems, codebooks-based precoding is used to reduce the complexity of feedback and overhead for transmitting CSI [7,9]. With this approach, a Precoding Matrix Indicator (PMI) is transmitted to the BS side using feedback channel, and the precoder is selected in accordance with a given optimization criteria (e.g., maximum throughput criteria). For 5G Advanced and future systems with higher throughput requirements, Discrete Fourier Transform (DFT) based codebook combined with a low-dimensional search procedure was proposed in [22] for PMI selection to improve the performance, with acceptable increase in computational complexity. The use of precoding matrix selection on the receiving side and PMI transmission over feedback channel allows to increase the communication efficiency for one subscriber, but does not solve the problems of the multi-user mode, since the precoding matrix selection is carried out by one user without taking into account the presence of others.

Another valuable approach to limited feedback precoding is based on the use of Grassmannian Codebooks [21,23,24,25,26]. In this case, the matrix closest to the actual channel matrix is selected from the Grassmannian codebook on the receiving side, and the index of this matrix is transmitted to the BS. All code matrices received from the MS side are processed at the BS side, and a precoding matrix is formed on this basis. This method can be classified as a multidimensional quantization and, like all quantization methods, it provides an estimate of the channel matrix with some error. This quantization error may be reduced by increasing the volume of code book (the number of quantized values), but with a large number of antennas at the BS, the required volume of the code book increases significantly, which complicates code matrices search process and increases the complexity of the algorithm for selecting a precoding matrix at the MS side. As a result, due to the inaccuracy of channel information, this type of Partial CSI precoding is significantly inferior to the full CSI precoding in terms of the number of available active users simultaneously served by the BS. There are the methods that partially solve this problem, e.g. in [25] dual stage Grassmannian product quantization approach for Massive MIMO systems was proposed. This approach is designed to solve the problem of synthesizing large codebooks for efficient quantization of CSI information; however, it only partially takes into account the quality of the CSI information and does not provide correction of the MIMO channel matrix estimates as CSI information arrives on the feedback channel from MSs.

It should be noted, that the retransmission of the code matrix index to the BS does not increase the CSI, since this is a normal duplication of the previously received information. In this paper, we propose a precoding method based on the fact, that the MS transmits new information via the feedback channel each time, which gets analyzed and accumulated together with the previously received CSI. This allows, after several transmission cycles via the feedback channel, to increase the accuracy and, as a result, to obtain almost full CSI and organize communication on the downlink for the maximum possible number of users. At the same time, the feedback transmission rate does not increase and CSI accumulates every transmission cycle.

2. Downlink MU-MIMO System Model

Let’s consider a mathematical model of Multiuser MIMO (MU-MIMO) system, where multiple users or mobile stations (MSs) are served simultaneously by one base station (BS) on the downlink, and Spatial-division multiple access (SDMA) technology allows the BS to communicate simultaneously with all MSs through multiple antennas. SDMA is possible with MIMO technology, and both the BS and the MS can be equipped with multiple antennas [2,6,7].

Let’s introduce the following notations: $N_{tx}$ - number of BS transmitting antennas; k – index of MS; $K_{us}$ - number of served MSs; $N_{rx}$ - number of receiving antetnnas at each MS; $K_{ch}$ - number of spatial streams between BS and MSs; H_k– complex downlink MIMO channel matrix between BS and k-th MS of dimension $\left(N_{rx}\times N_{tx}\right)$, consisting of complex transmission coefficients between the transmitting antennas of the BS and the receiving antennas of the k-th MS; ${\mathit{W}}_k$ - precoding matrix at the BS side of dimension $\left(N_{tx}\times K_{ch}\right)$ for k-th user’s signal generation; $\mathit{W}=\left[\begin{array}{cccc}{\mathit{W}}_1& {\mathit{W}}_2& ...& {\mathit{W}}_{K_{us}}\end{array}\right]$ - common precoding matrix of dimension $\left(N_{tx}\times K_{ch}{K}_{us}\right)$, consisting of matrixes ${\mathit{W}}_k$, $k=\overline{1,K_{us}}$. We also assume, for simplicity of further description, that the parameters of all MSs (number of antennas, type of modulation, etc.) are the same. If necessary, all the obtained results can be extended to any combination of MSs’ parameters.

In general, the model of the received signal at the k-th MS receiver input can be written as follows [27]:

$${\mathit{y}}_k={\mathit{H}}_k{\mathit{W}}_k{\mathit{s}}_k+{\sum }_{j=1,j\ne k}^{K_{us}}{\mathit{H}}_k{\mathit{W}}_j{\mathit{s}}_j+{\mathit{\eta }}_k={\mathit{H}}_k\mathit{W}\mathit{s}+{\mathit{\eta }}_k,$$

(1)

where ${\mathit{y}}_k$ is received signal of dimension $\left(N_{rx}\times 1\right)$; ${\mathit{s}}_k$ is complex vector of transmitted modulated symbols of dimension $\left(K_{ch}\times 1\right)$; $\mathit{s}$ denotes common vector of information symbols of all users of dimension $\left(K_{ch}{K}_{us}\times 1\right)$ ${\mathit{\eta }}_k$ is complex Gaussian random noise vector in communication channel of dimension $\left(N_{rx}\times 1\right)$, whose components have zero mean and variance $2{\sigma }_{\eta }^2$. Equation (1) can be considered as the sum of the useful signal, signals of neighboring MSs of the multi-user communication system, that are interference, and Additive White Gaussian Noise (AWGN) in the communication channel.

The task of BS is the simultaneous transmission of signals for $K_{us}$ users selected from the total number $K_{ch}$, using precoding technology in MIMO channel [2,6,7]. Precoding matrix $\mathit{W}$, used on the base station side, is calculated after receiving the channel state information from all MSs contained in the common channel matrix $\mathit{H}$. As a rule, this matrix must ensure the equality of signals’ powers transmitted to different users, i.e. the following condition must be met:

$$\mathit{trace}\left({{\mathit{W}}_k}^{\prime }{\mathit{W}}_k\right)=1,k=\overline{1,K_{us}},$$

(2)

where ${\mathit{A}}^{\prime }$ denotes the operation of Hermitian conjugation of matrix $\mathit{A}$.

3. Precoding in MU-MIMO System with Full and Partial Channel State Information

Let us consider MMSE precoding with fully available CSI information using the principle of reciprocity of signal propagation from the BS to the MSs [6,16,27]. To do this, we will solve the inverse problem when the BS receives signals from all MSs. For simplicity of further description and better understanding, we will limit ourselves to considering the case where all MSs have one receiving antenna. In this case, downlink channel matrix will be a vector ${\mathit{h}}_k$ of dimension $\left(1\times N_{tx}\right)$. This is the most common case and, if necessary, it is quite easy to extend it to any number of receiving antennas, provided that the total number of all MSs receiving antennas does not exceed the number of transmitting antennas on BS side. Let us consider a virtual model of receiving signals from all MSs at the base station:

$${\mathit{y}}_{BS}={\mathit{H}}^T{\mathit{s}}_{MS}+{\mathit{\eta }}_{BS},$$

(3)

where ${\mathit{y}}_{BS}$- vector of received signals from all users, $\mathit{H}={\left[{\mathit{h}}_1^T\dots {\mathit{h}}_{K_{us}}^T\right]}^T$ - downlink MU-MIMO channel matrix, and ${\mathit{H}}^T$ - MU-MIMO virtual channel matrix for the transmission from MSs to BS in reverse direction; ${\mathit{\eta }}_{BS}$ - complex AWGN vector with zero mean and and correlation matrix $2{\sigma }_{\eta }^2{\mathit{I}}_{N_{tx}}$; ${\mathit{s}}_{BS}={\left[s_1^{BS}\dots s_{K_{us}}^{BS}\right]}^T$ - vector of information symbols in the virtual model. Model (3) contains indexes «BS» and «MS» in order to distinguish the virtual model from model (1), in which the transmission is carried out from BS to MSs.

For convenience, we introduce the notation $\breve{\mathit{H}}\triangleq {\mathit{H}}^T$ and write MMSE algorithm to find estimates of the users symbol vector in the virtual channel:

$$\begin{gathered} {\widehat{\mathit{s}}}_{MS}=\breve{\mathit{G}}{\mathit{y}}_{BS}, \\ \breve{\mathit{G}}={\breve{\mathit{H}}}^{\prime }{\left(2{\sigma }_{\eta }^2{\mathit{I}}_{N_{tx}}+\breve{\mathit{H}}{\breve{\mathit{H}}}^{\prime }\right)}^{-1}={\left(2{\sigma }_{\eta }^2{\mathit{I}}_{K_{us}}+{\breve{\mathit{H}}}^{\prime }\breve{\mathit{H}}\right)}^{-1}{\breve{\mathit{H}}}^{\prime }, \end{gathered}$$

(4)

In this case, the correlation matrix of estimation errors will have the following form:

$$\mathit{V}=2{\sigma }_{\eta }^2{\left(2{\sigma }_{\eta }^2{\mathit{I}}_{K_{us}}+{\breve{\mathit{H}}}^{\prime }\breve{\mathit{H}}\right)}^{-1}.$$

(5)

Taking into account the reciprocity principle, the precoding matrix $\breve{\mathit{W}}$ is the transposed matrix $\breve{\mathit{G}}$ of the MMSE estimation algorithm for the virtual channel, [27], i.e.

$$\breve{\mathit{W}}={\breve{\mathit{G}}}^T={\left({\left(2{\sigma }_{\eta }^2{\mathit{I}}_{K_{ch}}+{\breve{\mathit{H}}}^{\prime }\breve{\mathit{H}}\right)}^{-1}{\breve{\mathit{H}}}^{\prime }\right)}^T={\breve{\mathit{H}}}^{*}{\left(2{\sigma }_{\eta }^2{\mathit{I}}_{K_{ch}}+{\breve{\mathit{H}}}^T{\breve{\mathit{H}}}^{*}\right)}^{-1},$$

(6)

where ${\mathit{A}}^{*}$ denotes the operation of matrix $\mathit{A}$ elements complex conjugation. Taking into account the previously introduced matrix notation $\breve{\mathit{H}}$ in equation (6), we obtain an expression for calculating the precoding matrix on the BS side without normalization:

$$\breve{\mathit{W}}={\mathit{H}}^{\prime }{\left(2{\sigma }_{\eta }^2{\mathit{I}}_{K_{ch}}+\mathit{H}{\mathit{H}}^{\prime }\right)}^{-1},$$

(7)

where $\breve{\mathit{W}}=\left[\begin{array}{cccc}{\breve{\mathit{w}}}_1& {\breve{\mathit{w}}}_2& ...& {\breve{\mathit{w}}}_{K_{us}}\end{array}\right]$ — common precoding matrix of dimension $\left(N_{tx}\times K_{us}\right)$, consisting of unnormalized column vectors $\breve{\mathit{w}}$ of dimension $\left(N_{tx}\times 1\right)$.

As already noted and expressed in (2), the precoding matrix must ensure equality and constancy of the transmitted signals in power domain. In this case, the normalization operation can be defined as follows:

$${\mathit{w}}_k={\displaystyle \frac{{\breve{\mathit{w}}}_k}{\sqrt{{{\breve{\mathit{w}}}_k}^{\prime }{\breve{\mathit{w}}}_k}}},k=\overline{1,K_{us}}.$$

(8)

Taking into account the normalization, we obtain the matrix $\mathit{W}=\left[\begin{array}{cccc}{\mathit{w}}_1& {\mathit{w}}_2& ...& {\mathit{w}}_{K_{us}}\end{array}\right]$, which is the common precoding matrix of dimension $\left(N_{tx}\times K_{us}\right)$, consisting of vectors ${\mathit{w}}_k$.

Thus, equations (7) and (8) describe an MMSE precoding algorithm with an accurately known channel matrix $\mathit{H}$ at the BS side. Let’s now consider the precoding on the BS side taking into account the inaccuracy of the channel parameters estimation. As an indicator characterizing the inaccuracy of channel matrix information, we will use the generalized scalar parameter of the total deviation from actual value, which we will call Channel Quality Information (CQI):

$$CQ{I}_k\triangleq {‖{\mathit{h}}_k-{\widehat{\mathit{h}}}_k‖}^2.$$

(9)

where ${\widehat{\mathit{h}}}_k$ - channel vector estimate.

Let us take into account the inaccuracy of the channel vector estimates ${\widehat{\mathit{h}}}_k$ on the BS side when forming the precoding matrix. Let us have estimates ${\widehat{\mathit{h}}}_k$ of vectors ${\mathit{h}}_k$, $k=\overline{1,K_{us}}$, whose accuracy is characterized by the corresponding indicators $CQ{I}_k$. We approximate the a priori distribution of the original vector ${\mathit{h}}_k$ by a Gaussian distribution with mean value ${\widehat{\mathit{h}}}_k$ and correlation matrix ${\mathit{V}}_{k,pr}=v_{k,pr}{\mathit{I}}_{N_{tx}}$, where $v_{k,pr}$ is a priori variance that will be calculated on the basis of the indicator $CQ{I}_k$ using equation $v_{k,pr}={\displaystyle \frac{CQ{I}_k}{N_{tx}}}$. Combining AWGN with the noise approximating the inaccuracy of the channel matrix, and considering the case of uncorrelated samples of this noise, we obtain the following expression for the unnormalized precoding matrix $\breve{\mathit{W}}$ (normalization is defined using the expression (8)):

$$\breve{\mathit{W}}={\widehat{\mathit{H}}}^{\prime }{\left(\left(2{\sigma }_{\eta }^2+{\displaystyle \frac{1}{N_{tx}}}{\sum }_{k=1}^{K_{ch}}CQ{I}_k\right){\mathit{I}}_{K_{ch}}+\widehat{\mathit{H}}{\widehat{\mathit{H}}}^{\prime }\right)}^{-1}.$$

(10)

where $\widehat{\mathit{H}}={\left[{\widehat{\mathit{h}}}_1^T{\widehat{\mathit{h}}}_2^T...{\widehat{\mathit{h}}}_{K_{us}}^T\right]}^T$ - inaccurately known channel matrix.

The approximate accuracy of the MMSE estimate will be determined by the diagonal elements of the following matrix (correlation matrix of estimation errors):

$${\mathit{V}}_{PCSI}=\left(2{\sigma }_{\eta }^2+{\displaystyle \frac{1}{N_{tx}}}{\sum }_{k=1}^{K_{ch}}CQ{I}_k\right){\left(\left(2{\sigma }_{\eta }^2+{\displaystyle \frac{1}{N_{tx}}}{\sum }_{k=1}^{K_{ch}}CQ{I}_k\right){\mathit{I}}_{K_{ch}}+\widehat{\mathit{H}}{\widehat{\mathit{H}}}^{\prime }\right)}^{-1}$$

(11)

Trace of matrix ${\mathit{V}}_{PCSI}$ can serve as a general indicator of precoding quality, and each diagonal value of this matrix $v_{PCSI,k}$ will characterize precoding efficiency for k-th user.

4. Users Selection MU-MIMO System Taking into Account Partial CSI

The performance of the MU-MIMO system with precoding is very sensitive to the accuracy of the channel vector estimates ${\widehat{\mathit{h}}}_k$, $k=\overline{1,K_{us}}$. When partial CSI information is used on the BS side for precoding, the performance of MU-MIMO system is significantly degraded. The lack of CSI information on the BS side leads to a decrease in the signal-to-noise ratio, and leads to a significant increase in interference from signals transmitted to other users [4,17,25].

To provide multi-user mode on the downlink with partial CSI to organize communication, an approach based on users selection from the total number of users waiting for service is used [12,16,26]. Due to inaccurate CSI, precoding does not provide full compensation for interference (signals from other users), especially when receiving signals from MSs with a small number of antennas. This problem can be partially solved by reducing the number of subscribers served, as well as by selecting and combining subscribers into groups that provide the least influence on each other, taking into account partial channel information.

The problem of users selection cannot be solved only by taking into account the accuracy of the channel information (CQI indicator), since this indicator does not take into account the influence of interference. More useful in this case is the variance of MMSE estimation errors $v_{PCSI,k}$ in virtual channel for one user or correlation matrix trace for the entire group of users, $\mathit{trace}\left({\mathit{V}}_{PCSI}\right)$, defined by the expression (11).

Let the MIMO system have $K_{us}$ users ready to receive information from the base station. Let’s assume that due to partial information about the channel, communication on the downlink can only be organized for $K_{us,sel}$ users only. Therefore, the task is to select $K_{us,sel}$ users out of the total number $K_{us}$, ensuring minimal mutual influence, i.e. the following condition must be met for the selected users:

$${\mathit{V}}_{PCSI}^{\left({\mathbb{K}}_{us,sel}\right)}=\underset{{\mathbb{K}}_{us}︸\left(\mathit{trace}\left(P_{NI}{\left(P_{NI}{\mathit{I}}_{K_{us,sel}}+{\widehat{\mathit{H}}}^{\left({\mathbb{K}}_{us}\right)}{\left({\widehat{\mathit{H}}}^{\left({\mathbb{K}}_{us}\right)}\right)}^{\prime }\right)}^{-1}\right)\right)}{\underbrace{min}}.$$

(12)

where $P_{NI}=\left(2{\sigma }_{\eta }^2+{\displaystyle \frac{1}{K_{us,sel}}}{\sum }_{k\in {\mathbb{K}}_{us,sel}}CQ{I}_k\right)$ - total power of AWGN and noise, taking into account the uncertainty of channel information, ${\mathbb{K}}_{us}$ - various sets of users’ numbers consisting of $K_{us,sel}$ elements, selected from the total number $K_{us}$, ${\mathbb{K}}_{us,sel}$ - a set of selected users’ numbers that provide a minimum trace of the matrix, i.e. optimal combination of users.

Finding the optimal combination of $K_{us,sel}$ users that satisfies condition (12), requires enumerating all combinations from $K_{us}$ of length $K_{us,sel}$ , and for each combination it is necessary to compute the inverse matrix of dimension $\left(K_{us,sel}\times K_{us,sel}\right)$. To simplify the user selection procedure, we propose to use an approach without trying all combinations, similar to the approach used in MIMO systems with antenna selection technology [28].

With respect to the considered precoding method, this approach is implemented as follows. We start the selection of combinations with a user with the best quality indicator $CQI$, then one of all remaining users is matched with this user, for which the minimum trace of matrix ${\mathit{V}}_{PCSI}^{\left({\mathbb{K}}_{us,sel}\right)}$ of dimension $\left(2\times 2\right)$ is ensured. Next, for these two users, another user is selected from all the remaining users, in combination with which the minimum trace of matrix ${\mathit{V}}_{PCSI}^{\left({\mathbb{K}}_{us,sel}\right)}$ of dimension $\left(3\times 3\right)$ is ensured. The process of adding the users continues until the specified number $K_{us,sel}$ of users is reached, or until some threshold of matrix ${\mathit{V}}_{PCSI}^{\left({\mathbb{K}}_{us,sel}\right)}$ will not be reached.

5. Channel Matrix Quantization and CSI Information Reduction Which Is Transmitted over Feedback Channel

The basis for the effective precoding is the availability of CSI on the transmitting side. As already mentioned, in most cases this information is not available at the BS for the downlink transmission, so a feedback channel from each MS to the BS is needed to transmit the channel information. As before, for simplicity of description, we will consider the case of MSs with one receiving antenna, i.e. the channel on the downlink for one subscriber is described by a complex channel vector ${\mathit{h}}_k$ ,$k=\overline{1,K_{us}}$, of dimension $\left(N_{tx}\times 1\right)$.

When the quantized values ​​of the channel matrix coefficients are directly transmitting to the BS side, the amount of transmitted information will be equal to $2N_{tx}{\mathit{log}}_2\left(L_q\right)$ bits, where $L_q$ is the number of quantization levels, so with a large number of antennas (Massive MIMO) this will require the allocation of a sufficiently large amount of resources [23,24]. Therefore, in order to reduce the amount of information transmitted via the feedback channel, another type of quantization is used, in which a limited set of vectors (codewords) are specified, specially selected and known at both the MS side and the BS side. From the total set of vectors (codebook), the code word closest to the original vector ${\mathit{h}}_k$ is selected, and only the codeword number is transmitted to the BS. This significantly reduces the amount of information transmitted. Vectors or matrices based on Grassmannians can be used as codebooks (Grassmannian Codebooks) [21,23,24,26].

For 3GPP standards, procedures have been developed for selecting and transmitting via feedback a codeword (the number of one of the codebook vectors) that is closest to the original channel vector according to some criteria. [7,9,12,15,22]. Additional information transmitted to the base station may be the following scalar parameters: coefficient ${\alpha }_k$ and quality indicator $CQ{I}_k$, characterizing the correspondence accuracy of this codeword to vector ${\mathit{h}}_k$.

Next, we consider the procedure when MS selects a codeword from the code book, calculates the complex weighting coefficient ${\alpha }_k$ and quality indicator $CQ{I}_k$, characterizing the correspondence accuracy of this codeword to vector ${\mathit{h}}_k$, and transmits this information along with selected codeword index $l_k$ to the BS.

Let's consider the procedure for selecting codeword index $l_k$ and estimation of parameters ${\alpha }_k$ and $CQ{I}_k$ in more detail. This procedure can be described by the following equations:

$$\begin{gathered} \left({\alpha }_k,l_k\right)=\underset{\alpha \in \mathbb{C},l=\overline{1,N_v}}{argmin}\left\{{‖{\mathit{h}}_k-\alpha {\mathit{c}}_l‖}^2\right\} \\ CQ{I}_k\triangleq {‖{\mathit{h}}_k-{\widehat{\mathit{h}}}_k‖}^2={‖{\mathit{h}}_k-{\alpha }_k{\mathit{c}}_{l_k}‖}^2, \end{gathered}$$

(13)

where ${\widehat{\mathit{h}}}_k={\alpha }_k{\mathit{c}}_{l_k}$ - quantized channel vector estimate, ${\mathit{c}}_l$ - l-th codeword (normalized vector) from a codebook $\mathit{C}$ of size $N_v$, $CQ{I}_k$ - quality indicator, which is an indicator of quantization quality of the original vector ${\mathit{h}}_k$ taking into account the complex weighting coefficient ${\alpha }_k$. Thus, the following values are transmitted to the BS side: ${\alpha }_k$, $CQ{I}_k$ and the closest code word index $l_k$.

The search for optimal values in (13) is carried out as follows. First, an estimate of complex weighting coefficient is found:

$${\alpha }_l={\mathit{h}}_k{{\mathit{c}}_l}^{\prime }{\left({\mathit{c}}_l{{\mathit{c}}_l}^{\prime }\right)}^{-1}={\mathit{h}}_k{{\mathit{c}}_l}^{\prime },$$

(14)

Substituting (14) in (13), we get

$$l_k=\underset{l=\overline{1,N_v}}{argmin}\left\{{‖{\mathit{h}}_k-{\mathit{h}}_k{{\mathit{c}}_l}^{\prime }{\mathit{c}}_l‖}^2\right\}=\underset{l=\overline{1,N_v}}{argmin}\left\{\left({\mathit{h}}_k-{\mathit{h}}_k{{\mathit{c}}_l}^{\prime }{\mathit{c}}_l\right){\left({\mathit{h}}_k-{\mathit{h}}_k{{\mathit{c}}_l}^{\prime }{\mathit{c}}_l\right)}^{\prime }\right\},$$

Considering that the codewords are normalized, i.e. ${\mathit{c}}_l{{\mathit{c}}_l}^{\prime }=1$, we will finally obtain the following optimal parameters values ​​for precoding:

$$l_k=\underset{l=\overline{1,N_v}}{argmax}\left\{{\left|{\mathit{h}}_k{{\mathit{c}}_l}^{\prime }\right|}^2\right\},{\alpha }_k={\mathit{h}}_k{{\mathit{c}}_{l_k}}^{\prime },CQ{I}_k={‖{\mathit{h}}_k-{\alpha }_k{\mathit{c}}_{l_k}‖}^2=\left({\mathit{h}}_k\left({\mathit{I}}_{N_{tx}}-{{\mathit{c}}_{l_k}}^{\prime }{\mathit{c}}_{l_k}\right){{\mathit{h}}_k}^{\prime }\right),$$

(16)

where ${\mathit{I}}_{N_{tx}}$ - identity matrix of dimension $\left(N_{tx}\times N_{tx}\right)$. Obtained in (16) parameters – codeword index $l_k$, quantized value of weighting coefficient ${\alpha }_k$ and quality indicator $CQ{I}_k$ - are transmitted to BS side. In this case, it is assumed that the BS side has exactly the same set of codebooks as the MS side.

The base station then reconstructs the channel vector estimates ${\widehat{\mathit{h}}}_k={\alpha }_k{\mathit{c}}_{l_k}$ for all users $k=\overline{1,K_{us}}$, selects $K_{us,sel}$ users for data transmission and calculates precoding matrix $\mathit{W}=\mathbb{F}\left\{\widehat{\mathit{H}}\right\}$, based on the selected precoding criteria $\mathbb{F}\left\{\right\}$. As such a criteria $\mathbb{F}\left\{\right\}$ we can use capacity, mutual information, symbols estimation errors in the virtual channel (10) or other criteria [26,27,28].

6. Algorithm for Cyclic Accumulation and Correction of Channel Vectors Estimates in MU-MIMO System

The precoding quality depends on the accuracy and amount of CSI information that the base station has. In turn, the requirement for high accuracy of CSI information is in conflict with the requirement to reduce the amount of information transmitted over the feedback channel. In addition, the requirement to increase quantization accuracy when using Grassmannian Codebook is accompanied by an increase in codebook size and, as a consequence, an increase in the complexity of choosing the appropriate codeword [23,24,25]. For example, if we need to transmit 16-bit codeword index, when choosing such a word, it will be necessary to perform $2^{16}$ operations of comparing the original channel vector with the corresponding codeword.

At the same time, the CSI information from the subscriber to the base station must be updated periodically (cyclically), since the position of the subscribers may change, as well as the number of subscribers participating in communication, etc. To improve the accuracy of the CSI information at the base station, the information cyclically transmitted over the feedback channel can be gradually accumulated and processed. However, if the same information is transmitted (codeword index $l_k$, coefficient ${\alpha }_k$ and quality indicator $CQ{I}_k$), then the quantization errors on each transmission will be highly correlated, especially when the channel parameters change slowly. Therefore, there will be no significant improvement in the accuracy of partial CSI. It is necessary to ensure that the quantization errors are uncorrelated, then the obtained information can be accumulated and the MU-MIMO channel matrix can be restored with higher accuracy.

To reduce the correlation of quantization errors we propose instead of a single codebook $\mathit{C}$ of size $N_v$ to use a set of codebooks ${\mathit{C}}^{\left(n\right)}$, where $n=\overline{1,N_c}$, $N_c$ - number of codebooks. Then before each n-th transmission over the feedback channel the corresponding code book ${\mathit{C}}^{\left(n\right)}$ is used, new values of the channel parameters ​​are calculated and transmitted to the BS side:

$$\begin{gathered} l_k^{\left(n\right)}=\underset{l=\overline{1,N_v}}{argmax}\left\{{\left|{\mathit{h}}_k{{\mathit{c}}_l^{\left(n\right)}}^{\prime }\right|}^2\right\}, \\ {\alpha }_k^{\left(n\right)}={\mathit{h}}_k{{\mathit{c}}_{l_k^{\left(n\right)}}^{\left(n\right)}}^{\prime }, \\ CQ{I}_k^{\left(n\right)}={‖{\mathit{h}}_k-{\alpha }_k^{\left(n\right)}{\mathit{c}}_{l_k^{\left(n\right)}}^{\left(n\right)}‖}^2, \end{gathered}$$

(17)

where ${\mathit{c}}_l^{\left(n\right)}\in {\mathit{C}}^{\left(n\right)}$ - $l$ -th codeword from $n$ -th codebook.

The uncorrelated nature of quantization errors in this case will largely depend on the correlation of codewords from different books. This creates a certain problem in searching for such books and, in addition, it is necessary to store in the memory of MSs a set of codebooks ($N_c$ codebooks) instead of single codebook.

Another approach for ensuring uncorrelated quantization errors is to use one codebook, but at each step it is not the channel vector itself is quantized, but a modified vector obtained as a result of a special orthogonal transformation of the original channel vector, for example:

$$\begin{gathered} {\mathit{t}}_k^{\left(n\right)}={\mathit{h}}_k{\mathit{T}}^{\left(n\right)}, \\ \left({\alpha }_{t,k}^{\left(n\right)},l_k^{\left(n\right)}\right)=\underset{\alpha \in \mathbb{C},l=\overline{1,N_v}}{argmin}\left\{{‖{\mathit{t}}_k^{\left(n\right)}-\alpha {\mathit{c}}_l‖}^2\right\},. \end{gathered}$$

(18)

where ${\mathit{T}}^{\left(n\right)}$ - matrix of $n$ -th orthogonal transformation of dimension $\left(N_{tx}\times N_{tx}\right)$, where $N_{tx}$ - number of antennas at the BS side, $N_{\nu }$ - size of original codebook $\mathit{C}$. As a set of such orthogonal matrices, we propose to use the powers of some initial orthogonal transformation ${\mathit{T}}_0$, i.e. ${\mathit{T}}^{\left(n\right)}={\left({\mathit{T}}_0\right)}^n$. In this case, to ensure maximum decorrelation, the original transformation must have the property ${\left({\mathit{T}}_0\right)}^n={\mathit{I}}_{N_{tx}}$ only for $n=i{N}_{tx},i=\mathrm{1,2},3,...$. As a result, similar with (17), we obtain the following expressions:

$$\begin{gathered} l_k^{\left(n\right)}=\underset{l=\overline{1,N_v}}{argmax}\left\{{\left|{\mathit{t}}_k^{\left(n\right)}{{\mathit{c}}_l}^{\prime }\right|}^2\right\}, \\ {\alpha }_{t,k}^{\left(n\right)}={\mathit{t}}_k^{\left(n\right)}{{\mathit{c}}_{l_k^{\left(n\right)}}}^{\prime }, \\ CQ{I}_{t,k}^{\left(n\right)}={‖{\mathit{t}}_k^{\left(n\right)}-{\alpha }_{t,k}^{\left(n\right)}{\mathit{c}}_{l_k^{\left(n\right)}}‖}^2. \end{gathered}$$

(19)

It can be shown that this approach is equivalent to the set of codebooks approach, in which there is one generating codebook and the others are generated by orthogonal transformation ${\mathit{T}}^{\left(n\right)}={\left({\mathit{T}}_0\right)}^n$, i.e.

$${\mathit{C}}^{\left(n\right)}={\mathit{C}}_0{\left({\mathit{T}}_0\right)}^n.$$

(20)

Selection of the appropriate codebook ${\mathit{C}}^{\left(n\right)}$ or orthogonal transformation ${\mathit{T}}^{\left(n\right)}$ is carried out at each MS according to an algorithm that is also known on the BS side. The base station at each cycle of receiving partial CSI restores channel vector estimate of the $k$ -th user. For the first approach, it is calculated simply:

$${\widehat{\mathit{h}}}_k^{\left(n\right)}={\alpha }_k^{\left(n\right)}{\mathit{c}}_{l_k^{\left(n\right)}}^{\left(n\right)},$$

(21)

where parameters ${\alpha }_k^{\left(n\right)},l_k^{\left(n\right)}$ and quality indicator $CQ{I}_k^{\left(n\right)}$ are calculated according to (17) using the set of codebooks ${\mathit{C}}^{\left(n\right)}n=\overline{1,N_c}$, and then transmitted over feedback channel.

For the second approach, the estimate of the channel vector is calculated through an auxiliary calculation of vector ${\mathit{t}}_k$ estimate, i.e. we have:

$${\widehat{\mathit{h}}}_k^{\left(n\right)}={\widehat{\mathit{t}}}_k^{\left(n\right)}{{\mathit{T}}^{\left(n\right)}}^{\prime }{\widehat{\mathit{t}}}_k^{\left(n\right)}={\alpha }_{t,k}^{\left(n\right)}{\mathit{c}}_{l_k^{\left(n\right)}},$$

(22)

where parameters ${\alpha }_k^{\left(n\right)},l_k^{\left(n\right)}$ are calculated according to expressions (19) using one generating codebook ${\mathit{C}}_0$. It can be shown that the quality of channel vector estimate ${\widehat{\mathit{h}}}_k^{\left(n\right)}$ will coincide with the quality of transformed vector estimate ${\widehat{\mathit{t}}}_k^{\left(n\right)}$:

$$\begin{gathered} CQ{I}_k={‖{\mathit{h}}_k-{\widehat{\mathit{h}}}_k^{\left(n\right)}‖}^2={‖{\mathit{h}}_k-{\alpha }_{t,k}^{\left(n\right)}{\widehat{\mathit{t}}}_k^{\left(n\right)}{\left({\mathit{T}}^{\left(n\right)}\right)}^{\prime }‖}^2= \\ ={‖{\mathit{h}}_k{\mathit{T}}^{\left(n\right)}-{\alpha }_{t,k}^{\left(n\right)}{\widehat{\mathit{t}}}_k^{\left(n\right)}{\left({\mathit{T}}^{\left(n\right)}\right)}^{\prime }{\mathit{T}}^{\left(n\right)}‖}^2={‖{\mathit{t}}_k-{\widehat{\mathit{t}}}_k^{\left(n\right)}‖}^2= \\ ={‖{\mathit{t}}_k-{\alpha }_{t,k}^{\left(n\right)}{\mathit{c}}_{l_k^{\left(n\right)}}‖}^2=CQ{I}_{t,k}. \end{gathered}$$

(23)

Equations (17), (21) or (19), (22) allow to obtain new channel vectors estimates after each new transmission on the feedback channel. Now the task is to combine all the estimates to improve the accuracy of the final estimate.

We will consider the current channel estimate ${\widehat{\mathit{h}}}_k^{\left(n\right)}$ as observation:

$${\widehat{\mathit{h}}}_k^{\left(n\right)}={\mathit{h}}_k+{\mathit{\mu }}_k^{\left(n\right)},$$

(24)

where ${\mathit{\mu }}_k^{\left(n\right)}$ - quantization noise, which we approximate by uncorrelated Gaussian noise with zero mean and variance $r_k^{\left(n\right)}$, defined by quality indicator $CQ{I}_k^{\left(n\right)}$, i.e. ${\mathit{\mu }}_k^{\left(n\right)}\sim \mathbb{N}\left(0,r_k^{\left(n\right)}{\mathit{I}}_{N_{tx}}\right)$, where the noise variance is determined by the expression $r_k^{\left(n\right)}={\displaystyle \frac{CQ{I}_k^{\left(n\right)}}{N_{tx}}}$. Let vector ${\mathit{h}}_k$ elements are a priori independent random variables with a Gaussian prior distribution with zero mean and variance $v_{pr}$, i.e. ${\mathit{h}}_k\sim \mathbb{N}\left(0,v_{pr}{\mathit{I}}_{N_{tx}}\right)$. Using well-known filtering relations (for example, Kalman filtering algorithm [29,30,31,32]) we obtain the following expressions for channel vectors estimates of the users and the variances of their estimation errors:

$$\begin{gathered} {\tilde{\mathit{h}}}_k^{\left(n\right)}={\tilde{\mathit{h}}}_k^{(n-1)}+{\kappa }_k^{\left(n\right)}\left({\widehat{\mathit{h}}}_k^{\left(n\right)}-{\tilde{\mathit{h}}}_k^{(n-1)}\right), \\ {v}_k^{\left(n\right)}={\displaystyle \frac{r_k^{\left(n\right)}{v}_k^{(n-1)}}{\left(r_k^{\left(n\right)}+v_k^{(n-1)}\right)}}, \\ {\kappa }_k^{\left(n\right)}={\displaystyle \frac{v_k^{(n-1)}}{\left(r_k^{\left(n\right)}+v_k^{(n-1)}\right)}}, \end{gathered}$$

(25)

where ${\kappa }_k^{\left(n\right)}$ - Kalman filter gain for n-th cycle estimation, $v_k^{\left(n\right)}$- variance of channel vector estimation errors. Variance $v_k^{\left(n\right)}$ can be used to calculate a new channel estimation quality indicator as follows:

$${\stackrel{⏜}{CQI}}_k^{\left(n\right)}=N_{tx}{v}_k^{\left(n\right)}.$$

(26)

The obtained estimates of channel vectors of all users ${\tilde{\mathit{h}}}_k^{\left(n\right)}$ and their quality indicators ${\stackrel{⏜}{CQI}}_k^{\left(n\right)}$ can be used to calculate the correlation matrix of estimation errors ${\mathit{V}}_{PCSI}$ (11) and users selection according to algorithm (12).

Considered algorithm (25) of cyclic correction of channel vector estimates for MU-MIMO system users was obtained for a constant MIMO channel and is intended to reduce quantization errors when using Grassmannians. However, the proposed algorithm can be modified to filter the parameters of a fluctuating MIMO channel. For this, we consider the first-order model of uncorrelated fading:

$${\mathit{h}}_k^{\left(n\right)}=a{\mathit{h}}_k^{(n-1)}+{\mathit{\xi }}_k^{\left(n\right)}.$$

(27)

where $a$ - model parameter determined by the nature of fading in the radio channel; ${\mathit{\xi }}_k^{\left(n\right)}$ - complex Gaussian noise vector of size $\left(1\times N_{tx}\right)$ with zero mean and correlation matrix $2{\sigma }_{\xi }^2{\mathit{I}}_{N_{tx}}$.

Using model (27) together with the observation equation (24), we write estimation algorithm expressions for channel vectors ${\mathit{h}}_k^{\left(n\right)}$, $k=\overline{1,K_{us}}$ for the n-th time point based on Kalman filter expressions:

(28)

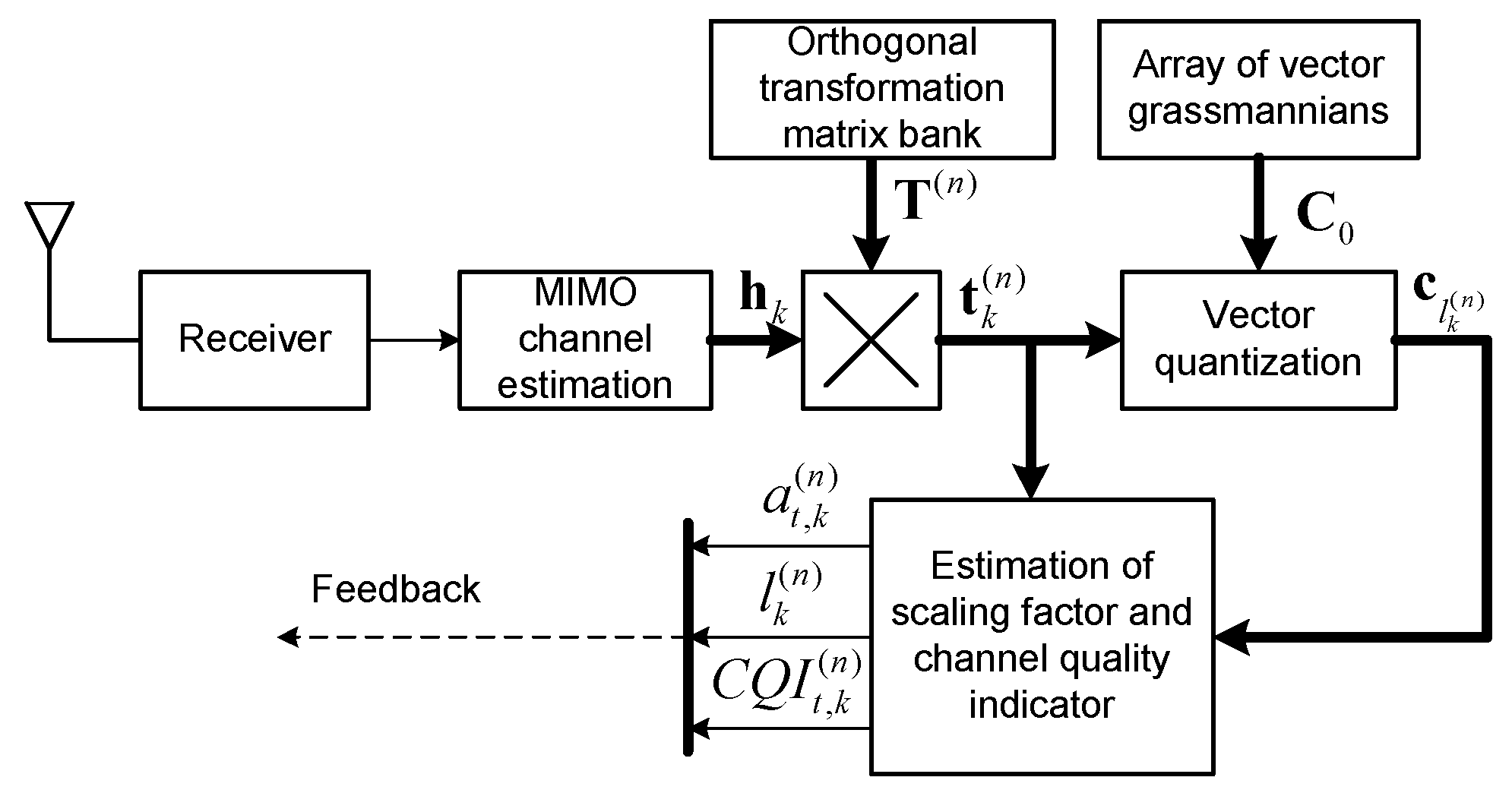
Block diagrams of the main processing stages on the BS side and on the MS side according to the proposed algorithm (equations (18), (19), (22), (28)), are shown on Figure 1 and Figure 2. Figure 2 additionally uses designations for the parameters of selected users: $b_{k,sel}^{\left(i\right)}$ - i-th bit for k-th user, $\left({\tilde{\mathit{h}}}_{k,sel}^{\left(n\right)},v_{k,sel}^{\left(n\right)}\right)$ - vector estimate and variance of these estimates for k-th user, where $k$ in this case there is the number of the selected user, which belongs to the set $k\in {\mathbb{K}}_{sel}$. Blocks designated as “Mx” perform combining function of symbols streams transmitted and pilot signals.

Thus, the following precoding algorithm is proposed for MU-MIMO system, which can be written in steps on the MS side and BS side (all these steps are repeated at each $n$ -th cycle of receiving new CSI from the MS side).

Algorithm 1. Algorithm a for cyclic accumulation and correction of channel vectors estimates in MU-MIMO system

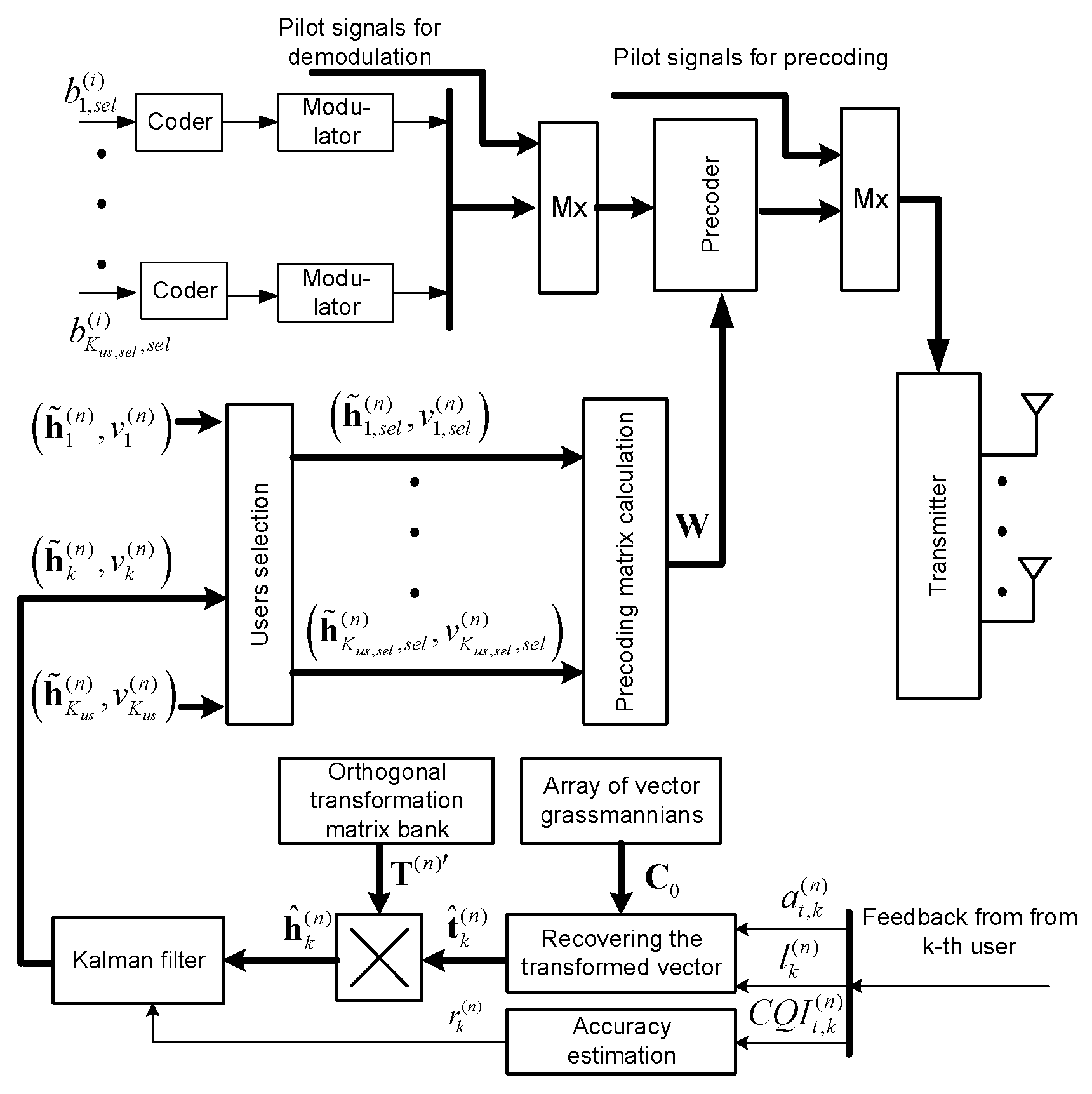
MS side Channel vector ${\mathit{h}}_{\mathit{k}}$ estimation using pilot signals. Channel vector transformation ${\mathit{t}}_{\mathit{k}}^{\left(\mathit{n}\right)}={\mathit{h}}_{\mathit{k}}{\mathit{T}}^{\left(\mathit{n}\right)}$ . Quantization of the transformed vector and calculation of parameters ${\mathit{\alpha }}_{\mathit{t},\mathit{k}}^{\left(\mathit{n}\right)},{\mathit{l}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ and quality of quantization parameter $\mathit{C}\mathit{Q}{\mathit{I}}_{\mathit{t},\mathit{k}}$ according to (18). Transmission of parameter values ${\mathit{\alpha }}_{\mathit{t},\mathit{k}}^{\left(\mathit{n}\right)},{\mathit{l}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ and $\mathit{C}\mathit{Q}{\mathit{I}}_{\mathit{t},\mathit{k}}$ via feedback channel.

BS side The base station, in accordance with(22), forms rough estimate ${\widehat{\mathit{h}}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ of channel vectors ${\mathit{h}}_{\mathit{k}}$ based on the current CSI received via feedback channel from the MSs. Using previous estimates ${\tilde{\mathit{h}}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ (in previous cycles), the BS performs correction of channel vector estimates for all MSs using Kalman filter (28). The estimates of channel vectors ${\tilde{\mathit{h}}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ and variance ${\mathit{v}}_{\mathit{k}}^{\left(\mathit{n}\right)}$ of their estimation error obtained as a result of filtering (cyclic correction and accumulation) are used to select users (according to condition (12)) and calculate the precoding matrix (10) taking into account normalization (8).

7. Simulation Results

To confirm the effectiveness of the proposed precoding algorithm with quantization, accumulation and correction of CSI, and user selection in the MU-MIMO system (equations (18), (19), (22), (28)), computer simulation was performed in the MATLAB system. The performance comparison was based on noise immunity and system capacity. The simulation parameters are listed in Table 1. Moreover, we considered a scenario where the maximum number of users was equal to the number of spatial channels, i.e. $K_{us}=K_{ch}$, and each user had one receiving antenna. The noise immunity characteristics were investigated for a fixed number of users equal to the maximum possible number $\left(K_{us,sel}=K_{ch}\right)$, with different number of transmission cycles on the feedback channel. The object for comparison was a precoding algorithm based on Grassmanian codebooks [23,24], which coincides with the algorithm described in this article (18)-(19), (22), (28), but doesn’t use orthogonal transformation before choosing the codeword. This algorithm corresponds to the case of the proposed precoding approach for n = 1 using Grassmanian codebook of the same size.

As the base orthogonal matrix ${\mathit{T}}_0$ selected permutation matrix was used for transformation to ensure the maximum repetition period, i.e. ${\left({\mathit{T}}_0\right)}^n={\mathit{I}}_{N_{tx}}$, only for $n=i{N}_{tx},i=\mathrm{1,2},3,...$

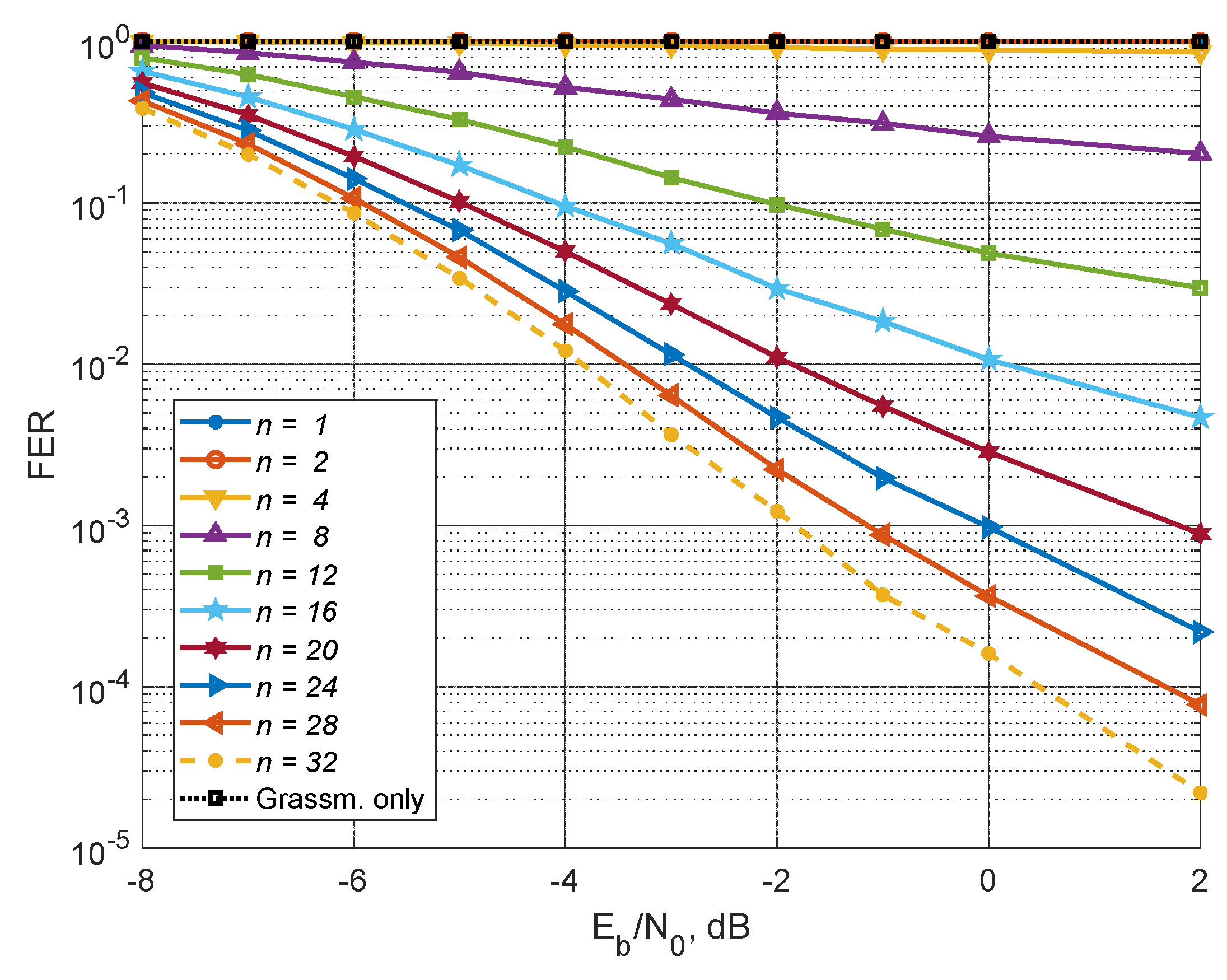
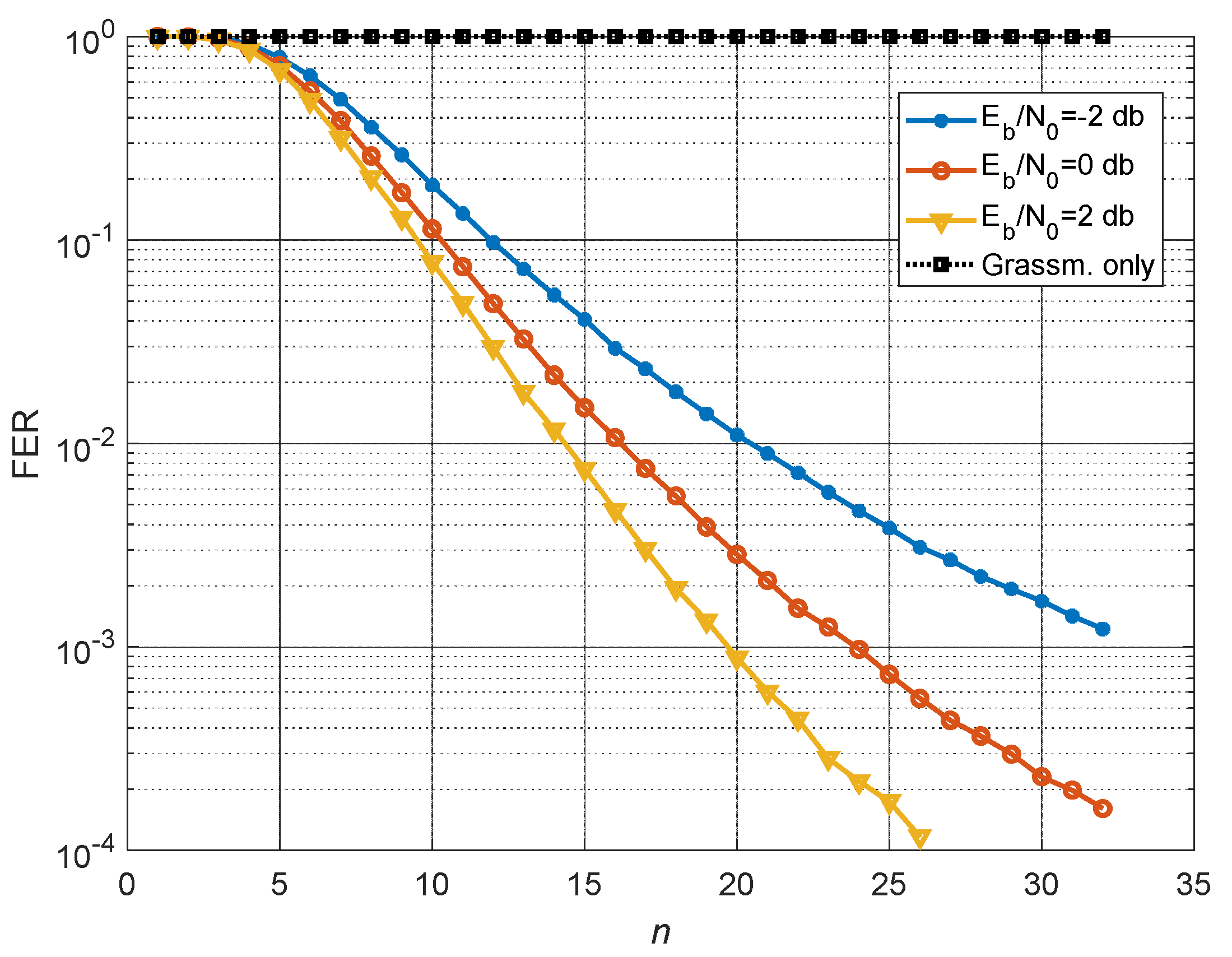
As a result of the simulation, curves were obtained (Figure 3), showing the dependence of the Frame Error Rate (FER) with channel coding versus Signal-to-Noise Ratio (SNR) per bit for different numbers of CSI information transmission cycles on feedback channel for the number of users served equal to the maximum number ($K_{us,sel}=32$). Figure 4 shows FER dependencies on the number of cycles for different SNR ​​ per bit values. It should be noted that the known precoding algorithm with the Grassmannian codebook is ineffective in this case. Its characteristics coincide with the characteristics of the proposed algorithm for n = 1 and each subsequent transmission over feedback channel does not improve the accuracy of the CSI.

From the above Figures it can be seen that, starting from the 4-th cycle, for the proposed algorithm, each new cycle of quantized CSI transmission from MSs to BS leads to a gradual improvement in the noise immunity characteristics of the MU-MIMO system, which confirms the effectiveness of the proposed precoding algorithm with CSI accumulation and correction of MIMO channel matrix estimates. The above Figures show that for all 32 users, the FER=0.01 level is achieved at 16-th cycle with SNR=0 dB, and FER=0.001 is achieved at 20-th cycle with SNR=2 dB, and when the number of cycles increases to 32, the energy efficiency increases by 4 dB for both FER values.

These simulation results confirm the effectiveness of the proposed precoding algorithm with CSI accumulation and correction of MIMO channel matrix estimates for a fixed number of active (served) users. However, of greater interest is the use of this approach in dynamic users selection scenario, where upon receipt of each new CSI transmission over the feedback channel, the channel matrix estimates are refined and the number of users selected to organize communication in the downlink increases. For this purpose, a preliminary simulation of the MU-MIMO system was carried out with different numbers of selected users. For each fixed number of users, the minimum number of transmission cycles on the reverse channel was determined to ensure the same FER=0.01 with approximately the same SNR ratio. Moreover, the approximate SNR value for the maximum number of selected users $K_{us,sel}=32$ was chosen.

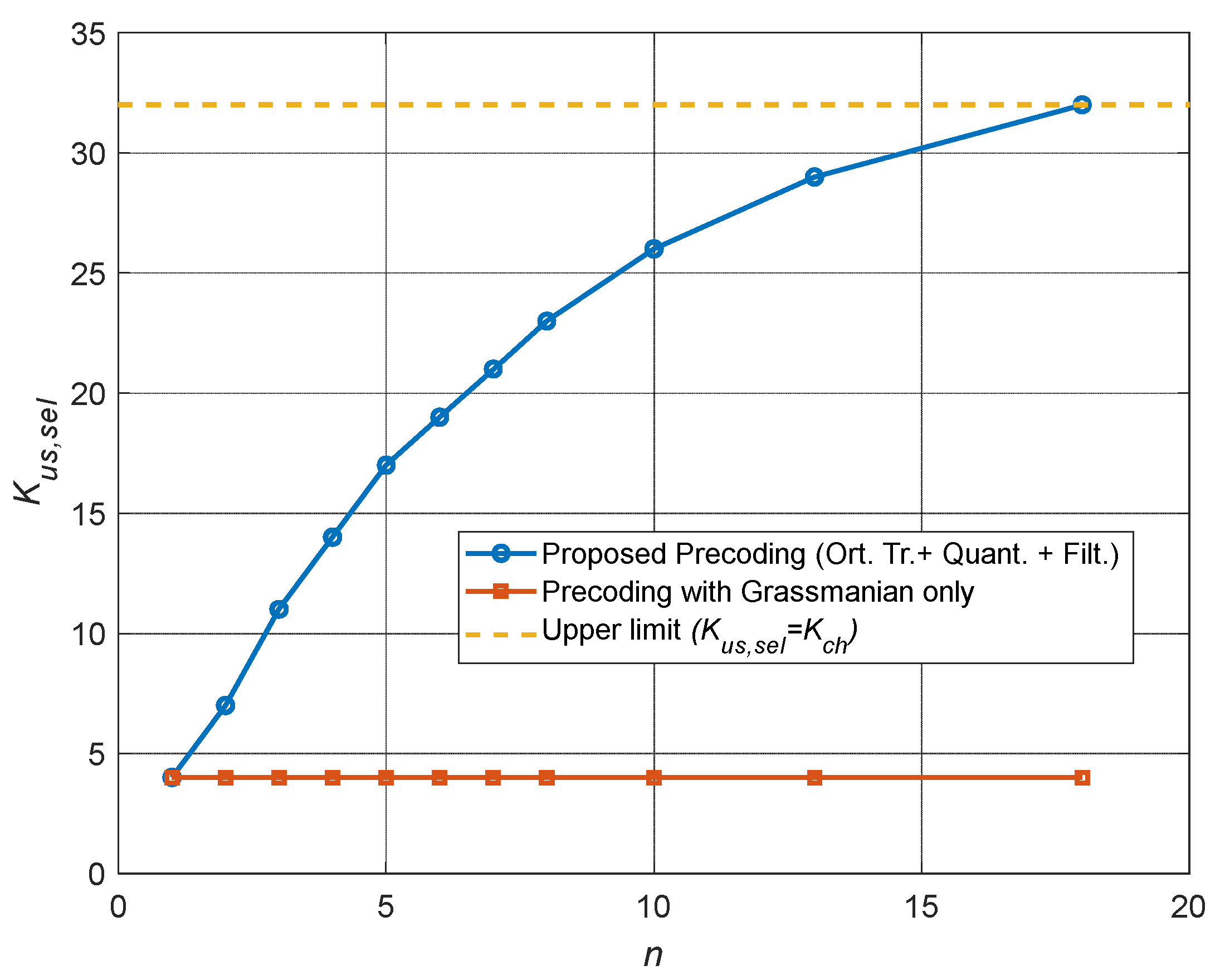
Figure 5 shows the dependence of the selected users number $K_{us,sel}$ on the cycle number $n$ (feedback channel transmission) for the proposed algorithm (curve marked ‘Proposed Precoding (Ort.Tr.+Quant.+Filt.)’), i.e. with orthogonal transformation of the channel vector, quantization and additional filtering of the quantized channel estimates. It also shows: the dependence for known precoding algorithm with single Grassmanian codebook (‘Precoding with Grassmanian only’), which is a horizontal line and does not depend on n, and the upper bound of selected users number $K_{us,sel}$ determined by channels number $K_{ch}$. Here we can see that compared to the single-codebook precoding algorithm, the proposed approach allows to consistently increase the number of active users from 4 to a maximum number of 32 in 18 cycles.

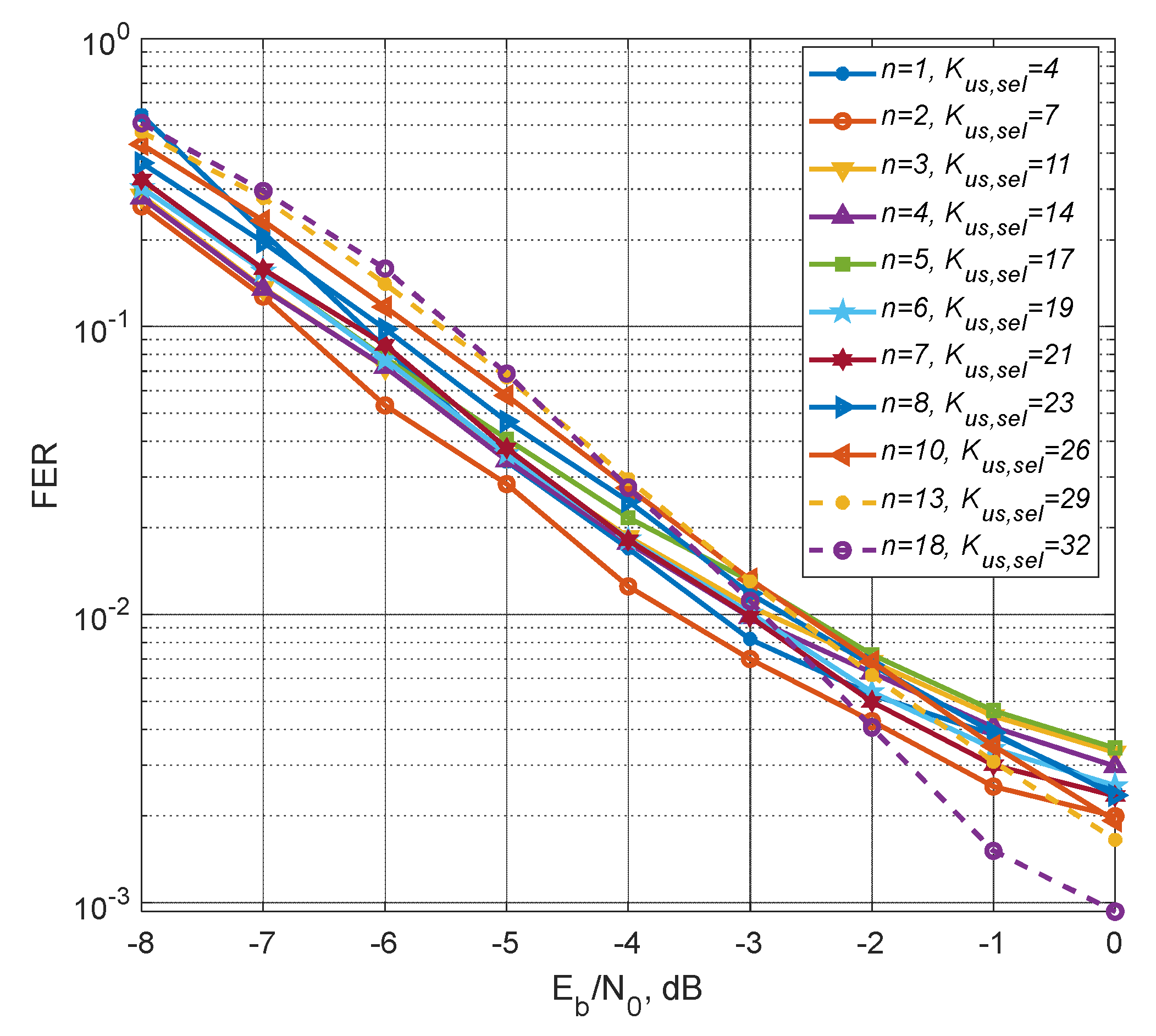
Figure 6 shows the dependencies of FER on SNR ratio per bit for different number of cycles and different number of selected users. These curves show that the noise immunity characteristics change insignificantly with a simultaneous increase in the number of cycles and the number of users, the spread of the noise immunity characteristics is ~ 1 dB at FER=0.01 (1%) level. Moreover, compared to simple precoding with one codebook (the characteristic coincides with the curve for n=1), there is an eightfold increase in the number of users for 18 CSI transmission cycles on the feedback channel.

8. Conclusions

The proposed precoding algorithm with quantization, CSI accumulation and correction, and user selection in MU-MIMO system (equations (18), (19), (22), (28)), can be used for dynamic downlink user selection in MU-MIMO systems with a large number of antennas (5G and B5G). By using special orthogonal transformations before quantization, the CSI at the BS side can be incrementally updated and improved without increasing the capacity of feedback channel. As the quality of the MIMO channel estimates improves, the number of active users supported by the MU-MIMO system grows and reaches the maximum number of users determined by the spatial resources allocated in the Massive MIMO system.

The proposed algorithm fits well with the algorithm for correcting estimates of the wireless communication channel, since the newly arriving channel state information through the feedback channel to the BS allows, at the same time, to refine the insufficiently accurate channel estimates previously obtained, as well as to correct them taking into account the change in the channel state for each user. Thus, the proposed approach for organizing communication with precoding, compared with the conventional precoding algorithm based on the use of codebooks, allows for a gradual increase in the number of active users and the achievement of precoding efficiency in MU-MIMO systems, but without increasing the transmission rate on the feedback channel.

In the future work, we plan to continue the study of the precoding approach with dynamic user selection, especially the influence of the total number of users requesting service in the Massive MIMO system on the speed of reaching the maximum number of active users, and also to consider scenarios when the total number of users in the MU-MIMO system exceeds the number of available spatial channels.