Optimizing Virtual Power Plants with Parallel Simulated Annealing on High-Performance Computing

1. Introduction

The increasing penetration of distributed energy resources (DERs), including renewable energy sources (RES) like wind and solar, presents both opportunities and complexities in managing modern power systems. VPPs have emerged as a powerful framework to integrate and coordinate DERs for enhanced grid stability, economic efficiency, and active participation in energy markets [1,2].

VPPs act as single aggregated entities, facilitating seamless interaction with the grid. They coordinate diverse energy sources, such as RES, electric vehicles (EVs), and energy storage systems (ESS) [3,4]. In the context of Smart Cities, VPPs serve as dynamic facilitators of decentralized energy management by aggregating DERs to balance supply and demand, reduce carbon emissions, and enhance energy efficiency [5]. By integrating advanced technologies like Vehicle-to-Grid (V2G), VPPs can provide ancillary services, improve grid resilience, and enable smart energy systems tailored to urban environments [6]. These systems also allow urban planners to optimize energy flows by leveraging real-time data from interconnected devices, including smart streetlights and EV charging stations, thus promoting sustainable urban development [7].

However, optimizing the scheduling and operation of VPPs poses substantial challenges due to the uncertainties associated with RES generation, load demand, and market prices. These challenges necessitate sophisticated optimization strategies that can balance the supply-demand dynamics while maximizing economic and social benefits for VPP participants [8,9]. As a central component of Smart City initiatives, VPPs must navigate the complexities of integrating diverse energy resources while maintaining operational flexibility and economic viability. The integration of EVs as mobile DERs adds further complexity, as their charging and discharging schedules impact not only grid stability but also the broader urban energy ecosystem [10,11].

Given the computational intensity of these tasks, especially for large-scale networks, leveraging High-Performance Computing (HPC) and heuristic approaches like Simulated Annealing (SA) becomes crucial for achieving efficient and scalable optimization.

Traditional optimization techniques, such as Mixed-Integer Linear Programming (MILP), often struggle to address the scalability and complexity requirements of large-scale VPP scheduling problems, especially under real-time constraints [12,13]. As the scale of VPPs grows, both in terms of the number of DERs and the sophistication of market mechanisms, there is a compelling need for robust optimization techniques capable of handling these demands efficiently [14]. Consequently, heuristic and metaheuristic methods, notably SA, have gained attention for their flexibility and effectiveness in navigating complex solution spaces typical in VPP scheduling [15,16].

SA, a stochastic optimization method inspired by the annealing process in metallurgy, has been widely applied to solve non-linear, multidimensional, and constraint-heavy optimization problems [17,18]. In VPP contexts, SA proves valuable in managing energy dispatch, balancing energy acquisition and storage usage, and optimizing market participation [14,19]. Recent research demonstrates that SA is effective in achieving competitive results in VPP scheduling, particularly when integrated with Demand Response (DR) programs and various DERs, including RES and storage units [9,16]. Nevertheless, standalone SA approaches can face scalability issues in large VPP configurations involving numerous DERs and complex market constraints [13,20].

To address these scalability constraints, researchers have turned to HPC to facilitate parallelized versions of SA. Parallel computing, with advancements in both hardware and software platforms, has shown significant potential in accelerating optimization processes and handling the extensive data required for real-time VPP scheduling [13,21]. HPC-enabled parallel SA implementations allow decomposition of large-scale optimization problems into manageable subproblems, enhancing computational efficiency while maintaining solution quality [22]. By leveraging multi-threading, parallel SA algorithms reduce convergence times and enable the management of large VPP networks, making it feasible to optimize energy acquisition and dispatch at a high temporal resolution [23]. The role of HPC in enabling real-time VPP optimization extends beyond simple computational speed-ups. Parallelized SA studies show that HPC systems efficiently manage complex scheduling by processing detailed, time-sensitive data in real-time. [20,24]. This capability is particularly valuable for VPP operators who must respond dynamically to fluctuations in renewable generation, load demand, and market conditions [25]. Moreover, parallel SA-based approaches enable simultaneous evaluation of bidding strategies for VPPs, streamlining decision-making processes within local energy markets [22].

This paper introduces a novel parallelized SA algorithm for VPP scheduling, implemented on HPC infrastructure using OpenMP. The model focuses on maximizing social welfare while respecting operational constraints, such as battery degradation and DER variability. This approach aims to achieve near-optimal scheduling solutions by leveraging parallelization to improve computational speed and solution quality. Through rigorous simulations, we demonstrate the effectiveness of our method in reducing optimization time while maintaining high-quality solutions across various VPP configurations [16,18].

The structure of this paper is designed to offer a comprehensive and sequential examination of our proposed approach. In  Section 2, we begin by reviewing recent literature on Virtual Power Plant (VPP) optimization, applications of SA in energy resource management, and the critical role of HPC in enhancing optimization strategies. This foundation sets the stage for  Section 3, where we outline the problem description and mathematical formulation of the VPP scheduling challenge. Within this section, a tailored search space representation is derived to address the specific requirements of parallelized algorithm design, and we introduce a customized parallel SA algorithm that efficiently navigates this search space by leveraging HPC capabilities.

Subsequently, the  Section 4 section details the parameter tuning and parallelization techniques used to maximize the algorithm’s performance, including an in-depth overview of the HPC environment configurations and essential parameters employed for the design of experiments.

We analyze the computational and scheduling outcomes in  Section 5, emphasizing the scalability and solution quality achieved with the parallelized SA approach. This analysis provides insights into the performance gains enabled by the HPC-enhanced framework. Finally, in  Section 6, we summarize our findings, highlighting the implications of this approach for advanced VPP scheduling and potential directions for future research in optimization and HPC applications in energy systems.

2. Related Works

The development of VPPs has become essential in modern power systems due to their ability to integrate DERs such as renewable energy sources (RES), electric vehicles (EVs), and energy storage systems (ESS). Effective VPP optimization frameworks are critical to ensuring these resources contribute positively to grid stability, operational efficiency, and market participation. This section examines recent methodologies and advancements in VPP optimization, focusing on approaches aimed at achieving effective scheduling, energy management, and market alignment for VPPs.

2.1. Optimization Strategies for Virtual Power Plants

A wide range of optimization strategies has been developed for VPPs, to integrate DERs while ensuring operational efficiency and profitability. Optimization techniques for VPPs include heuristic and metaheuristic methods, game-theoretic approaches, and multi-objective optimization models. [1] presents a categorization of 65 VPP optimization strategies, highlighting methods that integrate RES and energy storage. The study shows that combining wind power with demand response effectively mitigates intermittency challenges, making VPP scheduling more resilient. Additionally, VPPs have been identified as a critical strategy for integrating distributed energy resources into smart city power systems. Comprehensive reviews [5] emphasize the use of hierarchical control techniques and secure communication networks to manage DERs and energy storage systems effectively. These approaches enable demand-side frequency control ancillary services (D-FCAS), enhancing grid stability and supporting the development of sustainable energy systems [7]. Similarly, surveys on microgrid, smart grid, and VPP technologies [26] highlight the role of advanced control mechanisms and technical solutions in achieving energy sustainability. The integration of these technologies is vital for balancing operational efficiency with environmental goals in smart cities [27]. By leveraging advanced market mechanisms, VPPs facilitate participation in energy markets while balancing electricity supply and demand in dynamic smart grid environments [10].

The role of game theory in VPP optimization is particularly notable for its ability to handle the interactions between multiple prosumers in a VPP, allowing for dynamic energy scheduling that aligns generation and consumption with real-time pricing. For example, [8] demonstrates a game-theoretic model that successfully enhances VPP operations with prosumer participation, resulting in optimal payoff distribution across both residential and commercial VPP users. Such approaches underscore the flexibility required in VPPs to adapt to market fluctuations and DER uncertainties.

Multi-level and multi-objective optimization frameworks are also prominent in VPP scheduling, enabling VPPs to balance competing objectives like cost minimization, emission reduction, and customer satisfaction. [4] proposes a multi-level, multi-objective optimization model that leverages advanced algorithms to achieve effective load scheduling, energy cost reduction, and greenhouse gas minimization within VPPs. The approach, which applies algorithms like AMO-GWO, demonstrates the capability of advanced optimization frameworks to incorporate various real-time constraints while enhancing VPP performance.

To address the need for real-time adaptability in VPPs, researchers have developed hierarchical and adaptive optimization models. [28] explores an energy management approach using a teaching-and-learning-based optimization (TLBO) algorithm, showing that it can effectively minimize VPP operating costs. The TLBO-based model is particularly effective for optimizing over a 24-hour horizon, which is useful for applications that require short-term energy management and quick decision-making. Similarly, [29] introduces an adaptive, predictive energy management strategy that combines model predictive control (MPC) with feedback correction to optimize real-time VPP operations, improving both economic outcomes and grid stability by effectively handling uncertainties.

Robust optimization frameworks are also widely applied in VPP scheduling to handle the uncertainties associated with RES and fluctuating market conditions. For instance, [30] discusses a robust scheduling model for VPPs that uses a receding horizon dispatch approach, maximizing revenue while managing system and market uncertainties in a three-stage optimization framework. The methodology was validated in a real-world case study, demonstrating its effectiveness in maximizing VPP flexibility and revenue under uncertain operating environments.

Furthermore, multi-scale and multi-time-scale approaches enable VPPs to coordinate their operations over varying timeframes. [31] proposes a multi-time-scale scheduling strategy that aggregates and disaggregates deferrable loads in a VPP, enabling more effective participation in both energy and reserve markets. This strategy addresses the scheduling complexity of handling deferrable loads, achieving economic efficiency while maintaining operational reliability in VPP systems.

Finally, innovative bidding strategies are being developed to improve VPP profitability in competitive energy markets. For example, [32] proposes a coordinated bidding and operation model for VPPs, focusing on optimizing energy storage and demand response integration. By incorporating robust optimization techniques, the model adapts to uncertain energy prices and RES variability, demonstrating improved profit margins in both day-ahead and real-time markets.

Collectively, these studies highlight the diverse strategies available for VPP optimization, each offering unique contributions to the challenges of managing DERs and maximizing VPP efficiency. With advances in computational techniques and algorithmic frameworks, the VPP paradigm continues to evolve, providing effective solutions for integrating renewable resources and managing demand in modern energy systems.

SA is a metaheuristic optimization technique extensively applied in energy resource management for VPPs due to its ability to handle complex, multidimensional problems effectively. SA, inspired by the physical annealing process, operates by probabilistically accepting suboptimal solutions in the early stages of the optimization process, thus allowing the algorithm to escape local optima and explore the global solution space more comprehensively [9]. This characteristic makes SA well-suited to the non-linear, constraint-heavy nature of VPP scheduling, especially where DERs and market fluctuations contribute to significant uncertainties.

In recent years, researchers have leveraged SA in VPP contexts to address various challenges in energy dispatch, demand response integration, and grid stability. For instance, one study demonstrated that integrating SA with a custom heuristic improved the handling of electric vehicles (EVs) as distributed energy resources, optimizing charging and discharging schedules to enhance grid stability and maximize economic benefits for VPP operators [33]. Another application of SA in VPPs involved energy management systems that incorporate demand response strategies, showcasing SA’s capacity to adjust for demand fluctuations and reduce energy costs effectively. In simulations, the SA-based approach outperformed particle swarm optimization and other deterministic methods, indicating its robustness and adaptability under varying network conditions [34].

Furthermore, researchers have applied SA to optimize bidding strategies in electricity markets, with studies illustrating how SA-based algorithms can enhance the profitability of VPPs by strategically timing energy transactions [35]. By dynamically adjusting the bidding behavior based on real-time market data, SA-driven optimizations have demonstrated improvements in computational efficiency and revenue maximization, solidifying SA’s relevance in competitive energy markets.

In addition to market participation, SA has proven effective in addressing the dynamic economic dispatch problem within VPPs, particularly when integrating renewable resources such as wind energy. By accommodating the intermittent nature of renewable energy sources, SA-based algorithms can minimize generation costs and maximize social welfare, showcasing their potential for sustainable energy management [36]. Studies implementing SA in economic dispatch frameworks have achieved lower generation costs and increased utilization of renewable resources, demonstrating SA’s capacity to adapt to the evolving energy landscape and support sustainable energy goals.

The adoption of SA in energy resource management for VPPs thus highlights its versatility and efficacy across various operational scenarios. Its adaptability to real-time conditions and robustness in handling uncertainty positions SA as a crucial tool in the pursuit of optimized, resilient, and profitable VPP operations.

2.2. Parallel Computing for VPP Optimization

The computational complexity of Virtual Power Plant (VPP) optimization has driven interest in HPC and parallel computing methods as viable solutions to scale optimization processes effectively. Traditional optimization methods often fall short under the real-time constraints imposed by the dynamic and large-scale nature of VPPs, particularly as they expand in terms of DERs, market participation, and operational requirements [20]. Parallel computing, supported by HPC infrastructure, has demonstrated significant potential in accelerating optimization processes and enhancing solution quality, especially in VPP applications that require frequent adjustments based on real-time data.

A variety of studies have investigated parallel computing as a tool for addressing the high-dimensional optimization problem in VPPs. For instance, [23] explored the application of parallel processing in security-constrained optimal power flow analysis (SCOPF), demonstrating that parallelized models could reduce computational time without sacrificing solution quality. These methods are relevant in VPP contexts where security and contingency planning are essential for reliable grid integration.

Research has also highlighted the role of parallel computing in supporting stochastic and scenario-based optimization frameworks that manage uncertainty within VPP operations. A scalable framework for stochastic optimization of complex energy systems, as presented in [13], leveraged parallel interior-point methods to solve large-scale dispatch problems involving wind power, achieving significant scalability and efficiency improvements. This framework underscores the value of HPC-enabled optimization in VPP scheduling, where DER variability and market fluctuations pose challenges to deterministic methods.

Another promising application of parallel computing for VPPs is in demand response and market participation. Utilizing exhaustive search through parallel computing, [22] investigated bidding strategies for local energy markets, finding that metaheuristic approaches achieved near-optimal results within acceptable computational timeframes. These findings suggest that parallel processing can enhance the effectiveness of VPPs as market participants, providing competitive pricing and efficient resource allocation.

High-performance computing platforms such as the PIPS-IPM solver, as documented in [21], have enabled real-time stochastic optimization of power grids with large-scale variables, further validating the role of parallel architectures in solving computationally intensive VPP scheduling tasks. The application of HPC here not only supports rapid decision-making but also enhances grid stability by enabling VPPs to respond dynamically to load changes, renewable generation variability, and price signals.

Parallel computing approaches, when combined with adaptive optimization algorithms like SA, provide additional avenues for scaling VPP optimization. Hybrid methods incorporating SA with parallel processing have shown efficacy in handling the multidimensional, constraint-heavy optimization requirements inherent to VPPs, as demonstrated by [9]. This integration allows for distributed problem-solving, whereby each node in the HPC cluster optimizes a subset of the VPP’s DERs, leading to faster convergence and higher-quality solutions in comparison to serial approaches.

In summary, parallel computing represents a transformative approach for VPP optimization, especially as DER penetration increases and real-time market responsiveness becomes critical. Through multi-threading, distributed computation, and advanced parallel algorithms, VPP operators can efficiently schedule and manage a large network of DERs, ultimately contributing to a more flexible and responsive power grid.

2.3. Role of High-Performance Computing (HPC) in Advanced VPP Scheduling

The integration of HPC into Virtual Power Plant (VPP) scheduling represents a significant step forward in managing the complexities associated with large-scale energy systems. With the growing penetration of DERs and the increasing demand for responsive, dynamic power systems, HPC provides the computational power needed to enable real-time scheduling and management of VPPs. Researchers have demonstrated that HPC infrastructure can drastically enhance the scalability of optimization algorithms in energy systems, allowing for the decomposition of large-scale VPP scheduling tasks into manageable subproblems [20,21]. This scalability is crucial for maintaining solution quality as VPPs incorporate diverse and variable energy sources such as wind, solar, and electric vehicles (EVs) while adhering to market constraints.

Parallel computing frameworks, particularly those leveraging HPC clusters, have been applied to VPP scheduling to expedite solution times and handle increased complexity. Studies show that parallelized scheduling algorithms reduce computational times significantly, enabling VPP operators to make near-real-time adjustments based on load demand, renewable generation forecasts, and grid stability requirements [23]. These parallel architectures allow for the simultaneous optimization of multiple objectives, such as cost reduction, system reliability, and carbon emission minimization, which are essential in modern VPP operations [13].

Advanced HPC-enabled stochastic optimization techniques, like those developed for real-time power grid optimization, have also been adapted for VPP contexts. For instance, the PIPS-IPM solver, originally designed for complex power grid systems, has shown efficacy in addressing stochastic dispatch problems by supporting large datasets and processing power-intensive calculations in real-time [21]. This advancement underscores HPC’s role in improving the precision of VPP scheduling, as high-performance solvers facilitate the integration of uncertainty in demand and generation forecasts, ultimately enhancing the robustness of VPP management strategies [22].

Moreover, the use of HPC allows for enhanced simulation and optimization techniques, supporting sophisticated bidding strategies in energy markets. By implementing exhaustive search algorithms and metaheuristic optimization on HPC frameworks, VPPs can simulate a range of market scenarios and derive optimal bidding strategies that maximize profitability under market uncertainty [9]. These HPC-based methods ensure that VPPs remain competitive and adaptive, effectively responding to dynamic market conditions and integrating higher levels of renewable generation [13].

In summary, HPC plays an indispensable role in the evolution of VPP scheduling, enabling high-precision, scalable optimization and real-time responsiveness. The computational efficiency offered by HPC infrastructure is essential for managing the sophisticated requirements of modern VPPs, supporting advancements in scheduling accuracy, flexibility, and market participation.

3. Methodology

3.1. Problem Description

The VPP market optimization service is a critical framework designed to achieve efficient, real-time energy management by orchestrating the interactions between grid demands and prosumer activities. This service comprises two key components: forecasting and optimization. The forecasting component analyzes both real-time and historical data to predict future energy demand, supply trends, and market dynamics, providing the optimization module with essential insights. These forecasts enable the optimization service to determine prosumer schedules that maximize social welfare by balancing energy demand and supply across the VPP network.

At the heart of this optimization framework is the objective of maximizing social welfare through the strategic scheduling of energy transactions for each VPP entity. Each VPP functions as a prosumer, capable of buying or selling electricity to the grid within each period. The optimization service processes both forecasted and real-time data to compute the optimal quantities each prosumer can buy or sell. Importantly, the optimization does not involve price offers from prosumers; rather, it aligns prosumer transactions based on the predetermined price signals issued by the grid, which remain fixed per period.

The system architecture is supported by an Internet of Things (IoT) data streaming platform that facilitates continuous data flow between the prosumer devices and the optimization service. This platform manages the acquisition and storage of data from prosumer devices, including their energy generation, consumption, and battery states. Furthermore, it distributes the optimized scheduling decisions back to prosumer devices in real-time, enabling them to execute the prescribed buy or sell quantities. This IoT-enabled data infrastructure thus supports the real-time decision-making capabilities essential for responsive VPP market operations.

The optimization service operates within a structured ecosystem that includes three primary entities: the grid, the prosumers (VPPs), and the internal VPP market. The grid sets the electricity price per period, while prosumers, restricted to submitting quantity offers, adjust their buy or sell behaviors in response to this fixed pricing. Within the VPP market, the optimization service coordinates these transactions to maximize overall market welfare while satisfying operational constraints. The optimization ensures that the market functions effectively by aligning prosumer activities with grid-imposed conditions to maintain market stability and operational resilience.

The design requirements for this optimization framework are as follows:

• Rolling-based Social Welfare Optimization: The primary goal is to maximize social welfare by scheduling energy transactions in a way that meets the collective needs of the grid and prosumers. This optimization is conducted on a rolling basis, allowing the model to respond dynamically to real-time changes in demand and supply, ensuring alignment with current market dynamics.
• Scalability to Accommodate Expanding Market Demand: The framework must scale efficiently with an increasing number of prosumers, preserving computational efficiency and execution timeliness as the participant count grows. This scalability is essential to uphold the system’s performance standards within an expanding VPP market.
• Battery Health Constraints: To ensure the long-term operational viability of prosumer batteries, the optimization incorporates constraints that regulate battery charge and discharge cycles. These constraints maintain battery states within defined limits, promoting sustainable energy practices and prolonging battery life.
• Grid-Determined Pricing and Quantity-Based Scheduling: In this scenario, electricity prices are determined by the grid, with no price offers from prosumers. The optimization aligns each prosumer’s transactions with these predefined price signals, allowing prosumers to submit only the quantities they can generate or consume. This ensures a streamlined, price-sensitive scheduling approach within the VPP market.

Figure 1. Schematic of VPP management framework for a grid-regulated price environment, illustrating the core components and data flow between prosumers, the VPP market, and the grid. In this scenario, the VPP operates as an intermediary, orchestrating energy trading primarily between the VPP participants (prosumers) and the grid, with energy prices centrally regulated. Prosumers continuously stream real-time data on energy generation, consumption, and battery status to the VPP market via an IoT-enabled data streaming interface. The VPP’s energy management system, which functions as a central scheduler, consists of two principal components: a forecasting module that predicts consumption and generation patterns for VPP players, and an optimization module that dynamically schedules DERs. This scheduling determines optimal quantities for each prosumer to buy, sell, or charge/discharge within a given period, aligning with grid constraints to maximize efficiency and ensure a balanced and reliable energy supply.

Figure 1. Schematic of VPP management framework for a grid-regulated price environment, illustrating the core components and data flow between prosumers, the VPP market, and the grid. In this scenario, the VPP operates as an intermediary, orchestrating energy trading primarily between the VPP participants (prosumers) and the grid, with energy prices centrally regulated. Prosumers continuously stream real-time data on energy generation, consumption, and battery status to the VPP market via an IoT-enabled data streaming interface. The VPP’s energy management system, which functions as a central scheduler, consists of two principal components: a forecasting module that predicts consumption and generation patterns for VPP players, and an optimization module that dynamically schedules DERs. This scheduling determines optimal quantities for each prosumer to buy, sell, or charge/discharge within a given period, aligning with grid constraints to maximize efficiency and ensure a balanced and reliable energy supply.

The VPP market optimization model addresses a complex, dynamic problem that demands a seamless integration of forecasting, data streaming, and adaptive scheduling capabilities. To support the requirements of modern energy systems, this architecture must deliver scalability, real-time responsiveness, and robust data management. By harnessing predictive data and coordinating prosumer activities with established economic and operational constraints, the VPP optimization service strives to enhance market welfare, foster sustainable energy practices, and facilitate agile, market-aligned decision-making in real-world energy management scenarios.

This work aims to develop and evaluate an accelerated SA approach for Virtual Power Plant (VPP) planning and scheduling. The approach leverages OpenMP for parallel execution, significantly improving performance compared to traditional sequential implementations. The optimization problem is modeled as a Mixed-Integer Linear Programming (MILP) problem, integrating integer and continuous decision variables to represent energy acquisition, dispatch, and battery operations.

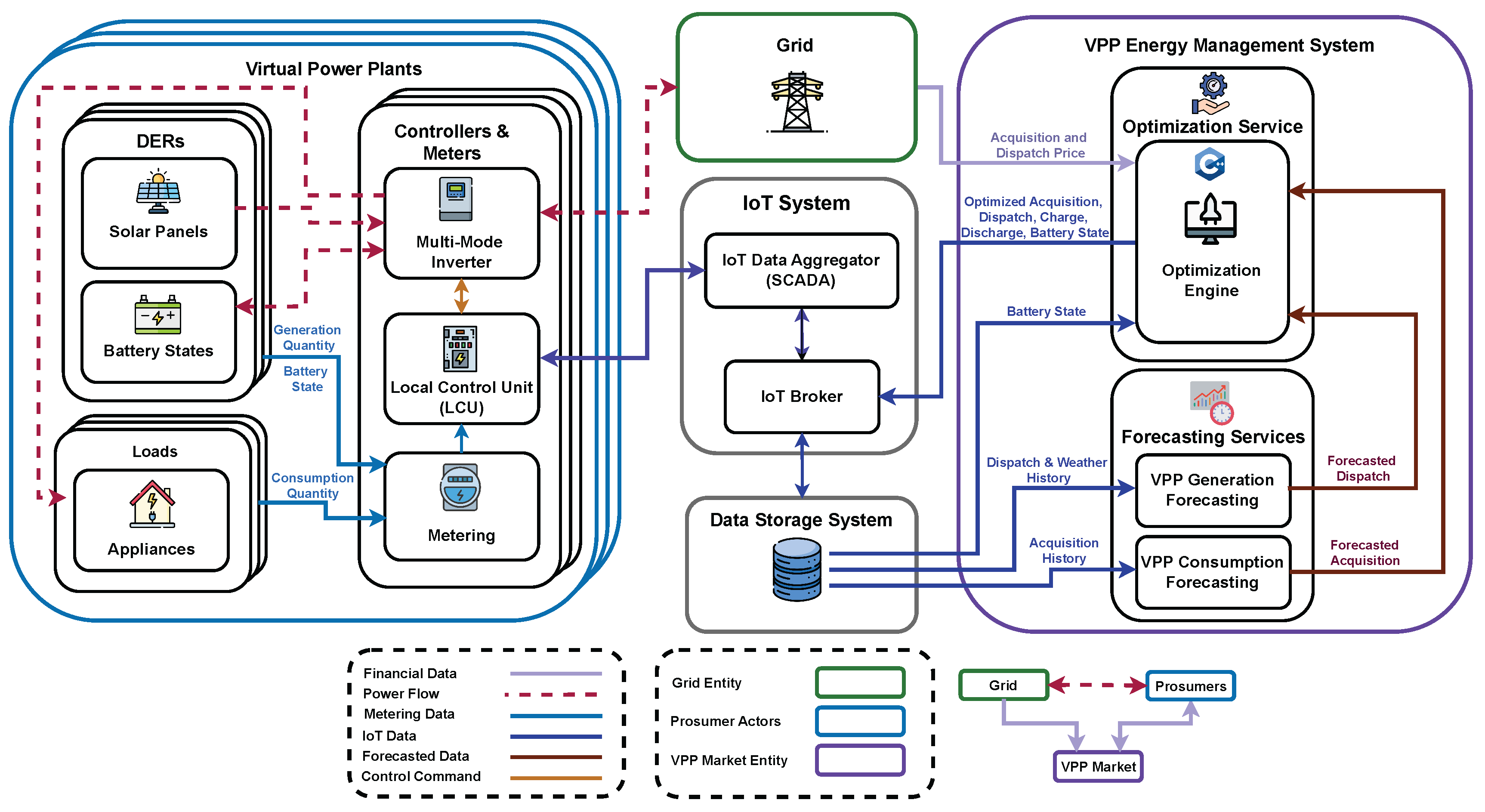
3.2. Problem Formulation

The VPP scheduling problem is modeled as a MILP problem to maximize the social welfare, subject to energy acquisition, dispatch, and battery dynamics constraints.

3.3. Parameters and Variables

The parameters and decision variables essential to the VPP market optimization model are defined in Table 1. These include key parameters like energy prices, battery limits, and time intervals, alongside decision variables governing acquisition, dispatch, and battery charge/discharge activities. The table categorizes each element by type and provides a clear notation for vectors and scalars, supporting an organized approach to modeling the system’s dynamic energy management requirements.

3.3.1. Objective Function

The primary objective is to minimize the total operational costs, which include energy acquisition, dispatch, battery-related costs, and fixed operational costs. The objective function is defined as:

$$\underset{{\mathbf{Q}}_{t,I}^{acq},{\mathbf{Q}}_{t,I}^{disp}}{min}Z=\sum _{t\in \mathcal{T}}\left({\left({\mathbf{Q}}_{t,I}^{acq}\right)}^{\top }{\Pi }_{t,I}^{acq}-{\left({\mathbf{Q}}_{t,I}^{disp}\right)}^{\top }{\Pi }_{t,I}^{disp}\right)\Delta t+\left(C^B+C^{\mathrm{fix}}\right)$$

(1)

3.3.2. Energy Balance Constraints

The energy balance ensures that, at any given time, the total energy input (acquisition, generation, discharge) equals the total output (dispatch, consumption, charge). This is mathematically expressed as:

$${\mathbf{Q}}_{t,I}^{acq}+{\mathbf{Q}}_{t,I}^{gen}+{\mathbf{Q}}_{t,I}^{dch}={\mathbf{Q}}_{t,I}^{disp}+{\mathbf{Q}}_{t,I}^{load}+{\mathbf{Q}}_{t,I}^{ch},\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(2)

3.3.3. Acquisition and Dispatch Decision Constraints

Binary decision variables control whether prosumers acquire or dispatch energy. The following constraints ensure proper acquisition and dispatch decisions:

$$0\le {\mathbf{Q}}_{t,I}^{acq}\le {\overline{\mathbf{Q}}}_{t,I}^{acq}·{\mathbf{\xi }}_{t,I}^{acq},0\le {\mathbf{Q}}_{t,I}^{disp}\le {\overline{\mathbf{Q}}}_{t,I}^{disp}·{\mathbf{\xi }}_{t,I}^{disp}$$

(3)

$$0\le {\mathbf{\xi }}_{t,I}^{acq},{\mathbf{\xi }}_{t,I}^{disp}\le 1,\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(4)

Additionally, the following constraint ensures that acquisition and dispatch actions are not performed simultaneously:

$${\mathbf{\xi }}_{t,I}^{acq}+{\mathbf{\xi }}_{t,I}^{disp}\le 1,\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(5)

3.3.4. Dispatch Breakdown

The energy dispatch ${\mathbf{Q}}_{t,I}^{disp}$ is composed of two parts:

$${\mathbf{Q}}_{t,I}^{disp}={\mathbf{Q}}_{t,I}^{disp,paid}+{\mathbf{Q}}_{t,I}^{disp,non-paid}$$

Where:

• ${\mathbf{Q}}_{t,I}^{\mathrm{disp},\mathrm{paid}}$: Paid energy dispatch at time t.
• ${\mathbf{Q}}_{t,I}^{\mathrm{disp},\mathrm{non}-\mathrm{paid}}$: Non-paid energy dispatch at time t.

The non-paid dispatch is subject to the following constraint:

$$0\le {\mathbf{Q}}_{t,I}^{disp,non-paid}\le {\overline{\mathbf{Q}}}_{t,I}^{non-paid}·{\mathbf{\xi }}_{t,I}^{disp},\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(6)

The variable ${\overline{\mathbf{Q}}}_{t,I}^{\mathrm{non}-\mathrm{paid}}$ is defined as being equal to ∞.

3.3.5. Battery Dynamics

The battery state at $t=1$ is initialized as:

$${\mathbf{S}}_{t,I}^{bat}={\mathbf{S}}_I^{bat,init}+\left({\mathbf{Q}}_{t,I}^{ch}-{\mathbf{Q}}_{t,I}^{dch}\right)\Delta t,t=1,\forall i\in \mathcal{I}$$

(7)

For subsequent time periods, the battery state is updated as:

$${\mathbf{S}}_{t,I}^{bat}={\mathbf{S}}_{t-1,I}^{bat}+\left({\mathbf{Q}}_{t,I}^{ch}-{\mathbf{Q}}_{t,I}^{dch}\right)\Delta t,\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(8)

3.3.6. Charge and Discharge Constraints

Charging and discharging constraints ensure non-simultaneous operations. Binary decision variables ${\mathbf{\rho }}_{t,I}^{ch}$ and ${\mathbf{\rho }}_{t,I}^{dch}$ control charging and discharging:

$$0\le {\mathbf{Q}}_{t,I}^{ch}\le {\overline{\mathbf{Q}}}_{t,I}^{ch}·{\mathbf{\rho }}_{t,I}^{ch},0\le {\mathbf{Q}}_{t,I}^{dch}\le {\overline{\mathbf{Q}}}_{t,I}^{dch}·{\mathbf{\rho }}_{t,I}^{dch}$$

(9)

$${\mathbf{\rho }}_{t,I}^{ch}+{\mathbf{\rho }}_{t,I}^{dch}\le 1,\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(10)

3.3.7. Battery Capacity Constraints

The battery state must remain within its capacity limits:

$$\underline{{\mathbf{S}}_{t,I}^{bat}}\le {\mathbf{S}}_{t,I}^{bat}\le \overline{{\mathbf{S}}_{t,I}^{bat}},\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(11)

3.4. Problem Exploration and Parallel Computation

In the VPP optimization framework, each player i at any time step t must ensure an energy balance among the grid, battery, and their local generation and consumption. Decisions related to energy acquisition (buying) and dispatch (selling) from the grid, as well as battery charging and discharging, are mutually exclusive and subject to upper-bound constraints. This section provides a formal derivation of the energy balance equation, integrating these exclusivity and constraint conditions. It also illustrates how the valid search space, confined to a line rather than a plane, can be efficiently solved in parallel for each player.

3.4.1. Energy Balance with Mutual Exclusivity and Constraints

At any time step t, the energy balance equation for player i can be formulated as:

$${\mathbf{q}}_{t,i}^{\mathrm{acq}}+{\mathbf{q}}_{t,i}^{\mathrm{gen}}+{\mathbf{q}}_{t,i}^{\mathrm{dch}}={\mathbf{q}}_{t,i}^{\mathrm{disp}}+{\mathbf{q}}_{t,i}^{\mathrm{load}}+{\mathbf{q}}_{t,i}^{\mathrm{ch}},\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(12)

Here, ${\mathbf{q}}_{t,i}^{\mathrm{acq}}$ is the energy acquired from the grid, ${\mathbf{q}}_{t,i}^{\mathrm{disp}}$ is the energy dispatched to the grid, ${\mathbf{q}}_{t,i}^{\mathrm{ch}}$ is the energy charged to the battery, ${\mathbf{q}}_{t,i}^{\mathrm{dch}}$ is the energy discharged from the battery, ${\mathbf{q}}_{t,i}^{\mathrm{gen}}$ is the energy generated (e.g., from solar PV), and ${\mathbf{q}}_{t,i}^{\mathrm{load}}$ is the energy consumed by the player’s loads.

3.4.2. Mutually Exclusive Flip-Flop Mechanism for Grid and Battery Operations

The energy interactions with the grid and battery in the VPP model are controlled through a mutually exclusive mechanism, ensuring that at any time t, each player i can either acquire or dispatch energy to the grid, and can either charge or discharge the battery—but never simultaneously. This mutual exclusivity not only maintains coherent energy flows but also prevents contradictory actions.

The conditions governing this mutual exclusivity are as follows:

$${\mathbf{q}}_{t,i}^{\mathrm{acq}}>0\Rightarrow {\mathbf{q}}_{t,i}^{\mathrm{disp}}=0,{\mathbf{q}}_{t,i}^{\mathrm{disp}}>0\Rightarrow {\mathbf{q}}_{t,i}^{\mathrm{acq}}=0$$

$${\mathbf{q}}_{t,i}^{\mathrm{ch}}>0\Rightarrow {\mathbf{q}}_{t,i}^{\mathrm{dch}}=0,{\mathbf{q}}_{t,i}^{\mathrm{dch}}>0\Rightarrow {\mathbf{q}}_{t,i}^{\mathrm{ch}}=0$$

To facilitate this exclusive control, the mechanism operates like a flip-flop. By using binary decision variables, the algorithm effectively "toggles" between states for each operation—either on or off—depending on the player’s action requirements. The flip-flop control ensures that once an energy acquisition action is set (e.g., charging), the opposite action (e.g., discharging) is automatically restricted.

The binary decision variables governing this flip-flop behavior are expressed as:

$${\xi }_{t,i}^{\mathrm{acq}}+{\xi }_{t,i}^{\mathrm{disp}}\le 1,{\rho }_{t,i}^{\mathrm{ch}}+{\rho }_{t,i}^{\mathrm{dch}}\le 1$$

where:

• ${\xi }_{t,i}^{\mathrm{acq}}=1$ enables energy acquisition while setting ${\mathbf{q}}_{t,i}^{\mathrm{disp}}=0$.
• ${\xi }_{t,i}^{\mathrm{disp}}=1$ enables energy dispatch while setting ${\mathbf{q}}_{t,i}^{\mathrm{acq}}=0$.
• ${\rho }_{t,i}^{\mathrm{ch}}=1$ initiates charging while setting ${\mathbf{q}}_{t,i}^{\mathrm{dch}}=0$.
• ${\rho }_{t,i}^{\mathrm{dch}}=1$ initiates discharging while setting ${\mathbf{q}}_{t,i}^{\mathrm{ch}}=0$.

This dual-layered design—mutual exclusivity and flip-flop functionality—ensures that all grid and battery operations remain coherent, maintaining stability within the VPP optimization model.

3.4.3. Upper Bound Constraints on Energy Flows

In addition to mutual exclusivity, the decision variables for energy acquisition, dispatch, charging, and discharging are constrained by upper bounds representing the maximum allowable energy flow in each case:

$$0\le {\mathbf{q}}_{t,i}^{\mathrm{acq}}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{acq}},0\le {\mathbf{q}}_{t,i}^{\mathrm{disp}}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{disp}}$$

$$0\le {\mathbf{q}}_{t,i}^{\mathrm{ch}}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{ch}},0\le {\mathbf{q}}_{t,i}^{\mathrm{dch}}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{dch}}$$

These constraints ensure that the player’s decisions remain within physically feasible limits.

3.4.4. Linearized Energy Balance Equation

To simplify the balance equation, we define two quantities that capture the net energy exchanged with the grid and battery, respectively:

$${\mathbf{X}}_{t,i}={\mathbf{q}}_{t,i}^{\mathrm{acq}}-{\mathbf{q}}_{t,i}^{\mathrm{disp}}(\mathrm{Net}\mathrm{grid}\mathrm{interaction})$$

$${\mathbf{Y}}_{t,i}={\mathbf{q}}_{t,i}^{\mathrm{ch}}-{\mathbf{q}}_{t,i}^{\mathrm{dch}}(\mathrm{Net}\mathrm{battery}\mathrm{activity})$$

Additionally, the net energy difference between the player’s generation and load is defined as:

$${\mathbf{B}}_{t,i}={\mathbf{q}}_{t,i}^{\mathrm{gen}}-{\mathbf{q}}_{t,i}^{\mathrm{load}}(\mathrm{Net}\mathrm{energy}\mathrm{surplus}/\mathrm{deficit})$$

Thus, the energy balance equation can be rewritten in a linear form:

$${\mathbf{Y}}_{t,i}={\mathbf{X}}_{t,i}+{\mathbf{B}}_{t,i},\forall t\in \mathcal{T},\forall i\in \mathcal{I}$$

(13)

Here: - ${\mathbf{Y}}_{t,i}$ represents the player’s net battery activity (charging/discharging). - ${\mathbf{X}}_{t,i}$ represents the net grid interaction (acquisition/dispatch). - ${\mathbf{B}}_{t,i}$ represents the net energy generated or consumed.

This equation captures the player’s energy balance at each time step, ensuring that the battery activity ${\mathbf{Y}}_{t,i}$ equals the available net energy from the grid and the player’s own generation and consumption.

3.4.5. Complete Energy Balance with Constraints

The complete energy balance equation for each player must satisfy both the mutual exclusivity and upper bound constraints. This yields the following system:

$${\mathbf{Y}}_{t,i}={\mathbf{X}}_{t,i}+{\mathbf{B}}_{t,i},-{\overline{\mathbf{q}}}_{t,i}^{\mathrm{disp}}\le {\mathbf{X}}_{t,i}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{acq}},-{\overline{\mathbf{q}}}_{t,i}^{\mathrm{dch}}\le {\mathbf{Y}}_{t,i}\le {\overline{\mathbf{q}}}_{t,i}^{\mathrm{ch}}$$

(14)

The binary decision variables ${\xi }_{t,i}^{\mathrm{acq}},{\xi }_{t,i}^{\mathrm{disp}},{\rho }_{t,i}^{\mathrm{ch}},{\rho }_{t,i}^{\mathrm{dch}}$ ensure that the player’s actions at each time step are mutually exclusive, preventing invalid combinations like acquiring and dispatching simultaneously.

Figure 2. Diagram of search space reduction for each prosumer: The left diagram represents the initial planar 2D search space allocated for each prosumer at each time. Optimization reduces this multidimensional search space to a linear path, simplifying each prosumer’s decision space. The resulting linear search spaces are then confined by specified lower and upper bounds, ensuring all decisions remain within feasible limits while optimizing resource allocation. This reduction enhances computational efficiency, allowing the system to manage larger networks of prosumers in real time.

Figure 2. Diagram of search space reduction for each prosumer: The left diagram represents the initial planar 2D search space allocated for each prosumer at each time. Optimization reduces this multidimensional search space to a linear path, simplifying each prosumer’s decision space. The resulting linear search spaces are then confined by specified lower and upper bounds, ensuring all decisions remain within feasible limits while optimizing resource allocation. This reduction enhances computational efficiency, allowing the system to manage larger networks of prosumers in real time.

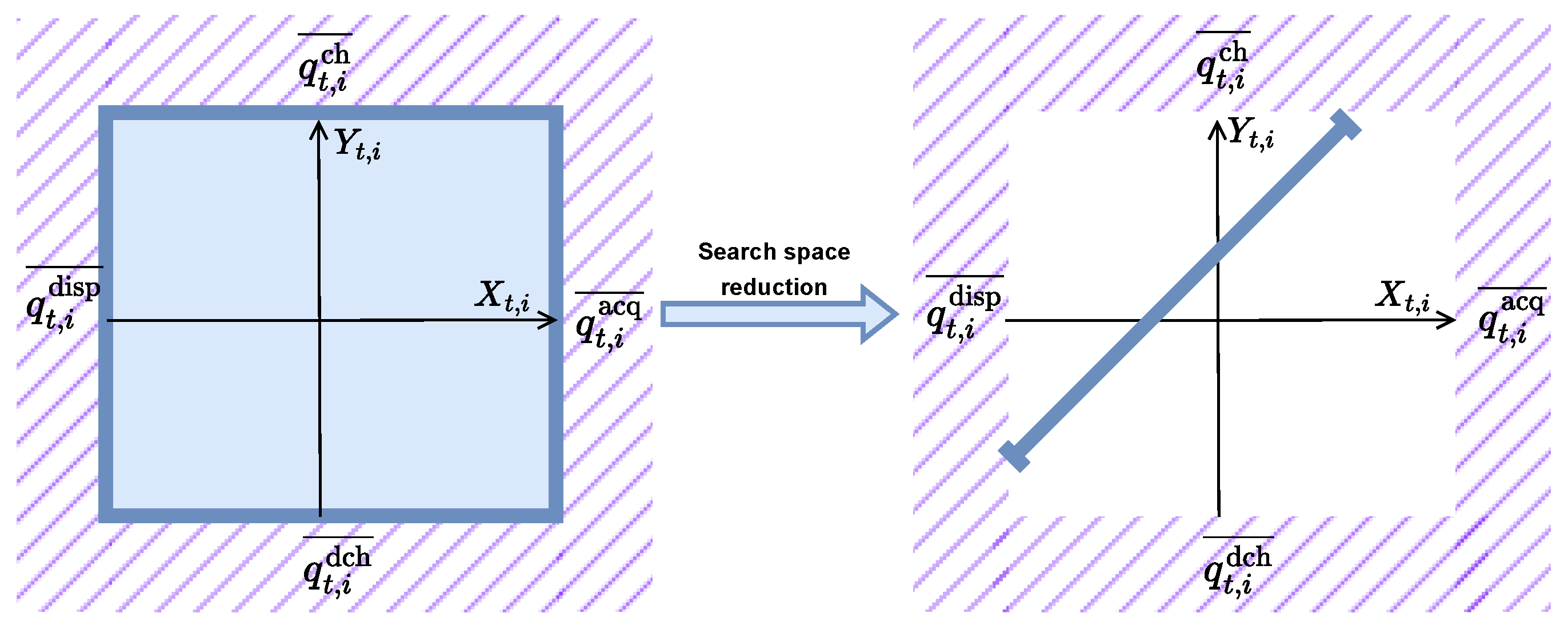
3.5. Solver Design and Algorithm Development

In order to address the VPP scheduling problem with computational precision and efficiency, we implemented two distinct solver approaches: an exact solver based on Mixed Integer Linear Programming (MILP) using Gurobi, and a parallelized SA algorithm. Each solver serves a different purpose: the exact solver is suitable for smaller instances requiring optimal precision, while the SA solver is designed for scalability and efficient performance on larger VPP configurations.

3.5.1. Exact Solver

The exact solver utilizes the Gurobi optimizer to solve the VPP scheduling problem formulated as a Mixed Integer Linear Programming (MILP) model.

Gurobi’s solver engine follows the conventional branch-and-bound method for MILP, incorporating advanced presolve techniques, heuristics, and cuts to expedite the search for an optimal solution within feasible timeframes. This approach ensures that the scheduling model achieves a precise, globally optimal solution.

3.5.2. Parallel Simulated Annealing Solver

While Gurobi, our chosen exact solver, offers robust scalability and efficiency, it is a licensed, paid software. To enhance computational flexibility and support scenarios where an alternative may be advantageous, we implemented a parallelized SA solver. This solver is designed to provide near-optimal solutions swiftly for large-scale VPP scheduling, leveraging adaptive, heuristic-driven search techniques to address the dynamic and complex nature of VPP optimization. SA is a probabilistic heuristic that mimics the physical annealing process, wherein a material is gradually cooled to reach a state of minimal energy. This technique is particularly effective for complex optimization problems with vast solution spaces, as it allows the search to explore beyond local minima, enhancing the likelihood of finding a globally optimal or near-optimal solution.

Our SA approach operates by iteratively adjusting the scheduling decisions for each player over all periods, minimizing the overall operational cost. To achieve scalability, we employed OpenMP to parallelize the optimization process across multiple threads, with each thread handling the scheduling optimization for an individual player. The structure of this parallel SA approach is outlined in Algorithm 1.

The SA process starts with an initial state ${\mathbf{S}}_0$ and a high-temperature $T_0$. This allows the algorithm to explore the solution space effectively by accepting suboptimal solutions, with the acceptance probability guided by the Boltzmann distribution. The acceptance probability decreases as the temperature is lowered, controlled by the cooling rate $\alpha$, leading to a gradual reduction in exploration in favor of exploitation. This process is effective in escaping local minima, thus increasing the chances of identifying a near-optimal solution for the VPP scheduling problem.

Algorithm 1:  Simulated Annealing with Parallel Optimization Using OpenMP

1: Input: Initial state ${\mathbf{S}}_0$, Initial temperature $T_0$, Cooling rate $\alpha$, Perturbation scale $\gamma$, Number of iterations $N_{\mathrm{iter}}$, Number of players $N_i$, Number of periods $N_t$, Battery dynamics, and cost parameters from the input. 2: Output: Best global state ${\mathbf{S}}_{\mathrm{best}}$, Best global cost $Z_{\mathrm{best}}$ 3: Initialize: Shared memory for global best state ${\mathbf{S}}_{\mathrm{best}}$ and global best cost $Z_{\mathrm{best}}$ to store optimization results. 4:    Initialize temperature $T_0$, objective function $Z\left(\mathbf{S}\right)$ for cost calculation. 5: #pragma omp parallel for shared(${\mathbf{S}}_{\mathrm{best}},Z_{\mathrm{best}}$) private(${\mathbf{S}}_i,Z_i,T_i$) reduction(+ : ${\mathbf{Z}}_{\mathrm{best}}$)     // Parallelized loop for each player i 6: for$i=1$ to $N_i$ do     // Each player is solved independently in parallel 7:     Initialize local state ${\mathbf{S}}_i={\mathbf{S}}_0$, local cost $Z_i=Z\left({\mathbf{S}}_i\right)$ 8:     Set ${\mathbf{S}}_{i,\mathrm{best}}={\mathbf{S}}_i$, $Z_{i,\mathrm{best}}=Z_i$, $T_i=T_0$ 9:     Initialize period states for player i across all periods. 10:     Calculate initial battery state $e_{i,t}$ based on input parameters and previous period states. 11:     for $k=1$ to $N_{\mathrm{iter}}$ do     // Iterative optimization process 12:         for $t=1$ to $N_t$do    // Optimize for each period t for player i 13:            Perturb player state ${\mathbf{S}}_i^{\mathrm{new}}$ for period t using $\gamma$ 14:            Compute new balance for the player, update charge/discharge states $q_{\mathrm{ch}},q_{\mathrm{dch}}$ 15:            Calculate new battery state $e_{\mathrm{bat}}^{\mathrm{new}}$ for period t 16:         end for 17:         Compute new cost $Z_i^{\mathrm{new}}=Z\left({\mathbf{S}}_i^{\mathrm{new}}\right)$     // Moved outside of inner loop 18:         Calculate acceptance probability $P=min\left(1,exp\left({\displaystyle \frac{Z_i-Z_i^{\mathrm{new}}}{T_i}}\right)\right)$ 19:         if $r<P$then    // Random value $r\in [0,1]$ 20:            Update ${\mathbf{S}}_i={\mathbf{S}}_i^{\mathrm{new}},Z_i=Z_i^{\mathrm{new}}$ 21:            if $Z_i<Z_{i,\mathrm{best}}$ then 22:                Update ${\mathbf{S}}_{i,\mathrm{best}}={\mathbf{S}}_i,Z_{i,\mathrm{best}}=Z_i$ 23:            end if 24:         end if 25:         Apply cooling schedule: $T_i=\alpha T_i$ 26:     end for 27:     Update global cost $Z_{\mathrm{best}}$ using OpenMP reduction. 28: end for 29: Return: Best global state ${\mathbf{S}}_{\mathrm{best}}$, Best global cost $Z_{\mathrm{best}}$

The use of OpenMP for parallelization allows each player’s problem to be optimized independently, where each thread adjusts player states across all periods based on the balance equation and battery constraints. This parallelized structure greatly reduces computation time and enhances scalability, making the SA highly suitable for large-scale, real-time VPP scheduling scenarios. By leveraging parallel SA, the solver achieves an efficient balance between computational performance and solution quality, supporting adaptive and cost-effective VPP operations in complex energy markets.

As illustrated in Figure 1, the HPC cluster architecture supports this parallelization by assigning each VPP to a separate physical node, where each node independently manages the VPP scheduling optimization process. Using parallel Simulated Annealing (SA) with OpenMP, each node efficiently computes the scheduling optimization, maximizing scalability and computational efficiency to meet the demands of real-time, responsive energy management.

Figure 3. Schematic of the high-performance computing cluster architecture: This diagram illustrates the HPC cluster infrastructure, where each physical node manages the optimization process of an independent VPP. Within each node, a soft computing layer executes parallel SA using OpenMP, enabling efficient parallelization across VPP operations and ensuring optimized scheduling. This configuration enhances scalability and computation speed, supporting real-time VPP management and maximizing energy system responsiveness.

Figure 3. Schematic of the high-performance computing cluster architecture: This diagram illustrates the HPC cluster infrastructure, where each physical node manages the optimization process of an independent VPP. Within each node, a soft computing layer executes parallel SA using OpenMP, enabling efficient parallelization across VPP operations and ensuring optimized scheduling. This configuration enhances scalability and computation speed, supporting real-time VPP management and maximizing energy system responsiveness.

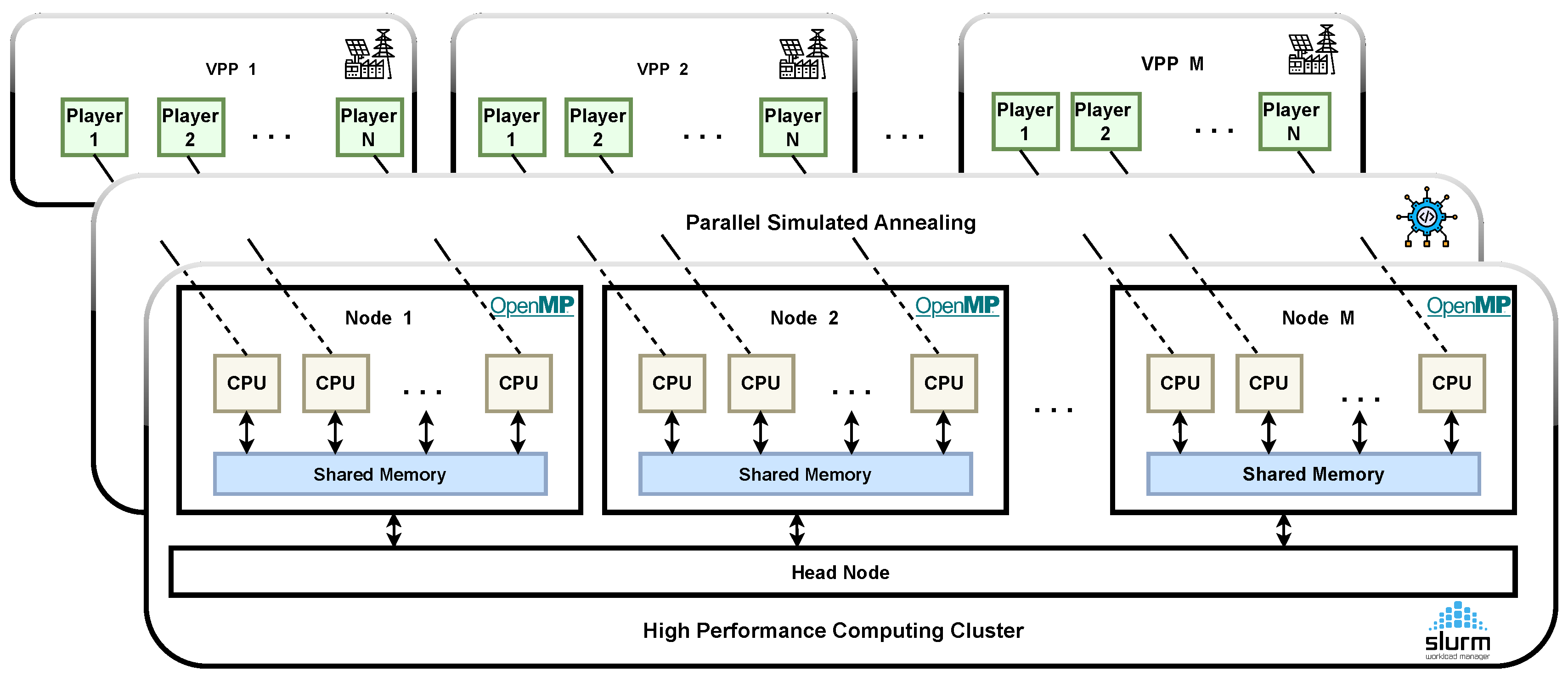
3.6. Experimental Design for High-Performance Computing

The experimental setup is structured to evaluate the computational performance of the parallel SA solver on a HPC infrastructure. The primary aim of these experiments is to assess the scalability and efficiency of the parallel SA algorithm under varying conditions, including the number of computational cores and the scale of the Virtual Power Plant (VPP) market, represented by the number of players (prosumers).

The independent variables in this experimental framework are defined as follows:

• Number of Cores: Experiments were conducted with the number of CPU cores varying from 1 to 32. This range allows us to evaluate the performance gains from parallelization at different levels of computational resources.
• Number of Players (Prosumers): To simulate the scalability of the algorithm in larger VPP markets, we varied the number of players from 32 to 1024. This variable directly influences the complexity of the optimization problem, as each player requires independent state updates and balancing within the SA framework.

The dependent variables, measured as indicators of performance, include:

• Averaged Execution Time (in seconds): This metric records the average time required to execute the SA algorithm across different core and player configurations. By observing how execution time scales with the number of cores and players, we assess the algorithm’s computational efficiency and identify any diminishing returns in speedup with increasing cores.
• Speedup Ratio: The speedup ratio is calculated as the ratio of execution time on a single core to that on multiple cores, providing a normalized measure of performance gain from parallelization. This metric is crucial for understanding the algorithm’s scalability in high-performance environments, particularly for identifying bottlenecks and parallel efficiency under increased core utilization.

Experimental Procedure

Each experiment initialized the SA solver with fixed parameters such as initial temperature, cooling rate, and perturbation scale, selected to balance exploration and precision, ensuring consistency across runs. The HPC environment was configured to allocate exclusive resources per experiment to eliminate variability from resource sharing. We executed the algorithm multiple times for each core-player configuration and recorded the averaged results to account for any fluctuations due to inherent stochasticity in the SA process.

The experiments were designed to simulate real-world VPP scheduling scenarios, where varying numbers of players engage in an energy market. The experimental design provides insights into the absolute and relative performance improvements achievable through parallel computing by systematically increasing the number of players and computational cores. In particular, the speedup ratio highlights the efficiency of the OpenMP-based parallelization as the number of players increases, reflecting the scalability potential of the SA solver in handling larger VPP markets.

Analysis and Interpretation

This experimental framework enables a comprehensive analysis of the SA algorithm’s performance, focusing on both execution time and speedup ratio across configurations. By observing the impact of core and player variations, we can quantify the effectiveness of parallelization in reducing execution time and identify optimal core allocations relative to problem size. This approach provides actionable insights for high-performance VPP scheduling, highlighting the computational gains achievable in complex, large-scale scenarios.

4. Implementation

4.1. HPC Environment Specifications

The virtual power plant scheduling simulations were executed on the Oblivion HPC cluster, consisting of 88 nodes with dual Intel Xeon Gold 6154 processors (36 cores per node) and 192 GB RAM per node, yielding a total of 3168 cores. This configuration provides the computational density and memory bandwidth necessary to support the extensive parallelism in our optimization framework.

The Oblivion HPC cluster provides low-latency communication and high throughput essential for parallelizing VPP optimization. Its multi-core architecture supports the decomposition of the scheduling problem, allowing each prosumer to be solved independently, thus significantly reducing execution time.

To ensure compatibility and optimal performance, GCC 11.3.0 was used in conjunction with Intel-specific optimizations and OpenMP support, tuned to fully exploit the Xeon architecture’s capabilities. This environment setup enabled high-resolution, efficient parallel processing, crucial for the scale and complexity of virtual power plant scheduling.

4.2. Model Parameters and Outputs

This section outlines the essential parameters and outputs for the virtual power plant (VPP) scheduling optimization model. The parameters define the model’s initial conditions and constraints, capturing the technical, operational, and economic aspects critical to effective energy management. The outputs represent the results of the optimization process, providing actionable insights for energy allocation and battery management.

4.2.1. Model Input Parameters

The parameters in Table 2 encompass time-based, operational, and economic factors that influence VPP decision-making. These inputs define the scope and constraints under which the optimization algorithm operates, ensuring that the model is responsive to varying energy demands, generation forecasts, and market conditions.

These parameters enable the VPP scheduling model to adapt to various operating scenarios, addressing both the technical limits and economic aspects of battery storage, energy acquisition, and dispatch. By defining clear boundaries, the model can optimize energy management decisions with precision, ensuring efficient use of resources in alignment with market constraints.

4.2.2. Optimization Outputs

The results produced by the optimization algorithm are detailed in Table 3. These outputs represent the optimized energy management actions for the VPP, covering energy acquisition, dispatch, storage, and cost-effective strategies.

These outputs include critical variables that influence operational decisions, from energy acquisition and dispatch volumes to battery charge and discharge levels. By providing optimized energy transactions and battery state trajectories, the outputs support cost-effective, balanced energy management strategies. The precision of these outputs allows for actionable insights, enabling the VPP to meet demand requirements while minimizing costs and enhancing operational efficiency.

4.3. Hyperparameter Optimization

Optimizing the SA approach for virtual power plant (VPP) scheduling requires careful tuning of key hyperparameters. In this study, we optimized four primary hyperparameters—initial temperature, cooling rate, maximum iterations, and perturbation scale—to balance solution quality with computational efficiency. A preliminary grid search was conducted to explore broad parameter ranges and understand initial trends, followed by targeted optimization using advanced methods, including Gaussian process minimization, random forest minimization, and gradient-boosted regression tree minimization.

4.3.1. Parameter Ranges and Search Strategy

The parameter ranges were established based on theoretical insights into SA behavior and initial grid search observations:

• Initial Temperature: Ranged from $50.0$ to $400.0$ to control the acceptance of worse solutions in early iterations.
• Cooling Rate: Varied from $0.85$ to $0.975$, determining the gradual decrease in temperature to ensure a controlled convergence.
• Perturbation Scale: Examined between $0.025$ and $0.2$ to manage the magnitude of solution adjustments at each step.

The initial grid search provided a foundational understanding of hyperparameter effects, indicating that higher initial temperatures and lower cooling rates tend to improve exploration in early phases of the search. Following these findings, three advanced optimization algorithms were employed to refine the configurations: Gaussian process minimization (GP), random forest minimization (RF), and gradient-boosted regression tree minimization (GBRT). Each of these algorithms has unique properties that contribute to hyperparameter tuning, with RF and GBRT showing particular strength in capturing non-linear interactions.

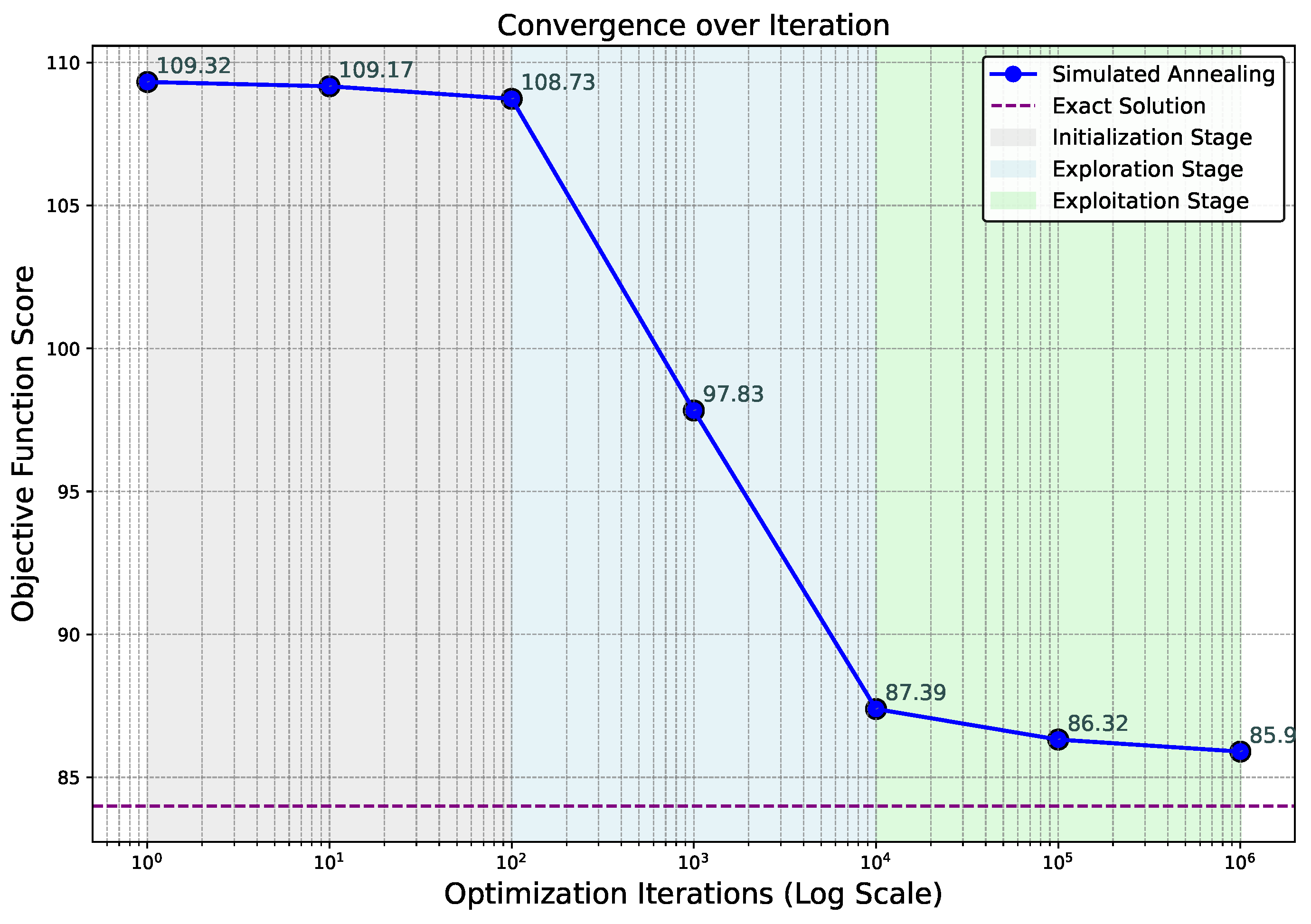
4.3.2. Analysis of Results

The optimization process revealed valuable insights into how each hyperparameter influences SA’s performance in the VPP scheduling problem. High initial temperature values (close to 400.0) were generally advantageous, allowing for extensive initial exploration and helping the algorithm avoid local minima in the early iterations. Conversely, a lower cooling rate (close to 0.85) was found to foster gradual convergence, maintaining solution diversity over extended iterations and reducing the risk of premature convergence.

The perturbation scale emerged as a pivotal parameter, with values around 0.065–0.077 providing a suitable balance between localized search precision and broader search space exploration. While the maximum iteration count showed limited impact due to its narrow predefined range, it provided a sufficient search depth to achieve stable convergence across all configurations.

Each optimization method demonstrated distinct strengths. Random forest minimization achieved the highest score, likely due to its effective handling of complex, non-linear interactions between parameters, which can be critical in SA’s adaptive search dynamics. Gradient-boosted regression trees also performed well, offering a competitive configuration with a slightly higher cooling rate, favoring faster convergence in later stages of the optimization.

4.4. Convergence Phases in Simulated Annealing

Following hyperparameter tuning in the VPP optimization framework, the convergence path of the SA algorithm is segmented into distinct phases: initialization, exploration, and exploitation. Each phase reflects the algorithm’s systematic approach, with initialization establishing a foundational search, broadly exploring the solution space, and exploitation honing in on optimal solutions within set parameter bounds. This structured convergence highlights the algorithm’s balance between global search diversity and local refinement, effectively achieving robust optimization outcomes in VPP scheduling.

Figure 4. Execution Time vs. Number of Cores for Different Player Counts.

Figure 4. Execution Time vs. Number of Cores for Different Player Counts.

4.5. Parallelization and Load Balancing Techniques

The design of the parallelized SA solver for Virtual Power Plant (VPP) optimization leverages OpenMP to achieve high computational efficiency and balance workload distribution effectively across multiple cores. The parallelization strategy centers on decomposing the optimization process into discrete, independent tasks, where each task corresponds to optimizing the scheduling decisions of an individual player within the VPP. This structure not only reduces computational overhead but also maximizes the scalability of the algorithm by allowing each player to be processed concurrently on separate threads.

Thread-Based Parallelization with OpenMP

In this implementation, OpenMP directives manage parallel threads to ensure optimal utilization of processing units. The parallel loop distributes each player’s optimization across multiple cores using the #pragma omp parallel for directive, which assigns players to threads at compile time using static scheduling. This approach leverages the uniformity in task complexity, as each player undergoes an identical optimization process over a consistent number of periods. Consequently, the computational demand is evenly distributed across threads, minimizing load imbalance and maximizing processing efficiency.

Static scheduling was selected due to the predictability of workload distribution, reducing runtime overhead associated with dynamic task assignment. By parallelizing the outer loop across players, the solver achieves high concurrency, while the inner loop within each player’s optimization cycle handles iterative temperature reduction, state perturbation, and cost evaluation. This structure allows each player’s state to be optimized independently, eliminating inter-thread dependencies and enabling a high degree of parallelism, which is crucial for scaling the approach to larger problem instances.

Unexplored Load Balancing Strategies

While this implementation uses OpenMP with static scheduling to handle the parallelization of player optimizations, certain load balancing strategies were not implemented. Specifically, dynamic scheduling and guided scheduling were not applied. These approaches, which assign tasks to threads at runtime, could dynamically redistribute workload among threads if computational variance existed. However, this added flexibility was deemed unnecessary for the current problem, where task complexity is uniform across players. Static scheduling’s pre-assignment of tasks proved sufficient and avoided the runtime overhead introduced by dynamic strategies.

Additionally, more advanced load balancing techniques, such as hierarchical or task-based parallelism, were not explored. These could be beneficial in cases involving highly irregular workloads, inter-thread dependencies, or a need for finer-grained parallelism. However, such complexity is not required for the homogeneous structure of this problem, where each player operates independently with consistent computational requirements.

Scalability and Computational Efficiency

The SA solver’s parallel design was tested across varying configurations of core counts, from a single core up to 32 cores. Each experiment measured the execution time and speedup ratio to evaluate scalability and the effectiveness of the load balancing technique. The results indicated that the solver maintained near-linear speedup up to 32 cores, with minimal deviation from the ideal speedup curve. This performance confirms that the parallelization strategy is highly scalable, capable of handling an increase in problem size (i.e., number of players) with consistent computational gains.

As the number of players scales up, the parallelization strategy effectively distributes the workload across cores, ensuring that additional computational resources lead to proportional reductions in execution time. This behavior is essential in VPP scheduling contexts where the system must adapt to real-time market fluctuations and evolving demand patterns. The observed results show that as the problem size grows, the parallelized SA solver not only maintains efficiency but also aligns closely with ideal speedup, making it robust for deployment in high-demand, real-time optimization environments.

5. Results and Discussion

The performance evaluation of the parallelized SA solver for the Virtual Power Plant (VPP) optimization problem was conducted on an HPC environment, with experiments designed to assess both computational efficiency and scalability. The experiments specifically explored the relationship between the number of computational cores and the number of players (prosumers) in the VPP market. This section presents the results in terms of execution time, speedup ratio, and scalability, with insights into how the parallelized SA solver performs under varying core and player configurations.

5.1. Execution Time and Speedup Analysis

The primary metrics for evaluating the parallel SA solver’s performance were Averaged Execution Time and Speedup Ratio. Figure 4 illustrates the execution time as a function of the number of cores for different player counts, ranging from 32 to 1024. Results show a consistent reduction in execution time with an increase in core count, demonstrating the efficacy of the OpenMP parallelization strategy. For each configuration, execution times were averaged across multiple runs to ensure robust results.

The speedup ratio, defined as the ratio of execution time on a single core to that on multiple cores, quantifies the computational gains from parallelization. As shown in Figure 6, it approaches the ideal linear curve, especially for larger player configurations (e.g., 256 and 512 players) due to more efficient task distribution across cores. The use of OpenMP’s default static scheduling ensures that iterations are pre-assigned to threads, reducing runtime overhead and maximizing throughput. This highlights the scalability of the parallelized SA approach in handling complex VPP markets with increasing computational demands.

Figure 5. Execution Time vs. Number of Cores for Different Player Counts.

Figure 5. Execution Time vs. Number of Cores for Different Player Counts.

Figure 6. Speedup Ratio vs. Number of Cores for Different Player Counts with Ideal Speedup Line.

Figure 6. Speedup Ratio vs. Number of Cores for Different Player Counts with Ideal Speedup Line.

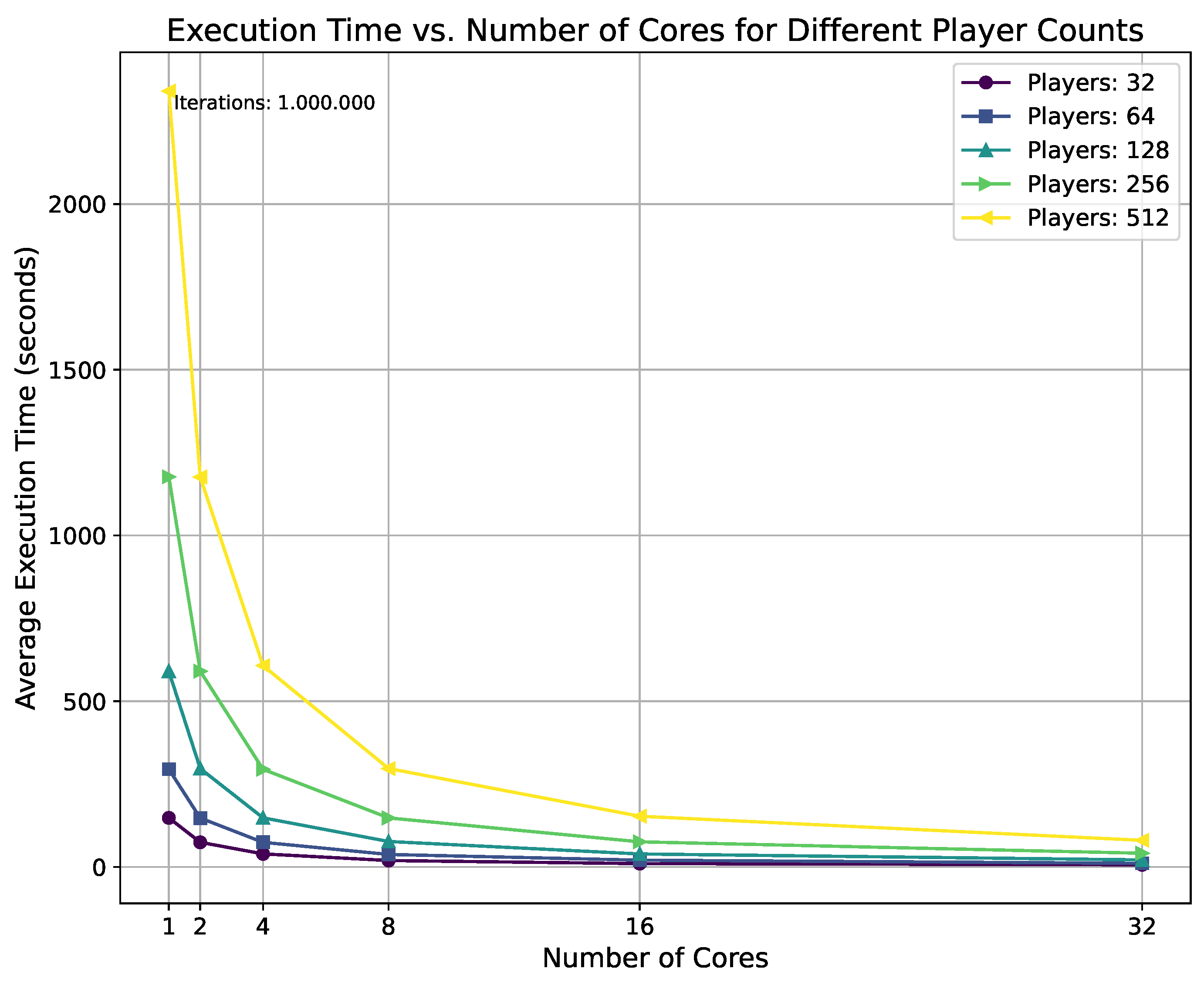
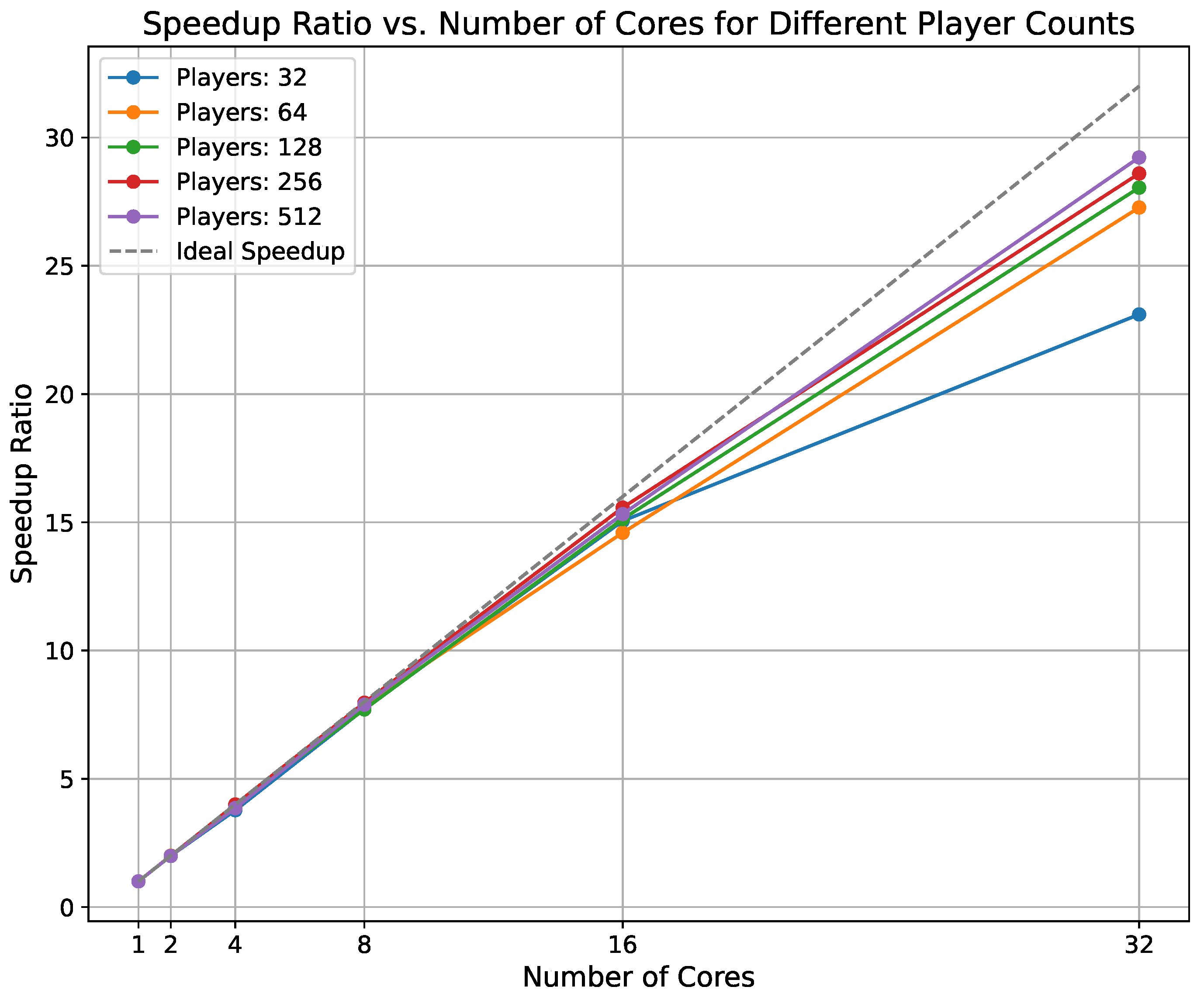
5.2. Scalability Assessment

Scalability is a critical aspect of the parallelized SA solver, particularly for large-scale VPP scenarios. A near-linear increase in speedup characterizes ideal scalability as the number of cores increases. The results demonstrate that the parallel SA solver achieves high scalability up to 32 cores, maintaining near-ideal speedup behavior across all player configurations. As the number of players increases, the algorithm’s scalability improves, with speedup curves for higher player counts closely following the ideal speedup line. This trend suggests that the parallelized SA is well-suited for large VPP problems where substantial computational resources are required to maintain efficiency.

The results indicate that the efficiency gains of the parallel SA approach are maintained even as the problem size scales, reflecting the robustness of the OpenMP-based parallelization in managing larger VPP markets. For configurations with 1024 players, the speedup performance remained stable and efficient, demonstrating the algorithm’s capability to handle extensive player interactions without a significant drop in parallel efficiency.

5.3. Efficiency and Resource Utilization

Efficiency in resource utilization is also crucial for high-performance computing applications. By monitoring CPU and memory usage during the experiments, we observed optimal resource distribution across the allocated cores. The CPU utilization remained high throughout the experiments, with minimal idle times, indicating that the parallelization strategy effectively distributed the computational workload. Memory usage remained within expected limits, ensuring stability and preventing resource contention issues.

The efficient use of computational resources underscores the effectiveness of the parallel SA solver in optimizing VPP operations in real-time. The scalability of the solver across different core and player configurations illustrates its adaptability in HPC environments, making it an effective tool for large-scale VPP scheduling.

5.4. Quality of Optimization Outcomes

A critical consideration in parallelization is the potential impact on solution quality. To ensure that parallel execution did not compromise the quality of the optimization results, we compared the solutions generated by the parallelized SA with those from a sequential SA implementation. Analysis confirmed that the parallel SA consistently reached comparable solution quality, maintaining optimal or near-optimal results across all core and player configurations. This validates the parallelization approach, as it enhances computational efficiency without sacrificing the algorithm’s ability to explore the solution space effectively.

5.5. Summary of Findings

The experimental results demonstrate that the parallelized SA solver for VPP scheduling achieves significant computational gains while maintaining solution quality. Key findings include:

• Near-ideal speedup ratio: The speedup ratio approached the ideal linear speedup curve, particularly at higher player counts, indicating strong scalability.
• High efficiency and optimal resource utilization: CPU and memory utilization were maintained at efficient levels, supporting stable execution across varied configurations.
• Consistent solution quality: Parallelization did not compromise optimization outcomes, as the parallel SA consistently delivered results comparable to the sequential version.

These findings underscore the effectiveness of the parallel SA solver in handling the complex, large-scale scheduling demands of VPP optimization, providing a reliable and efficient solution for high-performance computing applications.

6. Conclusion and Future Work

This study has successfully demonstrated the effectiveness of parallelized SA, facilitated by OpenMP, in optimizing Virtual Power Plant (VPP) scheduling for improved computational efficiency and responsiveness. By integrating OpenMP to parallelize SA operations, significant reductions in computation times were achieved, enabling the solver to handle large-scale VPP configurations with high efficiency. The experimental results showed that, with careful parameter selection and parallelization strategies, the SA solver achieved fast convergence towards near-optimal solutions, yielding substantial improvements in execution time and speedup ratio across varying player and core configurations.

The performance evaluation indicated that the parallelized SA algorithm maintained high scalability, with speedup ratios closely aligning with the ideal linear curve, particularly as the number of players increased. This behavior underscores the potential of parallel computing to enhance the scalability, adaptability, and computational feasibility of VPP operations, presenting a significant advancement in the field of energy system optimization. The results also validated that parallelization of the SA did not compromise solution quality, as the optimization outcomes consistently reached levels comparable to sequential SA. This balance between computational efficiency and solution integrity is essential for the real-world applicability of SA in dynamic and large-scale VPP scheduling scenarios.

Furthermore, the findings illustrate how the proposed optimization approach contributes to the broader objectives of sustainable urban energy management. By addressing challenges such as real-time decision-making, battery lifespan constraints, and dynamic energy pricing, the study advances the role of VPPs as integral components of smart city infrastructure. These advancements enable decentralized energy management, improve grid resilience, and support the seamless integration of renewable energy sources and electric vehicles, all of which are pivotal for achieving the energy efficiency and sustainability targets of smart cities.

Future work will focus on refining the parallelization approach to further reduce computational overhead and enhance scalability. This may include exploring advanced OpenMP features, dynamic scheduling mechanisms, and potentially integrating alternative parallel computing frameworks to boost performance in even larger VPP networks. Additionally, extending the application of the parallelized SA to more complex and dynamic VPP models—incorporating real-time market changes, demand fluctuations, and multi-energy interactions—will be a crucial area of future research. Efforts will also be directed towards creating robust simulation environments that replicate evolving smart city scenarios, ensuring that the proposed solutions remain adaptable and effective in meeting the demands of modern urban energy landscapes. Furthermore, a comprehensive benchmarking study will be undertaken to compare the performance of parallel and distributed computing implementations of other metaheuristic algorithms for the VPP optimization problem against commercial exact solvers. This analysis will provide deeper insights into the relative strengths and weaknesses of different approaches and their applicability to large-scale, real-world energy systems.