Mechanical Behavior of Auxetic Composite Panels for Civil Engineering Structures

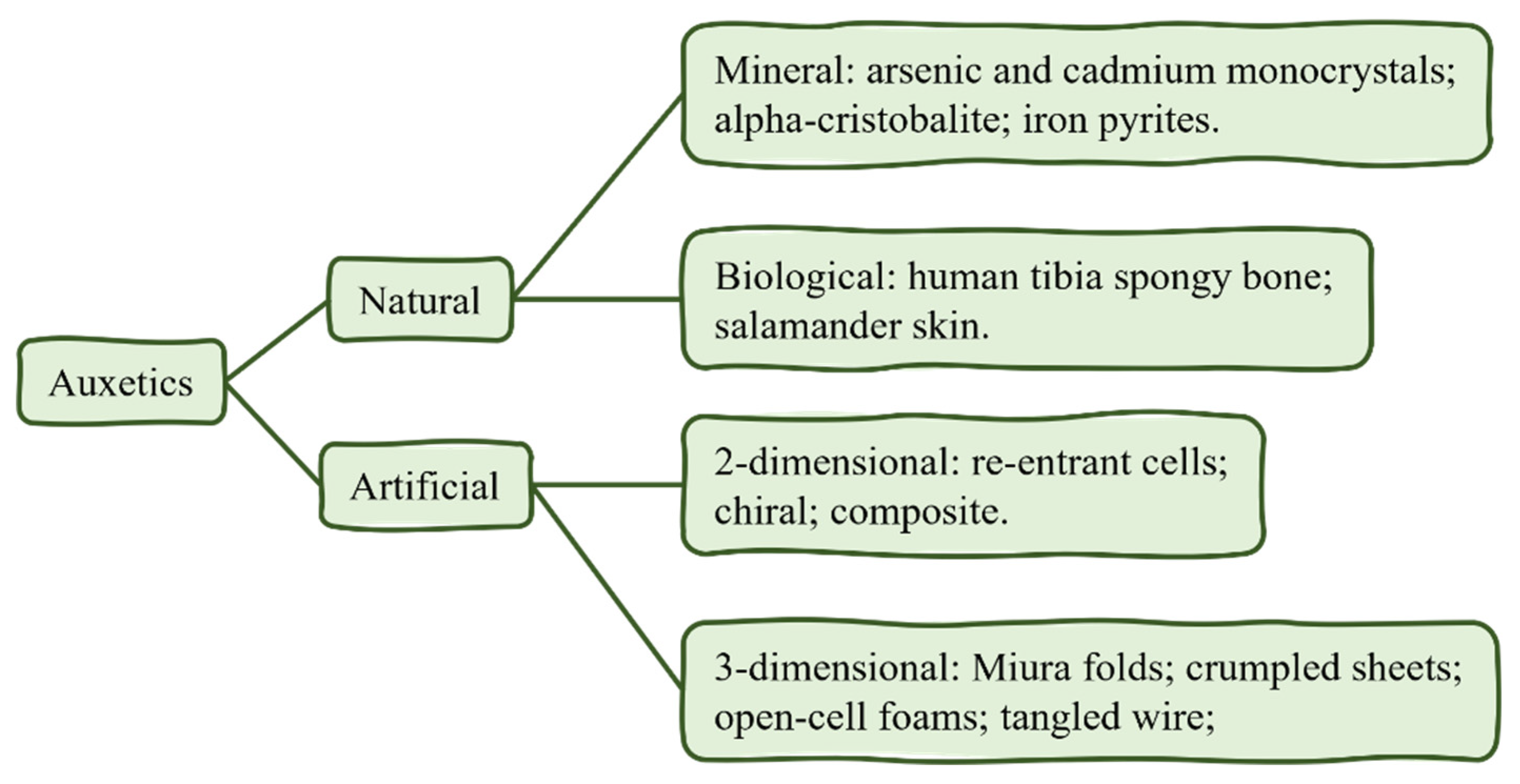
1. Introduction

The introduction should briefly place the study in a broad context and highlight why it is important. It should define the purpose of the work and its significance. The current state of the research field should be carefully reviewed and key publications cited. Please highlight controversial and diverging hypotheses when necessary. Finally, briefly mention the main aim of the work and highlight the principal conclusions. As far as possible, please keep the introduction comprehensible to scientists outside your particular field of research. References should be numbered in order of appearance and indicated by a numeral or numerals in square brackets—e.g., [1] or [2,3], or [4,5,6]. See the end of the document for further details on references.

Auxetics are considered metamaterials. A metamaterial is a composite whose properties are determined both by its constituent elements and its periodic structure of macroscopic elements [1]. An auxetic material has a negative Poisson ratio [2]. If Poisson's ratio is positive, the walls of the compressed sample, parallel to the external impact, bend outward (Figure 1a). In the case of an auxetic material, where Poisson's ratio is negative, the dimensions of the object begin to change under the external impact, as shown in Figure 1b.

Due to the negative Poisson's ratio, auxetics have unusual mechanical properties, and some of their properties exceed those of conventional materials. Many studies and comparisons of these properties have been conducted. For example, their increased resistance to deformation [3] can be attributed to their high shear strength [4]. This property of auxetic metamaterials is the basis of the present study. In addition, auxetics have high fracture toughness. That is, more energy is needed to crack them than conventional materials [5]. During the experiments, auxetics dampened vibrations and could be used as a soundproofing material [6]. There are many types of auxetic metamaterials. All of them can be divided into two-dimensional and three-dimensional types, which can reduce deformations in two or three directions, respectively [7]. The main properties of the auxetic materials and an overview of the most common auxetic configurations are described in [8,9,10,11,12,13,14,15].

The interrelation among structures, materials, properties, and applications of auxetic metamaterials and structures is studied in [11]. The most important properties of auxetics are the packing parameters and relative density of the material [9]. The main disadvantages of auxetic materials include high manufacturing cost, high porosity, insufficient bearing capacity, and suitability for only minor strain conditions [10,11]. It has been proposed that auxetics be divided into the following categories: natural auxetic materials, cellular auxetic materials, metallic auxetic materials, multi-material auxetics, and auxetic composites [10]. A rough classification is presented schematically in Figure 2. Studies [16,17,18] are devoted to the numerical analysis of auxetics, in particular, the relationship between the internal structure and the resulting properties of the material. The process of designing an auxetic structure considering the resulting properties and general purposes is described in [19].

The most popular and feasible way to manufacture artificial auxetic materials is to 3D print them. Various types of filaments can be used, e.g., silicone, polyvinyl acetate, rubber, thermoplastic polymers, and metal alloys. Another option is manufacturing an open-cell foam with auxetic properties [20]. Beyond that, folding is another approach. Crumpled aluminum foil [21], Miura-folded cells [22], and tangled wire [23] are folded auxetics.

The possible utility of auxetic properties for civil engineering purposes was assumed quite long ago [24]. However, for a long time, there was a lack of publications on this topic. The applicability of auxetics in civil engineering is mentioned in early reviews only a couple of times – with a reference in [8] to the work [25] devoted to braided composite rods with auxetic properties and a reference to auxetic nails in [11,26]. Recently, more research on the application of auxetic properties in civil engineering has emerged. Auxetic structures from braided composites for civil engineering purposes are studied in [27,28]. Experimental studies on reinforced auxetic fabrics are presented in [29,30,31]. It was proposed that the structure be modified with external auxetic foam layers to enhance the structural response of brittle panels under load [32].

A reduction in the initial yield stress of the studied composite under axial compression and an increase in the initial yield strength of the composite panel subjected to out-of-plane pressure loading were observed by finite element modeling. To reach the mentioned effect on the initial yield stress, the presence of a negative Poisson ratio was important, whereas the nuperical value of the Poisson ratio had little wffect on the results. An experimental consideration of this concept [32] was presented in [33,34,35,36]. The manufacturing process of auxetic foam samples, followed by the production and testing of cementitious composites with external auxetic foam layers, is described in [33]. The experimental analysis of the 3D-printed auxetics was presented in [37,38,39]. These studies obtained similar numerical and experimental results. The results revealed that, for auxetics, the ultimate force is greater than the yield force, and the energy absorption is higher than that for conventional materials. The concept of a fiber-reinforced plastic (FRP) sandwich structure was proposed in [40]. The load on this panel during testing was applied in the plane to the auxetic cellular structure. In the current study, it is proposed to consider the concept of a panel to bear out-of-plane loading, as in [41]. Reinforcing auxetic structures for concrete has notable potential for construction purposes [42,43,44]. Experimental reinforcement of concrete products with auxetic structures has shown an increase in the strength parameters of composites compared with unreinforced samples [44,45,46,47,48,49,50]. Despite the low strength of the polymers used to form a cellular auxetic mesh, its presence improved the properties of the concrete composite [45]. Such three-dimensional auxetic meshes can be considered "active reinforcement", in contrast to the "passive" classical reinforcement with straight bars [46].

At first sight, only plastic materials are suitable for auxetic structures. However, there are hypotheses that brittle and rigid materials, such as cementitious composites, may also have auxetic properties: the ability to absorb energy under loading and thus protect the building structure [51]. Polymer fiber reinforcement can improve the plasticity of the composite [51,52]. A comprehensive review of studies on concrete composites with auxetic properties was presented in [53]. The reviewers noted that there have been more theoretical studies on auxetic materials than experimental results [11,53]. The early reviews lacked data on true-life auxetic building structures. However, experimental studies on cementitious composites with an auxetic cellular structure have recently been conducted. The review [54] thus far mentions experimental research on the auxetic properties of cementitious structures. A numerical study on the auxetic behavior of cementitious cellular composites was reported in [55]. Experimental auxetic concrete samples have been studied elsewhere [51,56,57,58,59,60,61].

The manufacturing technology is simple yet intelligent. First, the auxetic structure was designed parametrically and printed on a 3D printer. A silicone-rubber mold was then made for concrete casting. Finally, the mortar was poured into a rubber-silicone mold. Most existing studies have used peanut- or ellipsoid-shaped auxetic configurations. Consistency between the numerical simulation and experimental results was reported in most of the studies. The material behavior can be modified by changing the parameters of the cellular structure. Due to the cellular configuration, the auxetic cementitious composites exhibited higher energy absorption capacities than the monolithic structures. Another option for manufacturing cellular cementitious composites is 3D printing [62]. Auxetic cellular composites are naturally associated with the existing internal configurations of 3D-printed walls [63]. 3D-printed concrete structures with cellular auxetic configurations have been presented in [64].

The construction of blast-resistant structures is a significant engineering task. Rooms with potentially explosive processes should be blast-resistant. From 2008 to 2019, at least 5 explosions occurred, with 7 victims in the laboratories of Russian research institutes. Residential buildings may also be exposed to explosion hazards. From January to September 2023, 28 cases of gas explosions in residential buildings in Russia. Some buildings or parts of them have become unsuitable for further use. Traditionally, massive monolithic structures provide blast resistance. These structures are expensive, resource-heavy, and not sustainable. Wide use of them is impossible due to their large weight. Auxetic materials are an option for lightweight blast-resistant structures that can absorb and dissipate explosive loads [18,65].

This study aimed to analyze the applicability of auxetics in civil engineering. The following objectives were set:

• Design and manufacture of auxetic samples based on existing research in the field.
• To evaluate the mechanical properties of the manufactured composites.
• To analyze the prospects of civil structures with auxetic configurations.

2. Materials and Methods

As stated earlier, auxetic metamaterials are the latest materials that require considerable research into their industrial applications. However, for any experiments, experts need standards that regulate and specify all the nuances of specimen testing, such as the size and shape of the specimen, the instrument on which the test is performed, and the temperature and humidity in the laboratory. None of these, of course, has yet been established for auxetic experiments. This study aims, among other things, to develop the prerequisites for laboratory testing of auxetics. As part of this study, the length, width, height, material, and honeycomb size of specimens for compression, tensile, and bending tests must be determined, and the test methods must be specified.

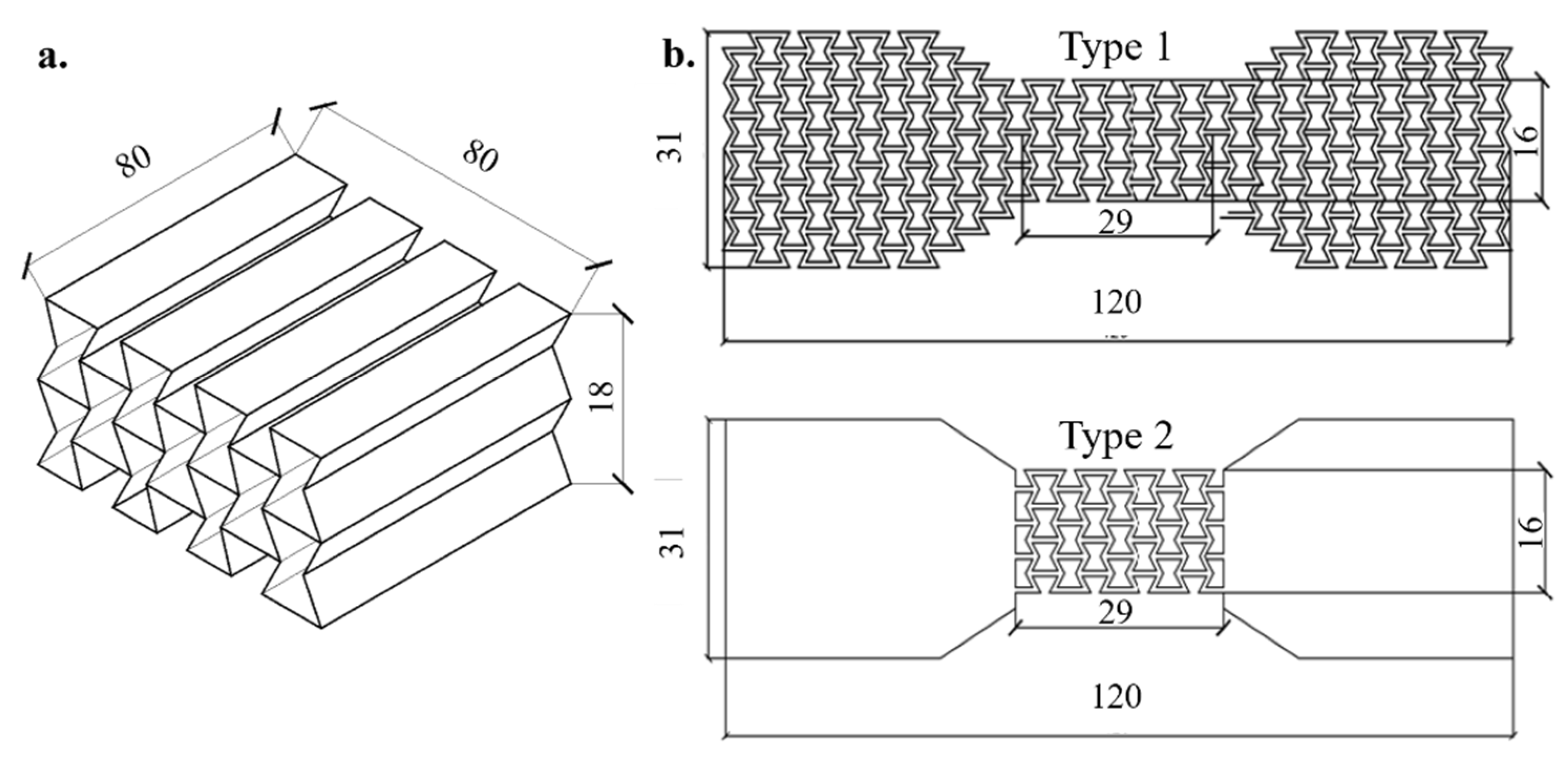
2.1. Sample Materials

The samples tested in this study were 3D-printed. The filaments used to print the samples were acrylonitrile butadiene styrene (ABS) and polylactide (PLA). The standard filament diamenter of 1.75 mm was used. These plastics are most commonly used for 3D printing and are economically accessible. Table 1 summarises the main mechanical properties of the fabricated plastics. The plastic manufacturer (“PrintProduct” LLC, Saint-Petersburg, Russia) provided information on the plastics that were not tested in the laboratory as part of this study.

2.2. Testing Methods

The manufactured auxetic structures were tested for compression and tension. Since the auxetics were made of polymer materials, the following standards were adopted as the methodological basis for the research: Russian state standard GOST 32656–2014 “Polymer composites. Test methods. Tensile test methods” (equivalent to ISO 527-4:1997, ISO 527-5:2009), Russian state standard GOST 11262-2017 “Plastics. Tensile test method” (equivalent to ISO 527-2:2012), and Russian standard GOST 4651-2014 “Plastics. Compression test method” (equivalent to ISO 604:2002). A universal electromechanical testing machine (Instron 5965, Instron, USA) was used for the testing.

For the compression test, samples with dimensions of 80x80x18 mm were manufactured. These samples are prototype blast-protecting modular panels. The samples were subjected to compression, as shown in Figure 3a. The samples were loaded at a constant rate until stability or integrity loss. The test assessed the auxetic properties of the resulting material and its response to a gradual, long-term loading on the working surface.

Flat samples with shoulders for serrated grips were manufactured for tension tests. The specimen sizes were 120x31x3.4 mm, and the test section size was 29x16 mm. Two types of specimens were prepared (Figure 3b): type 1 had filled areas outside the test section of the specimen; the whole type 2 samples had auxetic configuration. It was investigated whether the specimen exhibits auxetic behavior when stretched orthogonally to the auxetic cellular structure. The test results for type 1 and type 2 were compared to evaluate the influence of the shoulder design on the test results.

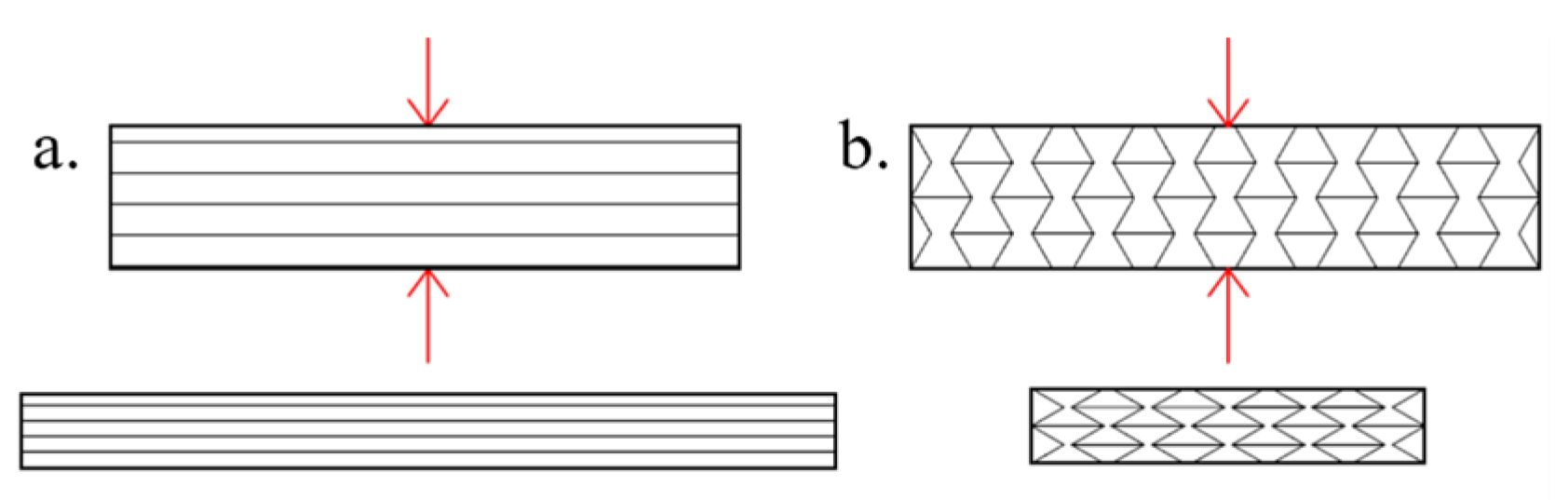
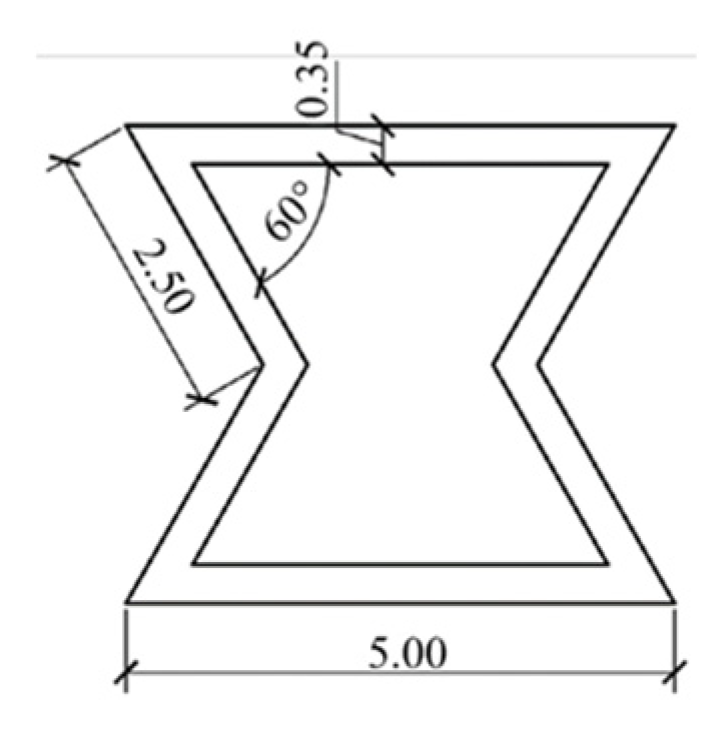
2.3. Cellular Configuration of the Samples

In this study, an hourglass-shaped auxetic internal structure was chosen as one of the most popular and described configurations [8,17,37,47]. The following parameters should be set during the design of the samples: the inclined wall length, the horizontal wall length, the wall thickness, and the inclination angle. The dimensions were chosen considering the 3D printer printing definition. The targeted result was the smallest possible dimensions of the cellular structure with the least amount of defects. Different models were used to compare the inclination angle sketches. The distance between the side walls of the cell was considered when choosing the best sketch. The greater the distance is for the unloaded sample, the better its auxetic properties should appear, as shown in Figure 4.

The following parameters were chosen: wall thickness 0.35 mm; horizontal wall length 5 mm; inclined wall length 2.5 mm; inclination angle 60°. The final design of the cell is shown in Figure 5.

A Raise 3D Pro2 Plus 3D printer (Raise 3D Technologies, Inc., USA) with a 0.4 mm nozzle diameter was used to print the samples. The printing process is shown in Figure 6.

The manufactured samples are shown in Figure 7.

3. Results

3.1. Compression Tests

The auxetic structure sample during the compression test is shown in Figure 8a. The deformed sample after the test is shown in Figure 8b.

Three samples with the exact dimensions but made of different materials were tested. Sample 1 was manufactured from PLA and printed with low printing accuracy. Sample 2 was made of PLA as well but printed with high printing accuracy. Sample 3 was made of ABS and printed with high printing accuracy. The yield point was established for all three samples during the test. The yield point and obtained Poisson ratio are presented in Table 2.

Load-deformation diagrams for compression tests are presented in Figure 9.

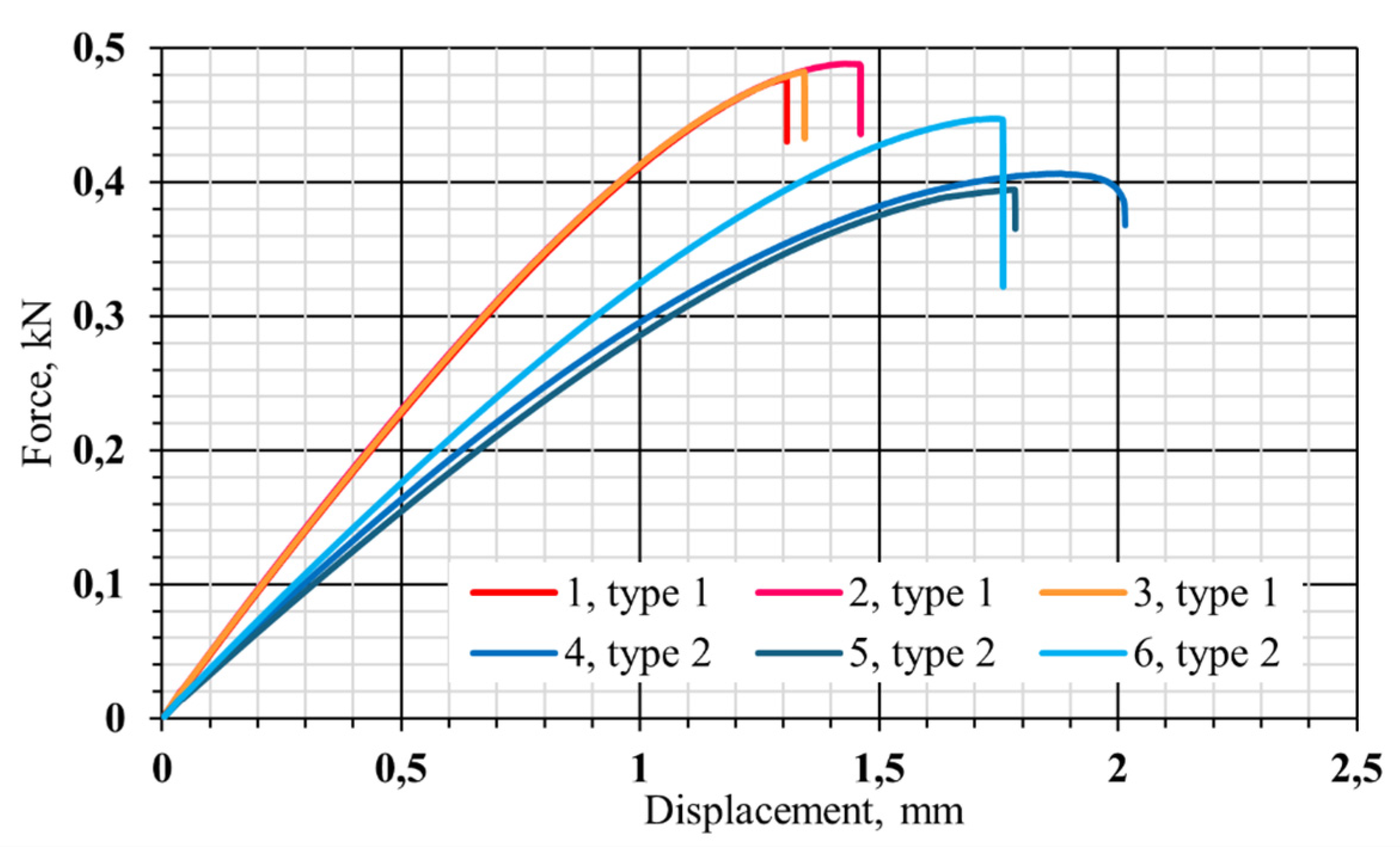
3.1. Tension Tests

A sample during tension test is shown in Figure 10a. The ruptured sample after the test is presented in Figure 10b.

The samples were stretched at a constant speed of 1 mm/min. Three identical samples of each type (Figure 3 and Figure 7) were tested, and no sample defects were detected during the testing process. The tension test results are presented in Table 3.

Load-deformation diagrams of tension tests for auxetic samples are presented in Figure 11.

4. Discussion

4.1. Compression Tests

A visual comparison of the samples before and after the compression test is shown in Figure 13. The PLA samples showed a lower Poisson ratio under compression (-0.06) than the ABS samples (-0.05). The obtained Poisson ratio values were consistent with experimental values obtained experimentally in a similar study [66]. The overall configuration of the samples was different in [66] than in this study. As expected, the auxetic structure properties depend on the properties of the original material. ABS is less ductile than PLA. It can be assumed that similar structures made of concrete exhibit even lower auxetic properties. This hypothesis was also mentioned in the literature review. Therefore, to fabricate an experimental auxetic concrete panel, it is necessary to obtain a cellular configuration with the lowest Poisson ratio. Polymer fiber reinforcement can enhance the plasticity of cementitious composites, as previously reported [51]. A visual comparison of the samples before and after the compression test is shown in Figure 12.

The printing accuracy with the selected cellular structure had little effect on the load perception of the structure because samples 1 and 2 showed similar results in compression tests. This conclusion enables cost reduction and acceleration of auxetic production by reducing the requirements for surface quality. Second, an optimistic forecast for the behavior of cementitious composite auxetics can be presented because the accuracy of concrete casting is lower than that of the 3D-printing. Note that although the results of the compression test are repeatable, they are limited by the small number of samples. In the future, it is necessary to expand the knowledge base by adding new experimental data.

4.2. Tension Tests

It was expected that the tension test results would be consistent regardless of the sample type, but this expectation was not confirmed. The results show that the shoulder structure of the samples significantly affects their tensile capacity. The average tensile strength of type 1 samples was 0.482 kN, whereas that of type 2 samples was 0.416 kN. The values differ by 13.7%. At the same time, cellular type 2 samples exhibited higher elongation at failure: 1.85 mm. The difference from 1.37 mm for type 1 is 35%. Based on the obtained results, it is possible to assume that the cellular structure exhibits auxetic properties even in the transverse direction. The presence of an auxetic mesh over the entire sample contributed to a more uniform stress distribution over the specimen and a higher capacity for deformation. In general, the load-displacement curves were similar to those reported in similar studies [67]. It can also be noted that all type 1 specimens failed in approximately the same part of the sample, whereas type 2 specimens ruptured at different parts. Pictures of the samples after testing are presented in Figure 13.

4.3. Auxetic Composite Panels for Civil Engineering Purposes

The present study focused on evaluating the auxetic properties of cellular composites. The negative Poisson ratio under compression was experimentally obtained in the designed cellular configuration. The manufactured samples can absorb energy under load. Constructions with such internal configurations can be used for blast protection, as described in [41]. Primary experiments were conducted on the 3D-printed polymer samples. In future research, fine-grained concrete samples with an auxetic configuration will be manufactured and tested. It is planned to use a 3D printer to prepare casting molds for concrete. The manufacturing technology should be similar to that described in [56]. In further research, calibration tests can also be initially carried out using polymer 3D printing, and for the most successful samples, concrete prototypes of structures can be manufactured. In future work, tests will also be conducted on the ability of auxetic panels to withstand blast loads. The ability of a structure to dissipate the energy of an explosion is a key property in the protection of buildings from explosions.

5. Conclusions

Although new and not fully understood, auxiliary metamaterials have already become a popular subject of research. The correct use of auxetic properties can lead to breakthroughs in various engineering fields. Auxetic metamaterials have great application potential in civil engineering and are expected to be fully developed soon. In this study, an experimental evaluation of the properties of auxetic cellular-configurated polymer structures was conducted. The possibility of manufacturing blast-resistant lightweight cementitious building structures was analyzed using existing studies and experimental results. In the experimental part of the study, tests using 3D-printed polymer modes were conducted. The following conclusions can be drawn based on the results of the study:

• The Poisson ratios of the PLA and ABS models were 0.06 and 0.05, respectively.
• The lower the plasticity of the material, the greater the "auxetic potential" of the cellular structure should be so that the resulting composite acquires sufficient auxetic properties. In this regard, in the future, experimentally evaluating the effect of the cellular structure configuration on the properties of the auxetic material by varying the cell parameters is planned.
• Manufacturing accuracy can be reduced without significantly affecting the results of compression tests.
• The average tensile strength of the samples with monolithic shoulders was 0.482 kN, whereas that of the samples with cellular shoulders was 0.416 kN, which is 13.7% lower.
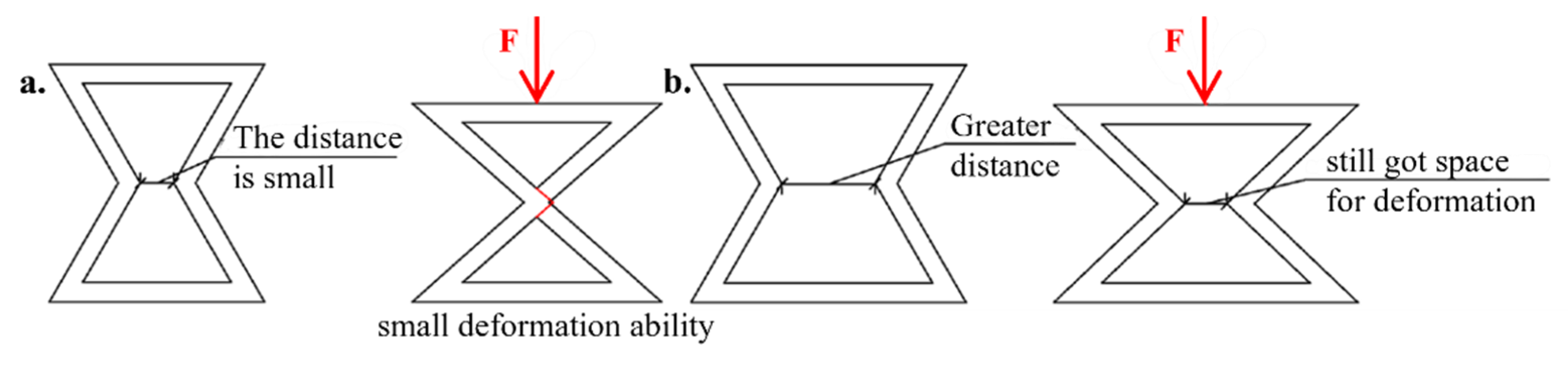
• The cellular structure exhibits auxetic properties when stretched transversely to the auxetic mesh. These properties manifest as a more uniform stress distribution across the sample.
• Cellular concrete panels with an auxetic structure can have auxetic properties and, as a result, the ability to absorb explosion energy. Therefore, further studies are planned to study the auxetic properties of such panels experimentally.