Introduction
The study of gravitational dynamics in systems with multiple massive bodies remains a central challenge in celestial mechanics. While the classical three-body problem offers foundational insights, introducing additional primaries—especially with spatial or physical perturbations—rapidly increases the system’s complexity. These models have relevance not only in theory but also in practical scenarios such as planetary rings, space debris environments, and exoplanetary systems, where idealized assumptions like symmetry or constancy often break down.This has prompted investigations into restricted N-body models, where the motion of a massless test particle is investigated under the gravitational effect of multiple gravitating sources. Such models are not only of theoretical curiosity but also describe the physical reality of many-body configurations in planetary ring systems, Trojan asteroid clouds, space debris fields, and young stellar environments.
Classical formulations of the restricted N-body problem commonly assume coplanar geometries, symmetric mass distributions, and time-invariant parameters. These idealizations simplify the mathematics but limit the applicability of the models to real astrophysical systems where asymmetry, radiative forces, and structural variations are more the rule than the exception. For instance, a central star’s gravitational field is often accompanied by strong radiation pressure that repels small bodies such as dust grains or micro-satellites. And this radiation is not static—solar flares, stellar variability, and rotational shading can create periodic or random intensity fluctuations, altering the system’s dynamical nature over time.
We address these problems in this paper by presenting an updated model for non-planar motion in a multi-primary rotating system. An asymmetric configuration with unequal mass distributions and orbital radii is coupled with a time-dependent radiation factor from the central primary. The paramount goal is to examine the implications of such perturbations on the existence, location, and stability of vertical equilibrium points. By incorporating time-varying radiative forcing, the research includes more realistic dynamics relevant to astrophysical environments that evolve dynamically.
Our approach uses analytic calculations and numerical simulations to identify potential regions of equilibrium and ascertain their linear stability via Jacobian eigenvalue analysis. We also investigate the influence of oscillatory radiation on particle orbits near such regions, gaining insight into the mechanisms whereby instability and chaos can develop. This study thus contributes to the overall understanding of spatial equilibria in gravitationally disturbed systems and opens up new avenues for investigating the complicated balance of forces in non-ideal celestial worlds.
Methodology
To investigate the vertical dynamics and stability properties of a test particle in a non-ideal gravitational environment, we construct a generalized multi-primary model inspired by the classical restricted N-body framework but extended to include several real-world complexities. The system consists of a radiating central primary and six peripheral massive bodies arranged in a rotating reference frame. Unlike classical formulations, this model introduces the following key physical extensions:
Asymmetric Mass Distribution: The six peripheral primaries are assigned non-uniform masses μi\mu_iμi, breaking the traditional assumption of mass symmetry. This choice simulates natural variability in body sizes or compositions, such as those found in asteroid fields or irregular planetary systems.
Variable Orbital Radius: Rather than maintaining a fixed radius for all peripheral bodies, we distribute them across a narrow band [aₘᵢₙ, aₘₐₓ] introducing spatial perturbation to the circular configuration. This models physical dispersion and natural orbital variations.
Time-Dependent Radiation: The central body emits radiation that exerts repulsive force on the test particle. The intensity of this radiation is governed by a time-varying function
q(t), reflecting dynamic phenomena such as pulsating stars, stellar flares, or shadowing effects in planetary systems. We consider both sinusoidal and piecewise profiles of
q(t), e.g.,
where
q₀ is the baseline radiation factor, δ is the amplitude, and ω the frequency of modulation.
Equations of Motion
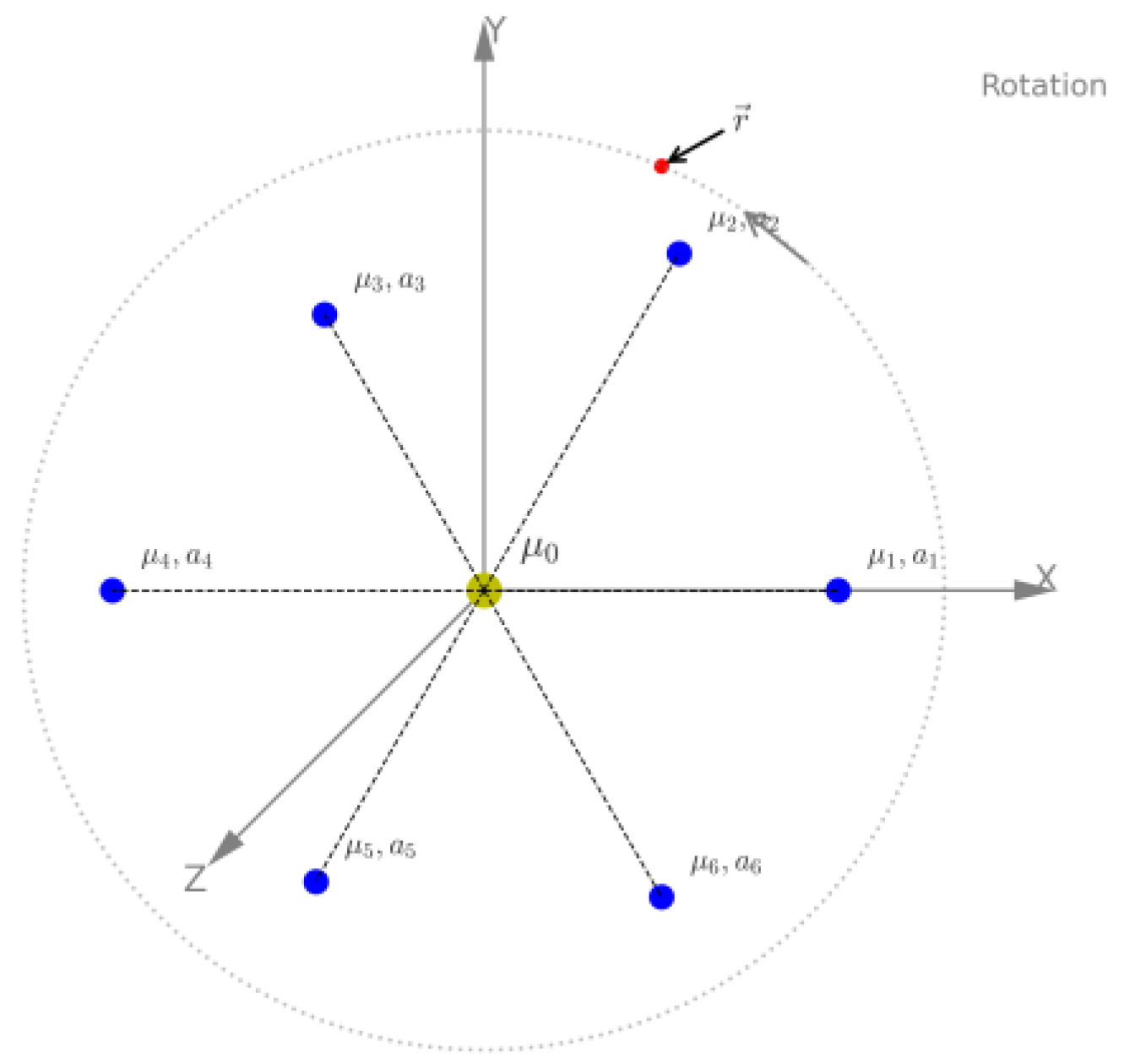
The test particle is considered massless and does not influence the motion of the primaries. The system consists of a central radiating body with mass μ₀, surrounded by six secondary primaries μᵢ (where i = 1…6), each moving in circular orbits at slightly different radii aᵢ. This asymmetry in orbital radius reflects natural dispersion as found in ring systems or multi-body debris structures.
To capture the dynamics of a massless particle within a rotating multi-body system, we adopt a co-rotating reference frame. In this frame, the fictitious forces, along with gravitational and radiative influences, define the net acceleration experienced by the particle. The governing equation takes the form:
where the effective potential U(r⃗,t)U(\vec{r}, t)U(r,t) includes both gravitational attractions from the primaries and a repulsive term representing time-dependent radiation from the central source.
Here,
μ₀ is the mass of the central radiating primary, and
q(t)∈(−1, 1) represents the time-dependent radiation factor that reduces the effective gravitational attraction. For simplification, we set
G = 1 and normalize
μ₀ = 1, unless otherwise specified.
The function
q(t) may follow different time profiles. In this study, we consider oscillatory radiation modeled by:
where
q₀ is the baseline radiation level,
δ is the oscillation amplitude, and
ω is the angular frequency of radiation variation.A schematic of the configuration is shown in
Figure 1, illustrating the central body, asymmetric placement of the six primaries, and the varying radii
aᵢ.
Locating Vertical Equilibrium Points
Vertical (out-of-plane) equilibrium points occur when the net vertical force acting on the test particle is zero. Assuming symmetry cancels the horizontal components, we focus on solving the scalar condition:
This equation is evaluated numerically using root-finding methods such as the bisection method and Newton-Raphson technique, applied across various configurations of q(t), μᵢ, and aᵢ.
Root-finding was performed using the bisection method, applied to the vertical force condition.
Linear Stability Analysis
To evaluate the local stability of the vertical equilibrium points z₀, we consider small perturbations around the equilibrium:
To evaluate the local stability near vertical equilibrium points, we perform linearization by introducing small perturbations around the steady state. The resulting system is characterized by the Jacobian matrix derived from the second-order partial derivatives of the effective potential. The real parts of the eigenvalues indicate stability: a positive real part implies exponential divergence, while purely imaginary eigenvalues correspond to oscillatory, neutrally stable behavior.
If any eigenvalue has a positive real part, the corresponding equilibrium is linearly unstable.
Parameter Space Exploration
To explore the behavior of the system under realistic perturbations, we simulate a wide range of parameter values:
Baseline radiation levels: q₀ ∈ [−1, 0]
Oscillation amplitudes: δ ∈ [0.01, 0.2]
Peripheral mass ratios: μᵢ ∈ [0.05, 0.25]
Orbital radii spread: aᵢ ∈ [0.8, 1.2]
Each combination is simulated over extended time intervals to observe the emergence of bounded motion, divergence, or chaotic dynamics in the neighborhood of the out-of-plane equilibria. The chosen amplitude range δ ∈ [0.01, 0.2] reflects realistic radiative fluctuation levels. Values below 0.01 led to negligible dynamical deviations, while values exceeding 0.2 introduced numerical instabilities in the simulations. The selected range ensures observable nonlinear effects without compromising computational stability.
All calculations were carried out using standard numerical methods implemented in a general-purpose programming environment. Root-finding and evaluation of stability were conducted numerically for a range of physical parameters.
Implications and Interpretation
The observed instability under varying radiation provides insights into the behavior of dust grains, small satellites, or particles in regions near variable stars, where radiation pressure fluctuates due to stellar pulsation, flares, or rotational modulation. The vertical displacement and loss of equilibrium could lead to the vertical thickening of dust rings or the ejection of particles from resonant orbital planes.
Additionally, the results imply that achieving vertical confinement of small particles in engineered orbital systems (e.g., satellite constellations or debris-mitigation structures) requires precise control of radiative forces or compensating stabilizers.
Results and Discussion
The system exhibits distinct behaviors depending on the strength and variability of radiation. In scenarios with constant radiation (q(t) = q₀), vertical equilibrium points exist within a limited range of q₀∈(−0.95, 0). These points are positioned symmetrically along the z-axis in ideal cases, but are displaced in asymmetric configurations.
Linear stability analysis indicates that all equilibrium points within this range are linearly unstable, with at least one positive real eigenvalue in the Jacobian matrix. When radiation varies with time, especially under the formq(t) = q₀ + δ·sin(ωt), the dynamics become richer. Small oscillations (δ ≤ 0.05) cause periodic motion around the equilibrium zone, while larger amplitudes (δ ≥ 0.1) disrupt the equilibrium, resulting in irregular, quasi-chaotic trajectories.
These findings demonstrate that radiative variability and structural asymmetry significantly affect the formation and persistence of vertical equilibrium points. Even slight deviations from symmetry or temporal constancy can lead to the collapse or migration of these equilibria. The dynamic behavior of the system was evaluated under a variety of initial conditions and parameter ranges, focusing particularly on the identification and stability of vertical equilibrium points under different radiation profiles and mass asymmetries.
Literature Review
The study of out-of-plane motion in multi-body gravitational systems has long been a subject of interest in celestial mechanics. The foundational work of Maxwell [
1] analyzed the dynamical stability of Saturn’s rings, establishing early insights into the behavior of particles in rotating systems. Later, Moser [
2] extended the understanding of orbital stability by exploring stable and chaotic motions in dynamical systems, emphasizing the sensitive dependence on initial conditions.
The concept of ring-like systems with multiple massive bodies was investigated in depth by Kalvouridis [
3], who analyzed (N+1)-body configurations over a decade of research. His findings demonstrated the structural complexity and resonance behaviors that arise in symmetrical multi-body systems. Building on these ideas, Singh et al. [
4] explored the stability of collinear equilibrium points within generalized three-body models, incorporating additional effects beyond Newtonian gravitation.
Further developments include the consideration of geometric distortions and external forces. Verma et al. [
5] examined the impact of oblateness and finite segments in the restricted 2+2 body problem, offering insight into the role of asymmetries in orbital dynamics. Similarly, Mahato et al. [
7] introduced a planetesimal belt into the gravitational model, revealing how additional mass distributions can significantly alter system behavior and lead to vertical instability.
A particularly relevant contribution is the study by Idrisi et al. [
6], which analyzed the out-of-plane dynamics of a massless particle in a circular restricted eight-body framework. Their model assumed perfect symmetry in the arrangement of the primaries and treated radiation pressure as a constant. They identified the existence of vertical equilibrium points and analyzed their stability under static conditions.A recent study by Idrisi et al. (2024) considered the vertical motion of a test particle in a circular eight-body configuration, focusing on gravitational interactions in a static radiative context.
However, the present work expands upon this foundation in several important ways. Most notably, it introduces a time-dependent radiation factor
q(t) = q₀ + δ·sin(ωt) to model stellar variability — a factor not considered in [
6]. Additionally, it allows for asymmetry in both mass distributions
μᵢ and orbital radii
aᵢ, making the model more representative of realistic astrophysical systems such as debris disks and satellite constellations. Finally, this study conducts a broader parameter space analysis, revealing the emergence of instability and chaotic behavior as radiative forcing increases. This work differs significantly from the study by Idrisi et al. (2024), which investigated vertical dynamics in a symmetric eight-body configuration with a constant radiation factor. In contrast, the present model introduces time-dependent radiation (q(t) = q₀ + δ·sin(ωt)) and incorporates asymmetry in both mass distribution and orbital radii of the peripheral bodies. These modifications result in new dynamical behaviors, including the disappearance of equilibrium points and the emergence of chaotic motion, which were not addressed in the earlier study.
By relaxing assumptions of symmetry and constancy, the current work provides a more generalized and flexible framework for analyzing vertical dynamics in perturbed multi-body systems.
Conclusions
This paper presents a modified formulation of the restricted multi-body problem that accounts for both structural asymmetry and time-dependent radiative forces. The model departs from classical configurations by allowing non-uniform mass distributions and orbital radii, as well as dynamically varying central radiation modeled as a sinusoidal perturbation.
Through numerical root-finding and linearized stability analysis, we identified vertical equilibrium points and evaluated their robustness under a range of physical conditions. In all scenarios, equilibrium points exhibited strong sensitivity to both geometric asymmetry and radiation variability, often becoming unstable or disappearing entirely when even modest perturbations were introduced.The methodology and results outlined here provide a foundation for more advanced modeling, including the application of machine learning to identify complex dynamical regimes, the extension to relativistic corrections, or the inclusion of other non-conservative forces such as drag or magnetic fields.
References
- Maxwell, J.C. On the Stability of the Motion of Saturn’s Rings; an Essay Which Obtained the Adams’ Prize for the Year 1856, in the University of Cambridge. Monthly Notices of the Royal Astronomical Society 1859, 19, 297–304. [Google Scholar] [CrossRef]
- MOSER, J. (1973). Stable and Random Motions in Dynamical Systems: With Special Emphasis on Celestial Mechanics (AM-77) (REV-Revised). Princeton University Press.
- Kalvouridis, Tilemahos. (2009). The Ring Problem of (N+1) Bodies: Ten Years of Research (1999-2009). Proceedings of SPIE - The International Society for Optical Engineering. 7651. [CrossRef]
- Singh, K. & Kushvah, Badam Singh & Ishwar, B.Hola. (2006). Stability of Collinear Equilibrium Points in Robes’s Generalised Restricted Three Body Problem. [CrossRef]
- Verma, Ravi & Pal, Ashok Kumar & Kushvah, Badam Singh & Mahato, Govind. (2023). Effect of finite straight segment and oblateness in the restricted 2+2 body problem. Archive of Applied Mechanics. 93. 1-17. [CrossRef]
- Idrisi, M. J., Ullah, M. S., Tenna, W., Khan, M. T., Khan, M. F., & Kamal, M. (2024). Out-of-plane dynamics: a study within the circular restricted eight-body framework. New Astronomy, 111, 102260. [CrossRef]
- Mahato, G., Pal, A. K., Alhowaity, S., Abouelmagd, E. I., & Kushvah, B. S. (2022). Effect of the Planetesimal Belt on the Dynamics of the Restricted Problem of 2+ 2 Bodies. Applied Sciences, 12(1), 424. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).