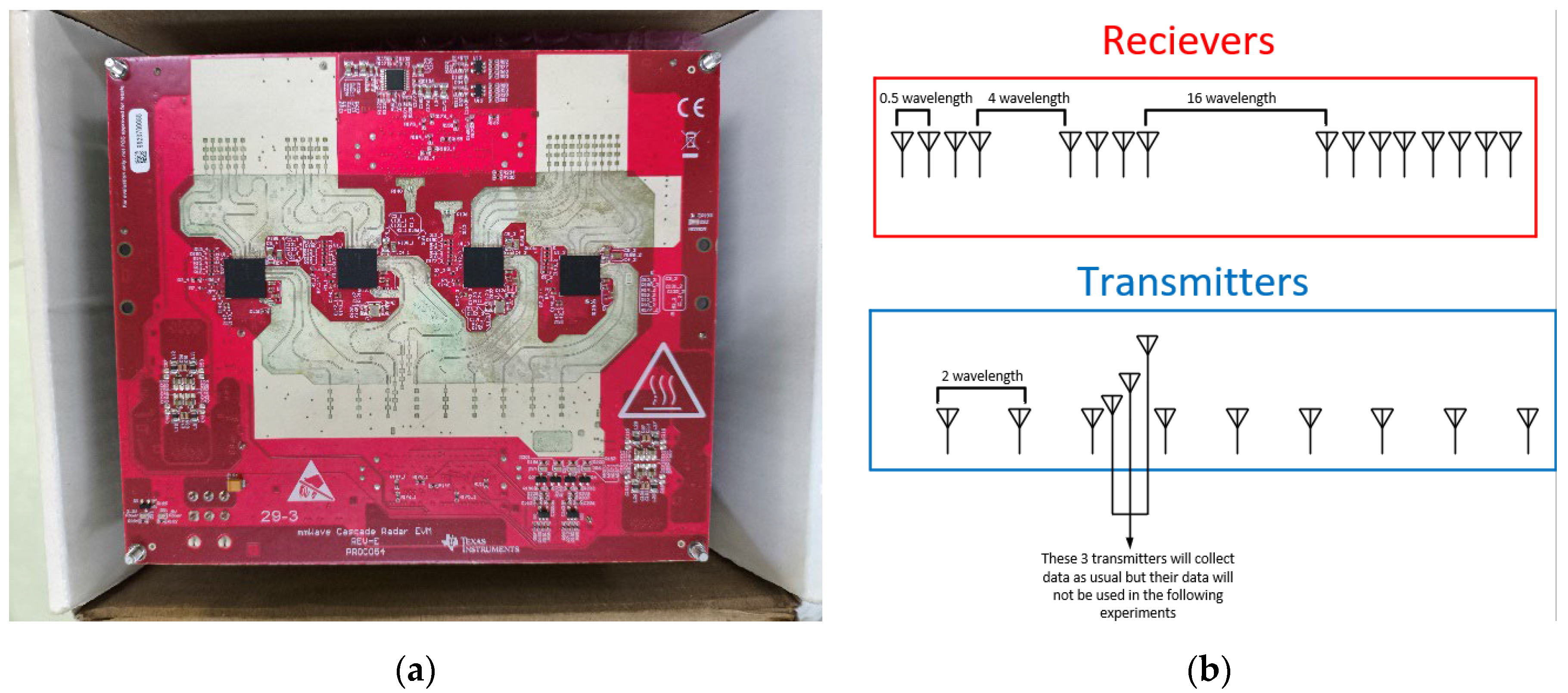
1. Introduction
In recent years, the Multiple Input Multiple Output (MIMO) technique, which achieves high Degree of Freedom (DOF) for radar systems, has drawn an increasing amount of attention in various applications, such as Autonomous Driving [
1], Ground Penetrating Radar [
2], Remote Sensing [
3], Through-wall Imaging [
4], etc. Orthogonal waveforms are radiated by transmitters (TXs), thus a MIMO system can separate different signals transmitted by different TXs. For example, a MIMO radar which has
transmitters and
receivers can generate
virtual antennas. There are three multiplexing schemes to obtain waveform diversity, namely Time-Division Multiplexing (TDM), Frequency-Division Multiplexing (FDM) and Code-Division Multiplexing (CDM). Due to the advantages of low hardware complexity and high signal separation, TDM-MIMO system is easy to implement, thus it has a wide range of applications [
5]. A large amount of research has focused on the algorithms and implementations for TDM-MIMO radar [
6,
7,
8]. However, a TDM-MIMO system has an inherent drawback which limits its performance. As transmitters take turns to transmit their signal, phase errors occur in nonstationary scenarios [
9]. In addition, more transmitters mean lower Pulse Repetition Frequency (PRF) and reduced maximum velocity that can be detected [
5].
Synthetic Aperture Radar (SAR) is an important technique for remote sensing and radar imaging. With the help of MIMO technology, a new architecture called MIMO-SAR not only increases spatial resolution [
10], but also provides novel imaging capability such as 3D imaging [
11] and Ground-Moving Target Indication (GMTI) [
12]. Due to the great potential of MIMO-SAR architecture, many researchers have contributed to various aspects of MIMO-SAR. In [
10], it is shown that the mere use of orthogonal waveforms is insufficient for most SAR applications, and thus a new class of waveform is introduced. Yanik et al. addressed the issues of the design process of MIMO-SAR systems and presents three versions of MIMO-SAR testbeds with different costs and performances [
13]. As in many cases, such as Unmanned Aerial Vehicle (UAV) imaging, irregular scanning geometries and computational complexity limit the capability of MIMO-SAR systems, Smith et al. proposed a new algorithm to leverage SAR and MIMO while achieving high resolution with high efficiency near field MIMO-SAR imaging [
14]. The effect of virtual array approximation in near field applications is studied by Hu et al., and a new design criterion is presented [
15]. An efficient image reconstruction algorithm which avoids time-consuming wavenumber accumulation by decomposing the range-wavenumber based on binomial approximation theory is proposed for MIMO-SAR 3D imaging [
16]. A beat frequency division (BFD) frequency-modulated continuous wave (FMCW) MIMO-SAR system and the corresponding signal process method which are suitable for UAV environments are presented [
17]. With appropriate transformation, MIMO-SAR 3D imaging can be achieved by inverse Fourier transform (IFT) [
18].
Apart from the imaging algorithms and array design of MIMO-SAR, it is the realization of MIMO systems that significantly affect both the performance and costs of MIMO-SAR. There are numerous studies discussing the problem of MIMO-SAR associated with a specific MIMO realization. Jin et al. proposed a novel MIMO-SAR scheme based on segmented-phase-code waveform which can relieve the short-term shift-orthogonality condition without losing imaging performance [
19]. In [
20], a MIMO-SAR system using chirp diverse waveform is discussed to achieve high resolution for wide-swath remote sensing, as chirp diverse waveform can easily provide high bandwidth which is necessary for this radar imaging. It is acknowledged that a large time-bandwidth product, low cross-correlation interferences and a low peak-average ratio have significant importance for MIMO radar imaging. To reach these aims, an orthogonal frequency division multiplexing (OFDM) chirp waveform with random matrix modulation is proposed for MIMO-SAR applications [
21]. As mentioned before, TDM-MIMO enjoys many advantages with respect to hardware complexity and cost. A forward-looking MIMO-SAR enhanced imaging scheme is presented, and its performance is validated with a TDM-MIMO radar [
22]. In [
23], the authors proposed a hierarchical high-resolution MIMO-SAR imaging algorithm which is derived in case of TDM-MIMO realization and the algorithm is tested on a TDM-MIMO system. There are also several researches focused on near-field imaging [
24], Ground Based SAR(GB-SAR) applications [
25]. To tackle the problem of ghost targets caused by sparse MIMO array, an algorithm called Sequential Spatial Masking (SSM) is proposed for forward-looking TDM-MIMO-SAR imaging [
26]. As discussed above, the nature of TDM-MIMO brings challenges to imaging algorithms in nonstationary scenarios because different transmitters are activated separately. Since Synthetic Aperture Radar (SAR) systems rely on the relative movement between platforms and targets, TDM-MIMO brings difficulties to using TDM-MIMO for SAR imaging [
27]. Besides, to achieve higher resolution with TDM-MIMO array, it is often required to have more transmitters, which leads to a lower PRF. However, if a MIMO-SAR system is installed on a fast-moving platform, such as a car or an aircraft, a low PRF means grating lobes and ghost targets appears in SAR imaging process. Notably, it is the time-division nature of TDM-MIMO that brings obstacles to its applications MIMO-SAR 3D imaging on a fast-moving platform.
To further improve imaging capabilities of MIMO-SAR technique, the super-resolution algorithms are also applied and modified for MIMO-SAR imaging. Traditional imaging methods, which lack the super-resolution ability, are well-researched in MIMO imaging scenarios. For instance, back projection (BP) [
28] and rang migration (RM) [
29] have been implemented in high-resolution MIMO imaging. However, the performances of these methods highly depend on the aperture of virtual array. To further improve imaging ability, the compressed sensing theory, which has been strictly proved [
30], are widely used in radar imaging, including MIMO imaging and ISAR imaging [
31]. Therefore, numerous research has been focused on modifying and improving CS-based methods for MIMO and MIMO-SAR 3D imaging. In [
32], the author proposed a CS-based method combined with a 2-step motion compensation process for MIMO-SAR imaging. In [
33], a L1-norm minimization method is used to do spatial filtering for deep neural network (DNN) for MIMO-SAR 3D imaging in low signal-to-noise ratio (SNR) scenarios. Z. Zhou et al. [
34] made a comparison of BP and sparse Bayesian recovery via iterative minimum (SBRIM) and concluded that generally SBRIM has better imaging ability but suffers from high computational complexity. A tensor compressed sensing algorithm is proposed for 3D imaging with Cross-MIMO array [
35]. An efficient MIMO-SAR imaging algorithm based on alternating direction method of multipliers (ADMM) is conducted and validated by experimental results [36]. Most existing researches focus on computational efficiency, motion compensation and multipath effect. However, few researchers pay attention to super-resolution MIMO-SAR 3D imaging while considering the unique nature of TDM-MIMO.
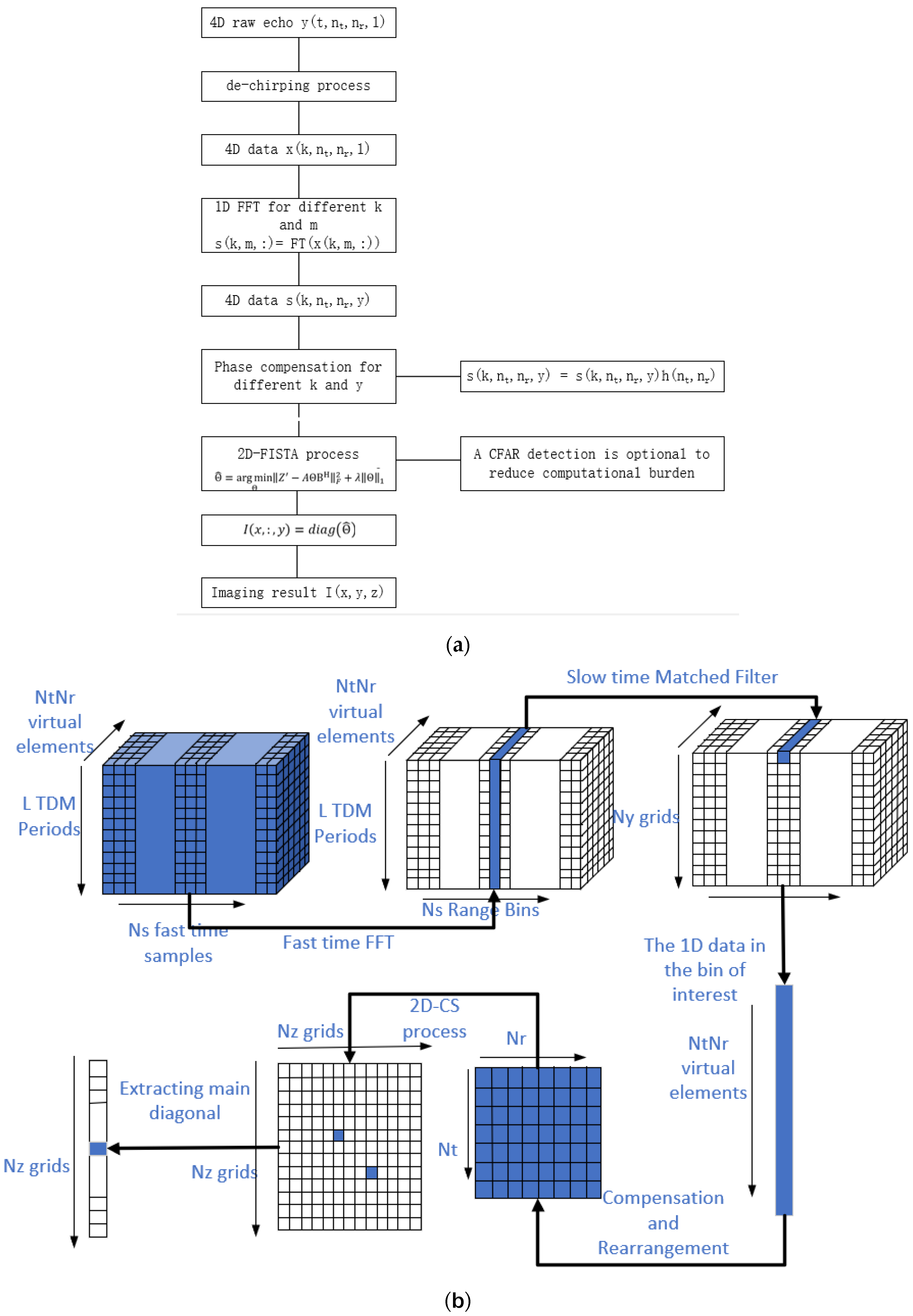
This article is mainly contributed to utilizing the property of TDM-MIMO to achieve unambiguous MIMO-SAR 3D imaging on a fast-moving platform. As discussed in paragraphs above, if a TDM-MIMO radar employs more transmitters to achieve high resolution, it will also have a lower PRF which makes MIMO-SAR imaging ambiguous on a fast-moving platform, such as a car or an aircraft. In this article, a novel CS-based super-resolution algorithm is proposed to achieve unambiguous MIMO-SAR 3D imaging by making good use of the phase shift caused by motion of platform. Through both simulation and real data experiments, we show that our algorithm perform well on a fast moving platform, while other methods fail.
The rest of this article is organized as follows. Details of the theory and the algorithm are shown in
Section 2. Simulation and experimental results are listed and discussed in
Section 3. Finally, a conclusion is presented in
Section 4.
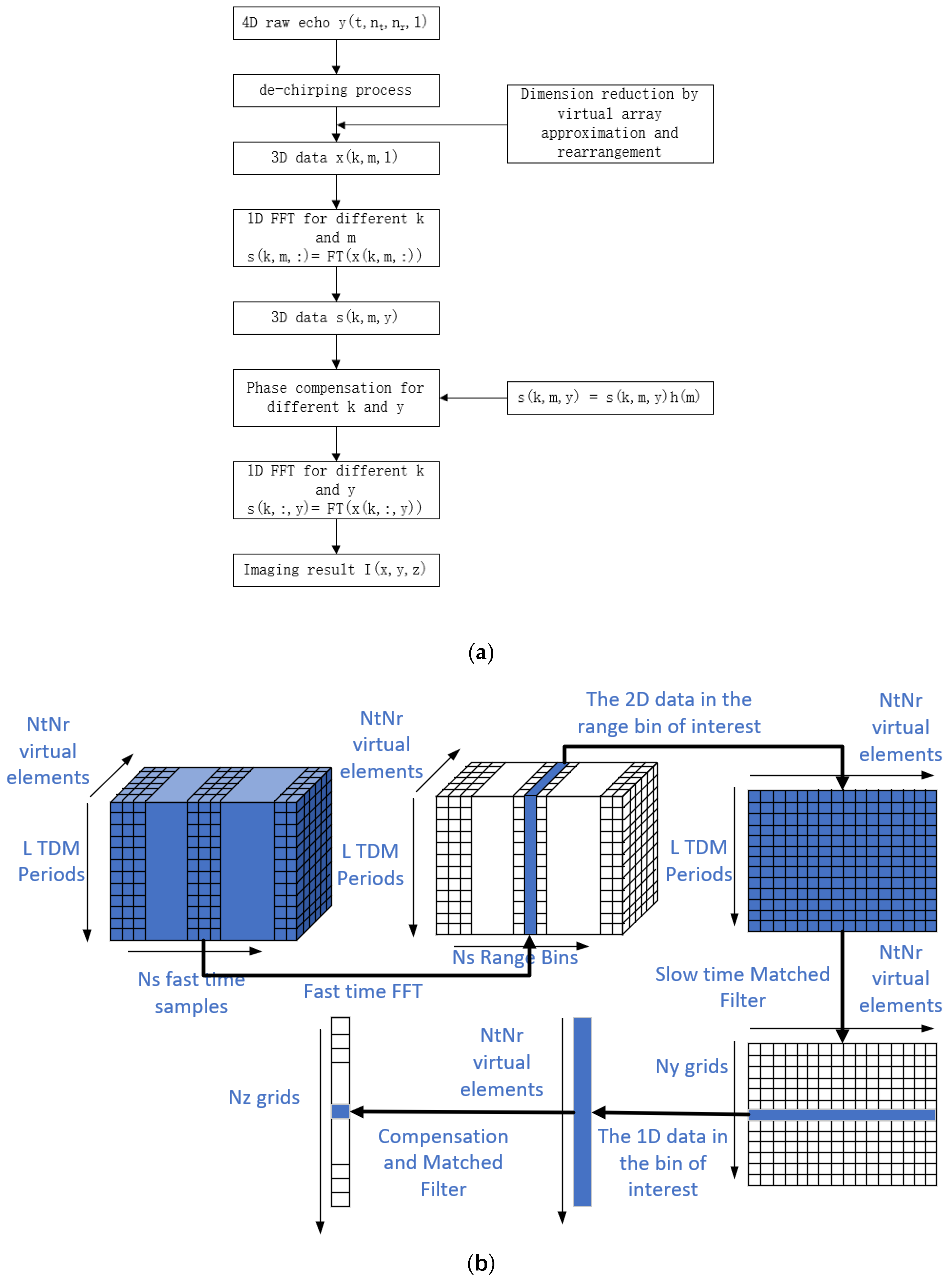
2. Signal Model
In this section, the signal model of TDM-MIMO-SAR 3D imaging is deduced and simplified. Moreover, our deductions are verified by simulation data.
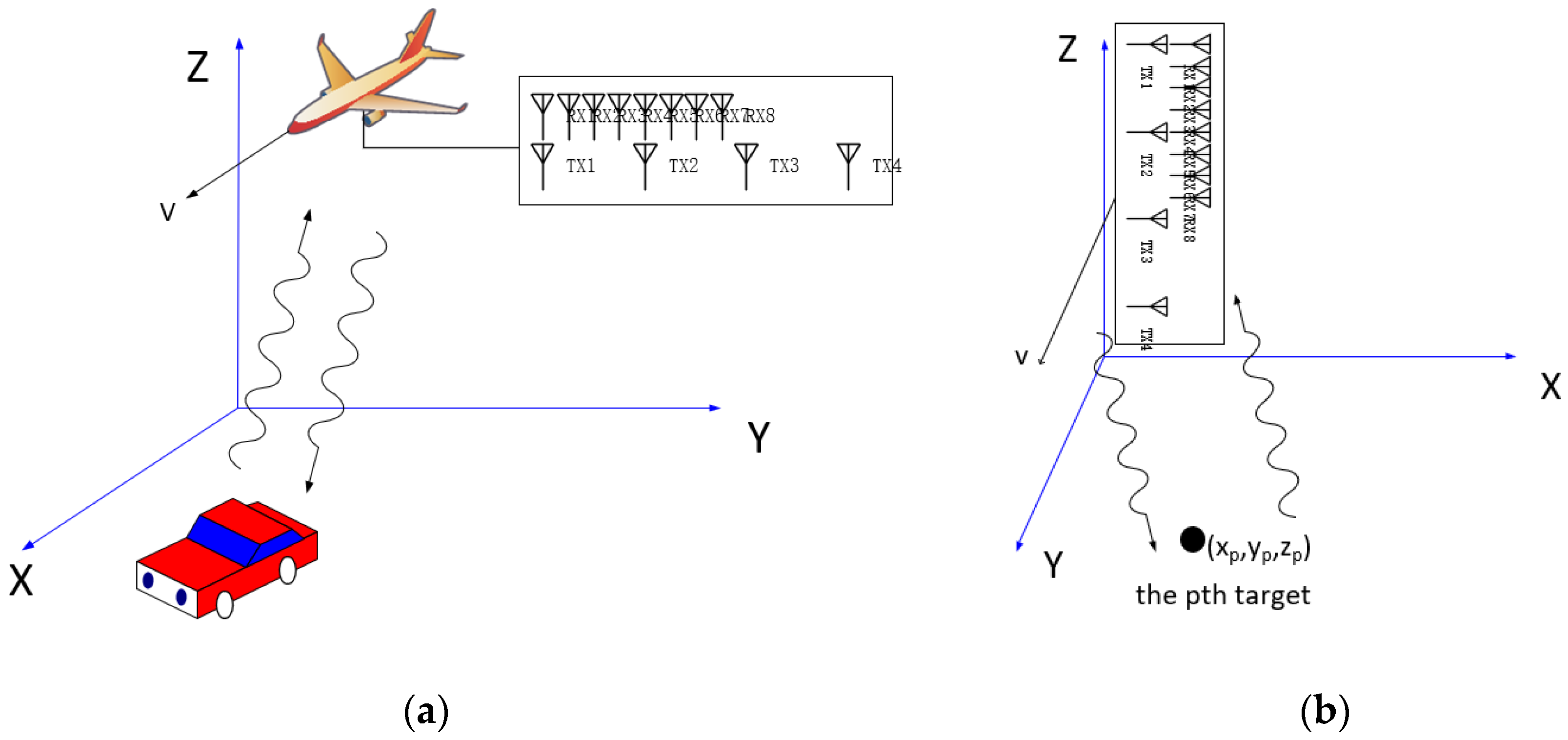
The geometry of TDM-MIMO-SAR 3D imaging is shown in
Figure 1.
Figure 1(a) demonstrates the imaging scenario of a typical airborne sensing application with a linear MIMO array of 4 transmitters and 8 receivers. For simplicity, an equivalent geometry is demonstrated in
Figure 1(b) where only one single point target is shown with its coordinates. In the following discussion, we will follow the notation and geometry depicted in
Figure 1(b), where the x axis, y axis and z axis stand for the cross-track direction, the track direction and the height direction. The linear TDM-MIMO array is distributed along the z axis, and thus the height resolution is provided by the MIMO array. The platform is moving along the y axis with a velocity
. The MIMO array composed of
transmitters and
receivers can be equivalent to
virtual elements. The inter-element space of transmitters and receivers are
and
.
stands for the wavelength of the transmitted signal. For a typical time-division working mode, it can be assumed that all receivers are activated during the entire TDM period, while transmitters take turns to transmit radar waves. A single TDM period contains
pulses and each pulse lasts for
seconds. So, a full TDM period lasts for
seconds. To complete a MIMO-SAR imaging working circle, it takes
TDM periods to transmit
pulses.
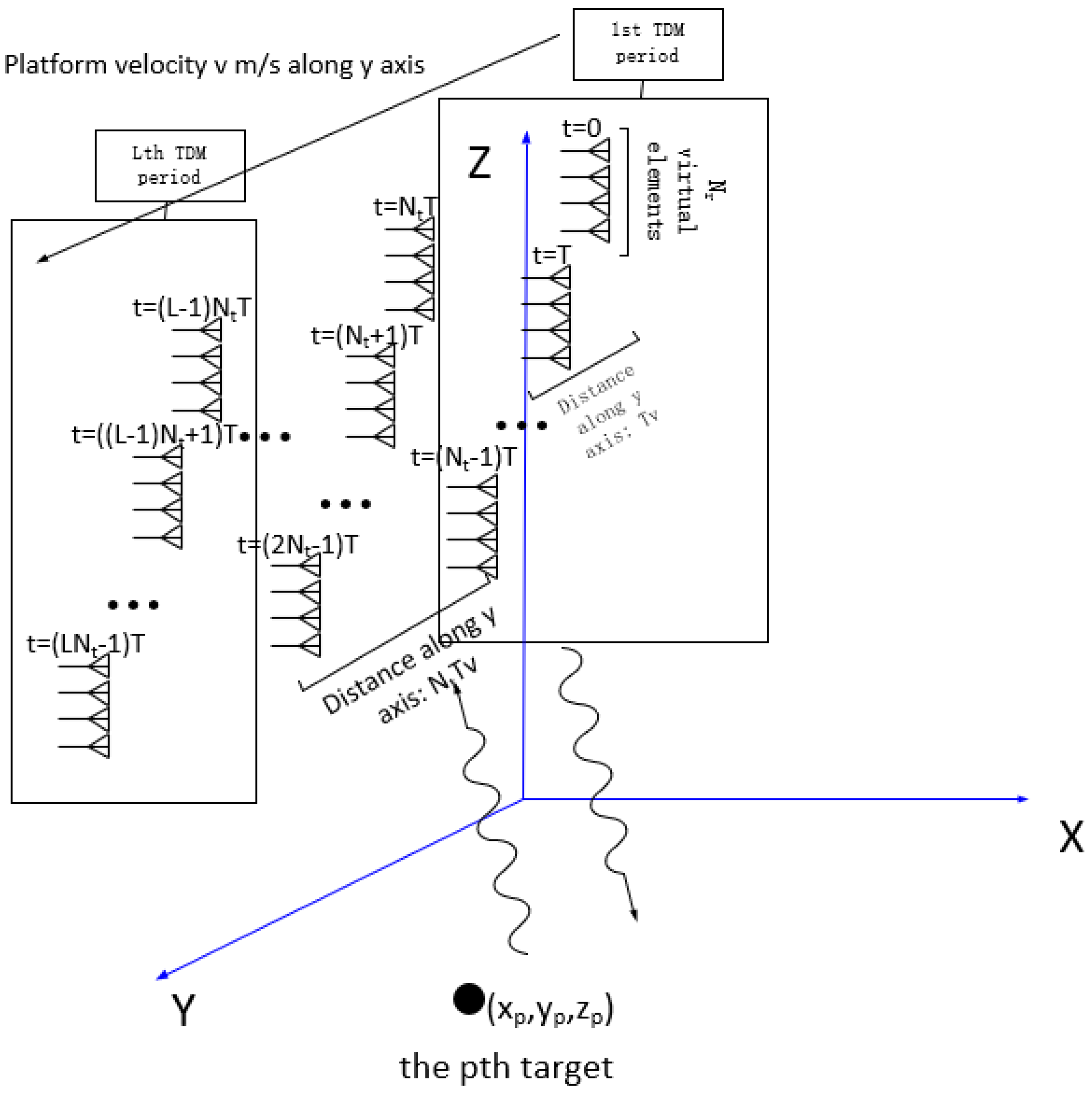
It is well known that virtual array approximation is useful and sufficient for most MIMO applications. In a TDM-MIMO-SAR working mode shown in
Figure 1(b), the equivalent virtual array is distributed in a two-dimensional aperture shown in
Figure 2. As discussed before, each TDM period costs for
seconds and the entire working circle which contains
TDM period lasts for
seconds. With a platform velocity of
m/s along y axis, the aperture length along y axis is
m, while the aperture length along z axis is
m. However, it is shown in
Figure 2 that due to the property of time-division working mode, virtual elements of the same TDM period are not exactly distributed on the same line. For instance, if we assume the coordinates of the first sub-aperture of
virtual elements in the first TDM period are
, the coordinates of the second sub-aperture in the first TDM period are
. There are several motion compensation methods developed to achieve 3D imaging for TDM-MIMO radar. However, these methods cannot exploit the full potential of TDM-MIMO-SAR. In the following sections, we will demonstrate a novel algorithm which can exploit this property of TDM-MIMO to achieve unambiguous 3D imaging.
For simplicity, we assume that the coordinates of the platform at time are , thus the transmitters are at and the receivers are at . With a velocity towards y axis, the platform moves to at the TDM period. Suppose that there are targets with corresponding coordinates . For a virtual element synthesized by the transmitter and the receiver, the baseband receiver signal reflected by the target is written as
Where denotes the fast time of one pulse, is the reflection coefficient of the targets and is the baseband signal transmitted by antennas. For simplicity, we assume that a chirp signal which is widely used in radar imaging is employed in the MIMO-SAR application.
Where represents the slope of the frequency change and is the carrier frequency. For a de-chirping process, the received signal is multiplied by the complex conjugate of the transmitted signal.
A Fast Fourier Transform (FFT) can be conducted to complete the de-chirping process.
Where represents the range bin. The equation above can be further simplified and rewritten as
means that the target is on the range bin. Sum up reflected signals of all targets and gaussian noise. After the de-chirping process, the four-dimensional sampled data can be expressed as
Where represents an additive white gaussian noise. According to the virtual array approximation, equation (7) can be approximated to a more concise form. The coordinates of virtual element of the transmitter and receiver discussed above, which is the virtual element, should be . For simplicity, this virtual element is called the virtual element and the distance between the virtual element and the target is denoted as .
Similarly, can also be approximated according to the virtual element approximation.
By combining the equation (12) and equation (13), we get an approximation of equation (7). The second approximation in equation (14) is done by the far field assumption.
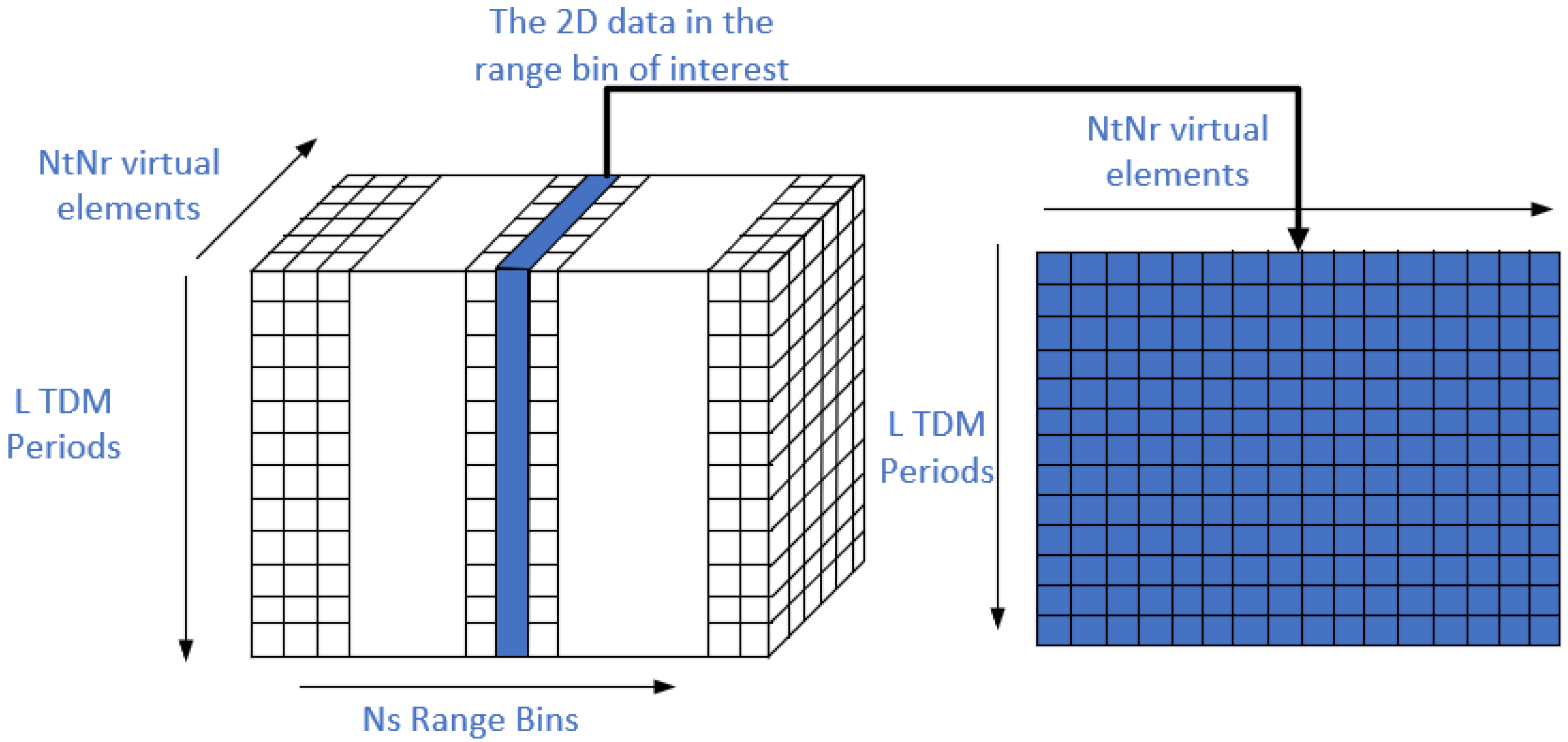
With the virtual array approximation, the four-dimensional data can be reshaped to a three-dimensional cube shown in
Figure 3. For simplicity, we assume that
is small enough that range cell migration does not happen in one MIMO-SAR working circle and both the synthetic aperture and MIMO aperture are significantly smaller than the rang distance of the target and the radar, such that the far field assumption can be established.
By dividing the data into separate 2d matrix, we can further simplify the 3D imaging problem to a 2D imaging problem in every range bins. Suppose that the target is in the range bin. The corresponding 2d data matrix can be denoted as
Where represents the virtual element and represents the TDM-period. The coordinates of this virtual element are . By introducing the far-field assumption, the equation (15) can be simplified.
Equation (17) is a result of ignoring constant term and quadratic term while substituting (16) for (15). The echo signal can be expressed as:
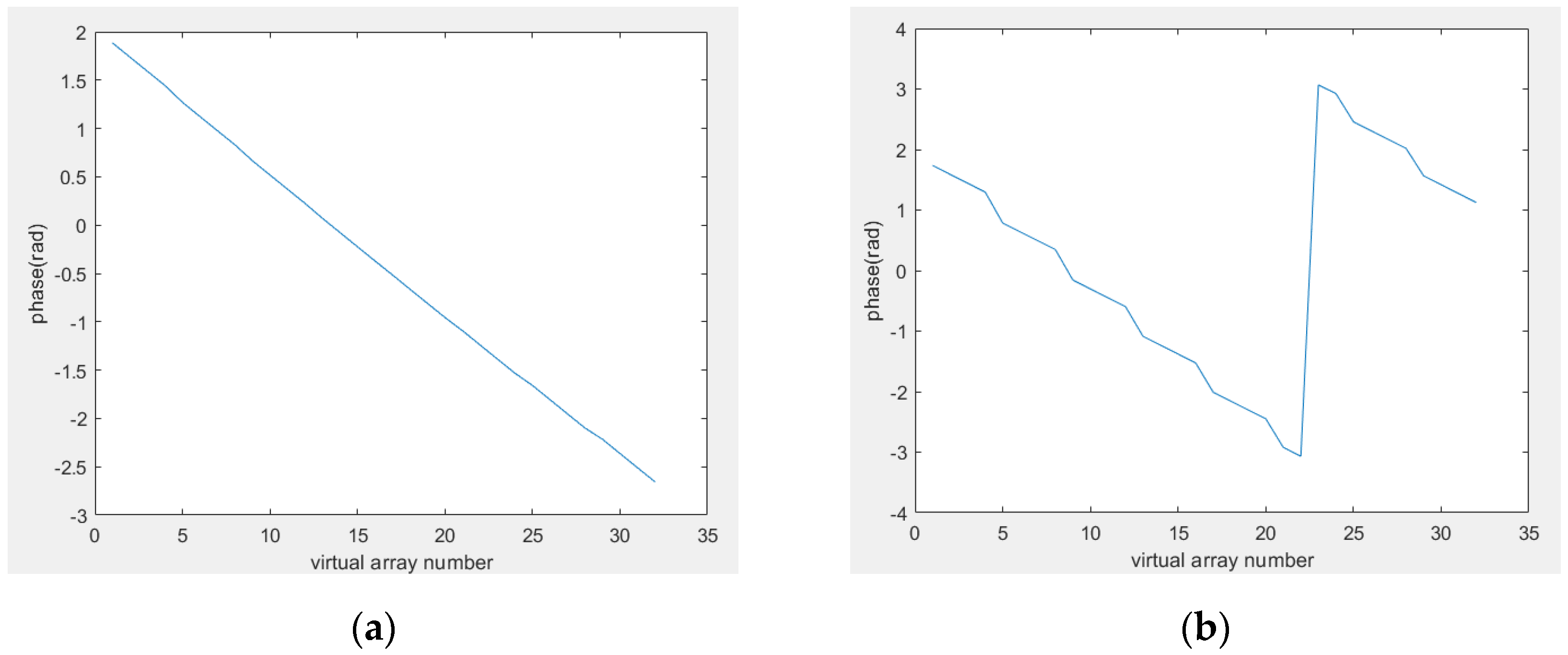
It is shown clearly in equation (18) that the TDM-MIMO-SAR 3D imaging is different from a naïve 2d imaging problem, as the property of time-division working mode introduces additional phase shift. Moreover, the phase shift is proportional to the exact
of the target location. By simulation, our deduction can be validated in
Figure 4.
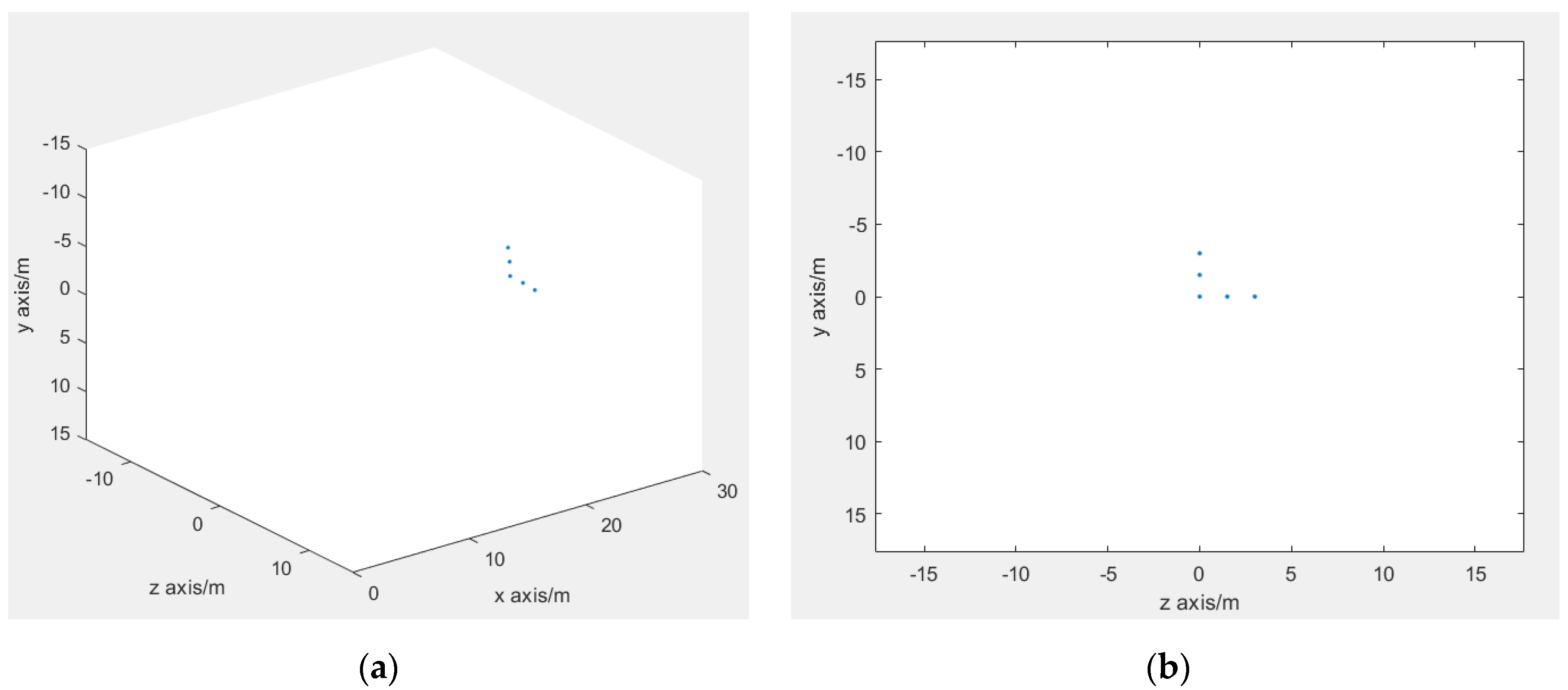
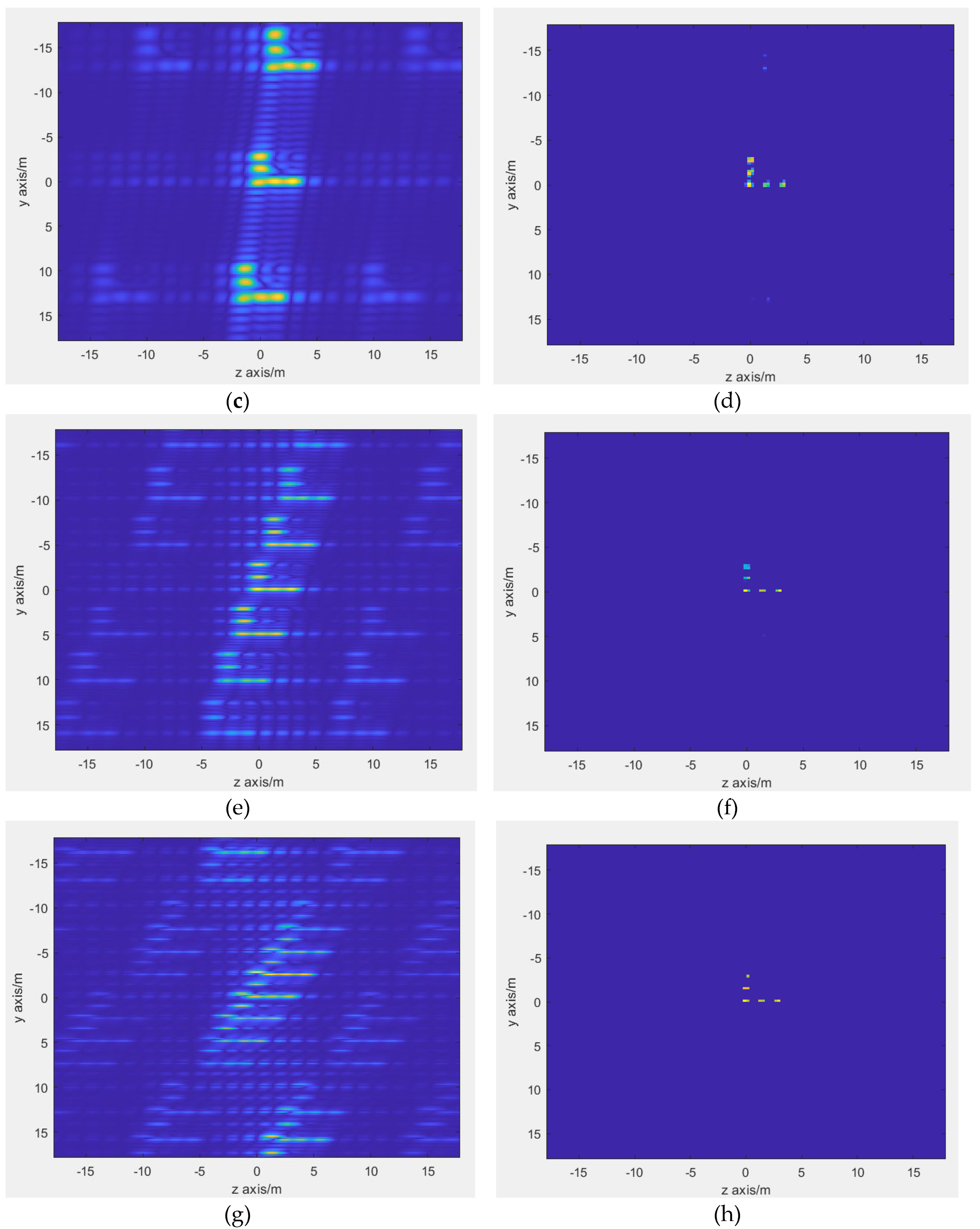
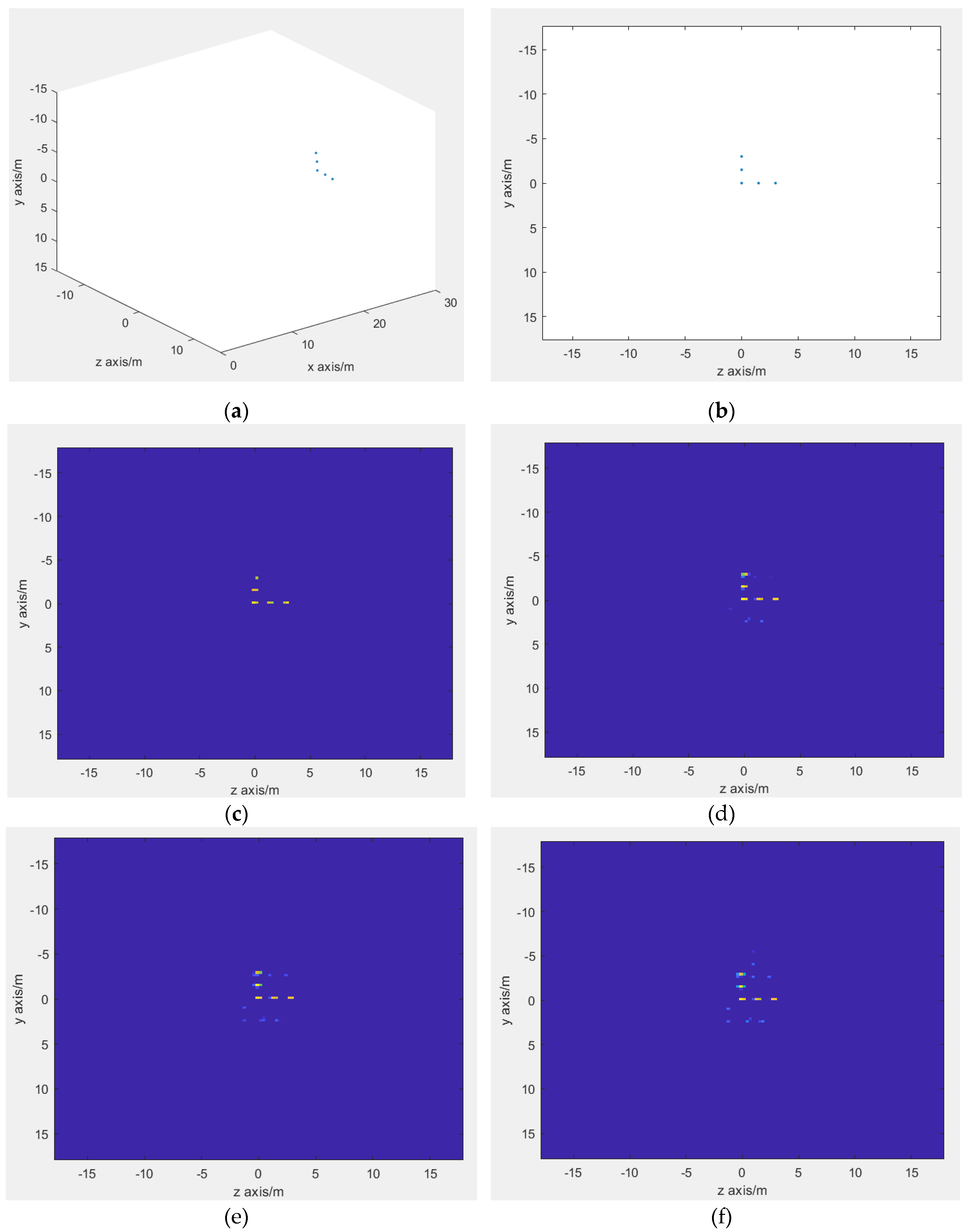
Figure 4 shows a simulation of a TDM-MIMO-SAR echo signal data after pulse compression. Details about the simulation settings are listed in
Table 1.