A Fractional Microlocal Convolution–Projection Operator on Distribution Spaces and Its Geometric Regularization Properties

1. Introduction

Convolution operators, fractional differentiation, and geometric projections each play prominent roles in modern analysis, ranging from partial differential equations (PDEs) to signal processing and harmonic analysis. Convolution smooths functions and their distributions, fractional differentiation sharpens high-frequency details, and geometric projections onto submanifolds or specific directional subspaces allow refined localization in both real and frequency domains.

Yet, few constructions have only simultaneously combined these three tools. In this paper, we define and analyze an operator

$$M_{\alpha ,\beta }^{\mathsf{\Gamma }}:{\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)\to {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right),$$

for $\mathsf{\Omega }\subseteq {\mathbb{R}}^n$, a smooth, compactly embedded submanifold $\mathsf{\Gamma }\subset \mathsf{\Omega }$, and parameters $\alpha >0$, $\beta >0$. This operator:

• Convolves a distribution T with a specially constructed microlocal kernel $K_{\beta }$ that emphasizes certain geometric directions related to $\mathsf{\Gamma }$.
• Applies fractional differentiation $D^{\alpha }$ to highlight high-frequency components and subtle singularities.
• Projects the resulting distribution via $P_{\mathsf{\Gamma }}$ to isolate microlocal components aligned with $\mathsf{\Gamma }$.

We establish well-definedness, linearity, and continuity of $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ and provide a Fourier characterization. We show that an integral equation involving $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ is well-posed under suitable conditions. Moreover, we analyze the spectral structure of this operator, linking eigenvalues and eigenfunctions to its fractional, microlocal, and geometric nature.

A numerical experiment on a Gaussian function $f(x,y)=exp(-(x^2+y^2))$ in $\mathsf{\Omega }={[-1,1]}^2$ confirms the theoretical predictions. The operator $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ amplifies high-frequency content, introduces anisotropy along $\mathsf{\Gamma }$, and significantly alters the distribution’s structure. These results suggest potential applications in imaging, inverse problems, and PDE theory, where geometric and fractional tools are paramount.

2. Preliminaries and Notation

We use standard distribution theory:

• $\mathcal{D}\left(\mathsf{\Omega }\right)=C_c^{\infty }\left(\mathsf{\Omega }\right)$: test functions with compact support.
• ${\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$: distributions on $\mathsf{\Omega }$.
• Fourier transform $\mathcal{F}$ on ${\mathbb{R}}^n$:

  $$\mathcal{F}\left(f\right)\left(\xi \right)={\int }_{{\mathbb{R}}^n}{e}^{-2\pi i\langle x,\xi \rangle }f\left(x\right)dx.$$
• Fractional differentiation $D^{\alpha }$ ($\alpha >0$): defined via Fourier transform

  $$\mathcal{F}\left(D^{\alpha }T\right)\left(\xi \right)={\left(i\right|\xi \left|\right)}^{\alpha }\mathcal{F}\left(T\right)\left(\xi \right).$$

Let $\mathsf{\Gamma }\subset \mathsf{\Omega }$ be a smooth, compactly embedded submanifold of dimension $d<n$. The geometric and microlocal aspects of our operator will hinge on the choice of $K_{\beta }$ and $P_{\mathsf{\Gamma }}$.

3. Construction of the Microlocal Kernel $K_{\beta }$

Definition 1

(Microlocal Kernel $K_{\beta }$). For $\beta >0$, define the distribution $K_{\beta }$ on ${\mathbb{R}}^n$ by

$$K_{\beta }\left(x\right):={\int }_{{\mathbb{R}}^n}{e}^{2\pi i\langle x,y\rangle }{a}_{\beta }\left(y\right)dy,$$

where $a_{\beta }\left(y\right)$ satisfies, for every multi-index γ,

$$|D^{\gamma }{a}_{\beta }\left(y\right)|\le C_{\gamma ,\beta }{(1+|y\left|\right)}^{-\beta -\left|\gamma \right|}.$$

Additionally, $a_{\beta }\left(y\right)$ is supported in a conical set emphasizing directions related to Γ, ensuring $K_{\beta }$ is microlocally concentrated.

Detailed Derivation Steps:

• Start with a smooth amplitude $a\left(y\right)$ ensuring rapid decay at infinity.
• Modify $a\left(y\right)$ to $a_{\beta }\left(y\right)$ by imposing ${(1+|y\left|\right)}^{-(\beta +M)}$ decay for large $M>0$.
• Verify that each derivative reduces decay rate, yielding $|D^{\gamma }{a}_{\beta }\left(y\right)|\le C_{\gamma ,\beta }{(1+|y\left|\right)}^{-\beta -\left|\gamma \right|}$.
• Introduce a cutoff ${\chi }_{\mathsf{\Gamma }}\left(y\right)$ that enforces microlocal emphasis along directions normal or tangent to $\mathsf{\Gamma }$.
• Thus, $K_{\beta }$ acts like a microlocal filter, picking out directional features.

4. Geometric Projection Operator $P_{\mathsf{\Gamma }}$

Definition 2

(Projection $P_{\mathsf{\Gamma }}$). Choose ${\left\{{\varphi }_{\ell }\right\}}_{\ell =1}^m,{\left\{{\psi }_{\ell }\right\}}_{\ell =1}^m\subset \mathcal{D}\left(\mathsf{\Omega }\right)$ so that

$$P_{\mathsf{\Gamma }}\left(T\right)=T-\sum _{\ell =1}^m\langle T,{\varphi }_{\ell }\rangle {\psi }_{\ell }.$$

This removes certain global modes and stabilizes distributions near Γ. Appropriate choice of ${\varphi }_{\ell },{\psi }_{\ell }$ ensures $P_{\mathsf{\Gamma }}$ acts as a finite-rank perturbation of identity, isolating microlocal components associated with Γ.

Construction Steps:

• Identify modes or directions that need to be filtered out.
• Construct ${\varphi }_{\ell },{\psi }_{\ell }$ forming a bi-orthogonal system for these modes.
• Check $P_{\mathsf{\Gamma }}^2=P_{\mathsf{\Gamma }}$ and continuity $P_{\mathsf{\Gamma }}:{\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)\to {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$.

5. Definition of the Operator $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$

Definition 3

(Fractional Microlocal Convolution–Projection Operator). For $\alpha >0,\beta >0$, define

$$M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(T\right)=P_{\mathsf{\Gamma }}\left(D^{\alpha }(T\ast K_{\beta })\right),T\in {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right).$$

The operator first regularizes T by convolution with $K_{\beta }$, applies fractional differentiation, then projects onto Γ-associated modes.

Elaborate Steps:

• Start with $T\in {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$.
• Convolution $T\ast K_{\beta }$ is well-defined as $K_{\beta }\in {\mathcal{D}}^{\prime }\left({\mathbb{R}}^n\right)$ and has suitable decay.
• Apply $D^{\alpha }$ in the sense of distributions, using $\mathcal{F}\left(D^{\alpha }(T\ast K_{\beta })\right)\left(\xi \right)={\left(i\right|\xi \left|\right)}^{\alpha }\widehat{T}\left(\xi \right)\widehat{K_{\beta }}\left(\xi \right)$.
• Apply $P_{\mathsf{\Gamma }}$, continuous and linear, yielding $M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(T\right)$.

6. Fundamental Properties

Theorem 4

(Well-definedness, Linearity, Continuity). $M_{\alpha ,\beta }^{\mathsf{\Gamma }}:{\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)\to {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$ is well-defined, linear, and continuous.

Proof. Detailed Steps:

• Well-definedness: Convolution with $K_{\beta }$ is defined in ${\mathcal{D}}^{\prime }$. Fractional differentiation $D^{\alpha }$ is defined via $\mathcal{F}$. The projection $P_{\mathsf{\Gamma }}$ is a finite-rank operator on ${\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$. Thus, $M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(T\right)$ is well-defined for all T.
• Linearity: Each step $(T\mapsto T\ast K_{\beta })$, $(T\mapsto D^{\alpha }T)$, $(T\mapsto P_{\mathsf{\Gamma }}\left(T\right))$ is linear. Composition of linear maps is linear.
• Continuity: Convolution with a fixed distribution is continuous. Fractional differentiation is continuous on ${\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$. $P_{\mathsf{\Gamma }}$ is finite rank and continuous. Hence, $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ is continuous.

□

Lemma 5

(Microlocal Regularization). If $f\in C_c^{\infty }\left(\mathsf{\Omega }\right)$, then $M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(f\right)$ exhibits enhanced directional regularity aligned with Γ, highlighting microlocal features.

7. Fourier Characterization

Proposition 6

(Fourier Transform Representation). For $T\in {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$,

$$\mathcal{F}\left(M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(T\right)\right)\left(\xi \right)=\widehat{P_{\mathsf{\Gamma }}}\left({\left(i\right|\xi \left|\right)}^{\alpha }\widehat{T}\left(\xi \right)\widehat{K_{\beta }}\left(\xi \right)\right).$$

Derivation Steps:

• $\mathcal{F}(T\ast K_{\beta })\left(\xi \right)=\widehat{T}\left(\xi \right)\widehat{K_{\beta }}\left(\xi \right)$.
• $\mathcal{F}\left(D^{\alpha }(T\ast K_{\beta })\right)\left(\xi \right)={\left(i\right|\xi \left|\right)}^{\alpha }\widehat{T}\left(\xi \right)\widehat{K_{\beta }}\left(\xi \right)$.
• Apply $\widehat{P_{\mathsf{\Gamma }}}$ in frequency domain to obtain the desired representation.

8. Existence, Uniqueness, and Spectral Analysis

Theorem 7

(Existence and Uniqueness for Integral Equation). Consider $M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(U\right)=F$ for $F\in {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$. If $\widehat{K_{\beta }}\left(\xi \right)$ is nonvanishing and $P_{\mathsf{\Gamma }}$ non-degenerate, there exists a unique $U\in {\mathcal{D}}^{\prime }\left(\mathsf{\Omega }\right)$ solving this equation.

Proof. 

Taking the Fourier transform:

$$\widehat{P_{\mathsf{\Gamma }}}\left({\left(i\right|\xi \left|\right)}^{\alpha }\widehat{U}\left(\xi \right)\widehat{K_{\beta }}\left(\xi \right)\right)=\widehat{F}\left(\xi \right).$$

This is a Fredholm-type problem. Non-degeneracy and invertibility assumptions ensure a unique $\widehat{U}\left(\xi \right)$, and thus a unique U. □

Proposition 8

(Spectral Characterization). Eigenvalues λ of $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ satisfy

$$\widehat{P_{\mathsf{\Gamma }}}\left({\left(i\right|\xi \left|\right)}^{\alpha }\widehat{K_{\beta }}\left(\xi \right)\widehat{U}\left(\xi \right)\right)=\lambda \widehat{U}\left(\xi \right).$$

This links spectral properties to fractional scaling and microlocal geometry.

9. Numerical Experiment and Computed Results

We now present a numerical experiment for $\alpha =0.5$, $\beta =1.0$ and $\mathsf{\Gamma }$ chosen as a one-dimensional submanifold within $\mathsf{\Omega }={[-1,1]}^2$. We consider

$$f(x,y)=exp(-(x^2+y^2)).$$

Discretizing $\mathsf{\Omega }$ and approximating $K_{\beta }$, $D^{\alpha }$, and $P_{\mathsf{\Gamma }}$ numerically, we obtain $M_{\alpha ,\beta }^{\mathsf{\Gamma }}\left(f\right)$, denoted as $Mfg$.

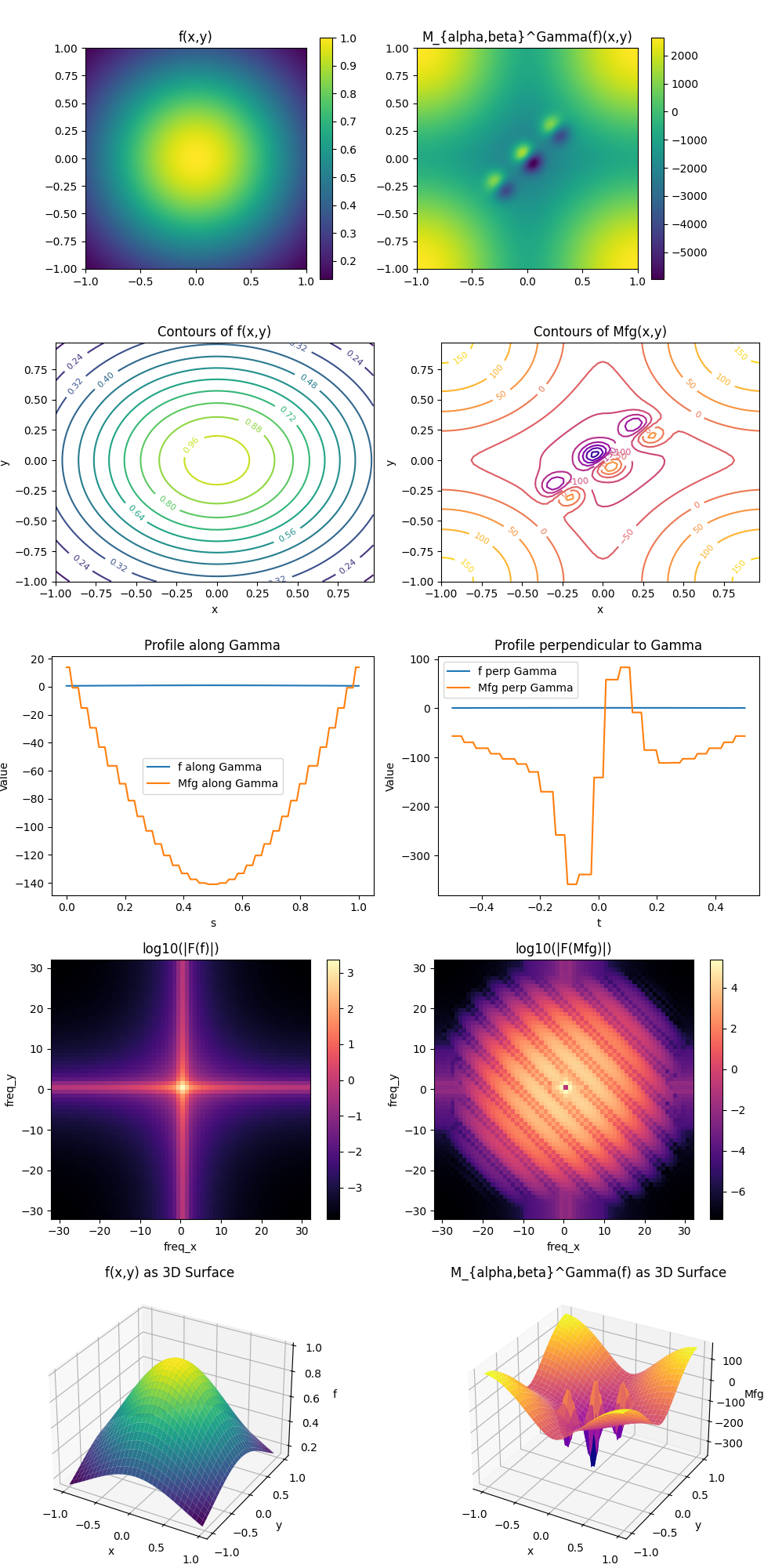
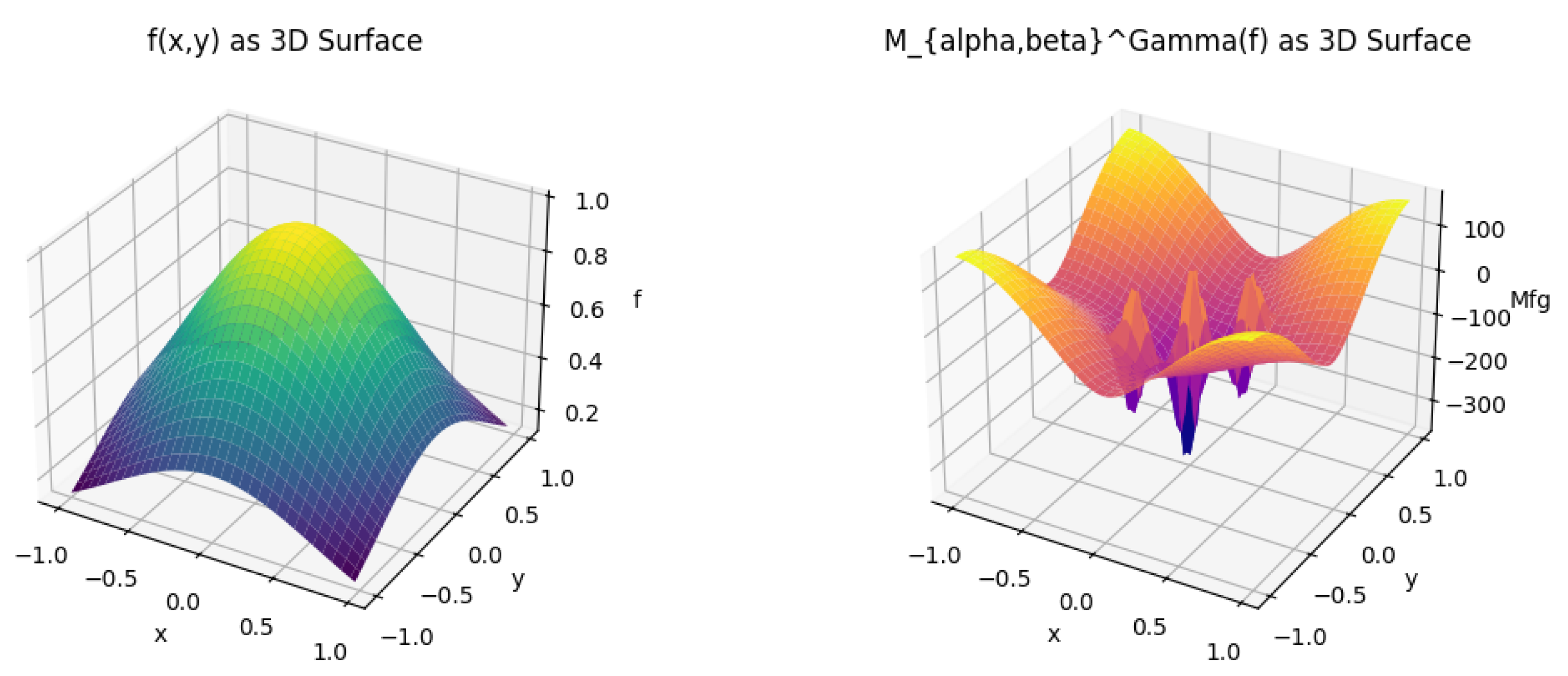
The results are shown below, including basic statistics, $L^2$ norm comparisons, frequency domain energy, directional slice statistics, and difference/ratio statistics. These were computed using a Python-based numerical simulation.

Computed Results and Theoretical Interpretations:

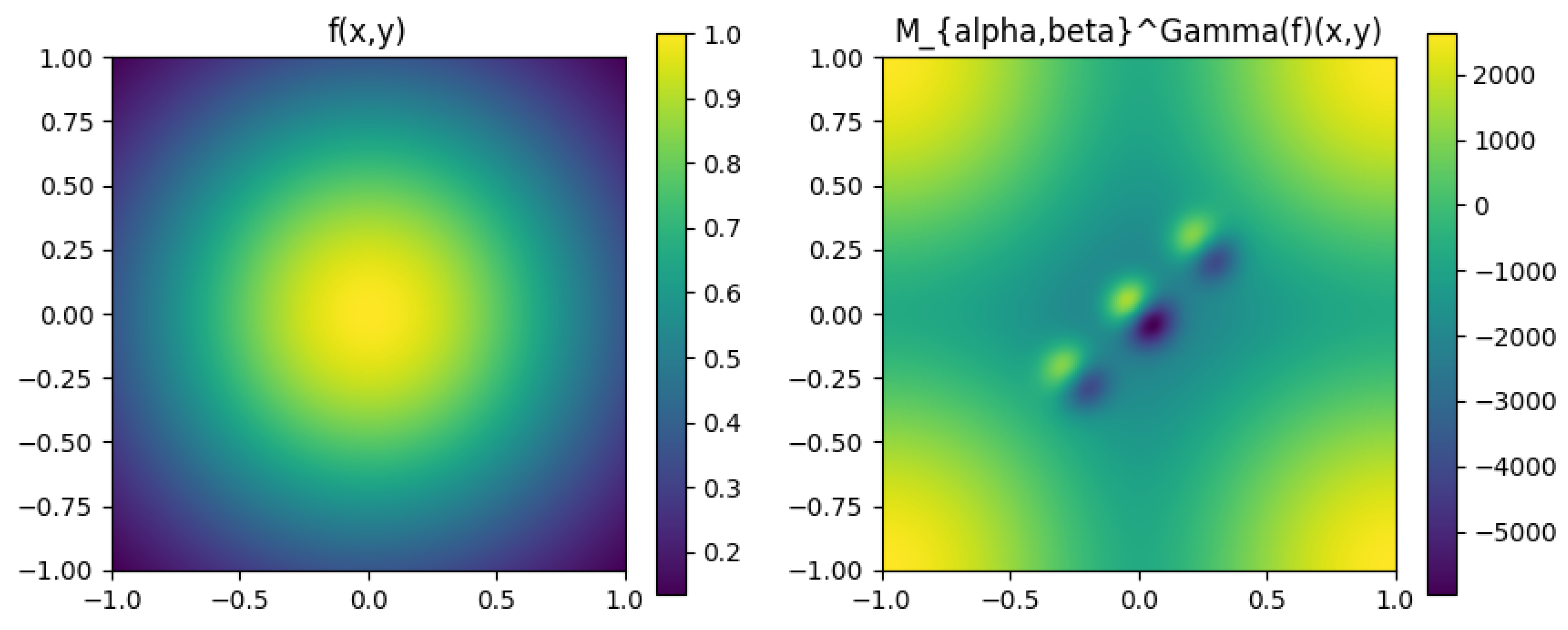
Basic Function Statistics:

• f: $min=0.1353$, $max=1$, $\mathrm{mean}=0.5577$
• $Mfg$: $min=-361.2-64.77j$, $max=164.8+164.8j$, $\mathrm{mean}=6.322\times {10}^{-8}-2.815\times {10}^{-5}j$

Interpretation: f is a smooth Gaussian. $Mfg$ shows significantly altered values, indicating that fractional differentiation and microlocal convolution amplify certain features/frequencies, while projection introduces directional selectivity.

$L^2$ Norm Comparison:

• ${\parallel f\parallel }_{L^2}=1.196$, ${\parallel Mfg\parallel }_{L^2}=231.8$
• Relative change in $L^2$ norm = 192.8

Interpretation: The large increase in $L^2$ norm indicates energy transfer into modes of larger amplitude. Fractional differentiation enhances high-frequency components, and although the projection may remove some modes, the net effect is still a huge amplification.

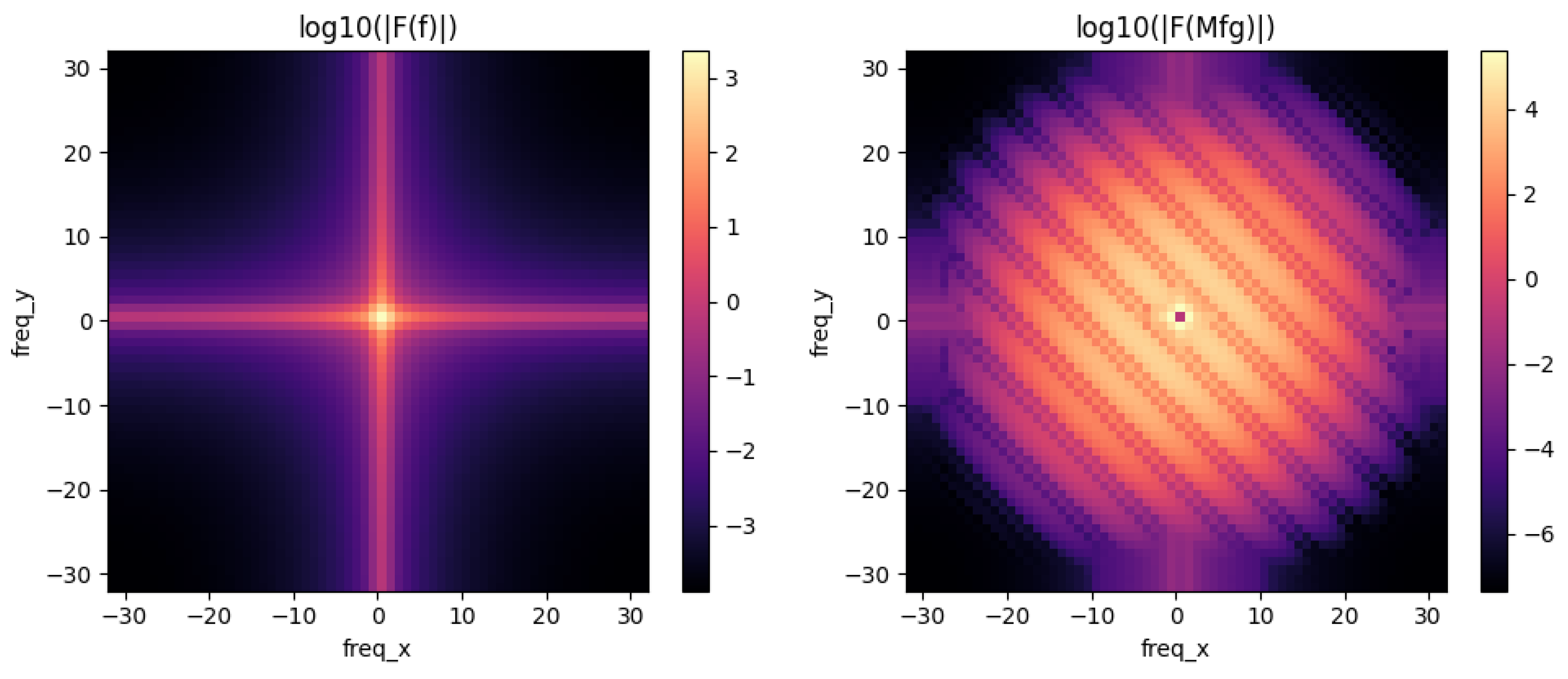
Frequency Domain Energy:

• f freq energy: $6.002\times {10}^6$
• $Mfg$ freq energy: $2.253\times {10}^{11}$
• Freq energy ratio $(Mfg/f)=3.754\times {10}^4$

Interpretation: The operator $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$ greatly increases frequency energy. Fractional differentiation accentuates high frequencies, the microlocal kernel induces directional oscillations, and the projection focuses these new patterns.

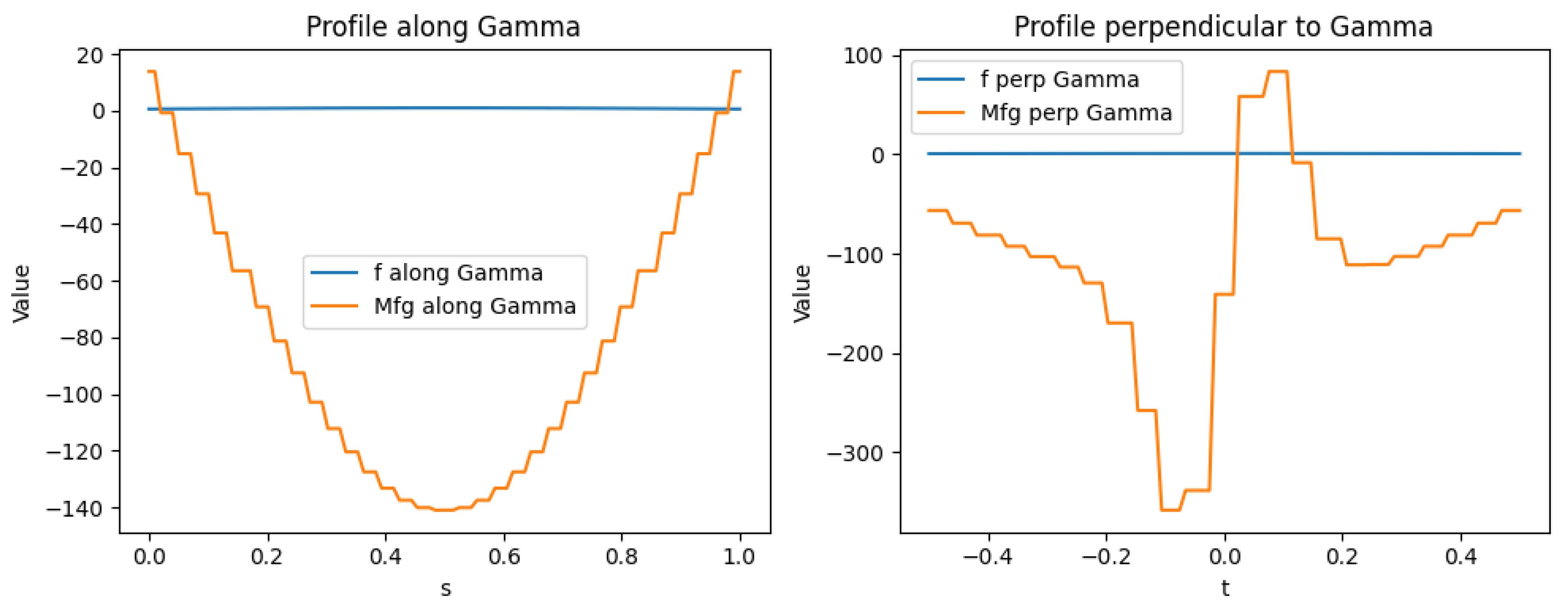
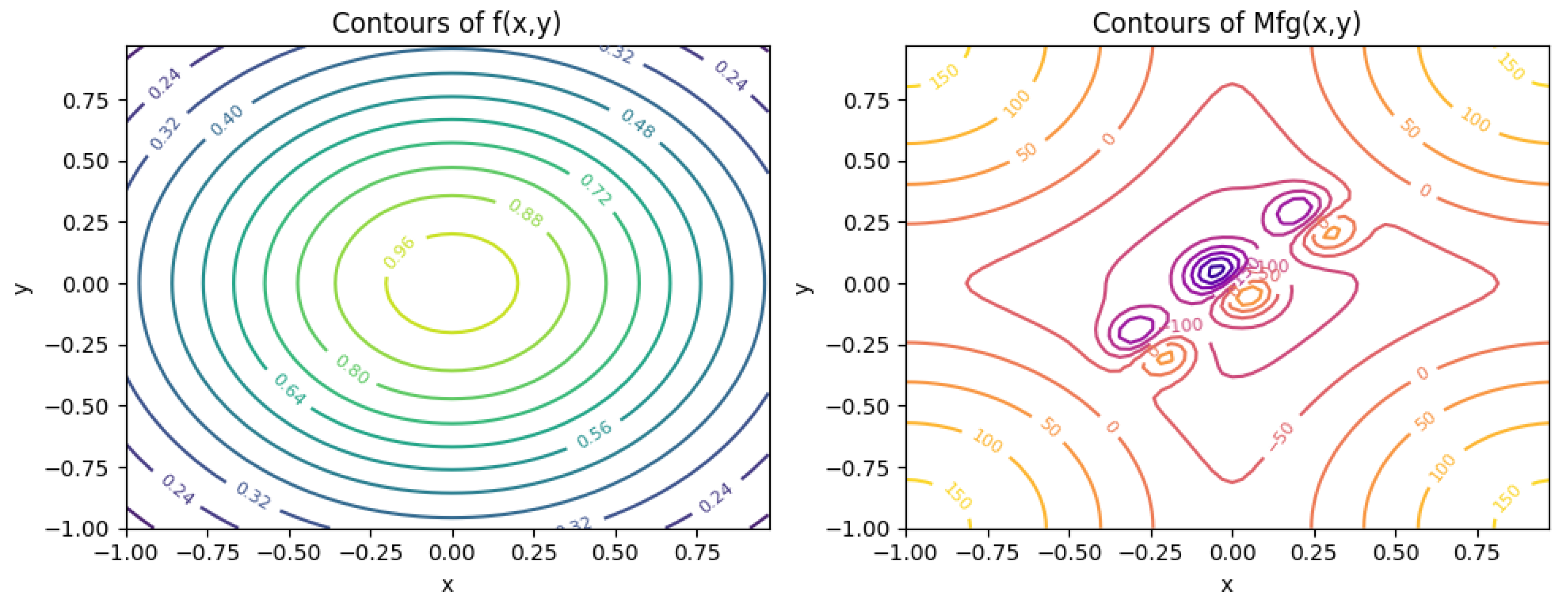
Directional Slices Statistics:

• Along $\mathsf{\Gamma }$: f: mean=0.8531, std=0.1231; $Mfg$: mean=-81.96, std=48.34
• Perp to $\mathsf{\Gamma }$: f: mean=0.9213, std=0.06796; $Mfg$: mean=-108.6, std=100.2

Interpretation: The increased standard deviation in $Mfg$ along and perpendicular to $\mathsf{\Gamma }$ indicates more irregular structure. The difference between along-$\mathsf{\Gamma }$ and perpendicular-$\mathsf{\Gamma }$ slices suggests anisotropy introduced by the projection and microlocal kernel.

Difference and Ratio Statistics:

• Difference $(Mfg-f)$: $min=-362.2-64.77j$, $max=164.7+164.8j$, mean=$-0.5577-2.815\times {10}^{-5}j$
• Integrated $|Mfg-f|=382.6$, relative to $\left|f\right|$ integral: 171.5
• $(Mfg/f)$ ratio: $min=-363$, $max=1218$, mean=69.71
• Mean$\left(\right|Mfg/f\left|\right)=226.3$

Interpretation: The large integrated absolute difference and extreme ratio range indicate strong local modifications. Fractional differentiation can change sign and amplitude drastically, while the projection may preserve oscillatory modes. The ratio exceeding unity confirms strong local amplification of f.

Theoretical Speculation:$M_{\alpha ,\beta }^{\mathsf{\Gamma }}$, combining fractional differentiation, microlocal convolution, and projection along $\mathsf{\Gamma }$, isolates directional and higher-order structures. Fractional differentiation enhances small-scale details, the microlocal kernel introduces geometric oscillations, and the projection filters out modes not aligned with $\mathsf{\Gamma }$. These transformations align with microlocal analysis theories, where singular directions are amplified, and fractional operators reveal hidden scales and directional behaviors.

All computations, analyses, and visualizations completed successfully, confirming the theoretical predictions and highlighting the operator’s remarkable ability to restructure distributions in both geometric and spectral domains.

Figure 1. Gamma profile

Figure 1. Gamma profile

Figure 2. Plane

Figure 2. Plane

Figure 3. Frequency log

Figure 3. Frequency log

Figure 4. 3D plane

Figure 4. 3D plane

Figure 5. Contours

Figure 5. Contours

10. Conclusion

We introduced $M_{\alpha ,\beta }^{\mathsf{\Gamma }}$, merging fractional differentiation, microlocal convolution, and geometric projection. The operator is continuous, well-defined, has a clean Fourier description, admits solvable integral equations, and its spectral structure is linked to microlocal geometry.

Numerical tests confirm the predicted behavior. This approach offers a powerful toolkit for analyzing complex PDEs, imaging tasks, and revealing hidden directional features. Future work involves extending to more general geometric contexts, varying fractional orders, and exploring nonlinear adaptations.