Optimal Control of Heat Equation by Coupling FVM and FEM Codes

1. Optimal Control Problem

The finite-volume framework, of which OpenFOAM is a prime example, is traditionally well-suited for flow applications of any kind. On the other hand, optimal control theory stems from the finite element framework and leverages many concepts that are naturally evaluated in that approach. In this section, we introduce the variational formulation of the optimal control problem to better understand what components are required for the implementation of an objective-oriented framework such as the one we display later in the paper. Each type of control is described considering the final equation system to be solved, and then the minimization algorithm is enforced by using a standard conjugate gradient method.

We recall some standard notation of functional spaces [10]. Let $\mathcal{O}$ be a domain $\Omega \subset {\mathbb{R}}^n$, with $n=2,3$, or its boundary $\Gamma$, or a part of it. Also, let $H^s\left(\mathcal{O}\right)$ be the standard Sobolev space of order s. Naturally, we have $H^0\left(\mathcal{O}\right)=L^2\left(\mathcal{O}\right)$. We now consider a cost function, or functional, in the following form

$$\mathcal{F}\left(u\right)={\displaystyle \frac{1}{2}}\left|\right|\varphi -{\varphi }_0{\left|\right|}_{L^2}+{\displaystyle \frac{\lambda }{2}}{\left|\right|u\left|\right|}_{H^S},$$

(1)

where $\varphi$ is a generic state variable subject to the control, ${\varphi }_0$ is the target, u is the control parameter and $\lambda$ represents a penalty coefficient. With the latter parameter, the regularization term can increase or decrease the penalization by different weights on the functional. We underline that regularization terms that involve the derivative of the control variable are not considered in this paper. Naturally, the first term in (1) represents the objective term or objective functional.

The control is performed on a steady-state temperature distribution without the convective term. Therefore, considering the gradient operator ∇ and the Laplacian operator $\Delta$, the state equation to be satisfied by the temperature $T\equiv \varphi$ is

$$\left\{\begin{array}{cccc}\hfill -\alpha \Delta T& =Q\hfill & \hfill & \mathrm{in}\Omega \hfill \\ \hfill T& =g_d\hfill & \hfill & \mathrm{on}{\Gamma }_D\hfill \\ \hfill \alpha \nabla T·\mathbf{n}& =g_n\hfill & \hfill & \mathrm{on}{\Gamma }_N,\hfill \end{array}\right.$$

(2)

where $\mathbf{n}$ represents the outward normal unit vector to the considered boundary, $\alpha$ is the thermal diffusivity, Q the volumetric source term, and $g_d$ and $g_n$ are two suitable functions defined on ${\Gamma }_D$ and ${\Gamma }_N$, respectively. The boundary $\partial \Omega$ is split into two parts: ${\Gamma }_N$ and ${\Gamma }_D$, with Neumann and Dirichlet boundary conditions applied. All the constraints of the problem are expressed in the Lagrangian, an auxiliary function defined as

$$\mathcal{L}(Q,T,T_a)=\mathcal{F}(T,Q)-{〈(-\Delta T-Q),T_a〉}_{L^2},$$

(3)

where $T_a$ is the Lagrangian multiplier or, in this case, the adjoint temperature. Naturally, we denote by $\langle ·,·\rangle$ the dot product.

For each type of control, the system of equations to be solved is derived, considering the state, the adjoint, and the control equation.

1.1. Distributed Control

The distributed control parameter is a volumetric heat source Q. Therefore, the functional is written as

$$\mathcal{F}(T,Q)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}{(T-T_d)}^{2}d\Omega +{\displaystyle \frac{\lambda }{2}}{\int }_{\Omega }{Q}^{2}d\Omega .$$

(4)

The adjoint problem is derived from the variational differentiation of the Lagrangian over the state variable. Thus, the equation for the adjoint temperature reads

$$\left\{\begin{array}{cccc}\hfill \alpha \Delta T_a& =-(T-T_d){\Theta }_{{\Omega }_d}\hfill & \hfill & \mathrm{on}\Omega ,\hfill \\ \hfill T_a& =0\hfill & \hfill & \mathrm{on}{\Gamma }_D,\hfill \\ \hfill \alpha \nabla T_a·\mathbf{n}& =0\hfill & \hfill & \mathrm{on}{\Gamma }_N,\hfill \end{array}\right.$$

(5)

where ${\Theta }_{{\Omega }_d}$ is the Heaviside function that is equal to one only in the target region ${\Omega }_d$. The adjoint equation is identical to the state formulation since we only consider the Laplacian operator. The right-hand side term is different from zero only in the target regions, as indicated by the Heaviside function.

The optimal control problem can be formulated as finding the minimum of the functional (4), condition for which the variables are considered optimal. We denote the optimal solution with an overline. Thus the optimal control $\overline{Q}$ must satisfy the Euler equation

$${\mathcal{F}}_F^{\prime }\left(\overline{Q}\right)=0,$$

(6)

where naturally ${\mathcal{F}}_F^{\prime }$ represents the Fréchet derivative of the functional $\mathcal{F}$ computed along the direction given by the control Q. Thus, deriving the functional with respect to the control parameter Q we obtain the following optimal control equation

$$\overline{Q}=-{\displaystyle \frac{\overline{T_a}}{\lambda }}.$$

(7)

The optimal control parameter $\overline{Q}$ follows exactly the optimal adjoint temperature $\overline{T_a}$ with an opposite sign and scaled by the parameter $\lambda$.

Although the Euler equation provides a definition of the optimal control variable, it is not sufficient for the numerical solution of the problem since it shows the behavior of the optimal solution of the optimization problem without any information on how to reach it. For most of the methods, the knowledge of the functional gradient is sufficient to calculate the direction for the functional minimization. For this reason, we consider the functional gradient

$${\mathcal{F}}_F^{\prime }\left(Q\right)=\lambda Q+T_a.$$

(8)

1.2. Neumann and Dirichlet Boundary Controls

For the Dirichlet boundary control, the control parameter is the imposed wall temperature $T_c$. Therefore, the state problem becomes

$$\left\{\begin{array}{cccc}\hfill -\alpha \Delta T& =Q\hfill & \hfill & \mathrm{in}\Omega ,\hfill \\ \hfill T& =g_d\hfill & \hfill & \mathrm{on}{\Gamma }_i,\hfill \\ \hfill T& =g_d+T_c\hfill & \hfill & \mathrm{on}{\Gamma }_c,\hfill \\ \hfill \alpha \nabla T·\mathbf{n}& =g_n\hfill & \hfill & \mathrm{on}{\Gamma }_N,\hfill \end{array}\right.$$

(9)

where ${\Gamma }_c$ is the controlled boundary. Note that for the Dirichlet boundary case, ${\Gamma }_D$ can be interpreted as the union of ${\Gamma }_i$ and ${\Gamma }_c$. The functional is rewritten as

$$\mathcal{F}(T,Q)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}{(T-T_d)}^{2}d\Omega +{\displaystyle \frac{\lambda }{2}}{\int }_{{\Gamma }_c}{T}_c^{2}d\Gamma ,$$

(10)

where the regularization term is calculated again in $L^2$. Note that, considering the temperature variable $T\in H^1(\Omega )$, its boundary value should be theoretically sought in the fractional space $H^{1/2}$. On the other hand, since the computation of fractional operators is not straightforward, we assume to compute the regularization term considering a standard $L^2$-norm. In this way, we expand the solution space for the control variable, considering less regularized solutions.

Similarly to the distributed control, the adjoint problem and the control equation are obtained through the differentiation of the Lagrangian functional. Therefore, we have the system for the adjoint variable

$$\left\{\begin{array}{cccc}\hfill \alpha \Delta T_a& =-(T-T_d){\Theta }_{{\Omega }_d}\hfill & \hfill & \mathrm{on}\Omega ,\hfill \\ \hfill T_a& =0\hfill & \hfill & \mathrm{on}{\Gamma }_i,{\Gamma }_c,\hfill \\ \hfill \alpha \nabla T_a·\mathbf{n}& =0\hfill & \hfill & \mathrm{on}{\Gamma }_N.\hfill \end{array}\right.$$

(11)

Again, writing explicitly the Euler equation, it is possible to find an optimal control definition for the problem as

$$\overline{T_c}=\alpha {\displaystyle \frac{\nabla \overline{T_a}{·\mathbf{n}|}_{{\Gamma }_c}}{\lambda }},$$

(12)

and the resulting functional gradient can be written as

$${\mathcal{F}}_F^{\prime }\left(T_c\right)=\lambda T_c-\alpha \nabla T_a{·\mathbf{n}|}_{{\Gamma }_c}.$$

(13)

For the Neumann boundary control, the control parameter is the heat flux H imposed at the wall. Therefore, the state problem and the functional are redefined as follows.

$$\left\{\begin{array}{cccc}\hfill -\alpha \Delta T& =Q\hfill & \hfill & \mathrm{in}\Omega ,\hfill \\ \hfill T& =g_d\hfill & \hfill & \mathrm{on}{\Gamma }_D,\hfill \\ \hfill \alpha \nabla T·\mathbf{n}& =g_n\hfill & \hfill & \mathrm{on}{\Gamma }_i,\hfill \\ \hfill \alpha \nabla T·\mathbf{n}& =H\hfill & \hfill & \mathrm{on}{\Gamma }_c,\hfill \end{array}\right.$$

(14)

where naturally now we have that ${\Gamma }_N={\Gamma }_i\cup {\Gamma }_c$. Therefore, the functional reads as

$$\mathcal{F}(\mathbf{u},T,g)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}{(T-T_d)}^{2}d\Omega +{\displaystyle \frac{\lambda }{2}}{\int }_{{\Gamma }_c}{H}^{2}d\Gamma .$$

(15)

Again, from the Lagrangian, the adjoint problem and the control equation can be derived and the adjoint system reads

$$\left\{\begin{array}{cccc}\hfill \alpha \Delta T_a& =-(T-T_d){\Theta }_{{\Omega }_d}\hfill & \hfill & \mathrm{on}\Omega ,\hfill \\ \hfill T_a& =0\hfill & \hfill & \mathrm{on}{\Gamma }_D,\hfill \\ \hfill \alpha \nabla T_a·\mathbf{n}& =0\hfill & \hfill & \mathrm{on}{\Gamma }_i,{\Gamma }_c.\hfill \end{array}\right.$$

(16)

From the Euler equation, the optimal control expression results

$$\overline{H}=-{\displaystyle \frac{\overline{T_a}}{\lambda }},$$

(17)

and the functional gradient becomes

$${\mathcal{F}}_F^{\prime }\left(H\right)=\lambda H+T_a.$$

(18)

1.3. Conjugate Gradient Method and Numerical Solution

To solve the stated problems numerically, we employ the conjugate gradient (CG) method [11]. This minimization technique belongs to the gradient descent family, along with the more common steepest gradient. These techniques are used for unconstrained optimization, where the control variable q is sought in the entire control space ${\mathbb{R}}^n$. The CG method approximates the optimal control $\overline{Q}$ through a sequence ${\left(Q^{\left(n\right)}\right)}_{n\in \mathbb{N}}$ such that, given a solution $Q^{\left(n\right)}$ at the n-th step, the solution at the following step is calculated using the formula

$${\mathbf{q}}^{\left(n+1\right)}={\mathbf{q}}^{\left(n\right)}+{\rho }^{\left(n\right)}{\mathbf{d}}^{\left(n\right)},$$

(19)

where the direction ${\mathbf{d}}^{\left(n\right)}$ is computed as

$${\mathbf{d}}^{\left(n\right)}=-\nabla \mathcal{F}\left({\mathbf{q}}^{\left(n\right)}\right)+{\beta }^{\left(n\right)}{\mathbf{d}}^{\left(n-1\right)}.$$

(20)

The parameter ${\beta }^{\left(n\right)}\in \mathbb{R}$ is obtained such that the directions ${\mathbf{d}}^{\left(n\right)}$ and ${\mathbf{d}}^{\left(n-1\right)}$ are conjugate with respect to the Hessian matrix $\mathbf{H}$, satisfying

$${\left({\mathbf{d}}^{\left(n\right)}\right)}^T\mathbf{H}{\mathbf{d}}^{\left(n-1\right)}=0,$$

(21)

and where $\mathbf{H}$ is constant, i.e. for a quadratic functional, we obtain the following expressions for $\beta$

$${\beta }^{\left(n\right)}={\displaystyle \frac{\nabla \mathcal{F}{\left({\mathbf{q}}^{\left(n\right)}\right)}^T\mathbf{H}{\mathbf{d}}^{\left(n-1\right)}}{{\left({\mathbf{d}}^{\left(n-1\right)}\right)}^T\mathbf{H}{\mathbf{d}}^{\left(n-1\right)}}}.$$

(22)

In order to make the computation easier, the formula (22) can be rewritten with the Fletcher-Reeves expression [12]

$${\beta }_{FR}^{\left(n\right)}={\displaystyle \frac{\left|\right|\nabla \mathcal{F}\left({\mathbf{q}}^{\left(n\right)}\right){\left|\right|}^2}{\left|\right|\nabla \mathcal{F}\left({\mathbf{q}}^{\left(n-1\right)}\right){\left|\right|}^2}},$$

(23)

that has been implemented in our numerical algorithm.

In (23) bold symbols have been used for scalar variables. Nevertheless, for the conjugate gradient method, the vectors must be interpreted as numeric vectors, i.e., the collection of the variable values on the degrees of freedom of the computational grid. Therefore, $\mathbf{q}$ represents the numeric vector that contains this value for each node, or a suitable numeric vector of values based on the specific discretization technique adopted for the system.

The numerical algorithm used for the minimization problem can be described in a number of steps. Initially, the vectors of the state variable $\mathbf{T}$, the adjoint variable ${\mathbf{T}}_a$, and the control variable $\mathbf{q}$ are initialized, along with the functional $\mathcal{F}$ and the auxiliary variable ${\mathbf{g}}_{old}$, which represents the functional gradient at the previous iteration. For the first iteration of the time loop, the descent direction ${\mathbf{d}}^{\left(0\right)}$ is initialized as the anti-gradient direction, similarly to the steepest gradient method.

After that, the time loop starts and the variables $\mathbf{T}$, ${\mathbf{T}}_a$, $\mathbf{q}$ and the functional $\mathcal{F}$ are updated. Naturally, the time loop must be interpreted as an iteration loop since our system is considered to be stationary. At this point, if the convergence conditions are not satisfied, the new search direction $\mathbf{d}$ is found calculating the current functional ${\mathbf{g}}_{new}$ and the parameter $\beta$. Otherwise, if the convergence is reached, the while loop is terminated, and the number of iterations and the value of the functional are collected.

Algorithm 1 illustrates only the mathematical aspects of the application since the coupling algorithm between the codes is shown in the next section. Therefore, this scheme does not take into account which code solves a specific numerical field but shows the logical order to find the numerical solution considering the necessary steps of the minimization procedure.

Algorithm 1 - Optimal Control

1: proceduremain()

Variables initialization.

2:     $n\leftarrow 0$    3:     ${\mathbf{q}}^{\left(0\right)}\leftarrow 0$    4:     ${\mathbf{T}}^{\left(0\right)}\leftarrow \mathbf{T}\left({\mathbf{q}}^{\left(0\right)}\right)$    5:     ${\mathbf{T}}_a^{\left(0\right)}\leftarrow {\mathbf{T}}_a\left({\mathbf{T}}^{\left(0\right)}\right)$    6:     ${\mathcal{F}}^{\left(0\right)}\leftarrow \mathcal{F}({\mathbf{T}}^{\left(0\right)},{\mathbf{q}}^{\left(0\right)})$    7:     ${\mathbf{g}}_{old}\leftarrow \nabla \mathcal{F}({\mathbf{q}}^{\left(0\right)},{\mathbf{T}}_a^{\left(0\right)})$    8:     $\mathbf{d}\leftarrow -{\mathbf{g}}_{old}$

Time loop.

9:     while not stop do   10:         ${\mathbf{q}}^{(n+1)}\leftarrow {\mathbf{q}}^{\left(n\right)}+\rho ·\mathbf{d}$   11:         ${\mathbf{T}}^{(n+1)}\leftarrow \mathbf{T}\left({\mathbf{q}}^{(n+1)}\right)$   12:         ${\mathbf{T}}_a^{(n+1)}\leftarrow {\mathbf{T}}_a\left({\mathbf{T}}^{(n+1)}\right)$   13:         ${\mathcal{F}}^{(n+1)}\leftarrow \mathcal{F}({\mathbf{T}}^{(n+1)},{\mathbf{q}}^{(n+1)})$   14:         if convergence then   15:            stop   16:         end if  17:         ${\mathbf{g}}_{new}\leftarrow \nabla \mathcal{F}({\mathbf{q}}^{(n+1)},{\mathbf{T}}_a^{(n+1)})$   18:         $\beta \leftarrow {\displaystyle \frac{\langle {\mathbf{g}}_{new},{\mathbf{g}}_{new}\rangle }{\langle {\mathbf{g}}_{old},{\mathbf{g}}_{old}\rangle }}$   19:         ${\mathbf{g}}_{old}\leftarrow {\mathbf{g}}_{new}$   20:         $\mathbf{d}\leftarrow -{\mathbf{g}}_{new}+\beta ·\mathbf{d}$   21:         $n\leftarrow n+1$   22:     end while  23: end procedure

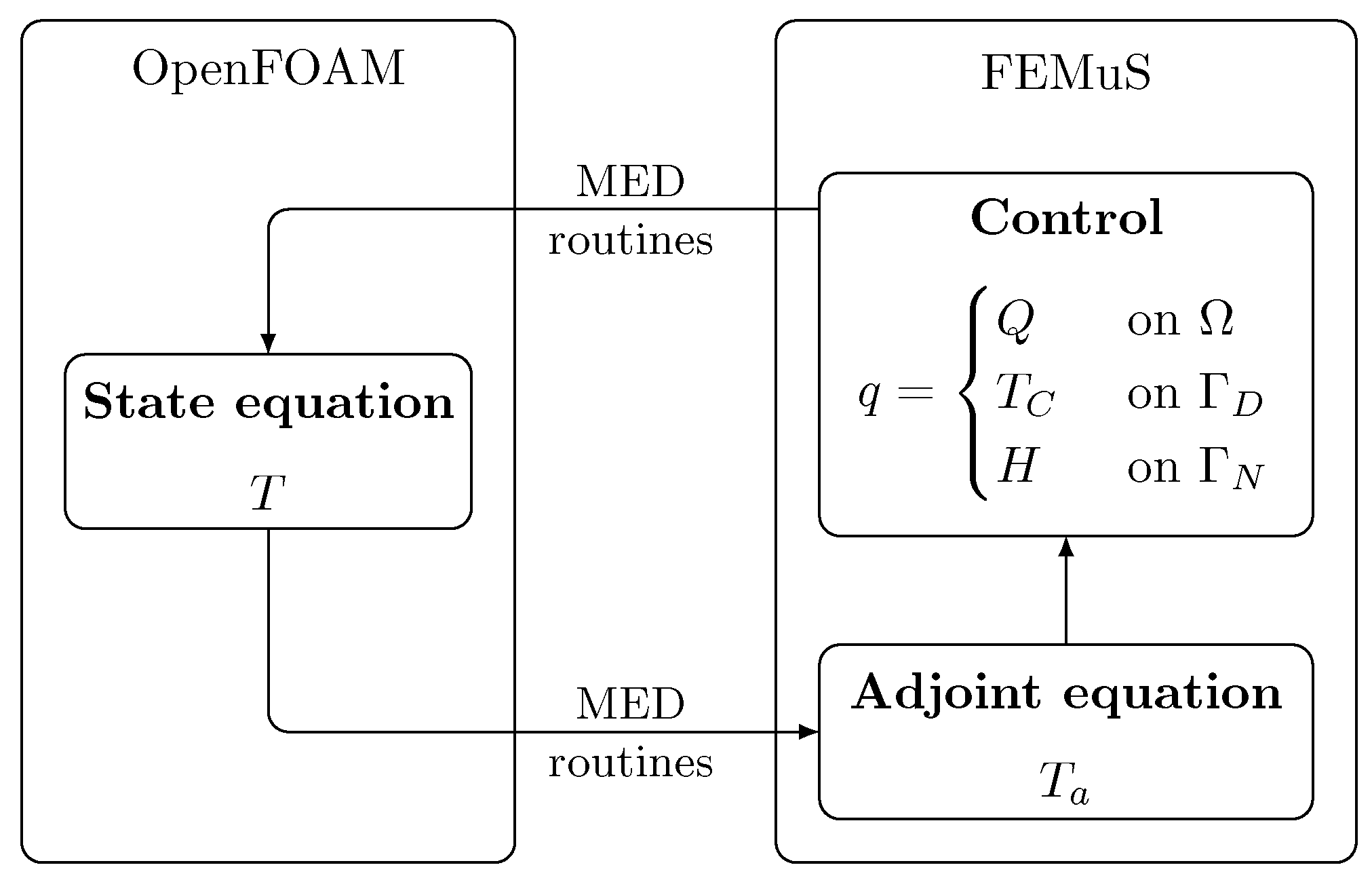
2. Coupling Algorithm

In this section, we briefly recall the algorithm for code coupling employed in this work, where an optimal control problem has been implemented considering two different numerical codes. The codes used in this work are FEMuS [13] and OpenFOAM [14], while the coupling interface has been built to exploit the MEDCoupling library [15]. While the first two codes are used to manage CFD problems, the MEDCoupling library is a module of the SALOME platform that is developed by CEA (Commissariat à l’énergie atomique et aux énergies alternatives) and EDF (Électricité de France) to share data at the memory level, avoiding the use of external files. The interested reader can consult [3] and reference therein for more details on the use of the library for coupling CFD codes.

Having in mind the mathematical setting of an optimal control problem as explained in Section 1, we briefly recall the coupling procedure between OpenFOAM and FEMuS in the optimal control context. The main idea presented in this work is to solve the state equation for the temperature field with OpenFOAM and the adjoint equation and the control q with FEMuS. Data transfer between state and adjoint variables is achieved through a class interface based on specific MEDCoupling functions. Specifically, following the equations described in Section 1, the state equation requires the evaluation of the control parameter q solved by FEMuS. In particular, for a distributed control, q is exchanged as a volumetric source for the temperature equation in OpenFOAM, while for the boundary control, q is transferred as a boundary condition. For the purpose of this specific paper, we added the possibility to exchange a normal gradient boundary condition from FEMus to OpenFOAM, as requested by the Neumann boundary control formulation in (14). A schematic representation of the coupling algorithm is presented in Figure 1, where ${\Omega }_D$ and ${\Omega }_N$ denote the Dirichlet and Neumann boundaries, respectively.

We remark that, in the coupling between a finite volume and a finite element mesh, the interpolation between the two computational grids assumes a pivotal role. Therefore, for the temperature field T solved in OpenFOAM, we exploit a $P_0-P_2$ interpolation towards FEMuS, where with $P_i$ we denote the polynomial of order $i-$th that approximates a numerical field. On the other hand, having solved q after the conjugate gradient step, we apply a $P_2-P_0$ interpolation from FEMuS to OpenFOAM, in order to set the control q as the volumetric source/boundary condition for T.

In Algorithm 2 we have reported a schematic overview of the coupling algorithm between FEMuS and OpenFOAM, including the routines employed. A brief description of each routine is reported on the right. The interested reader can find details in[3].

The coupling algorithm can also be divided into two main steps. The first collects the routines useful for the initialization of the interface between the two codes. Then, we have the iteration loop with the data transfer between the two codes, including the convergence criterion. Regarding the first block, the information related to both meshes is taken into account with the routine init_interface(). In fact, a MED mesh copy for each mesh is built knowing the connectivity map and the coordinate point set (create_mesh()). After that, MED fields for all relevant variables in the exchange can be built on top of the MED meshes. Each field is populated by the source code to prepare the transfer to the target code. This step can be done considering a cell/node-wise initialization depending on the source field type.

The first step of the iteration loop is to solve the state variable T in OpenFOAM and then extract its values. After that, these values, centered on cells, are interpolated into the biquadratic finite element mesh of FEMuS ($P_0-P_2$) and then stored in the corresponding data structure of the latter code. With this information, after the functional is evaluated, a convergence check is performed. Subsequently, the FEMuS code is equipped with all the information to solve its set of equations, i.e. the adjoint variable $T_a$ and the control q. The finite element solutions of these numerical fields are then interpolated from biquadratic FEM elements to piecewise value ($P_2-P_0$) in order to transfer these data into the OpenFOAM data structure. Naturally, only the control q is transferred, using the routine set_q_to_OF().

Algorithm 2 - Code Coupling

3. Numerical Results

In this section, we present some numerical results that outline the mathematical framework and numerical implementation described above. Specifically, we compare an optimal temperature control problem solved with two strategies. The first approach, which serves as a benchmark case, shows the results of the uncoupled case, i.e. only the FEMuS code is employed. The second approach exploits the coupling between FEMuS and OpenFOAM through the external library MEDCoupling for data transfer, as explained in Section 2.

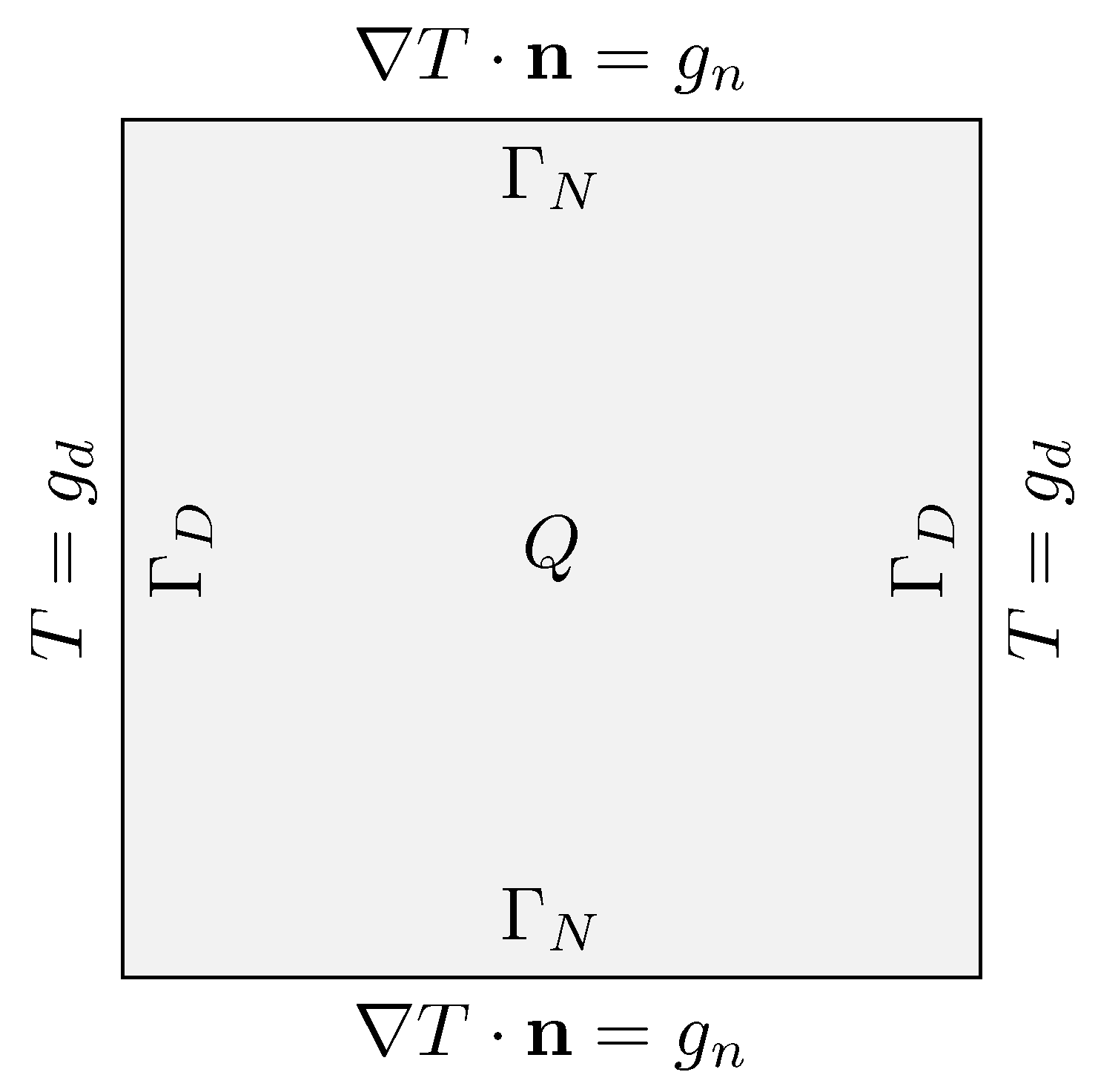
In both cases, we consider a square cavity as the problem domain, where a Poisson equation, i.e., the transport equation for the temperature field, is treated as the state equation and ${\Gamma }_D$ and ${\Gamma }_N$ represent boundaries with Dirichlet and Neumann conditions, respectively. The problem domain with the boundary conditions is reported in Figure 3. In particular, the steady-state case with a null convective term has been implemented and solved, leading to a Laplacian term equal to a right-hand side term in the form

$$\Delta T=Q.$$

(24)

The source field Q and the boundary conditions are described according to the different types of optimal control approach in the following sections. The boundary conditions $g_d,g_n$ are considered constant in ${\Gamma }_D$ and ${\Gamma }_N$, respectively. Boundary-type controls, which involve boundary conditions, are still initialized with $g_d$ or $g_n$, so at each step, we impose at the boundary $g_d$ (or $g_n$) plus $T_c$ (or H), where the control variable is initialized to zero.

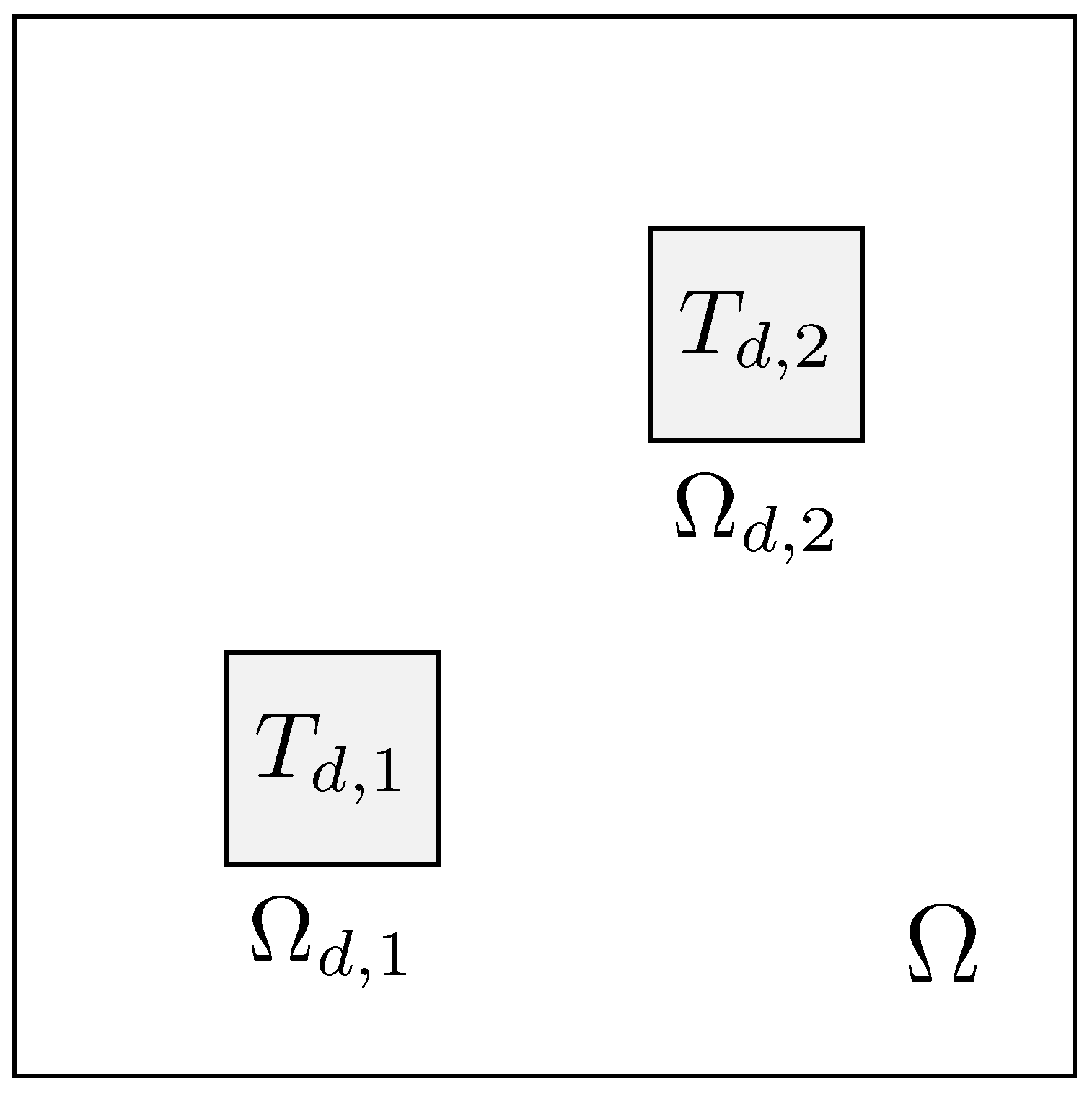
The objective functional, which relates the state variable T with the desired temperature $T_d$, remains the same for each type of control. In particular, we have

$$\mathcal{F}\left(T\right)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}{|T-T_d|}^{2}d\Omega ,$$

(25)

where ${\Omega }_d$ is made up of two square subregions of the domain $\Omega$. In Figure 4, a schematic representation of the domain is depicted, where we have $\Omega ={[0,L]}^2$, with $L=0.01$ m. In addition, for the target regions, we have ${\Omega }_{d,1}=[L/5,2L/5]\times [L/5,2L/5]$ and ${\Omega }_{d,2}=[3L/5,4L/5]\times [3L/5,4L/5]$ with targets $T_{d,1}$ and/or $T_{d,2}$, respectively.

For each simulation, we have considered $T_{d1}=-T_{d2}$.

Regarding the controlled regions, for each simulation, the regularization term is assumed to be solved on $\Omega$. Therefore, the considered functional is

$$\mathcal{F}(T,q)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}|T-T_d{|}^{2}d\Omega +{\displaystyle \frac{\lambda }{2}}{\int }_{\Omega }{\left|q\right|}^{2}d\Omega .$$

(26)

We recall that in the case of boundary control, the second integral on the right-hand side of (26) has a meaning only on the controlled portion of the domain, which is a portion of $\Gamma$, thus on the Dirichlet boundaries or on the Neumann ones.

Moreover, for each type of control, the results obtained with the coupled and uncoupled algorithms have been compared. In particular, we have considered the same $\lambda$, $\rho$, and the same criterion for the convergence. Specifically, considering the average functional of 10 iterations ${\overline{\mathcal{F}}}_i$ at the iteration i, the convergence has been obtained by

$${\displaystyle \frac{|{\overline{\mathcal{F}}}_i-{\overline{\mathcal{F}}}_{i-1}|}{{\mathcal{F}}_i}}<\epsilon ,$$

(27)

where $\epsilon$ has been set equal to ${10}^{-9}$. The average functional ${\overline{\mathcal{F}}}_i$ has been used instead of ${\mathcal{F}}_i$ to avoid false exits due to local plateaus encountered during oscillations in conjugate gradient descent.

A dimensionless formulation for the optimal control system is proposed to better show results with different dimensions or physical constants. Thus, the dimensionless state variable T, the dimensionless adjoint variable $T_a$ and the dimensionless control q are introduced as

$$\begin{array}{cccccc}\hfill T^{*}& ={\displaystyle \frac{T-g_d}{T_{ref}-g_d}},\hfill & \hfill T_a^{*}& ={\displaystyle \frac{T_a\alpha }{(T_{ref}-g_d)L^2}},\hfill & \hfill q^{*}& =\left\{\begin{array}{c}{Q}^{*}={\displaystyle \frac{Q{L}^2}{\alpha (T_{ref}-g_d)}},\hfill \\ T_c^{*}={\displaystyle \frac{T_c}{T_{ref}-g_d}},\hfill \\ H^{*}={\displaystyle \frac{HL}{\alpha (T_{ref}-g_d)}},\hfill \end{array}\right.\hfill \end{array}$$

(28)

where $T_{ref}=|T_{d,1}|=|T_{d,2}|$. Therefore, in our case, $T^{*}$ tends to $-1$ or 1 inside the controlled regions ${\Omega }_{d,1}$ and ${\Omega }_{d,2}$, respectively. Similarly, the space coordinates $\mathbf{x}$ are adimensionalized via the the square domain side L in ${\mathbf{x}}^{*}=\mathbf{x}/L$. In order for the optimal control system to remain coherent during the transition to these dimensionless variables, also the regularization factor $\lambda$ must be considered. Specifically, the following dimensionless transformations apply to the three types of control

$$\begin{array}{cccccc}\hfill {\lambda }_{dist}^{*}& ={\displaystyle \frac{\lambda {\alpha }^2}{L^4}},\hfill & \hfill {\lambda }_{Dir}^{*}& ={\displaystyle \frac{\lambda }{L}},\hfill & \hfill {\lambda }_{Neu}^{*}& ={\displaystyle \frac{\lambda {\alpha }^2}{L^3}}.\hfill \end{array}$$

(29)

In the following results, for the sake of simplicity, the parameter $\lambda$ will always be presented with its dimensional value, i.e., the value used in the simulations. However, its dimensionless value can be derived using formulas (29), with $L=0.01m$ and $\alpha =1.433·{10}^{-7}\frac{m^2}{s}$.

As mentioned in Section 2, one of the main issues related to the coupling of different codes is the interpolation of the numerical fields between two different computational grids. Therefore, it is important to take into account this aspect when we compare the numerical results between an uncoupled and a coupled algorithm. If we consider the temperature field obtained through the interpolation between the finite volume and the finite element grid, thus into FEMuS data structures, we should rewrite the functional in the case of the coupled algorithm. Therefore, considering the interpolator $\mathcal{I}\left(T\right):T\left(P_0\right)\to T\left(P_2\right)$ we have

$$\mathcal{F}\left(\mathcal{I}\left(T\right),\tilde{q}\right)={\displaystyle \frac{1}{2}}{\int }_{{\Omega }_d}|\mathcal{I}\left(T\right)-T_d{|}^{2}d\Omega +{\displaystyle \frac{1}{2}}{\int }_{{\Omega }_c}{\left|\tilde{q}\right|}^{2}d\Omega ,$$

(30)

where the control $\tilde{q}$ is obtained from the adjoint equation computed with the interpolated temperature, i.e.

$$\Delta {\tilde{T}}_a=\mathcal{I}\left(T\right)-T_d.$$

(31)

It is easy to understand that we have two different effects from the interpolation routine on the system of equations. The first interpolation acts directly on the functional, since we compute, in the FEM grid, the distance from the target temperature considering directly the interpolated temperature. The second interpolation, which indirectly arises from the control $\tilde{q}$, is evaluated considering a different equation for the adjoint variable. In fact, the effect of the interpolation can be seen on the right-hand side of (31), even if the Laplacian operator on the left-hand side acts as a smoother function, thus the error coming from the interpolation is lower. Naturally, we should also consider the interpolation error coming from the data transfer in the opposite direction, i.e. from FEMuS to OpenFOAM.

Regarding the computational grids employed for the coupling algorithm, we set to have the same number of degrees of freedom between the two codes. For this reason, to clarify the notation when the size of a grid is built with even numbers, e.g., $40\times 40$, we refer to the finite element grid, where these numbers represent the elements’ number $n_{el}$. As a result, the corresponding FV grid size is represented by odd numbers, such as $81\times 81$. Indeed, we recall that, considering biquadratic elements for finite element grids, its degrees of freedom are equal to ${(2n_{el}+1)}^2$ when considering a square domain with a structured quadrilateral mesh.

3.1. Distributed Control

In this section, we report the numerical results related to the distributed control, with both numerical methods, i.e. the coupled and uncoupled algorithm. We recall that for the distributed case, the control q acts as the volumetric source on the right-hand side of the temperature equation, i.e., Q. Regarding the boundary conditions, we have homogeneous Dirichlet and Neumann boundary conditions on ${\Gamma }_D$ and ${\Gamma }_N$, respectively.

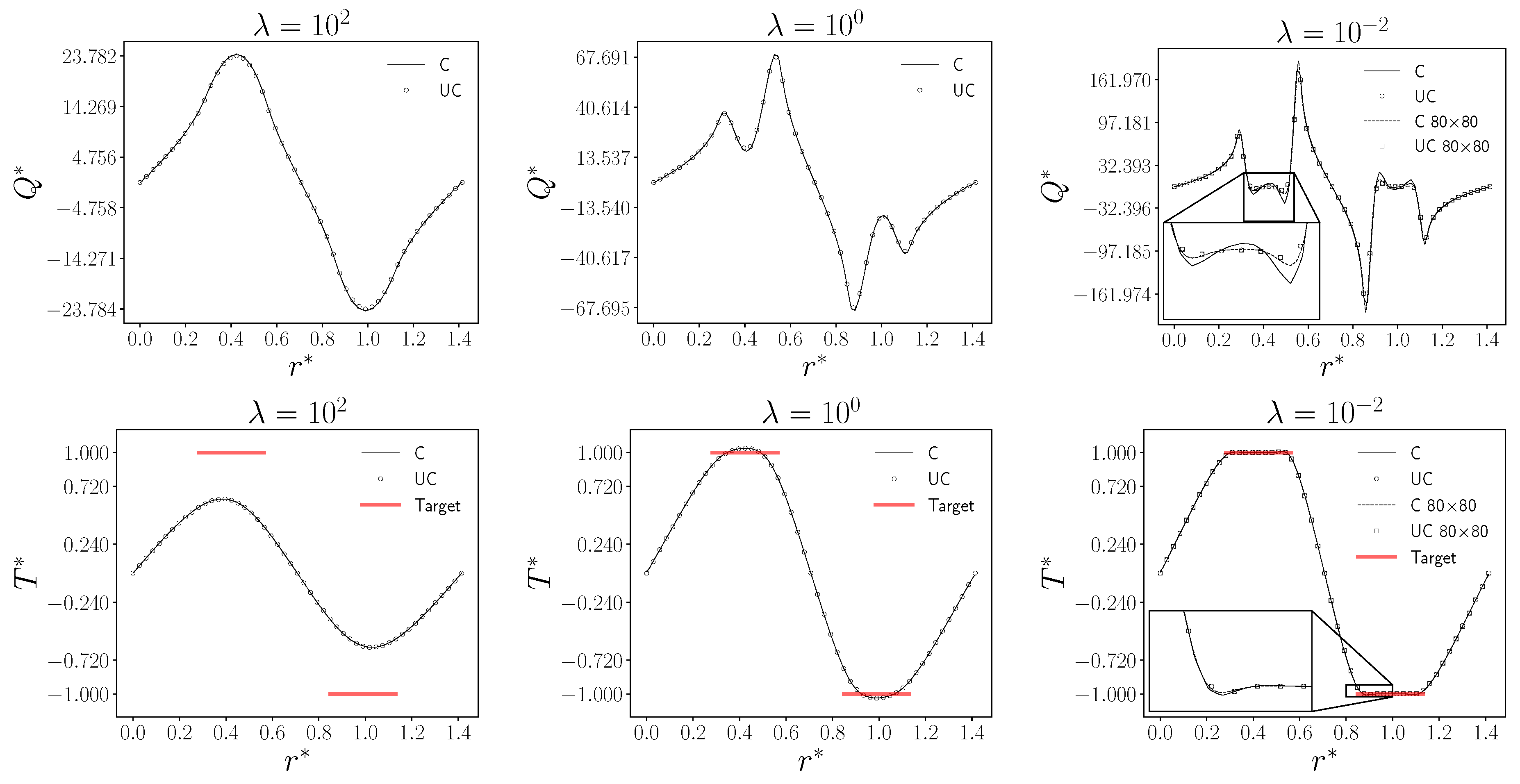
In Figure 5 the control $Q^{*}$ and the non-dimensional state variable $T^{*}$ are reported considering different values of the parameter $\lambda$, from ${10}^2$ to ${10}^{-2}$. In particular, the plots show the variables as a function of the dimensionless length $r^{*}=d/L$, which corresponds to the diagonal of the domain (from the lower left corner to the upper right corner), with a value ranging from 0 to $\sqrt{2}L$. The coordinate $r^{*}$ allows us to evaluate the state and the control variable in both controlled regions. In the following, we denote by UC the uncoupled results (circular marker), while with the label C the coupled codes results (solid line). The target value $T_d=\pm 1$ is represented with the solid line (red).

In Figure 5 we show the different behavior of the control parameter Q with different values of $\lambda$ and the corresponding effect on the state variable in the controlled regions. As $\lambda$ decreases, the control $Q^{*}$ becomes less smooth and produces a sharp behavior near the controlled regions, as expected. In fact, the case with $\lambda ={10}^{-2}$ represents the less regularized solution, with corresponding temperatures in the controlled region very close to the target value. Otherwise, with a $\lambda ={10}^2$ the control $Q^{*}$ has a low effect on the state variable that cannot reach the target value in the controlled regions.

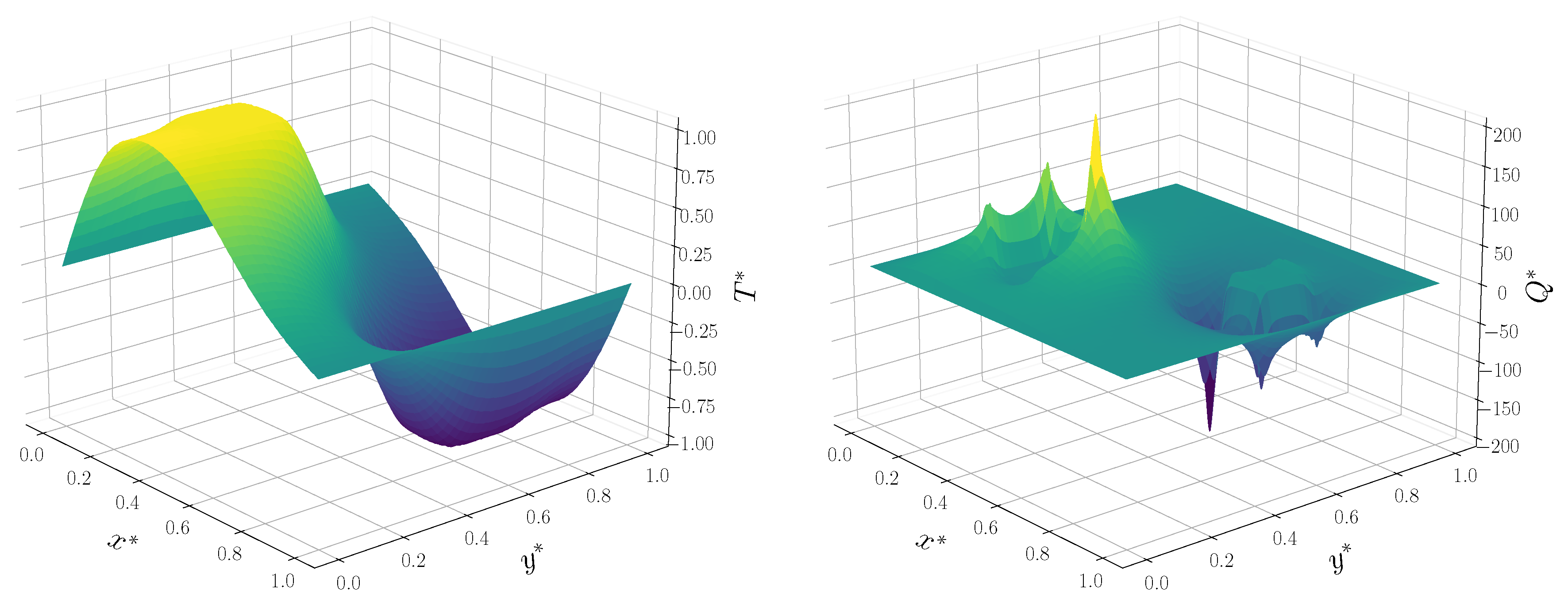
In Figure 6, a surface plot of the non-dimensional temperature and the non-dimensional control over the whole domain is reported. Specifically, we display only the case with the lowest $\lambda$, considering a $40\times 40$ finite element grid. The symmetric behavior of these variables is shown. Moreover, a sharp trend of $Q^{*}$ is present near the target regions, where several peaks can be observed. Regarding the temperature field, as expected, two plateaus are present in the target regions, with opposite values close to 1 and $-1$.

Table 1 reports the functional value and the number of iterations for the three different cases previously presented. the table lets us understand better the numerical results depicted in Figure 5. Indeed, for different $\lambda$ cases, the first column represents the minimum of the functional, while the second column reports the number of iterations needed to reach the convergence condition. The first row reports the results for the coupled case, while the second row represents the uncoupled scenario. We recall that these results refer to a computational FEM grid with $n\times n$ elements and a corresponding $2n+1\times 2n+1$ grid for the FVM to have the same number of degrees of freedom. Regarding $min\left(\mathcal{F}\right)$, with larger $\lambda$ values, we get a good match for both algorithms, while a larger difference can be noted for the lowest value of $\lambda$.

For $\lambda ={10}^{-2}$, we observe some discrepancies between coupled and uncoupled results. This phenomenon can be explained by considering the errors introduced during field interpolation and data transferred from one code to the other. As the optimal state is approaching, the distance $|T-T_d|$ of the state from the desired temperature decreases, making the interpolation error on T, at first negligible, increasingly important. This interpolation error limits the achievement of the real optimum state since we are not able to obtain a sufficiently accurate control.

The interpolation error can be improved by increasing the number of degrees of freedom. In fact, in Figure 5 on the right, we have also reported the same case of $\lambda ={10}^{-2}$ obtained with a refined grid, with a dashed line for the coupled case and with square markers for the uncoupled one. For the uncoupled case, small differences can be noticed because the simulation has already found its optimum, but in the coupled approach, improvement can be obtained to stir Q very close to the uncoupled results. These conclusions can be drawn from Table 1, where the distance between the two minima decreases considering the refined solution. In addition, the relative errors between the functional minimum increase by decreasing the value of $\lambda$, going from 1 to $10\%$. However, the latter value corresponding to the lowest $\lambda$ can be improved until around $2\%$ with a refined grid.

A measure of the quality of the optimization convergence can be obtained using the Euler expression defined in (7). In Figure 7 we compare the obtained control Q with its analytic optimal expression $-{\displaystyle \frac{T_a}{\lambda }}$. We can notice that, for the uncoupled approach, there is a perfect agreement between the two lines, while some differences are present for the coupled case. As said before, we obtain better results considering the refined coupled approach, which is shown on the right. This analysis reflects the considerations made earlier about the functional minimum and validates the accuracy of the uncoupled simulation, which is used as a reference case.

The number of iterations is different between the two algorithms. Actually, this is true considering the first two values of $\lambda$ where the coupled case needs more iterations to satisfy the convergence condition. For example, considering $\lambda ={10}^2$, we have an increase of almost one order of magnitude for the coupled case. However, this difference decreases when $\lambda$ decreases since for the most controlled case, i.e., $\lambda ={10}^{-2}$, the number of iterations is similar. In the last column, we report for the lowest $\lambda$ the results for a refined case. Refining the grid, we notice that we reach a lower functional value while the number of iterations increases.

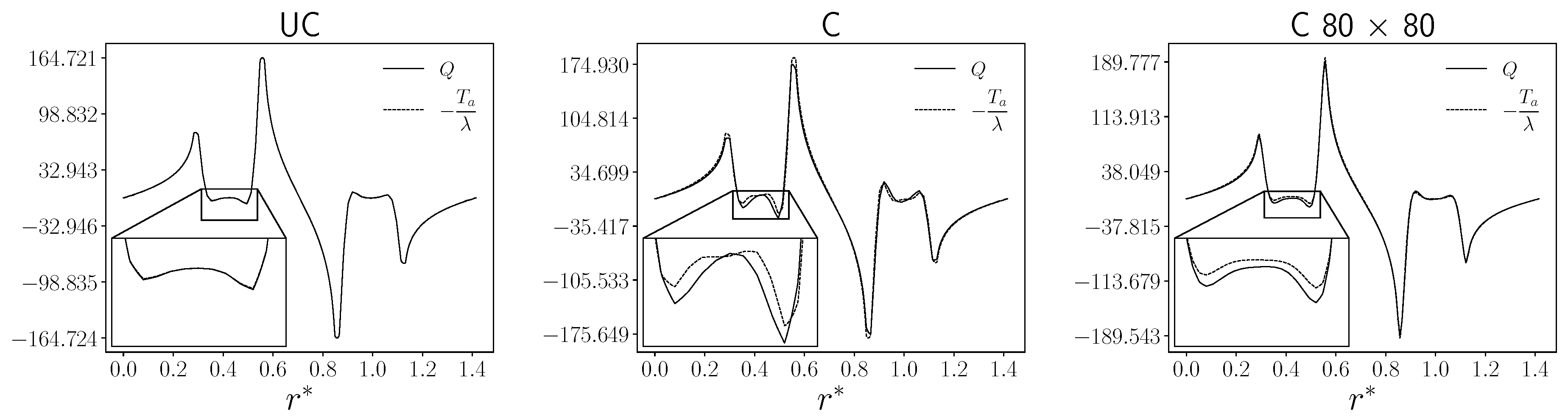
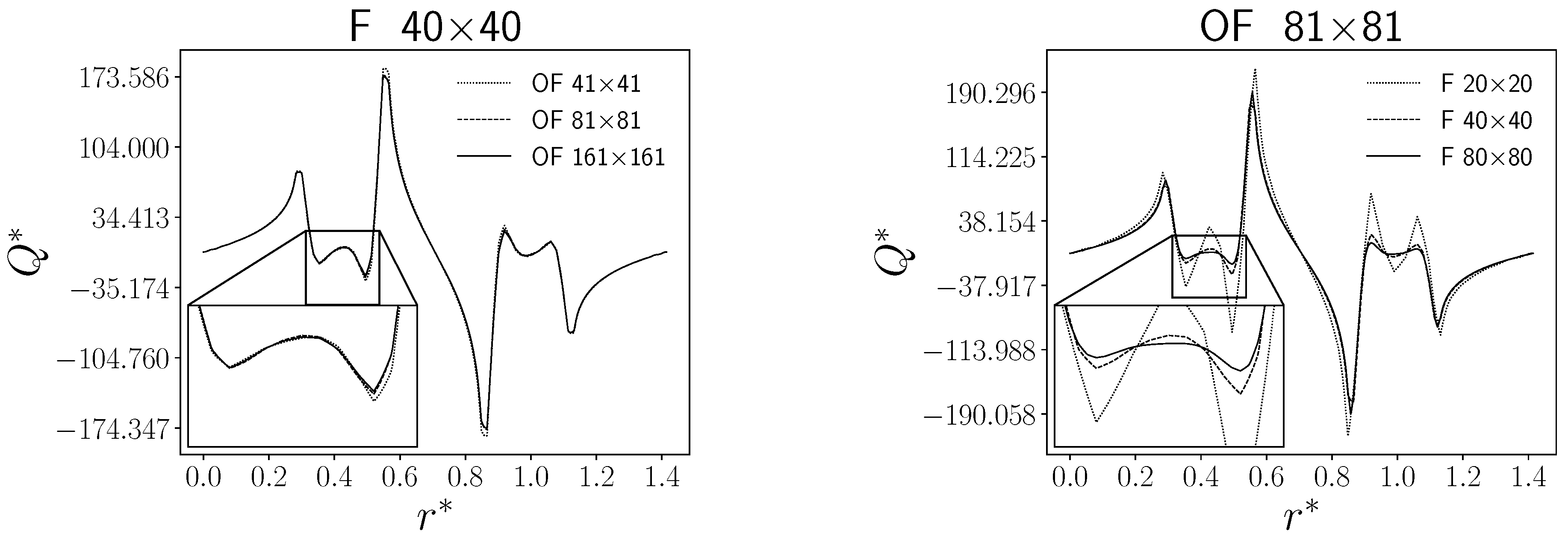
For the distributed case, we also investigate the influence of the difference between the degrees of freedom of the two meshes. This comparison aims to evaluate the impact of the MED-interpolating function on the overall behavior of the algorithm, especially for the shape of the control $Q^{*}$. Therefore, we consider three different grids of the FVM code (OpenFOAM), by fixing the FEM computational grid with the same degree of freedom as the intermediate FVM grid. On the other hand, the same simulations have been performed considering a fixed FVM grid and varying the FEM one. The results have been reported in Figure 8, where F denotes the FEMuS grid and OF the OpenFOAM grid. For these results, we have considered only the case with $\lambda ={10}^{-2}$, and the control $Q^{*}$ is reported as a function of the dimensionless diagonal coordinate $r^{*}$.

From Figure 8, one can see the difference in the control $Q^{*}$ as a function of the computational grids. On the left, the change of the FVM grid seems to have a small influence on the solution of the equation systems. On the right side, the situation is different when considering the coarsest FEM grid, while for finer grids, the results are comparable with the picture on the left.

We deduce that, at least for this application, the OpenFOAM grid has much less influence compared to the FEMuS grid on the shape of the control. The interpolation error occurs when the projected field no longer provides a good approximation of the original one, i.e. when the target grid is not fine enough. Reconfirming the observations made earlier, this shows that the error occurs when the temperature field is projected from the $P_0$ grid to the $P_2$ of the FEMuS grid, so when the interpolation control is not sufficiently detailed the error becomes significant.

In Table 2, we can confirm the effectiveness of grid refinement in the two codes: we have a much greater impact on the minimum of the functional by varying the FEMuS mesh compared to varying the OpenFOAM mesh. Moreover, it is interesting to note that the minimum number of iterations corresponds to the case where the two meshes have the same degrees of freedom.

3.2. Boundary Control

In this section, we report the boundary control cases, for two types of boundary conditions, Dirichlet and Neumann. The volumetric source of the state equation is equal to zero, leading to a Poisson equation for T. The boundary conditions correspond to the control q separately for the Dirichlet and the Neumann case, where the uncontrolled pair of boundaries stay homogeneous.

3.2.1. Dirichlet Boundary Control

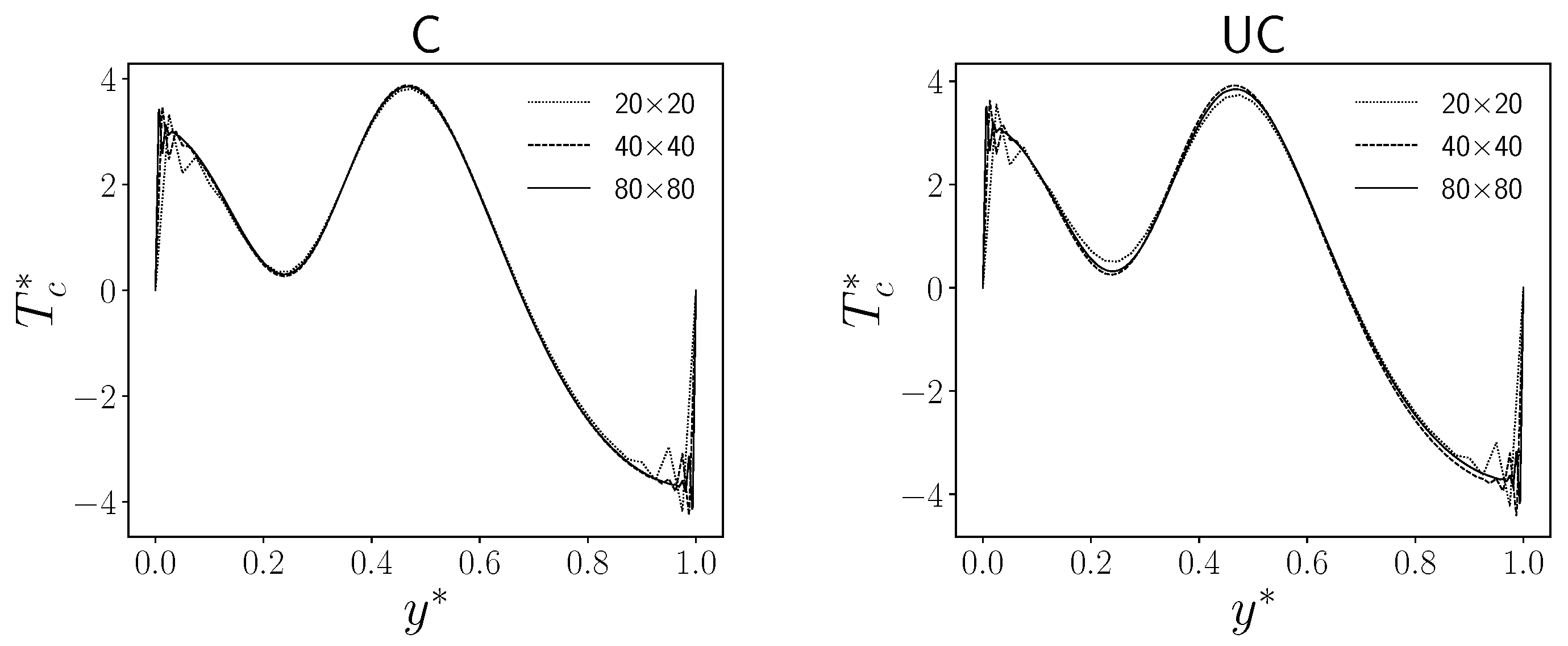
For the Dirichlet boundary control, we have also performed a standard grid convergence test to verify the goodness of the numerical results. In Figure 9, on the left, the state variable $T^{*}$ in the controlled domain, that is, the control parameter q ($T_c^{*}$), which is imposed as a boundary condition, is reported. Since the simulation is symmetric with respect to the y axes, we report only one boundary.

From Figure 9, a good grid convergence can be seen for both algorithms, confirming the reliability of the numerical approach. In fact, the finest grid presents a solution that tends to be smooth also close to the boundary of the control region. The boundary of $\Gamma$, corresponding to the corner nodes of the domain, is the most problematic region due to q being set to zero there.

In Figure 10, the control $T_c^{*}$ and the state variable $T^{*}$ have been reported for the Dirichlet boundary control for three values of $\lambda$ equal to ${10}^{-4},{10}^{-6}$ and ${10}^{-8}$. The notation adopted in the graphs is the same of the distributed case. Since the results are symmetric with respect to the line $x=0.5$, the control is reported only for the left boundary, while for the state variable, the plot has been made considering the match with the target region ${\Omega }_{d,1}$.

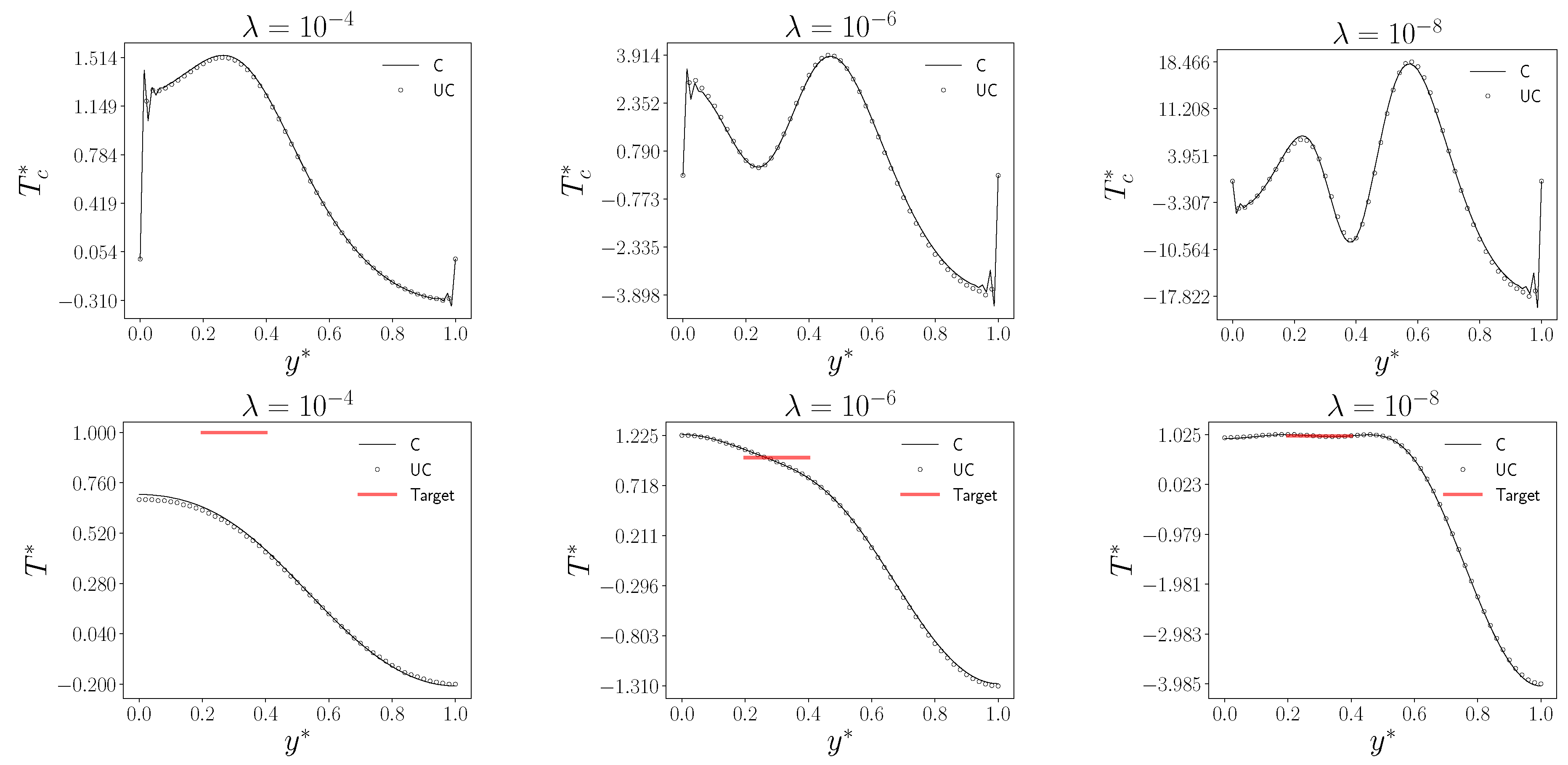
We can draw similar conclusions to those in the distributed case. Specifically, a good match with the temperature target value can be obtained with a low value of $\lambda$, which corresponds to the less regular trend of the control $T_c^{*}$. For this case, it can be noticed a flat behavior of $T^{*}$ very close to 1, i.e. the red line, in correspondence with the controlled region ${\Omega }_{d,1}$. The distance with the target region is higher considering the case with $\lambda ={10}^{-4}$, while with $\lambda ={10}^{-6}$, the temperature $T^{*}$ is able to only intersect $T_d$ without reproducing its constant value in the entire ${\Omega }_{d,1}$ region.

In Table 3, the functional minimum and the number of iterations are reported for the Dirichlet boundary control. We can observe a better behavior of the coupled code with respect to the uncoupled case on both the minimum reached and the number of iterations. In any case, the differences between the two cases are minimal.

3.2.2. Neumann Boundary Control

We present now the numerical results obtained with the Neumann boundary control, following (17). In this case, three values of $\lambda$ have been used to test the influence of the control H on the state equation. In Figure 11, the numerical results for the Neumann boundary control are reported with the considered $\lambda$. Due to symmetry, we report only one of the two boundaries (the bottom one) for the control H.

Similar comments of the previous cases are true for the Neumann boundary control as well. A good agreement between the state variable and the target temperature can be obtained only with small values of $\lambda$ since, for higher values of this parameter, the control $H^{*}$ does not sufficiently influence the temperature $T^{*}$. This consideration is graphically represented in Figure 11, where the variables are plotted as a function of the distance between the red line and the solutions for $T^{*}$. For low values of $\lambda$, the major difference is present near the target region, whereas for the uncoupled control, $H^{*}$ seems to be more flat with respect to the coupled result. Once again, we have reported the same case of $\lambda ={10}^{-1}$ obtained with a refined grid, with a dashed line for the coupled case and with square markers for the uncoupled one. Similarly, as in the distributed case, we can observe that the coupled and uncoupled results become similar as the grid becomes finer. On the other hand, these differences do not influence the state temperature $T^{*}$, which is in perfect agreement with the desired value for both algorithms. Small differences can be noticed for $x^{*}\approx 0.8$ (far from the target region), where the uncoupled algorithm $T^{*}$ reaches a lower value.

In Table 4, the functional minimum value and the number of iterations for both algorithms are reported. For the lower case of $\lambda$, which is the last column on the right, the results on a refined grid are also investigated. In this case, the number of iterations increases both in the coupled and in the uncoupled codes, decreasing the value of $\lambda$. For high values of $\lambda$, the functional minimum is similar in both algorithms, while the coupled case presents a higher number of iterations. A slightly different $min\left(\mathcal{F}\right)$ can be seen for the lowest value of $\lambda$. The case with $\lambda ={10}^{-1}$ shows the same pattern as the distributed case above. For finer grids on the coupled code, we obtain a lower minimum of the functional with a higher number of iterations, while in the uncoupled case, the number of iterations decreases. With refined meshes, the difference between the values of the functional minimum decreases, confirming the improvement of the results considering finer computational grids. This similarity can be justified considering the fact that both distributed and Neumann cases share the same control expression based on the adjoint temperature. In fact, this behavior is not present in the Dirichlet control since the gradient of the adjoint temperature is used as the control parameter.

4. Conclusions

In this work, an optimal control problem has been presented considering the steady-state heat equation with a vanishing convective term. Specifically, the minimization problem has been solved with the adjoint equation, while the control parameter is handled with a standard conjugate gradient technique.

Moreover, we have compared the simulation results considering also a numerical code coupling between the finite element FEMuS code and the finite volume code OpenFOAM. In particular, while the state equation has been solved in OpenFOAM, the adjoint and the control are solved in FEMuS. The data transfer has been managed by the external library MEDCoupling, which is able to take the state variable T from OpenFOAM for the FEMuS adjoint equation. The inverse path is followed by the control variable Q, obtained from FEMuS and transferred to OpenFOAM as the RHS (distributed control) or as a boundary condition (boundary control).

The numerical results obtained with the coupling framework are compared with the ones resulting from the standalone FEMuS solution. For the three types of control problems, a good agreement between the numerical solutions of the two algorithms has been obtained. Regarding the interpolation error, some differences can be seen considering low values of $\lambda$ since, for these cases, the result of the grid interpolation of T affects the control q, which is very sharp.

Extension to other systems of equations, from Navier-Stokes to turbulence modeling, will be studied in future work, with the purpose of searching boundary data that optimize multiphysics problems already validated in open-source codes such as OpenFOAM.