Submitted:
13 December 2024
Posted:
16 December 2024
Read the latest preprint version here
Abstract
This paper describes a new auto-associative network called a Unit Memory network. It is so-called because unit nodes in a network store binary input as integer values, representing binary words. The word size is critical and specific to the dataset and it also provides a first level of cohesion over the word values. A second cohesion network then links the unit network nodes, through layers of decreasing dimension, until the top layer contains only 1 node for any pattern. Thus, a pattern can be found using a search and compare technique through the two networks. The unit memory is compared to a Hopfield network and a Sparse Distributed Memory (SDM). It is shown that the memory requirements are not unreasonable and that it has a much larger capacity than a discrete Hopfield network, for example. It can also store dense or sparse data and can deal with maybe 30% noise. This is demonstrated with test results for 3 benchmark datasets. Apart from unit size, the rest of the configuration is automatic, and its simplistic design could make it attractive for some applications.
Keywords:
auto-associative
; Hopfield
; sparse distributed memory
; noise
1. Introduction
This paper describes a new design that can be used as an auto-associative memory. In this respect it is compared with a Discrete Hopfield Network [5], which was the original inspiration. Content-addressable memories can retrieve a full memory from any subpart of sufficient size. They are also able to retrieve the original memory when some of it has been corrupted by noise, which is of interest to this paper. As Hopfield also explains [5]: ‘Computational properties of use to biological organisms or to the construction of computers can emerge as collective properties of systems-having a large number of simple equivalent components (or neurons).’ This notes computational properties of neurons, which suggests some type of functional behaviour. Recent biological research suggests that it could be possible to have memory structures that are less functional as well, such as with glial cells. The main problem with discrete Hopfield networks is their memory capacity, which is only about 0.15 times the number of nodes. For example, a network with 100 nodes would only be able to store about 15 different patterns before they started to corrupt each other. This has now largely been solved with the new Modern Hopfield Network [8] that also does not need to be discrete. The memory structure tends to be dense however and so it may not deal so well with sparse data. The paper [6] presents one model designed to cope with sparse data, but it also notes that apart from some very nice advantages, the modern Hopfield models have been shown to be computationally heavy and vulnerable against noisy queries. In particular, the dense output alignments of the retrieval dynamics can be computationally inefficient, making models less interpretable and noise-sensitive.
This paper proposes a new model called a Unit Memory network. It is so-called because unit nodes in a network store binary input as integer values, representing binary words. Thus, a unit size is the first design feature and it is critical and specific to the dataset. It also provides a first level of cohesion over the word values, because specific word ‘patterns’ must be present for the related integer value to be flagged. A second cohesion network then links the unit network nodes, through layers of decreasing dimension, until the top layer contains only 1 node for any pattern. Thus, a pattern can be found using a search and compare technique through the two networks. The structure looks to be different, but one might think about a standard auto-encoder, with similar input and output layers and then a hidden layer that contains the common features. In this respect, that type of functionality is present in the unit memory as well.
2. Related Work
The paper [4] proposes to build a new Modern Hopfield Network that includes setwise links, creating a simplical complex. This is interesting because the simplical sets group base nodes, but into higher levels and degrees. Basically, the corollary 2.2 on page 5 states that the network capacity is proportional to the number of connections. To store more patterns, you need to add more connections. It cites earlier papers that also consider setwise links, but for a binary pairwise Hopfield network. The idea is to link non-linearly, in concentrations, where the nodes are associated. The linking process is entirely different to the cohesion network, however and continually changes the network topology. The appendices have biological reference, including neurons and synapses. A new design of Hopfield Network, described in [1], might in fact be closer. Their system still reduces an energy function, but it constructs a graph representation (discrete-graphical model) as the internal model, which is why it may be more similar. They argue for local learning rules, both in the human brain and their system. Because Deep Learning is often implemented with backpropagation, this is non-local learning and generally considered biologically implausible. They use a single forward-pass and backward-pass for retrieval, which looks to be similar, and also the one-shot integer value retrieval.
The paper [7] is the original work on sparse models. It uses a Hamming distance with the precept of: ‘The pursuit of a simple idea led to the discovery of the model, namely, that the distances between concepts in our minds correspond to the distances between points of a high-dimensional space. Strictly speaking, a mathematical space need not be a high-dimensional vector space to have the desired properties; it needs to be a huge space, with an appropriate similarity measure for pairs of points, but the measure need not define a metric on the space.’ Long (high-dimensional) binary vectors, or words, were used as the memory model and could handle 20% noise, but examples of noisy patterns were included in the memory, with a link to the correct one. Each memory address corresponded to a whole large word, not the smaller units that are used in this paper. Also with sparse data, the number of hard locations or addresses actually used was much less than the possible number from the size of the data, so a full list would contain a lot of redundancy, close to the Hopfield network capacity. Another problem with a flat list is if you are required to expand it at a particular point, then elements need to be moved. The tree structure in this paper can add new nodes more easily, but the problem still exists.
The paper [11] converted the binary numbers to decimal, which is also done in this paper, but again it was whole words not smaller units. Instead of cohesion, a Euclidean range around the selected memory was used to retrieve matching possibilities, which were then summed and a majority vote produced the final result. The paper [10] tested different methods of encoding the data stored into the SDM, including: Natural Binary Code (NBC), NBC with a different sorting of the numbers, integer values and a sum-code. But again, the stored patterns were whole images, not parts of images. They then also used a radius around the selected location, to compare with similar ones. The paper states that ‘Another big weakness of the original SDM model is that of using bit counters. This results in a low storage rate, which is about 0.1 bits per bit of traditional computer memory, huge consumption of processing power and a big complexity of implementation.’ The paper [11] notes problems with using Hamming distances, when converting binary to decimal: The integer representation has several advantages, such as a simpler encoding, it diminishes the effect of normalization when several vectors are combined and it avoids other undesirable effects. But decimal number and Hamming differences are not the same. For example, 0111 and 1000 would give decimal values of 7 and 8, with a hamming distance of 4, but a decimal difference of 1. The method of this paper still prefers the hamming difference. In their case, the decimal number is required to locate the position for a pattern in a vector list, whereas in this paper, patterns want to be clustered based on binary word similarity. The paper [10] however, describes that a conversion to the binary from some other form that also includes noise, is also a problem. For example, if there are greyscale images and 8-bit patterns are being stored, then a grey-level value of 127, or 01111111, could be converted with very little noise into 128, or 10000000, but the hamming distance between these two values is very large. The best method is therefore application-dependent, because either option is possible.
3. The Unit Memory Network
3.1. Network Construction
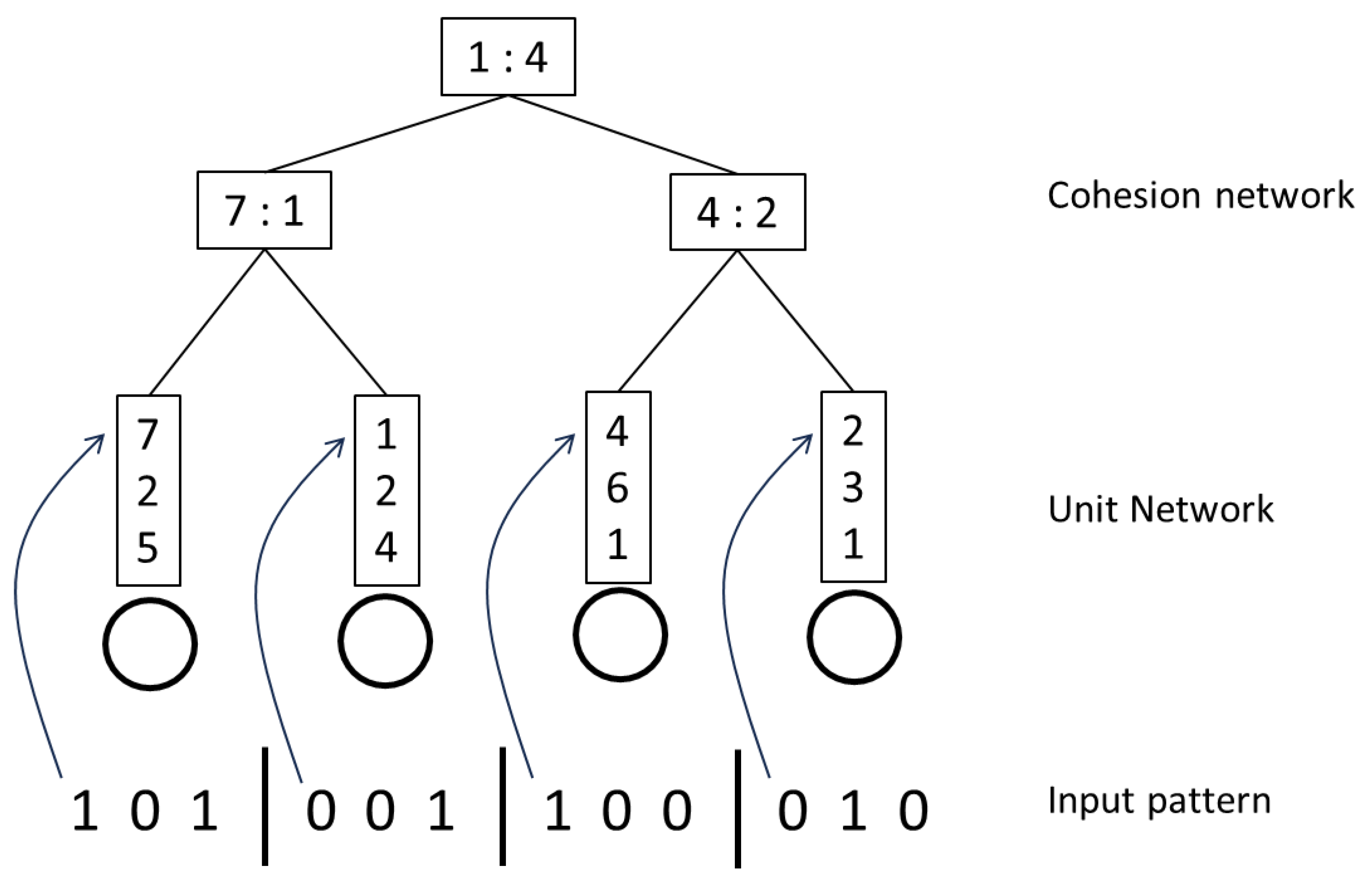
The model proposed in this paper is not a recursive Hopfield design, but is more like a Sparse Distributed Memory (SDM). The focus is on binary inputs only, with a value of 0 or 1. As the name suggests, the input pattern can be split up into units that each contain a certain number of the binary inputs. It could be 8 bits or 16 bits, for example and in fact the selected size is quite critical. When stored in the network, these binary numbers are converted to decimal first. Each network node therefore references words of this size and not individual binary values. This not only helps to reduce the size of the network but it adds a certain amount of cohesion, where these smaller ‘patterns’ need to occur for the unit value to be flagged. Then a second indexing network makes the retrieval and comparisons more efficient. It also adds cohesion across the units, by clustering the ones with shared values together. This cohesion network links all the base unit nodes through a number of layers that converges to a single final layer node. The dimension is reduced at each level by combining 2 values from the previous level into a compound one, and also leaving out 2 values. Figure 1 is a schematic of a unit memory network. Note that while a discrete Hopfield network is restricted to storing approximately 0.15N patterns or states, there is no such restriction with this design. A Modern Hopfield network does not have this restriction either, but it does need to add more dimensions to be able to store more information.
Binary is the chosen reduction method here, but it could be something else. The nodes at any level may therefore contain links for more than 1 base pattern and so there is a certain amount of search and comparison required, but the network structure is able to keep that to a minimum. While it may appear that this network simply stores every memory and then retrieves what is closest to the input, it does this using a lot of overlap in values that it stores and thereby reduces the memory requirements by a lot. In fact, it is probably more economic than a discrete Hopfield network for the same number of patterns. It is able to handle sparse or dense memory equally well and its simplistic structure makes it very quick to run. It is not completely deterministic however and can produce slightly different results on different test runs, but the only critical criterion is really the size of unit to use. The rest is mostly automatic. One unanswered question is how to cluster sibling nodes in a layer using the hamming distance, or at least the most economic way to do it. This would allow small traversals to neighbouring nodes, for example, but the current algorithm does not require that.
3.2. Network Use
Using the network therefore also consists of two stages. To train the network, the first stage creates the base unit nodes and assigns each node a list of integer values that represent any of the binary array words assigned to the unit. The second stage converts each pattern into a hierarchy of compound integer values and uses these to trace through the links in the trained network, that lead to the unit patterns at the base. Testing or using the network is essentially to match the new input with what base units are closest, but with some extra rules. The new input may be noisy and so if an input part does not match exactly with any values in the corresponding unit, then the unit value is set to ‘null’. A cohesion network is created for the new input pattern and the trained cohesion network is traced through to the base nodes using those values, where if a null value is encountered, then any match is allowed. This results in a small set of base unit values that are converted back to their binary equivalents, to produce a small set of whole train patterns. Each pattern is compared with the new input pattern and the one with the least hamming differences is selected as the correct pattern.
3.3. Train Algorithm
The structure consists of a unit network and a cohesion network and so both need to be built.
3.3.1. Unit Network
- Create a unit network, where each node stores integer values relating to an indicated number x of base binary values.
-
For each input pattern, split it up into words of the indicated unit size x. Note that the unit size is important and will separate out the values (and features) differently.
- o
- Convert a list of base words, representing a unit, from binary to decimal.
- o
- Store the number, only once in a list, for the unit at the corresponding position.
3.3.2. Cohesion Network
-
Link and add all decimal numbers for the current pattern to the cohesion network.o Create a layer of base compound keys by combining 2 adjacent unit node values.
- o
Then to reduce the dimensions, take the second compound value of the first node and the first compound value of the second node and create a new compound value and node in a new layer from it.- o
Repeat until there is only 1 node in the top layer. -
This creates a path which if followed, will lead to the input pattern at the end.
- o
- The paths are not unique however and because some information has been lost, there can be several instances at each node. But the numbers will be much smaller than for a flat list.
- o
- Thus, when there are several choices, a count of the most matching values can be used to select the best one.
- The process is described in Figure 1.
3.4. Test Algorithm
The retrieval process therefore also requires traversing both the unit and the cohesion networks.
3.4.1. Unit network
- Split the test input pattern into unit sizes and create the corresponding integer numbers.
-
Compare each number directly with the corresponding unit node value list.
- o
- If the value list contains the number, then keep the value for that position.
- o
- If the value list does not contain the number, then add a ‘null’ value for the position.
- This produces a list of integer or null values that represent the test pattern in the trained network.
3.4.2. Cohesion Network
- Create a cohesion network for the test pattern values only.
-
Traverse the trained cohesion network using these values.
- o
- If there is a null value at a branch, then any combination that includes the null value can be selected.
- o
- While there will be multiple options, the final branch(s) will have a much smaller subset of all patterns that the network was trained with.
- Retrieve all the selected base patterns and convert them back into binary patterns.
- Use a Hamming distance similarity count to select the pattern that is closest to the test input pattern.
- The finally selected pattern can thus have different values to the input pattern and thus remove noise from it.
Note that if there is no exact unit match, then do not include a closest match, because this leads to a combinatorial explosion that cannot be managed. It was much more economic to add a null value and leave the decision to the final set of patterns. At first sight, this does not seem to be a very economic solution, because it tries to store every train pattern as it is. However, a direct comparison with the memory requirements of a Hopfield network, for example, show that it is reasonably economic. Consider the following example: an auto-associative network with 100 nodes is to be used. The Hopfield network stores a weight from each node to every other node, which is 100 x 100 = 10000 weight values. Even if this is symmetric, so that ab == ba, then it is still 5000 in number. If a unit memory was to use units of size 4, then there would be 25 unit-network nodes. The cohesion network reduces these in binary style, from 13 to 7 to 4 to 2 to 1. Summing this gives 25 + 13 + 7 + 4 + 2 + 1 = 52 nodes. A Hopfield network can reliably store ≈ 0.15N nodes, or 15 patterns in this case. An upper limit would therefore be if every pattern value is different, leading to 52 x 15 = 780, which is much less than for the Hopfield network. This is only a crude estimate, but it shows that the memory requirements should be OK. For example, the Semeion dataset (see section 4) requires possibly 54579 values to be stored, whereas a fully-connected Hopfield network would require (256 x 256) = 65536 weight values, or if symmetry is considered then 32768 values. But that would be for 39 patterns, not the 1597 patterns that the unit memory stores.
4. Testing
The network was tested with 3 different image datasets. The Chars74k dataset [12] is a set of hand-written numbers, where only the numbers 1 to 9 were used. This produced approximately 55 examples for each number, or 360 images in total. The image was converted into a 32x32 black and white ascii image, which would also be a binary image with the values 1 or 0. The second dataset was another set of handwritten numbers called the Semeion dataset [2,3]. These were converted into 16x16 binary images, with a total of 1597 images. A third benchmark dataset, obtained from the UCI Machine Learning Repository [13], was a small subset of the Caltech 101 Silhouettes dataset [9]. These were converted into 64x64 binary images and placed into 8 different categories, with up to 10 images in a category, with 68 images in total.
4.1. Test Strategy
The only parameter that needs to be set is the unit size. Thus, a number of test runs could determine which unit size would give the best result for each dataset. The results were not exactly the same every time, but were close and so the results presented in Table 2 have been averaged over 50 test runs each. Testing a single row would take seconds or less to run. After determining what the best unit size was, the trained network was presented with the dataset again, but with a certain amount of noise added to each row. This included switching both the 1 and the 0 values, where a 10% noise factor would randomly switch 10% of the binary values, for example. With no noise, the network would be expected to recognise each train image again, but with noise, it would have to match partially to the image and then retrieve the train image that was closest. Because the images are placed in categories, the test also measured what category the finally selected image was from. Thus, two percentage scores were produced for each test run. The first was if the same data row (image) was returned and the second was if an image from the same category was returned. The results are presented in Table 2.
4.2. Test Results
The preferred unit size for each dataset was as shown in Table 1.
Table 1.
Preferred unit Sizes.
| Dataset | Dimensions | Unit Size |
|---|---|---|
| Chars74 | 32 x 32 | 12 |
| Semeion | 16 x 16 | 16 |
| Silhouettes | 64 x 64 | 4 |
Table 2.
Test results show the accuracy for exact row recall or correct category recall, with varying amounts of noise in the test pattern.
Table 2.
Test results show the accuracy for exact row recall or correct category recall, with varying amounts of noise in the test pattern.
| Dataset | Row Accuracy for Noise % | Category Accuracy for Noise % | ||||||
|---|---|---|---|---|---|---|---|---|
| 0% | 10% | 20% | 30% | 0% | 10% | 20% | 30% | |
| Chars74 | 100 | 98.7 | 91 | 75.9 | 100 | 98.9 | 91.5 | 76.1 |
| Semeion | 100 | 96.2 | 90.2 | 85.1 | 99.7 | 95.8 | 90 | 84.9 |
| Silhouettes | 100 | 98.4 | 95.3 | 87.4 | 100 | 98.5 | 94.9 | 87.2 |
The accuracy is expected to degrade when noise is added and the value is comparable with what other systems have produced. For example, the paper [4] quotes an 87% accuracy for its particular test, while [11] quotes 65% accuracy for 30% noise for its test. The category matching could be worse than exact row matching. It did involve a basic majority count over all rows in the category and that might be different to a single closest match. It should be noted that a test set with different images was not recognised very well, but that would not be the objective of an auto-associative network. It should also be noted that two fairly-basic discrete Hopfield networks failed this test completely. The digit images are quite sparse and so a Hopfield network may tend to move each node’s score to 0. This is what happened, with the returned patterns being all 0’s, because that was also the input to most nodes. Modern Hopfield networks [8] are addressing this problem by placing the minima more accurately, but they also need to be specialised to cope with sparse data [6].
5. Conclusions
A Unit Memory network has been shown to be very efficient, both in terms of processing time and memory requirements. It can handle dense or sparse data and does not require large basins of attraction, thereby allowing it to store a larger number of patterns safely. Noisy input is the primary concern in this paper and it is shown that for even 30% noise, the retrieval accuracy is as good as for other methods. The model has been compared to variants of the Hopfield network. It has an input/output layer (unit network) and a hidden layer (cohesion network) analogy and could be compared with a sparse quantized variant, but the 2 networks are constructed very differently. Although, both show that a graphical representation of the hidden layer is interesting. If the unit memory was to have an energy function, then it might be a shortest-path version, which could be a local rule. If the Hamming distance between sibling nodes could also be sorted, then they could be included as well. The best unit size would need to be decided first, but then online learning would be possible, which is another reason cited in [1] for their design. While the unit memory has a much simpler mathematical framework, this should not detract from the obvious importance of the Hopfield models. In fact, determining exactly what functionality they represent could make them all-the-more interesting. For example, they are thought to be a model for human memory as well. More recently however, it has been proposed that glial cells also play a part in memory and so if it is a simpler memory model analogy then maybe the simpler unit memory network could also be appropriate.
References
- Alonso, N. and Krichmar, J.L. A sparse quantized hopfield network for online-continual memory. Nature Communications 2024, 15, 3722. [Google Scholar] [CrossRef] [PubMed]
- Bouaguel, W. and Ben NCir, C.E., 2022. Distributed Evolutionary Feature Selection for Big Data Processing. Vietnam Journal of Computer Science, pp.1-20.
- Buscema, M. (1998). MetaNet: The Theory of Independent Judges, in Substance Use & Misuse, Vol. 33, No. 2, pp. 439 - 461.
- Burns, T.E. and Fukao, T. (2023). Simplical Hopfield Networks. burnsSimplicalHopfield23.pdf.
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Nat. Acad. Sci. 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.Y-C., Yang, D., Wu, D., Xu, C., Chen, B-Y. and Liu, H. (2023). On Sparse Modern Hopfield Model, 37th Conference on Neural Information Processing Systems (NeurIPS 2023).
- Kanerva, P. (1992). Sparse Distributed Memory and Related Models, NASA Technoical Report, Or, In M.H. Hassoun, ed., Associative Neural Memories: Theory and Implementation, pp. 50 - 76. New York: Oxford University Press, 1993.
- Krotov, D. and Hopfield, J. Dense Associative Memory Is Robust to Adversarial Inputs. Neural Computation 2018, 30, 3151–3167. [Google Scholar] [CrossRef] [PubMed]
- Marlin, B., Swersky, K., Chen, B. and Freitas, N., (2010). Inductive principles for restricted Boltzmann machine learning. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, JMLR Workshop and Conference Proceedings, pp. 509 - 516.
- Mendes, M., Coimbra, A.P. and Crisostomo, M. (2009). Assessing a Sparse Distributed Memory Using Different Encoding Methods, Proceedings of the World Congress on Engineering 2009 Vol I, WCE 2009, July 1 - 3, 2009, London, U.K.
- Snaider, J. and Franklin, S. (2012). Integer sparse distributed memory, In Twenty-fifth international flairs conference.
- The Chars74K dataset, http://www.ee.surrey.ac.uk/CVSSP/demos/chars74k/. (last accessed 10/12/24).
- UCI Machine Learning Repository. http://archive.ics.uci.edu/ml/. (last accessed 10/12/24).
Figure 1.
Unit and Cohesion Networks with unit size 3, for an input pattern.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
