Submitted:
19 November 2025
Posted:
20 November 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Materials and Methods:
2.1. Definitions of Probability Weighted Moments (PWMs)
2.2. Calculating PWMs for MBUW
2.2.1. Calculating : Equations (12-20)
2.2.2. Calculating Equations (21-26)
- Start with the initial guess of parameters (alpha and beta).
- Substitute these values in the objective function and the Jacobian.
- Choose the damping factor, say lambda=0.001
- Substitute in the equation (LM equation) to get the new parameters.
- Calculate the SSE at these parameters and compare this SSE value with the previous one when using the initial parameters to adjust for the damping factor.
- Update the damping factor accordingly as previously explained.
- Start new iteration with the new parameters and the new updated damping factor, i.e, apply the previous steps many times till convergence is achieved or a pre-specified number of iterations is accomplished.
2.2.3. Calculating Equation (29)
2.2.4. Calculating Equation (30)
2.3. Asymptotic Distribution of PWM Estimators
3. Monte Carlo Simulation Study
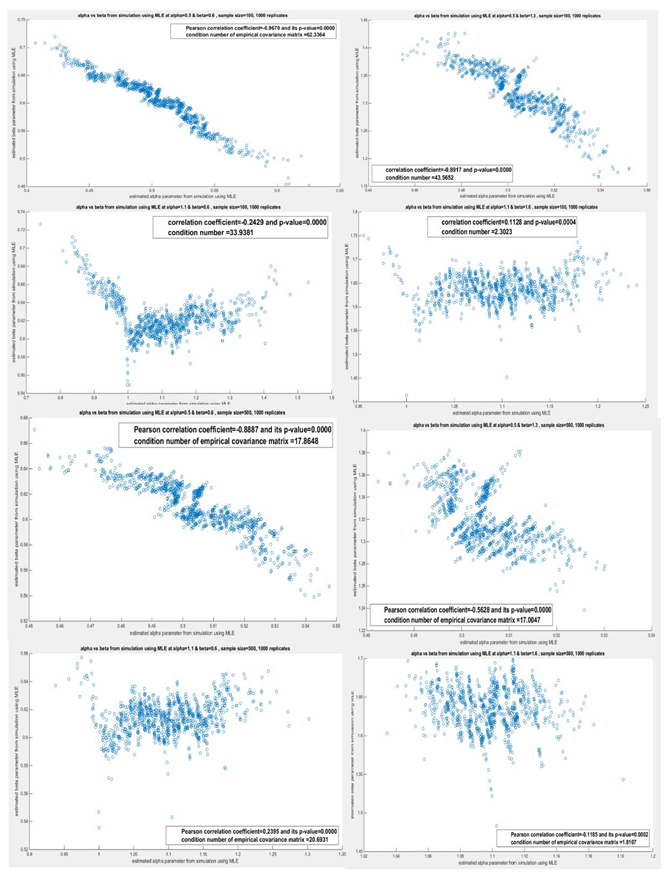
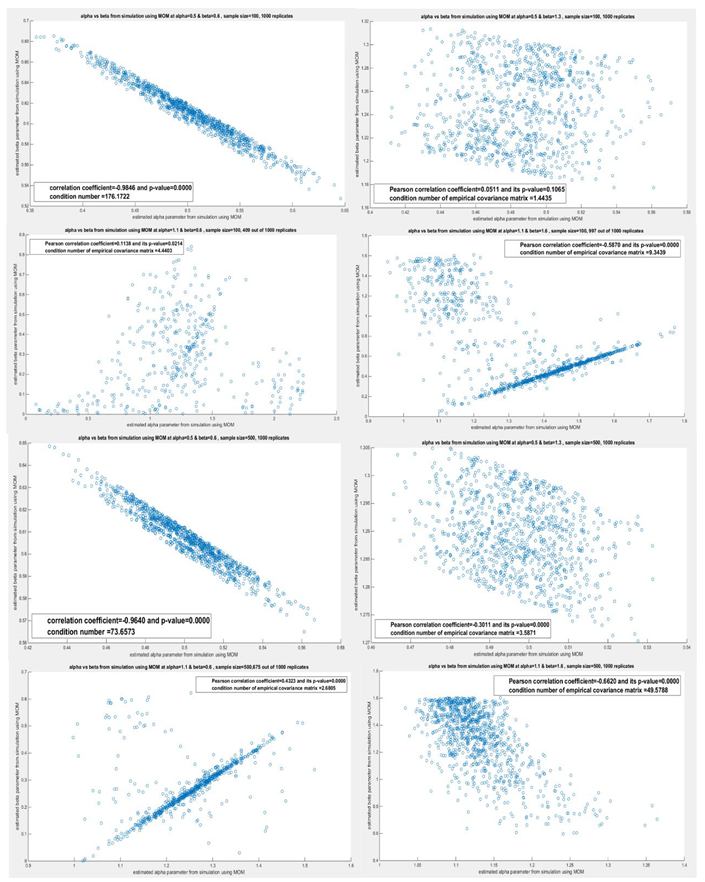
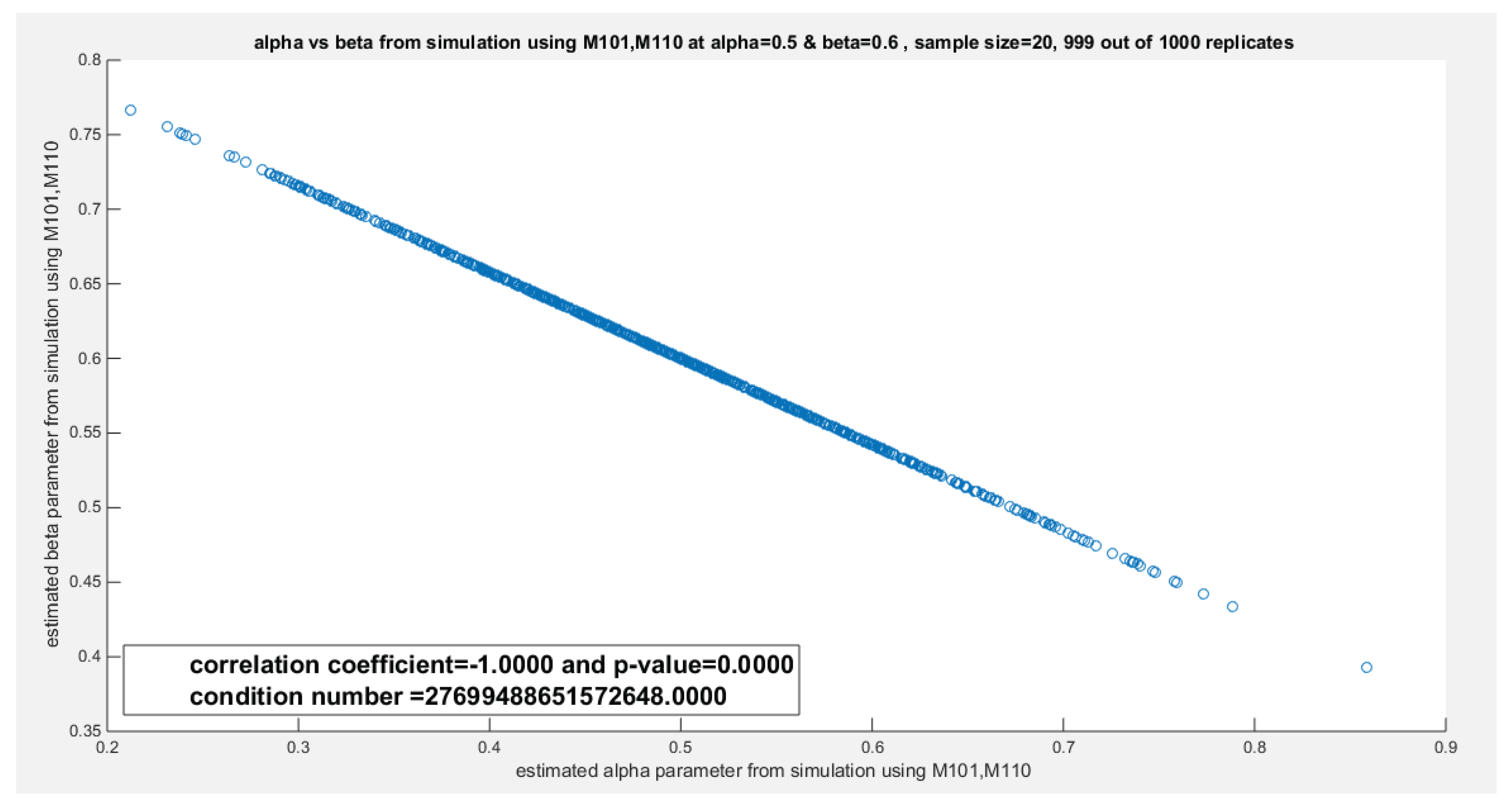
3.1. Simulation Study for the Parameters
3.2. Simulation Study for the Function of the Parameters (Validation of the Delta Method)
4. Results and Discussion of the Simulation Study
| PWM: M101,M110 |
PWM: M101,M110 |
PWM: M101,M110 |
PWM: M101,M110 |
|
|---|---|---|---|---|
|
Slope For |
||||
|
Slope For |
||||
|
PWM: M102,M120 & |
PWM: M102,M120 & |
PWM: M102,M120 & |
PWM: M102,M120 & |
|
|
Slope For |
||||
|
Slope For |
||||
|
MLE & |
MLE & |
MLE & |
MLE & |
|
|
Slope For α |
||||
|
Slope For |
||||
|
MOM & |
MOM & |
MOM & |
MOM & |
|
|
Slope For α |
||||
|
Slope For β |

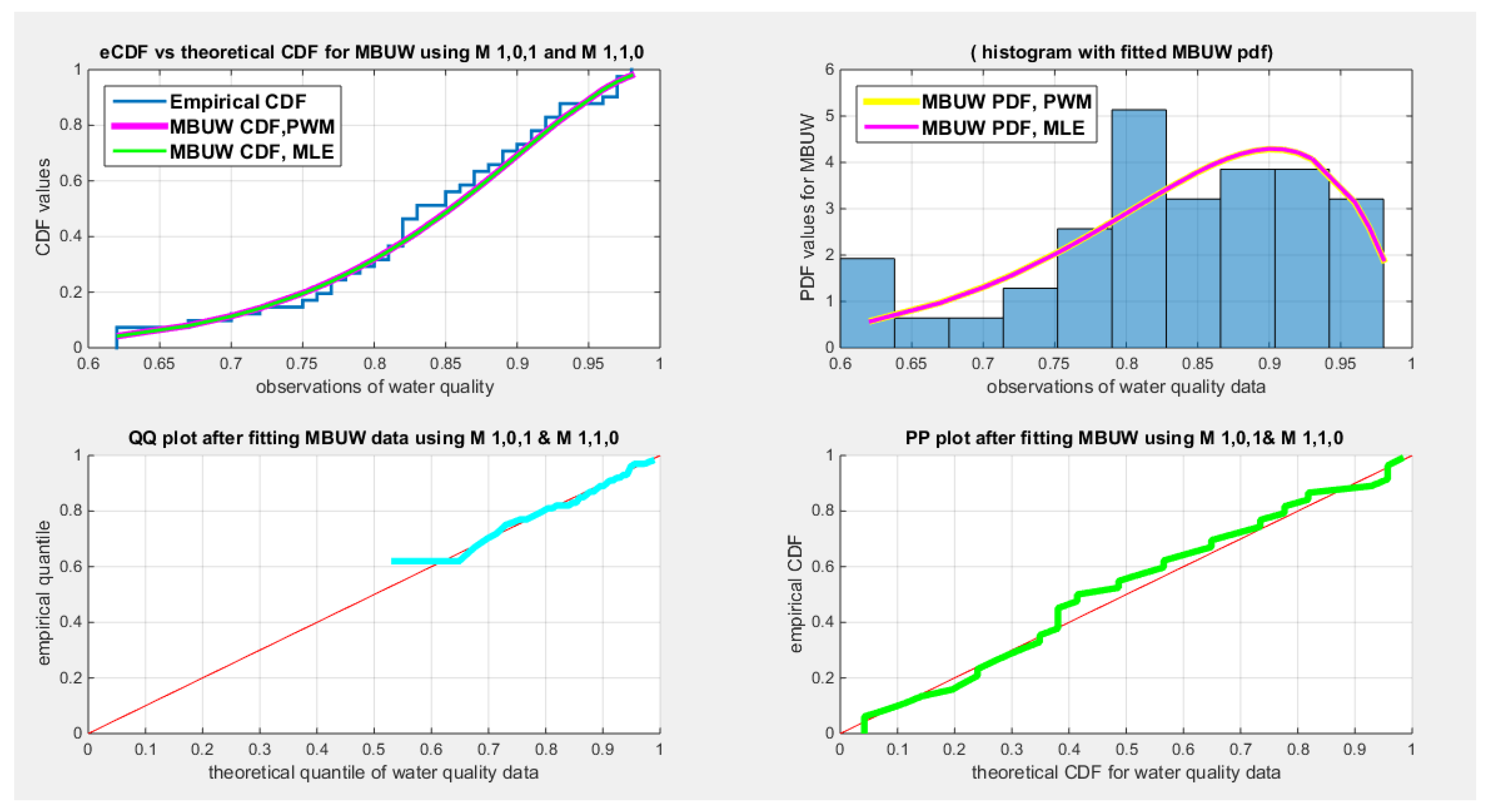
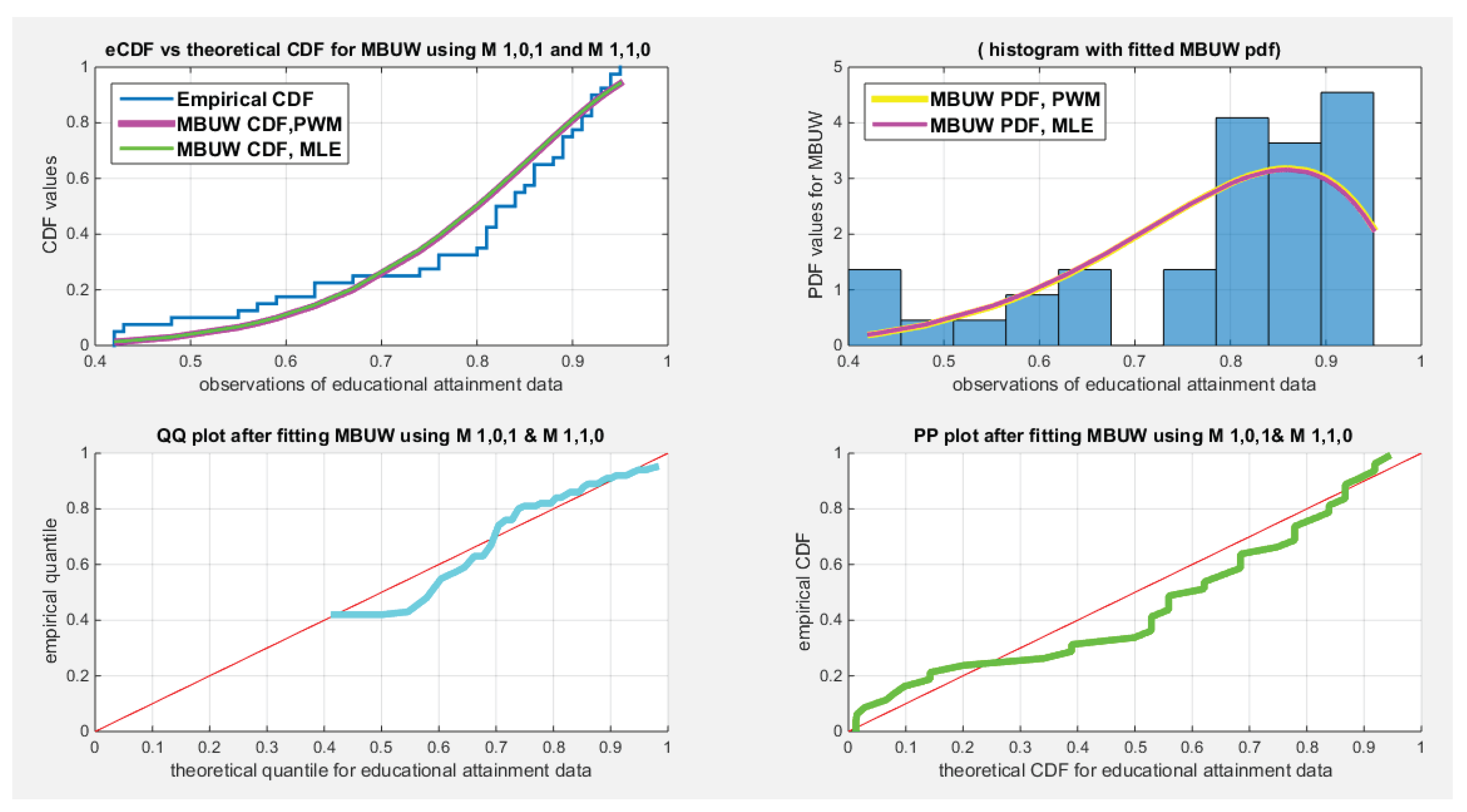
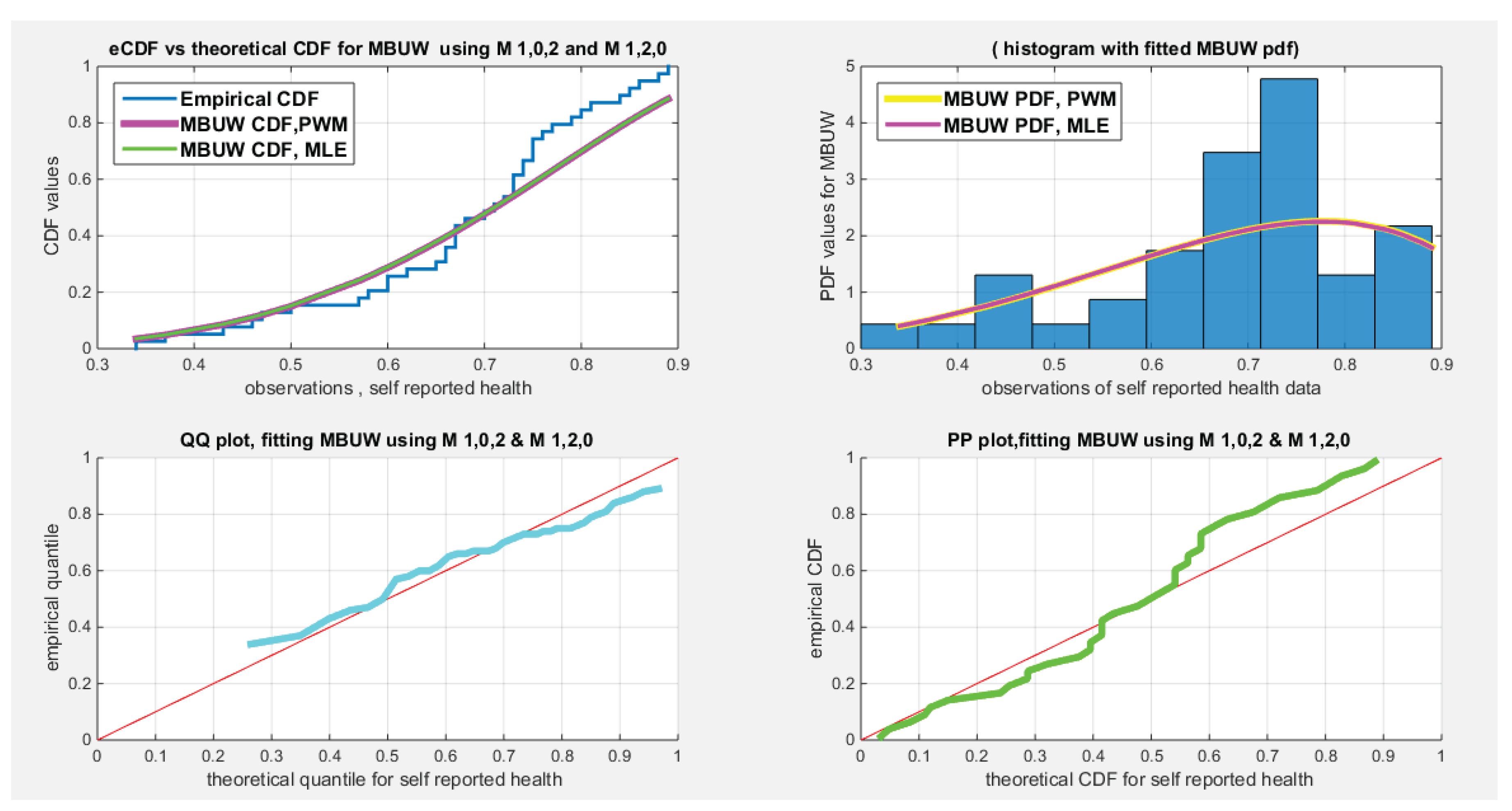
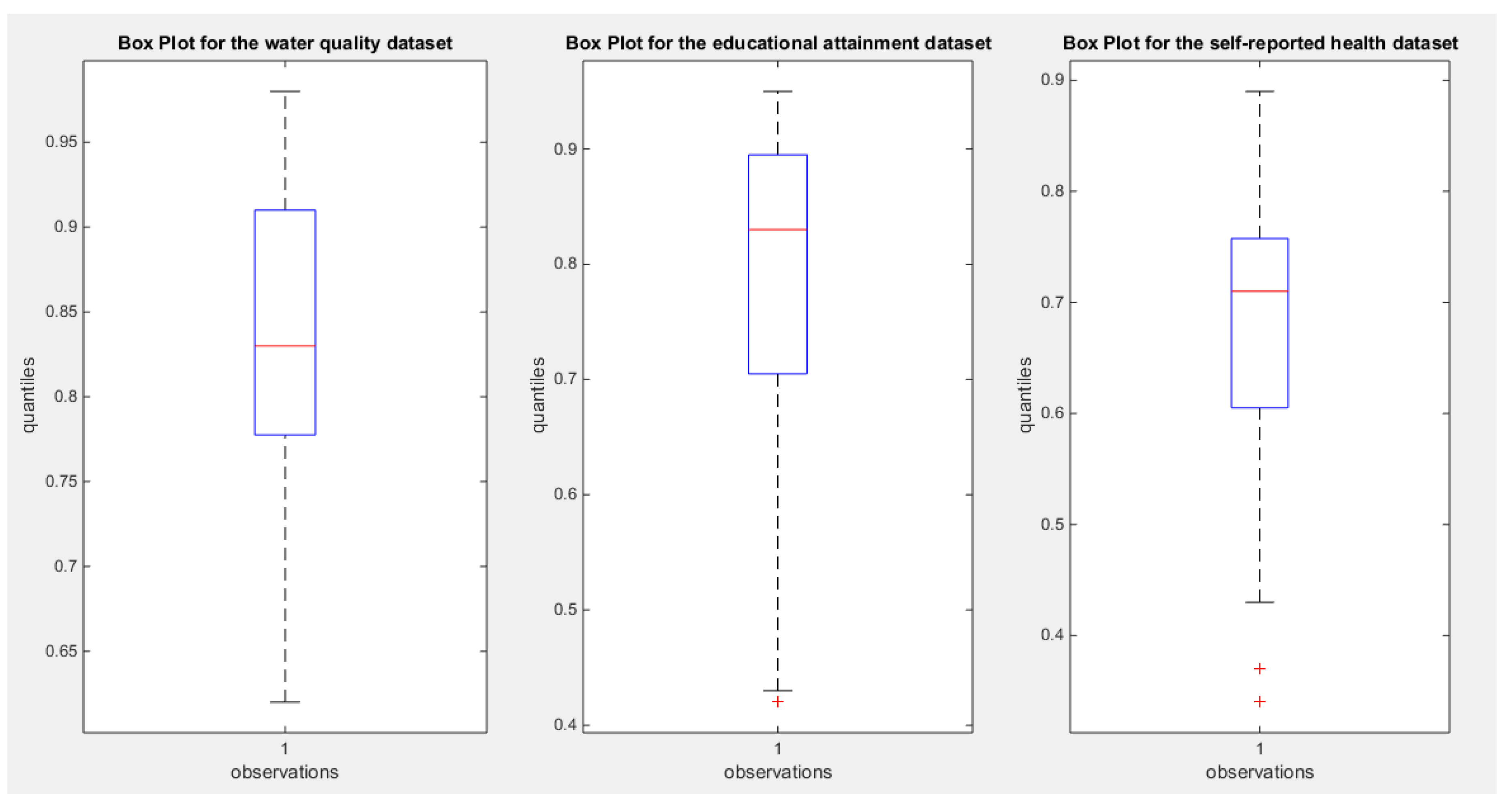
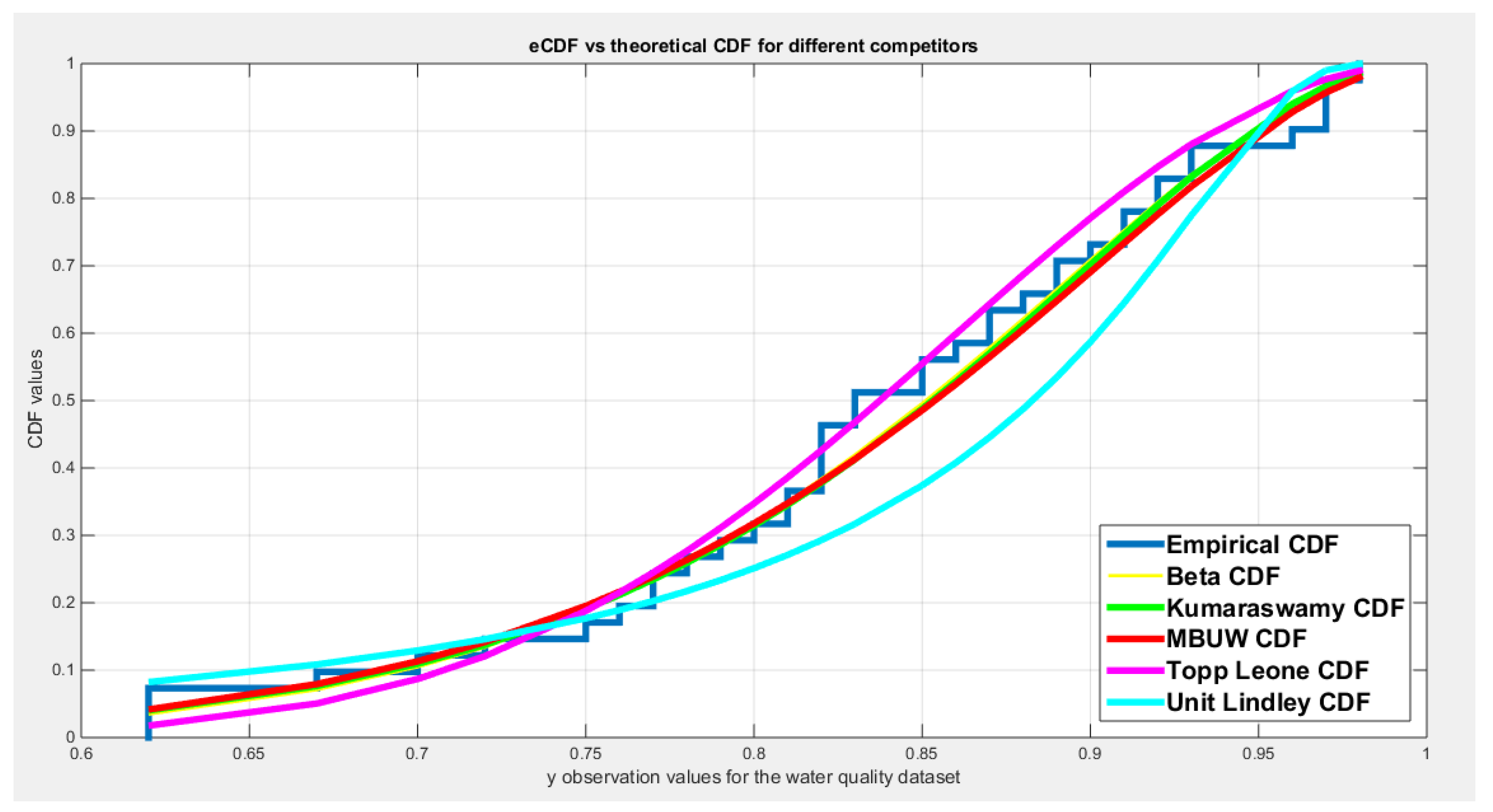
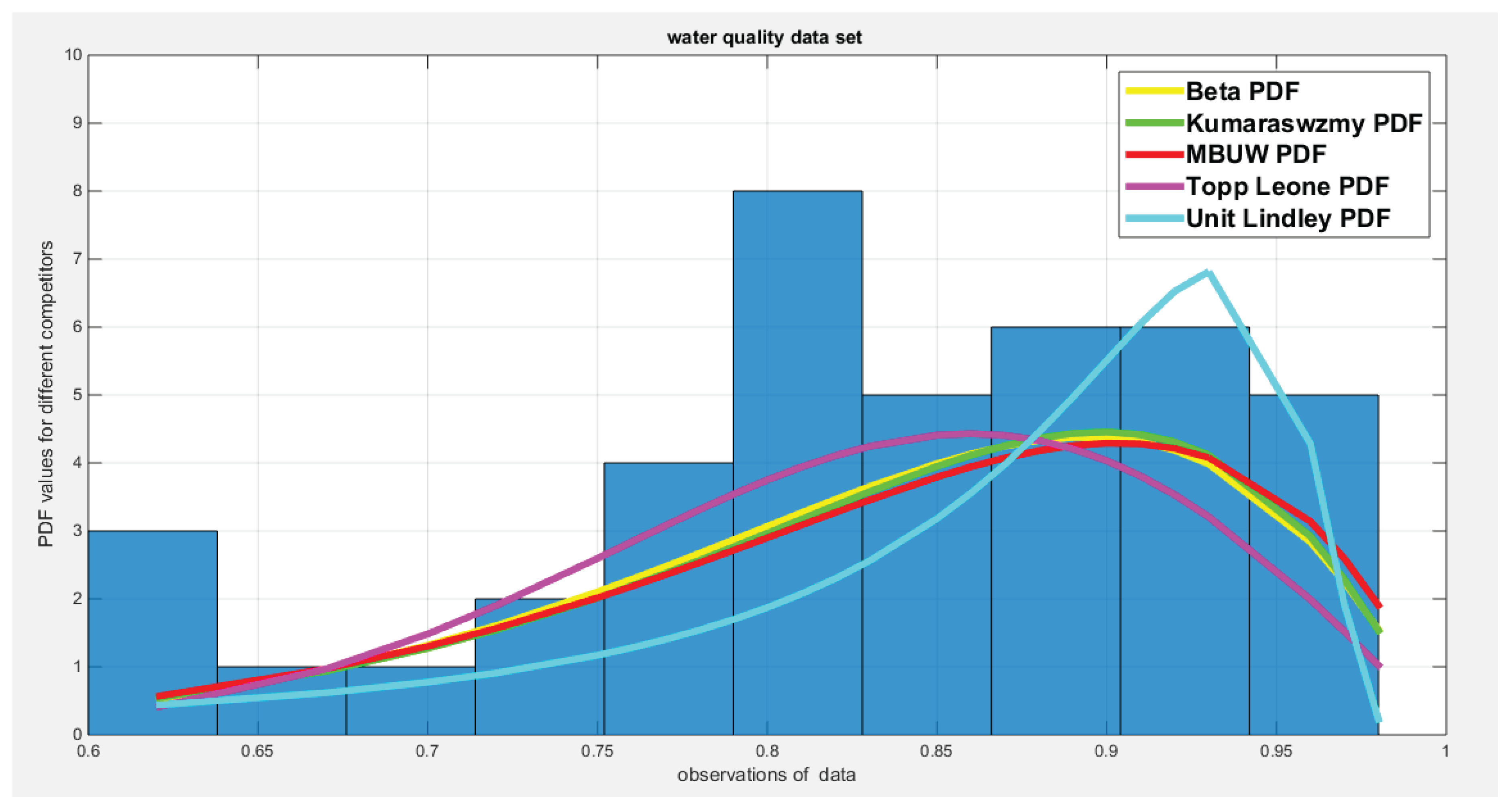
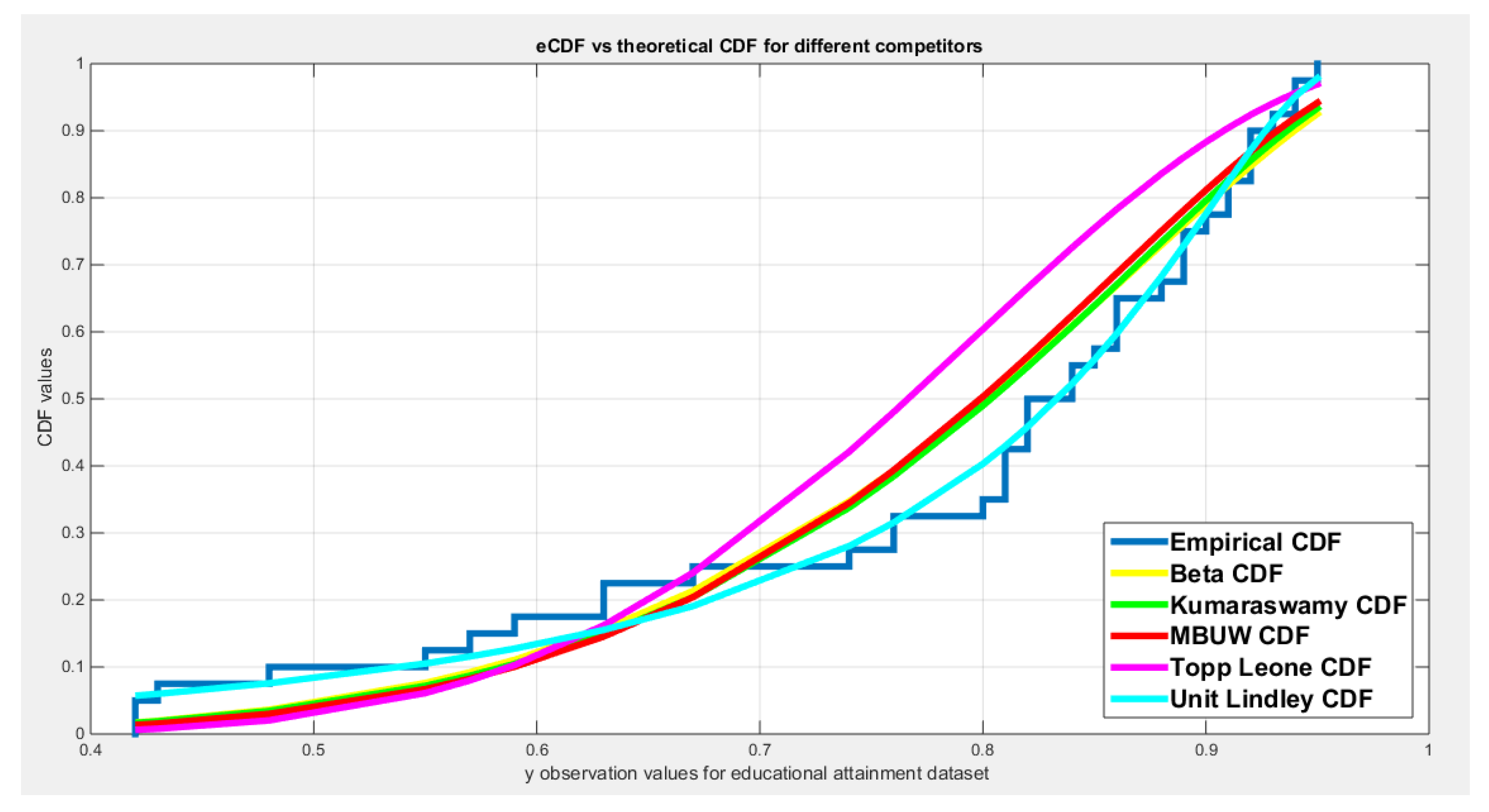
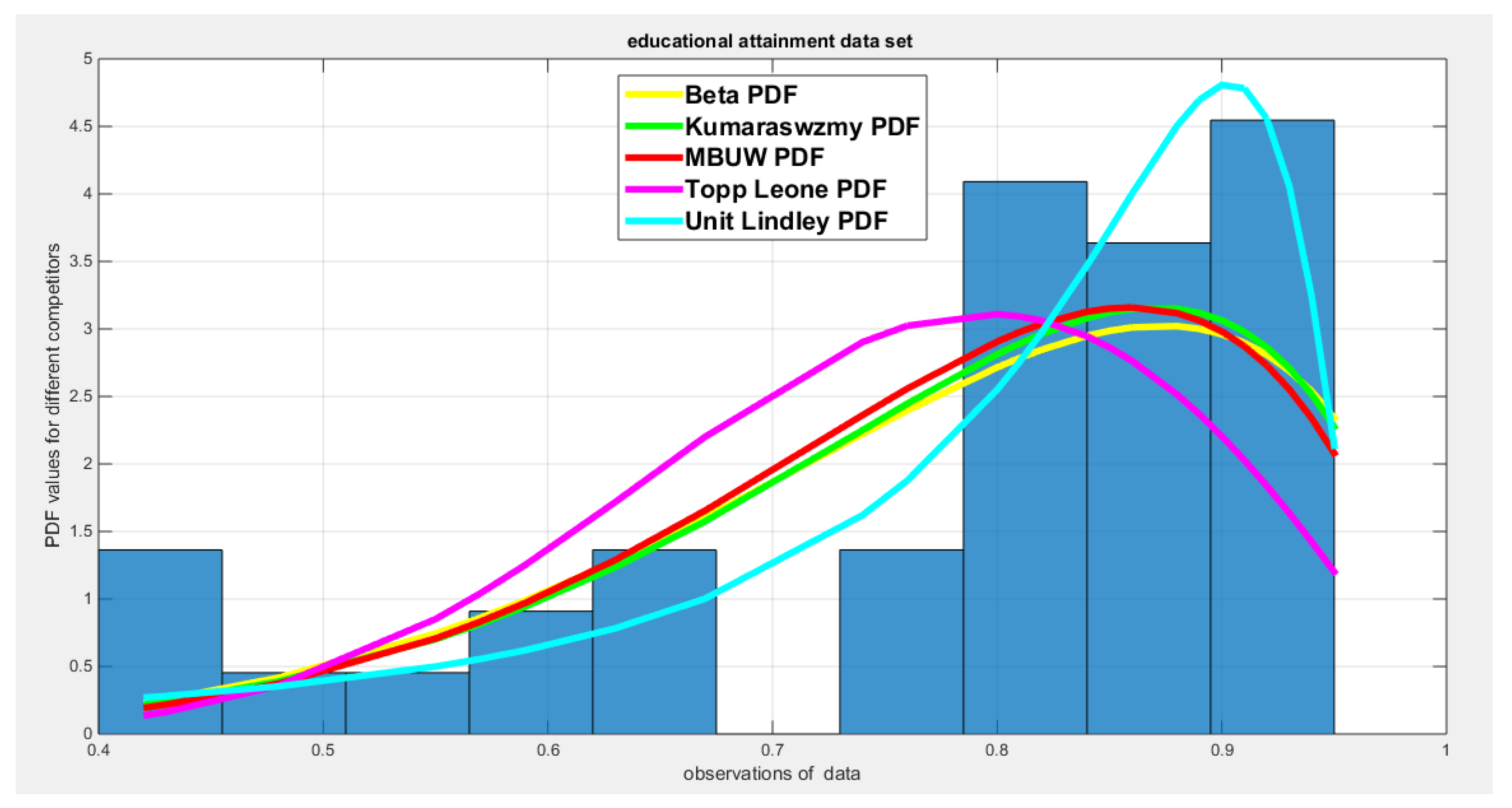
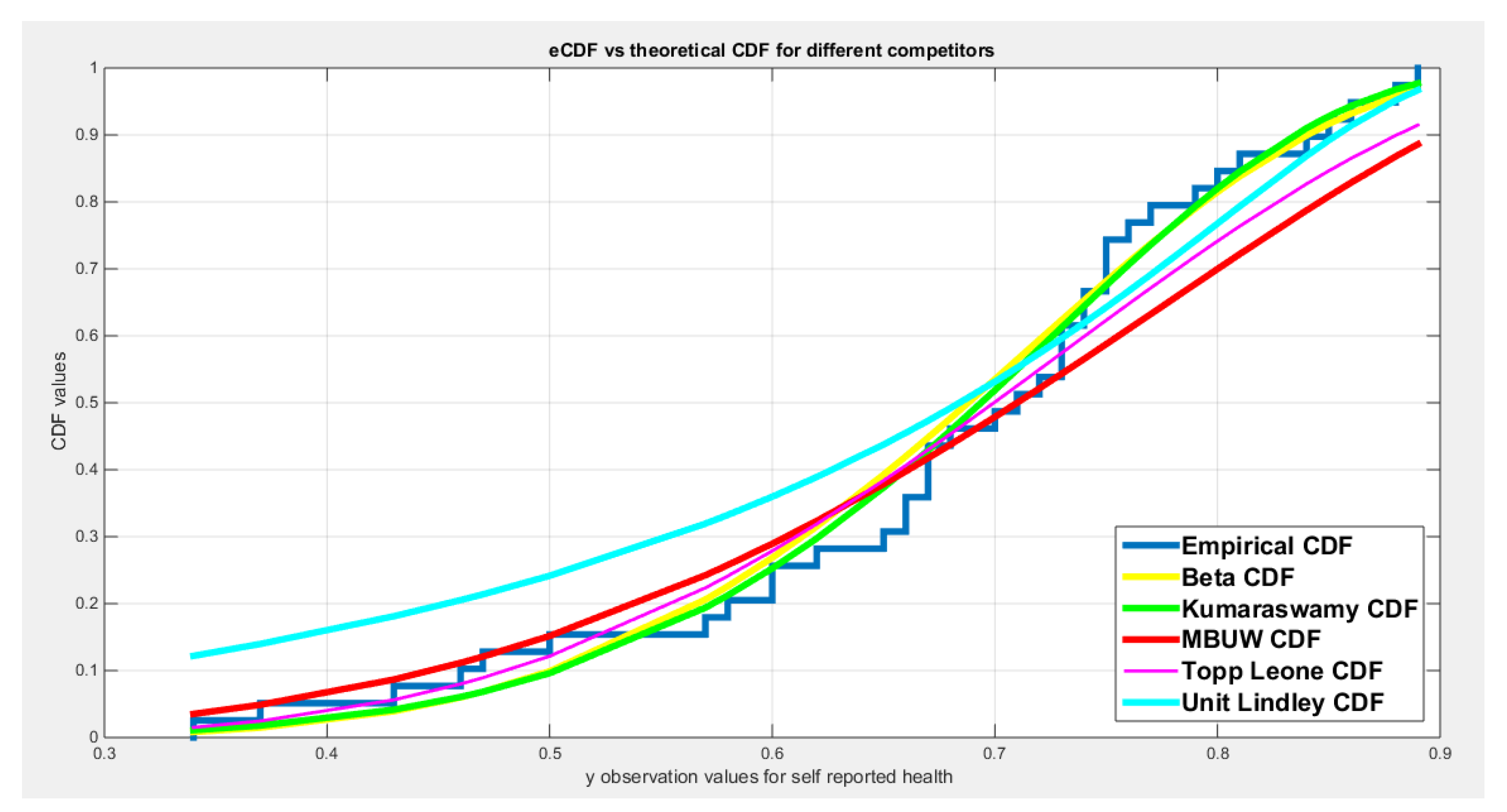
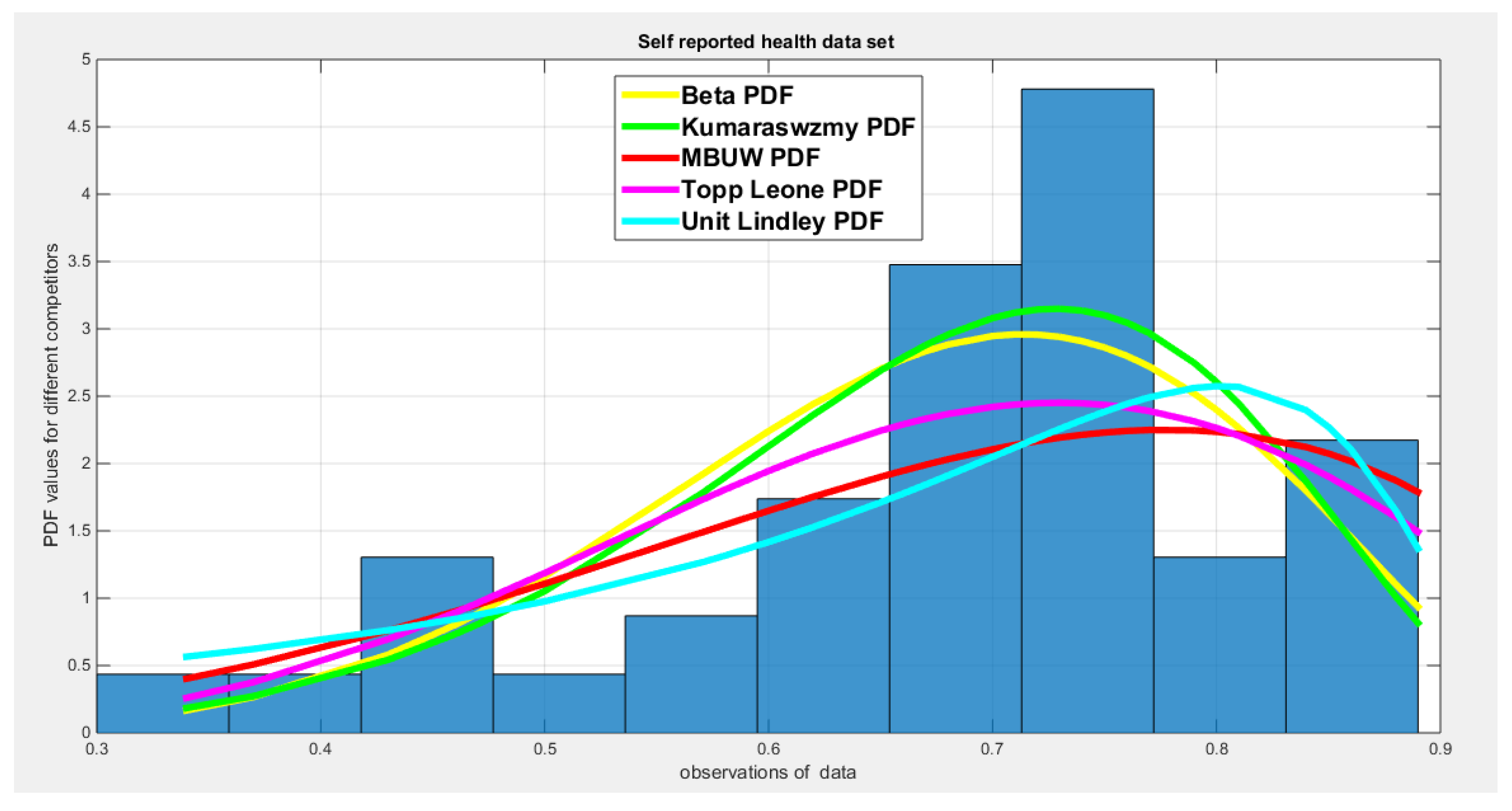
5. Real Data Analysis
| Beta | Kumaraswamy | MBUW | Topp-Leone | Unit-Lindley | ||||
| theta | 12.3585 | 0.2891 | ||||||
| Var-cov | 2.9116 | 0.9141 | 1.0268 | 0.3651 | 3.8183 | 0.0011 | ||
| 0.9141 | 0.3410 | 0.3651 | 0.2227 | |||||
| SE | 1.7063 | 1.0133 | 1.9540 | 0.0332 | ||||
| 0.5839 | 0.4719 | |||||||
| AIC | -48.1413 | -48.8385 | -48.0574 | -40.9642 | -57.3738 | |||
| CAIC | -47.817 | -48.5142 | -47.7331 | -40.8589 | -57.2685 | |||
| BIC | -44.7636 | -45.4607 | -44.6796 | -39.2753 | -55.6849 | |||
| HQIC | -46.92 | -47.6172 | -46.8361 | -40.3535 | -56.7631 | |||
| LL | 26.0707 | 26.4193 | 26.0287 | 21.4821 | 29.6869 | |||
| K-S Value | 0.1481 | 0.1434 | 0.1577 | 0.2598 | 0.0697 | |||
| H0 | Fail to reject | Fail to reject | Fail to reject | Reject | Fail to reject | |||
| P-value | 0.1613 | 0.1841 | 0.1219 | 0.0023 | 0.9442 | |||
| AD | 1.1861 | 1.1575 | 1.4386 | 4.5709 | 0.2596 | |||
| CVM | 0.2068 | 0.1985 | 0.2546 | 0.8485 | 0.0344 | |||
| Beta | Kumaraswamy | MBUW | Topp-Leone | Unit-Lindley | ||||
| theta | 7.3278 | 0.5929 | ||||||
| Var | 3.3978 | 1.6515 | 0.7936 | 1.2015 | 1.3768 | 0.0058 | ||
| 1.6515 | 0.9425 | 1.2015 | 2.5192 | |||||
| SE | 1.8433 | 0.8908 | 1.1734 | 0.0693 | ||||
| 0.9708 | 1.5872 | |||||||
| AIC | -46.2684 | -47.3865 | -38.5536 | -44.4298 | -40.09617 | |||
| CAIC | -45.9351 | -47.0531 | -38.2202 | -44.3217 | -39.9617 | |||
| BIC | -42.9413 | -44.0594 | -35.2264 | -42.7662 | -38.4062 | |||
| HQIC | -45.0746 | -46.1927 | -37.3598 | -43.8329 | -39.4729 | |||
| LL | 25.1342 | 25.6932 | 21.2768 | 23.2149 | 21.0349 | |||
| K-S Value | 0.0867 | 0.0684 | 0.1625 | 0.1234 | 0.1400 | |||
| H0 | Fail to reject | Fail to reject | Fail to reject | Fail to reject | Fail to reject | |||
| P-value | 0.6674 | 0.8577 | 0.2284 | 0.5512 | 0.2102 | |||
| AD | 0.4674 | 0.3414 | 1.4935 | 0.8744 | 1.6862 | |||
| CVM | 0.0807 | 0.0547 | 0.2492 | 0.1397 | 0.2886 | |||
| Using unbiased Sample estimator for |
Using unbiased Sample estimator for |
|||||
| thetas | 0.3564 | 0.3529 | ||||
| 1.4307 | 1.4316 | |||||
| Var-cov matrix of parameter |
10.7370 | 22.9418 | 627.8954 | 2.4064e+3 | ||
| 22.9418 | 94.1037 | 2.4064e+3 | 9.3821e+3 | |||
| Eigenvalues=4.8406, 100 | Eigenvalue=10.0408 , 1e+4 | |||||
| AD | 0.3418 ( p=0.8810) | 0.3820 (p=0.865) | ||||
| CVM | 0.0531 (p=0.8420) | 0.0637 (p=0.785) | ||||
| KS & p-value | 0.0980 (p=0.7901) | 0.1061 (p=0.7051 | ||||
| H0 | Fail to reject | Fail to reject | ||||
| SSE | 1.8169e-19 | 1.7110e-19 | ||||
| , unbiased estimator | 0.3891 | 0.2491 | ||||
| , unbiased estimator | 0.4441 | 0.3041 | ||||
| Sig.of parameter | 1.648(p=0.1072) | 0.5950(p=0.5552) | ||||
| Sig.of parameter | 3.3898(p=0.0016) | 1.2365(p=0.2235) | ||||
| Variance of the function of the parmaeter, after the delta method application. Determinant and trace of this matrix |
0.0181 | 0.0096 | 0.0214 | 0.0080 | ||
| 0.0096 | 0.0051 | 0.0080 | 0.0030 | |||
| Eigenvalues=0.0232, 8.6736e-19 Determinant=0 Trace=0.0232 |
Eigenvalues=0.0244 , -4.3368e-19 Determinant=0 Trace=0.0244 |
|||||
| Var-cov between M101&M110 | 8.8987e-4 | 0.0042 | ||||
| 0.0042 | 0.0020 | |||||
| Var-cov between M102 & M120 | 9.5798e-4 | 0.0197 | ||||
| 0.0197 | 0.002 | |||||
| and associated | 0.0468 | 0.0361 | 0.3518 | 0.2717 | ||
| 0.0361 | 0.1781 | 0.2717 | 1.3403 | |||
|
to achieved condition number=5 |
to achieved condition number=5 |
|||||
| Jacobian matrix | -0.3796 | 0.0977 | -0.2863 | 0.0735 | ||
| -1.4718 | 0.3786 | -0.1067 | 0.0274 | |||

| Using unbiased Sample estimator for |
Using unbiased Sample estimator for |
|||||
| thetas | 0.4310 | 0.4462 | ||||
| 1.3483 | 1.3442 | |||||
| Var-cov matrix of parameter |
679.8845 | 2.5075e+3 | 679.7206 | 2.4966e+3 | ||
| 2.5075e+3 | 9.3254e+3 | 2.4966e+3 | 9.3313e+3 | |||
| Eigenvalues=5.2672, 10000 | Eigenvalue=10.9762 , 1e+4 | |||||
| AD | 1.4027 ( p=0.2090) | 1.6993( p=0.1330) | ||||
| CVM | 0.2420 (p=0.1990) | 0.3333(p=0.1110) | ||||
| KS & p-value | 0.1787 (p=0.1371) | 0.2041(p=0.0615) | ||||
| H0 | Fail to reject | Fail to reject | ||||
| SSE | 2.2362e-19 | 2.4395e-19 | ||||
| , unbiased estimator | 0.3485 | 0.2139 | ||||
| , unbiased estimator | 0.4325 | 0.2979 | ||||
| Sig.of parameter | 2.0345(p=0.0487) | 0.6592(p=0.5136) | ||||
| Sig.of parameter | 3.2983(p=0.0021) | 1.0279(p=0.3104) | ||||
| Variance of the function of the parmaeter, after the delta method application. Determinant and trace of this matrix |
0.0190 | 0.0107 | 0.0213 | 0.0089 | ||
| 0.0107 | 0.0060 | 0.0089 | 0.0037 | |||
| Eigenvalues=0.0250, 2.6021e-18 Determinant=0 Trace=0.0250 |
Eigenvalues=0.0250 , 4.3368e-19 Determinant=0 Trace=0.0250 |
|||||
| Var-cov between M101&M110 | 6.7399e-4 | 0.0038 | ||||
| 0.0038 | 0.0020 | |||||
| Var-cov between M102 & M120 | 6.7302e-4 | 0.0264 | ||||
| 0.0264 | 0.0020 | |||||
| and associated | 0.0449 | 0.0355 | 0.4582 | 0.3613 | ||
| 0.0355 | 0.1671 | 0.3613 | 1.7103 | |||
|
to achieve a condition number=5 |
to achieve a condition number=5 |
|||||
| Jacobian matrix | -0.3668 | 0.0987 | -0.2691 | 0.0721 | ||
| -0.2059 | 0.0554 | -0.1119 | 0.0300 | |||

| Using unbiased Sample estimator for |
Using unbiased Sample estimator for |
|||||
| thetas | 0.5843 | 0.5752 | ||||
| 1.2806 | 1.2829 | |||||
| Var-cov matrix of parameter |
11.610 | 21.6717 | 71.1767 | 230.3148 | ||
| 21.6717 | 94.6865 | 230.3148 | 942.8902 | |||
| Eigenvalues=6.2964 , 100 | Eigenvalue=14.0669 , 1000 | |||||
| AD | 1.4443 ( p=0.2010) | 1.5100 ( p=0.1780) | ||||
| CVM | 0.2382 (p=0.2100) | 0.2529 (p=0.1900) | ||||
| KS & p-value | 0.1549 (p=0.2768) | 0.1645 (p=0.2167) | ||||
| H0 | Fail to reject | Fail to reject | ||||
| SSE | 5.9631e-19 | 0 | ||||
| , unbiased estimator | 0.3019 | 0.1865 | ||||
| , unbiased estimator | 0.3775 | 0.2621 | ||||
| Sig.of parameter | 2.7038(p=0.0102) | 0.7048 (p=0.4852) | ||||
| Sig.of parameter | 3.0045(p=0.0047) | 0.7988 (p=0.4293) | ||||
| Variance of the function of the parmaeter, after the delta method application. Determinant and trace of this matrix |
0.0172 | 0.0108 | 0.0205 | 0.0099 | ||
| 0.0108 | 0.0068 | 0.0099 | 0.0047 | |||
| Eigenvalues=0.0240, 1.7347e-18 Determinant=0 Trace=0.0240 |
Eigenvalues=0.0253 , 0 Determinant=0 Trace=0.0253 |
|||||
| Var-cov between M101& M110 | 4.0448e-4 | 0.0029 | ||||
| 0.0029 | 0.0020 | |||||
| Var-cov between M102 & M120 | 4.2498e-4 | 0.0347 | ||||
| 0.0347 | 0.0020 | |||||
| and associated | 0.0467 | 0.0352 | 0.6661 | 0.5053 | ||
| 0.0352 | 0.1817 | 0.5053 | 2.5787 | |||
| to achieve a condition number=5 | to achieve a condition number=5 | |||||
| Jacobian matrix | -0.3062 | 0.0717 | -0.2317 | 0.0574 | ||
| -1.5296 | 0.3579 | -0.1112 | 0.0276 | |||

6. Conclusions
7. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C


References
- Iman, M. Attia, “Median Based Unit Weibull (MBUW): ANew Unit Distribution Properties,” , vol. preprint article, Preprints.org, no. preprint article, Preprints.org, Oct. 2024. 25 October. [CrossRef]
- J. A. Greenwood, J. M. J. A. Greenwood, J. M. Landwehr, N. C. Matalas, and J. R. Wallis, “Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form,” Water Resources Research, vol. 15, no. 5, pp. 1049–1054, Oct. 1979. [CrossRef]
- J. R. M. Hosking, J. R. Wallis, and E. F. Wood, “Estimation of the Generalized Extreme-Value Distribution by the Method of Probability-Weighted Moments,” Technometrics, vol. 27, no. 3, pp. 251–261, Aug. 1985, Accessed: Dec. 08, 2024. [Online]. Available: https://www.tandfonline.com/doi/abs/10.1080/00401706.1985.
- J. R. M. Hosking and J. R. Wallis, “Parameter and Quantile Estimation for the Generalized Pareto Distribution,” TECHNOMETRICS, vol. 29, NO. 3, no. 3, pp. 251–261, 1987.
- Ekta Hooda, B K Hooda, and Nitin Tanwar, “Probability weighted moments (PWMs) and partial probability weighted moments (PPWMs) of type-II extreme value distribution,” in Conference: National Conference on Mathematics and Its applications in Science and technologyAt: Department of Mathematics, GJUS&T, Hisar, Haryana, India, India, Oct. 2018.
- Ashkar, F. and Mahdi S., “Comprison of two fitting methods for the log-logistic distribution,” Wter resources research, vol. 39, no. 8, 1217, pp. 1–8, 2003.
- F. Caeiro and A. Mateus, “A New Class of Generalized Probability-Weighted Moment Estimators for the Pareto Distribution,” Mathematics, vol. 11, no. 5, p. 1076, Feb. 2023. [CrossRef]
- Q. J. Wang, “Estimation of the GEV distribution from censored samples by method of partial probability weighted moments,” Journal of Hydrology, vol. 120, no. 1–4, pp. 103–114, Dec. 1990. [CrossRef]
- Caeiro,F. and Mateus, A., “A Log Probability Weighted Moments Method for Pareto distribution,” in Proceedings of the 17th Applied Stochastic Models and Data Analysis International Conference with 6th Demographics Workshop, London,UK,6-9 June2017,Skiadas,C.H.,ED.;2017;pp211-218, 2017, p. pp.211-218.
- F. Caeiro and D. Prata Gomes, “A Log Probability Weighted Moment Estimator of Extreme Quantiles,” in Theory and Practice of Risk Assessment, vol. 136, C. P. Kitsos, T. A. Oliveira, A. Rigas, and S. Gulati, Eds., in Springer Proceedings in Mathematics & Statistics, vol. 136., Cham: Springer International Publishing, 2015, pp. 293–303. [CrossRef]
- F. Caeiro, M. I. F. Caeiro, M. I. Gomes, and B. Vandewalle, “Semi-Parametric Probability-Weighted Moments Estimation Revisited,” Methodol Comput Appl Probab, vol. 16, no. 1, pp. 1–29, Mar. 2014. [CrossRef]
- F. Caeiro and M. Ivette Gomes, “Semi-parametric tail inference through probability-weighted moments,” Journal of Statistical Planning and Inference, vol. 141, no. 2, pp. 937–950, Feb. 2011. [CrossRef]
- F. Caeiro and M. I. Gomes, “A Class of Semi-parametric Probability Weighted Moment Estimators,” in Recent Developments in Modeling and Applications in Statistics, P. E. Oliveira, M. Da Graça Temido, C. Henriques, and M. Vichi, Eds., Berlin, Heidelberg: Springer Berlin Heidelberg, 2013, pp. 139–147. [CrossRef]
- Rizwan Munir,, Muhammad Saleem,, Muhammad Aslam, and and Sajid Ali, “Comparison of different methods of parameters estimation for Pareto Model,” Caspian Journal of Applied Sciences Research, 2(1), pp. 45-56, 2013, vol. 2, no. 1, pp. 45–56, 2013.
- H. Chen, W. H. Chen, W. Cheng, J. Zhao, and X. Zhao, “Parameter estimation for generalized Pareto distribution by generalized probability weighted moment-equations,” Communications in Statistics - Simulation and Computation, vol. 46, no. 10, pp. 7761–7776, Nov. 2017. [CrossRef]
- R. M. Vogel, T. A. R. M. Vogel, T. A. McMahon, and F. H. S. Chiew, “Floodflow frequency model selection in Australia,” Journal of Hydrology, vol. 146, pp. 421–449, 93. 19 June. [CrossRef]
- Hosking, J.R.M. , “L-moment: analysis and estimation of distributions using ;inear combinations of order statistics,” J.R.Statist. Soc, vol. 52, no. 1, pp. 105–124, 1990.
- Hosking,J.R.M., “The theory of probability weighted moments,” Res.Rep,RC12210, IBM ThomasJ. Watson Res. Cent., New York, 1986.
- P. F. Rasmussen, “Generalized probability weighted moments: Application to the generalized Pareto Distribution,” Water Resources Research, vol. 37, no. 6, pp. 1745–1751, 01. 20 June. [CrossRef]
- Jing, D., Dedun,S., Ronfu,Y., and Yu,H., “Expressions relating probability weighted moments to parameters of several distributions inexpressible in inverse form.,” J. Hydrol., vol. 110, no. J. Hydrol. 1989, 110, 259–270., pp. 259-270., 1989.
- J. M. Landwehr, N. C. J. M. Landwehr, N. C. Matalas, and J. R. Wallis, “Probability weighted moments compared with some traditional techniques in estimating Gumbel Parameters and quantiles,” Water Resources Research, vol. 15, no. 5, pp. 1055–1064, Oct. 1979. [CrossRef]
- J. M. Landwehr, N. C. J. M. Landwehr, N. C. Matalas, and J. R. Wallis, “Estimation of parameters and quantiles of Wakeby Distributions: 1. Known lower bounds,” Water Resources Research, vol. 15, no. 6, pp. 1361–1372, Dec. 1979. [CrossRef]
- Chernoff,H., Gastwirth, J.L., and HOHNSjohns, M.V., “Asymptotic distribution of linear combinations of functions of order statistics with applications to estimation,” Annals of Mathematical Statistics, vol. 38, pp. 52–72, 1967.
- Rao, C.R. , Linear Statistical Inference and Its Applications, 2nd ed. New York, NY: John Wiley, 1973.

| Statistical indices | MLE | MOM | PWM M101,M110 |
PWM M102,M120 |
|
|---|---|---|---|---|---|
|
|
0.5055,(0.0842) | 0.4943,(0.1113) | 0.4975,(0.1007) | 0.4978,(0.0985) | |
| 0.5963,(0.1077) | 0.6298,(0.0812) | 0.6014,(0.0581) | 0.6013,(0.0569) | ||
| 0.0647 | 0.0878 | 0.0798 | 0.078 | ||
| 0.0794 | 0.0648 | 0.0461 | 0.045 | ||
| 0.0071 | 0.0124 | 0.0101 | 0.0096 | ||
| 0.0116 | 0.0075 | 0.0034 | 0.0032 | ||
| 0.1293 | 0.1756 | 0.1596 | 0.1559 | ||
| 0.1324 | 0.1079 | 0.0768 | 0.0751 | ||
| (0.3653,0.7004) | (0.2838,0.7266) | (0.3008,0.7042) | (0.2961,0.6909) | ||
| (0.3366,0.7596) | (0.4767,0.8019) | (0.4821,0.7151) | (0.4897,0.7177) | ||
| Number of valid samples | 1000 of 1000 | 987 out of 1000 | 999 out of 1000 | 999 out of 1000 | |
|
|
0.5000 (0.0372) | 0.4441 (0.0648) | 0.4955 (0.0580) | 0.4954 (0.0578) | |
| 1.3210,0.0963 | 1.1365 (0.0724) | 1.3012 (0.0155) | 1.3012 (0.0154) | ||
| 0.02297 | 0.0706 | 0.0467 | 0.0468 | ||
| 0.0800 | 0.1637 | 0.0124 | 0.0125 | ||
| 0.0014 | 0.0073 | 0.0034 | 0.0034 | ||
| 0.0097 | 0.0320 | 2.4062e-4 | 2.3897e-4 | ||
| 0.0593 | 0.1412 | 0.0934 | 0.0936 | ||
| 0.0615 | 0.1259 | 0.0096 | 0.0096 | ||
| (0.4281,0.5786) | (0.2679,0.6069) | (0.3815,0.6117) | (0.3837,0.6118) | ||
| (1.111,1.5046) | (1.0330,1.3073) | (1.2702,1.3316) | (1.2702,1.3310) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.1056 (0.2651) | 1.1772 (0.3668) | 1.0920 (0.2883) | 1.0942 (0.2586) | |
| 0.6509 (0.0407) | 0.4717 (0.2795) | 0.5986 (0.0504) | 0.5990 (0.0452) | ||
| 0.2153 | 0.2933 | 0.2287 | 0.2052 | ||
| 0.0518 | 0.2534 | 0.0400 | 0.0359 | ||
| 0.0702 | 0.1371 | 0.0831 | 0.0668 | ||
| 0.0043 | 0.0926 | 0.0025 | 0.0020 | ||
| 0.1958 | 0.2666 | 0.2079 | 0.1865 | ||
| 0.0864 | 0.4224 | 0.0666 | 0.0598 | ||
| (0.6824,1.7008) | (0.5143.1.8809) | (0.5476,1.6682) | (0.6037,1.5896) | ||
| (0.5945,0.7521) | (0.0074,0.8971) | (0.5035,0.6993) | (0.5133,0.6856) | ||
| Number of valid samples | 1000 of 1000 | 40 out of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.0928 (0.1050) | 1.0979 (0.0172) | 1.0983 (0.1139) | ||
| 1.6595 (0.0546) | 1.5999 (0.0011) | 1.5999 (0.0075) | |||
| 0.086 | 0.0959 | 0.0927 | |||
| 0.0646 | 0.0063 | 0.0061 | |||
| 0.0111 | 0.0138 | 0.0130 | |||
| 0.0065 | 5.9109e-5 | 5.5617e-5 | |||
| 0.0782 | 0.0128 | 0.0843 | |||
| 0.0403 | 5.7592e-4 | 0.0038 | |||
| (0.8940,1.2883) | (0.8661,1.13024) | (8.700,1.3045) | |||
| (1.5711,1.7822) | (1.5847,1.6133) | (1.5849,1.6134) | |||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | ||
| Statistical indices | MLE | MOM | PWM M101,M110 |
PWM M102,M120 |
|
|---|---|---|---|---|---|
|
|
0.5052 (0.0533) | 0.4988 (0.074) | 0.5002 (0.0666) | 0.5001 (0.0645) | |
| 0.6012 (0.0652) | 0.6135 (0.0417) | 0.5999 (0.0385) | 0.5999 (0.0373) | ||
| 0.04427 | 0.0585 | 0.0540 | 0.0522 | ||
| 0.0520 | 0.0348 | 0.0312 | 0.0301 | ||
| 0.0029 | 0.0055 | 0.0044 | 0.0042 | ||
| 0.0042 | 0.0019 | 0.0015 | 0.0014 | ||
| 0.0854 | 0.1170 | 0.1080 | 0.1043 | ||
| 0.0866 | 0.0579 | 0.0520 | 0.0502 | ||
| (0.4097,0.6114) | (0.3495,0.6400) | (0.3693,0.6242) | (0.3718,0.6231) | ||
| (0.4535,0.7133) | (0.5302,0.6930) | (0.5283,0.6755) | (0.5289,0.6740) | ||
| Number of valid samples | 999 out of 1000 | 999 out of 1000 | 1000 of 1000 | 999 out of 1000 | |
|
|
0.5049 (0.0237) | 0.4699 (0.041) | 0.5015 (0.0374) | 0.5016 (0.0375) | |
| 1.3136 (0.0652) | 1.1947 (0.0546) | 1.2996 (0.0100) | 1.2996 (0.0100) | ||
| 0.0192 | 0.0415 | 0.0301 | 0.0302 | ||
| 0.0537 | 0.1057 | 0.0080 | 0.0081 | ||
| 5.8625e-4 | 0.0026 | 0.0014 | 0.0014 | ||
| 0.0044 | 0.0141 | 9.9379-5 | 1.0005e-4 | ||
| 0.0384 | 0.0830 | 0.0602 | 0.0605 | ||
| 0.0413 | 0.0813 | 0.0062 | 0.0062 | ||
| (0.4540,0.5486) | (0.3916,0.5492) | (0.4313,0.5756) | (0.4286,0.5769) | ||
| (1.1705,1.4177) | (1.1100,1.3013) | (1.2798,1.3183) | (1.2795,1.3190) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.1094 (0.1773) | 1.1040 (0.1804 | 1.1034 (0.1610) | ||
| 0.6336 (0.0282) | 0.6007 (0.0315) | 0.6006 (0.0281) | |||
| 0.1439 | 0.1444 | 0.1292 | |||
| 0.0351 | 0.0252 | 0.0226 | |||
| 0.0315 | 0.0325 | 0.0259 | |||
| 0.0019 | 9.9281e-4 | 7.9139e-4 | |||
| 0.1308 | 0.1312 | 0.1175 | |||
| 0.0584 | 0.0420 | 0.0376 | |||
| (0.8060,1.4720) | (0.7622,1.4710) | (0.7980,1.4223) | |||
| (0.5924,0.6997) | (0.5410,0.6648) | (0.5472,0.6563) | |||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | ||
|
|
1.0989 (0.0687) | 1.1014 (0.0747) | 1.1012 (0.0726) | ||
| 1.6399 (0.0394) | 1.6001 (0.0049) | 1.6001 (0.0048) | |||
| 0.0557 | 0.0597 | 0.0581 | |||
| 0.0458 | 0.0039 | 0.0038 | |||
| 0.0047 | 0.0056 | 0.0053 | |||
| 0.0031 | 2.3924e-5 | 2.2608e-5 | |||
| 0.0506 | 0.0543 | 0.0528 | |||
| 0.0286 | 0.0024 | 0.0024 | |||
| (0.9697,1.2345) | (0.9606,1.2525) | (0.9610,1.2454) | |||
| (1.5658,1.7226) | (1.5909,1.6100) | (1.5909,1.6095) | |||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | ||
| Statistical indices | MLE | MOM | PWM M101,M110 |
PWM M102,M120 |
|
|---|---|---|---|---|---|
|
|
0.5043 (0.0353) | 0.5027 (0.0484) | 0.5005 (0.0449) | 0.5001 (0.0434) | |
| 0.6042 (0.0433) | 0.6106 (0.0274) | 0.5997 (0.0259) | 0.5999 (0.0251) | ||
| 0.0282 | 0.0383 | 0.0359 | 0.0347 | ||
| 0.0349 | 0.0232 | 0.0207 | 0.0200 | ||
| 0.0013 | 0.0023 | 0.002 | 0.0019 | ||
| 0.0019 | 8.6160e-4 | 6.7061e-4 | 6.2760e-4 | ||
| 0.0564 | 0.0767 | 0.0718 | 0.0694 | ||
| 0.0581 | 0.0387 | 0.0345 | 0.0334 | ||
| (0.4332,0.5752) | (0.4059,0.5999) | (0.4118,0.5884) | (0.4110,0.5851) | ||
| (0.5107,0.6776) | (0.5577,0.6669) | (0.5490,0.6509) | (0.5509,0.6514) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 out of 1000 | 1000 of 1000 | |
|
|
0.5048 (0.0164) | 0.4845 (0.0277) | 0.5000 (0.0256) | 0.5002 (0.0253) | |
| 1.3183 (0.0441) | 1.247 (0.0330) | 1.3000 (0.0068) | 1.2999 (0.0067) | ||
| 0.0137 | 0.0254 | 0.0207 | 0.0204 | ||
| 0.0379 | 0.0534 | 0.0055 | 0.0054 | ||
| 2.9281e-4 | 0.001 | 6.5674e-4 | 6.4032e-4 | ||
| 0.0023 | 0.0039 | 4.6676e-5 | 4.5509e-5 | ||
| 0.0273 | 0.0508 | 0.0414 | 0.0407 | ||
| 0.0292 | 0.0411 | 0.0042 | 0.0042 | ||
| (0.4731,0.5354) | (0.4322,0.5397) | (0.4503,0.5508) | (0.4507,0.5494) | ||
| (1.2219,1.3884) | (1.1916,1.3021) | (1.2865,1.3132) | (1.2868,1.3131) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.1025 (0.122) | 1.2234 (0.4310) | 1.1006 (0.1254) | 1.1014 (0.1114) | |
| 0.6232 (0.0216) | 0.2910 (0.2066) | 0.6001 (0.0219) | 0.6002 (0.0195) | ||
| 0.0974 | 0.3368 | 0.0999 | 0.0888 | ||
| 0.0248 | 0.3267 | 0.0175 | 0.0155 | ||
| 0.0149 | 0.2005 | 0.0157 | 0.0124 | ||
| 0.0010 | 0.1381 | 4.7959e-4 | 3.7833e-4 | ||
| 0.0885 | 0.3062 | 0.0908 | 0.0807 | ||
| 0.0413 | 0.5445 | 0.0291 | 0.0259 | ||
| (0.8780,1.3561) | (0.2606,2.1869) | (0.8532,1.3501) | (0.8829,1.3176) | ||
| (0.5907,0.6774) | (0.0076,0.7279) | (0.5569,0.6437) | (0.5621,0.6380) | ||
| Number of valid samples | 1000 of 1000 | 409 out of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.0989 (0.0474) | 1.3354 (0.1711) | 1.1010 (0.0505) | 1.1008 (0.0492) | |
| 1.6365 (0.0318) | 0.6937 (0.3946) | 1.6001 (0.0033) | 1.6001 (0.0032) | ||
| 0.0379 | 0.2446 | 0.0409 | 0.0398 | ||
| 0.0405 | 0.9064 | 0.0027 | 0.0026 | ||
| 0.0022 | 0.0847 | 0.0026 | 0.0024 | ||
| 0.0023 | 0.9770 | 1.0953e-5 | 1.0394e-5 | ||
| 0.0345 | 0.2224 | 0.0372 | 0.0362 | ||
| 0.0253 | 0.5665 | 0.0017 | 0.0016 | ||
| (1.0089,1.1856) | (1.0331,1.6236) | (1.0036,1.1972) | (1.0056,1.1941) | ||
| (1.5761,1.6994) | (0.2126,1.5451) | (1.5937,1.6064) | (1.5938,1.6062) | ||
| Number of valid samples | 1000 of 1000 | 997 out of 1000 | 1000 of 1000 | 1000 of 1000 | |
| MLE | MOM | PWM M101,M110 |
PWM M102,M120 |
||
|---|---|---|---|---|---|
|
|
0.5044 (0.0162) | 0.5011 (0.0214) | 0.4988 (0.0202) | 0.4989 (0.0197) | |
| 0.6097 (0.0201) | 0.6066 (0.0123) | 0.6007 (0.0117) | 0.6006 (0.0114) | ||
| 0.0131 | 0.0171 | 0.0161 | 0.0156 | ||
| 0.0177 | 0.0110 | 0.0093 | 0.0090 | ||
| 2.8252e-4 | 4.5718e-4 | 4.1113e-4 | 3.8840e-4 | ||
| 4.9920e-4 | 1.9447e-4 | 1.3717e-4 | 1.2959e-4 | ||
| 0.0261 | 0.0341 | 0.0322 | 0.0312 | ||
| 0.0294 | 0.0184 | 0.0155 | 0.0150 | ||
| (0.4731,0.5360) | (0.4590,0.5431) | (0.4581,0.5388) | (0.4578,0.5380) | ||
| (0.5659,0.6457) | (0.5819,0.6303) | (0.5776,0.6242) | (0.5781,0.6244) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
0.5051 (0.0073) | 0.4971 (0.0118) | 0.5000 (0.0113) | 0.4999 (0.0113) | |
| 1.3195 (0.0242) | 1.2894 (0.0068) | 1.3000 (0.003) | 1.3 (0.0030) | ||
| 0.0068 | 0.0098 | 0.0092 | 0.0092 | ||
| 0.0237 | 0.0108 | 0.0024 | 0.0024 | ||
| 7.9362e-5 | 1.4693e-4 | 1.2707e-4 | 1.2682e-4 | ||
| 9.6674e-4 | 1.5855e-4 | 9.0313e-6 | 9.0134e-6 | ||
| 0.0137 | 0.0197 | 0.0183 | 0.0183 | ||
| 0.0182 | 0.0083 | 0.0019 | 0.0019 | ||
| (0.4932,0.5216) | (0.4753,0.5205) | (0.4795,0.5223) | (0.4793,0.5219) | ||
| (1.2824,1.3668) | (1.2766,1.3018) | (1.2940,1.3055) | (1.2942,1.3055) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.0978 (0.0556) | 1.2494 ( 0.0868) | 1.1001 (0.0548) | 1.1 (0.0488) | |
| 0.6137 (0.0126) | 0.2754 (0.1023) | 0.6000 (0.0096) | 0.6 (0.0085) | ||
| 0.0453 | 0.1532 | 0.0444 | 0.0396 | ||
| 0.0155 | 0.3247 | 0.0077 | 0.0069 | ||
| 0.0031 | 0.0299 | 0.0030 | 0.0024 | ||
| 3.4713e-4 | 0.1158 | 9.1734e-5 | 7.2737e-5 | ||
| 0.0412 | 0.1393 | 0.0403 | 0.0360 | ||
| 0.0258 | 0.5412 | 0.0129 | 0.0115 | ||
| (0.9962,1.2096) | (1.075, 1.4236) | (0.9952,1.2103) | (1.0074,1.1972) | ||
| (0.5904,0.6388) | (0.0953, 0.5332) | (0.5817,0.6193) | (0.5838,0.6170) | ||
| Number of valid samples | 1000 of 1000 | 675 out of 1000 | 1000 of 1000 | 1000 of 1000 | |
|
|
1.0976 (0.0213) | 1.1300 (0.0454) | 1.1001 (0.0227) | 1.1 (0.0220) | |
| 1.6352 (0.0279) | 1.3005 (0.23550 | 1.6000 (0.0015) | 1.6 (0.0014) | ||
| 0.0171 | 0.0388 | 0.0183 | 0.0178 | ||
| 0.0384 | 0.2995 | 0.0012 | 0.0012 | ||
| 4.5729e-4 | 0.0030 | 5.1549e-4 | 4.8480e-4 | ||
| 0.0020 | 0.1451 | 2.2133e-6 | 2.0816e-6 | ||
| 0.0155 | 0.0353 | 0.0167 | 0.0162 | ||
| 0.0240 | 0.1872 | 7.5140e-4 | 7.3023e-4 | ||
| (1.0584,1.1414) | (1.0631,1.248) | (1.0564,1.1454) | (1.0584,1.1441) | ||
| (1.5789,1.6842) | (0.6479,1.600) | (1.5971,1.6030) | (1.5973, 1.6029) | ||
| Number of valid samples | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | 1000 of 1000 | |
| n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | Var_cov | 4.1004e-4 | -2.368e-4 | 1.272e-4 | -3.391e-5 | 0.003 | 5.255e-4 | 5.1600e-4 | 3.3811e-5 | ||
| -2.368e-4 | 1.3681e-4 | -3.391e-5 | 9.0404e-6 | 5.255e-4 | 9.1825e-5 | 3.3811e-5 | 2.2155e-6 | ||||
|
Corr |
-1 | -1 | 1 | 1 | |||||||
|
Cond num. Eigen.val |
Cond. num=1.395e+16 Eigen_val=-1.3553e-20, 5.4685e-4 |
Cond_num=9.0086e+16 Eigen_val=1.6941e-21, 1.3624e-4 |
Cond_num=2.2935e+17 Eigen_val=0, 0.0031 |
Cond_num=6.692e+17 Eigen_val=0, 5.1822e-4 |
|||||||
| 100 | Var_cov | 0.0020 | -0.0012 | 6.574e-4 | -1.7526e-4 | 0.0157 | 0.0027 | 0.0026 | 1.6725e-4 | ||
| -0.0012 | 6.7119e-4 | 1.7526e-4 | 4.6723e-5 | 0.0027 | 4.8006e-4 | 1.6725e-4 | 1.0959e-5 | ||||
|
Corr |
-1 | -1 | 1 | 1 | |||||||
|
Cond num. Eigen.val |
Cond. num=1.632e+16 Eigen_val=1.0842e-19, 0.0027 |
Cond. num=5.8349e+16 Eigen_val=0, 7.0412e-4 |
Cond. num=1.2587e+17 Eigen_val=0.0162, 2.1684e-19 |
Cond. num=2.0801e+18 Eigen_val=0.0026, 3.3881e-21 |
|||||||
| 50 | Var_cov | 0.0044 | -0.0026 | 0.0014 | -3.7257e-4 | 0.0325 | 0.0057 | 0.0056 | 3.6534e-4 | ||
| -0.0026 | 0.0015 | -3.7257e-4 | 9.9325e-5 | 0.0057 | 9.9332e-4 | 3.6534e-4 | 2.3939e-5 | ||||
|
Corr |
-1 | -1 | 1 | 1 | |||||||
|
Cond num. Eigen.val |
Cond. num=2.548e+16 Eigen_val=0, 0.0059 |
Cond. num=5.654e+16 Eigen_val=0.0015, 1.3551e-20 |
Cond. num=5.2012e+16 Eigen_val=0.0335, 4.3368e-19 |
Cond. num=6.3331e+17 Eigen_val=0.0056, -6.7763e-21 |
|||||||
| 20 | Var_cov | 0.0101 | -0.0059 | 0.0034 | -8.9798e-4 | 0.0831 | 0.0145 | 0.0138 | 9.0267e-4 | ||
| -0.0059 | 0.0034 | -8.9798e-4 | 2.3940e-4 | 0.0145 | 0.0025 | 9.0267e-4 | 5.9148e-5 | ||||
|
Corr |
-1 | -1 | 1 | 1 | |||||||
|
Cond num. Eigen.val |
Cond.num=2.7699e+16 Eigen.val=0.0135, 4.3368e-19 |
Cond.num=1.0764e+17 Eigen.val=0.0036, 5.4210e-20 |
Cond.num=9.2362e+16 Eigen.val=0.0856, 4.3368e-20 |
Cond.num=1.328e+18 Eigen.val=0.0138, -1.3553e-20 |
|||||||
| n | PWM: M102,M120 |
PWM: M102,M120 |
PWM: M102,M120 |
PWM: M102,M120 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | Var_cov | 3.8765e-4 | -2.239e-4 | 1.2694e-4 | -3.384e-5 | 0.0024 | 4.1669e-4 | 4.8529e-4 | 3.1799e-5 | |||
| -2.239e-4 | 1.2934e-4 | -3.384e-5 | 9.0221e-6 | 4.1669e-4 | 7.281e-5 | 3.1799e-5 | 2.0836e-6 | |||||
| Corr | -1 | -1 | 1 | 1 | ||||||||
|
Cond num. Eigen.val |
Cond.num=4.1394e+17 Eigen.val=-4.0658e-20, 5.1700e-4 |
Cond.num=2.7053e+17 Eigen.val=3.3881e-21, 1.3596e-4 |
Cond.num=1.3574e+17 Eigen.val=1.3553e-20, 0.0025 |
Cond.num=7.5123e+17 Eigen.val=1.2705e-21, 4.8727e-4 |
||||||||
| 100 | Var_cov | 0.0019 | -0.0011 | 6.4091e-4 | -1.7086e-4 | 0.0124 | 0.0022 | 0.0024 | 1.5875e-4 | |||
| -0.0011 | 6.2822e-4 | -1.7086e-4 | 4.5552e-5 | 0.0022 | 3.7865e-4 | 1.5875e-4 | 1.0402e-5 | |||||
| Corr | -1 | -1 | 1 | 1 | ||||||||
|
Cond num. Eigen.val |
Cond.num=1.4424e+16 Eigen.val=1.0842e-19, 0.0025 |
Cond.num=1.0285e+17 Eigen.val=-1.3553e-20, 6.8647e-4 |
Cond.num=1.2979e+17 Eigen.val=-2.1684e-19, 0.0128 |
Cond.num=8.5287e+17 Eigen.val=-5.0822e-21, 0.0024 |
||||||||
| 50 | Var_cov | 0.0042 | -0.0024 | 0.0014 | -3.749e-4 | 0.0259 | 0.0045 | 0.0053 | 3.4528e-4 | |||
| -0.0024 | 0.0014 | -3.749e-4 | 9.9962e-5 | 0.0045 | 7.9183e-4 | 3.4528e-4 | 2.2625e-5 | |||||
| Corr | -1 | -1 | 1 | 1 | ||||||||
|
Cond num. Eigen.val |
Cond.num=1.8731e+16 Eigen.val=0, 0.0055 |
Cond.num=4.3350e+16 Eigen.val=-4.0658e-20, 0.0015 |
Cond.num=2.0248e+17 Eigen.val=1.0842e-19, 0.0267 |
Cond.num=4.8561e+17 Eigen.val=1.3553e-20, 0.0053 |
||||||||
| 20 | Var_cov | 0.0096 | -0.0056 | 0.0033 | -8.917e-4 | 0.0668 | 0.0117 | 0.0130 | 8.4944e-4 | |||
| -0.0056 | 0.0032 | -8.917e-4 | 2.3772e-4 | 0.0117 | 0.0020 | 8.4944e-4 | 5.5660e-5 | |||||
| Corr | -1 | -1 | 1 | 1 | ||||||||
|
Cond num. Eigen.val |
Cond.num=2.0154e+16 Eigen.val=8.6736e-19, 0.0128 |
Cond.num=3.6958e+17 Eigen.val=0.0036, 0 |
Cond.num=1.1993e+17 Eigen.val=8.6736e-19, 0.0689 |
Cond.num=6.3129e+17 Eigen.val=-2.7105e-20, 0.0130 |
||||||||
| n | MLE |
MLE |
MLE |
MLE |
|||||
|---|---|---|---|---|---|---|---|---|---|
| 500 | Var_cov | 2.631e-4 | -2.900e-4 | 5.368e-5 | -9.989e-5 | 0.0031 | 1.683e-4 | 4.522e-4 | -7.028e-5 |
| -2.900e-4 | 4.048e-4 | -9.989e-5 | 5.869e-4 | 1.683e-4 | 1.596e-4 | -7.028e-5 | 7.779e-4 | ||
| Corr | -0.8887(p=0) | -0.5628(p=1.26e-84) | 0.2395(p=1.644e-14) | -0.1185(p=1.729e-4) | |||||
|
Cond num. Eigen.val |
Cond_num=17.8648 Eigen_val=3.5402e-05, 6.3245e-4 |
Cond_num=17.0047 Eigen_val=3.5578e-05, 6.0499e-4 |
Cond_num=20.6931 Eigen_val=1.5003e-04, 0.0031 |
Cond_num=1.8107 Eigen_val=4.3764e-04, 7.9246e-4 |
|||||
| 100 | Var_cov | 0.0012 | -0.0015 | 2.699e-4 | -6.459e-4 | 0.0149 | -6.407e-4 | 0.0022 | 1.6973e-4 |
| -0.0015 | 0.0019 | -6.459e-4 | 0.0019 | -6.407e-4 | 4.676e-4 | 1.6973e-4 | 0.0010 | ||
| Corr | -0.9670(p=0) | -0.8917(p=0) | -0.2429(p=6.8e-15) | 0.1128(p=3.7e-4) | |||||
|
Cond num. Eigen.val |
Cond_num=62.3364 Eigen_val=4.9263e-05, 0.0031 |
Cond_num=43.5652 Eigen_val=4.9688e-05, 0.0022 |
Cond_num=33.9381 Eigen_val=4.3920e-04, 0.0149 |
Cond_num=2.3023 Eigen_val=9.8549e-04, 0.0023 |
|||||
| 50 | Var_cov | 0.0028 | -0.0034 | 5.626e-4 | -0.0014 | 0.0315 | -0.0013 | 0.0047 | -2.841e-4 |
| -0.0034 | 0.0042 | -0.0014 | 0.0043 | -0.0013 | 7.928e-4 | -2.841e-4 | 0.0016 | ||
| Corr | -0.9823(p=0) | -0.9326(p=0) | -0.2514(p=7e-16) | 0.1050(p=0.0009) | |||||
|
Cond num. Eigen.val |
Cond_num=116.3342 Eigen_val=6.0377e-05, 0.0070 |
Cond_num=72.3631 Eigen_val=6.5640e-05, 0.0047 |
Cond_num=42.4821 Eigen_val=7.4153e-04, 0.0315 |
Cond_num=3.1071 Eigen_val=0.0015, 0.0047 |
|||||
| 20 | Var_cov | 0.0071 | -0.0089 | 0.0014 | -0.0035 | 0.0703 | -0.0044 | 0.011 | -0.0013 |
| -0.0089 | 0.0116 | -0.0035 | 0.0093 | -0.0044 | 0.0017 | -0.0013 | 0.0030 | ||
| Corr | -0.9788(p=0) | -0.9683(p=0) | -0.4087(p=0) | -0.2297(p=0) | |||||
|
Cond num. Eigen.val |
Cond.num=99.0764 Eigen.val=0.0185, 1.8665e-4 |
Cond.num=139.9554 Eigen.val=0.0106, 7.5630e-5 |
Cond.num=51.2278 Eigen.val=0.0014, 0.0705 |
Cond.num=4.0477 Eigen.val=0.0028, 0.0112 |
|||||
| n | MOM |
MOM |
MOM |
MOM |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 500 | Var_cov | 4.565e-4 | -2.535e-4 | 1.385e-5 | -2.408e-5 | 0.0075 | 0.0038 | 0.0021 | -0.0071 | ||
| -2.535e-4 | 1.515e-4 | -2.408e-5 | 4.615e-5 | 0.0038 | 0.0105 | -0.0071 | 0.0555 | ||||
|
Corr |
-0.964(p=0) | -0.3011(p=2.09e-22) | 0.4323(p=4.0974e-32) | -0.662(p=4.0381e-127) | |||||||
|
Cond num. Eigen.val |
Cond_num=73.6573 Eigen_val=8.1441e-06, 5.9988e-4 |
Cond_num=3.5871 Eigen_val=4.0254e-5, 1.4440e-4 |
Cond_num=2.6805 Eigen_val=0.0049, 0.0131 |
Cond_num=49.5788 Eigen_val=0.0011, 0.0564 |
|||||||
| 100 | Var_cov | 0.0023 | -0.0013 | 7.66e-4 | 4.66e-5 | 0.1857 | 0.0101 | 0.0293 | -0.0396 | ||
| -0.0013 | 7.502e-4 | 4.66e-5 | 0.0011 | 0.0101 | 0.0427 | -0.0396 | 0.1557 | ||||
|
Corr |
-0.9846(p=0) | 0.0511(p=0.1065) | 0.1138(p=0.0214) | -0.587(p=2.2243e-93) | |||||||
|
Cond num. Eigen.val |
Cond. num=176.1722 Eigen_val=1.7454e-5, 0.0031 |
Cond. num=1.4435 Eigen_val=7.5939e-4 , 0.0011 |
Cond. num=4.4403 Eigen_val=0.042, 0.1864 |
Cond. num=9.3439 Eigen_val=0.0179, 0.1671 |
|||||||
| 50 | Var_cov | 0.0055 | -0.0030 | 0.0017 | 3.235e-4 | ||||||
| -0.0030 | 0.0017 | 3.235e-4 | 0.003 | ||||||||
|
Corr |
-0.9600(p=0) | 0.1444(p=4.525e-6) | |||||||||
|
Cond num. Eigen.val |
Cond. num=67.5162 Eigen_val=1.0526e-4, 0.0071 |
Cond. num=1.8992 Eigen_val=0.0016, 0.0031 |
|||||||||
| 20 | Var_cov | 0.0124 | -0.0041 | 0.0042 | 5.131e-4 | 0.1345 | 0.0016 | ||||
| -0.0041 | 0.0066 | 5.131e-4 | 0.0052 | 0.0016 | 0.0781 | ||||||
|
Corr |
-0.4506(p=1.619e-50) | 0.1093(p=-5.333e-4) | 0.0153(p=0.9255) | ||||||||
|
Cond num. Eigen.val |
Cond.num=3.2243, Eigen.val=0.0045, 0.0145 |
Cond.num=1.3664 Eigen.val=0.0040, 0.0055 |
Cond_num=1.724 Eigen_val=0.0781 , 0.1246 |
||||||||
| MLE vs. others | MOM vs. others | M101, M110 vs. others | M102, M120 vs. others | ||
|---|---|---|---|---|---|
| n=20 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE , M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is less efficient than MLE but is more efficient than MOM & M101 | |
|
MLE is less efficient than MOM, M101 &M102 |
MOM is more efficient than MLE but less efficient than M101& M102 | M101 is more efficient than MLE, MOM but less efficient than M102 | M102 is more efficient than MLE , MOM & M101 | ||
| time |
0.0307s per replicate Total time=30.7250s |
0.0220s per replicate Total time=22.0016 |
0.0423s per replicate Total time=42.2866 s |
0.0430s per replicate Total time=42.9643s |
|
| n=20 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE, M101 & M102 | M101 is less efficient than MLE but is more efficient than MOM and is likely as M102 | M102 is less efficient than MLE but more efficient than MOM & is likely as M101 | |
| MLE is more efficient than MOM but is less efficient than both M101 & M102 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MLE & MOM but is less efficient than M102 | M102 is more efficient than MLE, MOM & M101 | ||
| time |
0.0307s per replicate Total time=30.6922s |
0.0224 s per replicate Total time=22.4416s |
0.0430s per replicate Total time=43.0307s |
0.0442s per replicate Total time=44.2048s |
|
| n=20 | MLE is more efficient than MOM & M101 & is less efficient than M102 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MLE, MOM & M101 | |
| MLE is more efficient than MOM but is less efficient than M101 & M102 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MLE & MOM but is less efficient than M102 | M102 is more efficient than MLE, MOM & M101 | ||
| time |
0.0305s per replicate Total time=30.4843s |
0.0071s per replicate Total time=7.1177s |
0.0443s per replicate Total time=44.3011s |
0.0443 s per replicate Total time=44.2731s |
|
| n=20 | MLE is more efficient than M102 & M101 | M101 is less efficient than MLE & M102 | M102 is less efficient than MLE but is more efficient than M101. | ||
| MLE is markedly less efficient than M101 & M102 | M101 is more efficient than MLE but less efficient than M102 | M102 is more efficient than MLE & M101 | |||
| time |
0.0329s per replicate Total time=32.8729s |
0.0450s per replicate Total time=45.0361s |
0.0454s per replicate Total time=45.4295s |
| MLE vs. others | MOM vs. others | M101, M110 vs. others | M102, M120 vs. others | ||
|---|---|---|---|---|---|
| n=50 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE , M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
| MLE is less efficient than MOM,M101 &M102 | MOM is more efficient than MLE but is less efficient than M101 & M102 | M101 is more efficient than MLE, MOM but is less efficient than M102 | M102 is more efficient than MOM , M101 & MLE | ||
| time |
0.0342s per replicate Total time=34.1581s |
0.0248s per replicate Total time=24.8382s |
0.1227s per replicate Total time=122.7369s |
0.1285 s per replicate Total time=128.5091s |
|
| n=50 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE and is likely as M102 | M102 is more efficient than MOM but is less efficient than MLE& is likely as M101 | |
| MLE is more efficient than MOM but less efficient than both M101 & M102 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MLE, MOM & M102 | M102 is more efficient than MLE and MOM but is less efficient than M101 | ||
| time |
0.0342s per replicate Total time=34.2283s |
0.0255s per replicate Total time=25.5316s |
0.1289s per replicate Total time=128.9309s |
0.1264s per replicate Total time=126.4414s |
|
| n=50 | MLE is slightly more efficient than M101 but is less efficient than M102 | M101 is less efficient than MLE, & M102 | M102 is more efficient than MLE & M101 | ||
| MLE is less efficient than M101 & M102 | M101 is more efficient than MLE but is less efficient than M102 | M102 is more efficient than MLE & M101 | |||
| time |
0.0354s per replicate Total time=35.353s |
0.1266s per replicate Total time=126.6163s |
0.1281s per replicate Total time=128.0973s |
||
| n=50 | MLE is more efficient than M102 & M101 | M101 is less efficient than MLE & M102 | M102 is less efficient than MLE but is more efficient than M101 | ||
| MLE is markedly less efficient than M101 & M102 | M101 is more efficient than MLE but is less efficient than M102 | M102 is more efficient than MLE & M101 | |||
| time |
0.0340s per replicate Total time=34.0159s |
0.1276s per replicate Total time=127.5708s |
0.1344s per replicate Total time=134.377s |
| MLE vs. others | MOM vs. others | M101, M110 vs. others | M102, M120 vs. others | ||
|---|---|---|---|---|---|
| n=100 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE , M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
|
MLE is less efficient than MOM,M101 & M102 |
MOM is more efficient than MLE but is less efficient than M102 & M101 | M101 is more efficient than MLE & MOM but is less efficient than M102 | M102 is more efficient than MLE , MOM & M101 | ||
| time |
0.0377s per replicate Total time=37.7212s |
0.0262s per replicate Total time=26.2368s |
0.3503s per replicate Total time=350.3439s |
0.3536s per replicate Total time=353.56s |
|
| n=100 | MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient MLE | |
| ME is more efficient than MOM but less efficient than both M101 & M102 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MLE, MOM but is slightly less efficient than M102 | M102 is more efficient than MLE, MOM & M101 | ||
| time |
0.0364s per replicate Total time=36.4423s |
0.0270s per replicate Total time=27.0006s |
0.3519s per replicate Total time=351.9213s |
0.3612s per replicate Total time=361.189s |
|
| n=100 | MLE is more efficient than MOM & M101 but is less efficient than M102 | MOM is less efficient than MLE,M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM, MLE & M101 | |
| MLE is more efficient than MOM but is less efficient than M101, M102 | MOM is less efficient than MLE,M101 & M102 | M101 is more efficient than MOM, MLE but is less efficient than M102 | M102 is more efficient than MOM, MLE & M101 | ||
| time |
0.0356s per replicate Total time=35.5829s |
0.0126s per replicate Total time=12.6141s |
0.3094s per replicate Total time=309.4498s |
0.3746s per replicate Total time=374.639s |
|
| n=100 | MLE is more efficient than M102 , MOM & M101 | MOM is less efficient than MLE, M101, & M102. | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
| MLE is more efficient than MOM but is less efficient than M101 & M102 | MOM is less efficient than MLE, M101, & M102. | M101 is more efficient than MOM, MLE but is less efficient than M102 | M102 is more efficient than MOM, MLE & M101 | ||
| time |
0.0384s per replicate Total time=38.3641s |
0.0124s per replicate Total time=12.4405s |
0.3546s per replicate Total time=354.597s |
0.3627s per replicate Total time=362.7022s |
| MLE vs. others | MOM vs. others | M101, M110 vs. others | M102, M120 vs. others | ||
|---|---|---|---|---|---|
|
n= 500 |
MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE , M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
|
MLE is less efficient than MOM,M101 &M102 |
MOM is more efficient than MLE but is less efficient than M102 & M101 | M101 is more efficient than MLE, MOM but is less efficient than M102 | M102 is more efficient than MLE , MOM & M101 | ||
| time |
0.0569s per replicate Total time=56.8912s |
0.0296s per replicate Total time=29.5591s |
4.4784s per replicate Total time=4.4784e+3s |
5.5616s per replicate Total time=5.5616e+3s |
|
|
n= 500 |
MLE is more efficient than MOM , M102 & M101 | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
| MLE is less efficient than MOM, M101 & M102 | MOM is more efficient than MLE but is less efficient than M101 & M102 | M101 is more efficient than MLE, MOM but is less efficient than M102 | M102 is more efficient than MLE, MOM & M101 | ||
| time |
0.0608s per replicate Total time=60.8357 |
0.032s per replicate Total time=31.9762s |
4.2734s per replicate Total time=4.2734e+3s |
4.323s per replicate Total time=4.323e+3s |
|
|
n= 500 |
MLE is less efficient than M102 & M101 but is more efficient than MOM | MOM is less efficient than MLE,M101 & M102 | M101 is more efficient than MOM, MLE but is less efficient than M102 | M102 is more efficient than MOM , MLE & M101 | |
| MLE is less efficient than M102 & M101 but is more efficient than MOM | MOM is less efficient than MLE, M101 & M102 | M101 is more efficient than MOM, MLE but is less efficient than M102 | M102 is more efficient than MOM , MLE & M101 | ||
| time |
0.0542s per replicate Total time=54.1649s |
0.0404s per replicate Total time=27.245s |
4.486s per replicate Total time=4.486+3s |
4.267s per replicate Total time=4.267e+3s |
|
|
n= 500 |
MLE is more efficient than M102 , MOM & M101 | MOM is less efficient than MLE, M101, & M102. | M101 is more efficient than MOM but is less efficient than MLE & M102 | M102 is more efficient than MOM & M101 but is less efficient than MLE | |
| MLE is more efficient than MOM but is less efficient than M101 & M102 | MOM is less efficient than MLE, M101, & M102. | M101 is more efficient than MOM, MLE but is less efficient than M102 | M102 is more efficient than MOM, MLE &M101 | ||
| time |
0.0588s per replicate Total time=58.7812s |
0.0355s per replicate Total time=35.5128s |
4.519s per replicate Total time=4.519e+3s |
4.353s per replicate Total time=4.353e+3s |
| Water quality, n=41 | Educational attainment, n=40 | Self-reported Health, n=39 | |
| Mean | 0.8332 | 0.7810 | 0.6795 |
| Standard deviation | 0.0972 | 0.1568 | 0.1358 |
| Skewness | -0.6059 | -1.1480 | -0.8026 |
| Kurtosis | 2.9144 | 3.2077 | 3.2807 |
| Min | 0.62 | 0.42 | 0.3400 |
| Max | 0.98 | 0.95 | 0.8900 |
| 25th percentile | 0.7775 | 0.705 | 0.6050 |
| Median | 0.83 | 0.83 | 0.7100 |
| 75th percentile | 0.91 | 0.895 | 0.7575 |
| Beta | Kumaraswamy | MBUW | Topp-Leone | Unit-Lindley | ||||
| theta | 25.8989 | 0.2001 | ||||||
| Var-cov | 8.1698 | 1.2164 | 1.9713 | 0.5680 | 16.3599 | 0.000495 | ||
| 1.2164 | 0.2274 | 0.5680 | 0.2906 | |||||
| SE | 2.858 | 1.4040 | 4.0447 | 0.0222 | ||||
| 0.4769 | 0.5391 | |||||||
| AIC | -77.3397 | -76.8933 | -76.9952 | -78.5197 | -61.8161 | |||
| CAIC | -77.0239 | -76.5775 | -76.6794 | -78.4171 | -61.7135 | |||
| BIC | -73.9125 | -73.4662 | -73.5680 | -76.8061 | -60.1025 | |||
| HQIC | -76.0917 | -75.6453 | -75.7472 | -77.8957 | -61.1921 | |||
| LL | 40.6698 | 40.4467 | 40.4976 | 40.2599 | 31.9080 | |||
| K-S Value | 0.0929 | 0.0996 | 0.0991 | 0.0569 | 0.1952 | |||
| H0 | Fail to reject | Fail to reject | Fail to reject | Fail to reject | Fail to reject | |||
| P-value | 0.8387 | 0.7741 | 0.7789 | 0.9288 | 0.0765 | |||
| AD | 0.3114 | 0.3499 | 0.3463 | 0.5916 | 2.5329 | |||
| CVM | 0.0398 | 0.0483 | 0.0543 | 0.0567 | 0.4423 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





