Public Security Patrol Path Planning Recommendation Method based on Wolf-Pack Optimization Algorithm using DAF and BRS

1. Introduction

With the rapid development of human civilization, the public safety situation is also facing new and severe challenges. To create a good public safety environment, the public security patrol path planning plays an important role, which considers factors such as time, road conditions and distance, aiming to provide the shortest security patrol route for police to achieve higher duty efficiency.

Many scholars have reflected on the development of the policing model of public security patrols and the optimization of patrol routes, such as: Wang et al. designed a solution for collaborative execution of area coverage tasks by multiple unmanned ships for large-scale sea patrol tasks based on the multi unmanned ship area coverage traversal algorithm [1];Xiang et al. designed an improved Partheno-genetic Algorithm (IPGA) for quickly obtaining high-quality patrol task planning schemes [2];Li used the Rural Postman Problem (RPP) to construct a graph theory model for traffic police patrol path optimization based on the CE2 heuristic algorithm, effectively shortening the path length and saving costs [3];Both Zhang [4] and Kong et al [5] achieved path planning by improving ant colony algorithm and using distance discriminant analysis to select multiple parameter indicators; Jie et al. proposed a new multi-agent based reinforcement learning algorithm to plan the optimal patrol path under arbitrary conditions of multiple defenders and attackers [6];Liang adopted a combination of ant colony algorithm and genetic algorithm to improve the efficiency of sightseeing path planning in the intelligent navigation system of the park [7];Shi et al combined evolutionary algorithms with optimization experiments to establish a two-layer optimization model, and combines multi-agent genetic algorithms to solve multi-objective optimization scheduling problems in complex environments [8];Yan et al combined particle swarm optimization algorithm with predictive control, overcoming the disadvantage of traditional particle swarm optimization algorithm in generating infeasible paths during particle update process [9];Authors developed a two-layer optimization framework to solve the patrol police force allocation problem, and then used a new iterative Bender decomposition method to solve the potential optimization problem, thereby solving the spatial police patrol allocation problem with expected crime response time [10]. Unfortunately, various algorithms have their own shortcomings.

Over the past few decades, wolf-pack optimization algorithm has attracted widespread interest from researchers due to its high parallelism, good global convergence, and computational robustness, making it particularly suitable for solving high-dimensional, multi-modal complex functions [11];For instance, Tang et al. developed an automatic detection scheme for wolf pack hunting behavior in videos [12], which greatly improves the accuracy of motion state recognition, reaching up to 88%;Duan et al. proposed a target allocation method based on wolf behavior mechanism [13], which effectively solves the problem of collaborative target allocation among drone groups; In paper [14], an entropy-based grey wolf optimizer (IEGWO) algorithm was proposed to solve global optimization problems; Chen et al. developed a Hybrid Grey Wolf Optimizer (HGWO) that combines Halton sequences and multiple strategies, which can be used to solve practical engineering problems [15]; Authors modelled the behavioral characteristics of wolf packs in natural environments and used it to solve the dynamic task allocation problem of drone swarms in complex scenarios [16]; She et al. improved the wolf-pack optimization algorithm to enhance the accuracy and efficiency of solving highly nonlinear black box function structural reliability problems [17];In paper [18], researchers proposed a submarine cable positioning algorithm based on Improved Grey Wolf Optimization (IGWO), which achieves accuracy and effectiveness in submarine cable positioning.

Therefore, the effective utilization of the wolf-pack optimization algorithm mentioned above inspires us to intend to adopt an improved wolf-pack optimization algorithm to solve the optimization problem of public security patrol path planning, then this paper proposes a public security patrol path planning recommendation method based on an improved wolf-pack optimization algorithm (S3PRM-DAF-BRS-CWOA). Section 2 provides the related existing works about this new proposed method. Section 3 elaborates on the improvement and design of the new proposed method. Section 4 shows performance verification experiment and analysis of experimental results. Section 5 gives the conclusion of this article, summarizing its contributions, existing limitations, and future directions for improvement.

2. Related Works

2.1. Swarm Intelligence Optimization

In nature, a variety of creatures with limited individual ability show amazing abilities through constitutions and inter -individual information exchange, such as: ant colony, bee colony, wolves, and so on. The swarm intelligent optimization algorithm is designed by simulating the characteristics of biological group behaviors in nature. It uses simple rules and interactions between many bodies to optimize the optimization problem of complex functions. The origin of the swarm intelligent optimization algorithm dates back to the 1980s. At that time, some scholars began to study the calculation model of simulating the behavior of natural biological groups. In 1986, Garnier and others proposed an Ant Random Walking Model [19], which can be regarded as an early form of the swarm intelligent optimization algorithm. The swarm intelligent optimization algorithm provides new ways and shows excellent performance when solving many practical problems.

In recent years, in order to solve the limitations of traditional swarm intelligent algorithms on certain problems, scholars have proposed many new types of swarm intelligent optimization algorithms. These new algorithms have shown stronger applicability and experimental effects in solving complex practical problems, such as: Battle algorithm proposed by British scholar yang [20]. Essence These new algorithms can more effectively search for optimal solutions, strong adaptability, and can adapt to various types of optimization problems. However, there are still many shortcomings. For example, the adjustment of bat algorithm in certain parameters may affect the performance of the algorithm. There are few cases in practical applications, and more empirical research is required to verify its effects.

2.2. Wolf-Pack Optimization Algorithm

Among the new algorithms that have emerged in recent years, the wolf-pack optimization algorithm is a typical representative. Wolf-Pack Optimizaton Algorithm (WPOA) was first proposed by YANG et al. [21] by imitating the habit of imitating the group of raw animals, the intelligence shown in the simulation of the wolf-pack foraging and hunting in nature, mainly The three intelligent lines of the wolf hunting behavior, calling-galloping behavior and siege are abstracted to find the optimal solution to the problem. The algorithm process mainly includes parameter initialization, migration mechanism, summon-raid mechanism, siege mechanism, and regeneration mechanism.

Initialization: The algorithm first needs to set a series of parameters such as the size of the wolves, the location of each wolf, the step length, and the number of iterations. It is an important basis for the algorithm. Appropriate parameter settings can help algorithms to converge to optimal solutions faster, while maintaining sufficient search diversity to avoid local optimal. In the process, the wolf in the wolf-pack is assigned to the function of the function. Assuming that the number of wolves is n, and the dimension of the interpretation of the space is D, then the position of each wolf is as required as a formula (1).

$$x_{id}={rang}_{min}+rand(N,1)\mathrm{*}({rang}_{max}-{rang}_{min})$$

(1)

Migration-Mechanism: The process of searching the prey during the hunting of the wolf-pack in the natural environment, and searching the target separately in a certain field of a certain field of the wolf-pack members. In this process, each wolf searches the target in its nearby space according to the rules. The best Q -Po Wolf except the wolf in the solution space is regarded as the exploring wolf. The exploring wolf is centered on its own position, and the long -term searches are used as a search step to explore the prey around them. Degree value. If the adaptation value of the current wolf is greater than the point of adaptation of the position of the wolf, it indicates that the prey is relatively close to the wolf I and may capture the prey. The hunting process, that is, the current exploring wolf moves in the direction of H hunting and calculates the new location and the new adaptation value. For example, the formula (2) indicates that after moving the direction of P (P = 1,2, ..., H, H ≤D), the current wolf i is currently a new position in the D -dimensional space.

$$x_{id}^p=x_{id}+\mathit{sin}\left(2\pi \mathrm{*}{\displaystyle \frac{p}{h}}\right)\mathrm{*}{step}_a^d$$

(2)

Summon-Raid-Mechanism: After discovering the prey, the simulation wolf-pack will summon other wolves to quickly stride and participate in hunting by calling them by calling or other ways to increase the power of hunting. According to the formula (3), it is updated on the road of raid. If the new position obtained, the adaptation value is better than the current position, the wolf will move to the new position, otherwise it will stay in the current position. Among them, Z_id represented the position of the No. D-dimensional renewal of the No. i wolf in the wolf-pack; X_id is the current position of the D-dimension of the I wolf; RAND is a random number evenly distributed in the interval [-1,1]; Stepb is the step-size in the process of Summon-Raid; X_ld is the position of the leader wolf in d-th dimension.

$$z_{id}=x_{id}+Rand\times stepb\times \left(x_{ld}-x_{id}\right)$$

(3)

Siege-mechanism: During the capture process, the wolf-pack appeared around the leader wolf to adopt a small step to siege prey. That is, first generate a random number of RM in [0, 1]. If RM is smaller than θ (θ is a pre -set threshold), then the I wolf does not move. The wolf surrounded the prey with the leader wolf. The updated wolf position x_i^t+1 is shown in the formula (4), Stepc means the siege length; X_l is the position of the head wolf.

$$X_i^{t+1}=\left\{\begin{array}{c}{X}_i^t r_m<\theta \\ X_l+Rand\times stepc r_m>\theta \end{array}\right.$$

(4)

Regeneration-Mechanism: Simulation of the natural evolution of wolves is a key link in the iteration of the algorithm. Reserve strong performance in the wolves, eliminate wolves with poor performance, and then randomly supplement a certain number of artificial wolves. Update the population of the wolf by evaluating the adaptation value in the population, and the suspension conditions during iteration can be set. It ensures that the wolf clusters can adapt to evolution and eventually converge to the optimal solution, which improves the efficiency and effect of algorithms when solving complex optimization problems.

2.3. Data-Sets

In order to test the optimization ability of the DAF-BRS-CWOA proposed in this article, test comparison experiments with other optimization algorithms, and select some common functions and data sets of the test optimization algorithm as shown in Table 1 for testing. Select a variety of types of public test functions such as public test functions. Some test functions have the characteristics of multi -peak value, strong interference, high complexity, etc., and can fully test the global nature of the model. Some test functions are smooth, continuous, convex, and convex the characteristics such as the Single Peak are like a bowl shape; some test functions are very smooth and the change is relatively smooth, and test function formulas are shown in Table 1.

2.4. S3P-Function

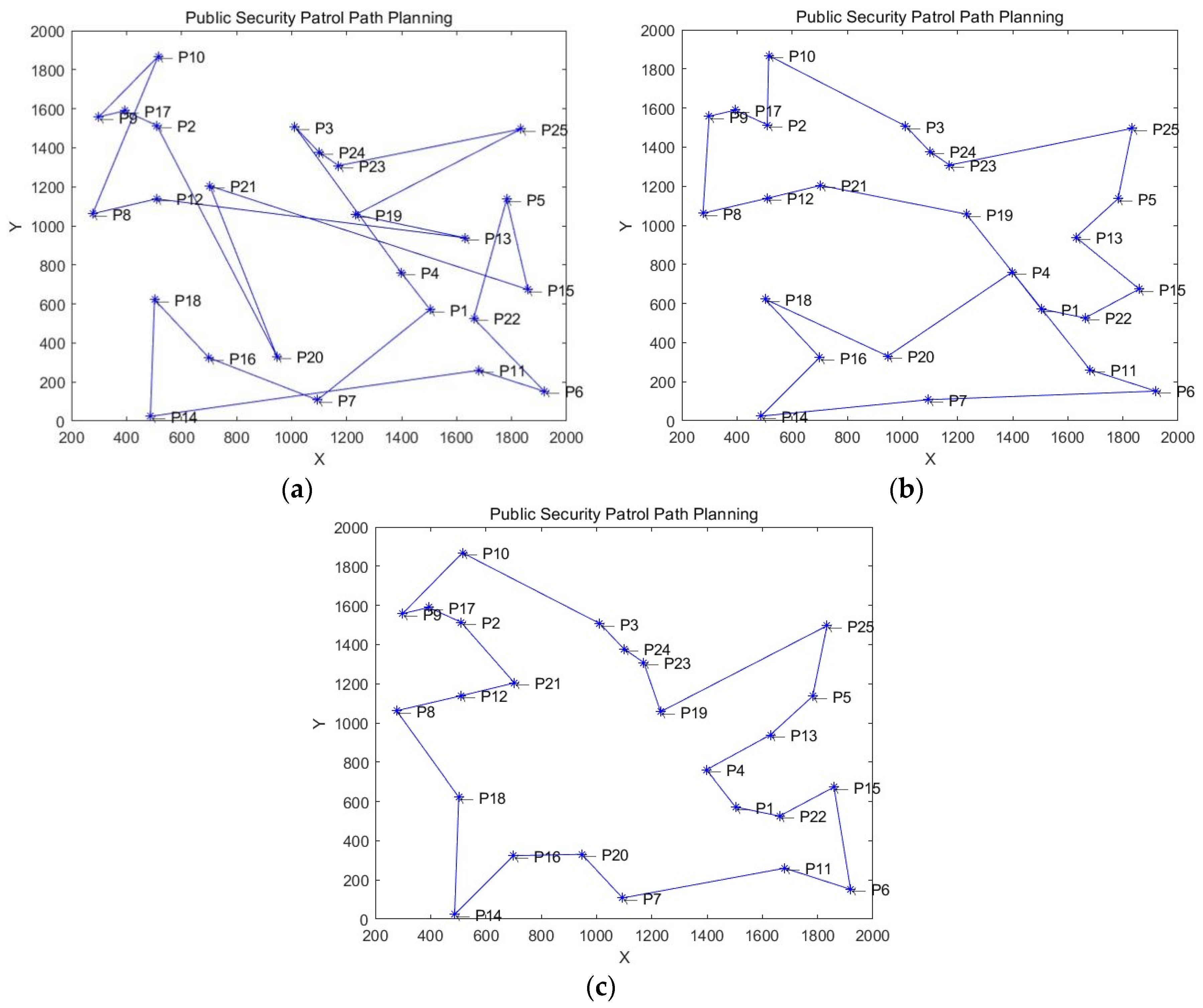
In the real social life, the task of public security patrols requires that the patrol paths of police officers must cover important nodes, and the number of important nodes is often large, so this results in multiple actual patrol paths with varying distances and disorganization, as shown in Figure 1(a). Fortunately, police officers often have rich patrol experience and have their own "optimal patrol path" based on this kind of experience, as shown in Figure 1(b). However, the "optimal patrol path" based on police officers' experience shown in Figure 1(b) is not truly optimal, especially in the case of a large number of important patrol nodes resulting to huge number of patrol path options, it is unlikely to find the globally optimal one due to limitations in human mental arithmetic ability, and Figure 1(c) gives the true global optimal patrol path compared to Figure 1(b).

It is based on the above problem that this article abstracts a problem model serving the planning of public security patrol paths. Without loss of generality, assuming that the security patrol task is carried out in a plain area and ignoring the influence of altitude, that is, the Euclidean distance is used to calculate the distance between all key points; thereby, this paper constructs an objective function of public security patrol path planning (S3P-Function), the calculation formula is as Equation5.(This paper takes a 2000 km by 2000 km area and 30 security patrol locations generated randomly).

$${Distance}_{total}=\sqrt{{\left(x_{p_n}-x_{p_1}\right)}^2+{\left(y_{p_n}-y_{p_1}\right)}^2}+{\displaystyle {\sum }_{n=2}^N}\sqrt{{\left(x_{p_n}-x_{p_{n-1}}\right)}^2+{\left(y_{p_n}-y_{p_{n-1}}\right)}^2}$$

(5)

Where, ${Distance}_{total}$ means the whole distance of some a public security patrol path; p_n means the n-th patrol point along some a security patrol path while p₁ means the first one; x_pn and y_pn present the horizontal and vertical coordinates respectively; N means the total number of patrol points along some a security patrol path.

Obviously, it is completely that different from classical test functions in 2.3 that the above description is a discrete problem. To solve this problem, this paper made a discrete algorithm based on the idea of WPOA to solve the discrete problem.

3. Improvement and Design of the New Proposed Method

Compared with the comparative algorithm in [22], the article titled " an adaptive distribution size (ADS) wolf-pack optimization algorithm using the strategy of jumping for raid (for short, WDX-WPOA)" demonstrates significant advantages in optimization capabilities, including higher global search accuracy, stronger robustness, and faster convergence speed. However, WDX-WPOA also has certain shortcomings, such as significantly longer iteration times in some test function applications shown in [23]; so this paper designed two following strategies to improve the optimization performance in response to this issue, and then the new proposed algorithm will be utilized to achieve a more efficient solution for the security patrol path planning problem.

3.1. Dynamic-Adjustment-Factor

During the raid process, in order to find the global optimal solution around the leader wolf, wolf-pack will be hoped to approach the leader wolf as soon as possible. However, the distance between wolves except the leader wolf should be precisely adjusted, that is, the distance should not be too small to avoid the wolf pack falling into local optimum, nor too large to prevent slow convergence. By setting reasonable distances, the efficiency of the optimization process can be improved while ensuring global search capability.

According to existing methods, the number of airdropped wolves in the ASGS-CWOA and WDX_WPOA does not change during the process of Summon-Raid. Obviously, this approach is insufficient to accurately reflect the dynamic changes during the raid process and may lead to a decrease in optimization performance, and to overcome this deficiency, Dynamic-Adjustment-Factor (DAF) was proposed to dynamically adjust the number of airdropped wolves based on real-time changes during the process of Summon-Raid, thereby improving the overall performance of the algorithm. The specific dynamic adjustment mechanism is shown in Equation (6) following.

$$\left\{\begin{array}{c}factor=(t/T)/2+1/2\\ {num}_{raid}=floor\left(numW*factor\right)\\ {new}_{raid-wolf-index}=inde{x}_{tem\left(1:nu{m}_{raid}\right)}\\ {old}_{raid-wolf-index}=index\_tem\left(\right({num}_{raid}+1):numW)\end{array}\right.$$

(6)

Where, factor depends the number of wolves following the old strategy of Summon-Raid as in ASGS-CWOA and the number of other wolves following the new proposed strategy of Summon-Raid ; t means the number of current iteration; T means the number of the maximum iteration; num_raid means the number of wolves to be replaced with new wolves; floor means a function that returns the calculated result rounded down to ensure that num_raid is an integer; numW means the number of wolf-pack that is 50 in this paper; new_{raid_wolf_index} means an index array that means the position of the wolf to be replaced with the new wolf while old_{raid_wolf_index} is the one in its original state; index_tem is an index array obtained by sorting the current fitness, from the worst fitness to the best fitness.

From the Equation (5), it’s observed that the factor will vary between 0.5 and 1, and it will increase the number of new_{raid_wolf_index} as the number of iterations increases, thereby allowing more wolves to participate in the raid process. This mechanism allows the algorithm to introduce fewer new wolves in the early stages to reduce computational complexity; In the later stage, the proportion of new wolves gradually increases to better explore the search space.

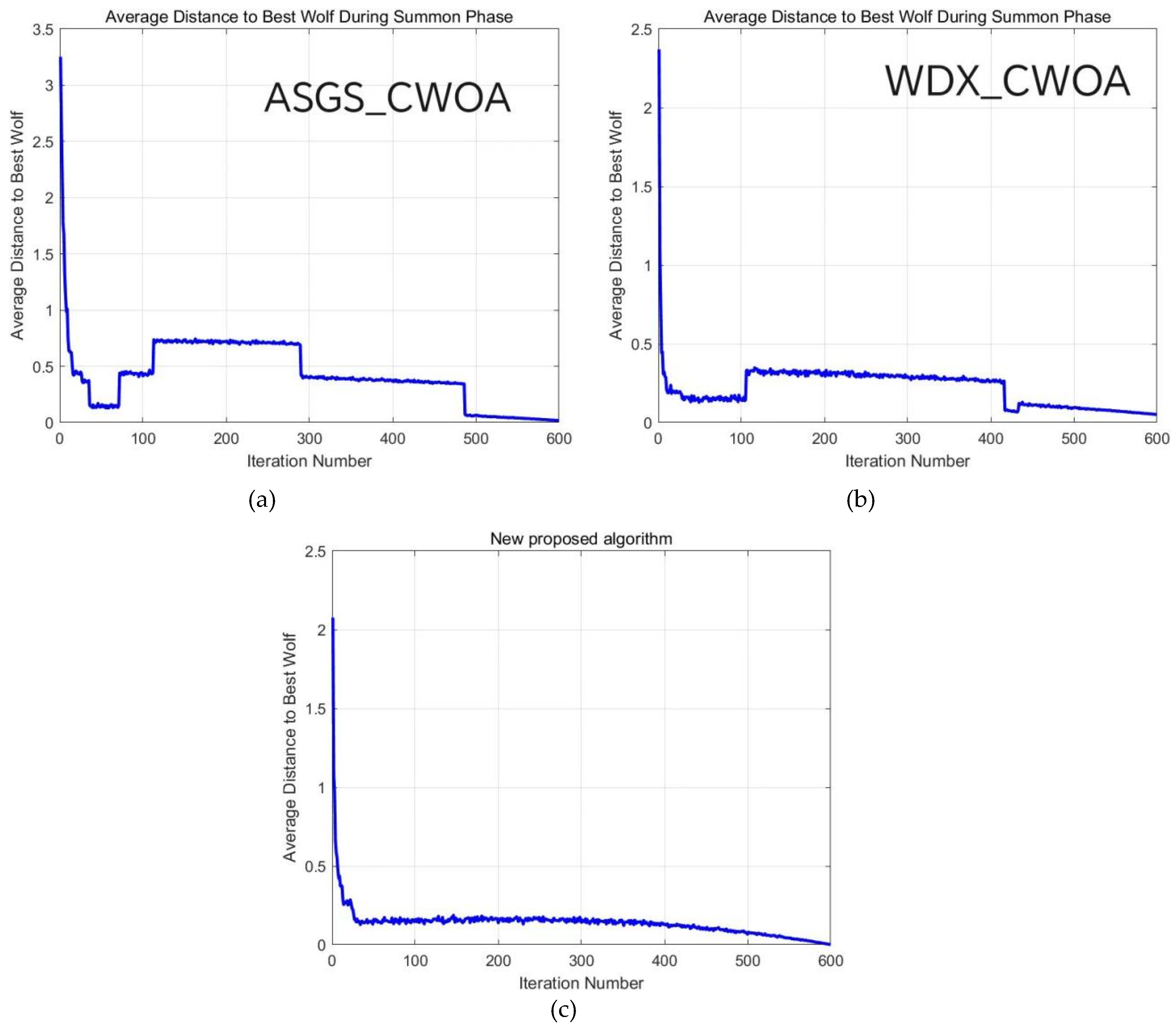
From Figure 2, it was seen that the convergence of the wolf-pack during the siege phase as the number of iterations increases. Obviously, the curve in the Figure 2(c) is smoother than the others, and the convergence speed of the wolf-pack is also faster. This indicates that introducing the DAF to dynamically adjust the number of airdropped wolves and wolves running according to the original strategy can not only improve the convergence speed of the wolf-pack and shorten the overall running time of the algorithm, but also not affect the algorithm's ability to globally find the optimal solution. In other words, as the number of iterations increases, the wolf-pack will get closer to the optimal solution..

3.2. Balanced-Raid-Strategy

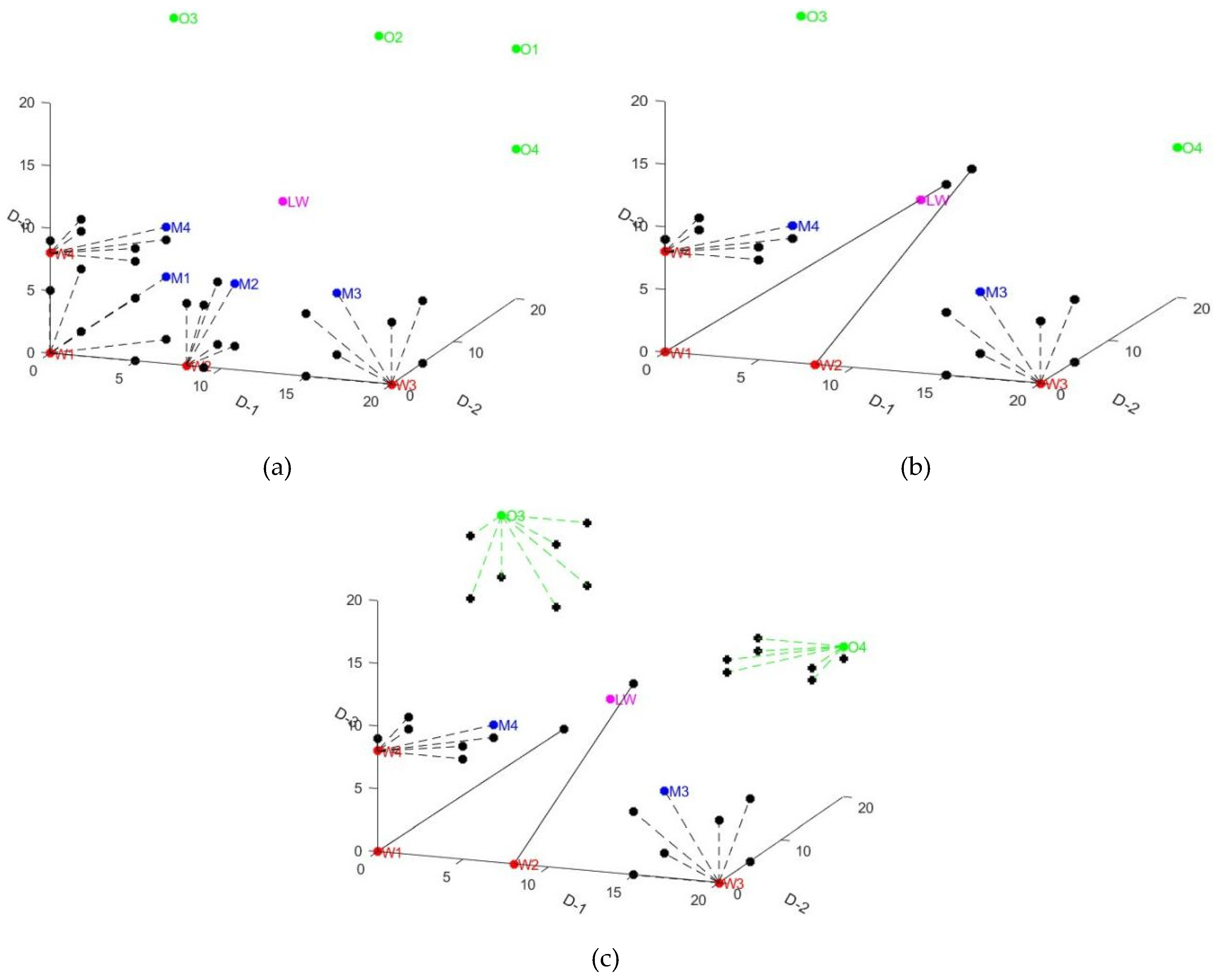
During the process of Summon-Raid, for every wolf, 2^D locations generated by the coordinate arrangement combination of current location and the middle one between the current wolf and the best wolf are checked up as well as the reverse location of the current wolf regarding the best wolf, shown in Figure 3(a) about ASGS-CWOA. Accordingly, in WDX-WPOA, half of the wolf-pack follows the Summon-Raid strategy in ASGS-CWOA, while the other half is directly airdropped to the surrounding of current optimal wolf, which means that only 2^(D-1) + 1 locations will be checked up per wolf on average and accelerates the gathering and siege rhythm of the wolf-pack, and accelerates the convergence speed of the algorithm in another word, shown in Figure 3(b).

Furthermore, Balanced-Raid-Strategy (BRS) was proposed in the new proposed algorithm to improve the existing original strategy of Summon-Raid by not only examining the reverse location of the current wolf, but also the ones generated according to certain rules between the reverse position of the current wolf regarding the current optimal wolf for half of wolf-pack, and in this way the search volume are increased during each iteration, which increases the possibility of finding the global optimal solution while increases the computational complexity and time consumption of the algorithm, shown in Figure 3(c).

$$\left\{\begin{array}{c}{wolf}_{i-opposite}=2*bestwolf-pop(i,:)\\ {locations}_{opposite}=original\_Summon\_Raid\_Mesh\_Process({wolf}_{i-opposite},bestwolf)\\ {ft}_{opposite-locations}=FitnessFunction\left({locations}_{opposite}\right)\\ [{ft}_{opposite-locations-best},{NO}_{opposite-locations-best}]=min\left({ft}_{opposite-locations}\right)\\ {wolf}_{oppsite-locations-best}={locations}_{opposite}({NO}_{opposite-locations-best},:)\end{array}\right.$$

(7)

Where, wolf_i-opposite means the opposite location of the current wolf while bestwolf means the current best wolf and pop(i,:) means the current wolf-ith; locations_opposite represents the locations between wolf_i-opposite and bestwolf according to the Summon-Raid rules in WDX-WPOA; original_Summon_Raid_Mesh_Process is a function that returns some related locations determined by Summon-Raid rules in WDX-WPOA while FitnessFunction is another one that returns the fitness of the given wolves or locations; ft_{opposite-locations} means the fitness regarding locations_opposite; ft_{opposite-locations-best} means the best one of ft_{opposite-locations} while NO_{opposite-locations-best} is the serial number of ft_{opposite-locations-best} in ft_{opposite-locations}, and wolf_{opposite-locations-best} is the best one of locations_opposite around wolf_i-opposite.

The Equation (7) gives the key rules regarding BRS during Summon-Raid process.

3.3. Steps Of DAF-BRS-CWOA

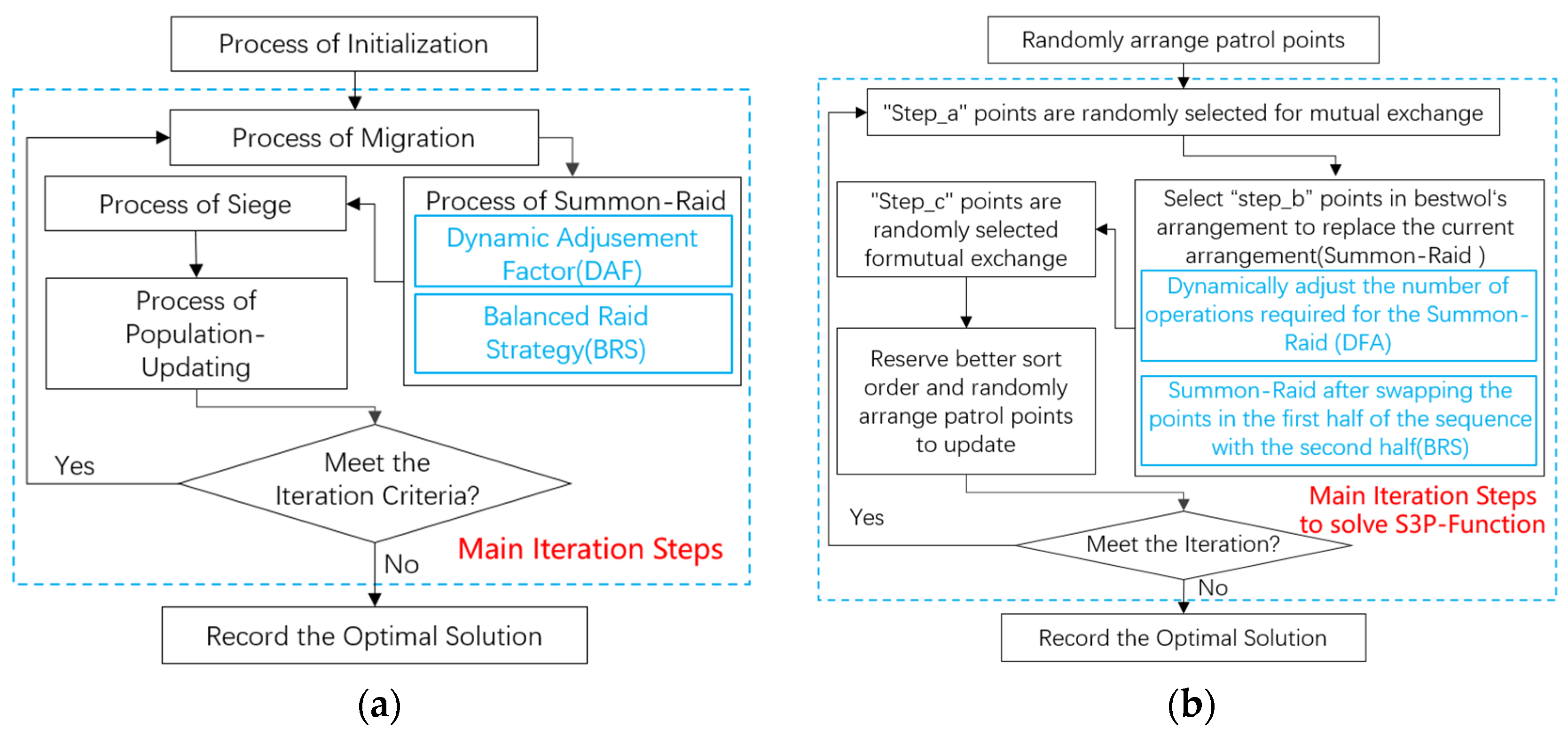
On the basis of the strategy of dynamically increasing the number of airdrop wolves and increasing the number of examined locations, WCOA was improved and DAF-BRS-CWOA was proposed. Here are the steps on how to implement the new improved algorithm, as shown in Figure 4(a).

All steps are consistent with WDX-WPOA except DAF and BRS are used in the Summon-Raid process, detailed in 3.1 and 3.2 respectively. At the same time, we made it as a discrete -type algorithm according to the idea of DAF-BRS-CWOA to solve the S3P-Function. The general process is as shown in Figure 4 (b).

4. Performance Verification Experiment

4.1. Experimental Designment

In order to test the optimization capabilities of DAF-BRS-CWOA, the classic genetic algorithm (GA), particle swarm algorithm (PSO) and WDX-WPOA three optimization algorithms shown in Table 2 are used to perform experiments. And 20 test functions such as 6 multi -model methods and the distance test function of the patrol path, the theoretical optimal of order, function, expression, dimension, characteristics, scope, and each test function is given. The numerical experiment results on the 21st test function for the next test can be analyzed and studied for the next step. Details are shown in tables following.

All numerical experiments are implemented on a computer equipped with Windows 11 Home 22H2 operating system, Intel(R) Core (TM) i7-12700H processor and 16G memory while the integrated development environment is MATLAB-2024a. For genetic algorithm, toolbox in Matlab 2017a is utilized for GA experiments; the PSO experiments were implemented by a “PSOt” toolbox for Matlab; Experiments on WDX-WPOA are done according to the steps from reference [23]; and the new algorithm DAF-BRS-CWOA is implemented by utilizing MATLAB-2024a with M programming language. The specific configuration of the above algorithms is shown in Table 2. In order to verify the excellent performance of the new algorithm, like the other three algorithms, it runs 30 optimization calculations on each test function. Then, all algorithms are evaluated from the aspects of the best value, worst value, average, standard deviation, the number of average iterations, and the average time of the global optimal.

4.2. Experimental Results and Analysis

Firstly, as shown in Table 3, seen from the optimal value, the DAF-BRS-CWOA can find the theoretical optimal values of all the test functions as well as WDX-WPOA, but no one else can do it; furthermore, seen from the worst value and average value, DAF-BRS-CWOA has the best performance in all 4 algorithms(PSO, GA, WDX-WPOA and DAF-BRS-CWOA) that its worst and average values both reach the theoretical optimal values while the other algorithms have no such ability. Therefore, DAF-BRS-CWOA has better optimization accuracy.

In addition, in 30 tests, the new algorithm had zero standard deviation on almost all test functions except function 2"Bukin6", function 4"Eggholder", function 6"Levy" and function 21" 3P-Function". Even so, in function 2 "Bukin6" and function 4 "Eggholder", the standard deviation of DAF-BRS-CWOA is better than the standard deviation of other algorithms. Although the standard deviation of DAF-BRS-CWOA in function 6 is larger than that of GA and PSO, GA and PSO cannot find the optimal value in 30 tests, while DAF-BRS-CWOA can, as show the standard deviation in Table 3. Therefore, DAF-BRS-CWOA has good stability in general.

Moreover, in term of average number of iterations, DAF-BRS-CWOA has smallest iterations on all test functions except function 2 "Bukin6", function 4 "Eggholder", function 21" S3P-Function", and on function 2, 4 and 21 the number of iterations is 600 which is same to the values on other algorithms, shown in Table 3 Average iteration. Hence, in general, DAF-BRS-CWOA has better advantage in terms of iteration.

Finally, as shown in Table 3 Average Time, the average time spent on Functions 14, 15, 18, and 19 is minimal for DAF-BRS-CWOA. Moreover, the four algorithms spend about the same amount of time on test functions 1, 9, and 20, and DAF-BRS-CWOA runs longer than PSO or GA on the rest of the test functions, but the performance of finding the optimal value is better than that of other algorithms (PSO and GA). Nonetheless, it is a consolation that the proposed algorithm outperforms WDX-WPOA in terms of running time without losing optimization accuracy. As shown in Table 4 and Figure 5, In all test functions, the DAF-BRS-CWOA is improved compared to WDX-WPOA. Therefore, the DAF-BRS-CWOA has a good convergence speed.

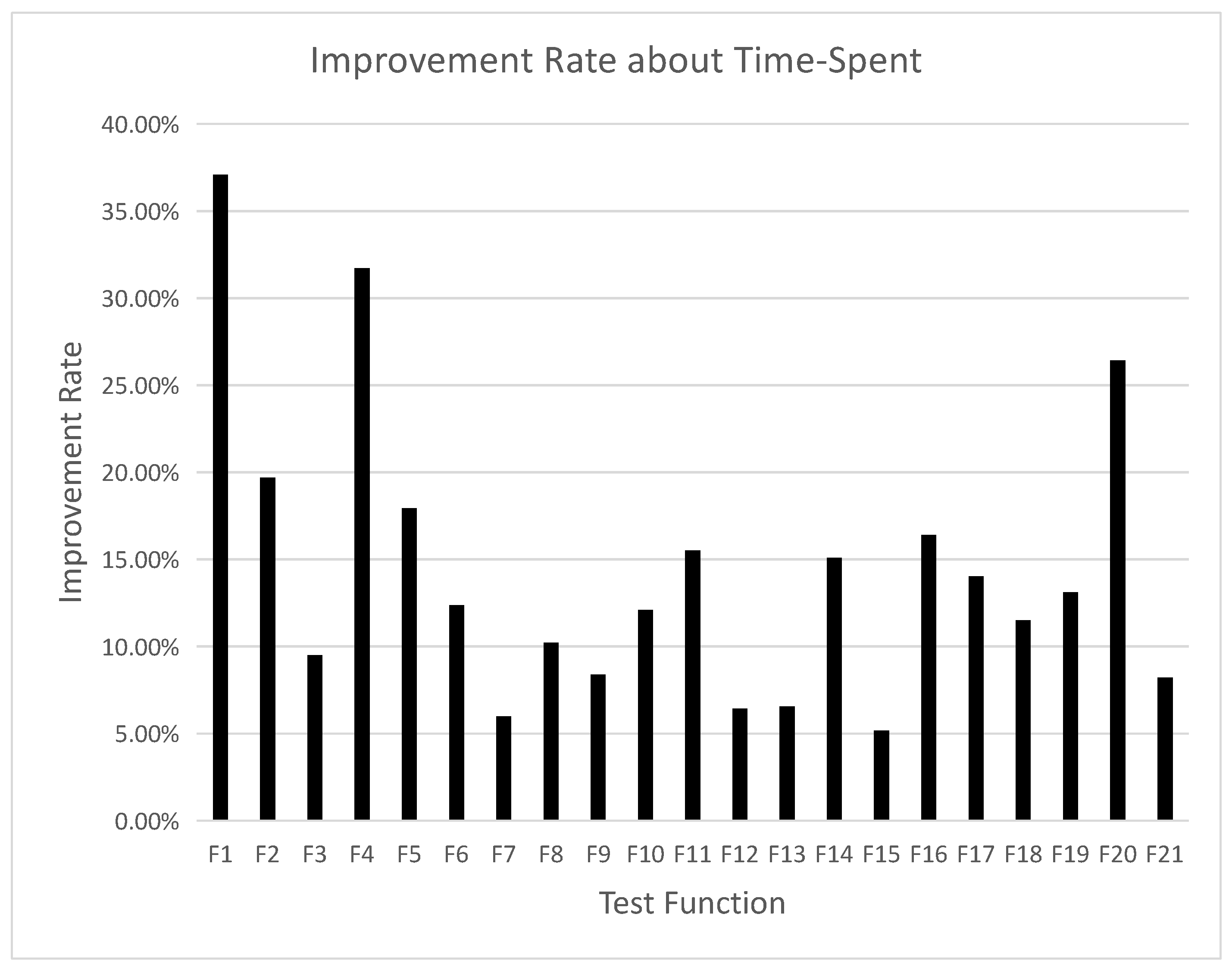
In fact, on the premise of guaranteeing the absolute global optimization ability, the conclusion shows that DAF-BRS-CWOA spent less time seen from Table 4 and Figure 3, it is seen that all the improvement rates are positive and that means DAF-BRS-CWOA spent less time than WDX-WPOA on all the 21 algorithms involved in this paper. Especially, it is worth mentioning that the improvement rates on function “Ackley’’ and “Eggholder” are both more than 30% and the value on function ‘‘Bohachevsky3’’ is more than 20% as well as most of the functions are both more than 10%. On the other functions, all the improvement rate are more than 5% and the worst improvement rate reaches about 5.17%.

Moreover, in the optimization of the function 21 patrol path, DAF-BRS-CWOA is the algorithm with the smallest path length, shortest time-spent, and smallest the length of the path among all algorithms (PSO, GA, WDX-WPOA and DAF-BRS-CWOA) during 30 independent experiments. DAF-BRS-CWOA has an absolutely small path length compared to GA and PSO. Compared to WDX-WPOA, the DAF-BRS-CWOA has a certain improvement in time-spent, as shown in Table 3. Therefore, DAF-BRS-CWOA has excellent performance in public security patrol path planning.

In a word, DAF-BRS-CWOA possesses excellent optimization accuracy, good stability, less time-spent and quick peed of convergence.

5. Conclusions

The public security patrol path planning is very important in public security work, however, the existing public security patrol path planning has some shortcomings to varying degrees. To address these shortcomings, this paper proposes a public security patrol path planning recommendation method based on an improved wolf-pack optimization algorithm, which mainly focuses on three aspects. Firstly, Dynamic-Adjustment-Factor was introduced in WDX-WPOA to dynamically adjust the number of airdropped wolves; Moreover, Balanced-Raid-Strategy with symmetric property was proposed to improve the existing original strategy of Summon-Raid by not only examining the reverse position of the current wolf, but also the ones generated according to certain rules between the reverse position of the current wolf and the current optimal wolf; Finally, an optimization objective function regarding the public security patrol path planning was abstracted and counted to obtain the optimal recommendation for the public security patrol path planning. Comparative and numerical experiments with four similar swarm intelligence optimization algorithms (PSO, GA, WDX-WPOA and DAF-BRS-CWOA) on 20 public datasets and the proposed objective function RPB Function were conducted and the results demonstrated that the DAF-BRS-CWOA has superior performance.

Although the algorithm proposed in this paper is superior, there are still some shortcomings. Such as shown in Table 3, DAF-BRS-CWOA spent more time than GA and PSO in 14 test functions. And it is in function-21 that DAF-BRS-CWOA spent a considerable amount of time as well as the results of each operation are not so stable due to the higher complexity, which confirms a principle: no perfect standard that applies universally. The authors will continuously improve this algorithm and make it play an increasingly important role in various different fields in the future work.