Retrial Queue with a Finite Number of Orbits for Failed Attempts to Access the Server and Search of Customers from Last Orbit

1. Introduction

The Retrial Queueing (RTQ) model under consideration is a single server model with a finite number of orbits arranged in hierarchical order, labeled as $1,2,\dots ,M$, and arranged in that order. Their capacities are respectively $K,2K,...(M-1)K$ and unlimited for the orbit-M. Further, the retrial rate of customers from these orbits has individual rates $\theta$, $2\theta$, ..., $M\theta$. These two facts together almost ensure minimum loss of customers, consequent to failed retrials, for a reason to be indicated in the descriptions to follow. If the server is busy at the time of arrival of a primary customer he/she will join the first orbit. Retrials are made from the first orbit and if those are unsuccessful, customers move to the next orbit and so on until they reach the last orbit. All the orbits except orbit-M are of finite capacity. The last orbit, orbit-M has infinite capacity and the customers in that orbit may either return to the same orbit or leaves the system forever, after each unsuccessful retrial attempt. Retrials from all the orbits follow linear retrial policy. Thus the model under consideration takes into account the impatience of customers in such queueing systems. On completion of service, the server transfers a customer from orbit M with probability p for the next service or stays idle with probability $1-p$. The time taken for transfer is negligible. Thus, customers in that orbit (who have already completed at least $M-1$ retrials) will get higher priority over all customers from other orbits and also the primary arrivals.

In the mathematical modeling of real-life problems, the theory of retrial queues plays a pivotal role. The monograph by Falin and Templeton [11], gives an introduction to the theory of retrial queues. Over the years, the theory of retrial queues has been developing and the literature covers various fields in which the theory can practically be applicable. The book by Artalejo and Gomez-Corral [4] includes comprehensive coverage of techniques for the computational analysis of retrial queues. It includes motivating examples in telephone and computer networks and a comparative analysis of the retrial queues versus standard queues with waiting lines and queues with losses. A modern treatment for the study of retrial queues can be seen in the books by Dudin et al. [9] and Chakravarthy [5,6]. Detailed and classified bibliography of articles on retrial queues can be found in [1,2]. The survey on retrial queues in [13,20] includes literature with algorithmic and computational aspects of retrial queues.

When we analyze most of the retrial queueing models, we can find that the server remains idle even if there are customers in the corresponding orbit/orbits. This happens just because of the fact that the retrying customers are unaware of the status of the server. Retrying customers will succeed in getting service only if the server is idle at the retrying epoch. To overcome the difficulties posed by such situations and to improve the utilization of the server the concept of orbital search in negligible time to the server at the end of a service completion epoch was introduced. In the classical queueing models the concept of searching of customers was introduced by Neuts and Ramalhoto [16]. It was extended to the case of retrial queues in 2002 by Artalejo et al. in [3]. Krishnamoorthy et.al.[14] extended the search mechanism to a queueing model in which the blocked customers leave the system forever. Orbital search in a wider sense is used in [7,8,12,15]. In these papers, the authors assume different distributions for the search time of customers from the orbit. However, in this, there is no guarantee that the customer so taken will be given the next service. This is because, during the search time, a primary or a retrial customer can access the server thereby failing the very objective of effectively reducing the idle time of the server and the waiting time of orbital customers.

The expanding(increasing) sizes of successive orbits compared to the previous one are to minimize customer loss due to retrials. Abandonment of the system due to failed retrials together with the additional feature of limited (finite) capacities and consequent loss of retrial customers from orbits 1, 2, ..., $M-2$ to orbits 2, 3, ..., $M-1$ lead to a more stable system. The increasing rate of retrials from successive orbits coupled with increasing rate of service of customers belonging to successive orbits and transfer of customers from orbit-M for service at a service completion epoch, ensure " almost sure" completion of service of customers reaching the final orbit within a specified time from the epoch of arrival of such customers.

A salient feature of this model is that we get a complete picture of customers in each of the orbits, namely the number of retrials each customer has made so far. 1, 2, ..., $M-2$ to orbits 2, 3, ..., $M-1.$ This feature is not seen in any RTQ models discussed in the literature so far with the exception that multiple hierarchical orbits are considered in [19].

Highlights

• Information about the number of retrials made by customers up to $(M-1)$th orbit.
• Customers from orbit- M are picked for service by the server immediately on completion of service, with a positive probability. If this probability is taken as one, then it represents the case of a queue of customers who have completed $M-1$ retrials
• This model considers separate orbits for customers who failed to access the server as a primary customer (orbit-1), completed one retrial (orbit-2, ...., completed $M-2$ retrials (orbit-$(M-1)$ and those who have completed $M-1$ or more retrials (orbit-M). Because of finite capacities of orbits$1,2,...,M-1$, a few primary customers, a few customers who retried once, ..., retried $M-2$ times might have been lost. However, this is not the case with the $M^{th}$ orbit. It has infinite capacity. The actual loss of customers from this orbit is due to failed retrial (${(M-1)}^{th}$or more retrials). We could have modified the last orbit customers’ status as those having completed $M-1$ retrials by assuming that customers who fail to access the server from this orbit NOT returning to orbit with probability 1. This is essentially a particular case of the model that we discuss in this paper.
• The increase in capacities in the ascending order of orbits$1,2,...M-1,M,$ ensures minimum loss of retrial customers from the immediately preceding orbits.
• The increase in the rates of retrials (in their ascending order) also ensures minimum loss of customers to orbit-j from orbit-$j-1$ for $j=1,2,..,M$ Here $j=1$ means orbit zero which "holds primary customers".
• Computation of certain probabilities (distributions) of significance is done in this paper.
• Because of abandonment of the system by customers in orbit-M upon a retrial,the RTQ under consideration is stable by Tweedie’s theorem
• The increasing nature of retrial rates from orbits can ensure minimum loss of retrial customers due to finite capacity restriction of orbits $1,2,\dots ,M-1.$
• The Idle time of the server also gets reduced due to increasing retrial rates.

Notations and Abbreviations

The following abbreviations and notations are used in this manuscript:

RTQ	Retrial Queue
CTMC	Continuous Time Markov chain
$QBD$ process	Quasi-Birth–Death Process
$LDQBD$ process	Level Dependent Quasi-birth–Death process
MAM	Matrix Analytic Method
P{a}	Probabilty of a
e	All one vector with appropriate dimension
$I_n$	Identity matrix of order $n\times n$
$A^{\prime }$	Transpose of matrix A
$\mathbf{0}$	Matrix whose entries are 0, of appropriate size
$A\otimes B$	Kronecker product; if $A=\left[a_{ij}\right]$ is a matrix of order $m\times n$ and if B is a matrix of order
	$p\times q$, then $A\otimes B=\left[a_{ij}B\right]$ will denote a matrix of order $mp\times nq$
$\lambda$	arrival rate
$\mu$	Service rate
$\theta$	retrial rate
p	probability with which search has been done
q	probability with which a customer returns to orbit M

The remainder of this paper is as follows. In Section 2, the description of the problem is given. In Section 3, the mathematical modeling of the problem and its analysis has been done. Steady-state analysis has been done in Section 4 and the steady-state probabilities were found. Section 5 contains performance measures. Section 6 contains some probability distributions of interest that are related to the model. Numerical and graphical illustrations that provide insight into the operation of the system are included in Section . Conclusions are provided in Section 7.

2. Model Description

The model considered in this paper is a single server retrial queue in which M orbits are available for retrial customers. These orbits are arranged in sequential order 1, 2,.....,$M.$ The first one is for primary customers who fail to access the server on their arrival; the second one is for failed retrials from orbit-1, the third one is for failed retrials from orbit-2, and so on. Finally, the $Mth$ orbit is for failed retrials from orbit-$(M-1)$. If a retrial attempt from orbit-M is not successful, the customer returns to the same orbit with some probability q. If a retrial from the $M^{th}$ orbit is not successful, with probability $(1-q)$ customers leave the system forever. The capacities of orbits $1,2,...,M-1$ are finite: $K,2K,....,(M-1)K$ respectively. This gives an exact picture of the number of retrials made by retrial customers up to orbit-$(M-1)$. The finite capacity restriction of these orbits may lead to loss of retrial customers. The retrial rates from these orbits are in increasing order. For easy exposition, we assume these to be $\theta ,2\theta ,\dots ,M\theta .$ The inter retrial time is exponentially distributed with parameter $r\theta$ for customers in the $r^{th}$ orbit for $r=1,2,\dots ,M.$ Retrial rates from all orbits are according to the linear retrial policy. The service rates of all customers are independent and identically distributed exponential random variables with parameter $\mu$. This can be made to depend on the nature of customers, for example, for primary customers, the parameter is $\mu$, for customers from orbits $1,2,3,\dots ,M$ the parameters are $2\mu ,3\mu ,\dots ,(M+1)\mu$, respectively. This will lead to an increase in the dimension of the resulting CTMC because we have to include the additional information on whether the customer in service is primary or from the orbit-j, $j=1,2,...,M$. This is what we consider in this manuscript. 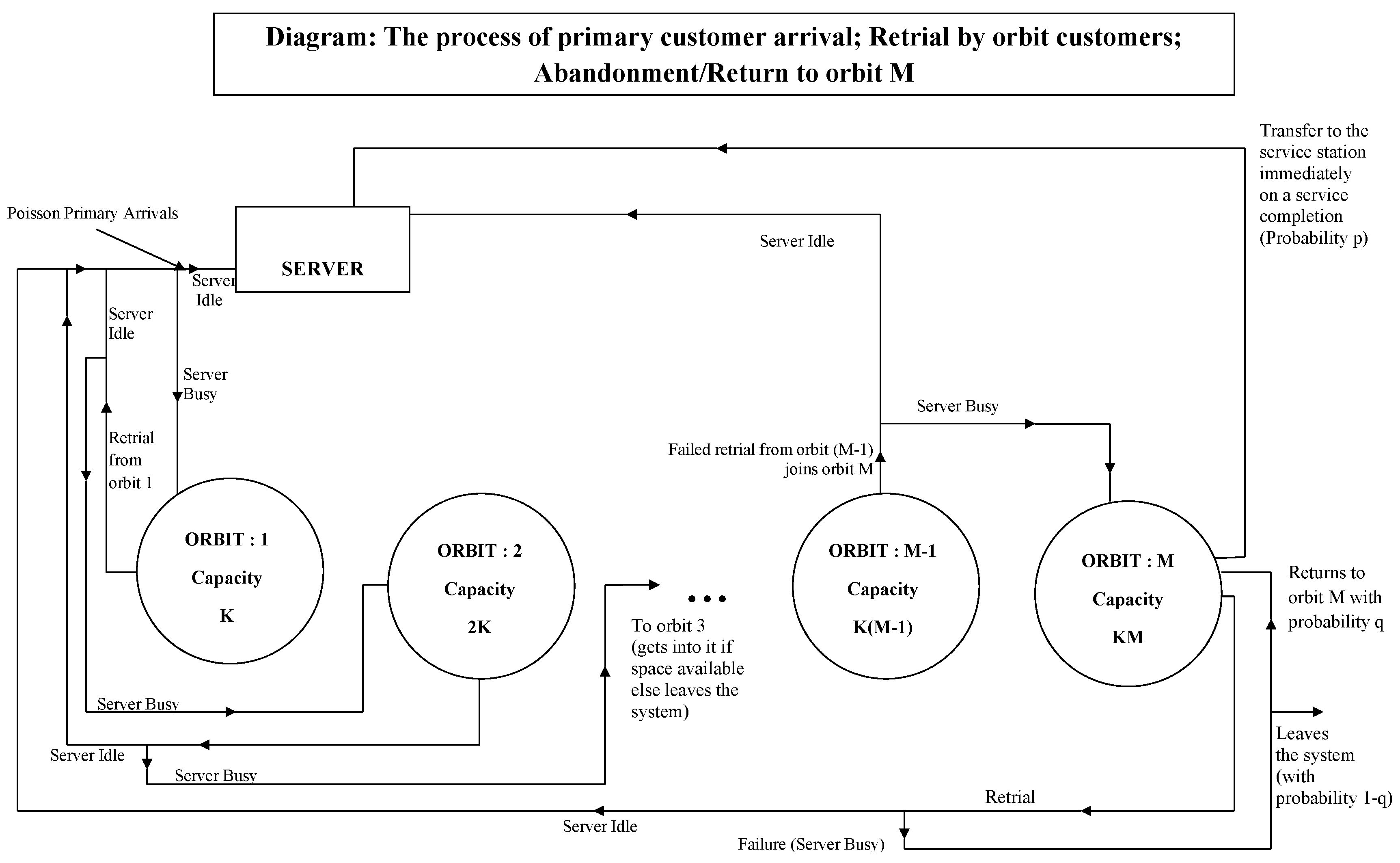After each service completion, with probability p the server searches for customers from orbit-M, and with probability $(1-p)$, it remains idle. The search time is assumed to be negligible. The diagram given in Figure 1 gives a representation of the process of primary customer arrival, retrial by orbit customers, and abandonment/return to orbit-M.

3. Mathematical Formulation

Let

• $N_i\left(t\right)$ be the number of customers in the orbit- i at time t for $i=1,2,\dots ,M;$
• $C\left(t\right)$ be the status of the server at time t

$$C\left(t\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{idle}\hfill \\ 1,\hfill & \mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{busy}\mathrm{with}\mathrm{a}\mathrm{primary}\mathrm{customer}\hfill \\ j+1,\hfill & \mathrm{if}\mathrm{the}\mathrm{server}\mathrm{is}\mathrm{busy}\mathrm{with}\mathrm{customers}\mathrm{from}\mathrm{orbit}\text{-}j,j=1,2\dots ,M\hfill \end{array}\right.$$

$$\varphi \left(t\right)=\{(N_M\left(t\right),N_{(M-1)}\left(t\right),\dots ,N_1\left(t\right),C\left(t\right));t\ge 0\}$$

is an irreducible continuous-time Markov chain and it describes the process under consideration.

The state space is $\Omega$ where

$$\Omega =\left\{(i_M,i_{(M-1)},\dots ,i_1,j)\right\}$$

where

$$i_M\ge 0;0\le i_r\le rK$$

Let the ordering of the elements of $\Omega$ be lexicographical. We form the so called states $(i_M,i_{(M-1)},\dots ,i_1,j)$ of the Markov chain $\varphi \left(t\right).$ We analyze the transitions of the Markov chain $\varphi \left(t\right)$ during an interval having an infinitesimal duration. We can form the matrices defining the transition rates of this chain. The infinitesimal generator Q of the LDQBD describing the model under consideration is of the form

$$Q=\left(\begin{array}{cccccc}{A}_1^0& A_0& & & & \\ A_2^1& A_1^1& A_0& & & \\ & A_2^2& A_1^2& A_0& & \\ & & \dots & \dots & \dots \end{array}\right)$$

(1)

where $A_0$ represents the rate matrix corresponding to the arrival of a customer to the $M^{th}$ orbit, that is the transition from level $i_M\to i_M+1$ where $i_M\ge 0$ and it is independent of $i_M$,

$A_2^i$ represents the rate matrix corresponding to the loss of a customer from the $M^{th}$ orbit as a result of the retrial, that is, transitions from level $i_M\to i_M-1;$ for $i_M=1,2,\dots ,$ and

$A_1$ describes all transitions in which the level does not change (transitions within levels $i_M$).

The structure of the $A_1^i,A_0,A_2^i$ for $i\ge 0$ can all be defined in terms of transition rates corresponding to the transitions of the states given in the Table 1 The first column defines the state from which a transition can occur, the second column defines a state to which a transition can occur, the third column describes the condition when this transition occurs and the last column contains the rate of the corresponding transition.

The retrial queueing model considered here can be studied as a level dependent Quasi Birth Death process and we apply Neuts-Rao truncation for the analysis of the model. We assume that when the number of customers in the $M^{th}$ orbit exceeds a certain limit, say N, retrial from that orbit occurs at constant rates $N\mu .$ In that situation the matrices $A_2^i$ becomes $A_2^N$ and $A_1^i$ becomes $A_1^N$ for $i\ge N$. The infinitesimal generator $Q^1$ of the modified model becomes

$$Q^1=\left(\begin{array}{cccccccc}{A}_1^0& A_0& & & & & & \\ A_2^1& A_1^1& A_0& & & & & \\ & A_2^2& A_1^2& A_0& & & & \\ & & \dots & \dots & \dots & & \\ & & & A_2& A_1& A_0\\ & & & & \dots & \dots & \dots \end{array}\right)$$

(2)

where

$$A_1=A_1^N,A_2=A_2^N$$

.

4. Steady-State Analysis

4.1. Stability Condition

Theorem 1. 

The system under consideration is always stable.

Proof. 

Let $\Psi$ be a Lyapunov test function defined by

$$\Psi \left(u\right)=i$$

(3)

where u denotes a state in the $i^{th}$ level. The mean drift for the state u belonging to the $i^{th}$ level is given by

$$y_u=\sum _{r\ne u}{q}_{ur}(\Psi \left(r\right)-\Psi \left(u\right))$$

(4)

$$=\sum _{u^{\prime }}{q}_{u{u}^{\prime }}(\Psi \left(u^{\prime }\right)-\Psi \left(u\right))+\sum _{u^{″}}{q}_{u{u}^{″}}(\Psi \left(u^{″}\right)-\Psi \left(u\right))+\sum _{u^{‴}}{q}_{u{u}^{‴}}(\Psi \left(u^{‴}\right)-\Psi \left(u\right))$$

(5)

where $u^{\prime }$ is a state in the ${(i-1)}^{th}$ level, $u^{″}$ is a state in the $i^{th}$ level and $u^{‴}$ is a state in the ${(i+1)}^{th}$ level, $q_{ij}$ is the ${(i,j)}^{th}$ entry of the infinitesimal generator. So $\Psi \left(u\right)=i,\Psi \left(u^{\prime }\right)=i-1,\Psi \left(u^{″}\right)=i,\Psi \left(u^{‴}\right)=i+1.$

$$y_u=\sum _{u^{\prime }}{q}_{u{u}^{\prime }}(i-1-i)+\sum _{u^{″}}{q}_{u{u}^{″}}(i-i)+\sum _{u^{‴}}{q}_{u{u}^{‴}}(i+1-i)$$

(6)

$$=\sum _{u^{\prime }}{q}_{u{u}^{\prime }}(-1)+\sum _{u^{″}}{q}_{u{u}^{″}}\left(0\right)+\sum _{u^{‴}}{q}_{u{u}^{‴}}\left(1\right)$$

(7)

$$=-\sum _{u^{\prime }}{q}_{u{u}^{\prime }}+\sum _{u^{‴}}{q}_{u{u}^{‴}}$$

(8)

We have, ${\sum }_{u^{‴}}{q}_{u{u}^{‴}}=c_1$, ${\sum }_{u^{\prime }}{q}_{u{u}^{\prime }}=c_2+i\theta$, where $c_1$ and $c_2$ are constants. So the mean drift

$$y_u=c_1-c_2-i\theta$$

(9)

which depends only on the level i. Thus for any $ϵ>0$, we can find $N^{\prime }$ large enough so that

$$y_u<-ϵ$$

(10)

for any u belonging to level $i\ge N^{\prime }$. Hence by Tweedie’s result [18], the theorem follows.

□

4.2. Stationary Distribution

The stationary distribution of the Markov process under consideration is obtained by solving the set of equations

$${\mathbf{xQ}}^{\mathbf{1}}=\mathbf{0},\mathbf{x}\mathbf{e}=\mathbf{1}.$$

Let $\mathbf{x}$ be the steady- state probability vector of $Q^1.$

Partition this vector in conformity with $Q^1$ as follows:

$$\mathbf{x}=\left(\mathbf{x}\right(\mathbf{0}),\mathbf{x}(\mathbf{1}),\mathbf{x}(\mathbf{2}),\dots ,)$$

$$\mathbf{x}\left(i\right)=\left(\mathbf{x}\right(i,0),\mathbf{x}(i,1),\dots ,\mathbf{x}(i,(M-1)K)$$

$\mathbf{x}(i,j)=\left(\mathbf{x}\right(i,j,0),\mathbf{x}(i,j,1),\dots ,\mathbf{x}(i,j,(M-2)K\left)\right)$ and so on. Finally we get elements of the form $x(i_M,i_{(M-1)},i_{(M-2)},\dots ,i_1,j)$ and it is the probability of being in state $(i_M,i_{(M-1)},i_{(M-2)},\dots ,i_1,j)$ $i_M\ge 0$; $0\le i_r\le rK$; $j=0,1,2,\dots ,M+1$

The steady-state probability vector is obtained as

$${\mathbf{x}}_{(N-1)+i}={\mathbf{x}}_{(N-1)}{R}^i,i\ge 0$$

(11)

where R is the minimal non-negative solution to the matrix quadratic equation

$$R^2{A}_2+R{A}_1+A_0=0$$

(12)

and the vectors ${\mathbf{x}}_{\mathbf{0}},\dots ,{\mathbf{x}}_{(\mathbf{N}-\mathbf{1})}$ are obtained by solving

$${\mathbf{x}}_{\mathbf{0}}{A}_1^0+{\mathbf{x}}_{\mathbf{1}}{A}_2^1=0$$

(13)

$${\mathbf{x}}_{(\mathbf{i}-\mathbf{1})}{A}_0+{\mathbf{x}}_{\mathbf{i}}{A}_1^i+{\mathbf{x}}_{(\mathbf{i}+\mathbf{1})}{A}_2^{(i+1)}=0$$

(14)

For $1\le i\le (N-2)$

$${\mathbf{x}}_{(\mathbf{N}-\mathbf{2})}{A}_0+{\mathbf{x}}_{(\mathbf{N}-\mathbf{1})}\left[A_1^{(N-1)}+A_{2}R\right]=0$$

(15)

subject to the normalizing condition

$$\sum _{i=0}^{(N-2)}{\mathbf{x}}_{\mathbf{i}}+{\mathbf{x}}_{(\mathbf{N}-\mathbf{1})}{(I-R)}^{-1}\mathbf{e}=1.$$

(16)

5. Performance Measures

Some measures of performance, which help the operators of the system to make decisions concerning the optimal values of the number M of hierarchical orbits to be maintained and the number K which decides customers to be allowed in those hierarchical orbits are evaluated. Following are some performance measures which help us to make a detailed study about the problem under consideration. For the evaluation of the performance measures we assume that summation w.r.t each $i_r$ is up to $rk$

• Expected number of customers in the $M^{th}$ orbit

  $$E\left[N_M\right]=\sum _{i=0}^{\infty }i\mathbf{x}\left(\mathbf{i}\right)\mathbf{e}$$

  (17)
• Expected number of customers in the $r^{th}$ orbit

  $$E\left[H\left(r\right)\right]=\sum _{i_M=1}^{MK}\sum _{i_{(M-1)}=1}^{(M-1)K}\dots ,\sum _{i_r=1}^{rK}\mathbf{x}(i_M,i_{M-1},i_{M-2},\dots ,i_r)\mathbf{e}$$

  (18)
• Probability that the server is busy with customers from orbit-r

  $$P_r=\sum _{i_M=1}^{MK}\sum _{i_{(M-1)}=1}^{(M-1)K}\dots ,\sum _{i_1=1}^K\mathbf{x}(i_M,i_{M-1},i_{M-2},\dots ,i_1,r+1)\mathbf{e}$$

  (19)
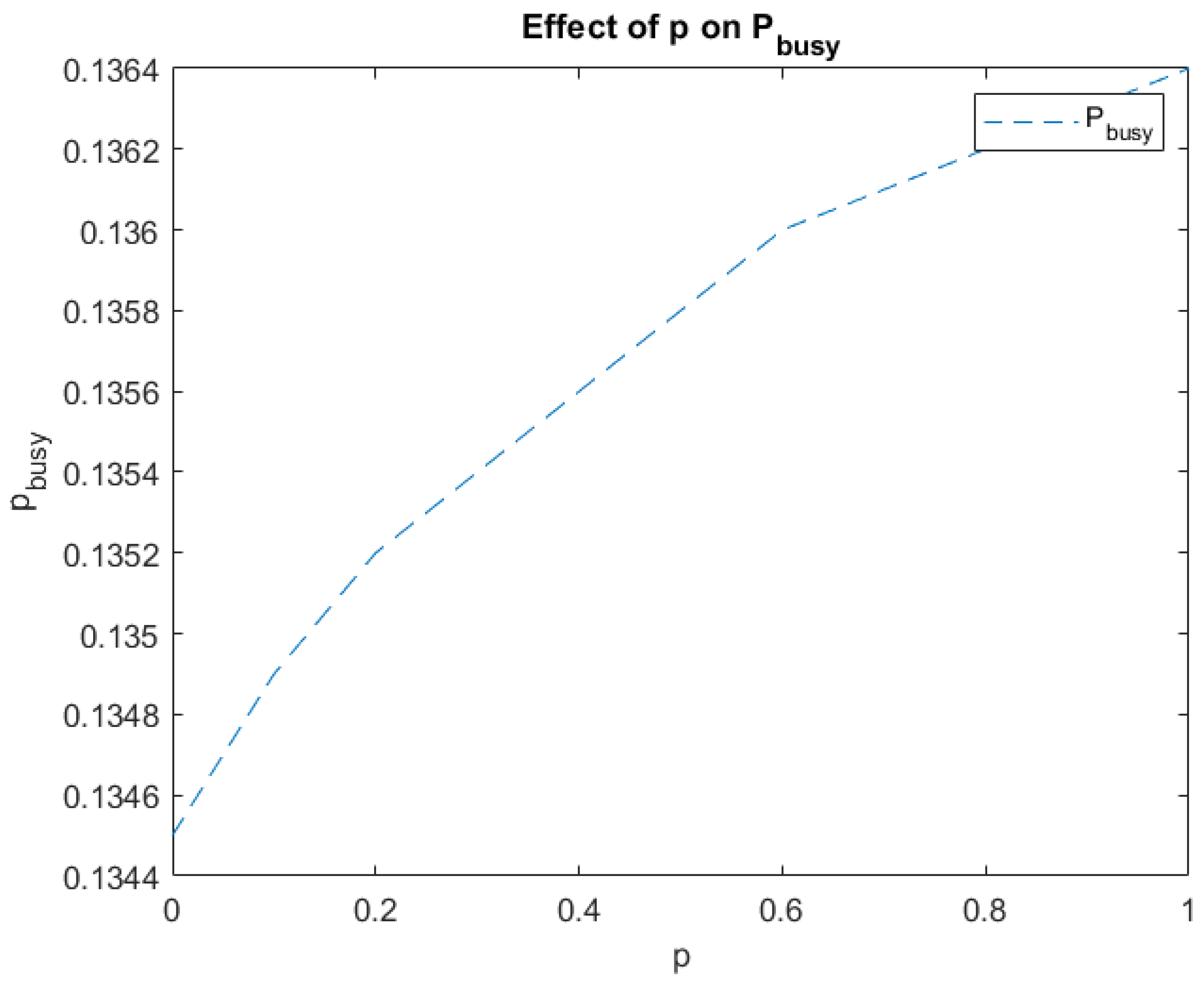
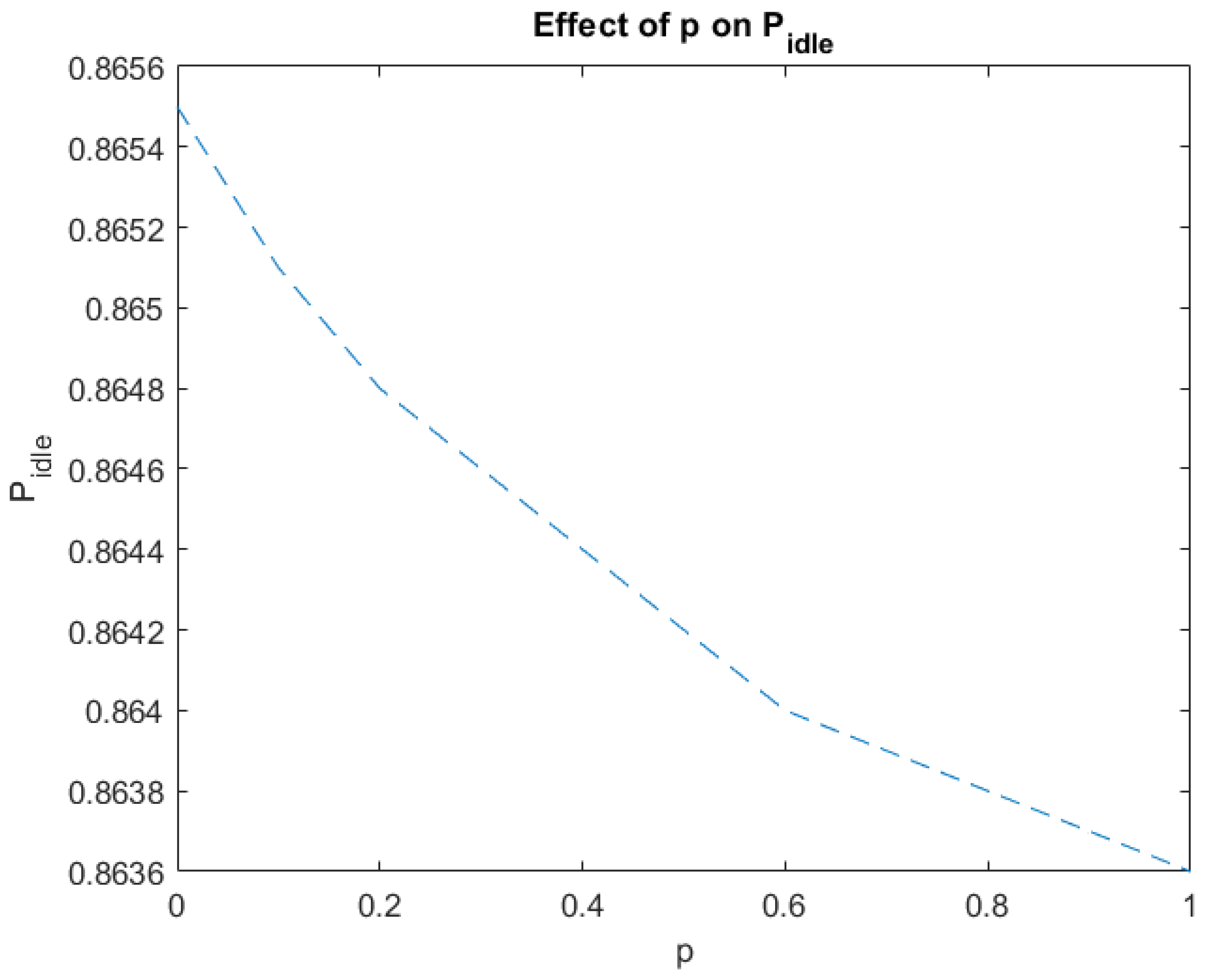
• Probability that the server is busy

  $$P_{busy}=\sum _{r=1}^{M+1}{P}_r$$

  (20)
• Probability that the server is idle

  $$P_{idle}=\sum _{i_M=1}^{MK}\sum _{i_{(M-1)}=1}^{(M-1)K}\dots ,\sum _{i_1=1}^K\mathbf{x}(i_M,i_{M-1},i_{M-2},\dots ,i_1,0)\mathbf{e}$$

  (21)
• Expected number of customers in the system

  $$E\left[N_s\right]=\sum _{r=1}^{M}E\left[H\left(r\right)\right]+P_{busy}$$

  (22)
• Expected number of customers entering the service facility as a result of orbital search

  $$E\left[S\right]=\sum _{i_M=0}^{\infty }\sum _{i_{(M-1)},\dots ,i_1}p*i_M*\mathbf{x}(i_{(M-1)},\dots ,i_1)\mathbf{e}$$

  (23)
• Expected number of customers leaving the system from orbit -M as a result of unsuccessful retrial

  $$E\left[L_M\right]=\sum _{i=0}^{\infty }(1-q)i*\mathbf{x}\left(i\right)\mathbf{e}$$

  (24)

6. Some Probability Distributions

Theorem 2. 

The probability of a primary customer accessing an idle server

$$P\left[R_p\right]=P_{idle}=\sum _{i_M=1}^{MK}\sum _{i_{(M-1)}=1}^{(M-1)K}\dots ,\sum _{i_1=1}^K\mathbf{x}(i_M,i_{M-1},i_{M-2},\dots ,i_1,0)\mathbf{e}$$

(25)

Theorem 3. 

The probability of a primary customer being able to get into orbit-1= $(1-P_{idle})$ *P{(orbit-1 is not full)}

Theorem 4. 

Probability of a customer in orbit-j, successfully accessing the server on retrial

$P\left[R_p\right]=P_{idle}*{\sum }_{k=1}^{jK}kj\theta$* P{ k customers in orbit -j} $j=1,2,M-1$

Theorem 5. 

Probability of a customer retrying to access the server $M-1$ times with the last retrial turning out to be a success= $P_{busy}^{M-1}$ *$P_{idle}$

Proof. 

In the primary arrival and subsequent $M-2$ retrials the customer encounters a busy server and in the $M-1$ retrial he is able to access the server □

6.1. A Lower Bound for the Time Taken to Access the Server

It is extremely hard to compute the exact distribution of the time until a customer is able to access the server. Statements of theorems 2to 5 given above provide certain probabilities in this connection; however those do not say anything about the distribution of time until a customer, starting from the time he gets into the system until either served out or leaves the system because of the orbit being full or could be because of impatience. We provide bounds on the distributions of the time to access the server or leave the system without taking service.

The following lemmas provide distribution of time till accessing the server

Lemma 1. 

The distribution of the time until accessing the server upon reaching the system immediately on arrival ie; τ=0is given by Prob{server seen idle upon primary arrival}=$P\{\tau =0\}$ =$P_{idle}$

Lemma 2. 

The distribution of the time until accessing the server upon reaching the system conditional on accessing the server at the first retrial is $Prob\{\tau ={T_1}^{\left(n\right)}\}$ where ${T_1}^{\left(n\right)}$ is the random variable representing the time to access the server conditional on n customers in that orbit. This has exponential distribution with parameter $2n\theta$ given by =

$$\sum _{n=1}^K(1-e^{-2n\theta t})*P_{idle}$$

(26)

Extending the above result to orbit-j, conditional on accessing the server by a retrial customer in orbit-j, the distribution of $\tau$ is given by the recursive relation

$${\tau }^{\left(j\right)}={\tau }^{(j-1)}+T_j$$

where ${\tau }^{(j-1)}$ is the random duration of time a customer spent until reaching orbit-j and $T_j$ is the duration of time he spends in that orbit.$T_j$ has the exponential distribution with parameter $nj\theta$ where n is the number of customers in orbit-j. Thus

$${\tau }^{\left(1\right)}=T_1$$

where $T_1\sim {\sum }_{n=1}^K(1-P_{idle})exp\left(\lambda \right)$, ${\tau }^{\left(2\right)}={\tau }^{\left(1\right)}+T_2$ where $T_2\sim exp\left(nj\theta \right)$ when there are n customers in orbit-j ; for $j=1,2,\dots ,M-1$. When $j=1$, ${\tau }^{(j-1)}={\tau }^{\left(0\right)}$ is defined as zero. Finally, for $j=M,$ ${\tau }^{\left(M\right)}={\tau }^{(M-1)}+T_M$ where $T_M\sim exp\left(nj\theta \right)$ when n customers are in orbit-M. Since we are looking for the distribution of the minimum time a customer spends in the system, conditional on meeting an idle server as a primary customer, or failing which access from orbit-1, failing which accessing the server from orbit-2,...and if all these retrials turn out to be failures, accessing the server from orbit-M in the first retrial on getting into that orbit or through the search by the system(negligible time, immediately on completion of service)

Important Note: It is to be noted that $T_1$ should be multiplied by the Probability that the server is idle at the time when the retrial customer tries to reach the server and ${\tau }^{\left(1\right)}$ has to be multiplied by the probability that the server busy when the customer tries to access the server. In general distribution, of${\tau }^{(j-1)}$ in

$${\tau }^{\left(j\right)}={\tau }^{(j-1)}+T_j$$

has to be multiplied probability that the server is busy when the customer retries from orbit-$j-1$ and distribution $T_j$ has to be multiplied by probability that server idle when the customer retries from orbit-j for $j=1,2,\dots ,M-1$

A customer on reaching orbit -M , will be either chosen for service through a search made at the end of a service completion or by repeated retrials. Assuming that the customer does not leave the system before accessing the server we get the following results:

Theorem 6. 

Denote by τ the random duration the customer spends in orbit before successfully accessing the server. Then with $\varphi =P\left\{serverbusy\right\},$

• $$P\{\tau \le t\}=\sum _{j=1}^{\infty }$$
  P{j-1 unsuccessful retrials followed by successful one before time t}

  $$=\sum _{n_1,...,n_j=1}^{\infty }{\varphi }^{(j-1)}(1-\varphi )n_1{n}_2\dots n_{(j-1)}{\theta }^{(j-1)}{M}^{j-1}{q}^{j-1}{\int }_0^{u_1}...{\int }_{u_{j-2}}^{u_{j-1}}{\int }_{u_{j-1}}^t{e}^{-n_1\theta M{u}_1}d{u}_1{e}^{-n_2\theta M{u}_2}d{u}_2\dots e^{-n_j\theta M{u}_j}d{u}_j$$
• Having failed j retrials($j=0,1,\dots )$, the customer is transferred to the service station at the end of a service:

  $$P\{\tau \le t\}=\sum _{j=0}^{\infty }{\varphi }^j{\int }_0^t\int \int \dots {\int }_{u_{j-1}}^{u_j}\sum _{n_1,...,n_j=1}^{\infty }{e}^{-n_1\theta M{u}_1}d{u}_1\dots e^{-n_j\theta M{u}_j}d{u}_j{n}_1{n}_2\dots n_{(j}{\theta }^{\left(j\right)}{M}^j{q}^j\left({\int }_{u_j}^t\sum _{k=0}^{\infty }k\theta e^{-k\theta \nu }d\nu \right)pd{u}_1\dots d{u}_j$$
  .

Here the last integral stands for the service completion of a customer in $(\nu ,\nu +d\nu )$ and immediately the customer in orbit is taken for service through search(probability p). The other integrals represent unsuccessful retrials by the customer j.

7. Numerical Examples

The following example gives an illustration of the effect of search probability on the performance measures of the system. Here we assume that the arrival follows Poisson distribution with parameter $\lambda .$. Also, the retrial rates are fixed for the customers from all the orbits, and we take $\theta$ as the retrial rate. The service rates for all customers are taken as $\mu$. In this example, the following values are kept fixed:

$$\lambda =2;\theta =3;\mu =18;K=3;M=2.$$

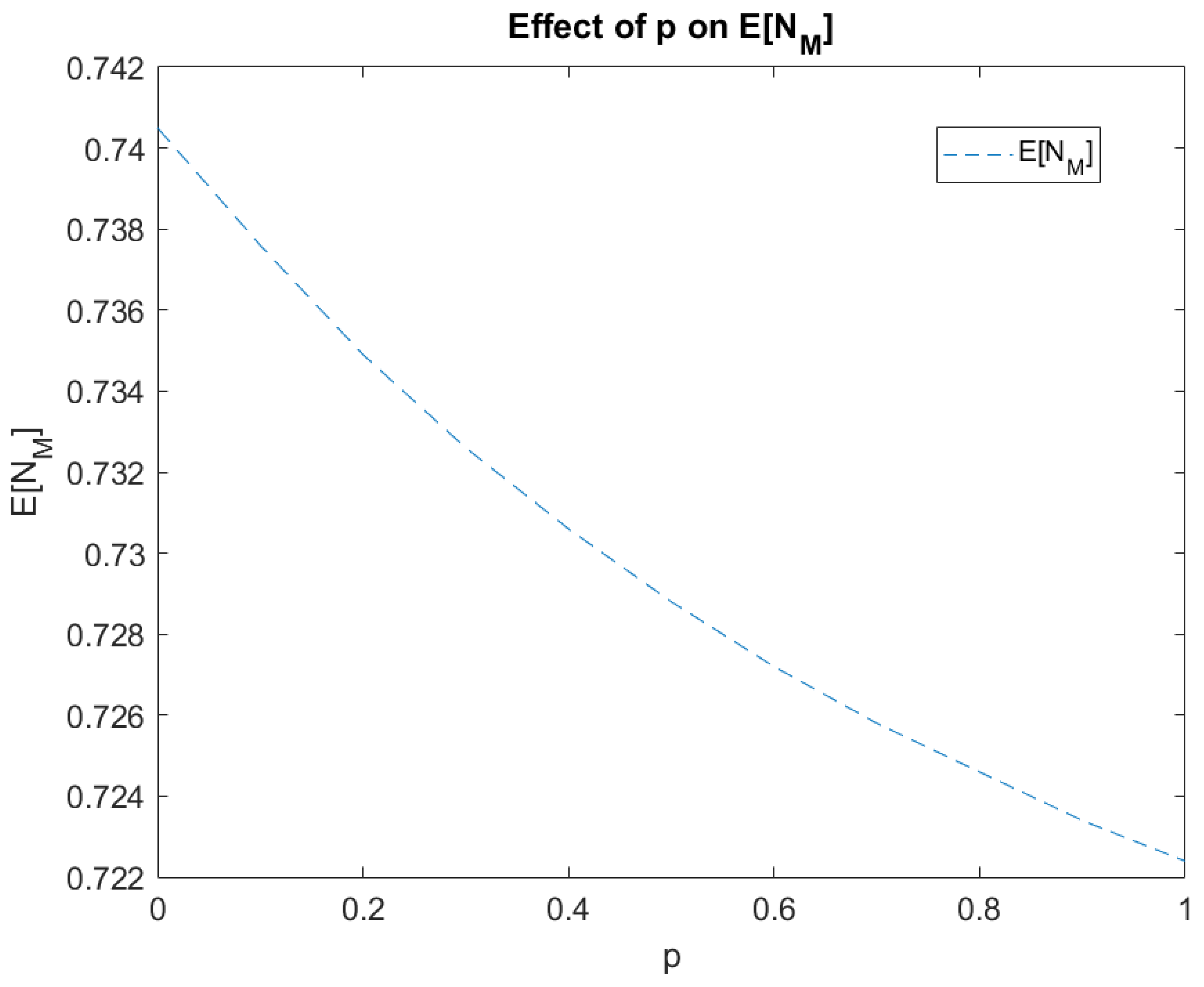
From Table 2 and the corresponding graphical illustrations, the following conclusions can be drawn:

• Figure 2 it can be seen that the expected number of customers in orbit-M decreases as p increases.
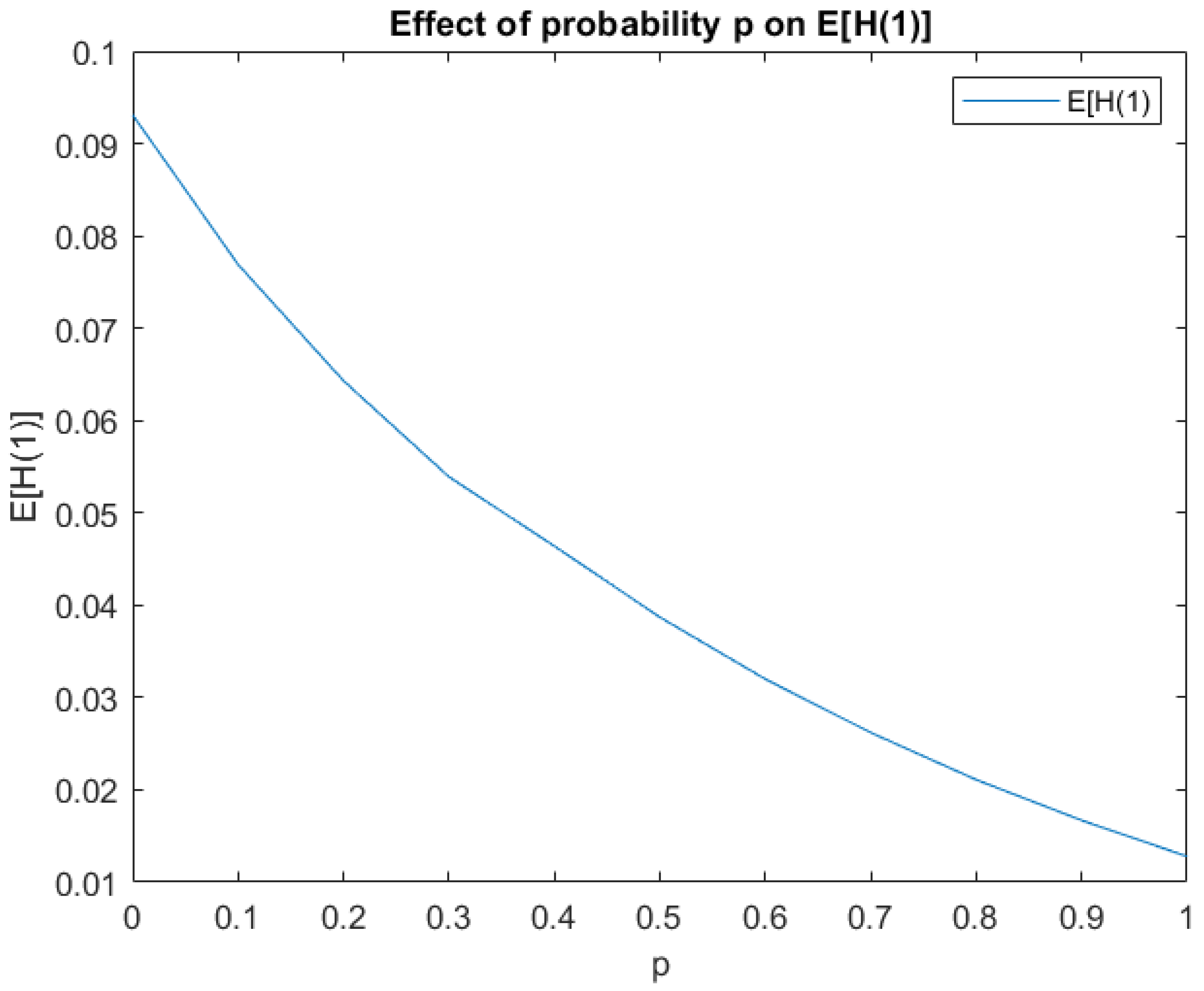
• From Figure 3 we can conclude that the expected number of customers in the first orbit decreases as p increases.
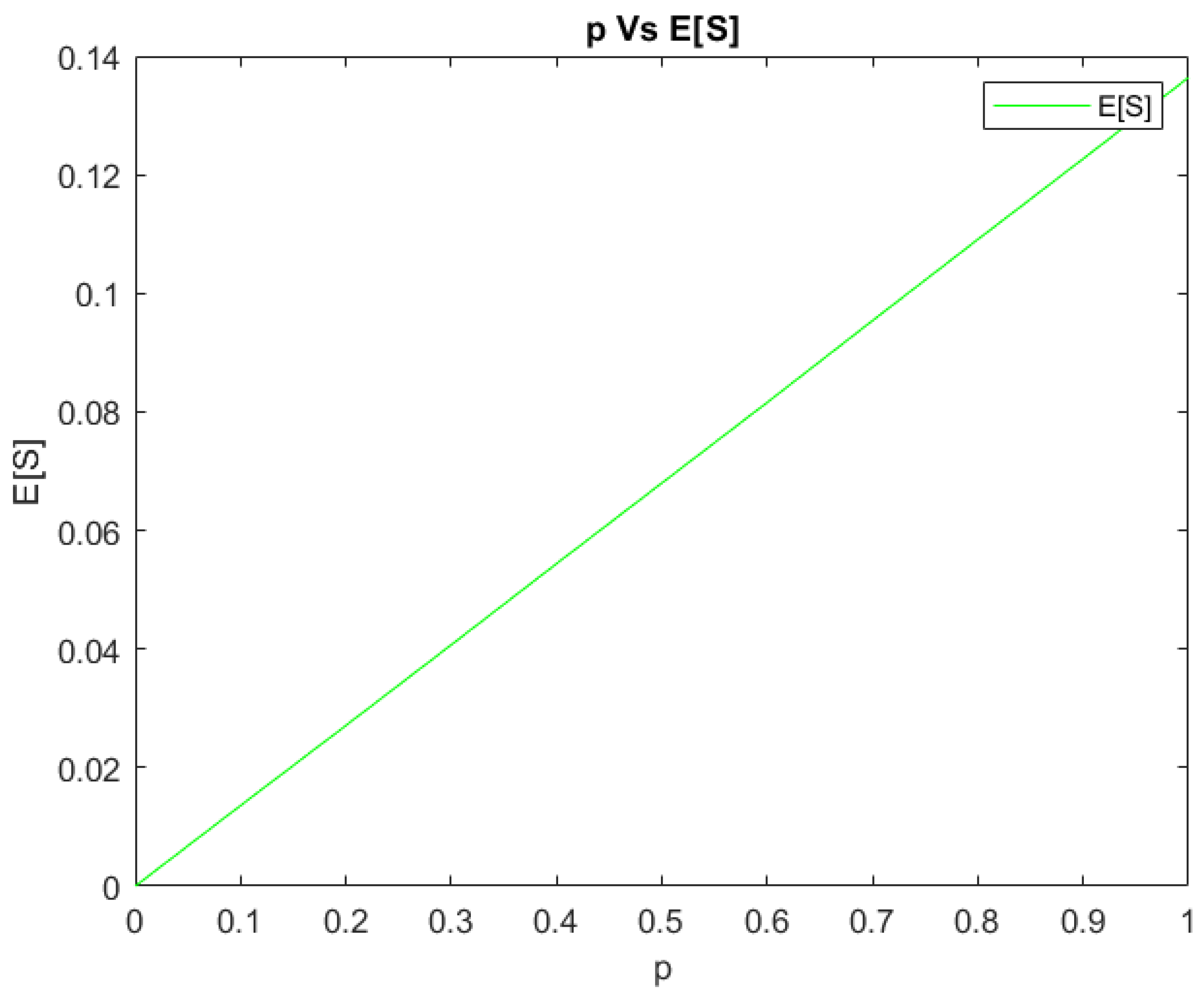
• Figure 4 shows that the expected number of customers getting service as a result of search increases as p increases.

• Figure 5 shows that, $P_{busy}$ increases with an increase in value of $p.$
• Figure 6 shows that $P_0$ decreases with an increase in value of $p.$
• Maximum server utilization is guaranteed if search is done after each service completion.