Submitted:
29 November 2024
Posted:
02 December 2024
You are already at the latest version
Abstract
Potential evapotranspiration (PET) is a significant factor contributing to water loss in hydrological systems, making it a critical area of research. However, accurately calculating and measuring PET remains challenging due to the limited availability of comprehensive data. This study presents a detailed model for predicting PET using the Thornthwaite equation, which requires only mean monthly temperature (Tmean) and latitude, with calculations performed using R-Studio. A geographic information system (GIS) was employed to interpolate meteorological data, ensuring coverage of all sub-basins within the Murat River basin, the study area. Additionally, Python libraries were utilized to implement artificial intelligence-driven models, incorporating both ma-chine learning and deep learning techniques. The study harnesses the power of artificial intelligence (AI), applying deep learning through a convolutional neural network (CNN) and machine learning techniques, including support vector machine (SVM) and random forest (RF). The results demonstrate promising performance across the models. For CNN, the coefficient of determination (R²) varied from 96.2 to 98.7%, the mean squared error (MSE) ranged from 0.287 to 0.408, and the root mean squared error (RMSE) was between 0.541 and 0.649. For SVM, the R² varied from 94.5 to 95.6%, MSE ranged between 0.981 and 1.013, and RMSE ranged from 0.990 to 1.014. RF showed the best performance, achieving R² of 100%, MSE values of 0.326 and 0.640, and corresponding RMSE values of 0.571 and 0.800. The climate and topography data used for all algorithms were consistent, and the results indicate that the RF model outperforms the others. Consequently, RF emerges as the most suitable method for calculating PET, followed by CNN and SVM. This study enhances methodologies for predicting PET, making a substantial contribution to hydrological science by addressing the critical need for data-efficient and accurate modeling techniques to tackle challenges associated with climate change and increasing water demand.
Keywords:
1. Introduction
2. Materials and Data Description
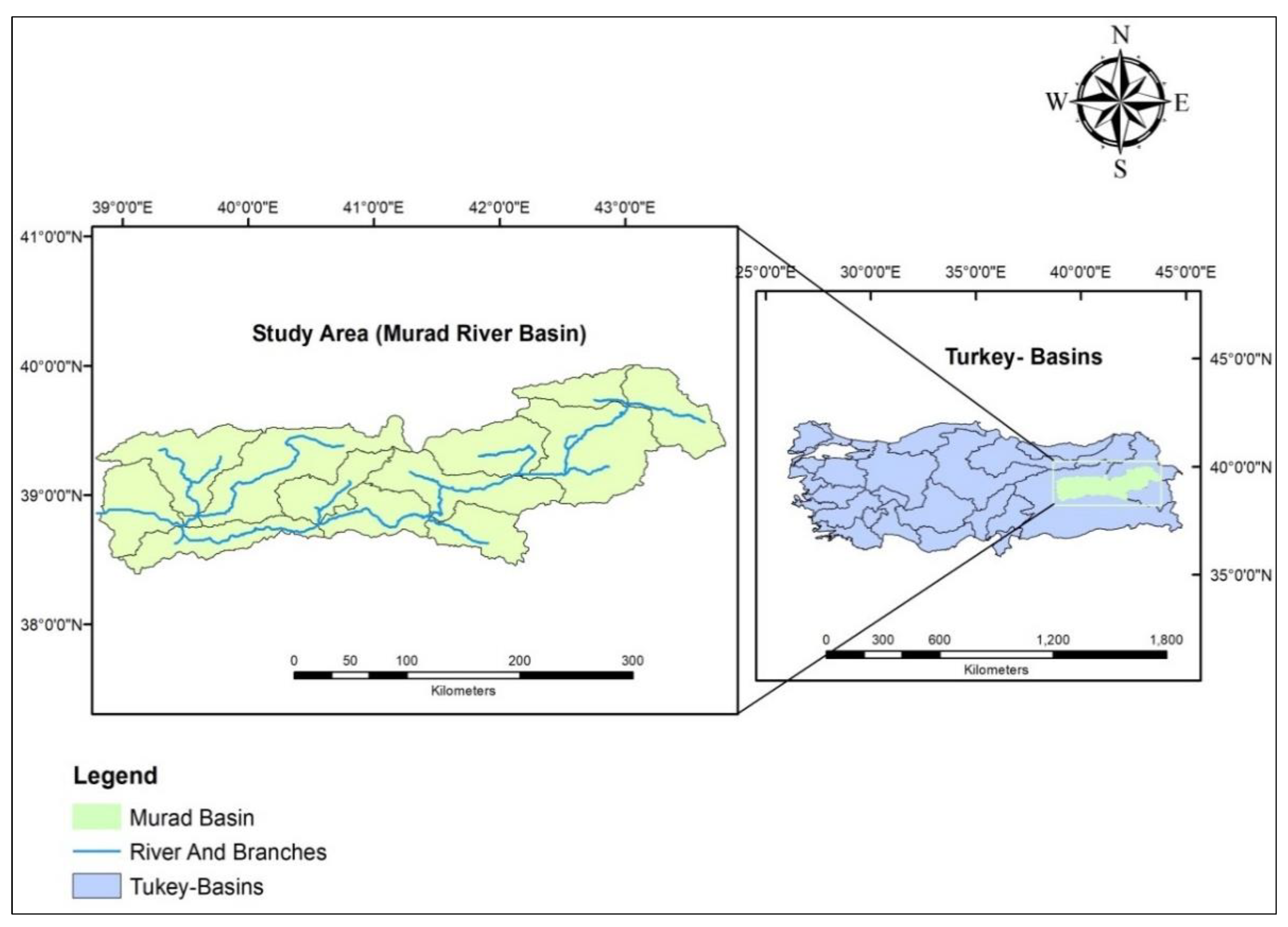
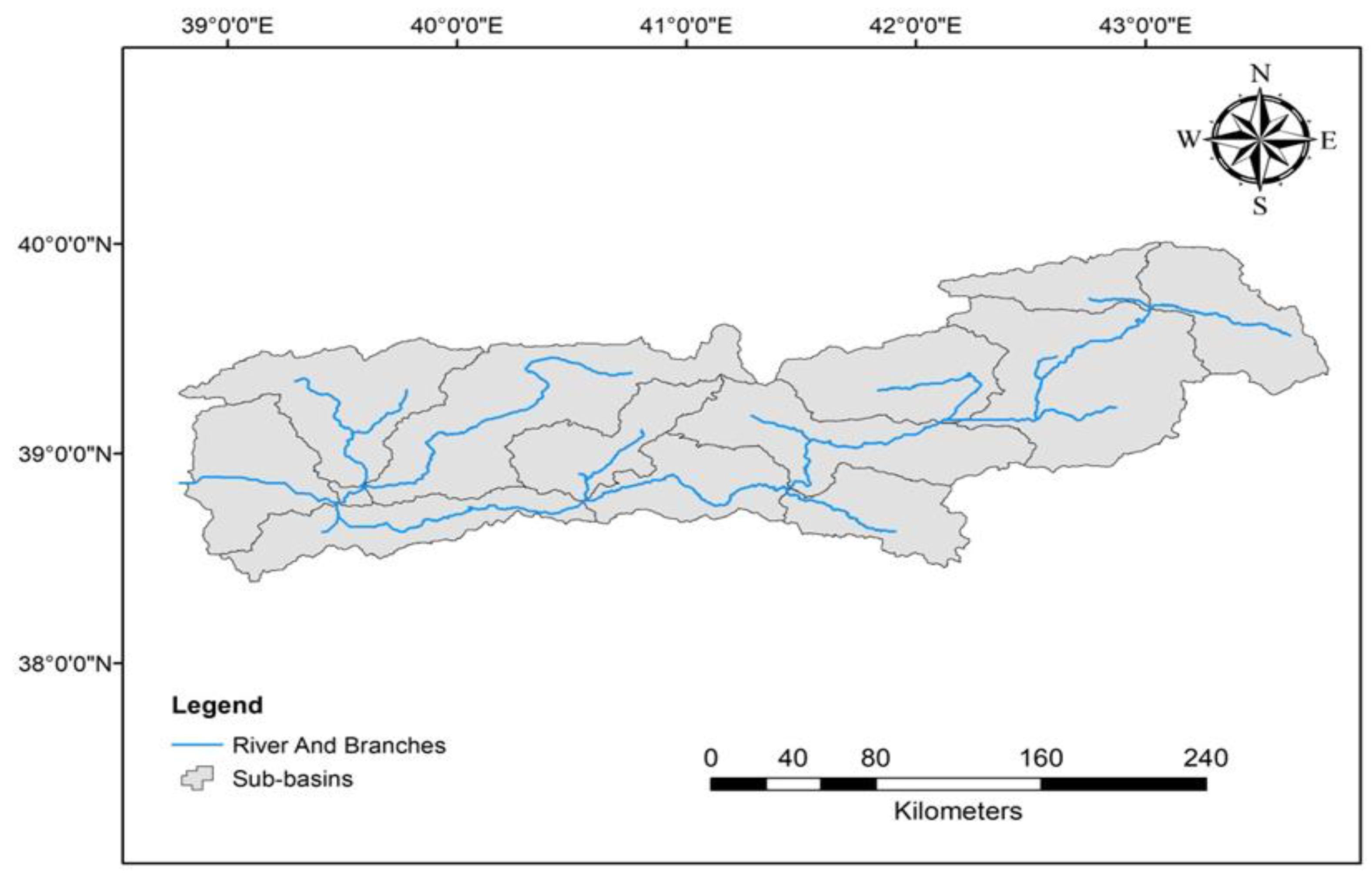
2.1. Study Area
2.2. Data Collection
3. Methodology
3.1. Geographic Information System (GIS) Spatial Analysis and Modeling Setup
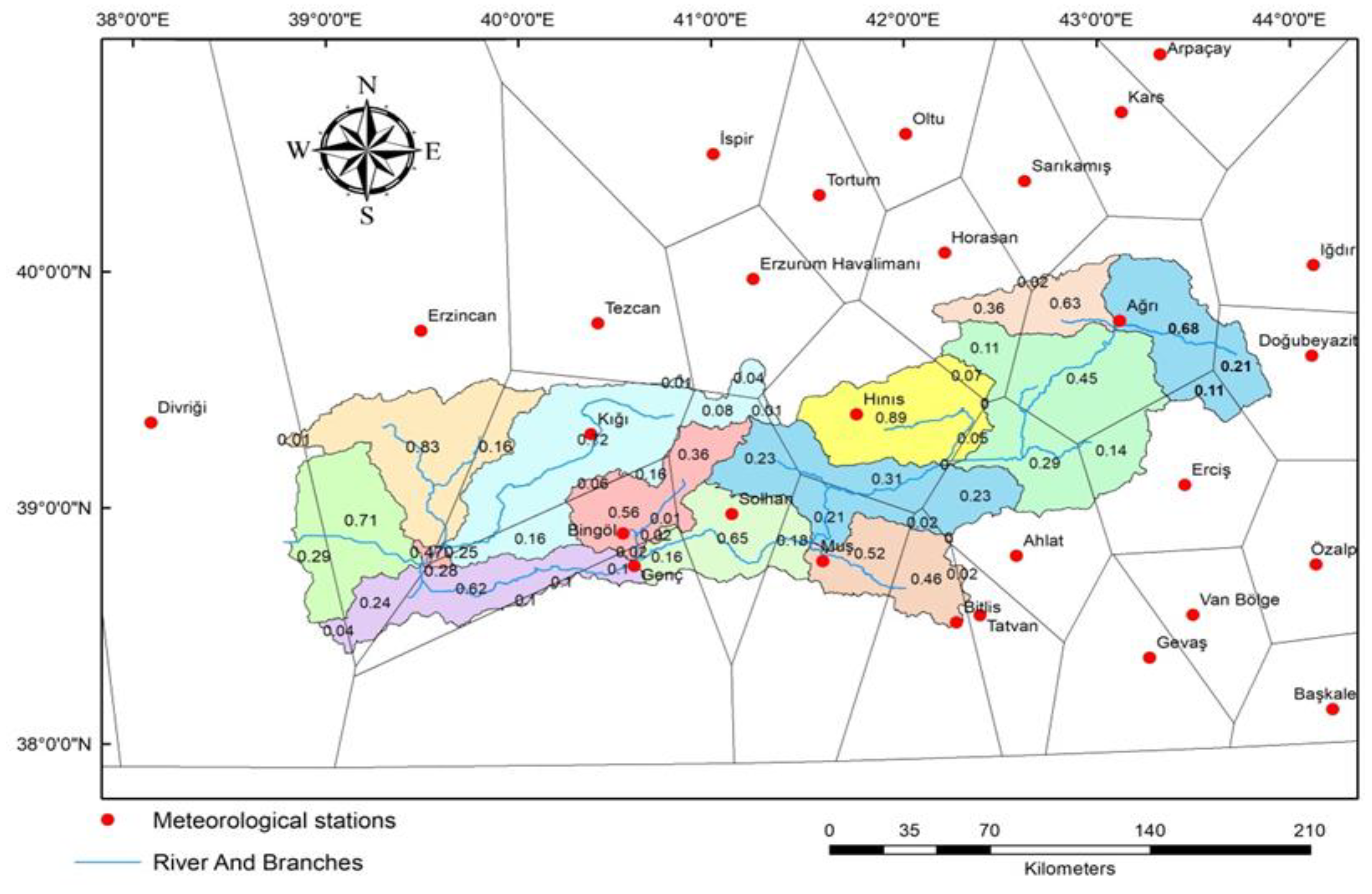
3.2. Interpolation Process Using the Thiessen Polygon Method
3.3. Computing Potential Evapotranspiration (PET)
3.4. Machine Learning and Deep Learning
3.4.1. Convolutional Neural Network (CNN)
3.4.2. Support Vector Machine (SVM)
3.4.3. Random Forest (RF)
3.5. Models’ Performance Validation
4. Results and Discussion
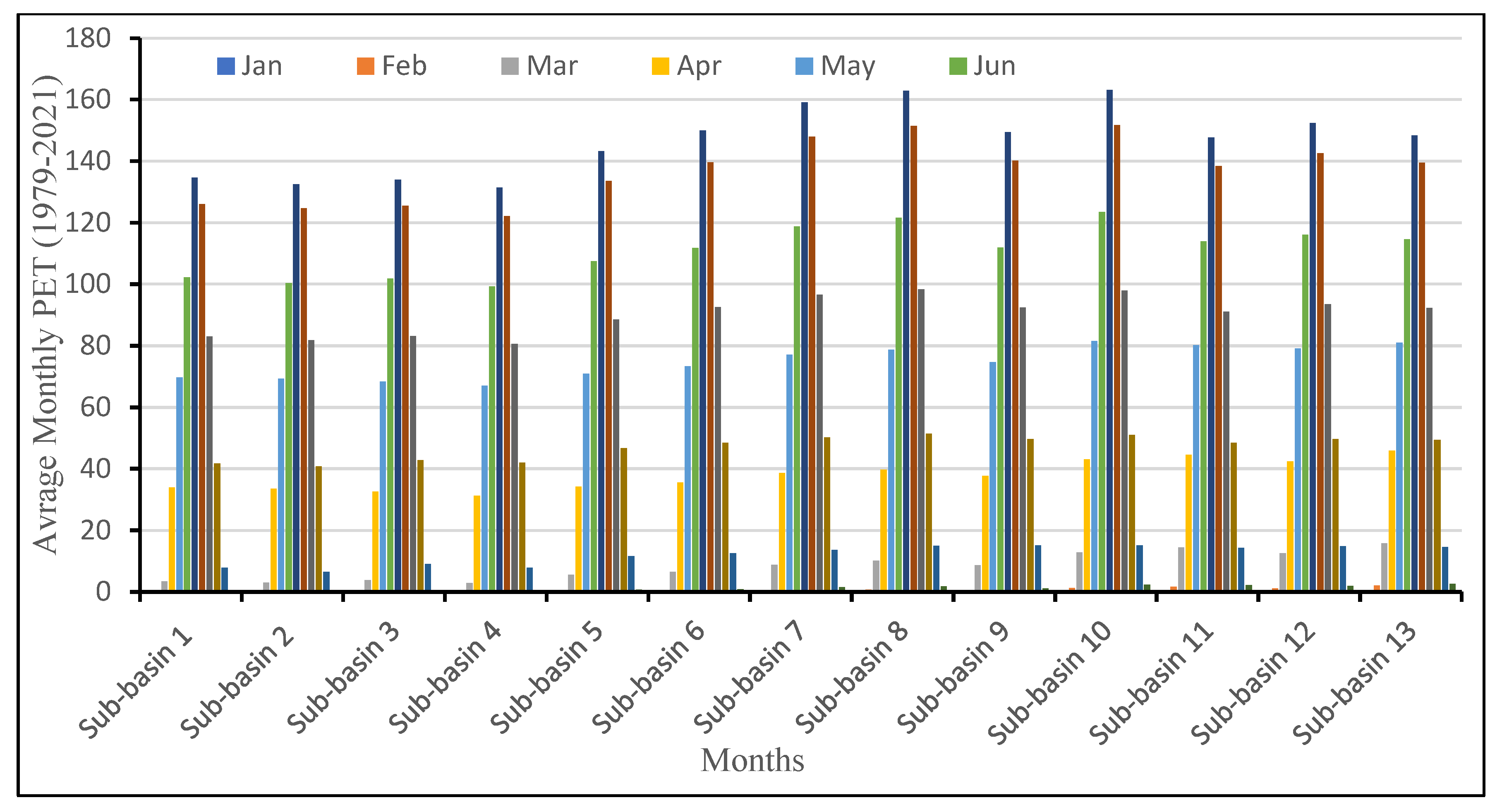
4.1. PET Calculated with the Thornthwaite Equation
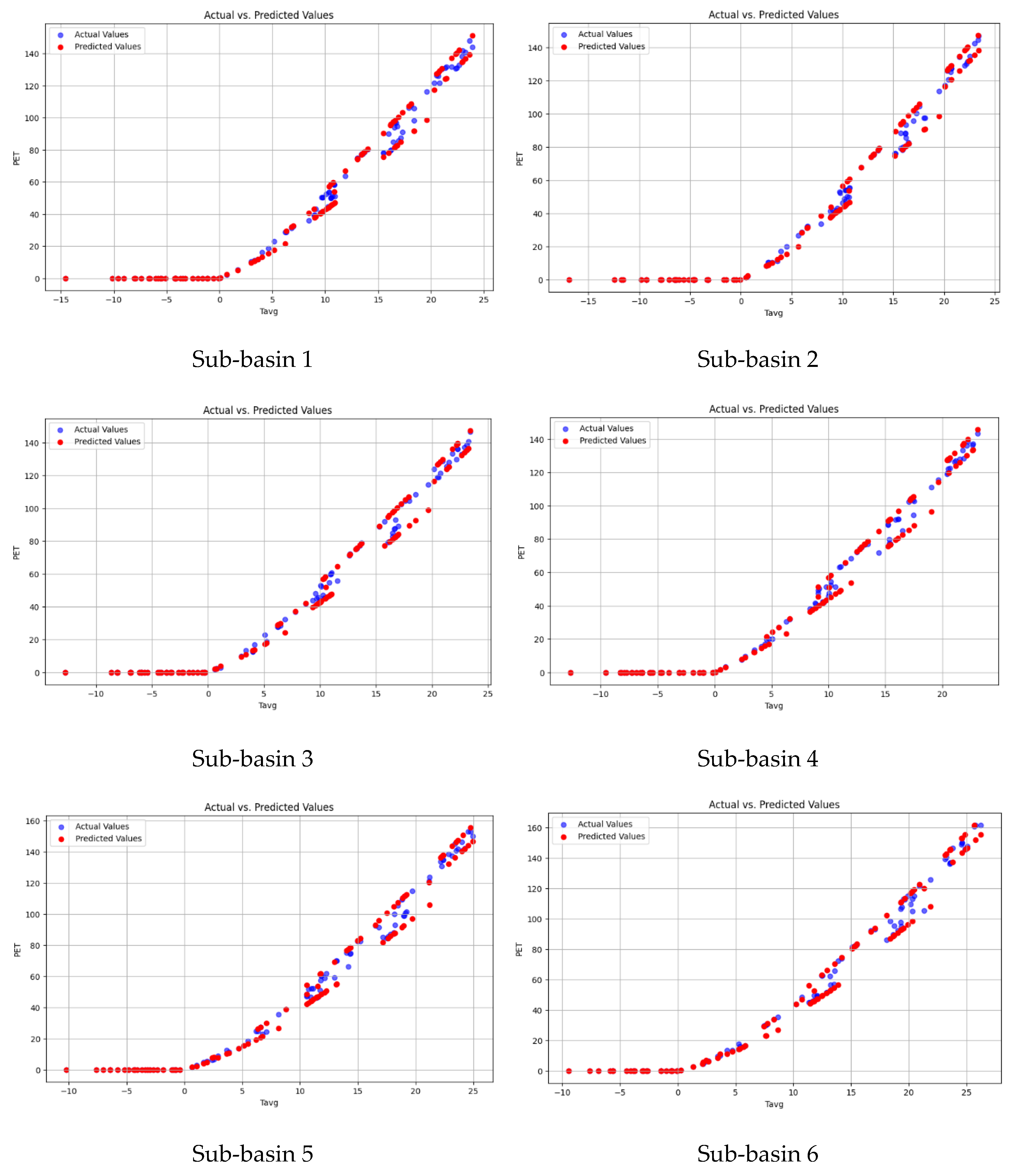
4.2. PET Prediction via CNN
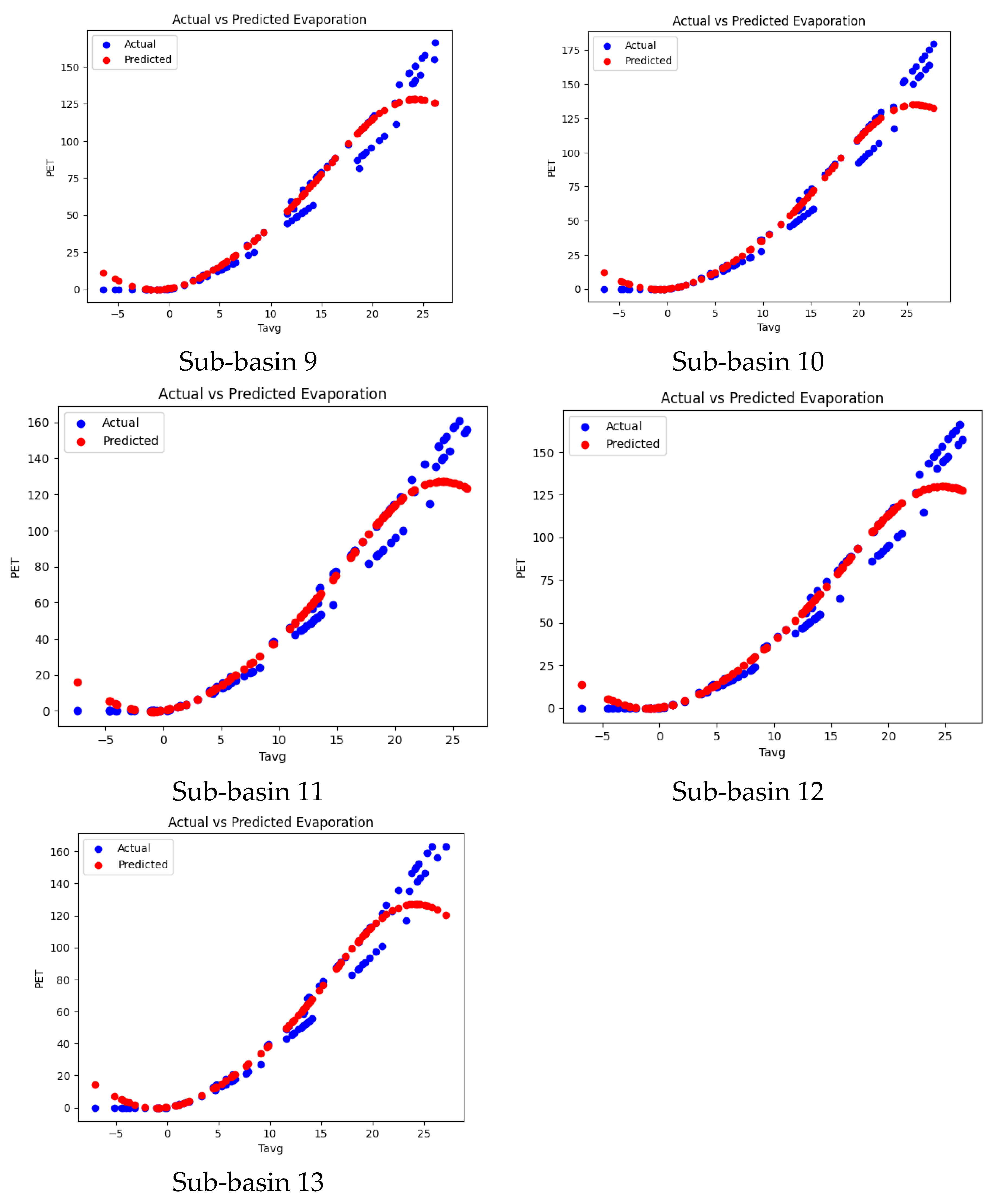
4.3. PET Prediction via SVM
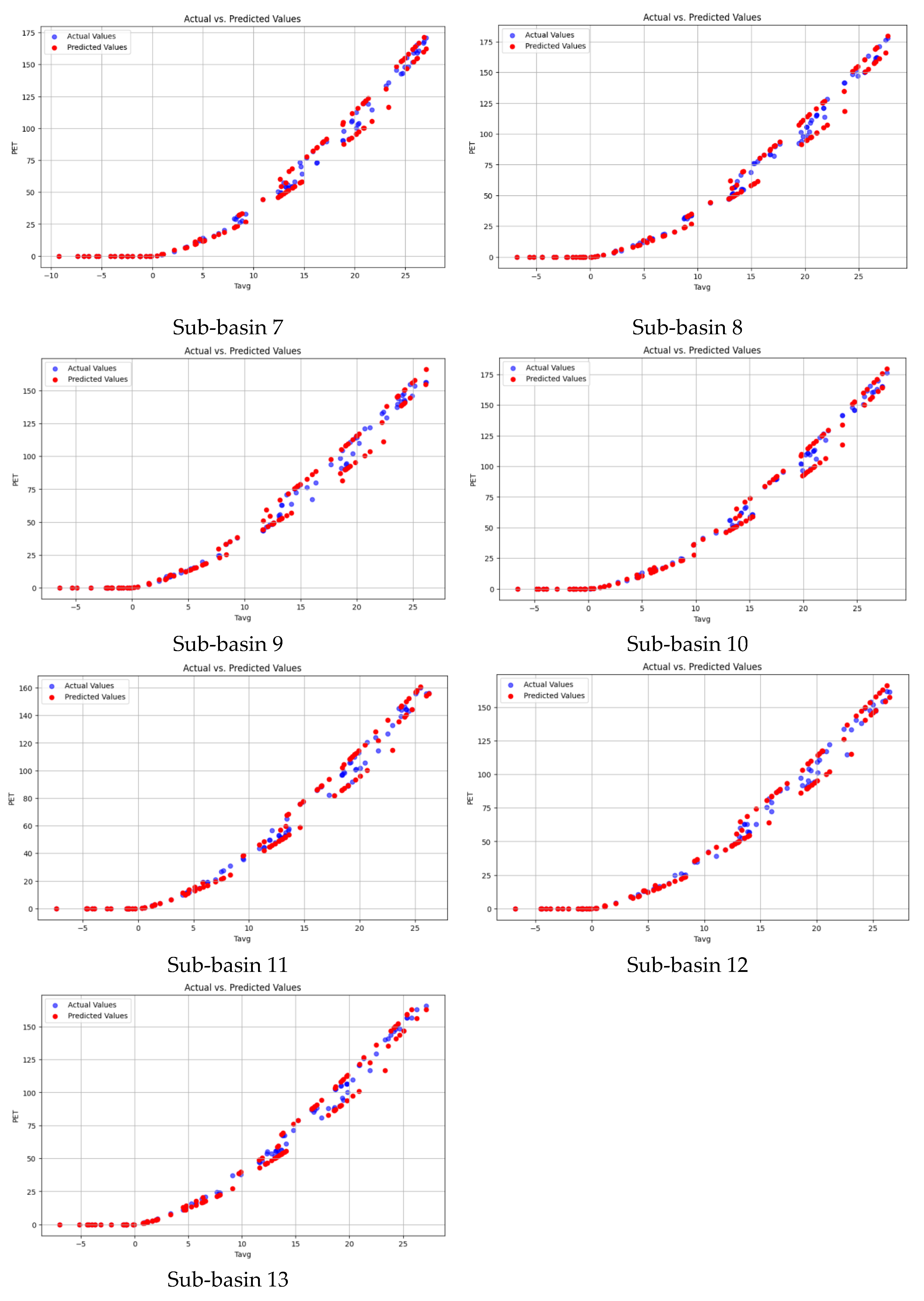
4.4. PET Prediction via RF
4.5. Performance of the Models
5. Conclusion
References
- Wood, E. F. , Su, H. , McCabe, M., & Su, B. (2003). Estimating evaporation from satellite remote sensing. Paper presented at the IGARSS 2003. 2003 IEEE International Geoscience and Remote Sensing Symposium. Proceedings (IEEE Cat. No. 03CH37477). [Google Scholar]
- Jing, W. , Yaseen, Z. M., Shahid, S., Saggi, M. K., Tao, H., Kisi, O.,... Chau, K.-W. Implementation of evolutionary computing models for reference evapotranspiration modeling: short review, assessment, and possible future research directions. Engineering applications of computational fluid mechanics 2019, 13, 811–823. [Google Scholar] [CrossRef]
- Raman, J. , Kim, J.-S., Choi, K. R., Eun, H., Yang, D., Ko, Y.-J., & Kim, S.-J. Application of lactic acid bacteria (LAB) in sustainable agriculture: Advantages and limitations. International Journal of Molecular Sciences 2022, 23, 7784. [Google Scholar] [PubMed]
- Pelosi, A. , Villani, P., Falanga Bolognesi, S., Chirico, G. B., & D’Urso, G. Predicting crop evapotranspiration by integrating ground and remote sensors with air temperature forecasts. Sensors 2020, 20, 1740. [Google Scholar]
- Penman, H. L. Natural evaporation from open water, bare soil, and grass. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences 1948, 193, 120–145. [Google Scholar]
- Shuttleworth, W. (1993). Evaporation Handbook of Hydrology ed DR Maidment. In: New York: McGraw-Hill) pp.
- Allen, R. G. , Clemmens, A. J., Burt, C. M., Solomon, K., & O’Halloran, T. Prediction accuracy for projectwide evapotranspiration using crop coefficients and reference evapotranspiration. Journal of irrigation and drainage engineering 2005, 131, 24–36. [Google Scholar]
- Aschonitis, V. , Touloumidis, D., ten Veldhuis, M.-C., & Coenders-Gerrits, M. Correcting Thornthwaite potential evapotranspiration using a global grid of local coefficients to support temperature-based estimations of reference evapotranspiration and aridity indices. Earth System Science Data 2022, 14, 163–177. [Google Scholar]
- Brutsaert, W. Global land surface evaporation trend during the past half-century: Corroboration by Clausius-Clapeyron scaling. Advances in Water Resources 2017, 106, 3–5. [Google Scholar] [CrossRef]
- Bouchet, R. (1963). Evapotranspiration reelle, evapotranspiration potentielle, et production agricole. Paper presented at the Annales agronomiques.
- Thornthwaite, C. W. An approach toward a rational classification of climate. Geographical Review 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Ahmadi, F. , Mehdizadeh, S., Mohammadi, B., Pham, Q. B., Doan, T. N. C., & Vo, N. D. Application of an artificial intelligence technique enhanced with intelligent water drops for monthly reference evapotranspiration estimation. Agricultural Water Management 2021, 244, 106622. [Google Scholar]
- Fahimi, F. , Yaseen, Z. M., & El-Shafie, A. Application of soft computing based hybrid models in hydrological variables modeling: a comprehensive review. Theoretical and applied climatology 2017, 128, 875–903. [Google Scholar]
- Mehr, A. D. , Nourani, V., Kahya, E., Hrnjica, B., Sattar, A. M., & Yaseen, Z. M. Genetic programming in water resources engineering: A state-of-the-art review. Journal of Hydrology 2018, 566, 643–667. [Google Scholar]
- Shahbazi, A. N. , Zahraie, B., & Nasseri, M. (2012). Seasonal meteorological drought prediction using support vector machine.
- Chen, Z. , Sun, S., Wang, Y., Wang, Q., & Zhang, X. Temporal convolution-network-based models for modeling maize evapotranspiration under mulched drip irrigation. Computers and electronics in agriculture 2020, 169, 105206. [Google Scholar]
- Hassan, M. A. , Khalil, A., Kaseb, S., & Kassem, M. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Applied Energy 2017, 203, 897–916. [Google Scholar]
- Papadopoulos, S. , Azar, E., Woon, W.-L., & Kontokosta, C. E. Evaluation of tree-based ensemble learning algorithms for building energy performance estimation. Journal of Building Performance Simulation 2018, 11, 322–332. [Google Scholar]
- Granata, F. , & Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agricultural Water Management 2021, 255, 107040. [Google Scholar]
- Deng, L. , & Yu, D. Deep learning: methods and applications. Foundations and trends® in signal processing 2014, 7, 197–387. [Google Scholar]
- Fattah, W. H. , & IMi, Y. Hydrological analysis of Murat river basin. International Journal of Applied 2015, 5, 47–55. [Google Scholar]
- Terakawa, A. (2003). Hydrological data management: Present state and trends: Secretariat of the World Meteorological Organization.
- Naoum, S. , & Tsanis, I. Ranking spatial interpolation techniques using a GIS-based DSS. Global Nest 2004, 6, 1–20. [Google Scholar]
- Chai, H. , Cheng, W., Zhou, C., Chen, X., Ma, X., & Zhao, S. Analysis and comparison of spatial interpolation methods for temperature data in Xinjiang Uygur Autonomous Region, China. Natural Science 2011, 3, 999. [Google Scholar]
- Anggraini, N. , & Slamet, B. (2021). Thornthwaite Models for Estimating Potential Evapotranspiration in Medan City. Paper presented at the IOP Conference Series: Earth and Environmental Science. [Google Scholar]
- Azman, R. , Noor, N., Abdullah, S., & Ideris, M. Analysis of Drought Index in Sub-Urban Area Using Standard Precipitation Evapotranspiration Index (SPEI). International Journal of Integrated Engineering 2022, 14, 157–163. [Google Scholar]
- Kim, S.-J. , Bae, S.-J., & Jang, M.-W. Linear regression machine learning algorithms for estimating reference evapotranspiration using limited climate data. Sustainability 2022, 14, 11674. [Google Scholar]
- Pramanik, M. , Chowdhury, K., Rana, M. J., Bisht, P., Pal, R., Szabo, S., Pal, I., Behera, B., Liang, Q., Padmadas, S. S., & Udmale, P. Climatic influence on the magnitude of COVID-19 outbreak: a stochastic model-based global analysis. International Journal of Environmental Health Research 2022, 32. [Google Scholar] [CrossRef]
- Wang, Q. , Ma, Y., Zhao, K., & Tian, Y. A Comprehensive Survey of Loss Functions in Machine Learning. Annals of Data Science 2022, 9. [Google Scholar] [CrossRef]
- Tian, Y. , Su, D., Lauria, S., & Liu, X. (2022). Recent advances in loss functions in deep learning for computer vision. In Neurocomputing (Vol. 497). [CrossRef]
- Lee, J. K. , Rouault, M., & Wyart, V. Adaptive tuning of human learning and choice variability to unexpected uncertainty. Science Advances 2023, 9. [Google Scholar] [CrossRef]
- Liu, S. , & Zhou, D. J. Using cross-validation methods to select time series models: Promises and pitfalls. British Journal of Mathematical and Statistical Psychology 2024, 77. [Google Scholar] [CrossRef]
- Siva, G. Matrix variate receiver operating characteristic curve for binary classification. Statistics 2024, 58. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Machine learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lazar, J. , Feng, J. H., & Hochheiser, H. (2017). Research methods in human-computer interaction: Morgan Kaufmann.
- Brito, L. C. , Pecanha, T. , Fecchio, R. Y., Rezende, R. A., Sousa, P., Silva-Junior, D.,... Halliwill, J. R. Morning versus evening aerobic training effects on blood pressure in treated hypertension. Medicine and science in sports and exercise 2019, 51, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Feng, F. , Tuomi, M., Jones, H. R., Barnes, J., Anglada-Escude, G., Vogt, S. S., & Butler, R. P. Color difference makes a difference: four planet candidates around τ ceti. The Astronomical Journal 2017, 154, 135. [Google Scholar]
- Yaseen, Z. M. , Al-Juboori, A. M., Beyaztas, U., Al-Ansari, N., Chau, K.-W., Qi, C.,... Shahid, S. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Engineering applications of computational fluid mechanics 2020, 14, 70–89. [Google Scholar] [CrossRef]
- Lee, Y. C. , Christensen, J. J., Parnell, L. D., Smith, C. E., Shao, J., McKeown, N. M., Ordovás, J. M., & Lai, C. Q. Using Machine Learning to Predict Obesity Based on Genome-Wide and Epigenome-Wide Gene–Gene and Gene–Diet Interactions. Frontiers in Genetics 2022, 12. [Google Scholar] [CrossRef]
- Wald, N. J. , & Bestwick, J. P. Is the area under an ROC curve a valid measure of the performance of a screening or diagnostic test? Journal of Medical Screening 2014, 21. [Google Scholar] [CrossRef]
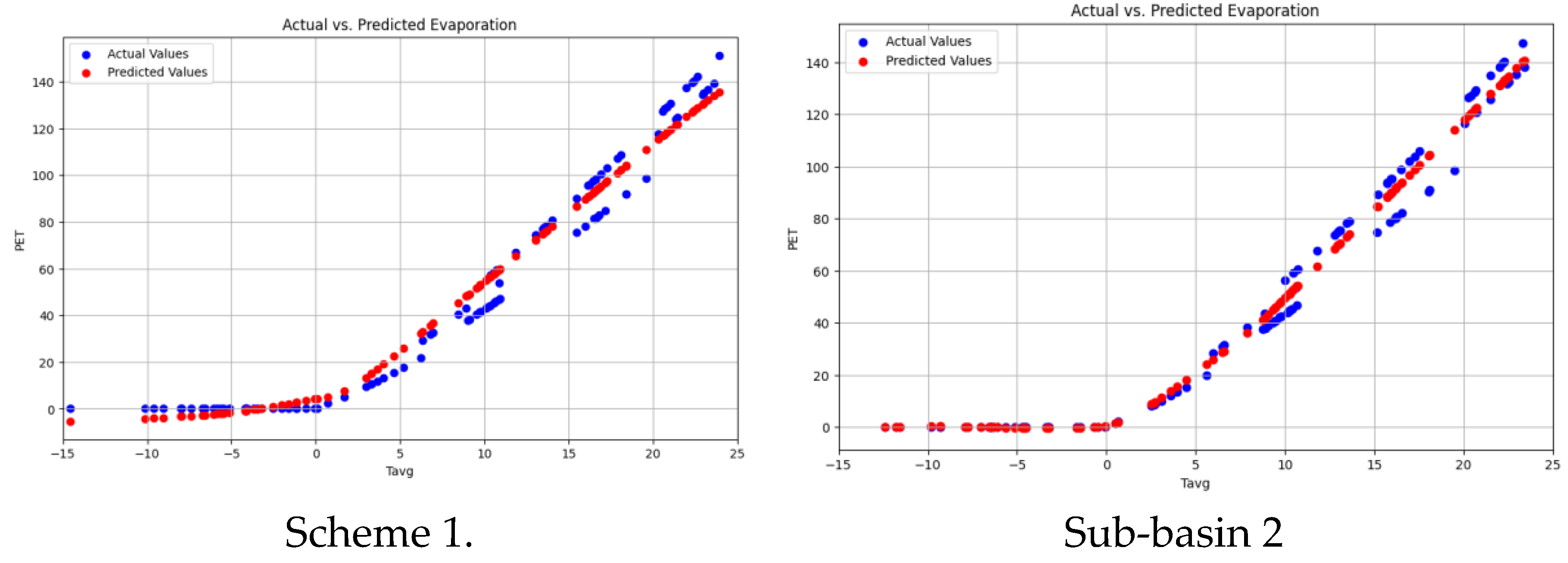
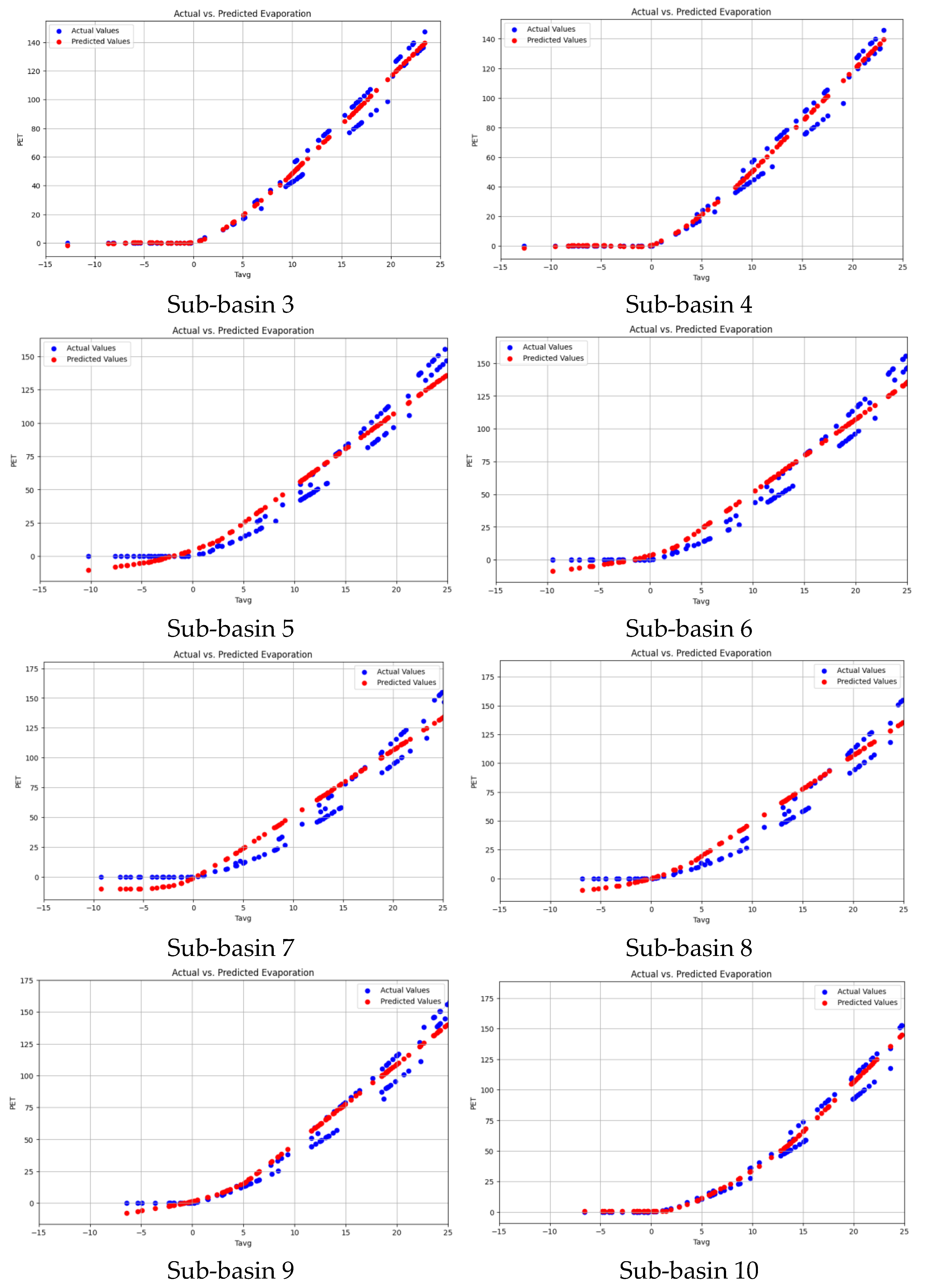
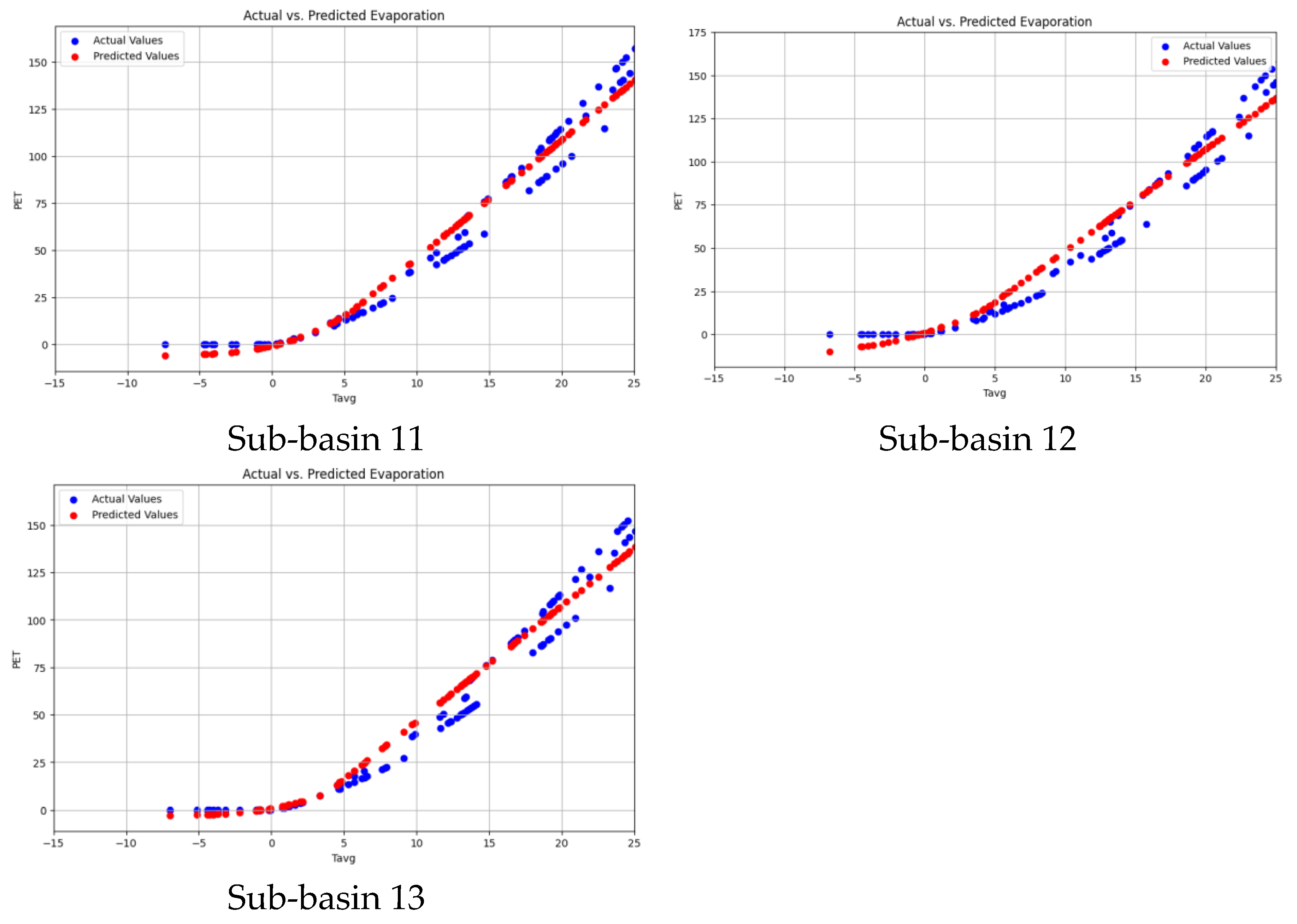
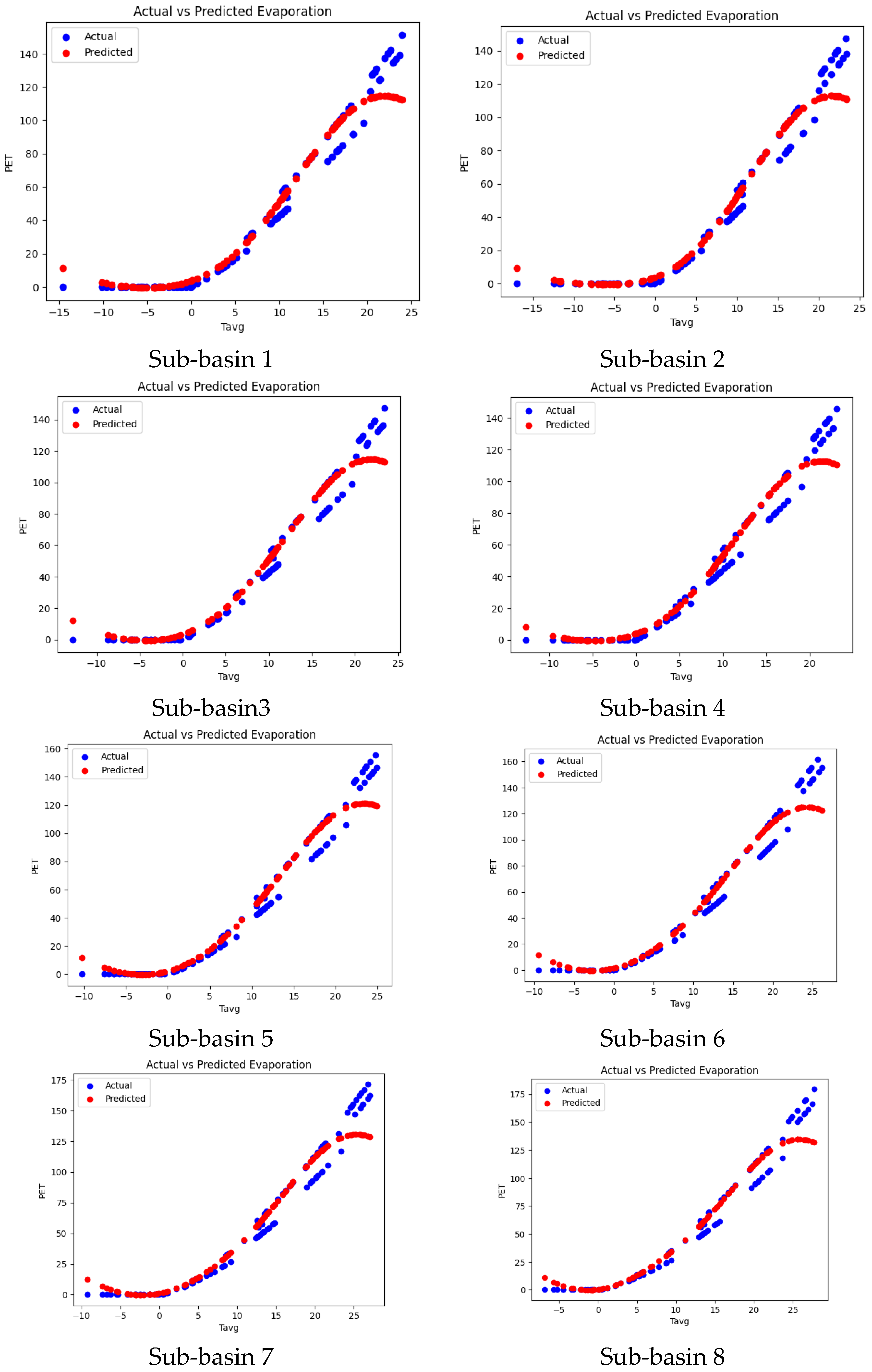
| SN | Station Name | Latitude | Longitude |
|---|---|---|---|
| 17099 | Ağrı | 39.7253 | 43.0522 |
| 17720 | Doğubeyazit | 39.5396 | 44.018 |
| 17203 | Bingöl | 38.8847 | 40.5007 |
| 17776 | Solhan | 38.9597 | 41.0503 |
| 17808 | Genç | 38.7477 | 40.5528 |
| 18176 | Kığı | 39.3086 | 40.3458 |
| 17205 | Tatvan | 38.5033 | 42.2808 |
| 17208 | Bitlis | 38.475 | 42.1625 |
| 17810 | Ahlat | 38.7487 | 42.475 |
| 17094 | Erzincan | 39.7523 | 39.4868 |
| 17718 | Tezcan | 39.7769 | 40.3906 |
| 17096 | Erzurum Havalimanı | 39.9529 | 41.1897 |
| 17666 | İspir | 40.4861 | 40.9996 |
| 17668 | Oltu | 40.5497 | 41.9951 |
| 17688 | Tortum | 40.3013 | 41.5409 |
| 17690 | Horasan | 40.0415 | 42.173 |
| 17740 | Hınıs | 39.3688 | 41.6957 |
| 17100 | Iğdır | 39.9227 | 44.0523 |
| 17097 | Kars | 40.6061 | 43.1119 |
| 17656 | Arpaçay | 40.8431 | 43.3278 |
| 17692 | Sarıkamış | 40.3329 | 42.5983 |
| 17204 | Muş | 38.7509 | 41.5023 |
| 17734 | Divriği | 39.3618 | 38.1142 |
| 17762 | Kangal | 39.2428 | 37.389 |
| 17172 | Van Bölge | 38.4693 | 43.346 |
| 17784 | Erciş | 39.0198 | 43.3386 |
| 17812 | Özalp | 38.6573 | 43.9767 |
| 17852 | Gevaş | 38.2963 | 43.1197 |
| 17880 | Başkale | 38.0435 | 44.0173 |
| Sub-basins | Area | Eff. Weight | Met. Stations |
|---|---|---|---|
| Sub-Basin 1 | 2957 | 0.68 | AĞRI |
| 0.11 | ERCİŞ | ||
| 0.21 | DOĞUBEYAZİT | ||
| Sub-Basin 2 | 1601 | 0.63 | AĞRI |
| 0.37 | HORASAN | ||
| Sub-Basin 3 | 5989 | 0.45 | AĞRI |
| 0.14 | ERCİŞ | ||
| 0.11 | HORASAN | ||
| 0.3 | AHLAT | ||
| Sub-Basin 4 | 3176 | 0.88 | HINIS |
| 0.07 | HORASAN | ||
| 0.05 | AHLAT | ||
| Sub-Basin 5 | 4047 | 0.32 | HINIS |
| 0.22 | MUŞ | ||
| 0.23 | AHLAT | ||
| 0.23 | SOLHAN | ||
| Sub-Basin 6 | 2259 | 0.53 | MUŞ |
| 0.47 | BITLIS | ||
| Sub-Basin 7 | 2437 | 0.18 | MUŞ |
| 0.65 | SOLHAN | ||
| 0.17 | GENÇ | ||
| Sub-Basin 8 | 2320 | 0.36 | SOLHAN |
| 0.08 | KIĞI | ||
| 0.56 | BİNGÖL | ||
| Sub-Basin 9 | 5836 | 0.1 | SOLHAN |
| 0.73 | KIĞI | ||
| 0.17 | BİNGÖL | ||
| Sub-Basin 10 | 2839 | 0.1 | GENÇ |
| 0.64 | BİNGÖL | ||
| 0.26 | ERZICAN | ||
| Sub-Basin 11 | 4039 | 0.84 | ERZICAN |
| 0.16 | KIĞI | ||
| Sub-Basin 12 | 137 | 0.28 | BİNGÖL |
| 0.47 | ERZICAN | ||
| 0.25 | KIĞI | ||
| Sub-Basin 13 | 3058 | 0.29 | DIVRIĞI |
| 0.71 | ERZICAN |
| Algorithms | Sub-basin 1 | Sub-basin 2 | Sub-basin 3 | Sub-basin 4 | Sub-basin 5 | Sub-basin 6 | Sub-basin 7 | Sub-basin 8 | Sub-basin 9 | Sub-basin 10 | Sub-basin 11 | Sub-basin 12 | Sub-basin 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | CNN | 0.962 | 0.987 | 0.987 | 0.987 | 0.962 | 0.975 | 0.987 | 0.975 | 0.984 | 0.986 | 0.986 | 0.986 | 0.985 |
| SVM | 0.954 | 0.954 | 0.956 | 0.956 | 0.953 | 0.950 | 0.945 | 0.945 | 0.954 | 0.945 | 0.953 | 0.953 | 0.948 | |
| RF | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| MSE | CNN | 0.293 | 0.287 | 0.309 | 0.277 | 0.345 | 0.353 | 0.405 | 0.422 | 0.408 | 0.400 | 0.377 | 0.376 | 0.387 |
| SVM | 0.375 | 0.348 | 0.287 | 0.267 | 0.484 | 0.661 | 0.981 | 1.028 | 0.548 | 1.013 | 0.527 | 0.610 | 0.680 | |
| RF | 0.409 | 0.326 | 0.389 | 0.338 | 0.439 | 0.407 | 0.485 | 0.640 | 0.605 | 0.412 | 0.331 | 0.439 | 0.385 | |
| RMSE | CNN | 0.541 | 0.536 | 0.556 | 0.526 | 0.587 | 0.594 | 0.637 | 0.649 | 0.639 | 0.632 | 0.614 | 0.613 | 0.622 |
| SVM | 0.612 | 0.590 | 0.536 | 0.517 | 0.696 | 0.813 | 0.990 | 1.014 | 0.740 | 1.006 | 0.726 | 0.781 | 0.825 | |
| RF | 0.640 | 0.571 | 0.624 | 0.582 | 0.663 | 0.638 | 0.696 | 0.800 | 0.778 | 0.642 | 0.575 | 0.663 | 0.621 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





