Application of Thermodynamic Methods to the Study of Plant Biomass and its Components – A Review

1. Basics of Chemical Thermodynamics

Chemical thermodynamics is an interdisciplinary science that combines thermodynamics, physical chemistry, statistical and chemical physics, and some other scientific areas. The main tasks of chemical thermodynamics are to determine thermodynamic functions, study the transformations of various forms of energy during chemical reactions and phase transitions, predict the feasibility and direction of chemical processes, and study the ability of chemical systems to perform useful work [1,2]. A section of chemical thermodynamics is thermochemistry, which studies the thermal effects of chemical reactions and physicochemical processes.

Chemical thermodynamics considers isolated, closed, and open systems. In an isolated system, there is no exchange of energy and matter with the external environment. In a closed system, there is no exchange of matter, but energy exchange with the external environment is carried out. In an open system, the exchange of both matter and energy with the external environment is possible.

There are also laws of thermodynamics. The zeroth law of thermodynamics states that an isolated thermodynamic system spontaneously passes over time into a state of thermodynamic equilibrium.

The first law of thermodynamics states that the heat received by a system from outside is used to increase the internal energy of the system and to perform work by this system.

According to the second law of thermodynamics, heat or thermal energy cannot spontaneously pass from a cooler body to a hotter body. Another formulation of the second thermodynamic law is as follows: in a nonequilibrium isolated system, entropy increases and reaches a maximum when thermodynamic equilibrium is established. The consequence of the second law is that a perpetual motion machine of the second kind is impossible.

The third law of thermodynamics states that the entropy of any equilibrium system, as the temperature approaches absolute zero, ceases to depend on any state parameters and tends to a certain limit close to zero. Moreover, all processes near absolute zero that transfer the system from one equilibrium state to another occur without changing the entropy.

Chemical thermodynamics operates with several terms, parameters, and thermodynamic functions such as temperature (T), pressure (P), volume (V), work (A), heat (Q), kinetic energy (E_k), internal energy (U), enthalpy (H), entropy (S), free energy or potential of Helmholtz (F) and Gibbs (G), etc.

In the case of an isolated system, the change in internal energy is zero: ΔU=0.

For a reaction occurring in closed or open systems at constant temperature and volume, the thermal effect (∆Q) of this reaction is equal to the change in the internal energy (∆U) of the system, i.e.,

∆Q = ∆U,

(1)

If a reaction occurs in an open system at constant temperature and pressure, then from the first law of thermodynamics it follows:

∆Q = ∆U + Р∆V = (U₂ + PV₂) - (U₁ + PV₁),

(2)

Denoting U + PV = H, where H is called enthalpy, we obtain:

∆Q = ∆Н,

(3)

Thus, in an open system at P=const, the thermal effect of the reaction is equal to the enthalpy change.

As a result of a chemical reaction, enthalpy can decrease (∆_rН < 0) when heat is released, or increase (∆_rН > 0) when heat is absorbed from outside. According to the Lavoisier-Laplace law, the thermal effect of a forward reaction is always equal to the thermal effect of a reverse reaction with the opposite sign. The second law of thermochemistry, proposed by Hess, states that the thermal effect of a reaction depends only on the initial and final state and does not depend on the intermediate stages of the reaction. There is also another formulation of this law, namely: if a chemical process occurs in several stages, then the overall thermal effect of the process is equal to the algebraic sum of the thermal effects of the individual, intermediate stages.

Two important consequences follow from Hess's law. Firstly. The thermal effect of a chemical reaction (∆_rН) is equal to the difference between the sums of the combustion enthalpies (∆_cН_r) of the starting reagents and the combustion enthalpies (∆_cН_p) of the reaction products, taking into account their stoichiometric coefficients:

∆_rН = ∑n_r ∆_cН_r - ∑n_p ∆_cН_p,

(4)

Secondly. The thermal effect of a chemical reaction is equal to the difference between the sums of the formation enthalpies (∆_fН_p) of the reaction products and the formation enthalpies (∆_fН_r) of the starting reagents, taking into account their stoichiometric coefficients.

∆_rН = ∑n_p ∆_fН_p - ∑n_r ∆_fН_r,

(5)

Numerical values of standard formation enthalpy for various substances under standard conditions (T_o=298.15 K, P_o = 0.1 MPa) are given in reference books.

The concept of entropy was first introduced by Rudolf Clausius in the late 19th century. Entropy is considered a function of the state of a thermodynamic system, related to the reduced thermal energy:

S = Q/T,

(6)

From the second law of thermodynamics, it follows that the spontaneous transfer of heat from a hotter region to a colder one is determined by the increase in the entropy of the system.

According to the Ludwig Boltzmann concept, entropy is a function of system state, characterizing the degree of statistical disorder (W) in the arrangement of elements of a system, ions, atoms, molecules, etc.:

S = R lnW,

(7)

If at Р = constant the temperature rises, then the disorder in the arrangement of atoms or molecules increases, which leads to an increase in the entropy, namely:

∆S = C_p ln(T₂/T₁),

(8)

where C_p is the specific heat capacity; and T₂ >T₁.

If the open system at Р = const is in equilibrium state, then the following equality is true:

∆Н = T∆S,

(9)

For example, at equilibrium between liquid and vapor at T_c, the change in entropy during vapor condensation (∆S_c) can be calculated if the condensation enthalpy (∆Н_c) is known:

∆S_c = ∆Н_c/T_c,

(10)

Similarly, one can find the change in entropy during melting at T_m of a crystalline substance:

∆S_m = ∆Н_m/T_m,

(11)

If a chemical reaction occurs, the change in entropy can be found using an equation similar to the Hess equation:

∆_rS = ∑n_p S_p - ∑n_r S_r,

(12)

where S_p and S_r are entropy values for obtaining products and starting reagents, respectively.

Numerical values of standard entropy for various substances under standard conditions (T_o=298.15 K, P_o = 0.1 MPa) are given in reference books.

Chemical thermodynamics can be also used to predict the feasibility and direction of chemical processes. For this purpose, special thermodynamic functions of the system state are used, which reflect the influence of two factors on the process, energy and entropy. These special thermodynamic functions have the property that their sign is a criterion for the feasibility or non-feasibility of a spontaneous reaction.

For isothermal reactions occurring at constant volume, such a function is the Helmholtz free energy, which is calculated using the equation:

∆_rF = ∆_rU - T∆_rS,

(13)

In the case of isothermal reactions occurring at constant pressure, a criterion for the feasibility of a spontaneous reaction is the Gibbs free energy or potential. The change in the Gibbs potential during the reaction is determined by the equation:

∆_rG = ∆_rH - T∆_rS.

(14)

These special thermodynamic functions characterize the degree of non-equilibrium of the reaction system. The more negative their values are, the greater the deviation of the system from equilibrium and the greater the probability of the reaction being feasible. The feasibility of a reaction is facilitated by a decrease in the internal energy or enthalpy and an increase in the disorder of the system, characterized by the entropy factor.

Thus, the criterion for the feasibility of a reaction in systems at constant volume is ∆_rF< 0. This can happen in the following cases:

∆_rU< 0, while ∆_rS > 0,

∆_rU >0, and ∆_rS >0, but T∆_rS >∆_rU,

∆_rU< 0, while ∆_rS< 0, but [∆_rU] > [T∆_rS]

For open systems proceeding at constant pressure, the criterion for reaction feasibility is ∆_rG < 0. This can happen when:

∆_rH< 0, while ∆_rS >0

∆_rH >0, and ∆_rS >0, but T∆_rS >∆_rH

∆_rH< 0, while ∆_rS< 0, but [∆_rH] > [T∆_rS]

If the reaction is reversible and an equilibrium is established between the forward and reverse reactions, such an equilibrium is characterized by a constant K_eq. According to Van't Hoff, the equilibrium constant of a chemical reaction is an exponential function of the thermodynamic potential:

at V = const, K_eq = EXP (-∆_rF/RT ),

(15)

at P= const, K_eq = EXP (-∆_rG/RT),

(16)

Vice versa, if the value of the equilibrium constant is known, then the thermodynamic potential of the reversible reaction can be calculated, as follows:

at V= const, ∆_rF = -RT lnK_eq,

(17)

at P= const, ∆_rG = -RT lnK_eq,

(18)

To describe the state of the multi-component system with a variable number of different components, a partial thermodynamic function of a component called chemical potential is used:

μ_k = (δG/δN_k)_{T, P, k ≠ i},

(19)

Such a function determines the change in thermodynamic potential when the number of components in the system changes. The importance of chemical potential is that one of the conditions of equilibrium in a system is the equality of the chemical potential of any component of the system in different phases and at different points of one phase. This function is widely used in physical chemistry to study the processes of dissolution, sorption, etc. For example, for a solution in equilibrium state at P and T = const, the following relationship exists:

Δμ_s = RT ln(P_s/P_o),

(20)

where P_s is the vapor pressure of the solvent above the solution, and P_o is the vapor pressure of the pure solvent.

If P_s < P_o the Δμ_s < 0, which is a criterion for good compatibility between the solvent and the polymer.

Thermodynamic analysis of nanoscale particles must take into account a great specific surface area (S_sp) of such particles and its change in various processes:

∆G_n = σV_m ΔS_sp,

(21)

where σ is the specific surface energy of particles; V_m is the molar volume.

Such nanoparticles tend to aggregate, which is thermodynamically favorable since this process leads to a decrease in the specific surface area (ΔS_sp < 0) and provides the negative value of the thermodynamic potential (∆G_n < 0).

Another example is the Gibbs-Thomson equation, according to which the melting point decreases with decreasing size of nanocrystallites. It was found that ∆G_n depends on the temperature change, as follows: ∆G_n = Δ_mH (ΔT/T_m). On the other hand, for nano- particles ΔS_sp = 4/L. Substituting the right parts of ∆G_n and ΔS_sp into eq. (21), the Gibbs-Thomson equation can be obtained:

T_n = T_m (1 - 4 σV_m/(L Δ_mH)),

(22)

where T_n and T_m are the melting points of nano-crystallites and macrocrystals, L is the size of nano-crystallite, and Δ_mH is the melting enthalpy.

2. Methods for Determining the Thermodynamic Characteristics of Substances

Values of standard thermodynamic functions (TDFs), such as the standard formation enthalpy (Δ_fH^o) and entropy (S^o), for various substances, can be found in reference books. However, if reference data is not available, the values of these TDFs are determined experimentally. The standard formation enthalpy of an organic substance C_xH_yO_z can be calculated from the experimentally determined combustion enthalpy (Δ_cH^o) of this substance at standard conditions (T_o=298.15 K, P=0.1 MPa). The combustion process of the substance is:

C_xH_yO_z + (x + 0.25y - 0.5z) O₂ → x CO₂ + 0.5y H₂O + Δ_cH^o(C_xH_yO_z),

The standard formation enthalpy of this substance can be calculated, as follows:

Δ_fH^o(C_xH_yO_z) = x Δ_fH^o(CO₂, g) + 0.5y Δ_fH^o(H₂O, l) - Δ_cH^o(C_xH_yO_z),

(23)

where Δ_fH^o(CO₂, g) = -393.51 kJ/mol and Δ_fH^o(H₂O, l) = -285.83 kJ/mol are standard enthalpies of the formation of carbon dioxide and liquid water, respectively.

Precision oxygen bomb calorimeters of various designs can be used to burn samples [3]. Typically, it consists of a strong stainless-steel bomb, which is placed in a water calorimeter. A small sample (0.5-1 g) is put in a crucible inside the bomb and 1 ml of water is added. Oxygen is pumped into the bomb to provide a pressure of 2.5 to 3 MPa. After temperature equilibrium is established, the sample is ignited, the temperature rise is measured with an accuracy of ±0.001 K, and the combustion enthalpy is calculated. The true mass of the used sample is determined from the mass of the produced CO₂. The corrections for ignition and forming of acid traces should be made. To adjust the enthalpy of combustion to standard conditions (T_o=298.15 K, P=0.1 MPa) the Washburn correction, as well as the correction for the change in the number of moles of gases before and after combustion are introduced. For each sample, several experiments are performed to obtain a reliable value of the combustion enthalpy and standard deviation.

To measure the specific heat capacity (C_p) of the dry sample, a scanning adiabatic vacuum calorimeter is used [3,4]. The experiments usually are carried out in the temperature range of 80-340 K. Below 80 K, C_p values can be estimated by the method of Kelly, et al. [5]. The accuracy of C_p determination is ±0.005 J/mol K. For each sample, several experiments should be performed to find the reliable C_p value and standard deviation.

The entropy value of the sample at temperature T is calculated, as follows:

$$\mathrm{S}\left(\mathrm{T}\right)={\int }_0^T\left({\displaystyle \frac{\mathrm{C}\mathrm{p}}{\mathrm{T}}}\right)\mathrm{dT},$$

(24)

If T is the standard temperature, T_o = 298.15 K, then the result of the calculation is the standard entropy of the sample, S^o.

Along with the bomb calorimeter and the scanning adiabatic calorimeter, other types of calorimeters are also used to study the thermochemical properties of samples. For example, to measure the enthalpy of sample wetting and dissolution, isothermal or adiabatic calorimeters, as well as microcalorimeters can be applied [6,7].

For example, to determine the wetting enthalpy of cellulose, a small sample (ca 1 g) is prepared. Before starting experiments, the air-dry sample is weighed into a special glass ampoule and dried in a vacuum at 378 K to a constant weight. The glass ampoule containing the dry sample is sealed and introduced into the calorimetric cell filled with distilled water. The calorimeter is thermostated at 298.15 K to achieve an equilibrium state. Thereafter, the sealed ampoule with the dry sample is broken to ensure that the sample is wetted with water. The released exothermic heat effect of wetting is measured with accuracy ±0.01 J. Several of the same samples usually are tested to calculate an average enthalpy value and standard deviation.

In addition to calorimetry, several other methods can be used to characterize samples. These methods may include X-ray scattering, NMR, FTIR-spectroscopy, DTA, electron microscopy, sorption, etc. [8,9,10,11].

This review article will show how thermochemical methods can be applied to the study of plant biomass and its main components, cellulose, hemicelluloses, lignin, etc. Considerable attention will be paid to the thermodynamics of physicochemical and chemical transformations of cellulose and nanocellulose, as well as other components of plant biomass. The thermodynamics of second solid, liquid, and gaseous biofuels released from the initial biomass was also considered.

3. Thermochemistry of Plant Biomass

There are many applications of chemical thermodynamics to various substances and diverse reaction classes (synthesis, decomposition, substitution, exchange, oxidation, reduction, etc.). Currently, due to the depletion of fossil fuel reserves and the harm that their use causes to the environment, much attention is paid to the use of renewable natural resources, including plant biomass.

The existence and further development of the present civilization require expanded consumption of energy, chemicals, and materials. Nowadays, the main energy sources are still fossil fuels, namely coal, petroleum, and natural gas [12]. However, the increased use of fossil fuels is causing acute environmental problems, since the combustion of such fuels is accompanied by the emission of carbon dioxide triggering the greenhouse effect and global warming.

An additional problem is that fossil resources are not reproduced in nature. Therefore, their reserves are exhausted and run down in an essentially permanent manner [13]. To eliminate the imbalance in the fossil sources, an increased utilization of alternative sources of energy and raw materials is required. Considerable attention in recent years has been given to plant biomass, which in contrast to fossil sources is continuously renewed in nature [14].

The total resources of plant biomass reach 1.5 trillion tons [15]. The potential resources of biomass among alternative and renewable energy sources is above 70% [16], while its share in the production of alternative energy exceeds 50% [17]. Despite advances in solar and wind energy, in many countries plant biomass still accounts for a significant share of energy production [17]. So in Africa, up to 60% of energy is generated from biomass. East Asia countries and China receive up to 25% of energy from biomass, while in Latin America, the share of biomass energy is 18%. Only in the USA, the European Union, and other developed regions and countries, the share of biomass in energy production is small and does not exceed 3%.

The plant biomass is formed in nature from carbon dioxide and water by photosynthesis absorbing solar energy. When the plant biomass is burned, it releases the accumulated solar energy in the form of heat, along with the release of used water and carbon dioxide stored in the biomass. Therefore, plant biomass is considered a CO₂-neutral source of renewable energy [17,18].

Currently implemented technologies for the production of liquid biofuels are based on the transformation of carbohydrates into bioethanol and vegetable oils into biodiesel fuel. The main sources of these carbohydrates are juices of sugarcane, sugar beet, and sweet sorghum, as well as starches of corn, wheat, potatoes, and some other agricultural plants. Since these carbohydrates and vegetable oils are required in the food industry, their use for the production of biofuels is limited. Moreover, further expansion of the production to a higher volume of bioethanol and/or biodiesel will cause a shortage of land areas, exhaustion of the soil, excessive consumption of water and energy, deficits of food and feed products, and increase their prices [19].

An alternative way to obtain biofuels without competing with the food and feed industry is the use of inedible biomass, which is an abundant, renewable, and inexpensive plant material. This biomass type involves energy crops (e.g., miscanthus, switchgrass, Bermuda grass, etc.), forest residues (e.g., sawdust, twigs, shrubs, etc.), residues of agricultural plants (e.g. stalks, husks, cobs, etc.), residues of textile, pulp, and paper, municipal paper waste, etc. Moreover, huge amounts of algae can be used as appropriate feedstock for the production of bioenergy or chemicals. The total resources of inedible biomass accumulated annually are estimated at 10 billion tons, the combustion of which could potentially generate about 150 EJ of bio-energy [20].

The main components of plant biomass are cellulose, hemicelluloses, and lignin (Table 1).

Cellulose is a linear, stereoregular, semicrystalline polysaccharide consisting of anhydroglucose units (AGUs) having a “chair” conformation and linked to each other in long macromolecules by chemical β-1,4-glycosidic bonds in a head-to-tail manner [16,22,23,24,25]. Macromolecules of natural cellulose from various origins may include 2,000 to 30,000 AGUs. During the process of cellulose isolation from plant materials and cellulose modification, partial depolymerization of the macromolecules is observed. Each AGU of cellulose contains three hydroxyl functional groups: one primary and two secondary groups. Hydroxyl groups of adjacent chains are linked by strong hydrogen bonds, which leads to the formation of thread-like elementary nanofibrils and their bundles, called microfibrils, which contain nanocrystallites and non-crystalline domains. Besides, hydroxyl groups can be replaced by various substituents, resulting in the formation of cellulose derivatives, such as ethers, esters, etc. [26,27].

Hemicelluloses are highly amorphous heteropolysaccharides [16,22,23,28,29]. In the cell walls of plant fibers, hemicelluloses fulfill the function of binder between cellulose fibrils and lignin. The chemical structure of hemicelluloses consists of chains of a variety of pentoses or hexoses units. Various plants and also its tissues contain different types of hemicelluloses. Agricultural and herbaceous plants, as well as hardwoods, contain mainly xylan, pentosan-type hemicellulose, while softwoods are enriched with mannan, which is hexosan-type hemicellulose. Hemicelluloses are heteropolymers. Xylan, for example, can be present in the form of glucuronoxylan (in hardwoods) or arabinoxylan (in grasses and grains), while mannan presents in the form of glucomannan (in softwoods) or galactomannan (in carob tree). The polysaccharide complex of biomass containing cellulose and hemicelluloses is called holocellulose.

Lignin is an aromatic, amorphous, and hydrophobic polymer [16,22,23,30,31]. It is a complex biopolymer of phenylpropane units, which are linked to each other with a variety of different chemical bonds with the formation three-dimensional network. Due to such structural organization, lignin is resistant to some chemical reagents and enzymes. This biopolymer consists of three main phenylpropane units such as guaiacyl (G), syringyl (S), and hydroxyphenyl (H). The relative ratios of these units can vary for different biomass sources. Lignin of softwoods is mainly of G-type, whereas lignin of hardwoods contains a mixture of G-and S-units. Lignin of herbaceous plants consists usually of all three types of phenylpropane units.

In addition to the main components, biomasses may contain inorganic substances (ash), organic extractives (lipids, waxes, and resins), starch, pectin, etc. If the initial biomass is subjected to chemical, physicochemical, or biological treatment, its chemical composition changes.

The chemical composition directly affects the calorific value of biomass. Increased content of lignin, lipids, resins, and waxes contributes to achieving a high calorific value of biomass [22,23,32]. This is due to the increased value of combustion enthalpy of lignin, Δ_cH from -25 to -26 MJ/kg [33] compared with polysaccharides, Δ_cH from -17.4 to -17.6 MJ/kg [3]. In addition, extractive substances of biomass, lipids, waxes, and resins have Δ_cH from -36 to -38 MJ/kg [20,34,35,36], which is much higher than that combustion enthalpy of polymeric components of the biomass, lignin, and polysaccharides.

Numerous experiments on measuring the combustion enthalpy or gross heating value (GHV) have shown that for dry wood samples of different species, the difference in the calorific values is small [37,38]. Softwood samples have an average value of Δ_cH = -20.5 MJ/kg, while hardwood samples have an average value of Δ_cH = -19.7 MJ/kg [38] (Table 2). Forest residues have a lower GHV with Δ_cH = -18.8 MJ/kg [39]. The calorific value of biomass of cereal crops and herbaceous plants turned out to be lower than that of woody biomass [20,40]. The lowest GHV was observed for paper waste containing a large amount of inorganic fillers [20,22,23], while olive samples having increased content of lignin and lipids are distinguished by quite high value of combustion enthalpy (Table 2).

There are several known methods for extracting energy from biomass. The most well-known method is the use of biomass as solid biofuel. In addition, biomass can be a feedstock for obtaining secondary biofuels from it, such as biochar, bio-oil, bioethanol, biodiesel, and biogas.

However, the direct use of biomass as a solid fuel raises several problems. The initial biomass is a non-dense and heterogeneous material consisting of pieces of various sizes [18]. Moreover, it can contain moisture and inorganic substances. These features of the initial biomass worsen its fuel properties, since moisture and inorganic admixtures decrease the calorific value, and the low bulk density of the initial biomass declines the density of thermal energy, which significantly reduces the productivity of furnaces.

To improve the fuel performance, the initial biomass should be demineralized, dried, and densified into briquets and pellets [41,42,43,44,45]. For example, it was shown that the initial unpressed Switchgrass biomass has unsatisfactory characteristics: bulk density, BD = 98 kg/m³, and thermal energy density, ED = 1.8 GJ/m³, while after pelletization these features increased 5 times [46]. When plastic waste is used as a binder, these features of the pelletized solid biofuel increase by 8 times, which is also accompanied by a rise in the GHV of the pellets.

Along with experimental methods, numerous attempts have been made to calculate the combustion heat of biomass. The most common approach is to use several correlation equations to calculate the calorific value of each type of biomass [32,33,47,48,49,50]. For the calculation, diverse variables were used such as ash content and moisture; individual biomass components, such as lignin; volatile matter and fixed carbon; various physical properties, etc. In addition, correlation equations based on the determination of the elemental composition of biomass were proposed [47,51,52,53]. However, since the amount of plant biomass species is unlimited, the number of correlation equations can also be unlimited. In addition, the articles [32,33,47] do not provide a critical analysis of the various mathematical models and correlation equations, so it is impossible to identify the equation that is best suited for specific biomass types. Analyzing calculation results of GHV for various biomasses [32,48], Park and co-authors [50] concluded that the discrepancies between calculations and experimental data are high, over 10%.

To improve the accuracy of calculations, it is necessary to use another method than finding correlations with some randomly selected biomass characteristics. In our studies, we used a method based on the rule of additive contributions [20]:

Δ_cH = 0.01 ∑ C_i Δ_cH _i,

(25)

where C_i is the percentage content of components (see e.g., Table 3); Δ_cH _i is GHV of the component of the biomass (Table 4).

The results revealed that the calculation method based on the rule of additive contributions gives values of combustion enthalpy for biomass samples that are very close to the experimental data (Table 3). More detailed studies have shown that the average deviation between calculated and experimental results does not exceed 3% [54].

Based on the carbon content [20,47,49], it can be calculated that burning 1 ton of plant biomass will release an average of 900 m³ of carbon dioxide, which is half the volume of this greenhouse gas produced by burning 1 ton of such solid fossil fuel as coal.

4. Thermal Energy Potential of Secondary Biofuels

Plant biomass is also a feedstock for producing secondary biofuels, such as biochar, bio-oil, and biogas. For this purpose, the initial biomass is pyrolyzed, i.e. subjected to heat treatment in the absence or lack of oxygen [16,22,55,56].

Slow pyrolysis of biomass is carried out with a heating rate below 60 degrees/min at temperatures of about 500^oC and residence time of 10-20 min with the formation of biochar, bio-oil, and biogas in approximately the same amounts. If slow pyrolysis is processed at high temperatures, from 600 to 1000^oC, then strong gasification of biomass with a predominant hydrogen fraction occurs [57,58]. Hydrothermal gasification of biomass, especially in the presence of a catalyst, significantly increases the hydrogen content in biogas.

Fast pyrolysis is performed at temperatures from 500 to 650^oC for short contact time. This pyrolysis type produces usually 60% bio-oil, 20% biochar, and 20% biogas.

In addition, flash pyrolysis is known, proceeding at temperatures higher than 650^oC with a contact time of less than 1 sec. The main product of flash pyrolysis is biogas.

It was found that biochar has GHV ca -27 MJ/kg [22]. The bio-oil is a dark and thick liquid containing a complex mixture of water and various organic substances (tar, hydrocarbons, furan derivatives, aldehydes, ketones, phenols, organic acids, methanol, etc.) with GHV ca -16 MJ/kg [22].

The biogas is a mixture, containing CO₂, CO, H₂, and CH₄, with a GHV ca -10 MJ/m³ [16,22]. This biogas is formed as a result of the following processes [16]:

1).

Oxidation of biochar at increased temperature

C + 0.5 O₂ → CO with Δ_rH (T) = -103.9 kJ/mol

C + O₂ → CO₂ with Δ_rH (T) = -370.1 kJ/mol

2).

Reduction reactions of gases at increased temperature

C + CO₂ $\leftrightarrow$ 2CO with Δ_rH (T) = 162.4 kJ/mol

C + H₂O $\leftrightarrow$ CO + H₂ with Δ_rH (T) = 131.9 kJ/mol

CO + H₂O $\leftrightarrow$ CO₂ + H₂ with Δ_rH (T) = -30.5 kJ/mol

C + 2H₂ $\leftrightarrow$ CH₄ with Δ_rH (T) = -65 kJ/mol

The average gasification temperature is 800^oC or 1073 K [57,58]. Therefore, instead of the standard enthalpies of reactions, Δ_rH^o, at 298.15 K, the enthalpies of these reactions, Δ_rH (T), at a temperature of T = 1073 K should be used. The calculated values of Δ_rH (T) are shown near the equation of the corresponding reaction.

To implement endothermic reactions that have positive values of reaction enthalpy, they must absorb thermal energy from the outside. Exothermic reactions can occur spontaneously without heat absorption from the outside, but often a temperature rise is necessary to increase the rate of such reactions.

Using slow pyrolysis of 100 kg woody biomass, the following yield of secondary biofuel was determined: 30 kg biochar, 18.1 kg bio-oil, and 14 m³ biogas [59]. It can be calculated that the total content of thermal energy (TEC) of such biofuel will be TEC = - 1.24 GJ, which is only 62% of the thermal energy content in 100 kg initial biomass equal to -2 GJ.

Another study [57] found that the yield of biogas after the gasification of pine wood was ca 37 m³ from 100 kg of wood. In this case, the TEC of such biogas volume does not exceed 20% of the TEC in 100 kg initial wood.

Biogas enriched with methane can be obtained by anaerobic digestion [60]. This process is performed at a pH 6-7 under the action of mesophilic bacteria at a temperature of 30-40 °C or thermophilic bacteria at a temperature of 50-60 °C. As a feedstock for biogas production, MSW, waste paper, residue of pulp and paper, agricultural waste, etc. can be used [16,60,61]. Lignocellulosic biomass is pretreated to loosen its physical structure and reduce the content of lignin hindering the bioconversion process. The pretreated biomass is diluted with water to prepare aqueous dispersion for anaerobic digestion.

The process of anaerobic biodegradation of organic substances usually takes 3 - 4 weeks and occurs in several stages. In the first stage, called hydrolysis, the complex organic molecules (СM) break down into simple molecules (SM). At the second stage, called acidogenesis, deeper biodegradation occurs with the release of volatile products and the formation of carboxylic acids (CA). In the third stage, called acetogenesis, simple molecules and carboxylic acids are converted to acetic acid (AA). In the last stage, called methanogenesis, acetic acid is converted to biogas (BG) containing mainly methane and carbon dioxide.

Thus, the anaerobic digestion process of biomass can be expressed, as follows:

CM → SM → CA → AA → BG

For example, in the first stage, cellulose and other C6-polysaccharides split into monomeric glucose (GL). Further, glucose forms carboxylic acids and acetic acid, which is transformed into biogas.

-(C₆ H₁₀O₅-)_n + n H₂O → nС₆H₁₂O₆

nС₆H₁₂O₆ → 3n CH₃COOH

3n CH₃COOH → 3n CH₄ + 3n CO₂

Total process: -(C₆H₁₀O₅-)_n + n H₂O → 3n CH₄ + 3n CO₂

The theoretical yield of this biogas from 1 t cellulose is 830 m³ and their thermal energy content TEC = -14.9 GJ, ca 86% from the TEC of initial cellulosic feedstock with TEC = - 17.4 GJ. However, due to increased cellulose crystallinity, the actual yield of biogas and its TEC from cellulose are 1.5 - 2 times lower than the theoretical values. An even lower biogas yield is observed during the anaerobic digestion of lignocellulosic raw materials.

To extract energy from plant biomass, it can be also hydrolyzed and transformed into monosaccharides, mainly glucose, followed by fermentation to produce bioethanol.

Features of the enzymatic hydrolysis of various plant materials have been discussed in many studies [62,63,64,65,66]. To implement the effective hydrolysis of biomass, enzyme preparations were used, which include at least three types of specific enzymes, such as endo-1,4-β-glucanases, exo-1,4-β-glucanases, and β-glucosidases. These enzymes act synergistically because endo-acting enzymes generate new chain ends for the exo-acting enzymes, which release the oligosaccharides that are converted into glucose by β-glucosidases [64].

The enzymatic hydrolysis of biomass is usually carried out at a temperature of 50 °C and pH 5 using a dose of enzyme preparation of 10 to 40 mg of protein per 1 g of substrate. It has been found that to achieve maximum glucose concentration during enzymatic hydrolysis, the optimal loading of the cellulose-containing substrate in the aqueous enzyme system should be at least 150 g/L [62,63,64]. At a higher substrate loading, enzymatic hydrolysis ceases due to a significant reduction in the mass transfer and inhibition of cellulolytic enzymes by a large amount of formed glucose [67].

In addition, it was established that the initial plant biomass exhibits high resistance to enzymatic cleavage due to the compact structure of the plant material and the presence of lignin and other non-cellulosic components hindering the hydrolysis process. Therefore, the plant biomass is pretreated to loosen its physical structure, eliminate non-cellulosic components, and increase cellulose accessibility to cellulolytic enzyme molecules. To reduce biomass recalcitrance, various pretreatment methods can be used such as steam explosion, acid hydrolysis, alkaline extraction, oxidation, and combined methods [68,69,70,71,72,73,74]. After the acidic pretreatment of the biomass, predominantly hemicelluloses are removed, which leads to an increase in the cello-lignin content. During alkaline and oxidative pretreatments, partial removal of hemicelluloses and lignin from the biomass occurs, which is accompanied by an increase in the cellulose content in the pretreated biomass and a reduction of biomass recalcitrance to enzymatic hydrolysis.

Combined pretreatment methods are considered the most effective for removing non-cellulosic components from biomass and improving enzymatic hydrolyzability. For example, 1 kg of switchgrass biomass was treated with dilute nitric acid and then with dilute alkali solution [46]. The result was 410 g of cellulose-enriched pre-treated biomass (PTB). After enzymatic hydrolysis of PTB, 320 g of glucose was obtained. In the fermentation stage, glucose produces 163 g bioethanol with a thermal energy content of TEC = -4.9 MJ, which however is only 27% of the TEC in 1 kg initial biomass equal to -18.3 MJ.

Special plant types containing vegetable oil are well known such as soybeans, rapeseed, olives, sunflower, palms, etc. However, these oil plants are in demand in the food industry, and their use for energy production is limited. For this purpose, it is desirable to use non-edible lipid sources such as camelina, jatropha, pongamia legume, crabapple, jojoba, castor oil plant, tung, algae, etc. Tall oil and waste cooking and frying oils are considered suitable feedstocks for biofuel production.

Though vegetable oils, technical oils, and other lipids have a high calorific value (-35 to -40 MJ/kg), they are less suitable as diesel fuel due to relatively low cetane number, low volatility, high flash point, and increased viscosity [22]. To improve fuel characteristics, lipids are subjected to transesterification. This process is carried out by reacting triglycerides (TGL) of lipids with alcohols, usually with methanol (MET), in the presence of catalysts. The final products are glycerol (GL) and ester of methanol and fatty acid (e.g. linoleic acid) used as a biodiesel fuel (BDF):

C₃H₅(O₂CR)₃ + 3CH₃OH → 3RCO₂CH₃ + C₃H₅(OH)₃

The glycerol fraction is separated from biodiesel fuel and the excess alcohol is removed by distillation or partial evaporation [16].

The following standard formation enthalpies were found or determined from combustion enthalpies of the starting reagents and products of this reaction (Table 5).

Using values of standard enthalpies, the enthalpy of the transesterification reaction was calculated as follows:

Δ_rH^o = Δ_fH^o(GL) + 3Δ_fH^o(BDF) - Δ_fH^o(TGL) - 3Δ_fH^o(MET),

(26)

As a result, it was found that the enthalpy of transesterification reaction Δ_rH^o = -363 kJ/mol. Thus, this reaction is exothermic and can proceed spontaneously without a temperature increase. However, to speed up the process, it is heated to 50-70^oC [16,75].

As with other types of biofuels, the TEC of biodiesel fuel can be also compared to the TEC of initial feedstock. Let's say, for example, that the source of vegetable oil is fallen olive fruits. From one ton of these fruits, 230 kg of oil can be extracted and subjected to transesterification. The calculations showed that the resulting biodiesel fuel will have a thermal energy content TEC= -7.4 GJ, which is however significantly less than the amount of energy TEC= -26. 1 GJ that can be obtained by burning 1 ton of fallen olives.

Although biomass is considered CO₂ neutral and the secondary biofuels extracted from it are CO₂ tolerant, the increasing greenhouse effect requires a reduction in CO₂ concentration in the atmosphere. Therefore, the process of converting carbon dioxide into biomethane, known as the Sabatier reaction, has attracted considerable attention [76,77].

The Sabatier reaction is expressed by the following equation:

CO₂ + 4H₂ ⇌ CH₄ + 2H₂O

Thus, it is the hydrogenation process of carbon dioxide. However, at normal or slightly increased temperatures and pressures, the rate of direct reaction probable is negligible, and the process is shifted to the left. To ensure the conversion of CO₂ to CH₄, the reaction should be carried out at elevated temperatures and pressures in the presence of a catalyst [78,79,80]. Studies have shown that a high yield of synthetic methane, over 90% of the theoretical yield. can be achieved if the reaction temperature is about 400^oC (673.15 K) and the pressure is about 3 MPa [79]. As catalysts, Ni and Ru on alumina and some others are used [76,80].

The Sabatier reaction most likely occurs in two stages. In the first stage, carbon dioxide is reduced with hydrogen to carbon monoxide, and in the second stage, carbon monoxide is converted to methane.

CO₂ + H₂ ⇌ CO + H₂O Δ_rH^o = 41.2 kJ/mol

CO + 3H₂ ⇌ CH₄ + H₂O Δ_rH^o = -206.2 kJ/mol

Total: CO₂ + 4H₂ ⇌ CH₄ + 2H₂O Δ_rH^o = -165 kJ/mol

It was found that the Sabatier reaction is exothermic [76]. Several references also indicated that the standard enthalpy of the Sabatier reaction, Δ_rH^o = -165 kJ/mol CH₄ when formed water is in the gaseous (vapor) state [76,81,82,83,84,85,86]. The standard Gibbs potential of this reaction was also estimated [85]. Unfortunately, in the case, when the formed water vapor condenses into liquid, the calculation of the standard enthalpy and Gibbs potential of the reaction was not performed. However, thermodynamic analysis requires calculating three thermodynamic functions, enthalpy, entropy, and Gibbs potential, not only for standard temperature and pressure but also for real conditions occurring at high temperature and pressure. For this purpose, a complete thermodynamic analysis of the Sabatier reaction was carried out under standard and real reaction conditions [87].

Using reference books, the standard enthalpies of formation (Δ_fH^o) and the standard enthalpies (S^o) for reagents and products of the Sabatier reaction were found (Table 6) and used for further calculations.

Thermodynamic analysis in the case of the gaseous (vapor) phase state of the formed water

The standard enthalpy of the Sabatier reaction was calculated using the equation:

Δ_rH^o(g) = Δ_fH^o(CH₄, g) + 2Δ_fH^o(H₂O, g) - Δ_fH^o(CO₂, g) - 4Δ_fH^o(H₂, g),

(27)

Similarly, the standard entropy of this reaction was calculated, as follows:

Δ_rS^o(g) = S^o(CH₄, g) + 2S^o(H₂O, g) - S^o(CO₂, g) - 4S^o(H₂, g),

(28)

In addition, the Gibbs potential of the reaction was found:

Δ_rG^o(g) = Δ_rH^o(g) -T_o Δ_rS^o(g),

(29)

where T_o = 298.15 K is the standard temperature.

Substituting the values of the required TDFs of reagents and products from Table 6 into these equations, the standard TDFs of the Sabatier reaction were obtained (Table 7).

Thermodynamic analysis in the case of the liquid phase state of the formed water

The calculations were performed using similar equations with the difference that standard TDF of liquid (l) water was used instead of gaseous (g) water.

The calculation results are presented in Table 7. When the resulting water is liquid, the exothermic thermal effect of the reaction is higher than in the case of gaseous water. The same relationship is observed for the Gibbs potential of the Sabatier reaction. A more negative value of the Gibbs potential means that the process that forms liquid water is more favorable than the process that produces gaseous water (vapor).

Despite the negative value of the Gibbs potential, the process of carbon dioxide hydrogenation under standard conditions, T_o= 298.15 K and P_o = 0.1 MPa, cannot be implemented, due to kinetic limitations [80]. As the temperature rises, the reaction rate increases, especially in the presence of a catalyst [76,78,79,80]. In addition, the elevation of pressure shifts the equilibrium of the reaction to the right and increases the methane yield [85,86].

Thermodynamic analysis of catalyzed Sabatier reaction at high temperatures and pressures

These calculations were carried out for real conditions of the Sabatier reaction, T_r = 673.15 K and P_r = 3 MPa in the catalyst presence, when the reaction rate is high enough to ensure a high yield of the formed methane. Under these conditions, the water is in a gaseous phase state. As is known, enthalpy is almost independent of pressure and the main influence on the enthalpy value is exerted by temperature. The enthalpy value of a gaseous substance at pressure P_r and temperature T_r can be found using the following equation:

$$\mathsf{\Delta }\mathrm{H}({\mathrm{P}}_{\mathrm{r}},{\mathrm{T}}_{\mathrm{r}})=\mathsf{\Delta }{\mathrm{H}}^{\mathrm{o}}\left(\mathrm{g}\right)+{\int }_{To}^{Tr}CpdT,$$

(30)

Unlike enthalpy, the entropy depends on both pressure and temperature. The value of enthalpy at pressure P_r = 3 MPa and standard temperature T_o = 298.15 K was calculated using the equation:

S(P_r,T_o) = S^o(g) - R ln(P_r/P_o),

(31)

where standard pressure P_o=0.1 MPa, and R=8.3145 (J/mol K) is the gas constant.

The calculated values of S(P_r,T_o) at P_r = 3 MPa for the studied substances are shown in Table 8.

Further, the entropy value of the gaseous substance at pressure P_r and temperature T_r was calculated, as follows:

$$\mathrm{S}({\mathrm{P}}_{\mathrm{r}},{\mathrm{T}}_{\mathrm{r}})=\mathrm{S}({\mathrm{P}}_{\mathrm{r}},{\mathrm{T}}_{\mathrm{o}})+{\int }_{To}^{Tr}Cp/TdT,$$

(32)

where C_p is the specific heat capacity of gaseous reagents and products.

The calculation results of TDFs are shown in Table 9.

Using these TDFs of gaseous substances, the enthalpy, entropy, and Gibbs potential of the Sabatier reaction at high temperature and pressure were obtained [87] (Table 10).

These results showed that the Sabatier reaction is highly exothermic also at increased temperature and pressure, while reaction entropy is negative. In addition, the Gibbs potential under these conditions is negative. Thus, the process of methane synthesis from carbon dioxide and hydrogen at elevated temperature T_r = 673.15 K and pressure P_r =3 MPa is energetically and thermodynamically favorable. Using the Van 't Hoff equation, it was found that the equilibrium constant of the reaction K_eq is 2.04 x 10³ [87]. Such a value of the equilibrium constant indicates that under real conditions the equilibrium of the Sabatier reaction is shifted to the right with the formation of methane and water vapor.

Calculations also showed that heating a compressed initial gas mixture from T_o to T_r requires the expenditure of 61.1 kJ/mol of thermal energy, which is 3 times less than the thermal energy released by the exothermic Sabatier reaction.

The Sabatier process continues to be improved. New designs of CO₂ hydrogenation reactors with an improved heat exchange have been proposed [76,83,88]. In addition, more efficient catalytic systems and the removal of resulting water vapor allow for optimization of reaction conditions and enhance methane yield [76,80,88,89]. The thermal energy of the Sabatier process can be utilized to heat the initial gas mixture and electrolyze water [90]. Moreover, constructions are being developed that combine a CO₂ hydrogenation reactor with a fuel combustion furnace [76], an electrolyzer [76,90], or an electrochemical cell [81,82].

5. Thermodynamic Characteristics for Main Components of Biomass

5.1. Thermodynamic Characteristics of Cellulose Samples

Standard combustion enthalpies (Δ_cH^o) of various semicrystalline cellulose I_β samples, including cellulose isolated from wood, cotton, bast cellulose fibers, and some other biomass types, were determined in [3,7,20,49,54,91,92,93,94]. It was established that the Δ_cH^o value of these samples varies within small limits of ± 0.08 MJ/kg and its average value is Δ_cH^o_av -17.41 MJ/kg or -2820.42 kJ/mol. Then, according to eq. (23), we can calculate that the standard enthalpy of cellulose formation is, on average Δ_fH^o_av = -969.79 kJ/mol. However, detailed studies have shown, that there is still a small but significant difference in the thermodynamic characteristics between cellulose I_β samples with different crystallinity [20].

Crystallinity is an important structural characteristic of cellulose, determining a complex of its physical, physiochemical, and chemical properties such as specific gravity, heat capacity, thermal expansion coefficient, sorption properties, hydrolyzability, etc. [24]. However, there is a problem associated with the lack of an accurate method for determining the degree of crystallinity of cellulose. There are only approximate methods for estimating the so-called crystallinity index (CrI) [11,95,96,97,98]. Moreover, different methods such as wide-angle X-ray scattering (WAXS), solid-state ¹³C-NMR, FTIR, Raman spectroscopy, etc. give different CrI values for the same cellulose sample; therefore, it is not clear which value of CrI should be preferred [99,100,101]. Even the same method, e.g., WAXS, also gives different CrI values for the same sample if different measurement techniques were used to separate X-ray scattering from the crystalline and amorphous domains [95,96,101]. For example, using different WAXS techniques, it was found that the CrI of the MCC Avicel sample varies from 49 to 82%, while the CrI of the cotton linter ranges from 55 to 87% [101].

Large discrepancies in the values of CrI when they are estimated by different methods or different measurement techniques of the same method are due to the use of different calculation equations, mathematical and structural models, and software. Secondly, this is due to the different experimental conditions of different methods. In addition, there are no standard protocols for preparing cellulose samples to determine their crystallinity. Thus, it is impossible to conclude which of the currently used methods and/or techniques for measuring cellulose crystallinity is the most suitable [101].

Therefore, a new method that works on other principles is advisable to develop. In our studies, a thermochemical method was proposed based on measuring the enthalpy of wetting (Δ_wH^o) of various cellulose samples [8,102]. It has been established that the interaction of cellulose with liquid water is accompanied by an exothermic thermal effect, i.e., the enthalpy of wetting. The higher the degree of amorphousness of the sample, the greater the exothermic value of the enthalpy of wetting [102]. As a result, the degrees of amorphicity (Y) and crystallinity (X) of cellulose samples were determined by a direct thermochemical method, as follows:

Y = Δ_wH^o/Δ_wH^o_am,

(33)

X = 1 - (Δ_wH^o/Δ_wH^o_am),

(34)

where Δ_wH^o is the enthalpy of wetting for the dry sample; and Δ_wH^o_am = -168 kJ/kg DM or -27.2 kJ/mol AGUs is the wetting enthalpy for completely amorphous cellulose in the dry state [102].

The results have shown that the thermochemical method provides the determination degrees of amorphicity and crystallinity of cellulose samples with a standard deviation of no more than ±0.01 (Table 11).

It can be noted that the thermochemical method is direct, simple, fast, accurate, reliable, and reproducible. To measure the enthalpy of wetting any precise calorimeter can be used. It does not require special models, complex software, and calculations. This method does not have special requirements for the shape and size of the samples. They do not need to be milled or pressed. It is possible to use cellulose samples with different morphology and types of crystal structure (I, II, III, or IV) in the form of pieces, fibers, or powders. There are only two main conditions for preparing cellulose samples for testing: they must be chemically pure and completely dry.

After measuring the degree of crystallinity by a thermochemical method, it is possible to study how this structural characteristic affects the thermodynamic functions of cellulose samples.

Studies have shown that with a change in the degree of crystallinity (X), there is a tendency for a noticeable change in the TDFs of cellulose I_β samples, which can be expressed with the following linear equations:

Δ_cH^o = Δ_cH^o_am + K X,

(35)

Δ_fH^o = Δ_fH^o_am - K X,

(36)

S^o = S^o_am - k X,

(37)

where Δ_cH^o_am, Δ_fH^o_am, and S^o_am are standard enthalpies of combustion and formation of AMC, and S^o_am is the standard entropy of AMC; coefficient K = 37. 2 kJ/mol, while coefficient k = 10.0 J/mol K.

Structural studies have shown that crystallites of celluloses of plants and tunicate have predominantly the allomorphic type I_β with a monoclinic crystalline cell, while crystallites of algal and bacterial cellulose are characterized predominantly by the unstable allomorphic type I_α with a monoclinic crystalline cell [103,104].

After the physicochemical modification of cellulose, three additional crystalline allomorphs, II, III, and IV, were obtained [103,104,105,106,107]. Samples containing cellulose II crystallites were prepared by alkaline treatment of natural cellulose or by regeneration from cellulose solutions. Cellulose samples with crystalline allomorph III are obtained from I or II samples by treatment with ethylenediamine or liquid ammonia. Samples with crystalline form IV are usually prepared by heating cellulose III samples in hot glycerol. Different crystalline allomorphs of cellulose have different parameters of crystalline unit cells [103,104,105]. Along with various crystalline allomorphs, amorphous cellulose is known, which is produced by dry grinding of semicrystalline cellulose samples, by saponification of amorphous cellulose acetate in a non-aqueous medium, and some other methods [108].

Due to the existence of various crystalline allomorphs (CAs) and amorphous cellulose, various studies have been conducted to evaluate their phase stability. The amorphous phase state is considered to be labile since amorphous cellulose can easily crystallize into any crystalline allomorph under certain conditions. This conclusion is also supported by the results of thermodynamic studies [3]. In the case of crystalline allomorphs of cellulose, the problem of the relative stability of the phase state has not been completely solved and remains open. The study of thermodynamic characteristics gave grounds to believe that the phase state of CA II is more stable than CA I [8]. In addition, it was found that CA III is more reactive than CA II [106]. However, other studies concluded that the phase state stability of different crystalline allomorphs cannot be estimated with a reasonable degree of accuracy [3,107].

Therefore, additional studies were conducted for detailed investigations of the thermodynamic characteristics of various crystalline allomorphs of cellulose and amorphous cellulose [20,104]. For this purpose, cellulose samples having different crystalline allomorphs and different degrees of crystallinity (X) were prepared, and their standard TDFs were determined [20,104] (Table 13).

The results showed that an increase in the degree of crystallinity of the samples with the same type of crystalline allomorph leads to a linear change in the TDFs similar to that observed for samples of cellulose I_β according to eq. (35)-(37). With a decreasing degree of crystallinity (X), the linear dependences of TDF converge to the same values ​​corresponding to X = 0. This indicates that the amorphous phase in cellulose samples with different crystalline allomorphs has similar thermodynamic characteristics. On the other hand, linear extrapolation of these dependencies to values corresponding to X = 1 yields TDFs for different crystalline allomorphs (Table 14). In addition, the values of melting enthalpy (Δ_mH^o) of cellulose crystallites with different crystalline allomorphs were calculated.

The standard Gibbs potential of formation (Δ_fG^o) of crystalline allomorphs was also calculated using the equation:

Δ_fG^o = Δ_fH^o - T_o (S^o - ∑ 𝑆𝑖)

(38)

where S^o is standard entropy, while ∑ Si is the sum of standard entropies of carbon atoms (graphite), molecules of H₂ and O₂ needed for forming one mole of AGUs.

Based on the obtained results, the thermodynamic stability of crystalline allomorphs I_β, II, III, IV and AMC was estimated. It can be assumed that the relative thermodynamic stability of cellulose crystalline allomorphs and AMC decreases in the following order:

CII > CIV ≥ CI > CIII > AmC

On the other hand, the relative reactivity of the different crystalline allomorphs and AMC will decrease in the reverse order:

AMC > CIII > CI ≥ CIV > CII

The obtained thermodynamic characteristics allow to explain the phase transitions and reactivity of cellulose samples with different crystalline allomorphs and AMC. Amorphous cellulose, AMC, is the most unstable and the most reactive, so it can crystallize into any crystalline allomorph under certain conditions [3,108]. For example, under the influence of moisture, amorphized cellulose recrystallizes into the most stable CA II. It is also known that after mercerization and regeneration from solutions, the structure of cellulose I_β always transforms into CA II. Thus, among the various crystalline allomorphs, CA II is probably the most stable, while CA III is the most labile. It was found that high-temperature treatment of the sample with CA III at 480–490 K triggers the reverse transformation of CA III into CA I_β [109], whereas, after treatment in glycerol above 533 K, CA III is transformed into CA IV [110].

As is known, the supramolecular architecture of cellulose consists of elementary nanofibrils and their bundles called microfibrils [24,111]. Moreover, each nanofibril is built of rod-like nanocrystallites with lateral size of 3-20 nm and length of 50-500 nm, as well as noncrystalline (amorphous) nanodomains. Due to this nanostructure, cellulose exhibits several specific properties.

The following example can be used to illustrate these specific properties. In plant biomass (e.g., softwood, SW) nano-fibrils are surrounded by an amorphous ligno-hemicellulose matrix and are separated from each other. During delignification at elevated temperatures in the cooking solution, the matrix is ​​removed. This ensures direct contact of nano-fibrils and leads to aggregation by co-crystallization of adjacent nano-crystallites, which leads to an increase in the lateral size (L) of crystallites in isolated cellulose. The process of spontaneous aggregation and co-crystallization of nano-crystallites is thermodynamically favorable since it leads to a decrease in the specific surface area (S_sp) and a negative value of the thermodynamic Gibbs potential according to eq. (21) (Table 15).

Another example is when nano-crystallites III are transformed to crystallites IV after treatment in glycerol at temperature above 533 K. As is known, the theoretical equilibrium melting point of cellulose macrocrystals is estimated at 750 K [112]. However, nano-crystallites can melt at much lower temperatures due to the dependence of melting point on the lateral size of nano-crystallites by the Gibbs-Thomson equation (22) [113].

Calculations showed that the equilibrium melting point of cellulose crystallites reduces and reaches 533 K for nanocrystallites with a lateral size of less than 4 nm [112]. Thus, the mechanism of the transformation of nano-crystallites III into crystallites IV consists of reducing the melting point of small nano-crystallites III (L = 3.3 nm) to processing temperature (533 K) in plasticizing glycerol medium, amorphization of these crystallites, the transition of plasticized amorphized cellulose in the viscoelastic state, and finally the crystallization of viscoelastic amorphized cellulose into relatively large crystallites IV (L = 6.0 nm) that are also more thermodynamic stable than crystallites of CIII.

A characteristic feature of cellulose nanocrystals is also an increase in solubility (SB) and a decrease in alkali concentration (C) for mercerization with a decrease in their lateral size, L [112], which is consistent with Gibbs-Thomson theory [114].

ln SB_n = ln SB_m + (4σV_m/L RT),

(39)

ln C_n = ln C_m - (4σV_m/L RT),

(40)

where index n is related to nano-crystallites, while index m to macrocrystals.

5.2. Thermodynamic Characteristics of Non-Cellulosic Components of Biomass

Non-cellulosic components of biomass include mainly hemicelluloses, starch, pectin, lignin, and extractives. Hemicelluloses can consist of C-6 polysaccharides called hexosans (mannans, glucans, galactans, etc.) and C-5 polysaccharides called pentosans (xylans, arabans, etc.). The article [115] notes that the gross heating value (GHV) of amorphized hexoses and amorphized cellulose should be close, while the GHV of pentoses is higher than hexoses. Other studies [54] showed that the standard enthalpy of combustion of samples of hexosans is on average Δ_cH^o = -2833.6 kJ/mol (GHV = -17.49 MJ/kg), and samples of pentosans Δ_cH^o = -2348.0 kJ/mol (GHV = -17.79 MJ/kg) (Table 16).

Based on the chemical structure, it can be concluded that the GHV of starch and hexoses must be identical [115]. But, in reality, this is not the case, since different starch types differ from each other in amylose content and degree of crystallinity [116,117]. Therefore, thermodynamic characteristics should be determined for specific types of starch. For example, it was found that for corn starch, the enthalpy of combustion Δ_cH^o = -2836.6 kJ/mol, and the enthalpy of formation Δ_fH^o = -953.6 kJ/mol.

The pectin sample showed the value of combustion enthalpy lower than hexosans but higher than pentosans [118].

After studying various lignin samples, it was found that the average GHV of lignin from coniferous trees is -26.8 MJ/kg, and for lignin from deciduous trees and grass plants -25.3 MJ/kg [115]. The values of combustion enthalpy Δ_cH^o = -5172.4 kJ/mol of lignin samples from softwood and Δ_cH^o = -4984.1 kJ/mol of lignin samples from hardwood obtained in [54,118] correspond to the results of [115] if calculate the combustion enthalpy in MJ/kg.

The article [115] reports that the GHV of extractive substances is not constant and can vary widely depending on the plant species and the extraction method. For example, the GHV of extractives from coniferous wood species was in the range from -30 to -39 MJ/kg. To improve the reliability of the results, the calorific values of resin acids (e.g., abietic acid, etc.), which constitute the main part of the extractives in coniferous wood, were studied [54,118]. The results showed that the value of combustion enthalpy of these components is higher than -11500 kJ/mol (-38 MJ/kg), while their formation enthalpy is above -570 kJ/mol (Table 16).

6. Thermodynamic of Chemical Reactions of Cellulose and other Polysaccharides

6.1. Thermodynamics of Bioethanol Production

Bioethanol is produced by fermentation of glucose solutions, usually using the yeast Saccharomyces cerevisiae [119,120]. The glucose substrate required for fermentation is obtained by enzymatic hydrolysis of carbohydrates, starch, and cellulose. In the USA, bioethanol is produced primarily from corn starch [22], with an annual production volume of over 15 giga gallons [121].

The production process involves the extraction and purification of starch from corn kernels, dissolution of the starch at elevated temperatures to gelatinization, hydrolysis of the starch gel with α-amylase and then glucoamylase, yeast fermentation of the formed glucose to produce a dilute ethanol solution, followed by distillation and dehydration of the ethanol.

To hydrolyze starch, gel-like starch solutions with a concentration of 150 to 200 g/L usually are used [122]. The starch gel is hydrolyzed by α-amylase to liquefy the gel and facilitate the subsequent transformation of starch to glucose [123]. Since α-amylase is an endo-acting enzyme, it catalyzes the hydrolysis of inner α-1, 4-glycosidic and branched α-1,6-glycosidic bonds with the formation of oligomeric products, mainly, dextrin and maltose [124,125]. Further, these oligomers are hydrolyzed by the exo-enzyme, glucoamylase, resulting in their conversion into glucose [126].

Next, the resulting glucose solution is fermented, usually with S. Cerevisiae yeast [119,120], to produce a diluted alcohol solution with a concentration of no more than 100 g/L to prevent yeast inhibition [127,128]. To obtain absolute alcohol, the diluted alcohol solution was distilled and dehydrated.

Despite the progress in hydrolysis and bioethanol production, thermodynamical aspects of various steps of these processes have not been studied sufficiently. It is not clear, which step is exothermic and which is endothermic. What determines the feasibility of these processes, enthalpy or entropy? To solve these problems a thermodynamic analysis should be performed.

Enzymatic hydrolysis of a starch gel with the formation of glucose solution occurs, as follows:

-C₆H₁₀O₅- x m H₂O → C₆H₁₂O₆ x (m-1) H₂O

The standard TDFs of the hydrolysis reaction were calculated using the following equations:

Δ_rH^o(H) = Δ_fH^o(GS) - Δ_fH^o(SG),

(41)

Δ_rS^o(H) = S^o(GS) - S^o(SG),

(42)

Δ_rG^o(H) = Δ_rH^o(H) -T_o Δ_rS^o(H),

(43)

where H, GS, and SG denote hydrolysis, glucose solution, and starch gel, respectively.

The values of standard thermodynamic functions of GS and SG can be experimentally determined or found in reference books.

The results presented in Table 17 show that the standard thermodynamic functions for the hydrolysis reaction of starch gel have the same values regardless of the gel concentration. Since the Gibbs potential (Δ_rG^o) of this reaction has a negative value, the hydrolysis process is thermodynamically favorable. The entropy of this reaction increases due to the cleavage of long chains and the conversion of a high-molecular polysaccharide into a low-molecular product such as glucose. The enthalpy of hydrolysis reaction (Δ_rH^o) is exothermic, but its value is too small. Moreover, the absolute value of enthalpy is significantly less than the value of temperature-entropy factor (T_oΔ_rS^o). Thus, the hydrolysis reaction of starch gel with the formation of the glucose solution is determined mainly by the contribution of the temperature-entropy factor to the Gibbs potential. Therefore the equilibrium constant of the hydrolysis process has a moderate value: K_eq = 2.65 x 10³.

Glucose solution required to bioethanol production can be obtained also by enzymatic hydrolysis of cellulose [62,64,129]. Production of glucose from non-edible cellulose substrates has been regarded as a promising way to obtain this valuable bioproduct without competing with the food industry.

For the hydrolysis of cellulose, enzyme preparations are used, which include at least three types of specific enzymes such as endo-1,4-β-glucanases, exo-1,4-β-glucanases, and β-glucosidases [64,128]. Numerous studies have shown that when using cellulose substrates, a problem arises due to their low enzymatic digestibility. This is explained by the crystallinity of cellulose, which is considered the most important structural factor hindering enzymatic hydrolysis [64,128,130]. Therefore, a thermodynamic analysis was carried out to study the thermodynamic mechanism of enzymatic hydrolysis of cellulose substrates with different crystallinity [131].

An attempt to perform a thermodynamic study of the enzymatic hydrolysis of completely crystalline and completely amorphous cellulose at temperatures from 273 to 373 K using a small mass ratio of an aqueous catalyst system to cellulose (SCR) to obtain saturated glucose solutions followed by their dilution was made in [132]. However, this theoretical study did not take into consideration such specific features of enzymatic hydrolysis as the negative impact of cellulose crystallinity on the hydrolysis process, limited cellulose accessibility, and cessation of enzymatic hydrolysis at small SCR, low hydrolysis rate below room temperature and the inactivation of cellulolytic enzymes at temperatures above 328 K. These factors should be taken into consideration when studying the thermodynamics of the real process of enzymatic hydrolysis of cellulose.

When a wet semicrystalline cellulose substrate is treated with an aqueous enzyme system, the accessible amorphous domains of cellulose and the outer paracrystalline surface layers of the crystallites are hydrolyzed and form a final glucose solution containing n moles of H₂O per mole of glucose (GL), while the internal highly ordered crystalline domains (CrD) remain unhydrolyzed. This process for one mole of AGUs of cellulose can be expressed, as follows:

-C6H10O5- x m H2O + (An + A - m) H2O → A (GL x n H2O) + (1-A) CrD

where A is the accessibility degree of cellulose, which is a function of cellulose amorphicity (Y), crystallinity (X), and paracrystallinity (p) degrees: A = Y + pX.

After the determination of standard TDFs of the wet cellulose substrates (CW), glucose solutions (GL x n H₂O), and highly ordered crystalline domains (CrD), the TDFs of the hydrolysis reaction were calculated [131]:

Δ_rH^o(H) = (1-A) Δ_fH^o(CrD) + A Δ_fH^o(GL x n H₂O) - Δ_fH^o(CW) - (An + A - m) Δ_fH^o(H₂O, _l),

(44)

Δ_rS^o(H) = (1-A) S^o(CrD) + A S^o(GL x n H₂O) – S^o(CW) - (An + A - m) S^o(H₂O,

(45)

Δ_rG^o(H) = Δ_rH^o(H) – T_o Δ_rS^o(H),

(46)

The obtained results showed [131] (Table 18) that the enthalpy of cellulose hydrolysis is small exothermic, like the hydrolysis enthalpy of starch. The value of the temperature-entropy factor (T_oΔ_rS^o) is significantly higher than the absolute value of the hydrolysis enthalpy. Therefore, the contribution of this factor to the negative Gibbs potential is predominant. In addition, with an increase in cellulose accessibility degree, the negative value of the Gibbs potential increases. Thus, the enzymatic hydrolysis of amorphous cellulose (AMC) is the most favorable. This is confirmed by the fact that the equilibrium constant of the hydrolysis reaction of AMC, K_eq = 5.82 x 10⁴, is more than a thousand times greater than that of semicrystalline cellulose substrates. In addition, the enzymatic hydrolysis of high-ordered crystalline domains of cellulose cannot be performed since the Gibbs potential of this process is close to zero.

Glucose solutions obtained after enzymatic hydrolysis of starch or cellulose can be used to produce bioethanol by yeast fermentation. The fermentation process can be described by the following equation:

0.5 C₆H₁₂O₆ x n H₂O → CO₂ + C₂H₆O x 0.5 n H₂O

To avoid producing an alcohol solution with a concentration higher than 100 g/L, which inhibits yeast, the concentration of the glucose solution should not exceed 196 g/L. In this case, the number of water molecules n per one mole of glucose is ca 51.

The standard TDFs of the fermentation process (F) of glucose solution (GS) conversion into ethanol solution (ES) were calculated using the following equations:

Δ_rH^o(F) = Δ_fH^o(CO₂) + Δ_fH^o(ES) - 0.5 Δ_fH^o(GS),

(47)

Δ_rS^o(F) = S^o(CO₂) + S^o(ES) - 0.5 S^o(GS),

(48)

Δ_rG^o(F) = Δ_rH^o(F) -T_o Δ_rS^o(F),

(49)

where Δ_fH^o(CO₂) and S^o(CO₂) are the standard formation enthalpy and entropy of carbon dioxide; Δ_fH^o(ES) and S^o(ES) are the standard formation enthalpy and entropy of ethanol solution; while Δ_fH^o(GS) and S^o(GS) are the standard formation enthalpy and entropy of glucose solution.

From the obtained results (Table 19) it follows, that the process of bioethanol production by fermentation of a glucose solution has a negative value of the Gibbs potential. In addition, the enthalpy of this process is quite exothermic and, together with the temperature-entropy factor, contributes to the negative Gibbs potential. Thus, the process of glucose conversion into bioethanol is both energetically and entropically favorable. In addition, it was found that the equilibrium constant of this process is very large: K_eq =1.35 x 10²⁰. Thus, the reaction equilibrium is strongly shifted towards the formation of bioethanol.

6.2. Thermochemistry of Cellulose Alkalization and Etherification

Treatment of cellulose with solutions of hydroxides of alkali metals is one of the most common methods of modification of this biopolymer. Currently, treatment with aqueous solutions of sodium hydroxide is used for the improvement of luster, hygroscopic properties, and dyeing of cellulose fibers and fabrics, for cellulose activation and refining, as well as in the production of cellulose ethers [133,134,135,136].

It has been established that after cellulose treatment with solutions of sodium hydroxide having a concentration of less than 10-11%, the crystalline structure of cellulose I remains unchanged [137]. However, when cellulose is alkalized with 16-20% alkali solutions the hydrated hydroxide ions penetrate between [1$\overline{1}$0] planes of the crystalline lattice of CA I and transform it into the swollen crystalline lattice of alkali cellulose (AlC) containing one molecule of NaOH and three molecules of H₂O per one anhydroglucose unit (AGU) in crystalline domains. Cellulose treatment with more concentrated sodium hydroxide solutions transforms the crystalline lattice of CA I into lattices of alkali celluloses containing one NaOH molecule and different numbers of water molecules n per one AGU [137]. For example, cellulose alkalization with 35-40% NaOH causes the formation of a crystalline lattice of AlC with the composition AGU$\bullet$NaOH$\bullet$H₂O, i.e., containing no more than one molecule of H₂O per AGU. During alkalization, the partial decrystallization of cellulose is observed.

After washing various alkali celluloses with water, hydroxide ions are replaced by water molecules resulting in the formation of the crystalline lattice of hydrate-cellulose, which after drying turns completely into the crystalline lattice of CA II [138]. It was also established that cellulose alkalization is accompanied by an exothermic heat effect, enthalpy of alkalization, Δ_alH^o [137] (Table 20).

The results show that the production of alkaline celluloses AlC 4, 5, and 6 is accompanied by a greater exothermic thermal effect than the production of alkaline celluloses AlC 1, 2, and 3.

Another significant thermodynamic characteristic is the standard enthalpy of the formation of alkali cellulose from one AGU and alkali solution containing m moles H₂O per one mole of NaOH. Following Hess’s law, the standard enthalpy of the formation of alkali cellulose after the alkalization of cotton cellulose (CC) can be calculated, as follows:

Δ_fH^o(AlC) = Δ_fH^o (CC) + Δ_fH^o(Alkali) – (m-n) Δ_fH^o(H₂O) + Δ_alH^o,

(50)

where Δ_fH (CC) = -969 kJ/mol is the standard enthalpy of formation of one mole of AGUs of original cotton cellulose [20], Δ_fH (H₂O) = -285.83 kJ/mol is the standard enthalpy of formation of liquid water, Δ_fH^o(Alkali) is the standard enthalpy of formation of alkali solutions [137].

From the presented results (Table 20) it follows that the enthalpy of the formation of various alkaline celluloses is exothermic. Thus, the process of AlCs formation is energetically advantageous. In addition, since the exothermic enthalpy of alkalization to obtain AlC 4-6 has the greatest value, these alkaline celluloses must be more reactive than AlC 1-3. For this reason, the stage of cellulose alkalization before etherification is carried out using 30-40% alkali solutions, which provide alkaline celluloses AlC 4-6 with increased reactivity.

Consider as an example the process of production of methylcellulose (MC) [137]. The first stage of this process is cellulose alkalization, e.g., with a 40% NaOH solution at room temperature, after which the excess alkali is removed to obtain a mass ratio of alkali to cellulose of 3:1. The resulting alkali cellulose such as AlC 6 is kept for 1-2 h, and then methylated with methyl chloride:

C₆H₇O₂ (OH)₃·NaOH · H₂O + (x-1) NaOH + x CH₃Cl → C₆H₇O₂ (OH)_3-x (OCH₃)_x + x NaCl + (1+x) H₂O

where x is the degree of substitution (DS) of MC. The DS of the samples, MC-1 and MC-2 was set to 1.3 and 1.8, respectively.

Taking into consideration the etherification process, the enthalpy of the methylation reaction of AlC 6 can be calculated using the equation:

Δ_rH^o = Δ_fH^o(MC) + xΔ_fH^o(NaCl) + (1+x) Δ_fH^o(H₂O) - Δ_fH^o(AlC 6) - (x-1) Δ_fH^o(NaOH) – x Δ_fH^o(CH₃Cl),

(51)

where Δ_fH^o(AlC 6) is the standard enthalpy of formation of AlC 6), while Δ_fH^o(NaCl), Δ_fH^o(NaOH, Δ_fH^o(CH₃Cl), and Δ_fH^o(H₂O) are the standard enthalpies of formation of the corresponding substances.

As a result, the following values of enthalpy of the methylation reaction of AlC 6 to obtain methylcellulose samples were found [137].

For MC 1 (DS = 1.3): Δ_rH^o (MC 1) = -184 kJ/mol.

For MC 2 (DS = 1.8): Δ_rH^o (MC 2) = -287 kJ/mol.

Since the enthalpy values of the methylation reaction of AlC 6 were quite exothermic, this means that the methylation reaction is energetically favorable. Moreover, obtaining methylcellulose with a higher degree of substitution is preferable.

6.3. Thermochemistry of Cellulose Esterification

Among diverse cellulose derivatives, two derivatives, namely the acetates, and nitrates, are of particular importance. To obtain cellulose acetates, the starting cellulose material is placed in a suitable organic liquid and treated with an anhydride of acetic acid in the presence of a small amount of a catalyst [139,140]. The esterification process is heterogeneous if cellulose and its ester do not dissolve in the organic liquid. When the organic liquid is a solvent for cellulose and its ester, the reaction is carried out under homogeneous conditions. The heterogeneous acetylation of cellulose proceeds in the solid phase according to the laws of topochemical reactions: rapidly in amorphous domains and more slowly inside the cellulose crystallites. On the contrary, the homogeneous acetylation proceeds fairly uniformly in liquid media that cause swelling or/and dissolution of cellulose.

Studies have shown that replacing cellulose hydroxyls with acetate groups leads to a significant increase in the hydrophobicity of the resulting derivative [141]. In addition, when moving from a monoester to a triester, a noticeable increase in hydrophobicity is observed, since in this case all three hydroxyls in the repeating cellulose unit are replaced by non-polar groups. Due to their performance properties, cellulose acetates can be used to produce cigarette filters, separating membranes, optical films, self-cleaning materials, protective coatings, anti-fog goggles, and other products [141,142,143,144].

Another significant cellulose esters are nitrates. To produce nitrocelluloses the starting cellulose material can be treated with mixtures of nitric with sulfuric, or phosphoric acids [145,146]. In addition, mixtures of nitric acid with anhydrides of phosphoric or acetic acids also can be used for nitration. Nevertheless, in industry, only mixtures of nitric with sulfuric acid are applied to synthesize nitrocelluloses. Cellulose nitrates are used for the production of plastics, membranes, films, protective coatings, adhesives, varnishes and enamels, smokeless powder, rocket fuels, explosives, etc. [147,148,149].

Although the chemistry of esterification reactions of cellulose has been studied quite well, their thermochemical aspects are largely unexplored. Since only a small research number has been devoted to this topic [150,151], the specificity of the thermochemistry of cellulose esterification remained unclear. Therefore, further research was undertaken with samples of cellulose acetates (AC) and nitrates (NC) with different degrees of substitution (DS) [20,152]. The thermochemical characteristics of these samples are presented in Table 21.

For comparison with the obtained TD characteristics, some literature data are shown in Figure 1 and Figure 2. As can be seen, the experimental results [20,152] are confirmed by the literature data [150,151].

From the linear dependences of TDFs on DS, the TD characteristics of cellulose esters can be calculated using the following correlation equations.

For cellulose nitrates

Δ_cH^o(NC) = Δ_cH^o(AMC) + DS K_c(NC),

(52)

Δ_fH^o(NC) = Δ_fH^o(AMC) + DS K_f(NC),

(53)

where K_c(NC) = 48 and K_f(NC) = 96

For cellulose acetates

Δ_cH^o(AC) = Δ_cH^o(AMC) - DS K_c(AC),

(54)

Δ_fH^o(AC) = Δ_fH^o(AMC) - DS K_f(AC),

(55)

where K_c(AC) = 889 and K_f(AC)= 186

Structural studies indicate that as a result of esterification, cellulose esters with an amorphized structure are formed [141,153]. Thus, the process of cellulose esterification is accompanied by decrystallization (melting) of cellulose crystallites and subsequent esterification of amorphized cellulose (AMC) with the formation of amorphous esters. This process can be expressed by the following TD equation:

Δ_rH^o(СС) = Δ_rH^o(AMC) + X Δ_mH^o,

(56)

where Δ_rH^o(СС) and Δ_rH^o(AMC) are enthalpies of esterification of cotton cellulose (CC) and amorphized cellulose (AMC), respectively; Δ_mH^o =37 (kJ/mol) is the melting enthalpy of cellulose I crystallites, while X=0.7 is the average crystallinity degree of CC sample.

The enthalpy of nitration of AMC can be expressed, as follows:

Δ_rH^o(AMC)_NC = Δ_fH^o(NC) + DS [Δ_fH^o(H₂O) - Δ_fH^o(HNO₃)] - Δ_fH(AMC),

(57)

On the other hand, the enthalpy of acetylation of AMC was calculated using the following equation:

Δ_rH^o(AMC)_AC = Δ_fH^o(AC) + DS [Δ_fH^o(AcAc) - Δ_fH^o(AcAn)] - Δ_fH^o(AMC),

(58)

The formation enthalpies of AMC, NC, and AC samples with various DS, reagents (HNO₃ and acetic anhydride, AcAn), as well as low-molecular-weight products of esterification (H₂O and acetic acid, AcAc), were determined experimentally or found in reference books.

The resulting enthalpies of cellulose esterification are shown in Table 22 and Table 23.

As can be seen from the results (Table 22), the nitration reaction of cellulose to DS of 1.5 is endothermic. In this case, the only possibility for the feasibility of nitration reaction is that the absolute value of the temperature-entropy factor must be greater than the absolute value of reaction enthalpy, so that the Gibbs potential of this reaction becomes negative, namely:

[TΔ_rS] > [Δ_rH] and Δ_rG = (Δ_rH -TΔS) < 0

where Δ_rG is the Gibbs potential of cellulose nitration, and T is the reaction temperature.

Thus, the nitration process of cellulose with a weak nitrating system to DS up to 1.5 can only be implemented if the temperature-entropy factor is positive and makes a predominant contribution to the Gibbs potential.

When cellulose is nitrated with concentrated nitrating systems to DS above 1.5, the reaction enthalpy becomes exothermic. In this case, the feasibility of the nitration process may depend on both the contribution of exothermic enthalpy and temperature-entropy factor to the Gibbs potential.

Unlike nitration, the acetylation of cellulose is always an exothermic process, regardless of the achieved DS value (Table 23). The more DS, the higher the exothermic heat effect of this reaction. Besides, an increase in exothermic reaction entropy and positive temperature-entropy factor will facilitate the implementation of the acetylation process.

The final conclusion is that the esterification of cellulose to high degrees of substitution is advantageous because it is an energetically favorable process. The results also showed that cellulose acetylation is accompanied by the release of significantly more thermal energy than the cellulose nitration process (Figure 3).

7. Discussion

As is known, renewable plant biomass is considered CO₂-neutral. Therefore, its combustion does not increase the concentration of this greenhouse gas in the atmosphere. It should also be noted that the volume of carbon dioxide formed during the combustion of 1 t biomass (ca 900 m³ CO₂) is two times less than when burning 1 t such solid fossil fuel as coal (ca 1870 m³ CO₂) and even 1.7 times less when burning 1 t of liquid or gaseous fossil fuels (ca 1600 m³ CO₂). In addition, CO₂ released during the combustion of plant biomass can be converted into gaseous biofuel, for example, bio-methane, using the Sabatier reaction.

Nevertheless, increased amounts of moisture and mineral impurities (ash) reduce the energy potential of biomass. Examples of such types of biomasses are fresh wood with high moisture content and office paper or rice husks with high ash content. On the other hand, it has been established that lipids, organic extractive substances, and lignin have increased calorific value, so their high content in biomass contributes to the extraction of elevated amounts of thermal energy during biomass combustion.

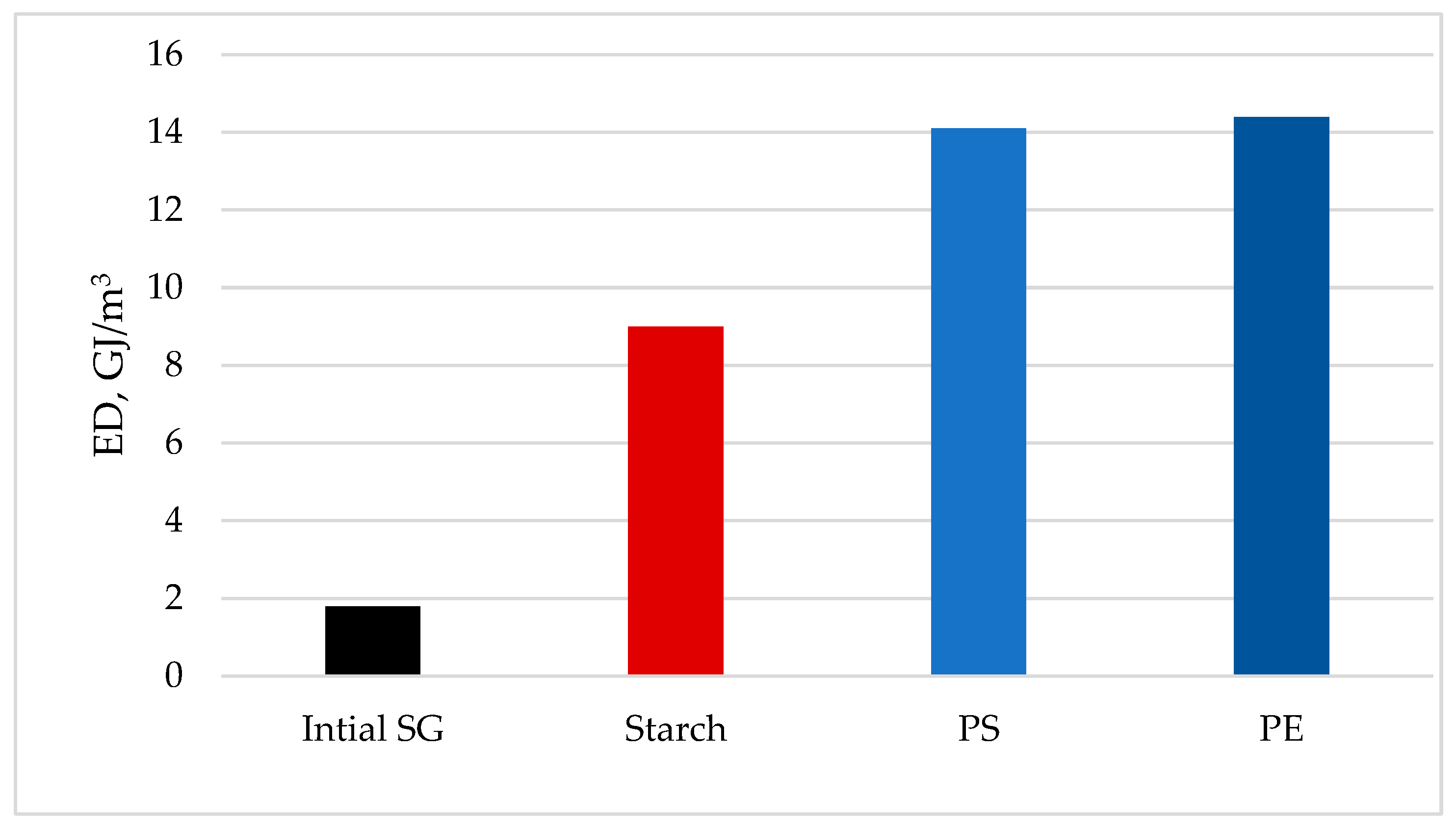
An additional problem is that the initial plant biomass is a loose and non-uniform material consisting of pieces of different sizes with low bulk density. These features of the biomass decline the density of thermal energy (ED), significantly reducing the productivity of the furnaces. To improve the fuel characteristics, the initial plant biomass should be demineralized, dried, and compacted. For example, if pelletize dried Switchgrass (SG) biomass with the addition of various binders such as starch and waste plastics, polystyrene (PS), and polyethylene (PE), then the density of thermal energy can be increased by 5-8 times (Figure 4). In terms of ED and GHV, biomass pelletized together with plastic binders is not inferior to coal, a traditional solid fossil fuel.

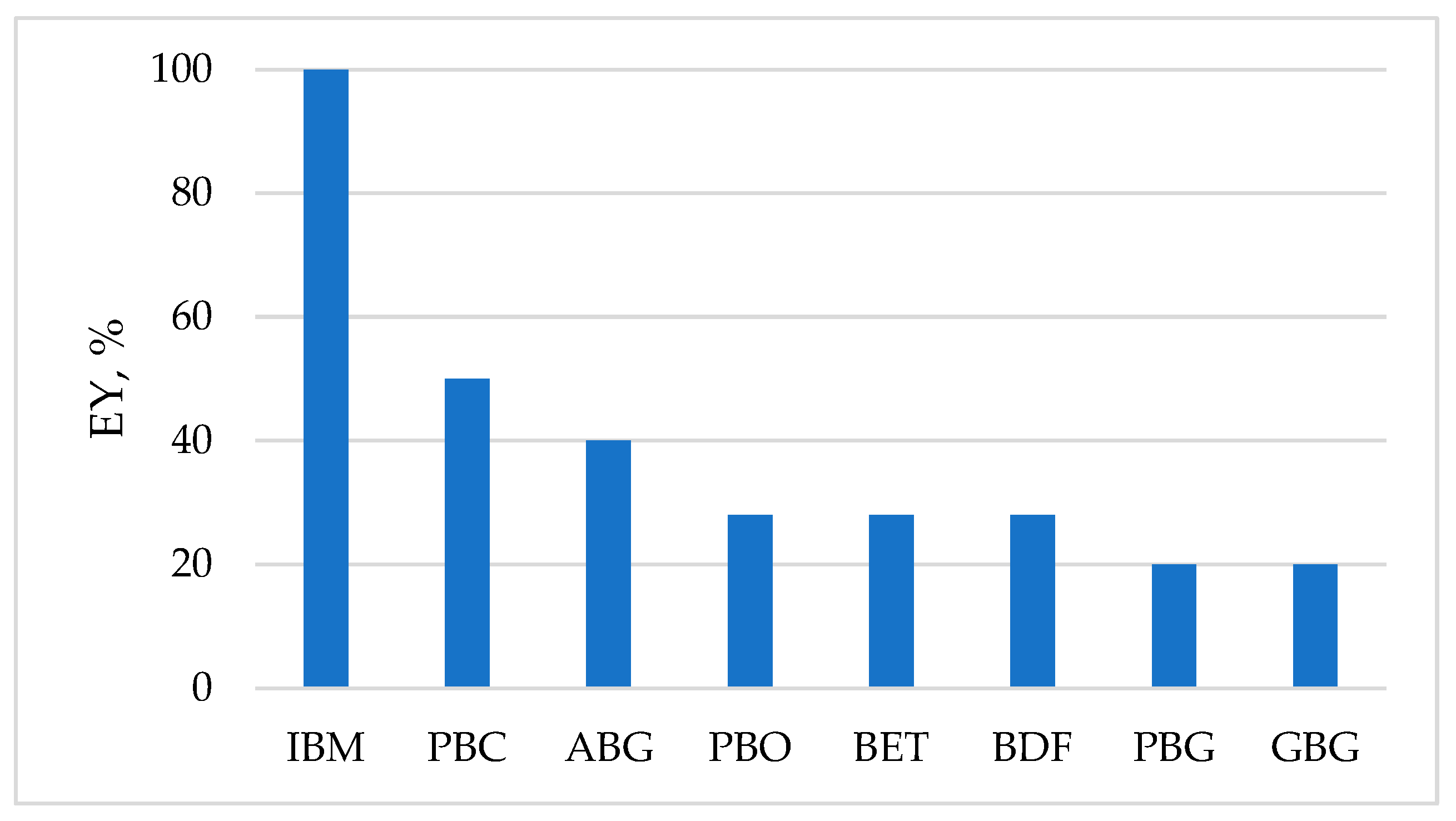
Initial plant biomass can be also a feedstock for producing secondary biofuels, such as biochar, bio-oil, bioethanol, biodiesel fuel, and biogases. From the chart (Figure 5), one can understand how profitable it is to produce various types of secondary biofuels. The following secondary biofuels were analyzed: biochar (PBC), bio-oil (PBO), and biogas (PBG) of slow pyrolysis of biomass; biogas produced by biomass gasification (GBG); biogas of anaerobic digestion of biomass (ABG); bioethanol (BET) and biodiesel fuel (BDF).

The analysis of thermal energy yield from initial biomass (IBM) and secondary biofuels shows that it is most advantageous to produce biochar of slow pyrolysis and, maybe, biogas by anaerobic digestion of cellulose or other polysaccharides. However, in general, one can conclude that if the ultimate goal is to obtain the maximum amount of thermal energy, then it is more profitable to directly burn the initial biomass (preferably in the form of pellets) than to burn such an amount of secondary solid, liquid or gaseous biofuel that can be extracted from this biomass.

As known, the most important component of biomass is cellulose. It is a semicrystalline biopolymer, many properties of which depend on crystallinity. Unfortunately, currently, existing research methods allow to determine only an estimated characteristic of cellulose crystallinity, the so-called crystallinity index. Therefore, to determine the crystallinity degree, a new thermochemical method was developed based on the measurement of the enthalpy of wetting of cellulose samples. This new method provides the determination degree of cellulose crystallinity with a standard deviation of no more than ±0.01. The thermochemical method is direct, simple, fast, accurate, reliable, and reproducible. It does not require special models, complex software, and calculations. In addition, this method does not have special requirements for the shape, size, morphology, and type of crystalline allomorph of cellulose samples.

In addition to determining the degree of crystallinity, a thermochemical method was used to characterize the thermodynamic stability of cellulose crystallites with different types of crystalline allomorphs (CAs), I_β, II, III, IV, and amorphous cellulose (AMC). The results showed that the relative thermodynamic stability of cellulose CAs and AMC decreases in the following order:

CII > CIV ≥ CI > CIII > AmC

On the other hand, the relative reactivity decreases in the reverse order:

AMC > CIII > CI ≥ CIV > CII

The obtained thermodynamic characteristics allow to explain the phase transitions and reactivity of AMC and cellulose samples with different crystalline allomorphs.

When discussing the thermodynamic properties of cellulose nanocrystallites, the Gibbs-Thomson theory should be used. This theory allows one to explain various specific features of the nanocrystallites such as their spontaneous aggregation, a decrease in the melting temperature and an increase in solubility with a decrease in the crystallites size, the phase transition of small nanocrystallites of CA III into larger crystallites of CA IV during high-temperature treatment, and other properties.

To study the thermodynamics of chemical reactions involving biomass and its components, it is necessary to know the standard thermodynamic functions (TDFs) such as the enthalpy of formation (Δ_fH^o) and the entropy (S^o) for the starting materials, reagents, and reaction products. The enthalpy of the formation of the main components of plant biomass, cellulose, lignin, hemicelluloses, and other organic substances, can be determined experimentally by studying the enthalpy of combustion (Δ_cH^o):

Δ_fH^o(C_xH_yO_z) = x Δ_fH^o(CO₂, g) + 0.5y Δ_fH^o(H₂O, l) - Δ_cH^o(C_xH_yO_z),

(59)

where Δ_fH^o(CO₂,g) = -393.51 kJ/mol and Δ_fH^o(H₂O,l) = -285.83 kJ/mol are standard enthalpies of the formation of carbon dioxide and liquid water, respectively.

To determine the standard entropy of a substance, measurements of its specific heat capacity are usually carried out using a scanning vacuum adiabatic calorimeter in the temperature range from 0 to standard temperature, 298.15 K.

Values of standard TDFs for cellulose and other components of plant biomass can be also found in scientific literature. In addition, standard TDFs for most reagents and reaction products are given in handbooks on chemical thermodynamics.

These TDFs are used to calculate the enthalpy (Δ_rH^o) and entropy (Δ_rS^o) values of diverse chemical reactions. For example, let a chemical reaction occur between a feedstock (F) and a reagent (R) to form a reaction product (P):

F + n R → m P

Then, the change in reaction enthalpy will be:

Δ_rH^o = m Δ_fH^o(P) - n Δ_fH^o (R) - Δ_fH^o(F),

(60)

while the change in reaction entropy:

Δ_rS^o = m S^o(P) - n S^o (R) - S^o(F),

(61)

The Gibbs potential of the reaction is calculated as follows

Δ_rG^o = Δ_rH^o - T Δ_rS^o,

(62)

Such a potential is used to predict the feasibility of a chemical reaction, namely, if the Gibbs potential has a negative value, then the reaction can occur, and in the case of a positive value of this potential, the reaction cannot proceed. Almost all reactions considered in this review article are feasible and therefore have a negative Gibbs potential.

In addition, the Gibbs potential determines the value of the equilibrium constant (K_eq) of reversible reactions:

K_eq = EXP (-Δ_rG^o/RT),

(63)

where EXP is the Euler's number “e”.

The more negative the value of Δ_rG^o, the greater the value of the equilibrium constant, and when the value of Δ_rG^o reaches -100, the reaction becomes practically irreversible. A typical example of such an irreversible reaction is the conversion of glucose solution into bioethanol with Δ_rG^o = -114.9 kJ/mol, the equilibrium constant of which has a very large value, K_eq = 1.35 x 10²⁰ (see section 6.1).

On the other hand, the value of Gibbs potential for the reaction of enzymatic hydrolysis of starch is not so large, Δ_rG^o = -19.54 kJ/mol; and therefore, the equilibrium constant of this process has a moderate value of K_eq = 2.64 x 10³, which indicates the possibility of reversibility of this reaction and a decrease in the yield of produced glucose compared to the theoretical value. The reaction of enzymatic hydrolysis of cellulose is also partially reversible.

Another important characteristic is the temperature coefficient of the reaction, which depends on the reaction enthalpy:

K_T = EXP (-Δ_rH^o/RT),

(64)

This coefficient allows to recommend whether to increase the reaction temperature or not. If the reaction is endothermic, then with increasing temperature the coefficient K_Т will increase, which improves the implementation of such a reaction. However, for exothermic reactions, an increase in temperature will cause a decrease in the coefficient K_T, which means a deterioration in the implementation of such a reaction.

An example of an endothermic reaction is the process of hydrothermal gasification of biochar obtained from plant biomass by the slow pyrolysis method:

$$\mathrm{C}+{\mathrm{H}}_2\mathrm{O}\leftrightarrow$$

It can be calculated that with an increase in the temperature of the gasification process from 973 to 1273 K, the value of the temperature coefficient will increase by 47 times, which should improve the yield of formed syngas. Further, this syngas can be used, e.g., for the synthesis of artificial hydrocarbon fuel by the Fischer-Tropsch method.

Almost all reactions involving cellulose considered in this review article are exothermic (Table 24). Therefore, an increase in the temperature of the cellulose reactions reduces the thermal coefficient, which indicates a deterioration in the implementation of these reactions. For this reason, cellulose reactions occur at normal or moderate temperatures, usually in the range of 293 to 333 K.

8. Conclusions

This review article shows the possibility of applying chemical thermodynamics to the study of plant biomass and its main components: cellulose, hemicelluloses, lignin, etc. The energy potential of various biomass types is determined. It is established that dry and demineralized biomass has a gross heating value (GHV) in the range from -17 to -21 MJ/kg. However, the GHV of biomass enriched with lignin, lipids, and other organic extractives can be significantly higher. To improve fuel properties and especially the density of thermal energy, the initial plant biomass should be densified and converted into pellets with the addition of various binders. It is shown that pelletized biomass is not inferior to fossil coal in its fuel properties, and when burned, it emits almost two times less carbon dioxide. In addition, it should be taken into account that biomass is considered CO₂-neutral and renewable, unlike fossil fuels. To calculate the combustion enthalpy of biomass, a method of additive contributions of combustion enthalpies of main components is proposed.

In addition to solid fuel, biomass can also be used as a raw material for the production of secondary biofuels such as biochar, bio-oil, biodiesel fuel, bioethanol, and biogases. However, it was shown that if the ultimate goal is to obtain the maximum amount of thermal energy, then it is more profitable to directly burn the biomass, preferably in pelletized shape, than to burn such an amount of secondary solid, liquid, or gaseous biofuel that can be extracted from starting amount of this biomass.

Using methods of chemical thermodynamics, the thermodynamic functions of cellulose and its derivatives were calculated. A new thermochemical method for the determination crystallinity degree of cellulose samples was also developed. In addition, the relative thermodynamic stability of different crystalline allomorphs of cellulose was estimated. It was found that the most stable allomorph is cellulose II, while the most labile is cellulose III, as well as amorphous cellulose. When studying the specific thermodynamic properties of cellulose nanocrystallites, the Gibbs-Thomson theory should be used.

Thermodynamic features of cellulose chemical reactions such as enzymatic hydrolysis, bioethanol production, alkalization, etherification, and esterification were analyzed. The thermodynamic functions of these reactions, as well as the equilibrium constants and temperature coefficients, were determined. Since most cellulose reactions are exothermic, increasing temperature is unfavorable for them. For this reason, these reactions should be carried out at normal and moderate temperatures.