1. Introduction
The problem of finding the maximum number of halving lines for subsets of the plane with n points (, see the definition below) has been widely treated in the Discrete Geometry literature.
In an informal way, a halving line of a set P is a line joining two points of P and that equally distribute the rest of the points of P in the two open half planes defined by the line (see the formal definition below).
The first asymptotic lower bound for the maximum number of these halving lines was given by Erdõs et al. in 1973 (see [
1]). They achieved the bound
. Later, this bound was improved to
by Eppstein (see [
2]).
More recently, Tóth found a lower bound that is asymptotically better than the bounds mentioned above:
(see [
3]). The constant in the exponent was improved by Nivasch [
4].
The up to date best upper bound of
is
, due to Dey [
5].
A problem related to the halving line problem is the rectilinear crossing number problem. It aims to find the minimum number of crossings for planar sets of n points if each two points of the set are connected with a segment (the rectilinear crossing number: See the formal definition below).
The attempts to find sets minimizing the number of crossings have carried out interesting conjectures about the properties of these sets. Two of these properties are the 3-decomposability and the 3-symmetry. This last property is about invariance of the set with respect to rotations of angles
,
. The conjecture linking the 3-symmetry with the rectilinear crossing number problem is that there are 3-symmetric sets of
n points that attains the rectilinear crossing number for every
n multiple of 3, see [
6] for more details.
A relation between the maximum number of halving lines and the rectilinear crossing number is given by the following conjecture of [
7]:
Conjecture 1. Every set attaining maximizes the number of halving lines.
The maximum number of halving lines is known for
and
is known for
and
(see [
8]). A table with the gaps between the best lower bound and the best upper bound of
for
can be found in [
8,
9].
An improvement of the best lower bound of
due to some of the authors of the present paper could yield the refutation of the conjecture (see [
10]).
In this paper we achieve an improvement of the current best lower bound of
,
,
and
. These results give more evidence against the conjecture but they do not imply its refutation by themselves. The result for
also implies an improvement by one of the current best lower bound of the maximum number of halving pseudolines for sets in the projective plane with 35 points (
. See [
11] for a formal definition of halving pseudolines).
The examples that give the shifted lower bounds have been obtained by removing two points of the sets that attain the current best lower bound of
,
,
and
included in the rectilinear crossing number web page by Aichholzer (see [
9]). They are inspired by a relation between
and
included in this paper.
These kind of recursive bounds for
are also treated in [
10] for
n an even number and may give new insights for the task of finding
.
We give the following definitions:
Definition 1.1. Given a finite set of points in the plane P, assume that we join each pair of points of P with a straight line segment. The rectilinear crossing number of P ( ) is the number of intersections out of the vertices of said segments. The rectilinear crossing number of n ( ) is the minimum of over all the sets P with n points.
Definition 1.2. Given a set of points , a k-edge of P is a line R that joins two points of P and leaves k points of P in one of the open half planes. We call it the k-half plane.
Definition 1.3. Given a set of points , a halving line of P is a line R that joins two points of P and leaves points of P in one of the open half planes (so a halving line of P partitions P in two equally sized or almost equally sized subsets).
Definition 1.4. Given a set of points , the graph of the halving lines of P is the graph , with and if the line that joins is a halving line of P
Notation: stands for the line joining the points .
We assume that all the sets in the paper are in general position (no three points in a line).
The outline of the rest of the paper is as follows: In section 2 we give the upper bound and the lower bound of in terms of , for n an odd number, in section 3 we give the examples that improve the lower bound of , , and , in section 4 we give a lower bound of in terms of that implies an improvement of the multiplicative constant in the asymptotic best lower bound of for odd values of n and in section 5 we give some concluding remarks.
2. The Relation Between ,
Let us see a result similar of that included in [
10] for even
n, but more general because we do not need the technical condition assumed there.
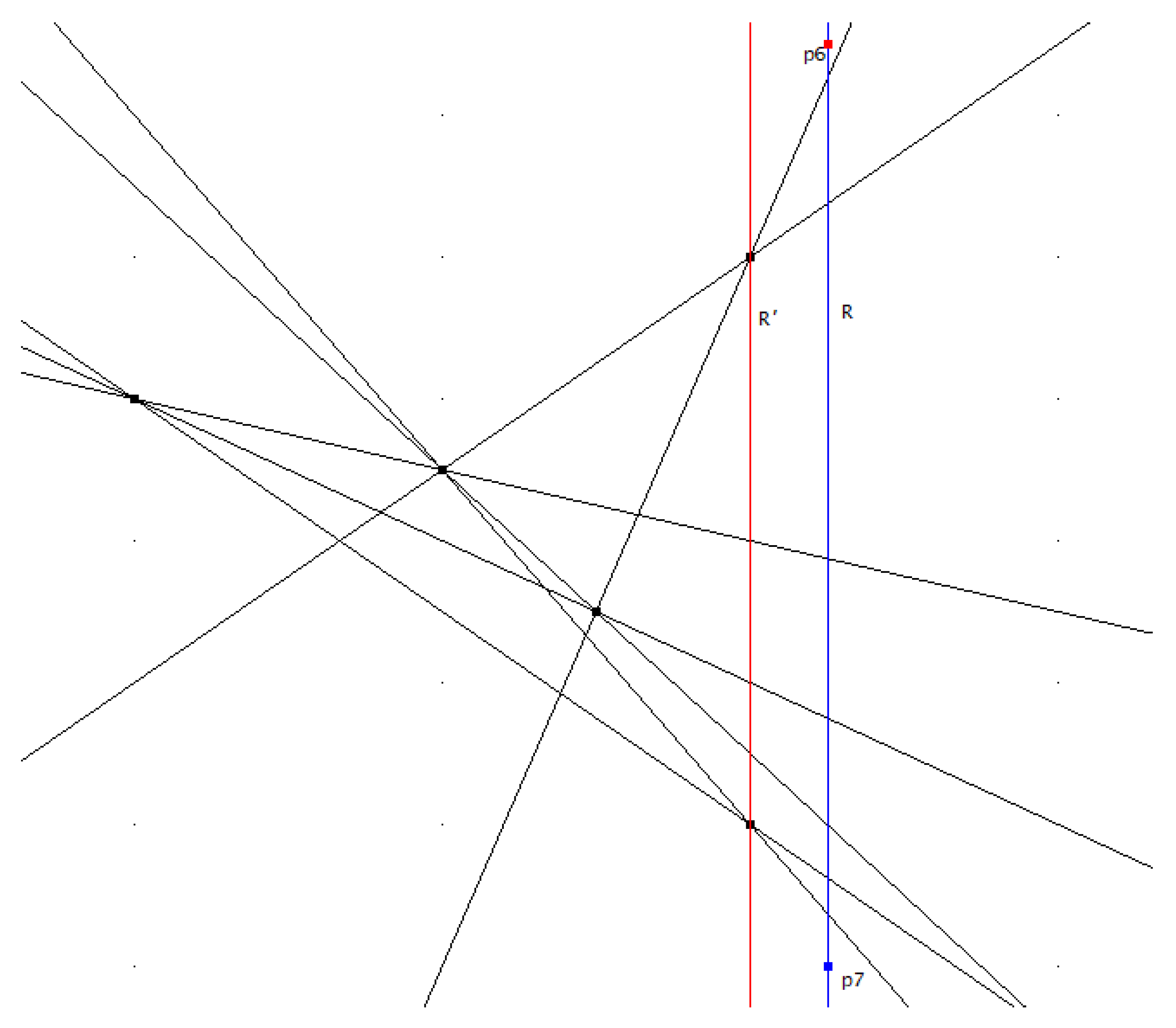
Proposition 2.1. For n an odd number, , it is satisfied that .
Proof. Consider a set
in which
is attained, for
n an odd number,
. Since
, there exist
-edges of
P. Then we take one of them,
, and define a line
R parallel to
, in the
-half plane, so that
R does not contain any point of
P. If we consider two points
in
R such that
is in the intersection of the upper half planes defined by halving lines of
P and
is in the intersection of the lower half planes defined by halving lines of
P, then we have that the halving lines of
P still are halving lines of
because they separate the points
. See
Figure 1 for the case
. We also have that
is now a halving line of
Q, because it leaves
points of
Q in one half plane. Moreover, since
is not a halving line of
Q because it is parallel to a halving line of
Q (
, there are at least other four halving lines of
Q, two containing
and two containing
because they must have an even (and positive) degree in the graph of the halving lines of
Q, as a consequence of the corollary 2.6 of [
1]. This implies that
, as desired. □
Now we see the lower bound of in terms of
Proposition 2.2. For
n an odd number,
, it is satisfied that
Proof. Consider a set
in which
is attained, for
n an odd number,
. Then we have that the number of pairs of points of
P with one of the points in the
-half plane and the other one in the
-half plane of some halving line of
P or in the
-half plane of some halving line of
P or in the
-half plane of some
-edge of
P, allowing repetitions, is:
where
is the number of
-edges of
P, so there exists a pair of points of
P, say
, that belongs to
s of said half planes, with:
If we remove
, then we obtain a set
such that the halving lines and
-edges corresponding to the
s half planes become halving lines of
Q: the halving lines for which we have removed a point in the
-half plane now have
points of
Q in one of the half planes, the halving lines for which we have removed two points in the
-half plane now have
points of
Q in one of the half planes and the
-edges for which we have removed two points in the
-half plane still have
points of
Q in the other half plane, so they are halving lines of
Q. Thus
where
is the number of halving lines of
Q.
By the corollary 1 of [
8] we have that
, so:
and we obtain the desired result by changing
n by
□
The multiplicative factor of the bound has limit as . Since it is close to 1, it gives us the following intuition: by removing two points, in all the possible ways, of a set for which is attained, we can obtain a set of n points with many halving lines. We apply this procedure in the following section to improve the current best lower bound of , , and .
3. The Improvement of the Lower Bound
The inequality of Proposition 2.2 is a worst case one. In particular cases, it may be improved to get better lower bounds for
when
n is an odd number. Concretely, to achieve an improvement for
, we use the example of [
9] of a set with 37 points that gives the current best upper bound of
, with 148 halving lines. The set is:
By the adequate removal of two points, we obtain the following result:
Proposition 3.1.
It is satisfied that
Proof. If we remove the points , from the set P defined above, then we obtain a set Q with 35 points and 137 halving lines, so , as desired.
The set is:
□
Remarks:
- 1.
A program that calculates the 127 halving lines is available upon petition to the authors;
- 2.
Another three sets Q with 35 points and 137 halving lines can be obtained by removing the following pairs of points from P: , , ;
- 3.
The crossing number of the four obtained sets with 137 halving lines is 18810;
- 4.
Since the set P attaining the current best upper bound of satisfies that , we have that if conjecture 1 was true, then .
- 5.
Since
, proposition 3.1 implies that
. This improves by one the current best lower bound of
included in [
11] (it is conjetured that
).
Now, to get an improvement for
, we use the example of [
9] of a set with 61 points that gives the current best upper bound of
, with 302 halving lines and remove two points from it. The set is:
Proposition 3.2.
It is satisfied that
Proof. If we remove the points , from the set P defined above, then we obtain a set Q with 59 points and 286 halving lines, so , as desired.
The set is:
□
Remarks:
- 1.
Another four sets Q with 59 points and 286 halving lines can be obtained by removing the following pairs of points from P: , , , ;
- 2.
The crossing number of the five obtained sets but the second one is 167510. The crossing number of the second set is 167526
- 3.
Since the set P attaining the current best upper bound of satisfies that , we have that if conjecture 1 was true, then .
Proposition 3.3.
It is satisfied that .
Proof. If we remove the points , from the set P included in that attains the current best lower bound for , then we obtain a set Q with 97 points and 553 halving lines, so , as desired.
Remarks:
- 1.
Another two sets Q with 97 points and 553 halving lines can be obtained by removing the following pairs of points from P: , ; , .
- 2.
The crossing number of the three obtained sets except the last one is 1292450; the crossing number of the last set is 1292418.
Proposition 3.4.
It is satisfied that .
Proof. If we remove the points , from the set Q described in Proposition 3.3 that attains the bound , then we obtain a set R with 95 points and 539 halving lines, so , as desired.
Remarks:
- 1.
Another set R with 95 points and 539 halving lines can be obtained by removing the following pair of points from Q: , . In the same way, other two sets with 95 points and 539 halving lines can be obtained by removing the following pairs of points from the first set in Remark 1 of Proposition 3.3: , ; , .
- 2.
The crossing number of the four obtained sets is 1187073. The best upper bound for the minimum crossing number for sets of 95 points is 1186887.
We summarize all the results in the following Table 1:

Table 1: results of the paper; stands for the current best lower bound of , stands for the lower bound of obtained in this paper and stands for the current best lower bound for the maximum number of halving pseudolines.
4. An Asymptotic Improvement
In this section, we apply the technique of the proof of Proposition 2.2 to shift, by a factor of , the multiplicative constant of the current best asymptotic bound of for odd numbers n by relating with .
Proposition 4.1. For an odd number n, , it is satisfied that .
Proof. Let
P be a set in which
is attained, where
is an even number. Then, we have that there are
points of
P (allowing repetitions) in the
-half planes generated by the halving lines of
P, or in the
-half planes generated by the
-edges of
P. Therefore, there exists a point
which belongs to
s of said half planes, with
So, if we remove
p, then we obtain a set
, for which the halving lines are either the halving lines of
P not containing
p or the
-edges of
P such that
p is contained in their
-half planes. Thus, if we call
the number of halving lines of
, we have that
As we have the lower bound
(see the proof of Corollary 2 in [
8]), we obtain
and we obtain the desired result by substituting
m by
. □
5. Conclusions
We have improved the current lower bound on the maximum number of halving lines for planar sets of , , and points. To do this, we have considered as basis sets, the sets P that attains the current best lower bound of , , , and we have removed two points of P in all the possible ways. This way we have obtained four different sets with the new lower bound for the case , five sets for the case , three sets for the case , four sets for the case . They are not combinatorially equivalent for the case because, despite they have the same crossing number, if we remove two points of each one of the four sets in all the possible ways we obtain different sequences of number of halving lines. The same applies for , and .
We have also given a lower bound of in terms of that can be considered as a generalization of the aforementioned examples and also a lower bound of in terms of for n an odd number.
A future line of work could be to try to obtain more examples that shift the current best lower bound of by applying slight perturbations to the points of the four examples. The new examples could yield an improvement of the lower bound of with the technique of removing two points performed in this paper. We could get the same for , and .
Author Contributions: Conceptualization, Javier Rodrigo, Estrella Alonso, Mariló López and Danilo Magistrali; Formal analysis, Javier Rodrigo; Investigation, Javier Rodrigo, Mariló López, Danilo Magistrali and Estrella Alonso; Methodology, Javier Rodrigo, Mariló López , Danilo Magistrali and Estrella Alonso; Software, Mariló López, Estrella Alonso and Danilo Magistrali; Validation, Javier Rodrigo.
Data Availability Statement: The data presented in this study are available on request from the corresponding author.
Conflicts of Interest: The authors declare no conflict of interest.
References
- P. Erdõs, L. Lovász, A. Simmons and E. G. Strauss, Dissection graphs of planar point sets, in: J. N. Srivastava (Ed.), A Survey of Combinatorial Theory, North-Holland, 1973, pp. 139-154.
- D. Eppstein, Set of points with many halving lines, Technical Report ICS-TR-92-86. University of California, Irvine, Department of Information and Computer Science, 1992.
- G. Tóth, Point sets with many k-sets, Discrete & Computational Geometry 2001, 26, pp. 187-194. [CrossRef]
- G. Nivasch, An improved, simple construction of many halving edges, in: J. E. Goodman et al., (Eds.), Surveys on Discrete and Computational Geometry: Twenty Years Later, Contemporary Mathematics, AMS, 2008, pp. 299-305.
- T. K. Dey, Improved bounds for planar k-sets and related problems. Discrete and Computational Geometry 1998, 19, pp. 373–382. [CrossRef]
- B. M. Ábrego, M. Cetina, S. Fernández-Merchant, J. Leaños and G. Salazar. 3-symmetric and 3-decomposable geometric drawings of Kn Discrete and Applied Mathematics 2010, 158, 1240–1258. [CrossRef]
- O. Aichholzer, J. García, D. Orden and P. Ramos. New lower bounds for the number of (<=k)-edges and the rectilinear crossing number of Kn. Discrete and Computational Geometry 2007, 38, 1–14. [CrossRef]
- B. M. Ábrego, M. Cetina, S. Fernández-Merchant, J. Leaños and G. Salazar. On (<=k)-edges, crossings, and halving lines of geometric drawings of Kn. Discrete and Computational Geometry 2012, 48, 192–215. [CrossRef]
- O. Aichholzer. On the rectilinear crossing number (2019). Available online: http://www.ist.tugraz.at/staff/aichholzer/crossings.html.
- J. Rodrigo and M. López. An improvement of the lower bound on the maximum number of halving lines in planar sets with 32 points. Electronic Notes in Discrete Mathematics 2018, 68, 305–310. [CrossRef]
- S. Bereg and M. Haghpanah. New algorithms and bounds for halving pseudolines. Discrete Applied Mathematics 2022, 319, 194–206. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).