Submitted:
20 December 2024
Posted:
24 December 2024
You are already at the latest version
Abstract
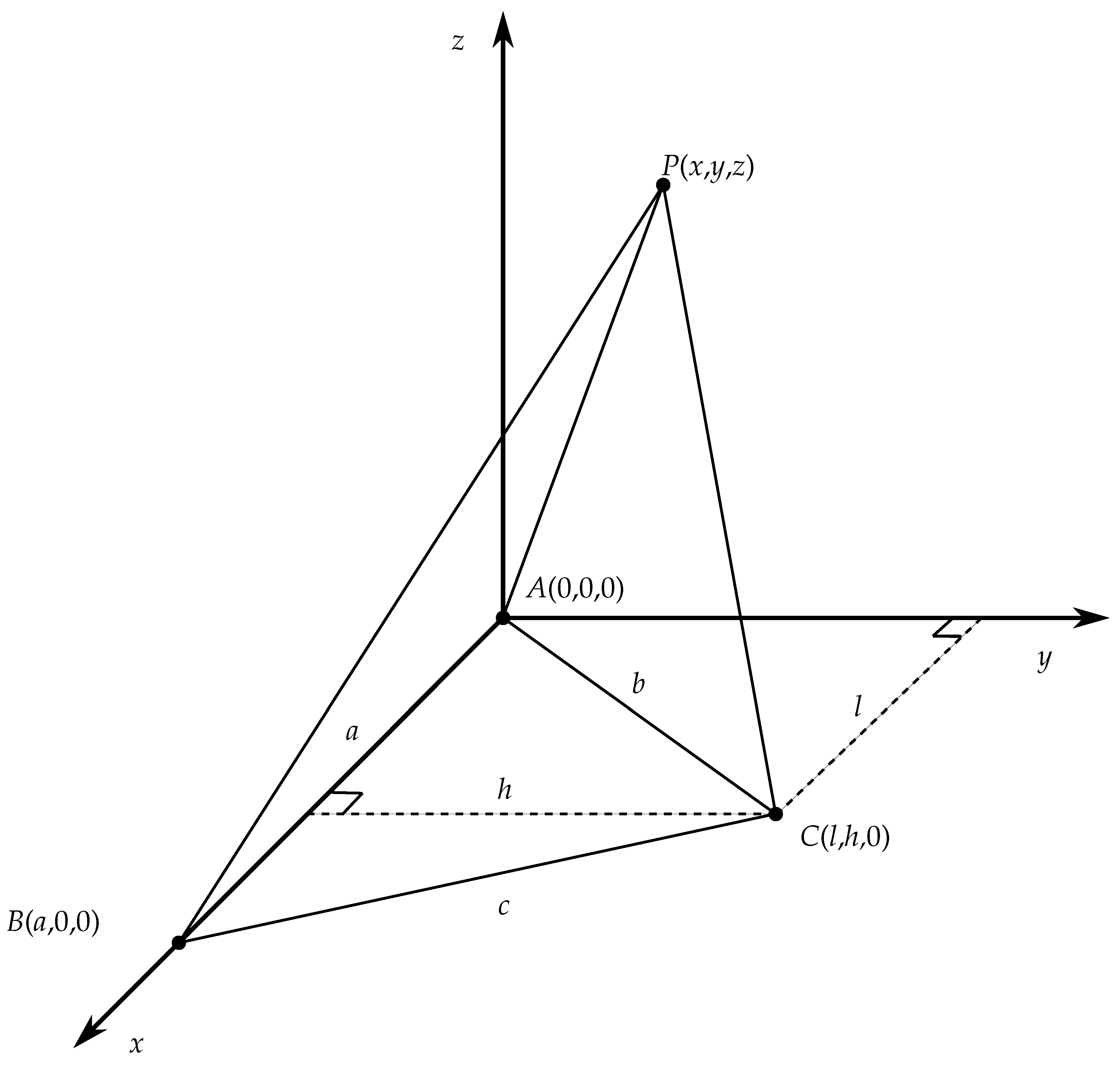
In a foundational study, dos Santos Bernardes 2024 explored how connecting points on a triangle's midsegment to its vertices forms triangles that conform to the Pythagorean theorem in both two- and three-dimensional spaces, unveiling deeper geometric relationships and extending Pythagorean principles to spatial geometry with an implicit solution. Building on this work, I present the derivation of an explicit solution, further elucidating these geometric relationships and enhancing our understanding of their spatial applications.
Keywords:
1. Introduction
2. Derivation of an explicit equation for the pythagorean tetrahedron
References
- dos Santos Bernardes, M. A. Introducing Novel Geometric Insights and Three-Dimensional Depictions of the Pythagorean Theorem for Any Triangles. International Journal of Pure and Applied Mathematics Research 2024, 4(2), 47–58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




