Optimal Control of a Harmonic Oscillator with Parametric Excitation

1. Introduction

Time-optimal control of dynamical systems is a fundamental problem in control theory, with widespread applications in engineering and physics [1,2]. This paper focuses on the optimal control of a harmonic oscillator subjected to excitation by a time-varying frequency, addressing the complexities associated with time-varying dynamics, parametric excitation, and frequency constraints. Optimal control problems involving time-dependent parameters and constraints have been extensively studied [3,4,5].However, to the best of our knowledge, the specific case of a harmonic oscillator with its frequency constrained to two discrete values, combined with the presence of viscous friction, poses a unique challenge [6,7]. Revisiting this problem, the natural question of determining the minimum time required for the system to transition between two given states was first raised in [8]. Our paper provides a comprehensive answer to that question.

The system’s dynamics are significantly affected by the switching between frequencies, making the determination of the optimal switching strategy a challenging and nontrivial task [9].

Our approach builds upon prior research in parametric excitation [10,11], where varying system parameters are employed to influence the system’s behavior, as well as on time-optimal control methods for systems with bounded control input [12,13]. An illustrative example closely related to our problem is the variable-length pendulum. In a classical pendulum, the length is fixed, resulting in a constant natural frequency. However, allowing the pendulum’s length to vary over time introduces parametric excitation, analogous to the frequency variation in the harmonic oscillator. The time-optimal control problem for the variable-length pendulum involves determining a length variation strategy that transitions the system from an initial state to a final state in minimal time.

Drawing inspiration from this analogy, we combine analytical techniques with control theory under constrained frequency parameters to develop methods for solving the optimal control problem for the harmonic oscillator. The significance of this study lies in its practical applications to systems requiring rapid state transitions under frequency constraints. For instance, in mechanical vibration systems, efficiently controlling oscillations is critical for ensuring stability and performance [14,15]. Similarly, in signal processing and communication systems, rapid frequency modulation can significantly enhance performance and adaptability [16]. In aerospace engineering and robotics, the ability to swiftly and precisely control oscillatory components within specified constraints is essential [17,18]. For example, the time-optimal control of a robotic arm with multiple joints involves solving a complex system of coupled equations, where the computational burden can become prohibitive for real-time applications. Autonomous vehicles also require near-instantaneous control adjustments to maintain safety and performance under dynamic conditions [19]. However, solving such complex optimal control problems in real time often proves infeasible due to the high computational demands. This study provides a framework to address these challenges, offering analytical and computational tools to improve the efficiency and practicality of time-optimal control solutions.

Optimal control strategies for such systems often require switching between discrete parameter values or continuously varying parameters within defined bounds. The primary challenge lies in designing a control law that minimizes the transition time while adhering to physical constraints and boundary conditions.

Previous studies have shown that efficient control strategies involve rapid adjustments of system parameters, similar to switching in harmonic oscillators. However, practical implementations must account for constraints, such as the maximum allowable rates of change, to ensure stability and prevent mechanical failure. These considerations are crucial for translating theoretical control strategies into real-world applications where robustness and safety are paramount.

In this paper, we provide a comprehensive analysis of the optimal control problem for a harmonic oscillator with frequency constraints. We investigate various boundary scenarios, construct feasible transition sets, and determine the optimal switching times between frequencies. The techniques developed in this study are adaptable to other systems facing similar control challenges, offering a robust and versatile framework for time-optimal control across a wide range of applications.

The remainder of the paper is structured as follows: Section 2: Formulation of the time-optimal control problem and discussion of mathematical preliminaries. Section 3: Development of analytical methods for determining optimal switching strategies. Section 4: Exploration of boundary scenarios with illustrative examples. Section 5: Practical implications and applications of the results. Section 6: Summary of the findings and directions for future research.

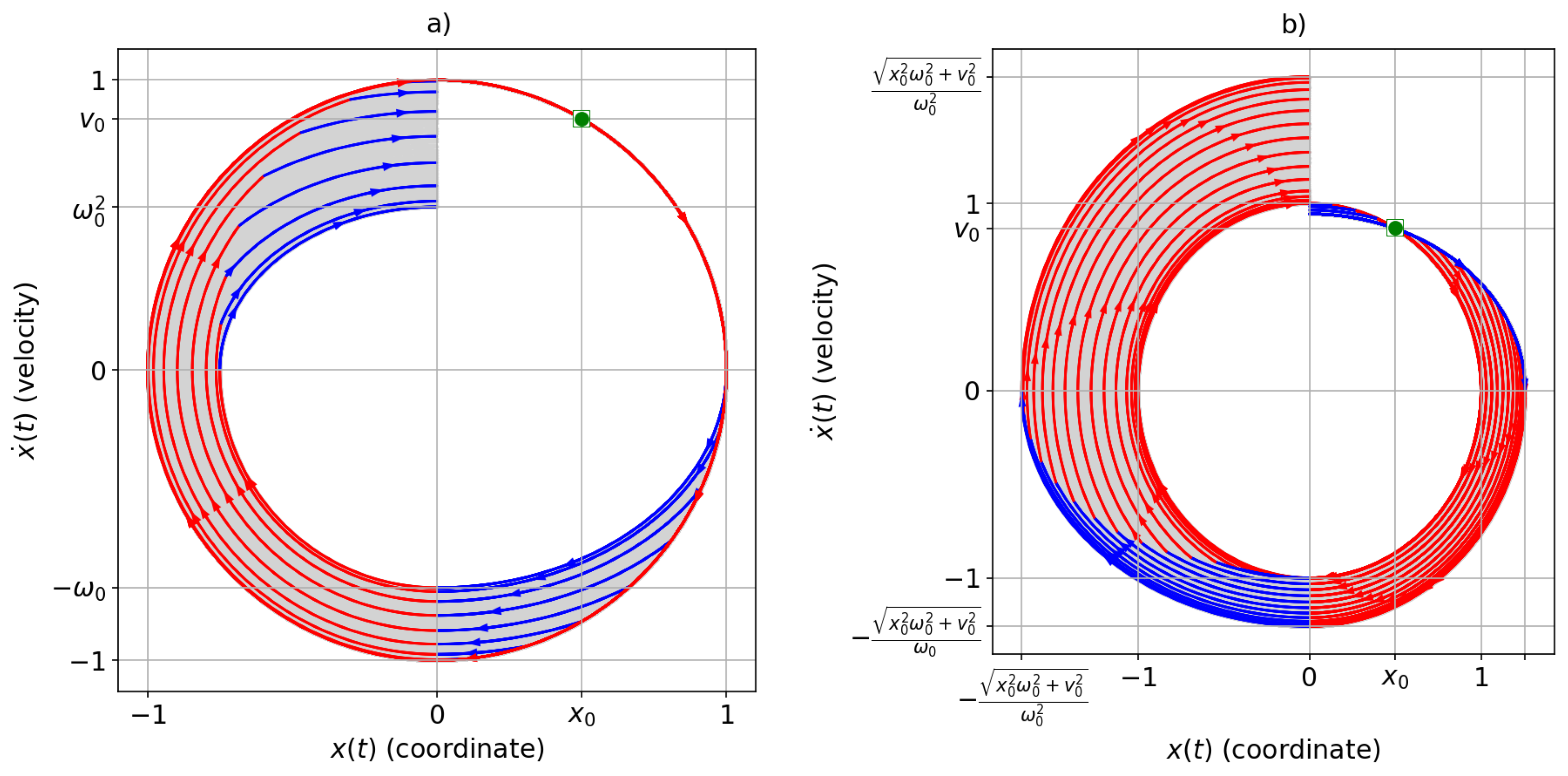
2. Preliminaries and Problem Formulation

Let us consider the following optimal control problem for a harmonic oscillator

$$\left\{\begin{array}{c}\ddot{x}\left(t\right)+{\omega }^2\left(t\right)x\left(t\right)=0,0\le t\le T;\hfill \\ x\left(0\right)=x_0,\dot{x}\left(0\right)=v_0,x_0^2+v_0^2\ne 0;\hfill \\ x\left(T\right)=x_T,\dot{x}\left(T\right)=v_T,x_T^2+v_T^2\ne 0;\hfill \\ 0<{\omega }_0\le \omega \left(t\right)\le 1,0\le t\le T;\hfill \\ T\to \underset{\omega \left(t\right)}{min}.\hfill \end{array}\right.$$

(1)

It is required to determine the control function $\omega \left(t\right)$ (frequency) to transfer the system from the initial state $(x_0,v_0)$ to the final state $(x_T,v_T)$ in minimal time. It is important to note that the boundary conditions cannot be zero, as the system described by $\left(\right)$ becomes uncontrollable in such cases.

This problem falls into the category of unstable bilinear optimal control problems.

In this paper, we will prove the existence of a solution to (1), outline its key properties, and present an algorithm for constructing both the optimal control and the corresponding optimal trajectory.

Remark 1.

Let us note two important properties that will be used later.

I. Let $x\left(t\right),$$\omega \left(t\right)$, and T be the solution to problem (1). Consider the substitution: $y\left(t\right)=x\left(t\right)/M,$$M=\mathrm{const},$ then the function $y\left(t\right)$ will solve the following problem

$$\left\{\begin{array}{c}\ddot{y}\left(t\right)+{\omega }^2\left(t\right)y\left(t\right)=0,0\le t\le T;\hfill \\ y\left(0\right)=x_0/M,\dot{y}\left(0\right)=v_0/M,y^2\left(0\right)+{\dot{y}}^2\left(0\right)\ne 0;\hfill \\ y\left(T\right)=x_T/M,\dot{y}\left(T\right)=v_T/M,y^2\left(T\right)+{\dot{y}}^2\left(T\right)\ne 0,\hfill \end{array}\right.$$

i.e., the trajectory $x\left(t\right)$ can be scaled.

II. Let $x\left(t\right),$${\omega }_x\left(t\right)$, and T be the solution to problem (1). Then the functions $y\left(t\right)=x(T-t)$ and ${\omega }_y\left(t\right)={\omega }_x(T-t)$ will solve the following problem

$$\left\{\begin{array}{c}\ddot{y}\left(t\right)+{\omega }_y^2\left(t\right)y\left(t\right)=0,0\le t\le T;\hfill \\ y\left(T\right)=x_0,\dot{y}\left(T\right)=-v_0,x_0^2+v_0^2\ne 0;\hfill \\ y\left(0\right)=x_T,\dot{y}\left(0\right)=-v_T,x_T^2+v_T^2\ne 0,\hfill \end{array}\right.$$

with reversed time dynamics, satisfying the corresponding boundary conditions for the reversed time interval. This symmetry property can be used to simplify the analysis of the problem or construct dual solutions based on the time-reversed control and trajectory. That is, the excitation problem ($x_0^2+v_0^2\le x_T^2+v_T^2$) and the damping problem ($x_0^2+v_0^2>x_T^2+v_T^2$) (see the Remark 2 to Theorem 1) of oscillations are equivalent.

In [3], a similar optimal control problem is analyzed for the specific case where $v_0=v_T=0$:

(2)

This scenario simplifies the boundary conditions, focusing on transferring the system between states with zero initial and final velocities. This serves as a foundational case for understanding more general boundary conditions in optimal control problems. It is demonstrated that the optimal solution to this problem exhibits an oscillatory nature, and the corresponding optimal control is a periodic function with a period equal to one semi-oscillation (Figure 1). The formulas for solving problem (2) are provided as a reference in Appendix A.

Next, the relationship between the solutions of problems (1) and (2) will be demonstrated. By utilizing the analytical solution formulas from problem (2), a general solution to system (1) with arbitrary boundary conditions will be derived.

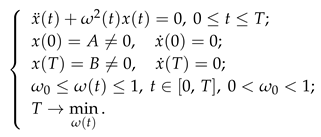
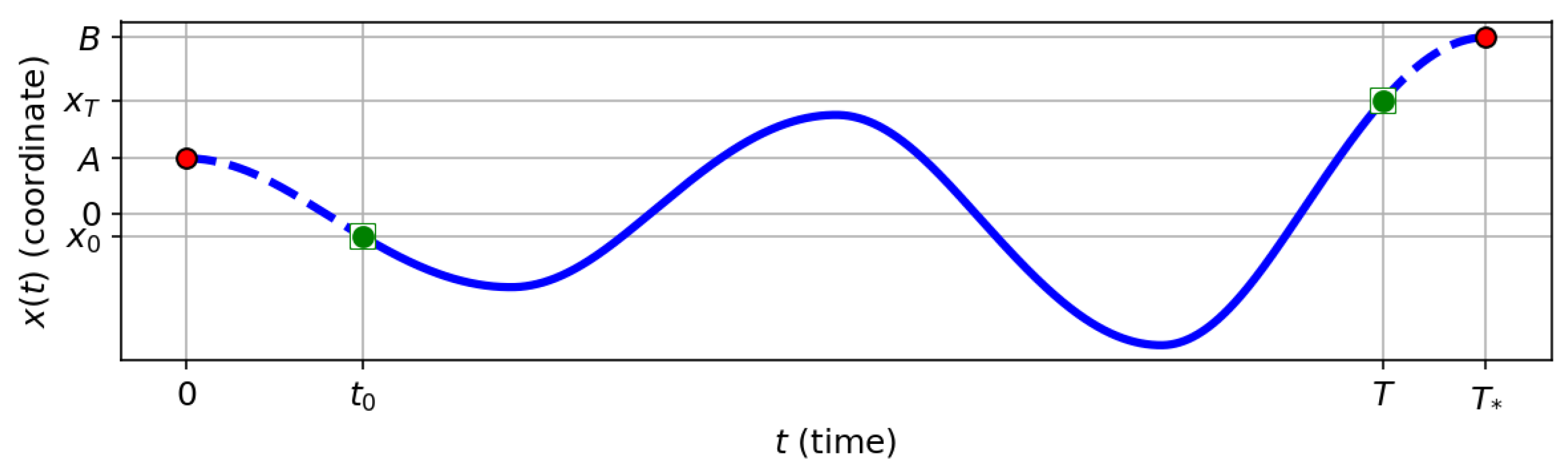
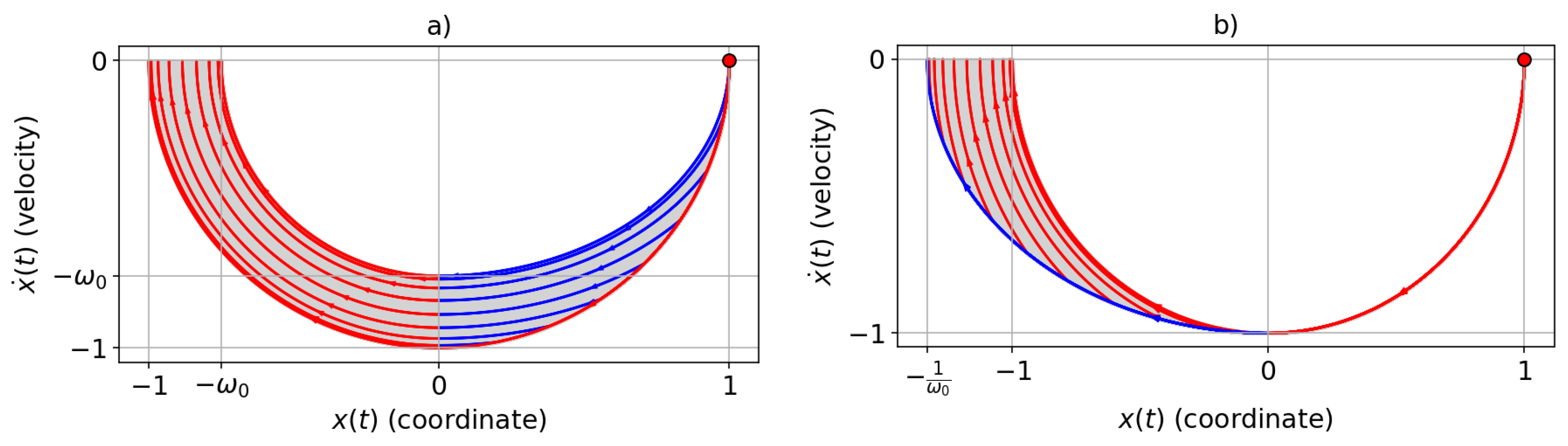
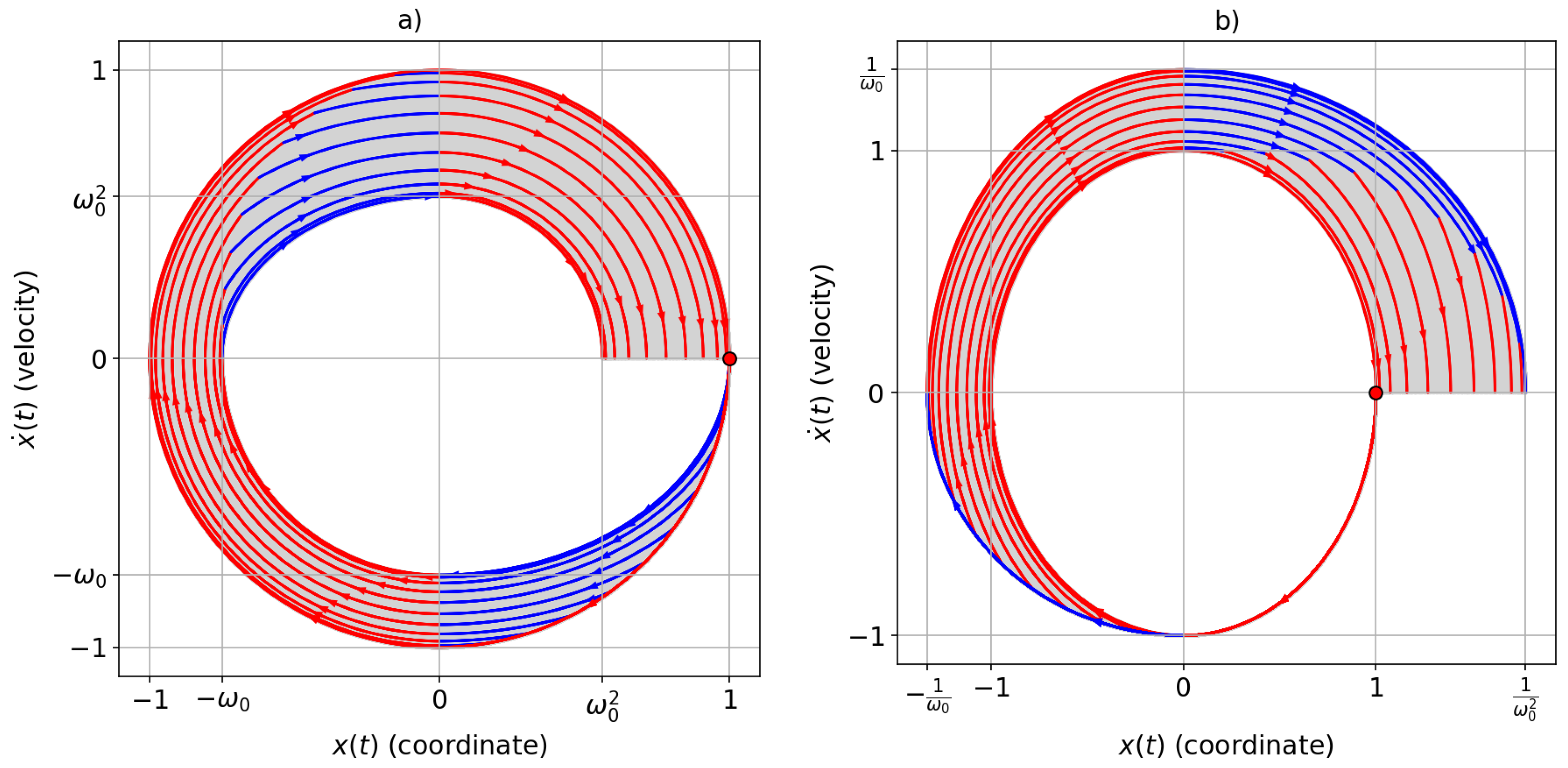
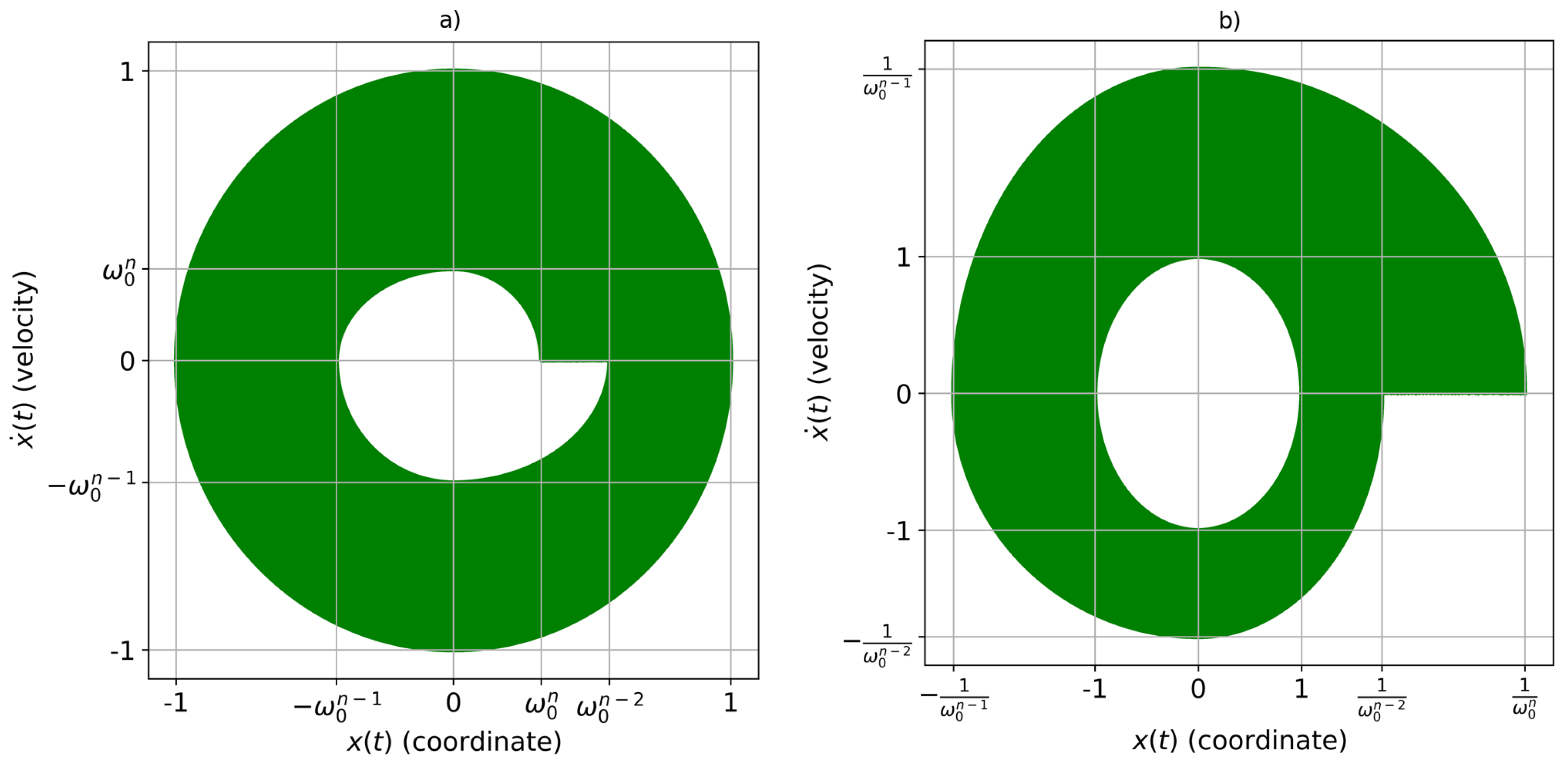
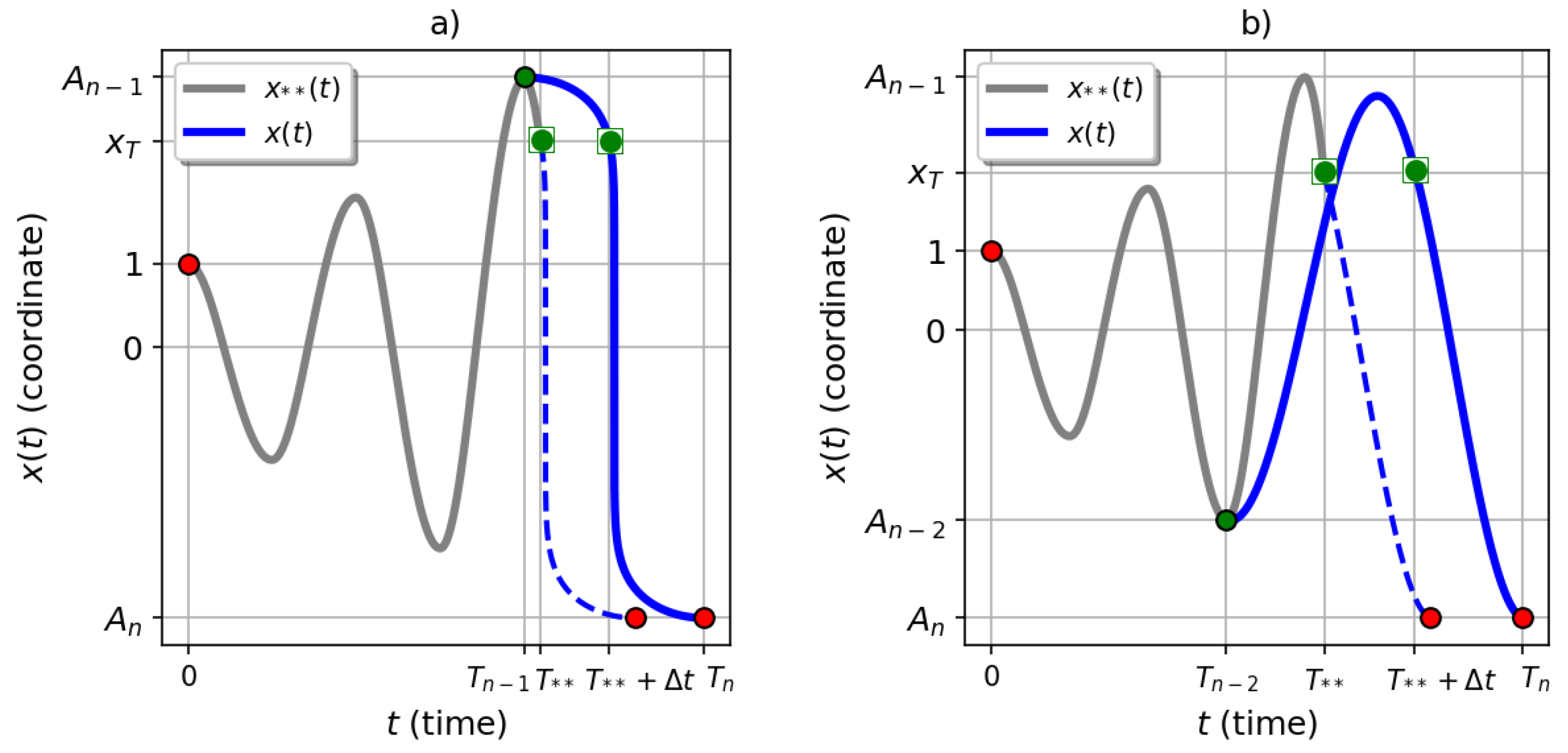
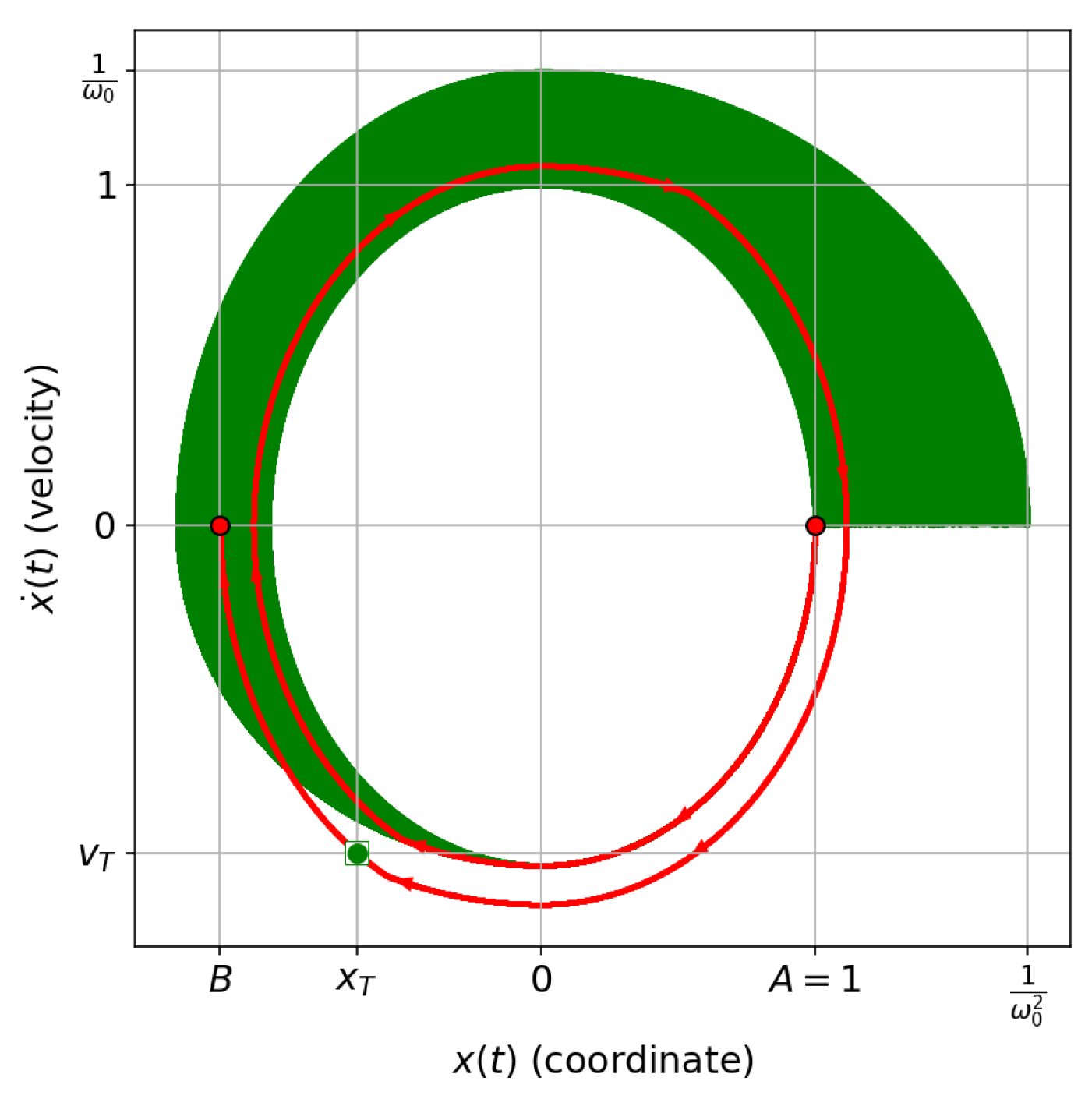
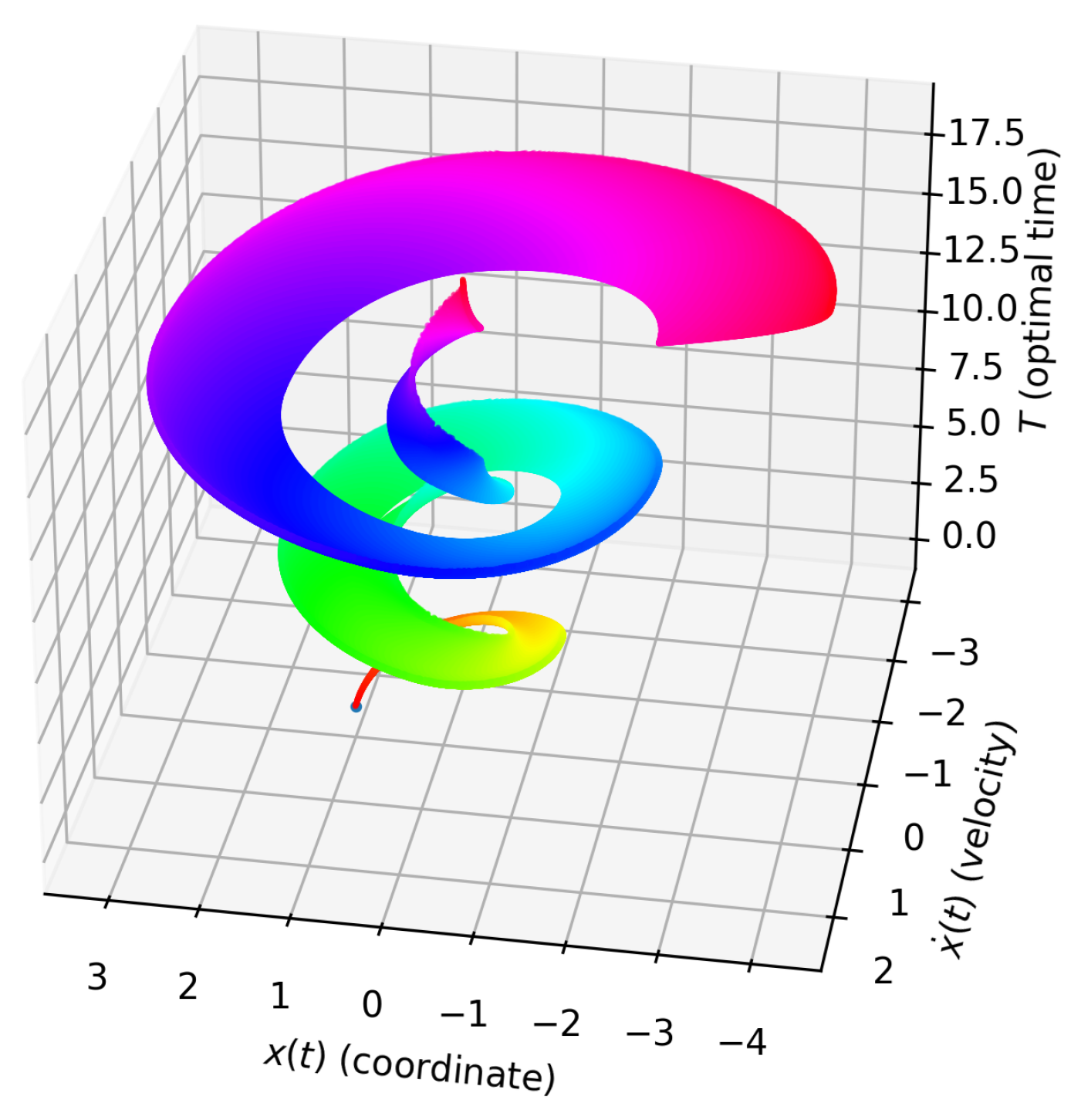
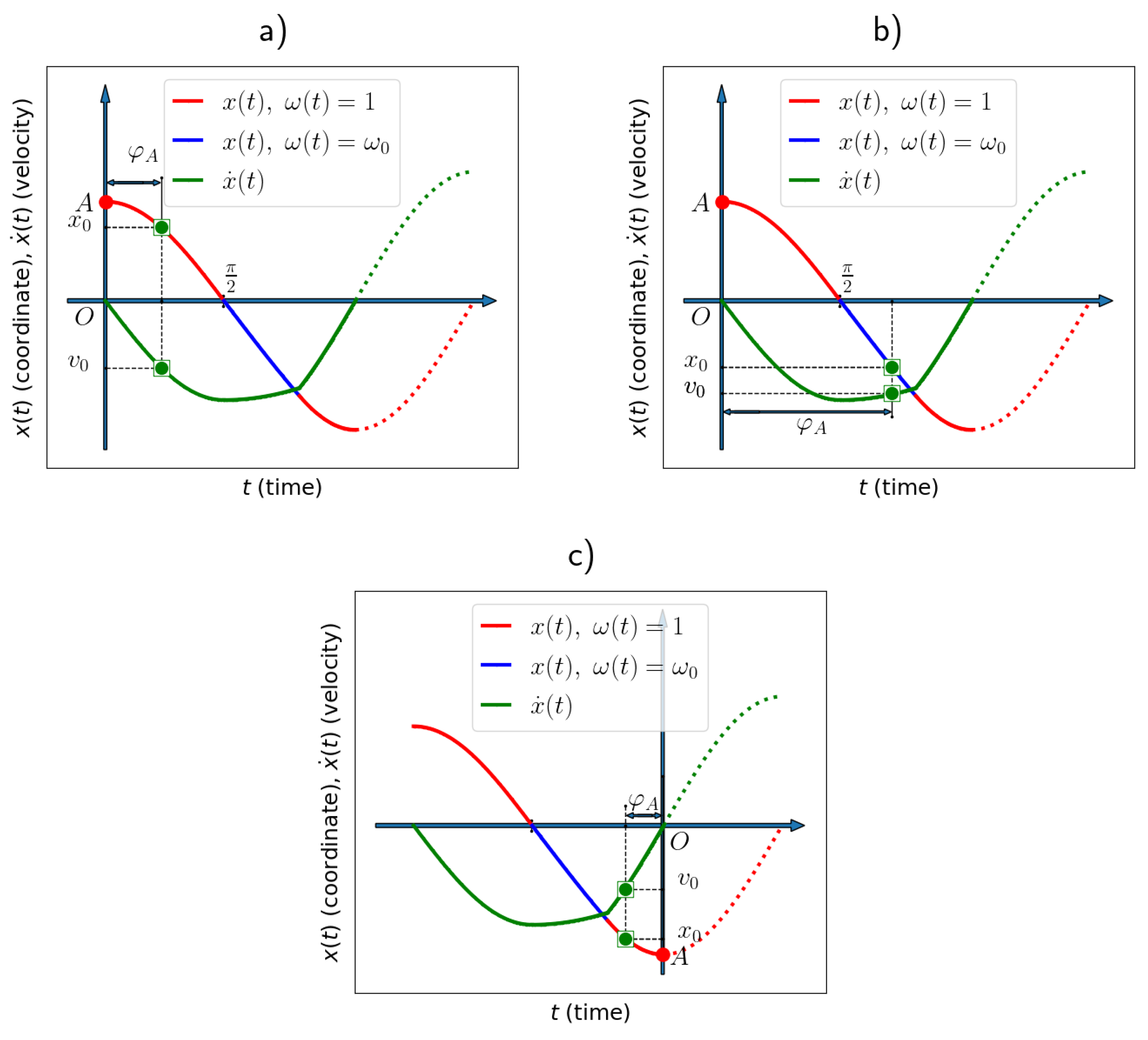
3. Solution of the Problem (1): Theoretical Analysis

The nature and structure of the solution to the optimal control problem (1), are determined by establishing a connection between the solutions of problems (1) and (2). Problem (1) addresses arbitrary initial and final velocities, while problem (2) focuses on the specific case where the initial and final velocities are zero $v_0=v_T=0$.

Theorem 1.

For any initial conditions $x_0$ and $v_0$ and final conditions $x_T$ and $v_T$ in problem (1), the following holds: there exist constants A and B, a periodic control ${\omega }_{*}\left(t\right)$ of the form shown in Figure 1, and a corresponding trajectory $x_{*}\left(t\right)$ that satisfies the differential equation and boundary conditions of system (2) on some interval $[0,T_{*}]$ (where $T_{*}$ may not be the optimal), such that:

1. Existence of Key Time Points: There exist two moments in time $t_0$ and T ($0\le t_0<T\le T_{*}$) such that $x_{*}\left(t_0\right)=x_0$, ${\dot{x}}_{*}\left(t_0\right)=v_0$, $x_{*}\left(T\right)=x_T$, ${\dot{x}}_{*}\left(T\right)=v_T$ These conditions ensure that the trajectory $x_{*}\left(t\right)$ passes through the specified initial and final states, as illustrated in Figure 2.

2. Optimal Solution to Problem (1): The pair $x_{*}\left(t\right)$, ${\omega }_{*}\left(t\right)$ for $t\in [t_0,T]$ is a solution to the optimal control problem (1).

Proof of Theorem 1.

The proof begins by considering a special case of the problem where $v_0=0$. For this case, it is shown that a periodic control $\omega \left(t\right)$ can be constructed to generate a trajectory $x\left(t\right)$ satisfying the required boundary conditions. Next, the method used for this special case is extended to the general scenario with arbitrary $v_0$ .

I. In the case $v_0=0$,the scaling property of the trajectory $x\left(t\right)$ allows the assumption $x_0=A=1$ and $t_0=0$. Under this assumption, the original problem can be reformulated into the following equivalent problem:

(3)

First, the existence of the value B in problem (2) will be established. In [3], it is demonstrated that the optimal control for problem (2) during each semi-oscillation takes the form illustrated in Figure 1. Here, $T_1$ denotes the duration of a single semi-oscillation, and at one of the control switching moments, $t=t_1$ or $t=t_2$, the condition $x\left(t\right)=0$ is satisfied.

Consider the reachable set of the controlled system (2) along trajectories generated by periodic controls of the form depicted in Figure 1.

First, construct the reachable set for a single semi-oscillation, which consists of the set of states $(x\left(t\right),\dot{x}\left(t\right))$ that the controlled system can achieve by performing at most one semi-oscillation, starting from the initial point $(1,0)$ corresponding to the initial condition of problem (3). It is known [3] that, on individual segments where the control is constant, the optimal trajectory is always described by one of two cosine functions: $Ccos(t+\phi )$ for control $\omega \left(t\right)=1$ or $Ccos({\omega }_{0}t+\phi )$ for control $\omega \left(t\right)={\omega }_0$. Here, C and $\phi$ are constants that depend on the specific segment where the control value remains constant.

For $\omega \left(t\right)=1$, the trajectory on the phase plane $(x,\dot{x})$ is represented by an arc of a circle, $x^2\left(t\right)+{\dot{x}}^2\left(t\right)=C^2$, as the solution is $x\left(t\right)=Ccos(t+\phi )$. For $\omega \left(t\right)={\omega }_0$, the trajectory becomes an arc of an ellipse, $x^2\left(t\right)+{\dot{x}}^2\left(t\right)/{\omega }_0^2=C^2$, since the solution takes the form $x\left(t\right)=Ccos({\omega }_{0}t+\phi )$.

The reachable set, depending on whether the amplitude of oscillations increases or decreases, is divided into two distinct parts, as shown in Figure 3. Over time, the motion along the trajectory on the phase plane consistently proceeds in a counterclockwise direction.

Figure 3 (a) illustrates oscillations with a decreasing amplitude. In this case, the second control switch occurs when the variable $x\left(t\right)$ changes sign. As a result, in the fourth quadrant, the reachable set is bounded by two curves: an arc of the circle $x^2\left(t\right)+{\dot{x}}^2\left(t\right)=1$ and an ellipse defined by $x^2\left(t\right)+{\dot{x}}^2\left(t\right)/{\omega }_0^2=1$. In contrast, in the third quadrant, no control switches occur, and all trajectories correspond to arcs of a circle.

Figure 3 (b) represents oscillations with an increasing amplitude. In this scenario, the first control switch occurs at the moment when the variable $x\left(t\right)$ changes its sign. Consequently, in the fourth quadrant, the reachable set is limited to an arc of a circle. In contrast, in the third quadrant, the reachable set starts to expand, bounded by two curves: an arc of the circle $x^2\left(t\right)+{\dot{x}}^2\left(t\right)=1$ and an ellipse defined by ${\omega }_0^2{x}^2\left(t\right)+{\dot{x}}^2\left(t\right)=1$.

Similarly, construct the reachable set for two semi-oscillations (Figure 4), and by continuing in the same manner, construct the reachable set for n (n even) semi-oscillations (Figure 5).

As n approaches infinity, the reachable set expands and encompasses all points on the phase plane except for the origin.

Thus, for any given terminal point $(x_T,v_T)$, there exists a trajectory in problem (2), generated under a specific type of control, that passes through this point at $t=T$. There may be multiple such trajectories; therefore, the one with the minimal time T is chosen. Extending this trajectory to its intersection with the x-axis,yields the required value of B and the final time $T_{*}$. Denote the selected trajectory and its corresponding control by $x_{*}\left(t\right)$ and ${\omega }_{*}\left(t\right)$ respectively (though this trajectory as a whole may not be optimal in problem (2)).

It has been shown that the pair $x_{*}\left(t\right)$, ${\omega }_{*}\left(t\right)$ satisfies the differential equation and boundary conditions (3) on $[0,T]$.

II. Now, it will be proven that $x_{*}\left(t\right)$, ${\omega }_{*}\left(t\right)$, $t\in [0,T]$ ($t_0=0$) , is also a solution to the optimal control problem (3), meaning that the time T is minimal.

Assume that this is not the case. Then there exist $x_{**}\left(t\right)$, ${\omega }_{**}\left(t\right)$, $T_{**}<T$, which satisfy the differential equation and the boundary conditions of problem (3) on the interval $[0,T_{**}]$, and the time $T_{**}$ is minimal in the problem (3) (Figure 6). The optimal trajectory $x_{**}\left(t\right)$ performs $n-1$ complete semi-oscillations and one final incomplete semi-oscillation. In the case where $n=1$, complete semi-oscillations may be absent. Let the moments when the derivative $x_{**}\left(t\right)$ equals zero be denoted as $T_1,T_2,\cdots ,T_{n-1}$, and the corresponding amplitudes as $A_i=x_{**}\left(T_i\right)$, where $i=1,\cdots ,n-1$.

According to Bellman’s principle of optimality [20], any part of the optimal trajectory $x_{**}\left(t\right)$ is also optimal in the problem (2) or (3). Here, the autonomy of the controlled system can be utilized, meaning the coefficients are independent of time. This allows any moment in time to be considered as the initial one, not necessarily $t=0$ .

Thus, on each semi-oscillation, as well as on any two consecutive semi-oscillations, the trajectory satisfies all the conditions of problem (2). Using the properties [3] of the solution to problem (2), it can be concluded that, over all complete semi-oscillations, the control ${\omega }_{**}\left(t\right)$ is a periodic function and takes the form depicted in Figure 1.

It remains to prove that on the final incomplete semi-oscillation the control has the same structure. From this, it will follow that the trajectories $x_{*}\left(t\right)$ and $x_{**}\left(t\right)$ coincide.

Let us consider the last incomplete semi-oscillation of the trajectory $x_{**}\left(t\right)$. Denote by $x\left(t\right)$ the trajectory obtained under the control of the type shown in Figure 1, satisfying the initial conditions $x\left(T_{n-1}\right)=A_{n-1}$, $\dot{x}\left(T_{n-1}\right)=0$, and at some moment $T_{**}+\Delta t$, also satisfying the boundary conditions of problem (3): $x(T_{**}+\Delta t)=x_T$, $\dot{x}(T_{**}+\Delta t)=v_T$. Here, $\Delta t\ge 0$ because the trajectory $x_{**}\left(t\right)$ is optimal (Figure 7 (a)).

Extend this trajectory up to the first moment $T_n$ where $\dot{x}\left(T_n\right)=0$. If this extension is not unique, select any control of the type shown in Figure 1 and the corresponding trajectory.

The resulting trajectory will be optimal on the interval $[T_{n-1},T_n]$ in a problem of the type (2).

Then, let us construct a new trajectory (Figure 7 (a)):

$$x_{***}\left(t\right)=\left\{\begin{array}{cc}{x}_{**}\left(t\right),\hfill & \mathrm{for}t\in [T_{n-1},T_{**}),\hfill \\ x(t+\Delta t),\hfill & \mathrm{for}t\in [T_{**},T_n-\Delta t].\hfill \end{array}\right.$$

(4)

This trajectory will satisfy the same boundary conditions as the trajectory $x\left(t\right)$, but on a smaller interval $[T_{n-1},T_n-\Delta t]$, which contradicts the optimality of $x\left(t\right)$.

Hence, $\Delta t=0$, and the trajectories $x_{**}\left(t\right)$ and $x\left(t\right)$ coincide. Consequently, the control ${\omega }_{**}\left(t\right)$ on the interval $[T_{n-1},T_{**}]$ has the same structure as shown in Figure 1.

It remains to prove that the switching points of the control on the last incomplete semi-oscillation (if they exist) coincide with the switching points on complete semi-oscillations.

Consider the last one complete and one incomplete semi-oscillation of the trajectory $x_{**}\left(t\right)$ (Figure 7 (b)). In a similar way, it can be shown that the control ${\omega }_{**}\left(t\right)$ on the interval $[T_{n-2},T_{**}]$ also has the same structure as shown in Figure 1.

Thus, the statement of the theorem for the case $v_0=0$ is proven.

The existence of a solution to problem (1) for arbitrary values of $x_0$ and $v_0$ is proven in a similar manner. Note some minor differences. Using the scalability property of the system (1), we can assume that $x_0^2+v_0^2=1$, meaning the initial point lies on the unit circle in the phase plane. Figure 8 shows the reachable set for no more than two semi-oscillations when the initial point is located in the first quadrant of the coordinate system. The reachable set is expanded similarly to the previous case and captures all points in the phase plane except the origin.

Thus, there exist a trajectory $x_{*}\left(t\right)$ and a control function ${\omega }_{*}\left(t\right)$ of the type shown in Figure 1, which satisfy the differential equation and the boundary conditions (1) on some interval $[t_0,T]$.

The proof is complete. □

Remark 2.

From the proof of the theorem (see Figure 8), it follows that $x^2\left(t\right)+{\dot{x}}^2\left(t\right)$ is non-decreasing in the case of excitation and non-increasing in the case of damping oscillations. Consequently, the boundary conditions uniquely determine the nature of the oscillations ($x_0^2+v_0^2<x_T^2+v_T^2$ indicates excitation, $x_0^2+v_0^2>x_T^2+v_T^2$ indicates damping, and if $x_0^2+v_0^2=x_T^2+v_T^2$, the oscillations have a constant amplitude).

Remark 3.

It is possible that the trajectory $x_{*}\left(t\right)$ is not optimal on the segment $[0,T_{*}]$. For example, Figure 9 shows the situation when the optimal trajectory (red curve) connecting the initial point $(1,0)$ and the final point $(x_T,v_T)$ extends to the intersection with the horizontal axis, and in this case the trajectory $x_{*}\left(t\right)$ contains 3 complete semi-oscillations. But the optimal trajectory connecting the points $(1,0)$ and the endpoint $(B,0)$ contains only one semi-oscillation, since the point $(B,0)$ belongs to the reachability set for at most two semi-oscillations (area highlighted in green).

Remark 4.

Using the established periodicity of the optimal control and its specific structure, combined with the method of constructing the reachable set from the proof of Theorem 1, it is possible to plot the dependence of the optimal time in problem 1, it is possible to plot the dependence of the optimal time in problem(3) on the endpoint $(x_T,v_T)$ (Figure 10). Notably, this plot reveals a discontinuous relationship between the optimal time and the endpoint.

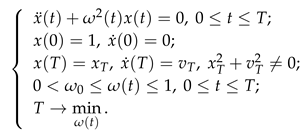
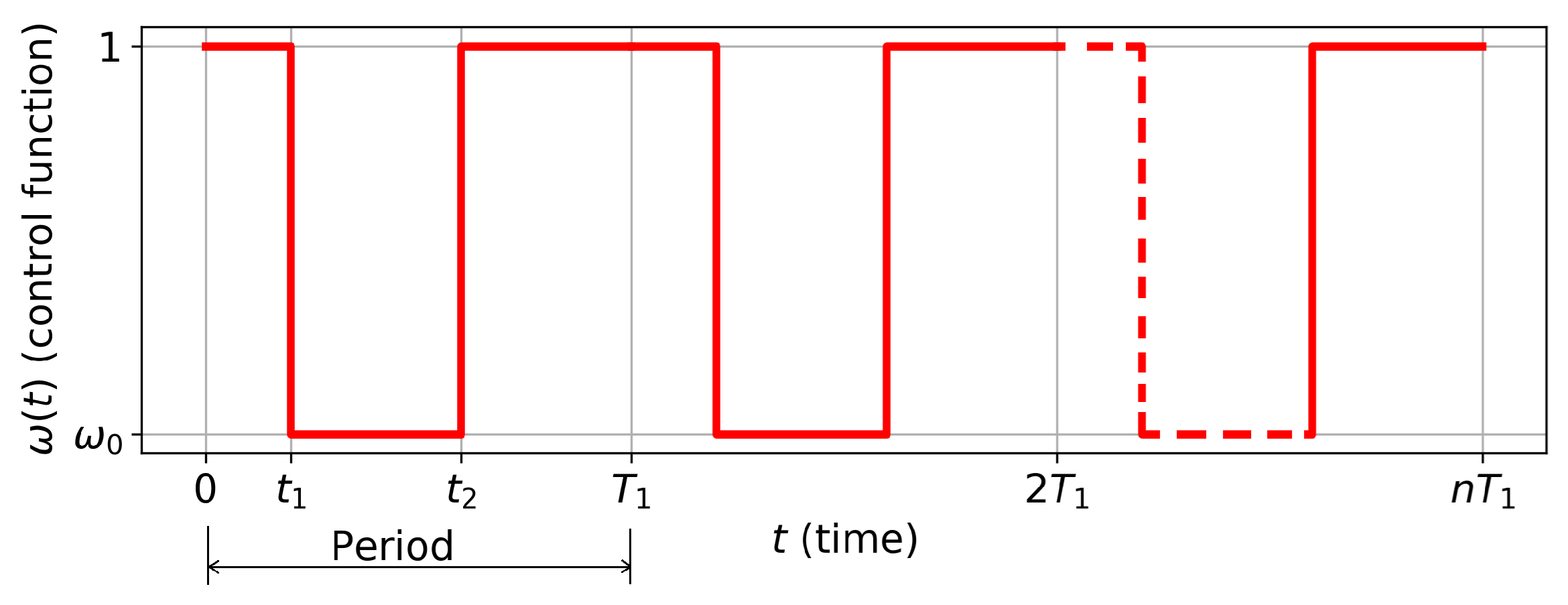
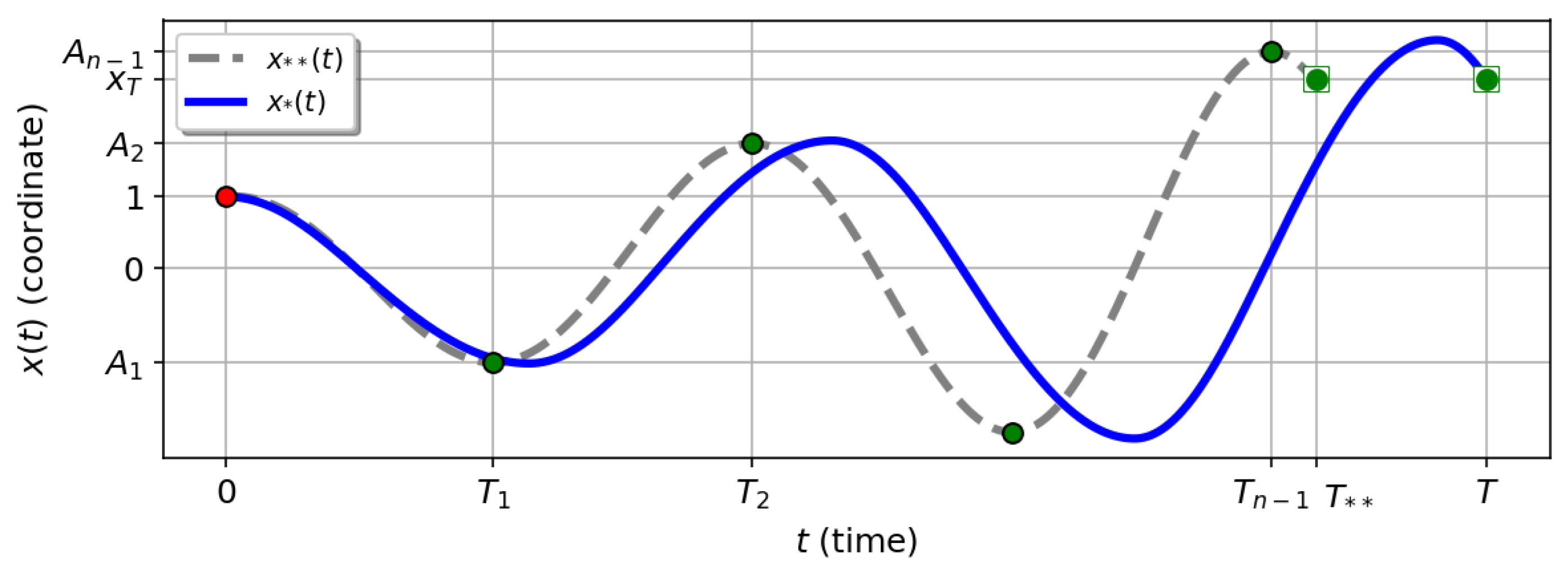
4. Algorithm for Constructing the Solution to Problem (1) via Reduction to a Problem with Zero Derivatives

In Section 3, Theorem 1 demonstrated that the optimal trajectory $x\left(t\right)$ in (1) corresponds to periodic control $\omega \left(t\right)$ as shown in Figure 1 over a certain time interval $[t_0,T]$.

To construct the solution, it is necessary to determine the number of internal semi-oscillations (which should be minimal and may be zero), the amplitudes of the first (left) and the last (right) semi-oscillations (which may be incomplete), and the time shifts (phase shift) that define the boundary points for the solution to (1) (Figure 2, or more precisely, Figure 11). These phase shifts are relative to the points where the derivative is zero.

First Step: Determining the Amplitudes of the Initial and Final Semi-Oscillations

It is assumed that $\left|A\right|\le \left|B\right|$, i.e., $x_0^2+v_0^2\le x_T^2+v_T^2$. The case $\left|A\right|>\left|B\right|$, i.e., $x_0^2+v_0^2>x_T^2+v_T^2$, is analyzed similarly using Remark 1$\left(II\right)$.

According to [3] (see Appendix A), for the oscillatory excitations, the control $\omega \left(t\right)$ and the corresponding trajectory $x\left(t\right)$ during the first semi-oscillation are described by the formulas provided in Figure 1 and Figure 11 during the first semi-oscillation are given by the formulas

$$\omega \left(t\right)=\left\{\begin{array}{cc}1,\hfill & 0\le t\le {\displaystyle \frac{\pi }{2}};\hfill \\ {\omega }_0,\hfill & {\displaystyle \frac{\pi }{2}}\le t\le t_2;\hfill \\ 1,\hfill & t_2\le t\le T_1,\hfill \end{array}\right.x\left(t\right)=\left\{\begin{array}{cc}Acos\left(t\right),\hfill & 0\le t\le {\displaystyle \frac{\pi }{2}};\hfill \\ -{\displaystyle \frac{A}{{\omega }_0}}sin\left({\omega }_0(t-{\displaystyle \frac{\pi }{2}})\right),\hfill & {\displaystyle \frac{\pi }{2}}\le t\le t_2;\hfill \\ Bcos(t-T_1),\hfill & t_2\le t\le T_1,\hfill \end{array}\right.$$

(5)

here $t_2$ is the second switching point, and $T_1$ is the period of one semi-oscillation.

The initial point lies either on the part of the trajectory corresponding to the control $\omega \left(t\right)=1$ (as described by formula (5), and shown by the blue curve in Figure 11 (a), (c)) or to the part of the trajectory that corresponds to the control $\omega \left(t\right)=0.5$ (as described by formula (5) and shown by the blue curve in Figure 11 (b)).

Thus, there are two cases to consider for the initial point.

Case A1

If the point $(x_0,v_0)$ belongs to the curve $x\left(t\right)=Acos\left(t\right)$ (Figure 11 (a), (c)), the amplitude A is uniquely determined from the system:

$$\left\{\begin{array}{c}{x}_0=Acos{\phi }_A;\hfill \\ v_0=-Asin{\phi }_A,\hfill \end{array}\right.$$

leading to

$$A=\left\{\begin{array}{cc}\mathrm{sgn}\left(x_0\right)\sqrt{x_0^2+v_0^2},\hfill & x_0\ne 0;\hfill \\ -\mathrm{sgn}\left(v_0\right)\sqrt{x_0^2+v_0^2},\hfill & x_0=0,\hfill \end{array}\right.{\phi }_A=\left\{\begin{array}{cc}-{\displaystyle \frac{v_0}{x_0}},\hfill & x_0\ne 0;\hfill \\ {\displaystyle \frac{\pi }{2}},\hfill & x_0=0.\hfill \end{array}\right.$$

(6)

Case A2

If the point $(x_0,v_0)$ belongs to the curve $x\left(t\right)=-{\displaystyle \frac{A}{{\omega }_0}}sin\left({\omega }_0\left(t-{\displaystyle \frac{\pi }{2}}\right)\right)$ (Figure 11 (b), which is possible for $x_0·v_0>0$), the value A is uniquely determined from the system:

$$\left\{\begin{array}{c}{x}_0=-{\displaystyle \frac{A}{{\omega }_0}}sin\left({\omega }_0\left({\phi }_A-{\displaystyle \frac{\pi }{2}}\right)\right);\hfill \\ v_0=-Acos\left({\omega }_0\left({\phi }_A-{\displaystyle \frac{\pi }{2}}\right)\right),\hfill \end{array}\right.$$

leading to

$$A=-\mathrm{sgn}\left(x_0\right)\sqrt{{\left({\omega }_0{x}_0\right)}^2+v_0^2},{\phi }_A={\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{1}{{\omega }_0}}{\displaystyle \frac{{\omega }_0{x}_0}{v_0}}.$$

(7)

Similarly, the final point $(x_T,v_T)$ is analyzed, and the amplitude B and phase shift ${\phi }_B$ (relative to the final time $T_{★}$) are determined using formulas analogous to (6) and (7):

Case B1

$$B=\left\{\begin{array}{cc}\mathrm{sgn}\left(x_T\right)\sqrt{x_T^2+v_T^2},\hfill & x_T\ne 0;\hfill \\ -\mathrm{sgn}\left(v_T\right)\sqrt{x_T^2+v_T^2},\hfill & x_T=0,\hfill \end{array}\right.{\phi }_B=\left\{\begin{array}{cc}-{\displaystyle \frac{v_T}{x_T}},\hfill & x_T\ne 0;\hfill \\ {\displaystyle \frac{\pi }{2}},\hfill & x_T=0.\hfill \end{array}\right.$$

(8)

Case B2

$$B=-\mathrm{sgn}\left(x_T\right)\sqrt{{\left({\omega }_0{x}_T\right)}^2+v_T^2},{\phi }_B={\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{1}{{\omega }_0}}{\displaystyle \frac{{\omega }_0{x}_T}{v_T}}.$$

(9)

Second Step: Choosing the Optimal Trajectory

After the first step there are two cases for initial point (A1 and A2) and two cases for final point (B1 and B2) leading to no more than four possible cases for the values of amplitudes of the initial and final semi-oscillations and phase shifts:

• Values A and ${\phi }_A$ are determined using formulas (6), B and ${\phi }_B$ are determined using formulas (8).
• Values A and ${\phi }_A$ are determined using formulas (7), B and ${\phi }_B$ are determined using formulas (8).
• Values A and ${\phi }_A$ are determined using formulas (6), B and ${\phi }_B$ are determined using formulas (9).
• Values A and ${\phi }_A$ are determined using formulas (7), B and ${\phi }_B$ are determined using formulas (9).

Accordingly, there are no more than four trajectories corresponding to these cases, one of which, according to Theorem 1, will be optimal.

The algorithm for constructing these trajectories and the criteria for selecting the optimal one are then considered.

First, for each case, the fulfillment of the condition $\left|A\right|\le \left|B\right|$ is checked. If $\left|A\right|>\left|B\right|,$ then this case is not suitable.

Next, for the remaining cases, the solution $x\left(t\right)$ is determined using the algorithm from Appendix A. The optimal trajectory must satisfy the boundary conditions of (1) on the interval $[{\phi }_A,T_{★}+{\phi }_B],$ i.e.

$$\left\{\begin{array}{c}x\left({\phi }_A\right)=x_0,\dot{x}\left({\phi }_A\right)=v_0;\hfill \\ x(T_{★}+{\phi }_B)=x_T,\dot{x}(T_{★}+{\phi }_B)=v_T.\hfill \end{array}\right.$$

(10)

If even one of these boundary conditions is not satisfied, the trajectory cannot be considered optimal.

It is possible that the trajectory over the entire interval $[0,T_{*}]$ is not optimal for problem (2), see Remark 3 to Theorem 1. In this case, the optimal number of complete semi-oscillations will differ from the required number.

From the set of trajectories, we select the trajectory with the minimal time. In accordance with Theorem 1, this trajectory will be the solution to the problem (1).

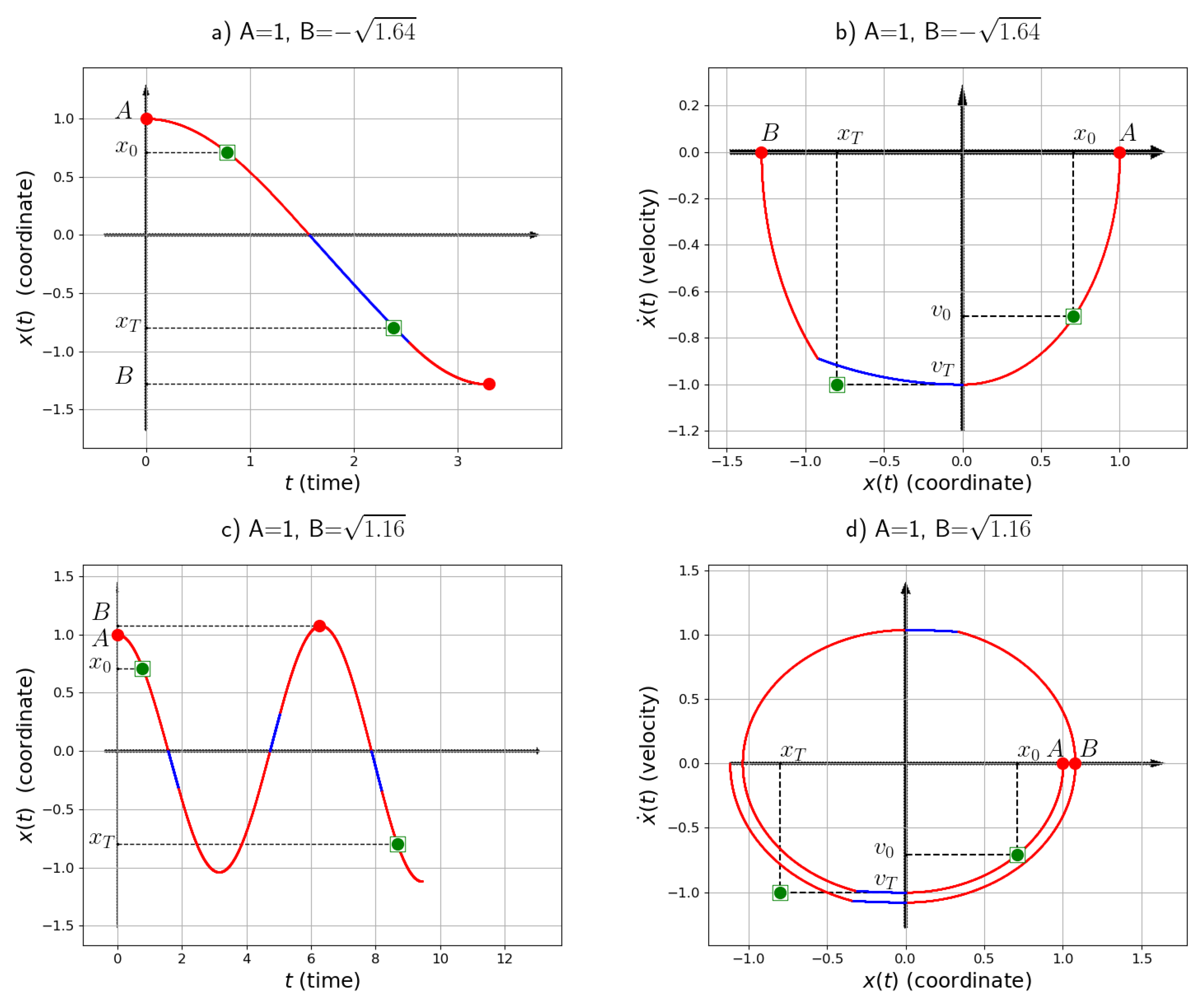
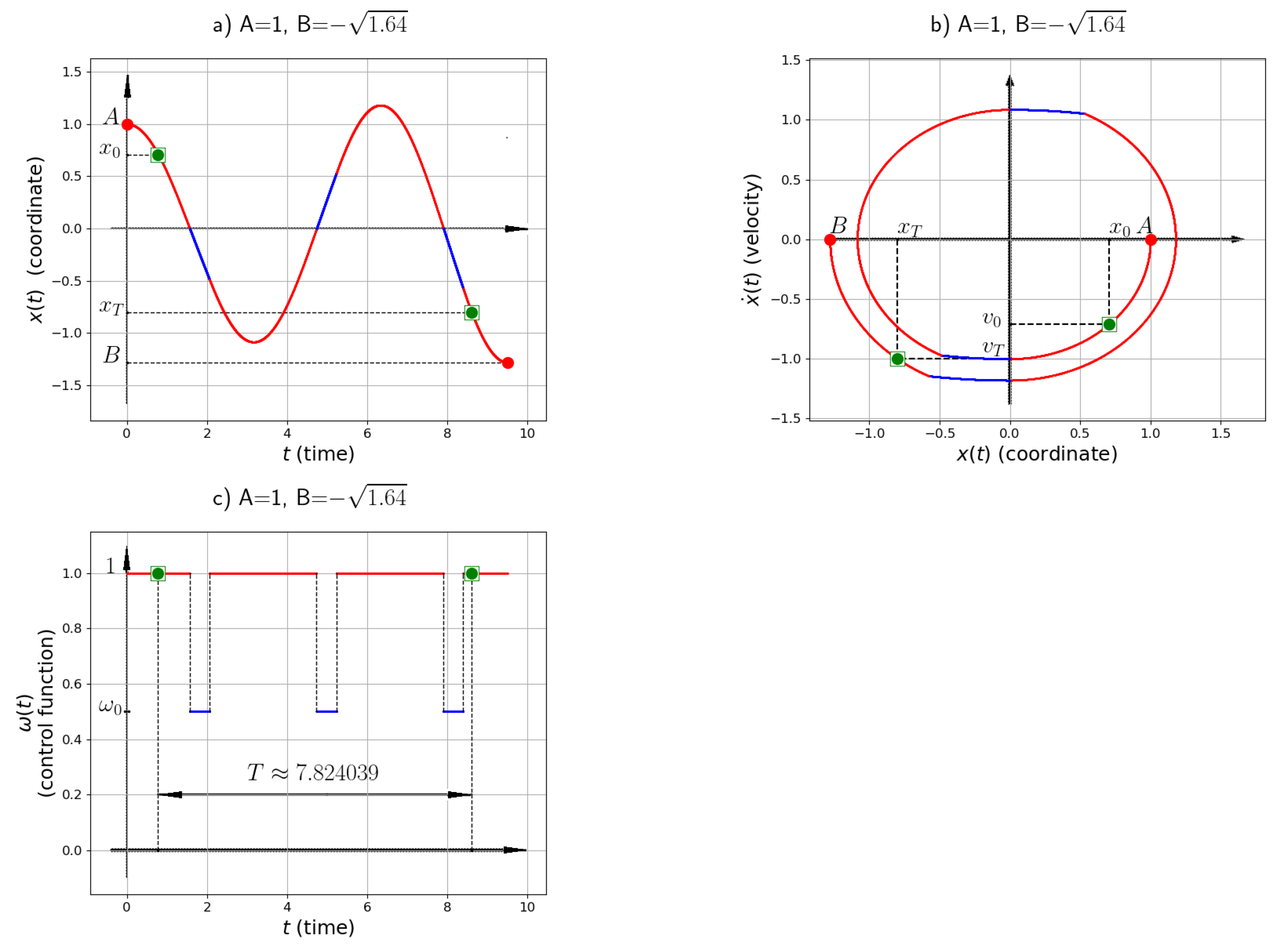
5. Simulation

Let us consider an example of constructing the optimal trajectory for problem with given boundary conditions to illustrate the application of the algorithm

$$\left\{\begin{array}{c}\ddot{x}\left(t\right)+{\omega }^2\left(t\right)x\left(t\right)=0,0\le t\le T;\hfill \\ x_0={\displaystyle \frac{\sqrt{2}}{2}},v_0=-{\displaystyle \frac{\sqrt{2}}{2}};\hfill \\ x_T=-0.8,v_T=-1;\hfill \\ 0<{\omega }_0=0.5\le \omega \left(t\right)\le 1,0\le t\le T;\hfill \\ T\to \underset{\omega \left(t\right)}{min}.\hfill \end{array}\right.$$

(11)

To apply the obtained algorithm, it is necessary to determine whether the dynamic process represents the excitation or damping of oscillations.

For the given boundary conditions, the condition of parametric excitation is fulfilled: $x_0^2+v_0^2=1\le x_T^2+v_T^2=1.64$. This characteristic will influence the choice of the optimal trajectory and the validation of the algorithm’s results (in the case of damped oscillations, see Remark 1$\left(II\right)$.

Determining Amplitudes and Phase Shifts

Initial point: the amplitude A and the phase shift ${\phi }_A$ are determined to correspond to the initial point $(x_0,v_0)$ using formulas (6) and (7).

From formulas (6), we find $A=1$ and ${\phi }_A={\displaystyle \frac{\pi }{4}}$ (red part of the trajectory, corresponding to the control $\omega \left(t\right)=1$, as shown in Figure 11 (a)).

The applicability condition for formulas (7) at the point $(x_0,v_0)$: $x_0·v_0>0$, is not satisfied. Therefore, the point cannot lie on the blue part of the trajectory, which corresponds to the control $\omega \left(t\right)={\omega }_0$, as illustrated in Figure 11 (b).

Final point: the amplitude B and the phase shift ${\phi }_B$, corresponding to the time moment T (boundary point $(x_T,v_T)$), are determined using formulas (8) and (9). Two values for the amplitude B and phase shift ${\phi }_B$ are derived as follows:

When the final point corresponds to the control $\omega \left(t\right)=1$ (the red part of the trajectory) using formulas (8) the values are: $B=-\sqrt{1.64},{\phi }_B=-{\displaystyle \frac{5}{4}}$.

When the boundary point corresponds to the control $\omega \left(t\right)={\omega }_0$ (the blue part of the trajectory) using formulas (9) the values are: $B=\sqrt{1.16},{\phi }_B={\displaystyle \frac{\pi }{2}}+2{\displaystyle \frac{2}{5}}.$

Trajectory Construction

From cases A1, B1 and B2, one option for the initial point and two options for the final point are identified, resulting in exactly two possible trajectories. These trajectories are constructed using formulas (A1) - (A3) (Appendix A) for each pair A and B (see Figure 12).

Trajectory 1: $A=1$ and $B=-\sqrt{1.64}$ as shown in Figure 12 (a), (b). This trajectory represents the optimal trajectory and phase portrait with the points $(x_0,v_0)$ and $(x_T,v_T)$.

Trajectory 2: $A=1$ and $B=\sqrt{1.16}$ as shown in Figure 12 (c), (d). This trajectory represents the optimal trajectory and phase portrait with the points $(x_0,v_0)$ and $(x_T,v_T)$.

Determining the Optimal Trajectory

In each case, it is verified whether the boundary conditions are satisfied by the constructed trajectory, specifically ensuring compliance with the conditions outlined in (10). In Figure 12 (b), (d), the boundary condition points (11) are marked, and it is evident that these conditions are not satisfied.

Following Remark 3, the number of internal oscillations must be increased. For the resulting trajectory, the fulfillment of the system conditions (10) satisfied. Thus, the solution of system (11) with nonzero boundary conditions has been obtained (see Figure 13).

Remark 5.

The resulting trajectory matches the optimal trajectory of a fading process with ${\omega }_0=0.5$ and the specified boundary conditions (see Remark 1 (II)):

$$\left\{\begin{array}{c}{x}_0=-0.8,v_0=1;\hfill \\ x_T={\displaystyle \frac{\sqrt{2}}{2}},v_T={\displaystyle \frac{\sqrt{2}}{2}}.\hfill \end{array}\right.$$

6. Main Results

• The problem of optimal control of an oscillatory process is considered in a general setting with non-zero boundary conditions for position and velocity (arbitrary boundary conditions).
• The existence and optimality of a solution to this problem is proven for any permissible boundary conditions. It is shown that the optimal trajectory is always a part of some trajectory that connects two points with zero velocities and is obtained using periodic control of a specific type.
• A method for solving the problem is proposed, based on extending the solution from the case of zero velocities.

7. Conclusion and Future Work

This paper presents a complete solution to the control problem for the harmonic oscillator with arbitrary boundary conditions, demonstrating the optimality of the coefficient control. Our analysis highlights the inherent complexity of the problem and its ill-posed nature with respect to numerical methods. The system’s dynamics are highly sensitive to variations in the control function $\omega \left(t\right)$, owing to the bilinear dependence in the term ${\omega }^2\left(t\right)x\left(t\right).$ Small numerical errors or approximations in $\omega \left(t\right)$ can lead to significant deviations in the system’s response, making numerical solutions unreliable. Moreover, the optimal process time can change abruptly when the boundary conditions change.

Using analytical techniques, explicit expressions were derived for the optimal control function $\omega \left(t\right)$ and the minimal time T required to transition the system from the initial to the final state. Determining the precise switching times analytically involves solving transcendental equations arising from the necessary conditions for optimality. The solution demonstrates that the optimal control strategy follows a bang-bang approach, where the control alternates between its minimum and maximum allowable values at analytically determined switching times.

This approach is applicable to the case ${\omega }_0=0$, where $x\left(t\right)$ is a composition of $Ccos(t+\phi )$ and linear functions $at+b$.

Although solutions for the time-optimal control of the harmonic oscillator under arbitrary boundary conditions have been derived, this study identifies several promising directions for future research:

• Robustness to Uncertainties: A rigorous examination of the robustness of optimal control strategies in the presence of system uncertainties, parameter variations, or external disturbances is warranted.
• Optimal Control with State Constraints: Extending the problem to incorporate state constraints such as limitations on the oscillator’s amplitude or velocity.
• Investigation of Multi-Input Control Systems: Expanding the analysis to encompass systems with multiple control inputs or coupled oscillators, which may exhibit more complex dynamics and control interactions, represents another avenue for research.