Submitted:
24 November 2024
Posted:
25 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Study Areas and Data
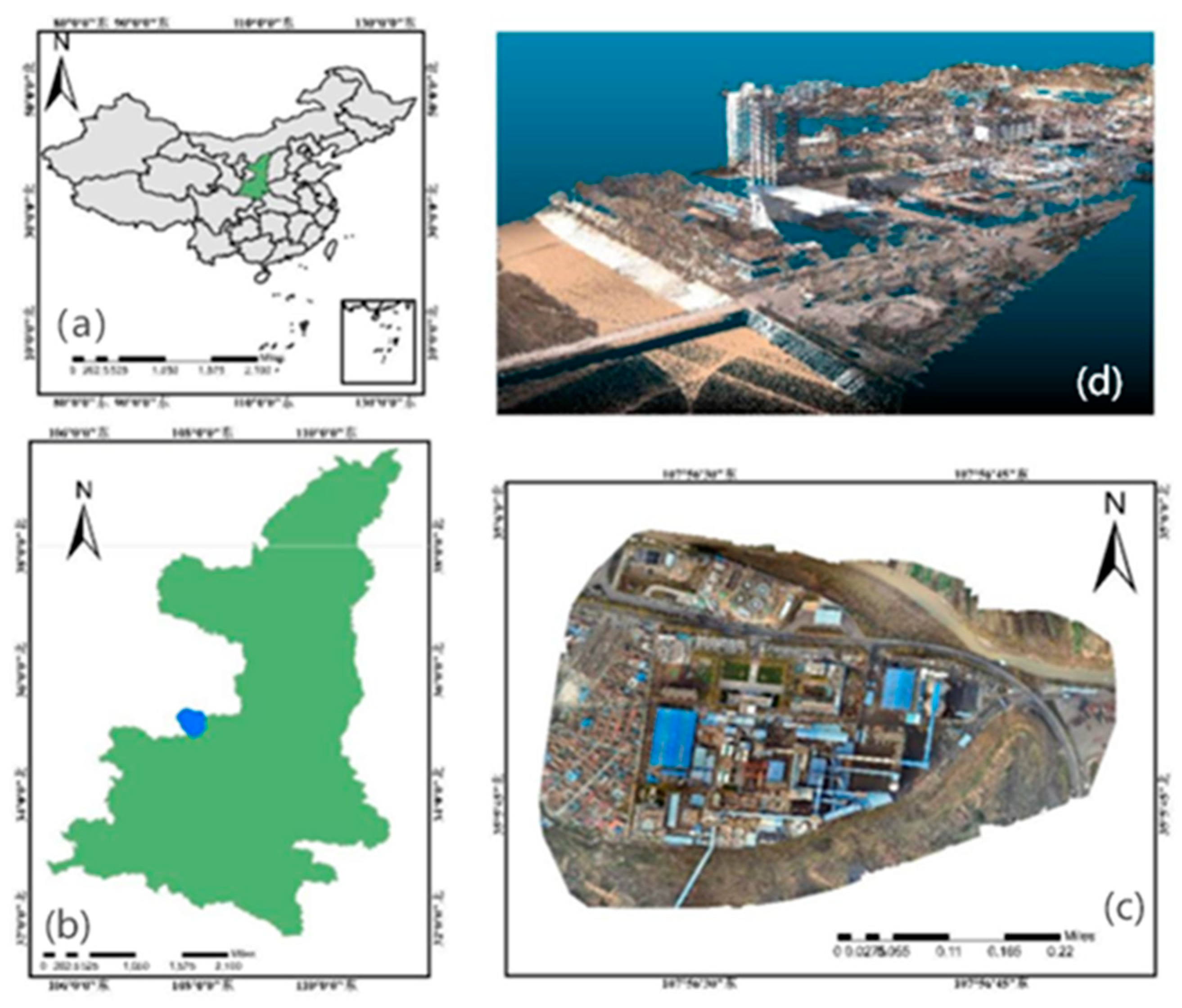
2.1. Study Area
2.2. Data Acquisition and Preprocessing

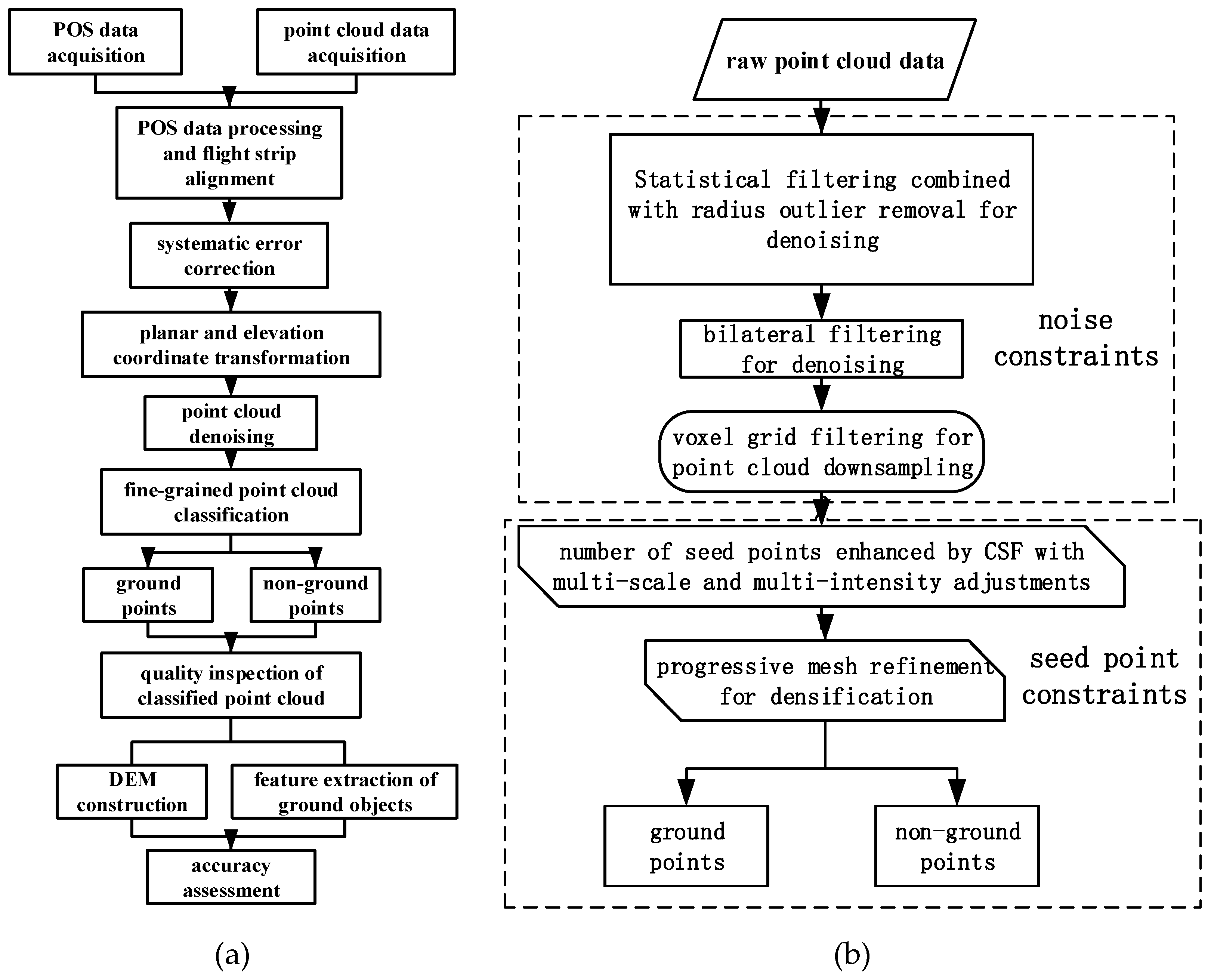
3. Methodology
3.1. Combinatorial Filtering Algorithm Based on Multiple Conditions
3.2. Establishment of DEM Interpolation Algorithm
3.3. DEM Accuracy Evaluation Index
4. Results and Discussion
4.1. Result Analysis of Combined Filtering Algorithm
4.1.1. Qualitative Analysis


4.1.2. Quantitative Analysis
| Terrain Data | a | b | c | d | Error1 | Error2 | Error |
|---|---|---|---|---|---|---|---|
| Flat Terrain | 7611447 | 42365 | 8562 | 4031680 | 0.55 | 0.21 | 1.26 |
| Ravine Terrain | 18451578 | 3528642 | 485642 | 16735268 | 16.05 | 2.82 | 10.24 |
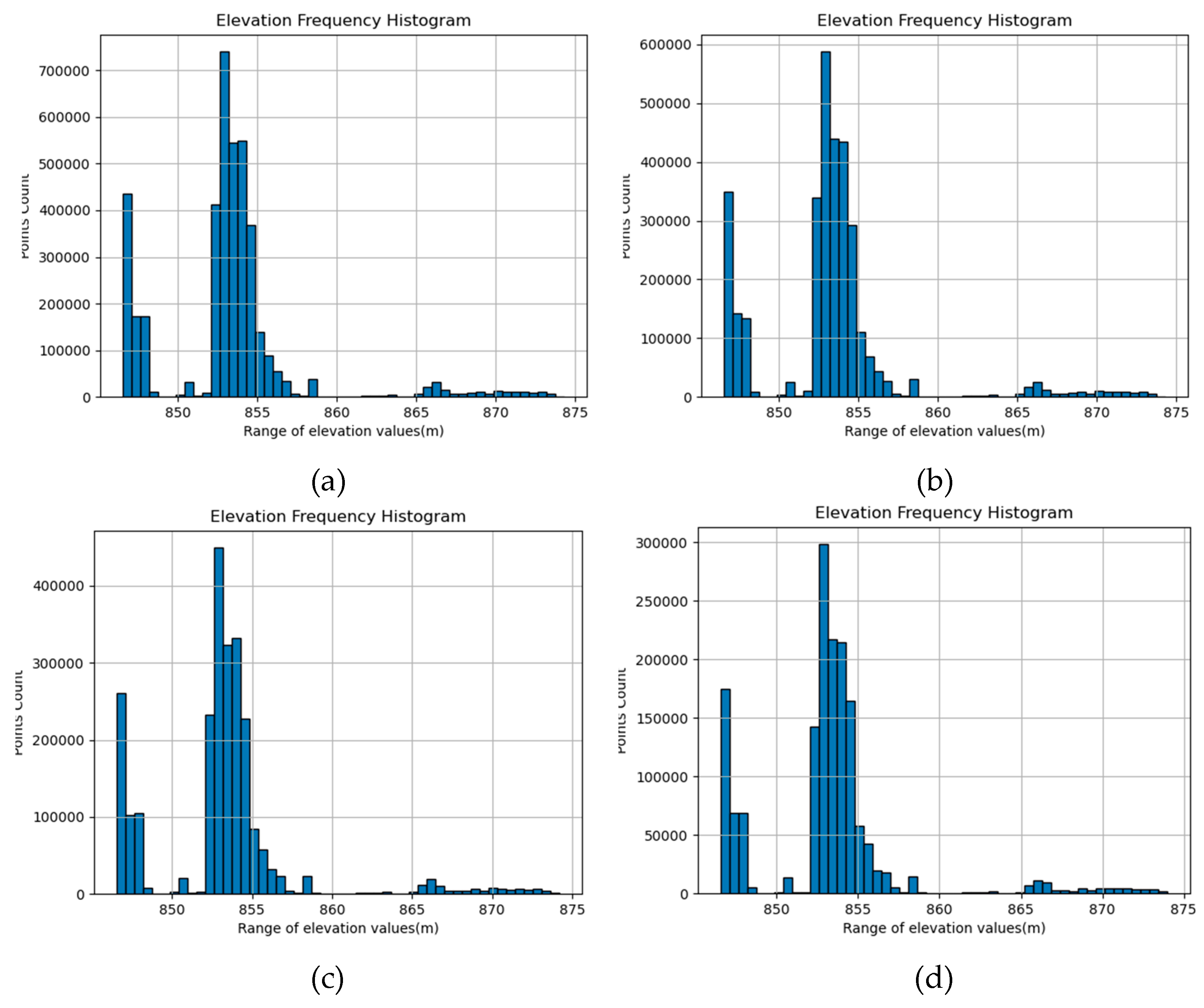
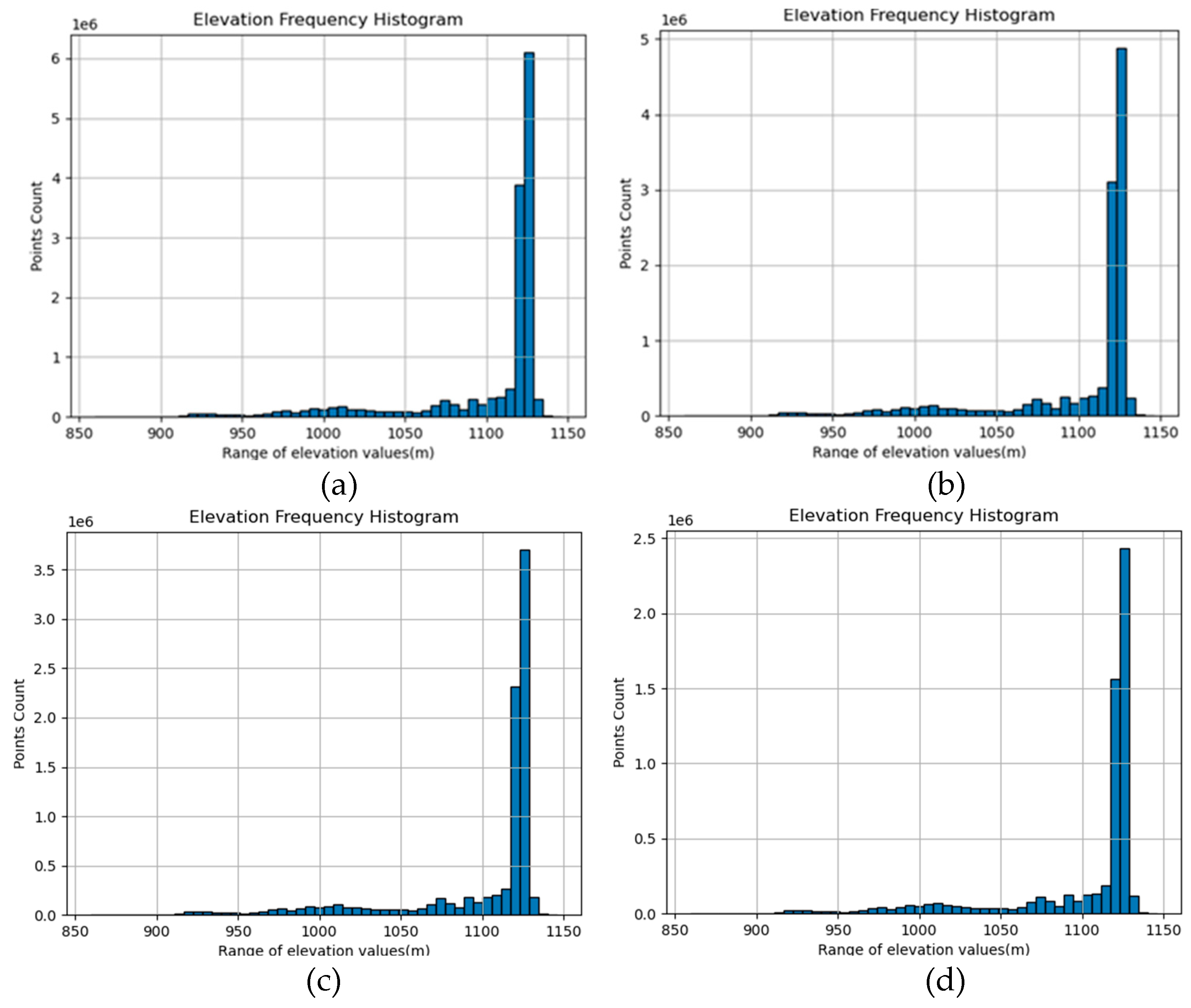
4.2. Analysis of DEM Results Formed at Different Cloud Densities
4.2.1. Selection of Point Cloud Density
| Resampling Percentage | Number of Flat Terrain Point Clouds | Average Elevation/m | Number of Point Clouds in Gully Terrain | Average Elevation/m |
|---|---|---|---|---|
| 90 | 3628512 | 867.71 | 15061742 | 1125.84 |
| 70 | 2539958 | 865.52 | 12049394 | 1125.71 |
| 50 | 1814256 | 862.63 | 9037045 | 1125.03 |
| 30 | 1088553 | 858.90 | 6024696 | 1124.07 |
| 10 | 362851 | 854.12 | 1506174 | 1102.36 |
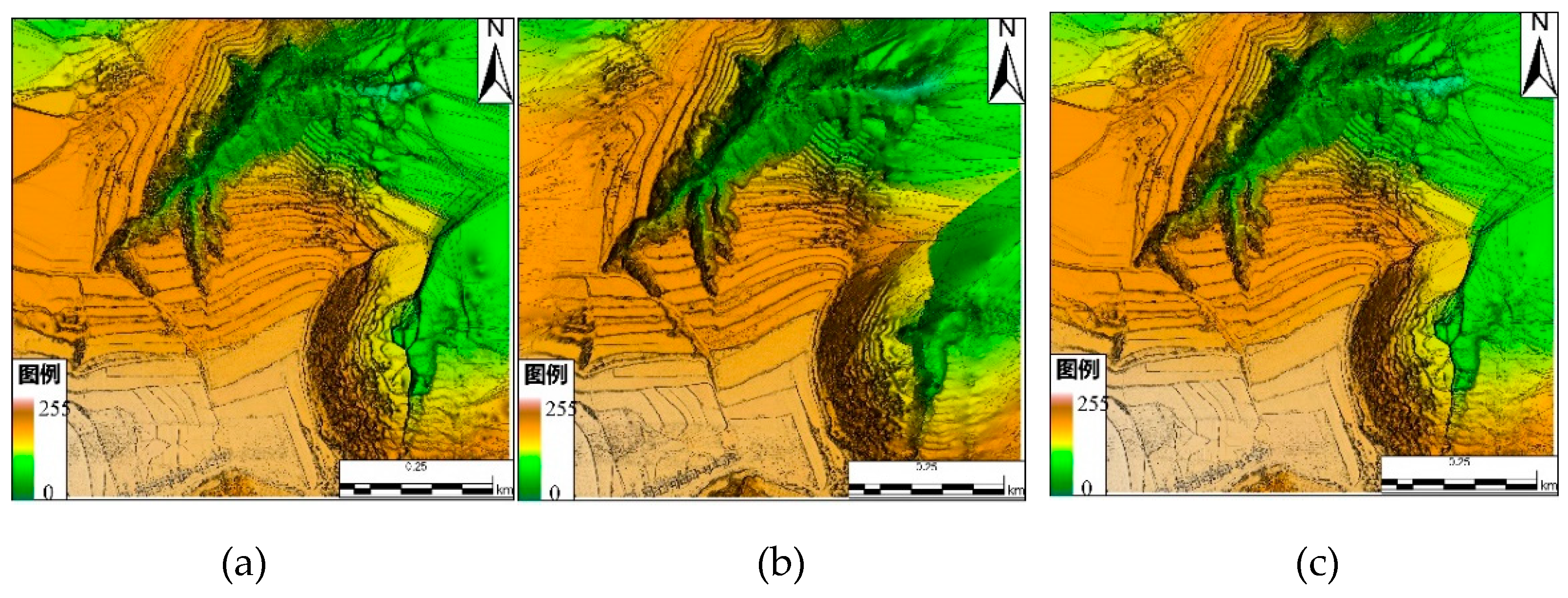
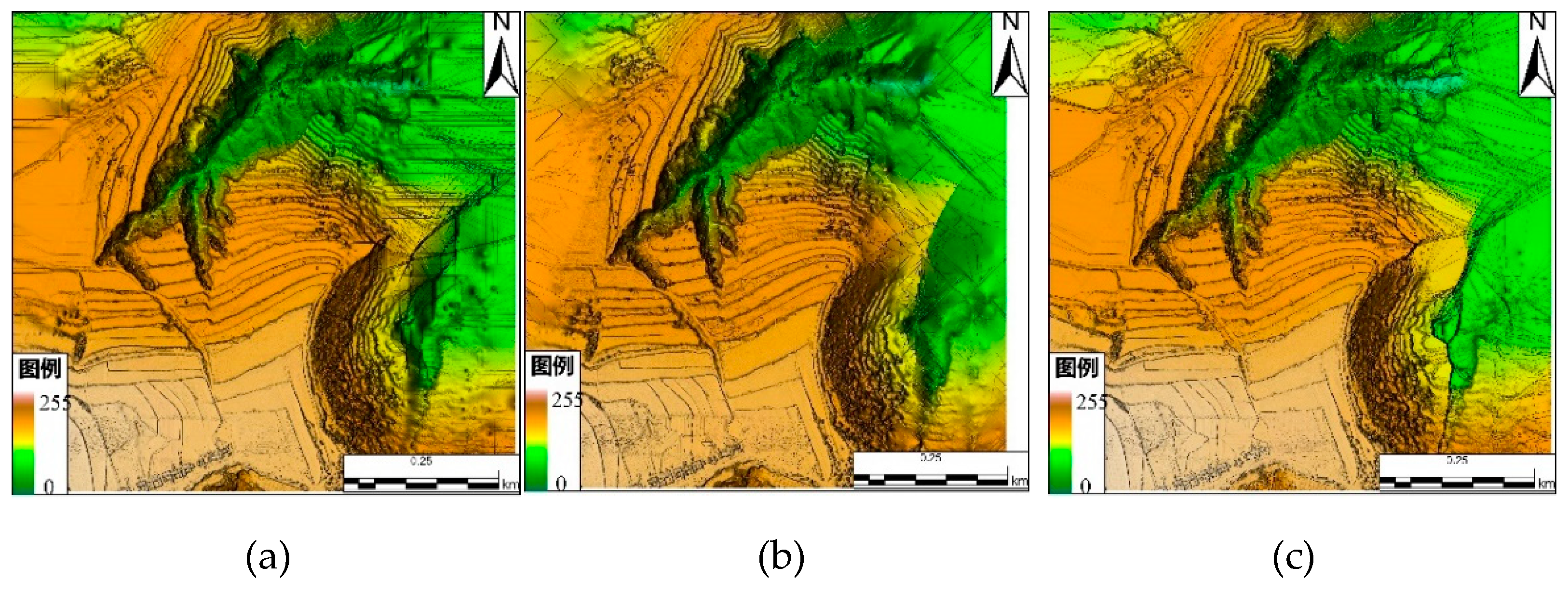
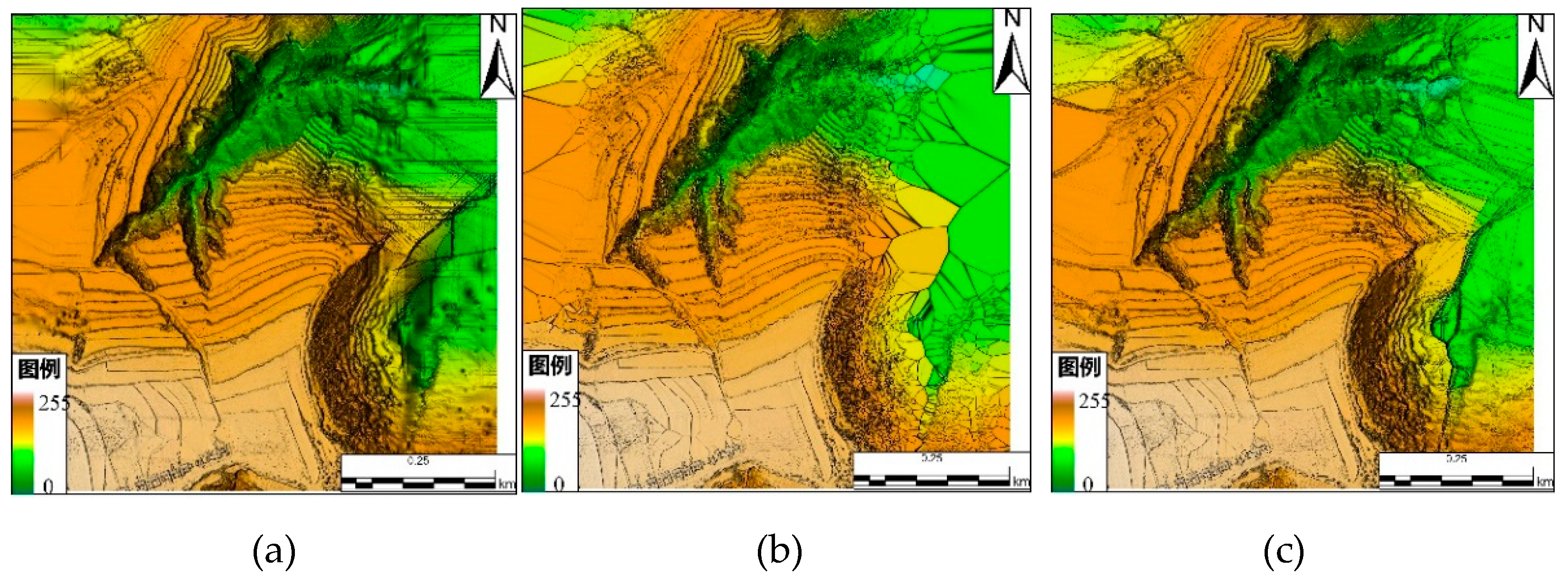
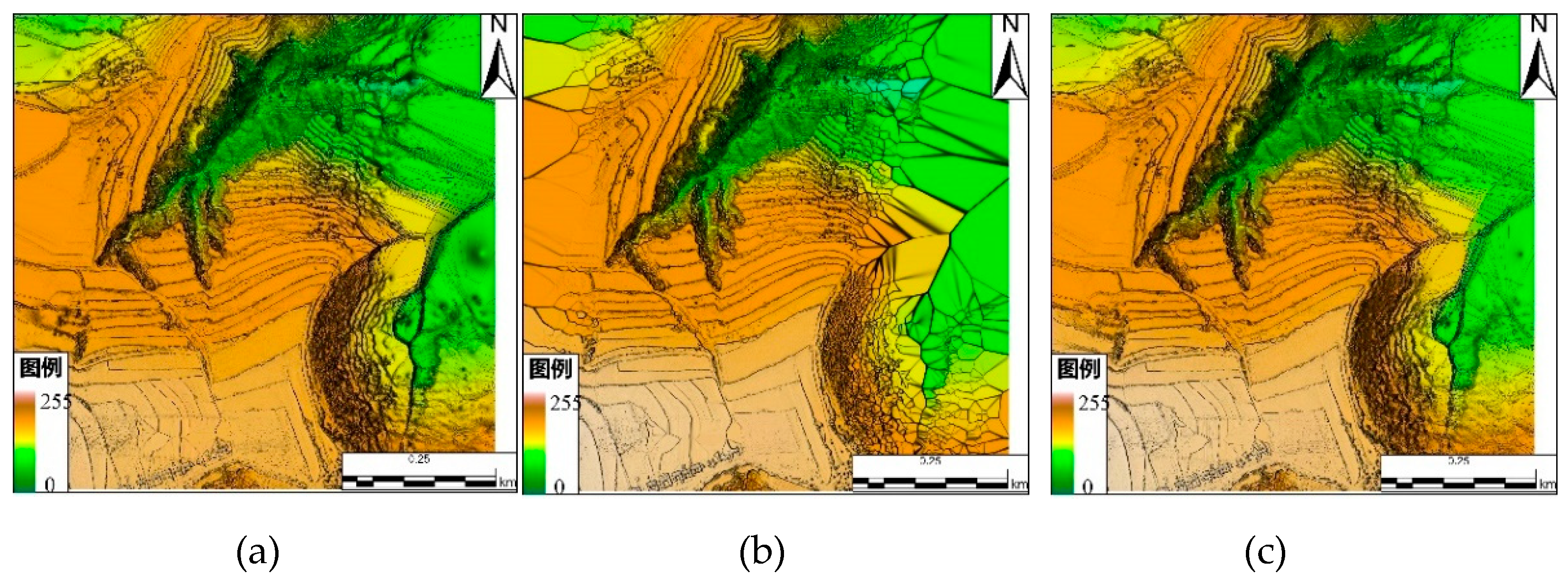
4.2.2. Analysis of DEM Results
4.3. Discussion and Analysis
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Thanks
Conflicts of Interest
References
- Wang Guofa, Pang Yihui, Ren Huaiwei, et al.Research and practice of intelligent mine system engineering and key technology[J].Journal of Coal,2024,49(01):181-202. [CrossRef]
- DING Enjie, YU Xiao, XIA Bing, et al.Development of mine informatisation and key technology of smart mine with digital twin as core[J].Journal of Coal,2022,47(01):564-578. [CrossRef]
- Zhang Jianzhong,Guo Jun. Discussion on the technical architecture of industrial internet for smart mines[J]. Coal Science and Technology, 2022,50(05):238-246. [CrossRef]
- CHEN Long,WANG Xiao,YANG Jianjian,et al. Parallel mining:from digital twin to mine intelligence[J].Journal of Automation,2021,47(07):1633 1645. [CrossRef]
- DING Enjie, YU Xiao, XIA Bing, et al.Development of mine informatisation and key technology of smart mine with digital twin as core[J].Journal of Coal,2022,47(01):564-578. [CrossRef]
- Khan R H N ,Kumar V S .Terrestrial LiDAR derived 3D point cloud model, digital elevation model (DEM) and hillshade map for identification and evaluation of pavement distresses[J].Results in Engineering,2024,23102680-102680. [CrossRef]
- Szafraniec E J .A dataset of high-resolution digital elevation models of the Skeiðarársandur kettle holes, Southern Iceland.[J].Scientific data,2024,11(1):660-660. [CrossRef]
- CHEN Chuanfa, WANG Mengzhu, YANG Shuai, et al.A multiresolution hierarchical interpolation filtering method applicable to airborne LiDAR point clouds in forest areas[J].Journal of Shandong University of Science and Technology(Natural Science Edition),2021,40(02):12-20. [CrossRef]
- Mengzhen Wang.Research on multi-resolution hierarchical interpolation filtering method for airborne LiDAR point cloud in forest area [D].Shandong University of Science and Technology,2020. [CrossRef]
- LIU Yan, SUN Yanning, CHEN Chuanfa, et al.Digital elevation model correction method for urban areas: an interpretable random forest model taking into account spatial heterogeneity[J].Journal of Geo-Information Science,2024,26(04):978-988.
- WU Fu, LIAO Zeyuan, HE Na, et al. Optimization of LiDAR point cloud density for geohazard investigation in mountainous areas with dense vegetation[J/OL]. Journal of Wuhan University (Information Science Edition),1-11[2024-08-22]. [CrossRef]
- LI Zihao, KUANG Haipeng, ZHANG Hong, et al.Target localisation method for aerial images based on fast iteration of digital elevation model elevation[J].Chinese Optics(in English),2023,16(04):777-787.
- H.M. Zhang, S.H. Fan, R.X. Chen, et al. Extraction method of river network in silt dam area based on digital elevation model[J].Journal of Agricultural Machinery,2023,54(09):246-253+269.
- YANG Zaisong, GAN Shu, YUAN Xiping, et al. Study on the construction of digital geomorphological model of backslope by UAV-LiDAR point cloud in Lufeng Dinosaur Valley[J].Laser and Infrared,2023,53(06):859-868.
- LUO Yuxuan, ZHU Peng, MOU Chao, et al. Application of Pegasus D20 LiDAR in the construction of digital twin watershed platform[J].Surveying and Mapping Bulletin,2023,(S1):130-135. [CrossRef]
- YANG Fan, REN Gang, QU Dan, et al. Application of airborne LiDAR technology in mine surface subsidence disaster monitoring[J].Surveying and Mapping Engineering,2023,32(04):59-68. [CrossRef]
- LIAO Xiaohan, ZHANG Jie, HUANG Yaohuan. Analysing the characteristics of low altitude geography and its expansion to geography[J].Journal of Geography,2024,79(03):551-564.
- TIAN Yuan, WU Feng, OU Yang Jun, et al.Analysis on the progress of UAV communication and standards for low altitude economy[J].Information and Communication Technology,2023,17(05):38-44.
- FAN Bangkui, LI Yun, ZHANG Ruiyu.Analysis of Low Altitude Intelligent Networking and UAV Industry Application[J].Progress in Geoscience,2021,40(09):1441-1450.
- Chen Bangsong, Sima Jinsong, Zhao Guangzu, et al.Experimental study on optimal density of airborne LiDAR data acquisition in densely vegetated mountainous areas[J/OL].Journal of Wuhan University (Information Science Edition),1-14.
- Bei Yixuan, Chen Chuanfa, Wang Xin, et al.Analysis of the impact of airborne LiDAR point cloud density and interpolation method on DEM and surface roughness accuracy[J].Journal of Geo-Information Science,2023,25(02):265-276.
- LIU Yicheng, LIU Bin, XIA Yan, et al.DEM construction of light airborne LiDAR data for complex mountainous areas with different point densities[J].Surveying and Mapping Bulletin,2023,(S1):32-35. [CrossRef]
- J. Xiao.Analysis of the impact of UAV-borne LiDAR point cloud density on DEM accuracy[J].Surveying and Mapping Bulletin,2024,(04):35-40. [CrossRef]
- HONGYUE ZHANG, XINXIAO SHI.Lake area point cloud processing and application based on fusion filtering algorithm[J].Applied Laser,2023,43(09):123-133. [CrossRef]
- Yuan Zhuang.Research on rock shift observation in mining area based on UAV three-dimensional laser scanning technology [D].Shandong University of Science and Technology,2020. [CrossRef]
- Zhou D , Wu K , Chen R ,et al.GPS/terrestrial 3D laser scanner combined monitoring technology for coal mining subsidence: a case study of a coal mining area in Hebei, China[J].Natural Hazards, 2014, 70(2):1197-1208. [CrossRef]
- Hao J , Zhang X , Wang H W H .Application of UAV Digital Photogrammetry in Geological Investigation and Stability Evaluation of High-Steep Mine Rock Slope[J].Drones, 2023, 7(3).
- Meng X , Lin Y , Yan L ,et al.Airborne LiDAR Point Cloud Filtering by a Multilevel Adaptive Filter Based on Morphological Reconstruction and Thin Plate Spline Interpolation[J].Electronics, 2019(10). [CrossRef]
- Li F , Zhu H , Luo Z ,et al.An Adaptive Surface Interpolation Filter Using Cloth Simulation and Relief Amplitude for Airborne Laser Scanning Data[J].Remote Sensing, 2021, 13(15):2938. [CrossRef]
- Lian X , Hu H .Terrestrial laser scanning monitoring and spatial analysis of ground disaster in Gaoyang coal mine in Shanxi, China: a technical note[J].Environmental Earth ences, 2017, 76(7):287. [CrossRef]
- Seafloor DEM modelling method based on improved inverse distance weighting algorithm; WANG Kewei, GAO Lihua, JIANG Feng.Seabed DEM modelling method based on improved inverse distance weighting algorithm[J].Marine Surveying and Mapping,2021,41(01):61-64.
- Sithole G, Vosselman G .Experimental comparison of filter algorithms for bare-Earth extraction from airborne laser scanning point clouds[J].ISPRS journal of photogrammetry and remote sensing, 2004(1/2):59. [CrossRef]
- Hengl T. Finding the right pixel size[J]. Computers & Geosciences, 2006,32(9):1283- 1298. [CrossRef]
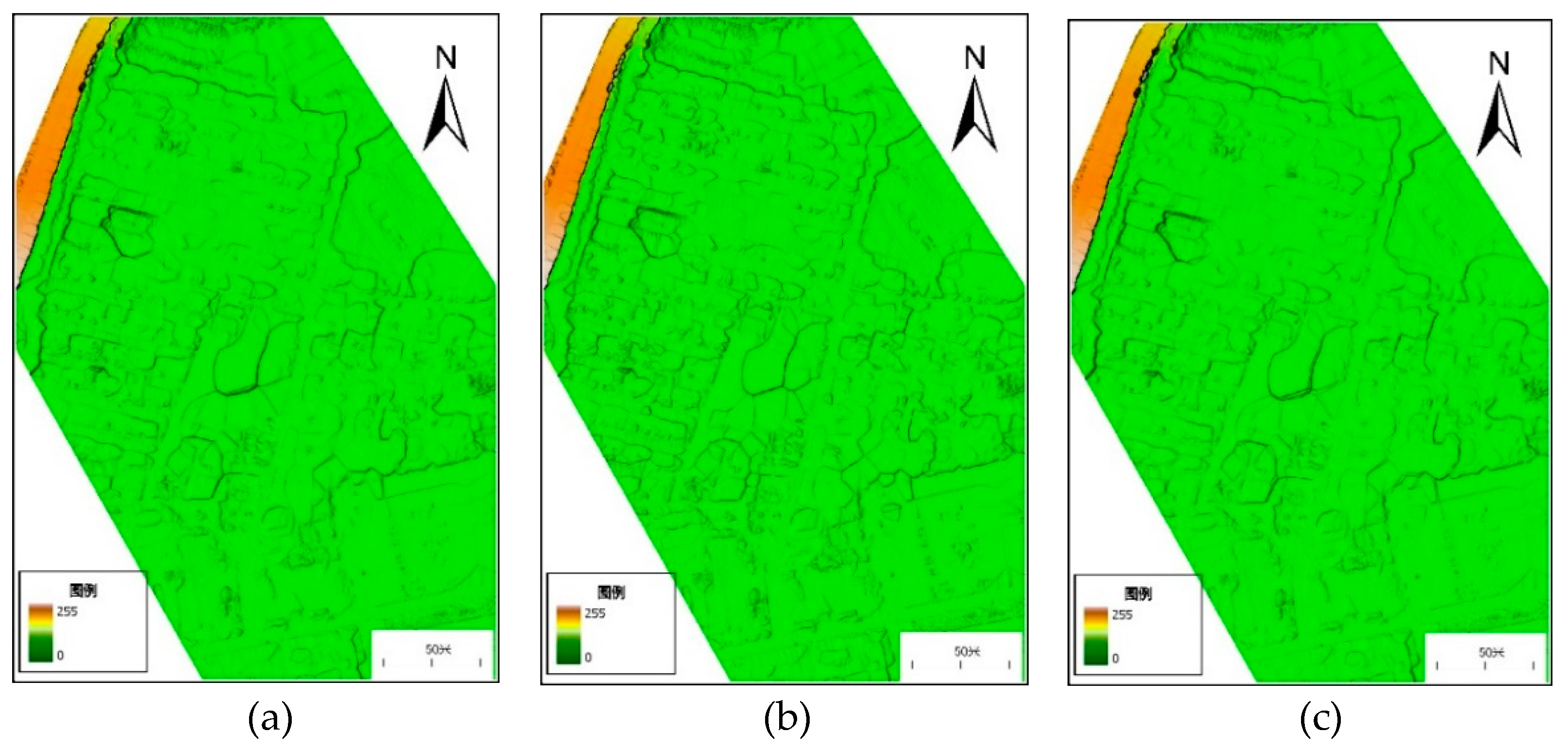
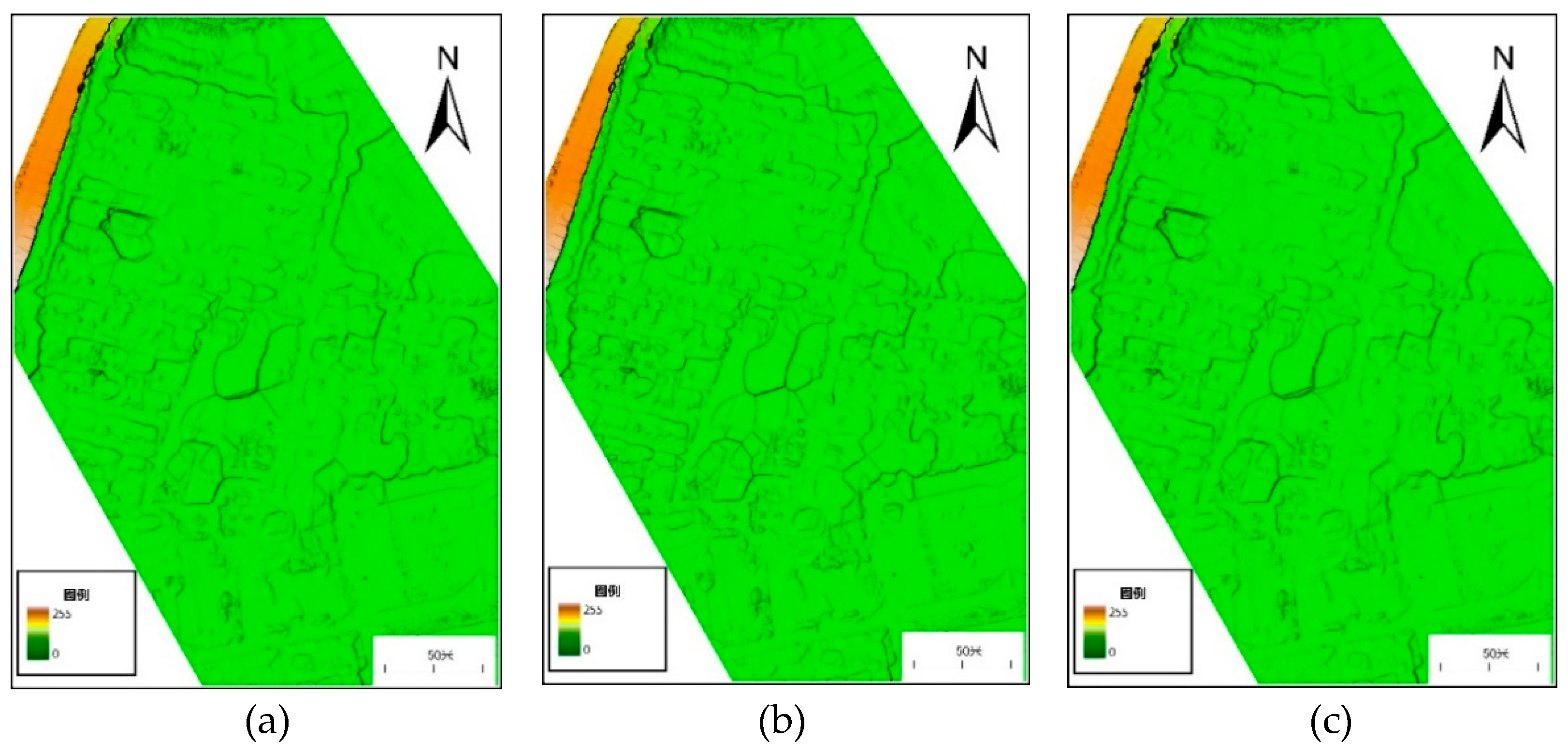
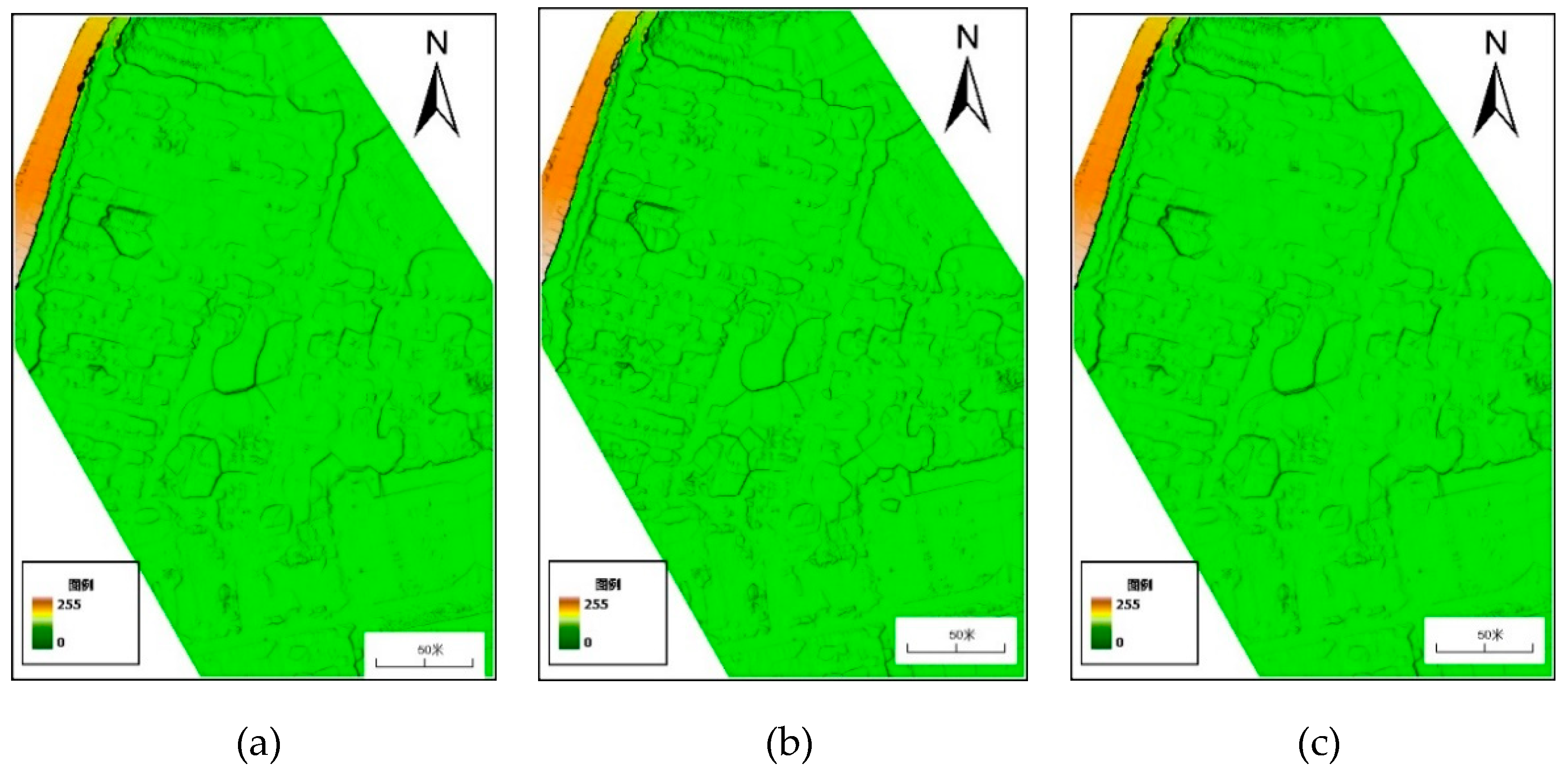
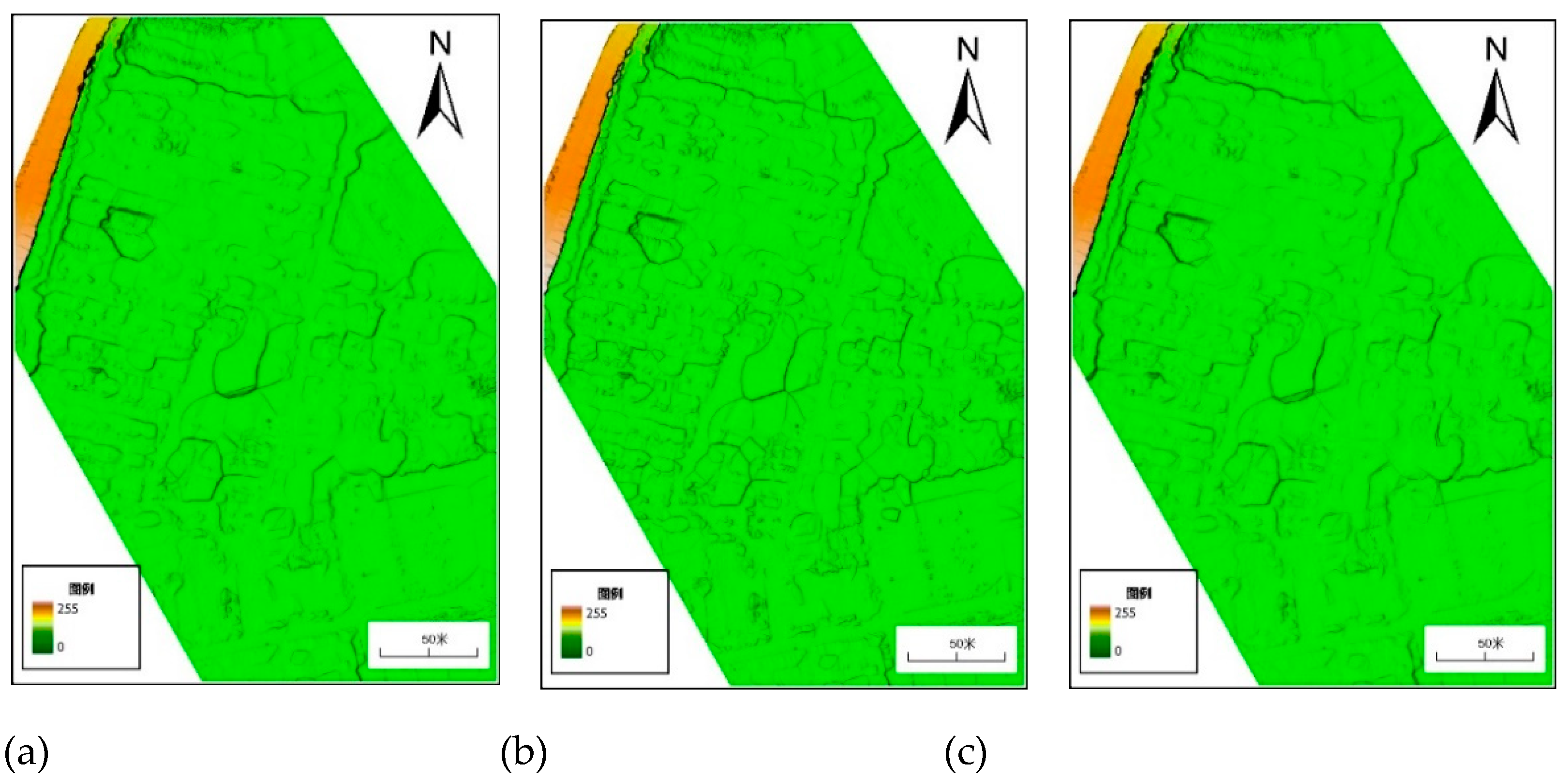
| Test Area | Density/(Points/m2) | Number of Laser Point Clouds/One | Elevation Range/m |
|---|---|---|---|
| Flat terrain | 350 | 14352663 | 850.49~901.79 |
| Gully relief | 420 | 21347990 | 954.79~1139.86 |
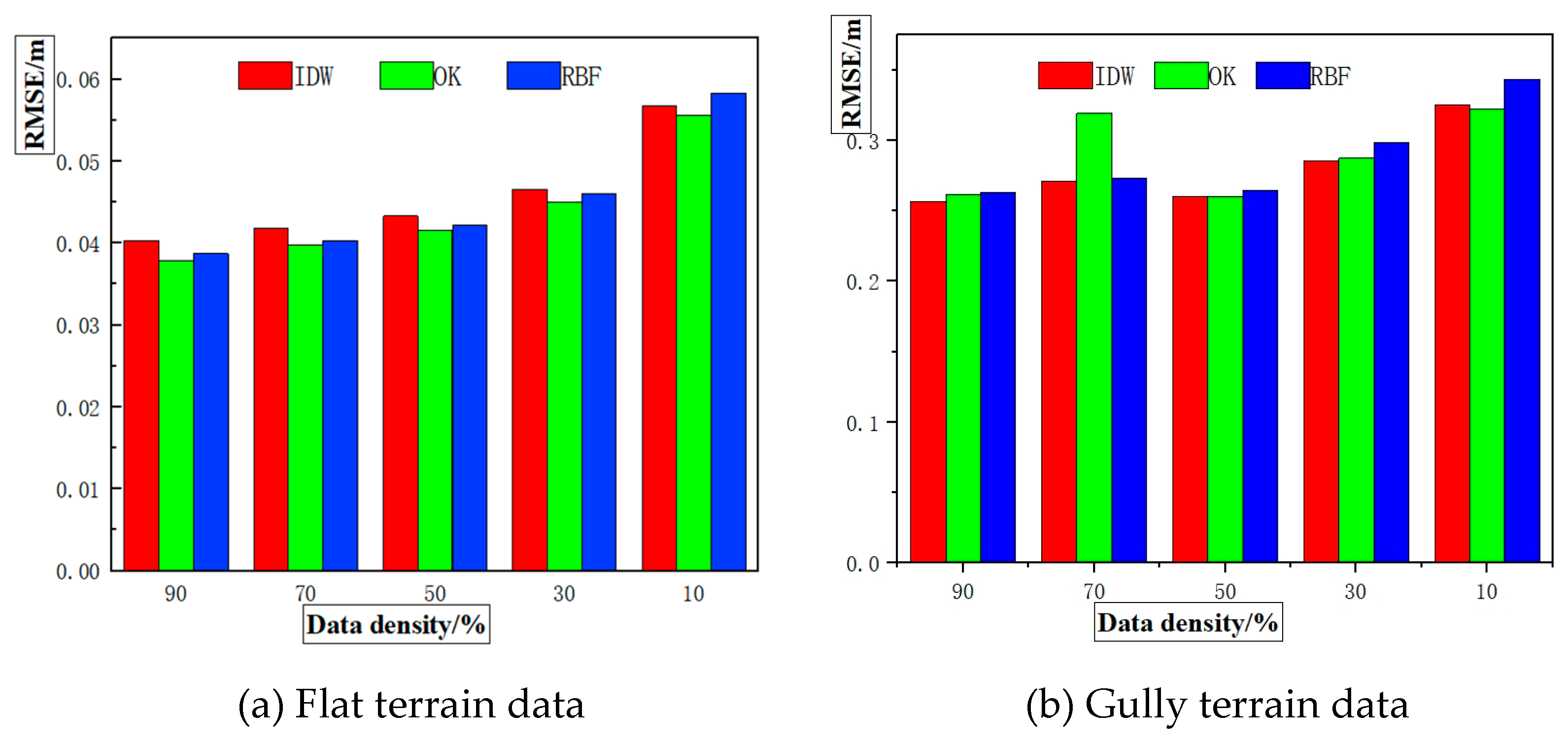
| Density/% | RMSE/m | |||||
|---|---|---|---|---|---|---|
| IDW | OK | RBF | ||||
| Test area | flat | gully | flat | gully | flat | gully |
| 90 | 0.0403 | 0.2565 | 0.0379 | 0.2619 | 0.0387 | 0.2629 |
| 70 | 0.0418 | 0.2708 | 0.0398 | 0.3192 | 0.0403 | 0.2731 |
| 50 | 0.0422 | 0.2599 | 0.0416 | 0.2598 | 0.0433 | 0.2648 |
| 30 | 0.0466 | 0.2857 | 0.0450 | 0.2874 | 0.0460 | 0.2985 |
| 10 | 0.0568 | 0.3255 | 0.0556 | 0.3220 | 0.0583 | 0.3435 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




