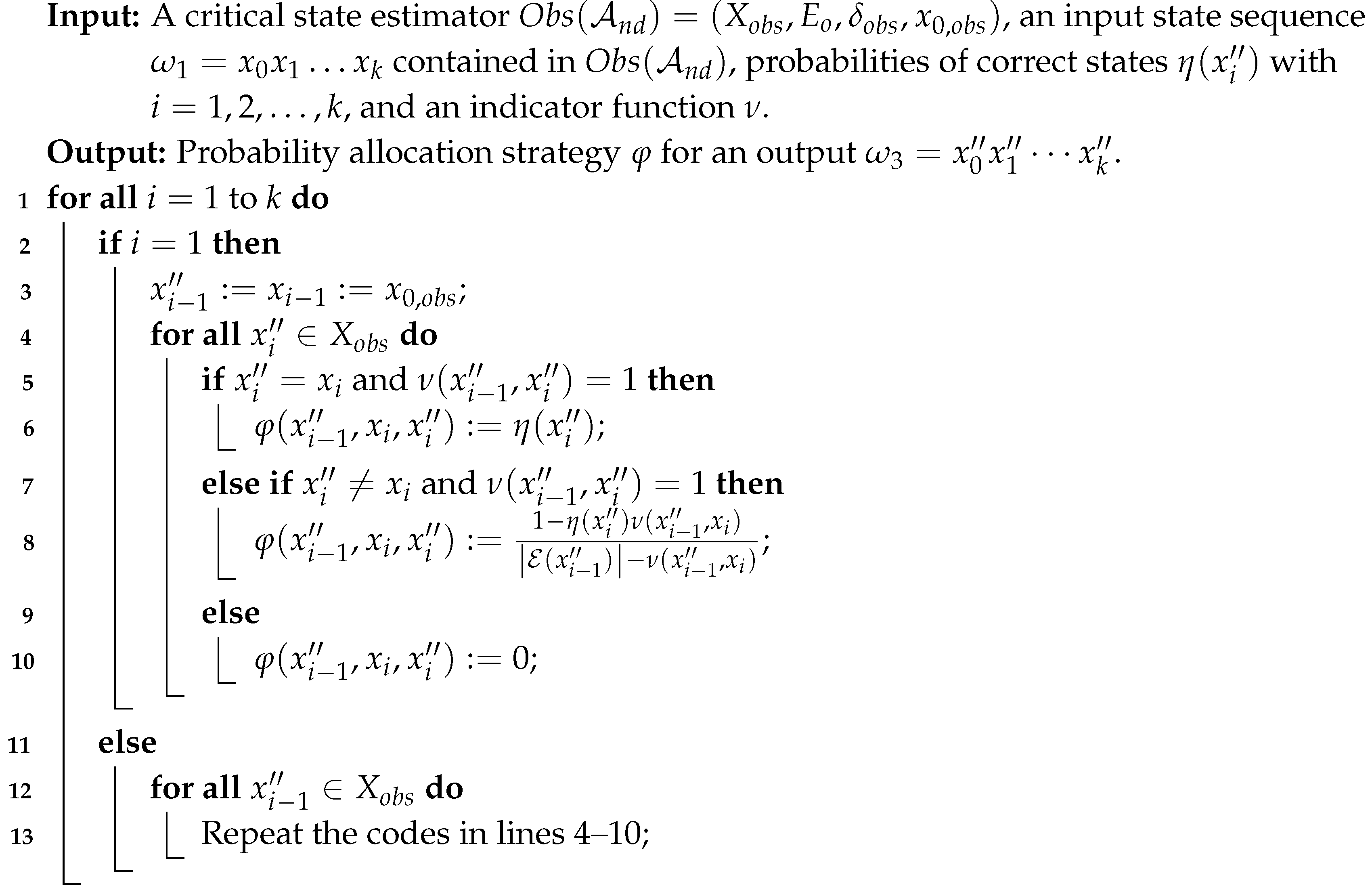Critical Observability Enforcement in Discrete-event Systems Using Differential Privacy

1. Introduction

Over the past decade, state estimation in discrete-event systems (DESs) (without a full sensor deployment) has received unprecedented interest thanks to the extensive deployment of cyber-physical systems that are mathematically characterized by discrete-event systems. Within this problem, several core challenges, such as opacity analysis [1,2,3], diagnosability assessment [4,5], detectability verification [6,7], and controller design optimization [8], are deeply dependent on the ability to accurately estimate the system states by its partially observed nature. Particularly, critical observability, as an important concern in the direction of state estimation, is the focus of our exploration in this research. The concept of critical observability, formulated in [9], is widely applied to networked systems, medical & health systems, semiconductor manufacturing, etc. A system is considered to be critically observable if, through the observation of a system output, it is possible to infer without ambiguity whether or not the current system states fully fall into a predefined set of critical states that can characterize several system properties of interest. Petri nets and automata are the main tools for the modeling and control of DESs with potential mutual transformation [10].

There are two commonly employed techniques for checking the critical observability of a DES that is modeled with finite state automata: regular language [11] and observer-based approaches [12,13,14]. In [11], the authors utilize the operations of regular languages to develop a computational procedure to address the observability verification problem, executable in polynomial time. In [12], k-step critical observability is defined and an observer called a k-extended detector is presented to verify k-step critical observability. The critical observability of large-scale finite-state automaton networks is considered in [13] and decentralized critical observers are designed. Lai et al. propose a novel method for constructing observers for polynomially-ambiguous max-plus automata to check their critical observability, which extends earlier work on unambiguous max-plus automata [14].

When a system is verified to be non-critically observable, a significant problem is how to make it critically observable. This research reports a mechanism that, borrowing from DP [15], aims to consolidate/enforce the critical observability for a non-critically observable system. Further, the mechanism ensures that the critical states of the system cannot be detected by an intruder, i.e., achieving critical state protection/concealment.

Differential privacy (DP) is a data processing technique within the field of cryptography, first proposed by Dwork [15]. Building on a solid mathematical foundation, DP guarantees that the statistical characteristics exhibited by the overall dataset will almost remain unchanged when a single entity (a user, a record, or any form of individual data point) is added to or removed from the dataset. In essence, the inclusion/exclusion of a single-record barely alters the computational outcomes of the dataset. Consequently, DP can withstand a wide range of privacy attacks, making it extremely difficult for attackers to accurately infer individual data by observing the calculation results.

The privacy protection mechanism due to DP is primarily achieved by introducing noise to obfuscate the original data during data processing, thereby concealing personal characteristics and sensitive information. The Laplace mechanism [16], which is particularly suited for protecting numerical data, and the exponential mechanism [17], designed for handling non-numerical data, are two of the most common and effective methods for injecting noise in order to implement DP.

As shown in the literature, DP has been widely applied in various fields, including big data analytics, federated learning, recommendation systems, and trajectory data publishing. In [18], DP is combined with the Haar Wavelet technique to protect the privacy of big data in body sensor networks. The authors developed a tree-based structure to analyze the data, reducing errors and enabling long-range queries. In [19], the authors concentrated on three aspects of DP protection for adolescents’ ultrasound examination health datasets: DP protection for basic statistical output perturbations, publication of DP marginal histograms and synthesized data, and machine learning DP learning algorithms. The problem of location and traffic information leakage in vehicular network environments is addressed in [20] by integrating local DP and federated learning. Specifically, the authors introduce four local DPMs, including the three-outputs and optimal piecewise mechanism, to perturb gradients from vehicles, ensuring privacy while maintaining model accuracy and minimizing communication overhead. In [21], Ren et al. employ the data from various social network platforms to generate personalized recommendations, where, to ensure the privacy of the users, DP is applied to the user attributes and the connections present in the social network graph. Presented in [22] and [23] is a privacy protection mechanism for symbolic systems whose traces (symbol sequences) can be protected. Based on this framework, the authors further develop an innovative exponential mechanism. In addition, DP finds its extensive applications in other domains such as logistics [24] and time series trajectories [25]. We believe that more research will be exposed as this kind of privacy protection paradigm prevails corresponding to the increasingly demanding requirements of system security.

Although DP is effective in protecting sensitive information within various information-intensive systems, its potential applications in DESs have yet to be fully explored. This paper primarily focuses on the problem how to utilize DP to enforce critical observability in DESs modeled with finite-state automata. Furthermore, we explore how DP is employed to guarantee that the critical states are not discovered by an intruder. The research follows the schematic illustrated in Figure 1. Specifically, given a system ${\mathcal{A}}_{nd}$ modeled with a nondeterministic finite-state automaton, a set of observable events ${\Sigma }_o$, a set of critical states $X_s$, and a set of non-critical states $X_{ns}$, we assume that the system is not critically observable with respect to (w.r.t.) the predefined set of observable events ${\Sigma }_o$ and critical states $X_s$. Using the standard determinization procedure presented in [26], we construct a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)$ w.r.t. observable events. The system’s behavior can be described as a scenario that the event sequence s generated by ${\mathcal{A}}_{nd}$ is transmitted to the critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)$, which then produces an observation $\rho$.

By estimating the state set that is consistent with an observation $\rho$, denoted by $\mathcal{C}\left(\rho \right)$, we draw a crucial conclusion. If this set is a subset of the non-critical states, i.e., $\mathcal{C}\left(\rho \right)\subseteq X_{ns}$, the observation $\rho$ is regarded as a safe observation. If the set is a subset of the critical states, i.e., $\mathcal{C}\left(\rho \right)\subseteq X_s$, the observation $\rho$ is considered an unsafe observation. In both cases, the critical states can be revealed/detected by an intruder. Otherwise, the set $\mathcal{C}\left(\rho \right)$ is neither a subset of the critical states nor a subset of the non-critical states, i.e, $\mathcal{C}\left(\rho \right)⊈X_s\wedge \mathcal{C}\left(\rho \right)⊈X_{ns}$. In this situation, the observation $\rho$ is also deemed unsafe since the critical observability of the system is violated. In other words, when $\rho$ is acquired by an intruder, he/she can determine that the system is not critically observable. To prevent unsafe observations from being captured, a DP module is introduced as a protection shield. The function of this module is that, when an unsafe observation $\rho$ is received, the module outputs a protected observation ${\rho }^{\prime }$ with a probability similar to that of another random observation, thereby obscuring the intruder such that it is difficult to trace back to the original unsafe observation. If the observation $\rho$ is safe, the system directly outputs the undecorated $\rho$.

We further analyze how DP works. For an unsafe observation $\rho$, it is first mapped into a state sequence $\omega$, which is a state string interleaved with $\rho$ in $Obs\left({\mathcal{A}}_{nd}\right)$, where $Obs\left({\mathcal{A}}_{nd}\right)$ is the observer of the plant ${\mathcal{A}}_{nd}$. Then, $\omega$ is sent to the DP module. We assume that the operational logic (running principals) of the DP module is public to an intruder, i.e., the intruder knows the probability distribution of the module generating all possible outputs ${\rho }^{\prime }$ w.r.t. an input observation $\rho$. However, when the two state sequences respectively corresponding to an unsafe observation $\rho$ and a random observation $\tau$ are input to the module, the protected output observation ${\rho }^{\prime }$ is highly similar in probability. This design guarantees that even if an intruder captures ${\rho }^{\prime }$, it is difficult to distinguish whether it originates from $\rho$ or $\tau$, thereby effectively protecting unsafe observations that violate critical observability (i.e., $\mathcal{C}\left(\rho \right)⊈X_s\wedge \mathcal{C}\left(\rho \right)⊈X_{ns}$) or reveal critical states (i.e., $\mathcal{C}\left(\rho \right)\subseteq X_s$). Under the aforementioned lines, the main contributions of this work are summarized as follows.

(1) A novel framework based on DP for the enforcement of critical observability for DESs is proposed. Given a non-critically observable system, we define an unsafe observation by computing the set of states consistent with it, i.e., an observational system output. In this paper, the designed method aims to confuse the unsafe observations with the randomly generated observations from a probabilistic viewpoint, such that a non-critically observable system satisfies critical observability. Moreover, this method guarantees that the critical states of the system cannot be detected by an intruder.

(2) To expand the application field of DP theory, we propose a new concept, called “state sequence DP” and apply it to finite state automata.

(3) Thanks to the concept of state sequence DP, we design an optimal DPM that ensures the optimal protection of unsafe observations.

The preliminaries of DESs and DP are presented in Section 2. The definition of critical observability is recalled in Section 3. In Section 4, a novel DPM specialized for the enforcement of critical observability of a system is designed. We discuss a realistic case of enforcing critical observability in Section 5 to show the practical applicability of the proposed approach. Finally, concluding remarks are given in Section 6.

2. Preliminaries

The basics of notations and notions necessary for the development of this research are presented, including languages and finite-state machines (deterministic finite automata–DFA and non-deterministic finite automata–NFA), as they are appropriate for the modeling of a DES. A reader is referred to [26]. Note that an NFA is equivalent to a DFA from the lens of languages that they can generate, i.e, they have the same modeling power.

2.1. Languages and Automata

Let E be a finite set of event labels a DES and $E^{*}$ be a set of the finite strings defined over E (the Kleene closure of set E), consisting of the empty string $\epsilon$. Given a string $\sigma \in E^{*}$, its length is the number of symbols contained in it, denoted by $\left|\sigma \right|$. In particular, we have $\left|\epsilon \right|=0$. Given two strings ${\sigma }_1$ and ${\sigma }_2$, the string $\sigma ={\sigma }_1{\sigma }_2$ is said to be the concatenation of ${\sigma }_1$ and ${\sigma }_2$.

A DFA is a quadruple ${\mathcal{A}}_d=(X_d,E,{\delta }_d,x_0)$, where $X_d$ is the finite set of states, E is, as previously stated, the collection of event labels, ${\delta }_d:X_d\times E\to X_d$ is the partially defined deterministic transition function, and $x_0\in X_d$ is the initial state. In order to facilitate the development of this research, one readily extends the transition function, as again denoted by ${\delta }_d$ in the case of no confusion, recursively defined from $X_d\times E\to X_d$ to $X_d\times E^{*}\to X_d$, where ${\delta }_d(x,se)={\delta }_d({\delta }_d(x,s),e)$ for $s\in E^{*}$ and $e\in E$ (specifically, we have ${\delta }_d(x,\epsilon )=x$ for all $x\in X_d$). Let $k\in \mathbb{N}$ with $\mathbb{N}=\{0,1,2,3,\dots \}$ be a non-negative integer. We use $E^k$ to denote the set of event sequences with length k, i.e., $E^k=\{s\in E^{*}\mid \left|s\right|=k\}$. Analogously, we write $X_d^k$ to represent the set of all state sequences with length k. The language generated by ${\mathcal{A}}_d$ is defined as $\mathcal{L}\left({\mathcal{A}}_d\right)=\{s\in E^{*}\mid {\delta }_d(x_0,s)\mathrm{is}\mathrm{defined}\}$. The set of events that are enabled (feasible) at a given state $x\in X_d$ is defined by $\mathcal{E}\left(x\right)=\{e\in E\mid {\delta }_d(x,e)\mathrm{is}\mathrm{defined}\}$. The number of enabled events at state x is thus $\left|\mathcal{E}\right(x\left)\right|$.

Given a DFA ${\mathcal{A}}_d=(X_d,E,{\delta }_d,x_0)$, a sequence $\xi$ (interleaving of states and events) starting from state $x_0$ and ending at a state in $X_d$, i.e., $\xi =x_0\stackrel{e_1}{\to }{x}_1\stackrel{e_2}{\to }\cdots \stackrel{e_k}{\to }{x}_k$ is said to be a production of ${\mathcal{A}}_d$ with $e_i\in \mathcal{E}\left(x_{i-1}\right)$ ($i=1,2,\dots ,k$). We write $\Xi$ to represent the set of all productions $\xi$ in the DFA ${\mathcal{A}}_d$. Given a production $\xi =x_0\stackrel{e_1}{\to }{x}_1\stackrel{e_2}{\to }\cdots \stackrel{e_k}{\to }{x}_k$ of ${\mathcal{A}}_d$, the state sequence $x_0{x}_1\cdots x_k$ associated with $\xi$ is called a production state sequence, denoted by $F\left(\xi \right)=x_0{x}_1\cdots x_k$. Analogously, the event sequence $e_1{e}_2\cdots e_k$ associated with $\xi$ is said to be a production event sequence, is denoted by $T\left(\xi \right)=e_1{e}_2\cdots e_k$. Let $\gamma =x_0{x}_1\cdots x_k$ with $k\ge 1$ be a non-empty state sequence. We write $\mathcal{T}\left(\gamma \right)=\{s\in E^{*}\setminus \left\{\epsilon \right\}\mid \exists \xi \in \Xi :F\left(\xi \right)=\gamma \&s=T\left(\xi \right)\}$ to represent the set of event sequences consistent with $\gamma$. Given a non-empty event sequence $s=e_1\cdots e_k$ with $k\ge 1$, its consistent state sequence set is defined as $\mathcal{F}\left(s\right)=\{\gamma \in X_d^{*}\setminus \left\{\epsilon \right\}\mid \exists \xi \in \Xi :T\left(\xi \right)=s\&\gamma =F\left(\xi \right)\}$. Note that $X_d^{*}$ is the set of all finite strings of elements in $X_d$.

Example 1.

Consider a DFA ${\mathcal{A}}_d=(X_d,E,{\delta }_d,x_0)$ shown in Figure 2, where $X_d=\{x_0,x_1,x_2,x_3,x_4\}$ and $E=\{\alpha ,\beta ,\lambda \}.$ We have ${\delta }_d(x_0,\beta )=x_1$, ${\delta }_d(x_0,\lambda )=x_2$, ${\delta }_d(x_0,\alpha )=x_3$, $\mathcal{E}\left(x_0\right)=\left\{\beta ,\lambda ,\alpha \right\}$, and $\left|\mathcal{E}\left(x_0\right)\right|=3$. Given a production $\xi =x_0\stackrel{\alpha }{\to }{x}_3\stackrel{\beta }{\to }{x}_4$, the production state sequence and the production event sequence associated with ξ are $F\left(\xi \right)=x_0{x}_3{x}_4$ and $T\left(\xi \right)=\alpha \beta$, respectively. Let us consider an event sequence $\lambda \alpha$ in ${\mathcal{A}}_d$. The set of state sequences consistent with $\lambda \alpha$ is $\mathcal{F}\left(\lambda \alpha \right)=\left\{x_0{x}_2{x}_2\right\}$. □

An NFA is a quadruple ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$, where $X_{nd}$ is the finite set of states, E is the same as before explained, ${\delta }_{nd}:X_{nd}\times E\to 2^{X_{nd}}$ is the (partial) transition function, and $X_0\subseteq X_{nd}$ is the set of initial states. The transition function ${\delta }_{nd}$ is similarly extended to ${\delta }_{nd}:X_{nd}\times E^{*}\to 2^{X_{nd}}$ by defining ${\delta }_{nd}(x,\epsilon )=\left\{x\right\}$ for all $x\in X_{nd}$ and ${\delta }_{nd}(x,se)={\bigcup }_{x^{\prime }\in {\delta }_{nd}(x,s)}{\delta }_{nd}(x^{\prime },e)$, where $s\in E^{*}$ and $e\in E$. The language generated by ${\mathcal{A}}_{nd}$ from state $x\in X_{nd}$ is formally defined as $\mathcal{L}({\mathcal{A}}_{nd},x)=\{s\in E^{*}\mid {\delta }_{nd}(x,s)\ne \varnothing \}$. Given a set of states $X\subseteq X_{nd}$, we define $\mathcal{L}({\mathcal{A}}_{nd},X)={\cup }_{x\in X}\mathcal{L}({\mathcal{A}}_{nd},x)$. The language of ${\mathcal{A}}_{nd}$ is $\mathcal{L}\left({\mathcal{A}}_{nd}\right)=\mathcal{L}({\mathcal{A}}_{nd},X_0)$.

Given an automaton, E is partitioned into two disjoint sets: $E=E_o\dot{\cup }{E}_{uo}$, where $E_o$ ($E_{uo}$) is the set of observable (unobservable) events. The natural projection $P:E^{*}\to E_o^{*}$ is defined by

$$P\left(\epsilon \right)=\epsilon \mathrm{and}P\left(se\right)=\left\{\begin{array}{cc}P\left(s\right)e,\hfill & \mathrm{if}e\in E_o;\hfill \\ P\left(s\right),\hfill & \mathrm{if}e\in E_{uo},\hfill \end{array}\right.$$

where $s\in E^{*}$ and $e\in E$. Function P can be extended to $P:2^{E^{*}}\to 2^{E_o^{*}}$, i.e., given $Z\subseteq E^{*}$, $P\left(Z\right)=\{z^{\prime }\in E_o^{*}\mid \exists z\in Z:z^{\prime }=P\left(z\right)\}$.

Given an NFA ${\mathcal{A}}_{nd}=(X_{nd},E_o\dot{\cup }{E}_{uo},{\delta }_{nd},X_0)$ and a state set $X\subseteq X_{nd}$, the set of states unobservably reached from X is defined as $UR\left(X\right)=\{x^{\prime }\in X_{nd}\mid \exists x\in X,\exists s\in E_{uo}^{*}:x^{\prime }\in {\delta }_{nd}(x,s)\}$. We use the notation $Ne(X,e)$ to represent the set of states reached by the occurrence of an observable event $e\in E_o$ from the states in X, i.e., $Ne(X,e)=\{x^{\prime }\in X_{nd}\mid \exists x\in X:x^{\prime }\in {\delta }_{nd}(x,e)\}$. The observer of ${\mathcal{A}}_{nd}$, denoted as $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$, can be computed following a standard procedure outlined in [26]. More specifically, $X_{obs}\subseteq 2^{X_{nd}}$ is the state set, $E_o$ is the set of observable events, ${\delta }_{obs}:X_{obs}\times E_o\to X_{obs}$ is the (partial) transition function (for all $x_{obs}\in X_{obs}$ and for all $e\in E_o$, ${\delta }_{obs}(x_{obs},e)=UR\left(Ne(x_{obs},e)\right)$), and $x_{0,obs}=UR\left(X_0\right)$ is the initial state.

Due to the nature of partial observation of a considered plant, we can only observe the observable event labels, while unobservable events can be directly observed. However, different event sequences may have the same observational results. Given an NFA ${\mathcal{A}}_{nd}$, a string $\rho \in P\left(\mathcal{L}\left({\mathcal{A}}_{nd}\right)\right)$ is said to be an observation. The state estimation w.r.t. $\rho$ can be expressed as $\mathcal{C}\left(\rho \right)=\{x\in X_{nd}\mid \exists x_0\in X_0,\exists s\in \mathcal{L}\left({\mathcal{A}}_{nd}\right):P\left(s\right)=\rho \&x\in {\delta }_{nd}(x_0,s)\}$. By definition, it comes $\mathcal{C}\left(\rho \right)={\delta }_{obs}(x_{0,obs},\rho )$. Note that an observer is a DFA where all events are observable.

2.2. Differential Privacy

Differential privacy is an effective vehicle for privacy protection by providing a mechanism (or a function) to protect sensitive personal information from being disclosed during statistical analysis or data dissemination. Broadly speaking, whenever we use a dataset as the input to this mechanism, the addition or removal of any single record from the dataset will not affect the data query results. This means that even if the dataset is slightly modified, it is difficult or impossible for external intruders to obtain any specific privacy information [15].

Definition 1

(Differential privacy  [27]). Let $ϵ$ be a positive real number and $\mathcal{M}$ be a randomized mechanism (function) that takes a dataset as input. Let $Im\left(\mathcal{M}\right)$ denote the image of $\mathcal{M}$. The mechanism $\mathcal{M}$ is said to provide $ϵ$-differential privacy if for any two datasets $D_1$ and $D_2$ that differ on a single element, and for any $O\subseteq Im\left(\mathcal{M}\right)$, it holds

$$\mathbb{P}\left[\mathcal{M}\left(D_1\right)\in O\right]\le exp\left(ϵ\right)\mathbb{P}[\mathcal{M}\left(D_2\right)\in O],$$

where the value of $\mathcal{M}$ at a dataset $D_1$ or $D_2$ is contained in the sample space, i.e., $Im\left(\mathcal{M}\right)$, with a probability decided by the randomness used in the mechanism, and $\mathbb{P}\left[\mathcal{M}\left(D_1\right)\in O\right]$ is the probability of $\mathcal{M}\left(D_1\right)\in O$ representing the possibility that the output of $\mathcal{M}$ at $D_1$ belongs to O. ♢

In Definition 1, the performance of DP is evaluated by the value of $ϵ$. Specifically, a smaller $ϵ$ indicates a more subtle distinction between the probabilities of events $\mathcal{M}\left(D_1\right)\in O$ and $\mathcal{M}\left(D_2\right)\in O$, signifying a lower likelihood for an intruder to distinguish between the two datasets. Conversely, a larger value of $ϵ$ implies a diminished level of protection for users’ private information.

Remark 1.

According to Definition 1, two datasets, namely $D_1$ and $D_2$, are required to differ in only one element. However, in this study, we extend the concept of DP to the field of DESs modeled with a DFA ${\mathcal{A}}_d$$=(X_d,E,{\delta }_d,x_0)$ (the formal definition of DP within the DFAs framework, called state sequence DP, will be presented in Section 4). In the definition of DP tailored for DESs, we define ${\mathcal{M}}_{\omega }:X_d^k\to X_d^k$ as a mechanism specifically designed for a set of state sequences. The input and output of ${\mathcal{M}}_{\omega }$ are two state sequences of equal length. The degree of similarity between these sequences is assessed based on their Hamming distance, as defined in Section 4.

3. Critical Observability for Automata

In this section, we recall the formalization of critical observability verification problems. Given an NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ that is partially observable, i.e., $E=E_o\dot{\cup }{E}_{uo}$, in practice, certain important physical states of the NFA are called critical states, represented by a subset of states $X_s\subseteq X_{nd}$. By acquiring a random sequence of observable events, if an intruder can always unambiguously infer whether the system is currently in a predefined set of critical states, ${\mathcal{A}}_{nd}$ is said to be critically observable.

Definition 2

(Critical observability [13]). Given an NFA ${\mathcal{A}}_{nd}$$=(X_{nd}$, $E,{\delta }_{nd},X_0)$, a set of observable events $E_o\subseteq E$, and a set of critical states $X_s\subseteq X_{nd}$, the system ${\mathcal{A}}_{nd}$ is said to be critically observable w.r.t. $E_o$ and $X_s$, if the following predicate holds

$$\forall \rho \in P\left(\mathcal{L}\left({\mathcal{A}}_{nd}\right)\right):\left[\mathcal{C}\left(\rho \right)\subseteq X_s\right]\vee \left[\mathcal{C}\left(\rho \right)\subseteq X_{nd}\setminus X_s\right].$$

♢

A critically observable system requires that, for any observation $\rho \in P\left(\mathcal{L}\left({\mathcal{A}}_{nd}\right)\right)$, the state set consistent with the observation should be either a subset of critical states or a subset of non-critical states. To verify whether an NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ is critically observable, one can construct a critical state estimator of ${\mathcal{A}}_{nd}$, i.e., the observer $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of ${\mathcal{A}}_{nd}$, which stores all possible state estimations [26]. Then, a system ${\mathcal{A}}_{nd}$ is critically observable w.r.t. $X_s$ and $E_o$, if for any state $x^{\prime }\in X_{obs}$, either $x^{\prime }\subseteq X_s$ or $x^{\prime }\subseteq X_{nd}\setminus X_s$ holds.

Let ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd}$, $X_0)$ be an NFA that is not critically observable, $E_o\subseteq E$ be a set of observable events, $X_s\subseteq X_{nd}$ be a set of critical states, and $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ be the critical state estimator of ${\mathcal{A}}_{nd}$. The set of critical observability violative states is denoted as $X_N=\{x\in X_{obs}\mid x⊈X_s\wedge x⊈X_{nd}\setminus X_s\}$.

Example 2.

Consider the NFA ${\mathcal{A}}_{nd}=\{X_{nd},E,{\delta }_{nd},X_0\}$ shown in Figure 3, where $X_{nd}=\{x_0,x_1,x_2,x_3,x_4,x_5\}$ is the set of states, $E=E_o\dot{\cup }{E}_{uo}=\{\alpha ,\beta ,\theta ,\lambda \}$ is the set of events with $E_o=\{\alpha ,\beta ,\lambda \}$ and $E_{uo}=\left\{\theta \right\}$, and $X_0=\left\{x_0\right\}$ is the set of initial states. The critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of ${\mathcal{A}}_{nd}$ is portrayed in Figure 4. We assume that the set of critical states is $X_s=\{x_3,x_4\}$. In Figure 4, by considering an observation $\rho =\beta \alpha \lambda$, the system ${\mathcal{A}}_{nd}$ is not critically observable w.r.t. $E_o$ and $X_s$, thanks to $\mathcal{C}\left(\beta \alpha \lambda \right)={\delta }_{obs}(x_{0,obs},\beta \alpha \lambda )=x_{o4}=\{x_3,x_4,x_5\}$, i.e, there exist a state $x_{o4}\in X_{obs}$ such that $x_{o4}⊈X_s$ and $x_{o4}⊈X_{nd}\setminus X_s$.

However, the NAF ${\mathcal{A}}_{nd}$ is critically observable if the critical state is $X_s=\left\{x_2\right\}$, since intruders can always determine whether the critical state is reached by observing the system’s behavior. That is, in $Obs\left({\mathcal{A}}_{nd}\right)$, for all $x\in X_{obs}$, $x\subseteq X_s$ or $x\subseteq X_{nd}\setminus X_s$ holds. □

Consider a system ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ that is not critically observable w.r.t. the set of observable events $E_o\subseteq E$ and the set of critical states $X_s\subseteq X_{nd}$. Let $Obs\left({\mathcal{A}}_{nd}\right)$ be the critical state estimator of ${\mathcal{A}}_{nd}$. Given a production $\xi =x_0\stackrel{e_1}{\to }{x}_1\stackrel{e_2}{\to }\cdots \stackrel{e_k}{\to }{x}_k$ of $Obs\left({\mathcal{A}}_{nd}\right)$ with the observation $\rho =e_1{e}_2\cdots e_k$, if the set of states consistent with $\rho$ is a subset of critical observability violative states or a subset of critical states, i.e., $\mathcal{C}\left(\rho \right)\subseteq X_N$ or $\mathcal{C}\left(\rho \right)\subseteq X_s$, the production is said to be unsafe. In this case, the corresponding sequences $F\left(\xi \right)=x_0{x}_1\cdots x_k$ and $T\left(\xi \right)=\rho =e_1{e}_2\cdots e_k$ are defined as an unsafe production state sequence and an unsafe production event sequence (or an unsafe observation), respectively. Otherwise, the set of states consistent with $\rho$ is included in $X_{nd}\setminus X_s$, i.e., $\mathcal{C}\left(\rho \right)\subseteq X_{nd}\setminus X_s$, the production is identified as safe. Its corresponding production event sequence $T\left(\xi \right)$ and production state sequence $F\left(\xi \right)$ are also considered safe. Once an unsafe observation is exposed to an intruder, he/she can determine that the system is not critically observable or the system’s critical states are revealed. In the following, we focus on how to make a non-critically observable system satisfy critical observability. Moreover, we guarantee that the critical states of the system cannot be revealed by an intruder.

4. Critical State Concealment Based on Differential Privacy

In this section, we aim to design a DPM to enforce critical observability for DESs modeled with DFAs, and to ensure that the predefined critical states cannot be detected to intruders. Specifically, we first define the Hamming distance of two state sequences in a DFA to describe the difference between them. Then, to prevent critical states or critical observability violative states from being captured by an intruder, we define a novel DPM for DFAs, called state sequence DP. Finally, an algorithm that provides a probability distribution for the generation of each state in an output state sequence is proposed and the DPM is designed.

4.1. Problem Statement

In $Obs\left({\mathcal{A}}_{nd}\right)$, when an unsafe observation $\rho$ is generated, we can design a DPM associated with $\rho$ to effectively conceal the unsafe observation. In particular, given an observation $\rho$, we derive its corresponding production state sequence ${\omega }_1\in \mathcal{F}\left(\rho \right)$. By inputting ${\omega }_1$ and a random production state sequence ${\omega }_2$, such that the Hamming distance between ${\omega }_1$ and ${\omega }_2$ is restricted to a bound $l\in \mathbb{N}$, into the designed mechanism, a protected production state sequence ${\omega }_3$ is output with approximate probability, where the lengths of ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are equal (i.e., $\left|{\omega }_1\right|=\left|{\omega }_2\right|=\left|{\omega }_3\right|$). Since both ${\omega }_1$ and ${\omega }_2$ can lead to the generation of ${\omega }_3$ with probabilities that are sufficiently close, it becomes impossible for an intruder to determine whether ${\omega }_1$ or ${\omega }_2$ is generated by the estimator $Obs\left({\mathcal{A}}_{nd}\right)$. In other words, from the observed behavior contained in $\mathcal{T}\left({\omega }_3\right)$, the intruder cannot infer its corresponding input behavior, and thereby the unsafe observation is not identifiable. Before discussing the use of DP to protect unsafe observations from being acquired, we first provide some definitions.

Definition 3

(Hamming distance). Given two production state sequences ${\omega }_1=x_0{x}_1\cdots x_k$ and ${\omega }_2=x_0^{\prime }{x}_1^{\prime }\cdots x_k^{\prime }$ generated by a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)$ with the same length ($\left|{\omega }_1\right|$ = $\left|{\omega }_2\right|$), the Hamming distance between ${\omega }_1$ and ${\omega }_2$ is defined as $\mathcal{J}({\omega }_1,{\omega }_2)=\left|\{j\mid {\omega }_1\left(j\right)\ne {\omega }_2\left(j\right)\}\right|$, where ${\omega }_i\left(j\right)$ represents the j-th entry of production state sequence ${\omega }_i$, $i=1,2$, and $j=1,2,\dots ,|{\omega }_1|$. ♢

Let $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ be a critical state estimator of ${\mathcal{A}}_{nd}$, $k\in {\mathbb{N}}^{+}=\{1,2,\dots \}$ be a positive integer representing the length of a production state sequence, and $l\in \mathbb{N}$ be a parameter. We define ${\mathcal{W}}_{k,l}$ as the set of all pairs of production state sequences $({\omega }_1,{\omega }_2)$ with $\left|{\omega }_1\right|=\left|{\omega }_2\right|=k$ and the Hamming distance $\mathcal{J}({\omega }_1,{\omega }_2)$ between them is less than or equal to l, i.e.,

$$\begin{array}{c}\hfill {\mathcal{W}}_{k,l}=\{({\omega }_1,{\omega }_2)\in X_{obs}^k\times X_{obs}^k\mid \mathcal{J}({\omega }_1,{\omega }_2)\le l\}.\end{array}$$

Considering Definition 1 and the properties of DES models, we now define state sequence DP in a DFA.

Definition 4

(State sequence differential privacy). Given an NFA ${\mathcal{A}}_{nd}$, let $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ be its critical state estimator and $X_{obs}^k$ be the set of state sequences with length k in $Obs\left({\mathcal{A}}_{nd}\right)$. Let $ϵ\ge 0$ be a real number. A mechanism ${\mathcal{M}}_{\omega }:X_{obs}^k\to X_{obs}^k$ is said to be of state sequence DP w.r.t. ${\mathcal{W}}_{k,l}$ if for all production state sequence pairs $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{k,l}$ and for all ${\omega }_3\in X_{obs}^k$, it holds

$$\begin{array}{c}\hfill \mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]\le exp\left(ϵ\right)\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3],\end{array}$$

(1)

where $\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_i\right)={\omega }_3]$ represents the probability of ${\mathcal{M}}_{\omega }\left({\omega }_i\right)={\omega }_3$ with $i\in \{1,2\}$. ♢

According to Definition 4, a mechanism that guarantees DP of state sequences w.r.t. ${\mathcal{W}}_{k,l}$ implies that for all pairs of production state sequences $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{k,l}$ with ${\omega }_1,{\omega }_2\in X_{obs}^k$, and for all possible output production state sequences ${\omega }_3\in X_{obs}^k$, the probability of ${\omega }_1$ being decorated as ${\omega }_3$ and that of ${\omega }_2$ being decorated as ${\omega }_3$ is close enough such that an intruder cannot identify which is the real input to ${\mathcal{M}}_{\omega }$.

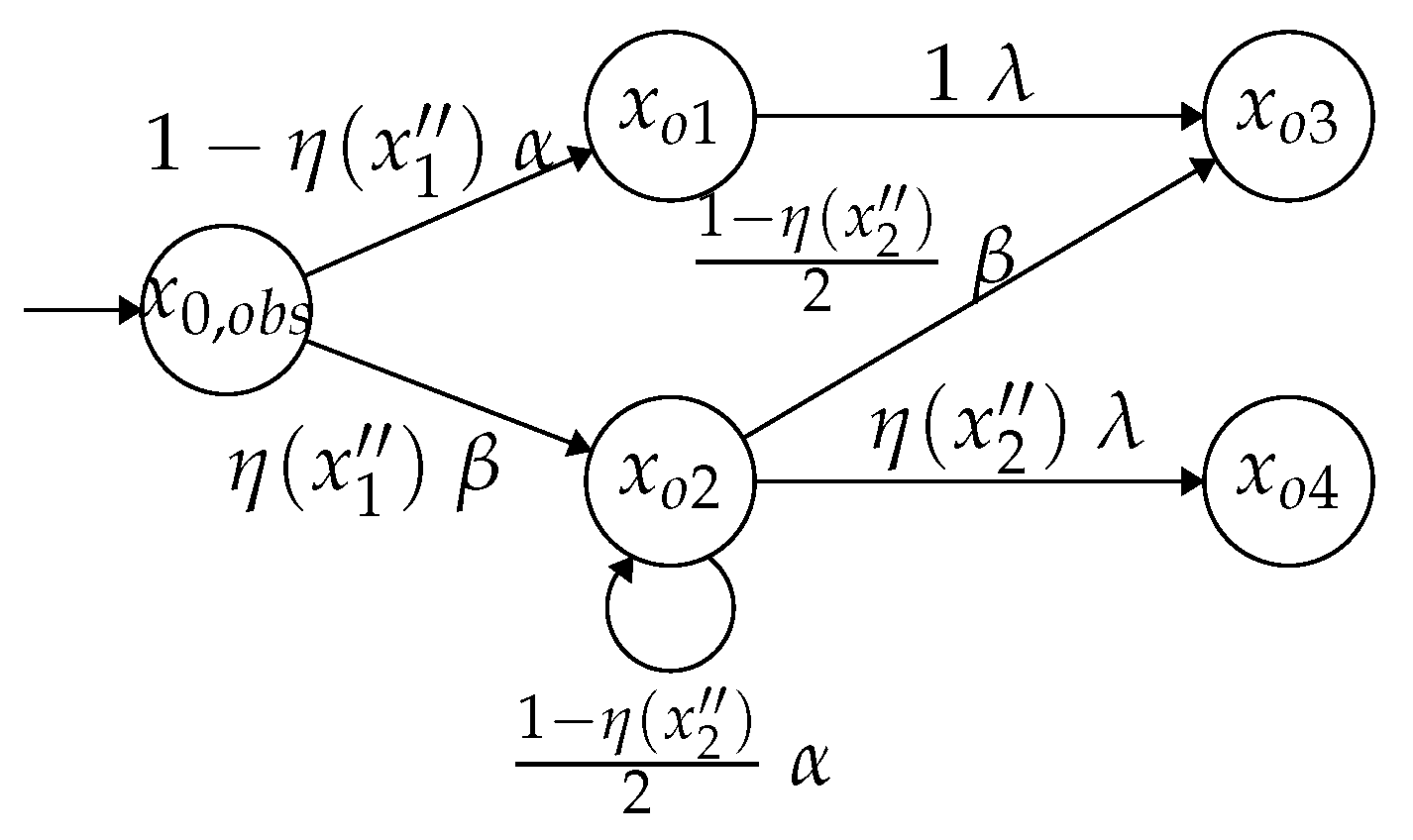
To evaluate the performance of the mechanism, we introduce the concept of the security degree of a state sequence. Given an NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$, a set of observable events $E_o\subseteq E$, a set of critical states $X_s\subseteq X_{nd}$, and the critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of ${\mathcal{A}}_{nd}$, let $\omega =x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$ be a state sequence in $Obs\left({\mathcal{A}}_{nd}\right)$. If the production state sequence $\omega$ is safe, the security degree of $\omega$ is defined as $deg\left(\omega \right)=|x_k|$, where $x_k=\mathcal{C}\left(\rho \right)$ with $\rho \in \mathcal{T}\left(\omega \right)$. Otherwise, the sequence $\omega$ is unsafe, whose security degree is defined as $deg\left(\omega \right)=0$. In other words, the state sequence $\omega$ consistent with an observation $\rho$ that violates critical observability or reveals the critical states (i.e., $\mathcal{C}\left(\rho \right)\subseteq X_N$ or $\mathcal{C}\left(\rho \right)\subseteq X_s$) has the lowest security level. Note that for all $\rho \in \mathcal{T}\left(\omega \right)$, $\mathcal{C}\left(\rho \right)$ is unique. Given a production state sequence $\omega$ in $Obs\left({\mathcal{A}}_{nd}\right)$, a larger value $deg\left(\omega \right)$ means that the set of critical observability violative states $X_N$ or the set of critical states $X_s$ is less likely to be detected by an intruder.

Consider a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)$ of a system ${\mathcal{A}}_{nd}$ and a parameter $k\in {\mathbb{N}}^{+}$. The maximum security degree of production state sequences $\omega =x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$ contained in $Obs(\left({\mathcal{A}}_{nd}\right)$ is defined as $de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)=max\{g\in \mathbb{N}\mid \exists \omega \in X_{obs}^{k+1}:deg\left(\omega \right)=g\}$1.

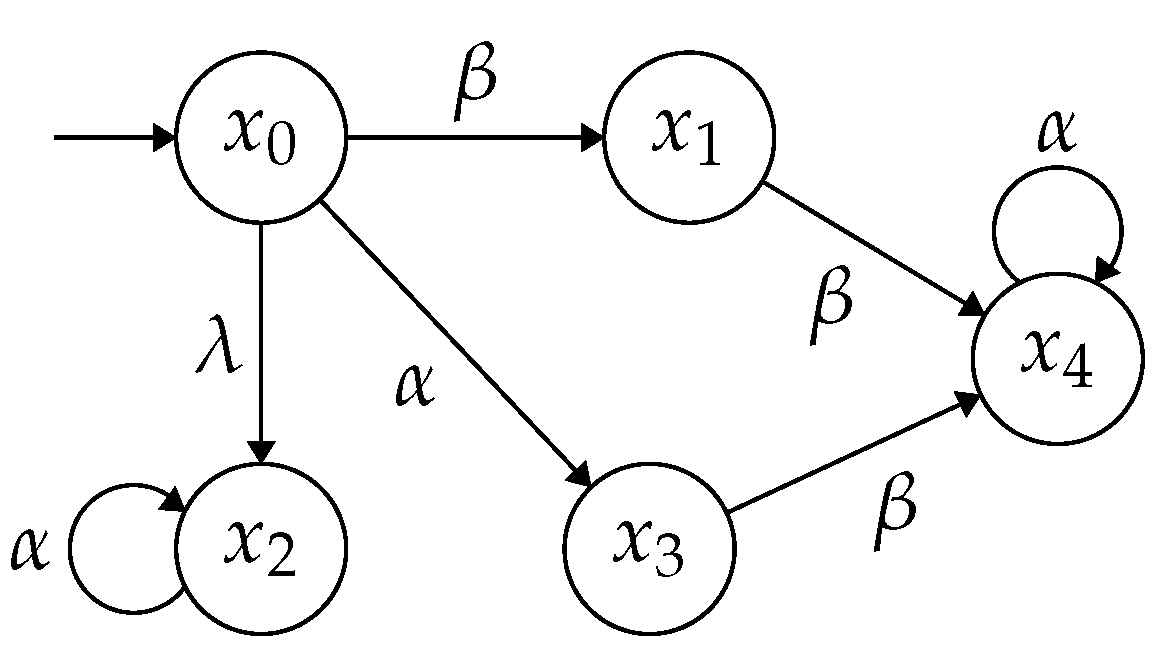
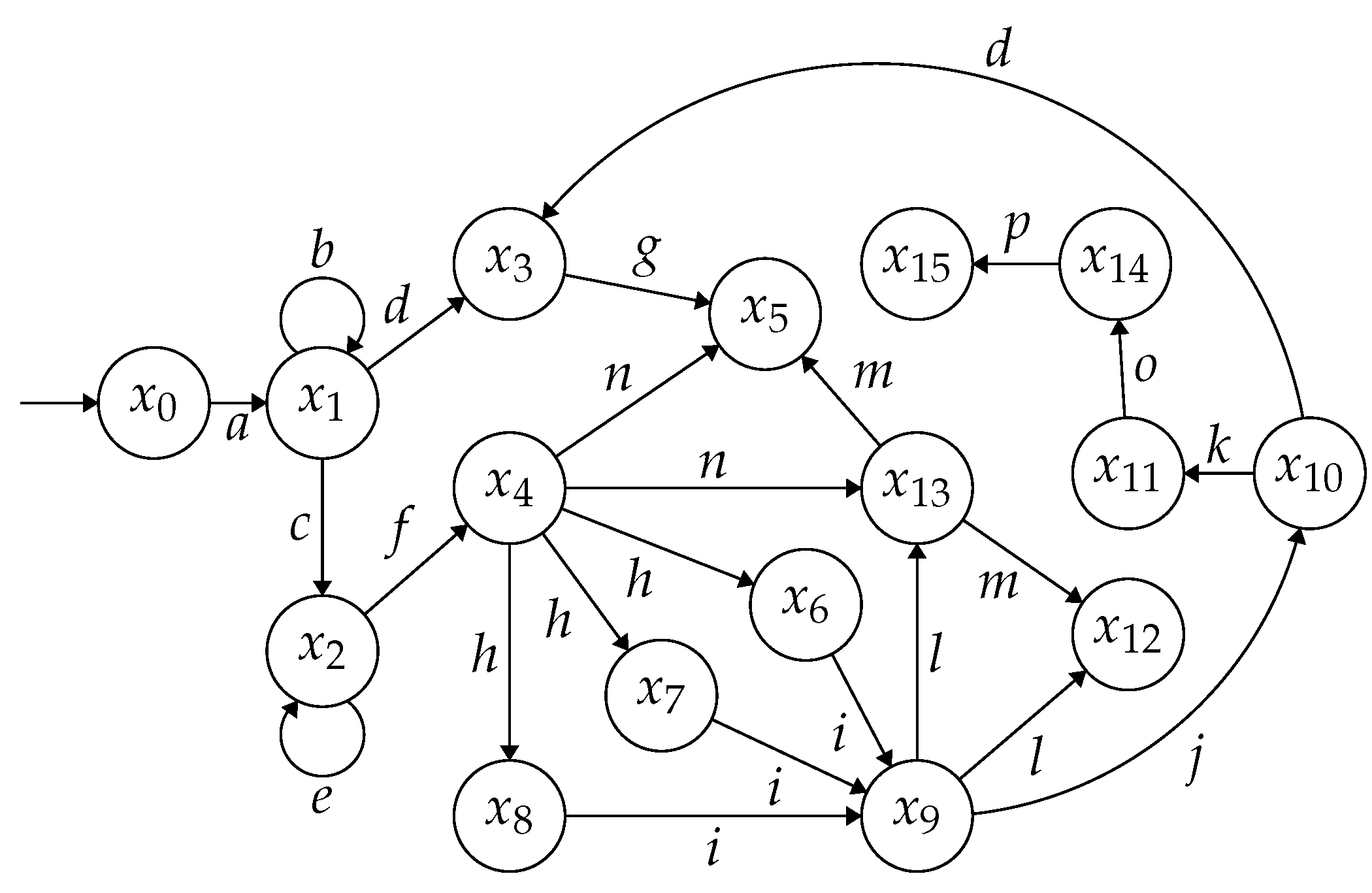
Example 3.

Consider the NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ and a set of critical states $X_s=\left\{x_3\right\}$ in Example 2. Let $\xi =x_{0,obs}\stackrel{\alpha }{\to }{x}_{o1}\stackrel{\lambda }{\to }{x}_{o3}\stackrel{\beta }{\to }{x}_{o1}$ be a production of $Obs\left({\mathcal{A}}_{nd}\right)$ portrayed in Figure 4 with $F\left(\xi \right)=\omega =x_{0,obs}{x}_{o1}{x}_{o3}{x}_{o1}$. The security degree of ω is 2, i.e., $deg\left(\omega \right)=|\{x_1,x_4\}|=2$. Given another production ${\xi }^{\prime }=x_{0,obs}\stackrel{\beta }{\to }{x}_{o2}\stackrel{\lambda }{\to }{x}_{o4}$, the production state sequence $F\left({\xi }^{\prime }\right)={\omega }^{\prime }=x_{0,obs}{x}_{o2}{x}_{o4}$ is unsafe and ${\omega }^{\prime }$ has the lowest security degree $deg\left({\omega }^{\prime }\right)=0$ thanks to $x_{o4}\subseteq X_N$. Given a non-negative integer $k=4$ representing the length of a state sequence, we have $de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),4)=2$. □

In this paper, we focus on a mechanism that provides the highest degree of protection for an unsafe production state sequence. In simpler terms, the mechanism is capable of confusing unsafe state sequences with safe ones that have the maximum security degree. In particular, the designed mechanism w.r.t. ${\mathcal{W}}_{k+1,l}$ ensures that, for an unsafe production state sequence ${\omega }_1=x_0{x}_1\cdots x_k$, there exists a production state sequence ${\omega }_2=x_0^{\prime }{x}_1^{\prime }\cdots x_k^{\prime }$ with maximum degree $de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)$ such that $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{k+1,l}$ and $\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]\le exp\left(ϵ\right)\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]$ for all ${\omega }_3\in X_{obs}^{k+1}$.

The distance bound l is another parameter that significantly impacts the performance of the mechanism ${\mathcal{M}}_{\omega }$. Given an unsafe state sequence ${\omega }_1$, it is crucial to select a value l that is as small as possible while guaranteeing that the mechanism ${\mathcal{M}}_{\omega }$ can maximally confuse ${\omega }_1$ with ${\omega }_2$. In other words, the state sequence ${\omega }_2$, which serves as a suitable alternative for ${\omega }_1$, should exhibit the utmost similarity to ${\omega }_1$.

Definition 5.

Let ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ be an NFA that is not critically observable, $X_s\subseteq X_{nd}$ be a set of critical states, $E_o\subseteq E$ be a set of observable events, $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ be a critical state estimator of ${\mathcal{A}}_{nd}$, and ${\mathcal{M}}_{\omega }:X_{obs}^{k+1}\to X_{obs}^{k+1}$ be a mechanism that provides state sequence DP w.r.t. ${\mathcal{W}}_{k+1,l}$. Given an unsafe state sequence ${\omega }_1$, the mechanism ${\mathcal{M}}_{\omega }$ is optimal w.r.t. ${\omega }_1$ if it satisfies the following statements:

• There exists a production state sequence ${\omega }_2$ in $Obs\left({\mathcal{A}}_{nd}\right)$ with $deg\left({\omega }_2\right)=$$de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)$ such that $({\omega }_1$, ${\omega }_2)\in {\mathcal{W}}_{k+1,l}$ holds;
• For all ${\omega }_3\in X_{obs}^{k+1}$, the inequality $\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]\le exp\left(ϵ\right)\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]$ holds;
• For all ${\omega }_2$ in $Obs\left({\mathcal{A}}_{nd}\right)$ with $deg\left({\omega }_2\right)=de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right)$, $k+1)$, there does not exist $l^{\prime }<l$ ($l,l^{\prime }\in \mathbb{N}$) such that $\mathcal{J}({\omega }_1$, ${\omega }_2)=l^{\prime }$. ♢

According to Definition 5, given an unsafe ${\omega }_1$, condition 1) ensures that there exists at least one state sequence ${\omega }_2$ with the maximum security degree such that $({\omega }_1,{\omega }_2)$ belongs to the set ${\mathcal{W}}_{k+1,l}$. Condition 2) indicates that an optimal mechanism provides (guarantees) the state sequence DP w.r.t. ${\mathcal{W}}_{k+1,l}$. Condition 3) implies that the parameter l with $l=\mathcal{J}({\omega }_1,{\omega }_2)$ must be minimal for all state sequences ${\omega }_2$ that satisfy $deg\left({\omega }_2\right)=$$de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)$. In the following, we will detail the design of an optimal mechanism ${\mathcal{M}}_{\omega }$ that satisfies the definition of state sequence DP.

4.2. State Sequence Differential Privacy

Based on Definitions 4 and 5, we first design a probability allocation strategy for the optimal mechanism ${\mathcal{M}}_{\omega }$ in a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of system ${\mathcal{A}}_{nd}$. Given an unsafe input production state sequence ${\omega }_1=x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$, the aim is to generate a random state sequence ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$ with a certain probability from ${\mathcal{M}}_{\omega }$ such that $\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]$. Specifically, the strategy to be defined enables assigning a probability $\mathbb{P}\left[x_i^{\prime \prime }\right]$ to each state included in the output production state sequence ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$, where $i=0,\dots ,k$. Then, by multiplying the probabilities $\mathbb{P}\left[x_i^{\prime \prime }\right]$ of all output states $x_i^{\prime \prime }\in X_{obs}$ ($i=0,1,\dots ,k$), we can obtain the probability of generating ${\omega }_3$, i.e., $\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]=\mathbb{P}\left[x_0^{\prime \prime }\right]\times \mathbb{P}\left[x_1^{\prime \prime }\right]\times \cdots \times \mathbb{P}\left[x_k^{\prime \prime }\right]$. In terms of the strategy, we explore the conditions for ensuring the DP of state sequences and further design an algorithm to synthesize this optimal mechanism ${\mathcal{M}}_{\omega }$.

Given a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs}$, $x_{0,obs})$, let ${\mathcal{M}}_{\omega }:X_{obs}^{k+1}\to X_{obs}^{k+1}$ be a mechanism that takes a production state sequence ${\omega }_1=x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$ as input and ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$ as output. Before elaborating on the probability allocation strategy to a state in ${\omega }_3$, we introduce an indicator function denoted as $\nu (x_{i-1}^{\prime \prime },x_i)$ for two states $x_{i-1}^{\prime \prime },x_i\in X_{obs}$, defined as follows:

$$\nu (x_{i-1}^{\prime \prime },x_i)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}\begin{array}{cc}\hfill & \exists e\in E_o:{\delta }_{obs}(x_{i-1}^{\prime \prime },e)=x_i;\hfill \end{array}\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where $i=1,2,\cdots ,k$. If $x_i^{\prime \prime }$ included in ${\omega }_3$ satisfies $x_i^{\prime \prime }=x_i$, it is considered a correct state. On the other hand, if $x_i^{\prime \prime }\ne x_i$, the state $x_i^{\prime \prime }$ is referred to as an incorrect state.

Now, we describe a probability allocation strategy that assigns a probability $\mathbb{P}\left[x_i^{\prime \prime }\right]$ to each state $x_i^{\prime \prime }$ in the state sequence ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$, where $i\in \{0,\dots ,k\}$. Given an input production state sequence ${\omega }_1=x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$, let ${\mathcal{X}}_{{\omega }_1}$ be the set that collects all the states in ${\omega }_1$, i.e., ${\mathcal{X}}_{{\omega }_1}=\{x_0,x_1,\dots ,x_k\}$. The strategy for ${\omega }_3$ associated with ${\omega }_1$ is a (partial) function $\phi :X_{obs}\times {\mathcal{X}}_{{\omega }_1}\times X_{obs}\to [0,1]$ that outputs a probability of generating state $x_i^{\prime \prime }\in X_{obs}$ in relation to two states $x_{i-1}^{\prime \prime }\in X_{obs}$ and $x_i\in {\mathcal{X}}_{{\omega }_1}$, where $(x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })\in X_{obs}\times {\mathcal{X}}_{{\omega }_1}\times X_{obs}$. Particularly, for the initial state, we define $x_0=x_0^{\prime \prime }=x_{0,obs}$, and it is assigned a probability value $\mathbb{P}\left[x_0^{\prime \prime }\right]=1$. Then, for all $i\in \{1,\dots ,k\}$, if $x_i^{\prime \prime }$ is a correct state, it is allocated a correct probability $\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })=\mathbb{P}\left[x_i^{\prime \prime }\right]=\eta \left(x_i^{\prime \prime }\right)$ (the value of $\eta \left(x_i^{\prime \prime }\right)$ is examined in detail in Theorem 1). On the other hand, if $x_i^{\prime \prime }$ is not a correct state, let

$$\phi ((x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })=\mathbb{P}\left[x_i^{\prime \prime }\right]={\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)\nu (x_{i-1}^{\prime \prime },x_i)}{\left|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)\right|-\nu (x_{i-1}^{\prime \prime },x_i)}}.$$

Algorithm 1: A probability Allocation Strategy $\phi$.

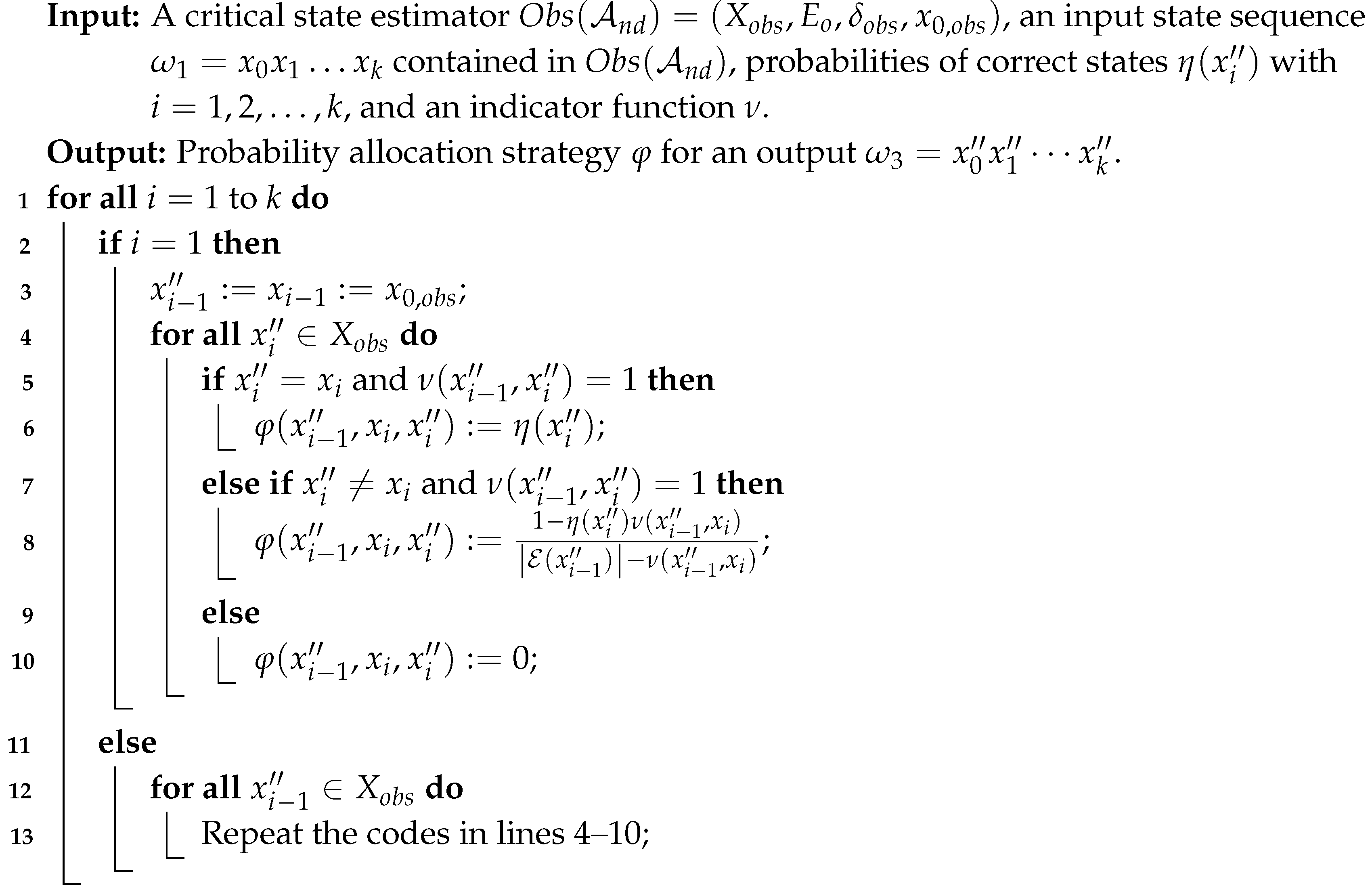Then, we design an algorithm (namely Algorithm 1) to compute the probability allocation strategy $\phi$ for a random output ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }$ associated with an input state sequence ${\omega }_1=x_0{x}_1\cdots x_k$. The algorithm takes as input a critical state estimator, an input state sequence, probabilities of correct states, and an indicator function. It iterates through each state in the input sequence and calculates the probability of generating each possible output state based on the given probabilities of correct states and the indicator function. In Algorithm 1, for all $i=1,\dots ,k$, if $i=1$, we have $x_0^{\prime \prime }=x_0=x_{0,obs}$. For each possible state $x_i^{\prime \prime }\in X_{obs}$, it checks whether $x_i^{\prime \prime }=x_i$ and whether the indicator function $\nu (x_{i-1}^{\prime \prime },x_i^{\prime \prime })=1$. If both conditions hold, the correct state $x_i^{\prime \prime }$ is allocated a correct probability $\eta \left(x_i^{\prime \prime }\right)$. If $x_i^{\prime \prime }\ne x_i$ and the indicator function $\nu (x_{i-1}^{\prime \prime },x_i^{\prime \prime })=1$, the state $x_i^{\prime \prime }$ is assigned an incorrect probability

$${\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)\nu (x_{i-1}^{\prime \prime },x_i)}{\left|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)\right|-\nu (x_{i-1}^{\prime \prime },x_i)}}.$$

Otherwise, if $\nu (x_{i-1}^{\prime \prime },x_i^{\prime \prime })=0$, $\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })=0$ is defined. If $1<i\le k$, for all $x_{i-1}^{\prime \prime }\in X_{obs}$, the codes in lines 4–10 are repeated. The computational complexity of Algorithm 1 is $\mathcal{O}(k\times \left|X_{obs}\right|)$.

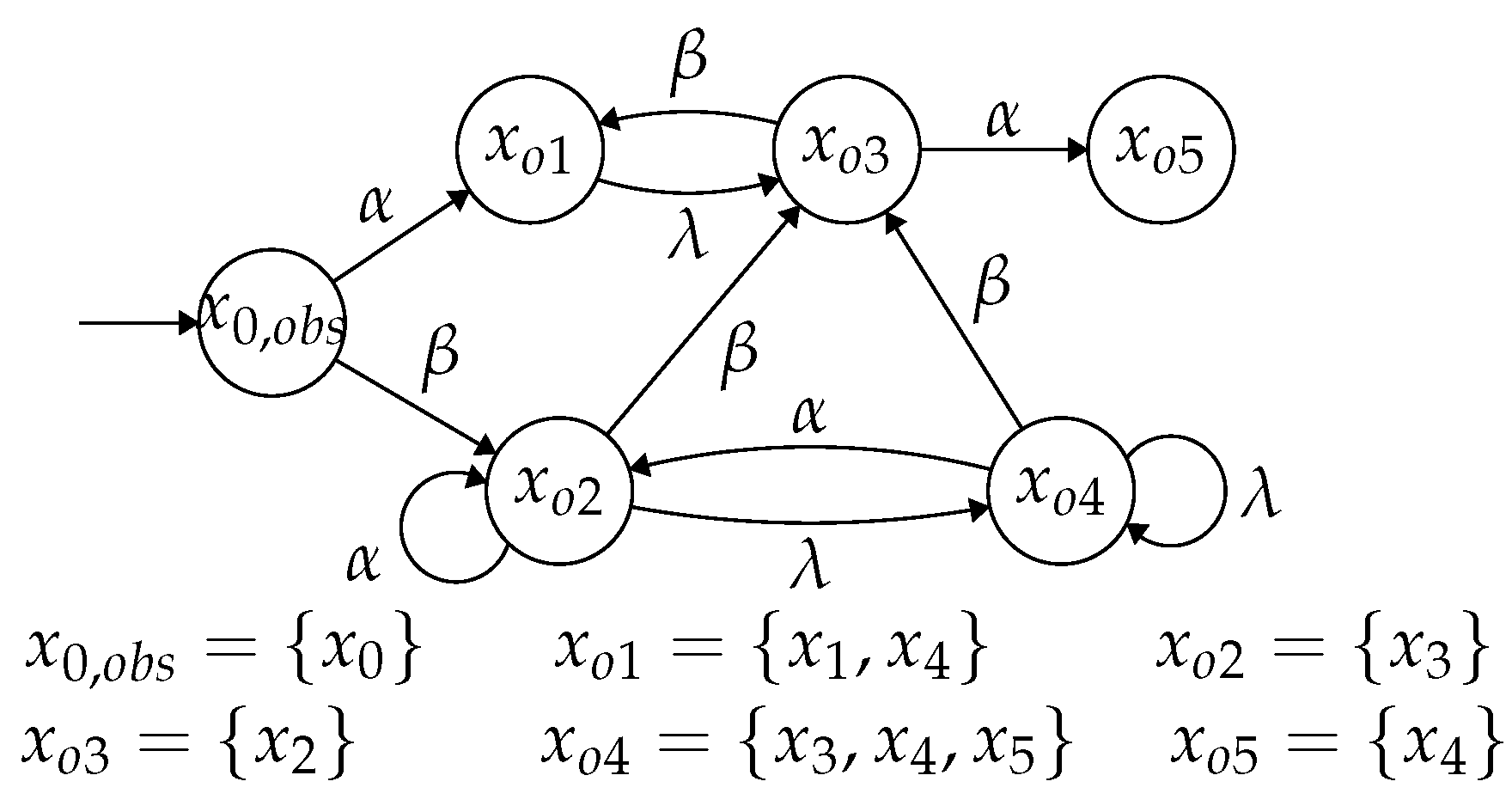
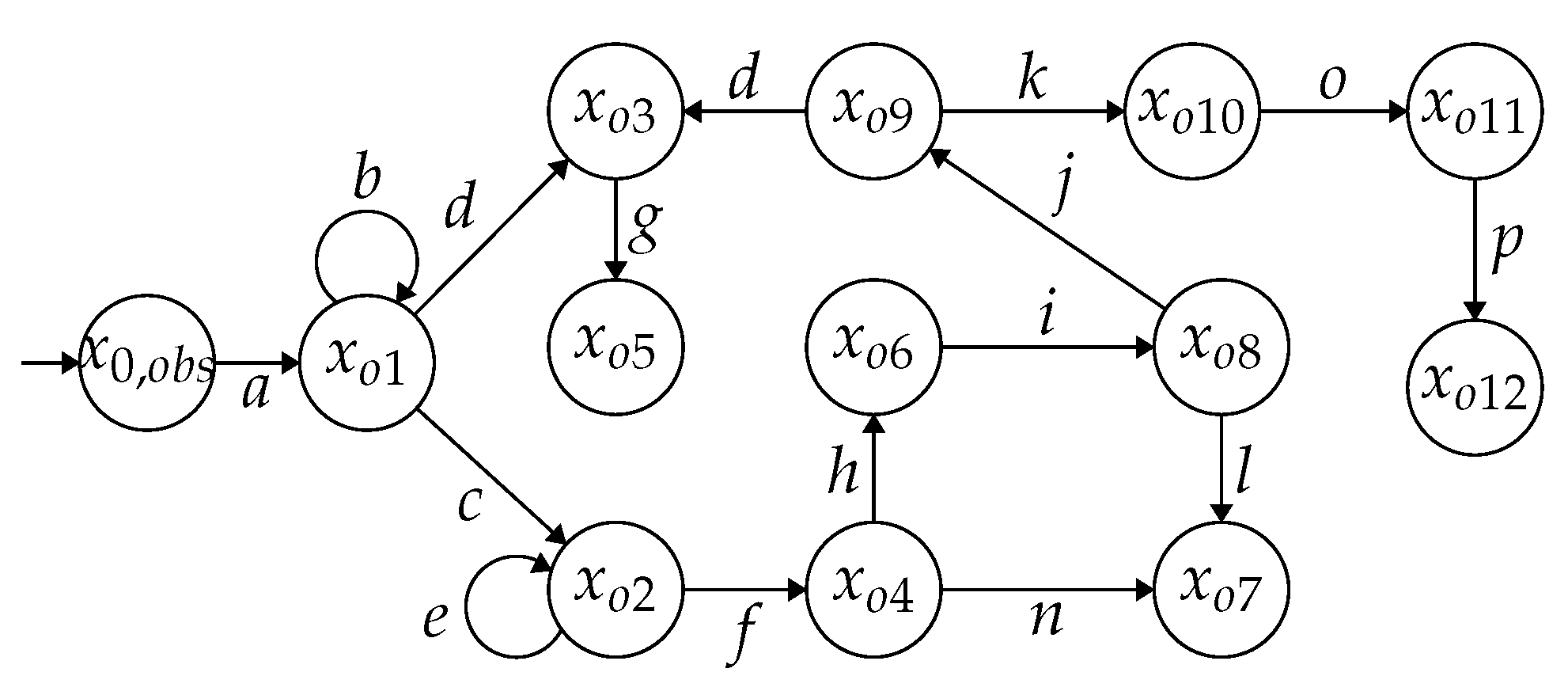
Example 4.

Consider a state sequence ${\omega }_1=x_0{x}_1{x}_2=x_{0,obs}{x}_{o2}{x}_{o4}$ in the critical state estimator in Figure 4 and feed into a mechanism ${\mathcal{M}}_{\omega }$. Let us elaborate on how to calculate the probability allocation strategy φ for a randomly generated output state sequence ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }{x}_2^{\prime \prime }$ with $x_0^{\prime \prime }=x_0=x_{0,obs}$ (all possible output state sequences ${\omega }_3$ with $\left|{\omega }_3\right|=3$ are illustrated in Figure 5).

If $x_1^{\prime \prime }=x_1=x_{o2}$, according to the strategy φ, the state $x_1^{\prime \prime }$ is correct and is assigned a correct probability $\eta \left(x_1^{\prime \prime }\right)$ with $\phi (x_0^{\prime \prime },x_1,x_1^{\prime \prime })=\phi (x_{0,obs},x_{o2},x_{o2})=\eta \left(x_1^{\prime \prime }\right)$ (the value of $\eta \left(x_1^{\prime \prime }\right)$ is discussed in Theorem 1); if $x_1^{\prime \prime }=x_{o1}$ with $x_{o1}\ne x_{o2}$, by the line 8 of Algorithm 1, we allocate an incorrect probability to state $x_{o1}$, i.e., $\phi (x_0^{\prime \prime },x_1,x_1^{\prime \prime })=\phi (x_{0,obs},x_{o2},x_{o1})={\displaystyle \frac{1-\eta \left(x_1^{\prime \prime }\right)\times 1}{2-1}}=1-\eta \left(x_1^{\prime \prime }\right)$.

At the state $x_1^{\prime \prime }=x_{o1}$, since the feasible state $x_2^{\prime \prime }=x_{o3}$ is not correct, i.e., $x_2^{\prime \prime }\ne x_2$ and $\nu (x_1^{\prime \prime },x_2^{\prime \prime })=\nu (x_{o1},x_{o3})=1$, we have $\phi (x_1^{\prime \prime },x_2,x_2^{\prime \prime })=\phi (x_{o1},x_{o4},x_{o3})={\displaystyle \frac{1-\eta \left(x_1^{\prime \prime }\right)\times 0}{1-0}}=1$. Analogously, at the state $x_1^{\prime \prime }=x_{o2}$, we have $\phi (x_{o2},x_{o4},x_{o4})=\eta \left(x_2^{\prime \prime }\right)$ and $\phi (x_{o2},x_{o4},x_{o2})=\phi (x_{o2},x_{o4},x_{o3})={\displaystyle \frac{1-\eta \left(x_2^{\prime \prime }\right)\times 1}{3-1}}={\displaystyle \frac{1-\eta \left(x_2^{\prime \prime }\right)}{2}}$. □

By utilizing the probability allocation strategy $\phi$, we are able to synthesize a mechanism that generates a production state sequence assigned with a probability. In other words, for all states contained in ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }$, the probability of generating ${\omega }_3$ is given by ${\prod }_{i=1}^k\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })$ with $\mathbb{P}\left[x_0^{\prime \prime }\right]=\mathbb{P}\left[x_{0,obs}\right]=1$. Now, we demonstrate the condition of $\eta \left(x_i^{\prime \prime }\right)$ for a mechanism ${\mathcal{M}}_{\omega }$ to provide state sequence DP w.r.t. ${\mathcal{W}}_{k+1,l}$, based on Algorithm 1.

Theorem 1.

Given a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of a system ${\mathcal{A}}_{nd}$ that is not critically observable, let $ϵ>0$ be a real number, $l\in \mathbb{N}$ be a parameter, $k\in {\mathbb{N}}^{+}$ be the length of a state sequence, ${\mathcal{M}}_{\omega }:X_{obs}^{k+1}\to X_{obs}^{k+1}$ be a mechanism whose probability allocation strategy is computed by Algorithm 1, and $x_i^{\prime \prime }$ ($0\le i\le k$) be a correct state contained in an output state sequence ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$ of ${\mathcal{M}}_{\omega }$. The mechanism ${\mathcal{M}}_{\omega }$ guarantees state sequence DP w.r.t. ${\mathcal{W}}_{k+1,l}$ if the probabilities of correct states $\eta \left(x_i^{\prime \prime }\right)$ satisfy the following condition:

$$\begin{array}{c}\hfill \eta \left(x_i^{\prime \prime }\right)={\displaystyle \frac{1}{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)exp(-\frac{ϵ}{l})+1}}.\end{array}$$

(2)

Proof. Let ${\omega }_1=x_0{x}_1\cdots x_k$ and ${\omega }_2=x_0^{\prime }{x}_1^{\prime }\cdots x_k^{\prime }$ be two production state sequences generated by $Obs\left({\mathcal{A}}_{nd}\right)$ such that $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{k+1,l}$. We consider ${\mathcal{M}}_{\omega }\left({\omega }_1\right)={\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3$ with ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$ (the initial states in ${\omega }_1$, ${\omega }_2$, and ${\omega }_3$ are the same, i.e., $x_0=x_0^{\prime }=x_0^{\prime \prime }=x_{0,obs}$). By Definition 4, we need to prove the following inequality:

$$\exp (-ϵ)\le {\displaystyle \frac{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]}{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]}}\le \exp \left(ϵ\right).$$

To begin with, we show ${\displaystyle \frac{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]}{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]}}\le \exp \left(ϵ\right)$. Using Algorithm 1, we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]}{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]}}& ={\displaystyle \frac{\eta \left(x_0^{\prime \prime }\right)\times {\prod }_{i=1}^k\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })}{\eta \left(x_0^{\prime \prime }\right)\times {\prod }_{j=1}^k\phi (x_{j-1}^{\prime \prime },x_j^{\prime },x_j^{\prime \prime })}}\hfill \\ \hfill & =\prod _{r\in R}{\displaystyle \frac{\phi (x_{r-1}^{\prime \prime },x_r,x_r^{\prime \prime })}{\phi (x_{r-1}^{\prime \prime },x_r^{\prime },x_r^{\prime \prime })}},\hfill \end{array}$$

where $R=\{r\in {\mathbb{N}}^{+}\mid x_r\ne x_r^{\prime }\}$ and $\left|R\right|\le l$.

Note that when $x_i^{\prime \prime }$ is an incorrect state, the values of $\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })$ depend on $\nu (x_{i-1}^{\prime \prime },x_i)$, i.e.,

$$\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })=\left\{\begin{array}{cc}{\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|-1}}\hfill & \mathrm{if}\nu (x_{i-1}^{\prime \prime },x_i)=1;\hfill \\ {\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

We now claim $\eta \left(x_i^{\prime \prime }\right)\ge {\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}\ge {\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|-1}}$.

1) First, we prove $\eta \left(x_i^{\prime \prime }\right)\ge {\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}$. One has

$$\begin{array}{cc}\hfill \eta \left(x_i^{\prime \prime }\right)-{\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}& ={\displaystyle \frac{1}{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)exp(-\frac{ϵ}{l})+1}}-{\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}\hfill \\ \hfill & ={\displaystyle \frac{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)(1-exp(-\frac{ϵ}{l}))}{\left(\right(|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)exp(-\frac{ϵ}{l})+1\left)\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|}}\ge 0.\hfill \end{array}$$

2) Let us prove the second inequality ${\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}\ge {\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|-1}}$.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|}}-{\displaystyle \frac{1-\eta \left(x_i^{\prime \prime }\right)}{\left|\mathcal{E}\right(x_{i-1}^{\prime \prime }\left)\right|-1}}\hfill \\ \hfill & ={\displaystyle \frac{|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1-|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|+|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|\eta \left(x_i^{\prime \prime }\right)}{|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|·(|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)}}\hfill \\ \hfill & ={\displaystyle \frac{|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|\eta \left(x_i^{\prime \prime }\right)-1}{|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|·(|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)}}={\displaystyle \frac{\frac{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)·(1-exp(-\frac{ϵ}{l}))}{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)·exp(-\frac{ϵ}{l})+1}}{|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|·(|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)}}\ge 0.\hfill \end{array}$$

Then we conclude that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]}{\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]}}& =\prod _{r\in R}{\displaystyle \frac{\phi (x_{r-1}^{\prime \prime },x_r,x_r^{\prime \prime })}{\phi (x_{r-1}^{\prime \prime },x_r^{\prime },x_r^{\prime \prime })}}\le \prod _{r\in R}{\displaystyle \frac{\eta \left(x_r^{\prime \prime }\right)}{\frac{1-\eta \left(x_r^{\prime \prime }\right)}{\left|\mathcal{E}\right(x_{r-1}^{\prime \prime }\left)\right|-1}}}\hfill \\ \hfill & =\prod _{r\in R}exp\left({\displaystyle \frac{ϵ}{l}}\right)=\prod _{i=1}^{\left|R\right|}exp\left({\displaystyle \frac{ϵ}{l}}\right)\le exp\left(ϵ\right).\hfill \end{array}$$

The constraint ${\prod }_{r\in R}{\displaystyle \frac{\phi (x_{r-1}^{\prime \prime },x_r,x_r^{\prime \prime })}{\phi (x_{r-1}^{\prime \prime },x_r^{\prime },x_r^{\prime \prime })}}\ge exp(-ϵ)$ can be proved similarly, which completes the proof. ▪

By Definition 4 and Theorem 1, Algorithm 2 computes an optimal mechanism for an unsafe input state sequence ${\omega }_1$, which aims to prevent the leakage of critical observability violative states or critical states in a non-critically observable system. [2]We use a number in square brackets after a tuple to represent the entries of the tuple.

[3]A number in square brackets after a set of tuples represents the set contained by the entries of the tuple set. Here, $B\left[2\right]=\{b_1\left[2\right],\dots ,b_m\left[2\right]\}$ with $b_i\in B(i=1,\dots ,m)$.

Algorithm 2: Construction of a mechanism ${\mathcal{M}}_{\omega }$.

Algorithm 2 first initializes two empty sets B and G for storing the triplet elements $b\in B$ and $g\in G$. Then, it iterates through all the productions $\xi =x_0\stackrel{e_1}{\to }{x}_1\stackrel{e_2}{\to }\cdots \stackrel{e_k}{\to }{x}_k$ with $F\left(\xi \right)={\omega }_2$. In lines 3–6, for each such sequence ${\omega }_2$, the algorithm executes three key computations: assigning ${\omega }_2$, the degree $deg\left({\omega }_2\right)$ of ${\omega }_2$, and the Hamming distance $\mathcal{J}({\omega }_1$,${\omega }_2)$ to $b\left[1\right]$, $b\left[2\right]$, and $b\left[3\right]$, respectively. In line 7, the maximum value in set $B\left[2\right]$ is computed and is stored in the variable s. Next, for each triplet b in the set B, check whether $b\left[2\right]$ is equal to the maximum number s. If the condition is true, then add this element b to the set G. In line 11, the value of the parameter h is obtained by calculating the minimum number in set $G\left[3\right]$. For all input state sequences $\omega =x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$ and for all ${\omega }_3=x_0^{\prime \prime }{x}_1^{\prime \prime }\cdots x_k^{\prime \prime }\in X_{obs}^{k+1}$, in line 15, we compute the correct probability $\eta \left(x_i^{\prime \prime }\right)$ for each output state $x_i^{\prime \prime }$. Finally, in lines 16–17, Algorithm 2 synthesizes the mechanism ${\mathcal{M}}_{\omega }$ by invoking the probability allocation strategy $\phi$ of Algorithm 1.

The computational complexity of Algorithm 2 is mainly decided by the synthesis of the mechanism ${\mathcal{M}}_{\omega }$ in lines 12–17. In lines 12–13, we enumerate all the input and output sequences, resulting in complexity $\mathcal{O}\left(\right|X_{obs}{|}^{2k})$. Furthermore, in lines 14–16, we compute $\eta \left(x_i^{\prime \prime }\right)$ and utilize Algorithm 1 to calculate $\phi$. This step has complexity $\mathcal{O}(k+k\times |X_{obs}\left|\right)$. Taking into account the above statements, the complexity can be expressed as $\mathcal{O}(k\times |X_{obs}{|}^{2k}\times (1+|X_{obs}\left|\right))$, i.e., $\mathcal{O}(k\times |X_{obs}{|}^{3k})$.

Theorem 2.

Consider a critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=(X_{obs},E_o,{\delta }_{obs},x_{0,obs})$ of a system ${\mathcal{A}}_{nd}$ that is not critically observable. Let ${\omega }_1=x_0{x}_1\cdots x_k\in X_{obs}^{k+1}$ be an unsafe production state sequence in $Obs\left({\mathcal{A}}_{nd}\right)$. The mechanism ${\mathcal{M}}_{\omega }$ computed by Algorithm 2 guarantees DP of state sequences w.r.t. ${\mathcal{W}}_{k+1,h}$, in which $h\in \mathbb{N}$ is a parameter calculated by Algorithm 2. Moreover, the mechanism is optimal w.r.t. an unsafe production state sequence ${\omega }_1$.

Proof. First, we prove that the mechanism ${\mathcal{M}}_{\omega }$ designed in Algorithm 2 provides DP of state sequences w.r.t. ${\mathcal{W}}_{k+1,h}$. Specifically, in lines 12–17, for all input state sequences $\omega$ and any possible output state sequence ${\omega }_3$, we have $\mathbb{P}[{\mathcal{M}}_{\omega }\left(\omega \right)={\omega }_3]={\prod }_{i=1}^k\phi (x_{i-1}^{\prime \prime },x_i,x_i^{\prime \prime })$. Besides, we accurately compute the correct state probability $\eta \left(x_i^{\prime \prime }\right)$ based on Equation (2). According to Theorem 1, the mechanism ${\mathcal{M}}_{\omega }$ provides DP of state sequences w.r.t. ${\mathcal{W}}_{k+1,h}$.

Then we show that the mechanism ${\mathcal{M}}_{\omega }$ is optimal w.r.t. the unsafe state sequence ${\omega }_1$. In lines 2–6, for all productions $\xi$, the security degrees of their corresponding state sequences $F\left(\xi \right)={\omega }_2$ are calculated and these values are stored in the set $B\left[2\right]$. Then the algorithm calculates the Hamming distance between ${\omega }_1$ and ${\omega }_2$, which reflects the degree of difference between them. In lines 7–10 of the algorithm, elements b are assigned to G such that $b\left[2\right]=s=deg\left({\omega }_2\right)=de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)$. In line 11, for all $g\left[3\right]\in G\left[3\right]$, the minimum value h in the set $G\left[3\right]$ is obtained, i.e., compute the minimum value h of the Hamming distance between ${\omega }_1$ and ${\omega }_2$. To this end, there exists a state sequence ${\omega }_2$ with $deg\left({\omega }_2\right)=de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),k+1)$ such that $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{k+1,h}$ and there does not exist $h^{\prime }<h$ such that $\mathcal{J}({\omega }_1,{\omega }_2)=h^{\prime }$ for all ${\omega }_2$ with the maximum degree. According to Definition 5, the mechanism ${\mathcal{M}}_{\omega }$ is optimal. ▪

In Algorithm 2, we design an optimal mechanism ${\mathcal{M}}_{\omega }$ w.r.t. an unsafe production state sequence ${\omega }_1$. When the mechanism ${\mathcal{M}}_{\omega }$ receives ${\omega }_1$ as input, a protected state sequence ${\omega }_3$ is probabilistically output. In addition, the mechanism guarantees that there exists at least one state sequence ${\omega }_2$ with the maximum security degree such that when ${\omega }_2$ is fed, it outputs ${\omega }_3$ with an approximate probability. Then, when an intruder obtains an observation ${\rho }^{\prime }\in \mathcal{T}\left({\omega }_3\right)$ derived from ${\omega }_3$, he/she is unable to infer whether ${\omega }_1$ or ${\omega }_2$ is generated in the critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)$. Consequently, the disclosure of critical states or critical observability violative states becomes unattainable for the intruder. Furthermore, in order to maximize the obfuscation effect between ${\omega }_1$ and ${\omega }_2$ , we especially emphasize the optimization of the parameter h in Algorithm 2, i.e., the Hamming distance between ${\omega }_1$ and ${\omega }_2$ is minimal.

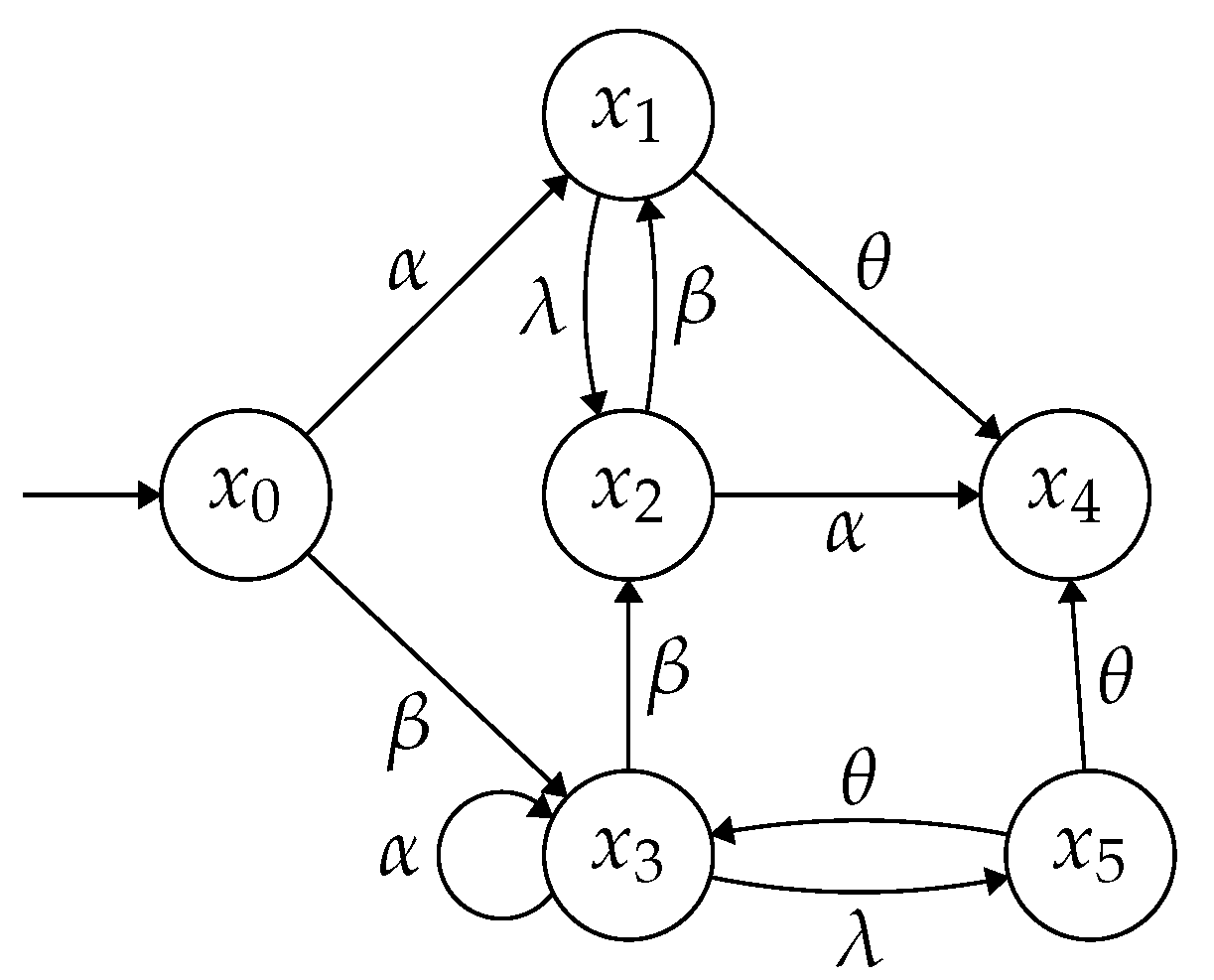
Example 5.

We consider the NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ shown in Figure 3. Based on the results in Example 2 by assuming that the observable event set is $E_o=\{\alpha ,\beta ,\lambda \}$ and the secret is $X_s=\left\{x_3\right\}$, the system ${\mathcal{A}}_{nd}$ is not critically observable. Suppose that an unsafe observation $\rho =\beta \alpha \lambda$ is generated, in which the state estimate $\mathcal{C}\left(\rho \right)=x_{o4}$ is neither a subset of the critical states nor a subset of the non-critical states. The unsafe state sequence ${\omega }_1=x_{0,obs}{x}_{o2}{x}_{o2}{x}_{o4}\in \mathcal{F}\left(\rho \right)$ corresponding to ρ is obtained in the critical state estimator shown in Figure 4. By lines 2–6 of Algorithm 2, we calculate the set B illustrated in Table 1 (the contents of columns 1, 2 and 3 record $B\left[1\right]$, $B\left[2\right]$ and $B\left[3\right]$, respectively). Then, we compute the maximum degree of the production state sequences in $B\left[1\right]$, i.e., $s=max\{b_1\left[2\right],b_2\left[2\right],\dots ,b_8\left[2\right]\}=2$ and choose the minimum parameter $h=3$.

We take the input sequence ${\omega }_1=x_{0,obs}{x}_{o2}{x}_{o2}{x}_{o4}$ and a random output ${\omega }_3=x_{0,obs}{x}_{o1}{x}_{o3}{x}_{o5}$ for an example. The probabilities of the correct states are

$$\begin{array}{c}\hfill \eta \left(x_i^{\prime \prime }\right)={\displaystyle \frac{1}{\left(\right|\mathcal{E}\left(x_{i-1}^{\prime \prime }\right)|-1)exp(-\frac{ϵ}{3})+1}}\end{array}$$

(3)

with $i=\{1,2,3\}$, where in general $ϵ\in [0.01,10]$. Here, we consider $ϵ=0.1$.

By Equation (3), we have

$$\begin{array}{cc}\hfill & \eta \left(x_0^{\prime \prime }\right)=\eta \left(x_{0,obs}\right)=1,\hfill \\ \hfill & \eta \left(x_1^{\prime \prime }\right)=\eta \left(x_{o2}\right)\approx 0.5083,\hfill \\ \hfill & \eta \left(x_2^{\prime \prime }\right)=\eta \left(x_{o2}\right)\approx 0.3408,\mathrm{and}\hfill \\ \hfill & \eta \left(x_3^{\prime \prime }\right)=\eta \left(x_{o4}\right)\approx 0.3408.\hfill \end{array}$$

The probability for generating ${\omega }_3$ is

$$\begin{array}{cc}\hfill & \mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]\hfill \\ & =\mathbb{P}\left[x_{0,obs}\right]\times \mathbb{P}\left[x_{o1}\right]\times \mathbb{P}\left[x_{o3}\right]\times \mathbb{P}\left[x_{o5}\right]\hfill \\ \hfill & =\eta \left(x_0^{\prime \prime }\right)\times {\displaystyle \frac{1-\eta \left(x_1^{\prime \prime }\right)}{2-1}}\times {\displaystyle \frac{1-0\times \eta \left(x_2^{\prime \prime }\right)}{1-0}}\times {\displaystyle \frac{1-0\times \eta \left(x_3^{\prime \prime }\right)}{2-0}}\hfill \\ \hfill & \approx 1\times (1-0.5083)\times 1\times {\displaystyle \frac{1}{2}}\hfill \\ \hfill & \approx 0.2458.\hfill \end{array}$$

Analogously, for another random input state sequence (e.g., ${\omega }_2=x_{0,obs}{x}_{o1}{x}_{o3}{x}_{o1}$ with the maximum security degree), we have probabilities for the correct states

$$\begin{array}{cc}\hfill & \eta \left(x_0^{\prime \prime }\right)=\eta \left(x_{0,obs}\right)=1,\hfill \\ \hfill & \eta \left(x_1^{\prime \prime }\right)=\eta \left(x_{o1}\right)\approx 0.5083,\hfill \\ \hfill & \eta \left(x_2^{\prime \prime }\right)=\eta \left(x_{o3}\right)=1,\mathrm{and}\hfill \\ \hfill & \eta \left(x_3^{\prime \prime }\right)=\eta \left(x_{o1}\right)\approx 0.5083.\hfill \end{array}$$

When considering ${\omega }_2$ as an input of ${\mathcal{M}}_{\omega }$, the probability of generating ${\omega }_3$ is

$$\begin{array}{cc}\hfill & \mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3]\hfill \\ & =\mathbb{P}\left[x_{0,obs}\right]\times \mathbb{P}\left[x_{o1}\right]\times \mathbb{P}\left[x_{o3}\right]\times \mathbb{P}\left[x_{o5}\right]\hfill \\ \hfill & =\eta \left(x_0^{\prime \prime }\right)\times \eta \left(x_1^{\prime \prime }\right)\times \eta \left(x_2^{\prime \prime }\right)\times {\displaystyle \frac{1-\eta \left(x_3^{\prime \prime }\right)}{2-1}}\hfill \\ \hfill & \approx 1\times 0.5038\times 1\times (1-0.5038)\hfill \\ \hfill & \approx 0.2499,\hfill \end{array}$$

and one has

$$\begin{array}{c}\hfill \mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3]\le exp\left(ϵ\right)\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3].\end{array}$$

In other words, if the observation $\rho =\beta \alpha \lambda$ is directly sent, the critical observability violative state $x_{o4}$ can be detected by an intruder due to $\mathcal{C}\left(\rho \right)=\{x_3,x_4,x_5\}⊈X_s$ and $\mathcal{C}\left(\rho \right)⊈X_{nd}\setminus X_s$. However, by inputting ${\omega }_1=x_{0,obs}{x}_{o2}{x}_{o2}{x}_{o4}\in \mathcal{F}\left(\rho \right)$ into the designed optimal DPM, a modified state sequence ${\omega }_3=x_{0,obs}{x}_{o1}{x}_{o3}{x}_{o5}$ is output. Just by acquiring the sequence ${\omega }_3$, it is difficult for an intruder to backtrack or infer the original sequence ${\omega }_1$, since there exists another random sequence ${\omega }_2=x_{0,obs}{x}_{o1}{x}_{o3}{x}_{o1}$ which can also generate ${\omega }_3$ with an approximate probability. □

5. Case Study

In this section, we consider a realistic case of enforcing critical observability in air traffic management (ATM) systems. In recent years, with the development of ATM systems, their network architecture has gradually shifted from closed, physically isolated networks to more interconnected and open cyber-physical systems. This evolution has made data exchange and information sharing efficient and convenient, but it has also created more possibilities for potential network attacks. Frequent and diverse types of network attacks pose a serious risk to the safety and stability of aviation. In this context, to strengthen security defenses by enhancing the system’s awareness and response capability to potential threats, we propose an innovative solution: unsafe observations protection based on DP.

An ATM system is illustrated in Figure 6, detailing the communication process between the airport control tower and the pilot during the various stages of flight. On the one hand, the control tower sends a series of instructions to the pilot, such as pre-flight/stop-flight instructions, engine start instructions, etc. These instructions guide the pilot’s actions and determine that the aircraft is airworthy and all parts of the system are operating normally. On the other hand, the pilot’s role is to wait for and follow instructions from the control tower, performing the corresponding operations. If there are any faults or abnormal situations during the flight, the pilot must immediately report to the tower. This real-time feedback mechanism allows the control tower to take action quickly to resolve issues that may threaten flight safety. The exchange of information between the control tower and the pilot runs throughout the entire flight process and jointly affects the aircraft’s maneuvers (represented by the downward arrows in Figure 6). A complete aerial flight can be divided into five stages: taxiing, climbing, cruising, descending, and landing. Each stage requires precise coordination between the pilot and the control tower. Based on Figure 6, we model an ATM system as an NFA (shown in Figure 7) by using a single aircraft as a study case and define a series of important physical states as critical states. The meanings of states and events in the NFA are listed in Table 2. We further assume that an intruder launches an attack as soon as he/she captures the critical states or critical observability violative states. To prevent the system ${\mathcal{A}}_{nd}$ from being corrupted, we introduce a DPM, such that the unsafe states are not accurately captured by an intruder. From a practical standpoint, this research establishes the groundwork for subsequent security defense of cyber-physical systems and has significant implications for safeguarding air transportation safety and maintaining airspace order.

In Figure 7, the pilot initially executes boarding and waits for instructions from the airport control tower (state $x_0$). When the pilot receives a pre-flight instruction sent by the tower (event a), the state is transferred from $x_0$ to $x_1$, at which point the pilot executes a pre-flight check. For any error found by the pilot during the check, an fault is reported (event d) to the tower, and the state $x_3$ is reached. In state $x_2$, the aircraft is waiting for the engine to start. If the engine fails to start (event e) due to safety issues or other conditions, the state remains in $x_2$; otherwise, the state transitions to $x_4$, where the pilot communicates with the tower in the hope of obtaining a taxi clearance. The taxiing process is represented by states $x_6$, $x_7$, and $x_8$, which correspond to different runways. The event h, obtaining taxi clearance, triggers the transition from $x_4$ to one of these taxing states. Once the taxi clearance is not granted (event n), the state transitions from $x_4$ to $x_{13}$ or $x_5$.

The event i, sending a climbing request, triggers the transition from one of the taxiing states ($x_6$, $x_7$, or $x_8$) to state $x_9$. If the climb request is granted (event j), the aircraft takes off and leaves the ground (state $x_{10}$). In addition, fault reports (event d) can lead to a transition from $x_{10}$ to $x_3$, allowing the aircraft to report any troubles encountered during the flight. However, if the climb request is rejected (event l), the state is switched from $x_9$ to $x_{12}$, in which case the flight is stopped and the aircraft returns to its origin. In exceptional cases, the aircraft may be started without authorization, resulting in a move from $x_9$ to $x_{13}$, as triggered by event l. In $x_{13}$, the pilot sends an anomaly report to the tower (event m), where the aircraft refuses to execute the flight mission and $x_{12}$ or $x_5$ is reached.

Example 6.

Let us consider the NFA ${\mathcal{A}}_{nd}=(X_{nd},E,{\delta }_{nd},X_0)$ portrayed in Figure 7, where $E=E_o\dot{\cup }{E}_{uo}$ is the set of events with $E_o=\{a,b,c,d,e,f,g,h,i,j,k,l,n,o,p\}$ and $E_{uo}=\left\{m\right\}$, and $X_0=\left\{x_0\right\}$ is the set of initial states. We assume that the set of critical states is $X_s=\{x_5,x_{12}\}$. The critical state estimator $Obs\left({\mathcal{A}}_{nd}\right)=\{X_{obs},E_o,{\delta }_{obs},x_{0,obs}\}$ of ${\mathcal{A}}_{nd}$ is shown in Figure 8, where the components of all states are listed in Table 3.

Given an observation $\rho =acfn$, we conclude that the critical observability is violated thanks to $\mathcal{C}\left(\rho \right)={\delta }_{obs}(x_{0,obs},acfn)=x_{o7}=\{x_5,x_{12},x_{13}\}⊈X_s$ and $\mathcal{C}\left(\rho \right)⊈X_{nd}\setminus X_s$. Therefore, ρ is an unsafe observation and ${\omega }_1=x_{0,obs}{x}_{o1}{x}_{o2}{x}_{o4}{x}_{o7}\in \mathcal{F}\left(\rho \right)$ is an unsafe production state sequence.

We now show how the unsafe production state sequence is protected by designed optimal mechanisms ${\mathcal{M}}_{\omega }$ that guarantees DP. Consider ${\omega }_1$ as an input of ${\mathcal{M}}_{\omega }$. By Algorithm 2, for all ${\omega }_2\in X_{obs}^5$, the security degrees $deg\left({\omega }_2\right)$ and Hamming distances $\mathcal{J}({\omega }_1,{\omega }_2)$ are listed in Table 4. Then we compute the maximum degree $s=3$ and for all ${\omega }_2$ with $deg\left({\omega }_2\right)=$$de{g}_{max}(Obs\left({\mathcal{A}}_{nd}\right),5)=3$, we select the minimum parameter $h=1$. For all $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{5,1}$, and for all ${\omega }_3\in X_{obs}^5$, it holds that

$$\begin{array}{c}\hfill \mathbb{P}\left[{\mathcal{M}}_{\omega }\left({\omega }_1\right)={\omega }_3\right]\le exp\left(ϵ\right)\mathbb{P}[{\mathcal{M}}_{\omega }\left({\omega }_2\right)={\omega }_3],\end{array}$$

where in general $ϵ\in [0.01,10]$. Here, we consider $ϵ=0.1$.

When observing $\rho =acfn$, the state that violates critical observability is detectable by an intruder. However, by applying the designed optimal mechanism that outputs a randomly modified production state sequence ${\omega }_3$, the unsafe sequence ${\omega }_1\in \mathcal{F}\left(\rho \right)$ cannot be ensured, since another sequence ${\omega }_2$ with $({\omega }_1,{\omega }_2)\in {\mathcal{W}}_{5,1}$ can generate ${\omega }_3$ with a similar probability. In this way, unsafe observations in the ATM system cannot be accurately captured. Thereby, the intruder is unable to launch an attack to the ATM system ${\mathcal{A}}_{nd}$. □

6. Conclusions

This work proposes a differential privacy (DP) mechanism for the enforcement of critical observability in DESs modeled with finite state automata. Meanwhile, the mechanism protects the predefined critical states from being captured by an intruder. We first recall the formalization of critical observability verification problems. Then, a mechanism called state sequence DP is introduced to protect critical states or critical observability violative states such that it cannot be detected by an intruder. Furthermore, in order to most effectively protect unsafe production state sequences, we define an optimal mechanism and design an algorithm for synthesizing the optimal mechanism. Finally, the problem of enforcing critical observability is explored in an ATM system, where model construction of the ATM system and protection implementation of unsafe observations using DP are illustrated in detail.

From a practical perspective, this research has potential applications in various cyber-physical systems. In the future, we will consider applying the differential privacy mechanism to the verification and enforcement of other properties such as k-step and infinite-step opacity. Moreover, it is worth exploring the critical observability problem when a system is subject to sensor attacks, i.e., sensor readings can altered by an external attacker.