Submitted:
08 November 2024
Posted:
12 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Fuzzy Concepts
2.1. Fuzzy Numbers and Fuzzy Partition
2.2. The F-Transform
2.3. Fuzzy Partial Derivatives
3. Classic Frankot-Chellappa Surface Normal Integration
4. Fuzzy Poisson Equation
5. Summary of Fuzzy Frankot-Chellappa Method
6. Experimental Results
6.1. Comparison in Terms of Accuracy
6.2. Comparison with Respect to Noise Suppression
7. Conclusion
References
- M. Abdi, T. Allahviranloo, Fuzzy finite difference method for solving fuzzy Poisson equation. Journal of Intelligent and Fuzzy Systems 2019, 37, 5281–5296. [CrossRef]
- T. Allahviranloo, Difference methods for fuzzy partial differential equations. Comput. Methods Appl. Math. 2006, 2, 233–242.
- M. Bähr, M. Breuß, An Improved Eikonal Method for Surface Normal Integration, Proceeding of the 37th German Conference on Pattern Recognition. Aachen, Germany (2015).
- M. Bähr, M. Breuß, Y. Queau, A.S. Boroujerdi J.D. Durou, LU-Fast and accurate surface normal integration on non-rectangular domains. Comput. Vis. Media. 2017, 3, 107–129. [CrossRef]
- J.D. Durou, J.F. Aujol, F. Courteille, Integrating the normal field of a surface in the presence of discontinuities. Energy Minimization Methods Comput. Vis. Pattern Recogn. 2009, 5681, 261–273.
- D. Dubois, H. Prade, Operations on fuzzy numbers. International Journal of Systems Science 1978, 9, 613–626. [CrossRef]
- R.T. Frankot, R. Chellappa, A method for enforcing integrability in shape from shading algorithms. IEEE Trans. Pattern Anal. Mach. Intell. 1988, 10, 576–593.
- R. Ghasemi Moghaddam, T. Allahviranloo, On the fuzzy Poisson equation. Fuzzy Sets Syst. 2018, 347, 105–128. [CrossRef]
- M. Harker, P. O’ Leary, Least squares surface reconstruction from measured gradient fields, In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition., (2008).
- B.K.P. Horn, Robot Vision, McGraw-Hill Book, (1986).
- Y. Queau, J-D. Durou, J-F. Aujol, Normal Integration: A survey. J Math Imaging Vis. 2018, 60, 576–593. [CrossRef]
- I. Perfilieva, Fuzzy transforms: Theory and applications. Fuzzy Sets Syst. 2006, 157, 993–1023. [CrossRef]
- I. Perfilieva, P. Valášek, Fuzzy Transforms in Removing Noise, in Computational Intelligence, Theory and Applications, International Conference 8th Fuzzy Days, Dortmund, Germany, (2004).
- T. Simchony, R.T. Frankot, Direct analytical methods for solving poisson equations in computer vision problems. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 435–446. [CrossRef]
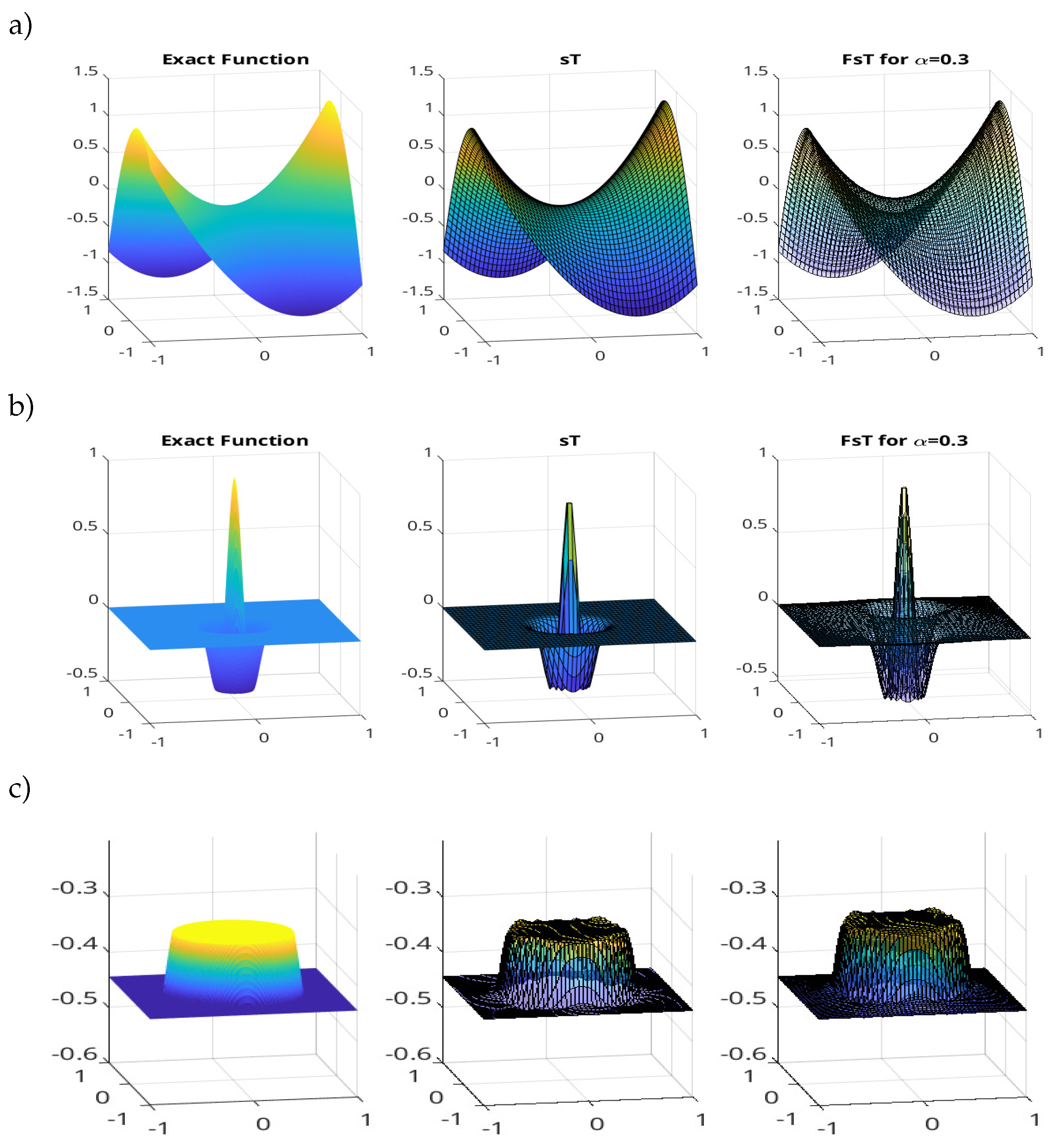
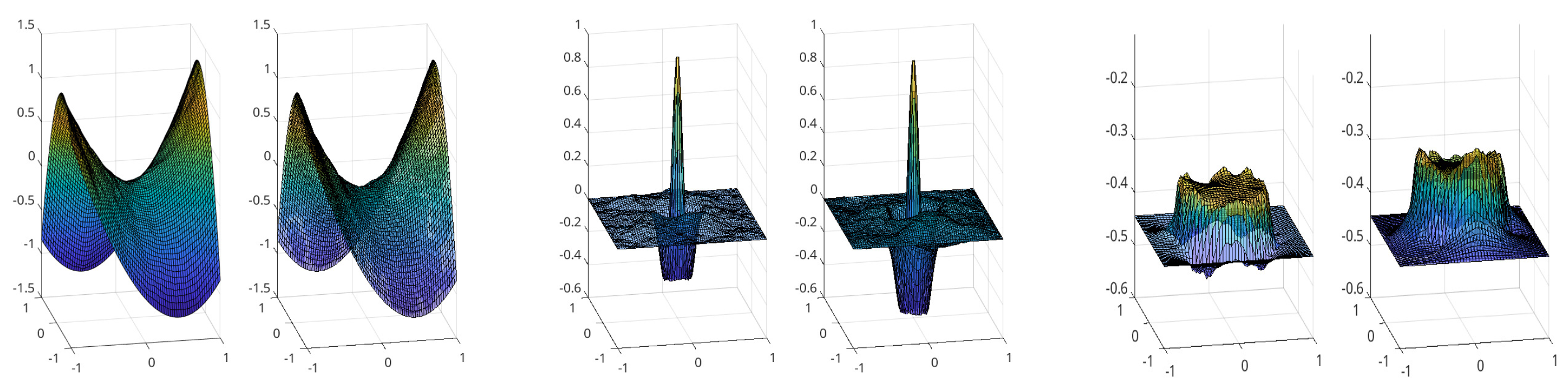
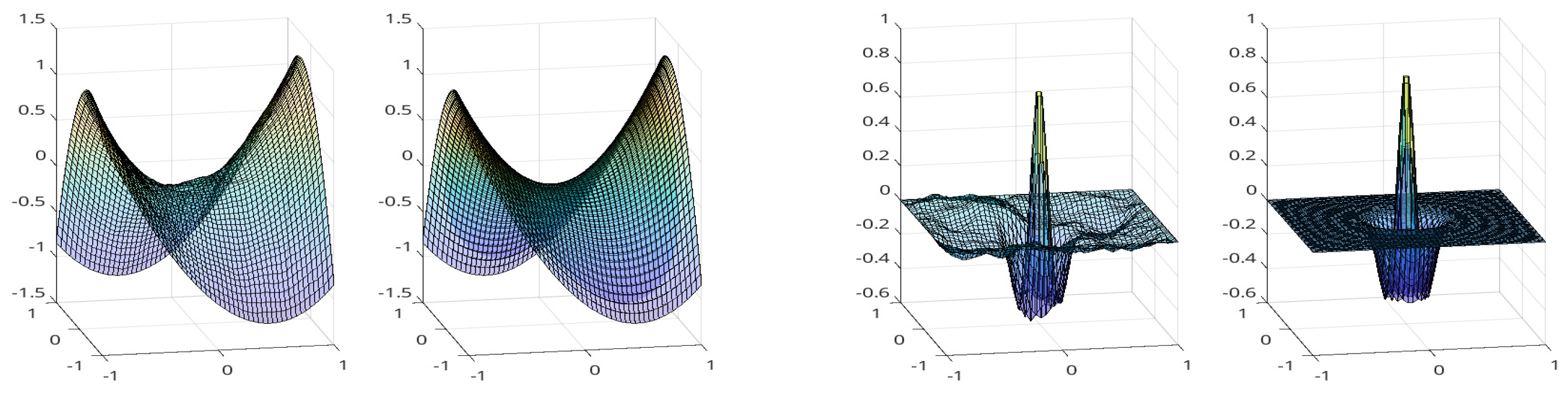
| Exact function z | d | D | d(noise ) | D(noise ) |
|---|---|---|---|---|
| 0.5704e-06 | 0.5704e-06 | 1.9234e-02 | 4.4535e-03 | |
| 1.1119e-06 | 1.1119e-06 | 2.6299e-03 | 1.6738e-03 | |
| 4.0103e-06 | 4.0103e-06 | 3.1116e-03 | 4.4851e-04 | |
| 8.3435e-05 | 8.3435e-05 | 4.4281e-04 | 7.3650e-05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




