Learning Optimal Strategies in a Duel Game

1. Game Description

The duel with which we are concerned is played between players $P_1$ and $P_2$, under the following rules.

• It is played in discrete rounds (time steps) $t\in \left\{1,2,...\right\}$.
• In the first turn, the players are at distance D.
• $P_1$ (resp. $P_2$) plays on odd (resp. even) rounds.
• On his turn, each player has two choices: (i) he can shoot his opponent or (ii) he can move one step forward, reducing their distance by one.
• If $P_n$ shoots, he has a kill probability$p_n\left(d\right)$ of hitting (and killing) his opponent, where d is their current distance. If he misses, the opponent can walk right next to him and shoot him for a certain kill.
• Each player’s payoff is 1 if he kills the opponent and $-1$ if he shoots and misses (in which case he is certain to be killed).

For $n\in \{1,2\}$, we will denote by $x_n\left(t\right)$ the position of $P_n$ at round t. The starting positions are $x_1\left(0\right)=0$ and $x_2\left(0\right)=D$, with $D=2N,N\in \mathbb{N}$. The distance between the players at time t is

$$d=|x_1\left(t\right)-x_2\left(t\right)|.$$

For $n\in \{1,2\}$, the kill probability is a decreasing function $p_n:\{1,2,\dots D\}\to [0,1]$ with $p_n\left(1\right)=1$. It is convenient to describe the kill probabilities as vectors:

$${\mathbf{p}}_n=\left(p_{n,1},...,p_{n,D}\right)=\left(p_n\left(1\right),...,p_n\left(D\right)\right).$$

This duel can be modeled as an extensive form game or tree game. The game tree is a directed graph $G=(V,E)$ with vertex set

$$V=\left\{1,2,...,2D\right\},$$

where

• the vertex $v=d\in \left\{1,2,...,D\right\}$ corresponds to a game state in which the players are at distance d and
• the vertex $v=d+D\in \left\{D+1,D+2,...,2D\right\}$ is a terminal vertex, in which the “active” player has fired at his opponent.

The edges correspond to state transitions; it is easy to see that the edge set is

$$E=\left\{\left(1,D+1\right),\left(2,1\right),\left(2,D+2\right),\left(3,2\right),\left(3,D+3\right),...,\left(D,D-1\right),\left(D,2D\right)\right\}.$$

An example of the game tree, for $D=6$, appears in Figure 1. The circular (resp. square) vertices are the ones in which $P_1$ (resp. $P_2$) is active and the rhombic vertices are the terminal ones.

To complete the description of the game, we will define the expected payoff for the terminal vertices. Note that the terminal vertex $d+D$ is the child of the nonterminal vertex d in which:

• The distance of the players is d and, assuming $P_n$ to be the active player, his probability of hitting his opponent is $p_{n,d}$.
• The active player is $P_1$ (resp. $P_2$) iff d is even (resp. odd).

Keeping the above in mind, we see that the payoff (to $P_1$) of vertex $d+D$ is

$$\forall d\in \left\{1,...,D\right\}:Q\left(d+D\right)=\left\{\begin{array}{cc}{p}_{1,d}·1+\left(1-p_{1,d}\right)·\left(-1\right)=2p_{1,d}-1,\hfill & \mathrm{when}d\mathrm{is}\mathrm{even};\hfill \\ p_{2,d}·\left(-1\right)+\left(1-p_{2,d}\right)·1=1-2p_{2,d}\hfill & \mathrm{when}d\mathrm{is}\mathrm{odd}.\hfill \end{array}\right.$$

The payoff to $P_2$ at vertex $d+D$ is $-Q\left(d+D\right)$. This completes the description of the duel.

2. Solution with Complete Information

It is easy to solve the above duel when each player knows D and both ${\mathbf{p}}_{\mathbf{1}}$ and ${\mathbf{p}}_{\mathbf{2}}$. We construct the game tree as described in Section 1 and we solve it by backward induction. Since the method is standard, we simply give an example of its application. Suppose that

$$\forall n,d:p_{n,d}=\left\{\begin{array}{cc}1\hfill & \mathrm{when}d=1,\hfill \\ min\left(1,{\displaystyle \frac{c_n}{d^{k_n}}}\right)\hfill & \mathrm{when}d>1.\hfill \end{array}\right.$$

We take $c_1=1$, $k_1=1$, $c_2=1$, $k_2={\displaystyle \frac{1}{2}}$. The kill probabilities are

The game tree with terminal payoffs is illustrated in Figure 2.

By the standard backward induction procedure we select the optimal action at each vertex and also compute the values of the nonterminal vertices. These are indicated in Figure 3 (optimal actions correspond to thick edges). We see that the game value is $-0.1547$, attained by $P_2$ shooting when the players are at distance 3 (which happens in round 4).

We next present a proposition which characterizes each player’s optimal strategy in terms of a shooting threshold. 1 In the following we use the standard notation by which “$-n$” denotes the “other player”. I.e., $p_{-1}=p_2$ and $p_{-2}=p_1$.2

Theorem 1. 

We define for $n\in \left\{1,2\right\}$ the shooting criterion vectors ${\mathbf{K}}_n=\left(K_{n,1},...,K_{n,D}\right)$ where

$$K_{n,1}=1\mathrm{and}\mathrm{for}d\ge 2:K_{n,d}=p_{n,d}+p_{-n,d-1}.$$

Then the optimal strategy for $P_n$ is to shoot as soon as it is his turn and the distance of the players is less than or equal to the shooting threshold $d_n$, where:

$$d_1=max\{d:K_{1,d}\ge 1\},d_2=max\{d:K_{2,d}\ge 1\}.$$

Proof. 

Suppose the players are at distance d and the active player is $P_n$.

• If $P_{-n}$ will not shoot in the next round, when their distance will be $d-1$, then $P_n$ must also not shoot in the current round, because he will have a higher kill probability in his next turn, when they will be at distance $d-2$.
• If $P_{-n}$ will shoot in the next round, when their distance will be $d-1$, then $P_n$ should shoot iff $p_{n,d}$ (his kill probability now) is higher then $1-p_{-n,d-1}$ ($P_{-n}$’s miss probability in the next round). In other words, $P_n$ must shoot iff

  $$p_{n,d}\ge 1-p_{-n,d-1}$$

  or, equivalently, iff

  $$K_{n,d}=p_{n,d}+p_{-n,d-1}\ge 1.$$

  (1)

Hence we can reason as follows.

• At vertex 1, $P_2$ is active and his only choice is to shoot.
• At vertex 2, $P_1$ is active and he knows $P_2$ will certainly shoot in the next round. Hence $P_1$ will shoot iff he has an advantage, i.e., iff

  $$Q_1\left(2\right)\ge Q_1\left(1\right)\iff 2p_{1,2}-1\ge 1-2p_{2,1}\iff p_{1,2}+p_{2,1}\ge 1.$$
  This is equivalent to $K_{1,1}\ge 1$ and will always be true.
• Hence at vertex 3, $P_2$ is active and he knows that $P_1$ will certainly shoot in the next round (at vertex d). So $P_2$ will shoot iff

  $$Q_1\left(3\right)\le Q_1\left(2\right)\iff 1-2p_{2,3}\le 2p_{1,2}-1\iff p_{2,3}+p_{1,2}\ge 1.$$

  which is equivalent to $K_{2,3}\ge 1$. Also, if $K_{2,3}<1$, then $P_1$ will know, when the game is at vertex 4, that $P_2$ will not shoot when at 3. So,  $P_1$ will not shoot when at 4. But then, when at 5, $P_2$ knows that $P_1$ will not shoot when at 4. Continuing in this manner we see that $K_{2,3}<1$ implies that firing will take place exactly at the vertex 2.
• On the other hand, if $K_{2,3}\ge 1$, then $P_1$ knows when at 4 that $P_2$ will shoot at the next round. So, when at 4, $P_1$ should shoot iff $K_{1,4}\ge 1$. If, on the other hand, $K_{1,4}<1$, then $P_1$ will not shoot when at 4 and $P_2$ will shoot when at 3.
• We continue in this manner for increasing values of d. Since both $K_{1,d}$ and $K_{2,d}$ are decreasing with d, there will exist a maximum $d_n$ value (it could equal D) in which some $K_{n,d}$ will be greater than one and $P_n$ will be active; then $P_n$ must shoot as soon as the game reaches or passes vertex $d_n$ and he “has the action”.

This completes the proof.    □

Returning to our previous example, we compute the vectors $K_n$ for $n\in \{1,2\}$ and list them in the following table.

Table 2. Shooting Criterion

d	1	2	3	4	5	6
Round	6	5	4	3	2	1
$K_{1,d}$		1.500	1.040	0.827	0.700	0.614
$K_{2,d}$		1.707	1.077	0.833	0.697	0.608

Table 2. Shooting Criterion

d	1	2	3	4	5	6
Round	6	5	4	3	2	1
$K_{1,d}$		1.500	1.040	0.827	0.700	0.614
$K_{2,d}$		1.707	1.077	0.833	0.697	0.608

For $P_1$ the shooting criterion is last satisfied when the distance is $d=3$; this happens at round 4 in which $P_1$ is inactive, so he should shoot at round 5. However, for $P_2$ the shooting criterion is also last satisfied at distance $d=3$ and round 4, in which $P_2$ is active; so he should shoot at round 4. This is the same result we obtained with backward induction.

3. Solution with Incomplete Information

We will now present an approach to the solution of the duel when each player has incomplete knowledge of his opponent’s kill probability function. More specifically, we assume that the players’s kill probabilities have, for all d, the form $f\left(d;\theta \right)$ where $\theta$ is a parameter vector. Assuming $P_1$ has $\theta ={\theta }_1$ and $P_2$ has $\theta ={\theta }_2$, we have

$$\forall d:p_{1,d}=f\left(d;{\theta }_1\right),p_{2,d}=f\left(d;{\theta }_2\right).$$

Furthermore, we assume that both players know the general form $f\left(d;\theta \right)$ and each $P_n$ knows his own parameter vector ${\theta }_n$ but not the ${\theta }_{-n}$ of his opponent.

Obviously in this case the players cannot perform the computations of either backward induction or the shooting criterion. Consequently we will propose an “exploration-and-exploitation” approach. In other words, under the assumption that multiple duels will be played, each player initially adopts a random strategy and, collecting information from played games, he gradually builds and refines an estimate of his optimal strategy.

We give now a more detailed description of our approach, by Algorithm 1, presented below in pseudocode.

Algorithm 1:Learning the Optimal Duel Strategy

1: Input: Duel parameters D, ${\theta }_1$, ${\theta }_2$; Learning parameters $\lambda$, ${\sigma }_0$; Number of plays R 2: ${\mathbf{p}}_1$=CompKillProb$\left({\theta }_1\right)$ 3: ${\mathbf{p}}_2$=CompKillProb$\left({\theta }_2\right)$ 4: Randomly initialize parameter estimates ${\theta }_1^0$, ${\theta }_2^0$ 5: for$r\in \{1,2,...,R\}$do 6:     ${\mathbf{p}}_1^r$=CompKillProb$\left({\theta }_1^{r-1}\right)$ 7:     ${\mathbf{p}}_2^r$=CompKillProb$\left({\theta }_2^{r-1}\right)$ 8:     $d_1^r$=CompShootDist$({\mathbf{p}}_1,{\mathbf{p}}_2^r)$ 9:     $d_2^r$=CompShootDist$({\mathbf{p}}_1^r,{\mathbf{p}}_2)$ 10:     ${\sigma }_r={\sigma }_{r-1}/\lambda$ 11:     X=PlayDuel$({\mathbf{p}}_1,{\mathbf{p}}_2,d_1^r,d_2^r,{\sigma }_r,X)$ 12:     $({\widehat{\mathbf{p}}}_1^r,{\widehat{\mathbf{p}}}_2^r)$=EstKillProb$\left(X\right)$ 13:     ${\theta }_1^r$=EstPars$({\widehat{\mathbf{p}}}_1^r,1)$ 14:     ${\theta }_2^r$=EstPars$({\widehat{\mathbf{p}}}_2^r,2)$ 15: end for 16: return$d_1^R$, $d_2^R$, ${\theta }_1^R$, ${\theta }_2^R$

The following remarks explain the operation of the algorithm.

• In line 1 the algorithm takes as input: (i) the duel parameters D, ${\theta }_1$, ${\theta }_2$, (ii) two learning parameters$\lambda ,{\sigma }_0$ and (iii) the number R of duels used in the learning process.
• Then, in lines 2-3, the true kill probability ${\mathbf{p}}_n$ (for $n\in \{1,2\}$) is computed by the function CompKillProb$\left({\theta }_n\right)$, which simply computes

  $$\forall n,d:p_n\left(d\right)=f_n\left(d;{\theta }_n\right).$$
  We emphasize that these are the true kill probabilities.
• In line 4 initial, randomly selected parameter vector estimates ${\theta }_1^0,{\theta }_2^0$ are generated.
• Then the algorithm enters the loop of lines 5-15 (executed for R iterations) which constitutes the main learning process.

  (a)

  In lines 6-7 we compute new estimates of the kill probabilities ${\mathbf{p}}_n^r$, by function CompKillProb, based on the estimates of parameters ${\theta }_n^{r-1}$:

  $$\forall n,d:p_n^r\left(d\right)=f_n\left(d;{\theta }_n^{r-1}\right).$$

  We emphasize that these are estimates of the kill probabilities, based on the parameter estimates ${\theta }_n^{r-1}$.

  (b)

  In lines 8-9 we compute new estimates of the shooting thresholds $d_n^r$, by function CompShootDist. For $P_n$, this is achieved by computing the shooting criterion ${\mathbf{K}}_n$ using the (known to $P_n$) ${\mathbf{p}}_n$ and the (estimated by $P_n$) ${\mathbf{p}}_{-n}^r$.

  (c)

  In line 10, ${\sigma }_r$ (which will be used as a standard deviation parameter) is divided by the factor $\lambda >1$.

  (d)

  In line 11 the result of the duel is computed by the function PlayDuel. This is achieved as follows:

  • For $n\in \left\{1,2\right\}$, $P_n$ selects a random shooting distance ${\widehat{d}}_n$ from the discrete normal distribution [6] with mean $d_n^r$ and standard deviation ${\sigma }_r$.
  • With both ${\widehat{d}}_1,{\widehat{d}}_2$ selected, it is clear which player will shoot first; the outcome of the shot (hit or miss) is a Bernoulli random variable with success probability $p_{n,{\widehat{d}}_n}$, where $P_n$ is the shooting player. Note that ${\mathbf{p}}_n$ is the true kill probability.

  The result is stored in a table X, which contains the data (shooting distance, shooting player, hit or miss) of every duel played up to the r-th iteration.

  (e)

  In line 12, the entire game records X are used by EstKillProb$\left(X\right)$ to obtain empirical estimates of the kill probabilities ${\widehat{\mathbf{p}}}_1^r,{\widehat{\mathbf{p}}}_2^r$. These estimates are as follows:

  $$\forall n,\forall d\in {\mathcal{D}}_n\text{:}{\widehat{p}}_{n,d}^r={\displaystyle \frac{{\sum }_{r\in {\mathcal{R}}_{n,d}}{Z}_r}{\left|{\mathcal{R}}_{n,d}\right|}}$$

  where

  $$\begin{array}{cc}\hfill {\mathcal{D}}_n& =\left\{d:d\mathrm{such}\mathrm{that}{P}_n\mathrm{may}\mathrm{shoot}\right\}\hfill \\ \hfill {\mathcal{R}}_{n,d}& =\left\{r:\mathrm{in}\mathrm{the}r-\mathrm{th}\mathrm{game}{P}_n\mathrm{actually}\mathrm{shot}\mathrm{from}\mathrm{distance}d\right\},\hfill \\ \hfill Z_r& =\left\{\begin{array}{cc}1\hfill & \mathrm{iff}\mathrm{the}\mathrm{shot}\mathrm{in}\mathrm{the}r-\mathrm{th}\mathrm{game}\mathrm{hit}\mathrm{the}\mathrm{target},\hfill \\ 0\hfill & \mathrm{iff}\mathrm{the}\mathrm{shot}\mathrm{in}\mathrm{the}r-\mathrm{th}\mathrm{game}\mathrm{missed}\mathrm{the}\mathrm{target}\hfill \end{array}\right.\hfill \end{array}$$

  (f)

  In line 13-14 the function EstPars uses a least squares algorithm to find (only for the $P_n$ who currently has the action) ${\theta }_n^r$ values which minimize the squared error

  $$J\left({\theta }_n\right)=\sum _{d\in {\mathcal{D}}_n}{\left(f_n\left(d;{\theta }_n\right)-{\widehat{p}}_{n,d}^r\right)}^2.$$

  (g)

  In line 21 the algorithm returns the final estimates of optimal shooting distances $d_1^R,d_2^R$ and parameters ${\theta }_1^R,{\theta }_2^R$.

Note that multiplication by $1/\lambda \in \left(0,1\right)$ results in ${lim}_{r\to \infty }{\sigma }_r=0$. Hence, while in the initial iterations of the learning process the players essentially use random shooting thresholds (exploration) with standard deviation ${\sigma }_r$, it is hoped that, as r increases and ${\sigma }_r$ of the used shooting thresholds goes to zero, the estimates of the kill probabilities and shooting thresholds will converge to their optimal values (exploitation). This is actually corroborated by the experiments we present in the next section.

4. Experiments

In this section we present numerical experiments to evaluate our approach.

4.1. Experiments Setup

In the following subsection we present several experiment groups, all of which share the same structure. Each experiment group corresponds to a particular form of the kill probability functions. In each case, the kill probability parameters, along with the initial player distance D, are the game parameters. For each choice of game parameters we proceed as follows.

First we select the learning parameters $\lambda ,\sigma$ and the number of learning steps R. These, together with the game parameters, are the experiment parameters. Then we select a number J of estimation experiments to run for each choice of experiment parameters. For each of the J experiments we compute the following quantities.

• The relative error of the final kill probability parameter estimates. For a given parameter ${\theta }_{n,i}$, this error is defined to be

  $$\mathrm{\Delta }{\theta }_{n,i}=\left|{\displaystyle \frac{{\theta }_{n,i}-{\theta }_{n,i}^R}{{\theta }_{n,i}}}\right|.$$
• The relative error of the shooting threshold estimates. Letting $d_n^R$ be the estimate of the shooting threshold based on the true kill probability vector $p_n$ and kill probability vector estimate $p_{-n}^R$, this error is defined to be

  $$\mathrm{\Delta }{d}_n=\left|{\displaystyle \frac{d_n-d_n^R}{d_n}}\right|.$$
• The relative error of the optimal payoff estimates. Letting $Q_n^R$ be the estimate of the optimal payoff (computed from the estimated shooting thresholds $d_1^R,d_2^R$) , this error is defined to be

  $$\mathrm{\Delta }{Q}_n=\left\{\begin{array}{cc}\left|{\displaystyle \frac{Q_n-Q_n^R}{Q_n}}\right|\hfill & \mathrm{iff}{Q}_n\ne 0\hfill \\ 0\hfill & \mathrm{iff}{Q}_n=0\mathrm{and}{Q}_n^R=Q_n\hfill \\ 1\hfill & \mathrm{iff}{Q}_n=0\mathrm{and}{Q}_n^R\ne Q_n\hfill \end{array}\right.$$
  Note that $\mathrm{\Delta }{Q}_2=\mathrm{\Delta }{Q}_1$, because the game is zero-sum.

4.2. Experiment Group A

In this group the kill probability function has the form:

$$n\in \left\{1,2\right\}:p_{n,d}=min\left({\displaystyle \frac{c_n}{d^{k_n}}},1\right).$$

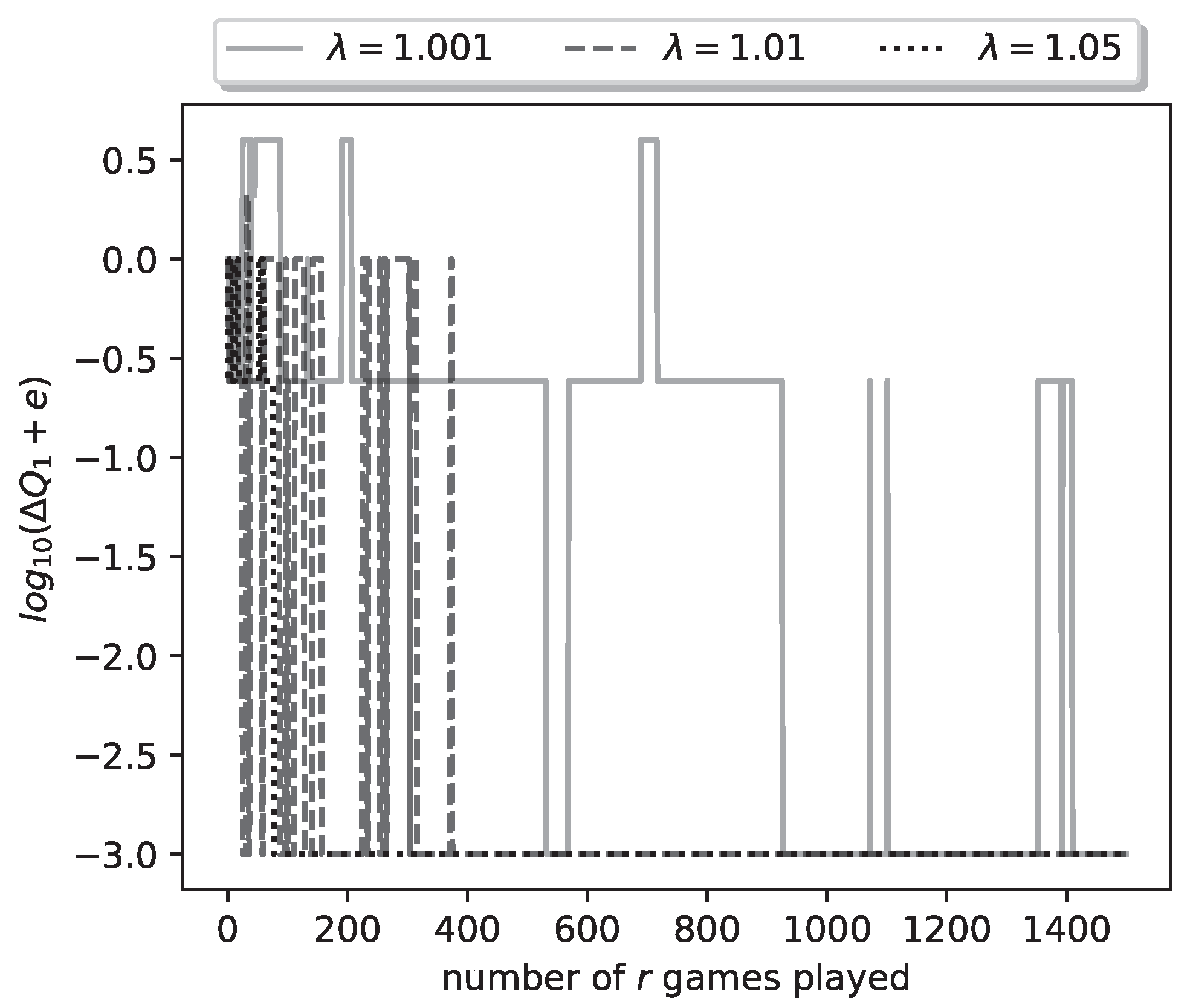
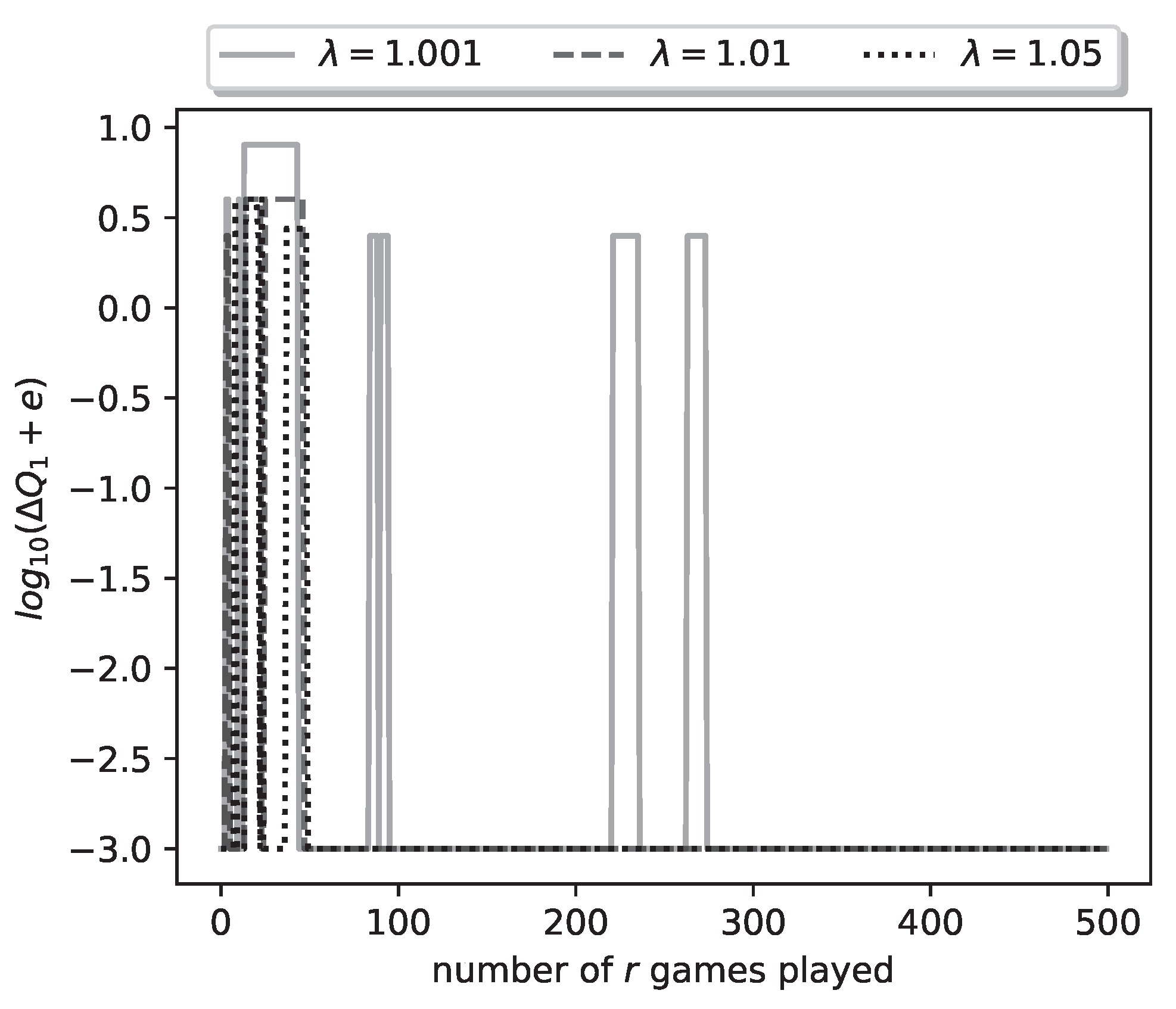
Let us look at the final results of a representative run of the learning algorithm. With $c_1=1$, $k_1=0.5$, $c_2=1$,$k_2=1$ and $D=10$, we run the learning algorithm with $R=1500$, ${\sigma }_0=6D$ and for three different values $\lambda \in \{1.001,1.01,1.05\}$. In Figure 4 we plot the logarithm (with base 10) of the relative payoff error $\mathrm{\Delta }{Q}_1+ϵ$ (we have added $ϵ={10}^{-3}$ to deal with the logarithm of zero error). The three curves plotted correspond to the $\lambda$ values 1.001, 1.01, 1.05. We see that, for all $\lambda$ values, the algorithm achieves zero relative error; in other words it learns the optimal strategy for both players. Furthermore convergence is achieved by the 1500-th iteration of the algorithm (1500-th duel played), as seen by the achieved logarithm value $-3$ (recall that we have added $ϵ={10}^{-3}$ to the error, hence the true error is zero). Convergence is fastest for the largest $\lambda$ value, i.e., $\lambda =1.05$, and slowest for the smallest value $\lambda =1.001$.

Figure 4. Plot of logarithmic relative error ${log}_{10}\mathrm{\Delta }{Q}_1$ of $P_1$’s payoff for a representative run of the learning process.

Figure 4. Plot of logarithmic relative error ${log}_{10}\mathrm{\Delta }{Q}_1$ of $P_1$’s payoff for a representative run of the learning process.

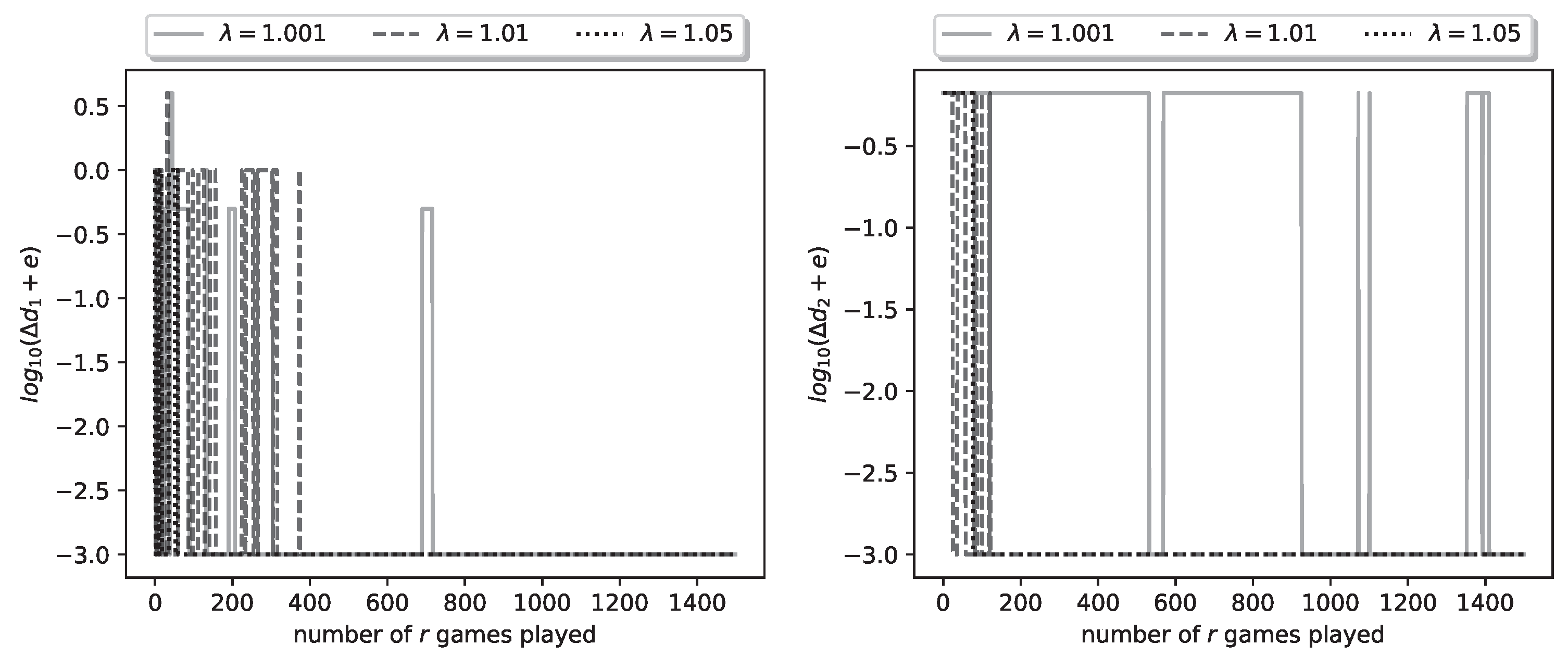
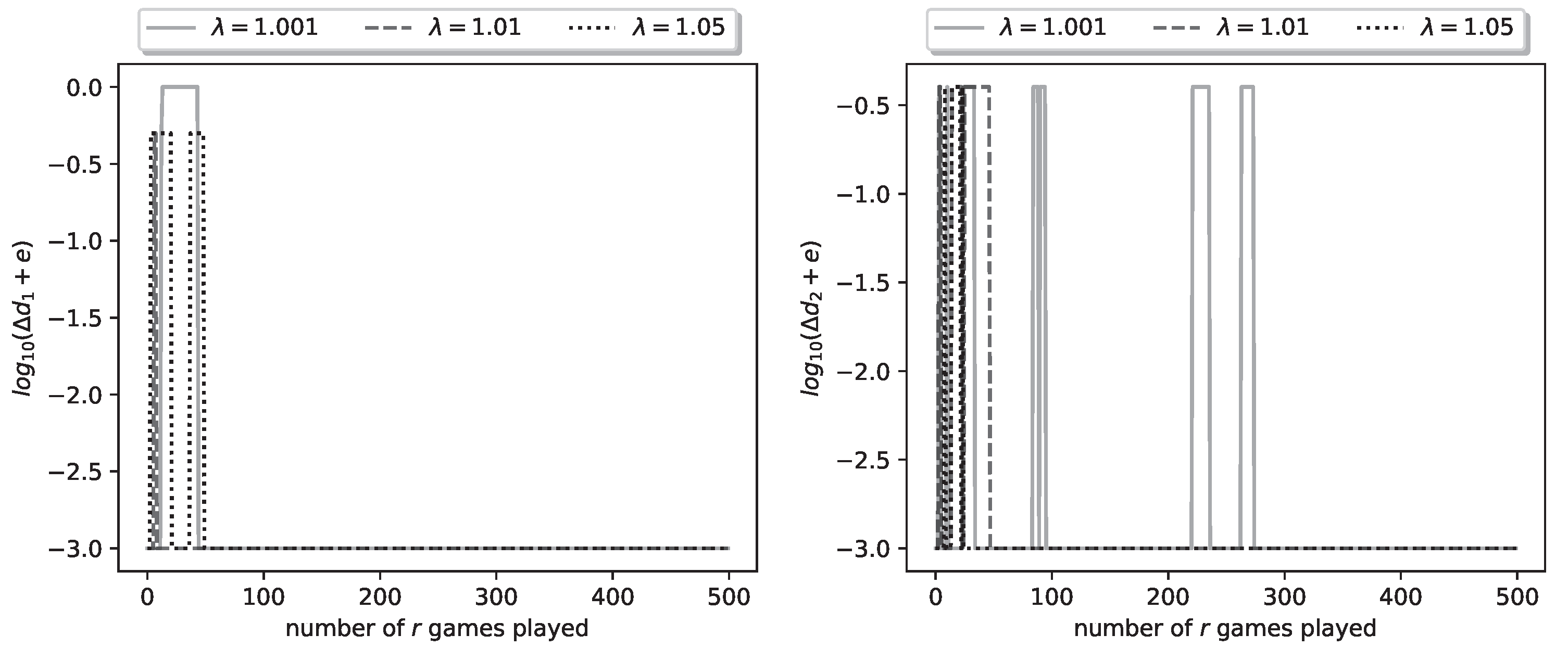
In Figure 5 we plot the logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_n$. These also, as expected, have converged to zero by the 1500-th iteration.

Figure 5. Plot of logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_1$, ${log}_{10}\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

Figure 5. Plot of logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_1$, ${log}_{10}\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

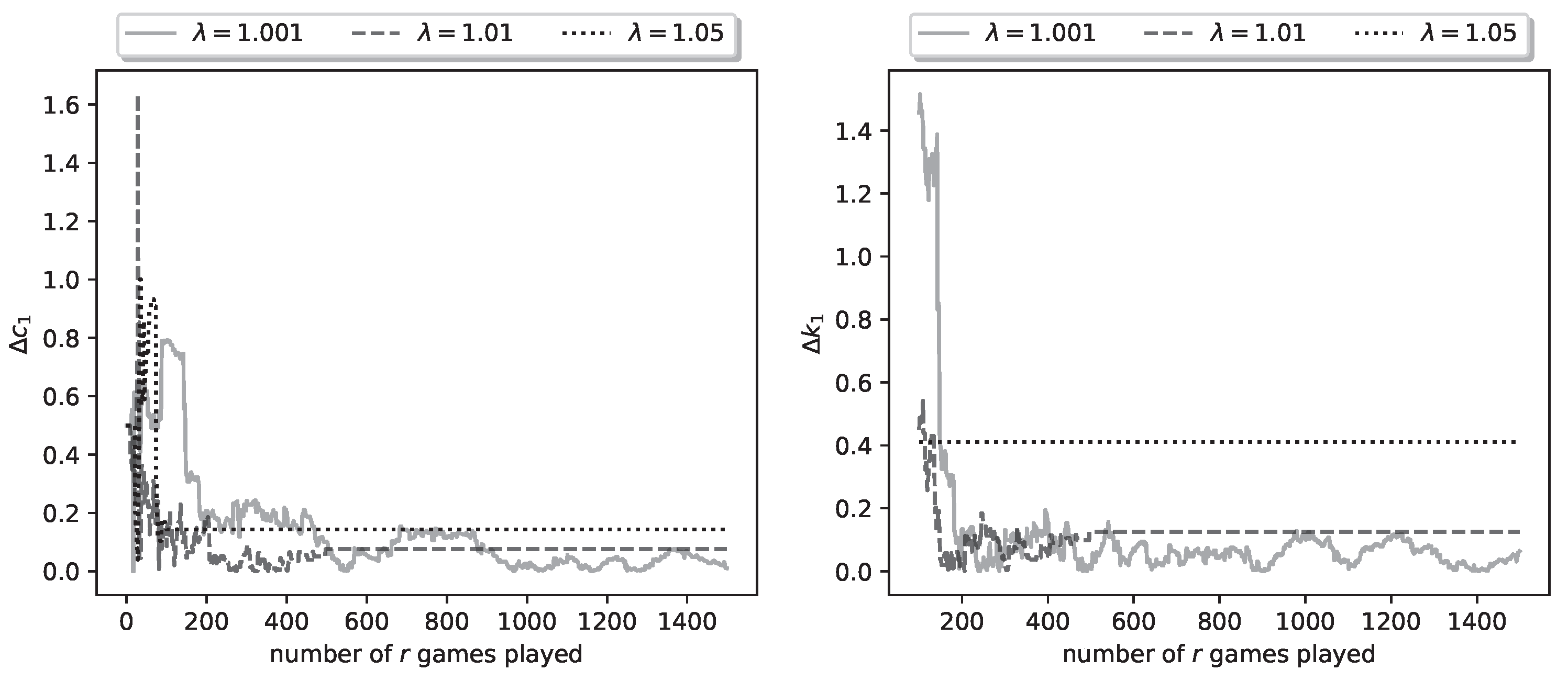
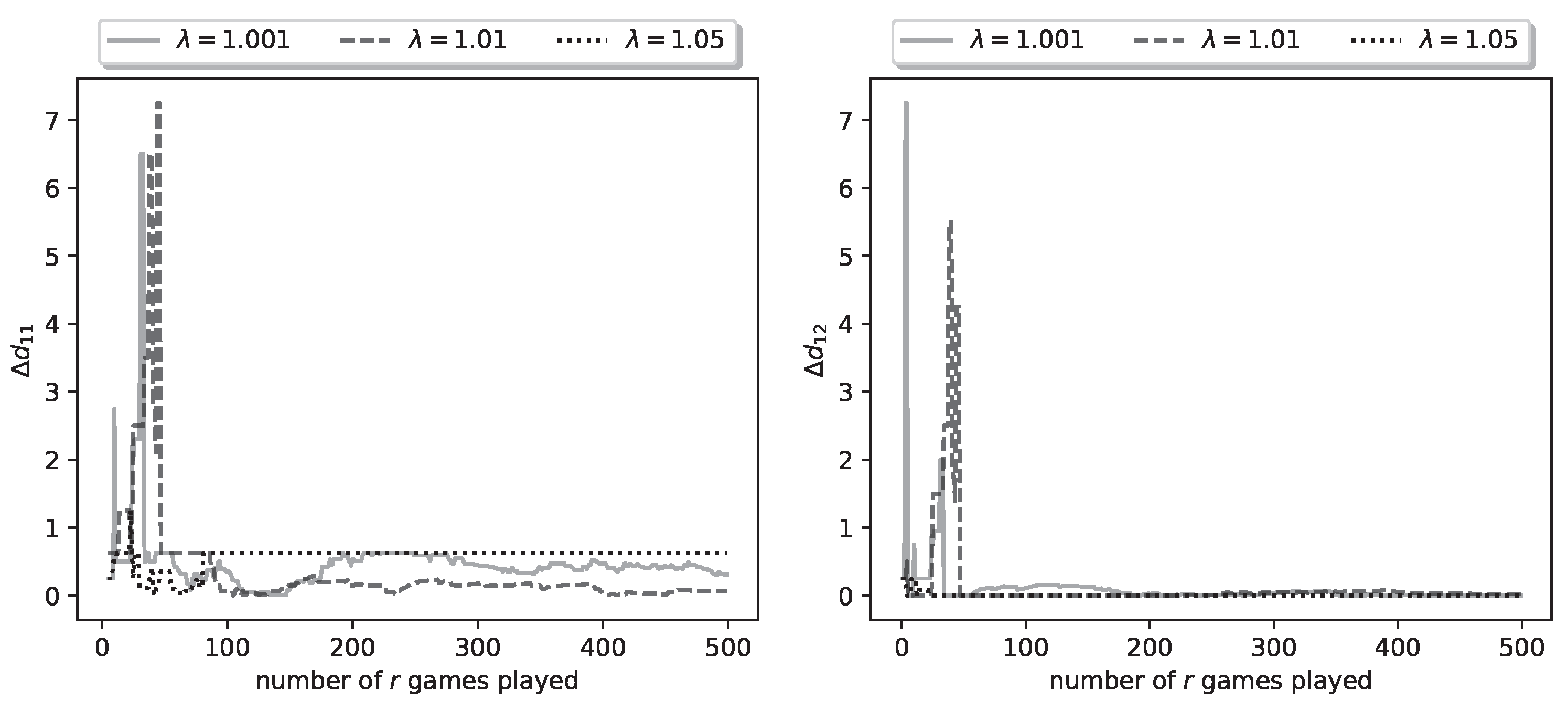
The fact that the estimates of the optimal shooting thresholds and strategies achieve zero error, does not imply that the same is true of the kill probability parameter estimates. In Figure 6 we plot the relative errors $\mathrm{\Delta }{c}_1$, $\mathrm{\Delta }{k}_1$.

Figure 6. Plot of relative parameter errors $\mathrm{\Delta }{c}_1$, $\mathrm{\Delta }{k}_1$ for a representative run of the learning process.

Figure 6. Plot of relative parameter errors $\mathrm{\Delta }{c}_1$, $\mathrm{\Delta }{k}_1$ for a representative run of the learning process.

It can be seen that these errors do not converge to zero; in fact, for $\lambda \in \{1.01,1.05\}$ the errors converge to fixed nonzero values, which indicates that the algorithm obtains wrong estimates. However, the error is sufficiently small to still result in zero-error estimates of the shooting thresholds. The picture is similar for the errors $\mathrm{\Delta }{c}_2$, $\mathrm{\Delta }{k}_2$, hence their plots are omitted.

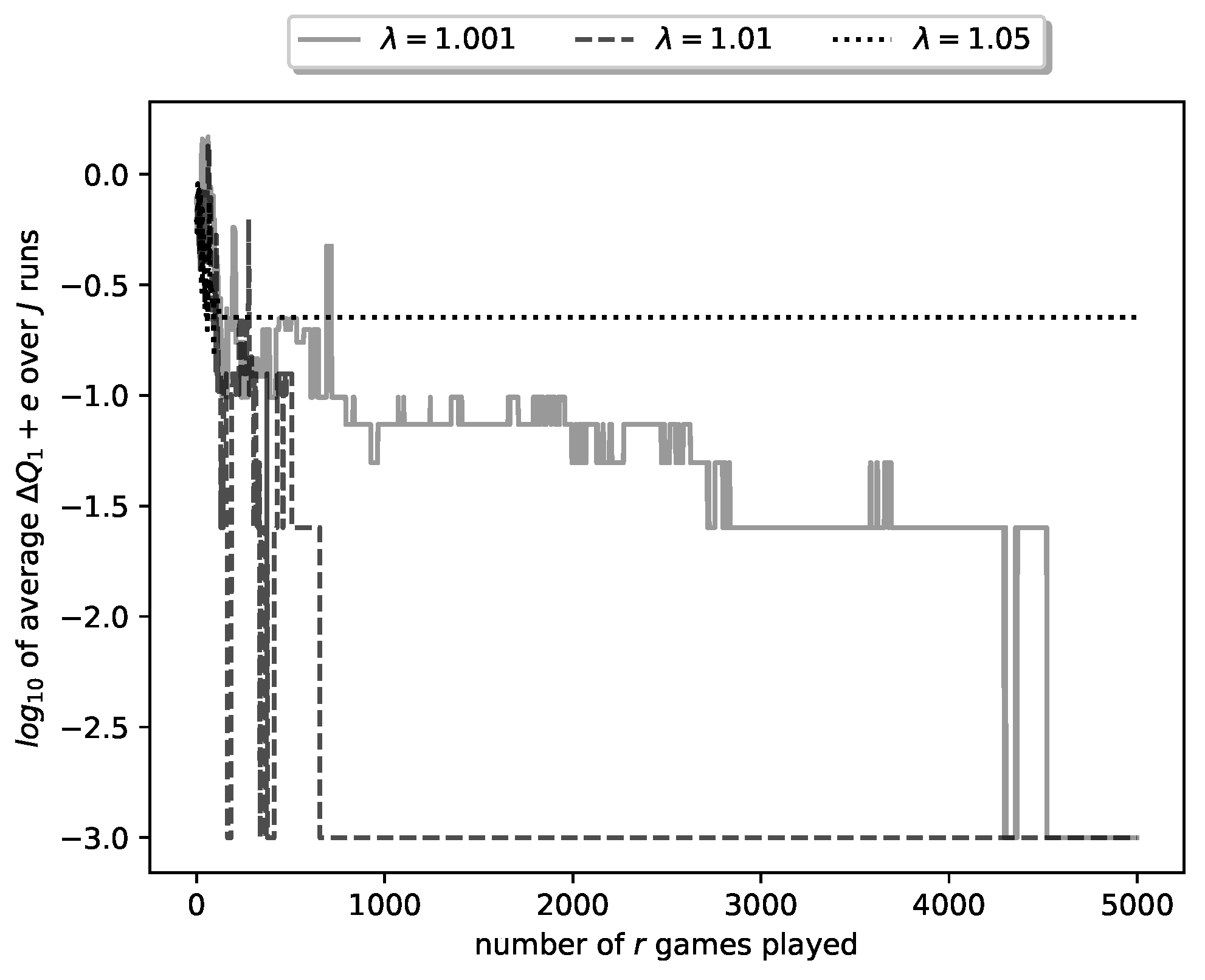
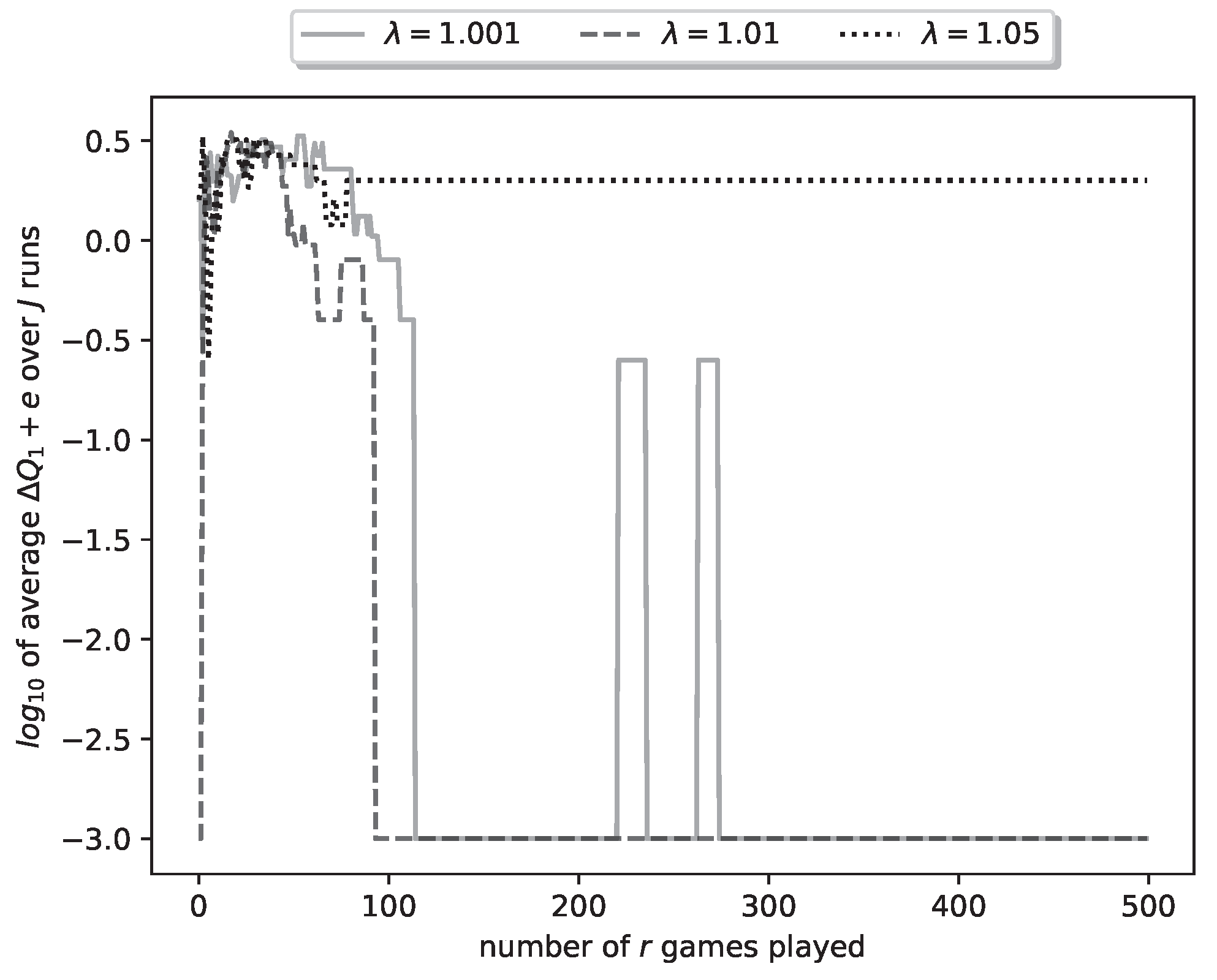
In the above we have given results for a particular run of the learning algorithm. This was a successful run, in the sense that it obtained zero-error estimates of the optimal strategies (and shooting thresholds). However, since our algorithm is stochastic, it is not guaranteed that every run will result in zero-error estimates. To better evaluate the algorithm, we have run it for $J=10$ times and averaged the obtained results. In particular, in Figure 7 we plot the average of ten curves of the type plotted in Figure 4. Note that now we plot the curve for $R=5000$ plays of the duel.

Figure 7. Plot of $Q_1$ ($P_1$’s payoff) for a representative run of the learning process.

Figure 7. Plot of $Q_1$ ($P_1$’s payoff) for a representative run of the learning process.

Several observations can be made regarding Figure 7.

• For the smallest $\lambda$ value, namely $\lambda =1.001$, the respective curve reaches $-3$ at $r=4521$. This corresponds to zero average error, which means that, in some algorithm runs, it took more than 4500 iterations (duel plays) to reach zero error.
• For the $\lambda =1.01$, all runs of the algorithm reached zero-error after $r=656$ runs.
• Finally, for $\lambda =1.05$, the average error never reached zero; in fact 3 out of 10 runs converged to nonzero-error estimates, i.e., to non-optimal strategies.

The above observations corroborate a fact well known in the study of reinforcement learning [7]. Namely, a small learning rate (in our case small $\lambda$) results in higher probability of converging to the true parameter values, but also in slower convergence. This can be explained as follows: a small $\lambda$ results in higher ${\sigma }_r$ values for a large proportion of duels played by the algorithm; i.e., in more extensive exploration, which however results in slower exploitation (convergence). 3

We conclude this group of experiments by running the learning algorithm for various combinations of game parameters; for each combination we record the average error attained at the end of the algorithm (i.e., at $r=R=5000$). The results are summarized at the following tables.

Table 3. Values of final average relative error $\mathrm{\Delta }{Q}_1$ for $c_2=1$, $k_2=1$ and various values of $c_1$, $k_1$, $\lambda$. D is fixed at $D=10$.

$\lambda$		1.001			1.01			1.05
$k_1$	0.50	1.00	1.50	0.50	1.00	1.50	0.50	1.00	1.50
$c_1$
1.00	0.000	0.000	0.000	0.000	0.100	0.482	0.224	0.500	1.207
1.50	0.000	0.000	0.000	0.059	0.049	1.748	0.215	0.480	3.777
2.00	0.000	0.000	0.048	0.074	0.199	0.097	0.144	0.980	0.072

Table 3. Values of final average relative error $\mathrm{\Delta }{Q}_1$ for $c_2=1$, $k_2=1$ and various values of $c_1$, $k_1$, $\lambda$. D is fixed at $D=10$.

$\lambda$		1.001			1.01			1.05
$k_1$	0.50	1.00	1.50	0.50	1.00	1.50	0.50	1.00	1.50
$c_1$
1.00	0.000	0.000	0.000	0.000	0.100	0.482	0.224	0.500	1.207
1.50	0.000	0.000	0.000	0.059	0.049	1.748	0.215	0.480	3.777
2.00	0.000	0.000	0.048	0.074	0.199	0.097	0.144	0.980	0.072

Table 4. Round at which $\mathrm{\Delta }{Q}_1$ converged to zero for all $J=10$ sessions for $c_2=1$, $k_2=1$ and various values of $c_1$, $k_1$, $\lambda$. D is fixed at $D=10$. If $\mathrm{\Delta }{Q}_1$ did not converge for all sessions we note for how many sessions it converged.

$\lambda$		1.001			1.01			1.05
$k_1$	0.50	1.00	1.50	0.50	1.00	1.50	0.50	1.00	1.50
$c_1$
1.00	4521	1456	2983	656	9/10	8/10	7/10	5/10	5/10
1.50	3238	2939	1754	7/10	9/10	9/10	0/10	8/10	6/10
2.00	4153	423	8/10	2/10	9/10	6/10	3/10	4/10	6/10

Table 4. Round at which $\mathrm{\Delta }{Q}_1$ converged to zero for all $J=10$ sessions for $c_2=1$, $k_2=1$ and various values of $c_1$, $k_1$, $\lambda$. D is fixed at $D=10$. If $\mathrm{\Delta }{Q}_1$ did not converge for all sessions we note for how many sessions it converged.

$\lambda$		1.001			1.01			1.05
$k_1$	0.50	1.00	1.50	0.50	1.00	1.50	0.50	1.00	1.50
$c_1$
1.00	4521	1456	2983	656	9/10	8/10	7/10	5/10	5/10
1.50	3238	2939	1754	7/10	9/10	9/10	0/10	8/10	6/10
2.00	4153	423	8/10	2/10	9/10	6/10	3/10	4/10	6/10

From Table 6 and Table 7 we see that for $\lambda =1.001$ almost all learning sessions conclude in zero $\mathrm{\Delta }{Q}_1$, while increasing the value of $\lambda$ results in more sessions concluding with non-zero error estimates. Furthermore, we observe that when the average $\mathrm{\Delta }{Q}_1$ converges to zero for multiple values of $\lambda$ the convergence is faster for bigger $\lambda$. These results highlight the trade off between exploration and exploitation discussed above.

Finally, in Table 8 we see how many learning sessions were run and how many converged to zero error estimate $\mathrm{\Delta }{Q}_1$ for different values of D and $\lambda$.

Table 5. Fraction of learning sessions that converged to $\mathrm{\Delta }{Q}_1-0$ for different values of D and $\lambda$.

$\lambda$	1.001	1.01	1.05
D
8	163/170	144/170	89/170
10	165/170	139/170	81/170
12	161/170	123/170	68/170
14	164/170	134/170	73/170
total	653/680	540/680	311/680

Table 5. Fraction of learning sessions that converged to $\mathrm{\Delta }{Q}_1-0$ for different values of D and $\lambda$.

$\lambda$	1.001	1.01	1.05
D
8	163/170	144/170	89/170
10	165/170	139/170	81/170
12	161/170	123/170	68/170
14	164/170	134/170	73/170
total	653/680	540/680	311/680

Table 6. Values of final average relative error $\mathrm{\Delta }{Q}_1$ for $d_{21}=1$, $d_{22}=D$ and various values of $d_{11}$, $d_{12}$, $\lambda$. D is fixed at $D=10$.

	$\lambda$	1.001	1.01	1.05
$d_{11}$	$d_{12}$
1	$D/2$	0.000	0.233	1.000
1	$2D/3$	0.000	0.000	0.799
1	D	$\sim 6·{10}^{-16}$	$\sim 2·{10}^{-16}$	0.800
$D/3$	$2D/3$	0.000	0.000	2.799
$D/3$	D	0.000	0.000	0.777
$D/2$	D	0.000	0.000	0.480

Table 6. Values of final average relative error $\mathrm{\Delta }{Q}_1$ for $d_{21}=1$, $d_{22}=D$ and various values of $d_{11}$, $d_{12}$, $\lambda$. D is fixed at $D=10$.

	$\lambda$	1.001	1.01	1.05
$d_{11}$	$d_{12}$
1	$D/2$	0.000	0.233	1.000
1	$2D/3$	0.000	0.000	0.799
1	D	$\sim 6·{10}^{-16}$	$\sim 2·{10}^{-16}$	0.800
$D/3$	$2D/3$	0.000	0.000	2.799
$D/3$	D	0.000	0.000	0.777
$D/2$	D	0.000	0.000	0.480

Table 7. Round at which $\mathrm{\Delta }{Q}_1$ converged to zero for all $J=10$ sessions for $d_{21}=1$, $d_{22}=D$ and various values of $d_{11}$, $d_{12}$, $\lambda$. D is fixed at $D=10$. If $\mathrm{\Delta }{Q}_1$ did not converge for all sessions we note for how many sessions it converged.

	$\lambda$	1.001	1.01	1.05
$d_{11}$	$d_{12}$
1	$D/2$	287	7/10	0/10
1	$2D/3$	812	333	9/10
1	D	7/10	9/10	9/10
$D/3$	$2D/3$	326	139	5/10
$D/3$	D	225	397	5/10
$D/2$	D	711	464	6/10

Table 7. Round at which $\mathrm{\Delta }{Q}_1$ converged to zero for all $J=10$ sessions for $d_{21}=1$, $d_{22}=D$ and various values of $d_{11}$, $d_{12}$, $\lambda$. D is fixed at $D=10$. If $\mathrm{\Delta }{Q}_1$ did not converge for all sessions we note for how many sessions it converged.

	$\lambda$	1.001	1.01	1.05
$d_{11}$	$d_{12}$
1	$D/2$	287	7/10	0/10
1	$2D/3$	812	333	9/10
1	D	7/10	9/10	9/10
$D/3$	$2D/3$	326	139	5/10
$D/3$	D	225	397	5/10
$D/2$	D	711	464	6/10

Table 8. Fraction of learning sessions that converged to $\mathrm{\Delta }{Q}_1-0$ for different values of D and $\lambda$.

$\lambda$	1.001	1.01	1.05
D
8	76/110	80/110	49/110
10	97/110	95/110	56/110
12	94/110	78/110	39/110
14	100/110	84/110	40/110
total	367/440	337/440	184/440

Table 8. Fraction of learning sessions that converged to $\mathrm{\Delta }{Q}_1-0$ for different values of D and $\lambda$.

$\lambda$	1.001	1.01	1.05
D
8	76/110	80/110	49/110
10	97/110	95/110	56/110
12	94/110	78/110	39/110
14	100/110	84/110	40/110
total	367/440	337/440	184/440

4.3. Experiment Group B

In this group the kill probability function is piecewise linear

$$p_{n,d}=\left\{\begin{array}{cc}1& \mathrm{when}d\in \left[1,d_{n1}\right]\\ -{\displaystyle \frac{1}{d_{n2}-d_{n1}}}d+{\displaystyle \frac{d_{n2}}{d_{n2}-d_{n1}}}& \mathrm{when}d\in \left[d_{n1},d_{n2}\right]\\ 0& \mathrm{when}d\in \left[d_{n2},D\right]\end{array}\right.$$

Let us look again at the final results of a representative run of the learning algorithm. With $d_{11}=D$, $d_{12}=D/3$, $d_{21}=1$, $d_{22}=D$ and $D=8$, we run the learning algorithm with $R=500$, ${\sigma }_0=6D$ and for the values $\lambda \in \{1.001,1.01,1.05\}$. In Figure 8 we plot the logarithm (with base 10) of the relative payoff error $\mathrm{\Delta }{Q}_1+ϵ$. We see similar results as in Group A, for all $\lambda$ values, the algorithm achieves zero relative error. Convergence is achieved by the 300-th iteration of the algorithm and it is fastest for $\lambda =1.05$, and slowest for $\lambda =1.001$.

Figure 8. Plot of logarithmic relative error ${log}_{10}\mathrm{\Delta }{Q}_1$ of $P_1$’s payoff for a representative run of the learning process.

Figure 8. Plot of logarithmic relative error ${log}_{10}\mathrm{\Delta }{Q}_1$ of $P_1$’s payoff for a representative run of the learning process.

In Figure 9 we plot the logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_n$. These also, as expected, have converged to zero by the 300-th iteration.

Figure 9. Plot of logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_1$, ${log}_{10}\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

Figure 9. Plot of logarithmic relative errors ${log}_{10}\mathrm{\Delta }{d}_1$, ${log}_{10}\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

As in Group A, the fact that the estimates of the optimal shooting thresholds and strategies achieve zero error does not imply that the same is true for the kill probability parameter estimates. In Figure 10, we plot the relative errors $\mathrm{\Delta }{d}_1$ and $\mathrm{\Delta }{d}_2$. The relative error $\mathrm{\Delta }{d}_2$ converges to zero quickly, but the relative error $\mathrm{\Delta }{d}_1$ does not converge to zero for $\lambda =1.05$. For $\lambda =1.05$ the error converges to a fixed nonzero value, which indicates that the algorithm obtains wrong estimates. However, the error is sufficiently small to still result in zero-error estimates of the shooting thresholds.

Figure 10. Plot of relative parameter errors $\mathrm{\Delta }{d}_1$, $\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

Figure 10. Plot of relative parameter errors $\mathrm{\Delta }{d}_1$, $\mathrm{\Delta }{d}_2$ for a representative run of the learning process.

As in group A, to better evaluate the algorithm, we have run it for $J=10$ times and averaged the obtained results. In particular, in Figure 11 we plot the average of ten curves of the type plotted in Figure 4. Note that now we plot the curve for $R=500$ plays of the duel.

Figure 11. Plot of $Q_1$ ($P_1$’s payoff) for a representative run of the learning process.

Figure 11. Plot of $Q_1$ ($P_1$’s payoff) for a representative run of the learning process.

We again run the learning algorithm for various combinations of game parameters and record the average error attained at the end of the algorithm (again at $r=R=5000$) for each combination. The results are summarized at the following tables.

From Table 6 and Table 7, we observe that for most parameter combinations, all learning sessions conclude with a zero $\mathrm{\Delta }{Q}_1$ for the smaller $\lambda$ values. However, for $\lambda =1.05$, the algorithm fails to converge and exhibits a high relative error. Notably, increasing $\lambda$ from 1.001 to 1.01 generally accelerates convergence, although this is not guaranteed in every case. In one instance, a higher $\lambda$ (specifically $1.01$) leads to a slower average convergence of $\mathrm{\Delta }{Q}_1$ to zero, indicating the importance of initial random shooting choices. We also observe that results for the highest $\lambda$ are suboptimal, with the algorithm failing to converge in varying numbers of sessions, such as in 1 out of 10 or even 5 out of 10 cases. Notably, when convergence does occur, it happens relatively quickly, with sessions typically completing in under 1000 iterations. These findings also highlight the trade-off between exploration and exploitation, as discussed earlier.

Finally, in Table 8 we see how many learning sessions were run and how many converged to zero error estimate $\mathrm{\Delta }{Q}_1$ for different values of D and $\lambda$.

5. Discussion

We proposed an algorithm for estimating the unknown game parameters and the optimal strategies through the course of repeated plays. We tested the algorithm for two models of the kill probability function and found that it converged for the majority of tests. Furthermore, we observed the established relationship between higher learning rates and reduced convergence quality, underscoring the trade-off between learning speed and stability in convergence. Future research could investigate additional models of the accuracy probability function, including scenarios where the two players employ distinct models, and work toward establishing theoretical bounds on the algorithm’s probabilistic convergence.