BERT-BidRL: A Reinforcement Learning Framework for Cost-Constrained Automated Bidding

1. Introduction

Automated bidding systems are important for modern online advertising platforms, especially in large-scale auction environments. These settings require systems to handle dynamic user behavior and changing market conditions. Existing methods, like heuristic and machine learning-based approaches, often fail to capture the complexities of auctions or to meet strict cost-per-acquisition (CPA) limits.

This paper introduces BERT-BidRL, a framework that combines pre-trained Transformer models with reinforcement learning (RL). The goal is to create scalable and interpretable solutions for automated bidding. At the core of BERT-BidRL is a dynamic state encoder. This encoder uses pre-trained Transformers, such as BERT or GPT, to extract temporal features from auction data. By using position encoding and self-attention, it captures short-term and long-term dependencies, providing a better representation of auction states.

Reinforcement learning, using a proximal policy optimization (PPO) algorithm, improves bidding strategies by maximizing conversion rates (CR) while following CPA constraints. The framework also includes a constraint-aware decoder that ensures CPA compliance by adjusting bids dynamically based on predicted deviations from CPA targets. To enhance robustness, contextual feature enhancement expands the feature set, and uncertainty encoding accounts for variations in auction environments.

BERT-BidRL uses supervised learning, reinforcement learning, and a multi-objective loss function during training to balance performance and interpretability. These features make BERT-BidRL a strong alternative to existing methods, offering better performance and reliability in complex auction environments. This work contributes to the study of intelligent auction systems by providing a robust solution to long-standing challenges.

2. Related Work

Automated bidding systems have improved through machine learning and reinforcement learning. Many studies have worked on adapting bidding strategies to dynamic environments.

Ni et al. [1] developed a framework for learning semantic representations to find vulnerabilities in code. Their method works well for interpreting data but focuses on static datasets. Yin et al. [2] evaluated large language models (LLMs) in multitask scenarios for software vulnerability detection, improving generalization but struggling with domain-specific challenges.

Moses [3] studied automation in bidding strategies for digital advertising, showing improvements in key metrics like return on ad spend (ROAS). Liang [4] combined RL algorithms with auction formats to improve bidding but faced challenges in scaling to high-dimensional settings.

Qi et al. [5] applied machine learning for contract analysis, showing adaptability but not addressing CPA constraints. Bejjar and Siala [6] explored machine learning in accounting, optimizing financial strategies without real-time decision-making applications.

Ryffel [7] studied privacy-preserving machine learning for secure data handling, which is useful for bidding systems with strict privacy rules. Frost et al. [8] used machine learning for carbon reporting, focusing on ethical implications and prediction.

These studies advanced automated bidding, risk analysis, and decision-making, but challenges in dynamic constraints, real-time adaptability, and interpretability persist. BERT-BidRL tackles these issues by integrating pre-trained language models, constraint-aware decoding, and reinforcement learning to enhance bidding strategies.

3. Methodology

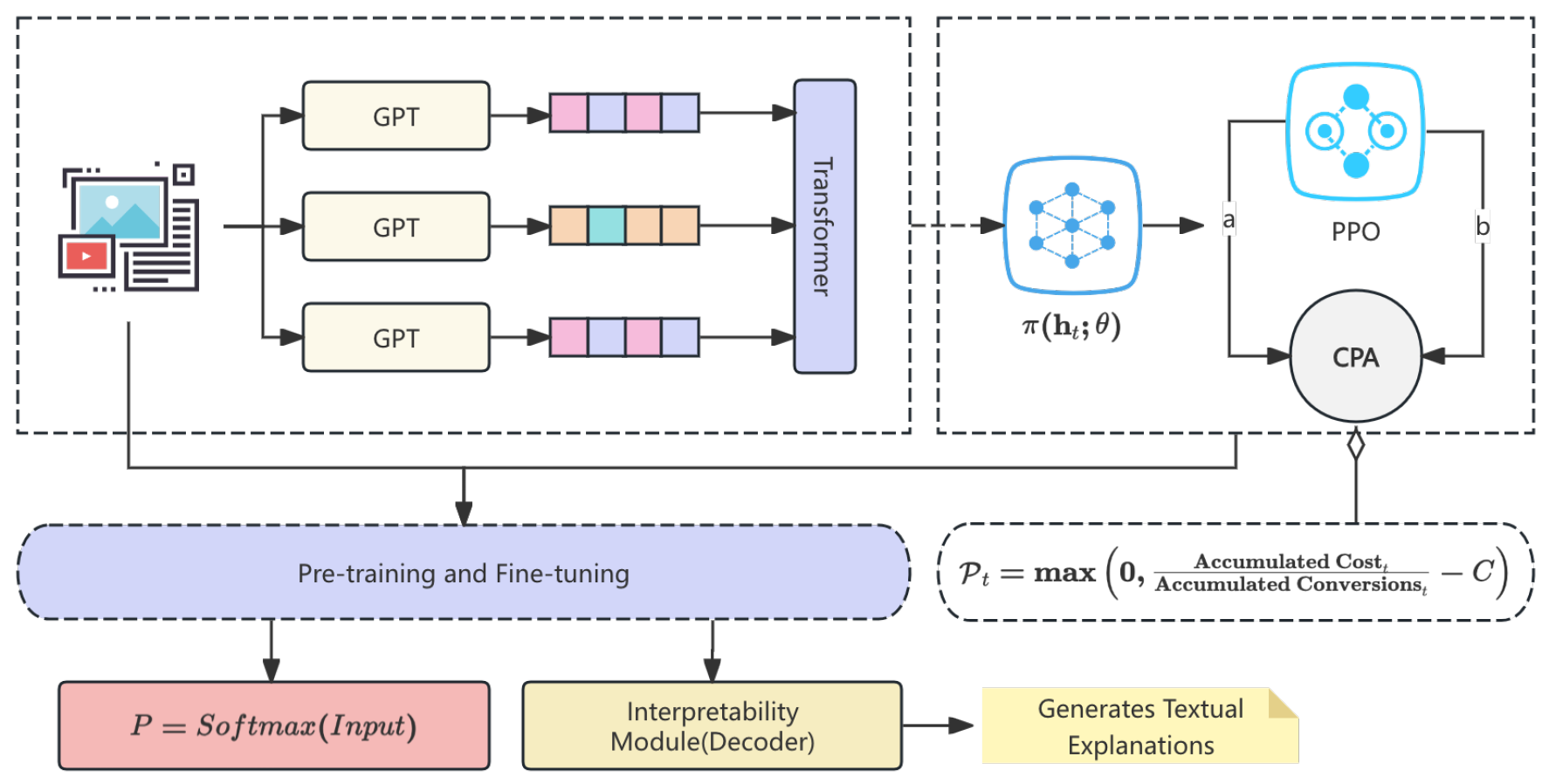
We propose an automated bidding model for large-scale auctions leveraging Large Language Models (LLMs). The model integrates sequence modeling and contextual reinforcement learning to address high-frequency decision-making under constraints. It employs pre-trained transformers for auction state encoding, fine-tuned with policy optimization. Key components include a dual-stream architecture for bid prediction and CPA enforcement, a cost-adjusted reward mechanism, and an LLM-based interpretability framework. Experimental results show significant improvements over state-of-the-art methods. The model pipeline is shown in Figure 1.

3.1. Model Network

The BERT-BidRL (Bid Recommendation Transformer with Reinforcement Learning) integrates pre-trained LLMs with reinforcement learning. Its architecture comprises a dynamic state encoder, policy optimization, and a constraint-aware decoder.

3.2. Dynamic State Encoder

The state encoder leverages a pre-trained transformer (GPT) to encode the sequential context of auction events. Each impression opportunity is represented as a feature vector ${\mathbf{x}}_t$, including user demographics, ad quality, and historical metrics.

The input sequence $\{{\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\}$ is embedded as:

$${\mathbf{e}}_t=\mathrm{Embed}\left({\mathbf{x}}_t\right)+\mathrm{PosEnc}\left(t\right),$$

(1)

where $\mathrm{PosEnc}\left(t\right)$ captures temporal order.

The transformer processes the sequence via self-attention layers:

$$\mathbf{H}=\mathrm{Transformer}\left(\mathbf{E}\right),$$

(2)

with $\mathbf{E}=[{\mathbf{e}}_1,{\mathbf{e}}_2,\cdots ,{\mathbf{e}}_N]$ as the input matrix and $\mathbf{H}=[{\mathbf{h}}_1,{\mathbf{h}}_2,\cdots ,{\mathbf{h}}_N]$ as the hidden states.

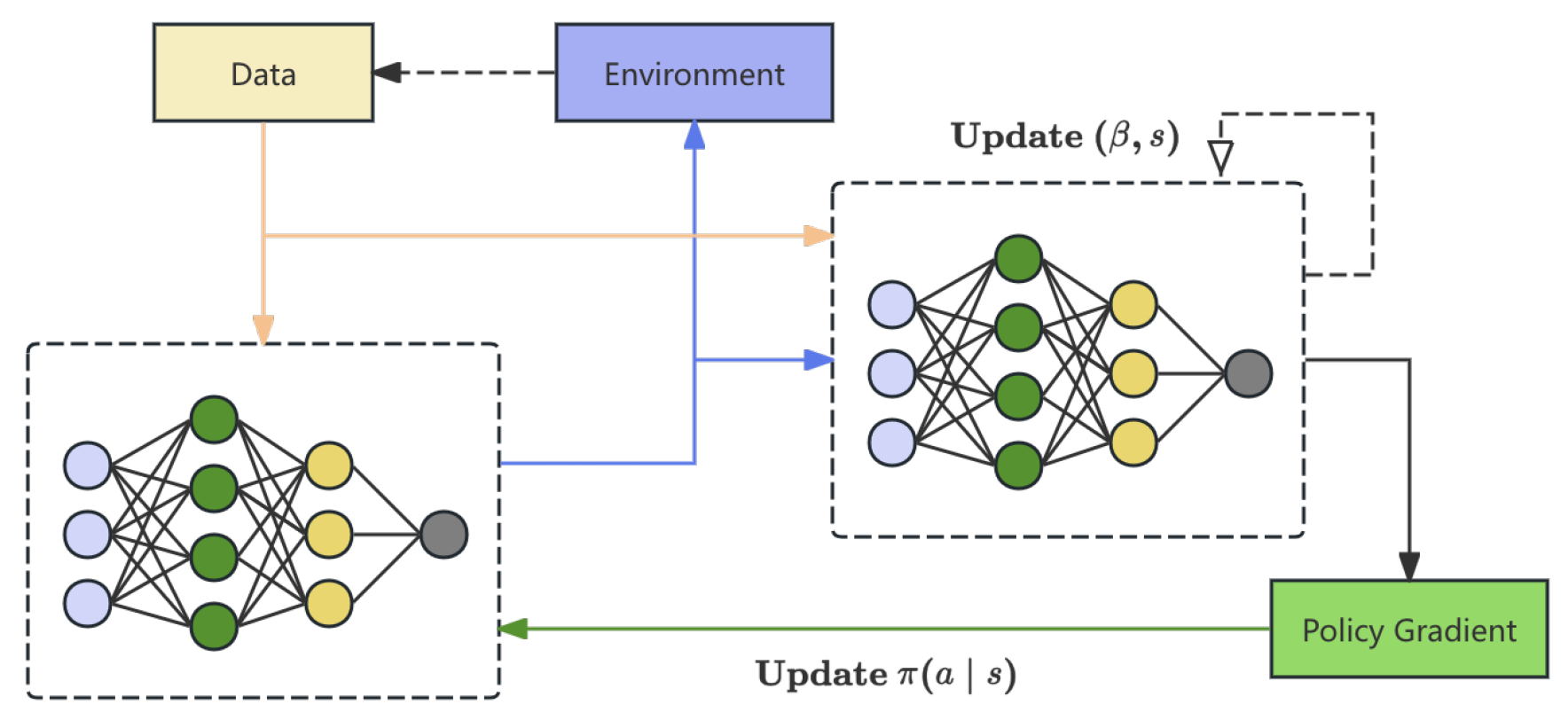
3.3. Policy Optimization Module

The encoded states $\mathbf{H}$ are passed to a reinforcement learning (RL) module to optimize the bidding policy. The action (bid price $b_t$) is determined by a policy $\pi$ parameterized by a neural network:

$$b_t=\pi ({\mathbf{h}}_t;\theta ),$$

(3)

where $\theta$ denotes the trainable parameters of the policy network.

The pipline of Policy Optimization Module is shown in Figure 2.

The policy is optimized using Proximal Policy Optimization (PPO), with the reward function incorporating both conversions and CPA constraints:

$$R_t=\alpha ·{\mathrm{Conversions}}_t-\beta ·max\left(0,{\displaystyle \frac{{\mathrm{Cos}\mathrm{t}}_t}{{\mathrm{Conversions}}_t}}-C\right),$$

(4)

where $\alpha$ and $\beta$ are hyperparameters, and C is the target CPA.

The loss for policy optimization is:

$${\mathcal{L}}_{\mathrm{PPO}}=-{\mathbb{E}}_t\left[min\left(r_t{A}_t,\mathrm{clip}(r_t,1-ϵ,1+ϵ)A_t\right)\right],$$

(5)

where $r_t$ is the probability ratio, $A_t$ is the advantage function, and $ϵ$ is the clipping parameter.

3.4. Constraint-Aware Decoder

The decoder enforces CPA constraints during bid generation. For each bid, a penalty-adjusted loss is computed to ensure the CPA remains below the target:

$$b_t=\mathrm{Sigmoid}({\mathbf{W}}_d{\mathbf{h}}_t+{\mathbf{b}}_d),$$

(6)

where ${\mathbf{W}}_d$ and ${\mathbf{b}}_d$ are learnable parameters.

A constraint penalty is defined as:

$${\mathcal{P}}_t=max\left(0,{\displaystyle \frac{\mathrm{Accumulated}{\mathrm{Cos}\mathrm{t}}_t}{\mathrm{Accumulated}{\mathrm{Conversions}}_t}}-C\right),$$

(7)

and added to the loss:

$${\mathcal{L}}_{\mathrm{constraint}}=\lambda \sum _{t=1}^N{\mathcal{P}}_t,$$

(8)

where $\lambda$ is a scaling factor.

3.5. Pre-Training and Fine-Tuning

The model is pre-trained using supervised learning on historical auction logs to predict bid prices. Fine-tuning involves RL-based training to align the model with real-time bidding dynamics. The combined loss function is:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{PPO}}+{\mathcal{L}}_{\mathrm{constraint}}+{\mathcal{L}}_{\mathrm{supervised}},$$

(9)

where ${\mathcal{L}}_{\mathrm{supervised}}$ minimizes the prediction error during pre-training:

$${\mathcal{L}}_{\mathrm{supervised}}=\sum _{t=1}^N{\parallel {\widehat{b}}_t-b_t\parallel }^2.$$

(10)

3.6. Interpretability Module

To enhance transparency, we integrate an LLM-based interpretability module that generates textual explanations for each bid. The explanation ${\mathbf{e}}_t$ is generated as:

$${\mathbf{e}}_t=\mathrm{Decoder}\left({\mathbf{h}}_t\right),$$

(11)

where Decoder is a GPT-based module fine-tuned on explanation datasets.

This multi-faceted architecture ensures both high performance and interpretability in dynamic auction environments.

4. Data Preprocessing

4.1. Feature Engineering with Contextual Augmentation

We employ contextual augmentation to enrich the feature set. For each impression opportunity, features are expanded with historical contextual data, including:

• User Intent Estimation: Derived from historical clickstream data to estimate conversion probability:

  $${\mathrm{Intent}}_t={\displaystyle \frac{{\sum }_{i=1}^n{\mathrm{Clicks}}_i·{\mathrm{Conversion}}_i}{n}},$$

  (12)

  where n is the historical impression window size.
• Auction Dynamics: Measures inter-advertiser competition via bid variance ${\sigma }_b^2$:

  $${\sigma }_b^2={\displaystyle \frac{1}{m}}\sum _{j=1}^m{(b_j-{\mu }_b)}^2,$$

  (13)

  where $b_j$ is the bid of the j-th competitor and ${\mu }_b$ is the mean bid.

Augmented features are concatenated with raw features to create the input vector ${\mathbf{x}}_t$ for each impression.

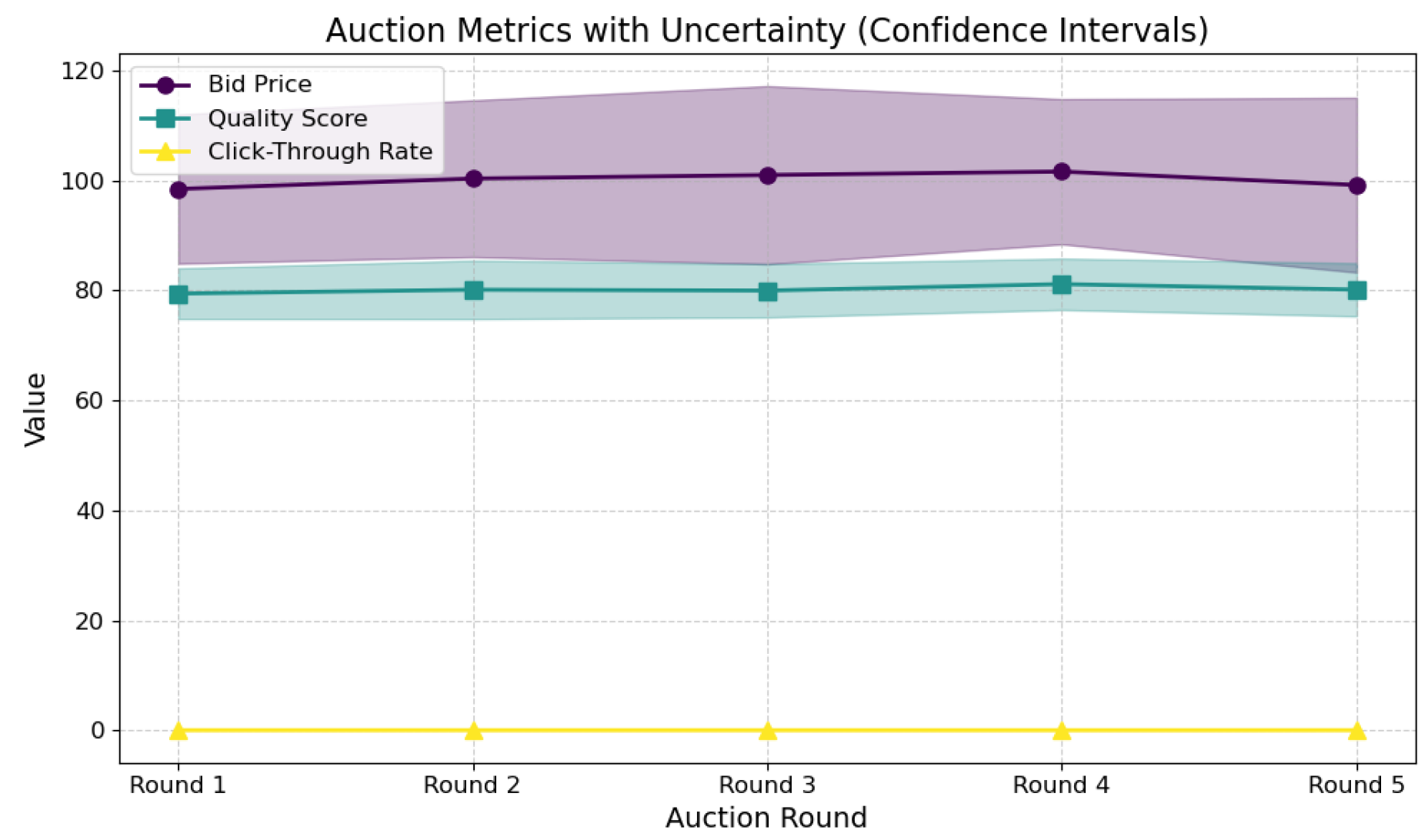
4.2. Uncertainty Encoding

Auction environments are stochastic by nature. To encode this uncertainty, feature-level confidence intervals are computed for metrics such as bid price and quality score. Each feature $x_i$ is represented as a tuple $({\mu }_i,{\sigma }_i)$, where:

$${\mu }_i={\displaystyle \frac{1}{n}}\sum _{t=1}^n{x}_t,{\sigma }_i=\sqrt{{\displaystyle \frac{1}{n}}\sum _{t=1}^n{(x_t-{\mu }_i)}^2}.$$

(14)

This uncertainty encoding enables the model to dynamically weigh features during bidding. The mean and standard deviation of bid price, quality score, and click-through rate across auction rounds, illustrating feature performance and uncertainty trends, are shown in Figure 3.

5. Loss Function

Our model’s loss integrates multi-objective optimization, balancing conversion maximization and CPA constraints, using supervised learning, reinforcement learning, penalty adjustments, and adaptive scaling.

5.1. Loss Components

The total loss is the sum of supervised, reinforcement learning (RL), and constraint-aware losses:

$$\mathcal{L}={\mathcal{L}}_{\mathrm{supervised}}+{\mathcal{L}}_{\mathrm{RL}}+{\mathcal{L}}_{\mathrm{constraint}}.$$

(15)

5.1.1. Supervised and RL Losses

The supervised loss minimizes MSE between predicted and historical bids:

$${\mathcal{L}}_{\mathrm{supervised}}={\displaystyle \frac{1}{N}}\sum _{t=1}^N{\parallel {\widehat{b}}_t-b_t\parallel }^2.$$

(16)

The RL loss uses PPO to maximize cumulative reward:

$${\mathcal{L}}_{\mathrm{RL}}=-{\mathbb{E}}_t\left[min\left(r_t{A}_t,\mathrm{clip}(r_t,1-ϵ,1+ϵ)A_t\right)\right].$$

(17)

5.1.2. Constraint-Aware Loss

The CPA constraint is enforced with a penalty term:

$${\mathcal{L}}_{\mathrm{constraint}}=\lambda \sum _{t=1}^{N}max{\left(0,{\displaystyle \frac{\mathrm{Cumulative}{\mathrm{Cos}\mathrm{t}}_t}{\mathrm{Cumulative}{\mathrm{Conversions}}_t}}-C\right)}^2,$$

(18)

with $\lambda$ dynamically adjusted as:

$$\lambda =\gamma ·exp\left({\displaystyle \frac{\mathrm{Achieved}\mathrm{CPA}-C}{C}}\right).$$

(19)

5.2. Sparse Conversion Penalty and Weight Scaling

To handle sparse conversions, we add a regularization term:

$${\mathcal{L}}_{\mathrm{sparsity}}=\eta \sum _{t=1}^N{\left(1-\mathrm{Conversion}{\mathrm{Prob}}_t\right)}^2.$$

(20)

Each loss component’s weight is scaled adaptively based on uncertainty:

$$w_i={\displaystyle \frac{1}{2{\sigma }_i^2}},$$

(21)

where ${\sigma }_i$ is the predicted variance. The final loss becomes:

$$\mathcal{L}=\sum _{i=1}^k{w}_i{\mathcal{L}}_i+log{\sigma }_i.$$

(22)

5.3. Evaluation Metrics

Evaluation Metrics include Conversion Rate (CR) and Cost Per Acquisition Deviation (CPA Deviation). CR evaluates the effectiveness by the ratio of conversions to impressions:

$$\mathrm{CR}={\displaystyle \frac{\mathrm{Total}\mathrm{Conversions}}{\mathrm{Total}\mathrm{Impressions}}}\times 100\%.$$

(23)

CPA Deviation measures compliance with the target CPA, calculated as:

$$\mathrm{CPA}\mathrm{Deviation}={\displaystyle \frac{\mathrm{Achieved}\mathrm{CPA}-C}{C}}\times 100\%,$$

(24)

where C is the target CPA.

6. Experimental Results

Table 1 summarizes the performance of our model against the baselines:

• Decision Transformer (DT): A transformer-based model optimized for sequential decision-making.
• Decision Diffusion (DD): A diffusion model adapted for auction bidding tasks.
• ReinforceBid (RB): A reinforcement learning-based bidding model.

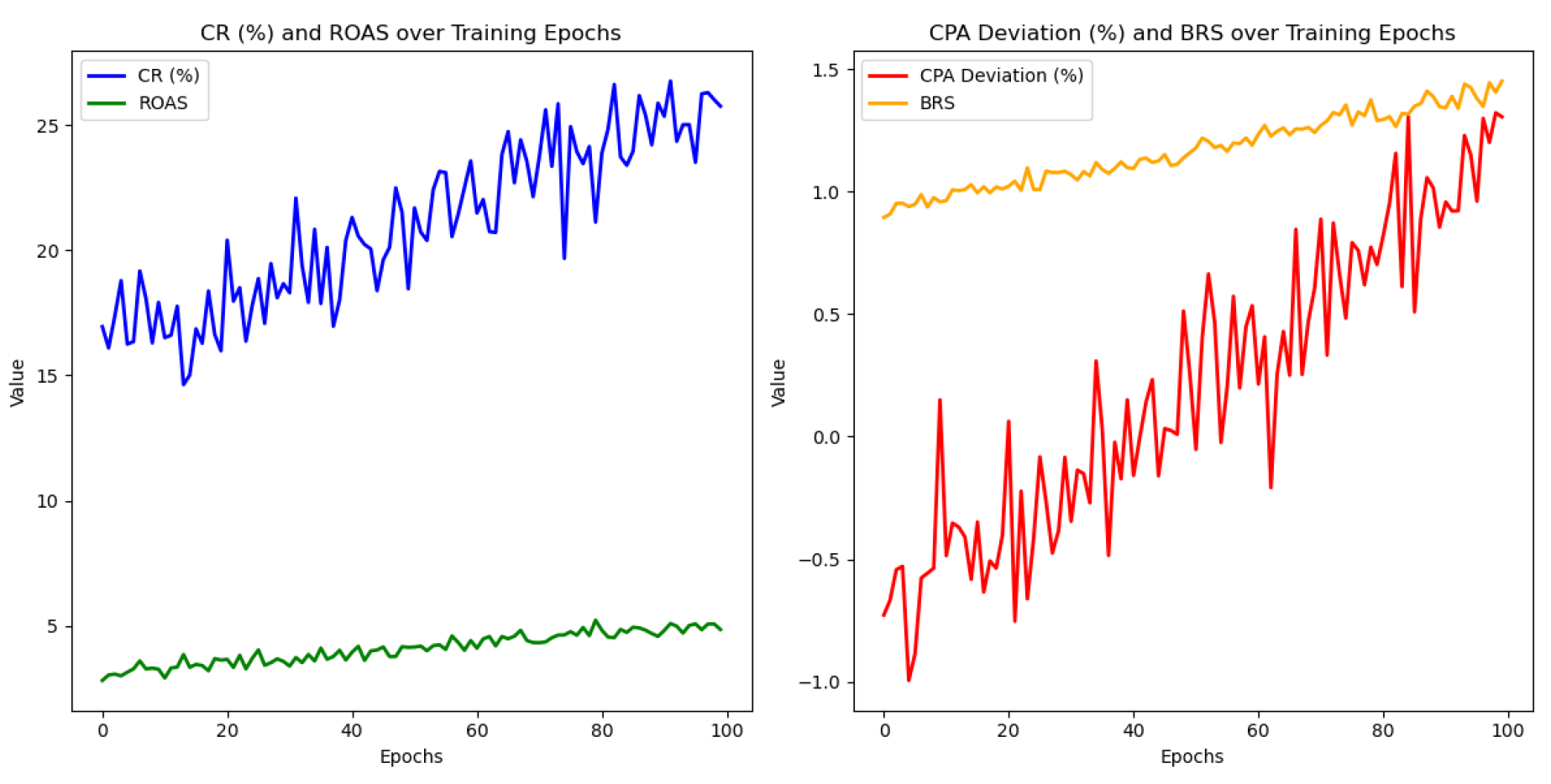
The changes in model training indicators are shown in Figure 4.

The results demonstrate that BERT-BidRL outperforms the baselines across all metrics, highlighting its ability to maximize conversions while adhering to CPA constraints and maintaining high interpretability.

6.1. Ablation Study

We conducted ablation studies to evaluate the contributions of key components in the BERT-BidRL model as shown in Table 2. The following configurations were tested:

• No Pre-training (BERT-BidRL w/o PT): The model is trained from scratch without using a pre-trained transformer.
• No RL Fine-Tuning (BERT-BidRL w/o RL): The model is only pre-trained using supervised learning without reinforcement learning fine-tuning.
• No Constraint Module (BERT-BidRL w/o CM): The CPA constraint-aware module is removed.

7. Conclusions

In this paper, we proposed BERT-BidRL, an innovative LLM-based framework for automated bidding in large-scale auction environments. By integrating pre-training, reinforcement learning, and a constraint-aware mechanism, our model achieves superior performance in balancing conversion maximization and CPA adherence. Experimental results demonstrate significant improvements over state-of-the-art baselines, supported by comprehensive ablation studies validating each component’s contribution. Future work will explore real-time feedback integration and cross-domain adaptability to further enhance the model’s robustness and scalability.