Submitted:
08 November 2024
Posted:
08 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Radon as Pollutant and as Tracer
1.2. Radon Source, Transport, and Temporal Variability
1.3. Low-Cost Radon Measurement and Citizen Science
1.4. Objective of the Paper
2. Methods 1: Hardware, Experimental Design and Data
2.1. The RadonEye Monitor
2.2. Measurement Locations and Periods
3. Methods 2: Statistical Analysis of Reported Rn Time Series
3.1. Box-Jenkins Scheme
3.1.1. Autoregressive Moving Average Model
3.1.2. Box-Jenkins Scheme - Autocorrelation and Partial Autocorrelation Functions (ACF and PACF)
3.2. Stationarity
3.3. Multifractal Methods
3.3.1. Hurst Coefficient
3.3.2. Multifractal Spectrum
3.3.3. Fractal Dimension of the Graph
3.3.4. Garger Exponent
3.3.5. Attractor Embedding Dimension
3.3.6. Lyapunov Exponent
4. Results 1: Aspects of Counting Statistics
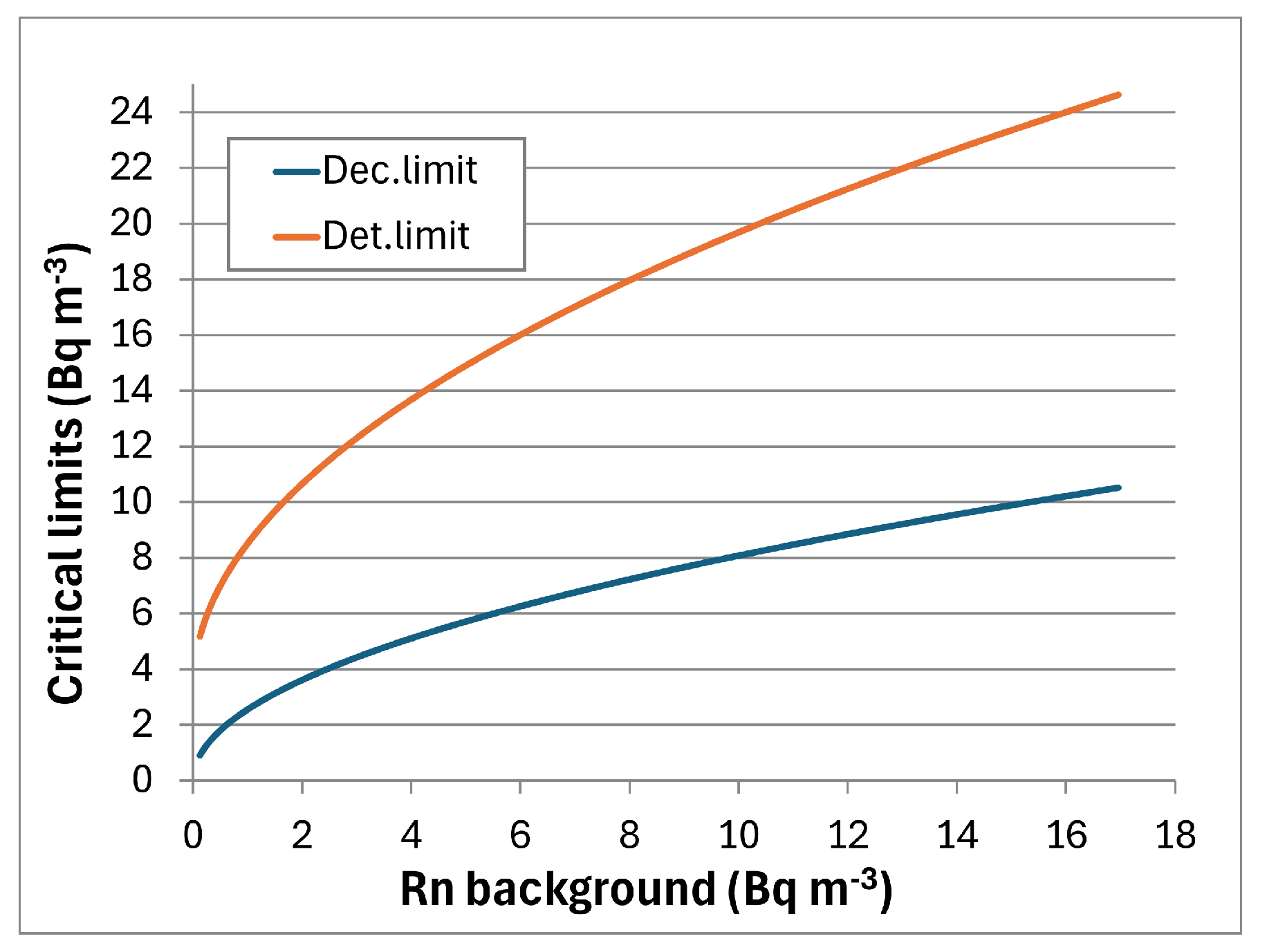
4.1. Critical Limits
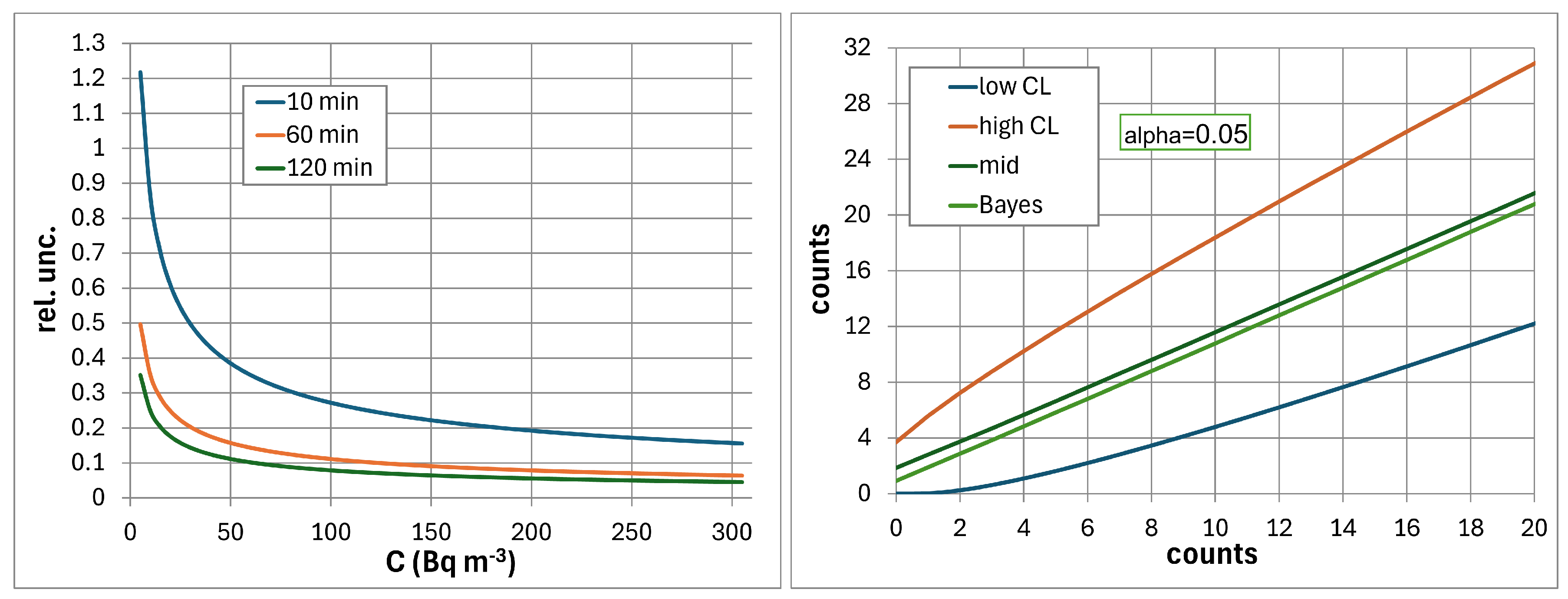
4.2. Frequentist Poisson Confidence Interval of Counts
4.3. Bayesian Estimate of the Expected True Count Rate
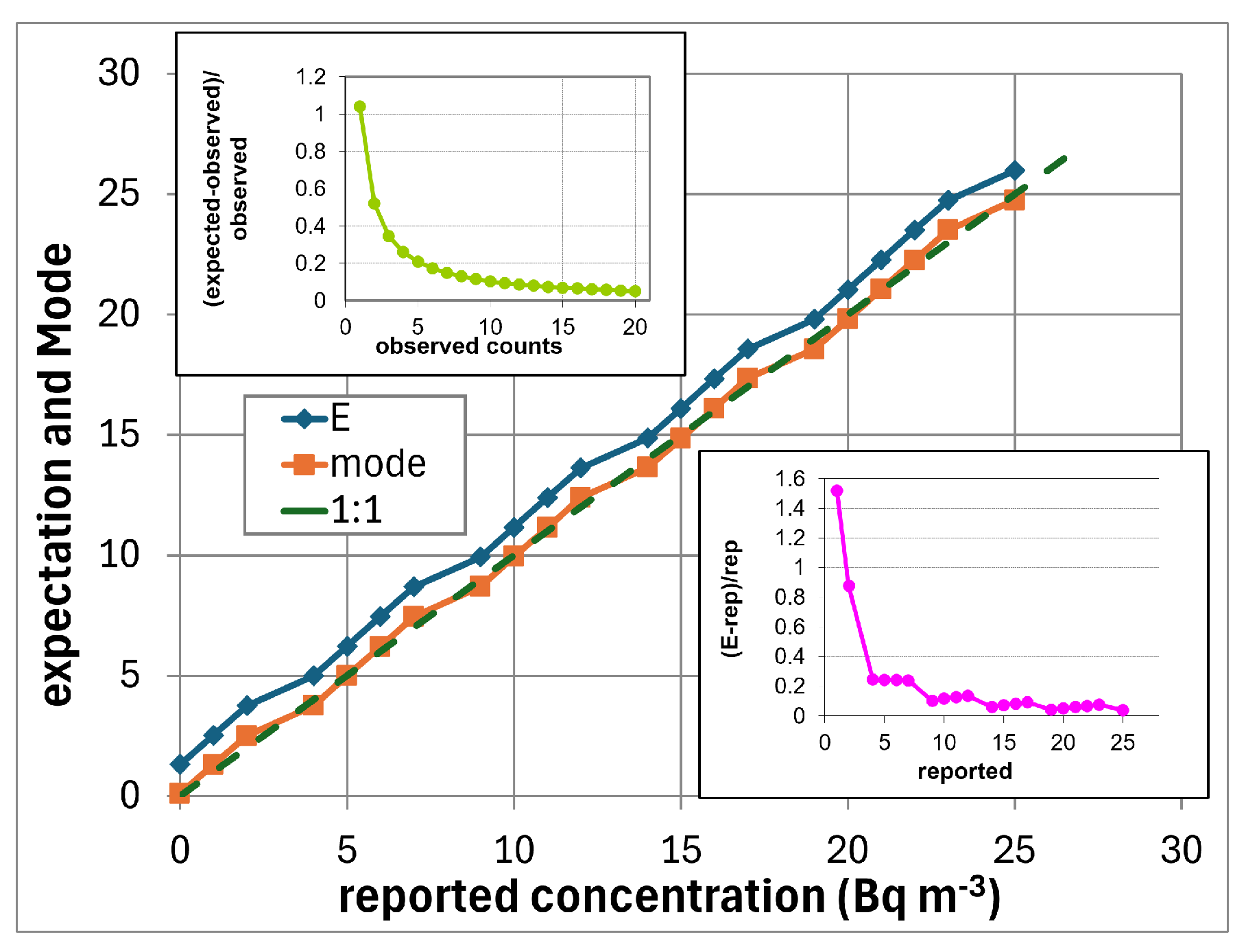
4.4. Bayesian Inversion of Reported Rounded Concentration Values
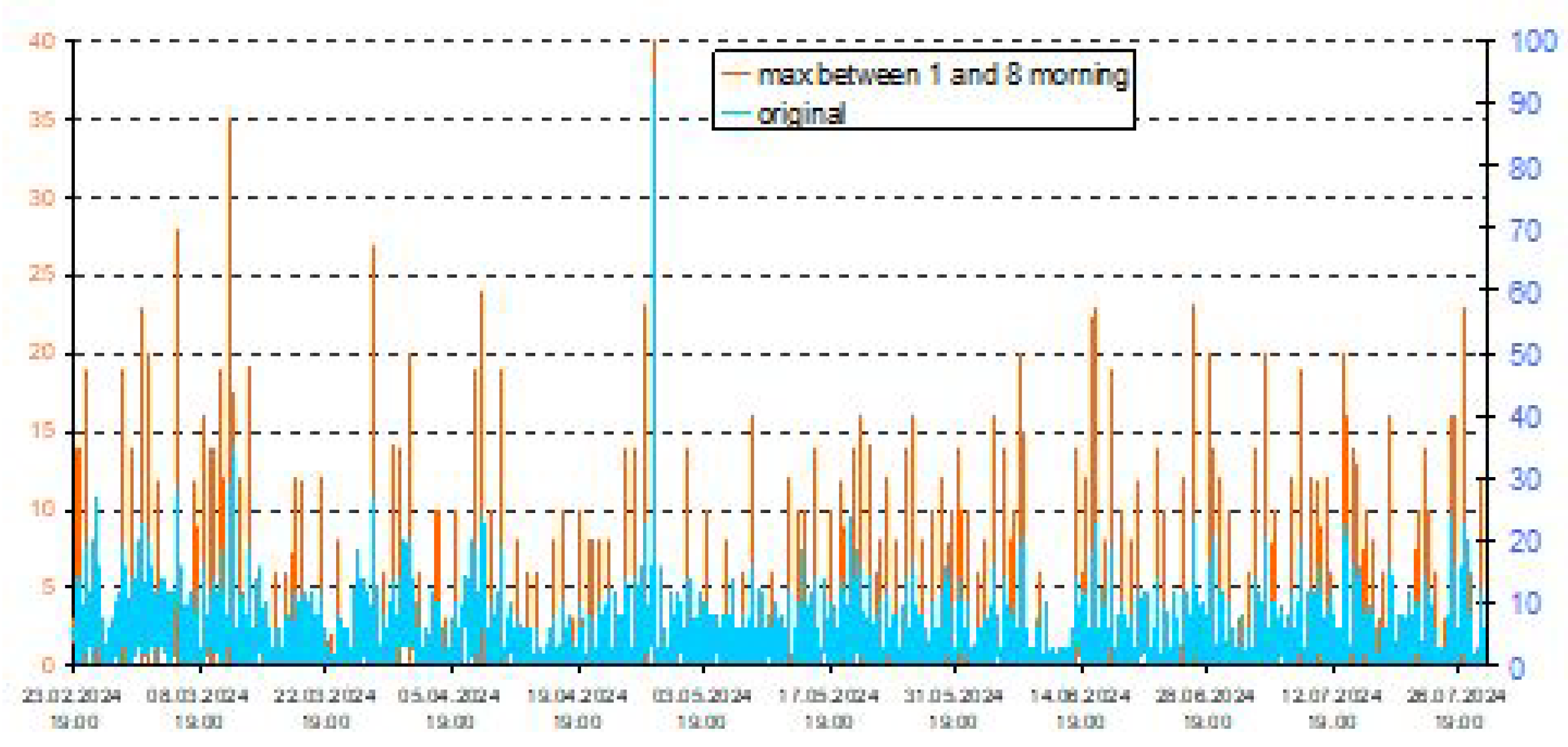
4.5. Missing Nominal Concentration Values
5. Results 2: Descriptive and Exploratory Statistics
5.1. Descriptive Statistics, Periodicity And Autocorrelation
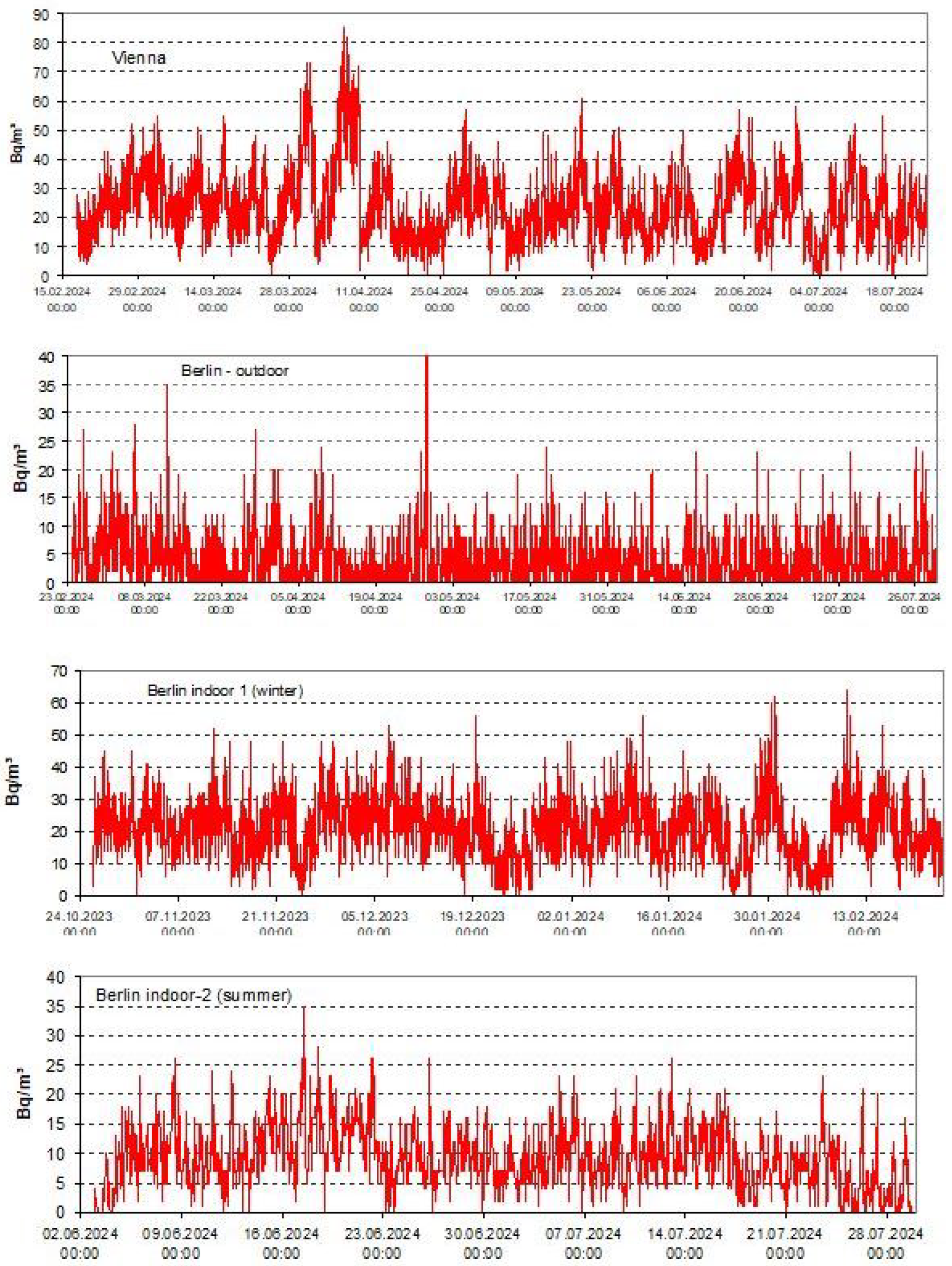
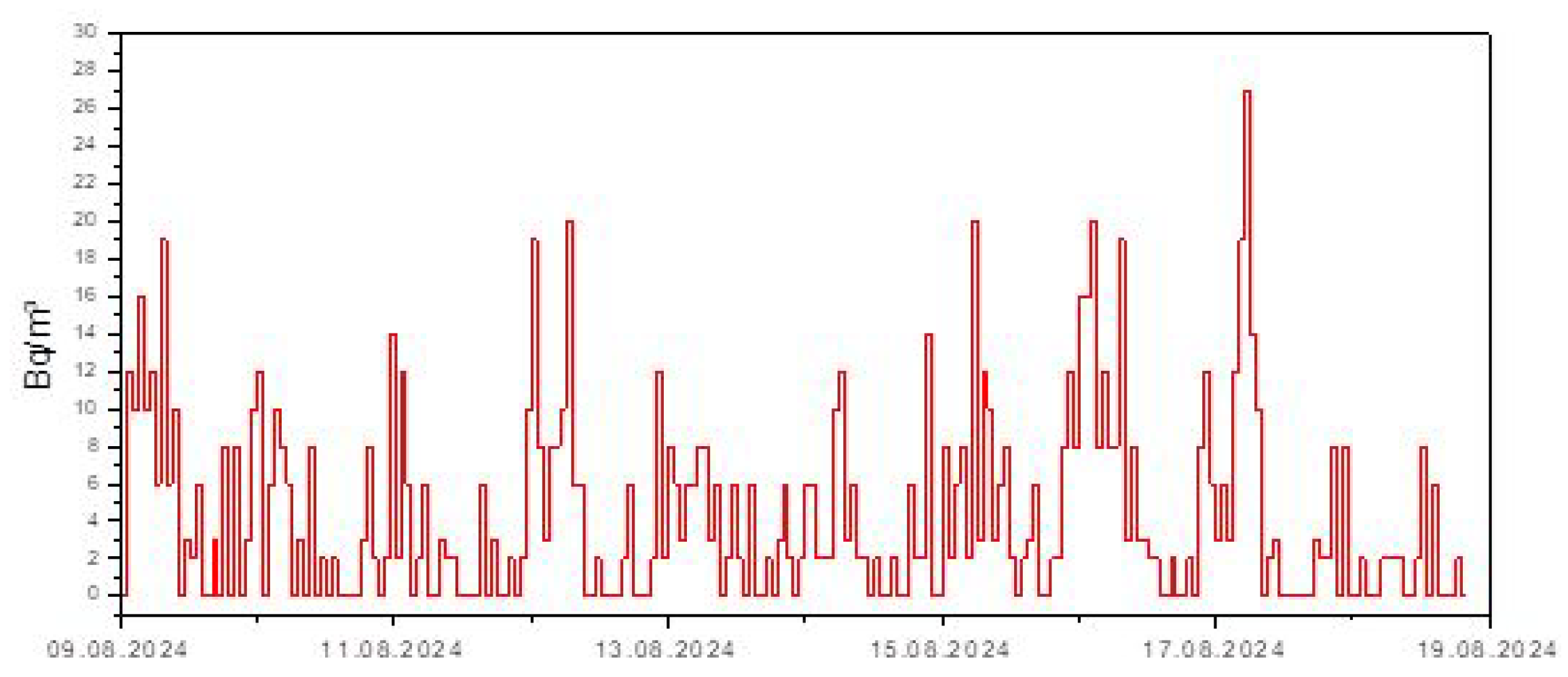
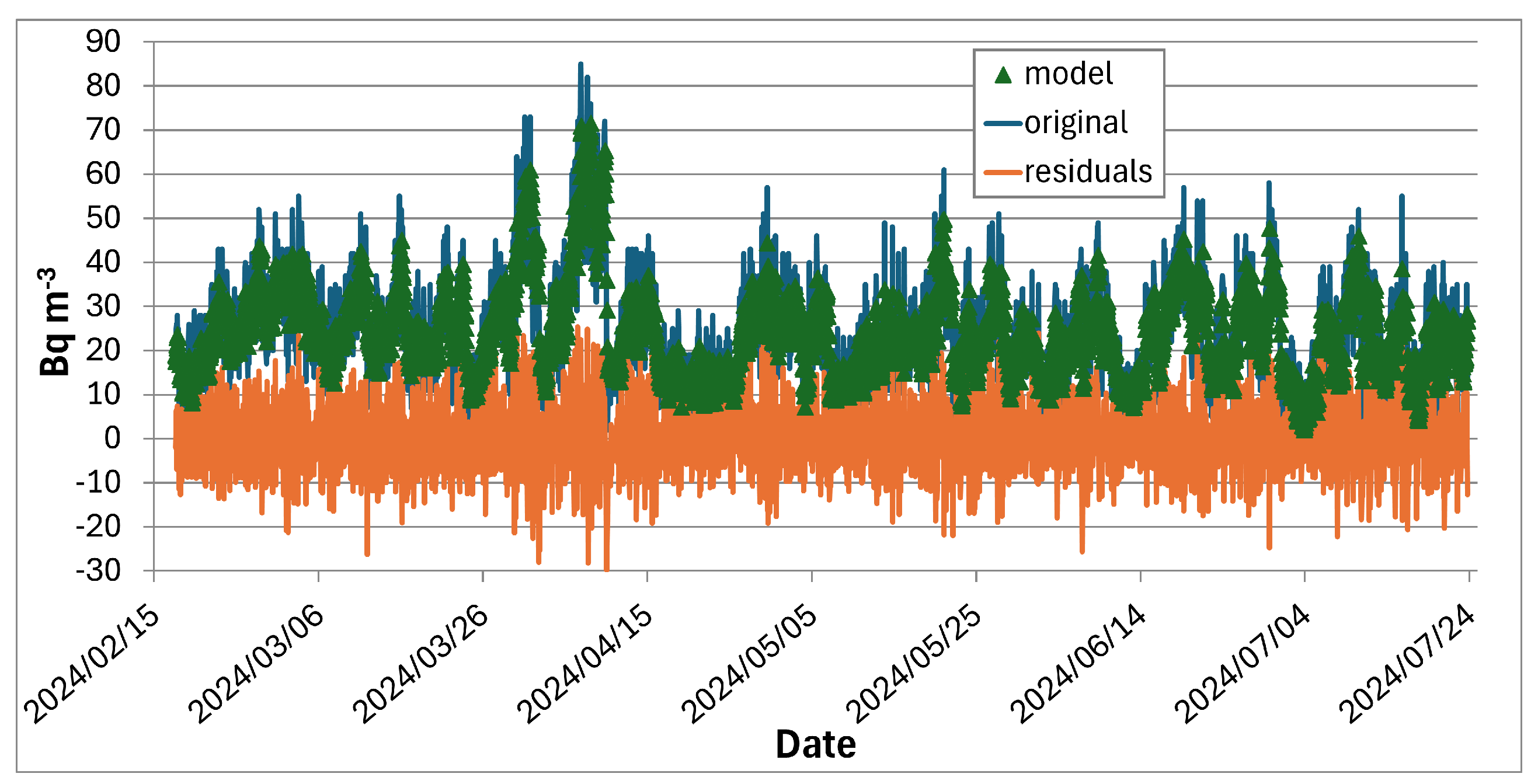
5.1.1. Time Series and Descriptive Statistics
5.1.2. Stationarity
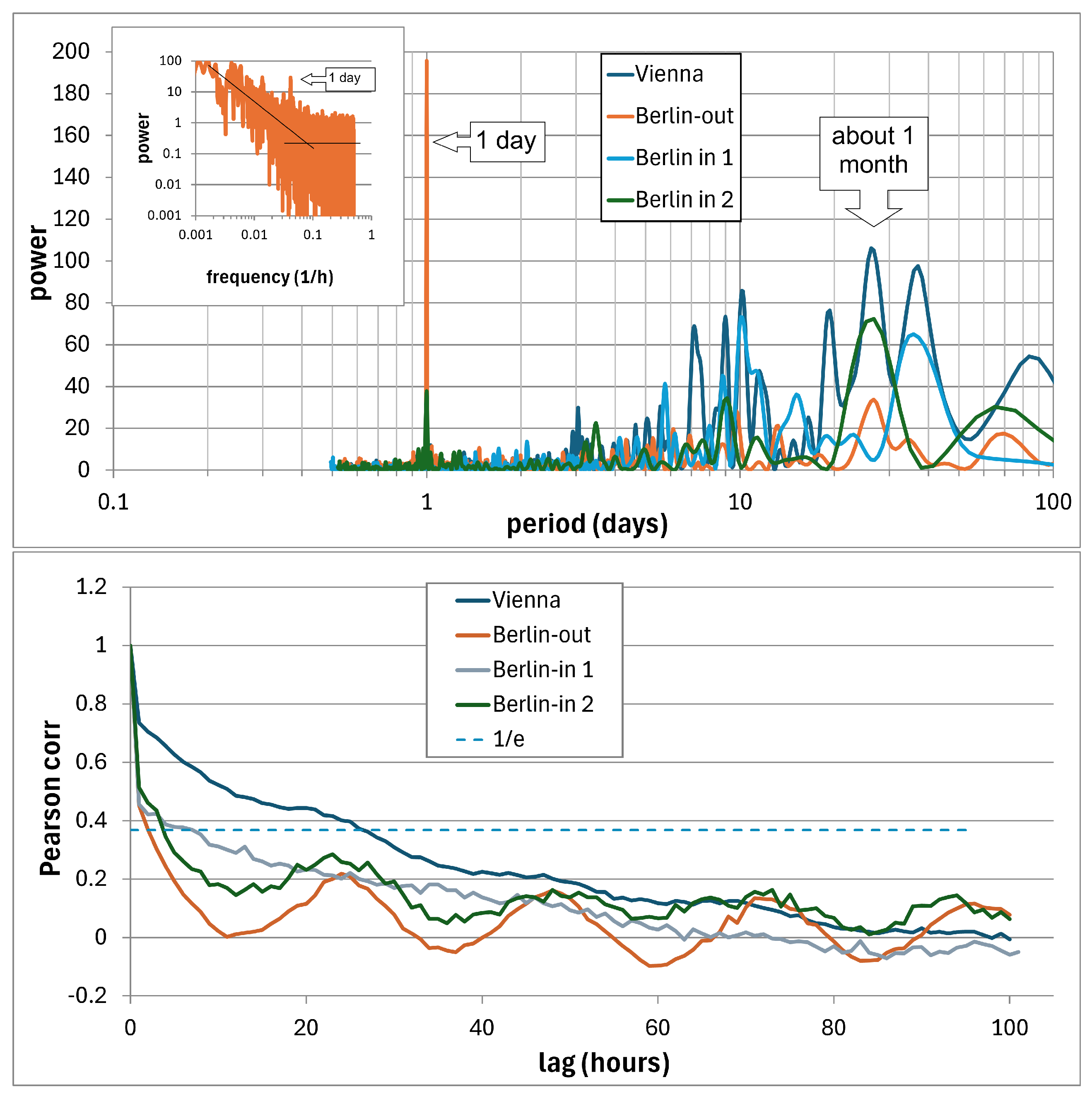
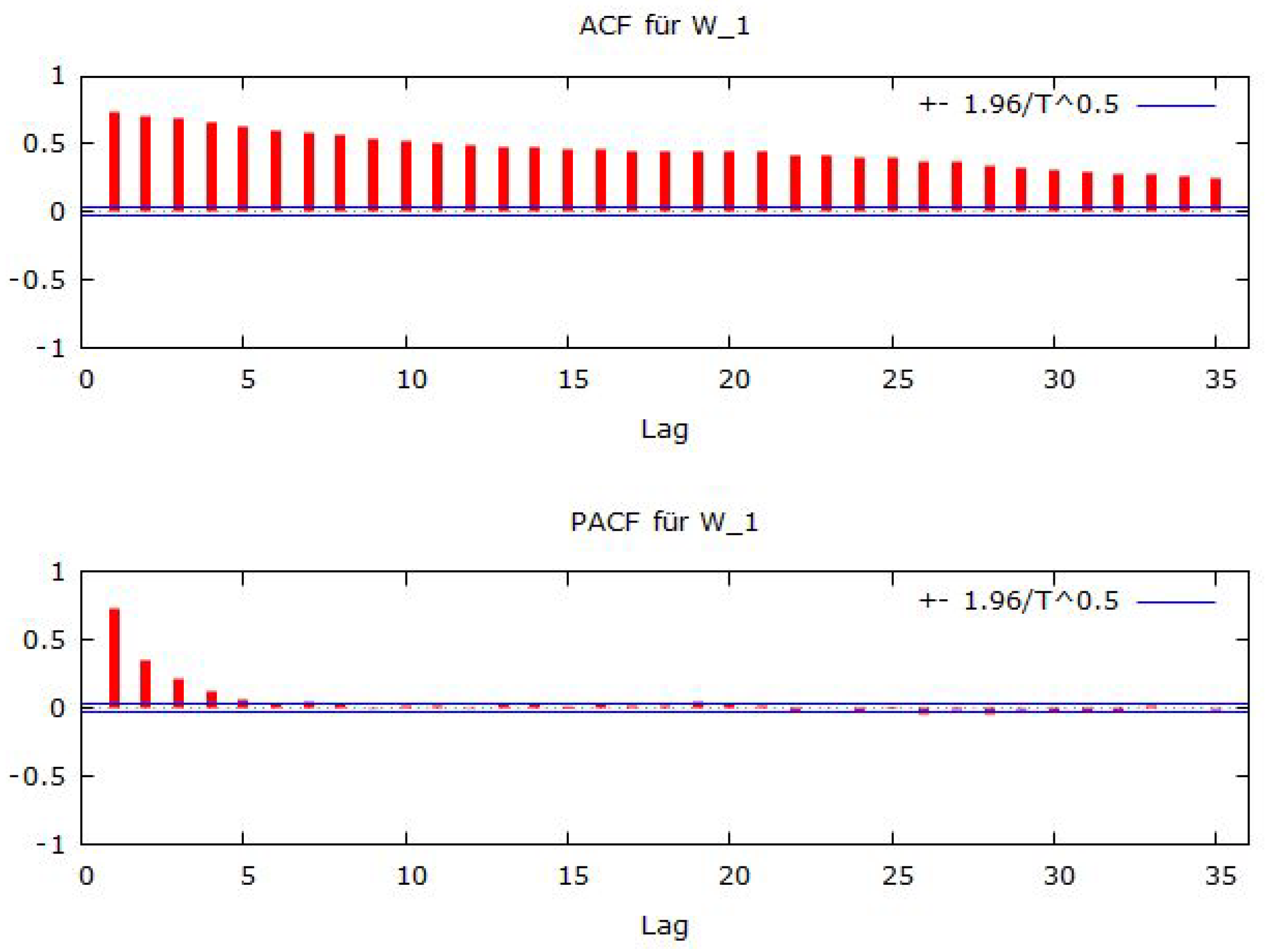
5.1.3. Periodicity and Autocorrelation
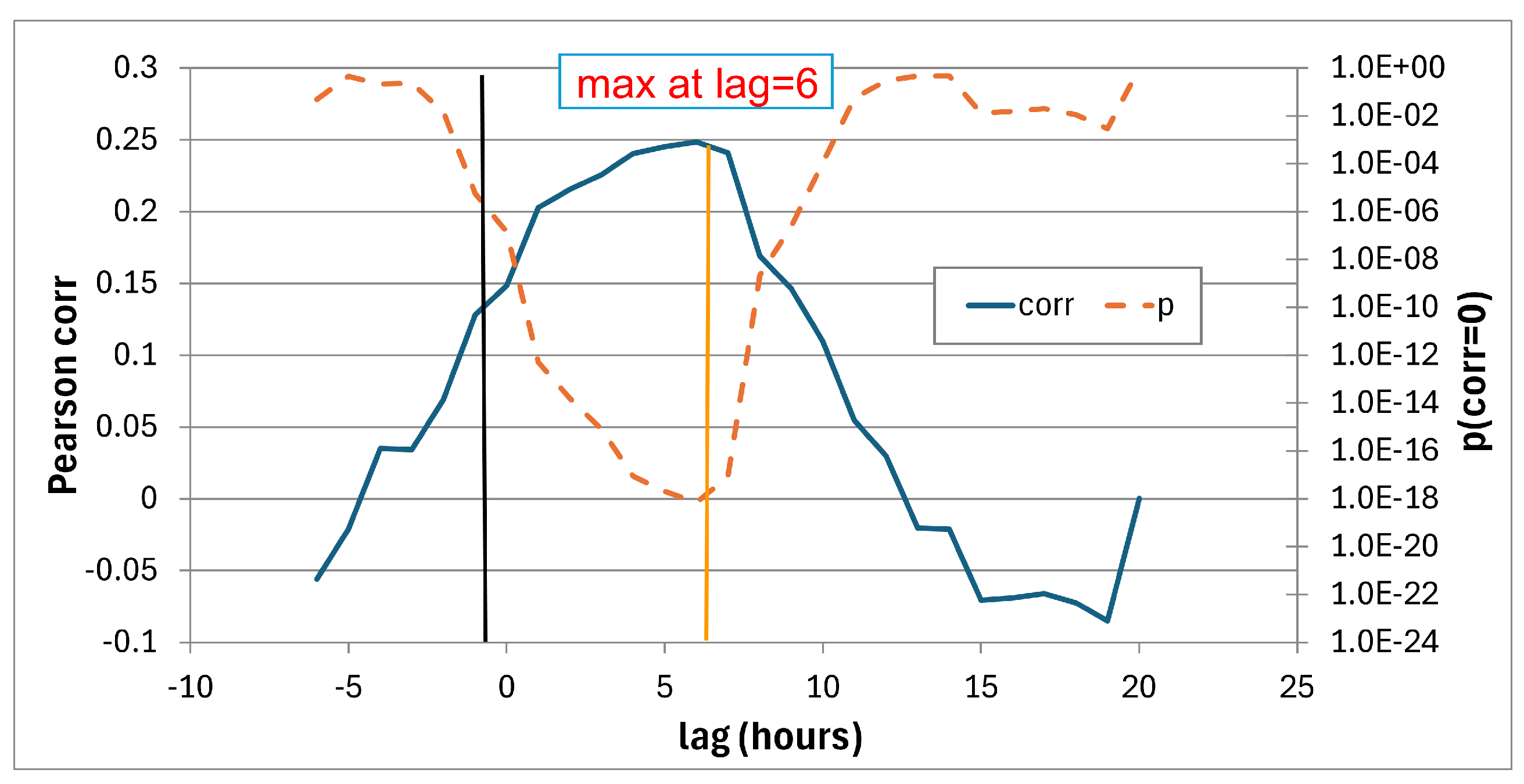
5.1.4. Cross-Correlation Indoor-Outdoor Radon
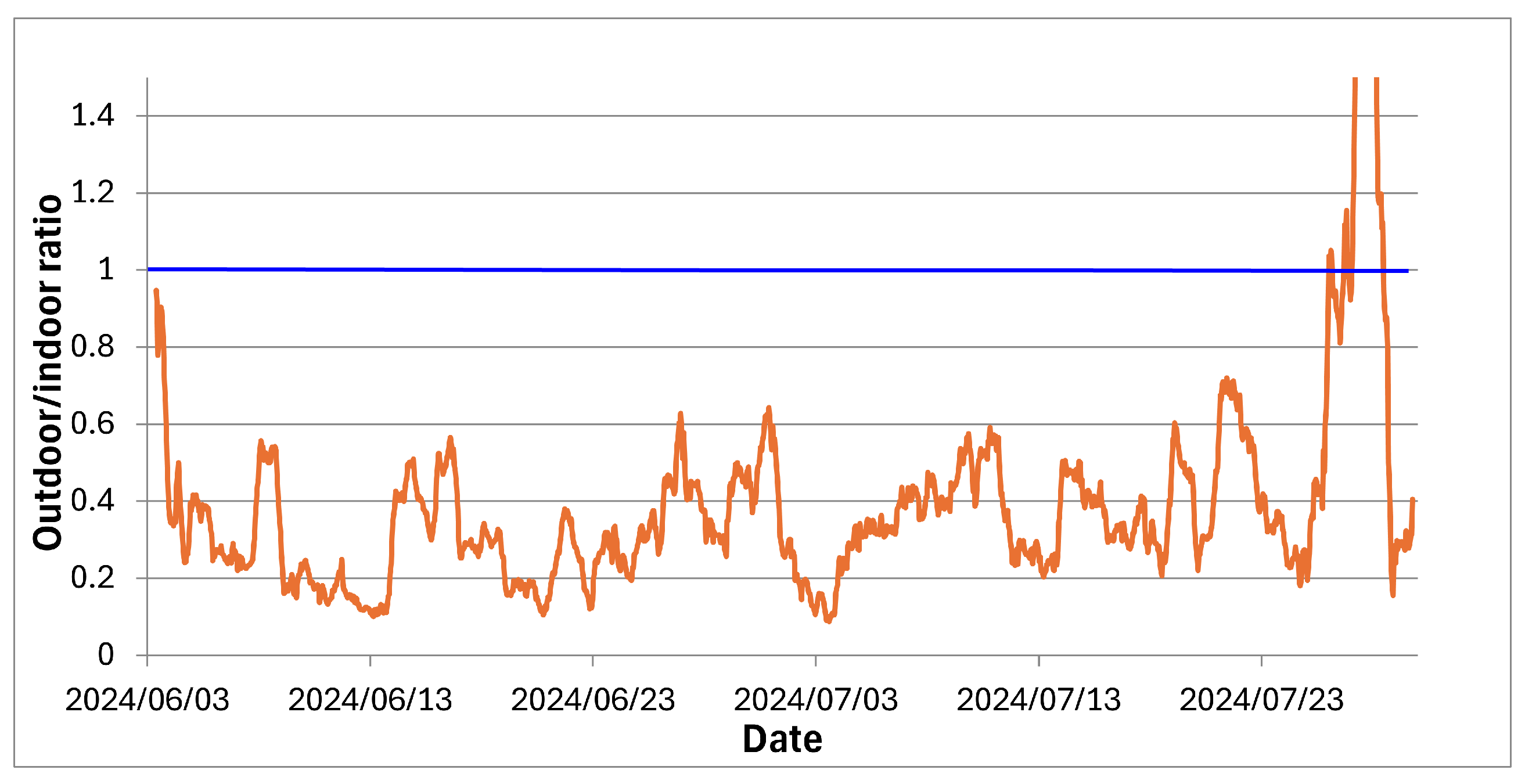
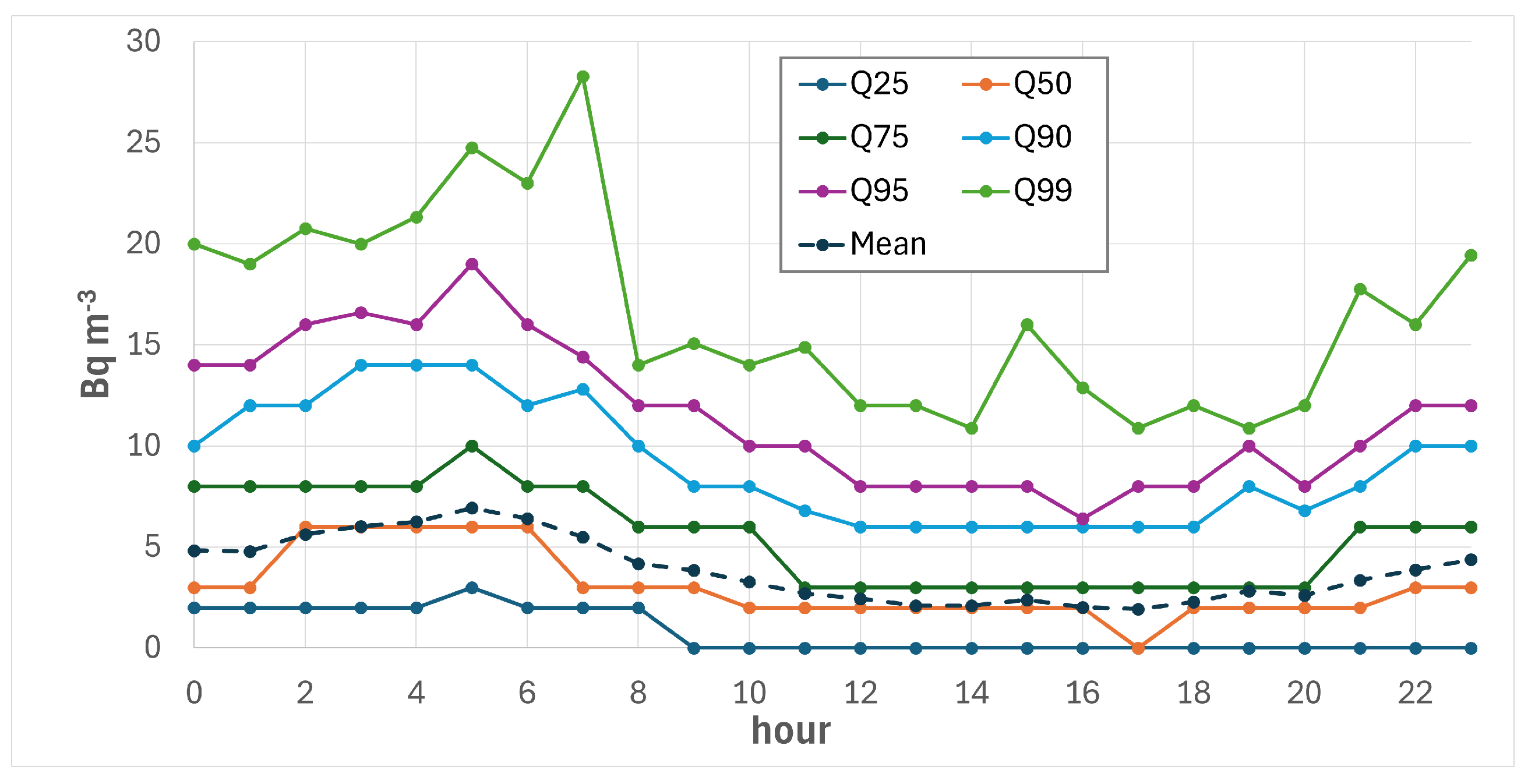
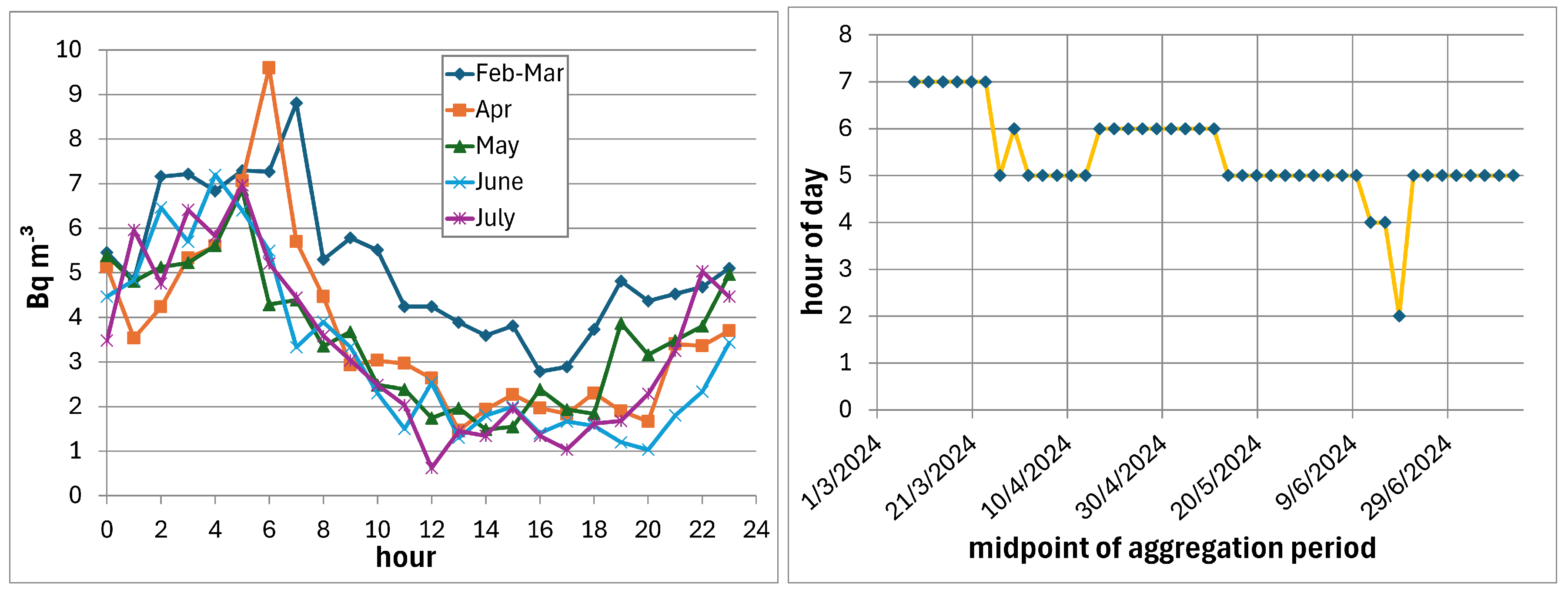
5.1.5. Outdoor Radon Diurnal Pattern
5.2. Autoregressive Modelling
5.2.1. Simple ARMA
5.2.2. Partial Autocorrelation
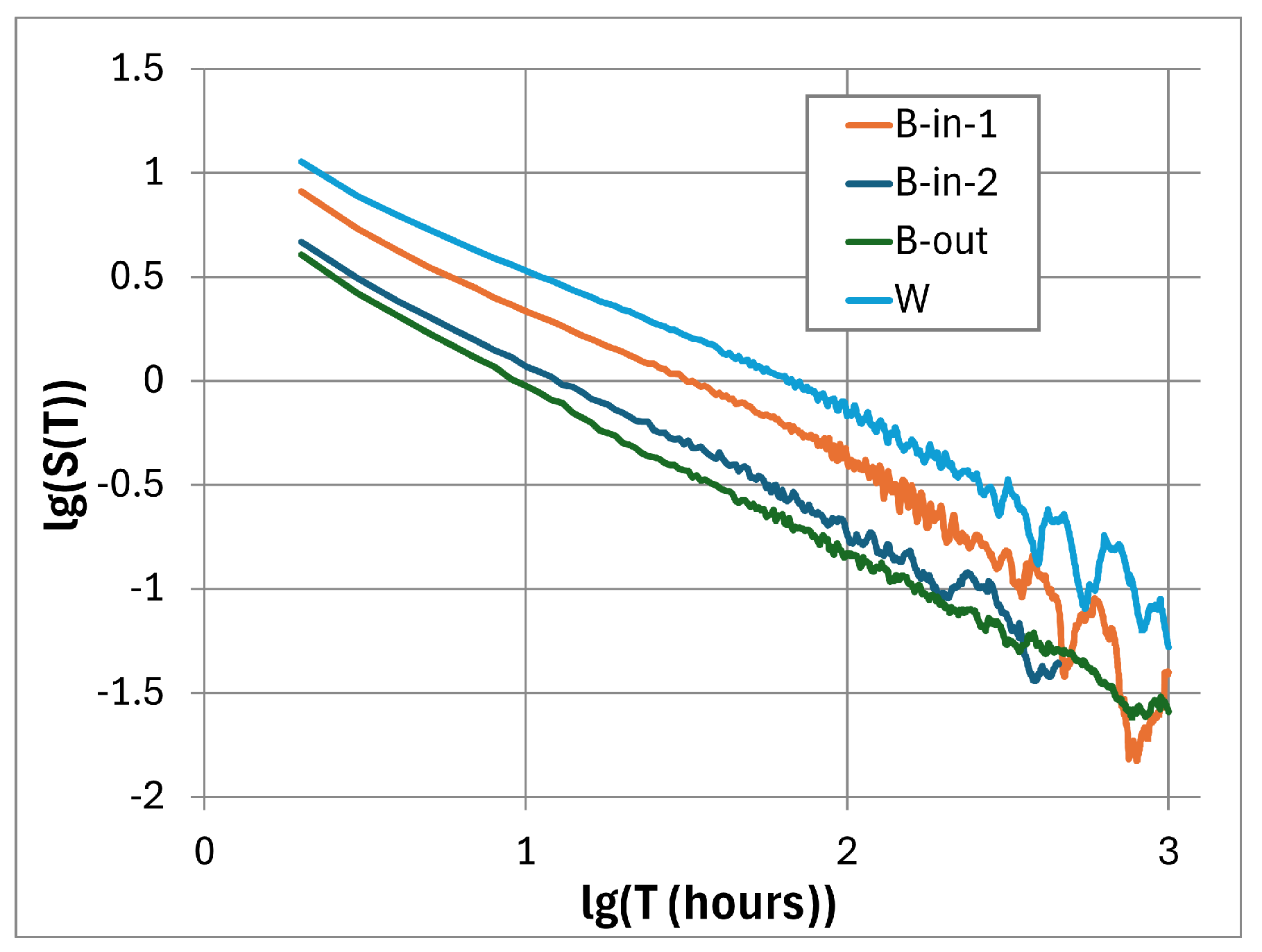
5.3. Fractal Analysis
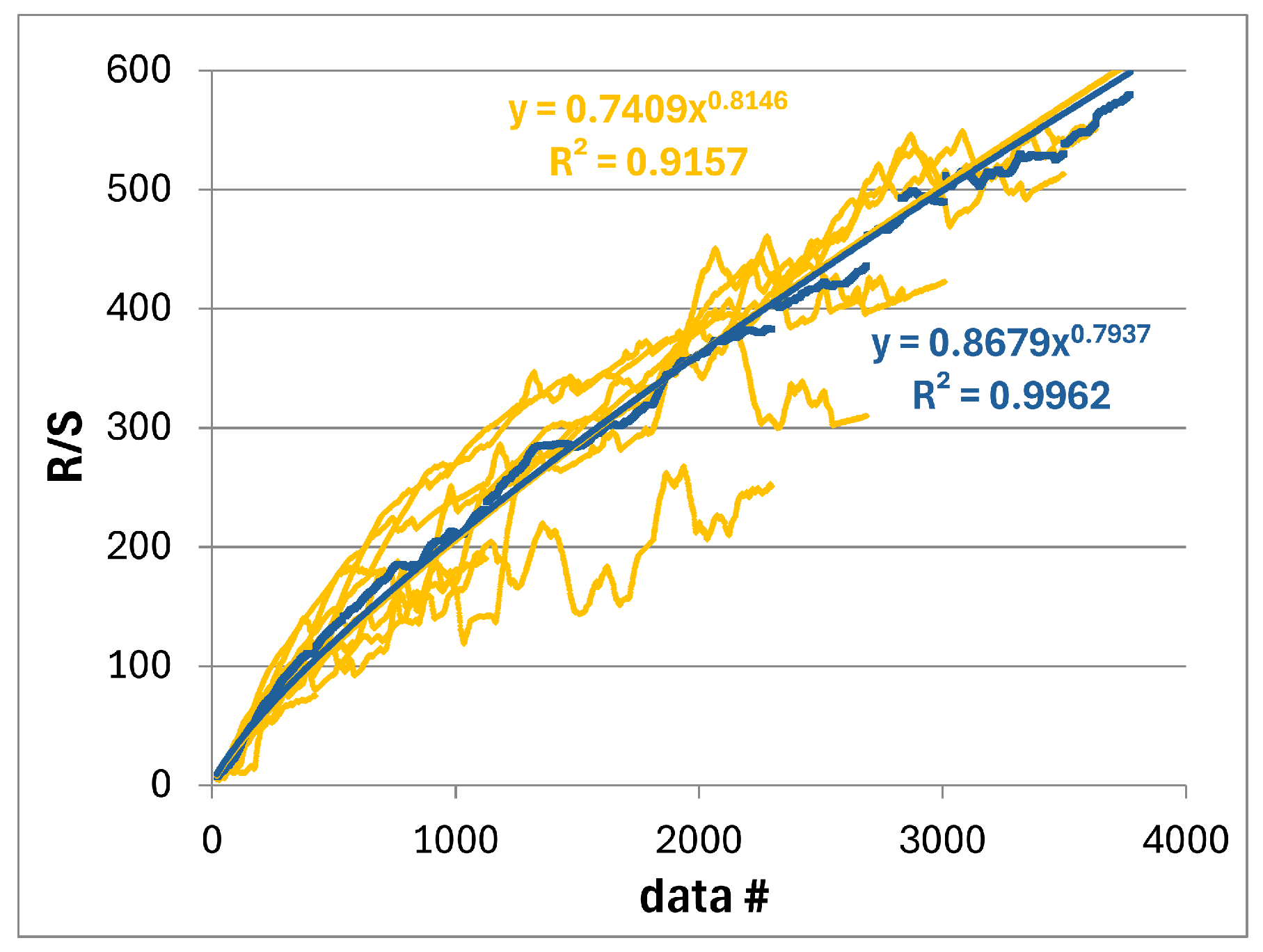
5.3.1. Hurst Exponent
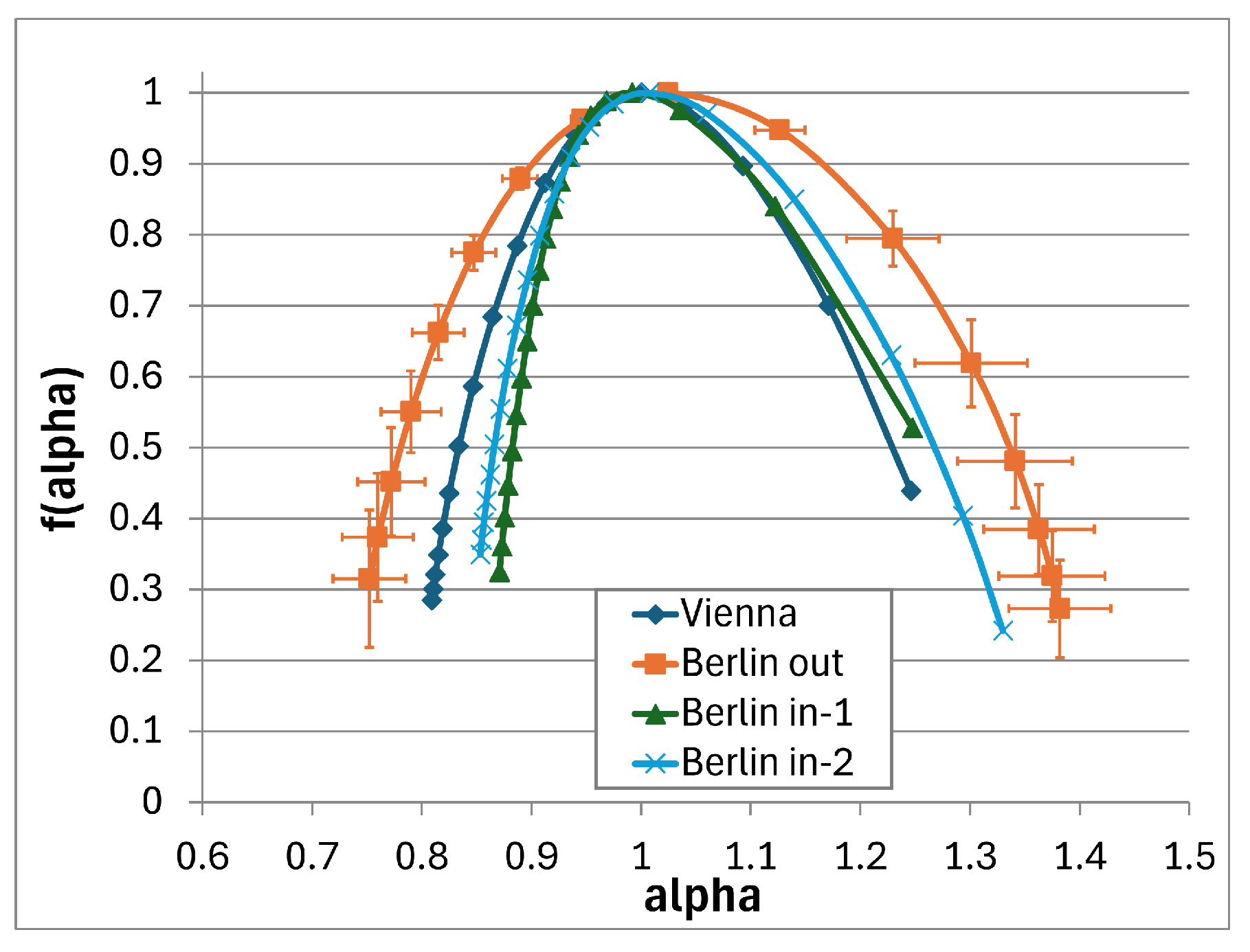
5.3.2. Multifractal Spectra
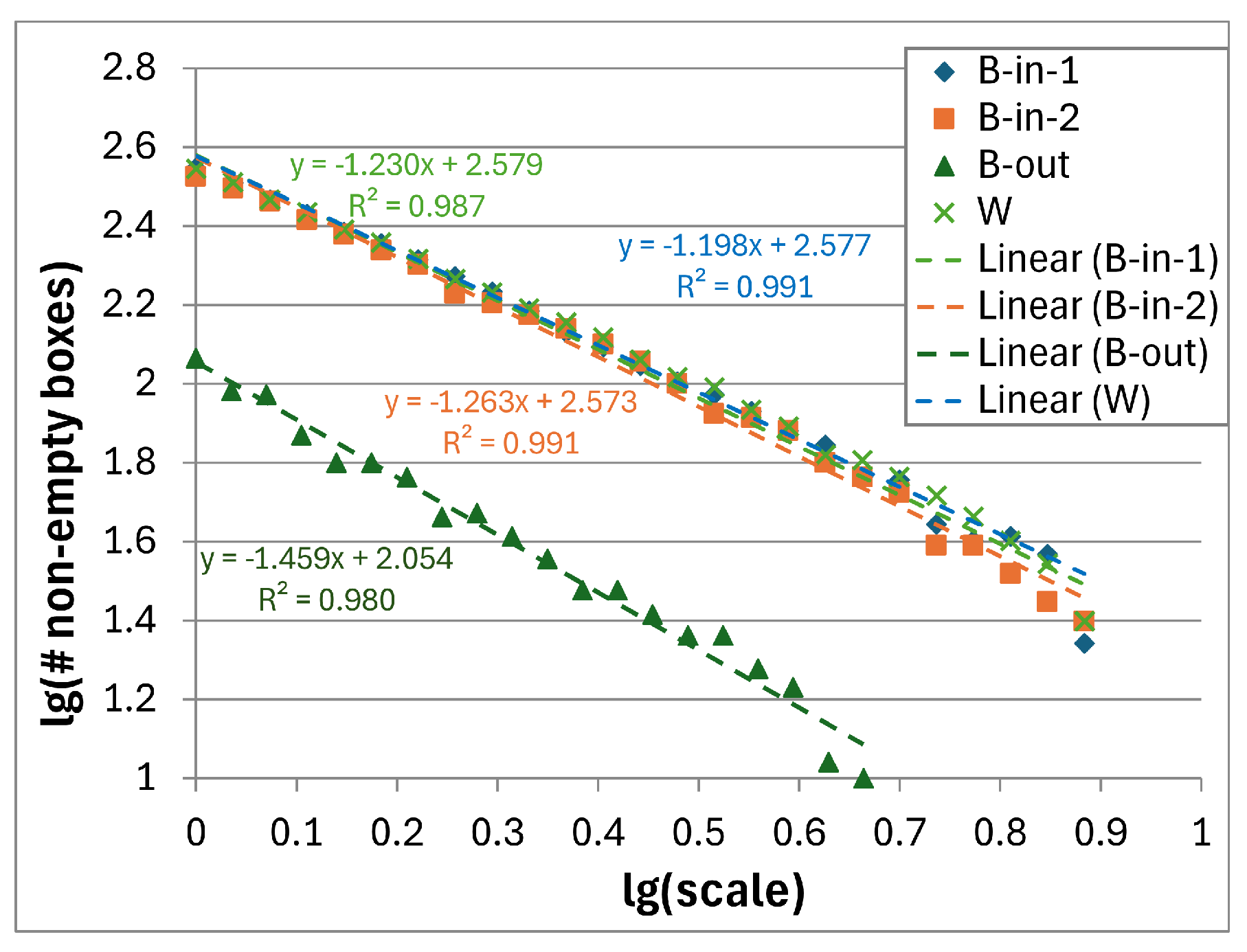
5.3.3. Graph Dimension
5.3.4. Garger Exponent
5.3.5. Attractor Embedding Dimension and Lyapunov Exponent
6. Conclusions
- Examine the relationship between recorded dynamics and their controlling physical environmental factors, particularly meteorological variability, with results intended for future publication.
- Refine the statistical methodology through ARFIMA (Autoregressive Fractionally Integrated Moving Average) analysis, leveraging the identified long-term memory structures; enhanced seasonal decomposition; application of detrended fluctuation analysis to reveal fractal structures; and development of techniques to identify chaotic patterns.
- Continue long-term measurements at the established locations to gain deeper insights into the temporal dynamics of radon concentrations and potential patterns that may emerge from extended datasets.
Supplemental Remark after Analysis Deadline
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization (WHO). WHO Handbook on Indoor Radon: A Public Health Perspective. Technical report, 2009. https://www.who.int/publications/i/item/9789241547673.
- European Commission (EC). Council Directive 2013/59/Euratom of laying down basic safety standards for protection against the dangers arising from exposure to ionising radiation, and repealing Directives 89/618/Euratom, 90/641/Euratom, 96/2, 2013. https://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=OJ:L:2014:013:0001:0073:EN:PDF. 5 December.
- Radulescu, I.; Calin, M.R.; Luca, A.; Röttger, A.; Grossi, C.; Done, L.; Ioan, M.R. Inter-comparison of commercial continuous radon monitors responses. Nuclear Instruments and Methods in Physics Research, Section A: Accelerators, Spectrometers, Detectors and Associated Equipment 2022, 1021, 165927. [Google Scholar] [CrossRef]
- Chambers, S.D.; Griffiths, A.D.; Williams, A.G.; Sisoutham, O.; Morosh, V.; Röttger, S.; Mertes, F.; Röttger, A. Portable two-filter dual-flow-loop 222Rn detector: stand-alone monitor and calibration transfer device. Advances in Geosciences 2022, 57, 63–80. [Google Scholar] [CrossRef]
- Beck, T.R.; Foerster, E.; Biel, M.; Feige, S. Measurement Performance of Electronic Radon Monitors. Atmosphere 2024, 15, 1180. [Google Scholar] [CrossRef]
- Mitev, K.; Georgiev, S.; Dimitrova, I.; Todorov, V.; Popova, A.; Dutsov, C.; Sabot, B. Recent work with electronic radon detectors for continuous Radon-222 monitoring. Journal of the European Radon Association. [CrossRef]
- Daraktchieva, Z.; Howarth, C.B.; Wasikiewicz, J.M.; Miller, C.A.; Wright, D.A. Long-term comparison and performance study of consumer grade electronic radon integrating monitors. Journal of Radiological Protection 2024, 44. [Google Scholar] [CrossRef] [PubMed]
- Dimitrova, I.; Georgiev, S.; Mitev, K.; Todorov, V.; Dutsov, C.; Sabot, B. Study of the performance and time response of the RadonEye Plus2 continuous radon monitor. Measurement: Journal of the International Measurement Confederation 2023, 207, 112409. [Google Scholar] [CrossRef]
- Dimitrova, I.; Georgiev, S.; Todorov, V.; Daraktchieva, Z.; Howarth, C.B.; Wasikiewicz, J.M.; Sabot, B.; Mitev, K. Calibration and metrological test of the RadonEye Plus2 electronic monitor. Radiation Measurements 2024, 175, 107169. [Google Scholar] [CrossRef]
- Rábago, D.; Fernández, E.; Celaya, S.; Fuente, I.; Fernández, A.; Quindós, J.; Rodriguez, R.; Quindós, L.; Sainz, C. Investigation of the Performance of Various Low-Cost Radon Monitors under Variable Environmental Conditions. Sensors 2024, 24. [Google Scholar] [CrossRef]
- Carmona, M.A.; Kearfott, K.J. Intercomparison of Commercially Available Active Radon Measurement Devices in a Discovered Radon Chamber. Health Physics 2019, 116, 852–861. [Google Scholar] [CrossRef]
- Bahadori, A.; Hanson, B. Evaluation of consumer digital radon measurement devices: a comparative analysis. Journal of Radiological Protection 2024, 44. [Google Scholar] [CrossRef]
- Cinelli, G.; De Cort, M.; Tollefsen, T. ; (Eds.). European Atlas of Natural Radiation; Publication Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Wilkening, M. Radon in the Environment; Elsevier, 1990. https://shop.elsevier.com/books/radon-in-the-environment/wilkening/978-0-444-88163-2.
- Baskaran, M. Radon: A Tracer for Geological, Geophysical and Geochemical Studies; Springer International Publishing: Cham, 2016. [Google Scholar] [CrossRef]
- Polian, G.; Lambert, G.; Ardouin, B.; Jegou, A. Long-range transport of continental radon in Subantarctic and Antarctic areas. Tellus 1986, 38 B, 178–189. [Google Scholar] [CrossRef]
- Whittlestone, S.; Zahorowski, W. Baseline radon detectors for shipboard use: Development and deployment in the First Aerosol Characterization Experiment (ACE 1). Journal of Geophysical Research: Atmospheres 1998, 103, 16743–16751. [Google Scholar] [CrossRef]
- Levin, I.; Born, M.; Cuntz, M.; Langendörfer, U.; Mantsch, S.; Naegler, T.; Schmidt, M.; Varlagin, A.; Verclas, S.; Wagenbach, D. Observations of atmospheric variability and soil exhalation rate of radon-222 at a Russian forest site: Technical approach and deployment for boundary layer studies. Tellus, Ser. B Chem. Phys. Meteorol. 2002, 54, 462–475. [Google Scholar] [CrossRef]
- Evangelista, H.; Pereira, E.B. Radon flux at King George Island, Antarctic Peninsula. Journal of Environmental Radioactivity 2002, 61, 283–304. [Google Scholar] [CrossRef] [PubMed]
- Wada, A.; Murayama, S.; Kondo, H.; Matsueda, H.; Sawa, Y.; Tsuboi, K. Development of a compact and sensitive electrostatic radon-222 measuring system for use in atmospheric observation. Journal of the Meteorological Society of Japan 2010, 88, 123–134. [Google Scholar] [CrossRef]
- Grossi, C.; Vargas, A.; Camacho, A.; López-Coto, I.; Bolívar, J.P.; Xia, Y.; Conen, F. Inter-comparison of different direct and indirect methods to determine radon flux from soil. Radiat. Meas. 2011, 46, 112–118. [Google Scholar] [CrossRef]
- Schmithüsen, D.; Chambers, S.; Fischer, B.; Gilge, S.; Hatakka, J.; Kazan, V.; Neubert, R.; Paatero, J.; Ramonet, M.; Schlosser, C.; et al. A European-wide 222radon and 222radon progeny comparison study. Atmos. Meas. Tech. 2017, 10, 1299–1312. [Google Scholar] [CrossRef]
- Wilkening, M.H.; Clements, W.E. Radon 222 from the ocean surface. Journal of Geophysical Research 1975, 80, 3828–3830. [Google Scholar] [CrossRef]
- Duenas, C.; Fernandez, M.C.; Martinez, M.P. Radon 222 from the ocean surface. Journal of Geophysical Research: Oceans 1983, 88, 8613–8616. [Google Scholar] [CrossRef]
- Fujiyoshi, R.; Sakamoto, K.; Imanishi, T.; Sumiyoshi, T.; Sawamura, S.; Vaupotic, J.; Kobal, I. Meteorological parameters contributing to variability in 222Rn activity concentrations in soil gas at a site in Sapporo, Japan. Sci. Total Environ. 2006, 370, 224–234. [Google Scholar] [CrossRef]
- Fujiyoshi, R.; Haraki, Y.; Sumiyoshi, T.; Amano, H.; Kobal, I.; Vaupotič, J. Tracing the sources of gaseous components (222Rn, CO2 and its carbon isotopes) in soil air under a cool-deciduous stand in Sapporo, Japan. Environmental geochemistry and health 2010, 32, 73–82. [Google Scholar] [CrossRef]
- Fujiyoshi, R.; Okabayashi, M.; Sakuta, Y.; Okamoto, K.; Sumiyoshi, T.; Kobal, I.; Vaupotič, J. Soil radon in winter months under snowpack in Hokkaido, Japan. Environmental Earth Sciences 2013, 70, 1159–1167. [Google Scholar] [CrossRef]
- Williams, A.G.; Zahorowski, W.; Chambers, S.; Griffiths, A.; Hacker, J.M.; Element, A.; Werczynski, S. The vertical distribution of radon in clear and cloudy daytime terrestrial boundary layers. Journal of the Atmospheric Sciences 2011, 68, 155–174. [Google Scholar] [CrossRef]
- Chambers, S.D.; Zahorowski, W.; Williams, A.G.; Crawford, J.; Griffiths, A.D. Identifying tropospheric baseline air masses at mauna loa observatory between 2004 and 2010 using radon-222 and back trajectories. Journal of Geophysical Research Atmospheres 2013, 118, 992–1004. [Google Scholar] [CrossRef]
- FTLAB Corp.. FTLAB Corp. http://radonftlab.com/.
- Di Carlo, C.; Ampollini, M.; Antignani, S.; Caprio, M.; Carpentieri, C.; Bochicchio, F. Thoron Interference on Performance of Continuous Radon Monitors: An Experimental Study on Four Devices and a Proposal of an Indirect Method to Estimate Thoron Concentration. International Journal of Environmental Research and Public Health 2022, 19. [Google Scholar] [CrossRef] [PubMed]
- Magistrat der Stadt Wien. Wien geo-map. https://www.wien.gv.at/verkehr/grundbau/images/geo-karte.jpg.
- Senatsverwaltung für Stadtentwicklung Bauen und Wohnen Berlin. Berlin geo-map. Available online: https://fbinter.stadt-berlin.de/fb/index.jsp?loginkey=showMap&mapId=k_inggeo@senstadt.
- Kümmel, M.; Dushe, C.; Müller, S.; Gehrcke, K. Outdoor 222Rn-concentrations in Germany - part 1 - natural background. Journal of Environmental Radioactivity 2014, 132, 123–130. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time series analysis: forecasting and control; John Wiley & Sons, 2015.
- Hoang, T.D.N. The Box-Jenkins Methodology for Time Series Models. SAS Global Forum 2013 2013, 6, 454–2013. [Google Scholar]
- NIST. NIST/SEMATECH e-Handbook of Statistical Methods, http://www.itl.nist.gov/div898/handbook/, 2012. [CrossRef]
- Bowers, M.C.; wen Tung, W. Variability and confidence intervals for the mean of climate data with short- and long-range dependence. Journal of Climate 2018, 31, 6135–6156. [Google Scholar] [CrossRef]
- Siino, M.; Scudero, S.; D’Alessandro, A. Stochastic Models for Radon Daily Time Series: Seasonality, Stationarity, and Long-Range Dependence Detection. Frontiers in Earth Science 2020, 8, 1–13. [Google Scholar] [CrossRef]
- Stránský, V.; Thinová, L. Radon concentration time series modeling and application discussion. Radiation Protection Dosimetry 2017, 177, 155–159. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series With a Unit Root. Journal of the American Statistical Association 1979, 74, 427. [Google Scholar] [CrossRef]
- Cottrell, A.; Lucchetti, R. Gretl User Guide. Gnu Regression, Econometrics and Time-series Library, /: 1–465. http.
- Robinson, P.M. Long-Memory Models. [CrossRef]
- Graves, T.; Gramacy, R.; Watkins, N.; Franzke, C. A brief history of long memory: Hurst, Mandelbrot and the road to ARFIMA, 1951-1980. Entropy 2017, 19, 1–21. [Google Scholar] [CrossRef]
- TAQQU, M.S.; TEVEROVSKY, V.; WILLINGER, W. ESTIMATORS FOR LONG-RANGE DEPENDENCE: AN EMPIRICAL STUDY. Fractals 1995, 03, 785–798. [Google Scholar] [CrossRef]
- Cuculeanu, V.; Pavalescu, M. Fractal analysis of the environmental radioactivity: A review. Annals of the Academy of Romanian Scientists Series on Physics and Chemistry 2019, 4, 45–84. [Google Scholar]
- Fuss, F.K.; Weizman, Y.; Tan, A.M. The non-linear relationship between randomness and scaling properties such as fractal dimensions and Hurst exponent in distributed signals. Communications in Nonlinear Science and Numerical Simulation 2021, 96, 105683. [Google Scholar] [CrossRef]
- Donner, R.V.; Potirakis, S.M.; Barbosa, S.M.; Matos, J.A.; Pereira, A.J.; Neves, L.J. Intrinsic vs. spurious long-range memory in high-frequency records of environmental radioactivity: Critical re-assessment and application to indoor 222Rn concentrations from Coimbra, Portugal. European Physical Journal: Special Topics 2015, 224, 741–762. [Google Scholar] [CrossRef]
- Chhabra, A.; Jensen, R.V. Direct determination of the f(α) singularity spectrum. Physical Review Letters 1989, 62, 1327–1330. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Physical Review A 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press, 1997. [CrossRef]
- Bossew, P. Multiplicative cascades as generators of log-normal fields; Case study: Environmental Radon. GeoENV-24, Chania, Greece, 19.-21.6.2024. In Proceedings of the geoENV2024 Book of Abstracts, 2024. [Google Scholar]
- Garger, E.; Kashpur, V.; Gurgula, B.; Paretzke, H.; Tschiersch, J. Statistical characteristics of the activity concentration in the surface layer of the atmosphere in the 30 km zone of Chernobyl. Journal of Aerosol Science 1994, 25, 767–777. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N. Fractal fluctuation of aerosol concentration near Chernobyl. Atmospheric Environment 1997, 31, 2297–2303. [Google Scholar] [CrossRef]
- Hatano, Y.; Hatano, N.; Amano, H.; Ueno, T.; Sukhoruchkin, A.K.; Kazakov, S.V. Aerosol migration near Chernobyl: Long-term data and modeling. Atmospheric Environment 1998, 32, 2587–2594. [Google Scholar] [CrossRef]
- Bossew, P.; Lettner, H. Statistische Analyse con Radondaten. (Statistical analysis of radon data; In German). Part of the project "Detailed statistical analysis of ÖNRAP data.". Technical report, BfS, 2002.
- Grassberger, P.; Procaccia, I. Measuring the strangeness of strange attractors. Physica D: Nonlinear Phenomena 1983, 9, 189–208. [Google Scholar] [CrossRef]
- Kodba, S.; Perc, M.; Marhl, M. Detecting chaos from a time series. European Journal of Physics 2005, 26, 205–215. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D. Fundamental limitations for estimating dimensions and Lyapunov exponents in dynamical systems. Physica D: Nonlinear Phenomena 1992, 56, 185–187. [Google Scholar] [CrossRef]
- Narzo, A.F. tseriesChaos: Analysis of Nonlinear Time Series, 2019. URL https://CRAN. R-project. org/package= tseriesChaos. R package version 0.1-13.1.[p 233].
- Garcia, C.A. nonlinearTseries: Nonlinear Time Series Analysis, 2024. https://constantino-garcia.r-universe.dev/nonlinearTseries.
- Hegger, R.; Kantz, H.; Schreiber, T. Practical implementation of nonlinear time series methods: The TISEAN package. Chaos 1999, 9, 413–435. [Google Scholar] [CrossRef]
- Shafique, B.; Kearfott, K.J.; Tareen, A.D.K.; Rafique, M.; Aziz, W.; Naeem, S.F. Time series analysis and risk assessment of domestic radon: Data collected in dwellings along fault lines. Indoor and Built Environment 2016, 25, 397–406. [Google Scholar] [CrossRef]
- Hammer. ; Harper, D.a.T.; Ryan, P.D. PAST: Paleontological Statistics Software Package for Education and Data Analysis. Palaeontologia Electronica 2001, arXiv:1011.1669v3]4(1), 1–9. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos data analyzer (professional version). Physics Academic Software.
- Smith, C.; Williams, S. QB64 (https://qb64.com/), 2024.
- Currie, L.A. Limits for Qualitative Detection and Quantitative Determination: Application to Radiochemistry. Analytical Chemistry 1968, 40, 586–593. [Google Scholar] [CrossRef]
- Currie, L.A. Lower Limit of Detection : Definition andi Elaboration of a Proposed Position for Radiological EHluent and Environmental Measurements (NUREG/CR-4007). US Nuclear Regulatory Commission 1984. [Google Scholar]
- IAEA/AQ/48. Determination and interpretation of characteristic limits for radioactivity measurements: Decision threshold, detection limit and limits of the confidence interval. Technical report, 2017. Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/AQ-48_web.pdf.
- Bruggeman, M. Implementing ISO11929 at our laboratories, 2020. Available online: http://www.lnhb.fr/pdf/ICRM_GSWG/2020/05.ISO11929_how_to_solve-M.Bruggeman.pdf.
- Kirkpatrick, J.M.; Venkataraman, R.; Young, B.M. Minimum detectable activity, systematic uncertainties, and the ISO 11929 standard. Journal of Radioanalytical and Nuclear Chemistry 2013, 296, 1005–1010. [Google Scholar] [CrossRef]
- Patil, V.V.; Kulkarni, H.V. Comparison of confidence intervals for the Poisson mean: Some new aspects. REVSTAT-Statistical Journal 2012, 10, 211–227. [Google Scholar] [CrossRef]
- Fink, D. A Compendium of Conjugate Priors. Technical report, Montana State Univeristy, Bozeman, 1997. Available online: https://www.johndcook.com/CompendiumOfConjugatePriors.pdf.
- Kikaj, D.; Vaupotič, J.; Chambers, S.D. Identifying persistent temperature inversion events in a subalpine basin using radon-222. Atmospheric Measurement Techniques 2019, 12, 4455–4477. [Google Scholar] [CrossRef]
- TraceRadon. EMPIR / 19ENV01 traceRadon (2023): Deliverable D7, Summary report on methodology for the characterization of RPA including outdoor radon and radon flux data. (D7 not available publicly). Technical report, EMPIR, 2023. http://traceradon-empir.eu/.
- Chambers, S.; Williams, A.G.; Zahorowski, W.; Griffiths, A.; Crawford, J. Separating remote fetch and local mixing influences on vertical radon measurements in the lower atmosphere. Tellus, Series B: Chemical and Physical Meteorology 2011, 63, 843–859. [Google Scholar] [CrossRef]
- Chambers, S.D.; Williams, A.G.; Crawford, J.; Griffiths, A.D. On the use of radon for quantifying the effects of atmospheric stability on urban emissions. Atmospheric Chemistry and Physics 2015, 15, 1175–1190. [Google Scholar] [CrossRef]
- Kikaj, D.; Chambers, S.D.; Kobal, M.; Crawford, J.; Vaupotič, J. Characterizing atmospheric controls on winter urban pollution in a topographic basin setting using Radon-222. Atmospheric Research 2020, 237. [Google Scholar] [CrossRef]
- Inoue, H.Y.; Zhu, C. Ecosystem respiration derived from 222Rn measurements on Rishiri Island, Japan. Biogeochemistry 2013, 115, 185–194. [Google Scholar] [CrossRef]
- Zimnoch, M.; Wach, P.; Chmura, L.; Gorczyca, Z.; Rozanski, K.; Godlowska, J.; Mazur, J.; Kozak, K.; Jericevi, A. Factors controlling temporal variability of near-ground atmospheric 222Rn concentration over central Europe. Atmospheric Chemistry and Physics 2014, 14, 9567–9581. [Google Scholar] [CrossRef]
- Pal, S.; Lopez, M.; Schmidt, M.; Ramonet, M.; Gibert, F.; Xueref-Remy, I.; Ciais, P. Investigation of the atmospheric boundary layer depth variability and its impact on the 222 Rn concentration at a rural site in France. Journal of Geophysical Research: Atmospheres 2015, 120, 623–643. [Google Scholar] [CrossRef]
- Kikaj, D.; Chambers, S.D.; Crawford, J.; Kobal, M.; Gregorič, A.; Vaupotič, J. Investigating the vertical and spatial extent of radon-based classification of the atmospheric mixing state and impacts on seasonal urban air quality. Science of the Total Environment 2023, 872. [Google Scholar] [CrossRef]
- Albarello, D.; Lapenna, V.; Martinelli, G.; Telesca, L. Extracting quantitative dynamics from 222Rn gaseous emissions of mud volcanoes. Environmetrics 2003, 14, 63–71. [Google Scholar] [CrossRef]
- Cuculeanu, V.; Lupu, A.; Sütö, E. Fractal dimensions of the outdoor radon isotopes time series. Environment International 1996, 22, 171–179. [Google Scholar] [CrossRef]
- Bejar, J.; Facchini, U.; Giroletti, E.; Magnoni, S. Low dimensional chaos is present in radon time variations. Journal of Environmental Radioactivity 1995, 28, 73–89. [Google Scholar] [CrossRef]
- Pacheco, P.; Ulloa, H.; Mera, E. Application of Chaos Theory to Time-Series Urban Measurements of Meteorological Variables and Radon Concentration: Analysis and Interpretation. Atmosphere 2022, 13. [Google Scholar] [CrossRef]
- LI, Y.; TAN, W.; TAN, K.; LIU, Z.; XIE, Y. Fractal and chaos analysis for dynamics of radon exhalation from uranium mill tailings. Fractals 2016, 24, 1650029. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Panayiotis, H.; Ermioni, P.; Matsoukas, C.; Demetrios, C.; Constantinos, N. Long-Memory and Fractal Trends in Variations of Environmental Radon in Soil: Results from Measurements in Lesvos Island in Greece. Journal of Earth Science and Climatic Change 2018, 09. [Google Scholar] [CrossRef]
- Planinić, J.; Vuković, B.; Radolić, V. Radon time variations and deterministic chaos. Journal of Environmental Radioactivity 2004, 75, 35–45. [Google Scholar] [CrossRef]
- Borchers, H.W. pracma: Practical Numerical Math Functions, 2023. https://cran.r-project.org/package=pracma.
- Weron, R. Estimating long range dependence: finite sample properties and confidence intervals. Physica A: Statistical Mechanics and its Applications 2002, 312, 285–299. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Kamphorst, S.O.; Ruelle, D.; Ciliberto, S. Liapunov exponents from time series. Physical Review A 1986, 34, 4971–4979. [Google Scholar] [CrossRef]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Physica D: Nonlinear Phenomena 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Sandubete, J.E.; Escot, L. DChaos: Chaotic Time Series Analysis, 2023. Available online: https://cran.r-project.org/package=DChaos.
- Strunk, G. GChaos 2012, 2012. Available online: https://www.complexity-research.com/GChaos.htm.
- Glushkov, A.V.; Yu Khetselius, O.; Buyadzhi, V.; Dubrovskaya, Y.V.; Serga, I.N.; Agayar, E.V.; Ternovsky, V.B. Nonlinear chaos-dynamical approach to analysis of atmospheric radon 222Rn concentration time series. Indian Academy of Sciences – Conference Series 2017, 1, 61–66. [Google Scholar] [CrossRef]


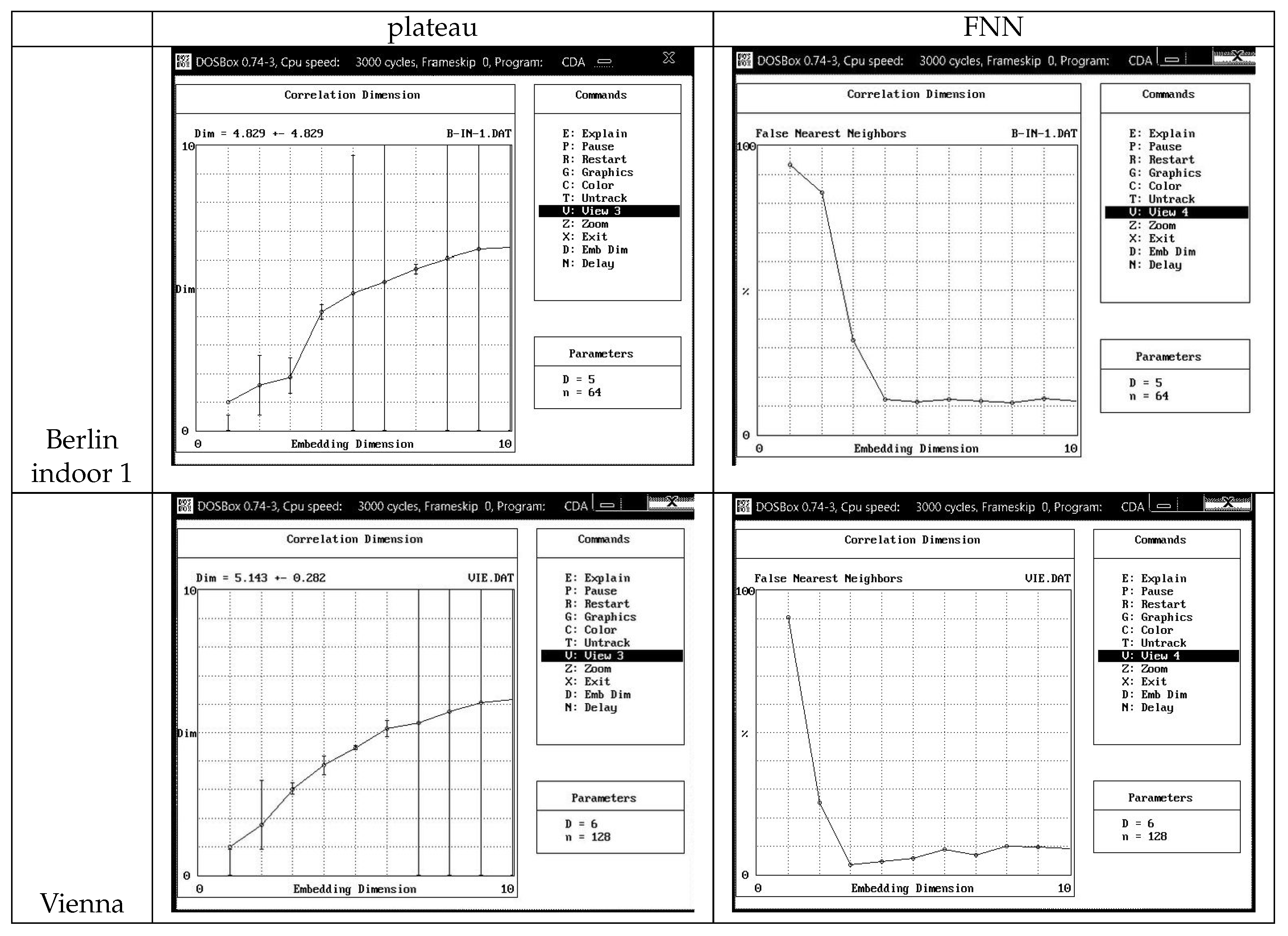
| plateau | FNN | |
| Berlin indoor 1 |
||
| Vienna |
| Berlin |
| indoor 1 |
| C(true)= → | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| = → | 0.405 | 0.81 | 1.215 | 1.62 | 2.025 | 2.43 | 2.835 | 3.24 | 3.645 | ||
| k= ↓ | C(reg)=↓ | C(rep)=↓ | p(k)= | ||||||||
| 0 | 0 | 0 | 0.667 | 0.445 | 0.297 | 0.198 | 0.132 | 0.088 | 0.059 | 0.039 | 0.026 |
| 1 | 1.234 | 1 | 0.27 | 0.36 | 0.361 | 0.321 | 0.267 | 0.214 | 0.166 | 0.127 | 0.095 |
| 2 | 2.469 | 2 | 0.055 | 0.146 | 0.219 | 0.26 | 0.271 | 0.26 | 0.236 | 0.206 | 0.174 |
| 3 | 3.704 | 4 | 0.007 | 0.039 | 0.089 | 0.14 | 0.183 | 0.211 | 0.223 | 0.222 | 0.211 |
| 4 | 4.938 | 5 | 7E-04 | 0.008 | 0.027 | 0.057 | 0.092 | 0.128 | 0.158 | 0.18 | 0.192 |
| 5 | 6.172 | 6 | 6E-05 | 0.001 | 0.007 | 0.018 | 0.037 | 0.062 | 0.09 | 0.117 | 0.14 |
| 6 | 7.407 | 7 | 4E-06 | 2E-04 | 0.001 | 0.005 | 0.013 | 0.025 | 0.042 | 0.063 | 0.085 |
| 7 | 8.642 | 9 | 2E-07 | 2E-05 | 2E-04 | 0.001 | 0.004 | 0.009 | 0.017 | 0.029 | 0.044 |
| 8 | 9.877 | 10 | 1E-08 | 2E-06 | 3E-05 | 2E-04 | 9E-04 | 0.003 | 0.006 | 0.012 | 0.02 |
| 9 | 11.11 | 11 | 5E-10 | 2E-07 | 5E-06 | 4E-05 | 2E-04 | 7E-04 | 0.002 | 0.004 | 0.008 |
| 10 | 12.35 | 12 | 2E-11 | 1E-08 | 6E-07 | 7E-06 | 4E-05 | 2E-04 | 5E-04 | 0.001 | 0.003 |
| 11 | 13.58 | 14 | 8E-13 | 1E-09 | 6E-08 | 1E-06 | 8E-06 | 4E-05 | 1E-04 | 4E-04 | 1E-03 |
| 12 | 14.82 | 15 | 3E-14 | 7E-11 | 6E-09 | 1E-07 | 1E-06 | 8E-06 | 3E-05 | 1E-04 | 3E-04 |
| 13 | 16.05 | 16 | 0 | 5E-12 | 6E-10 | 2E-08 | 2E-07 | 1E-06 | 7E-06 | 3E-05 | 8E-05 |
| 14 | 17.28 | 17 | 0 | 3E-13 | 5E-11 | 2E-09 | 3E-08 | 3E-07 | 1E-06 | 6E-06 | 2E-05 |
| 15 | 18.52 | 19 | 0 | 0 | 4E-12 | 2E-10 | 4E-09 | 4E-08 | 3E-07 | 1E-06 | 5E-06 |
| device id. | missing concentration values (Bq m) |
|---|---|
| GJ17RE000076 | 3, 6, 9, 12, 15, 18, 21, 24,... |
| RE22207111958 | 1, 3, 4, 5, 9, 11, 13, 15, 17, 18,... |
| HG04RE000641 | 3, 6 ,8, 11, 13,... |
| Vienna | Berlin-outdoor | Berlin-indoor 1 (winter) | Berlin-indoor 2 (summer) | |
|---|---|---|---|---|
| n | 3773 | 3768 | 2904 | 1365 |
| AM (Bq m) | 24 | 3.9 | 20.9 | 9.2 |
| SD (Bq m) | 12 | 4.7 | 9.5 | 5.3 |
| CV (%) | 51 | 123 | 46 | 58 |
| Min (Bq m) | 0 | 0 | 0 | 0 |
| Max (Bq m) | 85 | 60 (94) | 64 | 35 |
| Med (Bq m) | 22 | 2 | 20 | 9 |
| device # | GJ17RE000076 | RE22207111958 | RE22207111958 | HG04RE000641 |
| Vienna | Berlin outdoor | Berlin indoor 1 |
Berlin indoor 2 |
|
|---|---|---|---|---|
| Periods (d) | 1; 3.1; 26.2 | 1; 9.7; 13.2; 26.7 | 1; 5.8; 8.1; 10; 35.8 | 1; 3.5; 9.1; 26.7 |
| log-log slope | ≈ 0.9 | ≈ 0.4 | ≈ 0.7 | ≈ 0.6 |
| Autocorr ≥e-1=0.37 (h) | 26 | 2 | 6 | 4 |
| Autocorr ≥ p=0.05 (h) | 77 | 8 | 55 | 36 |
| coefficients | Berlin-out | Berlin-in 1 | Berlin-in 2 | Vienna |
|---|---|---|---|---|
| AR coefficients | ||||
| 1 | -1.32 | -0.997 | -1.28 | -1.29 |
| 2 | 0.165 | 0.119 | 0.128 | |
| 3 | 0.079 | 0.023 | 0.036 | |
| 4 | 0.035 | 0.137 | 0.058 | |
| 5 | 0.035 | 0.068 | ||
| AM coefficients | ||||
| 1 | -0.995 | -0.807 | -0.973 | -0.926 |
| AIC opt | 2.136e4 | 2.021e4 | 7874 | 2.586e4 |
| mean rel.res | 3.71 | 1.35 | 1.74 | 1.25 |
| statistic | Berlin out | Berlin in-1 | Berlin in-2 | Vienna |
|---|---|---|---|---|
| Custom | 0.64 | 0.76 | 0.84 | 0.82 |
| H=2-DB | 0.54 | 0.77 | 0.74 | 0.80 |
| Gretl | 0.73 | 0.81 | 0.86 | 0.87 |
| R, "corr. R/S" | 0.74 | 0.81 | 0.87 | 0.87 |
| R, "corr. empir" | 0.66 | 0.78 | 0.70 | 0.75 |
| statistic | Berlin out | Berlin in-1 | Berlin in-2 | Vienna |
|---|---|---|---|---|
| Garger g | 0.815 ± 0.005 | 0.698 ± 0.004 | 0.780 ± 0.005 | 0.658 ± 0.003 |
| Graph dim | 1.457 ± 0.049 | 1.230 ± 0.029 | 1.263 ± 0.026 | 1.198 ± 0.023 |
| Lyapunov L | low | low | low | low |
| Embed dim E | ∼6 | 4 - 6 | 5 | 3 - 5 |
| (h) | FNN | plateau | |
|---|---|---|---|
| Vienna | 128 | ∼ 3 | 6 ? |
| Berlin outdoor | 8 | n | 6 |
| Berlin indoor 1 | 64 | 5 | 5 ? |
| Berlin indoor 2 | 32 | 5 | 5 |
| (h) | E (tseriesChaos) |
E (nonlinearTseries) |
L (tseriesChaos) |
L (nonlinearTseries) |
|
|---|---|---|---|---|---|
| Vienna | 80 18 |
4 4 |
n.p. n.p. |
0.001 0.004 |
0.21 - 0.41 0.28 |
| Berlin outdoor | 8 30 |
6 7 |
n n.p. |
0.003 n |
0.055 - 0.35 0.28 - 0.52 |
| Berlin indoor 1 | 50 18 |
4 - 6 4 |
n.p. n.p. |
n 0.002 - 0.003 |
0.20 - 0.32 0.16 |
| Berlin indoor 2 | 36 18 |
5 - 6 5 |
n.p. n.p. |
0.002 0.001 |
0.19 0.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





