1. Introduction
Temporal effects in optics, and the corresponding spacetime symmetries, have been considered for a long time [
1,
2], but in recent years this area seems to observe a kind of explosion. The concept of time-refraction, which is an essential ingredient of what is now called spacetime optics, only emerged in recent years. It became one of the central pieces of our understanding of what is new area of optics, in both the classical and quantum regimes. This concept was formulated in classical terms by several authors [
3,
4,
5,
6,
7]. New theoretical approaches, such as generalized matrix methods to solve wave scattering by temporal structures [
9], have been implemented. In quantum optics, time-refraction was formulated by [
8], and more implicit terms by [
10]. Application of these concepts to quantum cosmology was also explored [
11]. Recent work shows an increase of interest on the quantum aspects of temporal optics [
12,
13,
14].
Experimental observation of time-refraction has been reported in several domains and in different configurations, well before the explicit formulation of the concept. The first possible observation was reported by Yablonovich in 1974 [
15], using laser-breakdown experiments. At that time, this was simply described as a
self-blue shift of the incident laser spectrum. It was clearly due to the sudden ionization of a neutral gas by the incoming laser beam, and was characterized by a spectral shift of the incident light spectrum towards the hight frequencies, in other words, a blue shift of the laser spectrum. Similar effects were later observed in laser and microwave ionization experiments [
16,
17] and it became a regular experimental evidence in intense laser-plasma interaction experiments. More recently, time-refraction was reported in experiments using microwaves in metamaterials [
18] and infrared subcycle pulses in epsilon near-zero optical conditions [
19]. Finally, it was reported in acoustic experiments, where the electromagnetic radiation is replaced by sound waves [
20]. Time-refraction in spin waves [
21] has also been considered.
This concept is therefore a general process, associated to any kind of wave propagating in a background non-stationary media. It opened the door to a new and increasingly active field. This topic is particularly relevant in the context of metallic thin films and metamaterials, as shown by a large number of recent publications [
22,
29,
30,
31,
32,
33,
34,
35,
36], as well as short [
37], and long reviews [
38]. It can used to manipulate the properties of metasurfaces, leading to the development of new optical devices, such as those to control wavefront shapes [
39]. Of particular relevance is the the use of highly-doped semi-conductors, showing reduced dissipation and remarkable optical properties in the near infrared, such as a negative refraction [
40] and a near-zero refractive index (see [
41] for an overview). It should be added that, in magnetized media, the occurrence of temporal boundaries can eventually induce Faraday rotation [
42], and more generally, the generation of photon angular momentum.
An important property of time-refraction is that it is a first order effect, which concerns every photon propagating in the medium, in the same way as the usual space-refraction. For that reason, it can easily be observed at the macroscopic classical level, using a photon beam of arbitrary intensity. Several manifestations of time-refraction have indeed been identified. In the classical regime they are mainly two: frequency shift and time-reflection. Light amplification by successive time-refraction events is also possible. The use of light amplification in temporal optics has been emphasised by several researchers (see, for instance, the references [
43,
44,
45]). We should also add the emission of photon-pairs, which is only relevant in the quantum regime.
Here we review time-refraction in classical and quantum regimes, describe its main physical features, including frequency shifts, temporal Snell’s and Fresnels laws, temporal Bragg effect and amplification. A first version of this review appeared as a conference paper in [
46]. The cases of i) a single temporal boundary, ii) a
temporal beam-splitter made of two consecutive temporal boundaries, iii) generalization to
time-crystals made of a succession of temporal beam-splitters, and more general temporally modulated media, are considered. A relevant aspect of these configurations is that they reveal the importance of temporal interference, which has been explored in the temporal version the Young’s double-slit experiment, discussed in [
47].
A quantum-optical description of these processes is also possible and reveals the creation of photon pairs in quantum vacuum. This photon pair creation is indeed very similar to that of the dynamical Casimir effect, and in some sense, time-refraction generalizes the dynamical Casimir picture, because no spatial boundary conditions are necessary. On the other hand, time-refraction is a first-order optical process, which exists in both classical and quantum regimes. It affects all the photons in the medium and is independent of boundaries. In contrast, the dynamical Casimir is usually identified as a second order quantum effect, which depends on the existence oscillating boundaries, although classical analogues can be envisaged.
Finally, we consider the strong field regime, associated with intense laser pulses, where temporal optical effects are related to possible electron-positron pair creation. This new regime is the so-called intense field or high energy QED. In order to illustrate it, we briefly mention the temporal Klein model, which is a temporal version of the well-known Klein paradox. This model describes a kind of time-refraction of the Dirac field, and explains the creation of particle pairs in a non-stationary vacuum. This is ultimately related with the predicted vacuum breakdown at ultrahigh laser intensities.
2. SpaceTime Boundaries
The simplest way to understand the main differences between space and time boundaries is to consider photon propagation across a moving boundary, where both the frequency (or energy)
and the wavevector (or momentum)
change across the boundary. We assume a sharp boundary between two media with refractive indices
and
, moving with an arbitrary velocity
v along an arbitrary axis
(see
Figure 1). The sharpness of the boundary is not a fundamental issue, and only simplifies our discussion. Using geometric optics or a more exact full wave description, it is then possible to the derive a
generalised Snell’s law, that follows from the existence of two independent invariants, of the form [
3,
48]
where
are the angles of propagation in the two media with respect to the axis
, and
. Notice that the frequencies
and
are, in general, different from each other. For a boundary at rest,
, we are reduced to pure space-refraction, described by the historical Snell’s law,
, and no frequency shift is observed
This is associated with a space symmetry breaking, where the presence of a boundary destroys translation invariance and introduces a change of the photon momentum, but not its energy.
Another relevant situation corresponds to an infinite velocity of the boundary, , where we are reduced to a purely temporal process, because the refractive index changes everywhere at the same time in the medium. In this case, we have and . By analogy with the previous space-refraction, we call it time-refraction. In this case, the photon frequency changes, but momentum is conserved. Notice that we can use proper Lorentz transformations to reduce the case of a finite velocity to these two extreme cases. The subliminal cases, , can be reduced to space-refraction, while the superluminal cases, , can be reduced to time-refraction.
As previously mentioned, the first reported observation of a frequency shift associated with the temporal change of the medium was probably made in 1974 [
15], when a
laser pulse was used to ionize Nitrogen and Helium gas jets. In these early experiments, the observed spectrum of the laser radiation was considerably blue-shifted after ionization. For that reason, the process was initially named
self-blue shift. It is now currently reported in laser pulse interactions with matter (see, for instance, [
49,
50,
51,
52,
53]). Recent experiments on time-refraction, not-related to ionization but to solid state materials, have also been reported [
18,
19].
A full wave description can be used to extend the Fresnel formulae onto the temporal domain. For that purpose, we use state the temporal continuity equations for the electromagnetic field. More specifically, the displacement and magnetic fields,
and
, will have to stay valid for all times, including the discontinuity time,
, in order to guarantee the validity of Maxwell’s equations [
8]. It is important to note that, in general conditions, these field continuity conditions imply the existence of a reflected signal. Therefore, time-refraction also necessarily (and surprisingly!) implies reflection in space. The emission of this reflected signal due to a temporal change of the medium can be called time-reflection [
4].
We therefore assume that, prior to time-discontinuity
, two beams of the same frequency are present in the medium, and propagate in opposite directions. Defining
as the amplitude of beam propagating with wavevector
, and
as the amplitude of beam propagating in the opposite direction,
, the reflection and transmission coefficients resulting from a temporal discontinuity are given by [
54]
where
is the ratio between the initial and the final refractive index of the optical medium. These expressions can be called the
temporal Fresnel’s laws. It should be noticed that they predict the occurrence of
total reflection,
, when the two initial field amplitudes satisfy the relation
. Similarly, we can have
total transmission,
, when
. Total transmission is the temporal analogue of the Brewster’s angle and defines a
temporal Brewster’s angle in the spacetime plan
. The concept was recently explored in [
58]. For isotropic media, there is no dependence of the field polarization direction, but this is not necessarily true for anisotropic media, as discussed below.
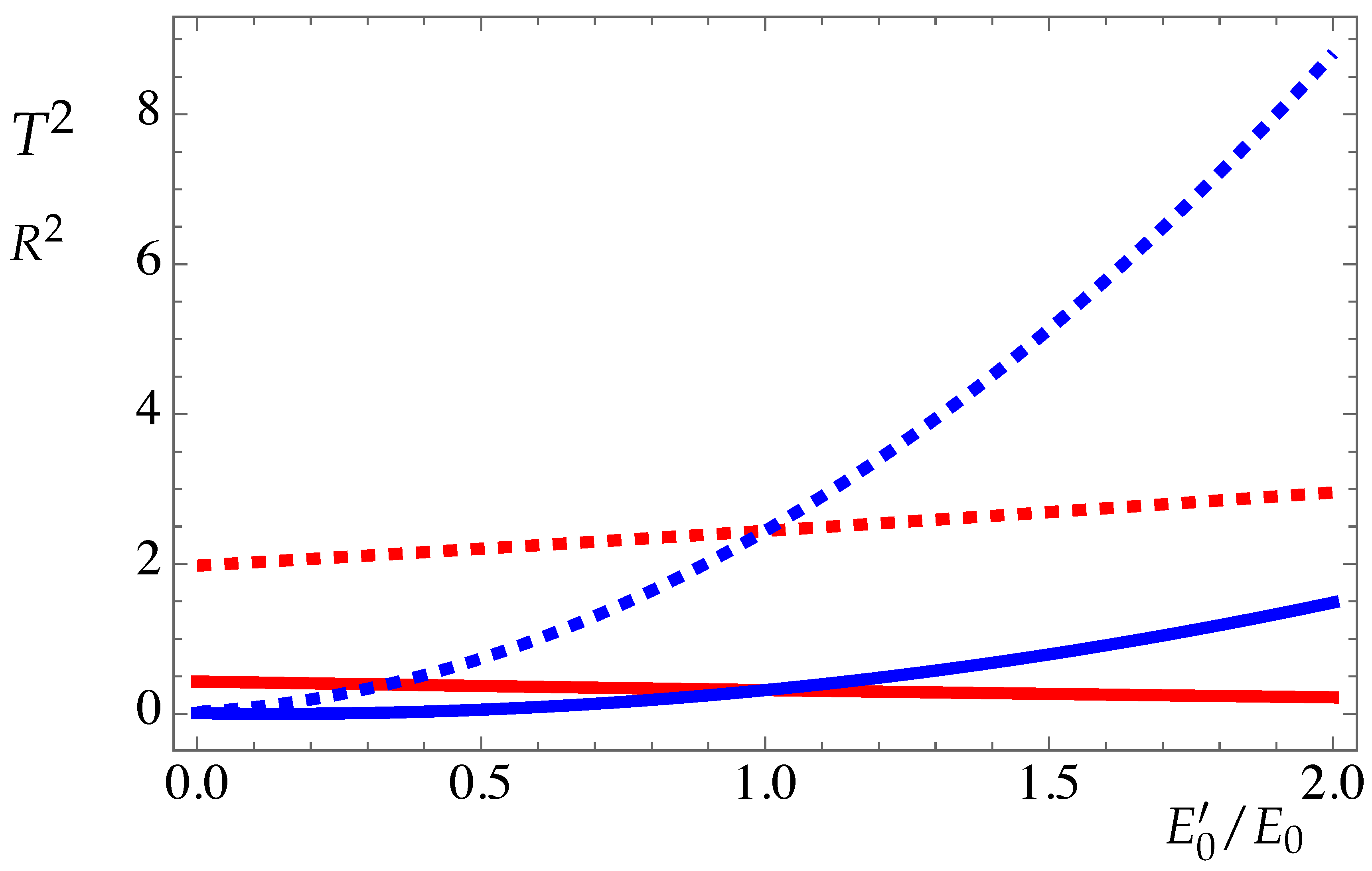
Notice that there is no energy conservation in time-refraction, and an exchange of energy always occurs between the electromagnetic field and the optical medium. This is associated with the fact that, in order to satisfy momentum conservation, the emission of a reflected signal implies the increase of momentum in the transmitted direction. As a result, if the frequency increases, there is an increase of the total electromagnetic energy. In order to illustrate this property we represent in
Figure 2 the quantities
and
, as a function of
, for different values of the ratio
.
Of course, in the simple case of a single initial mode, such that
, the above expressions reduce to
In this case, total reflection and total transmission are completely absent, except in the trivial case of
.
3. Quantum Time-Refraction
Although most of our present review is based on classical optics, it is useful to briefly consider the case of quantum optics. The concept of time-refraction can easily be transposed from classical to quantum optics, also sometimes called optical QED . Here, the field amplitudes have to be replaced by field operators, and similar continuity relations can be established for these operators. This quantum theory confirms the effects of frequency shift and time-reflection already known from the classical model, but a new effect also appears, which is the emission of photons from vacuum. This is an intrinsic quantum effect.
To understood this new effects, let us consider a Fock state of
n photons with frequency
propagating in the forward direction, with no photons in the backward direction, as defined by the state vector
. It can than be shown that, after a time-refraction event at
, we observe states with both forward and backward photons, defined by the new state vector
, where
s is the number of photon-pairs created by the temporal discontinuity. This photon-pair creation process can be described by [
8,
54]
where the probability for the occurrence of different photons states
is determined by
where the two coefficients
A and
B are defined by
Notice that these coefficients satisfy the hyperbolic relation
, characteristic of a bosonic field. Obviously, the
photons propagating in the forward direction, with wavevector
, correspond to the transmitted signal, while the
s photons propagating in the backward direction
correspond to the reflected signal. Given the final value
of the refractive index, both signals propagate in the new medium with a shifted frequency, determined by
. For recent discussions on quantum time-refraction, see [
55,
56,
57,
68].
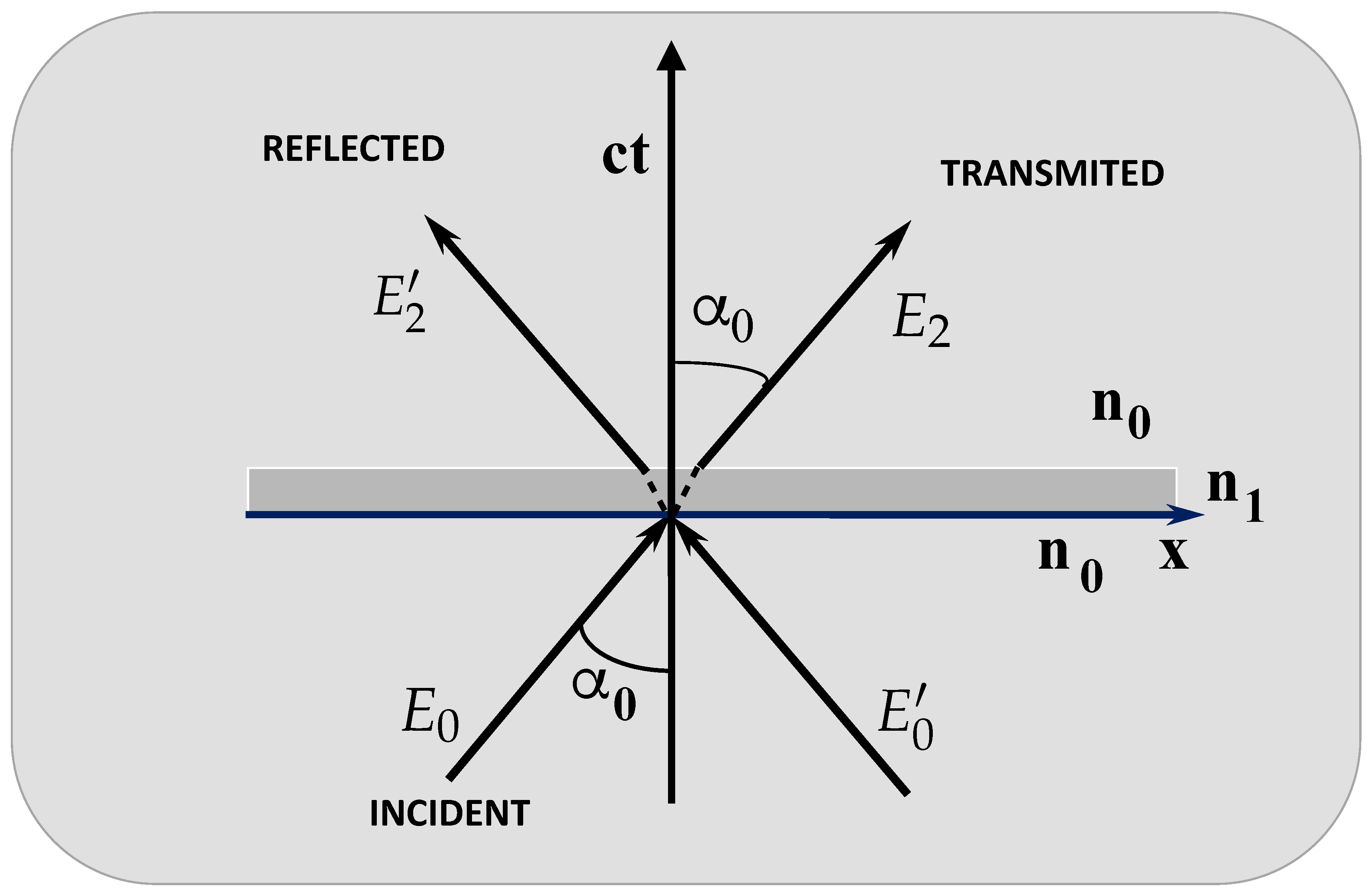
4. Temporal Beam-Splitters
As a natural extension of the basic time-refraction process described above, we can consider a temporal beam-splitter, which is the temporal analogue of the well-known optical beam-splitter. This is defined in the following way. We assume that, at
the refractive index suddenly changes from its initial value
to a different value
, and then, after a time interval
, the refractive index returns to its initial value
. This time interval is the analogue of the width of an optical beam-splitters. Of course, the main difference is that there are three independent directions in space, with only a single direction in time. Using the two consecutive continuity relations, as above, we can derive the time-transmitted and time-reflected coefficients in the form
and
where
and
are the final transmitted and reflected field amplitudes, after the two consecutive temporal discontinuities, as indicated in
Figure 3. For simplicity, we have assumed in these expressions that no reflected signal is initially present,
, as in eq. (
3). But the general case with
can be equally defined [
54].
We clearly see that these coefficients oscillate as a function of the temporal width . This is obviously a result of interferences created by the two temporal surfaces. As before, the maximum values of these coefficients are defined by the ratio between the two refractive indices, . Notice that, in the limit , or , the maximum reflected and transmitted fields can grow indefinitely, showing an unlimited increase of the total energy of the radiation field.
This concept of temporal beam-splitter was recently revisited, for short pulse propagation in metamaterials [
30], where the above analytical results were confirmed by numerical simulations, and more complicated temporal processes were also numerically solved. It should however be noticed that analytical solutions can also be derived for pulses with an arbitrary temporal shape. This analytical approach is based on the analogy with wave propagation in inhomogeneous optical media, such as, in stratified media. It is actually quite easy to derive time-transmission and time-reflection coefficients for propagation in a generic non-stationary medium, where the refractive index is an arbitrary function of time,
. This leads to the following expressions for the transmitted and reflected electric field amplitudes [
59]
and
where the phase
is defined by
Here, the time-dependent wave frequency
is determined by the instantaneous wave dispersion relation, assumed as locally valid, as indicated. But more intricate relations with nonlinear and nonlocal dispersion terms can also be derived. It is particularly useful to consider the case of a slowly varying medium, where the incident wave is always dominant, and we have
. In this case, the time-reflection and time-transmission coefficients are then given by
and
It is interesting to notice that these equations are the exact temporal analogues of the reflection and transmission coefficients defined in stationary inhomogeneous media, where the refractive index varies in space and not in time, as discussed in several books (see, for instance, [
60,
61]).
5. Temporal Rotations
We review the concept of temporal rotation, leading to a change in the angular momentum of light, in the presence of an axis of symmetry, as a static magnetic field. This includes temporally induced Faraday and Cotton-Mouton effects, which are first and second order polarimetric effects for propagation along and across the magnetic field. They could occur when a sudden change of the refractive index of the medium takes place in the presence of a static magnetic field. This means that temporal optics could be used to produce optical isolators. We limit our discussion here to the Faraday effect.
It should be noticed that we need two consecutive time boundaries, as in a temporal beam-splitter, to achieve rotation. An isolated time-boundary would only produce two distinct frequency shifts to the two modes polarized in orthogonal directions, such that we could not speak of a temporal rotation. This can be easily understood, if we consider a wave with frequency
propagation along the static magnetic field
, represented by a linearly polarized electric field
, where
are the circular polarization states. If the refractive index suddenly changes from
to
, due for instance to ionization of the medium, for
we have according to eq. (
3) a new electric field of the form
The quantities
can be represented as
where
is the plasma frequency, and
is the electron cyclotron frequency. We can see that the two orthogonal field components are no longer identical,
, and the initial linear polarization would be modified. But at the same time, the frequencies of these two components are no longer identical, according to
, which means that for
two separate spectral components propagate independently from each other. We therefore cannot talk about the polarization of a single wave mode.
Only when, after some interval
, the initial refractive index is recovered, as it occurs in a temporal beam-splitter as discussed above, can we talk again of a single wave mode and derive a Faraday rotation. This rotation (which is generally accompanied of a change in helicity) will be determined by the final field
, emerging from the temporal beam-splitter with the initial frequency
, which can be written as
where, using eq. (
8) for the two orthogonal modes, we have
with
. Other temporal process leading to the creation of photon angular momentum are due to spacetime non-uniformities of the refractive index, and not to optical anisotropy. This topic, related to both spin and orbital angular momentum, is phenomenologically very rich, and will be developed elsewhere.
6. Time-Crystals
Time-refraction and temporal beam-splitter are also intimately related with the concept of
time-crystal. This concept was initially imagined as a result of spontaneous symmetry breaking, leading a physical system to its lowest energy state [
62], in a way similar to (space) crystalization. In its final state, the system would spontaneously oscillate in time, in analogy with the periodic space arrangements of the ordinary crystals. However, it was soon realized that time crystalization cannot spontaneously occur, because it needs to be driven by an external energy source [
63], therefore is not a property of isolated systems. Subsequently, many different configurations of driven time crystals have been proposed in different media (see for a review [
64]), such as in ultra-cold atomic matter [
66]. Temporal multilayer structures, and their relation with non-Abelian gauge fields have recently been considered [
68]. Another way of describing this process is to consider multiple collisions of an optical pulse with a temporal boundary [
95]. A perturbation theory for spacetime periodic media has also been developed [
96]. Of particular interest in this context are the so-called
photonic time-crystals [
67,
69,
70,
71,
72], which are a natural extension of the previous concepts.
A closely related process is known as the dynamical Casimir effect [
23,
24,
25], which was developed quite independently. It is however physically distinct from a generic time-crystal because, while time-crystals can occur in unbounded time-varying media, the dynamical Casimir effect requires the existence of an oscillating boundary. In a more general field theory, these two concepts eventually coalesce, while keeping their specific identities. Historically, the dynamical Casimir is an extension of the original model associated with the Casimir force [
26,
27,
48], which is a property of quantum vacuum limited by static boundaries. Its dynamical version, was first studied by Moore [
23] and others [
24], and considered an oscillating instead of a static boundary. This property of photon-pair emission is a common property associated to time-refraction and as well as to the dynamical Casimir.
In contrast with classical effects, such as frequency shift and refraction, the quantum properties of time-refraction in a time-varying medium only concern a small number of photons, due to a very low emission probability. The same occurs for the dynamical Casimir effect associated with a moving boundary, which is a closely connected process. For that reason, the quantum manifestations of time-refraction are much more difficult to find. We should however mention that observation of the dynamical Casimir effect has be claimed in superconducting circuits [
28].
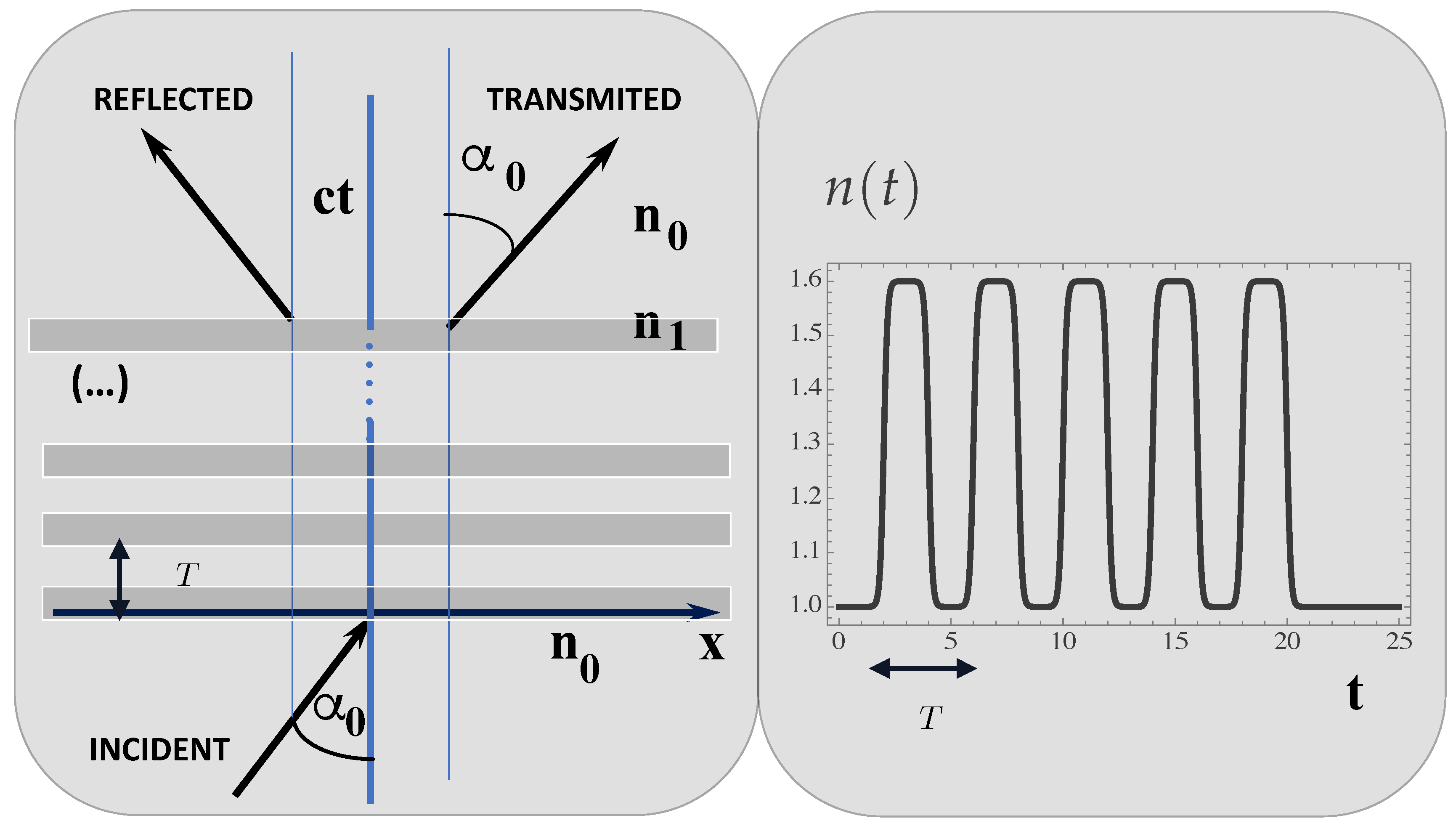
The simplest way to obtain a time-crystal is to superpose a large number
, of identical and equally spaced temporal beam-splitters, distant from each other by a duration
, as represented in
Figure 4. In alternative, we could assume periodic modulations of a continuously varying medium, where the influence of space boundaries can once more be forgotten. For this purpose, we consider an optical medium where the refractive index oscillates at a given frequency
, as described by
where
is the amplitude of the oscillation. Applying the quantum formulation for non-stationary media [
59], we can conclude that the number of photon pairs emitted in two opposite wavevector modes
and
with the same frequency, is given by
where the quantity
is defined as
where
are Bessel functions. The main contribution to the emission of photon pairs is clearly given by the constant part of the function
, because the integral of the oscillating terms over a long time interval in eq. (
19) will be averaged to zero. This constant part is defined by the condition
This formula defines what can be seen as a
temporal Bragg diffraction, which is the condition to attain a maximum value of backscattered (or time reflected) light. Recent developments on temporal Bragg diffraction can be found in [
73]. But, due to the need to satisfy total momentum conservation, it also corresponds to a maximum of time transmitted light. These peaks of the back and forward scattered signals occur when the frequency ratio
takes the value of
, for
, which is the well-known dynamical Casimir condition, and more generally of
, for
integer. This shows that a time-crystal is intimately related with the dynamical Casimir effect, as it is associated with a temporal oscillation of the optical path in the medium. Still, we are very far from the usual model of the dynamical Casimir effect, based on the oscillating mirror.
7. Superluminal fronts
Until now, we have only considered the case of temporal changes in unbounded media. But, if we assume the simultaneous effects of space and time variations, we can have access to new kinds of phenomena, such as photon acceleration (mainly studied in plasmas) and self-phase modulation (in nonlinear optics), which have been mainly discussed in the frame of classical physics. There are some particular cases, however, where simple quantum descriptions have been proposed. This is the case of perturbations moving with superluminal velocity, such as superluminal ionization fronts [
74] (see also the related work [
82,
83]), that we will now briefly discuss.
Relativistic ionization fronts usually move with velocities below the speed of light, and have been studied theoretical and experimentally for very long time [
17,
84]. They can be described by sharp boundary layers between a neutral and an ionized gas. The basic principle of ionization fronts is that of an optical boundary with relativistic velocity, produced by an intense laser pulse, in the absence of motion of atoms and charged particles. This relativistic boundary separates the plasma region from the neutral gas region. On one side of the front we have free electrons and ions, while on the other side we only have neutral atoms. The motion of this boundary is similar to that of a fire front, which can move very fast in a forest, even if the trees are immobile and attached to the ground. The behaviour of a probe beam with frequency
crossing this boundary can be described by a refractive index
of the form
The plasma frequency
is determined by the free electron density, and varies abruptly across the front. It can be described by an expression of the form
where we have assumed a front velocity moving along an arbitrary x-axis, with velocity
. The quantity
defines the width of the front, and
is a constant determining the maximum value of the plasma frequency attained behind the front. Chirp effects associated with the frequency distribution inside the pulse interacting with a moving boundary are very important for the final state of the transmitted pulse [
85,
86]. But, for simplicity, we only discuss here single frequency processes.
Superluminal fronts, with
, although not easy to create, are possible because these are optical boundaries, not related with any actual particle motion. There are several ways to produced these superluminal fronts in the laboratory, in particular, using the
flying focus concept [
87,
88]. This concept has recently been explored and is mainly based on the use of short laser pulses with a broad spectrum, combined with chromatic optical components. For instance, the use of a chromatic lens with a focal distance that depends on the frequency. When a short pulse is focused by such lenses, the different parts of the spectrum will focus at different positions and, if sufficiently intense, they will ionize the neutral gas at different instants and different locations, eventually creating an ionization front that moves with an arbitrarily velocity. Such optical arrangements have been explored by different groups in simulations and experiments, and are not in contradiction with special relativity.
Apart from a pioneering work based on geometric optics [
74], superluminal fronts have also been theoretically described in the frame of quantum optics, several years before the appearance of these recent flying focus devices, see [
59,
89]. Such theoretical models have shown that superluminal fronts can be reduced to a purely temporal process, identical to time-refraction, if we use an adequate reference frame. Making a Lorentz transformation to a moving frame
, such that it moves with respect the laboratory frame
S with an appropriate velocity
V, and considering the well-known velocity transformation formula [
91], we have
We realize that, for
, the front velocity in the new frame will diverge,
, if we choose
. Noting that the plasma frequency
is a relativistic invariant, we can easily conclude that, in the coordinates
of the moving frame, this quantity only depends on time, and will be described by
where
, with
. Notice that
is negative, because the front is superluminal,
. This expression shows that the superluminal front is reduced to a time-refraction event, occurring at
. Applying the above results for time-refraction to this new configuration, and transforming the frequency of the transmitted and reflected signals,
and
back to the laboratory frame
S, we are then led to the following results [
90]
where
is the frequency of the incident signal, and
pertains for parallel and anti-parallel propagation, such that
and
. This shows that, in contrast with the previous time-refraction process occurring in the laboratory frame, the two frequencies of the transmitted and reflected signals can now be very different. This is related to the fact that superluminal fronts break the symmetry of both space and time, and not just time. The physical consequences of this result are quite dramatic, because, for
one of these two frequencies becomes very large, according to the sign of
s. This means that superluminal fronts can considerably enhance the time-refraction process, in terms of frequency and energy upshifts.
8. Temporal Gates
These gates are associated with the temporal control of light propagation in a medium. They can be achieved by several different methods. An example is given here, for illustration, based on perturbed EIT in a gas of Rydberg atoms. But other space-time configurations are possible, such as a perturbed transmission near critical angles spatial Brewster’s angle and spatial total reflection [
75]. Another possible configuration explores the tunnelling process in superimposed space and time forbidden boundaries.
Let us assume a gas of Rydberg atoms, to which we suddenly apply an intense electric field. This will change the frequency of the atomic transmission lines, as well as the susceptibility of the medium, leading to an eventual inhibition of transmission during short time intervals. We consider the case of EIT configuration, which considerably amplifies these spectral effects. In this case, the susceptibility near an atomic transition takes the form [
76,
92,
93,
94]
where
is a reference value,
is the Rabi frequency,
is the transition bandwidth, and
is the frequency detuning associated with to the static or dynamical Stark effect, and due to a control field. A typical form of the frequency detuning s is given by
where
is a reference value and
the spectral detuning, induced on a fast time scale
. As a result of these spectral shifts, the properties of light propagation change across the gas, as illustrated by
Figure 5. This creates a time-gate with a duration of the order of
, and a correlated frequency shift,
. Temporal gates in the femtosecond time-scale seem possible, using dynamical Stark effect with current laser systems. See the related work of [
77] on the temporal analogs of EIT.
9. Time-Refraction Without Time
Let us now consider time-refraction in a completely different perspective, where instead of non-stationary effects related with light beams, we consider diffraction effects created by continuous light beams in stationary media. These diffraction effects can be described as waves, in the context of superfluid theory.
Superfluid light has indeed been considered in recent years, associated with continuous photon beams (laser beams) that propagate in nonlinear Kerr media [
78,
79,
80]. The diffraction fringes, created in the transverse beam structure by some eventual obstacle, are described in a way that is formally very similar to Bogolioubov modes in two-dimensional Bose-Einstein condensates. This formal analogy becomes apparent when we identify the axis of propagation in the Kerr medium as a kind of temporal direction. In this analogy, two transverse sections of the laser beam will be perceived as two different instants of "time". When such a description is possible, the transverse section of a laser beam behaves as a two-dimensional superfluid. This opens new opportunities for theory and experiments, and a new approach to superfluid phenomena, where we replace Bose-Einstein condensates by much simpler nonlinear optics media.
An interesting version of time-refraction was recently identified in superfluid light, where temporal processes are totally absent. It occurs when the photon beam propagating in a static Kerr medium, percieves a sharp discontinuity of the nonlinear susceptibility of the medium [
81]. While photons propagate in the stationary beam along some
z-direction of the medium, the existence of a sharp boundary at some location
, between two regions of the medium with two different nonlinear susceptibilities,
and
, leads to the excitation of diffraction waves in the perpendicular
-plane. These diffraction waves satisfy a dispersion relation that is formally identical to that of Bogolioubov oscillations in a Bose-Einstein condensate, and can therefore be called
bogolons. This is illustrated in
Figure 7. The sharp spatial boundary between the two nonlinear regions can then be perceived as a temporal boundary, where the time variable is now the axial variable
z divided by the velocity of light,
.
In order to describe this process, we use the envelope equation for the electric field, which is a nonlinear Schrödinger equation, written in terms of BEC variables. In such a specific context, this nonlinear equation can more appropriately be called a Gross-Pitaevskii equation. For that purpose, we start from the electric field associated with a photon beam (or laser beam) propagating in the Kerr medium, as described by
and use the paraxial approximation. After an appropriate change of variables [
48], the paraxial equation describing the slow evolution of the field amplitude can be written in the form
with
. This is formally identical to the Gross-Pitaevskii equation, used to describe a two-dimensional Bose-Einstein condensates in the mean-field approximation. But here, the role of the condensate wavefunction is played by the electric field amplitude
, and the time variable
t is just a rescaled space variable, where
z is divided by the speed of light,
. Furthermore, we have also introduced an effective photon mass
, and a coupling constant
describing the linear and nonlinear optical properties of the medium, as defined by
where
is the linear dielectric function. Here it is also assumed that the axial wavenumber
k is related to the wave frequency
by the linear dispersion relation of the medium, such that
.
If we further explore the analogy with a two-dimensional fluid, we can use a
Madelung transformation, such that
, where the square of the beam amplitude (the beam energy) is the fluid density
, and the gradient of the field phase is the fluid velocity
, as
This allows us to derive from eq. (
30) the equations for the photon fluid, which can be identified with
superfluid light. In particular, if this fluid is perturbed by some optical irregularity, the resulting density perturbations will satisfy a dispersion relation that is formally identical to the Bogoliubov dispersion relation for a BEC, of the form
where
is the Bogoliubov speed, and
is the unperturbed fluid density. This result is valid for density perturbations evolving with
frequency and wavevector
, defined in the perpendicular plane
. This is formally identical with what occurs in a two-dimensional Bose-Einstein condensate, but the quantity
is not a frequency in the usual sense, because the variable time
t is not a physical time but the beam propagation direction. These perturbations are indeed diffraction waves, defined as beam intensity modulations in the perpendicular plane, and by analogy with the condensates can be called
bogolons, because they satisfy identical dispersion relations.
Now, if at some point (which corresponds to an instant in temporal units) there is a sharp discontinuity of the nonlinear susceptibility, from an initial value to a different value , in temporal units this can be seen as time-refraction. Therefore, a description similar to the above time-refraction can be used to relate the initial wave "frequency" to the final one, , because has changed. This is a process that is formally identical to time-refraction, but occurs in a static configuration where the abrupt changes take place along the paraxial direction z, and not in physical time.
The elementary excitations of the medium are not photons, but bogolons, another kind of bosons. And, instead of photons propagating in the axial beam direction they are diffraction waves in the perpendicular plane. But we can nevertheless define temporal reflection and transmission coefficients, as [
81]
They are very similar, but not identical to the temporal Fresnel’s laws given by eqs. (
3). The new parameter
is determined by the Bogoliubov dispersion, valid on the two sides of the medium (
33), and is now equal to
. Another important difference with respect to photon time-refraction is that in bogolon time-refraction the sum of the refraction and transmission coefficients is independent of the parameter
, and always equal to one,
.
Simulations of the Gross-Pitaevskii equation (
30) confirm the validity of these analytical results, and allow us to explore further the time-refraction mechanism in the nonlinear bogolon regime. Furthermore, we can also define temporal beam-splitters for bogolons, as well as the equivalent of time-crystals, in this purely static problem. This illustrates the generally of the time-refraction concept, which can even survive the absence of temporal discontinuities.
10. High Energy QED
A further step in the theory of quantum time-refraction involves what is usually called
high energy QED, which assumes that quantum vacuum is not just made of virtual photons, but also of virtual electron-positron pairs. This new configuration is relevant to the physics of ultra-intense lasers, in the multi-Petawatt regime [
97,
98]. This more complete view of quantum vacuum includes, not only photons as considered above, but also electrons and positrons as described by Dirac’s equation.
In order to discuss this last topic, we assume the case of pure vacuum, where intense electromagnetic fields can be treated quasi-classically. Here, time-refraction is not related to a sudden change of refractive index, but to a sudden change of the vector potential, , and leads to the excitation of particle-pairs. Such an elementary process can be described by a temporal Klein model.
Almost one century ago, Oscar Klein solved Dirac’s equation for the case of a potential step , and showed that, for an incident electron, the reflection probability could be larger than one. This was initially called the Klein paradox, but was later understood in terms of particle-pair creation. The origin of this creation is the singularity of the electric field defined by the discontinuity of the static potential V.
A similar problem is associated wi9th a temporal step of the vector potential,
. In this case, the singularity of the electric field is created at
. The solution of Dirac’s equation for this temporal problem leads to the following probability for the electron-positron pair creation, f [
99]
where
is the normalized vector potential, and
specifies the particle momentum. This simple expression is valid for states such that
, and momentum parallel to the vector potential is negligible and assumes an infinitely fast time-step.
This can be generalized to more realistic configurations, associated with finite temporal variation of the vector potential
, where the electric field
can be created by intense laser pulses [
100]. This approach shows that pair production in vacuum can be described in the frame of a
temporal paradigm, that extends our previous discussion of time-refraction and spacetime optics.
11. Conclusions
In this paper, we have given an overview of spacetime optics, centred on the concept of time-refraction. This is a first order process, at the same level as the usual (space) reflection, and concerns every light beam propagating in a non-stationary medium. This process results from time symmetry breaking, and envolves the excitation of a reflected signal. Just as space-refraction, occurring at the space boundary between two media, time-refraction occurs at a temporal boundary and produces two beams, the transmitted and the reflected beam. Expressions for time-transmission and time-reflection coefficients were given. They show that photon momentum is conserved but not energy, because the radiation frequency of has to adjust to the new value of the refractive index.
Apart from these two distinct signatures, time-reflection and frequency shifts, when considered in the frame of quantum optics temporal discontinuities also imply photon creation in vacuum. We have discussed the concept of a temporal device called temporal beam-splitter, which is made of a sequence of two inverse time-refraction events, and can be seen as the temporal counterpart of the optical beam-splitter, one of the most basic devices used in both classic and quantum optics experiments [
48,
102]. More complicated temporal devices can also be imagined, such as time-cavities and photonic time-crystals, through the addition of periodically spaced temporal beam-splitters. These new temporal arrays display resonant transmission and reflection properties, that can be described by simple
temporal Bragg laws.
Time-crystals are closely related to the dynamical Casimir effect, a quantum process due to oscillating optical boundaries. Although defined in a different physical geometry, the dynamical Casimir effect and time-crystals rely essentially on the same elementary properties of quantum vacuum. However time-refraction and time-crystals are independent of optical boundaries, and can occur in unbounded and uniform media. Under certain conditions, a link with another quantum vacuum process can be established. This is known as
Unruh radiation, and is emitted by a particle moving in vacuum with uniform acceleration. To provide such a link the concept of
effective Unruh acceleration was proposed in [
101], but the physical picture is still not clear.
The basic concept of time-refraction is associated with sharp temporal boundaries, in analogy with space-refraction. But it can easily be extended to arbitrary non-stationary media, again in analogy with the optics of inhomogeneous and stratified media. Arbitrary temporal variations of the refraction index,
can be seen as a succession of infinitesimal events, and general expressions for time transmission and reflection coefficients can be derived, which resemble those of inhomogeneous optics. They provide an alternative approach to the case of temporally periodic media, such as time-crystals. They can also have relevance in different other areas of physics, such as that of Bose-Einstein condensates [
103,
104,
105], where time-symmetry breaking processes, such as expansion, quenching, and the Kibble-Zurek mechanism can be described in a similar way.
We have reviewed recent work on superluminal ionization fronts, which can be created by short laser pulses, using a flying focus configuration. Propagation across these fronts can lead to significant frequency shifts, as well as beam amplification, with relevance to future radiation sources. We have shown, using an appropriate reference frame called time-frame, that this process is equivalent to a purely temporal event, identical to time-refraction.
Furthermore, we have shown that time-refraction in anisotropic media is able to generate Faraday rotations and create angular momentum states of light. We have also shown the resilience of the time-refraction concept by applying it to a purely static process involving diffraction in superfluid light. And finally, we have discussed time-refraction in the context of high energy QED, and its relation with the possible creation of electron-positron pairs by intense laser fields in vacuum. Such a variety of examples clearly demonstrates the significance, the wide range of applications, and the universality of time-refraction. The field of spacetime optics is therefore able to influence several other areas of physics.
References
- F. R. Morgenthaler, "Velocity Modulation of Electromag-netic Waves", IRE Trans. Microwave Theory Tech. 6, 167 (1958).
- S.A. Akhmanov, A.P. Sukhorukov and A.S. Chirkin, "Nonstationary Phenomena and Space-Time Analogy in Nonlinear Optics", Sov. Phys. JETP 28, 748 (1969).
- J.T. Mendonça, Theory of Photon Acceleration, IOP Publishing, Bristol (2001).
- J.T. Mendonça and P.K. Shukla, "Time Refraction and Time Reflection: Two Basic Concepts", Phys. Scripta 65, 160 (2002).
- F. Biancalana, A. Amann, A.V. Uskov and E.P. O’Reilly, "Dynamics of Light Propagation in Spatiotemporal Dielectric Structures", Phys. Rev. E 75, 046607 (2007).
- Y. Xiao, D.N. Maywar and G.P. Agrawal, "Reflection and Transmission of Electromagnetic Waves at a Temporal Boundary", Opt. Lett. 39, 574 (2014).
- B.W. Plansinis, W.R. Donaldson and G.P. Agrawal, "What is the Temporal Analog of Reflection and Refraction of Optical Beams?", Phys. Rev. Lett. 115, 183901 (2015).
- J.T. Mendonça, A. Guerreiro and A.M. Martins, "Quantum Theory of Time Refraction", Phys. Rev. A 62, 033805 (2000).
- J. Xu, W. Mai and D.H. Werner, "Generalized temporal transfer matrix method: a systematic approach to solving electromagnetic wave scattering in temporally stratified structures", Nanophotonics 11, 1309 (2022).
- V.V. Dodonov, A.B. Klimov, and D.E. Nikonov, "Quantum Phenomena in Nonstationary Media", Phys. Rev. A 47, 4422 (1993).
- N. Westerberg, S. Cacciatori, F. Belgiorno, F. Dalla Piazza and D. Faccio, "Experimental Quantum Cosmology in Time-Dependent Optical Media", New J. Phys. 16, 075003 (2014).
- S. A. Horsley and J. B. Pendry, "Quantum Electrodynamics of Time-Varying Gratings", Proc. Nat. Academy of Sciences 120, e2302652120 (2023).
- J.E. Vásquez-Lozano and I. Liberal, "Shaping the Quantum Vacuum with Anisotropic Temporal Boundaries", Nanophotonics 12, 539 (2022).
- A. Svidzinsky, "Time Reflection of Light from a Quantum Perspective and Vacuum Entanglement", Opt. Express 32, 15623 (2024).
- E. Yablonovitch, "Self-phase Modulation and Short-Pulse Generation from Laser-Breakdown Plasmas", Phys. Rev. A 10, 1888 (1974).
- R. L. Savage, Jr., C. Joshi, and W. B. Mori, "Frequency Upconversion of Electromagnetic Radiation upon Tansmission into an Ionization Front", Phys. Rev. Lett. 68, 946 (1992).
- J.M. Dias, C. Stenz, N. Lopes, X. Badiche, F. Blasco, A. Dos Santos, L. O. Silva, A. Mysyrowicz, A. Antonetti and J.T. Mendonça, "Experimental Evidence of Photon Acceleration of Ultrashort Laser Pulses in Relativistic Ionization Fronts", Phys. Rev. Lett. 78, 4773 (1997).
- H. Moussa, G. Xu, S. Yin, E, Galiffi, Y. Radi and A. Alú, "Observation of Temporal reflection and Broadband Frequency Translation at Photonic Time Interfaces", Nature Phys. 19, 863 (2023).
- E. Lustig, O. Segal, S. Saha, E. Bordo, S.N. Chowdhury, Y. Sharabi, A.Fleischer, A. Boltasseva, O. Cohen, V.M. Shalaev and M. Segev, "Time-refraction optics with single cycle modulation", Nanophotonics 12, 2221 (2023).
- B. L. Kim, C. Chong and C. Daraio, “Temporal refraction in an acoustic phononic lattice” Phys. Rev. Lett. 133, 077201 (2024).
- K. Schultheiss, N. Sato, P.Matthies, L. Körber, K. Wagner, T. Hula, O. Gladii, J.E. Pearson, A. Hoffmann, M. Helm, J. Fassbender and H. Schultheiss, "Time Refraction of Spin Waves", Phys. Rev. Lett. 126, 137201 (2021).
- C. Caloz and Z.-L. Deck-Léger, “Spacetime metamaterials” IEEE Trans. Antennas Propag. 67,1569 ( 2019); 67, 1583 (2019).
- G. T. Moore, Quantum Theory of the Electromagnetic Field in a Variable-length One-dimensional Cavity, J. Math. Phys. 11, 2679 (1970).
- S.A. Fulling and P.C.W. Davies, "Radiation from a Moving Mirror in Two Dimensional Space-time: Conformal Anomaly", Proc. R. Soc. Lond. A 348, 393 (1976).
- V. Dodonov, Fifty Years of the Dynamical Casimir Effect, Physics 2, 67 (2020).
- H.B.G. Casimir, "On the Attraction Between Two Perfectly Conducting Plates", Proc. K. Ned. Akad. Wet. 51 793 (1948).
- K.A. Milton, "The Casimir Effect: Recent Controversies and Progress", J. Phys. A: Math. Gen. 37, R209 (2004).
- C.M. Wilson, G. Johansson, A. Pourkabirian, M. Simoen, J.R. Johansson, T. Duty, F. Nori, and P. Delsing, "Observation of the Dynamical Casimir Effect in a Superconducting Circuit", Nature 479, 376 (2011).
- L. Yuan, and S. Fan, "Temporal Modulation Brings Metamaterials Into New Era", Light Sci. Appl. 11, 173 (2022).
- C. Rizza, C. Castaldi and V. Galdi, "Sort-Pulsed Metamaterials", Phys. Rev. Lett. 128, 257402 (2022).
- Y. Zhou, M.Z. Alam, M. Karimi, J. Upham, O. Reshef, C. Liu, A.E. Willner and R.W. Boyd, "Broadband Frequency Translation Through Time Refraction in an Epsilon-Near-Zero Material", Nat. Commun. 11, 2180 (2020).
- O.Y. Long. K. Wang, A. Dutt and S. Fun, "Time Reflection and Refraction in Synthetic Frequency Dimension", Phys. Rev. Research 5, L012046 (2023).
- M.R. Shcherbakov, K. Werner, Z. Fan, N. Talisa, E. Chowdhury and G. Shvets, "Photon Acceleration and Tunable Broadband Harmonics Generation in Nonlinear Time-dependent Metasurfaces", Nat. Commun. 10, 1345 (2019). [CrossRef]
- V. Pacheco-Peña and N. Emgheta, "Spatiotemporal isotropic-to-Anisotropic Meta-Atoms", New J. Phys. 23, 095006 (2021).
- J.E. Vázquez-Lozano and I. Liberal, "Shaping the Quantum Vacuum with Anisotropic Temporal Boundaries", Nanophotonics 12, 539 (2023).
- J. Sisler, P. Thureja, M.Y. Grajower, R. Sokhoyan, I. Huang and H.A. Atwater, "Electrically tunable space–time metasurfaces at optical frequencies", Nat. Nanotechnol. 19, 1491 (2024).
- N. Engheta, "Four-dimensional optics using time-varying metamaterials", Science 379, 1190 (2023).
- E. Galiffi, R. Tirole, S. Yin, H. Li, S. Vezzoli, P.A. Huidobro, M.G. Silveirinha, R. Sapienza, A. Alù and J.B. Pendry, "Photonics of Time-Varying Media", Adv. Photonics 4, 014002 (2022).
- Q. Fan, A.M. Shaltout, J. van de Groep, M.L. Brongersma, and A.M. Lindenberg, "Ultrafast Wavefront Shaping via Space-Time Refraction", ACS Photonics 10, 2467 (2023).
- V. Bruno, C. DeVault, S. Vezzoli, Z. Kudyshev et al., "Negative Refraction in Time-Varying Strongly Coupled Plasmonic-Antenna Epsilon Near-Zero Systems", Phys. Rev. Lett. 124, 043902 (2020).
- W. Jaffray, S. Stengel, F. Biancalana, C.B. Fruhling, M. Ozlu, A. Boltassev, V.M. Shalaev and M. Ferrera, "Spatio-spectral Optical Fission in Time-varying Subwavelength Layers", arXiv:2406.04917 (2024).
- H. Li, S. Yin and A. Alú, "Nonreciprocity and Faraday Rotation at Time Interfaces", Phys. Rev. Lett. 128, 173901 (2022).
- M. Lyubarov, Y. Lumer, A. Dikopoltsev, E. Lustig, Y. Sharabi and M. Segev, "Amplified Emission and Lasing in Photonic Time Crystals", Science 377, 425 (2022).
- E. Galiffi, A.C, Harwood, S. Vezzoli, R. Tirole, A. Alú and R. Sapineza, "Optical coherent perfect absorption and amplification in a time-varying medium", arXiv:2410.16426 (2024).
- S.A.R. Horsley and J.B. Pendry, "Traveling Wave Amplification in Stationary Gratings", Phys. Rev. Lett. 133, 156903 (2024).
- J.T. Mendonça, ”Time-Refraction in Classical and Quantum Optics”, in A. Dodonov and C.C.H. Ribeiro (eds.) Proceedings of the 2nd International Workshop on Quantum Nonstationnary Systems, LF Editorial, São Paulo, Brazil (2024).
- R. Tirole, S. Vezzoli, E. Galiffi, I. Robertson, D. Maurice, B. Tilmann, S.A. Maier, J.B. Pendry and R. Sapienza, "Double-slit time diffraction at optical frequencies", Nat. Phys. 19, 999 (2023).
- J.T. Mendonça, The Quantum Nature of Light, IOP Publishing, Bristol (2022).
- S.P. Le Blanc, R. Sauerbrey, S.C. Rae and K. Burnett, "Spectral Blue Shifting of a Femtosecond Laser Pulse Propagating Through a High-Pressure Gas", J. Opt. Soc. Am. B 10, 1801 (1993).
- Y.M. Li and R. Fedosejevs, "Ionization-Induced Blue Shift of KrF Laser Pulses in an Underdense Plasma", Phys. Rev. E 54, 2166 (1996).
- H.J. Shin, D.G. Lee. Y.H. Cha, J.-H. Kim, K.H. Hong and C.H. Nam, "Nonadiabatic Blueshift of High-order Harmonics from Ar and Ne Atoms in an Intense Femtosecond Laser Field", Phys. REv. A 63, 053407 (2001).
- X. Xie, A.L. Cavalier and S.L. Johnson, "Self-Compression of Femtosecond Laser Pulses in Ambient Air Through Conical Radiation", Opt. Lett. 48, 5101 (2023).
- A. Giulietti and D. Giulietti, "Self-phase Modulation in Various Regimes of Intense Laser–Plasma Interactions", J. Plasma Phys. 81, 495810608 (2015).
- J.T. Mendonça, A.M. Martins and A. Guerreiro, "Quantum Theory of Time Refraction", Phys. Rev. A 68, 043801 (2003).
- A. Prain, S. Vezzoli, N. Westerberg, T. Roger, and D. Faccio, "Spontaneous Photon Production in Time-dependent Epsilon-near-zero Materials", Phys. Rev. Lett. 118, 133904 (2017).
- J.B. Pendry and S.A.R. Horsley, "QED in space–time varying materials", APL Quantum 1, 020901 (2024).
- C. Caloz, F. Ok and A. Bahrami, "Emergence of Quantum Space-Time Engineered Modulation (Q-STEM) Metamaterials", Proc. 4th URSI AT-RASC (2024).
- V. Pacheco-Peña and N. Engheta, "Temporal Equivalent of the Brewster angle", Phys. Rev. B 104, 214308 (2021).
- J.T. Mendonça and A. Guerreiro, "Time refraction and the quantum properties of vacuum", Phys. Rev. A 72, 063805 (2005).
- V.L. Ginzburg, Propagation of Electromagnetic Waves in Plasmas, Gordon and Breach, New Your (1961).
- M. Kline and I.W. Kay, Electromagnetic Theory and Geometric Optics, John Wiley & Sons, New York (1965).
- F. Wilczek, "Quantum Time Crystals", Phys. Rev. Lett. 109, 160401 (2012).
- P. Bruno, "Impossibility of Spontaneously Rotating Time Crystals: A No-Go Theorem", Phys. Rev. Lett, 111, 070402 (2013).
- K. Sacha ans J. Zakrzewski, "Time Crystals: a review", Rep. Prog. Phys. 81, 016401 (2018).
- Z. Dong, H. Li, T. Wan et al.,“Quantum Time Reflection and Refraction of Ultracold Atoms,” Nat. Photonics 18, 68 (2024).
- J.T. Mendonça and V.V. Dodonov, "Time Crystals in Ultracold Matter", J. Russian Laser Res. 35, 93 (2014).
- E. Lustig, O. Segal, S. Saha, C. Fruhling, V. M. Shalaev, A. Boltasseva, and M. Segev, "Photonic time- crystals - fundamental concepts," Optics Express 31, 9165 (2023).
- Z. Dong, X. Wu, Y. Yang, P, Yu, X. Chen and L. Yuan, "Temporal Multilayer Structures in Discrete Physical Systems Towards Arbitrary- Dimensional non-Abelian Aharonov-Bohm Interferences", Nat. Commun. 15, 7392 (2024).
- X. Wang, M. S. Mirmoosa, V. S. Asadchy, C. Rockstuhl, S. Fan and S. Tretyakov , “Metasurface-based realization of photonic time crystals,” Sci. Adv. 9, eadg7541 (2023).
- O. Shahariar and M.R.C. Mahdy, "An Idea of Implementing Photonic Space-Time Crystals Using Metasurfaces", arXiv:2409.00139 (2024).
- M.G. Ozlu, V. Mkhitaryan, C.B. Fruhling, A. Boltasseva and V.M. Shalaev, "Floquet Engineering of Polaritonic Amplification in Dispersive Photonic Time Crystals", arXiv:2408.00552 (2024).
- E.E. Narimanov, "Electromagnetic Response for Modulation at Optical Time Scale", arXiv:2409.19394 (2024).
- J. Zhang, W.R. Donaldson and G.P. Agrawal, "Spatiotemporal Bragg gratings forming inside a nonlinear dispersive medium", Opt. Lett. 49, 5854 (2024).
- L.O. Silva and J.T. Mendonça, "Photon Acceleration in Superluminous and Accelerated Ionization Fronts", IEEE Trans. Plasma Sci. 24, 316 (1996).
- L. Bar-Hillel, A. Dikopoltsev, A. Kam, Y. Sharabi, O. Segal, E. Lustig and M. Segev, "Time-refraction and time-reflection above critical angle for total internal reflection", Phys. Rev. Lett. 132, 263802 (2024).
- P. Valente, H. Failache and A. Lezama, "Temporal Build-up of Electromagnetically Induced Transparency and Absorption Resonances in Degenerate Two-Level Transitions", Phys. Rev. A 67, 013806 (2002).
- M. Akhtar and A. Naweed, "Temporal Analogs of Electromagnetically Induced Transparency, Induced Absorption, and Fano Resonance," Opt. Lett. 49, 5667 (2024).
- E.G. Khamis, A. Gammal, G.A. El, Yu.G. Gladuch and A.M. Kamchatnov, "Nonlinear Diffraction of Light Beams Propagating in Photorefractive Media with Embedded Reflecting Wire", Phys. Rev. A 78, 013829 (2008).
- C. Michel, O. Boughdad, M. Albert, P.-É. Larré, and M. Bellec, "Superfluid Motion and Drag-force Cancellation in a Fluid of Light", Nat. Commun. 9, 2108 (2018).
- Q. Fontaine et al., "Interferences Between Bogoliubov Excitations in Superfluids of Light", Phys. Rev. Research 2, 043297 (2020).
- J.T. Mendonça and I. Kourakis, "Propagation of Bogolons in Superfluid Light: Time-Like Effects in Non-Uniform Optical Media", Eur. Phys. J. Plus ´137, 1269 (2022).
- Y. Pan, M.-I. Cohen and M. Segev, "Superluminal k-Gap Solitons in Nonlinear Photonic Time Crystals", Phys. Rev. Lett. 130, 233801 (2023).
- C. Pan, X. Song, Y. Cao, L. Xiong, X. Lan, S. Wang, Y.Leng and Y.Pan, "Superluminal Spacetime Boundary, Time Reflection and Quantum Light Generation from Relativistic Plasma Mirrors", arXiv:2410.01287 (2024).
- M. Lampe, E. Ott and J.H. Walker, "Interaction of electromagnetic waves with a moving ionization front", Phys. Fluids 21, 42 (1978).
- L.O. Silva and J.T. Mendonça, "Photon Kinetic Theory of Self-Phase Modulation", Opt. Commun. 196, 285 (2001).
- W. Cai, Z. Yang, H. Wu, L. Wang, J. Zhang and L. Zhang, "Effect of Chirp on Pulse Reflection and Refraction at a Moving Temporal Boundary", Optics Express 30, 34875 (2022).
- A. Sainte-Marie, O. Gobert and F. Quéré, ”Controlling the Velocity of Ultrashort Light Pulses in Vacuum through Spatio-temporal Couplings”, Optica 4, 1298 (2017).
- D.H. Froula, D. Turnbull, A.S. Davies et al., ”Spatiotemporal Control of Laser Intensity”, Nature Photon 12, 262 (2018).
- A. Guerreiro, J.T. Mendonça and A.M. Martins, "New mechanism of vacuum radiation from non-accelerated moving boundaries", J. Opt. B: Quantum Semiclass. Opt. 7, S69 (2005).
- J.T. Mendonça, "Photon Acceleration by Superluminal Ionization Fronts", Symmetry 16, 112 (2024).
- L.D. Landau and E.M. Lifshitz, The Classical Theory of Fields, Elsevier Science, Amsterdam (2013).
- J.T. Mendonça, "Temporaal Optical Processes in a Rydberg Gas", J. Phys. B: At. Mol. Opt. Phys. 53, 164004 (2020).
- J. Gea-Banacloche, Y-q. Li, S-z. Jin and M. Xiao, "Electromagnetically Induced Transparency in Ladder-type Inhomogeneously Broadened Media: Theory and Experiment", Phys. Rev. A 51 576 (1995).
- S. Sevinçli, N. Henkel, C. Ates and T. Pohl, "Nonlocal Nonlinear Optics in Cold Rydberg Gases", Phys. Rev. Lett. 107 153001 (2011).
- M. Liu, F. Deng and W. Hong, "Parabolic-like Motion of an Optical Pulse Modulated by a Temporal Boundary in Highly Noninstantaneous Kerr Media", Phys. Rev. A 110, 043504 (2024).
- E.O. Hiltunen, "Perturbation theory for dispersion relations of spacetime-periodic materials", arXiv:2409.11514 (2024).
- J.W. Yoon et al., "Realization of Laser Intensity over 1023 W/cm2", Optica 8, 630 (2021).
- A. Fedotov, A. Ilderton, F. Karbstein, B. King, D. Seipt,H. Taya and G. Torgrimsson "Advances in QED with Intense Background Fields", Phys. Rep. 1010, 1 (2023).
- J.T. Mendonça, "Temporal Klein Model for Particle-Pair Creation", słSymmetry 13, 1361 (2021). [CrossRef]
- J.T. Mendonça, "Particle-Pair Creation by High-Harmonic Laser Fields", Phys. Scripta 98, 125606 (2023).
- J.T. Mendonça, G. Brodin and M. Marklund, "Vacuum Effects in a Vibrating Cavity: Time Refraction, Dynamical Casimir Effect, and Effective Unruh Acceleration", Phys. Lett. A 372, 5621 (2008).
- C.C. Gerry and P.L. Knight, Introductory Quantum Optics, Cambridge University Press, Cambridge (2005).
- A. Polkovnikov, K. Sengupta, A. Silva and M. Vengalattore, "Nonequilibrium Dynamics of Closed Interacting Quantum Systems", Rev. Mod. Phys.83, 863 (2011).
- A. del Campo and W.H. Zurek, "Universality of Phase Transition Dynamics: Topological Defects from Symmetry Breaking" Int. J. Mod. Phys. A 29, 1430018 (2014).
- J T Mendonça and A Gammal, "Time Symmetry Breaking in Bose–Einstein Condensates", J. Phys. A: Math. Theor. 50, 355501 (2017).
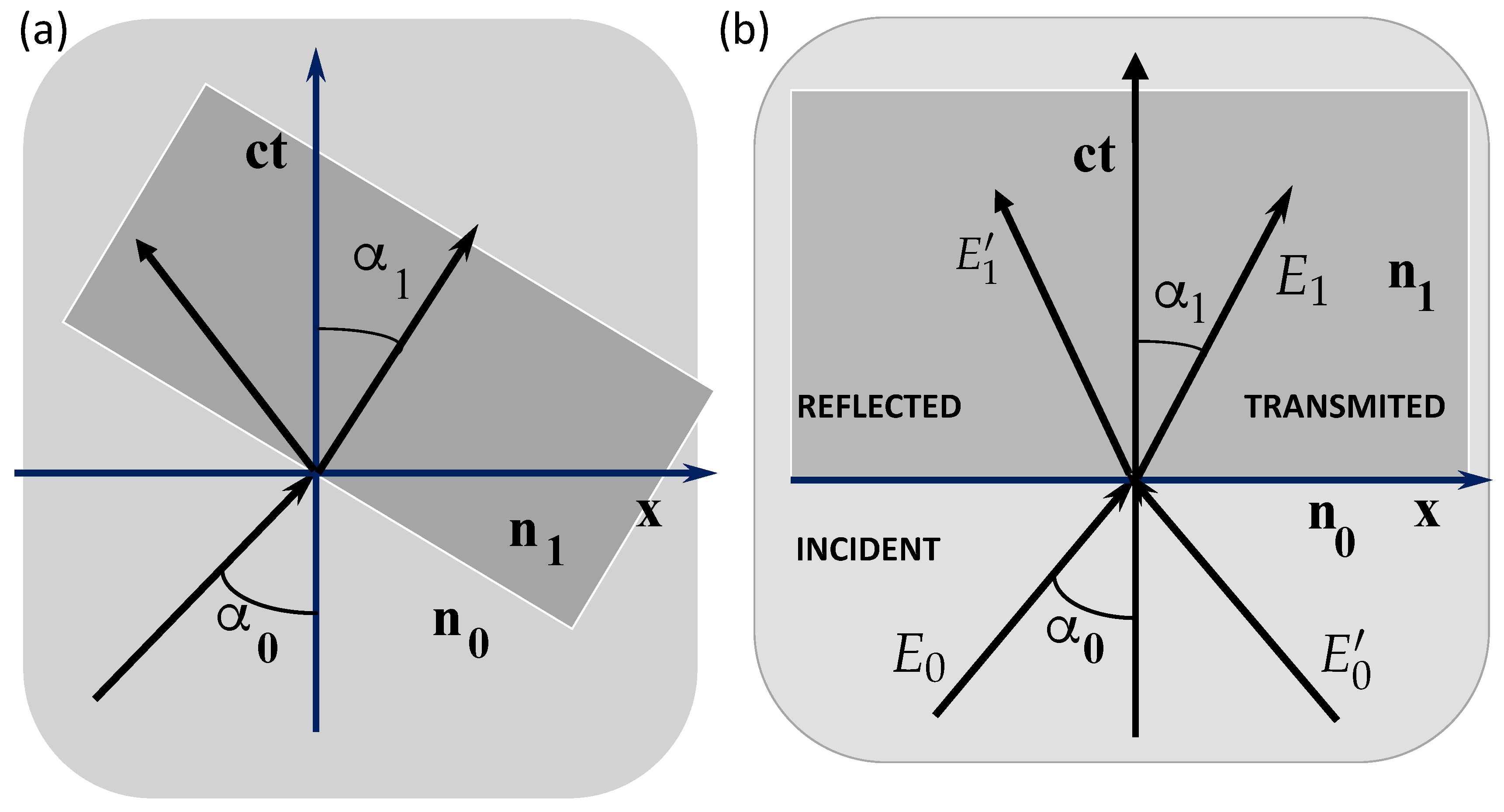
Figure 1.
Spacetime refraction: (a) boundary moving with velocity v along the x-axis, (b) boundary at rest, . We represent the plane, where two optical media with different refractive indices, to , are separated by a moving boundary (oblique line in the plane). The angles represent the photon velocity in the two media, . For the particular case of (b) where the boundary is at rest, we get a simpler picture, where the boundary coincides with the x-axis. In this case we include two initial beams moing with the same frequency but in opposite directions.
Figure 1.
Spacetime refraction: (a) boundary moving with velocity v along the x-axis, (b) boundary at rest, . We represent the plane, where two optical media with different refractive indices, to , are separated by a moving boundary (oblique line in the plane). The angles represent the photon velocity in the two media, . For the particular case of (b) where the boundary is at rest, we get a simpler picture, where the boundary coincides with the x-axis. In this case we include two initial beams moing with the same frequency but in opposite directions.
Figure 2.
(red curves) and (blue curves): as a function of the ratio , for and (dashed).
Figure 2.
(red curves) and (blue curves): as a function of the ratio , for and (dashed).
Figure 3.
Temporal beam-splitter, made of two successive time-refraction events: First, at the refractive index suddenly changes, from to , and then at , the refractive index returns to its initial value . Incident, reflected and transmitted rays across the temporal slab of duration τ are represented.
Figure 3.
Temporal beam-splitter, made of two successive time-refraction events: First, at the refractive index suddenly changes, from to , and then at , the refractive index returns to its initial value . Incident, reflected and transmitted rays across the temporal slab of duration τ are represented.
Figure 4.
Time-crystal, made of successive temporal beam-splitters events with the same duration τ, and the same refractive index , on a background of refractive index , separated by a time interval .
Figure 4.
Time-crystal, made of successive temporal beam-splitters events with the same duration τ, and the same refractive index , on a background of refractive index , separated by a time interval .
Figure 5.
Superluminal front: Electron plasma frequency in the time frame, moving with velocity with respect to the laboratory frame.
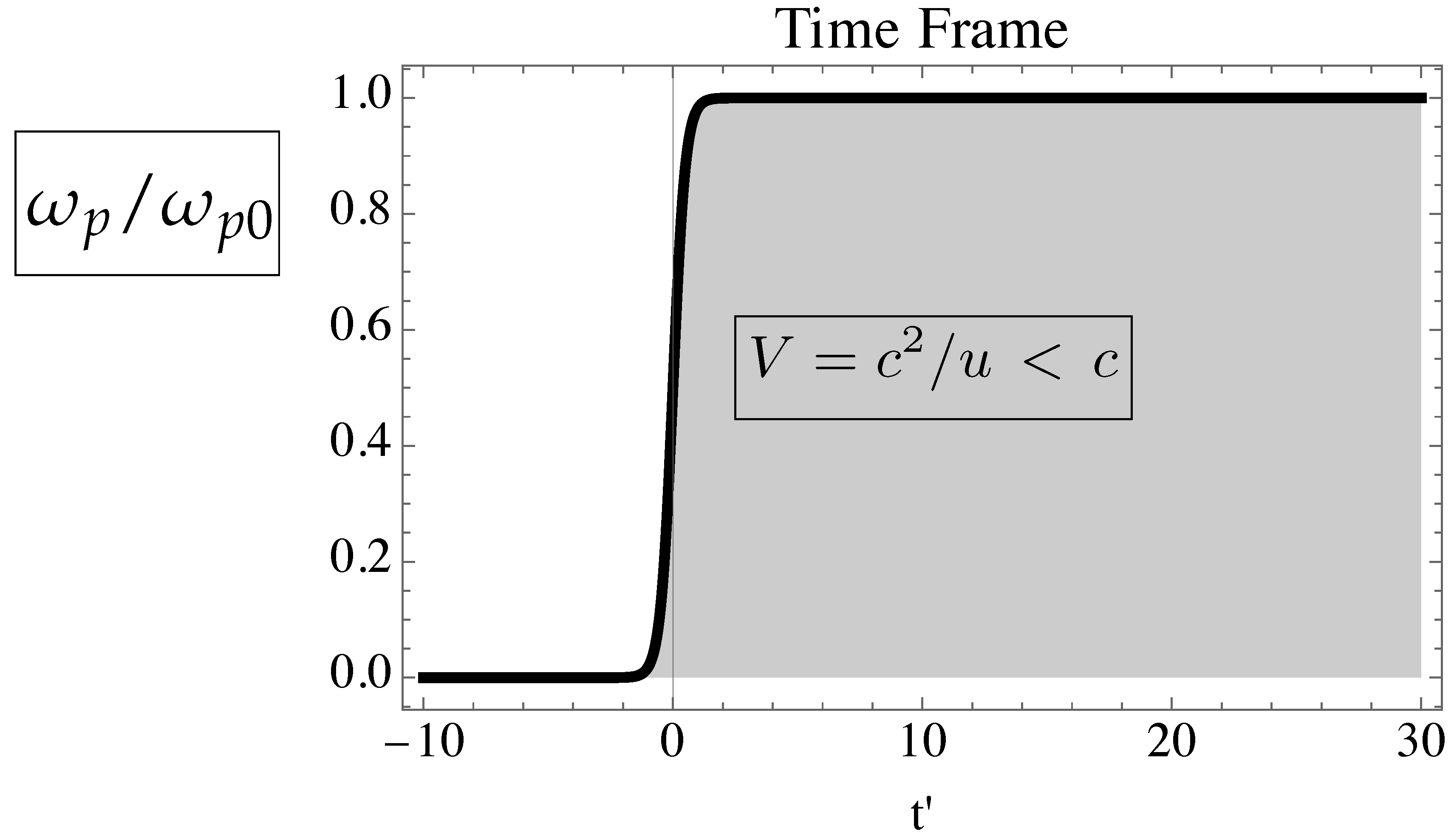
Figure 5.
Superluminal front: Electron plasma frequency in the time frame, moving with velocity with respect to the laboratory frame.
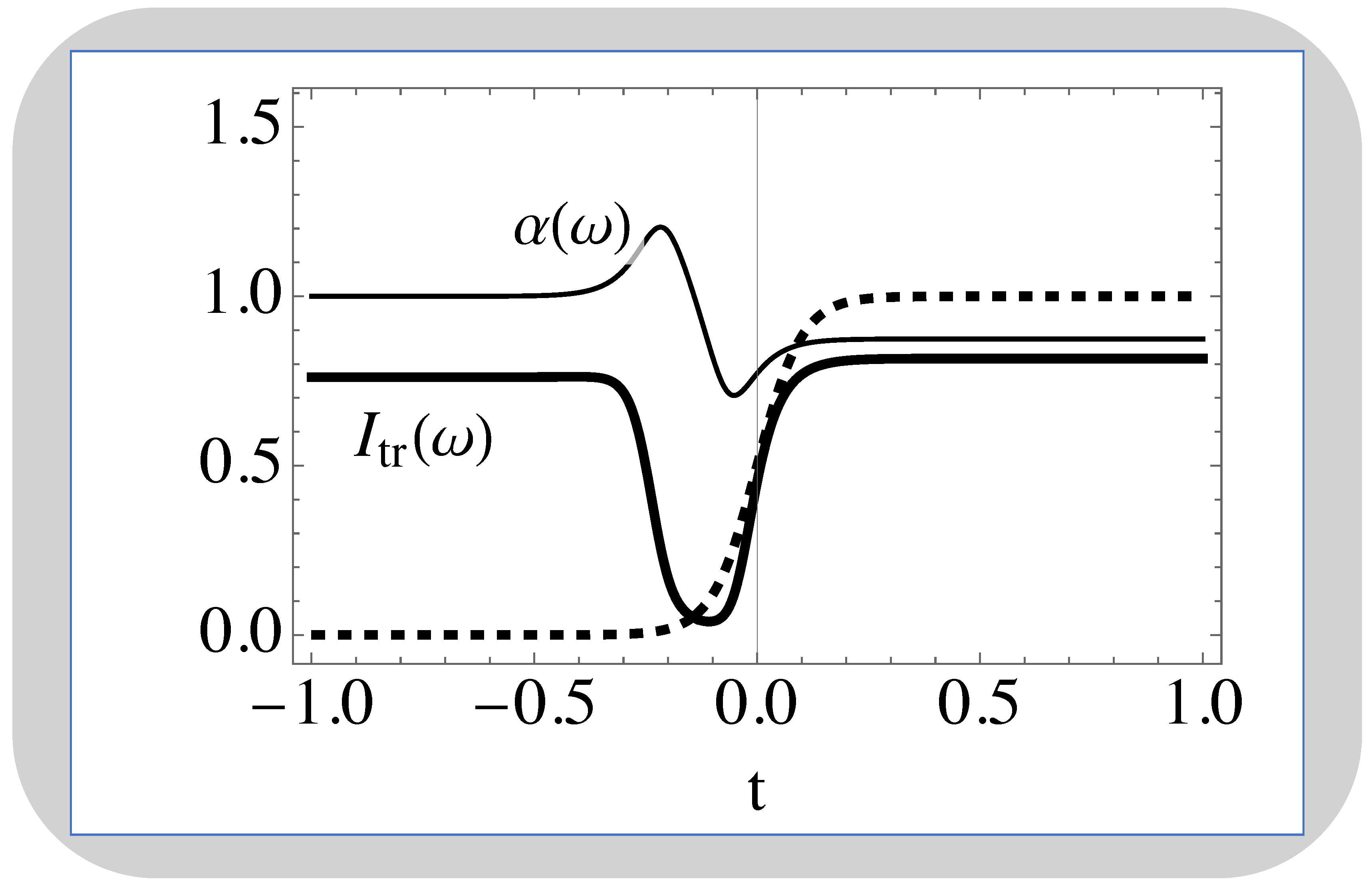
Figure 6.
Temporal Rydberg-EIT gate: Radiation intensity transmitted through the gas, (in bold), frequency shift , and Stark induced detuning, (dashed curve). Normalised units are used.
Figure 6.
Temporal Rydberg-EIT gate: Radiation intensity transmitted through the gas, (in bold), frequency shift , and Stark induced detuning, (dashed curve). Normalised units are used.
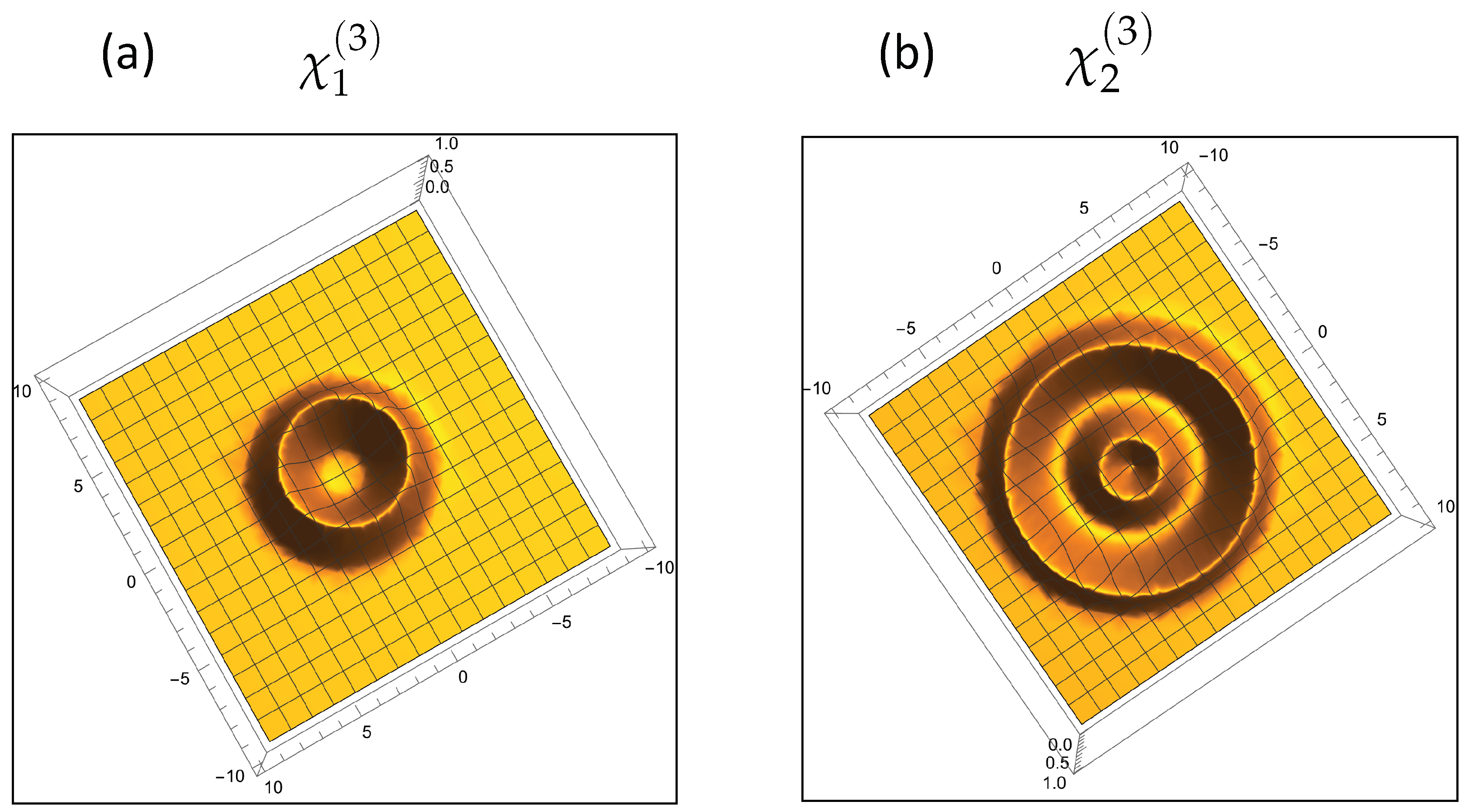
Figure 7.
Time-refraction in a static medium: diffraction ring at (a) , where the nonlinearity of the medium is described by , and at (b) where the nonlinearity susceptibility is .
Figure 7.
Time-refraction in a static medium: diffraction ring at (a) , where the nonlinearity of the medium is described by , and at (b) where the nonlinearity susceptibility is .
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).