Submitted:
30 October 2024
Posted:
30 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Results and Discussion
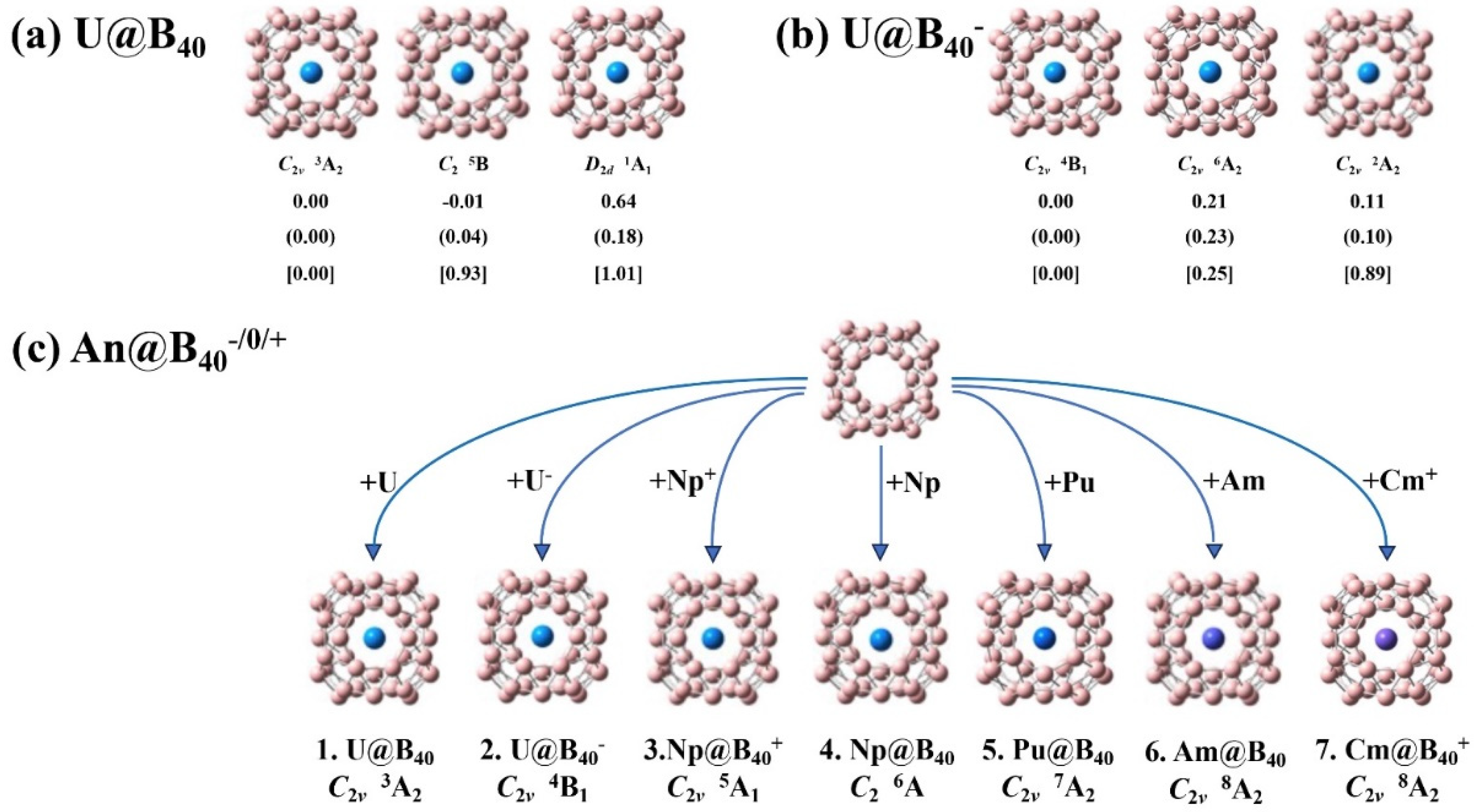
2.1. Structures and Stabilities
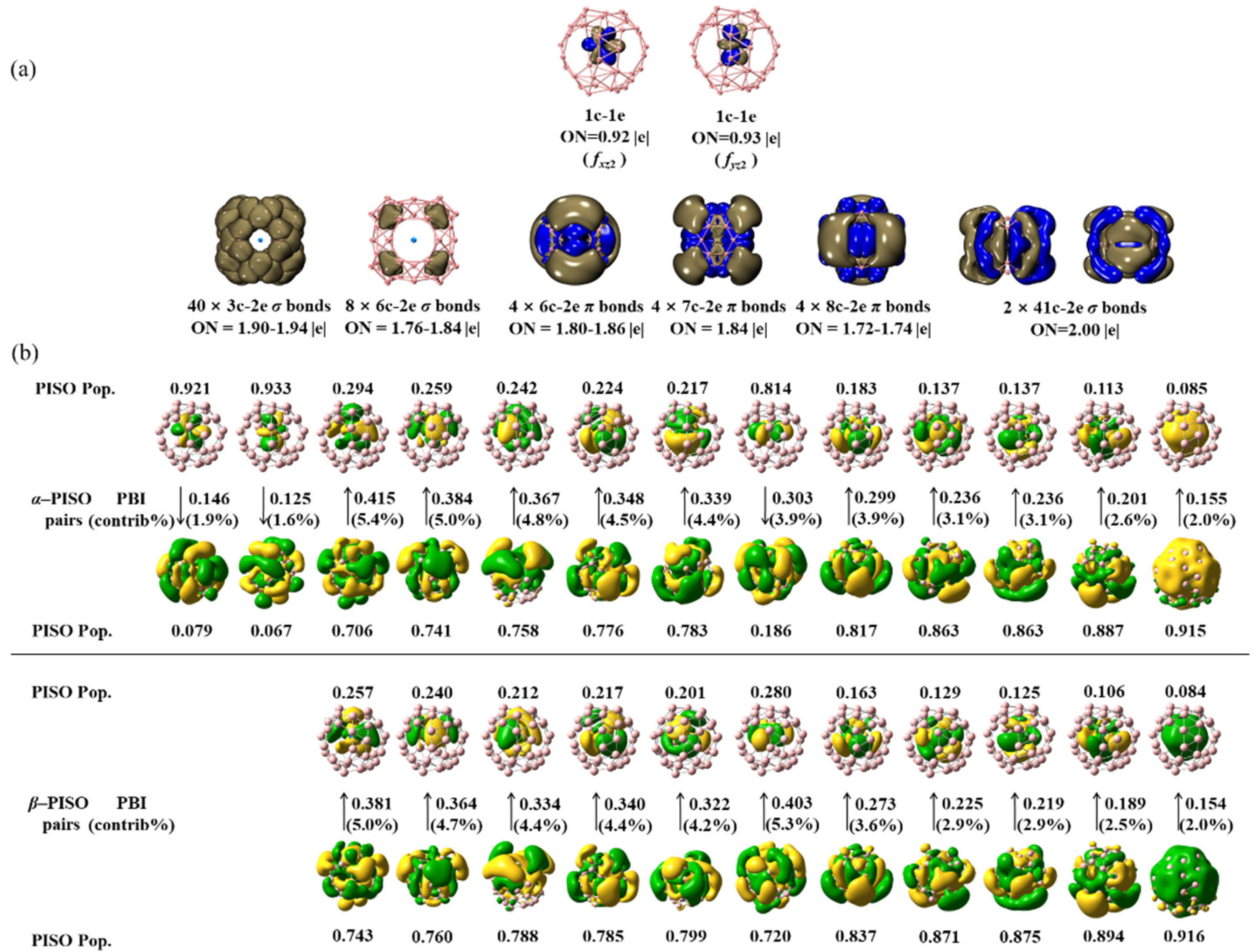
2.2. Bonding Pattern Analyses
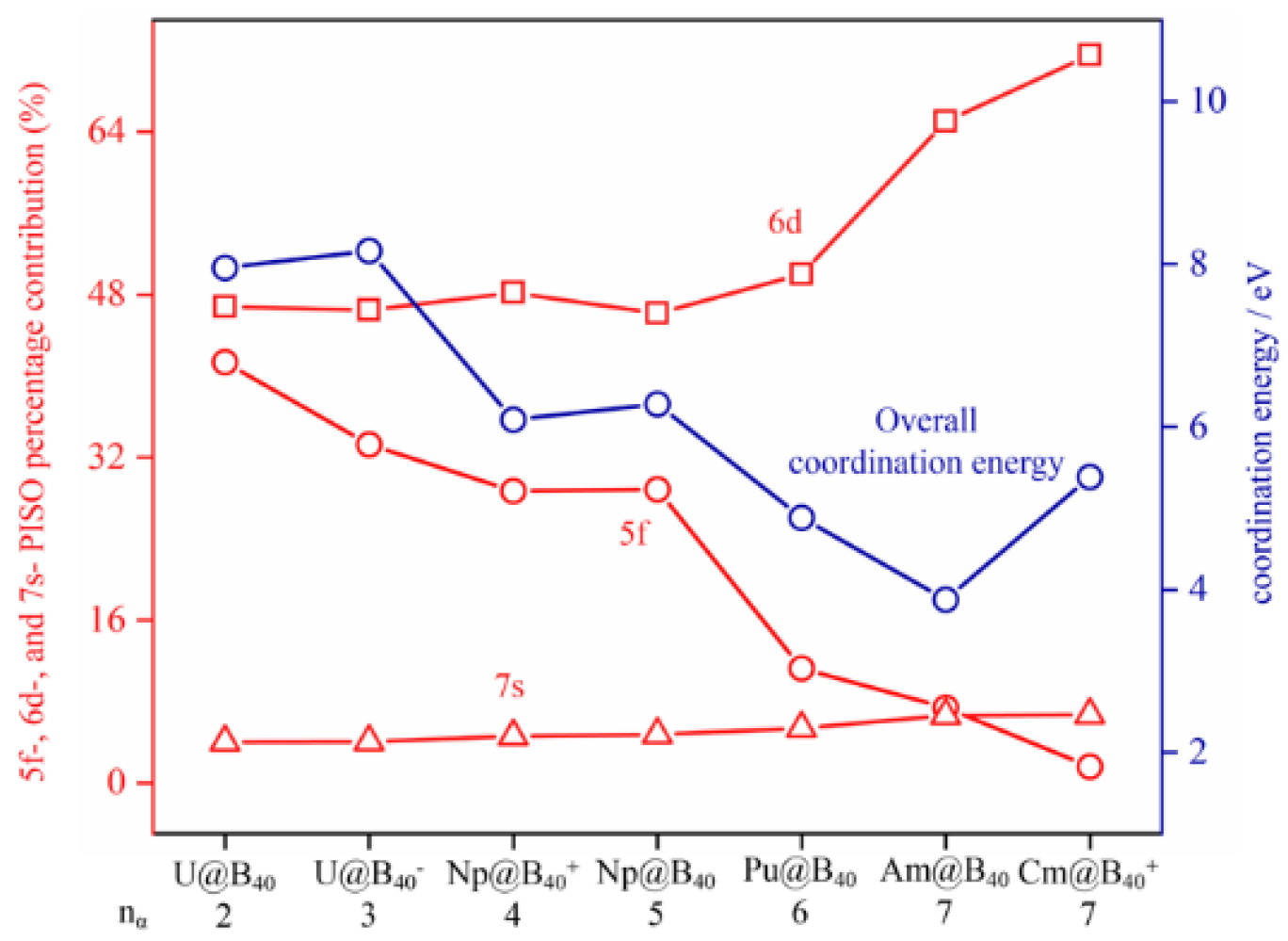
2.3. Percentage Contributions of An 5f-, 6d-, and 7s-Involved PISO Pairs to the Overall Coordination Interactions
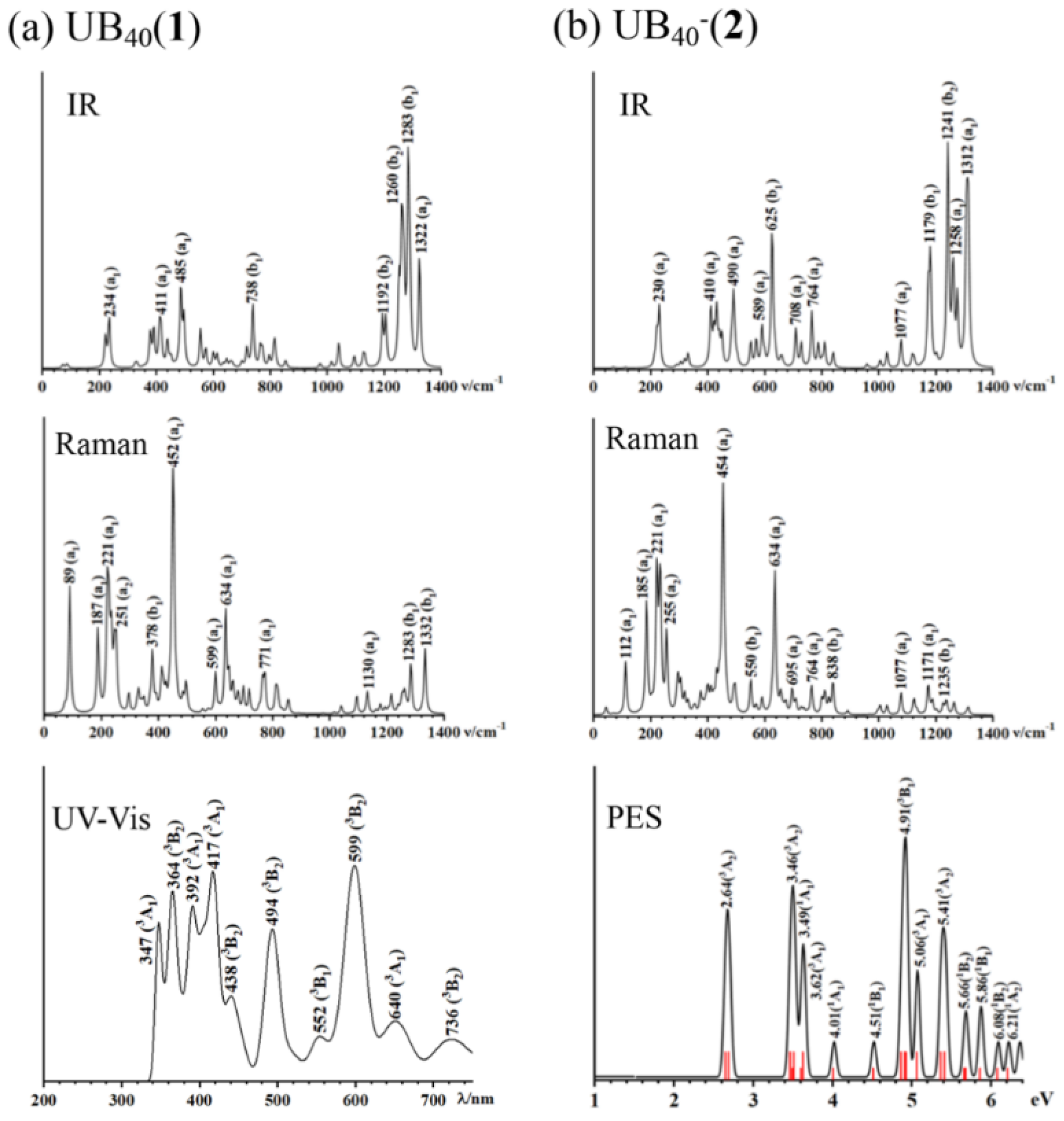
2.4. Simulated IR, Raman and PE Spectra
4. Theoretical Methods
5. Conclusions
Supplementary Materials
Author Contributions
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhai, H.J.; Zhao, Y.F.; Li, W.L.; Chen, Q.; Bai, H.; Hu, H.S.; Piazza, Z.A.; Tian, W.J.; Lu, H.G.; Wu, Y.B.; et al. Observation of an All-Boron Fullerene. Nat Chem 2014, 6, 727–731. [CrossRef]
- Chen, Q.; Li, W.L.; Zhao, Y.F.; Zhang, S.Y.; Hu, H.S.; Bai, H.; Li, H.R.; Tian, W.J.; Lu, H.G.; Zhai, H.J.; et al. Experimental and Theoretical Evidence of an Axially Chiral Borospherene. ACS Nano 2015, 9, 754–760. [CrossRef]
- Jian, T.; Chen, X.; Li, S.D.; Boldyrev, A.I.; Li, J.; Wang, L.S. Probing the Structures and Bonding of Size-Selected Boron and Doped-Boron Clusters. Chem Soc Rev 2019, 48, 3550–3591. [CrossRef]
- Bai, H.; Chen, Q.; Zhai, H.J.; Li, S.D. Endohedral and Exohedral Metalloborospherenes: M@B40 (M = Ca, Sr) and M&B40 (M = Be, Mg). Angewandte Chemie—International Edition 2015, 54, 941–945. [CrossRef]
- Jin, P.; Hou, Q.; Tang, C.; Chen, Z. Computational Investigation on the Endohedral Borofullerenes M@B40 (M = Sc, Y, La). Theor Chem Acc 2015, 134, 1–10. [CrossRef]
- Dong, H.; Hou, T.; Lee, S.T.; Li, Y. New Ti-Decorated B 40 Fullerene as a Promising Hydrogen Storage Material. Sci Rep 2015, 5, 1–8. [CrossRef]
- Fa, W.; Chen, S.; Pande, S.; Zeng, X.C. Stability of Metal-Encapsulating Boron Fullerene B40. Journal of Physical Chemistry A 2015, 119, 11208–11214. [CrossRef]
- An, Y.; Zhang, M.; Wu, D.; Fu, Z.; Wang, T.; Xia, C. Electronic Transport Properties of the First All-Boron Fullerene B40 and Its Metallofullerene Sr@B40. Physical Chemistry Chemical Physics 2016, 18, 12024–12028. [CrossRef]
- Jin, P.; Yang, L.; Liu, C.; Hou, Q.; Li, L. Computational Prediction of the Endohedral Metalloborofullerenes Tin@B40 (n = 1, 2). Theor Chem Acc 2017, 136, 1–12. [CrossRef]
- Li, H.R.; Tian, X.X.; Luo, X.M.; Yan, M.; Mu, Y.W.; Lu, H.G.; Li, S.D. Heteroborospherene Clusters Nin € B40 (n = 1-4) and Heteroborophene Monolayers Ni2 € B14 with Planar Heptacoordinate Transition-Metal Centers in H7-B7 Heptagons. Sci Rep 2017, 7, 1–7. [CrossRef]
- Li, S.X.; Zhang, Z.P.; Long, Z.W.; Qin, S.J. Structures, Stabilities and Spectral Properties of Metalloborospherenes MB 0/- 40 (M = Cu, Ag, and Au). RSC Adv 2017, 7, 38526–38537. [CrossRef]
- Yu, T.; Gao, Y.; Xu, D.; Wang, Z. Actinide Endohedral Boron Clusters: A Closed-Shell Electronic Structure of U@B40. Nano Res 2018, 11, 354–359. [CrossRef]
- Wang, J.; Xie, W.; Jiang, W.; Wu, X.; Wang, Z. The Reliability of the Density-Functional Theory in Actinide Endohedral Systems. Adv Theory Simul 2019, 2, 1–7. [CrossRef]
- Zhang, N.; Li, A.; Wang, C.; Wu, Q.; Lan, J.; Chai, Z.; Zhao, Y.; Shi, W. Theoretical Prediction of Chiral Actinide Endohedral Borospherenes. New Journal of Chemistry 2021, 45, 6803–6810. [CrossRef]
- Zhang, N.; Wang, C.; Wu, Q.; Lan, J.; Chai, Z.; Shi, W. Highly Stable Actinide(Iii) Complexes Supported by Doubly Aromatic Ligands†. Physical Chemistry Chemical Physics 2022, 24, 5921–5928. [CrossRef]
- Wang, C.Z.; Bo, T.; Lan, J.H.; Wu, Q.Y.; Chai, Z.F.; Gibson, J.K.; Shi, W.Q. Ultrastable Actinide Endohedral Borospherenes. Chemical Communications 2018, 54, 2248–2251. [CrossRef]
- Wang, J.; Wang, C.Z.; Wu, Q.Y.; Lan, J.H.; Chai, Z.F.; Nie, C.M.; Shi, W.Q. Construction of the Largest Metal-Centered Double-Ring Tubular Boron Clusters Based on Actinide Metal Doping. Journal of Physical Chemistry A 2022, 126, 3445–3451. [CrossRef]
- Zhang, N.; Wang, C.; Wu, Q.; Lan, J.; Chai, Z.; Shi, W. Highly Stable Actinide(Iii) Complexes Supported by Doubly Aromatic Ligands†. Physical Chemistry Chemical Physics 2022, 24, 5921–5928. [CrossRef]
- Xi, C.; Yang, L.; Liu, C.; You, P.; Li, L.; Jin, P. Lanthanide Metals in the Boron Cages: Computational Prediction of M@Bn (M = Eu, Gd; n = 38, 40). Int J Quantum Chem 2018, 118, 1–11. [CrossRef]
- Li, Y.; Wang, Y.; Zhou, Z.; Gao, Y.; Chen, Y.; Zhang, G.; Ma, C. Insights into ThB40: Stability, Electronic Structure, and Interaction. Molecules 2024, 29. [CrossRef]
- Wang, J.; Xie, W.; Jiang, W.; Wu, X.; Wang, Z. The Reliability of the Density-Functional Theory in Actinide Endohedral Systems. Adv Theory Simul 2019, 2, 1–7. [CrossRef]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. Journal of Chemical Physics 1999, 110, 6158–6170. [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative Assessment of a New Nonempirical Density Functional: Molecules and Hydrogen-Bonded Complexes. Journal of Chemical Physics 2003, 119, 12129–12137. [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J Chem Phys 1980, 72, 650–654. [CrossRef]
- Cao, X.; Dolg, M. Segmented Contraction Scheme for Small-Core Actinide Pseudopotential Basis Sets. Journal of Molecular Structure: THEOCHEM 2004, 673, 203–209. [CrossRef]
- Cao, X.; Dolg, M.; Stoll, H. Valence Basis Sets for Relativistic Energy-Consistent Small-Core Actinide Pseudopotentials. Journal of Chemical Physics 2003, 118, 487–496. [CrossRef]
- Guo, Y.; Riplinger, C.; Becker, U.; Liakos, D.G.; Minenkov, Y.; Cavallo, L.; Neese, F. Communication: An Improved Linear Scaling Perturbative Triples Correction for the Domain Based Local Pair-Natural Orbital Based Singles and Doubles Coupled Cluster Method [DLPNO-CCSD(T)]. Journal of Chemical Physics 2018, 148. [CrossRef]
- Neese, F. The ORCA Program System. Wiley Interdiscip Rev Comput Mol Sci 2012, 2, 73–78. [CrossRef]
- Pantazis, D.A.; Neese, F. All-Electron Scalar Relativistic Basis Sets for the Actinides. J Chem Theory Comput 2011, 7, 677–684. [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. Gaussian 09, Revision D.01, Gaussian, Inc.: Wallingford, CT, USA, 2013.
- Vandevondele, J.; Krack, M.; Mohamed, F.; Parrinello, M.; Chassaing, T.; Hutter, J. Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comput Phys Commun 2005, 167, 103–128. [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of Electronic Excitations within the Adiabatic Approximation of Time Dependent Density Functional Theory. Chem Phys Lett 1996, 256, 454–464. [CrossRef]
- Casida, M.E.; Jamorski, C.; Casida, K.C.; Salahub, D.R. Molecular Excitation Energies to High-Lying Bound States from Time-Dependent Density-Functional Response Theory: Characterization and Correction of the Time-Dependent Local Density Approximation Ionization Threshold. Journal of Chemical Physics 1998, 108, 4439–4449. [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing Paradigms of Chemical Bonding: Adaptive Natural Density Partitioning. Physical Chemistry Chemical Physics 2008, 10, 5207–5217. [CrossRef]
- Tkachenko, N. V.; Boldyrev, A.I. Chemical Bonding Analysis of Excited States Using the Adaptive Natural Density Partitioning Method. Physical Chemistry Chemical Physics 2019, 21, 9590–9596. [CrossRef]
- Zhang, J.X.; Sheong, F.K.; Lin, Z. Unravelling Chemical Interactions with Principal Interacting Orbital Analysis. Chemistry—A European Journal 2018, 24, 9639–9650. [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural Bond Orbital Analysis Program. J Comput Chem 2013, 34, 1429–1437. [CrossRef]
- Sheong, F.K.; Zhang, J.X.; Lin, Z. Principal Interacting Spin Orbital: Understanding the Fragment Interactions in Open-Shell Systems. Physical Chemistry Chemical Physics 2020, 22, 10076–10086. [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J Mol Graph 1996, 14, 33–38. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



