Submitted:
25 October 2024
Posted:
25 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
| Wells |
Barometric Efficiency, Eb, | Tidal Sensitivity, AV*, hPa/10−9 |
Skempton’s Coefficient, B |
Specific Elastic Capacity, SS, m−1×10−7 |
Porosity, φ |
Transmi-ssivity, Т, m2/day |
Hydraulic Conductivity, m/с |
|---|---|---|---|---|---|---|---|
| YuZ-5 | 0.40 | 0.161 | 0.67 | 16.9 | 0.11 | 7.8 | 9⋅10−7 |
| E-1 | 0.1 | 0.015 | 0.09 | 2.9 | 0.05 | 0.005 | 3.2⋅10−9 |
| 1303 | 0.43 | 0.215 | 0.64 | 10.3 | 0.07 | 0.32 | 3.7⋅10−8 |
Wells and Observations
| EQ Date |
EQ Time |
EQ Hypocenter Coordinates |
Mw | Earthquake Source Mechanism According to CMT https://www.globalcmt.org (accessed on 20 January 2024) |
Earthquake Source Dimensions**** |
Movement Along the Rupture***** U, m |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N, (°) |
E, (°) |
H, km |
Scalar Seismic Moment M0, N×m×1020 |
Strike, (°) |
Dip, (°) |
Rake, (°) |
W, m |
L, m |
||||
| 03.04.2023 | 03:06:59 | 52.58 | 158.76 | 95 | 6.6* 6.5** 6.6*** |
0.1 | 215(104) | 86(10) | 80(159) | 15798 | 41210 | 0.46 |
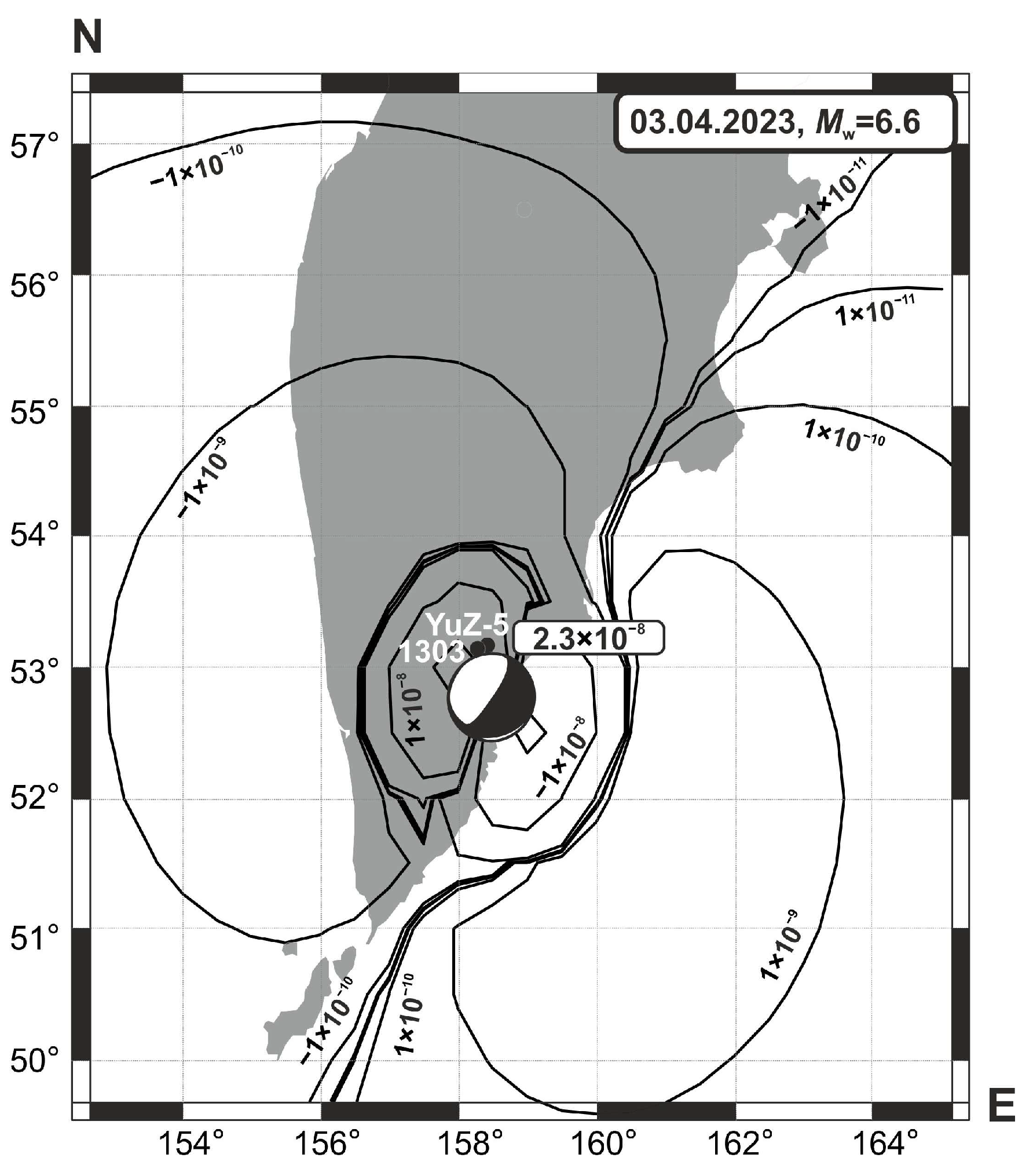
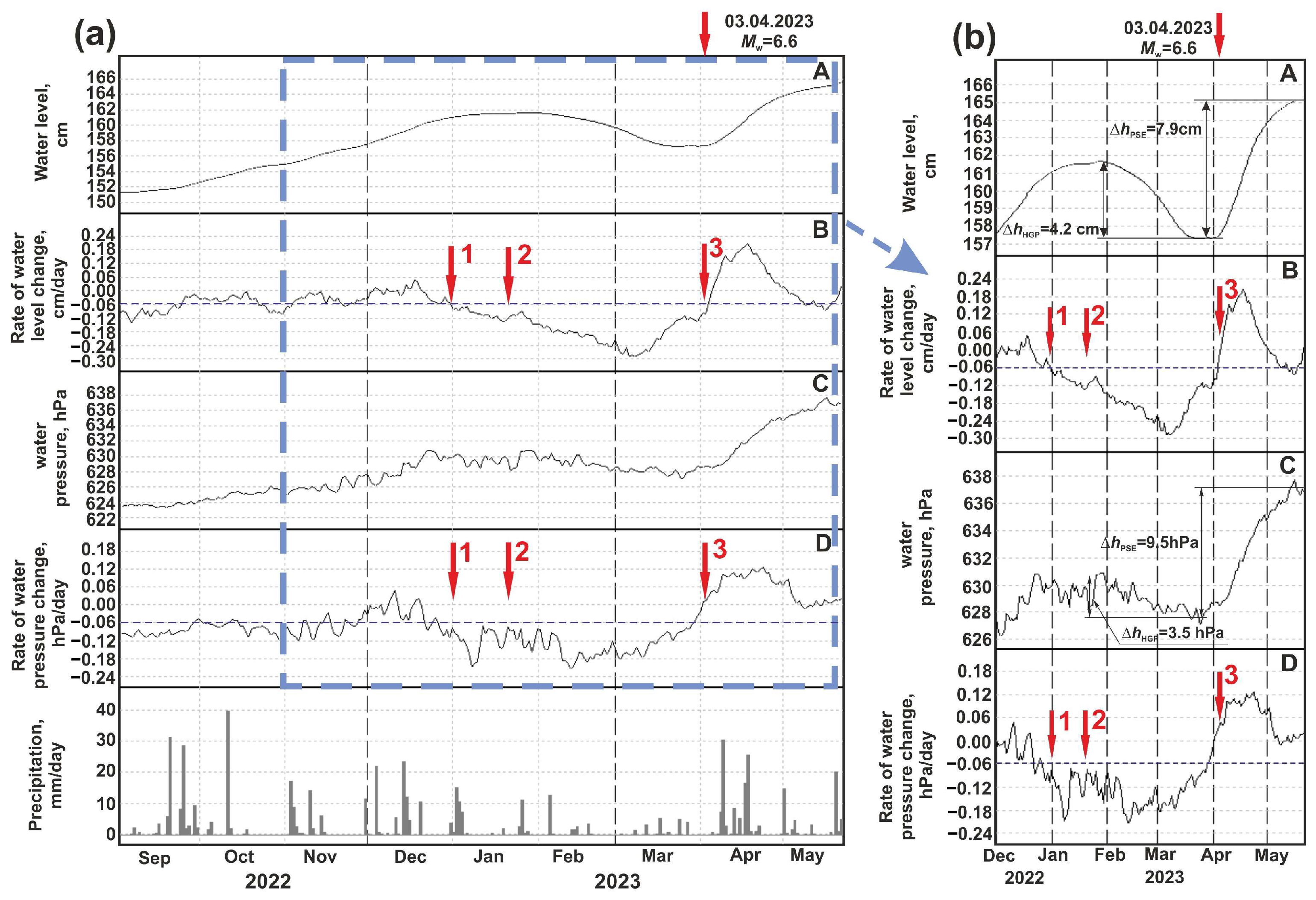
3 April 2023 Earthquake, Mw=6.6
2. Seismo-Hydrogeodynamic Effects
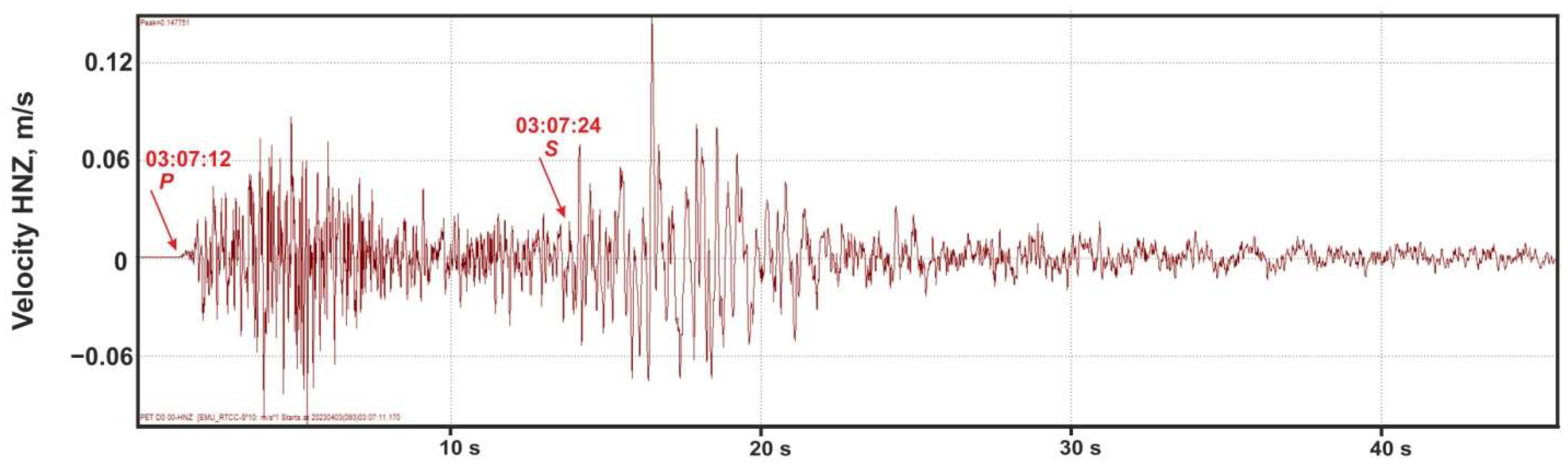
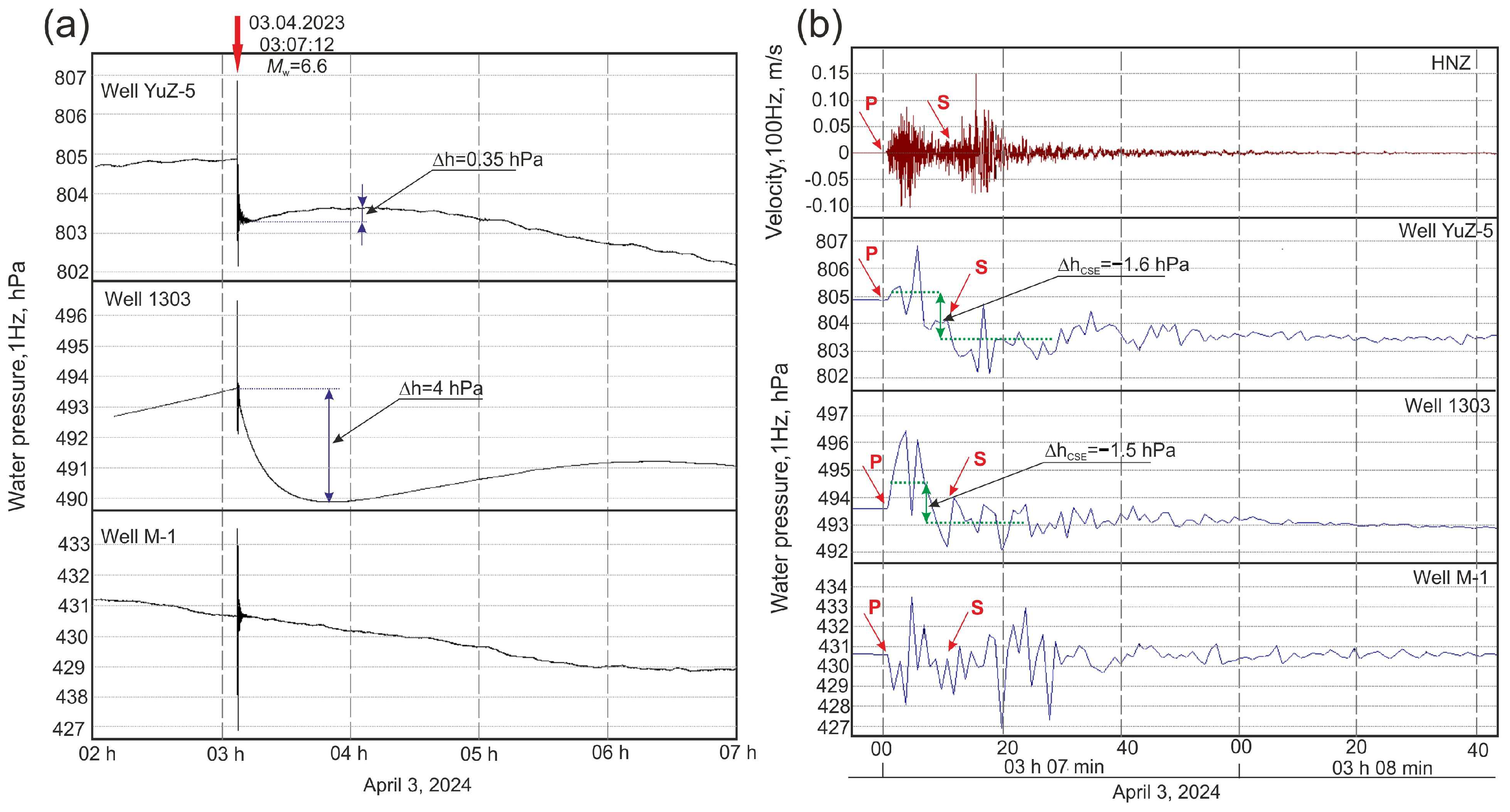
2.1. High-Frequency Records of Underground Water Pressure Variations
2.1.1. Coseismic Effects in Water Pressure Changes
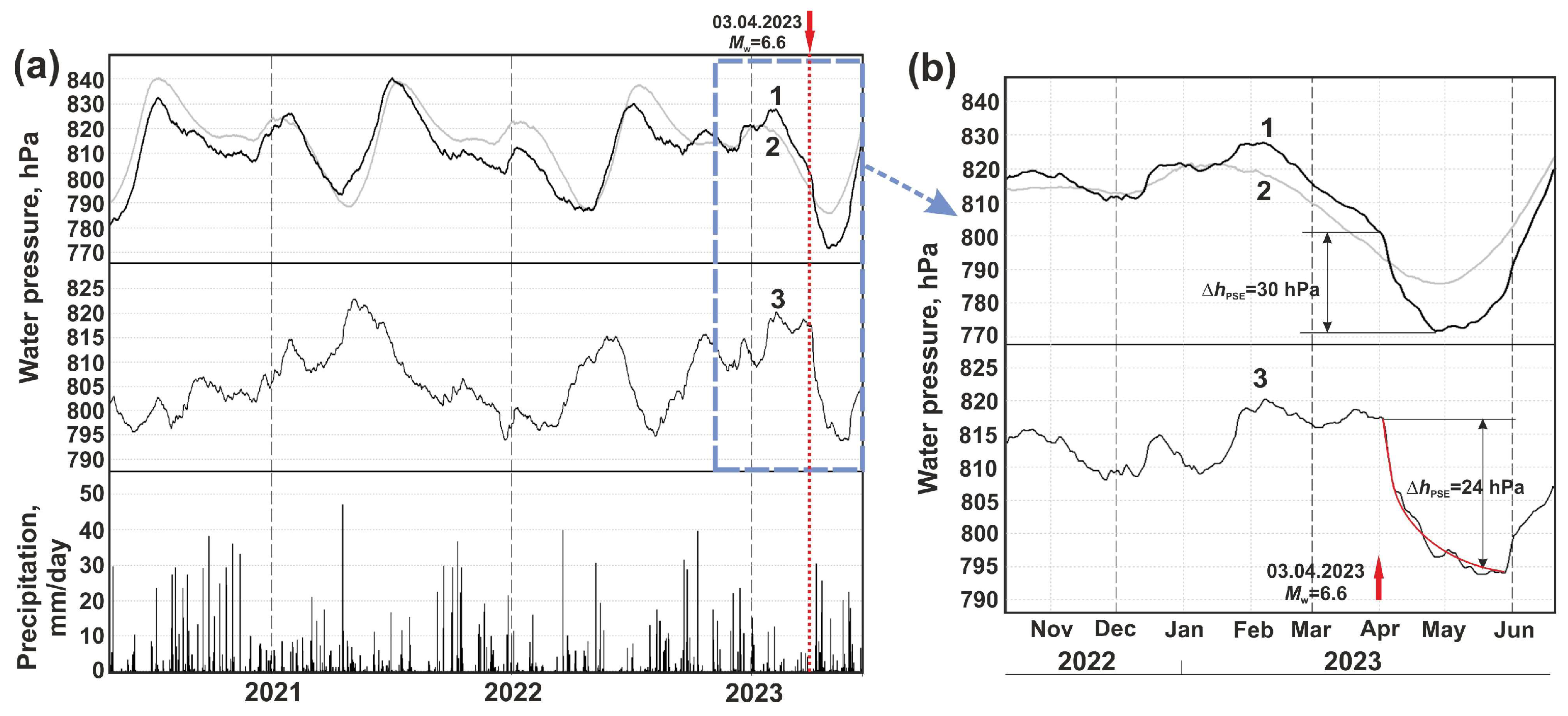
2.2. Average Hourly Variations of Water Pressure in Well YuZ-5
2.3. Average Daily Variations in Water Pressure in Well E-1
3. Discussion
3.1. Typification of Seismo-Hydrogeodynamic Effects in Wells YuZ-5 and E-1
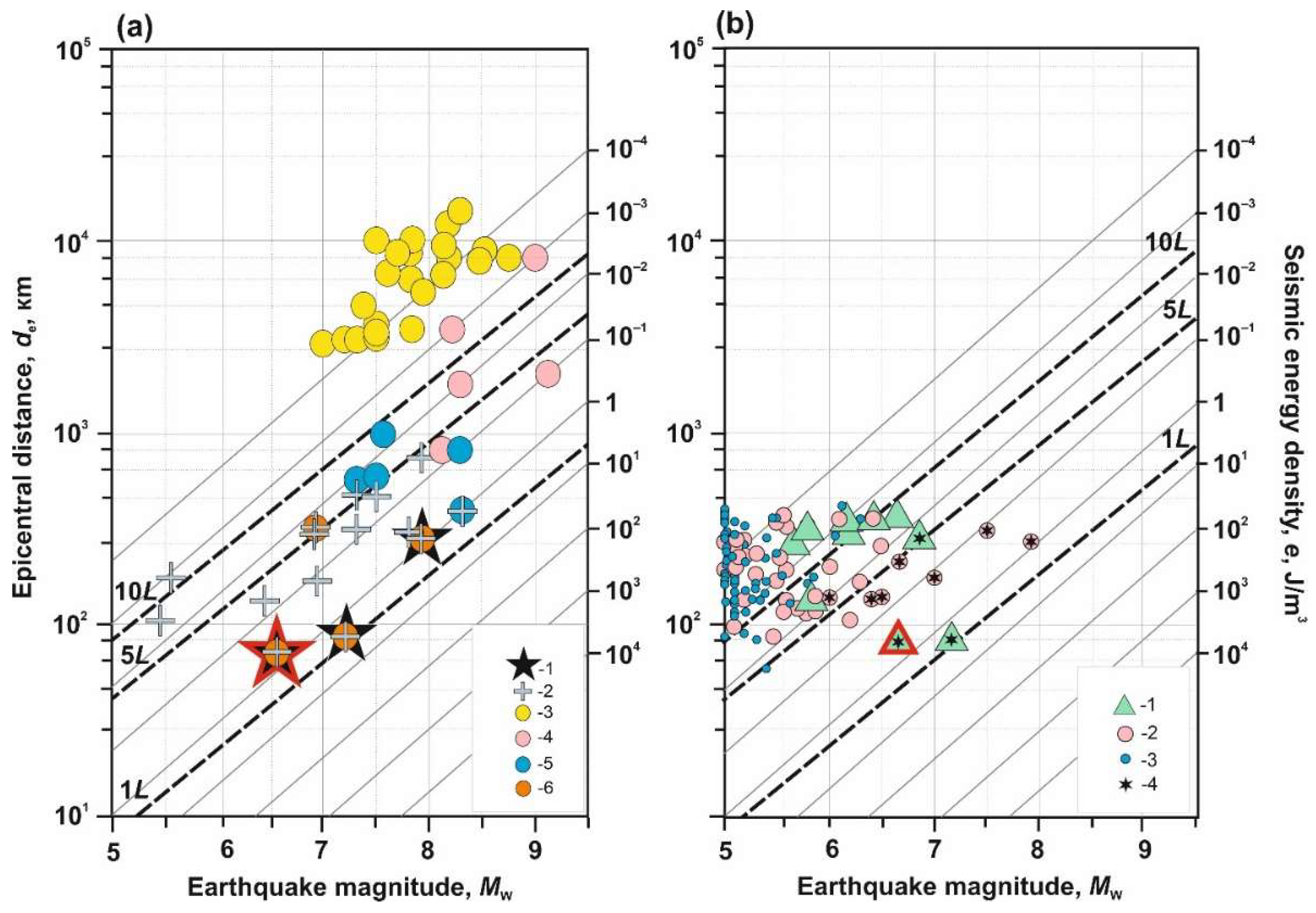
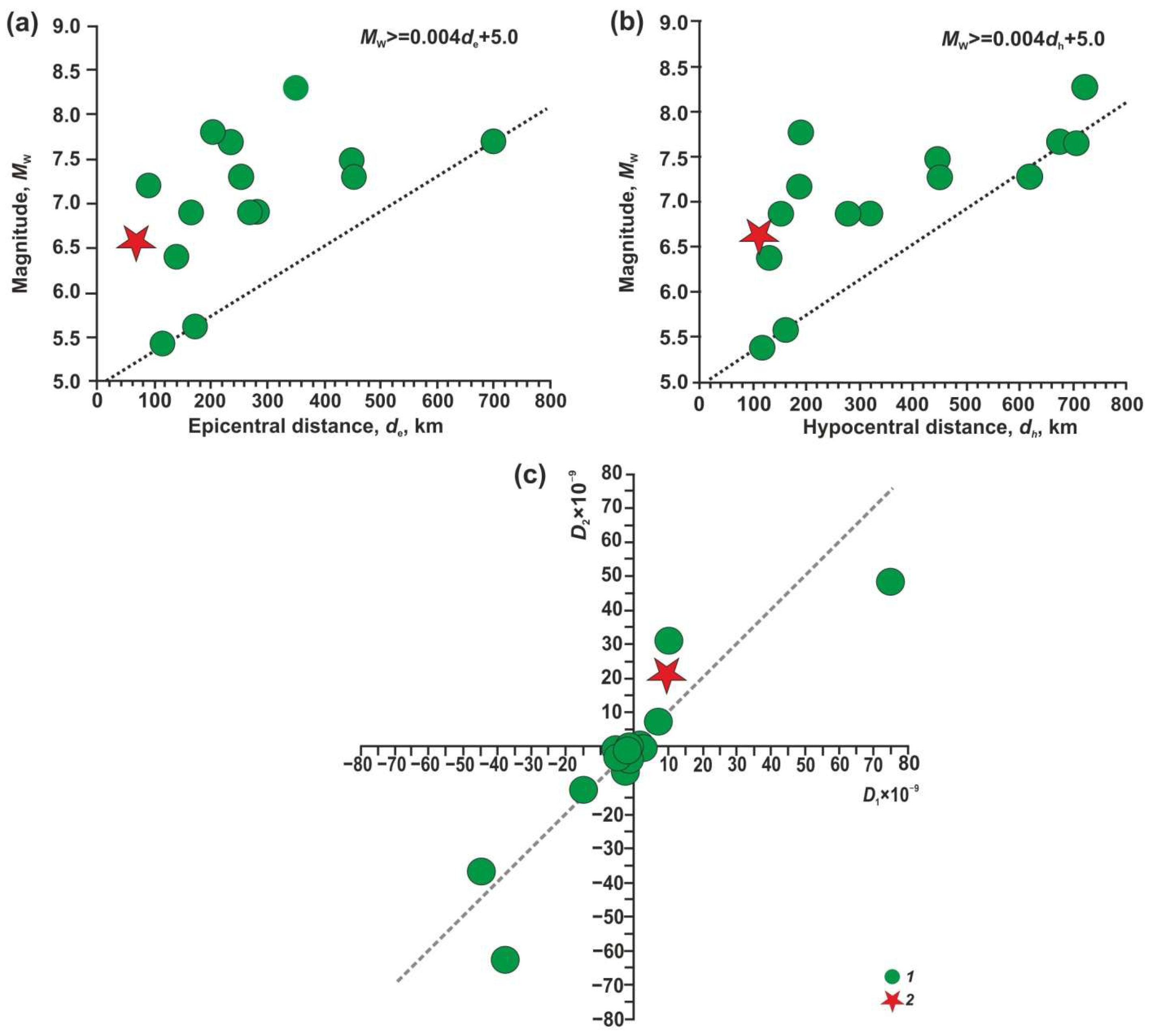
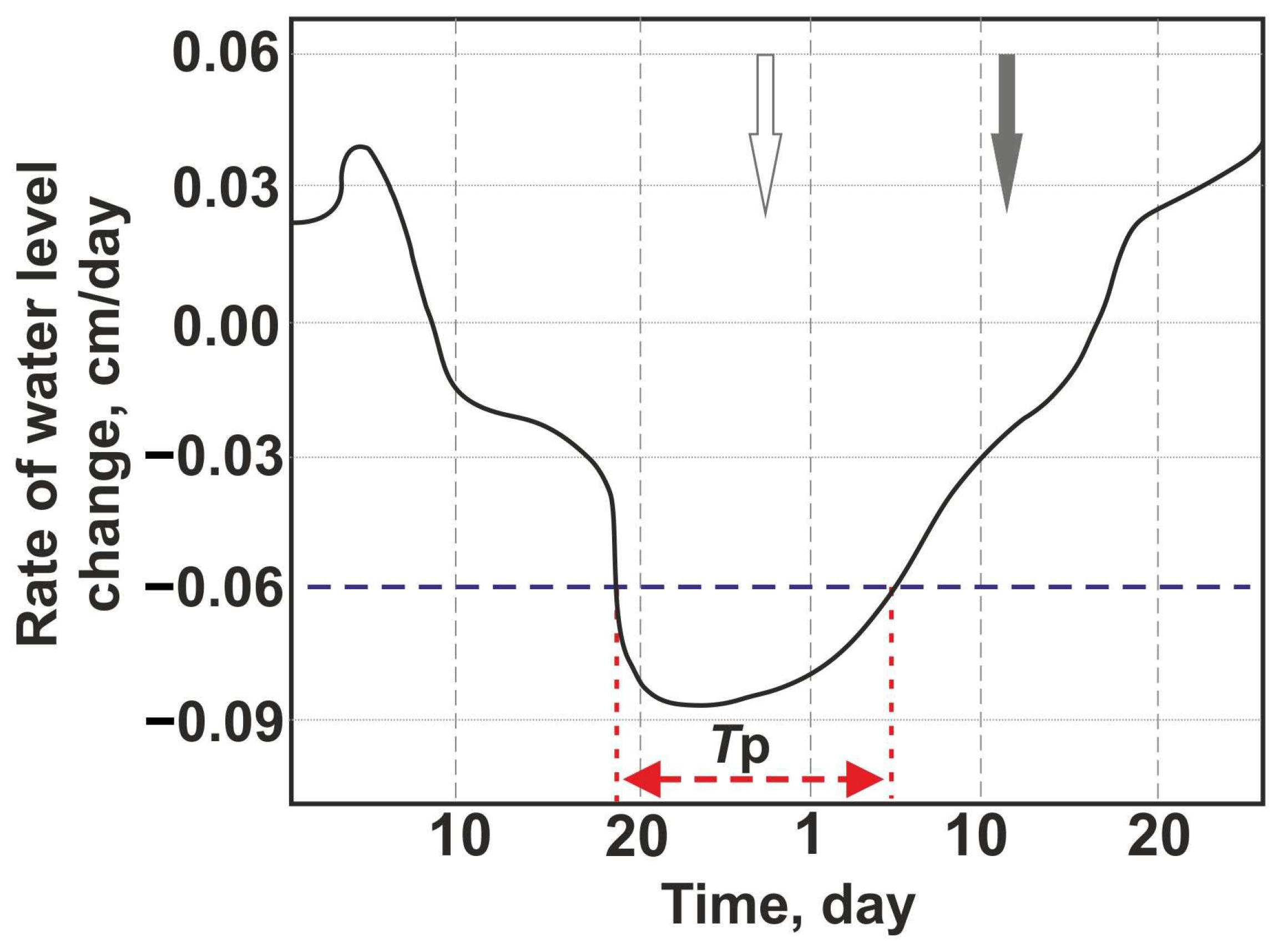
3.2. About the Forecast of 3 April 2023 Earthquake
3. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, C.-Y.; Manga, M. Earthquakes and Water. Lecture Notes in Earth Sciences; Springer: Berlin, Germany, 2010; p. 225. [CrossRef]
- Wang, C.-Y.; Manga, M. Water and Earthquakes. Lecture Notes in Earth System Sciences; Springer: Cham, Switzerland, 2021; p. 387. [CrossRef]
- Kopylova, G. N.; Boldina, S. V. Hydrogeological Earthquake Precursors: A Case Study from the Kamchatka Peninsula. Front. Earth Sci. 2020, 8, 576017. [CrossRef]
- Sheymovich, V. S. Explanation to the State Geological Map of the Russian Federation. Scale 1:200,000. Series South Kamchatka; VSEGEI: Moscow, Russia, 2000; p. 302. (In Russian).
- Kiryukhin, A.; Lavrushin, V.; Kiryukhin, P.; Voronin, P. System of Koryaksky–Avachinsky Volcanoes (Kamchatka, Russia). Geofluids 2017, 2017, 4279652. [CrossRef]
- Taran, Y.; Ryabinin, G.; Pokrovsky, B.; Malik, N.; Cienfuegos, E. Methane–rich thermal and mineral waters of the Avachinsky Depression, Kamchatka. Appl. Geochem. 2022, 145, 105414. [CrossRef]
- Boldina, S. V.; Kopylova, G. N.; Kobzev, V. A. Study of Seismic Effects on Changes in Groundwater Pressure: Equipment and Some Well Observastion Results for the Kamchatka Peninsula. Geodyn. Tectonophys. 2022, 13, 0594. (In Russian). [CrossRef]
- Kopylova, G.; Boldina, S. Seismo-Hydrogeodynamic Effects in Groundwater Pressure Changes: A Case Study of the YuZ-5 Well on the Kamchatka Peninsula. Water. 2023, 15, 2174. [CrossRef]
- Kopylova, G. N.; Boldina, S. V. On the Relationships of Water-Level Variations in the E-1 Well, Kamchatka to the 2008–2009 Resumption of Activity on Koryakskii Volcano and to Large (M ≥ 5) Earthquakes. J. Volcanol. Seismol. 2012, 6(5), 316–328. [CrossRef]
- Gordeev, E. I.; Pavlov, V. M. Subduction of the Pacific plate under Kamchatka: Seismic velocity of underthrust. Izv. Phys. Solid Earth 2009, 45(4), 326–337. [CrossRef]
- Gordeev, E. I.; Pinegina, T. K.; Lander, A. V.; Kozhurin, A. I. Beringia: Seismic Hazard and Fundamental Problems of Geotectonics. Izv. Phys. Solid Earth 2015, 51( 4), 512–521. [CrossRef]
- Kopylova, G. N.; Boldina, S. V. Hydrogeoseismological Research in Kamchatka: 1977–2017. J. Volcanol. Seismol. 2019, 13(2), 71–84. [CrossRef]
- Riznichenko, Y. V. The source dimensions of the crustal earthquakes and the seismic moment. In Issledovaniya po Fizike Zemletryasenii (Studies in Earthquake Physics); Nauka: Moscow, Russia, 1976; pp. 9–27. (In Russian).
- Rojstaczer, S. Determination of fluid flows properties from the response of water levels in wells to atmospheric loading. Water Resour. Res. 1988, 24, 1927–1938.
- Boldina, S. V.; Kopylova, G. N. Coseismic effects of the 2013 strong Kamchatka earthquakes in well YuZ-5. Bull. Kamchatka Reg. Assoc. “Educ.-Sci.” Cent. Earth Sci. 2016, 30, 66–76. (In Russian).
- Kopylova, G. N. Variations of Water Level Elizovskaya 1 Well, Kamchatka Due to Large Earthquakes: 1987–1998 Observations. J. Volcanol. Seismol. 2001, 2, 39–52. (In Russian).
- Kopylova, G. N.; Boldina, S. V.; Smirnov, A. A.; Chubarova, E. G. Experience in Registration of Variations Caused by Strong Earthquakes in the Level and Physicochemical Parameters of Ground Waters in the Piezometric Wells: The Case of Kamchatka. Seism. Instrum. 2017, 53, 286–295. [CrossRef]
- Kopylova, G. N.; Boldina, S. V. Effects of Seismic Waves in Water Level Changes in a Well: Empirical Data and Models. Izv. Phys. Solid Earth 2020, 56, 530–549. [CrossRef]
- Kopylova, G. N.; Boldina S. V. Seismohydrogeological Phenomena as an Earthquake’s Trigger Impact on Groundwater (by the Example of the Wells of the Petropavlovsk-Kamchatsky Test Site, Kamchatka Peninsula. Izv. Phys. Solid Earth 2023, 59(3), 405-420. [CrossRef]
- Kopylova, G. N.; Sugrobov, V. M.; Khatkevich, Yu. M. Variations in the regime of springs and hydrogeological boreholes in the Petropavlovsk polygon (Kamchatka) related to earthquakes. J. Volcanol. Seismol. 1994, 2, 53‒70. (in Russian).
- Kopylova, G.; Boldina, S. Anomalies in Groundwater Composition Caused by Earthquakes: Examples and Modeling Issues. E3S Web of Conferences 2019, 98, 01029. [CrossRef]
- Kopylova, G.; Boldina, S. Preseismic Groundwater Ion Content Variations: Observational Data in Flowing Wells of the Kamchatka Peninsula and Conceptual Model. Minerals 2021, 11, 731. [CrossRef]
- Kopylova, G. N.; Kulikov, G. V.; Timofeev, V. M. Otsenka sostoyaniya i perspektivy razvitiya gidrogeodeformatsionnogo monitoringa seysmoaktivnykh regionov Rossii (Assessment of the state and prospects for the development of hydrogeodeformational monitoring of seismically active regions of Russia). Razvedka i Okhrana Nedr (Exploration and Protection of Subsoil) 2007, 11, 75-83. (In Russian).
- Kopylova, G. N.; Smolina, N. N. Water-level changes in the wells of Kamchatka at the time of the Mw 7.6, April 20, 2006 Olyutorskii earthquake. J. Volcanolog. Seismol. 2010, 4, 180–192. [CrossRef]
- Wang, C.-Y. Liquefaction beyond the near field. Seismol. Res. Lett. 2007, 78, 512–517. [CrossRef]
- Medvedev, S. V.; Sponheuer, W.; Kárník, V. Seismic Intensity Scale MSK-64; Akad. Nauk SSSR, Geofiz. Kom: Moscow, Russia, 1965; p. 11. (In Russian).
- Okada, Y. Surface deformation due to shear and tensile faults in a half–space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154.
- Chia, Y.; Chiu, J.-J.; Chiang, Y.-H.; Lee, T.-P.; Wu, Y.-M.; Horng, M.-J. Implications of coseismic groundwater level changes observed at multiple-well monitoring stations. Geophys. J. Int. 2008, 172, 293–301. [CrossRef]
- Shi, Z.; Wang, G.; Liu, C. Co-seismic groundwater level changes induced by the May 12, 2008 Wenchuan earthquake in the near field. Pure Appl. Geophys. 2013, 170, 1773–1783. [CrossRef]
- Shi, Z.; Wang, G.; Manga, M.; Wang, C.-Y. Mechanism of co–seismic water level change following four great earthquakes—Insights from co-seismic responses throughout the Chinese mainland. Earth Planet. Sci. Lett. 2015, 430, 66–74. [CrossRef]
- Sun, X.; Wang, G.; Yang, X. Coseismic response of water level in Changping well, China, to the Mw 9.0 Tohoku earthquake. J. Hydrol. 2015, 531, 1028–1039. [CrossRef]
- Zhang, S.; Shi, Z.; Wang, G.; Zhang, Z. Quantitative Assessment of the Mechanisms of Earthquake–Induced Groundwater–Level Change in the MP Well, Three Gorges Area. Pure Appl. Geophys. 2018, 175, 2475–2484. [CrossRef]
- Shalev, E.; Kurzon, I.; Doan, M.-L.; Lyakhovsky, V. Sustained water-level changes caused by damage and compaction induced by teleseismic earthquakes. J. Geophys. Res. Solid Earth 2016, 121, 4943–4954. [CrossRef]
- Shalev, E.; Kurzon, I.; Doan, M.-L.; Lyakhovsky, V. Water–level oscillations caused by volumetric and deviatoric dynamic strains. Geophys. J. Int. 2016, 204, 841–851. [CrossRef]
- Kopylova, G. N.; Steblov, G. M.; Boldina, S. V.; Sdel’nikova I. A. The possibility of estimating the coseismic deformation from water level observations in wells. Izv. Phys. Solid Earth 2010, 46, 47–56. [CrossRef]
- Xiang, Y.; Sun, X.; Gao, X. Different coseismic groundwater level changes in two adjacent wells in a fault-intersected aquifer system. J. Hydrol. 2019, 578, 124123. [CrossRef]
- Kopylova, G. N.; Lyubushin, A. A.; Boldina, S. V. Statistical Analysis of Precision Water Level Data from Observations in a Seismoactive Region: Case Study of the YuZ-5 Well, Kamchatka. Seism. Instrum. 2019, 55, 507–523. [CrossRef]
- Cooper H. H.; Bredehoeft J. D.; Papadopulos I. S.; Bennet R.R. The response of well-aquifer system to seismic waves. Journal of Geophysical Research 1965, 70, 3915−3926.
- Boldina, S. V.; Kopylova, G. N. Effects of the January 30, 2016, Mw = 7.2 Zhupanovsky earthquake on the water level variations in wells YuZ-5 and E-1 in Kamchatka. Geodyn. Tectonophys. 2017, 8, 863–880. (In Russian). [CrossRef]
- Wang, C.-Y.; Manga, M. Changes in Tidal and Barometric Response of Groundwater during Earthquakes—A Review with Recommendations for Better Management of Groundwater Resources. Water 2023, 15, 1327. [CrossRef]
- Kopylova, G. N. Earthquake–induced Water Level Changes in the YuZ-5 Well Kamchatka. J. Volcanol. Seismol. 2006, 6, 52–64. (In Russian).
- Brodsky, E.E.; Roeloffs, E.; Woodcock, D.; Gall, I.; Manga, M.A. A Mechanism for sustained groundwater pressure changes induced by distant earthquakes. J. Geophys. Res. 2003, 108, 2390–2400. [CrossRef]
- Kopylova, G. N.; Boldina, S. V. The mechanism of the hydrogeodynamic precursor of the Мw = 7.8 Kronotsky earthquake of December 5, 1997. Russ. J. Pac. Geol. 2012, 5, 104–114. (In Russian).
- Kopylova, G. N. O veroyatnostnom srednesrochnom prognoze sil’nykh zemletryaseniy Kamchatki i parametrizatsii predvestnikov (On the probabilistic medium-term forecast of strong earthquakes in Kamchatka and the precursors parameterization). In Problemy kompleksnogo geofizicheskogo monitoringa Dal’nego Vostoka Rossii (Problems of complex geophysical monitoring of the Russian Far East), Chebrov, V. N., ed.; GS RAN: Obninsk, Russia, 2014; pp. 382-386. (In Russian).
- Kopylova, G. N., Boldina, S. V.; Serafimova, Yu. K. Earthquake Precursors in the Ionic and Gas Composition of Groundwater: A Review of World Data. Geochem. Int. 2022, 60, 928–946. [CrossRef]
- Zavyalov, A. D.; Zotov, O. D. A new way to determine the characteristic size of the source zone. J. Volcanol. Seismol. 2021, 15(1), 19-25. [CrossRef]
- Sil’nye Kamchatskie Zemletryaseniya 2013 Goda (Strong Earthquakes of Kamchatka in 2013), Chebrov, V. N., ed.; Novaya kniga: Petropavlovsk-Kamchatsky, Russia, 2014; p. 252. (In Russian).
- Chebrov, V. N.; Saltykov, V. A.; Serafimova, Yu. K. Identifying the Precursors of Large (M ≥ 6.0) Earthquakes in Kamchatka Based on Data from the Kamchatka Branch of the Russian Expert Council on Earthquake Prediction: 1998–2011. J. Volcanol. Seismol. 2013, 7(1), 76–85. [CrossRef]
- Chebrov, V.N.; Kugayenko, Y.A.; Abubakirov, I.R.; Droznina, S.Y.; Ivanova, Y.I.; Matveyenko, Y.A.; Mityushkina, S.V.; Ototyuk, D.A.; Pavlov, V.M.; Rayevskaya, A.A.; et al. The January 30th, 2016 earthquake with Кs = 15.7, Mw = 7.2, I = 6 in the Zhupanovsky region (Kamchatka). Bull. Kamchatka Reg. Assoc. “Educ.-Sci.” Cent. Earth Sci. 2016, 29, 5–16. (In Russian).
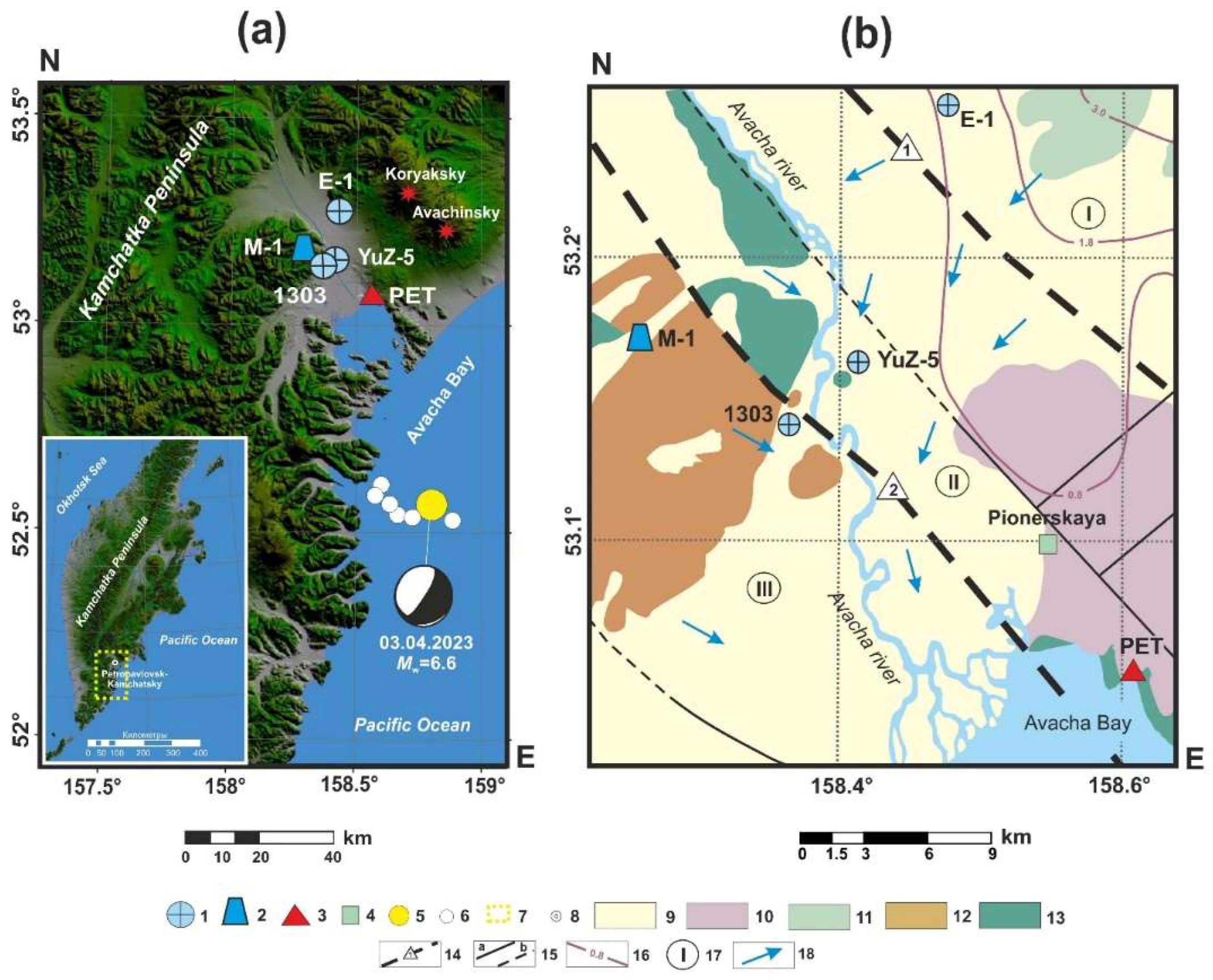
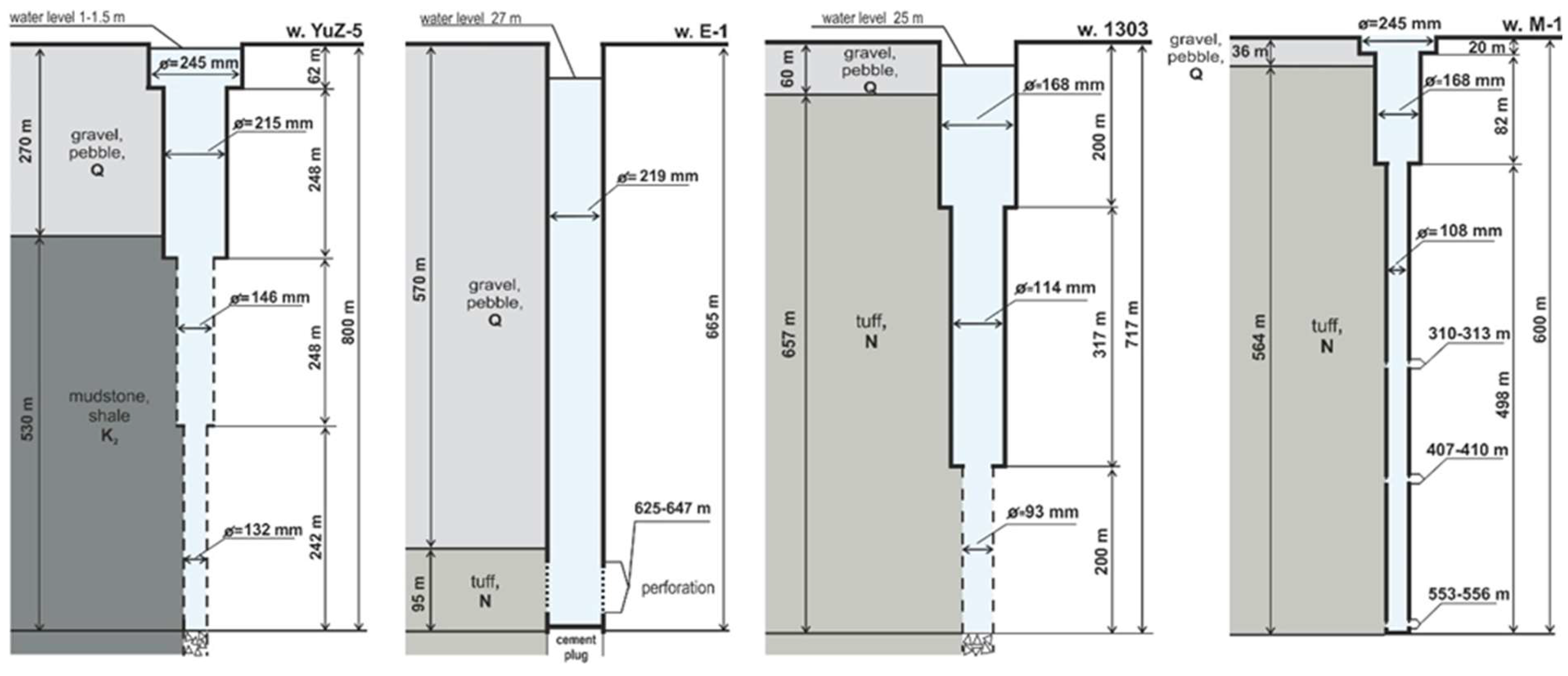
| Wells | Coor- dinates |
Precision observations start date (Precision observations duration*) |
Depth, m Open Interval, m |
Lithology: Age, Composition |
Water Level Depth, h, m Discharge rate, q, L/s; |
Water Temperature, °С |
Water Mineralization, g/L |
Water Type |
Gas Composition |
|---|---|---|---|---|---|---|---|---|---|
| YuZ-5 | 53.17°N 158.41°E |
Sept 1997 (26.4 years) |
800 310–800 |
К2, mudstone, shale |
piezometric h=1.5 |
14 | 0.45 | HCO3–SO4– Na–Ca |
dissolved gas, N2 |
| E-1 | 53.26°N 158.48°E |
Jan 1996 (28 years) |
665 625–645 |
N, Tuffs | piezometric h=27 |
10 | 1.5 | Cl–HCO3– Na |
free gas, N2–CH4 |
| 1303 | 53.14°N 158.36°E |
April 2021 (2.8 years) |
717 517–717 |
N, Tuffs | piezometric h=25 |
14 | 0.67 | HCO3–SO4– Na |
dissolved gas, N2 |
| M-1 | 53.18°N 158.28°E |
July 2020 (3.6 years) |
600 310–313 407–410 553–556 |
N, Tuffs | self-flowing, q=1.5 |
16 | 0.25 | SO4–Ca–Na | dissolved gas, N2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





