I. An Exceptional Multiplanetary Resonant Chain in TOI-270 and an Exact Laplace-like Resonance in HD 110067

1. Introduction

1.1. A New Beginning: Gravitational Landau Damping

Motivated by an unprecedented set of novel assumptions, we have embarked in a post-coronavirus study of mean-motion resonances (MMRs) occurring in (exo)planetary and satellite orbits [1]. Elements of the theory behind the challenge were laid out long ago (“Landau damping” [2,3,4,5,6,7,8]), but these studies were heretofore not applied to just a few major bodies orbiting around in the gravitational field of a central host in seemingly relaxed stable configurations.

In our view, the three pillars of planet/moon migration and eventual relaxation, after their rudimentary accretion disks were dispersed or accreted, are: (1) the ongoing global tidal transfer of angular momentum between surviving fragments that drives them all toward an unattainable intermediate orbit; (2) the dominant contributions of the most massive objects to the permeating tidal field; and (3) the gradual weakening of the mean tidal field, as massive objects halt their migration and no longer raise tides (“gravitational Landau damping”).

In this theory of planet and satellite evolution, when the global mean tidal field is erased due to the disappearance of radial excursions, all surviving objects should then be found orbiting in or near global MMRs [1,4]. Some natural predictions of such a final arrangement of orbits are (a) that the resulting MMR chain ought to be resonating globally, i.e., it should extend throughout all the survivors; and (b) that the survivors ought to also reside in or near local potential minima of the long-gone mean tidal field, creating thus a `regular’ radial profile of the presently observed orbital semimajor axes.

1.2. Global Mean-Motion Resonances

In planetary and satellite systems, the above predictions dictate a re-examination of the global chains of the orbital periods and the radial distributions of the semimajor axes, a program not easy to complete, but we are working on it. In this paper and in a companion Paper II [9], we study Laplace MMR chains of 3 objects and Laplace-like chains of 3 or 4 objects with an eye on the libration properties of these adjacent orbits and the spacings of the minima of the tidal potential, as they are revealed by the observed orbital configurations. In all cases, the most massive orbiting object in the system is assumed to define the location of the global 1:1 resonance.

Classical Laplace resonances (LRs) are characterized by orbital period ratios ${\displaystyle \frac{1}{4}}$:${\displaystyle \frac{1}{2}}$:1 (the Galilean moons [10]) or ${\displaystyle \frac{1}{2}}$:1:2 (GJ 876 [11]). LRs of the third type 1:2:4 have not so far been observed (see Table 2 below), and it is not known whether they can be formed at all.

Laplace-like resonances are generally similar; they show rational orbital-period ratios of 1:${\displaystyle \frac{3}{2}}$:2 (HD 110067 [12]; Table 3 below), or ${\displaystyle \frac{1}{2}}$:${\displaystyle \frac{3}{4}}$:1 (e.g., Kepler-90, TOI-1136, TRAPPIST-1), or ${\displaystyle \frac{2}{3}}$:1:${\displaystyle \frac{4}{3}}$ (e.g., Kepler-223, TOI-178). In these systems, the librating angle is precisely $2{\phi }_{\mathrm{L}}$ (Paper II), where ${\phi }_{\mathrm{L}}$ is the classical Laplace angle of LRs.

Other higher-order Laplace-like resonances show higher multiples of ${\phi }_{\mathrm{L}}$ and its few combinations with some typical basis angles. Such unusual resonances have been found in extensively modeled systems such as Kepler-60, K2-138, and TRAPPIST-1 [13,14,15,16,17,18,19,20,21]. The common factors in the librating angles were neglected during modeling, resulting in distorted values of the libration centers and amplitudes. These MMRs have thus provided the impetus for the work presented in Paper II.

It should be discernible from the preceding exposition that global MMRs do not rely or depend on local MMR pairs, the kinds that have been meticulously studied over many years in the past (e.g., Refs. [18,22,23,24,25], and references therein). Indeed, a number of previous N-body investigations [13,26,27] discovered that phase $\phi$ may be librating in the so-called type-II systems (`pure’ three-body MMRs), although one or both of the two-body MMRs do not librate. This surprising outcome is not as easily obtained from N-body models targeting local MMRs (e.g., Refs. [24,28,29]) in which each pair of adjacent planets is expected to lock into librations (the so-called type-I or `double’ MMRs [13,27]). On the other hand, Celletti et al. [26] classify three-body MMRs based on the orders of local pairs: if the local orders are same, so is the global order; otherwise, the MMR is of mixed order.

Furthermore, well-separated or distant bodies taking part in global MMR chains are not required or expected to show librations because of their large distances from the rest of the resonating bodies that may be closely-packed. Thus, the presence of librating phases is an independent property of global MMRs and not part of their definition. This point was also made by Lari and Saillenfest [30] who argued that, unlike triple ${\displaystyle \frac{1}{4}}$:${\displaystyle \frac{1}{2}}$:1 LRs, individual 2:1 commensurabilities are not genuine resonances because the trajectory of the system in phase space is not bounded by a separatrix (see also Refs. [31,32,33] for the first-order two-body Hamiltonian formalism).

1.3. Outline

In what follows, we concentrate on global Laplace-like MMRs between three adjacent planets, one of which resides in the 2:1 orbit. In the course of our investigation focusing on TOI-270 [34] and, in part, on HD 110067 [12], we also record the local MMR pairs needed in calculations. However, our conclusions are based on all three planetary orbits (their orbital periods and semimajor axes) that are relaxed, thus globally resonant in both space and time [1], yet they may or may not show librations.

In Section 2, we introduce physical and orbital characteristics of the TOI-270 system. In Section 3, we investigate several possible explanations for the 2:1 orbit of TOI-270 d, and we compare the ${\displaystyle \frac{3}{5}}$:1:2 MMR to classical LRs and the Laplace-like MMR of HD 110067. In Section 4, we summarize the few possibilities for the 2:1 orbit of TOI-270 d that we could not rule out with a high degree of confidence. In an Appendix, we discuss two potentially librating phase angles for the global MMR of TOI-270 that should be investigated further by N-body simulations.

2. The TOI-270 Exoplanetary System

Three planets were discovered in quiet M-dwarf TOI-270 by Günther et al. [35], and follow-up studies refined their orbits and masses [34,36]. Many researchers are presently turning their attention to the surface and atmospheric conditions of sub-Neptune TOI-270 d, using our best space telescopes to conduct transmission spectroscopic observations [37,38,39]; but the planetary system of TOI-270 also poses another problem of dynamical nature, and it is this problem that concerns us in the present investigation.

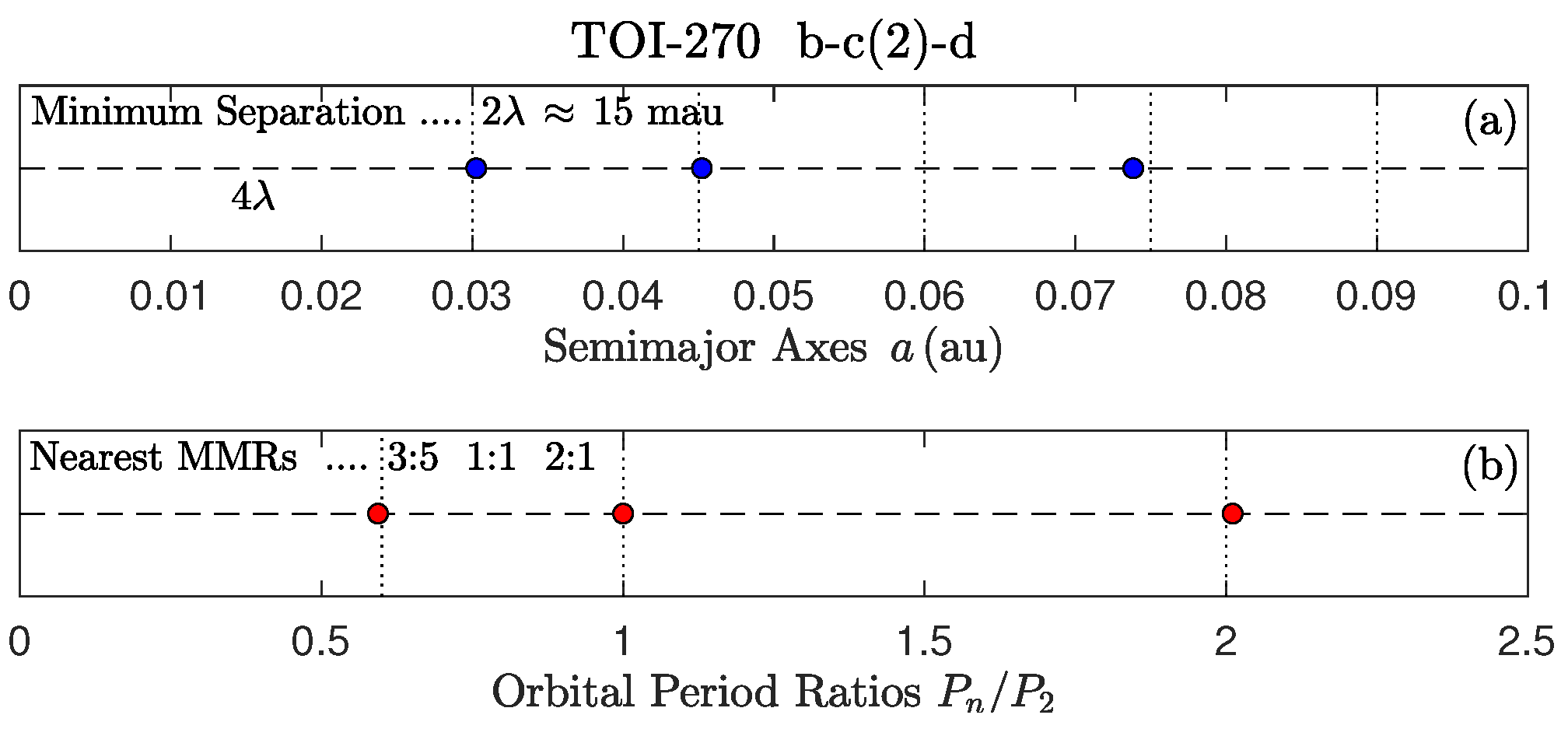
The best-fit solutions for the planetary orbits, masses, and radii have invariably converged to the values listed in Table 1 taken from Kaye et al. [34]. The last column shows the global MMRs calculated from the ratios $P_n/P_2$ ($n=1,2,3$) relative to the orbital period of the most massive planet c. The planetary configuration is also depicted in Figure 1. The dynamical problem is visible in Table 1 and in Figure 1: the 2:1 MMR is not vacant, although the planets are not trapped in a LR, nor is there a planet intervening between the 1:1 and 2:1 MMRs, as in the case of HD 110067 [12,40].

3. The Global 2:1 MMR Occupied by TOI-270 d

Except for the planetary system of HD 110067 and a few (6) known systems exhibiting LRs discussed below, no other extrasolar system had been discovered with its global 2:1 MMR being occupied by a planet—until the pair of planets TOI-270 c and d were detected [35]. The orbital period of planet d ($P_{\mathrm{d}}=273.2$ hr [34]) deviates from the exact 2:1 MMR by only +1.464 hr or 0.54% (Figure 1).

3.1. Possible Explanations

In general, any one of the following ideas could explain the surprising global 2:1 orbit of planet TOI-270 d:

(1)

A Laplace resonant chain (${\displaystyle \frac{1}{2}}$:1:2) between planets b, c, and d, as in GJ 876 [11,41]. But then, planet b would have to occupy instead the 1:2 MMR with an orbital period of about 2.83 d, i.e., shorter by 0.53 d than the current best-fit value. We explore this possibility in detail in Section 3.2 below.

(2)

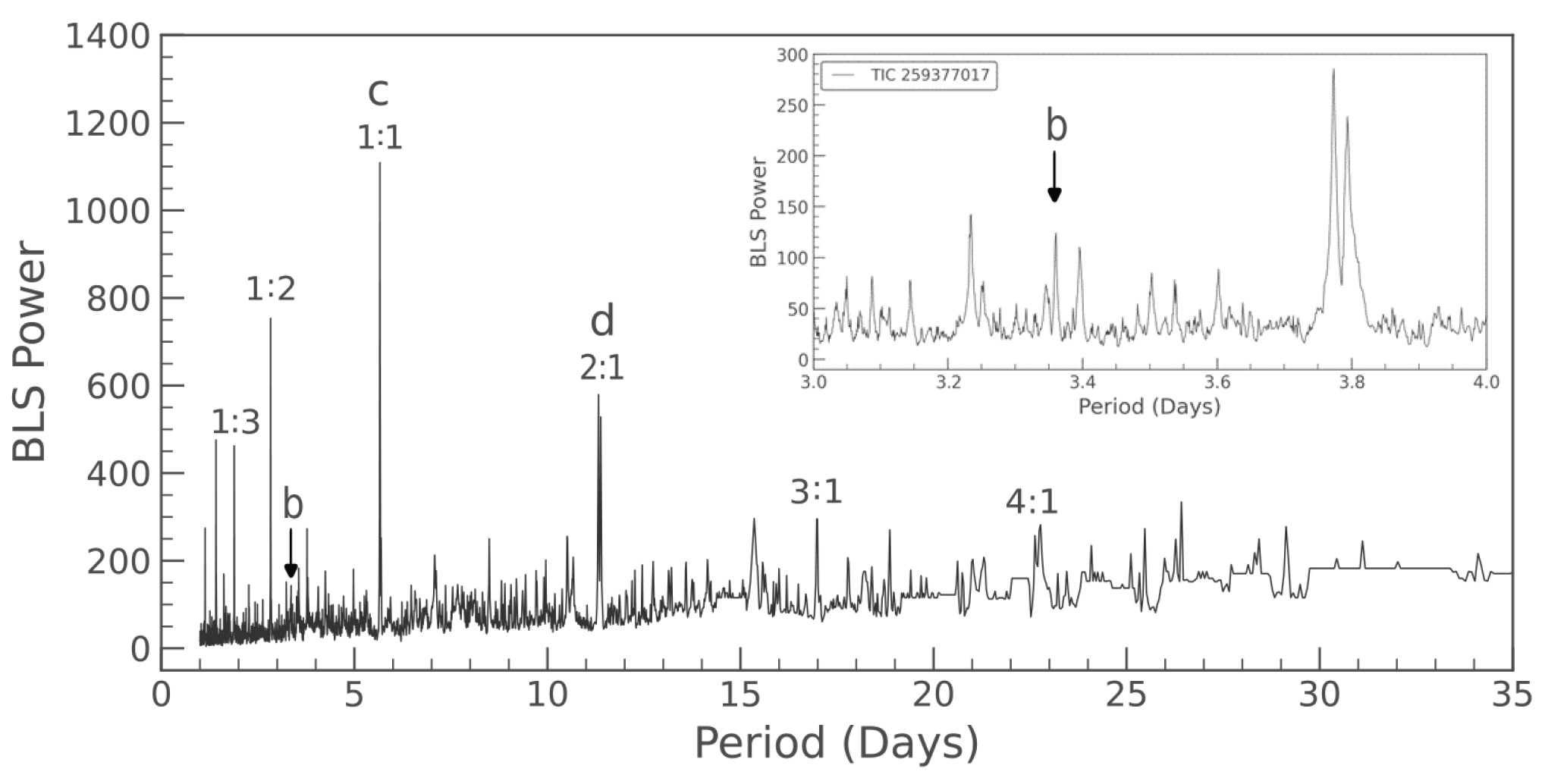
On the other hand, a yet undetected outer planet could complete a 1:2:4 Laplace chain in conjunction with planets c and d (although no LR is presently known with the most massive body in radial position $n=1$; see Table 2 below). We searched for a planetary signal at a period of 22.6-22.8 d with no success, although we found two distinct peaks in the periodogram within the targeted range (Figure 2). Past searches traversing this range have also produced negative results [34,35].

(3)

Another planet orbiting between the 1:1 and 2:1 orbits, as in the (1:1, 3:2, 2:1) chain of HD 110067 [12]. But no hint of such a planet has been found in any intervening orbit (Refs. [34,35,36], and this work).

(4)

Another planet more massive than any of the three known planets (i.e., with mass $M>M_{\mathrm{c}}=6.20M_{\oplus }$) would reset the location of the 1:1 MMR, resolving thus the issue. But no other planet has been detected out to an orbital period of at least ∼ 30 days (Ref. [35], and this work). At such large distances, more doubts are raised by the expanded projected aperture of a large planet on to the star that would be expected to produce very deep eclipses during transits—on the contrary, no eclipses of any depth are seen in the TESS data out to $P=35$ d.

(5)

Against the odds, the empirical rule calling for vacant non-LR 2:1 orbits adjacent to the principal 1:1 orbit could be invalid. We do not think this is a satisfactory resolution of the problem because this rule appears to be justified in 75 exosystems and solar-system satellite systems that we have analyzed so far (see also the results from a sample of 34 systems of Steffen [42]). In many of these systems, a body near the vacant 2:1 MMR has been clearly displaced out to a nearby higher-order MMR; in particular, 9:4 (e.g., Kepler-20 d, HD 108236 d), or 7:3 (e.g., Callisto, Kepler-80 b), or 5:2 (e.g., Saturn, HIP 9618 c). On the other hand, the most well-known system with an obviously vacant 2:1 MMR is the Plutonian satellites displaying a global MMR sequence of the form (1:1, 3:1, 4:1, 5:1, 6:1) [43,44].

(6)

A simple, yet surprising explanation would be that in TOI-270 we have encountered yet another stable triple chain of the type (3:5, 1:1, 2:1) in which the dominant planet c can stabilize the 3:5 MMR just as easily as the well-known Laplace 1:2 MMR. This novel hypothesis is also of theoretical interest (see Section 3.3 below), and it should be tested by numerical simulations.

Based on previous works and our analysis of the available TESS light curves, we believe that we can rule out cases 2-5 to some extent, but not cases 1 or 6 without further effort. We investigate these two cases in the following subsections.

3.2. Case-1: Potential Laplace Resonance Scrutinized

The case for $P_{\mathrm{b}}=3.36$ d in TOI-270 b appears to be weak for the following reasons:

(a)

The latest best-fit models [34,36] used narrow priors of width $P_{\mathrm{b}}\in [3.35,3.37]$ d, so they could have missed a best-fit value smaller by only 0.53 d falling within the error bars (case 1 in Section 3.1).

(b)

Both groups reported a shallow dip in relative flux for planet b of order ${10}^{-3}$, not discernible by eye in the data (see, e.g., section 5.2 in Ref. [34]); so, the latest models lean heavily on the initial determination of Günther et al. [35].

(c)

The periodogram combining all 5 sectors of TESS observations shows several distinct peaks in the interval of interest $P\in [2.5,3.5]$ d and a prominent peak at $P=2.830$ d (Figure 2).

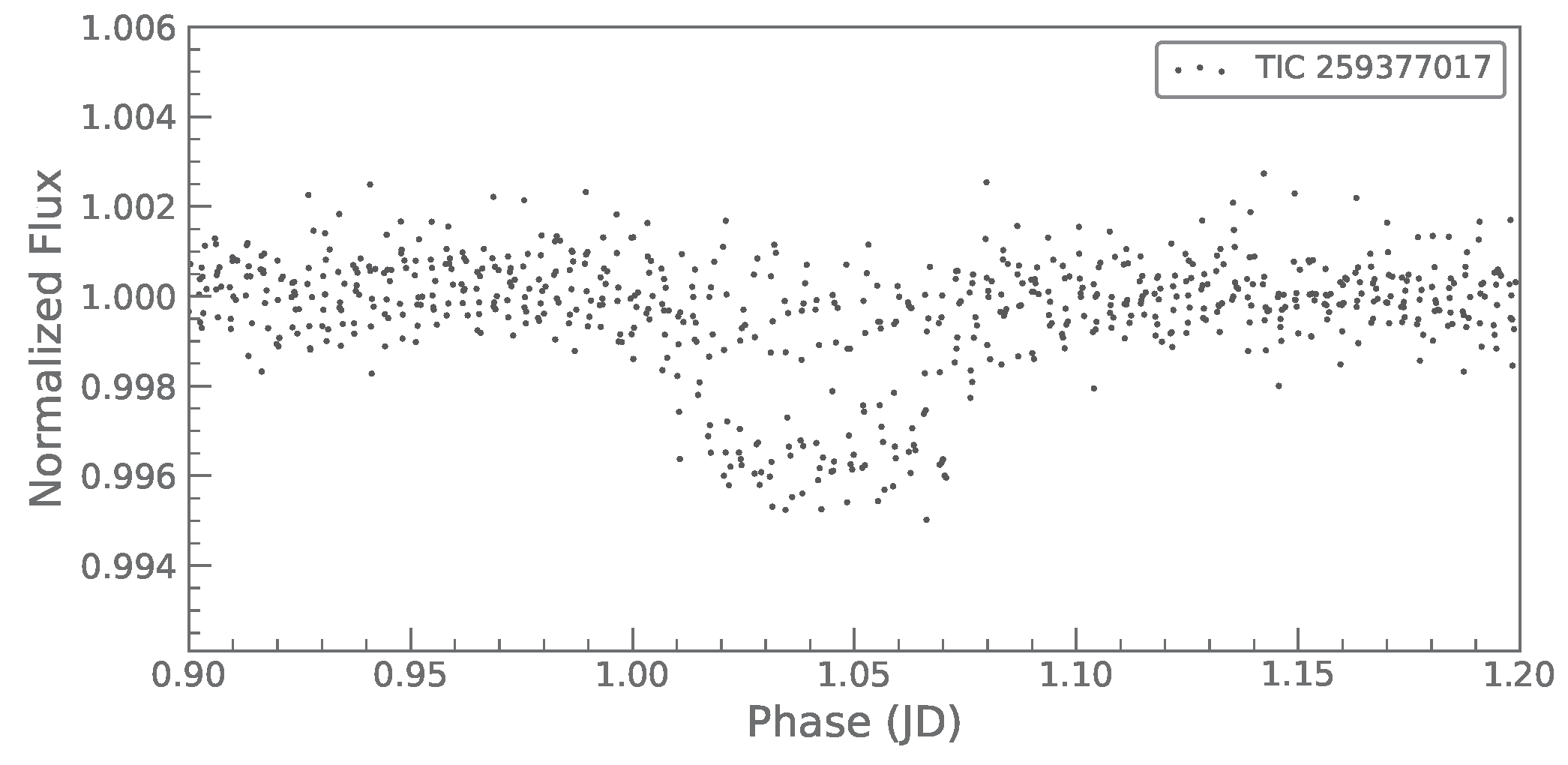
The $P=2.830$-d signal is a harmonic of the fundamental period $P_{\mathrm{c}}=5.6605$ d corresponding to planet c (Table 1), and it turns out that it is not caused by a transiting planet: We folded the TESS light curves at $P=2.830$ d, and the resulting light curve is shown in Figure 3. About one-half of the points are out of phase and do not highlight the observed dip; and the dip itself has the same depth and duration as the actual eclipse produced by transiting planet c at period $P_{\mathrm{c}}$. Thus, we can be fairly confident that the much weaker signal produced at the 3:5 MMR (Figure 2), in which virtually all points are in phase, corresponds to the actual orbit of planet b.

So, the results make a strong case against the presence of classical LRs in TOI-270 and point toward an investigation of the observed stable chain (${\displaystyle \frac{3}{5}}$:1:2) itself, which however lies quite close to the classical LR (${\displaystyle \frac{1}{2}}$:1:2). We explore the MMR chain of TOI-270 below in conjunction with the few known classical LRs and another unusual stable resonance (1:${\displaystyle \frac{3}{2}}$:2) recently discovered in HD 110067 [12].

3.3. Case-6: Laplace-like MMR Chains Explored in Conjunction with Classical LRs

We consider next the global MMR sequence of planetary orbits (3:5, 1:1, 2:1) observed in TOI-270. Kaye et al. [34] investigated the 2:1 MMR between planets c and d using N-body simulations designed to study primarily the long-term stability of the system. They found that the mean longitudes ${\lambda }_{\mathrm{c}}$ and ${\lambda }_{\mathrm{d}}$ circulate in the first 100 yr of evolution, so the two planets may not be locked together at present either. This outcome does not however preclude the existence of a new triple chain in TOI-270 in which the resonant phase angle (Paper II)

$$\phi =3{\lambda }_{\mathrm{b}}-7{\lambda }_{\mathrm{c}}+4{\lambda }_{\mathrm{d}}$$

(1)

could possibly librate (type-II resonance [13]) and the mean motions $3/P_{\mathrm{b}}-7/P_{\mathrm{c}}+4/P_{\mathrm{d}}$ combine to zero. For that reason, the planetary system of TOI-270 should be simulated again, hopefully in the near future.

Table 2. Laplace Resonant Chains and TOI-270 MMR Chain.

Host	Orbiting	Configuration
Body	Bodies	Mass Scheme	Refs.
Radial Position n:		1     2     3
Global MMRs of the form 1:4  1:2  1:1
Jupiter	I, E, G	$oo$   $\ell g$   $bb$	(1)
HIP 41378	b, c, g	$oo$   $\ell g$   $bb$	(2)
Global MMRs of the form 1:2  1:1  2:1
GJ 876	c, b, e	$oo$   $bb$   $\ell g$	(3)
Kepler-176‡	c, d, e★	$oo$   $bb$   $\ell g$	(4)
HR 8799	e, d, c	$\ell g$   $bb$   $oo$	(5)
HR 8832	f, d, g	$\ell g$   $bb$   $oo$	(6)
Global MMR of the form 3:5  1:1  2:1
TOI-270	b, c, d	$\ell g$   $bb$   $oo$	(7)
Key:
Mass scheme of the LR chain
$bb$ : Most massive body (`big boy’);
$\ell g$ : Least massive body (`little guy’);
$oo$ : Intermediate mass body (`other one’).
Jupiter’s moons
I: Io;  E: Europa;  G: Ganymede.

Notes: ^‡ The most massive planet Kepler-176 b is not part of the LR. ^★ Least massive exoplanet ever found ($M_{\mathrm{e}}=0.204M_{\oplus }$), other than the unusual `pulsar planet’ B1257+12 b ($M_{\mathrm{b}}=0.02M_{\oplus }$) [45]. References: (1) [10]. (2) [46,47]. (3) [11,41]. (4) [24,48]. (5) [49]. (6) [50,51,52]; also known as HD 219134 [52,53,54]. (7) [34].

Table 2. Laplace Resonant Chains and TOI-270 MMR Chain.

Host	Orbiting	Configuration
Body	Bodies	Mass Scheme	Refs.
Radial Position n:		1     2     3
Global MMRs of the form 1:4  1:2  1:1
Jupiter	I, E, G	$oo$   $\ell g$   $bb$	(1)
HIP 41378	b, c, g	$oo$   $\ell g$   $bb$	(2)
Global MMRs of the form 1:2  1:1  2:1
GJ 876	c, b, e	$oo$   $bb$   $\ell g$	(3)
Kepler-176‡	c, d, e★	$oo$   $bb$   $\ell g$	(4)
HR 8799	e, d, c	$\ell g$   $bb$   $oo$	(5)
HR 8832	f, d, g	$\ell g$   $bb$   $oo$	(6)
Global MMR of the form 3:5  1:1  2:1
TOI-270	b, c, d	$\ell g$   $bb$   $oo$	(7)
Key:
Mass scheme of the LR chain
$bb$ : Most massive body (`big boy’);
$\ell g$ : Least massive body (`little guy’);
$oo$ : Intermediate mass body (`other one’).
Jupiter’s moons
I: Io;  E: Europa;  G: Ganymede.

Notes: ^‡ The most massive planet Kepler-176 b is not part of the LR. ^★ Least massive exoplanet ever found ($M_{\mathrm{e}}=0.204M_{\oplus }$), other than the unusual `pulsar planet’ B1257+12 b ($M_{\mathrm{b}}=0.02M_{\oplus }$) [45]. References: (1) [10]. (2) [46,47]. (3) [11,41]. (4) [24,48]. (5) [49]. (6) [50,51,52]; also known as HD 219134 [52,53,54]. (7) [34].

3.3.1. Comparison with Known LRs and the Resonance in HD 110067

If it turns out that ${\displaystyle \frac{3}{5}}$:1:2 is a type-II resonance, we believe that the phase angle (1) will be found to librate about $\phi ={180}^{\circ }$, just as the Galilean LR between Io, Europa, and Ganymede [10], and unlike the LR of GJ 876 [11]. Our reasoning is described in detail in Paper II; our exploration started with a comparison between this resonance and five other classical LRs which we have found in extrasolar systems. All LRs are summarized in Table 2 that also includes the Galilean LR for completeness.

Although the list of 6 LRs in Table 2 is not long, we can infer the following trends:

(a)

No system has the most massive orbiting body ($bb$) in radial position $n=1$.

(b)

There is no system with $bb$ at $n=3$ and $\ell g$ at $n=1$.1

(c)

Only HIP 41378 has precisely the same arrangement of orbiting body masses as the famous Galilean LR with $bb$ at $n=3$ and $\ell g$ at $n=2$.

(d)

Except for HIP 41378, the other five exosystems have $bb$ at $n=2$ (including also TOI-270).

Because of trend (d), it would not come as a surprise if any of the three systems listed below GJ 876 in Table 2 showed a Laplace phase also librating about $\phi =0^{\circ }$ (see Rivera et al. [11] for a detailed analysis of the GJ 876 LR)—but this is not so for TOI-270 which shows only an approximate Laplace-like resonance.

We consider next trend (a), an unusual feature concerning the location of the most massive planet in each system. It certainly appears to be characteristic of the known LRs, and its violation by the global MMR of HD 110067 [12] led us to discover a new type of exact Laplace-like resonance of the form (1:1, 3:2, 2:1) with a phase of $\phi =2{\phi }_{\mathrm{L}}$ precisely. The proof follows after some preliminaries.

We list in Table 3 the detailed layouts of the four confirmed LRs and the two Laplace-like resonant chains observed in TOI-270 and HD 110067. Only HD 110067 has $bb$ at $n=1$ (planet d). The local MMR pairs $P_2$:$P_1$ & $P_3$:$P_2$ are also listed in Table 3; they are used in the determinations of phase angles. According to the classification of local MMR pairs given by Celletti et al. [26], HD 110067 shows a Laplace-like resonance of the first order, whereas TOI-270 shows a mixed (2&1) order.

Table 3. Confirmed LRs and Laplace-like Resonant Chains.

Host	Orbiting	Global	Local
Body	Bodies	Chaina	MMRsb	Refs.
Radial Position n:		1   2   3
	Confirmed Laplace Resonances
Jupiter	I, E, G	${\displaystyle \frac{1}{4}}$:$\left[{\displaystyle \frac{1}{2}}\right]$:1	2:1  &  2:1	(1)
GJ 876	c, b, e	${\displaystyle \frac{1}{2}}$:1:$\left[2\right]$	2:1  &  2:1	(2)
Kepler-176	c, d, e	${\displaystyle \frac{1}{2}}$:1:$\left[2\right]$	2:1  &  2:1	(3)
HR 8799	e, d, c	$\left[{\displaystyle \frac{1}{2}}\right]$:1:2	2:1  &  2:1	(4)
	Laplace-like Resonant Chains
HD 110067	d, e, f	1:$\left[{\displaystyle \frac{3}{2}}\right]$:2	3:2  &  4:3	(5)
TOI-270	b, c, d	$\left[{\displaystyle \frac{3}{5}}\right]$:1:2	5:3  &  2:1	(6)
Key:  I: Io;  E: Europa;  G: Ganymede;  $[·]=\ell g$.

Notes: ^a Orbital period sequence $P_1$:$P_2$:$P_3$. ^b Paired orbital periods $P_2$:$P_1=(r+1)$:r & $P_3$:$P_2=(s+1)$:s (except $P_2$:$P_1=(r+2)$:r in TOI-270). References: (1) [10]. (2) [11,41]. (3) [24,48]. (4) [49]. (5) [34]. (6) [12].

Table 3. Confirmed LRs and Laplace-like Resonant Chains.

Host	Orbiting	Global	Local
Body	Bodies	Chaina	MMRsb	Refs.
Radial Position n:		1   2   3
	Confirmed Laplace Resonances
Jupiter	I, E, G	${\displaystyle \frac{1}{4}}$:$\left[{\displaystyle \frac{1}{2}}\right]$:1	2:1  &  2:1	(1)
GJ 876	c, b, e	${\displaystyle \frac{1}{2}}$:1:$\left[2\right]$	2:1  &  2:1	(2)
Kepler-176	c, d, e	${\displaystyle \frac{1}{2}}$:1:$\left[2\right]$	2:1  &  2:1	(3)
HR 8799	e, d, c	$\left[{\displaystyle \frac{1}{2}}\right]$:1:2	2:1  &  2:1	(4)
	Laplace-like Resonant Chains
HD 110067	d, e, f	1:$\left[{\displaystyle \frac{3}{2}}\right]$:2	3:2  &  4:3	(5)
TOI-270	b, c, d	$\left[{\displaystyle \frac{3}{5}}\right]$:1:2	5:3  &  2:1	(6)
Key:  I: Io;  E: Europa;  G: Ganymede;  $[·]=\ell g$.

Notes: ^a Orbital period sequence $P_1$:$P_2$:$P_3$. ^b Paired orbital periods $P_2$:$P_1=(r+1)$:r & $P_3$:$P_2=(s+1)$:s (except $P_2$:$P_1=(r+2)$:r in TOI-270). References: (1) [10]. (2) [11,41]. (3) [24,48]. (4) [49]. (5) [34]. (6) [12].

For local resonances of the first order, $P_{n+1}$:$P_n=(p+1)$:p, where $p=r,s$ and $P_{n+1}>P_n$, two of the commensurability relations relating mean longitudes ${\lambda }_n$ [56] are

$$\begin{array}{ccc}{\theta }_1& =& (r+1){\lambda }_2-r{\lambda }_1-{\mathsf{\varpi }}_2\\ {\theta }_2& =& (s+1){\lambda }_3-s{\lambda }_2-{\mathsf{\varpi }}_2\end{array},$$

(2)

where ${\mathsf{\varpi }}_2$ is the longitude of the pericenter of planet $n=2$. Eliminating ${\mathsf{\varpi }}_2$ between these equations, we get the resonant phase angle $\phi ={\theta }_2-{\theta }_1$ [13], viz.

$$\phi =r{\lambda }_1-(r+s+1){\lambda }_2+(s+1){\lambda }_3.$$

(3)

In the HD 110067 system, $r=2$ and $s=3$ (Table 3), and equation (3) gives

$$\begin{array}{ccc}\phi & =& 2{\lambda }_1-6{\lambda }_2+4{\lambda }_3\hfill \\ & \equiv & 2{\phi }_{\mathrm{L}},\hfill \end{array}$$

(4)

where ${\phi }_{\mathrm{L}}\equiv {\lambda }_1-3{\lambda }_2+2{\lambda }_3$ is the classical Laplace phase angle [10]. This completes the proof.

Existing N-body models constructed with the parameters of HD 110067 have not been analyzed for librations yet, but the system is still under scrutiny (R. Luque, priv. comm.). The general-purpose (3:2 & 4:3) N-body simulations of Siegel and Fabrycky [29] indicate that the libration center of the Laplace-like angle (4) could be $\pm {18}^{\circ }$ off of ${180}^{\circ }$.

3.3.2. The Global Resonant Chain of TOI-270

The global MMR of TOI-270 is the only one in Table 3 that is of mixed order [26], so the equations of Section 3.3.1 are not valid. The local resonances are 5:3 and 2:1 for which the calculation of $\phi$ produces equation (1), where planet names b, c, d naturally correspond to 1, 2, 3 radially outward, respectively. Thus, we rewrite equation (1) with numerical subscripts, viz.

$$\phi =3{\lambda }_1-7{\lambda }_2+4{\lambda }_3,$$

(5)

and we proceed to decompose this phase angle into two parts, one of which is the Laplace angle ${\phi }_{\mathrm{L}}$, viz.

$$\phi ={\phi }_{\mathrm{L}}+2\left({\lambda }_1-2{\lambda }_2+{\lambda }_3\right).$$

(6)

The same phase angle $\phi$ is also found in the pure three-body first-order ${\displaystyle \frac{3}{4}}$:1:${\displaystyle \frac{4}{3}}$ MMR chain (not yet observed, but shown to be librating about ${180}^{\circ }$ in the 30 detailed N-body models of Siegel and Fabrycky [29]).

From our point of view, we can only probe analytically the second term in equation (6) as follows. Let

$${\phi }_{★}=2{\lambda }_1-4{\lambda }_2+2{\lambda }_3,$$

(7)

so that $\phi ={\phi }_{\mathrm{L}}+{\phi }_{★}$ in equation (6). Then, we find that phase ${\phi }_{★}$ corresponds to a first-order resonant pair [26] composed of the 3:2 & 2:1 local MMRs (equation (3) with $r=2$, $s=1$). In Appendix A, we describe this pair in conjunction with another stable first-order resonant pair (5:4 & 4:3; $\phi =2{\phi }_{★}$) observed in Kepler-60 [57] for which extensive N-body simulations have been published (e.g., Refs. [13,29]).

The global MMR chain corresponding to equation (7) is 2:3:6 (or 1:${\displaystyle \frac{3}{2}}$:3, to be compared to the Laplace-like chain 1:${\displaystyle \frac{3}{2}}$:2 in HD 110067; or ${\displaystyle \frac{2}{3}}$:1:2, specifically for systems with $bb$ at $n=2$). Then, we find that integer decomposition of global MMRs holds true, just as it does for the resonant phase angle of equation (6), viz.

$${\phi }_{\mathrm{L}}+{\phi }_{★}=\phi \Rightarrow [1:2:4]+[2:3:6]=[3:5:10].$$

(8)

This interesting property indicates that the Laplace-like phase angles of equations (5) and (7) are the ones to be investigated individually for oscillatory behavior by N-body simulations. Additional results pertaining to the arithmetic properties of the global MMR in TOI-270 are deferred to Appendix B.

3.4. The Long-Gone Tidal Field of TOI-270

Long ago, migrating planets in TOI-270 must have undergone radial oscillations about local minima of the global tidal potential [6,58] that they encountered, for as long as the collective mean tidal field had remained active in the system. During subsequent evolution, the tidal field was ultimately (and irrevocably) erased, presumably by the few-body gravitational analog of Landau damping [1,2,3,7,59,60], when all survivors had settled in or near their respective MMR orbits [4,40]; then, angular momentum redistribution and radial orbital evolution ceased in that eventual tidal-free environment.

The present-day arrangement of the planets illustrated in Figure 1(a) indicates that the longest tidal-field wavelength $\mathsf{\lambda }$ that was not Jeans unstable [5,7] must have had a value such that the minimum separation between planet orbits in the vicinity of the most massive planet presently is

$$2\mathsf{\lambda }\approx 15\mathrm{mau},$$

(9)

as highlighted in Figure 1(a) by vertical dotted lines. Indeed, planets b ($\ell g$) and d ($oo$) are separated from the most massive planet c ($bb$) by $2\mathsf{\lambda }$ and $4\mathsf{\lambda }$, respectively.

The value in equation (9) is corroborated by the few-body model of gravitational Landau damping [1] that predicts separations of nearest neighbors from the most massive planet c ($bb$ at $n=2$) of at least

$$2{\mathsf{\lambda }}_{\mathrm{c}}=4\pi h_{\mathrm{c}}=14.3\mathrm{mau},$$

(10)

where $h_{\mathrm{c}}$ is the radius of the Hill sphere of planet c at the pericenter of its orbit [61], viz.

$$h_{\mathrm{c}}=a_{\mathrm{c}}\left(1-e_{\mathrm{c}}\right){\left[{\displaystyle \frac{M_{\mathrm{c}}}{3\left(M_{★}+M_{\mathrm{c}}\right)}}\right]}^{1/3}=1.14\mathrm{mau},$$

(11)

as determined from the values listed in Table 1.

For comparison, $h_{\mathrm{c}}=0.171$ Gm is comparable to the Hill radius of Mercury (0.175 Gm); whereas the separation $2{\mathsf{\lambda }}_{\mathrm{c}}=2.145$ Gm is comparable to the major axis of Ganymede’s orbit (2.141 Gm) (for which its own minimum separation is $2{\mathsf{\lambda }}_{\mathrm{G}}=0.4$ Gm in the Galilean LR [1]).

For future reference, the same result can be obtained from the simpler equation (e.g., Ref. [62])

$$h_{\mathrm{c}}=a_{\mathrm{c}}{\left({\displaystyle \frac{{\mu }_{\mathrm{c}}}{3}}\right)}^{1/3},$$

(12)

for ${\mu }_{\mathrm{c}}\equiv M_{\mathrm{c}}/M_{★}\ll 1$ and $e_{\mathrm{c}}\ll 1$. We use this equation in Paper II to analyze the planetary orbits of HD 110067, Kepler-176, and Kepler-223.

4. Summary and Conclusions

Of the possible explanations for the appearance of a global non-Laplace 2:1 MMR in TOI-270 described in Section 3.1, some are open-ended in certain respects and cannot be ruled out entirely with a high degree of confidence. We summarize them below, where we retain the item numbers from Section 3.1.

(1) One idea that we investigated in depth in this work is that planet b may be orbiting a little closer to the star ($P=2.830$ d) than currently known ($P_{\mathrm{b}}=3.360$ d). That would produce a LR in the system which would resolve the issue in a familiar way. On the other hand, period P is the $m=2$ harmonic of the period $P_{\mathrm{c}}$ of the most massive planet, creating uncertainty in the interpretation of the signal seen in the periodogram of Figure 2. It turned out that we could not justify the presence of planet b at the 1:2 MMR based on the current TESS data (Figure 3). But the system is so close to a LR that we cannot dismiss the remote possibility of the signal generated at the 1:2 MMR and then somehow being shifted by half a day to the observed period $P_{\mathrm{b}}$ (see, e.g., Refs. [63,64]). An unabating observation in the periodogram (Figure 2 inset) is that the minor peak corresponding to planet b is less significant compared to some nearby peaks seen in the interval $P\in [3,4]$ d.

(4) An unseen distant planet (e.g., with $P>30$ d [35]), more massive than the three known planets, could resolve the issue by redefining the actual location of the principal 1:1 orbit, although one would expect such a planet to have produced deep eclipses during transits. As a case in point, a hypothetical planet at $P=34$ d occupying the 1:1 MMR would produce a typical sequence of inner resonances (1:10, 1:6, 1:3)—not too different than the inner MMRs of HD 10180 c-i-d (1:9, 1:5, 1:3 [65]), or HD 20781 b-c-d (1:16, 1:6, 1:3 [66]), or Kepler-20 b-e-c (1:9, 1:6, 1:3 [67]). However, there is no corroborating evidence in the TESS data for such an outer planet out to an orbital period of at least $P=35$ d.

(5) We would also not dismiss entirely the possibility that a non-LR 2:1 MMR adjacent to the principal 1:1 MMR may yet be stabilized or permitted in some special cases, providing thus a staggering exception to our empirical rule. This rule derives from 75 systems that we have analyzed so far and a subset of 34 systems analyzed by Steffen [42]; and 8% of them hosting classical LRs already make up an exception (Table 2). At any rate, this possibility has been weakened to a degree by the proof that in another system, HD 110067, the unusual occupancy of the 2:1 orbit is due to just another Laplace-like resonance (Section 3.3.1).

(6) A promising explanation for the stable ${\displaystyle \frac{3}{5}}$:1:2 resonant chain of TOI-270 is that we may be dealing with yet another type of a Laplace-like resonance. We explored this idea in Section 3.3.2 and in Appendix B. The calculations produced two relevant phase angles, $\phi$ and $\widehat{\phi }$ (see equations (5) and (A7)), related via the classical Laplace phase ${\phi }_{\mathrm{L}}$ by the equation $\widehat{\phi }={\phi }_{\mathrm{L}}+2\phi$. Potential librations of these angles should be monitored in numerical simulations of the TOI-270 system. The important question begging for an answer is which of the angles $\phi$ or $\widehat{\phi }$ might reveal a librating phase, so that we may determine with precision and rigor the nearest MMR (3:5 or 7:12) to the orbit of planet b (see Appendix B).