1. Introduction
In the past, a picture was worth a thousand words, but in the modern era of deepfakes and manipulated media, a picture now leads to a thousand doubts. Digital image manipulation has long posed a security threat to images shared on social media, causing people to increasingly distrust sensitive images circulating on these platforms, often requiring them to re-confirm the image source. Detecting forged images from simple editing operations, such as splicing and copy-move, remains challenging due to the increasing sophistication of these techniques. The rise of deepfakes [
1] has further worsened the credibility issue of social media images, as tampering and counterfeiting are no longer limited to experts.
Image forensics techniques [
2,
3] are considered passive approaches to proving content authenticity because they detect tampering by detecting signal inconsistencies in the image. These altered images are redistributed in either lossless or lossy formats. For lossless-encoded images, pixel-based characteristics such as noise [
4], patterns [
5], and camera properties [
6,
7] are analyzed to detect local inconsistencies and identify image forgery. In the case of lossy image codecs like JPEG, methods [
8,
9] exist to detect double JPEG compression, as JPEG exhibits specific characteristics in its DCT coefficients that help identify possible manipulated images. Active approaches, such as trustworthy cameras [
10,
11] or fragile digital watermarking [
12,
13], attempt to authenticate the image upon creation and detect later modifications by verifying embedded signatures or watermarks. These are considered active because any break in the signature or watermark serves as solid evidence of tampering. However, authenticity verification typically occurs only after counterfeiting has taken place.
We propose a novel proactive approach: the Secure Learned Image Codec (SLIC), designed to prevent image manipulation from the outset.
Figure 1 demonstrates the self-destruction effects of our proposed SLIC, which forces a malicious actor to obtain severely degraded visual content after re-compression. Once the content owner releases a sensitive image in SLIC format, the content is protected, as any subsequent re-compression–even after image editing–will result in eye-catching artifacts. In other words, SLIC is a non-idempotent codec. Because the content of a SLIC image is either original with good quality or visually damaged after tampering, images encoded with this secure codec hold greater credibility. If the public tends to trust only SLIC images, malicious actors will be forced to fabricate fake images in SLIC format to gain trust, a task that is considered non-trivial. Thus, counterfeiting can be prevented from the outset.
Designing a secure codec based on conventional codecs is challenging because most of them rely on linear and unitary transforms such as the Discrete Cosine Transform (DCT). In contrast, the non-linear transform employed by a learned image codec has the potential for a “destroy after re-compression” effect, as adversarial examples are known to neural networks. Adversarial attacks can introduce imperceptible perturbations into input images, leading to file size expansion [
14] or significant quality degradation [
15]. We think there are two approaches to developing a secure learned codec:
The first approach has been validated in [
16] but is limited to fixed image resolution and watermark secret bit length. In this work, we realize the second approach by generalizing the SLIC in full resolution and providing instant content protection right after compression. We summarize the contributions of this paper as follows:
We introduce the full resolution SLIC which verifies content authenticity through destructive re-compression. SLIC internally applies a universal adversarial attack to its output. We think developing a non-idempotent codec as a secure codec for authenticity verification will be a new area to explore to counter manipulated images.
We propose using perceptual quality metrics in the adversarial loss to fine-tune a learned image codec that effectively generates out-of-distribution perturbations in the decoder output. We analyze and compare the antagonistic effects of various perceptual quality metrics.
We point out the research opportunity of designing an efficient and effective perceptual metric to maximize perceptual loss. This may be an interesting topic for the study of adversarial attacks on learned image codecs.
2. Related Works
2.1. Watermarking to Defend Image Manipulation
Ensuring digital image integrity has long become a critical issue due to the widely available image manipulation software. Therefore, watermarking has become a popular technique for copyright enforcement and image authentication [
17]. The invention of deepfakes [
1] further exacerbated the credibility issue because the generative model to swap facial identities or revise the attributes of faces is also widely available on the internet.
Adversarial attacks [
18] to the generative models and adversarial watermarking [
19,
20] are well-known active defense strategies against Deepfakes. Lv [
19] proposed an adversarial attack-based smart watermark model to exploit Deepfake models. When Deepfake manipulates their watermarked images, the output images become blurry and easily recognized by humans. Yu et al. [
21] took a different approach by embedding watermarks as fingerprints in the training data for a generative model. They discovered the transferability of such fingerprints from training data to generative models, thereby enabling Deepfake attribution through model fingerprinting. Wang et al. [
22] proposed an invisible adversarial watermarking framework to enhance the copyright protection efficacy of watermarked images by misleading classifiers and disabling watermark removers. Zhang et al. [
23] developed a recoverable generative adversarial network to generate self-recoverable adversarial examples for privacy protection in social networks. More recently, EditGuard [
20] utilizes image steganography and watermarking techniques to unify copyright protection and tamper-agnostic localization.
These adversarial watermarking approaches are successful but focus on the image content without considering the image format, i.e., the container of the image content during transmission. We take a step further to develop a secure image codec with a learned image codec, which injects adversarial perturbations into the image content during the initial encoding and decoding process. The originality of the image is authenticated by its visual quality because any subsequent compressions after image editing will lead to severe quality degradation, as demonstrated in
Figure 1.
2.2. Learned Image Compression
The Learned Image Compression (LIC) technique is an end-to-end approach that automatically learns a pair of image encoders and decoders from a collection of images without the need for hand-crafted design of coding tools. This field of learned image compression has witnessed significant advancements [
24,
25,
26,
27] in the past few years, surpassing traditional expert-designed image codecs. Several comprehensive surveys and introductory papers [
28,
29,
30] have summarized these achievements.
However, by default, neural network-based codecs do not consider idempotence like traditional image codecs. The idempotence refers to image quality stability after a series of re-compressions, which is crucial to practical image codec. Kim et al. [
31] first identified the instability issue of successive deep image compression and proposed including a feature identity loss to mitigate it. Specific methods, such as invertible networks [
32,
33] have been proposed to improve the idempotence of neural codecs. Recent work from Xu et al. [
34] further proves that conditional generative model-based perceptual codec satisfies idempotence.
Meanwhile, neural image codecs are no exception to adversarial attacks. Liu et al. [
14] investigated the robustness of learned image compression, where imperceptibly manipulated inputs can significantly increase the compressed bitrate. Such attacks can potentially exhaust the storage or network bandwidth of computing systems. Chen and Ma [
15] examined the robustness of learned image codecs and investigated various defense strategies against adversarial attacks to improve robustness.
A non-idempotent image codec is not practical in image applications but is worth exploring for image authentication. If a neural codec could be self-destructive in quality after re-compression, it would be a roadblock for image tampering in this format. Thus, we can accumulate trust in such secure learned image codecs and deter counterfeiting behaviors.
2.3. Perceptual Distance Metrics
The evaluation of image distortion from lossy compression relies on full-reference image quality assessment metrics, which gauge the similarity between the distorted and the original images as human observers perceive. In addition to the traditional Mean Square Error (MSE), subjective metrics such as SSIM [
35], GMSD [
36], and NLPD [
37] have been widely employed. These quality metrics somehow represent the signal difference in a transformed domain (e.g., GMSD from the image gradient), hoping to align with human perceptual judgment. Recently, new DNN-based methods like VGG loss [
38], LPIPS [
39], PIM [
40], and DISTS [
41] have been proposed. These approaches have demonstrated superior predictive performance for subjective image quality. Their efficacy has been confirmed through validation against human judgments on benchmark datasets like BAPPS [
39] and CLIC2021 [
42], which comprise a comprehensive collection of two-alternative force choice (2AFC) human judgments. More recent works, such as Deep Distance Correlation (DeepDC) [
43], which focuses on feature space comparisons between pre-trained DNNs, improve on earlier metrics like LPIPS and DISTS by incorporating distance correlation to handle structure and texture similarities effectively.
In various computer vision tasks such as style transfer [
44], super-resolution [
45], and watermarking [
46], these quality metrics are often used in the loss function as perceptual loss to improve the image quality. In this work, we utilize and compare these quality metrics’ effectiveness as a perceptual loss to maximize the visual divergence as an adversarial attack.
2.4. Adversarial Attacks
Szegedy et al. [
47] first introduced the notion of adversarial examples and demonstrated that neural networks are vulnerable to small perturbations in input data. The goal of an adversarial attack is to find an adversarial example that is indistinguishable from the human eye but can lead to significant misclassifications. Adversarial attacks can be either targeted or untargeted.
Searching for adversarial examples was once considered computationally expensive because of its optimization nature. Szegedy et al. approximated it using a box-constrained L-BFGS. Goodfellow et al. [
48] proposed the Fast Gradient Sign Method (FGSM), a straightforward yet powerful approach for generating adversarial examples. FGSM is computationally efficient because it leverages the gradient of the loss function concerning the input data to create perturbations that maximize the model’s prediction error.
Later, more sophisticated attack techniques were introduced. Kurakin et al. [
49] extended FGSM by developing the iterative method I-FGSM, which applies FGSM multiple times with small step sizes. Madry et al. [
50] substituted FGSM with Projected Gradient Descent (PGD), which iteratively adjusts the perturbations based on the same calculation formula as FGSM but differs in introducing random noise to the original image and constraining total perturbation by clamping the noise in every iteration. Carlini and Wagner [
51] proposed the C&W attacks, which optimized a different objective function to generate adversarial examples. These attacks demonstrated a higher success rate in bypassing defenses.
Zhu et al. [
52] conduct iterative FGSM and PGD attacks on six LIC models and use PGD training as a defense method to improve the robustness. Chen and Ma [
15] propose the Fast Threshold-constrained Distortion Attack (FTDA) approach to generate adversarial examples with balanced performance and complexity compared to methods like C&W or I-FGSM. It is known that “adversarial examples are not bugs but features of neural networks.” However, for the context of developing a SLIC, it is not effective to perform an adversarial attack per image basis or even learn a universal adversarial perturbation to exploit the re-compression quality.
3. Proposed Method
3.1. Idempotence of Image Codec
The idempotence of image codec refers to the codec’s stability to recompression. For any input image
, the neural encoder
transforms
x into a latent representation
. The neural decoder
reconstructs an estimation of
x as
. Here, we denote
as the
n-th compression result of
x and
as the composition of the encode-then-decode function. We use a perceptual metric
to measure the distortion caused by a lossy image codec. A lossy image codec usually ensures
. We say that a image codec is idempotent if
That is, an idempotent codec always produces the same result when re-compressing a prior reconstruction. To create a non-idempotent image codec as a secure codec, we wish to make a visually destroyed second compressed image
, which satisfies
but its first compressed image
remains perceptually close to the original image
x as
3.2. Adversarial Loss for Perceptual Divergence
We fine-tune a neural encoder/decoder pair
and
with model parameters
and
to obtain a SLIC codec, such that the perceptual distance
between
and
diverges as much as possible, that is
where
and
are the first and second compression results, the perceptual distance
can be any previously discussed quality metrics such as
or
. Ideally, the perceptual distance between
is minimized through the rate-distortion optimization process.
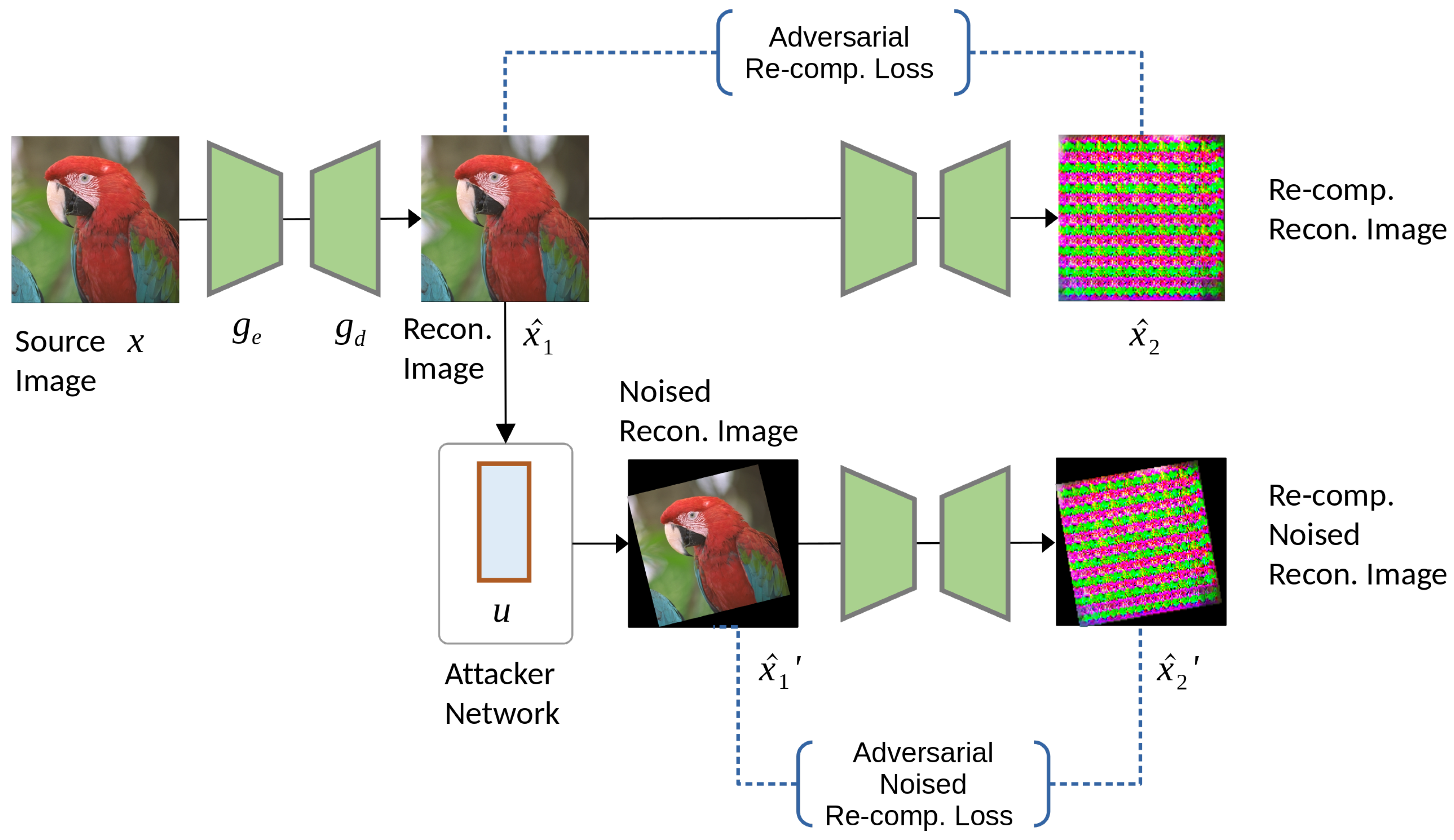
Figure 2 shows the SLIC training flow.
Our loss function to fine-tune the SLIC is defined as:
where
and
are hyper-parameters that control the trade-off between bitrate, distortion, and the loss caused by the adversarial re-compression,
. The
bitrate of the transformed discrete code
,
, is lower-bounded by the entropy of the discrete probability distribution
. Here, we estimate the discrete probability distribution
using a neural network and then encode it into a bitstream with an entropy coder. The
distortion is measured by a distance metric
, where MSE or SSIM is commonly used. We add the adversarial loss function in the training flow as:
Except for modeling the divergence between the encoded
and re-compressed
, we treat any possible image editing operation that comes with image tampering as a noise attack and use a noise-adding attacker
u to simulate it. The noised encoded image
and the noised second re-compression image
are also considered in the adversarial loss function. As indicated in
Figure 2, we denote the first and second terms of Equ.
6 as
adversarial re-compression loss and
adversarial noised re-compression loss, respectively. The adversarial re-compression losses use a constant
and ReLU function to maximize the perceptual loss divergence.
With the adversarial loss , we fine-tune the image codec to attack itself via generating invisible adversarial perturbation in the reconstructed image , if the reconstructed image is re-compressed, it exploits the image encoder and produces a severely damaged image .
3.3. Noise Attack Simulation
In practical scenarios, the published SLIC-encoded image may undergo various editing operations such as cropping, scaling, rotation, and lighting adjustment before the tampering behavior. These edits are considered noise attacks to the SLIC-encoded image, and our SLIC should be robust to those attacks. To simulate noise attacks, we use an attacker
u similar to [
53] and derive the noised encoded image as
, then re-compress it as
. We define eight types of editing operations commonly used in creating spliced fake images, including crop, Gaussian blur, median filtering, lightening, sharpening, histogram equalization, affine transform, and JPEG compression. We then test the resilience of our first encoded image against these image manipulations and evaluate the effectiveness of SLIC upon re-compression.
Surprisingly, our SLIC demonstrates robustness against non-filtering editing operations such as lightening, sharpening, and histogram equalization, even without noise attack simulation. These attacks tend to increase rather than decrease the magnitude of the adversarial perturbation. We classify Gaussian blur, median filtering, affine transform, and JPEG compression as filtering editing operations. These adversarial perturbations added to the first encoded image are partially filtered due to resampling. Therefore, to enhance robustness, we simulate three types of noise attacks in fine-tuning:
Gaussian blur: We randomly apply Gaussian blur with kernel size 3 and variance ranging from 0.1 to 1.5 on the first encoded images.
Affine transform: We randomly rotate from -10 to 10 degrees, translate from 0% to 10% in both axes and scale from 90% to 110% on the encoded images.
JPEG compression: We re-compress the encoded images with random JPEG quality from 70 to 95. Although there are differentiable JPEG quantization simulations have been proposed, such as mask-and-drop [
54] and cubic rounding [
55], we use an image transformation task to simulate the JPEG compression effects because of better robustness. More details are given in
Appendix A.1.
We do not simulate other attacks because, through experiments, we found that combining these three attacks randomly effectively enhances the robustness of the eight pre-defined noise attacks. Further discussion on this is provided in
Section 4.4.
4. Experimental Results
We implemented our SLIC using the CompressAI [
56] release of neural codecs [
24,
25,
26], denoted as Balle2018, Minnen2018, and Cheng2020. The MSE-optimized pre-trained models from CompressAI are used for fine-tuning. For training, we randomly selected 90% of the images from the COCO dataset [
57] as the training set and the remaining 10% as the validation set. We employed the PyTorch built-in Adam optimizer with a
learning rate to fine-tune a pre-trained LIC mode for 100 epochs. An early stopping criterion is implemented during training if the learning rate decays lower than
. Training images are randomly cropped as
patches with a batch size 12 using NVIDIA GeForce RTX 4090 GPU. We set
in the adversarial loss function from Equ.
6. In the overall rate-distortion-adversarial loss function from Equ.
5, we follow the same
value setting as CompressAI and tweak the
hyper-parameter as shown in
Table 1. We report the experimental numbers using a high bitrate setting as quality scale 8. However, the destructive re-compression effect can be observed in all quality settings.
We evaluated our SLIC on the Kodak [
58], FFHQ [
59], and DIV2K [
60] datasets. We use the original resolution images from Kodak (
) and FFHQ (
). Due to GPU memory constraints, we resize the DIV2K images to around
and pad the size with a multiple of 32 using replication mode. To evaluate our SLIC’s robustness, we define eight types of editing operations commonly mixed with image tampering: crop, Gaussian blur, median filtering, lightening, sharpening, histogram equalization, affine transform, and JPEG compression. The parameter settings are listed in
Table 2.
4.1. Perceptual Metrics Comparison
Since our adversarial re-compression loss leverages the perceptual metric
to divert the perceptual distance between re-compression results, we first test different perceptual metrics with the Balle2018 codec to observe the adversarial effects. The last two rows of
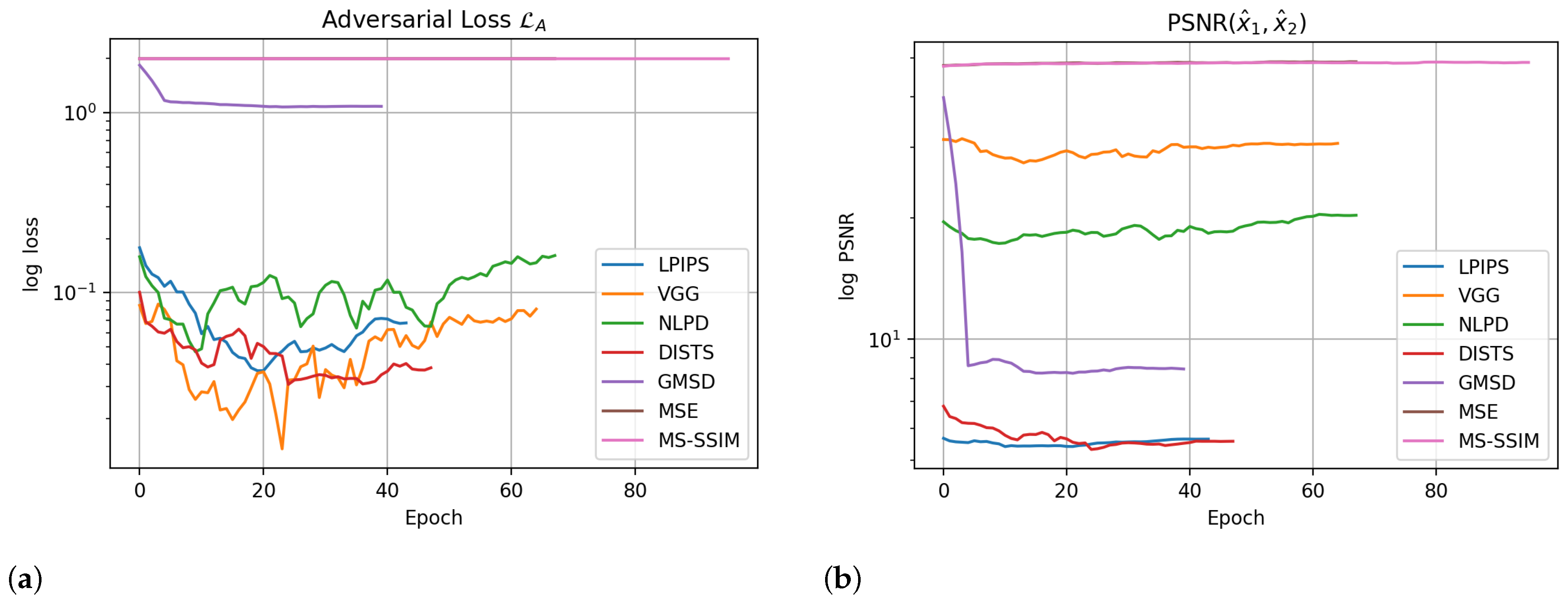
Table 3 show that the traditional metrics
and
are unsuccessful in achieving this goal. Their re-compression PSNR values are high, so the visual quality remains indistinguishable from human eyes. During the training, the adversarial loss of MSE and MS-SSIM in
Figure 3a and re-compression PSNR in
Figure 3b remain flat. We think that’s because the MSE is a summation-based metric, and the SSIM operates on a small local window with luminance, contrast, and structure components. Minimizing MSE or MS-SSIM for a reconstruction-based neural network is straightforward and efficient. Still, these pixel-based metrics cannot provide helpful perceptual features for the neural network to divert the re-compression quality.
Then, we test the DNN-based perceptual metrics
and
. The VGGLoss uses the intermediate feature activations of a pre-trained VGG network (precisely, layers like
conv1_2,
conv2_2,
conv3_3, and
conv4_3) to compute a perceptual loss, which captures image quality more effectively than simple pixel-wise losses. The LPIPS metric builds on a pre-trained VGG network and adds a linear layer as weights to re-calibrate each feature map’s importance with a human-rated ground truth. From
Figure 3a, using of
and
in the adversarial loss is efficient, as the loss decreases obviously through epochs. We observe a similar loss pattern on a recently developed DNN-based metric, DISTS.
However, the quality result from the PSNR value of
differs greatly from
and
, where its re-compression quality remains indistinguishable from the first compression result. The re-compression PSNR value of
or
shown in
Table 3 is significantly lower, so the SLIC trained with perceptual metric
or
effectively degrades visual quality. We think that’s because both LPIPS and DISTS learn a weighting layer on top of the VGG feature maps with a human-rated perceptual dataset, so the two metrics weigh more on features that are sensitive to human perception. As a result, a tiny invisible perturbation added to the compressed output will trigger a change in a perceptual sensitive feature map that causes severe quality damage in the re-compression. As for VGGLoss, feature maps are learned specifically for object detection purposes, and the magnitude of feature map coefficients highly impacts the calculation of VGGLoss (L1 or L2 norm). Therefore, we can observe that the adversarial loss of
decreases (which means increased quality divergence) during training in
Figure 3a, but the PSNR values remain high and less changed in
Figure 3b throughout the training process. That is, the increased distance of VGGLoss does not divert the actual perceptual distance of two images.
Except for the DNN-based perceptual metric, we include the test with the better-developed traditional quality metric GMSD and NLPD to compare their ability to divert the re-compression quality. The Gradient Magnitude Similarity Deviation (GMSD) [
36] is designed to measure perceptual similarity and focus on gradient information in both
x and
y directions, as human vision is highly sensitive to edges and gradient changes in images. The Normalized Laplacian Pyramid Distance (NLPD) [
37] is rooted in the Laplacian Pyramid decomposition, which captures image details at multiple scales and mimics the multi-scale nature of human visual perception.
Table 3 shows that both GMSD and NLPD reduce the PSNR of re-compression image
notably compared to MSE and MS-SSIM. However, the adversarial effect of NLPD is not robust to various editing operations like GMSD, which is showcased in
Section 4.3. We can think of NLPD as a metric scored from a simplified shallow network with Laplacian filters compared to the VGGLoss from a deep VGG network that learns filter maps from ImageNet. That may explain the lesser effectiveness of NLPD as a perceptual metric to diver the visual quality.
As GMSD computes the gradient magnitude similarity (GMS) between two images and uses the standard deviation of the GMS values to measure the difference, a minor update on the standard deviation of GMS may lead to regions of significant perceptual differences due to gradient change. That’s why the GMSD is quite effective in diverting the visual quality as PSNR decreases efficiently in
Figure 3b.
4.2. Destructive-Compression Effects
We present the qualitative re-compression results of
in
Figure 4. In the second and third rows of
Figure 4, the re-compression quality of SLIC codec trained with perceptual metric
and
is almost destroyed and unrecognizable from the prior compressed
, which aligns with the low averaged PSNR value around 5 in
Table 3. The quality damages introduced by perceptual metrics LPIPS and DISTS are far more severe than artifacts caused by other adversarial attacks [
15,
52]. It is interesting to note that LPIPS and DISTS have different artifact patterns, probably due to the design nature of the perceptual metric. The re-compression artifacts caused by metric
combined with neural codec Balle2018, Minnen2018, and Cheng2020 are presented in
Figure 5,
Figure A2 and
Figure A3, respectively. Their artifact patterns are similar except for the overflowed and truncated pixel colors, which should be affected by the randomness of image batches when we fine-tune the neural codec.
The re-compression artifacts caused by metric
have attractive uniform vertical black-and-white stripes, as shown in the fourth row of
Figure A1. We think the pattern may come from the image gradients in the
x direction. The metric
causes fewer artifacts than
but with similar vertical thicker red and light blue strips. The last row in
Figure 4 shows the re-compression result of metric
. The VGGLoss metric merely causes very few artifacts near image borders like the “48970” image of the FFHQ dataset, which echoes the findings we mentioned in the previous section; the VGGLoss is not an adequate metric to exploit the neural encoder for a degraded re-compression result.
We provide more destructive-compression results in
Appendix A.2. Pursuing a perfect perceptual metric that 100% matches human visual judgment is a holy grail of the image quality assessment research field. Most studies focus on minimizing perceptual loss, but almost zero studies have been conducted on effectively diverting one perceptual quality from another. This may be an interesting research topic for studying adversarial attacks on learned image codecs.
4.3. Robustness Against Editing Operations
Due to the victim image being manipulated for counterfeiting, which will undergo various image distortions, the SLIC must be robust enough for possible image editing. We present our SLIC’s robustness against eight pre-defined editing operations in
Table 4. We tested three selected neural codecs with perceptual metrics
and
, and the PSNR values were less than 10 in general across the tested SLICs.
Figure 5 shows Balle2018 +
codec’s re-compression quality degradation as an example; more results are listed in
Appendix A.2.
The robustness of cropping proves that the adversarial perturbations added to the compressed output are translation-invariant. Our SLIC is not impacted by the possible distortions such as sharpening, lighting adjustment, and color adjustment during image tampering because these edits will not smooth out the adversarial perturbations but magnify them. Filtering editing operations such as Gaussian blur, median filtering, affine transform, and JPEG compression will partially filter out adversarial perturbations. Still, the noise attacker simulates this kind of distortion during training. Therefore, our SLIC can still destroy the visual quality after re-compression, given challenging distortions such as blurring, rotation, scaling, and JPEG compression. The qualitative results in
Figure 5 demonstrate our SLIC’s robustness in being used as a secure image codec.
4.4. Robustness Against GenAI
In the era of AI-generated content, generative AI (GenAI) tools can manipulate images conveniently and provide more realistic outputs than traditional image editing software. For deepfakes, research efforts like FaceShifter [
61] have developed methods to transfer a target face onto a victim’s image, producing highly realistic results. Online tools such as Remaker AI [
62] provide vivid face swap tools that are freely available to the public. We test our SLIC with Remaker AI face swap and Stable Diffusion Inpaint [
63] to validate the robustness against GenAI tools.
Figure 6 demonstrates that our SLIC can still damage the image quality of a GenAI-manipulated image after re-compression.
We provide two face swap results and two inpainting results in
Figure 6. After re-compression, only the implanted regions with the target face or generated background are kept; the remaining areas are destroyed with adversarial artifacts. The last column of
Figure 6 shows our SLIC’s robustness in dealing with compound editing, which is rotated, scaled, and then inpainted. If an image is encoded in SLIC format, the whole image is protected unless the tampering behavior transplants a large portion of the region. In that case, almost all the essential information in the protected image is lost, which also means the integrity of the image is protected.
However, if the SLIC-encoded image contains a face we want to protect, the adversarial effect is lost after the victim’s face is re-generated onto the target image. In
Figure 7, the tampered image on the third comprises a non-SLIC encoded image and a SLIC-encoded faces. The adversarial perturbations on the victim’s face are transformed by the generative model’s encoder to a latent space representation and re-generated, aligned, and blended onto the target image. Face-swapping eliminates adversarial perturbations, so the re-compression result remains high quality. How to preserve the adversarial perturbations through the face re-generation process would be an essential research direction to explore.
4.5. Coding Efficiency Impact
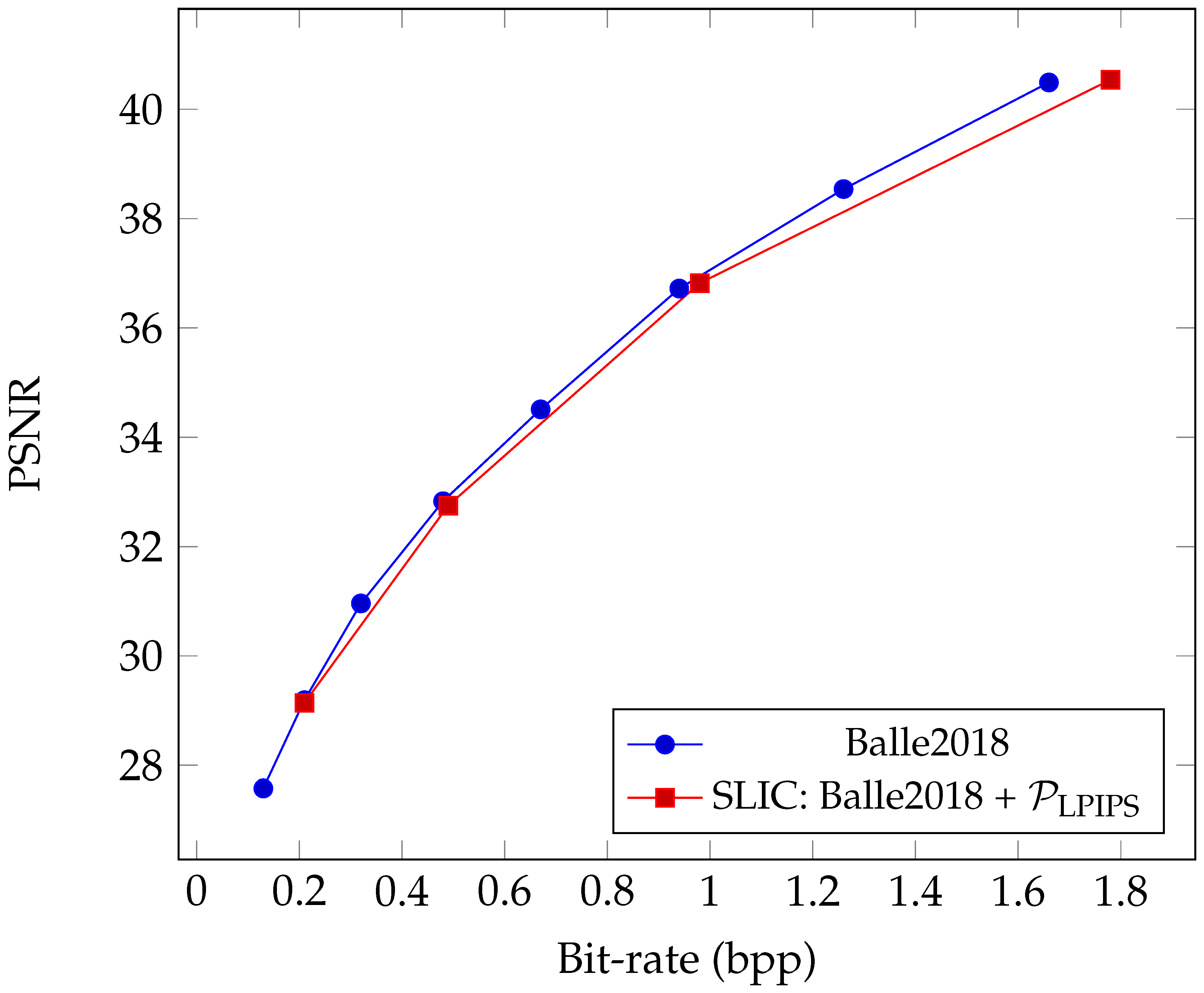
Conceptually, the proposed SLIC generates out-of-distribution noise signals as adversarial perturbations in the decoder output will reduce the coding efficiency of natural images. Therefore, when fine-tuning the neural codec, we keep the rate-distortion function and jointly optimize it with the adversarial loss. We present the rate-distortion curve of our SLIC evaluated on the Kodak dataset in
Figure 8. Our fine-tuned neural codec as SLIC remains optimal in coding efficiency compared to vanilla ones.
5. Discussion
Our work demonstrated the ability of SLIC to generate destructive results upon re-compression, effectively preventing unauthorized image modifications. However, several areas require further investigation to maximize its effectiveness and practical applicability.
5.1. Effectiveness of Perceptual Metrics
Our experiments highlighted that different perceptual metrics influence the performance of SLIC in generating destructive compression effects. We observed that deep-learning-based metrics like LPIPS and DISTS are more effective in creating visually disruptive artifacts compared to traditional metrics such as MSE or SSIM. Despite this, the selection of the most suitable perceptual metric for SLIC remains an open research question. Understanding why specific metrics better induce visual distortions requires further exploration into their internal mechanisms.
5.2. Adversarial Perturbation Preservation
One limitation we identified is the loss of adversarial perturbations when the protected image undergoes complex manipulations, such as face-swapping or deepfake generation using generative models. Preserving adversarial perturbations through such transformations is a critical area for future research. Investigating methods to make these perturbations invariant to transformations or exploring how to embed them more deeply within the image’s feature space could lead to more robust defenses against generative AI manipulations.
5.3. Optimizing Fine-Tuning Strategies
The fine-tuning process of the neural codec plays a crucial role in balancing image quality, compression rate, and adversarial robustness. In our experience, the GDN [
64] non-linear transform used in learned image codec Minnen2018 and Cheng2020 will cause numeric error when combined with perceptual metric
. While we identified effective hyperparameter settings for optimizing SLIC with existing metrics, more refined strategies could enhance its performance.
6. Conclusions
In this paper, we proposed the full resolution Secure Learned Image Codec (SLIC) as a proactive defense mechanism against image manipulation and tampering. Unlike traditional codecs, SLIC employs adversarial perturbations that degrade image quality upon subsequent re-compression, ensuring that any edited or tampered image is visually compromised. Our experiments demonstrate that SLIC effectively creates a non-idempotent codec, where the first encoded image remains high quality, while the second re-compressed version exhibits severe visual degradation. We achieved this by incorporating perceptual quality metrics into the adversarial loss, which enabled our codec to generate out-of-distribution perturbations. Among the tested perceptual metrics, LPIPS and DISTS were particularly effective in creating adversarial artifacts. Additionally, SLIC showed robustness against a variety of common image editing operations and GenAI-based manipulations, including face-swapping and inpainting. Our proposed SLIC highlights the potential of integrating adversarial training with learned image codecs as a novel approach to enhance image authentication and manipulation resistance. We believe that this proactive strategy paves a new way for digital content verification from the image format perspective, restoring trust in image credibility when faced with advancing image manipulation techniques.
Funding
This research was partially supported by the Minister of Science and Technology, Taiwan (grant number: MOST 111-2221-E-002-134-MY3) and National Taiwan University (grant number: NTU- 112L900902).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A.
Appendix A.1. UNetJPEG Image Transformation Task
In training our SLIC, we use a UNet-based architecture, UNetJPEG, as an image transformation task to approximate the effects of JPEG compression while conditioning on a specified quality factor. Our UNetJPEG is conditioned on the JPEG quality factor. The quality factor, which typically ranges from 10 to 100, is concatenated as an additional channel to the input image. This allows the network to adjust its output based on the provided quality factor, simulating the compression artifacts associated with various JPEG quality levels. The concatenated input is passed through the network, and the decoder reconstructs an image that mimics the distortions caused by JPEG compression at the given quality. During training, we use the standard JPEG encoder/decoder to create source and distorted image pairs for the neural network to approximate. We train the UNetJPEG network for 100 epochs on the COCO dataset.
The architecture of the
UNetJPEG is summarized in
Table A1. The network consists of four encoding layers, a middle bottleneck, and four decoding layers, each followed by ReLU activations. Skip connections are added between corresponding encoder and decoder layers, enabling the network to retain high-frequency details. Max pooling operations are used for downsampling in the encoder, and bilinear upsampling is employed in the decoder.
Table A1.
The architecture of the UNetJPEG.
Table A1.
The architecture of the UNetJPEG.
| Layer |
Operation |
Output Shape |
| Input |
Input image + quality factor (4 channels) |
|
| Encoder 1 |
Conv2d(4, 64, 3x3) + ReLU |
|
| Encoder 2 |
MaxPool2d + Conv2d(64, 128, 3x3) + ReLU |
|
| Encoder 3 |
MaxPool2d + Conv2d(128, 256, 3x3) + ReLU |
|
| Encoder 4 |
MaxPool2d + Conv2d(256, 512, 3x3) + ReLU |
|
| Middle |
MaxPool2d + Conv2d(512, 1024, 3x3) + ReLU |
|
| Decoder 4 |
Upsample + Conv2d(1024, 512, 3x3) + ReLU |
|
| Decoder 3 |
Upsample + Conv2d(512, 256, 3x3) + ReLU |
|
| Decoder 2 |
Upsample + Conv2d(256, 128, 3x3) + ReLU |
|
| Decoder 1 |
Upsample + Conv2d(128, 64, 3x3) + ReLU |
|
| Output |
Conv2d(64, 3, 1x1) + Sigmoid |
|
Table A2 shows the superior robustness against JPEG compression using
UNetJPEG on three test datasets. A significantly lower PSNR value indicates eye-catching artifacts that destroy the visual quality after re-compression.
Table A2.
The re-compression robustness comparison against JPEG on different simulation strategies. Here, the SLIC used is Balle2018 + .
Table A2.
The re-compression robustness comparison against JPEG on different simulation strategies. Here, the SLIC used is Balle2018 + .
| Simulation |
Kodak |
FFHQ |
DIV2K |
| JPEG↓ |
JPEG↓ |
JPEG↓ |
| UNetJPEG |
8.69 |
8.49 |
15.00 |
| Cubic round [55] |
25.89 |
27.62 |
36.52 |
Appendix A.2. More Destructive-Compression Effects
This section presents more qualitative re-compression results of SLICs trained with different perceptual metrics.
Figure A1.
The re-compressed results of Balle2018 + SLIC images after various editing operations.
Figure A1.
The re-compressed results of Balle2018 + SLIC images after various editing operations.
Figure A2.
The re-compressed results of Minnen2018 + SLIC images after various editing operations.
Figure A2.
The re-compressed results of Minnen2018 + SLIC images after various editing operations.
Figure A3.
The re-compressed results of Cheng2018 + SLIC images after various editing operations.
Figure A3.
The re-compressed results of Cheng2018 + SLIC images after various editing operations.
References
- Tolosana, R.; Vera-Rodriguez, R.; Fierrez, J.; Morales, A.; Ortega-Garcia, J. Deepfakes and beyond: A survey of face manipulation and fake detection. Information Fusion 2020, 64, 131–148. [Google Scholar] [CrossRef]
- Piva, A. An overview on image forensics. International Scholarly Research Notices 2013, 2013. [Google Scholar] [CrossRef]
- Zanardelli, M.; Guerrini, F.; Leonardi, R.; Adami, N. Image forgery detection: a survey of recent deep-learning approaches. Multimedia Tools and Applications 2023, 82, 17521–17566. [Google Scholar] [CrossRef]
- Mahdian, B.; Saic, S. Using noise inconsistencies for blind image forensics. Image and vision computing 2009, 27, 1497–1503. [Google Scholar] [CrossRef]
- Bayram, S.; Sencar, H.T.; Memon, N. An efficient and robust method for detecting copy-move forgery. 2009 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2009, pp. 1053–1056. [CrossRef]
- Ghosh, A.; Zhong, Z.; Boult, T.E.; Singh, M. SpliceRadar: A Learned Method For Blind Image Forensics. CVPR Workshops, 2019, pp. 72–79. [CrossRef]
- Popescu, A.C.; Farid, H. Exposing digital forgeries in color filter array interpolated images. IEEE Transactions on Signal Processing 2005, 53, 3948–3959. [Google Scholar] [CrossRef]
- Mahdian, B.; Saic, S. Detecting double compressed JPEG images. 3rd International Conference on Imaging for Crime Detection and Prevention (ICDP 2009). 2009. [Google Scholar] [CrossRef]
- Park, J.; Cho, D.; Ahn, W.; Lee, H.K. Double JPEG detection in mixed JPEG quality factors using deep convolutional neural network. Proceedings of the European conference on computer vision (ECCV), 2018, pp. 636–652. [CrossRef]
- Friedman, G.L. The trustworthy digital camera: Restoring credibility to the photographic image. IEEE Transactions on consumer electronics 1993, 39, 905–910. [Google Scholar] [CrossRef]
- Blythe, P.; Fridrich, J. Secure digital camera. Digital Investigation 2004. [Google Scholar]
- Kundur, D.; Hatzinakos, D. Digital watermarking for telltale tamper proofing and authentication. Proceedings of the IEEE 1999, 87, 1167–1180. [Google Scholar] [CrossRef]
- Lu, C.S.; Liao, H.Y.M. Structural digital signature for image authentication: an incidental distortion resistant scheme. Proceedings of the 2000 ACM workshops on Multimedia, 2000, pp. 115–118. [CrossRef]
- Liu, K.; Wu, D.; Wu, Y.; Wang, Y.; Feng, D.; Tan, B.; Garg, S. Manipulation Attacks on Learned Image Compression. IEEE Transactions on Artificial Intelligence 2023. [Google Scholar] [CrossRef]
- Chen, T.; Ma, Z. Towards robust neural image compression: Adversarial attack and model finetuning. IEEE Transactions on Circuits and Systems for Video Technology 2023. [Google Scholar] [CrossRef]
- Huang, C.H.; Wu, J.L. SLIC: Secure Learned Image Codec through Compressed Domain Watermarking to Defend Image Manipulation. Proceedings of the 6th ACM International Conference on Multimedia in Asia, 2024, pp. 1–7. [CrossRef]
- Rey, C.; Dugelay, J.L. A survey of watermarking algorithms for image authentication. EURASIP Journal on Advances in Signal Processing 2002, 2002, 1–9. [Google Scholar] [CrossRef]
- Ruiz, N.; Bargal, S.A.; Sclaroff, S. Disrupting Deepfakes: Adversarial Attacks Against Conditional Image Translation Networks and Facial Manipulation Systems 2020. arXiv:10.1007/978-3-030-66823-5_14.
- Lv, L. Smart watermark to defend against deepfake image manipulation. 2021 IEEE 6th international conference on computer and communication systems (ICCCS). IEEE, 2021, pp. 380–384. [CrossRef]
- Zhang, X.; Li, R.; Yu, J.; Xu, Y.; Li, W.; Zhang, J. Editguard: Versatile image watermarking for tamper localization and copyright protection. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2024, pp. 11964–11974. [CrossRef]
- Yu, N.; Skripniuk, V.; Abdelnabi, S.; Fritz, M. Artificial fingerprinting for generative models: Rooting deepfake attribution in training data. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 14448–14457. [CrossRef]
- Wang, J.; Wang, H.; Zhang, J.; Wu, H.; Luo, X.; Ma, B. Invisible Adversarial Watermarking: A Novel Security Mechanism for Enhancing Copyright Protection. ACM Transactions on Multimedia Computing, Communications and Applications. [CrossRef]
- Zhang, J.; Wang, J.; Wang, H.; Luo, X. Self-recoverable adversarial examples: A new effective protection mechanism in social networks. IEEE Transactions on Circuits and Systems for Video Technology 2022, 33, 562–574. [Google Scholar] [CrossRef]
- Ballé, J.; Minnen, D.; Singh, S.; Hwang, S.J.; Johnston, N. Variational image compression with a scale hyperprior. arXiv preprint 2018, arXiv:arXiv:1802.01436. [Google Scholar]
- Minnen, D.; Ballé, J.; Toderici, G.D. Joint autoregressive and hierarchical priors for learned image compression. Advances in Neural Information Processing Systems 2018, 31, 10771–10780. [Google Scholar] [CrossRef]
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Learned image compression with discretized gaussian mixture likelihoods and attention modules. CVPR, 2020, pp. 7939–7948. [CrossRef]
- Guo, Z.; Zhang, Z.; Feng, R.; Chen, Z. Causal contextual prediction for learned image compression. IEEE Transactions on Circuits and Systems for Video Technology 2021, 32, 2329–2341. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Jia, C.; Zhao, Z.; Wang, S.; Wanga, S. Image and video compression with neural networks: A review. IEEE Transactions on Circuits and Systems for Video Technology 2019. [Google Scholar] [CrossRef]
- Yang, Y.; Mandt, S.; Theis, L. An introduction to neural data compression. arXiv preprint 2022, arXiv:2202.06533. [Google Scholar] [CrossRef]
- Huang, C.H.; Wu, J.L. Unveiling the Future of Human and Machine Coding: A Survey of End-to-End Learned Image Compression. Entropy 2024, 26, 357. [Google Scholar] [CrossRef]
- Kim, J.H.; Jang, S.; Choi, J.H.; Lee, J.S. Instability of successive deep image compression. Proceedings of the 28th ACM International Conference on Multimedia, 2020, pp. 247–255. [CrossRef]
- Helminger, L.; Djelouah, A.; Gross, M.; Schroers, C. Lossy Image Compression with Normalizing Flows. Neural Compression: From Information Theory to Applications – Workshop @ ICLR 2021, 2021. [CrossRef]
- Li, Y.; Xu, T.; Wang, Y.; Liu, J.; Zhang, Y.Q. Idempotent learned image compression with right-inverse. Advances in Neural Information Processing Systems 2024, 36. [Google Scholar]
- Xu, T.; Zhu, Z.; He, D.; Li, Y.; Guo, L.; Wang, Y.; Wang, Z.; Qin, H.; Wang, Y.; Liu, J. ; others. Idempotence and perceptual image compression. arXiv preprint 2024, arXiv:2401.08920. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X.; Bovik, A.C. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index. IEEE transactions on image processing 2013, 23, 684–695. [Google Scholar] [CrossRef]
- Laparra, V.; Ballé, J.; Berardino, A.; Simoncelli, E.P. Perceptual image quality assessment using a normalized Laplacian pyramid. Electronic Imaging 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual losses for real-time style transfer and super-resolution. Proceedings of the European Conference on Computer Vision (ECCV). Springer, 2016, pp. 694–711. [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. CVPR, 2018. [CrossRef]
- Bhardwaj, S.; Fischer, I.; Ballé, J.; Chinen, T. An unsupervised information-theoretic perceptual quality metric. Advances in Neural Information Processing Systems 2020, 33, 13–24. [Google Scholar] [CrossRef]
- Ding, K.; Ma, K.; Wang, S.; Simoncelli, E.P. Image quality assessment: Unifying structure and texture similarity. IEEE transactions on pattern analysis and machine intelligence 2020, 44, 2567–2581. [Google Scholar] [CrossRef] [PubMed]
- CLIC 2021: Workshop and Challenge on Learned Image Compression.
- Zhu, H.; Chen, B.; Zhu, L.; Wang, S.; Lin, W. DeepDC: Deep Distance Correlation as a Perceptual Image Quality Evaluator. arXiv e-prints, 2022; arXiv:2211.04927. [Google Scholar] [CrossRef]
- Gatys, L.A.; Ecker, A.S.; Bethge, M. A neural algorithm of artistic style. arXiv preprint 2015, arXiv:1508.06576. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z. ; others. Photo-realistic single image super-resolution using a generative adversarial network. CVPR, 2017, pp. 4681–4690. [CrossRef]
- Huang, C.H.; Wu, J.L. Image Data Hiding in Neural Compressed Latent Representations. IEEE International Conference on Visual Communications and Image Processing (VCIP). IEEE, 2023. [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv preprint 2013, arXiv:1312.6199. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv preprint 2014, arXiv:1412.6572. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial intelligence safety and security; Chapman and Hall/CRC, 2018; pp. 99–112. [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. arXiv preprint 2017, arXiv:1706.06083. [Google Scholar] [CrossRef]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. 2017 ieee symposium on security and privacy (sp). Ieee, 2017, pp. 39–57. [CrossRef]
- Zhu, T.; Sun, H.; Xiong, X.; Zhu, X.; Gong, Y.; Fan, Y. ; others. Attack and defense analysis of learned image compression. arXiv preprint 2024, arXiv:2401.10345. [Google Scholar] [CrossRef]
- Huang, C.H.; Wu, J.L. Joint Image Data Hiding and Rate-Distortion Optimization in Neural Compressed Latent Representations. International Conference on Multimedia Modeling. Springer, 2024, pp. 94–108. [CrossRef]
- Zhu, J.; Kaplan, R.; Johnson, J.; Fei-Fei, L. Hidden: Hiding data with deep networks. Proceedings of the European conference on computer vision (ECCV), 2018, pp. 657–672. [CrossRef]
- Shin, R.; Song, D. Jpeg-resistant adversarial images. NIPS 2017 Workshop on Machine Learning and Computer Security, 2017, Vol. 1.
- Bégaint, J.; Racapé, F.; Feltman, S.; Pushparaja, A. CompressAI: a PyTorch library and evaluation platform for end-to-end compression research. arXiv preprint 2020, arXiv:2011.03029. [Google Scholar] [CrossRef]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; others. Imagenet large scale visual recognition challenge. International journal of computer vision 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Kodak PhotoCD dataset. http://r0k.us/graphics/kodak/, 1999.
- Karras, T.; Laine, S.; Aila, T. A Style-Based Generator Architecture for Generative Adversarial Networks. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2019, pp. 4401–4410. [CrossRef]
- Agustsson, E.; Timofte, R. NTIRE 2017 Challenge on Single Image Super-Resolution: Dataset and Study. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, 2017. [CrossRef]
- Li, L.; Bao, J.; Yang, H.; Chen, D.; Wen, F. Faceshifter: Towards high fidelity and occlusion aware face swapping. arXiv preprint, arXiv:1912.13457.2019. [Google Scholar]
- Remaker Face Swap Online Free. https://remaker.ai/face-swap-free/.
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-Resolution Image Synthesis with Latent Diffusion Models. 2021. [Google Scholar] [CrossRef]
- Ballé, J.; Chou, P.A.; Minnen, D.; Singh, S.; Johnston, N.; Agustsson, E.; Hwang, S.J.; Toderici, G. Nonlinear transform coding. IEEE Journal of Selected Topics in Signal Processing 2020, 15, 339–353. [Google Scholar] [CrossRef]
Figure 1.
The proposed Secure Learned Image Codec (SLIC) will be self-destroyed after re-compression. Top images from left to right: the first encoded image, blurred encoded image, JPEG compressed image, affine transformed image (shift 10 pixels, rotated 5°, scaled 95%), face swapped image, and inpainted image. The bottom re-compressed images are severely damaged.
Figure 1.
The proposed Secure Learned Image Codec (SLIC) will be self-destroyed after re-compression. Top images from left to right: the first encoded image, blurred encoded image, JPEG compressed image, affine transformed image (shift 10 pixels, rotated 5°, scaled 95%), face swapped image, and inpainted image. The bottom re-compressed images are severely damaged.
Figure 2.
The SLIC training flow. In a rate-distortion optimized neural codec, we introduce the adversarial re-compression and the adversarial noised re-compression losses.
Figure 2.
The SLIC training flow. In a rate-distortion optimized neural codec, we introduce the adversarial re-compression and the adversarial noised re-compression losses.
Figure 3.
The trending of (a) adversarial loss and (b) re-compression PSNR among various perceptual metrics during training.
Figure 3.
The trending of (a) adversarial loss and (b) re-compression PSNR among various perceptual metrics during training.
Figure 4.
The re-compression visual quality of the SLICs. The top row is the source image, and the remaining rows are the re-compressed images of Balle2018 codecs, adversarial trained with different perceptual metrics.
Figure 4.
The re-compression visual quality of the SLICs. The top row is the source image, and the remaining rows are the re-compressed images of Balle2018 codecs, adversarial trained with different perceptual metrics.
Figure 5.
The re-compressed results of Balle2018 + SLIC images after various editing operations.
Figure 5.
The re-compressed results of Balle2018 + SLIC images after various editing operations.
Figure 6.
The results of Balle2018 + SLIC images were re-compressed after GenAI manipulation: FaceSwap and Stable Diffusion Inpaint.
Figure 6.
The results of Balle2018 + SLIC images were re-compressed after GenAI manipulation: FaceSwap and Stable Diffusion Inpaint.
Figure 7.
The failed case: a SLIC-protected face will lose its adversarial perturbations after deepfake re-generating the victim face on the target image.
Figure 7.
The failed case: a SLIC-protected face will lose its adversarial perturbations after deepfake re-generating the victim face on the target image.
Figure 8.
The rate–distortion curve of SLIC Balle2018 + compared with the original codec. They are evaluated on the Kodak dataset.
Figure 8.
The rate–distortion curve of SLIC Balle2018 + compared with the original codec. They are evaluated on the Kodak dataset.
Table 1.
The values for different LIC quality scales.
Table 1.
The values for different LIC quality scales.
| Quality |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
0.2 |
0.3 |
0.45 |
0.6 |
0.8 |
1 |
1.75 |
2.5 |
Table 2.
The parameter settings of editing operation used for evaluation.
Table 2.
The parameter settings of editing operation used for evaluation.
| Editing operation |
Setting |
| Crop |
Crop center 80% rectangle and paste into another blank image. |
| Gaussian Blur |
Gaussian blur with window size and . |
| Median Filtering |
Median filtering with window size . |
| Lightening |
Increase luminance by 150%. |
| Sharpening |
Sharpen image with filter kernel
|
| Histogram Equalization |
Histogram equalization in RGB channel. |
| Affine Transform |
Rotate image by , translate 10 pixels, and scale to 95%. |
| JPEG Compression |
JPEG compression with quality . |
Table 3.
The re-compression quality degradation in PSNR of the SLICs. We use Balle2018 as the primary codec with different perceptual metrics to fine-tune the SLICs. A significantly low PSNR indicates the destructiveness of re-compression.
Table 3.
The re-compression quality degradation in PSNR of the SLICs. We use Balle2018 as the primary codec with different perceptual metrics to fine-tune the SLICs. A significantly low PSNR indicates the destructiveness of re-compression.
| SLIC |
Kodak |
FFHQ |
DIV2K |
|
|
|
|
|
|
| Balle2018 +
|
39.74 |
5.68 |
40.83 |
5.56 |
38.28 |
5.26 |
| Balle2018 +
|
39.81 |
5.11 |
40.95 |
4.96 |
38.25 |
5.41 |
| Balle2018 +
|
39.74 |
8.42 |
40.86 |
7.62 |
38.31 |
8.17 |
| Balle2018 +
|
40.67 |
30.64 |
41.33 |
19.16 |
38.92 |
25.81 |
| Balle2018 +
|
40.72 |
43.05 |
41.38 |
31.33 |
39.01 |
44.53 |
| Balle2018 +
|
40.70 |
47.87 |
41.36 |
47.30 |
39.02 |
47.86 |
| Balle2018 +
|
40.60 |
47.27 |
41.20 |
46.70 |
38.97 |
47.46 |
Table 4.
The re-compression quality degradation on edited images in PSNR. The SLICs are trained using different neural codecs and percpetual metrics and evaluated on test datasets.
Table 4.
The re-compression quality degradation on edited images in PSNR. The SLICs are trained using different neural codecs and percpetual metrics and evaluated on test datasets.
| SLIC |
|
|
Re-compress after |
| |
|
Crop↓ |
G.Blur↓ |
M.Filter↓ |
Sharp↓ |
Light↓ |
H.Equ.↓ |
Affine↓ |
JPEG↓ |
| Kodak |
| Balle2018 +
|
39.74 |
5.68 |
7.20 |
6.62 |
5.75 |
5.89 |
5.75 |
5.22 |
6.54 |
8.69 |
| Balle2018 +
|
39.81 |
5.11 |
6.50 |
7.48 |
6.04 |
5.14 |
6.44 |
5.37 |
9.68 |
7.29 |
| Minnen2018 +
|
40.35 |
5.52 |
6.99 |
6.39 |
6.07 |
6.77 |
5.72 |
6.07 |
7.89 |
11.55 |
| Cheng2020 +
|
39.53 |
5.79 |
5.85 |
7.41 |
6.81 |
6.99 |
7.17 |
5.83 |
6.42 |
8.19 |
| FFHQ |
| Balle2018 +
|
40.83 |
5.56 |
6.45 |
6.44 |
5.64 |
5.51 |
5.40 |
5.04 |
6.24 |
8.49 |
| Balle2018 +
|
40.95 |
4.96 |
5.84 |
8.19 |
6.18 |
4.77 |
6.31 |
5.25 |
10.16 |
7.55 |
| Minnen2018 +
|
40.86 |
5.06 |
6.00 |
5.76 |
5.38 |
5.55 |
5.37 |
5.57 |
7.32 |
12.20 |
| Cheng2020 +
|
40.59 |
5.34 |
4.05 |
6.56 |
6.03 |
5.46 |
5.61 |
4.94 |
6.46 |
7.40 |
| DIV2K |
| Balle2018 +
|
38.28 |
5.26 |
7.08 |
7.18 |
5.56 |
6.11 |
5.59 |
5.80 |
7.64 |
15.00 |
| Balle2018 +
|
38.25 |
5.41 |
7.18 |
8.76 |
6.81 |
5.50 |
6.71 |
5.99 |
11.40 |
10.25 |
| Minnen2018 +
|
38.82 |
5.67 |
7.14 |
6.71 |
6.44 |
8.01 |
6.61 |
7.67 |
9.34 |
24.20 |
| Cheng2020 +
|
37.62 |
5.59 |
4.97 |
9.19 |
6.82 |
7.05 |
6.69 |
7.00 |
6.98 |
9.80 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).