1. The Haug and Tatum Cosmological Model
The Haug and Tatum cosmological model (HTC) [
1] has integrated some newly-discovered fundamental relationships between certain cosmological parameters such that it even appears to resolve the Hubble tension. In the following sections, we will explore different aspects of the model and compare each with the
-CDM model. HTC is a variant of the
cosmology model that satisfies the Friedmann [
2] equation, making it consistent with Einstein’s [
3] general relativity. One of the fundamental breakthroughs of this model is its ability to provide a robust mathematical framework relating the CMB temperature to other cosmological parameters, all in accordance with general relativity. For an in-depth study of the model, one must consult the many references we provide in this paper. To facilitate such study, we herein summarize the key features and compare them with the
-CDM model. Based on our analysis so far, HTC appears to outperform the
-CDM model, although there may still be challenges as we continue to test it with pending observational studies.
2. -CDM Cannot Predict Current CMB Temperature, Whereas HTC Can Precisely Predict
The current CMB temperature
is the most precisely measured cosmological parameter. For example, the recent Dhal et al. [
4] study reports a CMB temperature of
. Unfortunately,
-CDM cannot predict
, as pointed out by Narlikar and Padmanabhan [
5]:
“The present theory is, however, unable to predict the value of T at . It is therefore a free parameter in SC (Standard Cosmology)."
In sharp contrast, HTC can accurately predict the current CMB temperature according to:
Equation (
1) was first introduced within
cosmology by Tatum et al. [
6]. It was later fundamentally derived from the Stefan-Boltzmann law by Haug and Wojnow [
7]. Since then, it has also been derived using a geometric mean approach by Haug and Tatum [
8], which also seems valid in
black hole cosmology.
3. -CDM Cannot Derive , Whereas HTC Does So
HTC reference [
1] gives distance-vs-redshift scaling according to
. When used in combination with equation (
1), the following well-known observational relation can be easily derived:
Whereas, in standard cosmology, the
relation appears to be mostly an assumption based upon observations see [
9,
10,
11], rather than a prediction based on derivation and then confirmed by observations, as in the HTC model.
4. -CDM Cannot Yet Resolve the Hubble Tension, Whereas HTC Appears to Resolve the Hubble Tension
In
-CDM cosmology, the Hubble tension has not yet been satisfactorily resolved, as noted by Valentino et al. [
12]. Haug and Tatum, however, have recently demonstrated that the Hubble tension appears to be resolved within HTC. By using the measured CMB temperature, Haug and Tatum [
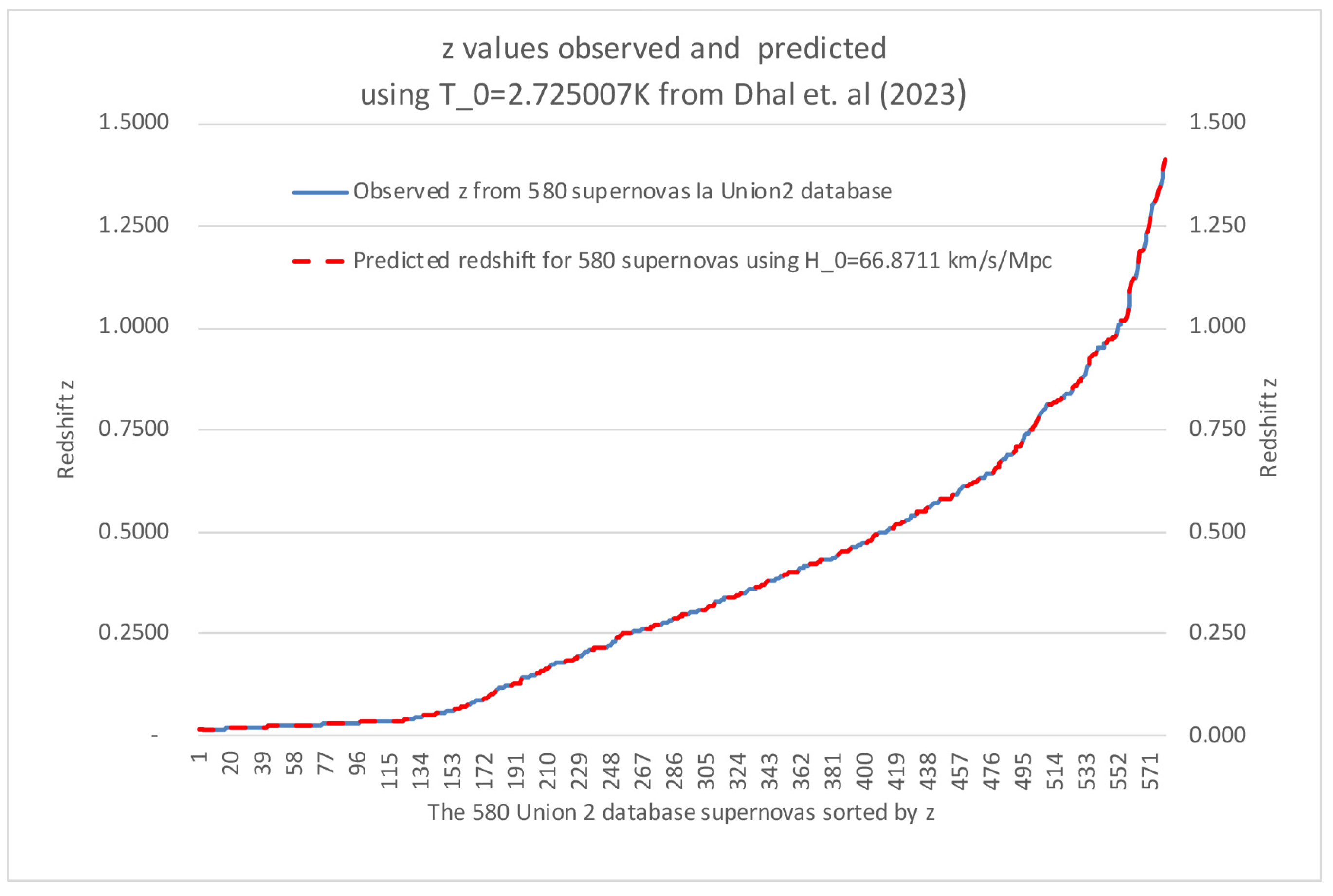
1] demonstrated that, through either a simple but tedious trial-and-error method or a more sophisticated and automated “intelligent search” algorithm, one can readily find the single optimal value of
which allows their redshift function to match the full distance ladder of supernovae (SN Ia) in the Union2 database. Haug [
13] has further discussed this and even provided an additional mathematical proof that the Hubble tension is resolved within the HTC model. In
Figure 1, we show the graph of the predicted redshifts in HTC versus the actual observed redshifts across the full Union2 distance ladder. We simply start out with the measured CMB value of Dhal et al. [
4]
and then, by the trial-and-error method or alternatively by the closed-form solution method (both methods described in the papers just mentioned), find the one single
value that gives a near-perfect match between observed redshifts and our HTC predicted redshifts. Naturally, there is a very small residual uncertainty in
due to the minimal residual uncertainty in
. Of course, we have also incorporated the latest NIST CODATA uncertainties in the physical constants used.
Moreover, if one starts out by already assuming the CMB temperature and
values of
Figure 1, one can also use the observed full distance redshift ladder of the Union2 supernovae to extract the Planck length value matching the NIST CODATA; this is yet another convincing way that HTC resolves the Hubble tension, see [
14]. Such a result also demonstrates that HTC is linked to the Planck scale, and that all of these parameters are mathematically connected within HTC.
5. -CDM Has Much Higher Uncertainty in Comparison to HTC in Measured
Despite considerable recent improvements in the measurements of
, there is still significant uncertainty in the measured Hubble constant value. The Planck Collaboration study [
15] gives
. In contrast, the SH0ES study of the local universe by Riess et al. [
16] gives
. These two very different results are the basis for the Hubble tension in standard cosmology, which we have already shown that HTC appears to resolve in favor the Planck Collaboration value.
Fortunately, HTC also dramatically improves the precision of
. This is possible because, unlike the
-CDM model, HTC has established an exact mathematical relationship between
and
(derivable from equation
1). As a result, we can simply use the most precisely measured value of either
or
and calculate the other parameter. For example, if we use the Dhal et al. [
4] study, which provides a high-precision CMB temperature, we obtain
, see [
1,
17]. This is a dramatic improvement in precision in comparison to the Planck Collaboration and Riess et al. measurements.
6. HTC Provides for Markedly Increased Precision in Predictions of a Series of Cosmological Parameters
Since HTC has achieved much higher precision in
, we can significantly increase the precision in predicting any of the usual cosmological parameters in which uncertainty in
has been the main source of uncertainty.
Table 1, for example, shows a sampling of cosmological parameters for which HTC provides for greatly reduced uncertainty compared to what is currently possible in the
-CDM model. An important question, of course, is whether any of this can be supported by observations. We believe this is already the case. To give but one example, the approximately 14.6 billion-year HTC cosmic age estimate provides about 800 million more years for early galaxy formation than predicted by the
-CDM model, which aligns much better with observations made by JWST. See
Section 8 for more details and specific references on this topic. The
in the table is a composite constant that we represent with the Latin symbol for Upsilon, see [
17,
18].
7. -CDM Operates with Three Different Distances for a Given Red-Shift, Whereas They Are Unified in HTC
In the -CDM model, for an object at a given observed redshift, there are potentially three different distances, each governed by a different -CDM distance-vs-redshift formula. These are: the luminosity distance; the angular diameter distance; and the co-moving distance. These distances can be quite different, even for the same z value. This remarkable fact could be an artifact of the -CDM concept of accelerated expansion, in order to keep the model internally consistent. In HTC, the luminosity distance, angular diameter distance, and co-moving distance are derived to be one and the same for any given redshift. This is because HTC uses only a single derived distance-vs-redshift formula. It should be remembered that HTC, like any cosmology, models cosmic coasting at constant velocity rather than cosmic acceleration. Researchers should ask themselves how such a simple model, with only one distance for a given redshift, can fit the entire distance ladder of all supernovae without the need for cosmic acceleration. While HTC certainly needs to undergo more observational testing, and may require some modifications, it performs remarkably well on all aspects that we have examined so far.
8. -CDM Appears to Be Less Compatible with Recent Early Universe Observations than HTC
Melia [
23], who has a different type of
model than ours, recently pointed out that:
“JWST’s recent discovery of well-formed galaxies and supermassive black holes only a few hundred million years after the Big Bang seriously challenges the timeline predicted by Λ-CDM,"
Like Melia, we believe that these findings strongly support the
principle of cosmic coasting at constant velocity, which extrapolates to a greater current cosmic age than estimated by
-CDM. Haug and Tatum have recently demonstrated that, within HTC, the age of the universe appears to be
years. This is about 800 million years more than predicted by the
-CDM model. The discovery of surprisingly large and well-formed galaxies in the early universe studied by JWST therefore appears to be more in-line with HTC [
19,
20].
9. HTC Is Consistent with both the Standard Friedmann Equation and Our Thermodynamic Friedmann Equation, Whereas -CDM Has No Solid Mathematical Foundation Relating CMB Temperature with Other Cosmic Parameters
Haug and Tatum [
21] have introduced a thermodynamic version of the Friedmann equation, in which the critical Friedmann universe behaves according to:
wherein
is our composite Upsilon constant. This is fully compatible with the standard critical Friedmann equation. So, we now have a direct mathematical relationship between the CMB temperature and other cosmological parameters. The thermodynamic Friedmann equation is simply the Friedmann equation expressed through the CMB temperature rather than simply the Hubble constant. The
-CDM model is unlikely to achieve this, as it would require predicting
in the first place, which it cannot do, owing to the lack of a rigorous mathematical relationship between
and
.
10. -CDM Has Horizon Problems, Whereas HTC Has No Horizon Problem
Measurements of the CMB anisotropy show that the observable universe has a remarkably uniform thermal blackbody radiation spectrum in all observational directions. Melia [
24,
25] has clearly shown that the horizon problem emerges only within the
-CDM model and not within
cosmology. Since HTC is clearly a
type model, there is also no horizon problem in HTC.
The rationale for Melia’s conclusion concerning
models is remarkably straightforward. As best explained in his reference [
25], there are now two phase transitions during the
-CDM model expansion which appear to present a horizon problem for
-CDM. The first of these could be solved, in theory, by an unobservable inflationary epoch of accelerated early cosmic expansion from about
seconds to about
seconds following the Big Bang. This would be according to the well-known theory of cosmic inflation. The second of these phase transitions would likely have been an electroweak phase transition (EWPT) event occurring at a critical temperature of
, at approximately
seconds following the Big Bang. Such an event would, by virtue of the apparent uniformity of the vacuum expectation value of the Higgs field, present the second horizon problem within the
-CDM model. This event would be well beyond the inflationary epoch and require an entirely different
-CDM horizon problem solution. As Melia nicely explains, neither phase transition “would have created observable sub-horizon features in the
model.” This would be because such phase transition events in the early
universe would have occurred within a causally-connected region now filling the entire visible
universe of today.
11. Summary and Conclusions
We have compared numerous categories within the HTC model and the -CDM model. From these comparisons, we must conclude that HTC is a simpler and yet more powerful and integrated cosmological model than -CDM. HTC can predict , while -CDM cannot. HTC resolves the Hubble tension (in favor of the Planck Collaboration measurement), which remains an unresolved problem within -CDM. Furthermore, we believe that the Hubble tension itself indicates a breakdown in the -CDM model’s ability to describe the cosmos. HTC also significantly reduces uncertainty in cosmological parameters such as , , , and . For example, the predicted age of the universe in HTC is about 800 million years greater than that in -CDM, a result which appears to be more consistent with the discovery of “surprisingly early” developed galaxies in recent JWST studies.
Despite these initial successes, there are likely still a number of outstanding issues in our model. However, we must bear in mind that literally thousands of researchers have been working on the -CDM model for several decades, whereas the HTC model in particular, and models in general, are newer and less well-explored. It would be a mistake, we think, to dismiss such an alternative model based upon prejudice. Instead, we believe that HTC should be currently viewed as an intriguing alternative to -CDM, one that many more researchers could, and probably should, explore.
References
- E. G. Haug and E. T. Tatum. Solving the Hubble tension using the Union2 supernova database. Preprints.org, 2024. [CrossRef]
- A. Friedmann. Über die krüng des raumes. Zeitschrift für Physik, 1922; 10, 377. [CrossRef]
- A. Einstein. Näherungsweise integration der feldgleichungen der gravitation. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin, 1916.
- Dhal, S. Singh, K. Konar, and R. K. Paul. Calculation of cosmic microwave background radiation parameters using cobe/firas dataset. Experimental Astronomy (2023), 56:715, 2023. [CrossRef]
- J. V. Narlikar and T. Padmanabhan. Standard cosmology and alternatives: A critical appraisal. Annual Review of Astronomy and Astrophysics, 1979; 39, 211. [CrossRef]
- E. T. Tatum, U. V. S. E. T. Tatum, U. V. S. Seshavatharam, and S. Lakshminarayana. The basics of flat space cosmology. International Journal of Astronomy and Astrophysics, 2015; 5, 116. [Google Scholar] [CrossRef]
- E. G. Haug and S. Wojnow. How to predict the temperature of the CMB directly using the Hubble parameter and the Planck scale using the Stefan-Boltzman law. Journal of Applied Physics and Mathematics, accepted and forthcoming, 2024. [CrossRef]
- E. G. Haug and E. T. Tatum. The Hawking Hubble temperature as a minimum temperature, the Planck temperature as a maximum temperature and the CMB temperature as their geometric mean temperature. Journal of Applied Physics and Mathematics (accepted and forthcoming), 2024.
- I. de Martino et. al. Measuring the redshift dependence of the cosmic microwave background monopole temperature with planck data. The Astrophysical Journal, 2012; 757, 144. [CrossRef]
- L. Yunyang. Constraining cosmic microwave background temperature evolution with sunyaev–zel’dovich galaxy clusters from the atacama cosmology telescope. The Astrophysical Journal, 2021; 922, 136. [CrossRef]
- D.A. Riechers, A. D.A. Riechers, A. Weiss, and F. et al. Walter. Microwave background temperature at a redshift of 6.34 from h2o absorption. Nature, 2022; 602, 58. [Google Scholar] [CrossRef]
- E. Valentino et. al. In the realm of the Hubble tension – a review of solutions. Classical and Quantum Gravity, 2021; 38, 153001. [CrossRef]
- E. G. Haug. Closed form solution to the Hubble tension based on Rh=ct cosmology for generalized cosmological redshift scaling of the form: z=(Rh/Rt)x-1 tested against the full distance ladder of observed SN Ia redshift. Preprints.org, 2024. [CrossRef]
- E. G. Haug and E. T. Tatum. Planck length from cosmological redshifts solves the Hubble tension. ResearchGate.org, 2024. [CrossRef]
- N. Aghanim et al. (the Planck Collaboration). Planck 2018 results. vi. cosmological parameters. Astronomy & Astrophysics, 2021; 652. [CrossRef]
- A. G. Riess et. al. A comprehensive measurement of the local value of the Hubble constant with 1 km s-1 Mpc-1 uncertainty from the Hubble space telescope and the sh0es team. The Astrophysical Journal, 2021; 934. [CrossRef]
- E. T. Tatum, E. G. E. T. Tatum, E. G. Haug, and S. Wojnow. High precision Hubble constant determinations based upon a new theoretical relationship between CMB temperature and H0. Journal of Modern Physics, Accepted and forthcoming. Pre-print version at Hal-archive, 2024. [Google Scholar]
- E. T. Tatum. Upsilon constants and their usefulness in Planck scale quantum cosmology. Journal of Modern Physics, 2024; 15, 167. [CrossRef]
- E. T. Tatum and E. G. Haug. Extracting a cosmic age of 14.6 billion years from all 580 type Ia supernova redshifts in the Union2 database. ResearchGate.org, 2024. [CrossRef]
- E. G. Haug and E. T. Tatum. How a thermodynamic version of the Friedmann equation appears to solve the early galaxy formation problem. PrePrints.org, 2024. [CrossRef]
- E. G. Haug and E. T. Tatum. Friedmann type equations in thermodynamic form lead to much tighter constraints on the critical density of the universe. https://www.preprints.org/manuscript/202403.1241/v2. 2024.
- E. G. Haug and E. T. Tatum. Cosmic entropy prediction with extremely high precision in Rh=ct cosmology. Preprints.org, 2024. [CrossRef]
- F. Melia. Strong observational support for the Rh=ct timeline in the early universe. Physics of the Dark Universe, 2024; 46, 101587. [CrossRef]
- F. Melia and Shevchuk A. S. H. The Rh=ct universe. Monthly Notices of the Royal Astronomical Society, 2012; 419, 2579. [CrossRef]
- F. Melia. A solution to the electroweak horizon problem in the Rh=ct universe. Eur. Phys. J. 2018; 78, 739. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).