The Bluegill Game: How Do Team and Individual Sports Specialists Play the “Bluegill Game”? An Illustration of a Perverse Side Effect of Altruism

1. Introduction. The Question of Cooperation between “Teammates”

Are team sports specialists predisposed to cooperation? This is an important question in the fields of teaching and business [1] and is subject to much debate in the literature. On one hand, team sports (such as soccer, basketball, volleyball, handball and rugby) can be viewed as zero-sum duels between two teams (i.e. what one team wins, the other loses) in which each team represents a sort of perfectly exclusive, stable "super player" [2]. The balanced nature of teams ("my teammates' teammates are my teammates, my teammates' opponents are my opponents and my opponents' teammates are my opponents") favours clear relationships and disfavours cheating. Team sports develop “decentration capabilities” [3]. The members of a group with the same objectives improve their mutually empathic clairvoyance and are more open with each other. They share a common reference framework [4], which helps them to build a collective understanding of the situation [5,6,7]. On the other hand, only antagonistic motor interactions (shots, smashes, drop goals, etc.) change the score in team sports. Cooperation is only a by-product of having opponents. Furthermore, team sports players do not appear to be particularly predisposed to sociability outside sport [8] and the functional cohesion observed during a match ("who plays with whom?") is unrelated to socio-affective cohesion ("who likes whom?")[9].

The results of the present study showed that a certain number of apparently contradictory traits - the empathy felt by team sports players and their collective understanding of shared situations on one hand and their opponent-driven cooperation and the lack of a relationship between functional cohesion and socio-affective cohesion on the other – are different aspects of the same relational skill.

To this end, we asked a group of team sports specialists to play a game derived from the well-known Prisoner's Dilemma [10]. This paradoxical game opposes selfish and altruistic tactics. It embodies the concept whereby the aggregation of individual preferences does not necessarily result in an optimum for the group as a whole. When interrogated separately by the police for the same crime, two accomplices must choose between (i) denouncing the other prisoner and risking a minor sentence and (ii) denying any involvement and being releasing from prison due to a lack of evidence, as long as he/she is not denounced by the other prisoner at the same time: the prisoner having remained silent will then receive a stiff sentence, whereas the selfish betrayer will go free and receive a payoff. The Prisoner's Dilemma is a non-zero sum, non-cooperative game. The term "non-cooperative" applies here because the players sometimes have diverging interests; when one player remains silent and the other betray his/her accomplice, the rewards are clearly unequal. The term "non-zero sum" applies because even when one player makes a gain, the other does not automatically lose (as would happen in a duel). When both players either remain silent or betray each other, their respective gains are the same. It is therefore possible for a player to cooperate for opportunistic reasons in a non-cooperative game. The ambivalence of this interaction – a mixture of competition and cooperation, "coopetition" – favours the emergence of irrational relationships and means that beliefs have to be taken into account[11,12,13]. Even when the mathematical resolution of the game prompts a player to betray another (even when not guilty [14,15,16]), observed the survival of conciliatory strategies as long as the game is iterated a certain number of times. In fact, the game used in the present study (the "Bluegill Game" [17]) is a form of Prisoner's Dilemma with a mixed-strategy Nash equilibrium.

The Prisoner's Dilemma has been tested in many different experimental situations (with over 1000 published between 1950 and 1980!) and has often been reformulated [18]. It has become one of the best-known models in game theory. However, this famous dilemma has hardly ever been resolved in the context of a physical game [19]. This is surprising, given the very physical consequences of remaining in jail or being freed... The mathematicians' version of the game is an entirely abstract system; when a player has chosen his/her strategy, he/she can hand over a paper and leave the room, so that the game is over before it has even begun! So, how do team sports player in behave "in the heat of the fight" when prompted to choose between selfishness and altruism? To the best of our knowledge, the present study is the first to have imported a Prisoner's Dilemma model into the world of sporting games. Once a strategy has been chosen, it has to be implemented; regardless of the abstract schemes underlying the game, the result depends on completion of a motor action. In sporting games, motor situations can be considered as a laboratory for studying human behaviour [20,21,22]. The played is completely immersed in the game. We can see his hesitations, his pleasure, his taste for domination and/or aggressiveness. In fact, this immersion in the game is not simply recreational; it is a way of measuring the cooperative abilities of team sports players in vivo.

2. Methods. The Implementation of a Motor Action Dilemma

2.1. The Mechanism of Dilemma

In the classic Prisoner's Dilemma, a strategy in which both prisoners defect (P, P) for ("poor", "poor") – is the only Nash equilibrium (Figure 1); i.e. the only solution for which neither of the player’s gains by changing tactics if the other maintains his/her tactics [23]. The situation is ambiguous because although each player is better off if both cooperate by remaining silent (S, S): ("satisfactory", "satisfactory"), neither will take the risk because the personal cost will be very high if the other defects.

Matrix 1. The payoff matrix for the Prisoner’s Dilemma.

Prisoner’s dilemma	Cooperate	Defect
Cooperate	(S, S)	(VP, VS)
Defect	(VS, VP)	(P, P)

NB: VP = Very Poor; P = poor; S = satisfactory; VS = very satisfactory.

"Cooperate" and "Defect" are the game's two tactics. The first and second letter in each parenthesis corresponds to the respective payoffs for the "line" player and the "column player". The game has a Nash equilibrium with a pure strategy (P, P): the prisoner is always better off defecting.

As the Prisoner's Dilemma stands, the solution is to always defect because the opponent(s) will defect. In this configuration, defecting is the only pure-strategy Nash equilibrium ("pure" because the game is only played once, as opposed to a "mixed strategy" based on probabilities over iterated games). However, this equilibrium is fundamentally suboptimal. How, then, can one "succeed in a world of egoists?" Another option has been suggested by John Harsanyi - another winner of the 1994 Nobel Prize in Economics (1977, 1995).

Following on from Rousseau (1756) and Piaget (1932)[20,24], Harsanyi introduced a key concept: moral behaviour. He drew a distinction between two forms of rationality. Nashian (primary) rationality corresponds to purely individual logic and leads individuals to maximise their gains through fear of retaliation. "Secondary" rationality (referred to below as "Harsanyian") is guided by social conscience and leads individuals to maximise the average gain for the group as a whole. When confronted with a Prisoner's Dilemma, a Harsanyian player will choose rationally to cooperate: he/she will remain silent because the decision is based on an ethical principle: compliance with a "social contract", as described by Rousseau [24]: "a form of association that will defend and protect with the whole common force the person and goods of each associate, and in which each, while uniting himself with all, may still obey himself alone, and remain as free as before" (p. 359).

According to Harsanyi, the aggregation of shared, ethically held tactics in the Prisoner's Dilemma lead to a cooperative equilibrium. Given that the players maximize their gains by remaining silent, the two should cooperate and stick to the founding contract without needing to discuss matters. This cooperation is motivated by individual interests, rather than altruism (i.e. disinterested benevolence): "In a context of reciprocity, cooperation is not altruistic" [25]. Furthermore, even though Nash equilibrium is more robust in mathematical terms, it is subject to huge bias: it is in the players' interests to admit to the crime… even when they have committed none! The Harsanyi equilibrium is precarious and is not stable when a "freeloader" is involved.

So, should the prisoners "play Harsanyi" or "play Nash"? Should they cooperate or act selfishly? It is impossible to answer these questions with confidence because the strategies are conditional. What does one player believe that the other is thinking? And what does the other player believe that the first one will do? Marc Barbut [26] paraphrased a famous line by [2]: "The best way to stop your opponent from guessing what you are going to do is to not know yourself" (p. 850).

This paradox can be partially solved by testing the dilemma through behavioural game theory [27,28,29,30].

This is precisely what we set out to do, although our payoff matrix differed significantly from that used in the classic Prisoner's Dilemma (Figure 2). We used the paradoxical "bluegill game" [17] with three Nash equilibria: two suboptimal, pure strategies (("Poor", "Very Satisfactory") and ("Very Satisfactory", "Poor")) and an optimal, mixed strategy that consists in playing altruistically half the time (if one considers VS>S>P>VP, with a uniform difference between these four payoffs). This game also has a Harsanyi equilibrium based on constant compliance with ethics and tacit cooperation via the presumption of reciprocity: "do not unto others that which you would not have them do unto you".

The game was inspired by a curious phenomenon in nature. The bluegill (Lepomis macrochirus) is a member of the perch family of fish. There are two types of males. The first corresponds to a Guardian. He builds a nest to attract females that are about to spawn. After the spawning, the male not only fertilises the eggs but also guards the fry when the female leaves the nest for some reason. The second type of male (a "Sneaker") does not look after a family. After hiding in the shade until a female has spawned (in response to signals sent by a Guardian), the Sneaker then hurries to fertilize the eggs before the Guardian does. If the Sneaker is successful, the Guardian will defend an unrelated family that carries the Sneaker's genes. The two types of males coexist in a 1:1 ratio [17]. Of course, this animal-based illustration is metaphorical. In the present study, Guardian and Sneaker correspond to tactics with an equal likelihood of being played, according to the mixed Nashian equilibrium.

Matrix 1. the payoff matrix for the Bluegill Game.

Bluegill Game	Guardian	Sneaker
Guardian	Satisfying for both even if each miss opportunities (S, S)	Bad for the Guardian who makes the dirty work for the benefit of the Sneaker, Very Satisfied (P, VS)
Sneaker	Bad for the Guardian who makes the dirty work for the benefit of the Sneaker, Very Satisfied (VS, P)	Very bad for both: it is the anarchy (‘every man for himself’) (VP, VP)

"Guardian" and "Sneaker" are the game's two tactics. In contrast to the conventional prisoner's dilemma, there are two Nash equilibria with a pure strategy ((VS, P) and (P, VS)), so that neither of the players will gain by changing his/her tactic if the other player does not change as well.

2.2. A Motor Implementation of the Bluegill Game

How, then, can the male bluegill's Guardian and Sneaker habits be turned into a motor-action game? Two teams (each wearing distinctive jersey) competed on a handball court. Each team had its own half and goal. Each match lasted for 15 minutes. Players were allowed to touch the ball (a handball ball) with their hands and feet, with no other restrictions on the technique. The players were allowed to score by throwing the ball into either goal. If the score took place in the opponent's goal, the scorer and the members of his/her nominal team received one point each. In the event of an own goal (i.e. a goal against the scorer's own team), only the scorer won a point. After each goal, the players returned to their own half. The paradox is as follows. If all the members of a team cooperate to score a point, everybody is satisfied (the Harsanyian solution) but the situation is not balanced in the Nashian sense; it is in each player's interest to become a turncoat at the least opportunity. However, if every team member plays egotistically, it is "every man for himself" and the chances of anyone scoring fall. Hence, in a context in which there is always doubt as to the honesty of a team member and betrayal is authorized by the rules, we decided to determine who would score the most points by recording direct motor interactions (passes and shots), Guardian behavior (cooperation within a team) and Sneaker behavior (egotistical behavior: shots and passes against a player's nominal team).

2.3. The Players’ Characteristics

We formed two groups of volunteer sports students in their late teens or early twenties: 25 team sports specialists (the TeamSport group) and 23 individual specialists from individual sports not requiring motor interaction between players (i.e. gymnastics, athletics and swimming) as the IndividualSport control group. The students were attending the Faculty of Sports Science at the University of Caen (Caen, France) and were participating in the bluegill game as practical work for a game theory course. A second control group comprised non-sporting students from the human and social sciences (the NoSport group) attending the same university. None of the NoSport students had played sport at higher than county level and none had knowledge of game theory. The measurements were not invasive. All participants received information on the protocol prior to inclusion in the study. Participation was voluntary and all participants gave their prior, written consent, in compliance with the precepts of the Declaration of Helsinki.

The fact that two of the three groups were familiar with the concepts of game theory (notably the concept of a Nash equilibrium – presented as the optimal solution in this type of game) could conceivably have influenced the players' decisions and thus was controlled for in our subsequent analysis of the results. The gender ratio was fairly homogenous, with the exception of the TeamSport group (in which male players were more numerous).

Each of the three groups was split in three teams (Table 1). The intra-team gender distribution was as well balanced as possible. Each player played two matches within his/her group, with the exception of one player in the TeamSport group (who played only once) and one player in the IndividualSport subgroup (who played three times). The three groups did not play against each other. During the matches, a referee checked for dangerous play. The goal keepers were the only players who had to remain loyal to their team throughout the match and had to defend their respective goals regardless of where the shot came from. After a goal or a save, they always had to pass the ball to one of their teammates. Hence, we did not study the goalkeepers' behavior.

While two teams were playing their 15-minute match, the third team watched. Each observer filled out two forms (one per player observed) specifying the number and nature (cooperative or egotistical) of passes and shots and the number of goals scored.

Each of the three subgroups played 15-minute matches in groups of 8.

3. Results. Which Sports Players are the Most Egotistical?

3.1. Harsanyi vs. Nash

We first looked at the "sport" variable – probably the most determinant, in view of the game's motor features - and its possible effect on the players immersed in this paradoxical game.

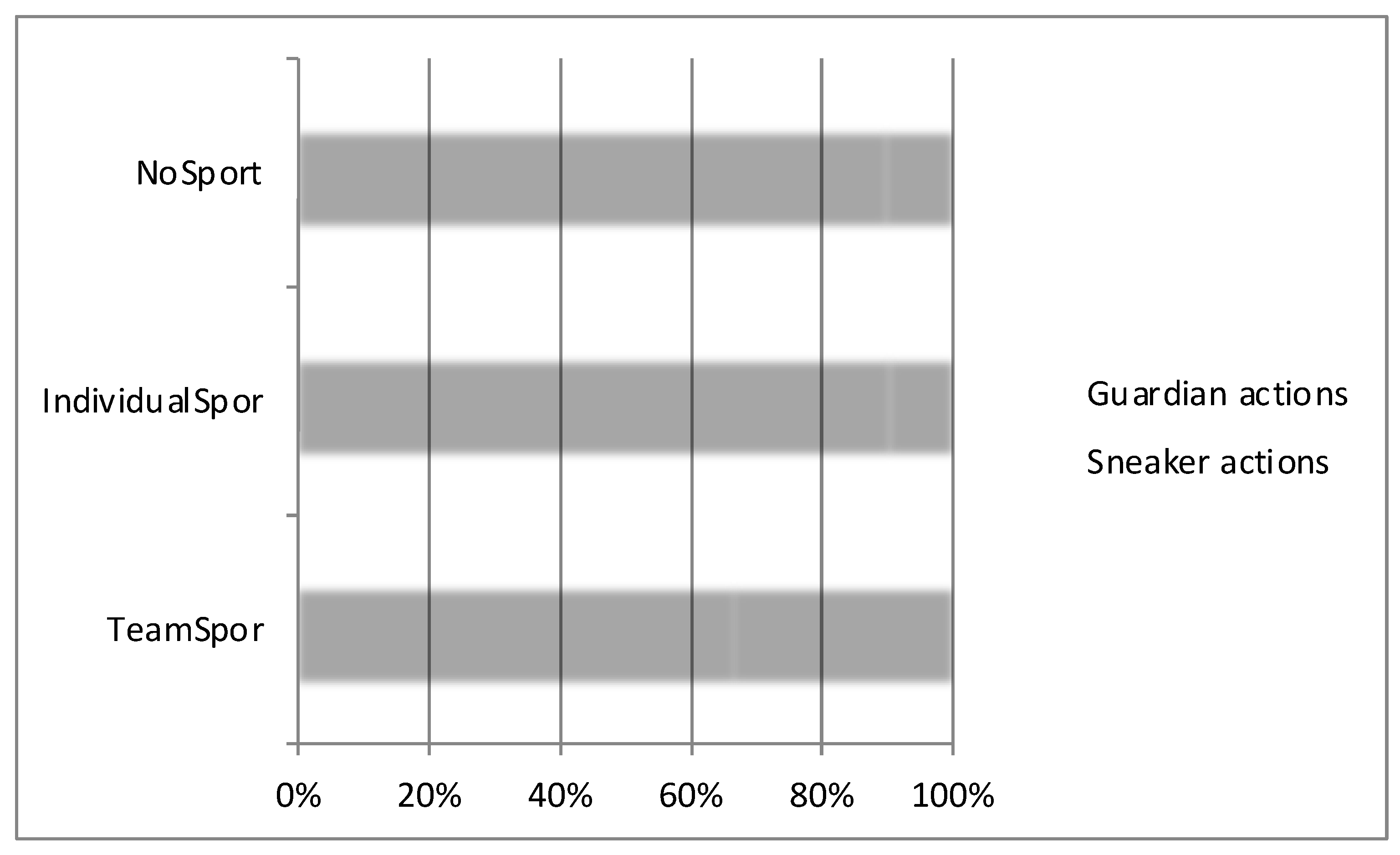
The total number of Sneakers or Guardian passes and shots were counted. A "Sneaker shot" was an own goal and a "Sneaker pass" was a pass to the other team, whereas Guardians shots and passes were "loyal" to the player's nominal team. So, did the sportspeople in the TeamSport group "play Guardian" more than the others? Did they cooperate more? The answer is no. Figure 3 shows the distribution of the 616 direct interactions observed (as a percentage), whereas Table 2 shows the raw data and distinguishes between shots and passes.

The TeamSport group was significantly more Sneaker-like than the two other groups (chi2 (2, N= 616) = 7.01; p<.05). In contrast, there was no statistically significant differences between the IndividualSport and NoSport groups (chi2 (1, N= 366) = 0.1; ns) in terms of playing tactics.

There were more "guardians" than "sneakers" in all three subgroups.

There was a higher percentage of "sneakers" in the TeamSport group than in the two other subgroups. The team sports group made more passes and shots in general.

However, all three groups played Guardian more than they did Sneaker. Perfectly Harsanyian behavior would correspond to a Guardian play rate of 100%, whereas perfectly Nashian behavior would correspond to a Guardian play rate of 50%. Hereafter and by convention, Guardian play rates of between 75% and 100% will be referred to as Harsanyian strategies and rates of between 50 and 74% will be referred to as Nashian strategies.

The female players differed in their approach, relative to male players (chi2 (1, N= 72) = 5.8; p<0.04): they were more Harsanyian and complied more with team ethics (Table 3).

The female players were more show solidarity (Harsanyian) than the male players.

Note: "GameT+" corresponds to a grade in the game theory course module of more than 15 out of 20; "GameT=" corresponds to a grade of between 10 and 15 out of 20; "GameT-" corresponds to a grade of less than 10 out of 20; "NoGameT" means that the student had not taken the Game Theory course module.

On average, there was no correlation between a player's knowledge of game theory and the tactics adopted in the Bluegill Game.

Students familiar with game theory could potentially have favoured the Nash equilibrium, since the latter had been presented in class as the be all and end all for this type of game. However, having been taught about game theory at university did not significantly influence tactics during the bluegill game itself (chi2 (3, N= 72) = 3.6; ns). This lack of significance is worrying. Most of the data from experimental game theory come from surveys that focus on verbal situations [31]. If mastery (or lack of mastery) of a problem on the purely cognitive level has no incidence on its resolution in an ecological context, how much weight should be given to the theoretical knowledge? This observation was made by Parlebas [32] for the Four Coins game, in which children sometimes played irrationally (with the deliberate intention of losing).

3.2. Logistic Regression

The three study groups were not matched for gender or their knowledge of the Nash equilibrium. Furthermore, the cross-correlation tables are not sufficient. For example, there was a higher proportion of males in the TeamSport group (16 out of 25) and all of the group members had taken the game theory course. If they showed themselves to be more Nashian than Harsanyian (which was the case), was this due to their sporting specialization, their gender or their theoretical knowledge of the Nash equilibrium? In order to see whether an egotistical tendency (Nash) or cooperative tendency (Harsanyi) was indeed related to the sport practised and not linked to other explanatory factors (gender, knowledge of the best game tactics after having taken the course), we performed a logistic regression using the latest update of Tri2 software [33,34,35].

Nashian (egotistical) behaviour was taken as the explanatory factor. The reference situation was set to Male gender + NoSport + NoGameT (Table 5), corresponding to 28.8% of the study population. For each of the other modes, we calculated the marginal effects with all other factors being equal. Female gender had an impact on Nashian behaviour (-16%, relative to the reference situation. This confirms the conclusions of Table 3: the women cooperated more (chi2= 3.8, p=0.048**). Knowledge of game theory (GameT+) tended to make the player more egotistical (+4.9%, suggesting some degree of uptake of the course about the Nash equilibrium), whereas the absence of knowledge (GameT-) had the opposite effect (-11.7%). These last two trends did not achieve statistical significance. In contrast, the TeamSport factor had significant explanatory power at (p<0.05**, +20.6 %) for Nashian tactics. During the bluegill game, the team sports players were seen to be less cooperative than the individual sports players and the non-sportspeople. That said, and as is always the case in quasi-experimental research, it is not possible to affirm that this correlation constitutes a causal relationship.

Belonging to the team sports group was significantly correlated (p<0.05) with "sneaker" behaviour.

4. Discussion. Bad Guys Finish First

"Survival of the fittest" [36] applies as much to sport as it does to the animal kingdom. Similarly, Voltaire commented that "better is the enemy of good". However, "good" is defined in the dictionary as "benevolent, kind" as well as "suitable". According to Dawkins, "niceness dies a Darwinian death." [37]. According to the pioneer of ethology [36], slight hereditary variations in a given species may make an organ "better" and enable the bearer and its descendants to ultimately triumph over individuals with hitherto "suitable" characteristics. In the animal kingdom, being good is not enough for survival: you have to be the best.

In the game studied here, the "best" player escapes from the usual, "suitable" Harsanyian moral habits by adopting Nashian egoism. Cooperative behaviour (which is "suitable" most of the time) is cruelly equivocal: cooperative players give the bluegill game the stability and continuity that it needs to guarantee maintenance of a moral order. Without co-operators, the game would turn into anarchy and no-one would have any chance of scoring at all. "Every man for himself" would turn into "everyone against the ball carrier", with the worst possible outcome (("Very Poor", "Very Poor"); Figure 2). We observed this situation for a few brief moments – generally after a player had betrayed his/her team. However, it is not in anyone's interest to see this situation last because the game will stagnate. Furthermore, the Harsanyian players – the "good guys" – keep the game alive by putting together scoring opportunities as a team. Nevertheless, overly docile players can fail to show the essential qualities needed for victory; they merely constitute "solid teammates" and are not strong players. In fact, for maximum efficacy, the Harsanyian solution drives all the players to play Guardian. The prime beneficiaries in this game are the players (mainly team sport players; Figure 3) who disdain the collective optimum and focus on their own interests. This was always the case on the pitch: the winners (those with the best scores after 15 minutes) were always the most Nashian players. Each player sought to renege on the "social contract", while hoping that the other players would not do likewise. He/she then obtains the maximum payoff (("Very Satisfactory", "Poor"); Figure 2). Furthermore, this corresponds to the Nash equilibrium and is therefore likely to last. This egotistical role corresponds to a "freeloader" or "free rider": someone who profits from a situation without paying for a "ticket". Here, the "fittest" player is the entrepreneurial player and not one who saves face by not betraying his/her team complying. The "good guy" is the one you can count but who will turn his/her coat at the first sign of trouble. Being "good" means "wanting the best" for the other players. In the bluegill game (as in sport in general), the "bad guys" finish first. The "fittest" sportsperson is one who does not wish you well.

These observations help us to interpret the more egotistical behaviour of the TeamSport players, who are more used to deciphering the opponents' behaviour and masking their own behaviour. The team sport players' empathic acuity gives them opportunistic skills that they can exploit during the bluegill game. The collaboration shown by soccer or rugby players during a match is intended to beat the opponents. The aim is never just to pass the ball for its own sake but to do so to beat the opposing team. In duels (i.e. strictly competitive, excellence-dominated games, such as judo, tennis, chess, etc.), antagonism is at its height. The objective of the "group intelligence" referred to in the literature is to create "excluante" competition [21]. Also, certain apparently contradictory aspects of research on team sports players – the collective conscience of shared situations on one hand and the absence of a link between functional cohesions and socio-affective cohesion on the other – are in fact just different aspects of a same-relational skill.

We found that female players cooperated more than male players. This finding is in agreement with the psychosociological and sociological literature. Our culture favours an arrangement between the sexes, in which women are given pacific and conciliatory roles [38,39,40,41,42].

5. Conclusion. A Perverse Effect of Cooperation

For team sports specialists, the Nash equilibrium [23] is more robust than the Harsanyi equilibrium [43]. The principles of equilibrium and exclusivity are inappropriate in the bluegill game and were abandoned by the team sports specialists. These players are opportunists and focus solely on winning.

The losers in the bluegill game were the most cooperative players. How different is this game from social situations? The Prisoner's Dilemma did not become a successful paradigm by chance. It has been likened to a large number of cooperative, human-human interactions. John Nash was awarded the Nobel Prize for "simply" having extended the Minimax theorem [2] to non-cooperative and not strictly competitive situations, which are more similar to true interpersonal relationships [44]. There are many applications of this dilemma. The arms race between nations is one example. The group optimum (the Harsanyi position) would be to spend the military budget on something else. However, disarmament does not constitute a Nash equilibrium because to assert its supremacy, each country will gain by arming itself if its enemy disarms. As the arms race escalates, the financial cost and the risk of war increase. In other words, the balanced strategy (arms for everyone) is not satisfactory but the satisfactory strategy (disarmament for everyone) is not balanced. The same mechanism applies to the limitation of fishing quotas or environmental protection. It is wise to limit fishing or polluting activities, in order to replenish stocks and enable fishermen to continue to ply their trade. However, if everyone stops fishing (or polluting), some people will then be tempted to grab some of the recovering resources. If everyone adopts this approach, then the cumulative effects of overfishing (or polluting) activities will lead to the extinction of the fish stocks (or irreversible degradation of living conditions). A third example illustrates the conflict between individual choice and collective interests: doping in sport. For sport in general, doping is harmful. The absence of doping gives participants more similar chances of winning on merit alone and thus creates more excitement and suspense. But if one player dopes, the others would be silly not to do likewise. The doped competitor will win fame and fortune, whereas the others will finish with nothing. In the doubt on what the other one is going to, the other player can take the risk of doping. The players end up by coordinating their doping, which will turn out to be bad for them all: if opponents have access to the same doping products, they will once again have similar chances of winning but, unlike the starting situation, will be endangering their health.

There is a perverse side effect when the accumulation of individually coherent choices leads to an unwanted and aberrant outcome for the group [45]. In the bluegill game, the rational solution is to betray one's team every other time (a Nashian strategy). However, the universal application of these rational choices would probably end up in a stagnant game, with a trend towards anarchy and "every man for himself". This is an unwanted, perverse group effect. According to Boudon, the suppression of perverse effects is part of social regulation. The social order gains its substance from a set of more or less visible adjustments that favour the group as a while (by punishing freeloaders, dopers, polluters, etc.).

However, the sociologist's statement can be turned on its head. A coherent, collective result can be the fruit of a combination of absurd individual actions. This is what we observed. By playing more often altruistically than egotistically, our players showed Nashian irrationality. Nevertheless, they kept the game alive, which would otherwise have stagnated. Is, then, this sacrifice for the good of the group is not a perverse effect?